Как учесть инфляцию в расчетах в excel

Временная стоимость денег (Time Value of Money, TVM) – это важный показатель в бухгалтерской и финансовой отрасли. Идея заключается в том, что рубль сегодня стоит меньше чем тот же самый рубль завтра. Разница между этими двумя финансовыми значениями является прибыль, которую можно извлечь с одного рубля или убыток. Например, данная прибыль может быть получена с процентов, начисленных на банковском счете или в качестве дивидендов от инвестиций. Но также может быть убыток при оплате процентов за погашение кредитного долга.

Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel

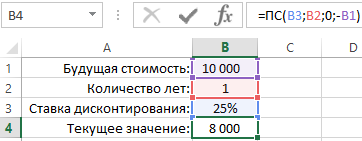
Программа Excel предлагает несколько финансовых функций для вычисления стоимости денег во времени. Например, функция ПС (приведенная стоимость) возвращает текущую стоимость инвестиций. Простыми словами, данная функция снижает сумму на размер процента дисконтирования и возвращает текущую стоимость для этой суммы. Если инвестиционный проект предполагает принести прибыль в размере 10 000 через год. Вопрос: какой максимальной суммой рационально рискнуть чтобы инвестировать в данных проект?

Например, в России розничный бизнес иногда делает прибыль до 35% годовых, а оптовый не более 15%. Учитывая небольшую сумму инвестиций предполагается, что инвестиционный объект не является оптовым бизнесом, а значит следует ожидать прибыль больше чем 15% годовых. Ниже на рисунке провиден пример формулы калькулятора доходности инвестиций в процентах:

Как мы видим на рисунке калькулятор нам отображает, чтобы получить сумму 10 000 за 1 год при доходности 25% нам необходимо вложить 8 000 финансовых средств. То есть если бы у нас была сумма 8 000 и мы вложили ее под 25% годовых через год мы заработали бы 10 000.

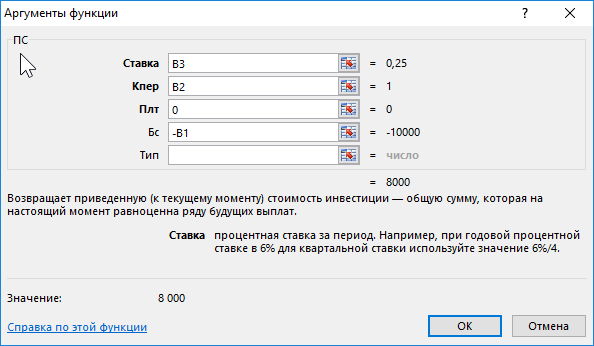
Функция ПС имеет 5 аргументов:

1. Ставка – процентная ставка дисконтирования. Это прибыль в процентах, на которую можно рассчитывать за период дисконтирования. Это значение имеет наибольшее влияние на вычисление текущей стоимости инвестиций, но его наиболее сложно точно определить. Осторожные инвесторы чаще всего занижают процентную ставку до максимально реально достижимого уровня при тех или иных условиях. Если же финансовые средства предназначены для погашения кредита, в таком случае данный аргумент определяется легко.
2. Количество периодов (Кпер) – период времени на протяжении которого дисконтируется будущая сумма. В данном примере указан 1 год (записанный в ячейке B2). Процентная ставка и количество лет должны быть выражены в соответственных единицах измерения. Это значит, что вы используете годовую ставку, тогда числовое значение в данном аргументе значит количество лет. Если указана процентная ставка в первом аргументе для месяцев (например, 2,5% ежемесячных), тогда число во втором аргументе значит количество месяцев.
3. Платеж (Плт) – сумма, которая периодически платится на протяжении периода дисконтирования. Если предусмотрен в условиях инвестирования только один платеж, как в выше приведенном примере, тогда данная сумма является будущей стоимостью денег, а сам платеж равен =0. Данный аргумент должен быть согласован со вторым аргументом количества периодов. Если количество периодов дисконтирования равно 10, а третий аргумент не равен <>0, тогда функция ПС посчитает как 10 платежей на сумму, указанную в третьем аргументе (Плт). Ниже на следующем примере изображено как вычисляется текущая стоимость денег при нескольких взносах отдельными платежами.
4. Будущая стоимость (БС) – это сумма, которую следует получить в конце периода дисконтирования. Финансовые функции Excel основаны на вычислениях наличного потока. Это значит, что будущая стоимость и текущая стоимость инвестиций имеют противоположные знаки чисел. В данном примере будущая стоимость является отрицательным числом, поэтому формула в результате вычислений возвращает положительное число.
5. Тип – данный аргумент должен иметь значение 0, если выплата итоговой суммы припадает на конец периода дисконтирования, или число 1 – если на его начало. В данном примере значение данного аргумента не имеет значения и никак не повлияет на итоговый результат вычисления. Так как платежный взнос равен нулю и аргумент определяющий тип может быть опущен. В таком случае функция по умолчанию присваивает данному аргументу значение 0.



Формула расчета текущей стоимости денег с учетом инфляции в Excel

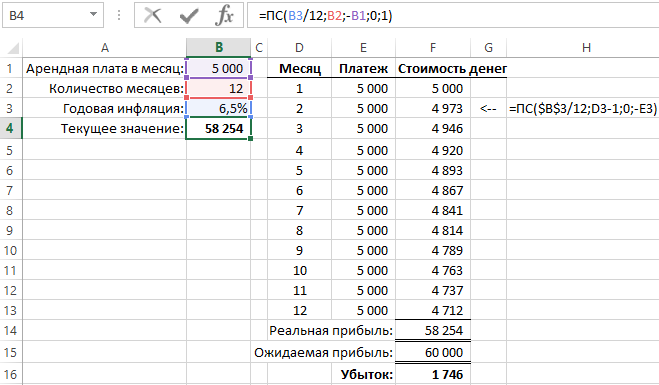
В другом примере применения функции ПС выполняется вычисление будущей стоимости денег сразу для целой серии будущих равных платежных взносов. Если, например, по договору аренды офиса арендатор должен платить по 5000 каждый месяц на протяжении одного года, тогда арендодатель с помощью функции ПС сможет посчитать сколько он потеряет дохода при учете 6,5% годовой инфляции:

В данном примере пятый аргумент «Тип» имеет числовое значение 1, так как оплата за аренду платится в начале каждого месяца.

В случае наличия суммы регулярных платежей функция ПС в реальности вычисляет текущую стоимость денег отдельно для каждого платежа и суммирует полученные результаты. На рисунке видны результаты вычисления стоимости для каждого платежа. Текущая стоимость первого платежа такая же, как и сумма платежа, так как платится сейчас по факту. Платеж в следующем месяце будет проплачен через месяц и уже уменьшается его текущая денежная стоимость (обесценивается). Он дисконтирован до суммы 4 973. Изменения не значительные, но последний платеж, который буде проплачен через 11 месяцев имеет стоимость уже существенно ниже – 4 712. Все результаты вычисления значений текущей стоимости инвестиций необходимо суммировать. Функция ПС выполняет всю эту работу автоматически без необходимости составления хронологического графика платежей за весь период.

As you might guess, one of the domains in which Microsoft Excel really excels is finance math. Brush up on the stuff for your next or current job with this how-to. In this tutorial from everyone’s favorite digital spreadsheet guru, YouTube’s ExcelIsFun, the 54th installment in his «Excel Finance Class» series of free video lessons, you’ll learn how to make inflation calculations.

Want to master Microsoft Excel and take your work-from-home job prospects to the next level? Jump-start your career with our Premium A-to-Z Microsoft Excel Training Bundle from the new Gadget Hacks Shop and get lifetime access to more than 40 hours of Basic to Advanced instruction on functions, formula, tools, and more.

Buy Now (97% off) >

Other worthwhile deals to check out:

• 97% off The Ultimate 2021 White Hat Hacker Certification Bundle
• 98% off The 2021 Accounting Mastery Bootcamp Bundle
• 99% off The 2021 All-in-One Data Scientist Mega Bundle
• 59% off XSplit VCam: Lifetime Subscription (Windows)
• 98% off The 2021 Premium Learn To Code Certification Bundle
• 62% off MindMaster Mind Mapping Software: Perpetual License
• 41% off NetSpot Home Wi-Fi Analyzer: Lifetime Upgrades

Никак, для процента в год и процента в месяц разные формулы расчета. Так годовой — это просто коэффициент, а месячный — типа сложный процент.
Любую формулу можно написать с помощью простых операторов: +-*/^, стандартные функции можно не использовать (БС), но если все же используете, то точно надо понимать как они работают, там масса нюансов!

Кстати, БС предполагает один платеж в период, т.е. для ежемесячной инфляции предполагается 12 платежей в год, т.е. формула будет работать для года, но не для месяца.

Изменено: TheBestOfTheBest — 11.05.2017 11:15:50

Создание электронной таблицы для определения влияния инфляции на стоимость денег

Действительная
стоимость денег зависит от инфляции и
определяется по следующей формуле:

,
(2)

где

процент инфляции за период (например,
за год).

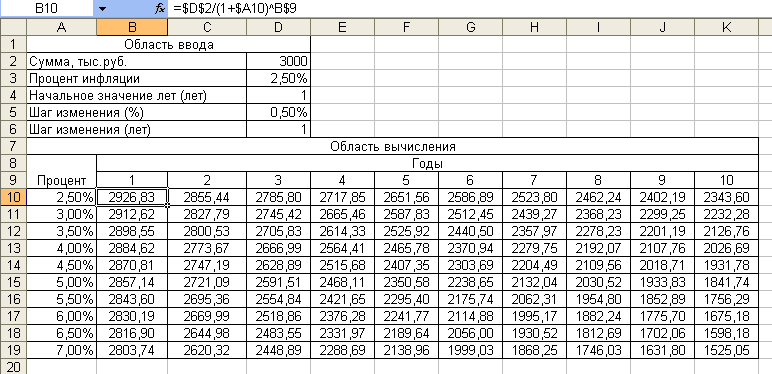
Задание 1.2

Аналогично
рассмотренному примеру создайте таблицу
для расчета реальной стоимости денег
с возможностью изменения суммы и процента
инфляции (рисунок 2).

Решение:

Рисунок
2 Таблица расчета реальной стоимости
денег с возможностью изменения суммы
и процента инфляции

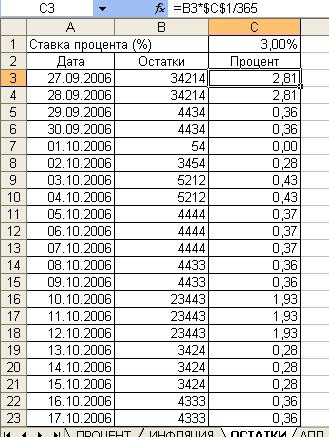
Создание электронной таблицы для расчета процентов по остаткам на расчетном счете в банке

Задание 1.3

На конец каждого
операционного дня на расчетном счете
присутствуют остатки денежных средств:

Дата	27.09	29.09	01.10	02.10	03.10	05.10	08.10	10.10	13.10	16.10	20.10	23.10	25.10
Остатки	34214	4434	54	3454	5212	4444	4433	23443	3424	4333	5613	2215	60

Банк начисляет на
них проценты из расчета 3,0% годовых.
Датой поступления процентов на расчетный
счет является 26 число каждого месяца.
Выбран период с 27.09.2006г. по 26.10.2006 г.

Необходимо
произвести расчет суммы начисленных
процентов.

Решение:

Составим таблицу,
в которую внесем даты и суммы остатков
на расчетном счете на конец каждого
операционного дня.

Столбец А отведем
для дат, столбец В – для остатков на
расчетном счете, а столбец С – для
определения суммы ежедневно начисляемого
процента (рисунок 3).

Рисунок
3 Таблица для расчета процентов по
остаткам

на
расчетном счете

В ячейку А3 введем
начальную дату 27.09.2006, а в ячейку А4
формулу:

=
А3 + 1. Для
заполнения
диапазона
А5:А32 применим метод автозаполнения.

Изменение даты в
ячейки А3 повлечет за собой соответствующее
изменение дат в области А4:А32. Это позволит
нам в следующем месяце, изменив дату в
ячейке А3, изменить весь временной
интервал.

В ячейку В4 введем
формулу: =
В3.

Таким образом,
сумма остатка на следующий день будет
равна сумме остатка предыдущего дня.
Это позволяет сэкономить время при
вводе данных в столбце остатков.
Аналогичным образом заполните все
пустые ячейки в столбце В.

Формула для
определения суммы процента (столбец С)
имеет следующий вид: =
B3*$C$1/365.

В данном случае
сумма денежных средств на расчетном
счете на каждую конкретную дату (ячейка
В3) умножается на процент банка (абсолютная
ссылка на ячейку С1) и делится на количество
дней в году (365).

2 Лабораторная работа №2. Обработка и анализ экономической информации с помощью финансовых функций ms Excel

Цель работы
−
формирование теоретических знаний и
практических навыков использования
финансовых
функций MS
Excel
для обработки, анализа экономической
информации и решения финансовых задач.

Задачи работы:

− уяснить сущность
и аргументы основных финансовых функций;

− определить
будущую стоимость на основе постоянной
и переменной процентных ставок;

− рассчитать
доходность ценных бумаг;

− определить
амортизационные отчисления;

− овладеть навыками
выбора финансовых функций для решения
экономических задач в зависимости от
исходных данных.

Теоретические
положения

В состав табличного
процессора Microsoft
Excel
входит более 300 встроенных функций,
дающих возможность выполнять самую
разнообразную обработку данных. Следует
различать понятия «встроенная функция»
(один из множества вычислительных
элементов Excel)
и «формула» (конкретное выражение,
возможно, включающее в себя более чем
одну функцию и выполняющее действия на
основе одного или нескольких значений).

Встроенные функции
MS
Excel
традиционно разделяются на следующие
категории:

− финансовые
функции;

− математические;

− функции для
работы с базами данных, массивами и
ссылками;

− функции работы
с датой и временем;

− логические
функции;

− статистические
функции и др.

Финансовые функции
применяются при планировании и анализе
финансово-хозяйственной деятельности
предприятия, а также при решении задач,
связанных с инвестированием средств.

В качестве
аргументов функций могут использоваться
константы, ссылки на ячейки, имена
диапазонов ячеек, а также другие функции
(вложенные функции). Рассмотрим основные
финансовые функции Microsoft
Excel.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В прошлой статье из курса «ФИНАНСОВАЯ МАТЕМАТИКА» мы рассмотрели понятие инфляции и статистические показатели для ее измерения, а сейчас закрепим полученные знания на практике.

Итак, убедившись, что с теорией у нас все ОК, учимся решать задачи: смотрим видеоурок и внимательно читаем примеры ниже.

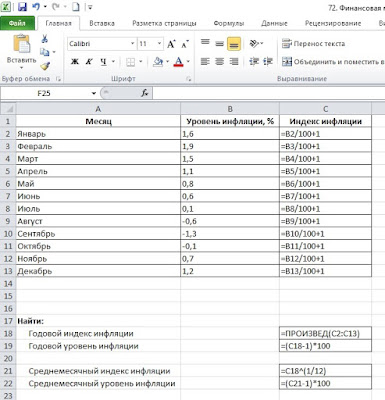
Пример 1.

На рисунке 1 приведены исходные данные помесячных уровней инфляции на протяжении года (диапазон ячеек А1:В13 рабочего листа Excel). Например, за январь общий уровень повышения цен, или общий уровень инфляции составил 1,6%; в феврале — +1,9% и так далее. Вплоть до июля месяца мы видим ежемесячный рост цен. С августа по октябрь мы наблюдали снижение общего уровня цен, то есть, дефляцию. И в последние месяцы года инфляция вновь возобновилась. 

Рис. 1. Исходные данные

*Каждый рисунок можно увеличить щелчком левой кнопки мыши

Необходимо найти годовой индекс и годовой уровень инфляции, а также, среднемесячный индекс и среднемесячный уровень инфляции. 

Решение.

Для нахождения годовых и среднемесячных показателей, прежде всего, нам необходимо перейти от  исходных месячных уровней инфляции (колонка В) к соответствующим индексам инфляции (колонка С). Взаимосвязь между этими показателями демонстрирует первая формула, изображенная на рис. 1. Где лямбда — это уровень инфляции, %; І — индекс инфляции.

Выразив индекс инфляции через уровень инфляции, получим выражение: 

I = лямбда / 100% + 1.

Собственно, эту формулу и следует ввести в каждую из ячеек диапазона С2:С13.

Получив, таким образом, в ячейках С2:С13 месячные индексы инфляции, найдем в ячейке С18 годовой индекс инфляции с использованием второй формулы, рис. 1. То есть, общий индекс инфляции за весь период равен произведению частных индексов инфляции за все периоды, которые входят в его состав. В ячейку С18 введем формулу: 

=ПРОИЗВЕД(С2:С13).

Зная годовой индекс инфляции, рассчитаем в ячейке С19 годовой уровень инфляции с испоьзованием первой формулы, рис. 1. Для этого в ячейку С19 введем формулу: 

=(С18-1)*100.

Для нахождения среднемесячного индекса инфляции нам поможет третья формула, изображенная на рис. 1. То есть, зная общий индекс инфляции, мы должны найти корень n-ой степени из нее. Где n — количество рассчитанных месячных индексов инфляции, в нашем случае n=12. Итак, в ячейку С21 введем формулу: 

=С18^(1/12).

Теперь, зная среднемесячный индекс инфляции, переходим к среднемесячному уровню инфляции. В ячейку С22 вводим формулу: 

=(С21-1)*100.

Итак, все формулы, которые мы ввели на рабочий лист Excel показаны на рис. 2.

Рис. 2. Формулы для расчета требуемых показателей

Если теперь от формул перейти к результатам расчетов, то будем иметь, рис. 3.

Рис. 3. Результаты расчета годовых и среднемесячных показателей инфляции

По данным рисунка 3 можно сделать следующие выводы:

— в целом за год общий уровень цен в экономике вырос в 1,077 раза или на +7,71%;

— при этом, среднемесячный рост уровня цен составлял +0,621%.

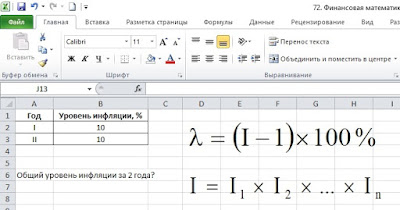
Пример 2.

Уровень инфляции на протяжении двух лет составлял по 10% ежегодно. Найти общий уровень инфляции за эти два года. Условие задачи и необходимые для ее решения формулы приведены на рис. 4. 

Рис. 4. Исходные данные

Решение.

Распространенная ошибка при решении подобных задач: общий уровень инфляции за два года 10% + 10% = 20% — НЕПРАВИЛЬНО!

Общий уровень инфляции всегда находится только исходя из общего индекса инфляции, первая формула на рис. 4. Но для нахождения общего индекса инфляции, нам нужно знать частные индексы инфляции за каждый период, формула 2 на рис. 4.

Поэтому, в колонке С сначала найдем индексы инфляции для каждого года, используя формулу: I = лямбда / 100% + 1 = 10% / 100% + 1 = 1,1.

Далее, в ячейке С4 находим общий индекс инфляции за два года: 1,1 * 1,1 = 1,21. Ну и напоследок, в ячейке С7 найдем общий уровень инфляции за 2 года: (1,21 — 1) * 100% = 21%. Формулы для расчета требуемых показателей приведены на рис. 5.

Рис. 5. Формулы для расчета требуемых показателей

Таким образом, общий уровень инфляции за два года составил не 20%, как можно было подумать сначала, а ровно 21%.

Есть, со вторым примером разобрались. И еще один интересный и очень актуальный пример связанный с тем, что покупательная способность денег, вследствие инфляции, со временем падает.

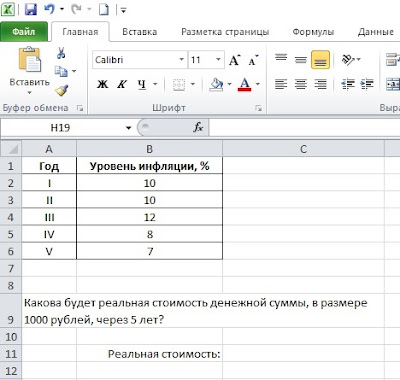
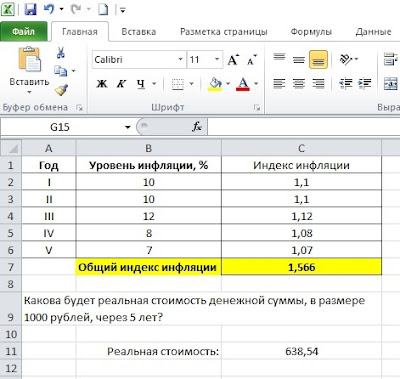
Пример 3.

Имеются прогнозные данные о возможном уровне инфляции на протяжении следующих 5 лет. Необходимо определить, какова будет реальная стоимость денежной суммы, в размере 1000 руб. через 5 лет? Исходные данные приведены на рис. 6.

Рис. 6. Исходные данные

Решение.

Практическое решение данной задачи снова сводится к нахождению общего индекса инфляции.

Сначала в колонке С находим индексы инфляции за каждый год. Далее в ячейке С7 рассчитываем общий индекс инфляции путем перемножения годовых индексов между собой. По результатам расчетов он будет равен 1,566. То есть, за 5 лет общий уровень цен в экономике вырастет в 1,566 раза. И ровно во столько же раз упадет покупательная способность наших 1000 руб.

В ячейке С11 рассчитываем реальную стоимость 1000 руб., как 1000 / 1,566 = 638,54 руб. Соответствующие результаты расчетов приведены на рис. 7.

Рис. 7. Результаты расчетов

Таким образом, через 5 лет за 1000 руб. мы сможем приобрести ровно такое же количество товаров и услуг, как и сегодня за 638,54 руб.

Все видеоуроки по курсу ФИНАНСОВОЙ МАТЕМАТИКИ вы можете найти на нашем Youtube-канале «Учите компьютер вместе с нами!»