Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Содержание
- Что это такое
- А нужно ли это
- Как построить график уравнения регрессии в Excel
- Подготовительные работы
- Как пользоваться
- Анализ
- Как построить график квадратного уравнения в Excel
- Как построить график линейного уравнения
- Вывод
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите:
Выберите раздел:
Далее:
Прокрутите окно вниз, выберите:
Отметьте пункт:
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите:
Выберите:
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат.
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
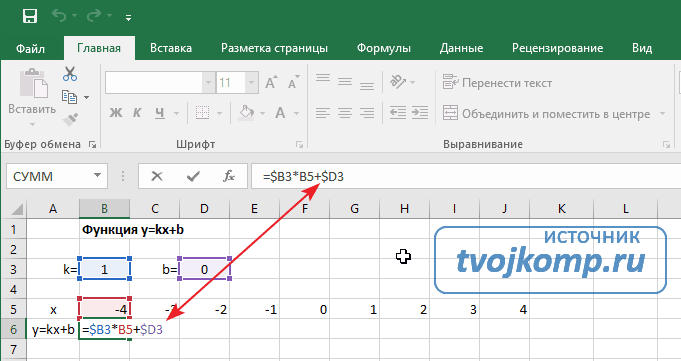
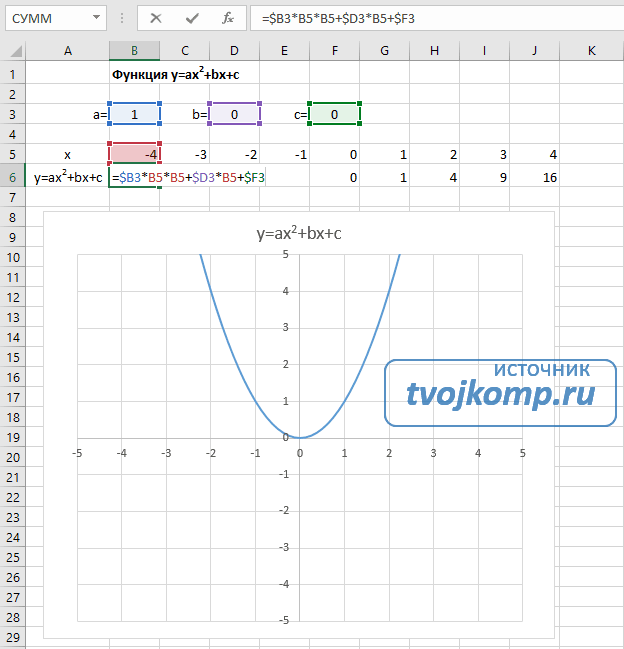
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;

При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите:
Поместите график в свободное место на листе.
Как построить график линейного уравнения
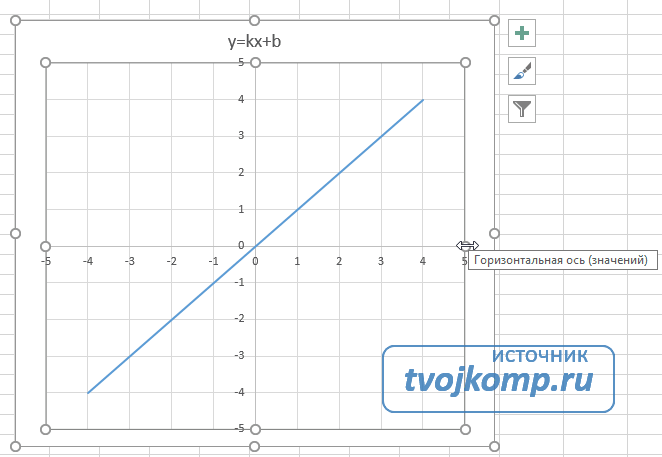
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.

График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
Варианты построения графика функции в Microsoft Excel
Вариант 1: График функции X^2
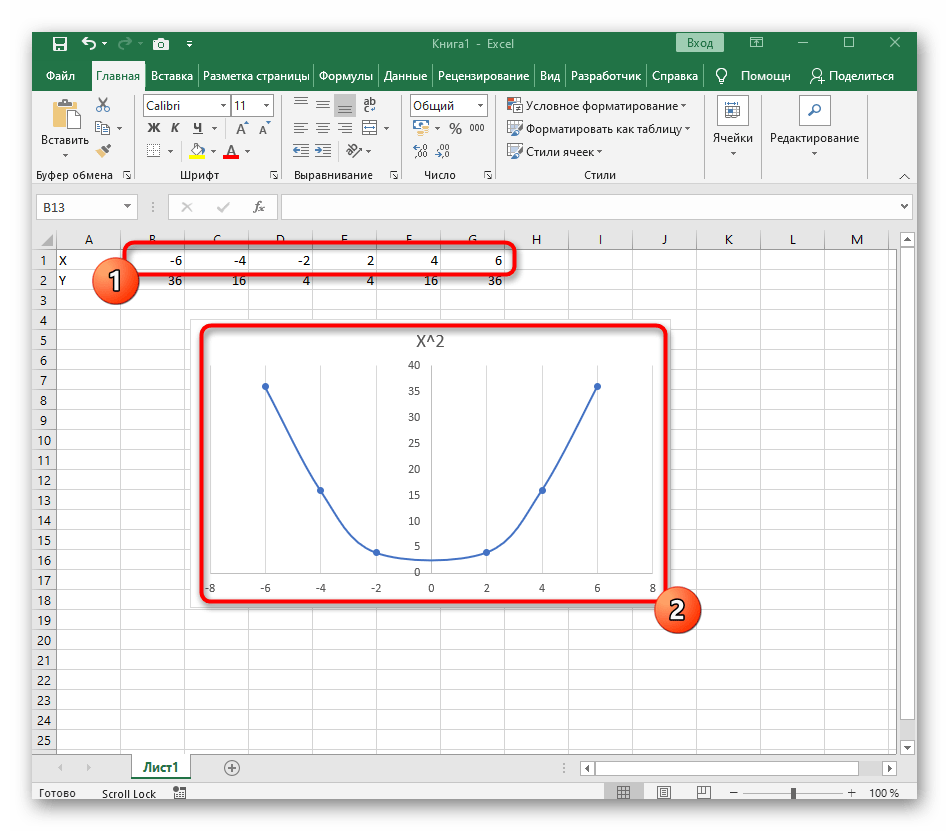
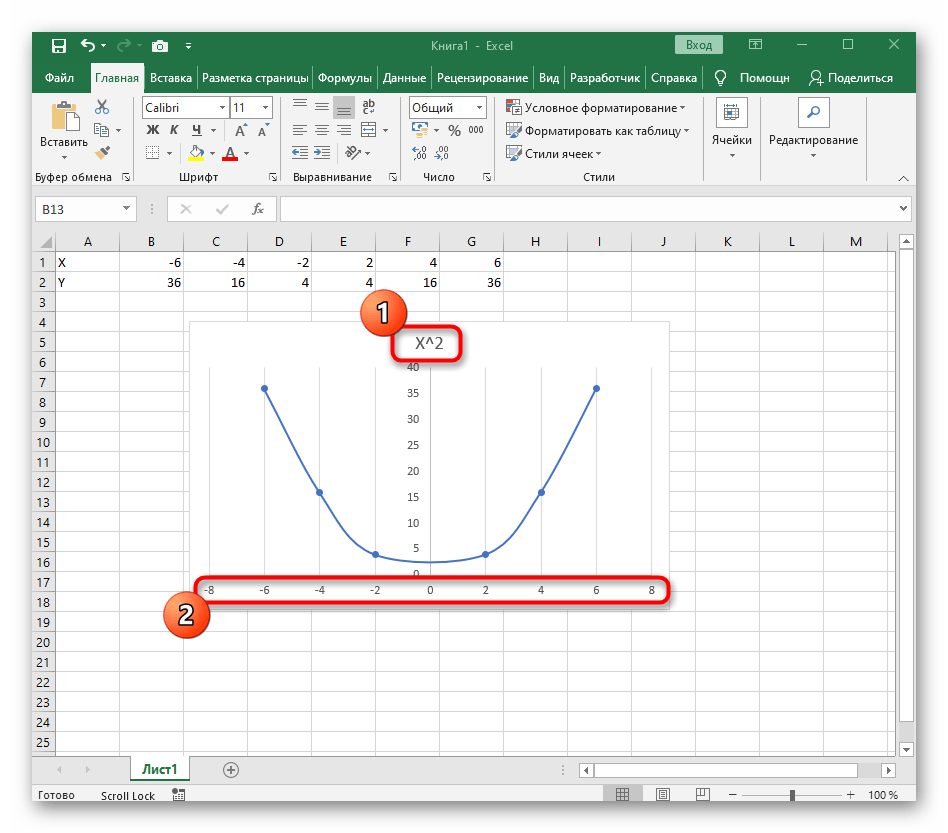
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
-
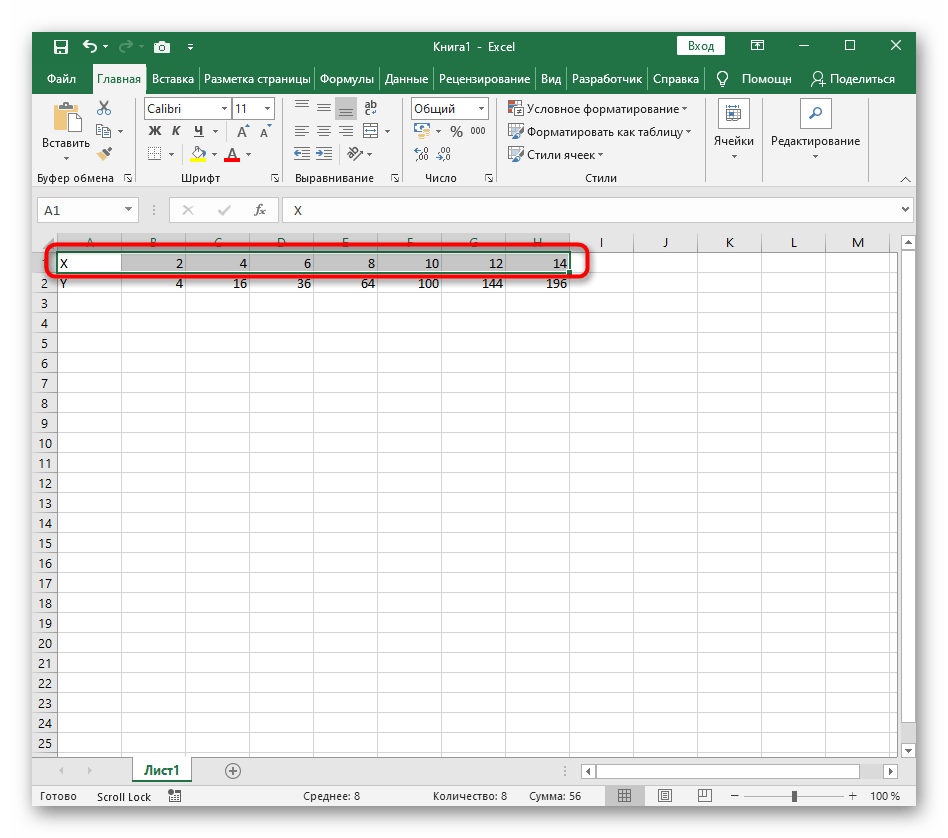
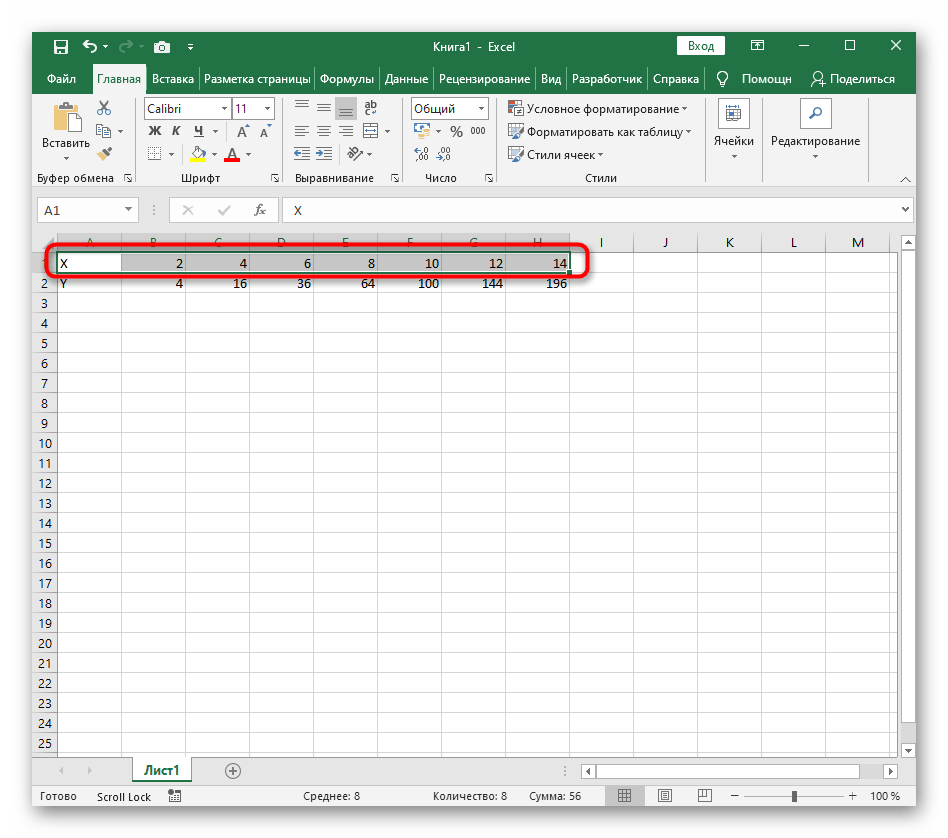
Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
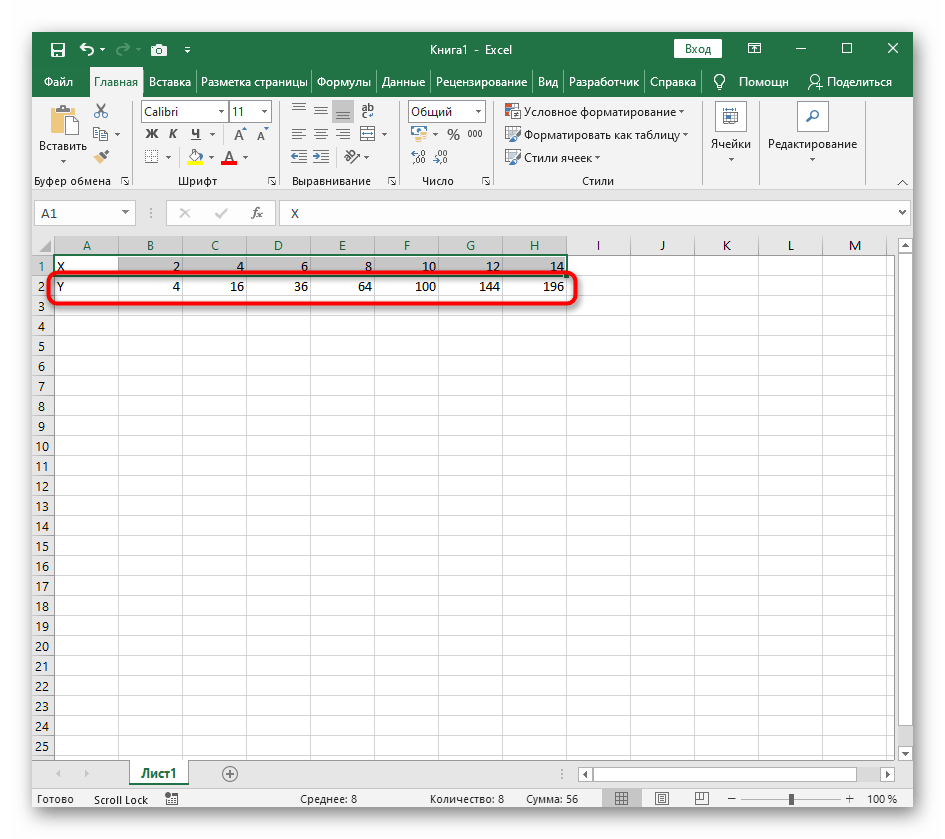
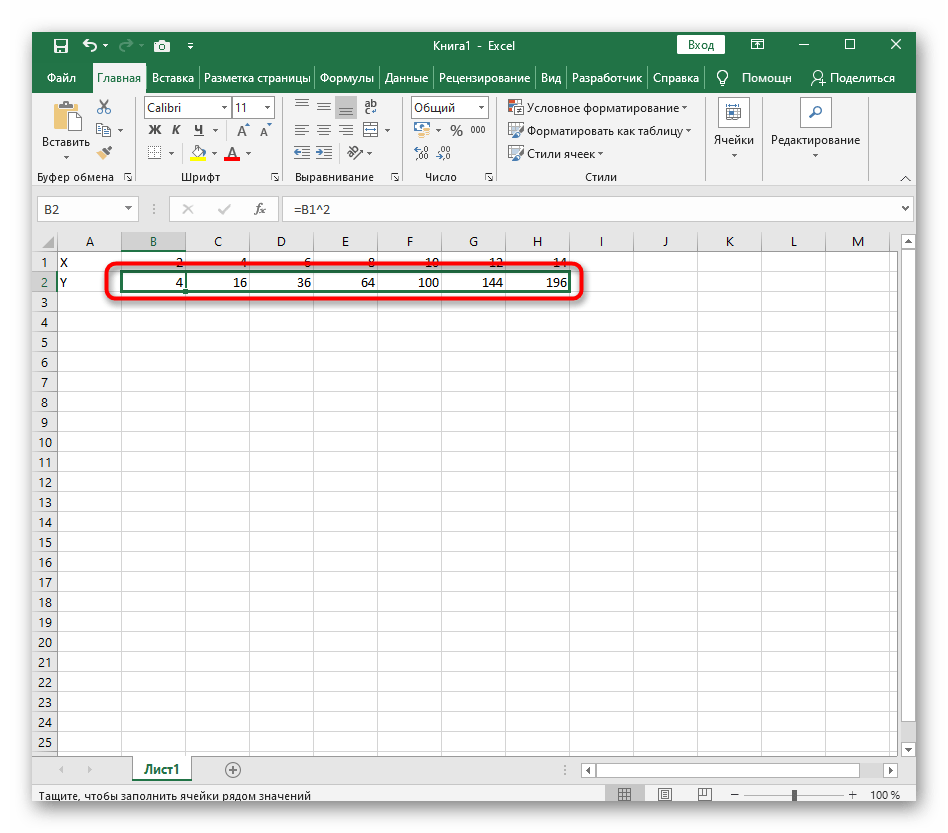
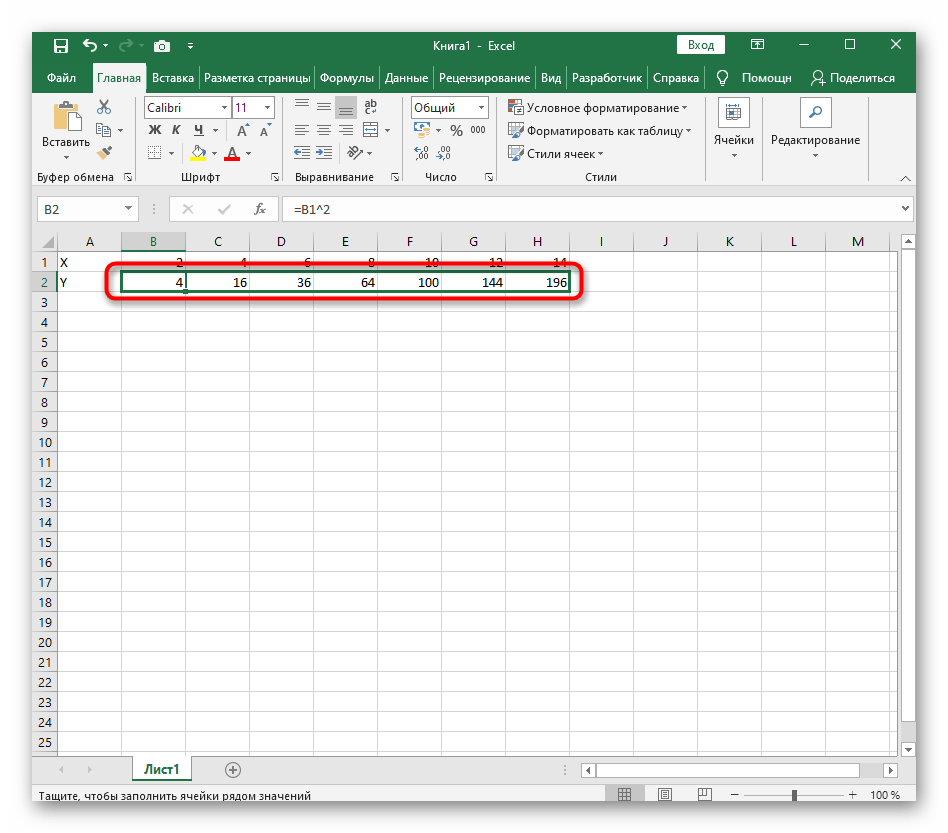
Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
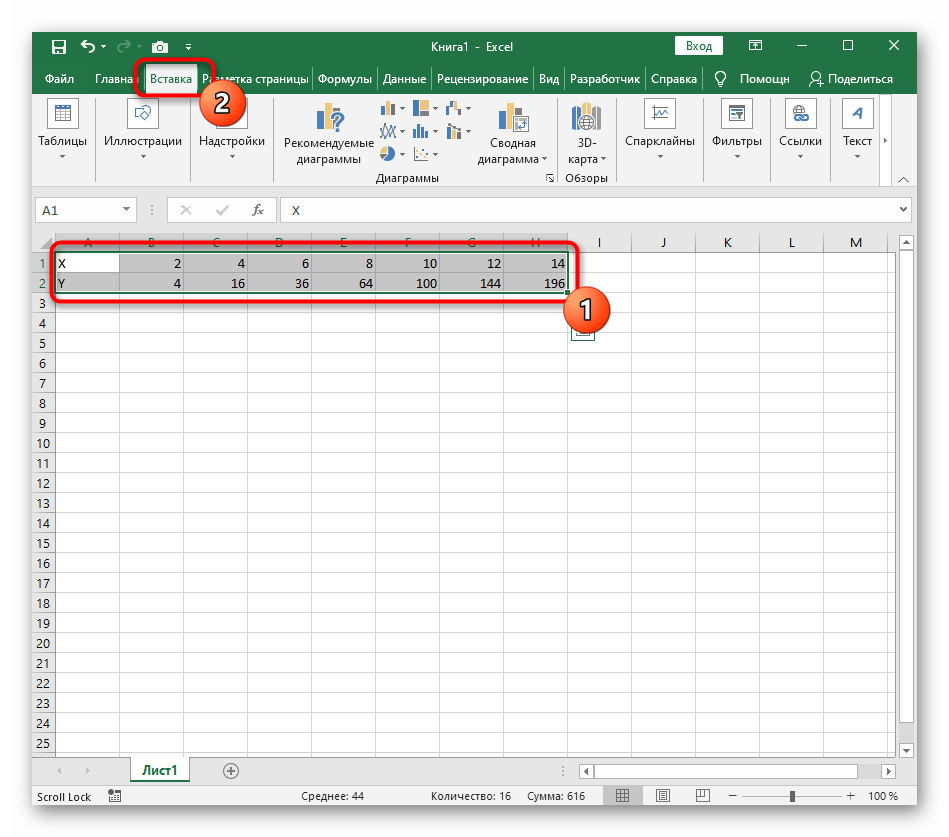
Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
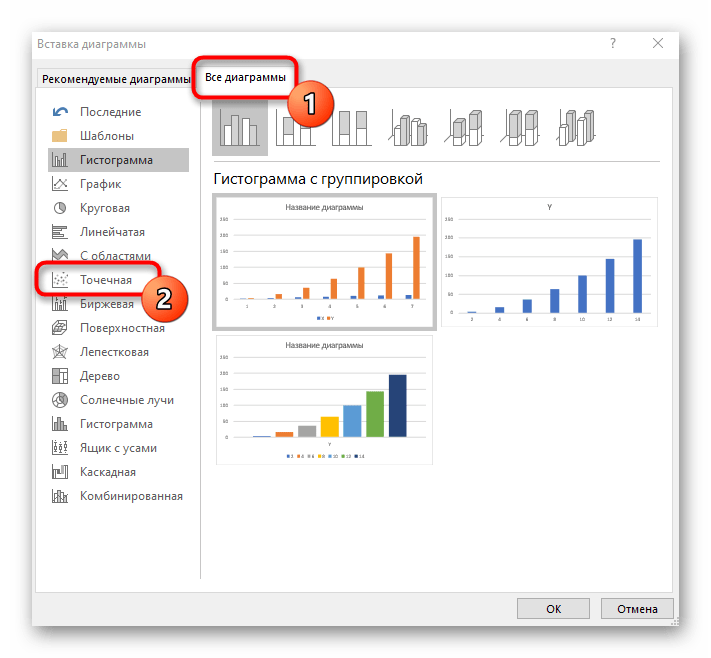
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
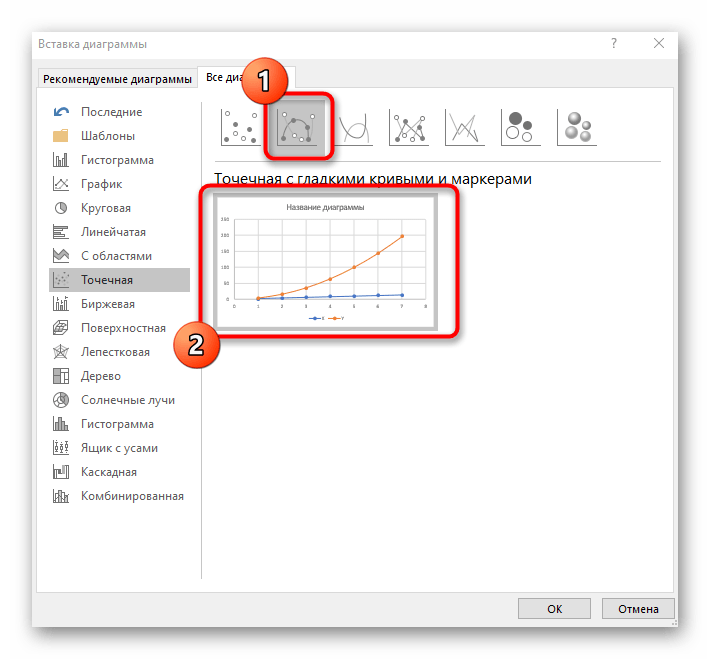
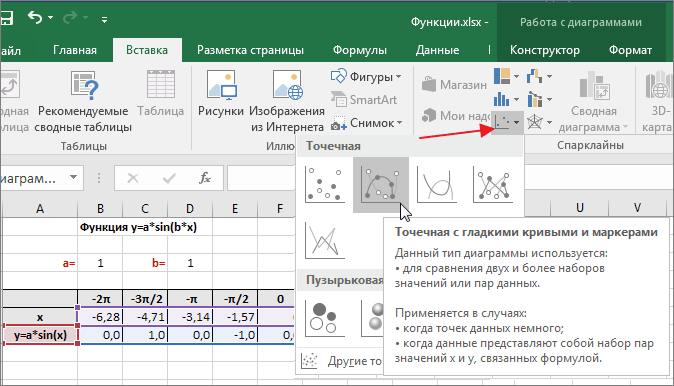
Подойдет вариант «Точечная с гладкими кривыми и маркерами».
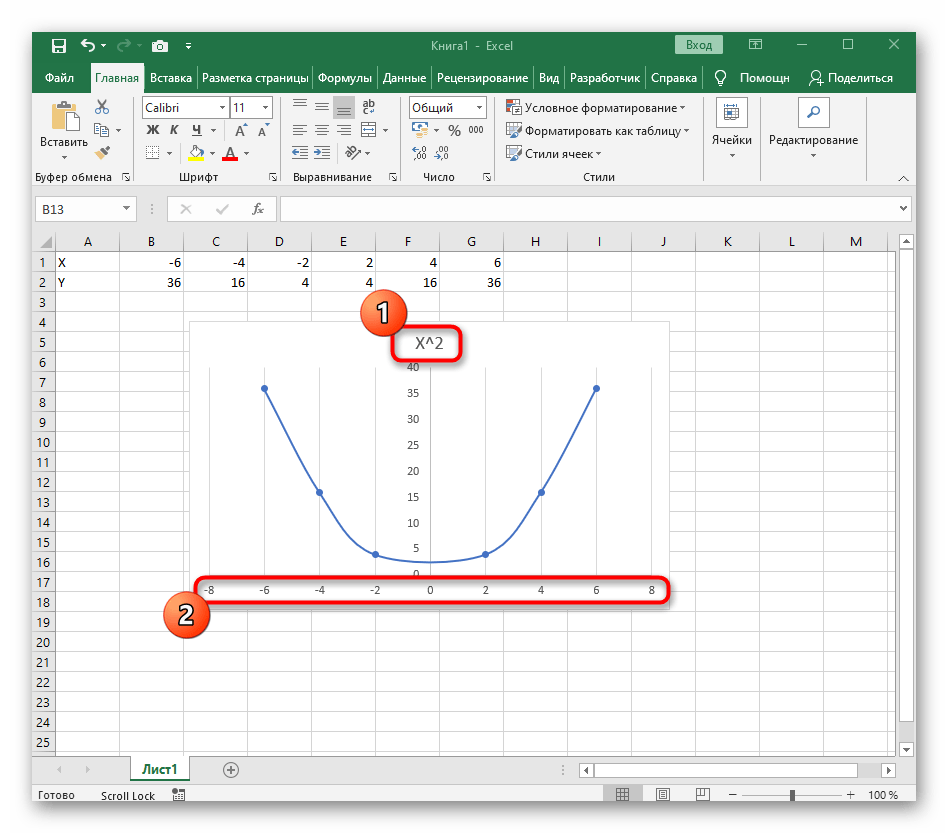
После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
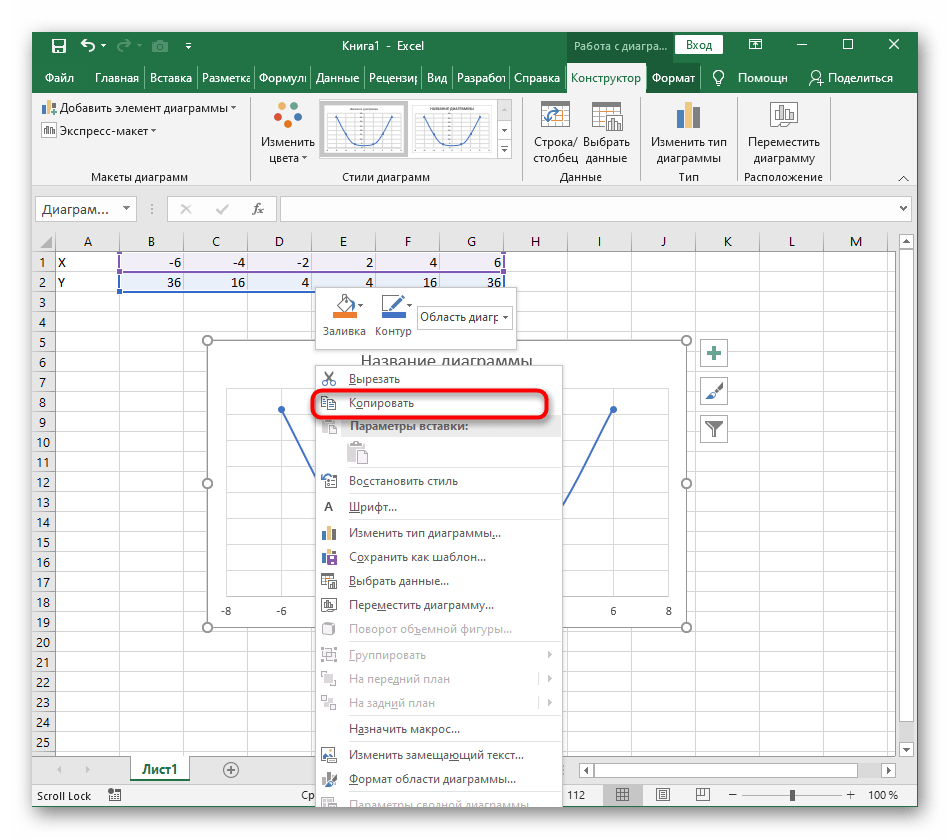
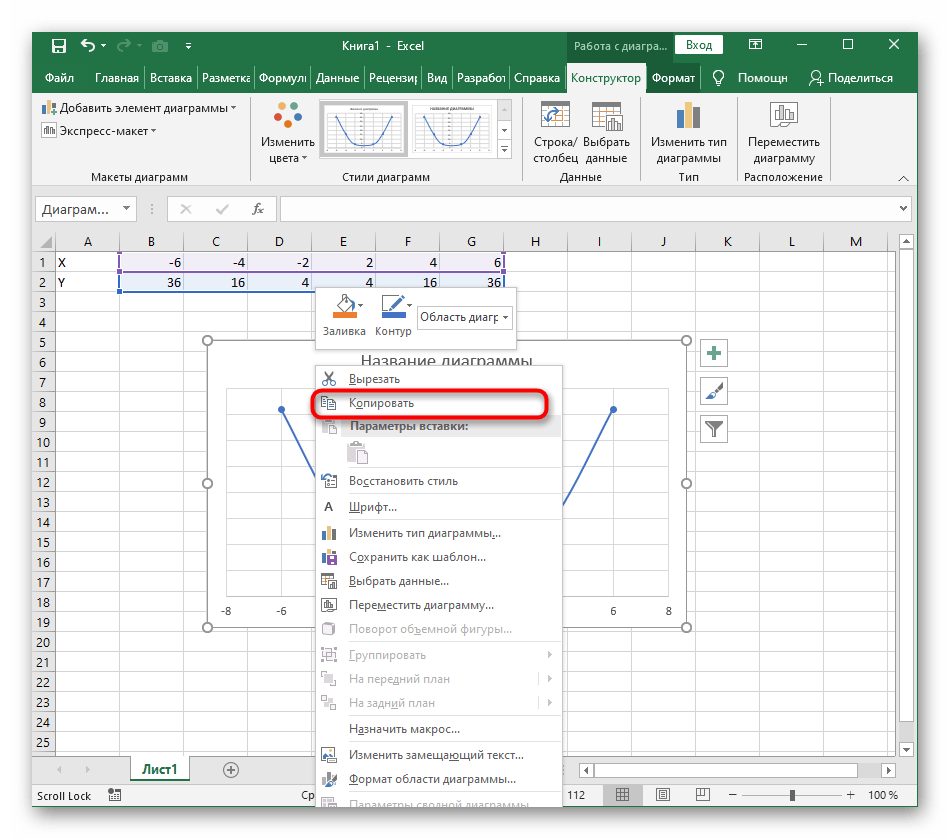
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
-
Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
Создайте сразу два столбца — X и Y, куда будете записывать данные.
Запишите самостоятельно первые два или три значения с указанным шагом.
Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
Перейдите к столбцу Y и объявите функцию =SIN( , а в качестве числа укажите первое значение X.
Сама функция автоматически высчитает синус заданного числа.
Растяните столбец точно так же, как это было показано ранее.
Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
Выделите столбец с Y и перейдите на вкладку «Вставка».
Создайте стандартный график, развернув выпадающее меню.
График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
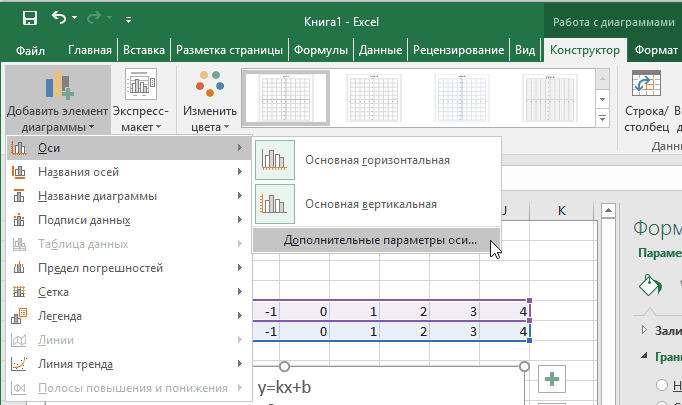
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://urok.1sept.ru/articles/564361
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
Содержание
- 1 Процедура создания графика
- 1.1 Способ 1: создание графика зависимости на основе данных таблицы
- 1.2 Способ 2: создание графика зависимости с несколькими линиями
- 1.3 Способ 3: построение графика при использовании различных единиц измерения
- 1.4 Способ 4: создание графика зависимости на основе алгебраической функции
- 1.5 Помогла ли вам эта статья?
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке . Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Поделитесь статьёй с друзьями:
Добрый день. А есть возможность в Excele создать график с тремя переменными, но на одном графике? 2 параметра как обычно, координаты х и у, а третий параметр чтоб отражался размером метки? Вот как пример, такой график —
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графика линейной функции в Excel
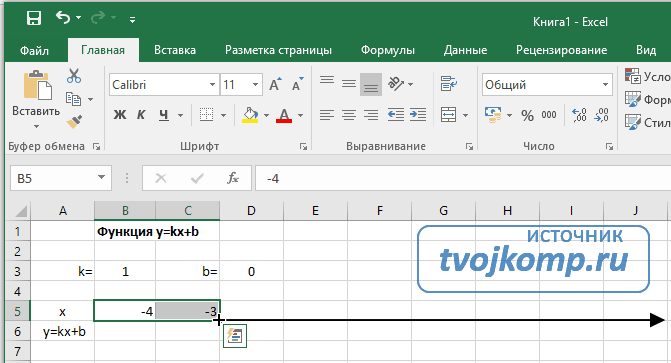
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале .
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.

Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
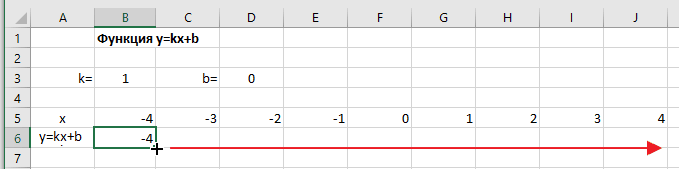
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.

Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.

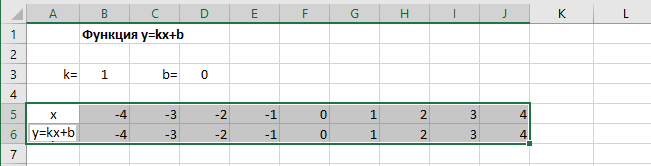
Выделяем прямоугольный диапазон ячеек A5:J6.

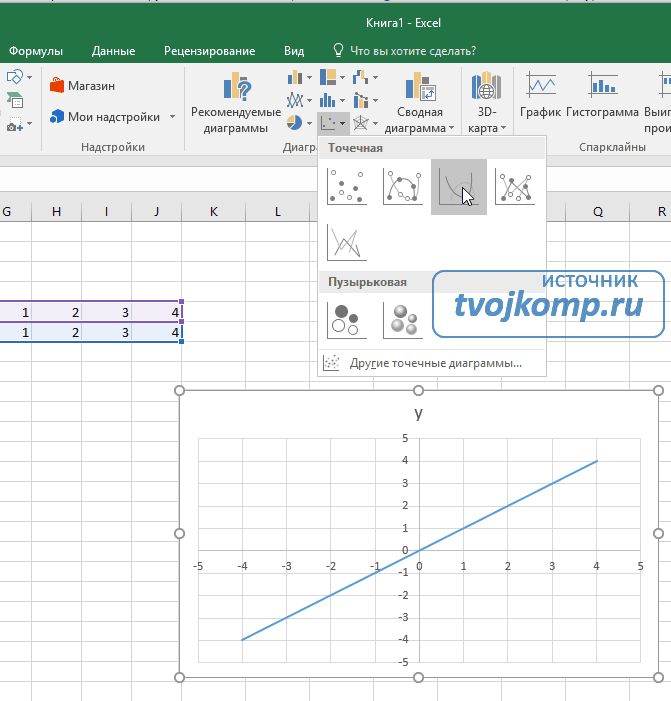
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
Построение диаграммы типа «График»
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
График линейной функции
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
Вход в режим изменения параметров координатных осей
В правой части окна появиться боковая панель настроек Формат оси.
Редактирование параметров координатной оси
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
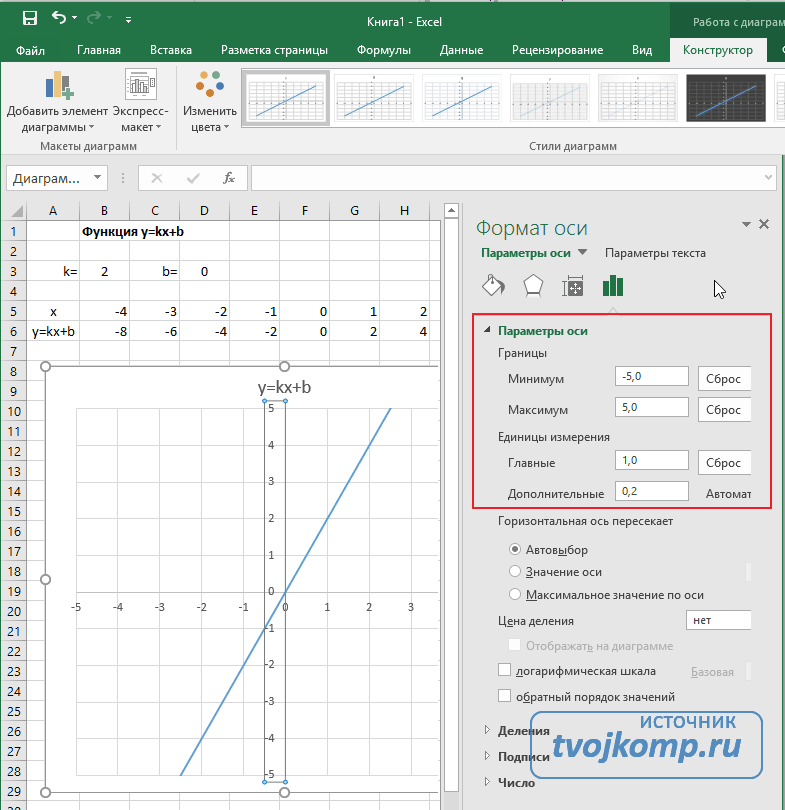
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
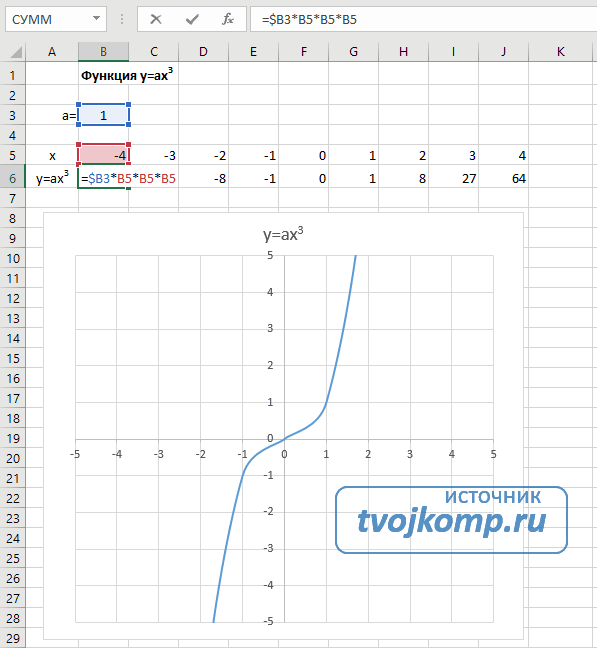
График квадратичной функцииКубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
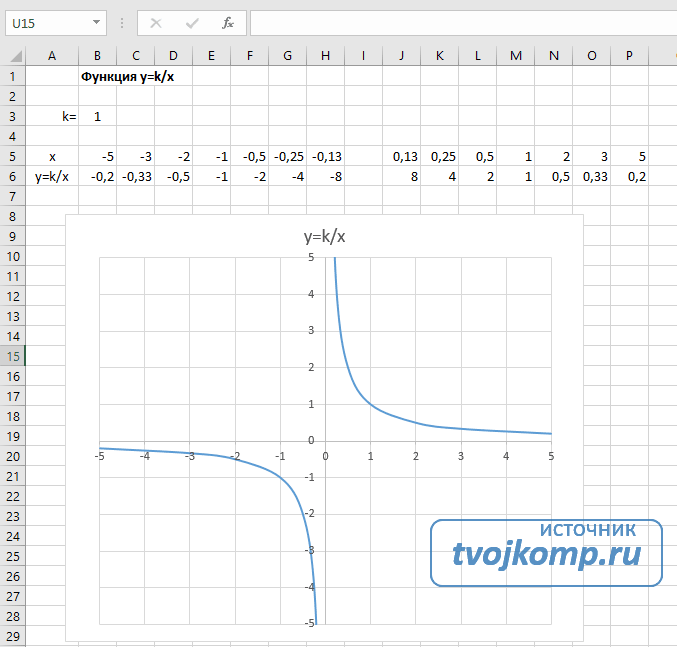
График кубической параболыГипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
График гиперболыПостроение тригонометрических функций sin(x) и cos(x)
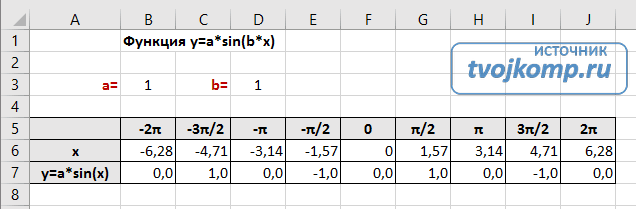
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
Таблица значений функции sin(x)
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
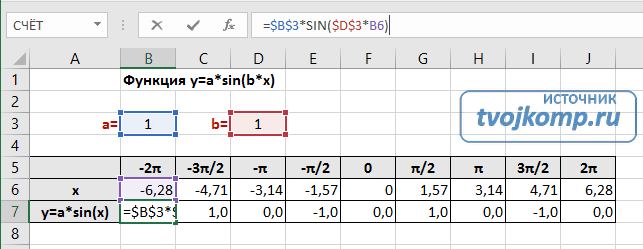
В седьмой строке записываются расчетные формулы тригонометрической функции.
Запись расчетной формулы функции sin(x) в Excel
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
Построение диаграммы Точечная с гладкими кривыми
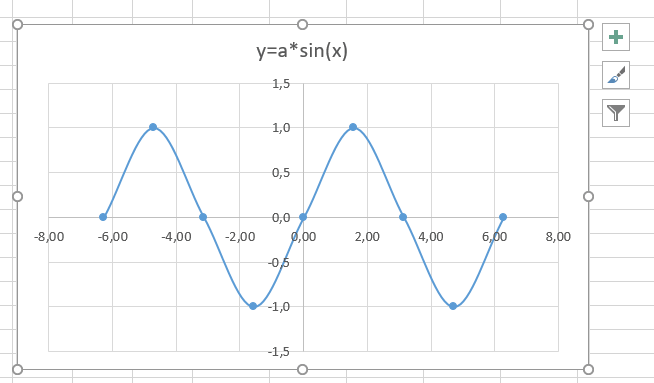
В итоге получим диаграмму.
График sin(x) после вставки диаграммы
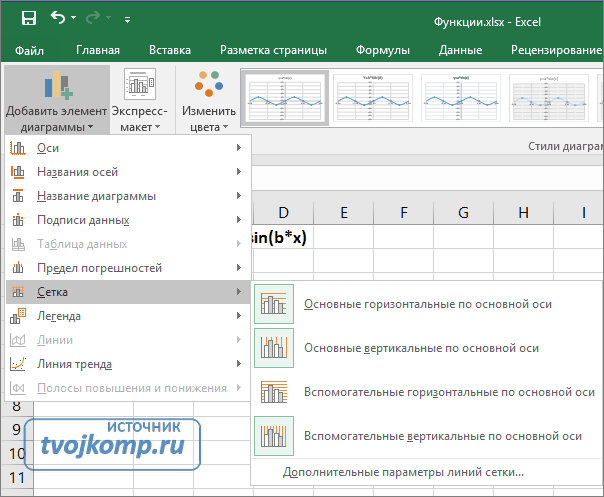
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Настройка сетки при построении графика
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
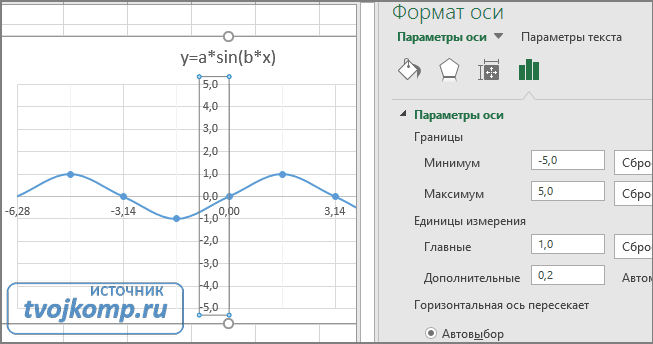
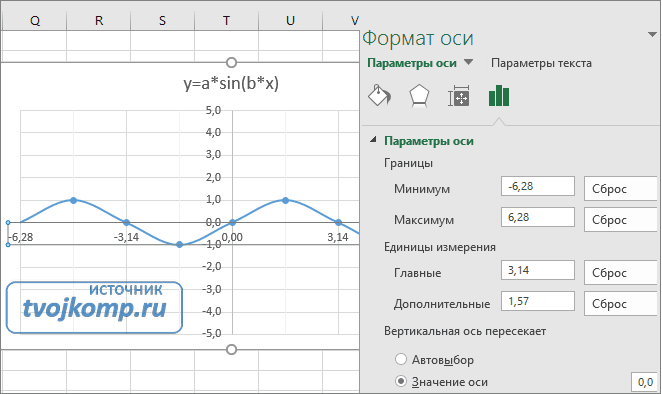
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Настройка формата горизонтальной оси Х графика функции
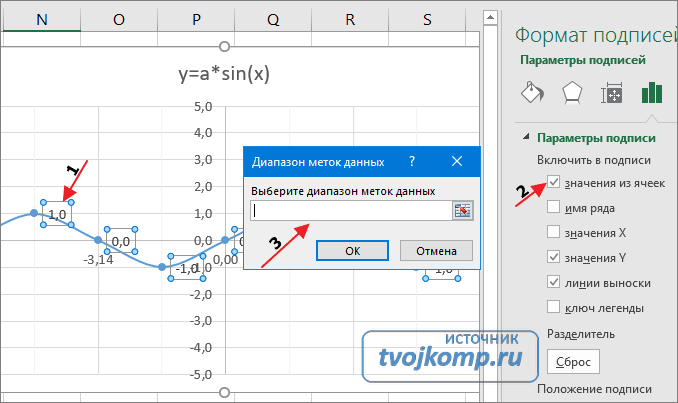
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
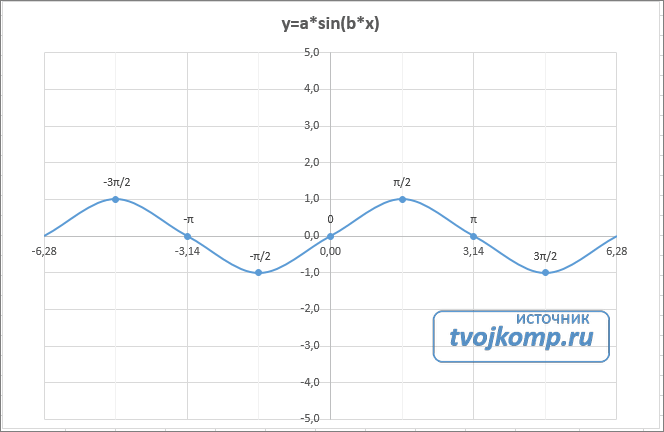
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дорогой читатель! Вы посмотрели статью до конца. Получили вы ответ на свой вопрос? Напишите в комментариях пару слов.Если ответа не нашли, укажите что искали.
Рекомендовано Вам:
Построение графиков функций в Excel
Февраль 9th, 2014
Andrey K
(
голос, значение:
из 5)
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
(
голос, значение:
из 5)
Вы можете
оставить комментарий
, или
ссылку
на Ваш сайт.
Душевые термостаты, лучшие модели на
http://tools-ricambi.ru/
изготавливаются из материалов высшего качества
Одной из типичных математических задач является построение графика зависимости. В нем отображается зависимость функции от изменения аргумента. На бумаге выполнить данную процедуру не всегда просто. Но инструменты Excel, если в должной мере овладеть ими, позволяют выполнить данную задачу точно и относительно быстро. Давайте выясним, как это можно сделать, используя различные исходные данные.
Процедура создания графика
Зависимость функции от аргумента является типичной алгебраической зависимостью. Чаще всего аргумент и значение функции принято отображать символами: соответственно «x» и «y». Нередко нужно произвести графическое отображение зависимости аргумента и функции, которые записаны в таблицу, или представлены в составе формулы. Давайте разберем конкретные примеры построения подобного графика (диаграммы) при различных заданных условиях.
Способ 1: создание графика зависимости на основе данных таблицы
Прежде всего, разберем, как создать график зависимости на основе данных, предварительно внесенных в табличный массив. Используем таблицу зависимости пройденного пути (y) от времени (x).
- Выделяем таблицу и переходим во вкладку «Вставка». Кликаем по кнопке «График», которая имеет локализацию в группе «Диаграммы» на ленте. Открывается выбор различных типов графиков. Для наших целей выбираем самый простой. Он располагается первым в перечне. Клацаем по нему.
- Программа производит построение диаграммы. Но, как видим, на области построения отображается две линии, в то время, как нам нужна только одна: отображающая зависимость пути от времени. Поэтому выделяем кликом левой кнопки мыши синюю линию («Время»), так как она не соответствует поставленной задаче, и щелкаем по клавише Delete.
- Выделенная линия будет удалена.
Собственно на этом построение простейшего графика зависимости можно считать завершенным. При желании также можно отредактировать наименования диаграммы, её осей, удалить легенду и произвести некоторые другие изменения. Об этом подробнее рассказывается в отдельном уроке.
Урок: Как сделать график в Экселе
Способ 2: создание графика зависимости с несколькими линиями
Более сложный вариант построения графика зависимости представляет собой случай, когда одному аргументу соответствуют сразу две функции. В этом случае потребуется построить две линии. Для примера возьмем таблицу, в которой по годам расписана общая выручка предприятия и его чистая прибыль.
- Выделяем всю таблицу вместе с шапкой.
- Как и в предыдущем случае, жмем на кнопку «График» в разделе диаграмм. Опять выбираем самый первый вариант, представленный в открывшемся списке.
- Программа производит графическое построение согласно полученным данным. Но, как видим, в данном случае у нас имеется не только лишняя третья линия, но ещё и обозначения на горизонтальной оси координат не соответствуют тем, которые требуются, а именно порядку годов.
Сразу удалим лишнюю линию. Ею является единственная прямая на данной диаграмме — «Год». Как и в предыдущем способе, выделяем линию кликом по ней мышкой и жмем на кнопку Delete.
- Линия удалена и вместе с ней, как вы можете заметить, преобразовались значения на вертикальной панели координат. Они стали более точными. Но проблема с неправильным отображением горизонтальной оси координат все-таки остается. Для решения данной проблемы кликаем по области построения правой кнопкой мыши. В меню следует остановить выбор на позиции «Выбрать данные…».
- Открывается окошко выбора источника. В блоке «Подписи горизонтальной оси» кликаем по кнопке «Изменить».
- Открывается окошко ещё меньше предыдущего. В нём нужно указать координаты в таблице тех значений, которые должны отображаться на оси. С этой целью устанавливаем курсор в единственное поле данного окна. Затем зажимаем левую кнопку мыши и выделяем всё содержимое столбца «Год», кроме его наименования. Адрес тотчас отразится в поле, жмем «OK».
- Вернувшись в окно выбора источника данных, тоже щелкаем «OK».
- После этого оба графика, размещенные на листе, отображаются корректно.
Способ 3: построение графика при использовании различных единиц измерения
В предыдущем способе мы рассмотрели построение диаграммы с несколькими линиями на одной плоскости, но при этом все функции имели одинаковые единицы измерения (тыс. руб.). Что же делать, если нужно создать графики зависимости на основе одной таблицы, у которых единицы измерения функции отличаются? В Экселе существует выход и из этого положения.
Имеем таблицу, в которой представлены данные по объему продаж определенного товара в тоннах и по выручке от его реализации в тысячах рублей.
- Как и в предыдущих случаях выделяем все данные табличного массива вместе с шапкой.
- Клацаем по кнопке «График». Снова выбираем первый вариант построения из перечня.
- Набор графических элементов сформирован на области построения. Тем же способом, который был описан в предыдущих вариантах, убираем лишнюю линию «Год».
- Как и в предыдущем способе, нам следует на горизонтальной панели координат отобразить года. Кликаем по области построения и в списке действий выбираем вариант «Выбрать данные…».
- В новом окне совершаем щелчок по кнопке «Изменить» в блоке «Подписи» горизонтальной оси.
- В следующем окне, производя те же действия, которые были подробно описаны в предыдущем способе, вносим координаты столбца «Год» в область «Диапазон подписей оси». Щелкаем по «OK».
- При возврате в предыдущее окно также выполняем щелчок по кнопке «OK».
- Теперь нам следует решить проблему, с которой ещё не встречались в предыдущих случаях построения, а именно, проблему несоответствия единиц величин. Ведь, согласитесь, не могут располагаться на одной панели координат деления, которые одновременно обозначают и денежную сумму (тыс. рублей) и массу (тонны). Для решения данной проблемы нам потребуется произвести построение дополнительной вертикальной оси координат.
В нашем случае для обозначения выручки оставим ту вертикальную ось, которая уже имеется, а для линии «Объём продаж» создадим вспомогательную. Клацаем по данной линии правой кнопкой мышки и выбираем из перечня вариант «Формат ряда данных…».
- Запускается окно формата ряда данных. Нам нужно переместиться в раздел «Параметры ряда», если оно было открыто в другом разделе. В правой части окна расположен блок «Построить ряд». Требуется установить переключатель в позицию «По вспомогательной оси». Клацаем по наименованию «Закрыть».
- После этого вспомогательная вертикальная ось будет построена, а линия «Объём продаж» переориентируется на её координаты. Таким образом, работа над поставленной задачей успешно окончена.
Способ 4: создание графика зависимости на основе алгебраической функции
Теперь давайте рассмотрим вариант построения графика зависимости, который будет задан алгебраической функцией.
У нас имеется следующая функция: y=3x^2+2x-15. На её основе следует построить график зависимости значений y от x.
- Прежде, чем приступить к построению диаграммы, нам нужно будет составить таблицу на основе указанной функции. Значения аргумента (x) в нашей таблице будут указаны в диапазоне от -15 до +30 с шагом 3. Чтобы ускорить процедуру введения данных, прибегнем к использованию инструмента автозаполнения «Прогрессия».
Указываем в первой ячейке столбца «X» значение «-15» и выделяем её. Во вкладке «Главная» клацаем по кнопке «Заполнить», размещенной в блоке «Редактирование». В списке выбираем вариант «Прогрессия…».
- Выполняется активация окна «Прогрессия». В блоке «Расположение» отмечаем наименование «По столбцам», так как нам необходимо заполнить именно столбец. В группе «Тип» оставляем значение «Арифметическая», которое установлено по умолчанию. В области «Шаг» следует установить значение «3». В области «Предельное значение» ставим цифру «30». Выполняем щелчок по «OK».
- После выполнения данного алгоритма действий весь столбец «X» будет заполнен значениями в соответствии с заданной схемой.
- Теперь нам нужно задать значения Y, которые бы соответствовали определенным значениям X. Итак, напомним, что мы имеем формулу y=3x^2+2x-15. Нужно её преобразовать в формулу Excel, в которой значения X будут заменены ссылками на ячейки таблицы, содержащие соответствующие аргументы.
Выделяем первую ячейку в столбце «Y». Учитывая, что в нашем случае адрес первого аргумента X представлен координатами A2, то вместо представленной выше формулы получаем такое выражение:
=3*(A2^2)+2*A2-15Записываем это выражение в первую ячейку столбца «Y». Для получения результата расчета щелкаем по клавише Enter.
- Результат функции для первого аргумента формулы рассчитан. Но нам нужно рассчитать её значения и для других аргументов таблицы. Вводить формулу для каждого значения Y очень долгое и утомительное занятие. Намного быстрее и проще её скопировать. Эту задачу можно решить с помощью маркера заполнения и благодаря такому свойству ссылок в Excel, как их относительность. При копировании формулы на другие диапазоны Y значения X в формуле будут автоматически изменяться относительно своих первичных координат.
Наводим курсор на нижний правый край элемента, в который ранее была записана формула. При этом с курсором должно произойти преображение. Он станет черным крестиком, который носит наименование маркера заполнения. Зажимаем левую кнопку мыши и тащим этот маркер до нижних границ таблицы в столбце «Y».
- Вышеуказанное действие привело к тому, что столбец «Y» был полностью заполнен результатами расчета формулы y=3x^2+2x-15.
- Теперь настало время для построения непосредственно самой диаграммы. Выделяем все табличные данные. Снова во вкладке «Вставка» жмем на кнопку «График» группы «Диаграммы». В этом случае давайте из перечня вариантов выберем «График с маркерами».
- Диаграмма с маркерами отобразится на области построения. Но, как и в предшествующих случаях, нам потребуется произвести некоторые изменения для того, чтобы она приобрела корректный вид.
- Прежде всего, удалим линию «X», которая разместилась горизонтально на отметке 0 координат. Выделяем данный объект и жмем на кнопку Delete.
- Легенда нам тоже не нужна, так как мы имеем только одну линию («Y»). Поэтому выделяем легенду и снова жмем по клавише Delete.
- Теперь нам нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «X» в таблице.
Кликом правой кнопки мыши выделяем линию диаграммы. В меню перемещаемся по значению «Выбрать данные…».
- В активировавшемся окне выбора источника клацаем по уже хорошо знакомой нам кнопке «Изменить», располагающейся в блоке «Подписи горизонтальной оси».
- Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «X». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».
- Вернувшись к окну выбора источника данных, клацаем по кнопке «OK» в нём, как до этого сделали в предыдущем окне.
- После этого программа произведет редактирование ранее построенной диаграммы согласно тем изменениям, которые были произведены в настройках. График зависимости на основе алгебраической функции можно считать окончательно готовым.
Урок: Как сделать автозаполнение в Майкрософт Эксель
Как видим, с помощью программы Excel процедура построения графика зависимости значительно упрощается в сравнении с созданием его на бумаге. Результат построения можно использовать как для обучающих работ, так и непосредственно в практических целей. Конкретный вариант построения зависит от того, на основе чего строится диаграмма: табличные значения или функция. Во втором случае перед построением диаграммы придется ещё создавать таблицу с аргументами и значениями функций. Кроме того, график может быть построен, как на основе одной функции, так и нескольких.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Задача решения уравнения встает не только перед студентами и школьниками. В Excel можно использовать различные способы выполнения этой задачи. О способе решения путем подбора параметра пойдет речь в этой статье.
Нахождение корней нелинейного уравнения с использованием средства
«Подбор параметра» сводится в двум этапам:
- определение приблизительных границ отрезков и количества корней графическим методом;
- подбор на каждом отрезке значения корня, удовлетворяющего заданной точности вычислений.
Примером может служить решение квадратного уравнения, которое в общем виде задается выражением
«Y(x) = ax2 + bx +
c» . Для того, чтобы построенная электронная таблица позволяла бы находить решения подобных уравнений с любыми коэффициентами, лучше вынести коэффициенты в отдельные ячейки, а в формулах для вычисления значений функции использовать ссылки на эти ячейки. Впрочем, это дело вкуса. Можно при составлении формулы использовать значения коэффициентов, а не ссылки на них.
Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «
А6» . Для вычисления следующего значения в ячейку
«А7» введена формула «
=А6+$
B$4» , т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
Далее с помощью
маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Вводится формула для вычисления значения функции (для рассматриваемого примера в ячейку «
В6» ) и формируется ряд аналогичных формул для остальных ячеек. В формуле использованы абсолютные ссылки на ячейки с коэффициентами уравнения.
По построенной таблице строится
точечная диаграмма .
Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Можно было бы найти решение уже на этом шаге, но для этого понадобилось бы гораздо больше ячеек и шаг, равный заданной точности вычислений (0,001). Чтобы не создавать громоздких таблиц, далее используется
«Подбор параметра» из группы
«Прогноз» на вкладке
«Данные» . Предварительно необходимо выделить место под начальные значения переменной (корней в примере два) и соответствующие значения функции. В качестве «
х1» выбирается первое из значений, дающих наиболее близкое к нулю значение функции (в примере 0,5). В
ячейку
L6 введена формула для вычисления функции. В окне подбора параметра необходимо указать для какой ячейки (
L6 ), какое значение (
) нужно получить, и в какой ячейке для этого изменять значения (
К6 ).
Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки
L9 (в ячейку скопирована формула из ячейки
L6 ).
Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
Подбор параметра имеется и в более ранних версиях программы.
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
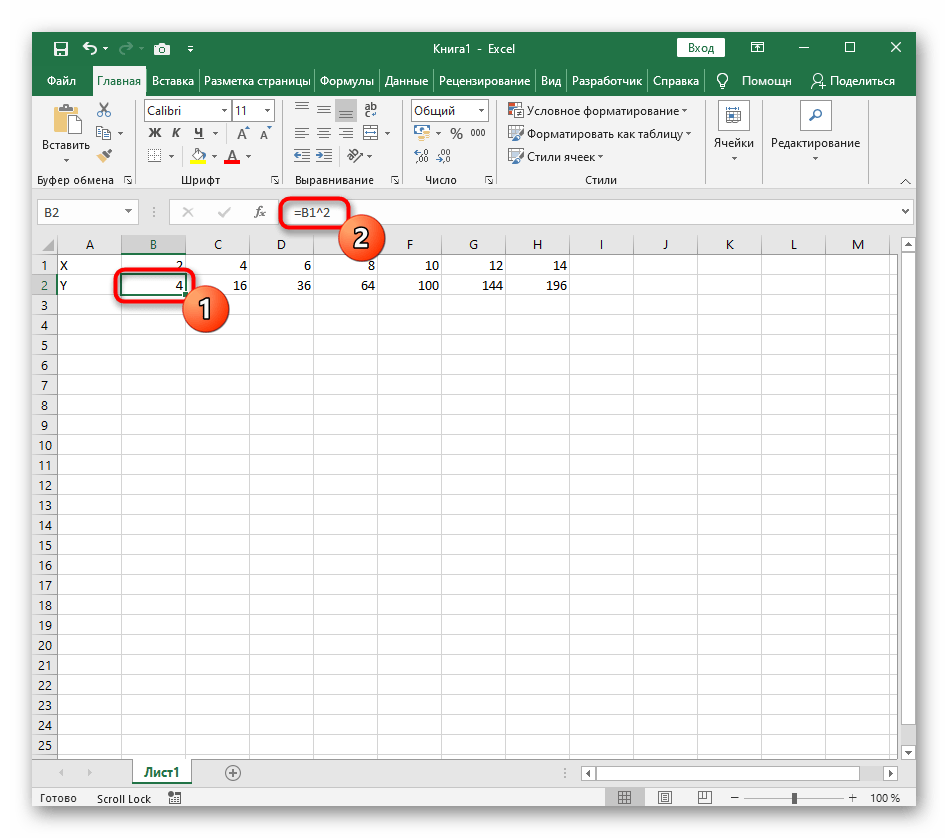
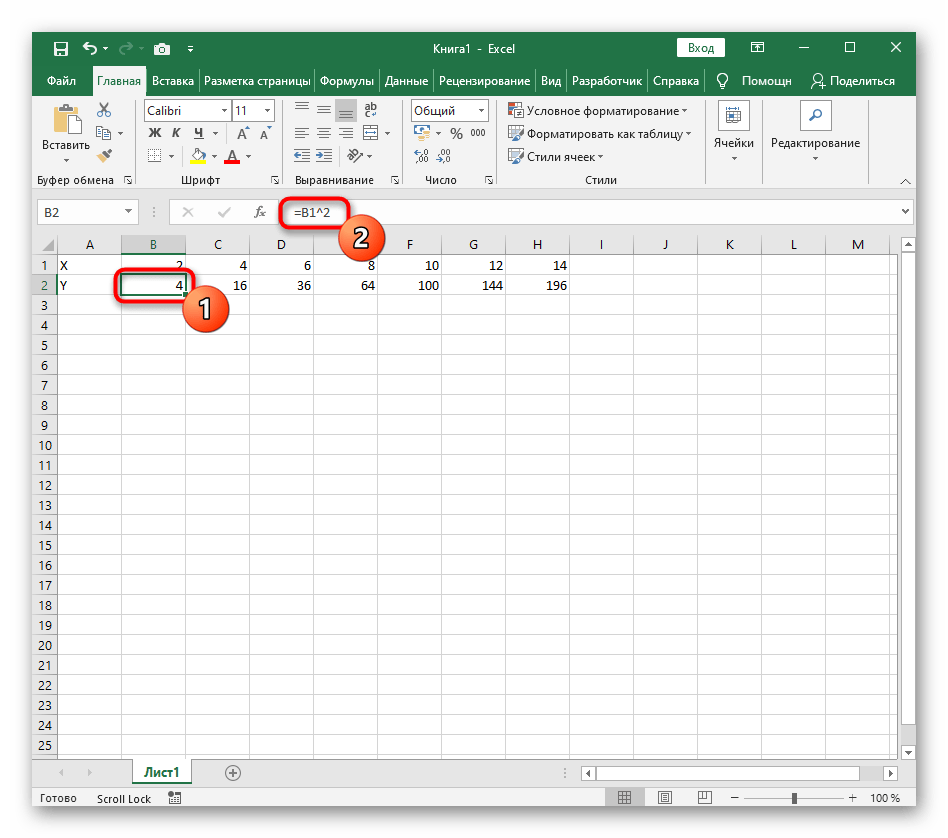
- Нажмите по первой ячейке и впишите
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
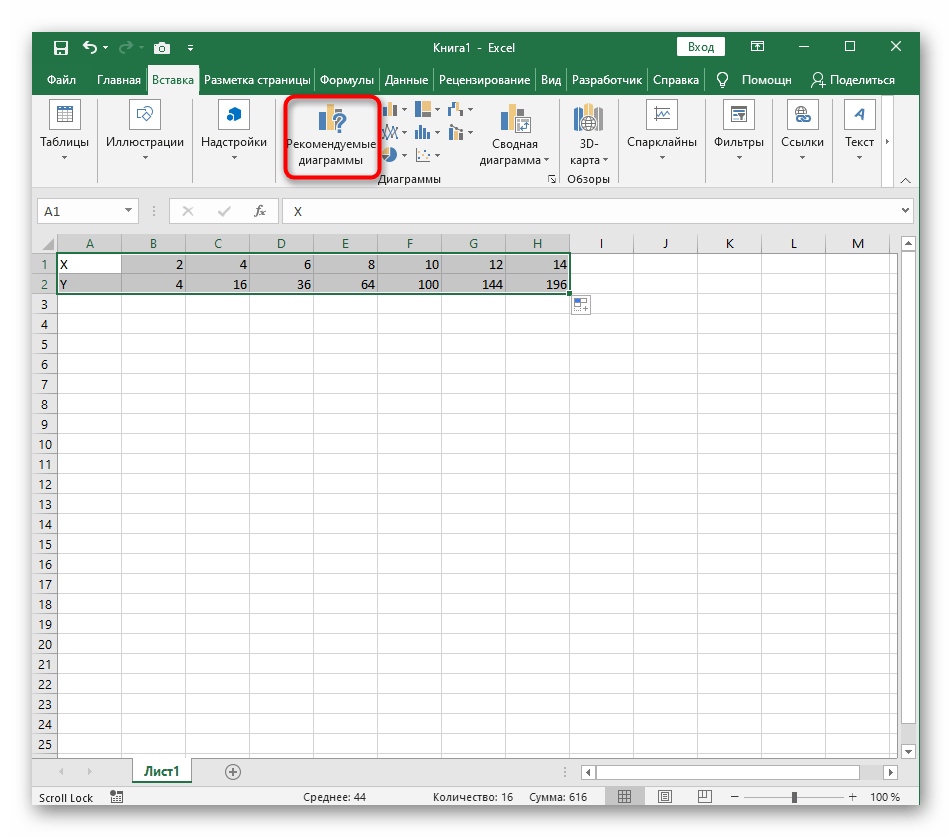
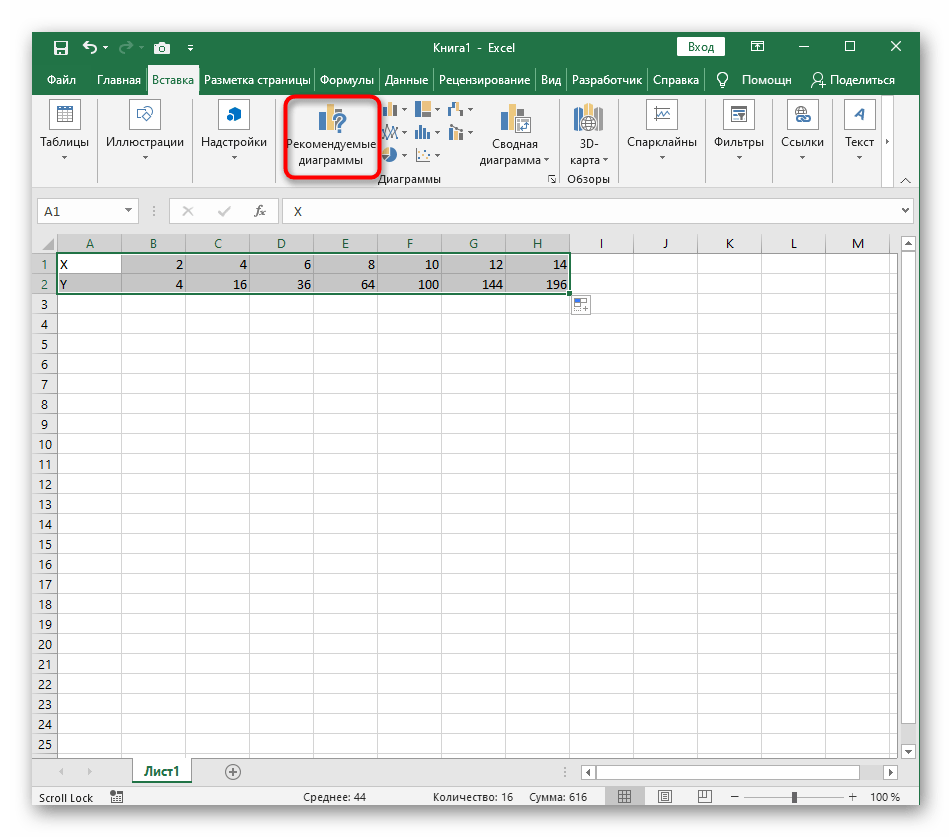
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
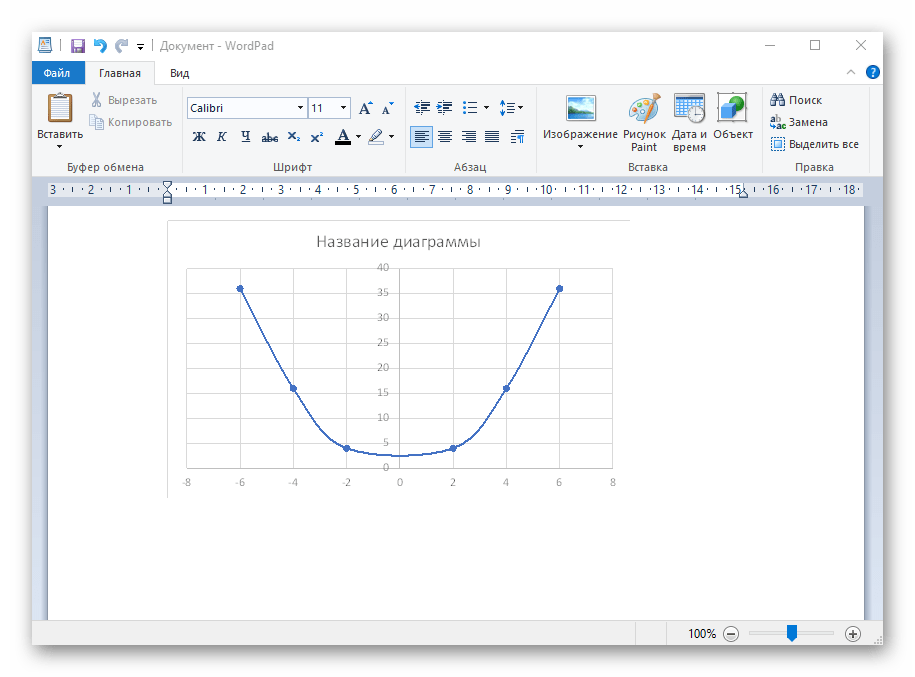
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
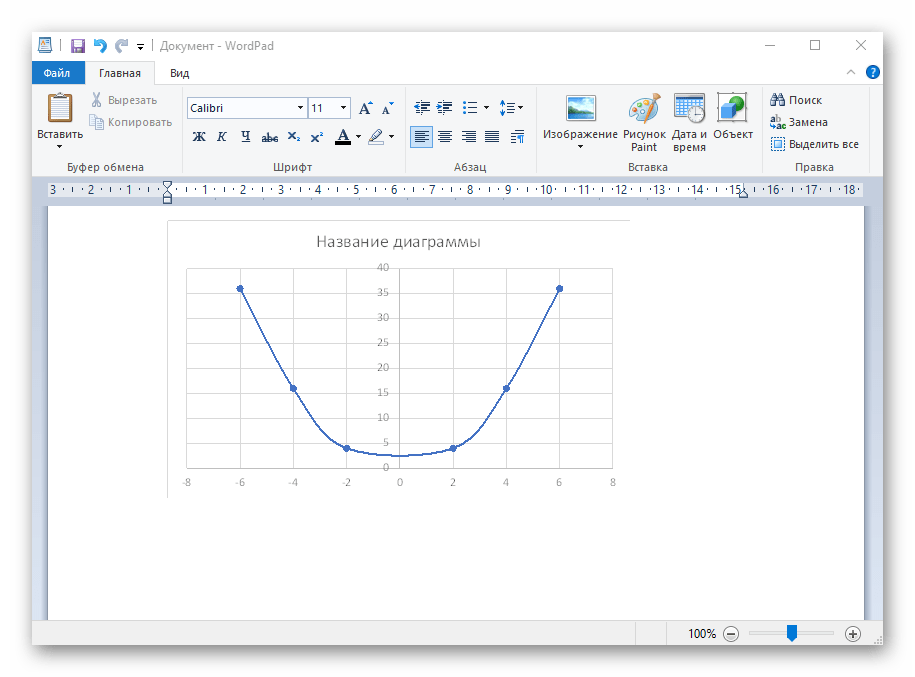
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
В итоге получим диаграмму.
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!



































 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):