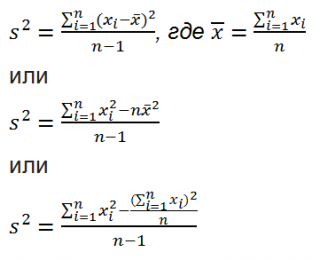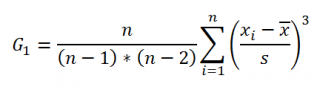Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Применение инструмента «Описательная статистика»
- Вопросы и ответы
Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.
Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
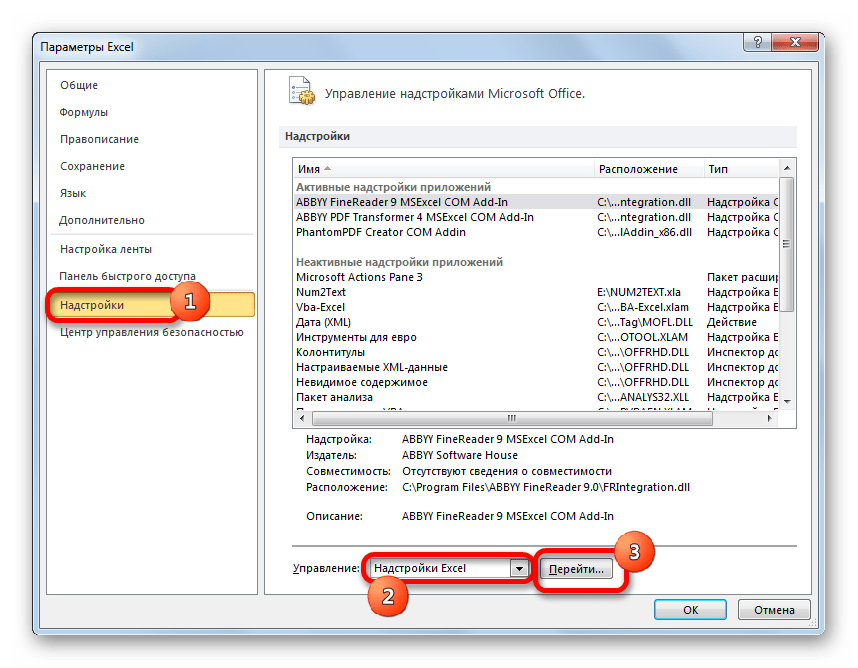
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
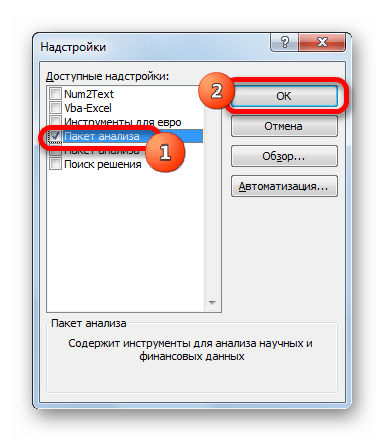
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Применение инструмента «Описательная статистика»
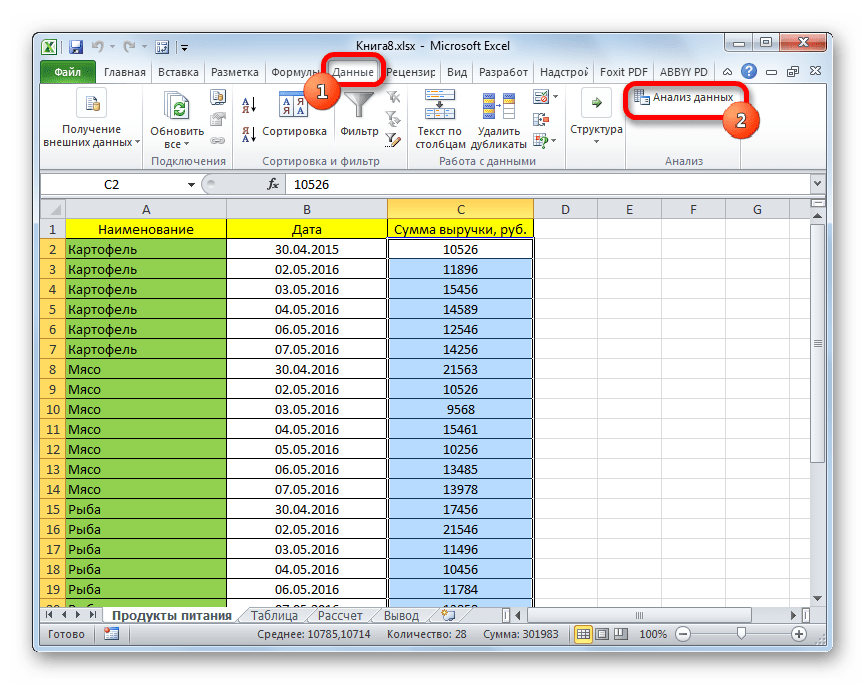
Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.
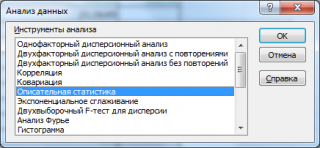
- Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
- Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
- После выполнения данных действий непосредственно запускается окно «Описательная статистика».
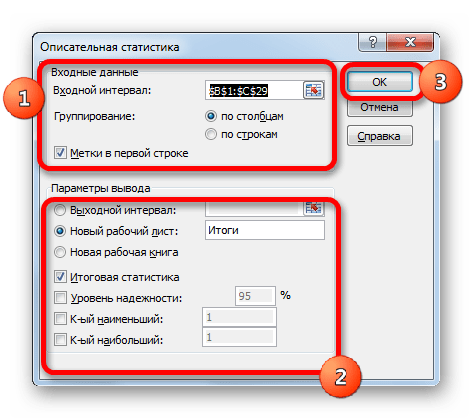
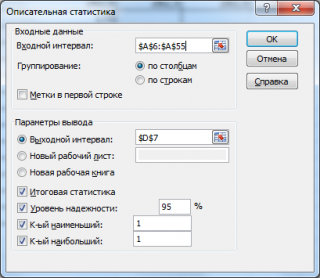
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.
Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».
Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.
Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.
После того, как все указанные данные внесены, жмем на кнопку «OK».
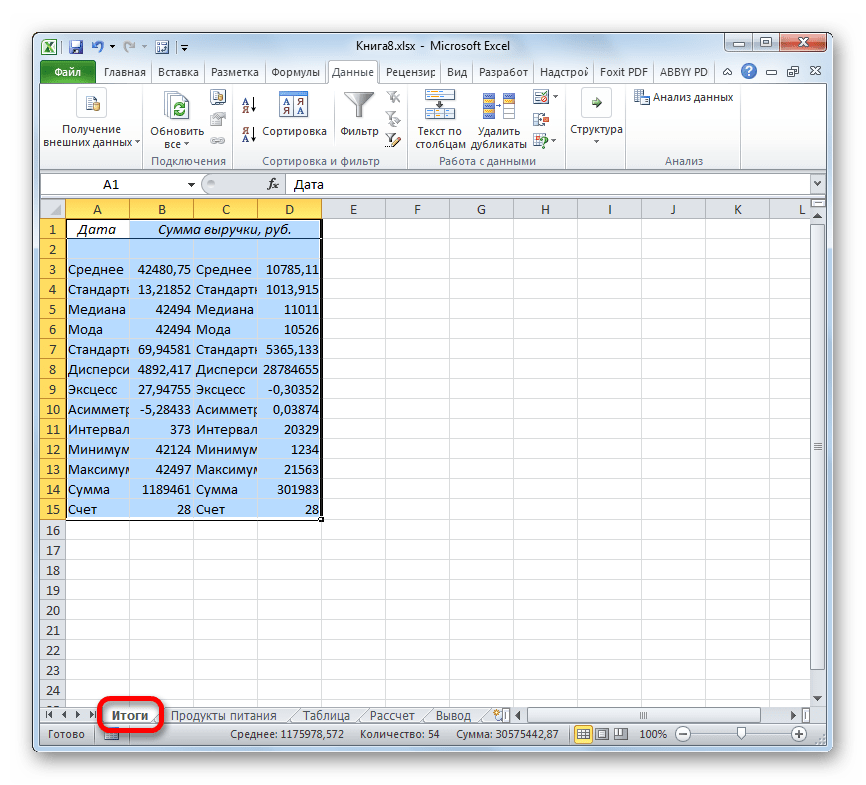
- После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.
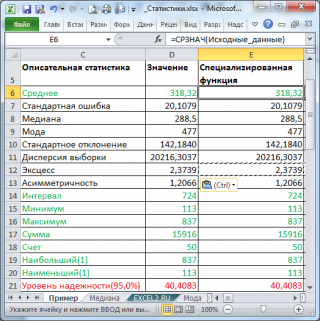
- После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.
Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.
Урок: Статистические функции в Excel
Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.
Еще статьи по данной теме:
Помогла ли Вам статья?
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно,
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
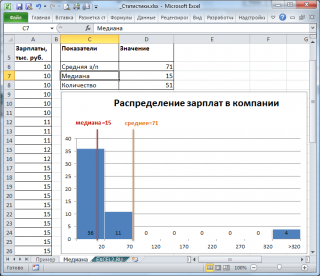
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
МОДА.НСК()
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
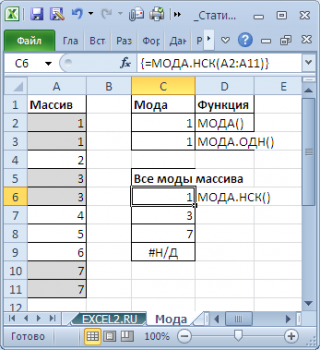
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
, творится, что-то не то. Действительно,
модой
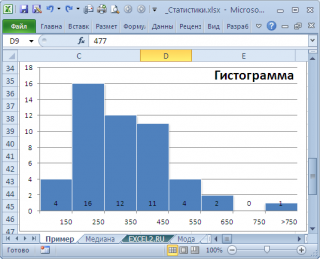
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
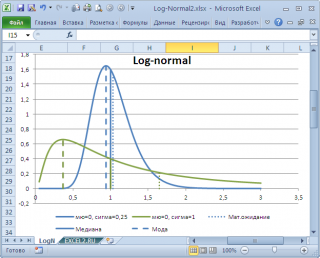
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
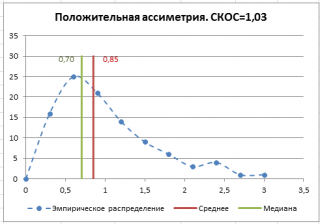
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Содержание
- 1 СРЗНАЧ()
- 2 СРЗНАЧЕСЛИ()
- 3 МАКС()
- 4 МИН()
- 5 НАИБОЛЬШИЙ()
- 6 НАИМЕНЬШИЙ()
- 7 МЕДИАНА()
- 8 МОДА()
- 9 Как создать таблицу в Excel для чайников
- 9.1 Как выделить столбец и строку
- 9.2 Как изменить границы ячеек
- 9.3 Как вставить столбец или строку
- 9.4 Пошаговое создание таблицы с формулами
- 10 Как создать таблицу в Excel: пошаговая инструкция
- 11 Как работать с таблицей в Excel
- 11.1 Выделение всех ячеек одним кликом
- 11.2 Открытие нескольких файлов одновременно
- 11.3 Перемещение по файлам Excel
- 11.4 Добавление новых кнопок на панель быстрого доступа
- 11.5 Диагональная линия в ячейках
- 11.6 Добавление в таблицу пустых строк или столбцов
- 11.7 Скоростное копирование и перемещение информации
- 11.8 Быстрое удаление пустых ячеек
- 11.9 Расширенный поиск
- 11.10 Копирование уникальных записей
- 11.11 Создание выборки
- 11.12 Быстрая навигация с помощью Ctrl и стрелки
- 11.13 Транспонирование информации из столбца в строку
- 11.14 Как скрывать информацию в Excel
- 11.15 Объединение текста с помощью «&»
- 11.16 Изменение регистра букв
- 11.17 Внесение информации с нулями в начале
- 11.18 Ускорение ввода сложных слов
- 11.19 Больше информации
- 11.20 Переименование листа с помощью двойного клика
Функции категории Статистические предназначены в первую очередь для анализа диапазонов ячеек в Excel. С помощью данных функций Вы можете вычислить наибольшее, наименьшее или среднее значение, подсчитать количество ячеек, содержащих заданную информацию, и т.д.
Данная категория содержит более 100 самых различных функций Excel, большая часть из которых предназначена исключительно для статистических расчетов и обычному рядовому пользователю покажется темным лесом. Мы же в рамках этого урока рассмотрим самые полезные и распространенные функции данной категории.
В рамках данной статьи мы не будем затрагивать такие популярные статистические функции Excel, как СЧЕТ и СЧЕТЕСЛИ, для них подготовлен отдельный урок.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
НАИБОЛЬШИЙ()
Возвращает n-ое по величине значение из массива числовых данных. Например, на рисунке ниже мы нашли пятое по величине значение из списка.
Чтобы убедиться в этом, можно отсортировать числа в порядке возрастания:
НАИМЕНЬШИЙ()
Возвращает n-ое наименьшее значение из массива числовых данных. Например, на рисунке ниже мы нашли четвертое наименьшее значение из списка.
Если отсортировать числа в порядке возрастания, то все станет гораздо очевидней:
МЕДИАНА()
Статистическая функция МЕДИАНА возвращает медиану из заданного массива числовых данных. Медианой называют число, которое является серединой числового множества. Если в списке нечетное количество значений, то функция возвращает то, что находится ровно по середине. Если же количество значений четное, то функция возвращает среднее для двух чисел.
Например, на рисунке ниже формула возвращает медиану для списка, состоящего из 14 чисел.
Если отсортировать значения в порядке возрастания, то все становится на много понятней:
МОДА()
Возвращает наиболее часто встречающееся значение в массиве числовых данных.
Если отсортировать числа в порядке возрастания, то все становится гораздо понятней:
Статистическая функция МОДА на данный момент устарела, точнее, устарела ее форма записи. Вместо нее теперь используется функция МОДА.ОДН. Форма записи МОДА также поддерживается в Excel для совместимости.
Как известно, категория Статистические в Excel содержит более 100 самых разноплановых функций. Но, как показывает практика, львиная доля этих функций практически не применяется, а особенно начинающими пользователями. В этом уроке мы постарались познакомить Вас только с самыми популярными статистическими функциями Excel, которые Вы рано или поздно сможете применить на практике. Надеюсь, что данный урок был для Вас полезен. Удачи Вам и успехов в изучении Excel.
Оцените качество статьи. Нам важно ваше мнение:
Программа Microsoft Excel удобна для составления таблиц и произведения расчетов. Рабочая область – это множество ячеек, которые можно заполнять данными. Впоследствии – форматировать, использовать для построения графиков, диаграмм, сводных отчетов.
Работа в Экселе с таблицами для начинающих пользователей может на первый взгляд показаться сложной. Она существенно отличается от принципов построения таблиц в Word. Но начнем мы с малого: с создания и форматирования таблицы. И в конце статьи вы уже будете понимать, что лучшего инструмента для создания таблиц, чем Excel не придумаешь.
Работа с таблицами в Excel для чайников не терпит спешки. Создать таблицу можно разными способами и для конкретных целей каждый способ обладает своими преимуществами. Поэтому сначала визуально оценим ситуацию.
Посмотрите внимательно на рабочий лист табличного процессора:
Это множество ячеек в столбцах и строках. По сути – таблица. Столбцы обозначены латинскими буквами. Строки – цифрами. Если вывести этот лист на печать, получим чистую страницу. Без всяких границ.
Сначала давайте научимся работать с ячейками, строками и столбцами.
Как выделить столбец и строку
Чтобы выделить весь столбец, щелкаем по его названию (латинской букве) левой кнопкой мыши.
Для выделения строки – по названию строки (по цифре).
Чтобы выделить несколько столбцов или строк, щелкаем левой кнопкой мыши по названию, держим и протаскиваем.
Для выделения столбца с помощью горячих клавиш ставим курсор в любую ячейку нужного столбца – нажимаем Ctrl + пробел. Для выделения строки – Shift + пробел.
Как изменить границы ячеек
Если информация при заполнении таблицы не помещается нужно изменить границы ячеек:
- Передвинуть вручную, зацепив границу ячейки левой кнопкой мыши.
- Когда длинное слово записано в ячейку, щелкнуть 2 раза по границе столбца / строки. Программа автоматически расширит границы.
- Если нужно сохранить ширину столбца, но увеличить высоту строки, воспользуемся кнопкой «Перенос текста» на панели инструментов.
Для изменения ширины столбцов и высоты строк сразу в определенном диапазоне выделяем область, увеличиваем 1 столбец /строку (передвигаем вручную) – автоматически изменится размер всех выделенных столбцов и строк.
Примечание. Чтобы вернуть прежний размер, можно нажать кнопку «Отмена» или комбинацию горячих клавиш CTRL+Z. Но она срабатывает тогда, когда делаешь сразу. Позже – не поможет.
Чтобы вернуть строки в исходные границы, открываем меню инструмента: «Главная»-«Формат» и выбираем «Автоподбор высоты строки»
Для столбцов такой метод не актуален. Нажимаем «Формат» — «Ширина по умолчанию». Запоминаем эту цифру. Выделяем любую ячейку в столбце, границы которого необходимо «вернуть». Снова «Формат» — «Ширина столбца» — вводим заданный программой показатель (как правило это 8,43 — количество символов шрифта Calibri с размером в 11 пунктов). ОК.
Как вставить столбец или строку
Выделяем столбец /строку правее /ниже того места, где нужно вставить новый диапазон. То есть столбец появится слева от выделенной ячейки. А строка – выше.
Нажимаем правой кнопкой мыши – выбираем в выпадающем меню «Вставить» (или жмем комбинацию горячих клавиш CTRL+SHIFT+»=»).
Отмечаем «столбец» и жмем ОК.
Совет. Для быстрой вставки столбца нужно выделить столбец в желаемом месте и нажать CTRL+SHIFT+»=».
Все эти навыки пригодятся при составлении таблицы в программе Excel. Нам придется расширять границы, добавлять строки /столбцы в процессе работы.
Пошаговое создание таблицы с формулами
- Заполняем вручную шапку – названия столбцов. Вносим данные – заполняем строки. Сразу применяем на практике полученные знания – расширяем границы столбцов, «подбираем» высоту для строк.
- Чтобы заполнить графу «Стоимость», ставим курсор в первую ячейку. Пишем «=». Таким образом, мы сигнализируем программе Excel: здесь будет формула. Выделяем ячейку В2 (с первой ценой). Вводим знак умножения (*). Выделяем ячейку С2 (с количеством). Жмем ВВОД.
- Когда мы подведем курсор к ячейке с формулой, в правом нижнем углу сформируется крестик. Он указываем на маркер автозаполнения. Цепляем его левой кнопкой мыши и ведем до конца столбца. Формула скопируется во все ячейки.
- Обозначим границы нашей таблицы. Выделяем диапазон с данными. Нажимаем кнопку: «Главная»-«Границы» (на главной странице в меню «Шрифт»). И выбираем «Все границы».
Теперь при печати границы столбцов и строк будут видны.
С помощью меню «Шрифт» можно форматировать данные таблицы Excel, как в программе Word.
Поменяйте, к примеру, размер шрифта, сделайте шапку «жирным». Можно установить текст по центру, назначить переносы и т.д.
Как создать таблицу в Excel: пошаговая инструкция
Простейший способ создания таблиц уже известен. Но в Excel есть более удобный вариант (в плане последующего форматирования, работы с данными).
Сделаем «умную» (динамическую) таблицу:
- Переходим на вкладку «Вставка» — инструмент «Таблица» (или нажмите комбинацию горячих клавиш CTRL+T).
- В открывшемся диалоговом окне указываем диапазон для данных. Отмечаем, что таблица с подзаголовками. Жмем ОК. Ничего страшного, если сразу не угадаете диапазон. «Умная таблица» подвижная, динамическая.
Примечание. Можно пойти по другому пути – сначала выделить диапазон ячеек, а потом нажать кнопку «Таблица».
Теперь вносите необходимые данные в готовый каркас. Если потребуется дополнительный столбец, ставим курсор в предназначенную для названия ячейку. Вписываем наименование и нажимаем ВВОД. Диапазон автоматически расширится.
Если необходимо увеличить количество строк, зацепляем в нижнем правом углу за маркер автозаполнения и протягиваем вниз.
Как работать с таблицей в Excel
С выходом новых версий программы работа в Эксель с таблицами стала интересней и динамичней. Когда на листе сформирована умная таблица, становится доступным инструмент «Работа с таблицами» — «Конструктор».
Здесь мы можем дать имя таблице, изменить размер.
Доступны различные стили, возможность преобразовать таблицу в обычный диапазон или сводный отчет.
Возможности динамических электронных таблиц MS Excel огромны. Начнем с элементарных навыков ввода данных и автозаполнения:
- Выделяем ячейку, щелкнув по ней левой кнопкой мыши. Вводим текстовое /числовое значение. Жмем ВВОД. Если необходимо изменить значение, снова ставим курсор в эту же ячейку и вводим новые данные.
- При введении повторяющихся значений Excel будет распознавать их. Достаточно набрать на клавиатуре несколько символов и нажать Enter.
- Чтобы применить в умной таблице формулу для всего столбца, достаточно ввести ее в одну первую ячейку этого столбца. Программа скопирует в остальные ячейки автоматически.
- Для подсчета итогов выделяем столбец со значениями плюс пустая ячейка для будущего итога и нажимаем кнопку «Сумма» (группа инструментов «Редактирование» на закладке «Главная» или нажмите комбинацию горячих клавиш ALT+»=»).
Если нажать на стрелочку справа каждого подзаголовка шапки, то мы получим доступ к дополнительным инструментам для работы с данными таблицы.
Иногда пользователю приходится работать с огромными таблицами. Чтобы посмотреть итоги, нужно пролистать не одну тысячу строк. Удалить строки – не вариант (данные впоследствии понадобятся). Но можно скрыть. Для этой цели воспользуйтесь числовыми фильтрами (картинка выше). Убираете галочки напротив тех значений, которые должны быть спрятаны.
Если вы никогда раньше не использовали табличный процессор для создания документов, советуем прочитать наше руководство Эксель (Excel) для чайников.
После этого вы сможете создать свой первый табличный лист с таблицами, графиками, математическими формулами и форматированием.
Подробная информация о базовых функциях и возможностях табличного процессора MS Excel.
Описание основных элементов документа и инструкция для работы с ними в нашем материале.
Кстати, чтобы эффективнее работать с таблицами Exel можете ознакомиться с нашим материалом Горячие клавиши Excel — Самые необходимые варианты.
Содержание:
Работа с ячейками. Заполнение и форматирование
Прежде чем приступать к конкретным действиям, необходимо разобраться с базовым элементом любого документа в Excel.
Файл Эксель состоит из одного или нескольких листов, разграфленных на мелкие ячейки.
Ячейка – это базовый компонент любого экселевского отчета, таблицы или графика. В каждой клеточке содержится один блок информации. Это может быть число, дата, денежная сумма, единица измерения или другой формат данных.
Чтобы заполнить ячейку, достаточно просто кликнуть по ней указателем и ввести нужную информацию.
Чтобы отредактировать ранее заполненную ячейку, нажмите на неё двойным кликом мышки.
Рис. 1 – пример заполнения ячеек
Каждая клеточка на листе имеет свой уникальный адрес. Таким образом, с ней можно проводить расчеты или другие операции.
При нажатии на ячейку в верхней части окна появится поле с ее адресом, названием и формулой (если клеточка учуствует в каких-либо расчетах).
Выберем ячейку «Доля акций». Адрес её расположения – А3. Эта информация указана в открывшейся панели свойств. Также мы можем увидеть содержимое.
Формул у этой клетки нет, поэтому они не показываются.
Больше свойств ячейки и функций, которые можно задействовать по отношению к ней, доступны в контекстном меню.
Кликните на клеточку правой клавишей манипулятора.
Откроется меню, с помощью которого можно отформатировать ячейку, провести анализ содержимого, присвоить другое значение и прочие действия.
Рис. 2 – контекстное меню ячейки и ее основные свойства
вернуться к меню ↑ Сортировка данных
Часто пользователи сталкиваются с задачей сортировки данных на листе в Эксель. Эта функция помогает быстро выбрать и просмотреть только нужные данные из всей таблицы.
Перед вами уже заполненная таблица (как её создать разберемся дальше в статье). Представьте, что вам нужно отсортировать данные за январь по возрастанию.
Как бы вы это сделали? Банальное перепечатывание таблицы – это лишняя работа, к тому же, если она объемная, делать этого никто не будет.
Для сортировки в Excel есть специально отведенная функция. От пользователя требуется только:
- Выделить таблицу или блок информации;
- Открыть кладку «Данные»;
- Кликнуть на иконку «Сортировка»;
Рис. 3 – вкладка «Данные»
- В открывшемся окошке выберите колонку таблицы, над которой будем проводить действия (Январь).
- Далее тип сортировки (мы выполняем группировку по значению) и, наконец, порядок – по возрастанию.
- Подтвердите действие, нажав на «ОК».
Рис. 4 – настройка параметров сортировки
Произойдет автоматическая сортировка данных:
Рис. 5 – результат сортировки цифр в столбце «Январь»
Аналогичным образом можно проводить сортировку по цвету, шрифту и другим параметрам.
вернуться к меню ↑ Математические расчеты
Главное преимущество Excel – возможность автоматического проведения расчетов в процессе заполнения таблицы. К примеру, у нас есть две ячейки со значениями 2 и 17. Как в третью ячейку вписать их результат, не делая расчеты самостоятельно?
Для этого, вам необходимо кликнуть на третью ячейку, в которую будет вписан конечный результат вычислений.
Затем нажмите на значок функции f(x), как показано на рисунке ниже.
В открывшемся окошке выберите действие, которое хотите применить. СУММ – это сумма, СРЗНАЧ – среднее значение и так далее.
Полный список функций и их наименований в редакторе Excel можно найти на официальном сайте компании Microsoft.
Нам нужно найти сумму двух ячеек, поэтому нажимаем на «СУММ».
Рис. 6 – выбор функции «СУММ»
В окне аргументов функции есть два поля: «Число 1» и «Число 2». Выберите первое поле и кликните мышкой на ячейку с цифрой «2».
Её адрес запишется в строку аргумента.
Кликните на «Число 2» и нажмите на ячейку с цифрой «17». Затем подтвердите действие и закройте окно.
Если необходимо выполнить математические действия с тремя или большим количеством клеточек, просто продолжайте вводить значения аргументов в поля «Число 3», «Число 4» и так далее.
Если в дальнейшем значение суммируемых ячеек будет изменяться, их сумма будет обновляться автоматически.
Рис. 7 – результат выполнения подсчетов
вернуться к меню ↑ Создание таблиц
В экселевских таблицах можно хранить любые данные.
С помощью функции быстрой настройки и форматирования, в редакторе очень просто организовать систему контроля личного бюджета, список расходов, цифровые данные для отчетности и прочее.
Таблицы в Excel имеют преимущество перед аналогичной опцией в Word и других офисных программах.
Здесь у вас есть возможность создать таблицу любой размерности. Данные заполняются легко. Присутствует панель функций для редактирования содержимого.
К тому же, готовую таблицу можно интегрировать в файл docx с помощью обычной функции копирование-вставка.
Чтобы создать таблицу, следуйте инструкции:
- Откройте вкладку «Вставка». В левой части панели опций выберите пункт «Таблица». Если вам необходимо провести сведение каких-либо данных, выбирайте пункт «Сводная таблица»;
- С помощью мышки выделите место на листе, которое будет отведено для таблицы. А также вы можете ввести расположение данных в окно создания элемента;
- Нажмите ОК, чтобы подтвердить действие.
Рис. 8 – создание стандартной таблицы
Чтобы отформатировать внешний вид получившейся таблички, откройте содержимое конструктора и в поле «Стиль» кликните на понравившийся шаблон.
При желании, можно создать собственный вид с другой цветовой гаммой и выделением ячеек.
Рис. 9 – форматирование таблицы
Результат заполнения таблицы данными:
Рис. 10 – заполненная таблица
Для каждой ячейки таблицы также можно настроить тип данных, форматирование и режим отображения информации. Окно конструктора вмещает в себя все необходимые опции для дальнейшей конфигурации таблички, исходя из ваших требований.
Читайте также:
вернуться к меню ↑ Добавление графиков/диаграмм
Для построения диаграммы или графика требуется наличие уже готовой таблички, ведь графические данные будут основываться именно на информации, взятой из отдельных строк или ячеек.
Чтобы создать диаграмму/график, нужно:
- Полностью выделить таблицу. Если графический элемент нужно создать только для отображения данных определенных ячеек, выделите только их;
- Откройте вкладку вставки;
- В поле рекомендуемых диаграмм выберите иконку, которая, по вашему мнению, наилучшим образом визуально опишет табличную информацию. В нашем случае, это объемная круговая диаграмма. Поднесите к иконке указатель и выберите внешний вид элемента;
Рис. 11 – выбор типа используемой диаграммы
- Кликните на необходимую форму. На листе автоматически отобразится уже заполненная диаграмма:
Рис. 12 – результат добавление диаграммы
Если нужно изменить внешний вид получившейся визуализации, просто кликните по ней два раза.
Произойдёт автоматическое перенаправление в окно конструктора.
С его помощью можно применить другой стиль к диаграмме, изменить её тип, цветовую гамму, формат отображения данных, добавить новые элементы и провести их настройку.
Аналогичным образом можно создать точечные графики, линейные диаграммы и схемы зависимости элементов таблицы.
Все полученные графические элементы также можно добавить в текстовые документы Ворд.
В табличном редакторе Excel присутствует множество других функций, однако, для начальной работы будет достаточно и приемов, которые описаны в этой статье. В процессе создания документа многие пользователи самостоятельно осваивают более расширенные опции. Это происходит благодаря удобному и понятному интерфейсу последних версий программы.
Читайте также:
Тематические видеоролики:
Эксель (Excel) для чайников: работа с таблицами, графиками, сортировкой данных и математическими расчетами
Проголосовать
Пользуетесь ли вы Excel? Мы выбрали 20 советов, которые помогут вам узнать его получше и оптимизировать свою работу с ним.
Выпустив Excel 2010, Microsoft чуть ли не удвоила функциональность этой программы, добавив множество улучшений и нововведений, многие из которых не сразу заметны. Неважно, опытный вы пользователь или новичок, найдется немало способов упростить работу с Excel. О некоторых из них мы сегодня расскажем.
Выделение всех ячеек одним кликом
Все ячейки можно выделить комбинацией клавиш Ctrl + A, которая, кстати, работает и во всех других программах. Однако есть более простой способ выделения. Нажав на кнопку в углу листа Excel, вы выделите все ячейки одним кликом.
Открытие нескольких файлов одновременно
Вместо того чтобы открывать каждый файл Excel по отдельности, их можно открыть вместе. Для этого выделите файлы, которые нужно открыть, и нажмите Enter.
Перемещение по файлам Excel
Когда у вас открыто несколько книг в Excel, между ними можно легко перемещаться с помощью комбинации клавиш Ctrl + Tab. Эта функция также доступна по всей системе Windows, и ее можно использовать во многих приложениях. К примеру, для переключения вкладок в браузере.
Добавление новых кнопок на панель быстрого доступа
Стандартно в панели быстрого доступа Excel находятся 3 кнопки. Вы можете изменить это количество и добавить те, которые нужны именно вам.
Перейдите в меню «Файл» ⇒ «Параметры» ⇒ «Панель быстрого доступа». Теперь можно выбрать любые кнопки, которые вам нужны.
Диагональная линия в ячейках
Иногда бывают ситуации, когда нужно добавить в таблицу диагональную линию. К примеру, чтобы разделить дату и время. Для этого на главной странице Excel нажмите на привычную иконку границ и выберите «Другие границы».
Добавление в таблицу пустых строк или столбцов
Вставить одну строку или столбец достаточно просто. Но что делать, если их нужно вставить гораздо больше? Выделите нужное количество строк или столбцов и нажмите «Вставить». После этого выберите место, куда нужно сдвинуться ячейкам, и вы получите нужное количество пустых строк.
Скоростное копирование и перемещение информации
Если вам нужно переместить любую информацию (ячейку, строку, столбец) в Excel, выделите ее и наведите мышку на границу, чтобы изменился указатель. После этого переместите информацию в то место, которое вам нужно. Если необходимо скопировать информацию, сделайте то же самое, но с зажатой клавишей Ctrl.
Быстрое удаление пустых ячеек
Пустые ячейки — это бич Excel. Иногда они появляются просто из ниоткуда. Чтобы избавиться от них всех за один раз, выделите нужный столбец, перейдите на вкладку «Данные» и нажмите «Фильтр». Над каждым столбцом появится стрелка, направленная вниз. Нажав на нее, вы попадете в меню, которое поможет избавиться от пустых полей.
Расширенный поиск
Нажав Ctrl + F, мы попадаем в меню поиска, с помощью которого можно искать любые данные в Excel. Однако его функциональность можно расширить, используя символы «?» и «*». Знак вопроса отвечает за один неизвестный символ, а астериск — за несколько. Их стоит использовать, если вы не уверены, как выглядит искомый запрос.
Если же вам нужно найти вопросительный знак или астериск и вы не хотите, чтобы вместо них Excel искал неизвестный символ, то поставьте перед ними «~».
Копирование уникальных записей
Уникальные записи могут быть полезными, если вам нужно выделить в таблице неповторяющуюся информацию. К примеру, по одному человеку каждого возраста. Для этого выберите нужный столбец и нажмите «Дополнительно» слева от пункта «Фильтр». Выберите исходный диапазон (откуда копировать) и диапазон, в который нужно поместить результат. Не забудьте поставить галочку.
Создание выборки
Если вы делаете опрос, в котором могут участвовать только мужчины от 19 до 60, вы легко можете создать подобную выборку с помощью Excel. Перейдите в пункт меню «Данные» ⇒ «Проверка данных» и выберите необходимый диапазон или другое условие. Вводя информацию, которая не подходит под это условие, пользователи будут получать сообщение, что информация неверна.
Быстрая навигация с помощью Ctrl и стрелки
Нажимая Ctrl + стрелка, можно перемещаться в крайние точки листа. К примеру, Ctrl + ⇓ перенесет курсор в нижнюю часть листа.
Транспонирование информации из столбца в строку
Довольно полезная функция, которая нужна не так уж и часто. Но если она вдруг понадобится, вряд ли вы будете транспонировать по одной. Для транспонирования в Excel есть специальная вставка.
Скопируйте диапазон ячеек, который нужно транспонировать. После этого кликните правой кнопкой на нужное место и выберите специальную вставку.
Как скрывать информацию в Excel
Не знаю, зачем это может пригодиться, но тем не менее такая функция в Excel есть. Выделите нужный диапазон ячеек, нажмите «Формат» ⇒ «Скрыть или отобразить» и выберите нужное действие.
Объединение текста с помощью «&»
Если вам нужно объединить текст из нескольких ячеек в одну, необязательно использовать сложные формулы. Достаточно выбрать ячейку, в которой будет соединен текст, нажать «=» и последовательно выбрать ячейки, ставя перед каждой символ «&».
Изменение регистра букв
С помощью определенных формул можно менять регистр всей текстовой информации в Excel. Функция «ПРОПИСН» делает все буквы прописными, а «СТРОЧН» — строчными. «ПРОПНАЧ» делает прописной только первую букву в каждом слове.
Внесение информации с нулями в начале
Если вы введете в Excel число 000356, то программа автоматически превратит его в 356. Если вы хотите оставить нули в начале, поставьте перед числом апостроф «’».
Ускорение ввода сложных слов
Если вы часто вводите одни и те же слова, то обрадуетесь, узнав, что в Excel есть автозамена. Она очень похожа на автозамену в смартфонах, поэтому вы сразу поймете, как ей пользоваться. С ее помощью можно заменить повторяющиеся конструкции аббревиатурами. К примеру, Екатерина Петрова — ЕП.
Больше информации
В правом нижнем углу можно следить за различной информацией. Однако мало кто знает, что, нажав туда правой кнопкой мыши, можно убрать ненужные и добавить нужные строки.
Переименование листа с помощью двойного клика
Это самый простой способ переименовать лист. Просто кликните по нему два раза левой кнопкой мыши и введите новое название.
Часто ли вы пользуетесь Excel? Если да, то у вас наверняка есть свои секреты работы с этой программой. Делитесь ими в комментариях.
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html
Расчет процентного прироста аналогичен. Допустим, наше первое измерение — 129, а второе — 246. Каков процент увеличения?
Для начала вам нужно найти необработанное увеличение, поэтому вычтите начальное значение из второго значения. В нашем случае мы будем использовать = 246-129, чтобы получить результат 117.
Теперь возьмите полученное значение (необработанное изменение) и разделите его на исходное измерение. В нашем случае это = 117/129 . Это дает нам десятичное изменение 0,906. Вы также можете получить всю эту информацию в одной формуле, например:
Используйте тот же процесс, что и выше, чтобы преобразовать это в процент, и вы увидите, что у нас есть 91-процентное изменение. Сделайте быструю проверку: 117 почти равно 129, так что это имеет смысл. Если бы мы рассчитали значение изменения 129, процентное изменение составило бы 100 процентов.
Как рассчитать среднее (среднее) в Excel
Одна из самых полезных встроенных функций рассчитывает среднее (среднее) из набора чисел. Если вы раньше не использовали функцию Excel, вы будете поражены тем, насколько это просто. Просто введите имя функции, выберите ячейки, к которым вы хотите применить ее, и нажмите Enter.
В нашем примере у нас есть ряд измерений, из которых нам нужно среднее значение. Мы нажмем на новую ячейку и наберем = AVERAGE ( затем с помощью мыши выберите соответствующие ячейки (вы также можете ввести диапазон ячеек, если хотите). Закройте скобки с помощью a ), и вы получите формула, которая выглядит следующим образом: = СРЕДНИЙ (B4: B16)
Нажмите Enter , и вы получите среднее значение! Это все, что нужно сделать.
Как рассчитать T-тест студента в Excel
T- тест Стьюдента вычисляет шансы, что две выборки были получены из одной популяции. Урок статистики выходит за рамки этой статьи, но вы можете прочитать больше о различных типах студенческих t- тестов с помощью этих бесплатных ресурсов для изучения статистики. (Статистика Ад — мой личный фаворит).
Короче говоря, значение P, полученное из t- теста Стьюдента, скажет вам, есть ли существенная разница между двумя наборами чисел.
Допустим, у вас есть два измерения из одной группы, и вы хотите увидеть, отличаются ли они. Скажем, вы взвесили группу участников, попросили их пройти персональное обучение, а затем снова взвесили их. Это называется парным t- тестом, и мы начнем с этого.
Функция Excel T.TEST — это то, что вам нужно здесь. Синтаксис выглядит так:
=T.TEST(array1, array2, tails, type) массив1 и массив2 — это группы чисел, которые вы хотите сравнить. Аргумент tails должен быть установлен в «1» для одностороннего теста и «2» для двустороннего теста.
Аргумент типа может быть установлен в «1», «2» или «3». Мы установим его в «1» для этого примера, потому что именно так мы сообщаем Excel, что проводим парное t- тестирование.
Вот как будет выглядеть формула для нашего примера:
Теперь мы просто нажимаем Enter, чтобы получить наш результат! Важно помнить, что этот результат является значением P. В большинстве полей значение P меньше 0,05 указывает на значительный результат.
Основы теста одинаковы для всех трех типов. Как уже упоминалось, «1» в поле типа создает парный t- тест. «2» запускает тест с двумя выборками с одинаковой дисперсией, а «3» — тест с двумя выборками с неравной дисперсией. (При использовании последнего Excel запускает t- тест Уэлча.)
Как рассчитать стандартное отклонение в Excel
Вычислить стандартное отклонение в Excel так же просто, как вычислить среднее значение. На этот раз вы будете использовать функции STDEV.S или STDEV.P.
STDEV.S следует использовать, когда ваши данные являются выборкой населения. STDEV.P, с другой стороны, работает, когда вы рассчитываете стандартное отклонение для всей совокупности. Обе эти функции игнорируют текстовые и логические значения (если вы хотите включить их, вам понадобится STDEVA или STDEVPA).
Чтобы определить стандартное отклонение для набора, просто введите = STDEV.S () или = STDEV.P () и вставьте диапазон чисел в скобки. Вы можете нажать и перетащить или ввести диапазон.
В конце у вас будет число: это ваше стандартное отклонение.
Как рассчитать стандартную ошибку в Excel
Стандартная ошибка тесно связана со стандартным отклонением. И хотя в Excel нет функции для ее вычисления, вы можете быстро найти ее с минимальными усилиями.
Чтобы найти стандартную ошибку, разделите стандартное отклонение на квадратный корень из n , количество значений в вашем наборе данных. Вы можете получить эту информацию с помощью одной формулы:
=STDEV.S(array1)/SQRT(COUNT(array1))
Если вы используете текстовые или логические значения в вашем массиве, вам нужно будет использовать COUNTA.
Вот как мы можем рассчитать стандартную ошибку с нашим набором данных:
Использование Excel для статистики: не очень хорошо, но выполнимо
Можете ли вы использовать Excel для статистики и сложных расчетов? Да. Будет ли оно работать так же хорошо, как специализированное статистическое программное обеспечение, такое как SPSS или SAS? Нет. Но вы все равно можете рассчитывать проценты, средние значения, стандартные отклонения и даже t- тесты.
Когда вам нужен быстрый расчет, и ваши данные находятся в Excel, вам не нужно импортировать их в другое программное обеспечение. И это сэкономит вам время. Вы также можете использовать функцию поиска целей в Excel, чтобы еще быстрее решать уравнения. решение задач
Не забудьте поместить свои данные в эстетически привлекательные и информативные графы. прежде чем показывать его своим коллегам! И это также поможет освоить операторы IF в Excel. операторы операторы