1. Построение вариационного ряда
Нужно выделить ячейки содержащие результаты эксперимента, и воспользоваться операцией сортировка по возрастанию (либо с панели инструментов, либо через главное меню Данные>Сортировка), и в появившемся окне сообщения – «обнаружены данные выходящие за пределы выделенного диапазона» выбрать действие – «сортировать в пределах указанного выделения»
2. Построение группировочного статистического ряда
Для вычисления абсолютной частоты нужна статистическая функция ЧАСТОТА. При её использовании нужно выполнить следующие действия:
а) выделить весь диапазон ячеек, в которых будет располагаться результат подсчёта частот (т.е. это ячейки под заголовком Абсолютная частота в количестве равном числу промежутков)
b) не снимая выделения, поставить курсор в строку формул и нажать на кнопку вставка функции (чуть левее курсора) или Главное меню – вставка – формула.
с) выбрать функцию ЧАСТОТА
d) ввести Массив_данных – диапазон, содержащий элементы выборки (в файле 2.xls это ячейки) B2:B101
e) ввести Массив_интервалов – диапазон ячеек под заголовком Начало промежутка начиная со строчки, соответствующей промежутку под номером 2 до строчки, соответствующей последнему промежутку.
f) нажмите на кнопку ОК и после закрытия окна для ввода аргументов функции ЧАСТОТА поставьте курсор обратно в строку формул.
g) Нажмите на три кнопки Ctrl+Shift+Enter (сначала на первые две, а потом, не отпуская их, нажмите на Enter).
Примечание. Формулу вычисления абсолютной частоты необходимо ввести как формулу массива. Нажатие комбинации клавиш CTRL+SHIFT+ENTER позволяет определить формулу как формулу массива. Если формула не будет введена как формула массива, единственное значение будет равно 1.
В результате изначально выделенный диапазон будет содержать абсолютные частоты попадания во все промежутка. Проверьте, что сумма всех абсолютных частот равна общему числу элементов выборки (100).
3. Построение гистограммы группировочного статистического ряда
Задание
Для
случайной выборки объемом n=50
с несовпадающими числами выполнить
следующую последовательность действий:
1.Вывести
на лист Excel
исходные статистические данные.
2. Построить
вариационный ряд.
3. Вычислить
статистические характеристики.
4. Построить
интервальный статистический ряд.
5.Построить
гистограмму частот.
6. Составить
статистическую функцию распределения
статистического ряда.
7.
Составить и постоить статистическую
функцию распределения группированного
статистического ряда.
В качестве примера
рассмотрим следующую выборку
Порядок выполнения работы
1.Ввод исходных статистических данных.
Вводим данные в
первый столбец таблицы (рис.1).
рис.1
2. Построение вариационного ряда.
Производим
сортировку данных в порядке возрастания.
Для этого:
а) выделяем первый
столбец;
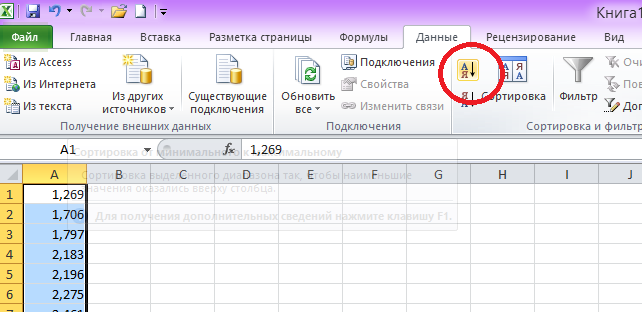
б)
на ленте
во вкладке «Данные» выбираем «Сортировка
и фильтр» (рис.2)
рис. 2
3. Вычисление статистических характеристик.
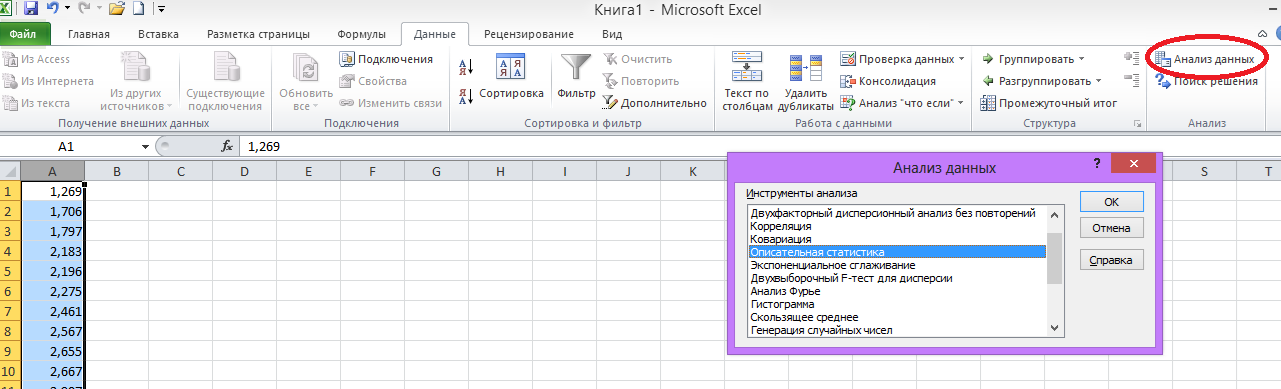
На ленте
во вкладке «Данные» выбираем «Анализ
данных» меню «Описательная статистика»
нажимаем ОК.
рис. 3
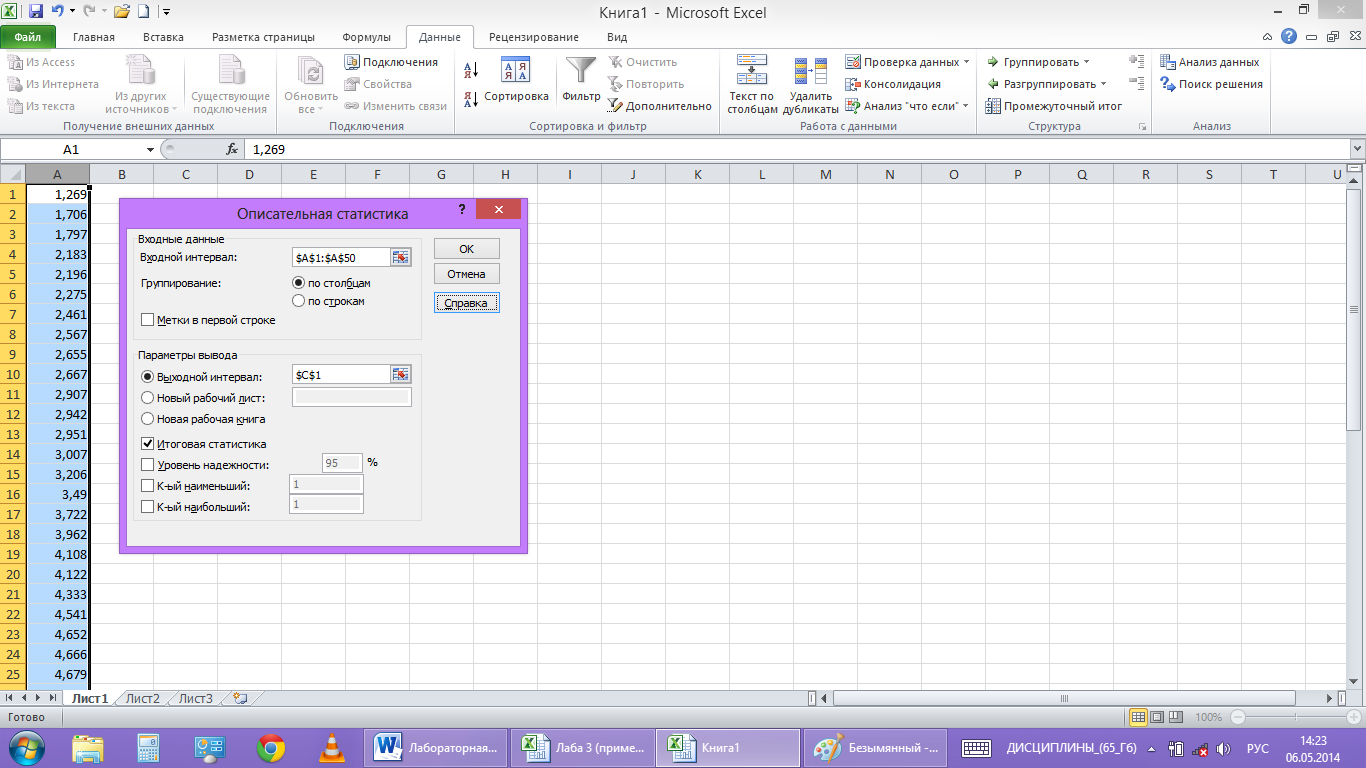
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
а в пункте «Выходной интервал» обозначим
первую ячейку для записи результаов
$C$1.
Ставим флажок напротив пункта «Итоговая
статистика» и нажимаем ОК.(рис.4)
рис. 4
На
рабочем листе появляется таблица с
вычисленными значениями числовых
характеристик выборки (рис.5)
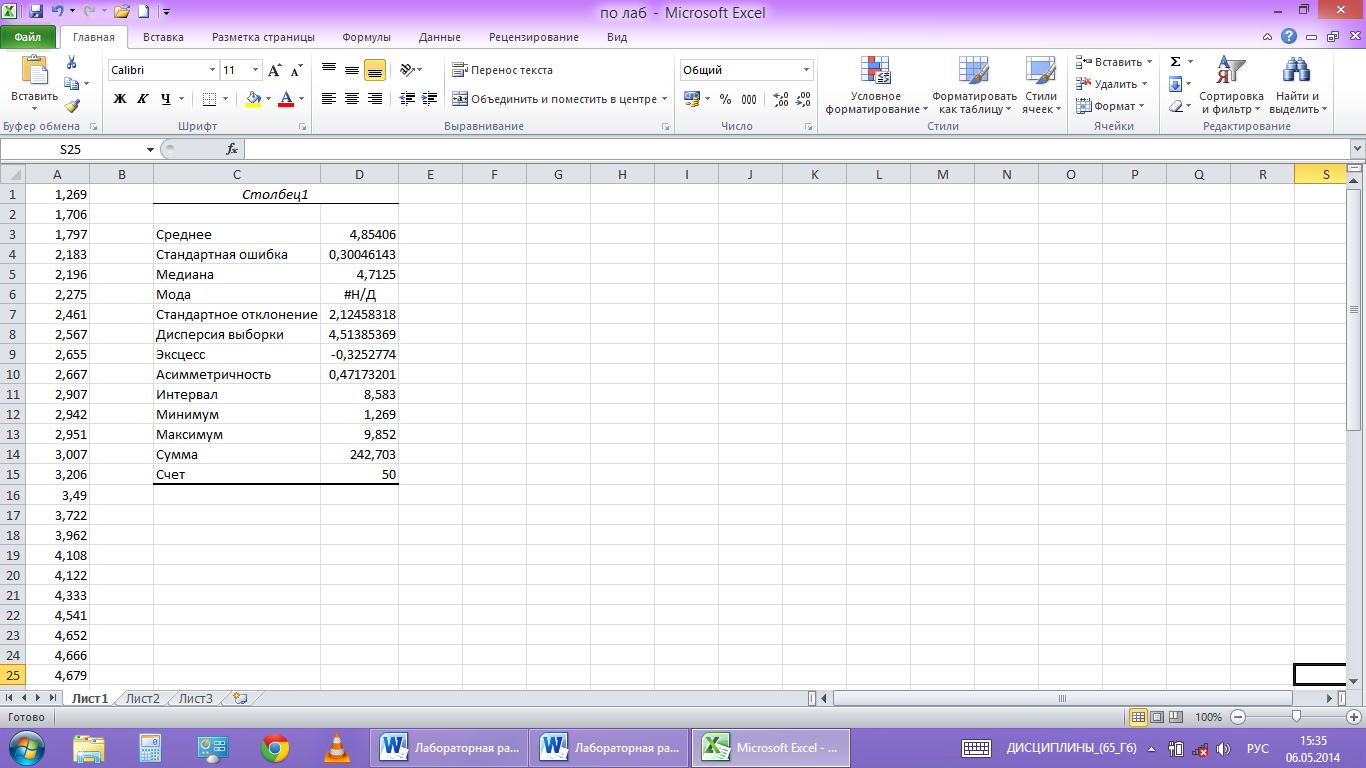
рис. 5
Здесь
«Среднее»означает математическое
ожидание выборки, а «Стандартная ошибка»
— погрешность ее значения. «Дисперсия
выборки» означает исправленную выборочную
дисперсию, а «Стандартное отклонение»
— исправленное среднее квадратичное
отклонение. Положительное значение
«Асимметричности» означает, что «длинная
часть» кривой лежит правее моды.
Отрицательное значение «Эксцесса»
означает, что кривая имеет более низкую
и «плоскую» вершину, чем нормальная
кривая. «Интервал» равен разности
Xmax−Xmin.
«Сумма»
дает результат суммирования всех
элементов выборки. «Счет» задает общее
число элементов выборки.
4. Построение интервального статистического ряда.
Длину интервала
группировки определяем по формуле
Необходимые данные
имеем в таблице: Xmax
– в ячейке D13,
Xmin–
в ячейке D12,
число элементов выборки n
— в ячейке D15.
В ячейку С16 вводим
слово «Интервал», в ячейку D16
вводим формулу
в ячейке D16
появится значение числа h.
В ячейку C17
вводим букву h.
В ячейку D17
вводим формулу
В ячейке
D17
получаем округленное до одного знака
после запятой значение интерала h.
Проведем формирование
интервалов. Для этого от Xmin
отступим влево примерно на h/2
и получим начальную точку отсчета.
Последовательно прибавляя к ней целое
число отрезков h,
получим все граничные точки интервалов.
В ячейку
F1
вводим формулу
В этой
ячейке появляется значение начальной
точки отсчета. В ячейку F2
вводим формулу
В этой
ячейке появляется значение второй
граничной точки первого интервала.
Возвращаемся в ячейку F2,
ставим курсор в правый нижний угол рамки
и двигаем его вниз, не отпуская левую
кнопку мыши. В результате такой процедуры
(протяжка) столбец F
заполнят граничные точки интервалов.
Самый нижний интервал должен включать
Xmax
(рис.6).
Проведем подсчет
числа вариант, попавших в каждый интервал,
определим относительные частоты и
серединные точки этих интервалов.
Для
этого на ленте во вкладке «Данные»
выбираем «Анализ данных» меню
«Гистограмма». (рис.
7)
|
|
|
|
рис. 6 |
рис. 7 |
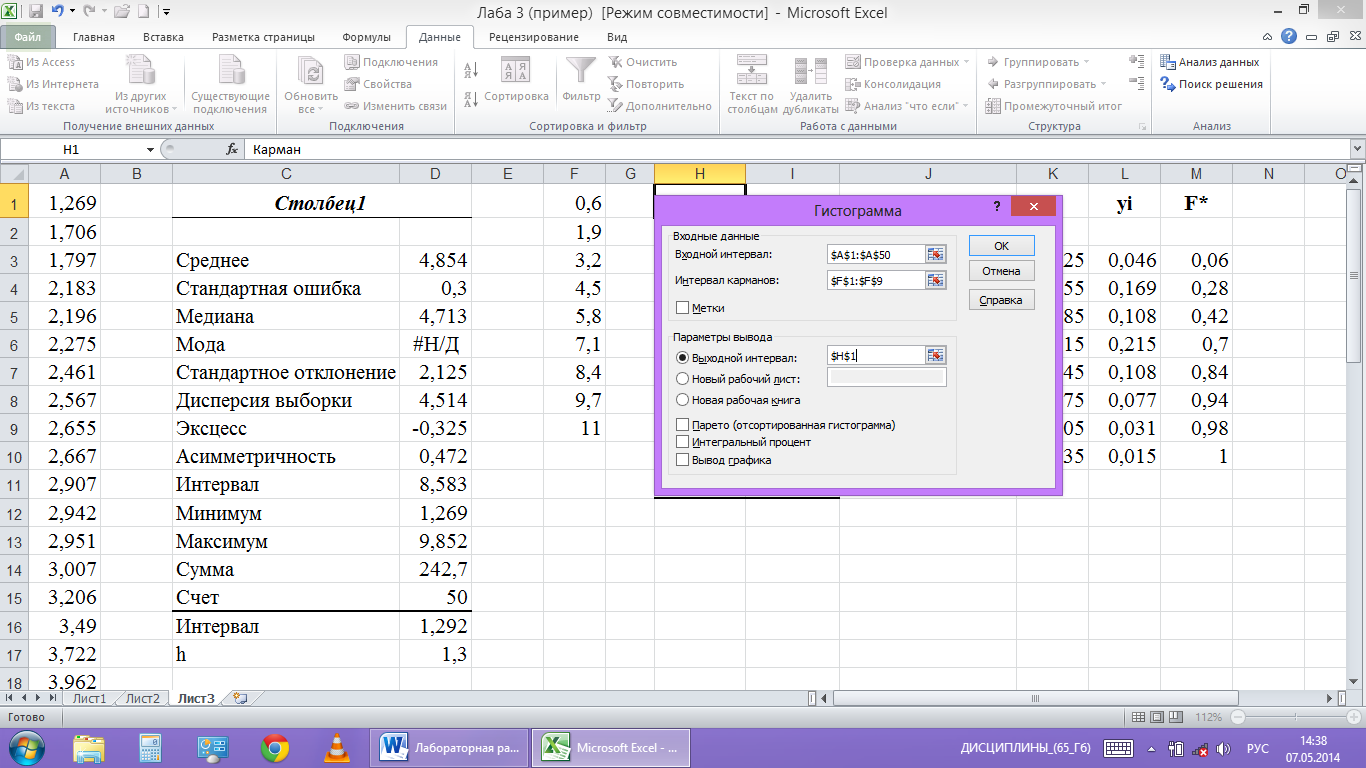
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
в пункт «Интервал карманов» — диапазон
ячеек с границами интервалов $F$1:$F$9.
Отметим точкой пункт «Выходной интервал»
и введем в него адрес первой ячейки для
записи результатов $Н$1. Появится таблица
из двух столбцов с обозначениями «Карман»
и «Частота» (рис.8).
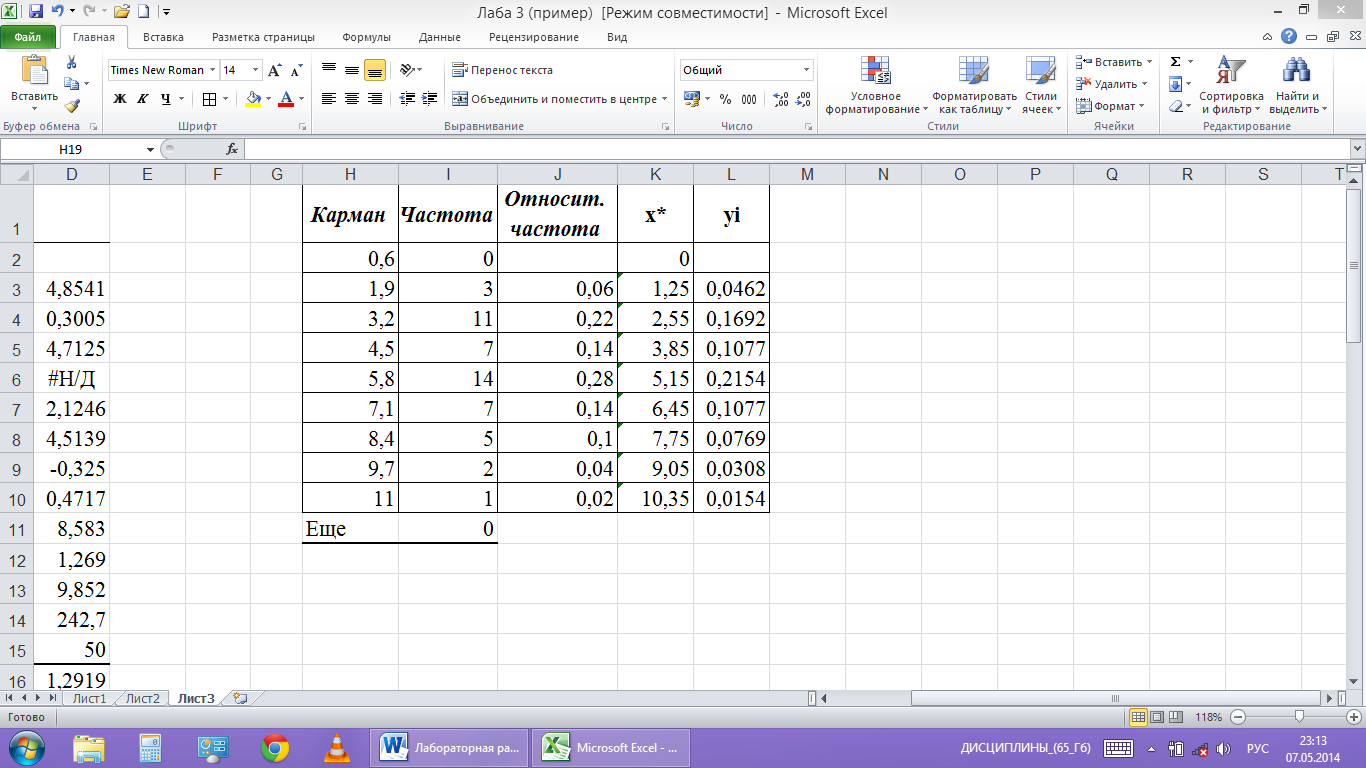
Определим
относительные частоты рi*,
значения серединных точек интервалов
и высоты
прямоугольников
Для этого
-
в ячейку
J1
введем заголовок «Относительная
частота»; -
В ячейку
J3
введем формулу
и
протягиваем её вниз до ячейки J10.
В результате к таблице из двух столбцов
добавится третий столбец (рис.8). В этой
таблице частота появления случайной
величины в каждом интервале записана
в одной строке с концом интервала;
-
в ячейку
K1
введем заголовок столбца Х*; -
в ячейку
К3 введем формулу
Протягиваем
эту формулу до ячейки К10. В результате
в четвертом столбце таблицы (рис.8)
появятся значения серединных точек
интервалов;
-
в ячейку
L1
введем заголовок столбца Уi; -
в ячейку
L3
введем формулу
Протягиваем
её вниз до ячейки L10.
В
результате в пятом столбце таблицы
(рис.8) появятся значения Уi.
рис.8
Соседние файлы в папке Лаб.работы
- #
- #
- #
- #
- #
- #
- #
Построение рядов распределения
Любой ряд распределения характеризуется двумя элементами:
— варианта(хi) – это отдельные значения признака единиц выборочной совокупности. Для вариационного ряда варианта принимает числовые значения, для атрибутивного – качественные (например, х=«государственный служащий»);
— частота (ni) – число, показывающее, сколько раз встречается то или иное значение признака. Если частота выражена относительным числом (т.е. долей элементов совокупности, соответствующих данному значению варианты, в общем объеме совокупности), то она называется относительной частотойили частостью.
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Интервальный ряд может строиться как с интервалами равной длины (равноинтервальный ряд) так и с неодинаковыми интервалами, если это диктуется условиями статистического исследования. Например, может рассматриваться ряд распределения доходов населения со следующими интервалами:
где k – число интервалов, n – объем выборки. (Конечно, формула обычно дает число дробное, а в качестве числа интервалов выбирается ближайшее целое к полученному число.) Длина интервала в таком случае определяется по формуле
При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:
— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.
Проиллюстрируем процесс первичной обработки данных на следующих примерах.
Пример 1.1. имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Теперь построим полигон: выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Пример 1.2. Имеются данные о выбросах загрязняющих веществ из 50 источников:
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Составить равноинтервальный ряд, построить гистограмму
Внесем массив данных в лист Excel, он займет диапазон А1:J5 Как и в предыдущей задаче, определим объем выборки n, минимальное и максимальное значения в выборке. Поскольку теперь требуется не дискретный, а интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу =1+3,322*LOG10(B7).
Рис.1.4. Пример 2. Построение равноинтервального ряда
Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(В9-В8)/С10.
Рис.1.5. Пример 2. Построение равноинтервального ряда
Теперь заполним массив «карманов» при помощи функции ЧАСТОТА, как это было сделано в примере 1.
Рис.1.6. Пример 2. Построение равноинтервального ряда
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Расчет ширины интервала и таблица интервалов приведены в файле примера на листе Гистограмма . Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() . О вводе этой функции см. статью Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL .
Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Стиль и внешний вид гистограммы
После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:
- добавить заголовок и другие дополнительные данные для отображения. Для того, чтобы добавить данные на график, кликните на пункт “Добавить элемент диаграммы”, затем, выберите нужный пункт из выпадающего списка:
Вы также можете использовать кнопки быстрого доступа к редактированию элементов гистограммы, стиля и фильтров:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Например:
Для распределения учеников по росту получаем: begin S^2=fraccdot 104,1approx 105,1\ sapprox 10,3 end Коэффициент вариации: $ V=fraccdot 100textapprox 6,0textlt 33text $ Выборка однородна. Найденное значение среднего роста (X_)=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
- если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
1. Построение вариационного ряда
Нужно выделить ячейки содержащие результаты эксперимента, и воспользоваться операцией сортировка по возрастанию (либо с панели инструментов, либо через главное меню Данные>Сортировка), и в появившемся окне сообщения – «обнаружены данные выходящие за пределы выделенного диапазона» выбрать действие – «сортировать в пределах указанного выделения»
2. Построение группировочного статистического ряда
Добавьте и заполните, введя соответствующие формулы, две таблицы:
Таблица №1
Для вычисления минимального и максимального элемента воспользуйтесь встроенными в Excel статистическими формулами (главное меню – вставка – функция…) МИН и МАКС.
Таблица №2
начало промежутка
конец промежутка
Середина промежутка
Абсолютная частота
Относи-тельная частота
Накопленная частота
1
2
Для вычисления абсолютной частоты нужна статистическая функция ЧАСТОТА. При её использовании нужно выполнить следующие действия:
а) выделить весь диапазон ячеек, в которых будет располагаться результат подсчёта частот (т.е. это ячейки под заголовком Абсолютная частота в количестве равном числу промежутков)
b) не снимая выделения, поставить курсор в строку формул и нажать на кнопку вставка функции (чуть левее курсора) или Главное меню – вставка – формула.
с) выбрать функцию ЧАСТОТА
d) ввести Массив_данных – диапазон, содержащий элементы выборки (в файле 2.xls это ячейки) B2:B101
e) ввести Массив_интервалов – диапазон ячеек под заголовком Начало промежутка начиная со строчки, соответствующей промежутку под номером 2 до строчки, соответствующей последнему промежутку.
f) нажмите на кнопку ОК и после закрытия окна для ввода аргументов функции ЧАСТОТА поставьте курсор обратно в строку формул.
g) Нажмите на три кнопки Ctrl+Shift+Enter (сначала на первые две, а потом, не отпуская их, нажмите на Enter).
Примечание. Формулу вычисления абсолютной частоты необходимо ввести как формулу массива. Нажатие комбинации клавиш CTRL+SHIFT+ENTER позволяет определить формулу как формулу массива. Если формула не будет введена как формула массива, единственное значение будет равно 1.
В результате изначально выделенный диапазон будет содержать абсолютные частоты попадания во все промежутка. Проверьте, что сумма всех абсолютных частот равна общему числу элементов выборки (100).
3. Построение гистограммы группировочного статистического ряда
В качестве элементов группировочного ряда надо взять середины промежутков и приведённые частоты.
Для построения гистограммы выполните следующие действия:
- Главное меню: Вставка – Диаграмма.
- Тип: точечная.
- Диапазон данных: выделите ячейки содержащие значения абсолютных частот.
- Ряд: Значения по X: укажите диапазон ячеек содержащий значения середины промежутков.
- Готово.
Использование Excel для расчета статистических характеристик случайной величины
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xiслучайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Содержание
- Лабораторная работа № 3 Обработка статистических данных на основе приложения ms excel
- Порядок выполнения работы
- 1.Ввод исходных статистических данных.
- 2. Построение вариационного ряда.
- 3. Вычисление статистических характеристик.
- 4. Построение интервального статистического ряда.
- Как построить вариационный ряд в excel
Лабораторная работа № 3 Обработка статистических данных на основе приложения ms excel
Для случайной выборки объемом n=50 с несовпадающими числами выполнить следующую последовательность действий:
1.Вывести на лист Excel исходные статистические данные.
2. Построить вариационный ряд.
3. Вычислить статистические характеристики.
4. Построить интервальный статистический ряд.
5.Построить гистограмму частот.
6. Составить статистическую функцию распределения статистического ряда.
7. Составить и постоить статистическую функцию распределения группированного статистического ряда.
В качестве примера рассмотрим следующую выборку
Порядок выполнения работы
1.Ввод исходных статистических данных.
Вводим данные в первый столбец таблицы (рис.1).
2. Построение вариационного ряда.
Производим сортировку данных в порядке возрастания. Для этого:
а) выделяем первый столбец;
б) на ленте во вкладке «Данные» выбираем «Сортировка и фильтр» (рис.2)
3. Вычисление статистических характеристик.
На ленте во вкладке «Данные» выбираем «Анализ данных» меню «Описательная статистика» нажимаем ОК.
В пункт «Входной интервал» вводим диапазон ячеек с исходными данными $A$1:$A$50, а в пункте «Выходной интервал» обозначим первую ячейку для записи результаов $C$1. Ставим флажок напротив пункта «Итоговая статистика» и нажимаем ОК.(рис.4)
На рабочем листе появляется таблица с вычисленными значениями числовых характеристик выборки (рис.5)
Здесь «Среднее»означает математическое ожидание выборки, а «Стандартная ошибка» — погрешность ее значения. «Дисперсия выборки» означает исправленную выборочную дисперсию, а «Стандартное отклонение» — исправленное среднее квадратичное отклонение. Положительное значение «Асимметричности» означает, что «длинная часть» кривой лежит правее моды. Отрицательное значение «Эксцесса» означает, что кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. «Интервал» равен разности Xmax−Xmin. «Сумма» дает результат суммирования всех элементов выборки. «Счет» задает общее число элементов выборки.
4. Построение интервального статистического ряда.
Длину интервала группировки определяем по формуле
Необходимые данные имеем в таблице: Xmax – в ячейке D13, Xmin– в ячейке D12, число элементов выборки n — в ячейке D15.
В ячейку С16 вводим слово «Интервал», в ячейку D16 вводим формулу
в ячейке D16 появится значение числа h. В ячейку C17 вводим букву h. В ячейку D17 вводим формулу
В ячейке D17 получаем округленное до одного знака после запятой значение интерала h.
Проведем формирование интервалов. Для этого от Xmin отступим влево примерно на h/2 и получим начальную точку отсчета. Последовательно прибавляя к ней целое число отрезков h, получим все граничные точки интервалов.
В ячейку F1 вводим формулу
В этой ячейке появляется значение начальной точки отсчета. В ячейку F2 вводим формулу
В этой ячейке появляется значение второй граничной точки первого интервала. Возвращаемся в ячейку F2, ставим курсор в правый нижний угол рамки и двигаем его вниз, не отпуская левую кнопку мыши. В результате такой процедуры (протяжка) столбец F заполнят граничные точки интервалов. Самый нижний интервал должен включать Xmax (рис.6).
Проведем подсчет числа вариант, попавших в каждый интервал, определим относительные частоты и серединные точки этих интервалов.
Для этого на ленте во вкладке «Данные» выбираем «Анализ данных» меню «Гистограмма». (рис. 7)
В пункт «Входной интервал» вводим диапазон ячеек с исходными данными $A$1:$A$50, в пункт «Интервал карманов» — диапазон ячеек с границами интервалов $F$1:$F$9. Отметим точкой пункт «Выходной интервал» и введем в него адрес первой ячейки для записи результатов $Н$1. Появится таблица из двух столбцов с обозначениями «Карман» и «Частота» (рис.8).
Определим относительные частоты рi * , значения серединных точек интервалов
и высоты прямоугольников
в ячейку J1 введем заголовок «Относительная частота»;
В ячейку J3 введем формулу
и протягиваем её вниз до ячейки J10. В результате к таблице из двух столбцов добавится третий столбец (рис.8). В этой таблице частота появления случайной величины в каждом интервале записана в одной строке с концом интервала;
в ячейку K1 введем заголовок столбца Х*;
в ячейку К3 введем формулу
Протягиваем эту формулу до ячейки К10. В результате в четвертом столбце таблицы (рис.8) появятся значения серединных точек интервалов;
в ячейку L1 введем заголовок столбца Уi;
в ячейку L3 введем формулу
Протягиваем её вниз до ячейки L10.
В результате в пятом столбце таблицы (рис.8) появятся значения Уi.
Источник
Как построить вариационный ряд в excel
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, – генеральной совокупностью.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
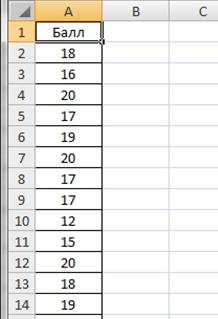
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
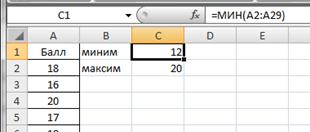
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
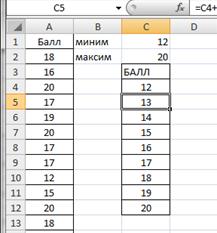
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
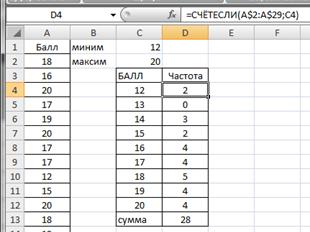
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
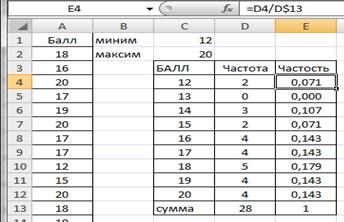
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
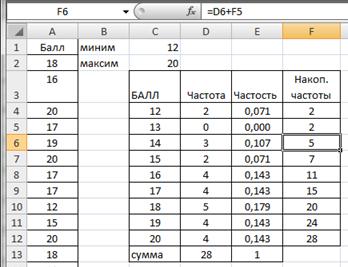
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
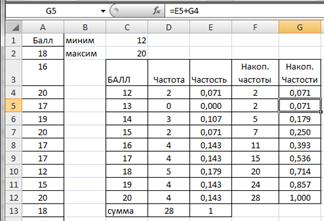
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.
Рисунок 2.13. Полигон распределения частот
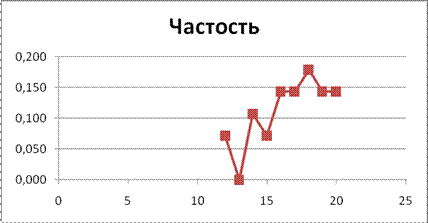
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
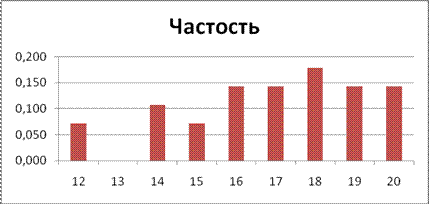
Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» – «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
Пример 2.2.
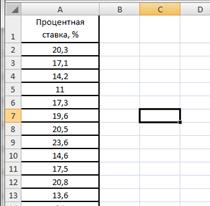
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
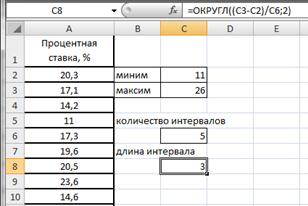
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
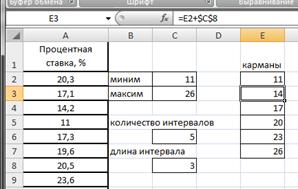
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
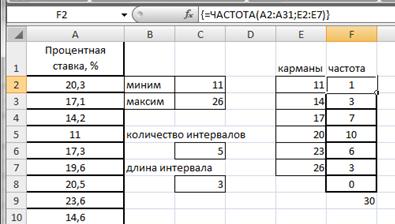
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
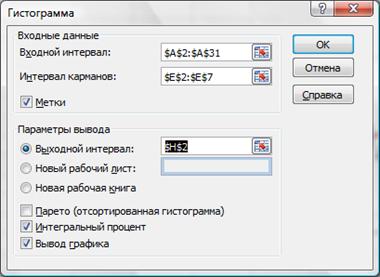
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
Рисунок 2.22. Построение гистограммы
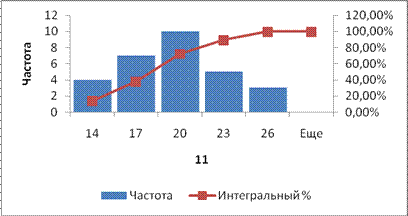
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Дата добавления: 2018-11-12 ; просмотров: 1065 | Нарушение авторских прав
Вариационный ряд может быть:
– дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
– интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение .
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа – в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).
Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).
Размахом вариации называется число
где хтах — наибольший вариант;
x min — наименьший вариант.
Сумма всех частот равна определенному числу л, которое называется объемом совокупности:
Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:
Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.
Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.
В результате получим дискретный вариационный ряд (табл. 3.10).
Ранжированный ряд успеваемости
Число студентов, л,
Относительная частота, А
В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).
Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).
Рис. 3.13. Контекстное меню строки состояния
Рассмотрим два варианта подсчета частот:
- 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
- 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.
Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»
В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).
Рис. 3.15. Результаты применения инструмента «Гистограмма)
Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).
В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.
Источник