Содержание:
- 1 Шаг 1
- 2 Шаг 2
- 3 Шаг 3
- 4 Шаг 4
- 5 Шаг 5
- 6 Шаг 6
-
- 6.0.1 Дубликаты не найдены
-
Тангенциальная линия — это прямая линия на графике, которая проходит по касательной к кривой линии, составленной из точек данных. В Excel есть возможность автоматически создавать линию тренда, или вы можете вручную нарисовать касательную линию на графике. Тангенциальная линия рисуется касаясь изогнутой линии, так что когда кривая отходит от линии, она равноудалена от линии. В то время как функция линии тренда в Excel покажет тренд всей линии, ручное рисование линии создаст истинную касательную.
Кредит: Драган Радоевич / iStock / Getty Images
Шаг 1
Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.
Шаг 2
Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.
Шаг 3
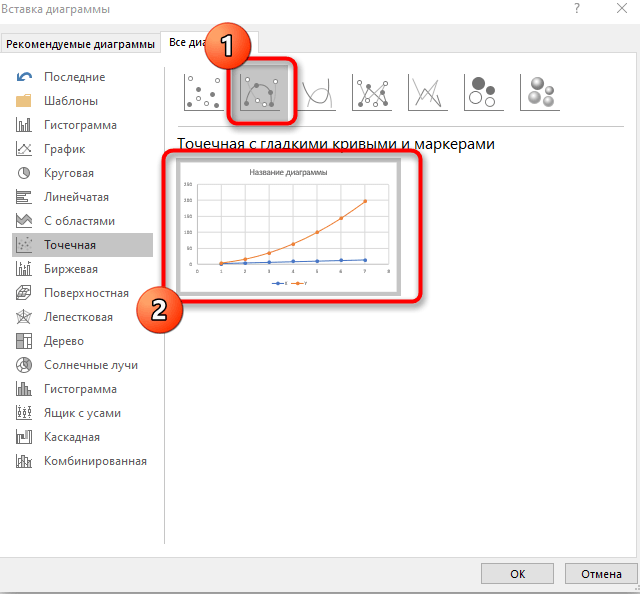
Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.
Шаг 4
Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.
Шаг 5
Нажмите на вкладку «Вставка», а затем нажмите «Фигуры». Выберите «Линия» и нарисуйте линию так, чтобы она просто касалась одной из точек на вашей кривой.
Шаг 6
Нажмите на вкладку «Инструменты рисования: Формат» и нажмите кнопку «Повернуть» справа. Выберите «Дополнительные параметры вращения». Нажмите стрелку «Вверх» или «Вниз» рядом с полем «Поворот» в диалоговом окне, которое появляется, чтобы повернуть линию на кривой. Когда линия будет равноудалена от обеих сторон кривой, нажмите «ОК».
Дубликаты не найдены
ЕСЛИ(условие;выполнить_если_истина;выполнить_если_ложь)
[в eng версии соответственно это IF(. )]
Условие — что угодно, что может интерпретироваться как булевская функция. Например, дано, что a=2, b=3. Тогда IF(a>b;»истина»;»ложь») вернёт «ложь».
Сделать разветвление на несколько вариантов — IF(условие1;действие1;IF(условие2;действие2;..))
В качетсве крайнего «ложь» блока ЕСЛИ можно писать что угодно [если уверены, что рассмотрели все возможные варианты].
Вообще, насколько помню, годная в экселе справка была.. Так что традиционное — RTFM.
В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.
Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:
где к = /'(хо) — угловой коэффициент;
Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (хмин и хмакс) и ординат (умин и умакс).
Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х2,у2), которые располагаются на границах прямоугольника.
Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х) . Значения углового коэффициента
могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.
Пусть к > 0. Остановимся на всех возможных вариантах расположения точек. При хх = хмин с учетом формулы ух = к * (хмин — х) + у .
Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем х2 = хмакс и у2 = к * (хмакс — х) + у.
Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)
Формируем таблицы начальных условий задачи.
координат заданной точки функции(х, у) (F2 и G2);
углового коэффициента к = /'(х) (Н2);
граничных значений диапазонов (хмин, хмакс, умин, умакс) (A2:D5).
Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения уг при хг = хмин и у2 при х2 = хмакс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).
Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы — Точечная, а вид — Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.
Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.
Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у — к * х. Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.
Изменяя значения координаты х, осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.
При необходимости можно дополнительно построить график производной заданной функции.
Касательная к графику из определенной точки
Автор mulder777, 29.03.2012, 04:38
« назад — далее »
Ребята, здравствуйте! Несколько лет ломаю голову над вопросом построения касательной к графику из определенной точки. Пример в прикрепленном файле. Только не нужно писать мне об всяких апроксимациях и т.п. Я прошу реальной помощи на основании представленного примера, чтобы посмотрев на ваше решение, смог в дальнейшем использовать ваше уравнение или функцию или т.п.
Нда….. Я так и понял, что на этом сайте и не пахнет реальными мозгами… 
mulder777, а вы уверены, что нашли правильную касательную?
например судя по графику, если сильно увеличить масштаб, то прямая не касается графика.
Предположительно касание происходит при х=60, но это не так,
можно проверить формулой:
=ПРЕДСКАЗ(60;{0,04686;0,255};{-23,03;80})
в результате получается значение 0,214596234106571, что выше табличных данных при х=60 (0,213)
Есть вопросы:
откуда взялась точка [-23,03;0,04686]?
если бы график не стал бы опускатся после х=60 (например это была бы парабола), как бы Вы строили касаткльную?
я бы так стал решать
PS: поломал голову минут 10
PPS: на текущий момент исходный файл скачен 2 раза, из них второй раз мной, так что не нужно «брать на слабо»
и неуважительно высказыватся об участниках форума
Если нужна только правая сторона, то так будет лучше
Если нужна касательная к сглаженной линии, то без аппроксимации (интерполяции) не обойтись
Аппроксимирующую (интерполирующую) функцию повзаимствовал у С.М. (все копирайты сохранил)
PS: сдается мне, что здесь «пахнет» игрой на бирже
Качество автоматического построения касательной к сглаженной кривой можете оценить при масштабе 400%
Уважаемый MCH! Здравствуйте!
Этот график представляет собой диаграмму динамической остойчивости судна на плаву. Точка, с которой я провожу касательную — это пересечение этой диаграммы с перпендикуляром, восстановленным из определенного значения угла (амплитуда качки судна), которая тоже расчитывается определенным способом и мне известна. Касательная из этой точки к этой диаграмме мне нужна для определения опрокидывающего плеча судна. В моем случае не обязательно находить значение Y при Х=80, достаточно найти просто координаты места касания к диаграмме. По поводу вашего вопроса о том, как бы я строил касательную, если бы график не опускался после 60-ти — отвечаю, во всех случаях динамической остойчивости судна этот график выглядит однообразно и всегда имеет такую форму. Скачал все ваши варианты, сижу, думаю, анализирую, спасибо за уделенное мне время, о результатах отпишусь. Но в последнем варианте касательной вообще не вижу
P.S. Игрой на бирже тут не пахнет. Я моряк, пытаюсь автоматизировать и без того свой нелегкий труд.
Нда… Вопросов оказывается еще больше…. Откуда вы взяли эти функции типа «MaxRight» и «Non…….»
Цитата: mulder777 от 01.04.2012, 06:33
Откуда вы взяли эти функции типа «MaxRight» и «Non…….»?? При переносе этих функций в свой файл — они не работают!!!??? КАК!?
сами же просили:
ЦитироватьТолько не нужно писать мне об всяких апроксимациях и т.п.
Поэтому промолчу
Смотрите решение, пробуйте в дальнейшем использовать функции MaxRight и NonLinearInterpolation
Определяем точку касания
PS: Все функции можно увидеть нажав Alt+F11
Понятно, видимо все это связано с введением новой нестандартной функции при помощи программирования. Короче я поступил проще, ввел все свои таблицы и расчеты в ваш файл, там они все считают. А как перенести эти новые функции на новую книгу — это для меня дремучий лес! Спасибо за поддержку!
Здравствуйте господа! Вопрос о касательной не совсем полный. Простое построение самой касательной к графику не дает ответ на ее применение. Так, только графическое удовлетворение. Хочется пояснить для чего строится касательная. Дело в том, что кроме создания самой касательной, еще требуется, используя дополнительные построения, вытянуть некие данные из построенного. Возможно ли это вообще? Пользовательские функции не пугают, правда я в них тоже ни-фига… 
А в чем вопрос?
Необходимо рассчитать все коэффициенты Kрад, Кзал, Ккас?
Формулу для расчета значения в ячейке S21 можно брать не «с потолка»:
=NonLinearInterpolation($H$11:$T$11;$H$12:$T$12;-$U$12)
расчетное значение получилось: 0,1099736328125
Точка касания: 66,05
=TangentPoint(H11:T11;H12:T12;-U12;U15;0,1)
значение в точке касания = 1,165977702
=NonLinearInterpolation(H11:T11;H12:T12;66,05)
Ккас = 1,47328386794217
=ПРЕДСКАЗ(90;{0,1099736328125:1,165977702};{-16,25:66,05})
Кзал = 0,981850625537781
=ПРЕДСКАЗ(51,7;{0,1099736328125:1,165977702};{-16,25:66,05})
Kрад = 0,84519882314596
=ПРЕДСКАЗ(57,3-16,25;{0,1099736328125:1,165977702};{-16,25:66,05})
- Профессиональные приемы работы в Microsoft Excel
-
►
Обмен опытом -
►
Microsoft Excel -
►
Касательная к графику из определенной точки
Функция TAN Excel (касательная)
Функция TAN Excel — это встроенная тригонометрическая функция в excel, которая используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.
Функция TAN Excel
Функция TAN Excel — это встроенная функция, относящаяся к категории Math / Trig function, которая возвращает значение тангенса угла. Формула для TAN всегда возвращает числовое значение.
В тригонометрии тангенс угла эквивалентен отношению перпендикуляра к основанию прямоугольного треугольника.
TAN Θ = противоположная сторона / смежная сторона
Следовательно, TAN Θ = a / b
Формула TAN в Excel
Ниже приведена формула TAN в Excel.
Где число — это аргумент, передаваемый функции в радианах.
Угол, который мы указываем в качестве входных данных, распознается функцией Tangent, только если он указан как Radians.
Чтобы преобразовать угол в радианы, используйте функцию РАДИАНЫ или преобразуйте угол в радианы с помощью математического соотношения
Радиан = угол в градусах * (π / 180)
π в Excel представлена функцией PI ()
Следовательно, радиан = градус * (PI () / 180)
Расчет значения TAN с использованием функции TAN и RADIANS
Расчет значения TAN с использованием TAN и функции PI
У функции касательной есть много реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Функция касания, используемая в системах навигации и GPS, в аэронавтике.
Например, если самолет летит на высоте 3000 м и делает угол к наблюдателю на земле 26 °, и мы хотим найти расстояние от самолета до наблюдателя.
Как мы знаем, TAN Θ = противоположная сторона / смежная сторона
Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.
А соседняя сторона = горизонтальное расстояние самолета от земли, которое неизвестно, и нам нужно его вычислить.
Итак, используя формулу для TAN, мы имеем
TAN (26 °) = 3000 / x
Следовательно, x = 3000 / (TAN (26 °))
В Excel, взяв относительные контрольные значения, мы имеем
Икс = B2 / (TAN (B3 * (PI () / 180))))
X = 6150.91 метров
Как использовать TAN в Excel?
Функция Excel TAN очень проста и удобна в использовании. Позвольте мне понять, как работает формула TAN в Excel на нескольких примерах.
Касательная в Excel, пример # 1
Мужчина ростом 6 футов находится в 55 метрах от дерева. Он делает угол обзора 47 ° параллельно земле. Мы хотим рассчитать высоту дерева.
Чтобы найти высоту дерева, мы будем использовать TAN Θ. В контексте Excel мы будем использовать функцию Tangent.
Высота дерева будет
Высота Человека + Расстояние Человека от дерева * TAN (47 °)
Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра).
Поместив все относительные значения в Excel, формула для высоты дерева будет
= (0,3 * B2) + (B3 * TAN ((B4 * (PI () / 180))))
Выходные данные TAN Excel:
Высота дерева 60,78 метра.
Касательная в Excel, пример # 2
Предположим, у нас есть пять прямоугольных треугольников с указанием их углов и длины с одной стороны, и нам нужно вычислить длину двух других сторон.
Сумма всех углов треугольника равна 180 °; следовательно, мы можем легко вычислить третий угол.
Мы знаем, Sin Θ = противоположное / гипотенуза
Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза
В Excel длина Противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN.
= E2 * SIN (C2 * (PI () / 180))
Применяя формулу TAN для пяти треугольников, мы можем получить длину перпендикуляров треугольников
Теперь у нас есть две стороны треугольника: гипотенуза и перпендикулярная сторона. Мы можем легко вычислить третью сторону (основание), используя TAN в Excel.
Мы знаем, что TAN Θ = противоположная сторона / смежная сторона.
Таким образом, длина прилегающей стороны будет Обратная сторона/ТАН Θ.
В Excel длина прилегающей стороны (основания) будет рассчитываться по формуле TAN.
= F2 / (TAN (РАДИАНЫ (C2)))
Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника.
TAN в выводе Excel:
Касательная в Excel, пример №3
Самолет делает разворот радиусом 160 м и летит с постоянным углом крена 87 °, в идеальных условиях (без колебаний ветра) рассчитайте постоянную путевую скорость самолета.
Радиус поворота задается формулой.
Радиус поворота = V 2 / g * TAN Θ
Радиус поворота 160 метров; Постоянный угол крена 87 °, g — ускорение свободного падения, значение которого составляет 9,8 м / с. 2 , поэтому путевая скорость будет
V = (Радиус поворота * (g * TAN Θ)) 1/2
Применяя приведенную выше формулу TAN в Excel со справочными значениями, мы получаем формулу TAN.
= КОРЕНЬ (B2 * (9,8 * (TAN (РАДИАНЫ (B3)))))
SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.
TAN в выводе Excel:
Итак, путевая скорость самолета составляет 172,97 м / с.
Пример функции касания # 4
У нас есть формула для TAN, обозначенная f (x) = 2c * TAN2Θ, где c — постоянное значение, равное 0,988. Значение варианта — это значение, а формула для TAN зависит от значения. Нам нужно построить график заданной функции касания.
Используя функцию Excel TAN, мы затем вычислим значения функции, поэтому, взяв контрольные значения в качестве входных данных, мы получим формулу TAN,
Как можно провести касательную к графику в экселе?
Excel всё-таки не бумага, чтобы на ней что-то можно было провести.
Вы табулировали некую функцию и отобразили её график. Вам надо выбрать точку и табулировать функцию производной в некой заранее заданной точке.
Уравнение касательной к табулированной функции находят разными способами на выч. методах. В сети можно найти уже готовые формулы. Если хотите сами, то надо выбрать 3 точки, наиболее близкие к заданной, представить функцию параболой, проходящей через них, а потом построить касательную к этой параболе.
Как только у вас будет уравнение прямой, табулируйте её функцию и выведите на график результат.
ЗЫ
Табулировать функцию — найти множесто пар (аргумент, значение) и вывести их в табличном виде.
Как построить касательную в excel к точке
Тангенциальная линия — это прямая линия на графике, которая проходит по касательной к кривой линии, составленной из точек данных. В Excel есть возможность автоматически создавать линию тренда, или вы можете вручную нарисовать касательную линию на графике. Тангенциальная линия рисуется касаясь изогнутой линии, так что когда кривая отходит от линии, она равноудалена от линии. В то время как функция линии тренда в Excel покажет тренд всей линии, ручное рисование линии создаст истинную касательную.
Кредит: Драган Радоевич / iStock / Getty Images
Шаг 1
Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.
Шаг 2
Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.
Шаг 3
Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.
Шаг 4
Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.
Шаг 5
Нажмите на вкладку «Вставка», а затем нажмите «Фигуры». Выберите «Линия» и нарисуйте линию так, чтобы она просто касалась одной из точек на вашей кривой.
Шаг 6
Нажмите на вкладку «Инструменты рисования: Формат» и нажмите кнопку «Повернуть» справа. Выберите «Дополнительные параметры вращения». Нажмите стрелку «Вверх» или «Вниз» рядом с полем «Поворот» в диалоговом окне, которое появляется, чтобы повернуть линию на кривой. Когда линия будет равноудалена от обеих сторон кривой, нажмите «ОК».
Дубликаты не найдены
ЕСЛИ(условие;выполнить_если_истина;выполнить_если_ложь)
[в eng версии соответственно это IF(. )]
Условие — что угодно, что может интерпретироваться как булевская функция. Например, дано, что a=2, b=3. Тогда IF(a>b;»истина»;»ложь») вернёт «ложь».
Сделать разветвление на несколько вариантов — IF(условие1;действие1;IF(условие2;действие2;..))
В качетсве крайнего «ложь» блока ЕСЛИ можно писать что угодно [если уверены, что рассмотрели все возможные варианты].
Вообще, насколько помню, годная в экселе справка была.. Так что традиционное — RTFM.
В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.
Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:
где к = /'(хо) — угловой коэффициент;
Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (хмин и хмакс) и ординат (умин и умакс).
Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х2,у2), которые располагаются на границах прямоугольника.
Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х ) . Значения углового коэффициента
могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.
Пусть к > 0. Остановимся на всех возможных вариантах расположения точек. При хх = хмин с учетом формулы ух = к * (хмин — х ) + у .
Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем х2 = хмакс и у2 = к * (хмакс — х ) + у .
Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)
Формируем таблицы начальных условий задачи.
координат заданной точки функции(х , у ) (F2 и G2);
углового коэффициента к = /'(х ) (Н2);
граничных значений диапазонов (хмин, хмакс, умин, умакс) (A2:D5).
Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения уг при хг = хмин и у2 при х2 = хмакс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).
Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы — Точечная, а вид — Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.
Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.
Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у — к * х . Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.
Изменяя значения координаты х , осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.
При необходимости можно дополнительно построить график производной заданной функции.
Как можно провести касательную к графику в экселе?
Excel всё-таки не бумага, чтобы на ней что-то можно было провести.
Вы табулировали некую функцию и отобразили её график. Вам надо выбрать точку и табулировать функцию производной в некой заранее заданной точке.
Уравнение касательной к табулированной функции находят разными способами на выч. методах. В сети можно найти уже готовые формулы. Если хотите сами, то надо выбрать 3 точки, наиболее близкие к заданной, представить функцию параболой, проходящей через них, а потом построить касательную к этой параболе.
Как только у вас будет уравнение прямой, табулируйте её функцию и выведите на график результат.
ЗЫ
Табулировать функцию — найти множесто пар (аргумент, значение) и вывести их в табличном виде.
Функция TAN Excel (касательная)
Функция TAN Excel — это встроенная тригонометрическая функция в excel, которая используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.
Функция TAN Excel
Функция TAN Excel — это встроенная функция, относящаяся к категории Math / Trig function, которая возвращает значение тангенса угла. Формула для TAN всегда возвращает числовое значение.
В тригонометрии тангенс угла эквивалентен отношению перпендикуляра к основанию прямоугольного треугольника.
TAN Θ = противоположная сторона / смежная сторона
Следовательно, TAN Θ = a / b
Формула TAN в Excel
Ниже приведена формула TAN в Excel.
Где число — это аргумент, передаваемый функции в радианах.
Угол, который мы указываем в качестве входных данных, распознается функцией Tangent, только если он указан как Radians.
Чтобы преобразовать угол в радианы, используйте функцию РАДИАНЫ или преобразуйте угол в радианы с помощью математического соотношения
Радиан = угол в градусах * (π / 180)
π в Excel представлена функцией PI ()
Следовательно, радиан = градус * (PI () / 180)
Расчет значения TAN с использованием функции TAN и RADIANS
Расчет значения TAN с использованием TAN и функции PI
У функции касательной есть много реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Функция касания, используемая в системах навигации и GPS, в аэронавтике.
Например, если самолет летит на высоте 3000 м и делает угол к наблюдателю на земле 26 °, и мы хотим найти расстояние от самолета до наблюдателя.
Как мы знаем, TAN Θ = противоположная сторона / смежная сторона
Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.
А соседняя сторона = горизонтальное расстояние самолета от земли, которое неизвестно, и нам нужно его вычислить.
Итак, используя формулу для TAN, мы имеем
TAN (26 °) = 3000 / x
Следовательно, x = 3000 / (TAN (26 °))
В Excel, взяв относительные контрольные значения, мы имеем
Икс = B2 / (TAN (B3 * (PI () / 180))))
X = 6150.91 метров
Как использовать TAN в Excel?
Функция Excel TAN очень проста и удобна в использовании. Позвольте мне понять, как работает формула TAN в Excel на нескольких примерах.
Касательная в Excel, пример # 1
Мужчина ростом 6 футов находится в 55 метрах от дерева. Он делает угол обзора 47 ° параллельно земле. Мы хотим рассчитать высоту дерева.
Чтобы найти высоту дерева, мы будем использовать TAN Θ. В контексте Excel мы будем использовать функцию Tangent.
Высота дерева будет
Высота Человека + Расстояние Человека от дерева * TAN (47 °)
Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра).
Поместив все относительные значения в Excel, формула для высоты дерева будет
= (0,3 * B2) + (B3 * TAN ((B4 * (PI () / 180))))
Выходные данные TAN Excel:
Высота дерева 60,78 метра.
Касательная в Excel, пример # 2
Предположим, у нас есть пять прямоугольных треугольников с указанием их углов и длины с одной стороны, и нам нужно вычислить длину двух других сторон.
Сумма всех углов треугольника равна 180 °; следовательно, мы можем легко вычислить третий угол.
Мы знаем, Sin Θ = противоположное / гипотенуза
Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза
В Excel длина Противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN.
= E2 * SIN (C2 * (PI () / 180))
Применяя формулу TAN для пяти треугольников, мы можем получить длину перпендикуляров треугольников
Теперь у нас есть две стороны треугольника: гипотенуза и перпендикулярная сторона. Мы можем легко вычислить третью сторону (основание), используя TAN в Excel.
Мы знаем, что TAN Θ = противоположная сторона / смежная сторона.
Таким образом, длина прилегающей стороны будет Обратная сторона/ТАН Θ.
В Excel длина прилегающей стороны (основания) будет рассчитываться по формуле TAN.
= F2 / (TAN (РАДИАНЫ (C2)))
Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника.
TAN в выводе Excel:
Касательная в Excel, пример №3
Самолет делает разворот радиусом 160 м и летит с постоянным углом крена 87 °, в идеальных условиях (без колебаний ветра) рассчитайте постоянную путевую скорость самолета.
Радиус поворота задается формулой.
Радиус поворота = V 2 / g * TAN Θ
Радиус поворота 160 метров; Постоянный угол крена 87 °, g — ускорение свободного падения, значение которого составляет 9,8 м / с. 2 , поэтому путевая скорость будет
V = (Радиус поворота * (g * TAN Θ)) 1/2
Применяя приведенную выше формулу TAN в Excel со справочными значениями, мы получаем формулу TAN.
= КОРЕНЬ (B2 * (9,8 * (TAN (РАДИАНЫ (B3)))))
SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.
TAN в выводе Excel:
Итак, путевая скорость самолета составляет 172,97 м / с.
Пример функции касания # 4
У нас есть формула для TAN, обозначенная f (x) = 2c * TAN2Θ, где c — постоянное значение, равное 0,988. Значение варианта — это значение, а формула для TAN зависит от значения. Нам нужно построить график заданной функции касания.
Используя функцию Excel TAN, мы затем вычислим значения функции, поэтому, взяв контрольные значения в качестве входных данных, мы получим формулу TAN,
помогите по учебе, пожалуйста
Впервые я дрался из-за женщины в семь лет. Она была второй женой деда. Высокая, с гвардейской выправкой и полуседыми усиками над губой.Носила прямые яркие платья с коротким рукавом, плотно облегающим завидный бицепс. Голос имела зычный. Он раскатывался по двору как гром:»Бор-р-рык! Кушать!». Это если я гулял один. А если с дедом, тогда: «Охламоны! Хавать!»
И, когда она в очередной раз вышла на балкон позвать меня, я услышал как Толька Коршунов выкрикнул: «Гвардеец кардинала на посту!» И я вцепился в него, хотя Тольке было целых одиннадцать лет и он даже уже был влюблен в Таньку, о чем поведал всему двору вырезанным на тополе объявлением «Я люблю тебя».Имя вырезать не стал, проявив не детскую мудрость.
Толька валялся в пыли, совершенно не сопротивляясь, а только удивленно таращась на меня. Я пытался молотить его, приговаривая: «Гад, гад!» Под очередное «гад» меня подняла в воздух неведомая сила. Мелькнул яркий рукав, бицепс, усы и я оказался за обеденным столом с моей «не моей» бабой Феней.
Мама назвала ее официально — Феодосия Николаевна и всегда повторяла: «Она не твоя бабушка».Моя бабушка была первая жена деда, баба Женя. Она жила в одном городе с нами, в центре России, а дед с Феней жили у моря.
Оно — море — и стало причиной нашего знакомства. Я был худющим болезненным ребенком, и педиатр убедила мать, что море положительно скажется на моем здоровье. «Но обязательно не меньше месяца,» — повторяла она. Когда мне было почти четыре года, меня повезли знакомить с дедом, морем и Феней. Феодосией Николаевной. Как бы не хотели мама с «моей» бабушкой изъять ее из этого уравнения. В первый раз мама была со мной две недели, натянуто общаясь с дедом и Феней. Убедившись, что старики вполне способны управиться с ее чахлым «цветком» жизни, она начала часто уходить в гости к подругам детства и задерживаться там допоздна.
Я не хотел спать без нее. Ходил по квартире, поднывая. Дед уговаривал спать, а Феня сгребалав охапку, и говорила: «Борык, не куксись. Пойдем встречать маму!» Мы выходили в притихший двор, она сажала меня на качели.
Качелей я боялся, мне казалось, что меня, такого легкого, подхватит ветер и унесет, но Феня мощной фигурой вставала ровно напротив качелей и и заключала подвешенное сиденье в свои уверенные руки, прежде,чем снова толкнуть. «Будешь наверху — смотри маму,» — напутствовала она и легонько толкала качель. «Не виднооо,» — ныл я, а она отвечала: «Значит, надо повыше. Не боишься?» Я мотал головой в разные стороны, и она толкала сильней. И в один день, взлетая до ветки тополя, я понял, что хочу, чтоб мама не торопилась.
И мама, наверное, поняла. Она уехала, оставив меня с дедом и Феней на лето. Мы посадили ее на поезд,помахали в окошко и пошли домой обедать. А вечером мне почему-то захотелось плакать. Я помню ощущение полной опустошенности, и помню, как оно появилось. Оно появилось, когда я думал, что сегодня вечером не надо встречать маму и мы с Феней не пойдем качаться. Но после ужина она объявила:»Борык, не куксись, пойдем смотреть, как мама едет на паровозе.»
Мы ходили качаться каждый вечер. Дед поначалу говорил, что поздно, и «ребенку нужен режим», но Феня обрывала его на полуслове: «Не гунди, охламон, рыбенку много чего нужно.»
Охламон улыбался внутрь себя и капитулировал. Мы с Феней выходили, когда последние бабульки снимались с лавочек у подъезда, а возвращались к полуночи, покусанные комарами и абсолютно счастливые.
Качели были моим личным раем. Качели которые качала Феня. Она раскачивала меня, а потом притормаживала и влепляла поцелуй в неожиданное место. Когда качели начинали останавливаться, а я просить: «Еще, еще!», Феня принималась щекотать меня. Я вертелся волчком, заливался на весь тихий гулкий двор, но не слезал с сиденья.
Здоровье мое, несмотря на отсутствие режима, улучшилось. Встретив меня, загоревшего и слегка отъевшегося, на вокзале, бабушка Женя поджала губки. Стройность была одной из основных ее добродетелей, и она весьма боялась жирного и сдобного греха.
Очень скоро после приезда домой я спросил, когда снова поеду к деду и Фене.
— Лен, ты слышала?— крикнула бабушка моей маме, и не дождавшись ответа повторила:
—Ты это слышала?
— Мам, не начинай снова, это ребенок, — мама подошла ко мне и внезапно погладила по голове. Она редко так делала, мне стало так хорошо, и я снова вспомнил качели. Мне хотелось повторить свой вопрос маме, но я не стал. А в конце длинной-длинной зимы, когда я свалился с ужасной ангиной, мама сидя у моей кровати сказала: «Бобка, ну что же ты, выздоравливай!Скоро ведь поедем к деду!»
Я выздоровел и мы поехали. Мама уехала через три дня. Была середина мая. Раз в месяц Феня наряжала нас с дедом «в парадное», и мы шли в переговорный пункт: попросить маму оставить меня еще на месяц. Вышло три раза.
Дед работал сутки через трое, и в свободные дни старательно просаливал меня в море. А вечера были мои с Феней. И качелями. Взлет— посадка — поцелуй, взлет — посадка — объятия.
— Борык, маму видишь?
— Вижу! В окно! Она спит!
— А Москву видишь?
— Вижу!
— Кремль красный?
— Синий!
— Значит, вечер!
Смех-посадка-поцелуй, тихий подъезд, мы играем в шпионов, и, чтобы не будить деда, укладываемся вместе спать на диване.
Находясь между этим хитросплетением взрослых, я совершал детские ошибки, но учился на них. Однажды я попросил бабушку Женю испечь оладушки как у Фени. «Борис, питаться жареным — вредно!» — выпалила она, но не преминула заметить под нос: «Своих детей сгубила, за моего взялась. «В моем сознании эта фраза повисла вопросом, но я промолчал. Летом меня снова отправили «на море»: у мамы появился перспективный кавалер, и без меня было сподручней.
Вопрос, зародившийся после обмолвки «моей» бабушки терзал меня, и я не знал, как поступить. Мне было уже шесть лет,и я начал ощущать какую-то неловкость в стальных объятиях Фени. К тому же я маялся, гадая, как она сгубила своих детей.Решился однажды спросить у деда. Он вздохнул, но ответил: «Утонули они на лодке с отцом их. Она с тех пор на море и несмотрит.И забудь, что я сказал, и с ней не говори.»Я и не говорил, и даже позабыл, ибо мучивший меня вопрос разрешился. А качели так и были нашими, хоть я и мог уже качаться сам. Но не мог же я сам себя целовать?
К следующему лету у деда начались проблемы со здоровьем, и вместо моря я отправлялся гулять во двор. А после драки с Толькой Коршуновым из-за Фени меня приняли в дворовое сообщество и я даже был частью «живой пирамиды», на которой стоял Толька, чтобы вырезать на тополе сердце, пронзенное стрелой, под своим «я люблю тебя». Да что там, и на море мы тоже гоняли, и строили шалаши, и даже пробовали влюбляться, и я еще не раз подрался из-за женщин. Было не до качелей.
Феня ухаживала за дедом, и в квартире поселился тонкий, но устойчивый запах лекарств. А мама вышла замуж. За Толика. За другого, конечно, но вроде он тоже намекал, что «я люблю тебя». Эту новость мне сообщила Феня и, глядя на меня, добавила: «Не куксись! Это хорошо. Вы подружитесь.» Я подумал:»Никогда!», а она оказалась права.
Все эти события: дедова болезнь, замужество мамы, драка с Толькой и дворовая дружба подвели итог моего дошкольного детства. Остались лишь воспоминания: разрозненные, малосвязные, но при этом яркие до осязаемости. И в главном из них я подлетаю на качелях вверх, а потом меня целует в макушку Феня.
Больше выездов «на море» не было, потому что началась другая жизнь. Мы приехали к деду через четыре года. На похороны.Я помню, как зашел в ту самую квартиру, а посреди большой комнаты стоял гроб. Феня провела нас с мамой мимо него в спальню и уложила спать с дороги. Назавтра была суета, похороны, поминки, и во всем этом я затерялся и чувствовал себя лишним.
Я потихоньку вышел из-за поминального стола и пошел в маленькую комнату. Сел на кровать, уставился в стену. Не знаю, сколько так просидел, но зашла Феня. Она обняла меня, и внезапно я разрыдался. Феня гладила меня по голове, а затем внимательно посмотрев в глаза, сказала: «Борык, деда все равно тебя любит. Ну, не куксись. «
Мы с мамой уехали после девятого дня. Феня предлагала мне остаться. Я выжидательно посмотрел на мать, рассчитывая, что она заявит о полной невозможности оставить меня. Но она молчала. Я отрицательно мотнул головой.
— Ну поезжайте, поезжайте, выберете время еще приехать. — Феня была тише, чем обычно, да и понятно почему.
А потом жизнь меня закружила. Это был, наверное, не тот танец, который я хотел, но отказаться не получалось. Свадьбы, рождения, болезни, похороны, встречи, расставания. Жизненное колесо неслось все быстрей, пока не застопорилось о диагноз моего собственного сына. Лейкоз. Помню глаза жены как провалы в ад и ее же бесстрастный голос, когда она перечисляла, что нужно купить в больницу. Еще доктора помню, который сказал, что «большинство случаев разрешаются благоприятно». В интернете писали, что большинство — это семьдесят процентов. И наш ребенок должен был в них попасть. Должен! И не должен в тридцать. Пусть не он. Мы стали командой по попаданию в семьдесят процентов: жена взяла на себя всё, связанное с сыном, а я должен был зарабатывать. Общение превратилось в сводки анализов. Лучше, хуже, хуже, лучше, лучше, немного хуже, немного лучше, еще немного лучше.
Мы победили. Мы попали в семьдесят. А я понял, что не чувствую ничего.
Я боялся посмотреть в глаза сыну и жене, потому что они бы это поняли. На работе подвернулась командировка, поехал. И вдруг как током дернуло: «А ведь Феня еще может быть жива! Есть шанс!»Не сама собой, конечно, эта мысль пришла, я рядом с теми местами оказался. Сделал крюк, нашел тот двор. Дверь в квартиру никто не открыл. Значит, не выпал шанс. Она бы точно дома была.
Вышел из подъезда — на лавочке тип алкоголического вида сидит. Аккуратно у него поинтересовался, не знает ли он, кто в шестьдесят четвертой квартире живет.
А он как заорет:
— Боб, ты? Точно ты! Ну ты же!
Друган детства оказался. В квартире пара молодая живет, дальние родственники Фени. А она сама давно уж померла. А до того как будто с ума сошла немного. Выходила вечерами гулять до ночи. На качелях раскачивалась и улыбалась. А потом соседи по запаху нашли ее.
— Боб, на пиво не подкинешь? Давай за встречу, — закончил он свой рассказ вполне ожидаемо.Я подкинул, а «за встречу» не стал. Он сразу побежал отовариваться, и я оглядываясь, как шпион, подошел к качелям. Всё те же. Вечная металлоконструкция. Сел боком, оттолкнулся ногой. Тополь тот же, вон на нем вырезано «Я люблю тебя» и сердце, пронзенное стрелой. Только еще что-то сверху накарябали, раньше не было. «Не куксись». «Не куксись. Я люблю тебя». Нет, не может быть. Точно: «Не куксись».
Я уперлся лбом в ствол дерева,а потом обхватил руками. Меня трясло. Нет, меня «типало». Так говорила Феня в минуты особого волнения: «Меня типает». Внезапно с утробным рыком я набрал полную грудь воздуха и разрыдался.
Я тоже люблю тебя, Феня. Я люблю тебя, дед. Я люблю жену и сына. И маму, и отчима, и сестру. И даже когда меня не станет, эта любовь останется. Но еще рано, я еще должен сказать им всем об этом хотя бы раз.
Содержание
- Как построить касательную к графику в excel
- КАК НАРИСОВАТЬ КАСАТЕЛЬНУЮ ЛИНИЮ В EXCEL — ВОКРУГ-ДОМ — 2022
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Как нарисовать цветную линию в фотошопе
- Как нарисовать линию в фотошопе
- Как нарисовать линию в Excel
- Моделирования касательной в заданной точке функции
- Как можно провести касательную к графику в экселе?
- Как построить уравнение касательной в экселе
- Как сделать касательную в excel к графику
- Как нарисовать касательную линию в Excel — Вокруг-Дом — 2021
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Как нарисовать цветную линию в фотошопе
- Как нарисовать линию в фотошопе
- Как нарисовать линию в Excel
- Как сделать касательную в excel к графику
- Метод касательной сделать в MS Excel
- Функция TAN Excel (касательная)
- Функция TAN Excel
- Формула TAN в Excel
- Как использовать TAN в Excel?
- Касательная в Excel, пример # 1
- Касательная в Excel, пример # 2
- Касательная в Excel, пример №3
- Пример функции касания # 4
- Как построить уравнение касательной в экселе
Как построить касательную к графику в excel
КАК НАРИСОВАТЬ КАСАТЕЛЬНУЮ ЛИНИЮ В EXCEL — ВОКРУГ-ДОМ — 2022
Тангенциальная линия — это прямая линия на графике, которая проходит по касательной к кривой линии, составленной из точек данных. В Excel есть возможность автоматически создавать линию тренда, или вы можете вручную нарисовать касательную линию на графике. Тангенциальная линия рисуется касаясь изогнутой линии, так что когда кривая отходит от линии, она равноудалена от линии. В то время как функция линии тренда в Excel покажет тренд всей линии, ручное рисование линии создаст истинную касательную.
Кредит: Драган Радоевич / iStock / Getty Images
Шаг 1
Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.
Шаг 2
Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.
Шаг 3
Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.
Шаг 4
Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.
Шаг 5
Нажмите на вкладку «Вставка», а затем нажмите «Фигуры». Выберите «Линия» и нарисуйте линию так, чтобы она просто касалась одной из точек на вашей кривой.
Шаг 6
Нажмите на вкладку «Инструменты рисования: Формат» и нажмите кнопку «Повернуть» справа. Выберите «Дополнительные параметры вращения». Нажмите стрелку «Вверх» или «Вниз» рядом с полем «Поворот» в диалоговом окне, которое появляется, чтобы повернуть линию на кривой. Когда линия будет равноудалена от обеих сторон кривой, нажмите «ОК».
Как нарисовать цветную линию в фотошопе
Инструменты рисования в Photoshop позволяют создавать векторные фигуры с различными атрибутами. Линии являются настолько важным элементом дизайна, что Photoshop включает в себя инструмент для рисования .
Как нарисовать линию в фотошопе
В Photoshop есть несколько способов рисования линий. Узнайте, когда и как использовать инструменты «Кисть», «Линия» и «Перо» для прямых линий и кривых.
Как нарисовать линию в Excel
Excel, программа для работы с электронными таблицами, является частью Microsoft Office Suite. В Excel 2007 есть опции для включения изображений, картинок, фигур и SmartArt. Формы включают объекты, такие как .
Моделирования касательной в заданной точке функции
В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.
Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:
где к = /'(хо) — угловой коэффициент;
Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (хмин и хмакс) и ординат (умин и умакс).
Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х2,у2), которые располагаются на границах прямоугольника.
Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х0) . Значения углового коэффициента
могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.
Пусть к > 0. Остановимся на всех возможных вариантах расположения точек. При хх = хмин с учетом формулы ух = к * (хмин — х0) + у0 .
Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем х2= хмакс и у2 = к * (хмакс — х0) + у0.
Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)
Формируем таблицы начальных условий задачи.
координат заданной точки функции(х0, у0) (F2 и G2);
углового коэффициента к = /'(х0) (Н2);
граничных значений диапазонов (хмин, хмакс, умин, умакс) (A2:D5).
Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения уг при хг = хмин и у2 при х2 = хмакс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).
Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы — Точечная, а вид — Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.
Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.
Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у0 — к * х0. Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.
Изменяя значения координаты х0, осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.
При необходимости можно дополнительно построить график производной заданной функции.
Как можно провести касательную к графику в экселе?
Excel всё-таки не бумага, чтобы на ней что-то можно было провести.
Вы табулировали некую функцию и отобразили её график. Вам надо выбрать точку и табулировать функцию производной в некой заранее заданной точке.
Уравнение касательной к табулированной функции находят разными способами на выч. методах. В сети можно найти уже готовые формулы. Если хотите сами, то надо выбрать 3 точки, наиболее близкие к заданной, представить функцию параболой, проходящей через них, а потом построить касательную к этой параболе.
Как только у вас будет уравнение прямой, табулируйте её функцию и выведите на график результат.
ЗЫ
Табулировать функцию — найти множесто пар (аргумент, значение) и вывести их в табличном виде.
Источник
Как построить уравнение касательной в экселе
Как сделать касательную в excel к графику
Как нарисовать касательную линию в Excel — Вокруг-Дом — 2021
Тангенциальная линия — это прямая линия на графике, которая проходит по касательной к кривой линии, составленной из точек данных. В Excel есть возможность автоматически создавать линию тренда, или вы можете вручную нарисовать касательную линию на графике. Тангенциальная линия рисуется касаясь изогнутой линии, так что когда кривая отходит от линии, она равноудалена от линии. В то время как функция линии тренда в Excel покажет тренд всей линии, ручное рисование линии создаст истинную касательную.
Кредит: Драган Радоевич / iStock / Getty Images
Шаг 1
Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.
Шаг 2
Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.
Шаг 3
Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.
Шаг 4
Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.
Шаг 5
Нажмите на вкладку «Вставка», а затем нажмите «Фигуры». Выберите «Линия» и нарисуйте линию так, чтобы она просто касалась одной из точек на вашей кривой.
Шаг 6
Нажмите на вкладку «Инструменты рисования: Формат» и нажмите кнопку «Повернуть» справа. Выберите «Дополнительные параметры вращения». Нажмите стрелку «Вверх» или «Вниз» рядом с полем «Поворот» в диалоговом окне, которое появляется, чтобы повернуть линию на кривой. Когда линия будет равноудалена от обеих сторон кривой, нажмите «ОК».
Как нарисовать цветную линию в фотошопе
Инструменты рисования в Photoshop позволяют создавать векторные фигуры с различными атрибутами. Линии являются настолько важным элементом дизайна, что Photoshop включает в себя инструмент для рисования .
Как нарисовать линию в фотошопе
В Photoshop есть несколько способов рисования линий. Узнайте, когда и как использовать инструменты «Кисть», «Линия» и «Перо» для прямых линий и кривых.
Как нарисовать линию в Excel
Excel, программа для работы с электронными таблицами, является частью Microsoft Office Suite. В Excel 2007 есть опции для включения изображений, картинок, фигур и SmartArt. Формы включают объекты, такие как .
Как сделать касательную в excel к графику
Argument ‘Topic id’ is null or empty
© Николай Павлов, Planetaexcel, 2006-2021
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
За изображения спасибо Depositphotos.com
ИП Павлов Николай Владимирович
ИНН 633015842586
ОГРН 310633031600071
Метод касательной сделать в MS Excel
Помощь в написании контрольных, курсовых и дипломных работ здесь.

Как найти производную? У меня программа для решения уравнения методом касательной. На форме.
Метод касательной (Ньютона). Нужно исправить программу
Program kasat; var a,b,x,eps:real;n:integer; function f (x:real):real; begin.
Как сделать вылет шара по касательной
Добрый день! Столкнулся со следующей проблемой. В моем примере два шара А и Б. А — неподвижный.

Доброго времени! За несколько часов так и не решил задачку. Файл Excel в столбце D имеет.
Как сделать в Excel сделать матрицу из коэффициентов и столбца свободных членов (ТММ)
В общем мне нужно рассчитать Синтез и кинематику шарнирного четырехзвенного механизма в Excel.
Метод SaveAs в Excel
Всем доброго времени суток.Помогите разобраться с методом SaveAs Есть,ну назовем ее,небольшая.
Метод дихотомии — MS Excel
Здравствуйте) помогите пожалуйста найти минимум функции f(X) = 2*Х^2 + EXP(-X). Есть пример этого.

Доброго времени суток! Прошу помощи с работой в MS Exel. Низко кланяюсь и извиняюсь за.
Функция TAN Excel (касательная)
Функция TAN Excel — это встроенная тригонометрическая функция в excel, которая используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.
Функция TAN Excel
Функция TAN Excel — это встроенная функция, относящаяся к категории Math / Trig function, которая возвращает значение тангенса угла. Формула для TAN всегда возвращает числовое значение.
В тригонометрии тангенс угла эквивалентен отношению перпендикуляра к основанию прямоугольного треугольника.
TAN Θ = противоположная сторона / смежная сторона
Следовательно, TAN Θ = a / b
Формула TAN в Excel
Ниже приведена формула TAN в Excel.
Где число — это аргумент, передаваемый функции в радианах.
Угол, который мы указываем в качестве входных данных, распознается функцией Tangent, только если он указан как Radians.
Чтобы преобразовать угол в радианы, используйте функцию РАДИАНЫ или преобразуйте угол в радианы с помощью математического соотношения
Радиан = угол в градусах * (π / 180)
π в Excel представлена функцией PI ()
Следовательно, радиан = градус * (PI () / 180)
Расчет значения TAN с использованием функции TAN и RADIANS
Расчет значения TAN с использованием TAN и функции PI
У функции касательной есть много реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Функция касания, используемая в системах навигации и GPS, в аэронавтике.
Например, если самолет летит на высоте 3000 м и делает угол к наблюдателю на земле 26 °, и мы хотим найти расстояние от самолета до наблюдателя.
Как мы знаем, TAN Θ = противоположная сторона / смежная сторона
Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.
А соседняя сторона = горизонтальное расстояние самолета от земли, которое неизвестно, и нам нужно его вычислить.
Итак, используя формулу для TAN, мы имеем
TAN (26 °) = 3000 / x
Следовательно, x = 3000 / (TAN (26 °))
В Excel, взяв относительные контрольные значения, мы имеем
Икс = B2 / (TAN (B3 * (PI () / 180))))
X = 6150.91 метров
Как использовать TAN в Excel?
Функция Excel TAN очень проста и удобна в использовании. Позвольте мне понять, как работает формула TAN в Excel на нескольких примерах.
Касательная в Excel, пример # 1
Мужчина ростом 6 футов находится в 55 метрах от дерева. Он делает угол обзора 47 ° параллельно земле. Мы хотим рассчитать высоту дерева.
Чтобы найти высоту дерева, мы будем использовать TAN Θ. В контексте Excel мы будем использовать функцию Tangent.
Высота дерева будет
Высота Человека + Расстояние Человека от дерева * TAN (47 °)
Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра).
Поместив все относительные значения в Excel, формула для высоты дерева будет
= (0,3 * B2) + (B3 * TAN ((B4 * (PI () / 180))))
Выходные данные TAN Excel:
Высота дерева 60,78 метра.
Касательная в Excel, пример # 2
Предположим, у нас есть пять прямоугольных треугольников с указанием их углов и длины с одной стороны, и нам нужно вычислить длину двух других сторон.
Сумма всех углов треугольника равна 180 °; следовательно, мы можем легко вычислить третий угол.
Мы знаем, Sin Θ = противоположное / гипотенуза
Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза
В Excel длина Противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN.
= E2 * SIN (C2 * (PI () / 180))
Применяя формулу TAN для пяти треугольников, мы можем получить длину перпендикуляров треугольников
Теперь у нас есть две стороны треугольника: гипотенуза и перпендикулярная сторона. Мы можем легко вычислить третью сторону (основание), используя TAN в Excel.
Мы знаем, что TAN Θ = противоположная сторона / смежная сторона.
Таким образом, длина прилегающей стороны будет Обратная сторона/ТАН Θ.
В Excel длина прилегающей стороны (основания) будет рассчитываться по формуле TAN.
= F2 / (TAN (РАДИАНЫ (C2)))
Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника.
TAN в выводе Excel:
Касательная в Excel, пример №3
Самолет делает разворот радиусом 160 м и летит с постоянным углом крена 87 °, в идеальных условиях (без колебаний ветра) рассчитайте постоянную путевую скорость самолета.
Радиус поворота задается формулой.
Радиус поворота = V 2 / g * TAN Θ
Радиус поворота 160 метров; Постоянный угол крена 87 °, g — ускорение свободного падения, значение которого составляет 9,8 м / с. 2 , поэтому путевая скорость будет
V = (Радиус поворота * (g * TAN Θ)) 1/2
Применяя приведенную выше формулу TAN в Excel со справочными значениями, мы получаем формулу TAN.
= КОРЕНЬ (B2 * (9,8 * (TAN (РАДИАНЫ (B3)))))
SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.
TAN в выводе Excel:
Итак, путевая скорость самолета составляет 172,97 м / с.
Пример функции касания # 4
У нас есть формула для TAN, обозначенная f (x) = 2c * TAN2Θ, где c — постоянное значение, равное 0,988. Значение варианта — это значение, а формула для TAN зависит от значения. Нам нужно построить график заданной функции касания.
Используя функцию Excel TAN, мы затем вычислим значения функции, поэтому, взяв контрольные значения в качестве входных данных, мы получим формулу TAN,
= 2 * 0,988 * (ТАН (РАДИАНЫ (2 * B3)))
Применяя формулу TAN к другим ячейкам, которые у нас есть,
TAN в выводе Excel:
График касательной функции:
Как построить уравнение касательной в экселе
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
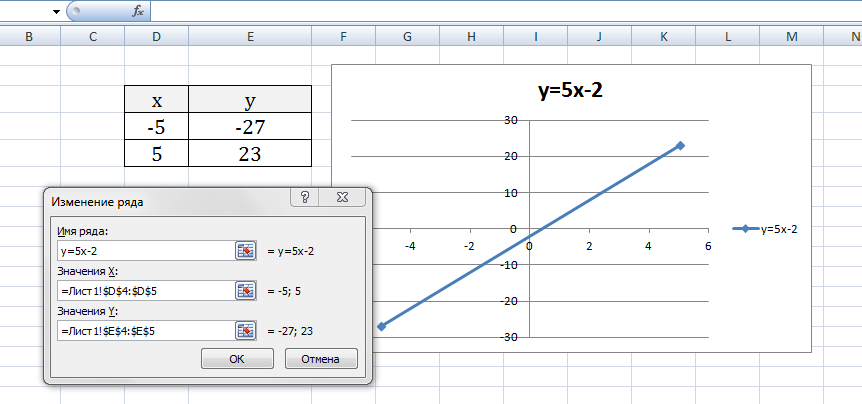
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x 2 -2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
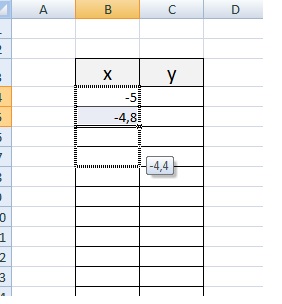
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
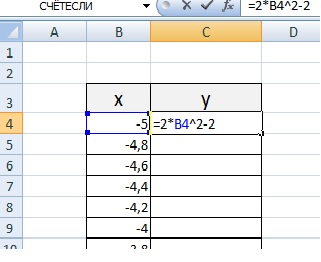
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
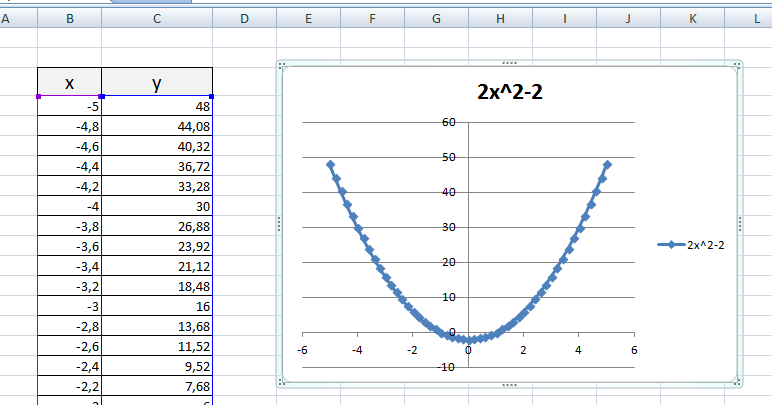
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
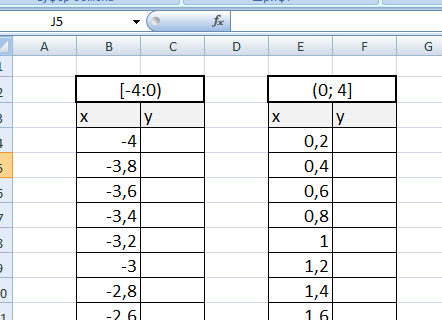
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
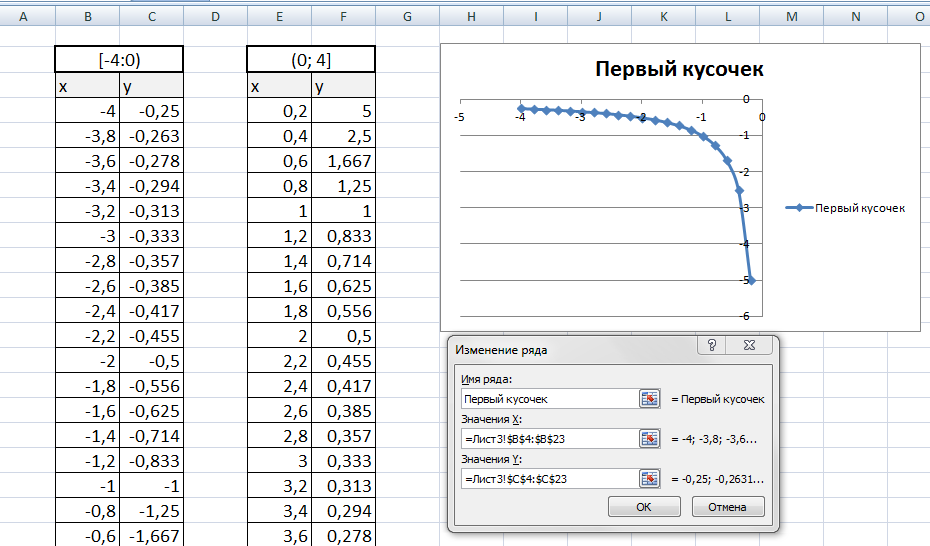
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
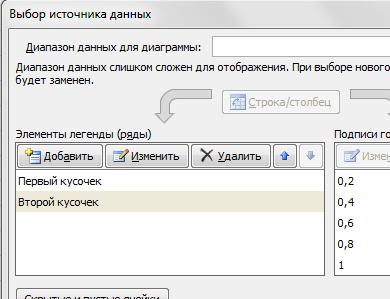
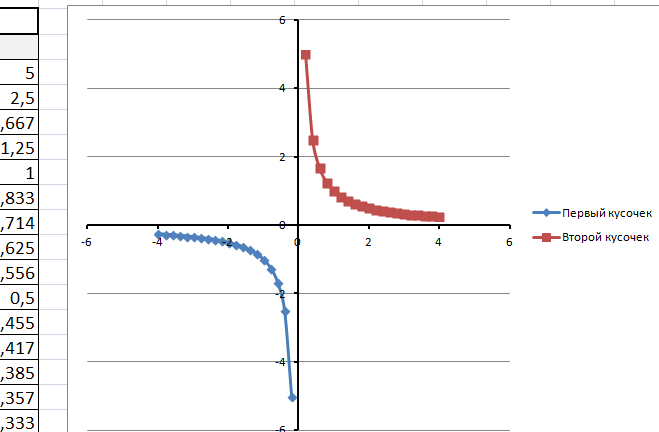
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Источник
Как нарисовать касательную линию в Excel – Вокруг-Дом – 2021 Тангенциальная линия – это прямая линия на графике, которая проходит по касательной к кривой
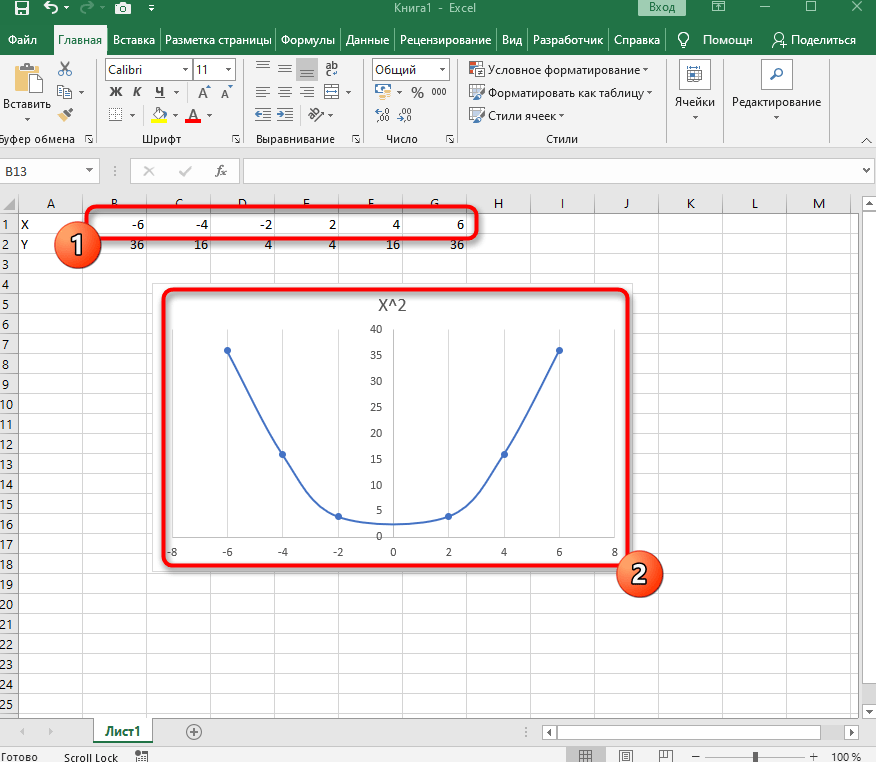
График функции F(x) = X^2
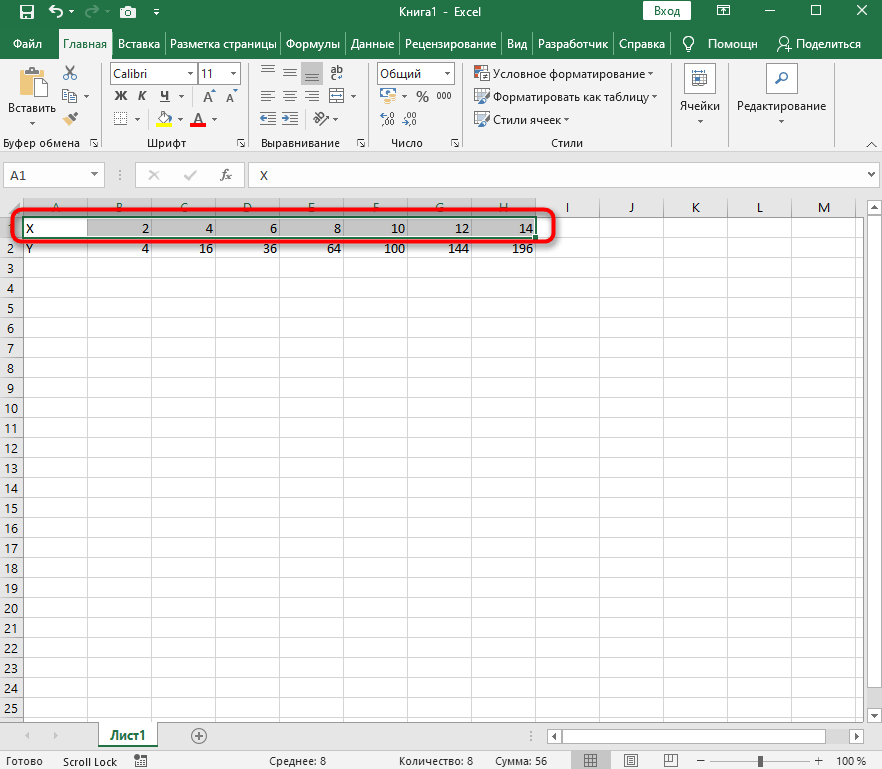
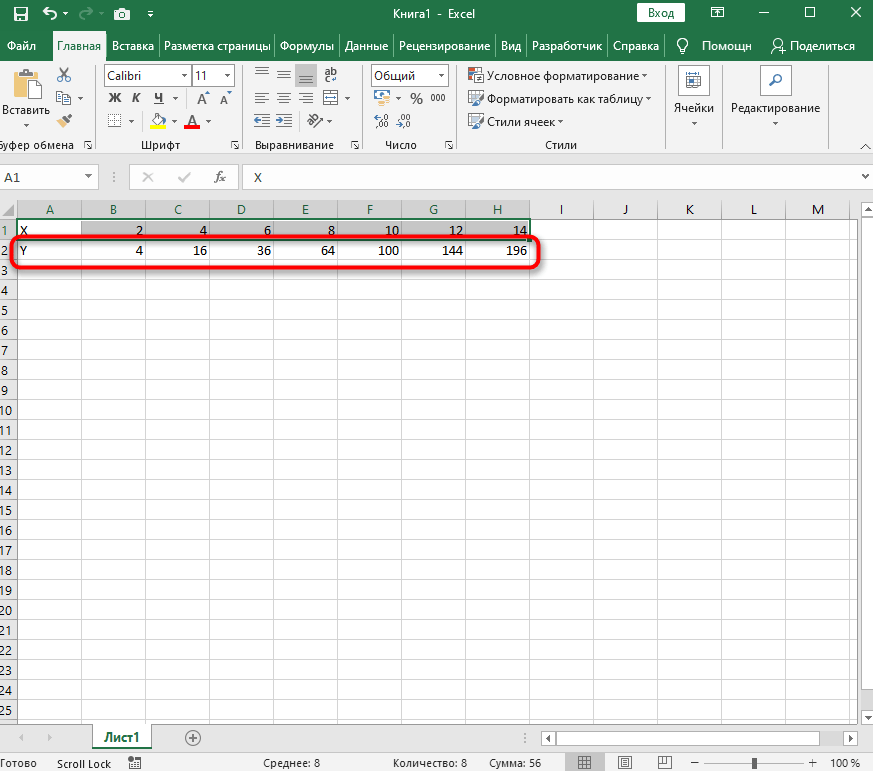
Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:
-
Создайте строку на листе в программе, вписав туда известные значения X.
-
Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.
-
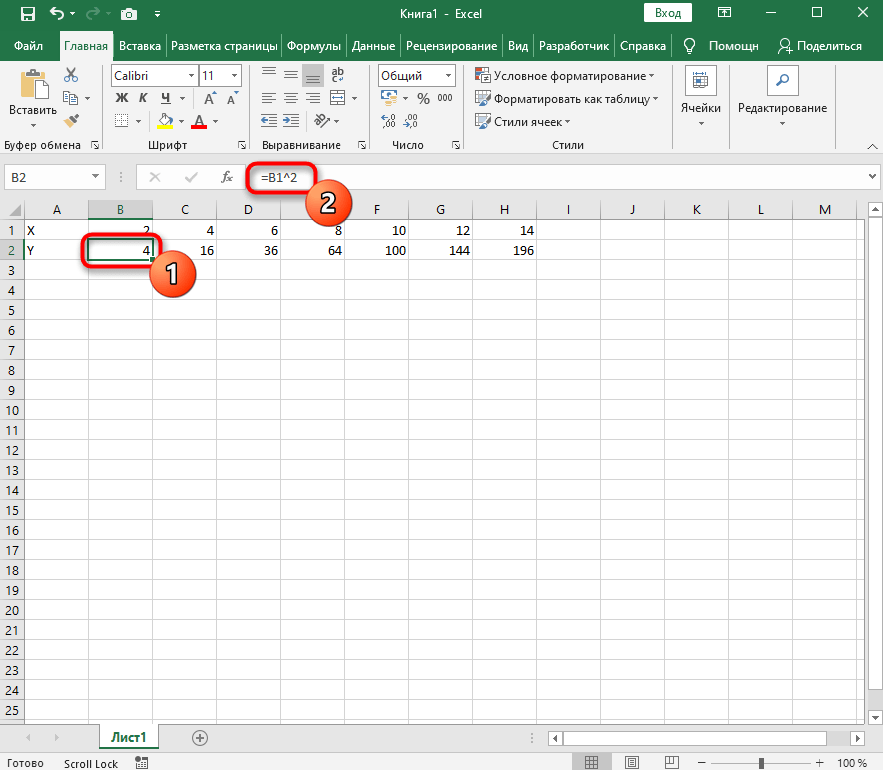
Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.
-
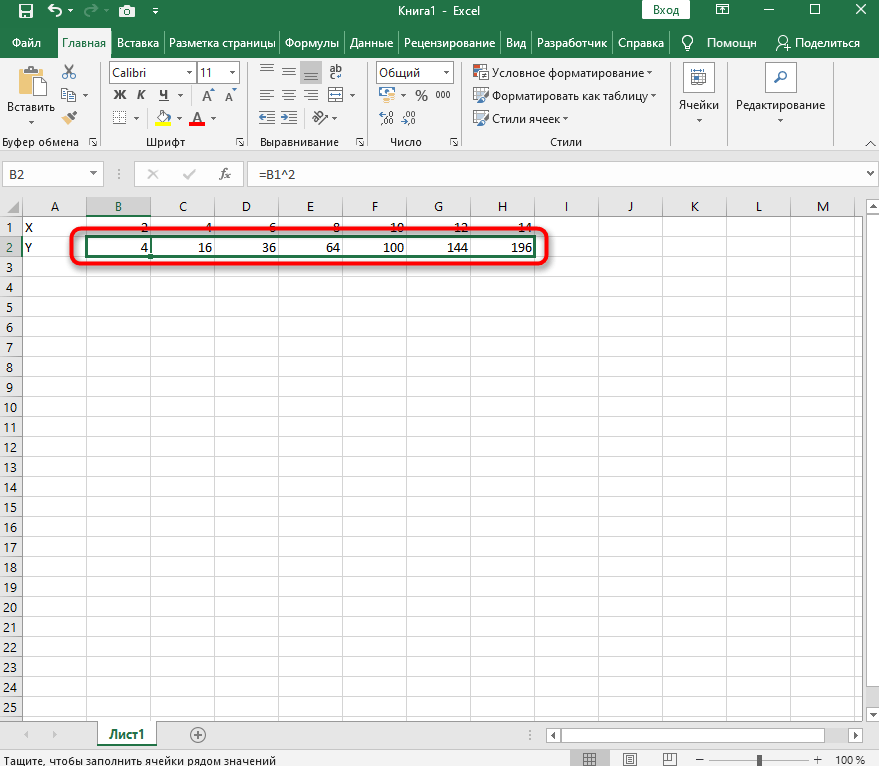
Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.
-
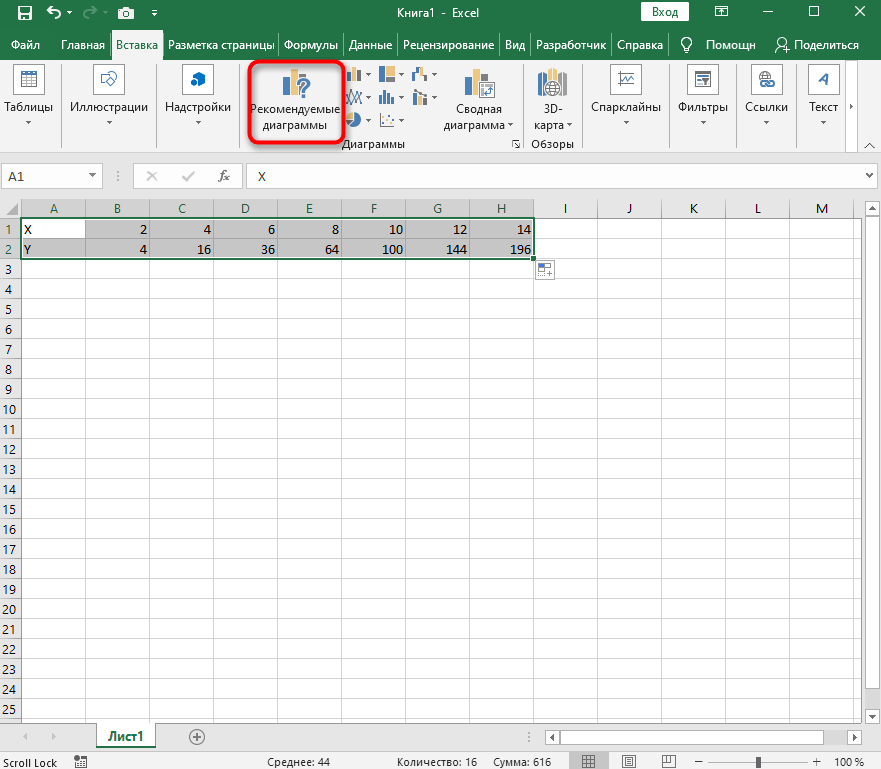
Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.
-
В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.
-
Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).
Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.
Источник: http://timeweb.com/ru/community/articles/kak-postroit-grafik-funkcii-v-excel
Шаг 1
Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.
Источник: http://ru.univdesigntechnologies.com/89-how-to-draw-a-tangential-line-in-excel-36643
Шаг 2
Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.
Источник: http://ru.univdesigntechnologies.com/89-how-to-draw-a-tangential-line-in-excel-36643
Argument ‘Topic id’ is null or empty
© Николай Павлов, Planetaexcel, 2006-2021
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
За изображения спасибо Depositphotos.com
ИП Павлов Николай Владимирович
ИНН 633015842586
ОГРН 310633031600071
Источник: http://programka.com.ua/instrukcija/excel/kak-sdelat-kasatelnuju-v-excel-k-grafiku
Шаг 3
Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.
Источник: http://ru.univdesigntechnologies.com/89-how-to-draw-a-tangential-line-in-excel-36643
Шаг 4
Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.
Источник: http://ru.univdesigntechnologies.com/89-how-to-draw-a-tangential-line-in-excel-36643
Метод касательной сделать в MS Excel
Помощь в написании контрольных, курсовых и дипломных работ здесь.

Как найти производную? У меня программа для решения уравнения методом касательной. На форме.
Метод касательной (Ньютона). Нужно исправить программу
Program kasat; var a,b,x,eps:real;n:integer; function f (x:real):real; begin.
Как сделать вылет шара по касательной
Добрый день! Столкнулся со следующей проблемой. В моем примере два шара А и Б. А — неподвижный.

Доброго времени! За несколько часов так и не решил задачку. Файл Excel в столбце D имеет.
Как сделать в Excel сделать матрицу из коэффициентов и столбца свободных членов (ТММ)
В общем мне нужно рассчитать Синтез и кинематику шарнирного четырехзвенного механизма в Excel.
Метод SaveAs в Excel
Всем доброго времени суток.Помогите разобраться с методом SaveAs Есть,ну назовем ее,небольшая.
Метод дихотомии — MS Excel
Здравствуйте) помогите пожалуйста найти минимум функции f(X) = 2*Х^2 + EXP(-X). Есть пример этого.

Доброго времени суток! Прошу помощи с работой в MS Exel. Низко кланяюсь и извиняюсь за.
Источник: http://programka.com.ua/instrukcija/excel/kak-sdelat-kasatelnuju-v-excel-k-grafiku
( 1 оценка, среднее 5 из 5 )
Задача приближенного вычисления производной может возникнуть в тех случаях, когда неизвестно аналитическое выражение для исследуемой функции. Функция может быть задана таблично, или известен только график функции, полученный, например, в результате показаний датчиков параметров технологического процесса.
Иногда, при решении некоторых задач на компьютере, из-за громоздкости выкладок может оказаться более удобным вычисление производных численным методом, чем аналитическим. При этом, разумеется, необходимо обосновать применяемый численный метод, т. е. убедиться в том, что погрешность численного метода находится в приемлемых границах.
Одним из эффективных методов решения дифференциальных уравнений является разностный метод, когда вместо искомой функции рассматривается таблица ее значений в определенных точках, при этом производные приближенно заменяются разностными формулами.
Пусть известен график функции у = f (х ) на отрезке [а ,b ].Можно построить график производной функции, вспомнив ее геометрический смысл. Воспользуемся тем фактом, что производная функции в точке х равна тангенсу угла наклона к оси абсцисс касательной к ее графику в этой точке.
у 1 = = tgα = f ¢ (x 0), и точка М 0 (х 0 , у 1) принадлежит графику производной.
Чтобы построить график производной, необходимо разбить отрезок [а , b ]на несколько частей точками х i , затем для каждой точки графически построить значение производной и соединить полученные точки плавной кривой с помощью лекал.
На рис. 5.2 показано построение пяти точек М 1, М 2 . , М 5 и графика производной.
1. Строим касательную к графику функции у = f (x )в точке (х 1 , f (x 1));из точки (-1, 0) параллельно касательной в точке (х 1 , f (x 1)) проведем прямую до пересечения с осью ординат; эта точка пересечения дает значение производной f ¢ (х 1).Строим точку М 1 (х 1 , f ¢ (х 1)).
2. Аналогично построим остальные точки М 2 , М 3 , М 4 и М 5 .
3. Соединяем точки М 1 , М 2 , М 3 , М 4 , М 5 плавной кривой.
Точность графического способа определения производной невысока. Мы приводим описание этого способа только в учебных целях.
Замечание . Если в алгоритме построения графика производной вместо точки (-1, 0) взять точку (-l ,0), где l > 0, то график будет построен в другом масштабе по оси ординат.
5 . 2 .Разностные формулы
а) Разностные формулы для обыкновенных производных
Разностные формулы для приближенного вычисления производной подсказаны самим определением производной. Пусть значения функции в точках x i обозначены через y i :
y i = f (x i ), x i = a+ ih , i = 0, 1, . , n; h =
Мы рассматриваем случай равномерного распределения точек на отрезке [a , b ]. Для приближенного вычисления производных в точках x i можно использовать следующие разностные формулы , или разностные производные .
Так как предел отношения (5.1) при h ® 0 равен правой производной в точке х i , то это отношение иногда называют правой разностной производной в точке x i .По аналогичной причине отношение (5.2) называют левой разностной производной в точке x i .Отношение (5.3) называют центральной разностной производной в точке x i .
Оценим погрешность разностных формул (5.1)–(5.3), предполагая, что функция f (x ) разлагается в ряд Тейлора в окрестности точки x i :
Полагая в (5.4) х = x i + h или х = х i — h , получим
Непосредственной подстановкой разложений (5.5) и (5.6) в формулу (5.10) можно получить зависимость между второй производной функции и разностной формулой для производной второго порядка .
Первый заключается в том, что мы наш набор точек аппроксимируем стандартной функцией Excel, то есть подбираем функцию, которая лучше всего ложится на наши точки (в Excel это линейная функция, логарифмическая, экспоненциальная, полиномиальная и степенная). Второй способ – численное дифференцирование, для которого нам нужно будет только умение вводить формулы.
Производной функции f (x) в точке x называется предел отношения приращения Δf функции в точке x к приращению Δx аргумента, когда последнее стремится к нулю:
Вот и воспользуемся этим знанием: будем просто брать для расчета производной очень маленькие значения приращения аргумента, т.е. Δx.
Для вычисления этой производной в каждой точке мы производим вычисления с использованием двух соседних точек: первая с координатой ε 0 по горизонтальной оси, а вторая с координатой x 0 + Δx, т.е. одна – производную в которой вычисляем и та, что поправее. Вычисленная таким образом производная называется разностной производной вправо (вперед) с шагом Δ x .
Можем поступить наоборот, взяв уже другие две соседние точки: x 0 — Δx и x 0 , т.е интересующую нас и ту, что левее. Получаем формулу для вычисления разностной производной влево (назад) с шагом — Δ x .
Предыдущие формулы были «левые» и «правые», а есть еще одна формула, которая позволяет вычислять центральную разностною производную с шагом 2 Δx, и которая чаще других используется для численного дифференцирования:
Для проверки формулы рассмотрим простой пример с известной функцией y=x 3 . Построим таблицу в Excel с двумя с столбцами: x и y, а затем построим график по имеющимся точкам.
Производная функции y=x 3 это y=3x 2 , график которой, т.е. параболу, мы и должны получить с использованием наших формул.
Попробуем вычислить значения центральной разностной производной в точках х. Для этого. В ячейке второй строки нашей таблицы забиваем нашу формулу (3), т.е. следующую формулу в Excel:
Теперь строим график с использованием уже имеющихся значений х и полученных значений центральной разностной производной:
А вот и наша красненькая парабола! Значит, формула работает!
Вот наша кривая в координатах «истинное напряжение — истинная деформация» σ-ε:
Действуем так же, как и в предыдущем примере и получаем вот такую кривую:
Это и есть изменение скорости упрочнения по ходу деформации. Что с ней делать, это уже отдельный вопрос.
Известно, что численными приближенными методами производная функции в заданной точке может быть вычислена с использованием формулы конечных разностей. Выражение для вычисления производной функции одной переменной в точке х k записанное в конечных разностях, имеет вид
При достаточно малых значениях Δх, можно с приемлемой точностью получить величину производной функции в точке. Для вычисления производной в MS Excel будем использовать приведенную выше формулу. Рассмотрим технологию вычисления производной на примере .
Пример 1.18 Найти производную функции у = 2х 3 + х 2 в точке х=3. Заметим, что производная приведенной функции в точке х=3, вычисленная аналитическим методом, равна 60 — это значение нам понадобится для проверки результата, полученного путем вычисления численным методом.
Задачу вычисления производной в табличном процессоре можно решать двумя способами.
Введем в ячейку рабочего листа формулу правой части заданной функциональной зависимости например в ячейку В2, как показано на рисунке, делая ссылку на ячейку, где будет находиться значение х, например А2,
Зададим окрестность точки х=3 достаточно малого размера, например значение слева х k =2,9999999, а значение справа х k +1 =3,00000001, и введем эти значения в ячейку А2 и А3 соответственно. В ячейку С2 введем формулу вычисления производной =(В3-В2)/(А3-А2).
В результате вычисления в ячейку С2 будет выведено приближенное значение производной заданной функции в точке х=3, величина которой равна 60, что соответствует результату, полученному аналитически (рис.1.24).
Введем в ячейку рабочего листа А2 заданное значение аргумента, равное 3, в ячейке В2 укажем достаточно малое приращение аргумента — (1E — 9), в ячейку С2 введем формулу для вычисления производной
После нажатия клавиши получим результат вычисления 60,0000.
Как видим, результат получен такой же, как и при первом способе. Приведенный второй способ является более предпочтительным в случаях, когда нужно построить таблицу значений производной функции для заданных значений аргумента.
Напомним, что функция Y=f(x) имеет экстремум при значении х = х k если производная функции в этой точке равна нулю.
Если функция f(x) непрерывна на отрезке [а, b] и имеет внутри этого отрезка локальный экстремум, то его можно найти, используя надстройку Excel Поиск решения.
Рассмотрим последовательность нахождения экстремума функции на примере
Пример 1.19 Задана неразрывная функция у = х 2 + х + 2. Требуется найти ее экстремум (минимальное значение) на отрезке [-2; 2].
В ячейку A3 рабочего листа введем любое число, принадлежащее заданному отрезку, в этой ячейке будет находиться значение х.
В ячейку В3 введем формулу, определяющую заданную функциональную зависимость. Вместо переменной х в этой формуле должна быть ссылка на ячейку А3: =А3^2+A3+2.
В открывшемся окне диалога Поиск решения в поле Установить целевую ячейку укажем адрес ячейки, содержащей формулу (В3), установим переключатель Минимальному значению, в поле Измени ячейки укажем адрес ячейки, в которой содержится переменная х-A3.
Добавим два ограничения в соответствующее поле: A3 > = — 2 и A3 ) i =(y i +1 -y i -1 )/(x i +1 -x i -1 )
Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.
В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.
Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.
Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
Предполагается, что балка до приложения нагрузок была абсолютно прямой, а после нагружения находится в зоне упругих деформаций.
На рисунке ниже показана расчетная схема задачи и общий вид эпюр.
На следующем скриншоте представлены исходные данные.
10. Так как балка нагружена симметрично относительно своей середины, то реакции обеих опор одинаковы и равны каждая половине суммарной нагрузки:
R =(q *z max +8*F 1 +2*F 2 )/2=(0,985*8000+8*9000+2*50000)/2=85 440 Н
Задача:
Найти значения изгибающего момента M xi в сечениях балки аналитически по формулам сопротивления материалов и методом численного дифференцирования расчетной линии прогибов. Сравнить и проанализировать полученные результаты.
Решение:
Первое, что мы сделаем, это выполним расчет в Excel поперечных сил Q y , изгибающих моментов M x , углов поворота U x оси балки и прогибов V x по классическим формулам сопромата во всех сечениях с шагом h . (Хотя, в принципе, значения сил и углов нам в дальнейшем не понадобятся.)
Результаты вычислений находятся в ячейках I5-L54. На скриншоте ниже показана половина таблицы, так как значения во второй ее части зеркальны или аналогичны представленным значениям.
Использованные в расчетах формулы можно посмотреть .
Итак, нам известны точные значения моментов и прогибов.
Угол поворота – это первая производная прогиба U =V’ .
Предположим, что столбец точных значений прогибов получен не аналитическими расчетами, а замерами на реальной балке и у нас больше нет никаких других данных. Вычислим вторые производные от точных значений прогибов, используя формулу (6) из таблицы предыдущего раздела статьи, и найдем значения моментов методом численного дифференцирования.
Точные значения моментов, рассчитанные по аналитическим формулам сопромата с учетом веса самой балки, отличаются от найденных по приближенным формулам вычисления производных незначительно. Моменты определены весьма точно, судя по относительным погрешностям, рассчитанным в процентах в ячейках N5-N54.
Поставленная задача решена. Мы выполнили вычисление производной второго порядка по приближенной формуле с использованием центральных конечных разностей и получили отличный результат.
Зная точные значения прогибов можно методом численного дифференцирования с высокой точностью найти действующие в сечениях моменты и определить степень нагруженности балки!
Однако.
Увы, не стоит думать, что на практике легко получить необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!
Дело в том, что измерения прогибов требуется выполнять с точностью ~1 мкм и стараться максимально уменьшать шаг замеров h , «устремляя его к нулю», хотя и это может не помочь избежать ошибок.
Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.
Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$.
Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i =4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении (ε 21 =1,813%).
Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.
Вычисление производной численными методами всегда необходимо выполнять очень осторожно!
Уважаемые читатели, отзывы и комментарии к статье, размещайте в специальном блоке ниже статьи.
Чтобы получать информацию о выходе новых статей на блоге, подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи.
Прошу УВАЖАЮЩИХ труд автора скачать файл с примером ПОСЛЕ ПОДПИСКИ на анонсы статей.
[expert_bq id=»1570″]y — 1 15 x 3 18 x 2 105 x 176 , x — ; — 2 1 15 x 3 — 6 x 2 9 x 12 , x — 2 ; y — 1 5 x 2 12 x 35 , x — ; — 2 1 5 x 2 — 4 x 3 , x — 2 ;. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5
Урок по теме: уравнение касательной к графику функции
Непосредственной подстановкой разложений (5.5) и (5.6) в формулу (5.10) можно получить зависимость между второй производной функции и разностной формулой для производной второго порядка .
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 < α < π 2 или 0 ° < α 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 < α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.
Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.
Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .
Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .
Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x < 0 .
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .
Необходимо найти производную в точке со значением — 1 . Получаем, что
y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Ответ: уравнение касательной приобретает вид
y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5
Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что
y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )
y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )
Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3
Вычисляем значение функции в точке х = — 2 , где получаем, что
- y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
- Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .
Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .
— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞
y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3
Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 < 0
Другое уравнение имеет два действительных корня, тогда
1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3
Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.
y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk
3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3
y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3
Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Данное равенство может быть записано как объединение двух функций:
y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.
Касательная к эллипсу
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид
y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5
Касательная к гиперболе
Гипербола может быть представлена в виде двух объединенных функций вида
В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .
Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3
Ответ: уравнение касательной можно представить как
Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a
Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Начинаем решение с представления параболы в качестве двух функций. Получим, что
— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4
Касательная к графику функции
2 способ.
1) Находим уравнение касательной к графику функции у=f(х) в точке с абсциссой а.
2) Находим уравнение касательной к графику функции у=g(х) в точке с абсциссой а.
3) Полученные прямые должны совпадать, т. е. решаем систему:
k1=k2,
b1=b2.
[expert_bq id=»1570″]Решение таких задач основывается на том, что координаты точки А n;m должны удовлетворять искомому уравнению касательной решая уравнение m f a f a m-a найдем а и, таким образом, приходим к задаче первого типа; находим точки пересечения двух графиков, решая уравнения f x g x и у g х или у f x ; находим корень данной системы уравнений. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$.
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 < α < π 2 или 0 ° < α 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 < α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
2 способ.
Прямая у=kх+b является касательной к графику функции у=f(x) в том и только том случае, если существует такое значение а, при котором совпадают значения данных функций и значения их производных, т. е. Совместна система
f(a)=ka+b,
f’(a)=k.