Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Кроме неожиданных результатов, формулы иногда возвращают значения ошибок. Ниже представлены некоторые инструменты, с помощью которых вы можете искать и исследовать причины этих ошибок и определять решения.
Примечание: В статье также приводятся методы, которые помогут вам исправлять ошибки в формулах. Этот список не исчерпывающий — он не охватывает все возможные ошибки формул. Для получения справки по конкретным ошибкам поищите ответ на свой вопрос или задайте его на форуме сообщества Microsoft Excel.
Ввод простой формулы
Формулы — это выражения, с помощью которых выполняются вычисления со значениями на листе. Формула начинается со знака равенства (=). Например, следующая формула складывает числа 3 и 1:
=3+1
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
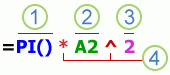
Части формулы
-
Функции: это специальные формулы Excel, которые выполняют определенные вычисления. Например, функция ПИ() возвращает значение числа Пи: 3,142…
-
Ссылки: это ссылки на отдельные ячейки или диапазоны. Например, A2 возвращает значение ячейки A2.
-
Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.
-
Операторы: оператор * (звездочка) служит для умножения чисел, а оператор ^ (крышка) — для возведения числа в степень. С помощью + и – можно складывать и вычитать значения, а с помощью / — делить их.
Примечание: Для некоторых функций требуются так называемые аргументы. Аргументы — это значения, которые некоторые функции используют при вычислениях. Аргументы функции указываются в ее скобках (). Функция ПИ не требует аргументов, поэтому у нее пустые скобки. У некоторых функций несколько аргументов, в том числе необязательные. Аргументы разделяются точкой с запятой (;).
Например, функция СУММ требует только один аргумент, но у нее может быть до 255 аргументов (включительно).
Пример одного аргумента: =СУММ(A1:A10).
Пример нескольких аргументов: =СУММ(A1:A10;C1:C10).
В приведенной ниже таблице собраны некоторые наиболее частые ошибки, которые допускают пользователи при вводе формулы, и описаны способы их исправления.
|
Рекомендация |
Дополнительные сведения |
|
Начинайте каждую формулу со знака равенства (=) |
Если опустить знак равенства, введенные данные могут отображаться в виде текста или даты. Например, при вводе СУММ(A1:A10)Excel отображает текстовую строку SUM(A1:A10) и не выполняет вычисление. Если ввести значение 11/2, вместо деления 11 на 2 Excel отображается дата 2–ноя (при условии, что ячейка имеет формат «Общий«) вместо деления 11 на 2. |
|
Следите за соответствием открывающих и закрывающих скобок |
Все скобки должны быть парными (открывающая и закрывающая). Если в формуле используется функция, для ее правильной работы важно, чтобы все скобки стояли в правильных местах. Например, формула =ЕСЛИ(B5<0);»Недопустимо»;B5*1,05) не будет работать, поскольку в ней две закрывающие скобки и только одна открывающая (требуется одна открывающая и одна закрывающая). Правильный вариант этой формулы выглядит так: =ЕСЛИ(B5<0;»Недопустимо»;B5*1,05). |
|
Для указания диапазона используйте двоеточие |
Указывая диапазон ячеек, разделяйте с помощью двоеточия (:) ссылку на первую ячейку в диапазоне и ссылку на последнюю ячейку в диапазоне. Например, =SUM(A1:A5), а не =SUM(A1 A5), которые возвращают #NULL! Ошибка. |
|
Вводите все обязательные аргументы |
У некоторых функций есть обязательные аргументы. Старайтесь также не вводить слишком много аргументов. |
|
Вводите аргументы правильного типа |
В некоторых функциях, например СУММ, необходимо использовать числовые аргументы. В других функциях, например ЗАМЕНИТЬ, требуется, чтобы хотя бы один аргумент имел текстовое значение. Если использовать в качестве аргумента данные неправильного типа, Excel может возвращать непредвиденные результаты или ошибку. |
|
Число уровней вложения функций не должно превышать 64 |
В функцию можно вводить (или вкладывать) не более 64 уровней вложенных функций. |
|
Имена других листов должны быть заключены в одинарные кавычки |
Если формула содержит ссылки на значения или ячейки на других листах или в других книгах, а имя другой книги или листа содержит пробелы или другие небуквенные символы, его необходимо заключить в одиночные кавычки (‘), например: =’Данные за квартал’!D3 или =‘123’!A1. |
|
Указывайте после имени листа восклицательный знак (!), когда ссылаетесь на него в формуле |
Например, чтобы возвратить значение ячейки D3 листа «Данные за квартал» в той же книге, воспользуйтесь формулой =’Данные за квартал’!D3. |
|
Указывайте путь к внешним книгам |
Убедитесь, что каждая внешняя ссылка содержит имя книги и путь к ней. Ссылка на книгу содержит имя книги и должна быть заключена в квадратные скобки ([Имякниги.xlsx]). В ссылке также должно быть указано имя листа в книге. В формулу также можно включить ссылку на книгу, не открытую в Excel. Для этого необходимо указать полный путь к соответствующему файлу, например: =ЧСТРОК(‘C:My Documents[Показатели за 2-й квартал.xlsx]Продажи’!A1:A8). Эта формула возвращает количество строк в диапазоне ячеек с A1 по A8 в другой книге (8). Примечание: Если полный путь содержит пробелы, как в приведенном выше примере, необходимо заключить его в одиночные кавычки (в начале пути и после имени книги перед восклицательным знаком). |
|
Числа нужно вводить без форматирования |
Не форматируйте числа, которые вводите в формулу. Например, если нужно ввести в формулу значение 1 000 рублей, введите 1000. Если вы введете какой-нибудь символ в числе, Excel будет считать его разделителем. Если вам нужно, чтобы числа отображались с разделителями тысяч или символами валюты, отформатируйте ячейки после ввода чисел. Например, если для прибавления 3100 к значению в ячейке A3 используется формула =СУММ(3 100;A3), Excel не складывает 3100 и значение в ячейке A3 (как было бы при использовании формулы =СУММ(3100;A3)), а суммирует числа 3 и 100, после чего прибавляет полученный результат к значению в ячейке A3. Другой пример: если ввести =ABS(-2 134), Excel выведет ошибку, так как функция ABS принимает только один аргумент: =ABS(-2134). |
Вы можете использовать определенные правила для поиска ошибок в формулах. Они не гарантируют исправление всех ошибок на листе, но могут помочь избежать распространенных проблем. Эти правила можно включать и отключать независимо друг от друга.
Существуют два способа пометки и исправления ошибок: последовательно (как при проверке орфографии) или сразу при появлении ошибки во время ввода данных на листе.
Ошибку можно исправить с помощью параметров, отображаемых приложением Excel, или игнорировать, щелкнув команду Пропустить ошибку. Ошибка, пропущенная в конкретной ячейке, не будет больше появляться в этой ячейке при последующих проверках. Однако все пропущенные ранее ошибки можно сбросить, чтобы они снова появились.
-
Для Excel в Windows щелкните Параметры > файла > формулы.
Для Excel на Mac щелкните меню Excel > Параметры > проверки ошибок.В Excel 2007 нажмите кнопку Microsoft Office
и выберите Параметры Excel > Формулы.
-
В разделе Поиск ошибок установите флажок Включить фоновый поиск ошибок. Все найденные ошибки помечаются треугольником в левом верхнем углу ячейки.
-
Чтобы изменить цвет треугольника, которым помечаются ошибки, выберите нужный цвет в поле Цвет индикаторов ошибок.
-
В разделе Правила поиска ошибок установите или снимите флажок для любого из следующих правил:
-
Ячейки, содержащие формулы, которые приводят к ошибке. Формула не использует ожидаемый синтаксис, аргументы или типы данных. Значения ошибок: #DIV/0!, #N/A, #NAME?, #NULL!, #NUM!, #REF!и #VALUE!. Каждое из этих значений ошибок имеет разные причины и разрешается по-разному.
Примечание: Если ввести значение ошибки прямо в ячейку, оно сохраняется как значение ошибки, но не помечается как ошибка. Но если на эту ячейку ссылается формула из другой ячейки, эта формула возвращает значение ошибки из ячейки.
-
Несогласованная формула вычисляемого столбца в таблицах. Вычисляемый столбец может содержать отдельные формулы, отличающиеся от формулы главного столбца, что создает исключение. Исключения вычисляемого столбца возникают при указанных ниже действиях.
-
Ввод данных, не являющихся формулой, в ячейку вычисляемого столбца.
-
Введите формулу в ячейку вычисляемого столбца, а затем нажмите клавиши CTRL+Z или нажмите кнопку Отменить
на панели быстрого доступа.
-
Ввод новой формулы в вычисляемый столбец, который уже содержит одно или несколько исключений.
-
Копирование в вычисляемый столбец данных, не соответствующих формуле столбца. Если копируемые данные содержат формулу, эта формула перезапишет данные в вычисляемом столбце.
-
Перемещение или удаление ячейки из другой области листа, если на эту ячейку ссылалась одна из строк в вычисляемом столбце.
-
-
Ячейки, содержащие годы, представленные в виде 2 цифр: ячейка содержит текстовую дату, которая может быть неправильно интерпретирована как неправильный век, если она используется в формулах. Например, дата в формуле =ГОД(«1.1.31») может относиться как к 1931, так и к 2031 году. Используйте это правило для выявления дат в текстовом формате, допускающих двоякое толкование.
-
Числа в формате текста или предшествуют апострофу. Ячейка содержит числа, хранящиеся в виде текста. Обычно это является следствием импорта данных из других источников. Числа, хранящиеся как текст, могут стать причиной неправильной сортировки, поэтому лучше преобразовать их в числовой формат. ‘=SUM(A1:A10) рассматривается как текст.
-
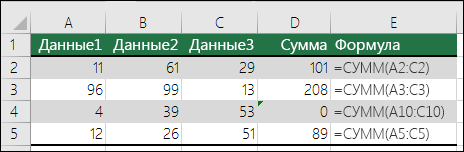
Формулы, несовместимые с другими формулами в регионе. Формула не соответствует шаблону других формул, расположенных рядом с ней. Во многих случаях формулы, соседствующие с другими формулами, отличаются только используемыми ссылками. В следующем примере из четырех смежных формул Excel отображает ошибку рядом с формулой =СУММ(A10:C10) в ячейке D4, так как смежные формулы увеличиваются на одну строку, а одна — на 8 строк. Excel ожидает формулу =СУММ(A4:C4).
Если используемые в формуле ссылки не соответствуют ссылкам в смежных формулах, приложение Microsoft Excel сообщит об ошибке.
-
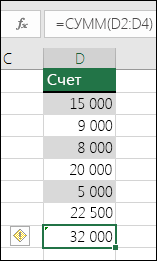
Формулы, опускающие ячейки в области. Формула не может автоматически включать ссылки на данные, которые вы вставляете между исходным диапазоном данных и ячейкой, содержащей формулу. Это правило позволяет сравнить ссылку в формуле с фактическим диапазоном ячеек, смежных с ячейкой, содержащей формулу. Если смежные ячейки содержат дополнительные значения и не являются пустыми, Excel отображает рядом с формулой ошибку.
Например, при использовании этого правила Excel отображает ошибку для формулы =СУММ(D2:D4), поскольку ячейки D5, D6 и D7, смежные с ячейками, на которые ссылается формула, и ячейкой с формулой (D8), содержат данные, на которые должна ссылаться формула.
-
Незаблокированные ячейки, содержащие формулы. Формула не заблокирована для защиты. По умолчанию все ячейки на листе блокируются, поэтому их нельзя изменить при защите листа. Это поможет избежать случайных ошибок, таких как случайное удаление или изменение формул. Эта ошибка указывает, что ячейка была разблокирована, но лист не был защищен. Убедитесь, что ячейка не заблокирована.
-
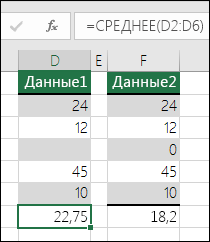
Формулы, ссылающиеся на пустые ячейки. Формула содержит ссылку на пустую ячейку. Это может привести к неверным результатам, как показано в приведенном далее примере.
Предположим, требуется найти среднее значение чисел в приведенном ниже столбце ячеек. Если третья ячейка пуста, она не используется в расчете, поэтому результатом будет значение 22,75. Если эта ячейка содержит значение 0, результат будет равен 18,2.
-
Данные, введенные в таблицу, недопустимы. В таблице возникает ошибка проверки. Проверьте параметр проверки ячейки, перейдя на вкладку Данные > группу Data Tools > Проверка данных.
-
-
Выберите лист, на котором требуется проверить наличие ошибок.
-
Если расчет листа выполнен вручную, нажмите клавишу F9, чтобы выполнить расчет повторно.
Если диалоговое окно Поиск ошибок не отображается, щелкните вкладку Формулы, выберите Зависимости формул и нажмите кнопку Поиск ошибок.
-
Чтобы повторно проверить пропущенные ранее ошибки, щелкните Файл > Параметры > Формулы. Для Excel на Mac щелкните меню Excel > Параметры > проверки ошибок.
В разделе Поиск ошибок выберите Сброс пропущенных ошибок и нажмите кнопку ОК.
Примечание: Сброс пропущенных ошибок применяется ко всем ошибкам, которые были пропущены на всех листах активной книги.
Совет: Советуем расположить диалоговое окно Поиск ошибок непосредственно под строкой формул.
-
Нажмите одну из управляющих кнопок в правой части диалогового окна. Доступные действия зависят от типа ошибки.
-
Нажмите кнопку Далее.
Примечание: Если нажать кнопку Пропустить ошибку, помеченная ошибка при последующих проверках будет пропускаться.
-
Рядом с ячейкой нажмите кнопку «Проверка ошибок »
, а затем выберите нужный параметр. Доступные команды различаются для каждого типа ошибки, и первая запись описывает ошибку.
Если нажать кнопку Пропустить ошибку, помеченная ошибка при последующих проверках будет пропускаться.
Если формула не может правильно вычислить результат, в Excel отображается значение ошибки, например #####, #ДЕЛ/0!, #Н/Д, #ИМЯ?, #ПУСТО!, #ЧИСЛО!, #ССЫЛКА!, #ЗНАЧ!. Ошибки разного типа имеют разные причины и разные способы решения.
Приведенная ниже таблица содержит ссылки на статьи, в которых подробно описаны эти ошибки, и краткое описание.
|
Статья |
Описание |
|
Исправление ошибки #### |
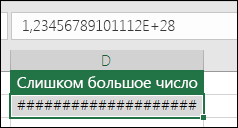
Эта ошибка отображается в Excel, если столбец недостаточно широк, чтобы показать все символы в ячейке, или ячейка содержит отрицательное значение даты или времени. Например, результатом формулы, вычитающей дату в будущем из даты в прошлом (=15.06.2008-01.07.2008), является отрицательное значение даты. Совет: Попробуйте автоматически изменить ширину ячейки, дважды щелкнув между заголовками столбцов. Если ### отображается потому, что Excel не может отобразить все знаки, эта проблема будет исправлена. |
|
Исправление ошибки #ДЕЛ/0! #ПУСТО! |
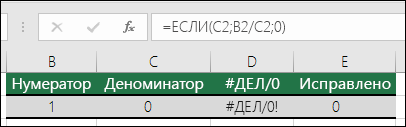
Эта ошибка отображается в Excel, если число делится на ноль (0) или на ячейку без значения. Совет: Добавьте обработчик ошибок, как в примере ниже: =ЕСЛИ(C2;B2/C2;0). |
|
Исправление ошибки #Н/Д |
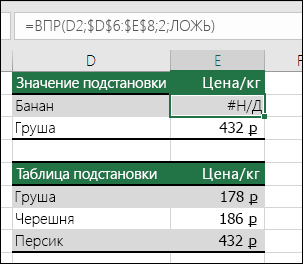
Эта ошибка отображается в Excel, если функции или формуле недоступно значение. Если вы используете такую функцию, как ВПР, есть ли для искомого значения соответствие в диапазоне поиска? Скорее всего, нет. Используйте функцию ЕСЛИОШИБКА для подавления ошибки #Н/Д. В этом случае можно ввести следующее: =ЕСЛИОШИБКА(ВПР(D2;$D$6:$E$8;2;ИСТИНА);0) |
|
Исправление ошибки #ИМЯ? #ПУСТО! |
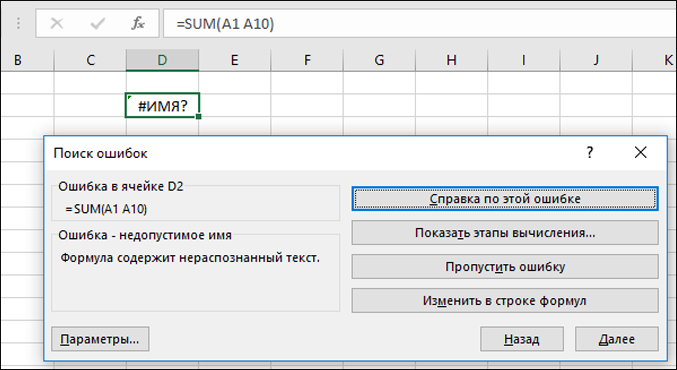
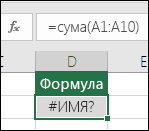
Эта ошибка отображается, если Excel не распознает текст в формуле. Например имя диапазона или имя функции написано неправильно. Примечание: Если вы используете функцию, убедитесь, что ее имя написано неправильно. В данном случае слово СУММ введено с ошибкой. Удалите «а», и Excel исправит формулу. |
|
Исправление ошибки #ПУСТО! |
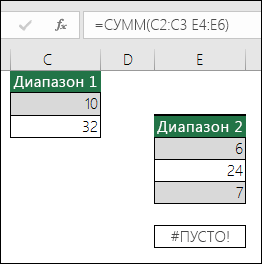
Эта ошибка отображается в Excel, когда вы указываете пересечение двух областей, которые не пересекаются. Оператором пересечения является пробел, разделяющий ссылки в формуле. Примечание: Убедитесь, что диапазоны разделены правильно: области C2:C3 и E4:E6 не пересекаются, поэтому ввод формулы =СУММ(C2:C3 E4:E6) возвращает #NULL! Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!. Если поставить запятую между диапазонами C и E, она будет исправлена =СУММ(C2:C3;E4:E6) |
|
Исправление ошибки #ЧИСЛО! #ПУСТО! |
Эта ошибка отображается в Excel, если формула или функция содержит недопустимые числовые значения. Используете ли вы функцию, которая выполняет итерацию, например IRR или RATE? Если да, то #NUM! ошибка, вероятно, из-за того, что функция не может найти результат. Инструкции по устранению неполадок см. в разделе справки. |
|
Исправление ошибки #ССЫЛКА! #ПУСТО! |
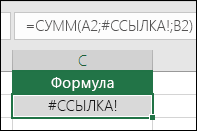
Эта ошибка отображается в Excel при наличии недопустимой ссылки на ячейку. Например, вы удалили ячейки, на которые ссылались другие формулы, или вставили поверх них другие ячейки. Вы случайно удалили строку или столбец? Смотрите, что произошло после удаления столбца B в формуле =СУММ(A2;B2;C2). Нажмите кнопку Отменить (или клавиши CTRL+Z), чтобы отменить удаление, измените формулу или используйте ссылку на непрерывный диапазон (=СУММ(A2:C2)), которая автоматически обновится при удалении столбца B. |
|
Исправление ошибки #ЗНАЧ! #ПУСТО! |
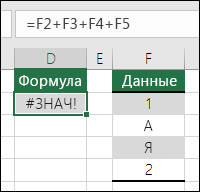
Эта ошибка отображается в Excel, если в формуле используются ячейки, содержащие данные не того типа. Вы используйте математические операторы (+, -, *, / ^) с разными типами данных? В таком случае попробуйте использовать вместо них функцию. В этом случае =СУММ(F2:F5) поможет устранить проблему. |
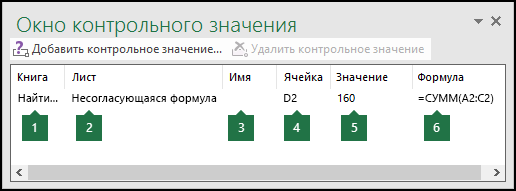
Если ячейки не видны на листе, для просмотра их и содержащихся в них формул можно использовать панель инструментов «Окно контрольного значения». С помощью окна контрольного значения удобно изучать, проверять зависимости или подтверждать вычисления и результаты формул на больших листах. При этом вам не требуется многократно прокручивать экран или переходить к разным частям листа.
Эту панель инструментов можно перемещать и закреплять, как и любую другую. Например, можно закрепить ее в нижней части окна. На панели инструментов выводятся следующие свойства ячейки: 1) книга, 2) лист, 3) имя (если ячейка входит в именованный диапазон), 4) адрес ячейки 5) значение и 6) формула.
Примечание: Для каждой ячейки может быть только одно контрольное значение.
Добавление ячеек в окно контрольного значения
-
Выделите ячейки, которые хотите просмотреть.
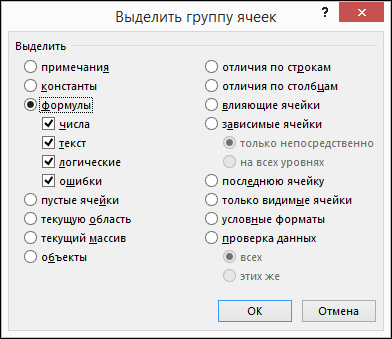
Чтобы выделить все ячейки с формулами, на вкладке Главная в группе Редактирование нажмите кнопку Найти и выделить (вы также можете нажать клавиши CTRL+G или CONTROL+G на компьютере Mac). Затем выберите Выделить группу ячеек и Формулы.
-
На вкладке Формулы в группе Зависимости формул нажмите кнопку Окно контрольного значения.
-
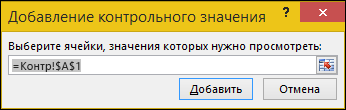
Нажмите кнопку Добавить контрольное значение.
-
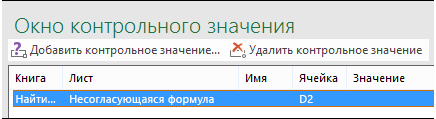
Убедитесь, что вы выделили все ячейки, которые хотите отследить, и нажмите кнопку Добавить.
-
Чтобы изменить ширину столбца, перетащите правую границу его заголовка.
-
Чтобы открыть ячейку, ссылка на которую содержится в записи панели инструментов «Окно контрольного значения», дважды щелкните запись.
Примечание: Ячейки, содержащие внешние ссылки на другие книги, отображаются на панели инструментов «Окно контрольного значения» только в случае, если эти книги открыты.
Удаление ячеек из окна контрольного значения
-
Если окно контрольного значения не отображается, на вкладке Формула в группе Зависимости формул нажмите кнопку Окно контрольного значения.
-
Выделите ячейки, которые нужно удалить.
Чтобы выделить несколько ячеек, щелкните их, удерживая нажатой клавишу CTRL.
-
Нажмите кнопку Удалить контрольное значение.
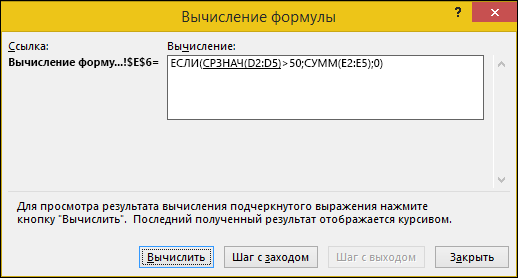
Иногда трудно понять, как вложенная формула вычисляет конечный результат, поскольку в ней выполняется несколько промежуточных вычислений и логических проверок. Но с помощью диалогового окна Вычисление формулы вы можете увидеть, как разные части вложенной формулы вычисляются в заданном порядке. Например, формулу =ЕСЛИ(СРЗНАЧ(D2:D5)>50;СУММ(E2:E5);0) будет легче понять, если вы увидите промежуточные результаты:
|
В диалоговом окне «Вычисление формулы» |
Описание |
|
=ЕСЛИ(СРЗНАЧ(D2:D5)>50;СУММ(E2:E5);0) |
Сначала выводится вложенная формула. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ. Диапазон ячеек D2:D5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(D2:D5) возвращает результат 40. |
|
=ЕСЛИ(40>50;СУММ(E2:E5);0) |
Диапазон ячеек D2:D5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(D2:D5) возвращает результат 40. |
|
=ЕСЛИ(ЛОЖЬ;СУММ(E2:E5);0) |
Поскольку 40 не больше 50, выражение в первом аргументе функции ЕСЛИ (аргумент лог_выражение) имеет значение ЛОЖЬ. Функция ЕСЛИ возвращает значение третьего аргумента (аргумент значение_если_ложь). Функция СУММ не вычисляется, поскольку она является вторым аргументом функции ЕСЛИ (аргумент значение_если_истина) и возвращается только тогда, когда выражение имеет значение ИСТИНА. |
-
Выделите ячейку, которую нужно вычислить. За один раз можно вычислить только одну ячейку.
-
Откройте вкладку Формулы и выберите Зависимости формул > Вычислить формулу.
-
Нажмите кнопку Вычислить, чтобы проверить значение подчеркнутой ссылки. Результат вычисления отображается курсивом.
Если подчеркнутая часть формулы является ссылкой на другую формулу, нажмите кнопку Шаг с заходом, чтобы отобразить другую формулу в поле Вычисление. Нажмите кнопку Шаг с выходом, чтобы вернуться к предыдущей ячейке и формуле.
Кнопка Шаг с заходом недоступна для ссылки, если ссылка используется в формуле во второй раз или если формула ссылается на ячейку в отдельной книге.
-
Продолжайте нажимать кнопку Вычислить, пока не будут вычислены все части формулы.
-
Чтобы посмотреть вычисление еще раз, нажмите кнопку Начать сначала.
-
Чтобы закончить вычисление, нажмите кнопку Закрыть.
Примечания:
-
Некоторые части формул, в которых используются функции ЕСЛИ и ВЫБОР, не вычисляются. В таких случаях в поле Вычисление отображается значение #Н/Д.
-
Если ссылка пуста, в поле Вычисление отображается нулевое значение (0).
-
Некоторые функции вычисляются заново при каждом изменении листа, так что результаты в диалоговом окне Вычисление формулы могут отличаться от тех, которые отображаются в ячейке. Это функции СЛЧИС, ОБЛАСТИ, ИНДЕКС, СМЕЩ, ЯЧЕЙКА, ДВССЫЛ, ЧСТРОК, ЧИСЛСТОЛБ, ТДАТА, СЕГОДНЯ, СЛУЧМЕЖДУ.
Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Отображение связей между формулами и ячейками
Рекомендации, позволяющие избежать появления неработающих формул
Нужна дополнительная помощь?
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12678 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://exceltable.com/otchety/reshenie-uravneniy
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
Идентификация ошибок осуществляется несколькими способами. Один из них реализуется через отображение кода ошибки в ячейке.
|
Ошибка |
Описание |
|
#Н/Д |
Н/Д – является сокращением термина Неопределённые данные. Помогает предотвратить использование ссылки на пустую ячейку |
|
#ЧИСЛО! |
Функция с числовым аргументом использует неприемлемый аргумент |
|
#ИМЯ? |
Ошибка в написании имени или используется несуществующее имя |
|
#ССЫЛКА! |
Используется ссылка на несуществующую ячейку |
|
#ЗНАЧ! |
Вместо числового или логического значения введён текст, и Excel не может преобразовать его к нужному типу данных |
|
#ДЕЛ/0! |
В качестве делителя используется ссылка на ячейку, в которой содержится нулевое или пустое значение (если ссылкой является пустая ячейка, то её содержимое интерпретируется как ноль) |
|
#ПУСТО! |
Используется ошибочная ссылка на ячейку |
|
############# |
Данные не помещаются в ячейку по ширине, следует увеличить ширину столбца или применить более компактное форматирование |
Второй способ обнаружения ошибок – Excel отображает в левом верхнем углу ячейки зелёный треугольник (индикатор ошибки). При выборе такой ячейки появляется смарт-тег проверки ошибок.
Для проверки ошибок необходимо выполнить следующие шаги:
1. Выберите лист, который требуется проверить на наличие ошибок.
2. На вкладке Формулы в группе Зависимости формул нажмите кнопку Проверка наличия ошибок. Откроется окно диалога Контроль ошибок.
3. В окне диалога Контроль ошибок просмотрите информацию о текущей ошибке в левой части окна.
4. Для просмотра более детального описания ошибки и возможных вариантов её исправления нажмите кнопку Справка по этой ошибке.
5. Нажмите кнопку Показать этапы вычисления. MS Excel откроет окно диалога Вычисление формулы, где вы сможете просмотреть значения различных частей вложенной формулы, вычисляемые в порядке расчёта формулы:
a) нажмите кнопку Вычислить, чтобы проверить значение подчёркнутой ссылки. Результат вычислений показан курсивом;
b) если подчёркнутая часть формулы является ссылкой на другую формулу, нажмите кнопку Шаг с заходом, чтобы отобразить другую формулу в поле Вычисление. Нажмите кнопку Шаг с выходом, чтобы вернуться в предыдущую ячейку и формулу;
c) Выполняйте указанные действия, пока не будет вычислена каждая часть формулы;
d) Чтобы снова увидеть вычисления, нажмите кнопку Заново;
e) Чтобы завершить вычисления, нажмите кнопку Закрыть.
6. Для изменения формулы в строке формул нажмите кнопку Изменить в строке формул.
7. Если ошибка является несущественной, вы можете нажать кнопку Пропустить ошибку. Помеченная ошибка при последующих проверках будет пропускаться.
8. Для перехода к следующей ошибке нажмите кнопку Далее. Для возврата к предыдущей – кнопку Назад.
9. Доведите до конца проверку ошибок и закройте окно диалога Контроль ошибок.
Трассировка связей между формулами и ячейками
Для удобства поиска причин ошибок, а также и в некоторых других случаях можно графически отобразить связь между
ячейками в формуле.
Для отображения ячеек, входящих в формулу в качестве аргументов, необходимо выделить
ячейку с формулой и нажать кнопку Влияющие ячейки в группе Зависимости формул вкладки Формулы.
Один щелчок по кнопке Влияющие ячейки отображает связи с
ячейками, непосредственно определяющими результат вычисления. Если в этих ячейках также находятся формулы, то следующий щелчок отображает связи с
ячейками, являющимися аргументами этих формул. И так далее.
Для отображения ячеек, в формулы которых входит какая-либо ячейка, её следует выделить и нажать кнопку Зависимые ячейки в группе Зависимости формул вкладки Формулы.
Один щелчок по кнопке Зависимые ячейки отображает связи с
ячейками, непосредственно зависящими от выделенной
ячейки. Если эти
ячейки также влияют на другие
ячейки, то следующий щелчок отображает связи с зависимыми
ячейками. И так далее.
Связи в пределах текущего листа отображаются синими стрелками. Связи с
ячейками других листов и книг отображаются чёрными пунктирными линиями и значком листа. Красные стрелки показывают
ячейки, вызывающие ошибки.
Для скрытия стрелок связей следует нажать кнопку Убрать все стрелки в группе Зависимости формул вкладки Формулы. Использование окна контрольных значений.
Если вы работаете с большой таблицей, содержащей формулы, которые ссылаются на различные ячейки текущей таблицы и/или ячейки другого листа, достаточно сложно отследить их взаимосвязи.
В этом случае вашим помощником может выступать панель инструментов Окно контрольного значения.
Окно контрольного значения значительно упрощает анализ, проверку зависимостей и подтверждение вычислений и результатов формул на больших листах. Благодаря окну контрольного значения не требуется постоянно прокручивать лист, когда вы работаете с большой таблицей, переходить к различным его частям.
Добавление ячеек в окно контрольных значений
Для добавления на панель контрольных значений выполните следующие действия:
1. Выделите ячейки, контрольные значения которых нужно поместить на панель.
Чтобы выделить все ячейки листа с формулами, на вкладке Главная в группе Правка нажмите кнопку Найти и выделить и выберите команду Формулы.
2. На вкладке Формулы в группе Зависимости формул нажмите кнопку Окно контрольного значения.
.
4. В окне диалога Добавление контрольного значения проверьте правильность выбранного диапазона и нажмите кнопку Добавить.
Циклические ссылки
Циклические ссылки возникают, когда формула в какой-либо ячейке посредством других ячеек ссылается сама на себя.
Например, ячейка С4 = Е7, Е7 = С11, С11 = С4. В итоге С4 ссылается на С4.
Появление циклических ссылок очень легко определить. При их возникновении или наличии в уже созданной книге Excel сразу же появляется предупреждение о циклической ссылке, которое и описывает суть явления.
При нажатии на кнопку OK сообщение будет закрыто, а в ячейке, содержащей циклическую ссылку, в большинстве случаев появится 0.
Предупреждение, как правило, появляется при первоначальном создании циклической ссылки или открытии книги, содержащей циклические ссылки. Если предупреждение принято, то при дальнейшем возникновении циклических ссылок оно может не появляться.
Циклические ссылки в Excel могут создаваться преднамеренно, для решения тех или иных задач финансового моделирования, а могут возникать случайно, в виде технических ошибок и ошибок в логике построения модели.
В первом случае мы знаем об их наличии, так как сами их предварительно создали, и знаем, зачем они нам нужны.
Во втором случае мы можем вообще не знать, где они находятся, например, при открытии чужого файла и появлении сообщения о наличии циклических ссылок.
Найти циклическую ссылку можно несколькими способами. Например, чисто визуально формулы и ячейки, участвующие в образовании циклических ссылок в Excel, отмечаются синими стрелками.
Если циклическая ссылка – одна на листе, то в строке состояния будет выведено сообщение о наличии циклических ссылок с адресом ячейки.
Если циклические ссылки есть ещё и на других листах кроме активного, то будет выведено сообщение без указания ячейки.
Найти циклическую ссылку можно также при помощи инструмента поиска ошибок.
На вкладке Формулы в группе Зависимости формул выберите элемент Поиск ошибок и в раскрывающемся списке пункт Циклические ссылки.
Вы увидите адрес ячейки с первой встречающейся циклической ссылкой. После её корректировки или удаления – со второй и т. д.
Итак, используя вышеперечисленные инструменты и приёмы, вы сможете облегчить поиск, исправление и предупреждение ошибок в рабочих книгах Excel.
Успехов!!!
Свидетельство о регистрации СМИ: Эл № ФС77-67462 от 18 октября 2016 г.
Контакты редакции: +7 (495) 784-73-75, smi@4dk.ru
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12677 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Поиск ошибок в формулах
Кроме неожиданных результатов, формулы иногда возвращают значения ошибок. Ниже представлены некоторые инструменты, с помощью которых вы можете искать и исследовать причины этих ошибок и определять решения.
Примечание: В статье также приводятся методы, которые помогут вам исправлять ошибки в формулах. Этот список не исчерпывающий — он не охватывает все возможные ошибки формул. Для получения справки по конкретным ошибкам поищите ответ на свой вопрос или задайте его на форуме сообщества Microsoft Excel.
Ввод простой формулы
Формулы — это выражения, с помощью которых выполняются вычисления со значениями на листе. Формула начинается со знака равенства (=). Например, следующая формула складывает числа 3 и 1:
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
Функции: это специальные формулы Excel, которые выполняют определенные вычисления. Например, функция ПИ() возвращает значение числа Пи: 3,142.
Ссылки: это ссылки на отдельные ячейки или диапазоны. Например, A2 возвращает значение ячейки A2.
Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.
Операторы: оператор * (звездочка) служит для умножения чисел, а оператор ^ (крышка) — для возведения числа в степень. С помощью + и – можно складывать и вычитать значения, а с помощью / — делить их.
Примечание: Для некоторых функций требуются так называемые аргументы. Аргументы — это значения, которые некоторые функции используют при вычислениях. Аргументы функции указываются в ее скобках (). Функция ПИ не требует аргументов, поэтому у нее пустые скобки. У некоторых функций несколько аргументов, в том числе необязательные. Аргументы разделяются точкой с запятой (;).
Например, функция СУММ требует только один аргумент, но у нее может быть до 255 аргументов (включительно).
Пример одного аргумента: =СУММ(A1:A10).
Пример нескольких аргументов: =СУММ(A1:A10;C1:C10).
В приведенной ниже таблице собраны некоторые наиболее частые ошибки, которые допускают пользователи при вводе формулы, и описаны способы их исправления.
Начинайте каждую формулу со знака равенства (=)
Если не упустить знака равно, введите текст или дату. Например, если ввести СУММ(A1:A10),Excel отображает текстовую строку СУММ(A1:A10) и не выполняет вычисления. Если ввести 11/2,Excel отобразит дату 2-ноя (предполагается, что формат ячейки — Общий),а не деление 11 на 2.
Следите за соответствием открывающих и закрывающих скобок
Все скобки должны быть парными (открывающая и закрывающая). Если в формуле используется функция, для ее правильной работы важно, чтобы все скобки стояли в правильных местах. Например, формула =ЕСЛИ(B5 =ЕСЛИ(B5 Для указания диапазона используйте двоеточие
Указывая диапазон ячеек, разделяйте с помощью двоеточия (:) ссылку на первую ячейку в диапазоне и ссылку на последнюю ячейку в диапазоне. Например, =СУММ(A1:A5), а не =СУММ(A1 A5),который возвращает #NULL! Ошибка.
Вводите все обязательные аргументы
У некоторых функций есть обязательные аргументы. Старайтесь также не вводить слишком много аргументов.
Вводите аргументы правильного типа
В некоторых функциях, например СУММ, необходимо использовать числовые аргументы. В других функциях, например ЗАМЕНИТЬ, требуется, чтобы хотя бы один аргумент имел текстовое значение. Если использовать в качестве аргумента данные неправильного типа, Excel может возвращать непредвиденные результаты или ошибку.
Число уровней вложения функций не должно превышать 64
В функцию можно вводить (или вкладывать) не более 64 уровней вложенных функций.
Имена других листов должны быть заключены в одинарные кавычки
Если формула содержит ссылки на значения или ячейки на других листах или в других книгах, а имя другой книги или листа содержит пробелы или другие небуквенные символы, его необходимо заключить в одиночные кавычки (‘), например: =’Данные за квартал’!D3 или =‘123’!A1.
Указывайте после имени листа восклицательный знак (!), когда ссылаетесь на него в формуле
Например, чтобы возвратить значение ячейки D3 листа «Данные за квартал» в той же книге, воспользуйтесь формулой =’Данные за квартал’!D3.
Указывайте путь к внешним книгам
Убедитесь, что каждая внешняя ссылка содержит имя книги и путь к ней.
Ссылка на книгу содержит имя книги и должна быть заключена в квадратные скобки ( [Имякниги.xlsx]). В ссылке также должно быть указано имя листа в книге.
В формулу также можно включить ссылку на книгу, не открытую в Excel. Для этого необходимо указать полный путь к соответствующему файлу, например: =ЧСТРОК(‘C:My Documents[Показатели за 2-й квартал.xlsx]Продажи’!A1:A8). Эта формула возвращает количество строк в диапазоне ячеек с A1 по A8 в другой книге (8).
Примечание: Если полный путь содержит пробелы, как в приведенном выше примере, необходимо заключить его в одиночные кавычки (в начале пути и после имени книги перед восклицательным знаком).
Числа нужно вводить без форматирования
Не форматируйте числа, которые вводите в формулу. Например, если нужно ввести в формулу значение 1 000 рублей, введите 1000. Если вы введете какой-нибудь символ в числе, Excel будет считать его разделителем. Если вам нужно, чтобы числа отображались с разделителями тысяч или символами валюты, отформатируйте ячейки после ввода чисел.
Например, если для прибавления 3100 к значению в ячейке A3 используется формула =СУММ(3 100;A3), Excel не складывает 3100 и значение в ячейке A3 (как было бы при использовании формулы =СУММ(3100;A3)), а суммирует числа 3 и 100, после чего прибавляет полученный результат к значению в ячейке A3. Другой пример: если ввести =ABS(-2 134), Excel выведет ошибку, так как функция ABS принимает только один аргумент: =ABS(-2134).
Вы можете использовать определенные правила для поиска ошибок в формулах. Они не гарантируют исправление всех ошибок на листе, но могут помочь избежать распространенных проблем. Эти правила можно включать и отключать независимо друг от друга.
Существуют два способа пометки и исправления ошибок: последовательно (как при проверке орфографии) или сразу при появлении ошибки во время ввода данных на листе.
Ошибку можно исправить с помощью параметров, отображаемых приложением Excel, или игнорировать, щелкнув команду Пропустить ошибку. Ошибка, пропущенная в конкретной ячейке, не будет больше появляться в этой ячейке при последующих проверках. Однако все пропущенные ранее ошибки можно сбросить, чтобы они снова появились.
Чтобы Excel на Windows, щелкните Файл > Параметры > Формулыили
для Excel на Mac щелкните меню Excel параметры > параметры > проверки ошибок.
В Excel 2007 нажмите кнопку Microsoft Office 
В разделе Поиск ошибок установите флажок Включить фоновый поиск ошибок. Все найденные ошибки помечаются треугольником в левом верхнем углу ячейки.
Чтобы изменить цвет треугольника, которым помечаются ошибки, выберите нужный цвет в поле Цвет индикаторов ошибок.
В разделе Правила поиска ошибок установите или снимите флажок для любого из следующих правил:
Ячейки, содержащие формулы,которые могут привести к ошибке. Формула не использует ожидаемый синтаксис, аргументы или типы данных. Значения ошибок: #DIV/0!, #N/A, #NAME?, #NULL!, #NUM!, #REF! и #VALUE!. Каждое из этих значений ошибок имеет разные причины и решается разными способами.
Примечание: Если ввести значение ошибки прямо в ячейку, оно сохраняется как значение ошибки, но не помечается как ошибка. Но если на эту ячейку ссылается формула из другой ячейки, эта формула возвращает значение ошибки из ячейки.
Несогласоваемая формула вычисляемого столбца в таблицах. Вычисляемая формула может включать отдельные формулы, отлича которые отличаются от формулы этого столбца, что создает исключение. Исключения вычисляемого столбца возникают при указанных ниже действиях.
Ввод данных, не являющихся формулой, в ячейку вычисляемого столбца.
Введите формулу в ячейку вычисляемого столбца и нажмите CTRL+Z или кнопку Отменить 
Ввод новой формулы в вычисляемый столбец, который уже содержит одно или несколько исключений.
Копирование в вычисляемый столбец данных, не соответствующих формуле столбца. Если копируемые данные содержат формулу, эта формула перезапишет данные в вычисляемом столбце.
Перемещение или удаление ячейки из другой области листа, если на эту ячейку ссылалась одна из строк в вычисляемом столбце.
Ячейки, содержащие годы,представленные в виде двух цифр. Ячейка содержит дату в текстовом сообщении, которая может быть неправильно интерпретирована как неправильное век, если оно используется в формулах. Например, дата в формуле =ГОД(«1.1.31») может относиться как к 1931, так и к 2031 году. Используйте это правило для выявления дат в текстовом формате, допускающих двоякое толкование.
Числа, отформатированные как текстили предшествующие апострофом: ячейка содержит числа, хранимые как текст. Обычно это является следствием импорта данных из других источников. Числа, хранящиеся как текст, могут стать причиной неправильной сортировки, поэтому лучше преобразовать их в числовой формат. ‘=СУММ(A1:A10) — это текст.
Формулы, несогласованныес другими формулами в регионе: формула не соответствует шаблону других формул рядом с ней. Во многих случаях формулы, смежные с другими формулами, отличаются только от ссылок. В следующем примере четырех смежных формул Excel отображает ошибку рядом с формулой =СУММ(A10:C10) в ячейке D4, так как смежные формулы приращены на одну строку, а эта формула приращена на 8 строк — Excel ожидает формулу =СУММ(A4:C4).
Если используемые в формуле ссылки не соответствуют ссылкам в смежных формулах, приложение Microsoft Excel сообщит об ошибке.
Формулы,которые не содержат ячеек в области. Формула не может автоматически включать ссылки на данные, вставленные между исходным диапазоном данных и ячейкой, содержаной формулу. Это правило позволяет сравнить ссылку в формуле с фактическим диапазоном ячеек, смежных с ячейкой, содержащей формулу. Если смежные ячейки содержат дополнительные значения и не являются пустыми, Excel отображает рядом с формулой ошибку.
Например, при использовании этого правила Excel отображает ошибку для формулы =СУММ(D2:D4), поскольку ячейки D5, D6 и D7, смежные с ячейками, на которые ссылается формула, и ячейкой с формулой (D8), содержат данные, на которые должна ссылаться формула.
Незаблокировка ячеек с формулами:формула не заблокирована для защиты. По умолчанию все ячейки на этом сайте заблокированы, поэтому их нельзя изменить, если он защищен. Это поможет избежать случайных ошибок, таких как случайное удаление или изменение формул. Эта ошибка указывает на то, что ячейка разблокирована, но лист не защищен. Убедитесь, что ячейка не заблокирована.
Формулы, ссылающие на пустые ячейки:формула содержит ссылку на пустую ячейку. Это может привести к неверным результатам, как показано в приведенном далее примере.
Предположим, требуется найти среднее значение чисел в приведенном ниже столбце ячеек. Если третья ячейка пуста, она не используется в расчете, поэтому результатом будет значение 22,75. Если эта ячейка содержит значение 0, результат будет равен 18,2.
Данные, введенные в таблицу,недопустимы: в таблице есть ошибка проверки. Проверьте параметры проверки для ячейки, на вкладке Данные в группе > Data Tools > проверки данных.
Выберите лист, на котором требуется проверить наличие ошибок.
Если расчет листа выполнен вручную, нажмите клавишу F9, чтобы выполнить расчет повторно.
Если диалоговое окно Поиск ошибок не отображается, щелкните вкладку Формулы, выберите Зависимости формул и нажмите кнопку Поиск ошибок.
Чтобы повторно проверить пропущенные ранее ошибки, щелкните Файл > Параметры > Формулы. Для Excel Mac щелкните меню Excel параметры > параметры > проверки ошибок.
В разделе Поиск ошибок выберите Сброс пропущенных ошибок и нажмите кнопку ОК.
Примечание: Сброс пропущенных ошибок применяется ко всем ошибкам, которые были пропущены на всех листах активной книги.
Совет: Советуем расположить диалоговое окно Поиск ошибок непосредственно под строкой формул.
Нажмите одну из управляющих кнопок в правой части диалогового окна. Доступные действия зависят от типа ошибки.
Нажмите кнопку Далее.
Примечание: Если нажать кнопку Пропустить ошибку, помеченная ошибка при последующих проверках будет пропускаться.
Рядом с ячейкой нажмите кнопку Проверка ошибок 
Если нажать кнопку Пропустить ошибку, помеченная ошибка при последующих проверках будет пропускаться.
Если формула не может правильно вычислить результат, в Excel отображается значение ошибки, например #####, #ДЕЛ/0!, #Н/Д, #ИМЯ?, #ПУСТО!, #ЧИСЛО!, #ССЫЛКА!, #ЗНАЧ!. Ошибки разного типа имеют разные причины и разные способы решения.
Приведенная ниже таблица содержит ссылки на статьи, в которых подробно описаны эти ошибки, и краткое описание.
Эта ошибка отображается в Excel, если столбец недостаточно широк, чтобы показать все символы в ячейке, или ячейка содержит отрицательное значение даты или времени.
Например, результатом формулы, вычитающей дату в будущем из даты в прошлом (=15.06.2008-01.07.2008), является отрицательное значение даты.
Совет: Попробуйте автоматически изменить ширину ячейки, дважды щелкнув между заголовками столбцов. Если ### отображается потому, что Excel не может отобразить все знаки, эта проблема будет исправлена.
Эта ошибка отображается в Excel, если число делится на ноль (0) или на ячейку без значения.
Совет: Добавьте обработчик ошибок, как в примере ниже: =ЕСЛИ(C2;B2/C2;0).
Эта ошибка отображается в Excel, если функции или формуле недоступно значение.
Если вы используете такую функцию, как ВПР, есть ли для искомого значения соответствие в диапазоне поиска? Скорее всего, нет.
Используйте функцию ЕСЛИОШИБКА для подавления ошибки #Н/Д. В этом случае можно ввести следующее:
Эта ошибка отображается, если Excel не распознает текст в формуле. Например имя диапазона или имя функции написано неправильно.
Примечание: Если вы используете функцию, убедитесь, что ее имя написано неправильно. В данном случае слово СУММ введено с ошибкой. Удалите «а», и Excel исправит формулу.
Эта ошибка отображается в Excel, когда вы указываете пересечение двух областей, которые не пересекаются. Оператором пересечения является пробел, разделяющий ссылки в формуле.
Примечание: Убедитесь, что диапазоны правильно разделены — области C2:C3 и E4:E6 не пересекаются, поэтому при вводе формулы =СУММ(C2:C3 E4:E6) возвращается #NULL! ошибку «#ВЫЧИС!». Если ввести между диапазонами C и E запятую, это исправит ошибку =СУММ(C2:C3;E4:E6)
Эта ошибка отображается в Excel, если формула или функция содержит недопустимые числовые значения.
Вы используете функцию, которая итерирует, например IRR или СТАВКА? В этом случае #NUM! вероятно, функция не может найти результат. По шагам решения проблемы обратитесь к разделу справки.
Эта ошибка отображается в Excel при наличии недопустимой ссылки на ячейку. Например, вы удалили ячейки, на которые ссылались другие формулы, или вставили поверх них другие ячейки.
Вы случайно удалили строку или столбец? Смотрите, что произошло после удаления столбца B в формуле =СУММ(A2;B2;C2).
Нажмите кнопку Отменить (или клавиши CTRL+Z), чтобы отменить удаление, измените формулу или используйте ссылку на непрерывный диапазон (=СУММ(A2:C2)), которая автоматически обновится при удалении столбца B.
Эта ошибка отображается в Excel, если в формуле используются ячейки, содержащие данные не того типа.
Вы используйте математические операторы (+, -, *, / ^) с разными типами данных? В таком случае попробуйте использовать вместо них функцию. В этом случае =СУММ(F2:F5) поможет устранить проблему.
Если ячейки не видны на листе, для просмотра их и содержащихся в них формул можно использовать панель инструментов «Окно контрольного значения». С помощью окна контрольного значения удобно изучать, проверять зависимости или подтверждать вычисления и результаты формул на больших листах. При этом вам не требуется многократно прокручивать экран или переходить к разным частям листа.
Эту панель инструментов можно перемещать и закреплять, как и любую другую. Например, можно закрепить ее в нижней части окна. На панели инструментов выводятся следующие свойства ячейки: 1) книга, 2) лист, 3) имя (если ячейка входит в именованный диапазон), 4) адрес ячейки 5) значение и 6) формула.
Примечание: Для каждой ячейки может быть только одно контрольное значение.
Добавление ячеек в окно контрольного значения
Выделите ячейки, которые хотите просмотреть.
Чтобы выделить все ячейки с формулами, на вкладке Главная в группе Редактирование нажмите кнопку Найти и выделить (вы также можете нажать клавиши CTRL+G или CONTROL+G на компьютере Mac). Затем выберите Выделить группу ячеек и Формулы.
На вкладке Формулы в группе Зависимости формул нажмите кнопку Окно контрольного значения.
Нажмите кнопку Добавить контрольное значение.
Убедитесь, что вы выделили все ячейки, которые хотите отследить, и нажмите кнопку Добавить.
Чтобы изменить ширину столбца, перетащите правую границу его заголовка.
Чтобы открыть ячейку, ссылка на которую содержится в записи панели инструментов «Окно контрольного значения», дважды щелкните запись.
Примечание: Ячейки, содержащие внешние ссылки на другие книги, отображаются на панели инструментов «Окно контрольного значения» только в случае, если эти книги открыты.
Удаление ячеек из окна контрольного значения
Если окно контрольного значения не отображается, на вкладке Формула в группе Зависимости формул нажмите кнопку Окно контрольного значения.
Выделите ячейки, которые нужно удалить.
Чтобы выделить несколько ячеек, щелкните их, удерживая нажатой клавишу CTRL.
Нажмите кнопку Удалить контрольное значение.
Иногда трудно понять, как вложенная формула вычисляет конечный результат, поскольку в ней выполняется несколько промежуточных вычислений и логических проверок. Но с помощью диалогового окна Вычисление формулы вы можете увидеть, как разные части вложенной формулы вычисляются в заданном порядке. Например, формулу =ЕСЛИ(СРЗНАЧ(D2:D5)>50;СУММ(E2:E5);0) будет легче понять, если вы увидите промежуточные результаты:
В диалоговом окне «Вычисление формулы»
Сначала выводится вложенная формула. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Диапазон ячеек D2:D5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(D2:D5) возвращает результат 40.
Диапазон ячеек D2:D5 содержит значения 55, 35, 45 и 25, поэтому функция СРЗНАЧ(D2:D5) возвращает результат 40.
Поскольку 40 не больше 50, выражение в первом аргументе функции ЕСЛИ (аргумент лог_выражение) имеет значение ЛОЖЬ.
Функция ЕСЛИ возвращает значение третьего аргумента (аргумент значение_если_ложь). Функция СУММ не вычисляется, поскольку она является вторым аргументом функции ЕСЛИ (аргумент значение_если_истина) и возвращается только тогда, когда выражение имеет значение ИСТИНА.
Выделите ячейку, которую нужно вычислить. За один раз можно вычислить только одну ячейку.
Откройте вкладку Формулы и выберите Зависимости формул > Вычислить формулу.
Нажмите кнопку Вычислить, чтобы проверить значение подчеркнутой ссылки. Результат вычисления отображается курсивом.
Если подчеркнутая часть формулы является ссылкой на другую формулу, нажмите кнопку Шаг с заходом, чтобы отобразить другую формулу в поле Вычисление. Нажмите кнопку Шаг с выходом, чтобы вернуться к предыдущей ячейке и формуле.
Кнопка Шаг с заходом недоступна для ссылки, если ссылка используется в формуле во второй раз или если формула ссылается на ячейку в отдельной книге.
Продолжайте нажимать кнопку Вычислить, пока не будут вычислены все части формулы.
Чтобы посмотреть вычисление еще раз, нажмите кнопку Начать сначала.
Чтобы закончить вычисление, нажмите кнопку Закрыть.
Некоторые части формул, в которых используются функции ЕСЛИ и ВЫБОР, не вычисляются. В таких случаях в поле Вычисление отображается значение #Н/Д.
Если ссылка пуста, в поле Вычисление отображается нулевое значение (0).
Некоторые функции вычисляются заново при каждом изменении листа, так что результаты в диалоговом окне Вычисление формулы могут отличаться от тех, которые отображаются в ячейке. Это функции СЛЧИС, ОБЛАСТИ, ИНДЕКС, СМЕЩ, ЯЧЕЙКА, ДВССЫЛ, ЧСТРОК, ЧИСЛСТОЛБ, ТДАТА, СЕГОДНЯ, СЛУЧМЕЖДУ.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://support.microsoft.com/ru-ru/office/%D0%BF%D0%BE%D0%B8%D1%81%D0%BA-%D0%BE%D1%88%D0%B8%D0%B1%D0%BE%D0%BA-%D0%B2-%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0%D1%85-3a8acca5-1d61-4702-80e0-99a36a2822c1
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
Skip to content
В статье описано, как использовать функцию ЕСЛИОШИБКА в Excel для обнаружения ошибок и замены их пустой ячейкой, другим значением или определённым сообщением. Покажем примеры, как использовать функцию ЕСЛИОШИБКА с функциями визуального просмотра и сопоставления индексов, а также как она сравнивается с ЕСЛИ ОШИБКА и ЕСНД.
«Дайте мне точку опоры, и я переверну землю», — сказал однажды Архимед. «Дайте мне формулу, и я заставлю ее вернуть ошибку», — сказал бы пользователь Excel. Здесь мы не будем рассматривать, как получить ошибки в Excel. Мы узнаем, как предотвратить их, чтобы ваши таблицы были чистыми, а формулы — понятными и точными.
Итак, вот о чем мы поговорим:
Что означает функция Excel ЕСЛИОШИБКА
Функция ЕСЛИОШИБКА (IFERROR по-английски) предназначена для обнаружения и устранения ошибок в формулах и вычислениях. Это значит, что функция ЕСЛИОШИБКА должна выполнить определенные действия, если видит какую-либо ошибку. Более конкретно, она проверяет формулу и, если вычисление дает ошибку, то она возвращает какое-то другое значение, которое вы ей укажете. Если же всё хорошо, то просто возвращает результат формулы.
Синтаксис функции Excel ЕСЛИОШИБКА следующий:
ЕСЛИОШИБКА(значение; значение_если_ошибка)
Где:
- Значение (обязательно) — что проверять на наличие ошибок. Это может быть формула, выражение или ссылка на ячейку.
- Значение_если_ошибка (обязательно) — что возвращать при обнаружении ошибки. Это может быть пустая строка (получится пустая ячейка), текстовое сообщение, числовое значение, другая формула или вычисление.
Например, при делении двух столбцов чисел можно получить кучу разных ошибок, если в одном из столбцов есть пустые ячейки, нули или текст.
Рассмотрим простой пример:
Чтобы этого не произошло, используйте формулу ЕСЛИОШИБКА, чтобы перехватывать и обрабатывать их нужным вам образом.
Если ошибка, то пусто
Укажите пустую строку (“”) в аргументе значение_если_ошибка, чтобы вернуть пустую ячейку, если обнаружена ошибка:
=ЕСЛИОШИБКА(A4/B4; «»)
Вернемся к нашему примеру и используем ЕСЛИОШИБКА:
Как видите по сравнению с первым скриншотом, вместо стандартных сообщений мы видим просто пустые ячейки.
Если ошибка, то показать сообщение
Вы также можете отобразить собственное сообщение вместо стандартного обозначения ошибок Excel:
=ЕСЛИОШИБКА(A4/B4; «Ошибка в вычислениях»)
Перед вами – третий вариант нашей небольшой таблицы.
5 фактов, которые нужно знать о функции ЕСЛИОШИБКА в Excel
- ЕСЛИОШИБКА в Excel обрабатывает все типы ошибок, включая #ДЕЛ/0!, #Н/Д, #ИМЯ?, #NULL!, #ЧИСЛО!, #ССЫЛКА! и #ЗНАЧ!.
- В зависимости от содержимого аргумента значение_если_ошибка функция может заменить ошибки вашим текстовым сообщением, числом, датой или логическим значением, результатом другой формулы или пустой строкой (пустой ячейкой).
- Если аргумент значение является пустой ячейкой, он обрабатывается как пустая строка (»’), но не как ошибка.
- ЕСЛИОШИБКА появилась в Excel 2007 и доступна во всех последующих версиях Excel 2010, Excel 2013, Excel 2016, Excel 2019, Excel 2021 и Excel 365.
- Чтобы перехватывать ошибки в Excel 2003 и более ранних версиях, используйте функцию ЕОШИБКА в сочетании с функцией ЕСЛИ, например как показано ниже:
=ЕСЛИ(ЕОШИБКА(A4/B4);»Ошибка в вычислениях»;A4/B4)
Далее вы увидите, как можно использовать ЕСЛИОШИБКА в Excel в сочетании с другими функциями для выполнения более сложных задач.
ЕСЛИОШИБКА с функцией ВПР
Часто встречающаяся задача в Excel – поиск нужного значения в таблице в соответствии с определёнными критериями. И не всегда этот поиск бывает успешным. Одним из наиболее распространенных применений функции ЕСЛИОШИБКА является сообщение пользователям, что искомое значение не найдено в базе данных. Для этого вы заключаете формулу ВПР в функцию ЕСЛИОШИБКА примерно следующим образом:
ЕСЛИОШИБКА(ВПР( … );»Не найдено»)
Если искомое значение отсутствует в таблице, которую вы просматриваете, обычная формула ВПР вернет ошибку #Н/Д:
Для лучшего понимания таблицы и улучшения ее внешнего вида, заключите функцию ВПР в ЕСЛИОШИБКА и покажите более понятное для пользователя сообщение:
=ЕСЛИОШИБКА(ВПР(D3; $A$3:$B$5; 2;ЛОЖЬ); «Не найдено»)
На скриншоте ниже показан пример ЕСЛИОШИБКА вместе с ВПР в Excel:
Если вы хотите перехватывать только #Н/Д, но не все подряд ошибки, используйте функцию ЕНД вместо ЕСЛИОШИБКА. Она просто возвращает ИСТИНА или ЛОЖЬ в зависимости от появления ошибки #Н/Д. Поэтому нам здесь еще понадобится функция ЕСЛИ, чтобы обработать эти логические значения:
=ЕСЛИ(ЕНД(ВПР(D3; $A$3:$B$5; 2;ЛОЖЬ)); «Не найдено»;ВПР(D3; $A$3:$B$5; 2;ЛОЖЬ))
Дополнительные примеры формул Excel ЕСЛИОШИБКА ВПР можно также найти в нашей статье Как убрать сообщение #Н/Д в ВПР?
Вложенные функции ЕСЛИОШИБКА для выполнения последовательных ВПР
В ситуациях, когда вам нужно выполнить несколько операций ВПР в зависимости от того, была ли предыдущая ВПР успешной или неудачной, вы можете вложить две или более функции ЕСЛИОШИБКА одну в другую.
Предположим, у вас есть несколько отчетов о продажах из региональных отделений вашей компании, и вы хотите получить сумму по определенному идентификатору заказа. С ячейкой В9 в качестве критерия поиска (номер заказа) и тремя небольшими таблицами поиска (таблица 1, 2 и 3), формула выглядит следующим образом:
=ЕСЛИОШИБКА(ВПР(B9;A3:B6;2;0);ЕСЛИОШИБКА(ВПР(B9;D3:E6;2;0);ЕСЛИОШИБКА(ВПР(B9;G3:H6;2;0);»Не найден»)))
Результат будет выглядеть примерно так, как на рисунке ниже:
То есть, если поиск завершился неудачей (то есть, ошибкой) первой таблице, начинаем искать во второй, и так далее. Если нигде ничего не нашли, получим сообщение «Не найден».
ЕСЛИОШИБКА в формулах массива
Как вы, наверное, знаете, формулы массива в Excel предназначены для выполнения нескольких вычислений внутри одной формулы. Если вы в аргументе значение функции ЕСЛИОШИБКА укажете формулу или выражение, которое возвращает массив, она также обработает и вернет массив значений для каждой ячейки в указанном диапазоне. Пример ниже поможет пояснить это.
Допустим, у вас есть Сумма в столбце B и Цена в столбце C, и вы хотите вычислить Количество. Это можно сделать с помощью следующей формулы массива, которая делит каждую ячейку в диапазоне B2:B4 на соответствующую ячейку в диапазоне C2:C4, а затем суммирует результаты:
=СУММ(($B$2:$B$4/$C$2:$C$4))
Формула работает нормально, пока в диапазоне делителей нет нулей или пустых ячеек. Если есть хотя бы одно значение 0 или пустая строка, то возвращается ошибка: #ДЕЛ/0! Из-за одной некорректной позиции мы не можем получить итоговый результат.
Чтобы исправить эту ситуацию, просто вложите деление внутрь формулы ЕСЛИОШИБКА:
=СУММ(ЕСЛИОШИБКА($B$2:$B$4/$C$2:$C$4;0))
Что делает эта формула? Делит значение в столбце B на значение в столбце C в каждой строке (3500/100, 2000/50 и 0/0) и возвращает массив результатов {35; 40; #ДЕЛ/0!}. Функция ЕСЛИОШИБКА перехватывает все ошибки #ДЕЛ/0! и заменяет их нулями. Затем функция СУММ суммирует значения в итоговом массиве {35; 40; 0} и выводит окончательный результат (35+40=75).
Примечание. Помните, что ввод формулы массива должен быть завершен нажатием комбинации Ctrl + Shift + Enter (если у вас не Office365 или Excel2021 – они понимают формулы массива без дополнительных телодвижений).
ЕСЛИОШИБКА или ЕСЛИ + ЕОШИБКА?
Теперь, когда вы знаете, как использовать функцию ЕСЛИОШИБКА в Excel, вы можете удивиться, почему некоторые люди все еще склоняются к использованию комбинации ЕСЛИ + ЕОШИБКА. Есть ли у этого старого метода преимущества по сравнению с ЕСЛИОШИБКА?
В старые недобрые времена Excel 2003 и более ранних версий, когда ЕСЛИОШИБКА не существовало, совместное использование ЕСЛИ и ЕОШИБКА было единственным возможным способом перехвата ошибок. Это просто немного более сложный способ достижения того же результата.
Например, чтобы отловить ошибки ВПР, вы можете использовать любую из приведенных ниже формул.
В Excel 2007 — Excel 2016:
ЕСЛИОШИБКА(ВПР( … ); «Не найдено»)
Во всех версиях Excel:
ЕСЛИ(ЕОШИБКА(ВПР(…)); «Не найдено»; ВПР(…))
Обратите внимание, что в формуле ЕСЛИ ЕОШИБКА ВПР вам нужно дважды выполнить ВПР. Чтобы лучше понять, расшифруем: если ВПР приводит к ошибке, вернуть «Не найдено», в противном случае вывести результат ВПР.
А вот простой пример формулы Excel ЕСЛИ ЕОШИБКА ВПР:
=ЕСЛИ(ЕОШИБКА(ВПР(D2; A2:B5;2;ЛОЖЬ)); «Не найдено»; ВПР(D2; A2:B5;2;ЛОЖЬ ))
ЕСЛИОШИБКА против ЕСНД
Представленная в Excel 2013, ЕСНД (IFNA в английской версии) — это еще одна функция для проверки формулы на наличие ошибок. Его синтаксис похож на синтаксис ЕСЛИОШИБКА:
ЕСНД(значение; значение_если_НД)
Чем ЕСНД отличается от ЕСЛИОШИБКА? Функция ЕСНД перехватывает только ошибки #Н/Д, тогда как ЕСЛИОШИБКА обрабатывает все типы ошибок.
В каких ситуациях вы можете использовать ЕСНД? Когда нецелесообразно скрывать все ошибки. Например, при работе с важными данными вы можете захотеть получать предупреждения о возможных ошибках в вашем наборе данных (случайном делении на ноль и т.п.), а стандартные сообщения об ошибках Excel с символом «#» могут быть яркими визуальными индикаторами проблем.
Давайте посмотрим, как можно создать формулу, отображающую сообщение «Не найдено» вместо ошибки «Н/Д», которая появляется, когда искомое значение отсутствует в наборе данных, но при этом вы будете видеть все другие ошибки Excel.
Предположим, вы хотите получить Количество из таблицы поиска в таблицу с результатами, как показано на рисунке ниже. Проще всего было бы использовать ЕСЛИОШИБКА с ВПР. Таблица приобрела бы красивый вид, но при этом за надписью «Не найдено» были бы скрыты не только ошибки поиска, но и все другие ошибки. И мы не заметили бы, что в исходной таблице поиска у нас есть ошибка деления на ноль, так как не заполнена цена персиков. Поэтому более разумно использовать ЕСНД, чтобы с ее помощью обработать только ошибки поиска:
=ЕСНД(ВПР(F3; $A$3:$D$6; 4;ЛОЖЬ); «Не найдено»)
Или подойдет комбинация ЕСЛИ ЕНД для старых версий Excel:
=ЕСЛИ(ЕНД(ВПР(F3; $A$3:$D$6; 4;ЛОЖЬ));»Не найдено»; ВПР(F3; $A$3:$D$6; 4;ЛОЖЬ))
Как видите, формула ЕСНД с ВПР возвращает «Не найдено» только для товара, которого нет в таблице поиска (Сливы). Для персиков она показывает #ДЕЛ/0! что указывает на то, что наша таблица поиска содержит ошибку деления на ноль.
Рекомендации по использованию ЕСЛИОШИБКА в Excel
Итак, вы уже знаете, что функция ЕСЛИОШИБКА — это самый простой способ отлавливать ошибки в Excel и маскировать их пустыми ячейками, нулевыми значениями или собственными сообщениями. Однако это не означает, что вы должны обернуть каждую формулу в функцию обработки ошибок.
Эти простые рекомендации могут помочь вам сохранить баланс.
- Не ловите ошибки без весомой на то причины.
- Оберните в ЕСЛИОШИБКА только ту часть формулы, где по вашему мнению могут возникнуть проблемы.
- Чтобы обрабатывать только определенные ошибки, используйте другую функцию обработки ошибок с меньшей областью действия:
- ЕСНД или ЕСЛИ ЕНД для обнаружения только ошибок #H/Д.
- ЕОШ для обнаружения всех ошибок, кроме #Н/Д.
Мы постарались рассказать, как можно использовать функцию ЕСЛИОШИБКА в Excel. Примеры перехвата и обработки ошибок могут быть полезны и для «чайников», и для более опытных пользователей.
Также рекомендуем: