Построение графика проверки распределения на нормальность (
Normal
Probability
Plot
) является графическим методом определения соответствия значений выборки нормальному распределению.
Предположим, что имеется некий набор данных. Требуется оценить, соответствует ли данная
выборка
нормальному распределению
.
Рассмотренный ниже графический метод основан на субъективной визуальной оценке данных. Объективным же подходом является, например,
анализ степени согласия гипотетического распределения с наблюдаемыми данными
(goodness-of-fit test), который рассмотрен в статье
Проверка простых гипотез критерием Пирсона ХИ-квадрат
.
Из-за наличия неустранимой статистической ошибки выборки, присущей случайной величине, невозможно однозначно ответить на вопрос «Взята ли данная выборка из
нормального распределения
или нет». Поэтому, рассмотренный графический метод, скорее, дает ответ на вопрос «Разумно ли предположение, что оцениваемая выборка взята из
нормального распределения
»?
Рассмотрим алгоритм построения графика проверки распределения на нормальность (
Normal
Probability
Plot
)
:
-
Отсортируйте значения выборки по возрастанию
(значения выборки x
j
будут отложены по горизонтальной оси Х); -
Каждому значению x
j
выборки
поставьте в соответствие значения (j-0,5)/n, где n – количество значений в
выборке
, j –порядковый номер
значения от 1 до n. Этот массив будет содержать значения от 0,5/n до (n-0,5)/n. Таким образом, диапазон от 0 до 1 будет разбит на равномерные отрезки. Этот диапазон соответствует
вероятности наблюдения значений случайной величины
Z<=z
j
; -
Преобразуем значения массива, полученные на предыдущем шаге, с помощью
обратной функции
стандартного нормального распределения
НОРМ.СТ.ОБР()
и отложим их по вертикальной оси Y.
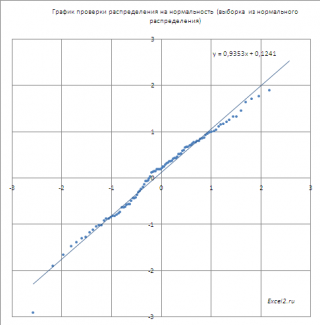
Если значения
выборки
, откладываемые по оси Х, взяты из
стандартного нормального распределения
, то на графике мы получим приблизительно прямую линию, проходящую примерно через 0 и под углом 45 градусов к оси х (если масштабы осей совпадают).
Расчеты и графики приведены в
файле примера на листе Нормальное
. О построении диаграмм см. статью
Основные типы диаграмм в MS EXCEL
.
Примечание
: Значения
выборки
в
файле примера
сгенерированы с помощью формулы
=НОРМ.СТ.ОБР(СЛЧИС())
. При перерасчете листа или нажатии клавиши
F9
происходит обновление данных в
выборке
. О генерации чисел, распределенных по
нормальному закону
см. статью
Нормальное распределение. Непрерывные распределения в MS EXCEL
. Таже значения выборки могут быть сгенерированы с помощью надстройки
Пакет анализа
.
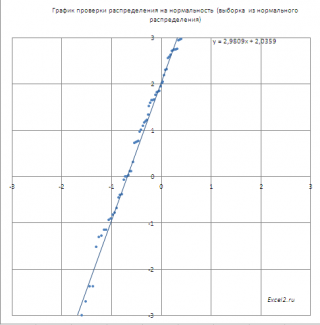
Если значения
выборки
взяты из
нормального распределения
(μ не обязательно равно 0, σ не обязательно равно 1), то угол наклона кривой даст оценку
стандартного отклонения
σ, а ордината точки пересечения оси Y – оценку
среднего значения
μ.
Данные оценки несколько отличаются от оценок параметров, полученных с помощью функций
СРЗНАЧ()
и
СТАНДОТКЛОН.В()
, т.к. они получены
методом наименьших квадратов
, рассмотренного в статье про регрессионный анализ.
Примечание
: Рассмотренный выше метод в отечественной литературе имеет название
Метод номограмм
. Номограмма – это листы бумаги, разлинованные определенным образом. Номограмма используется в различных областях знаний. В
математической статистике
номограмма называется вероятностной бумагой. Такую «вероятностную бумагу» мы практически построили самостоятельно, когда нелинейно изменили масштаб шкалы ординат:
=НОРМ.СТ.ОБР((j-0,5)/n)
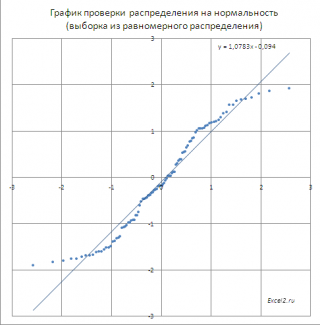
Интересно посмотреть, как будут выглядеть на диаграмме данные, полученные из
выборок
из других распределений (не из
нормального
). В
файле примера на листе Равномерное
приведен график, построенный на основе
выборки
из непрерывного равномерного распределения.
Очевидно, что значения
выборки
совсем не ложатся на прямую линию и предположение о
нормальности выборки
должно быть отвергнуто.
Подобная визуальная проверка
выборки
на соответствие другим распределениям может быть сделана при наличии соответствующих
обратных функций
. В статье
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
приведены
графики
для следующих распределений:
Стьюдента
,
ХИ-квадрат распределения
,
F-распределения
. Подобный график также приведен в статье про
распределение Вейбулла
.
17 авг. 2022 г.
читать 2 мин
Многие статистические тесты предполагают, что значения в наборе данных имеют нормальное распределение .
Один из самых простых способов проверить это предположение — выполнить тест Харке-Бера , который представляет собой тест согласия, который определяет, имеют ли выборочные данные асимметрию и эксцесс, соответствующие нормальному распределению.
В этом тесте используются следующие гипотезы:
H 0 : Данные нормально распределены.
H A : Данные не распределены нормально.
Тестовая статистика JB определяется как:
JB = (n/6) * (S 2 + (C 2 /4))
куда:
- n: количество наблюдений в выборке
- S: асимметрия выборки
- C: образец эксцесса
При нулевой гипотезе нормальности JB ~ X 2 (2).
Если значение p , соответствующее тестовой статистике, меньше некоторого уровня значимости (например, α = 0,05), то мы можем отклонить нулевую гипотезу и сделать вывод, что данные не распределены нормально.
В этом руководстве представлен пошаговый пример того, как выполнить тест Харке-Бера для заданного набора данных в Excel.
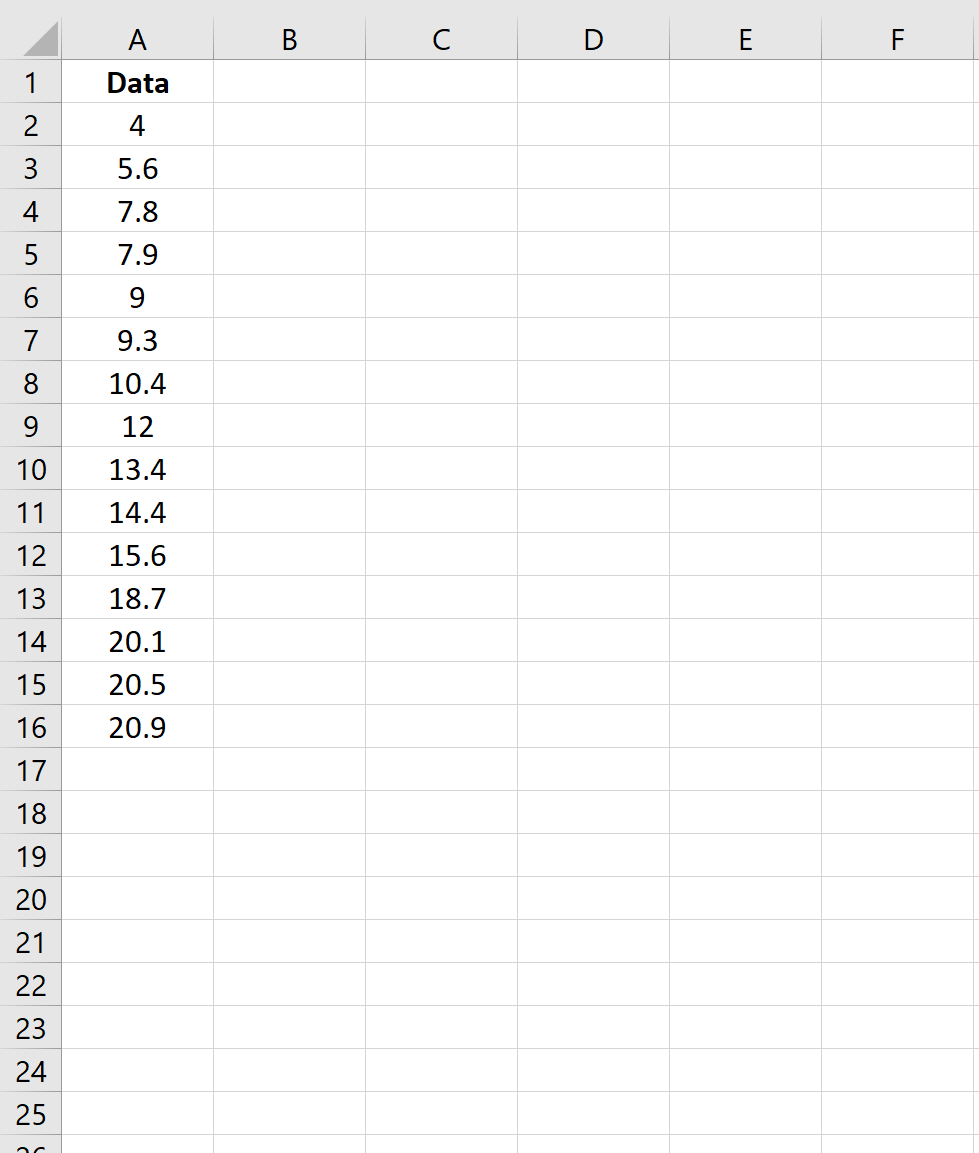
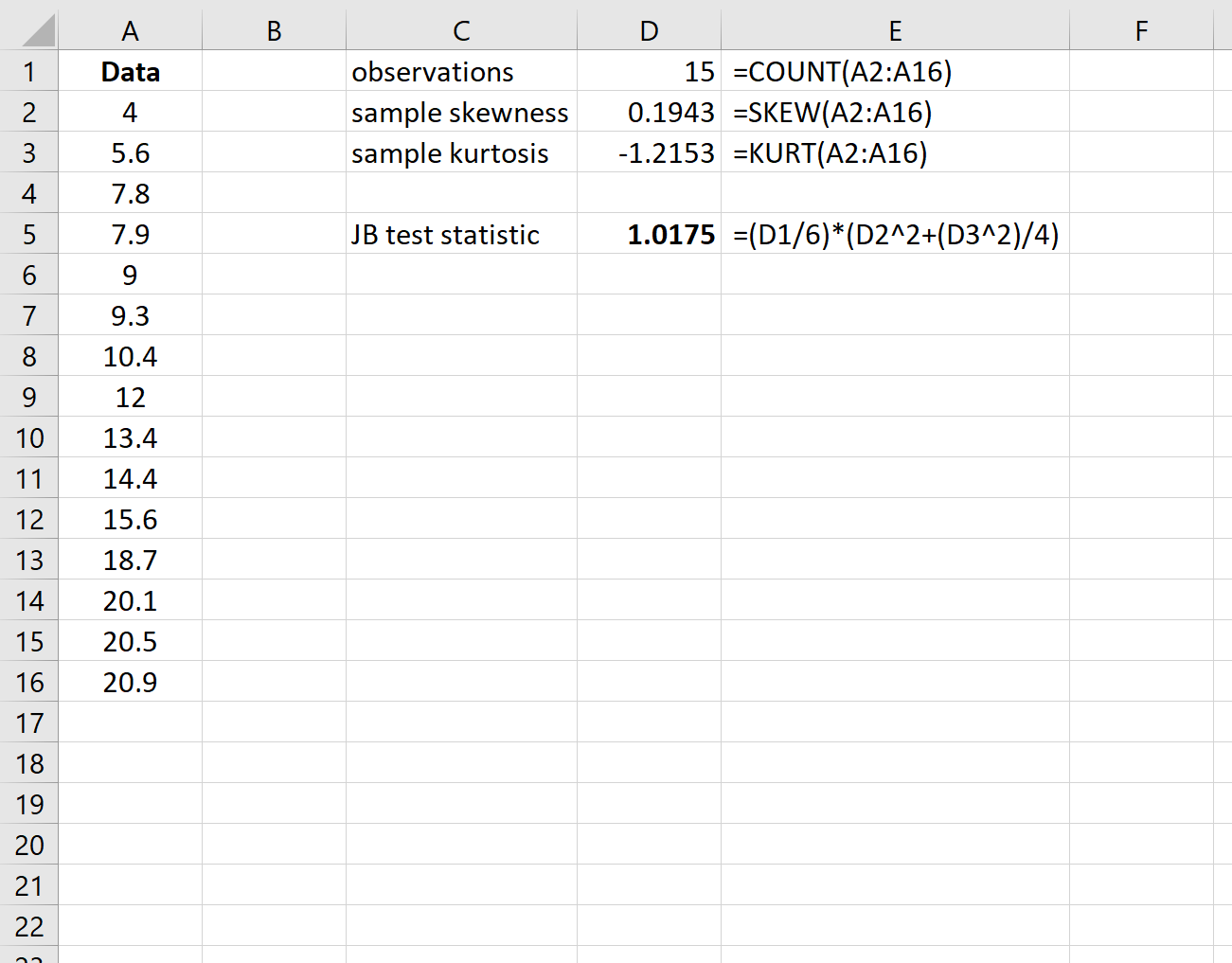
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных с 15 значениями:
Шаг 2: Рассчитайте тестовую статистику
Затем рассчитайте статистику теста JB. В столбце E показаны используемые формулы:
Тестовая статистика оказывается 1,0175 .
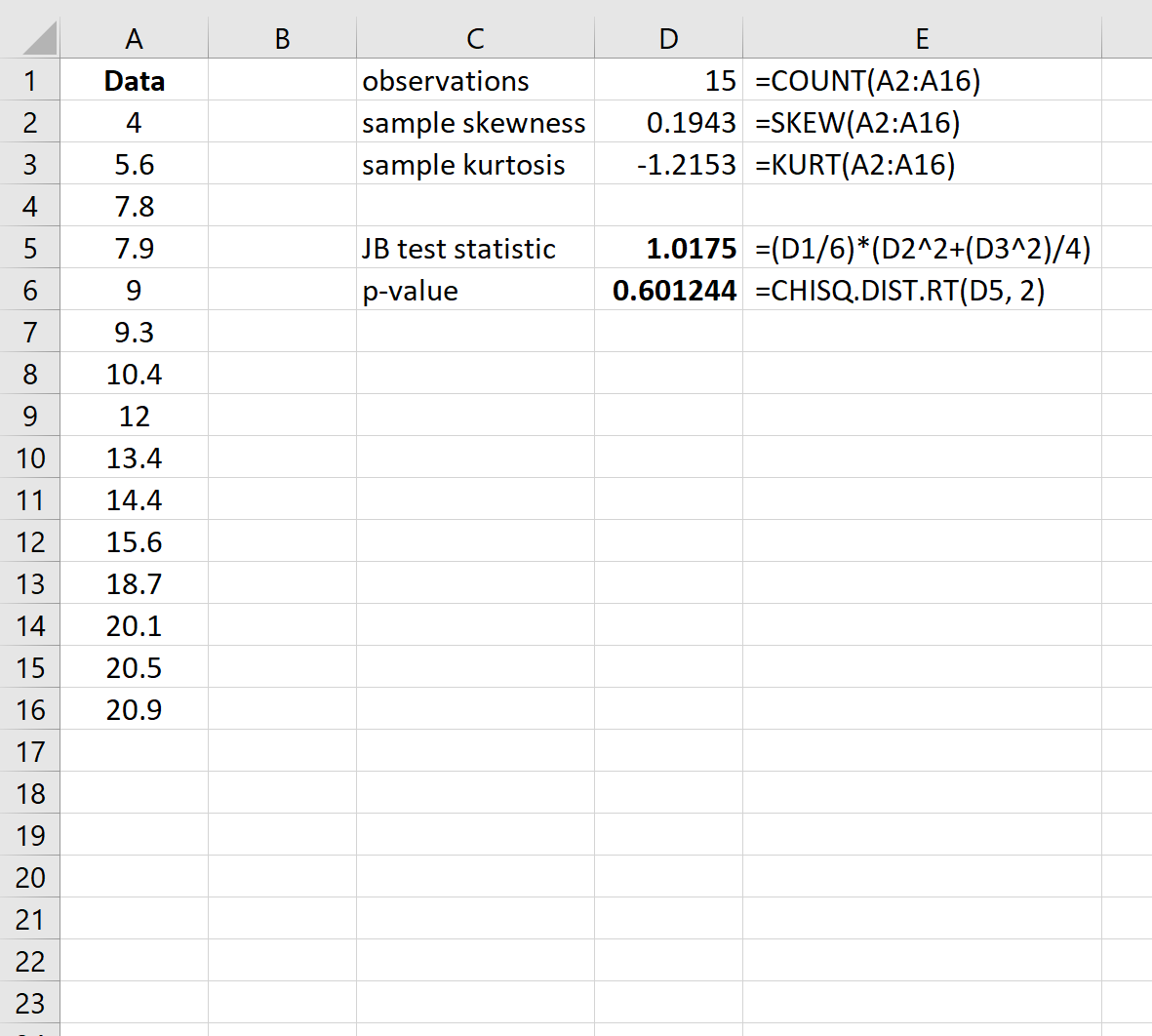
Шаг 3: Рассчитайте P-значение
При нулевой гипотезе нормальности тестовая статистика JB следует распределению хи-квадрат с 2 степенями свободы.
Итак, чтобы найти p-значение для теста, мы будем использовать следующую функцию в Excel: =CHISQ.DIST.RT(статистика теста JB, 2)
Значение p теста составляет 0,601244.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств того, что набор данных не имеет нормального распределения.
Другими словами, мы можем предположить, что данные распределены нормально.
Дополнительные ресурсы
Как создать график QQ в Excel
Как выполнить критерий согласия хи-квадрат в Excel
Many statistical tests make the assumption that the values in a dataset are normally distributed.
One of the easiest ways to test this assumption is to perform a Jarque-Bera test, which is a goodness-of-fit test that determines whether or not sample data have skewness and kurtosis that matches a normal distribution.
This test uses the following hypotheses:
H0: The data is normally distributed.
HA: The data is not normally distributed.
The test statistic JB is defined as:
JB =(n/6) * (S2 + (C2/4))
where:
- n: the number of observations in the sample
- S: the sample skewness
- C: the sample kurtosis
Under the null hypothesis of normality, JB ~ X2(2).
If the p-value that corresponds to the test statistic is less than some significance level (e.g. α = .05), then we can reject the null hypothesis and conclude that the data is not normally distributed.
This tutorial provides a step-by-step example of how to perform a Jarque-Bera test for a given dataset in Excel.
Step 1: Create the Data
First, let’s create a fake dataset with 15 values:
Step 2: Calculate the Test Statistic
Next, calculate the JB test statistic. Column E shows the formulas used:
The test statistic turns out to be 1.0175.
Step 3: Calculate the P-Value
Under the null hypothesis of normality, the test statistic JB follows a Chi-Square distribution with 2 degrees of freedom.
So, to find the p-value for the test we will use the following function in Excel: =CHISQ.DIST.RT(JB test statistic, 2)
The p-value of the test is 0.601244. Since this p-value is not less than 0.05, we fail to reject the null hypothesis. We don’t have sufficient evidence to say that the dataset is not normally distributed.
In other words, we can assume that the data is normally distributed.
Additional Resources
How to Create a Q-Q Plot in Excel
How to Perform a Chi-Square Goodness of Fit Test in Excel
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в учебном процессе. Показываются преимущества данного метода перед ручным счетом по проверке рассмотренного критерия.
Ключевые слова: шаблон Excel, гистограмма, кривая распределения, критерий согласия Пирсона
В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: металлургии, а также в экономике, биологии, политике, социологии и т. д. Рассмотрим использование некоторых средств статистического анализа, а именно — гистограмм для обработки больших массивов данных.
Целью первичной обработки экспериментальных наблюдений обычно является выбор закона распределения, наиболее хорошо описывающего случайную величину, выборку которой мы наблюдали. Проверка того, насколько хорошо наблюдаемая выборка описывается теоретическим законом, осуществляется с использованием различных критериев согласия. Целью проверки гипотезы о согласии опытного распределения с теоретическим является стремление удостовериться в том, что данная модель теоретического закона не противоречит наблюдаемым данным, и использование ее не приведет к существенным ошибкам при вероятностных расчетах. Некорректное использование критериев согласия может приводить к необоснованному принятию или необоснованному отклонению проверяемой гипотезы [1].
Сходимость результатов наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными. Сама процедура проверки нормальности распределения относится к распространенной стандартной и довольно тривиальной задаче обработки данных и достаточно подробно и широко описана в различной литературе по метрологии и статистической обработке данных измерений [2- 4].
Данные, получаемые в результате измерений при контроле технологических процессов, оценке характеристик различных объектов и др. для дальнейшей обработки желательно представлять в виде теоретического распределения, максимально соответствующего экспериментальному распределению. Проверку гипотезы о виде функции распределения в настоящее время проводят по различным критериям согласия — Пирсона, Колмогорова, Смирнова и другим в соответствии с новыми разработанными нормативными документами — рекомендациями по стандартизации [5, 6].
Наиболее часто используется критерий Пирсона 2. Однако применение критериев согласия требует обычно довольно значительного объёма данных. Так, критерий Пирсона обычно рекомендуется использовать при объёме выборки не менее 50…100. Поэтому при небольшом объёме выборки проверку гипотезы о виде функции распределения проводят приближёнными методами — графическим методом или по асимметрии и эксцессу. Применение критерия Пирсона для ручной обработки данных очень подробно было изложено в известной работе [2]. Как свидетельствует опыт проверок согласия экспериментальных данных с теоретическими по различным критериям, эта процедура является очень трудоемкой, требует некоторой усидчивости и особого внимания при обработке от исследователя, как правило, не исключает ошибок в работе и не вызывает особого энтузиазма у выполняющего эту работу.
Решение задач статистического анализа связано со значительными объемами вычислений. Проведение реальных многовариантных статистических расчетов в ручном режиме является очень громоздкой и трудоемкой задачей и без использования компьютера в настоящее время практически невозможно. В настоящее время разработано достаточное количество универсальных и специализированных программных средств для статистического анализа и обработки экспериментальных данных. Автор предлагает к рассмотрению достаточно простой и эффективный шаблон для быстрого построения гистограммы и кривой нормального распределения.
По виду гистограммы можно предположить (принять гипотезу) о том, что выборка случайных чисел подчиняется нормальному закону распределения. Далее, для того чтобы убедиться в правильности выбранной гипотезы надо, первое — построить график гипотетического нормального закона распределения, выбрав в качестве параметров (математического ожидания и среднего квадратического отклонения) их оценки (среднее и стандартное отклонение), и совместить график гипотетического распределения с графиком гистограммы. И, второе — используя в данном случае, как пример, критерий согласия Пирсона, установить справедливость выбранной гипотезы.
Рассмотрим порядок действий при работе с критерием Пирсона в среде Excel.
1. Полученные в результате измерений значения 100 случайных результатов измерений внести в ячейки A1:A100 шаблона Excel и приступить к построению гистограммы на основе данных, назначая длину интервала (карман) и выбирая необходимое число интервалов.
2. Затем на этом же листе создается таблица, в которую посредством формул Excel вносятся основные расчетные величины, используемые для построения гистограммы и кривой Гаусса: среднее арифметическое, стандартное отклонение, минимальное и максимальное значения выборки, размах, величина кармана (рис. 1).
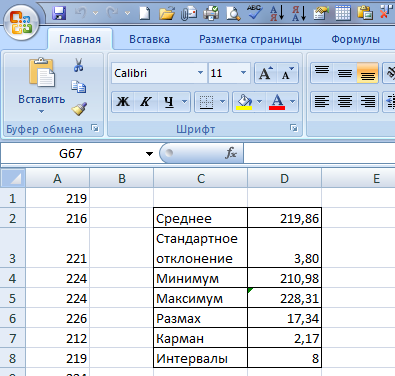
Рис. 1. Фрагмент таблицы с исходными данными
В ячейку D2 вносится формула =СРЗНАЧ(A1:A100), D3: =СТАНДОТКЛОН(A1:A100), D4: =МИН(A1:A100), D5: =МАКС(A1:A100), D6: =D5-D4, D7: =D6/D8. В ячейку D8 вводится число интервалов, которое для числа измерений, равным 100, может быть принято от 7 до 12.
Для оценки оптимального для нашего массива данных количества интервалов можно воспользоваться формулой Стерджесса: k~1+3,322lgN, где N— количество всех значений величины. Например, для N = 100, n = 7,6, которое должно быль округлено до целого числа, округляем до n = 8.
3. Интервал карманов вычисляют так: разность максимального и минимального значений массива, деленная на количество интервалов: .
4. Теперь в каждой ячейке шаг за шагом прибавляем полученное значение ширины кармана: сначала к минимальному значению нашего массива (ячейка D4), затем в следующей ячейке ниже — к полученной сумме и т. д. Так постепенно доходим до максимального значения. Таким образом, мы и построили интервалы карманов в виде столбца значений.
Интервалом считается следующий диапазон: (i-1; i] или i<значения<=i (нестрогая верхняя граница интервала — это значение в ячейке, нижняя строгая граница — значение в предыдущей ячейке).
5. Выделяем столбец рядом с нашими карманами, нажимаем «F2» и вводим функцию: =ЧАСТОТА (массив данных; диапазон карманов) и нажимаем Ctr+Shift+Enter.
6. В выделенном нами столбце напротив границ интервалов (а мы знаем, что это нестрогие верхние границы) появилось количество значений исходного массива, которые попадают в интервал (рис. 2).
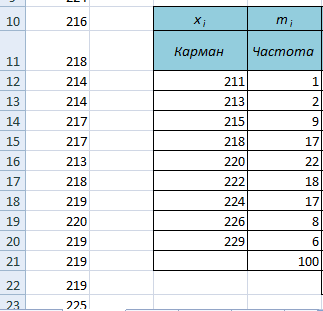
Рис. 2. Количество значений исходного массива, попавших в интервалы (частоты)
Построение теоретического закона распределения
Для построения теоретического закона распределения совместно с гистограммой и проверкой согласия по критерию хи-квадрат Пирсона автоматически заполняется таблица 1 после ввода экспериментальных данных в ячейки A1:A100.
Таблица 1
|
xi |
mi |
n∙pi |
|
|
карманы |
частота |
теоретическая частота |
статистика U |
Для построения этой таблицы надо воспользоваться таблицей карман — частота процедуры Гистограмма. В этой таблице обозначены:
xi — границы интервалов группировки (карманы — получены как результат выполнения процедуры Гистограмма);
mi — количество элементов выборки, попавших в i–ый интервал (частота — получена в результате процедуры Гистограмма).
Для построения этой таблицы в Excel к столбцам карман — частота процедуры Гистограмма надо добавить столбцы n∙pi (теоретическая частота) и (статистика U).
Проверка согласия эмпирического и теоретического законов распределения по критерию хи-квадрат Пирсона.
В ячейку столбца, помеченного именем U, вводим формулу,
, (1)
Критическое значение статистики U, которая имеет распределениес r степенями свободы (число степеней свободы определяется как число частичных интервалов минус 1), определяется при помощи функции ХИ2ОБР.
Функция ХИ2ОБР вызывается следующим образом. В главном меню Excel выбирается закладка Формулы → Вставить функцию →в диалоговом окне Мастер функций— шаг 1 из 2 вкатегории Статистические →ХИ2ОБР (рис. 3).
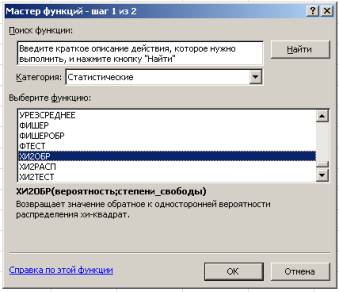
Рис. 3. Диалоговое окно выбора функции ХИ2ОБР
В диалоговом окне Аргументы функции ХИ2ОБР заполняются поля как показано на рис. 4, задаваясь уровнем значимости (например, 0,05, что соответствует доверительной вероятности Р = 0,95) и предварительно выбрав ячейку для результата вычисления функции.
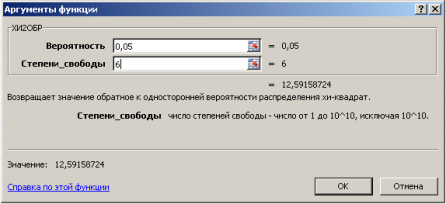
Рис. 4. Диалоговое окно функции ХИ2ОБР с заполненными полями ввода
Размножим формулу (1) в диапазонах ячеек [F12; F20] и [F51; F61]. В ячейке F21 получим сумму содержимого ячеек F12; F20 (рис. 5). В ячейке F62 получим сумму содержимого ячеек F51; F61 (рис. 6).
В ячейке F21 получено значение статистики: U = 2,09, а в ячейке F62 — U = 3,43 при доверительной вероятности Р = 0,95.
Теперь с помощью стандартного инструмента для построения гистограмм («вставка/гистограмма» и т. д.) на этом же листе Excel можно построить гистограммы распределения с кривой Гаусса для разных чисел интервалов (в данном случае n = 8 и n = 10) (рис. 5 и 6).
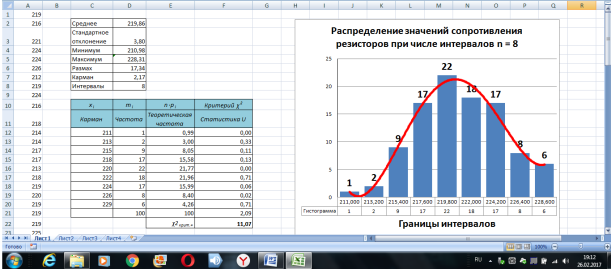
Рис. 5. Вид гистограммы и кривой распределения при числе интервалов n = 8 (пример)
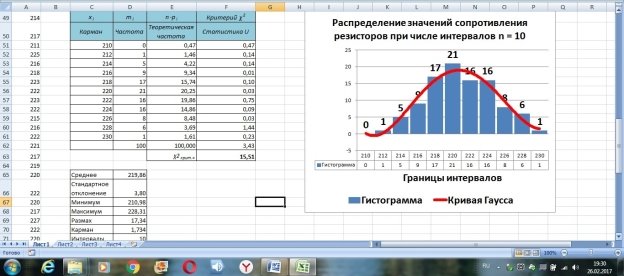
Рис. 6. Вид гистограммы и кривой распределения при числе интервалов n = 10 (пример)
Шаблон позволяет варьировать числом интервалов и величиной кармана, при этом автоматически изменяется внешний вид гистограммы и кривой нормального распределения. Исследователь может подобрать наиболее «красивый» вид гистограммы и аппроксимирующей кривой Гаусса, одновременно изменив значение доверительной вероятности и числа степеней свободы и добившись при этом выполнения критерия Пирсона.
Если значение статистики U оказалось меньше критического значения при заданной доверительной вероятности, то гипотеза, состоящая в том, что исследуемая выборка подчиняется нормальному закону распределения, принимается. Вданном примере значение обеих статистик U оказалось меньше критического значения
и
Следовательно, мы можем распространить данный закон распределения на всю генеральную совокупность исследуемых объектов (партию изделий, сменную выработку, месячный план и т. д.).
Более подробно указанная тема была рассмотрена в статье автора в сборнике «Законодательная и прикладная метрология» [7].
Выводы
- Существовавшая ранее традиционная «ручная» обработка данных при проверке нормального (и других) законов распределения и построении гистограмм являлась достаточно трудоемкой задачей, не исключавшей появление ошибок, обнаружение которых зачастую требовало значительных затрат времени и моральных сил исследователя.
- Появление пакетов офисных программ, в частности Excel 2010 и ее последующих версий, позволяет значительно сократить трудоемкость обработки данных и практически исключает появление ошибок в расчетах.
Литература:
1. Лемешко Б. Ю., Постовалов С. Н. О правилах проверки согласия опытного распределения с теоретическим. — Методы менеджмента качества. Надежность и контроль качества. — 1999, № 11. — С. 34–43.
2. Бурдун Г. Д., Марков Б. Н. Основы метрологии. Учебное пособие для вузов. — М.: Изд. стандартов, 1975. — 336 с.
3. Сулицкий В. Н. Методы статистического анализа в управлении: Учеб. пособие. — М.: Дело, 2002. — 520 с.
4. Иванов О. В. Статистика / Учебный курс для социологов и менеджеров. Часть 2. Доверительные интервалы. Проверка гипотез. Методы и их применение. — М.: Изд. МГУ им. М. В. Ломоносова, 2005. — 220 с.
5. Рекомендации по стандартизации Р 50.1.033–2001. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть 1. Критерии типа хи-квадрат. — М.: ФГУП «Стандартинформ», 2006. — 87 с.
6. Рекомендации по стандартизации Р 50.1.037–2002. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. — М.: ИПК Изд. стандартов, 2002. — 62 с.
7. Фаюстов А. А. Проверка гипотезы о нормальном распределении выборки по критерию согласия Пирсона средствами приложения Excel. — Законодательная и прикладная метрология, 2016, № 6. — С. 3–9.
Основные термины (генерируются автоматически): статистический анализ, критерий согласия, массив данных, вид функции распределения, интервал карманов, максимальное значение, минимальное значение, построение гистограммы, различный критерий согласия, стандартное отклонение.
Как определить, является ли распределение нормальным?
Если
установлено, что исследуемые значения
имеют количественный характер, следует
проверить выборку на нормальность
распределения. Это можно сделать
несколькими способами.
Первый
способ проверки выборки на нормальность
распределения
Прежде
всего, нужно вычислить показатели
асимметрии и эксцесса, используя
программу Excel,
имеющуюся практически на всех компьютерах.
Для этого в таблицу программы следует
поместить результаты измерений. Пусть
это будет ряд значений, полученных на
выборке из 25 объектов: 9 10 10 10 11
11 11 11 12 12 12 12 12 12 12 13 13 13 13
14 14 15 15 16 17
Данные
могут располагаться как в виде строки,
так и в виде колонки. Далее, нажатием
кнопки с символами fx,
расположенной
ниже панели инструментов, вызываем
мастер функций. В верхнем окне выбираем
категорию «Статистические», а в нижнем
— пункт «Скос». Возвращаемся к таблице
с результатами измерений, и, выделяя
набранные ранее цифры, помещаем их
значения в открывшееся окно «Аргументы
функций». На правой стороне окна
появляется результат вычислений –
0,579. Это и есть значение показателя
асимметрии, характеризующего степени
отклонения вершины кривой распределения
от его центра. Можно сказать, что
показатель асимметрии отражает отклонение
вершины реальной кривой распределения
от идеальной по оси абсцисс.
По
схожему алгоритму вычисляем величину
показателя эксцесса характеризующего
подъем или снижение вершины распределения,
то есть – отклонения по оси ординат.
Для того, чтобы произвести расчет данного
показателя, следует выбрать пункт
«эксцесс». В окне «Аргументы функций»
получим его значение – 0,116.
При
наличии статистических таблиц критических
значений асимметрии и эксцесса (в данном
учебном пособии это таблицы 9 и 10)
вычисленные значения сравниваются с
табличными. Если оба
(!) показателя окажутся меньше табличных
величин, то распределение может считаться
нормальным.
Для
нашего примера табличное значение
показателя асимметрии находим на
пересечении строки n
= 25 и колонки
р ≤ 0,01
(предположим,
что мы
анализируем
результаты
достаточно важных экспериментов и
считаем, что вероятность ошибки
статистического заключения не должна
превышать 1%). Это число составляет 1,061.
Так как вычисленное значение показателя
асимметрии 0,579 оказывается гораздо
меньше табличной величины 1,061, можно
сделать заключение, что отклонение
вершины распределения по оси абсцисс
не столь значительно, чтобы отказаться
от применения параметрических методов.
В
таблице 10 находим критическое значение
показателя эксцесса.
Для
n
= 26 (так как
в таблице
отсутствует строка для n
= 25, переходим
к ближайшей строке)
и
р
≤ 0,01 оно
составляет 0,869.
И снова
фактическое значение показателя 0,116
оказывается меньше табличного 0, 869.
Отсюда следует, что отклонение вершины
распределения по оси ординат также
несущественно и его можно считать
нормальным. То, что оба показателя
оказались меньше критических табличных
величин, дает основание для последующего
применения параметрических критериев.
Второй
способ проверки выборки на нормальность
распределения
При
отсутствии таблиц критических значений
асимметрии и эксцесса следует произвести
расчеты не только этих показателей, но
и их выборочных ошибок.
Ошибка
показателя асимметрии производится по
формуле:
Для
нашего примера
она составит:
Выборочная
ошибка эксцесса рассчитывается по
другой формуле:
в
результате получим:
Далее
следует разделить показатели асимметрии
и эксцесса на их ошибки.
Частное
от деления показателей асимметрии и
эксцесса на их ошибки определяется как
tф (фактическое
значение) и сравнивается с tт,табличное
значение),
взятым из
таблицы Стьюдента (таблица 6), при
соответствующем уровне значимости и
числе степеней свободы. Если фактическое
значение критерия Стьюдента окажется
меньше табличного, распределение
признается нормальным, и, наоборот, если
фактическое значение окажется больше
табличного, следует сделать вывод о
несоответствии распределения нормальному
закону.
Для
показателя асимметрии получаем следующее
значение t-критерия:
Число
степеней свободы (df),
определяющее строку в таблице Стьюдента,
находим как n-1.
Следовательно, df
= 25-1=24. Уровень значимости (вероятность
ошибки статистического заключения),
определяющий колонку в таблице Стьюдента,
оставляем 1%. На пересечении строки df
=24 и колонки р
≤ 0,01 находим
табличное значение критерия tт
= 2,80.
Так как tф (1,25)
оказывается
гораздо
меньше чем tт
(2,80), можно
заключить, что и второй способ проверки
указывает на незначительность асимметрии
кривой распределения.
Фактическое
значения t-критерия
для показателя эксцесса рассчитываем
по формуле
Таким образом, не только для асимметрии,
но и для эксцесса tф
(0,129)
оказывается
существенно
меньше чем tт
(2,80), что опять
же указывает на нормальность распределения.
Третий
способ проверки выборки на нормальность
распределения
Проще всего задача
решается, если имеется компьютер с
установленной на ней программой
Statistica. После ввода данных в таблицу
вызывается стартовая панель модуля
Основные
статистики и таблицы
(Basic
Statistics/Tables).
В средней части окна Descriptive
Statistics
(Описательные статистики) слева находится
блок проверки распределений (Distribution).
Чтобы проверить, относятся ли показатели
выбранной переменной к распределяемым
по нормальному закону, нужно поставить
галочку в окне возле пункта K-S
and Lilliefors test for normality (Критерий
Колмогорова-Смирнова и Лилиефорса для
нормальности)
и нажать на кнопку Histograms
(гистограммы). В появившемся окне
приводятся гистограмма распределения
значений переменной и наложенная на
нее кривая нормального распределения,
сопоставление которых позволяет
визуально оценить характер распределения.
В
верхней части окна указывается
достоверность отличия проверяемого
распределения от нормального,
характеризуемая уровнем значимости р
(вероятность неправильного отвержения
гипотезы, если она верна). Если уровень
значимости р<0,05, то распределение
отлично от нормального на основании
соответствующего критерия. И наоборот,
если р>0,05, как на рисунке, то наблюдаемая
величина распределена нормально. Зная
вид распределения, в дальнейшей обработке
можно применить оптимальные статистические
методы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
This question borders on statistics theory too — testing for normality with limited data may be questionable (although we all have done this from time to time).
As an alternative, you can look at kurtosis and skewness coefficients. From Hahn and Shapiro: Statistical Models in Engineering some background is provided on the properties Beta1 and Beta2 (pages 42 to 49) and the Fig 6-1 of Page 197. Additional theory behind this can be found on Wikipedia (see Pearson Distribution).
Basically you need to calculate the so-called properties Beta1 and Beta2. A Beta1 = 0 and Beta2 = 3 suggests that the data set approaches normality. This is a rough test but with limited data it could be argued that any test could be considered a rough one.
Beta1 is related to the moments 2 and 3, or variance and skewness, respectively. In Excel, these are VAR and SKEW. Where … is your data array, the formula is:
Beta1 = SKEW(...)^2/VAR(...)^3
Beta2 is related to the moments 2 and 4, or the variance and kurtosis, respectively. In Excel, these are VAR and KURT. Where … is your data array, the formula is:
Beta2 = KURT(...)/VAR(...)^2
Then you can check these against the values of 0 and 3, respectively. This has the advantage of potentially identifying other distributions (including Pearson Distributions I, I(U), I(J), II, II(U), III, IV, V, VI, VII). For example, many of the commonly used distributions such as Uniform, Normal, Student’s t, Beta, Gamma, Exponential, and Log-Normal can be indicated from these properties:
Where: 0 <= Beta1 <= 4
1 <= Beta2 <= 10
Uniform: [0,1.8] [point]
Exponential: [4,9] [point]
Normal: [0,3] [point]
Students-t: (0,3) to [0,10] [line]
Lognormal: (0,3) to [3.6,10] [line]
Gamma: (0,3) to (4,9) [line]
Beta: (0,3) to (4,9), (0,1.8) to (4,9) [area]
Beta J: (0,1.8) to (4,9), (0,1.8) to [4,6*] [area]
Beta U: (0,1.8) to (4,6), [0,1] to [4.5) [area]
Impossible: (0,1) to (4.5), (0,1) to (4,1] [area]
Undefined: (0,3) to (3.6,10), (0,10) to (3.6,10) [area]
Values of Beta1, Beta2 where brackets mean:
[ ] : includes (closed)
( ) : approaches but does not include (open)
* : approximate
These are illustrated in Hahn and Shapiro Fig 6-1.
Granted this is a very rough test (with some issues) but you may want to consider it as a preliminary check before going to a more rigorous method.
There are also adjustment mechanisms to the calculation of Beta1 and Beta2 where data is limited — but that is beyond this post.
Нормальность распределения
В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями —
обновите страницу .
Некоторые статистические инструменты исходят из предположения, что распределение
является нормальным. Ниже будет приведён алгоритм проверки нормальности распределения,
а также пример в excel.
Закон распределения
Проверка на соответствие нормальному распределению — это частный случай решения задачи
о нахождении среди известных функций распределения такой, максимально точно описывающей
данное распределение.
В первую очередь, необходимо структурировать имеющиеся значения, в статье
свойства
распределения
описано, как строится ряд распределения, поэтому здесь я опущу детали и приведу
исходные данные и обработанные значения:
| 150 | 149 | 157 | 152 | 140 | 152 | 160 | 149 | 150 | 149 |
| 144 | 131 | 138 | 147 | 151 | 139 | 146 | 159 | 155 | 158 |
| 166 | 161 | 155 | 147 | 136 | 169 | 145 | 169 | 161 | 147 |
| 129 | 158 | 154 | 138 | 136 | 136 | 140 | 150 | 161 | 157 |
| 136 | 143 | 155 | 151 | 158 | 140 | 136 | 137 | 156 | 144 |
| 162 | 151 | 151 | 147 | 155 | 154 | 147 | 138 | 171 | 134 |
| 143 | 131 | 149 | 137 | 146 | 162 | 138 | 138 | 156 | 133 |
| 147 | 167 | 154 | 154 | 164 | 160 | 135 | 144 | 144 | 159 |
| 162 | 138 | 162 | 145 | 135 | 162 | 131 | 145 | 155 | 150 |
| 149 | 151 | 140 | 154 | 152 | 143 | 171 | 136 | 166 | 144 |
| Таблица 1. Исходные данные для проверки нормальности распределения |
| # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 5 | 11 | 11 | 11 | 13 | 17 | 12 | 12 | 3 | 3 |
| pi | 0.05 | 0.11 | 0.11 | 0.11 | 0.13 | 0.17 | 0.12 | 0.12 | 0.03 | 0.03 |
| Таблица 2. Количество элементов в каждом интервале |
График 1. Ряд распределения
Независимо от того, что мы видим на графике, нам необходимо проверить, является
ли распределение нормальным.
Характеристики нормального распределения — это среднее значение и стандартное отклонение.
Вычислим эти значения для нашего распределения:
μ = 149.09
σ = 10.23
Расчёт среднего значения и стандартного отклонения описан в статье параметры распределения
Нормальное распределение
Кривая нормального распределения для μ=149.09 и σ=10.23:
P(x) = e^[-0.5((x-149.09)/10.23)2] / [10.23√2π]
Формула нормального распределения
График 2. Ряд распределения и нормальное распределение, μ = 149.09, σ = 10.23
Первое приближение
Попробуем изобрести критерий нормальности, самое простое,
что приходит в голову — это определить процент соответствия
нормальной кривой и существующего распределения.
Для этого сложим абсолютные значения разниц по всем точкам графика,
найдём площадь под графиком нормального распределения и вычислим
интересующее отклонение, я назову такой критерий
«критерий нормальности» и постановлю, что если отклонение
больше, допустим 30%, то распределение не является нормальным.
diff = Σ|D(X) — P(X)|
S = ΣP(X)
Δ = diff / S
diff = 22.59
S = 105.23
Δ = 21%
Отклонение составляет 21%, а значит я делаю вывод, что распределение является нормальным
по критерию нормальности со средним значением
μ=149.09 и стандартным отклонением σ=10.23.
Скачать статью в формате PDF.
Автор статьи:
Дата редакции статьи: 19.12.2019
Вам понравилась статья?
/
Просмотров: 3 739