Как пропорционально уменьшить сумму в excel - Word и Excel

СУММПРОИЗВ (SUMPRODUCT) в Excel. Гораздо больше, чем сумма произведений

Разберем, казалось бы, простую функцию СУММПРОИЗВ ( SUMPRODUCT ). В конце будет просто бомба для тех, кто строит отчеты в одних файлах, а хранит данные — в других.

Из русскоязычного написания функции можно догадаться, что СУММПРОИЗВ — это сумма произведений. Классический и самый примитивный способ её использования — перемножить значения из двух или более диапазонов и затем просуммировать. Посмотрим, как это работает.

Как и в первой варианте, нам нужно зафиксировать цифру по итоговым продажам, однако, так как в расчетах не принимает участие отдельная ячейка с нужным значением, нам нужно проставить знаки “$” перед обозначениями строк и столбцов в адресах ячеек диапазона суммы: =D2/СУММ($D1500:$D$15) .

Как посчитать процент от числа и долю в Эксель

Вычислить сумму конкретных чисел в столбцах Excel можно как автоматически, так и вручную, используя стандартные инструменты программы. Помимо этого, имеется возможность просто просмотреть итоговый результат, не записывая его в ячейку. Начнем с последнего и самого простого способа.

Вариант №1: просматриваем всю сумму

В том случае, когда необходимо просто посмотреть всю сумму по столбцу, где ячейки содержат конкретные данные, и при этом не нужно постоянно удерживать сумму для дальнейших расчетов, делаем следующее:

Примечание: с левой стороны от суммы указываются число выделенных ячеек и усредненное значение по выбранному диапазону.

EXCEL — как распределить сумму X на N месяцев — CodeRoad

При необходимости проверки большего количества условий, выполняемых одновременно (аналог логическому оператору И ), добавляем их в формулу через знак умножения и не забываем взять новое условие в круглые скобки.

Находим процент от числа

А сейчас давайте попробуем вычислить процент от числу в виде абсолютного значения, т.е. в виде другого числа.

Математическая формула для расчета выглядит следующим образом:

Например, давайте узнаем, какое число составляет 15% от 90.

Подобные знания помогают решать множество математических, экономических задач, физических и других задач. Допустим, у нас есть таблица с продажами обуви (в парах) за 1 квартал, и мы планируем в следующем продать на 10% больше. Нужно определить, какому количеству пар для каждого наименования соответствуют эти 10%.

В случаях, когда нам нужно получить разные проценты от разных чисел, соответственно, нужно создать отдельный столбец не только для вывода результатов, но и для значений процентов.

Расчет пропорций при распределении расходов | Такском

Чтобы использовать эту функцию, на вкладке «Данные» выберите кнопку «Из интернета» и вставьте адрес надежного источника, например cbr.ru. Эксель предложит выбрать, какую именно таблицу нужно загрузить с сайта — отметьте нужную галочкой.

1 ответ

Возможный Дубликат : Пропорционально распределить (пропорционально распределить) значение по набору значений Я искал алгоритм, чтобы распределить общую сумму ежемесячно на основе количества дней в году в C# так, чтобы сумма всех пропортонов была равна общей стоимости. Диапазон дат в течение года и.

B1 , B2 и B3 являются входными ячейками. B1 должна быть датой, а не строкой.

D1 — O1 — это месяцы. Значения должны быть датами, а не строками, но затем могут быть отформатированы так, чтобы показывать только месяц и год. Например, формат MMM YYYY .

Вам нужно только ввести D1 и E1 в качестве дат 2017-01-01 и 2017-02-01 , затем выберите D1:E1 и заполните справа. Затем будет создана серия , имеющая от шага к шагу разницу в E1 — D1 , что в данном примере составляет 1 месяц.

и может быть заполнен справа по мере необходимости. В примере до O2 .

Теперь, если вы изменяете какую-либо из входных ячеек, значения в D2 на O2 также изменятся из-за формулы.

7 полезных формул для тех, кто считает деньги в эксель-таблице

То, что я рассказываю вам в своей статье это детский лепет. Если посмотреть, что вытворяют ребята завершившие обучение на курсе “EXCEL”, то захочется научиться делать также. Поэтому посоветую вам зарегистрироваться на обучение.

Как посчитать процентное распределение в Excel по формуле

Процентное распределение отображает нам как определенное значение (например, показатель суммарного дохода) разделяется на отдельные составляющие, которые образуют его целостность.

Формула процентного распределения в Excel

Как видно ниже на рисунке ниже формула вычисления процентного распределения в Excel очень проста:

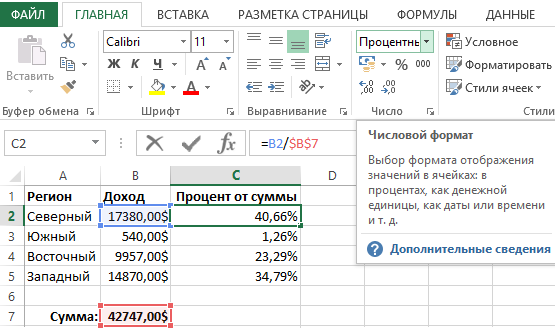
Каждую часть необходимо разделить на сумму всех частей. В данном случаи ячейка B7 содержит значение суммарного дохода всех отделов регионов. Чтобы вычислить процентное распределение суммарного дохода по всем регионам, достаточно лишь поделить значение отдельного показателя по каждому региону на суммарный доход.

Как видно формула не очень сложна. Она использует просто относительные ссылки на доходы регионов, чтобы поделить их на абсолютную ссылку на суммарный доход. Обратите внимание на абсолютную ссылку. Указанные символы доллара позволяют заблокировать ссылку на одну, конкретную ячейку. Благодаря этому адрес абсолютной ссылки не изменяется при копировании формул в другие ячейки.

Процентное распределение по динамической формуле Excel

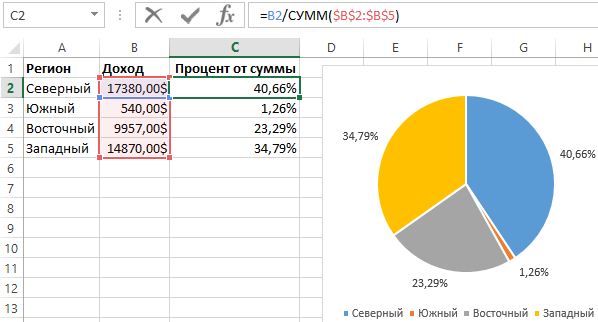
Отдельное вычисление для хранения суммарного дохода в отдельной ячейке как константу – не обязательно. Если мы добавим в формулу функцию =СУММ(), тогда мы можем динамически выполнять вычисление процентного распределения. Ниже на рисунке показано решение для создания динамической формулы процентного распределения отдельных значений.

Примечание: Для тех, кто не в курсе – функция СУММ суммирует все значения, которые заданы в ее аргументах.

Снова обратите внимание на то, что все адреса ссылок, которые заданы в аргументах функции СУММ должны быть абсолютными (в данном случаи). Благодаря зафиксированный абсолютными ссылками диапазон ячеек в аргументе функции СУММ, не изменяться в процессе копирования формулы в другие ячейки.

Как раскидать сумму пропорционально в excel

В общем и целом написать данную статью подвигла меня очередная лекция на тему себестоимости. Кстати, крайне рекомендую курс для ИТ-менеджеров в открытом университете, который там сейчас находится в открытом доступе.

Итак, классика!

Суть в том, что везде, где я встречаю код распределения (размазывания) одной суммы на другую по некому базису, всё всегда сводится к нахождению коэффициента распределения (когда мы делим распределяемую сумму на сумму базы) и последующего умножения этого коэффициента на базу по строке (например, если мы распределяем пропорционально количеству, то на количество).

Таким образом все сводится к такому вот методу:

Здесь базой является количество, сумма базы = 6, распределяемая сумма = 100. Коэффициент = распределяемая сумма / сумма базы = 100 / 6 = 16,(6) («Шесть в скобках» — это то, как нас учили записывать периодичские дроби. Если кого-то учили иначе — проьба иметь это ввиду). Далее в каждой строке я округляю результат до копеек.

В принципе мы получили то, что хотели — распределили нужную сумму пропорционально количеству. В данном случае у нас крайне удачно получилось с округлением — в первой строке мы округлили вверх и получили одну лишнюю копейку, во второй строке мы округлили вниз и потеряли копейку. И то, что нам так повезло — это воля парня, сказавшего парню из эпиграфа сказать древним грекам все те умные вещи, о которых он им сказал.

Давайте рассмотрим случай, когда тот парень был к нам не так благосклонен, а именно — давайте распределим 10 на 3:

В итоге у нас не хватило одной копейки. Для того, чтобы решить эту проблему, необходимо учесть остаточек в конце. У нас распределенная сумма получилась равна 9,99, а сумма, которую нужно распределить — 10. Разницу, обычно, добавляют к последней строке. Т.е. в последней строке у нас будет 3,34, «чтобы не нарушать отчетности» (с).

Все хрошо, пока потерянная в ходе округления сумма мала и не играет большой роли. Но если мы попытаемся таким же образом распределить 10 на 30 строк, то внезапно окажется, что к последней строке нам нужно прибавить уже не 1 копейку, а 10. Можно, конечно, прибавить сумму остатка к последней строке:

В последней строке в итоге будет сумма 0,33 + 0,10 = 0,43. Если мы распределяем какие-нибудь ксвенные затраты на количество выпуска, то для каждой статьи затрат может набраться весьма большое отклонение, которое все целиком упадет на последнюю строчку. Таким образом продукт, выпущенный нами в последнюю очередь, вберет в свою себестоимость все те отклонения и станет «золотым» )))

Если мы будем дораспределять остаток, то, в принципе, мы также можем попасть на округление и дораспределять нам придется до тх пор, пока все копейки не израсходуются. Это, как мне кажется, несколько неудобно, непрозрачно да и затратно.

Новое решение!

Давным-давно, кажется в позапрошлую работу, меня попросили создать обработку, которая бы перекраивала контуры полей, перераспределяя на их новую площадь какие-то старые остатки на счетах учета затрат на дату распределения. Там как раз сумма распределялась между новыми площадями пропорционально новому метражу. Звучит пространно, но примите на веру (как древние греки), что это относится к обсуждаемой нами задаче распределения суммы по базе. И тогда я как раз «родил» (ага, прям как Авраам Исаака) алгоритм распределения, после которого нет остатка. Странно, но тогдашний мой руководитель так и не понял суть алгоритма, хотя после теста сказал, что все работает и оставил как есть. Западные программисты в таких случаях просто стараются не использовать подобные алгоритмы, так что честь и хвала программистам российским, которые используют и то, в чем не понимают )))

В принципе все просто: мы каждую итерацию должны пересчитывать коэффициент распределения. Давайте построим таблицу с 30-ю записями и добавим колонки для нового коэффициента и по-новому распределенной суммы:

Пример 1. Распределение премии

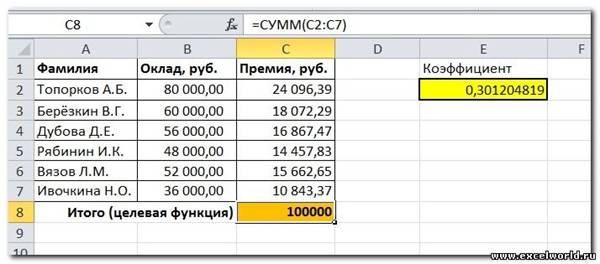
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.

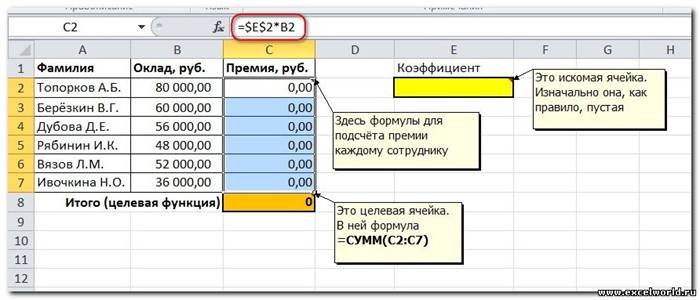
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).

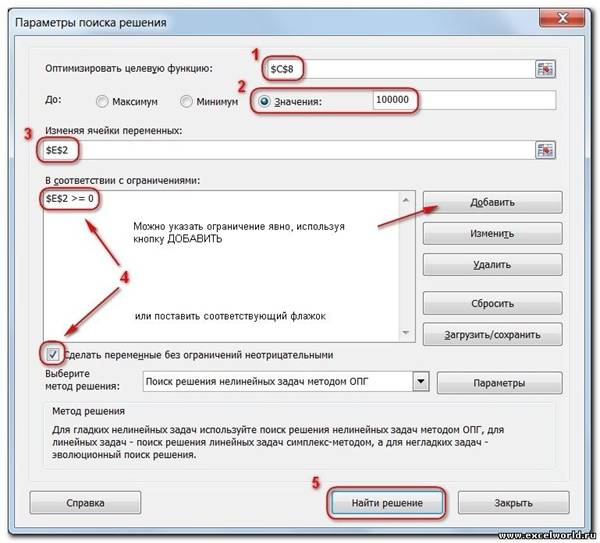
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:

Начиная с Excel 2010

1. Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна

2. Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода

3. Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение

4. Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=,

5. Кнопка, включающая итеративные вычисления с заданными параметрами.

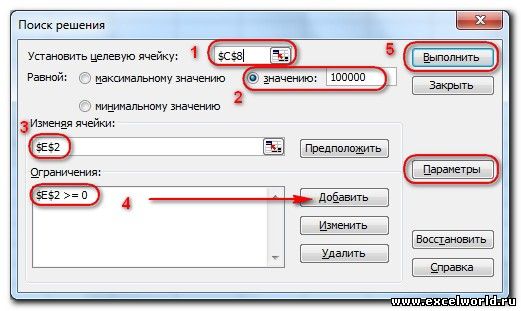
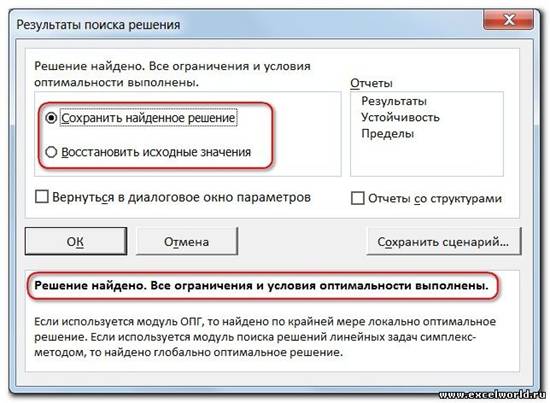
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.

Начиная с Excel 2010

Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОКи фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отменаи возвращаетесь к предыдущему состоянию таблицы.

Решение данной задачи выглядит так

Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.

Разберём еще одну задачу оптимизации (получение максимальной прибыли)

Пример 2. Мебельное производство (максимизация прибыли)

Фирма производит две модели А и В сборных книжных полок.

Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.

Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?

Порядок действий нам уже известен.

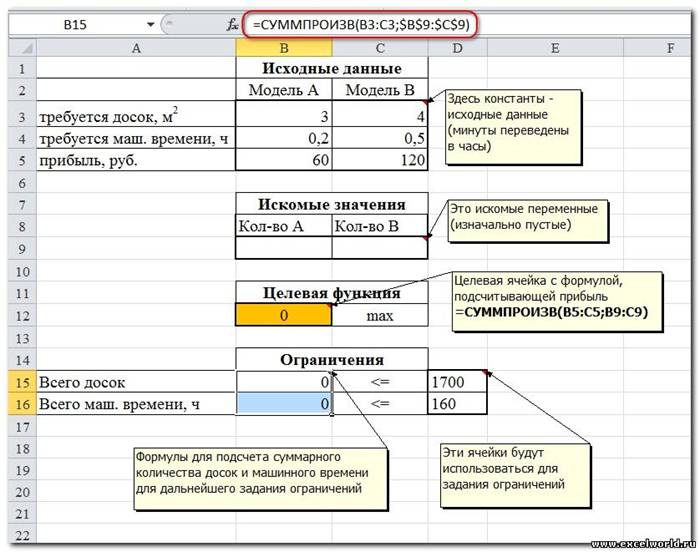
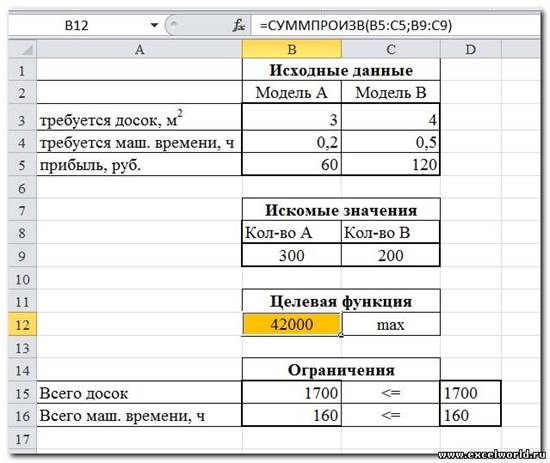
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке

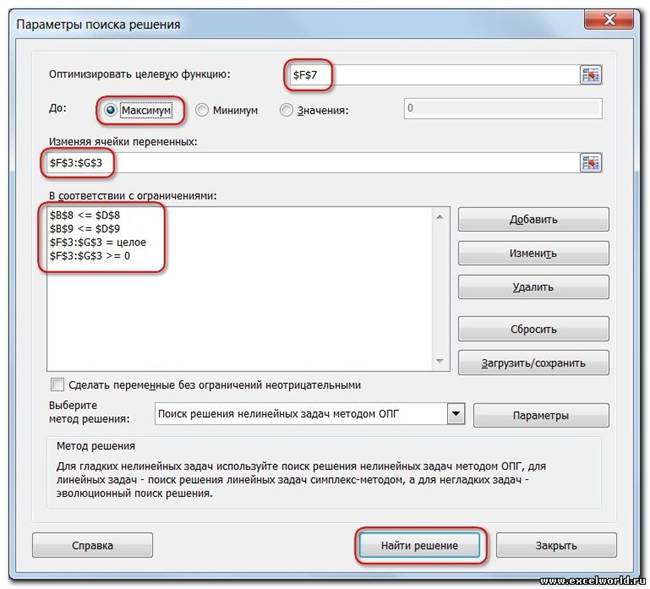
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры

1. Целевая ячейка F7 содержит формулу для расчёта прибыли

2. Параметр оптимизации — максимум

3. Изменяемые ячейки F3:G3

4. Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D9); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D8). Здесь вместо ссылок на ячейки D8 и D9 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице

5. Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат

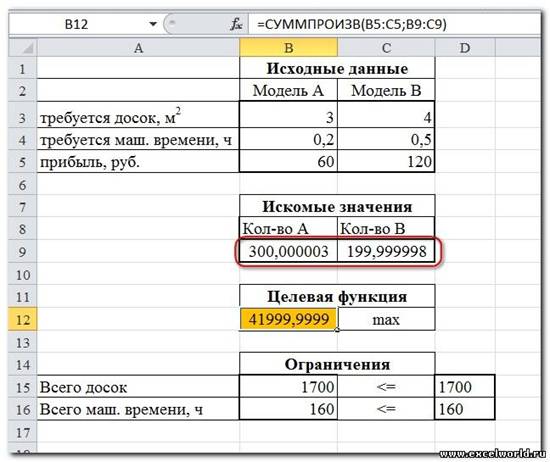
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:

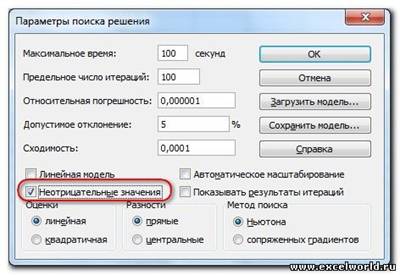
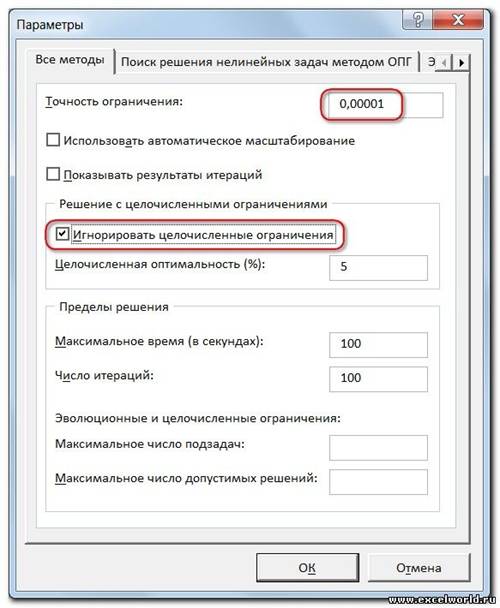
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметрыи попадаем в одноимённое диалоговое окно

Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.

Пример 3. Транспортная задача (минимизация затрат)

На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.

Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».

Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.

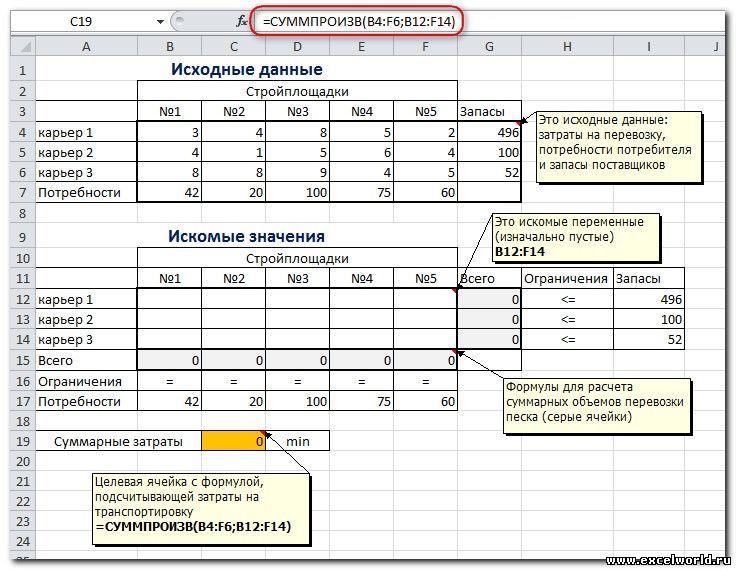
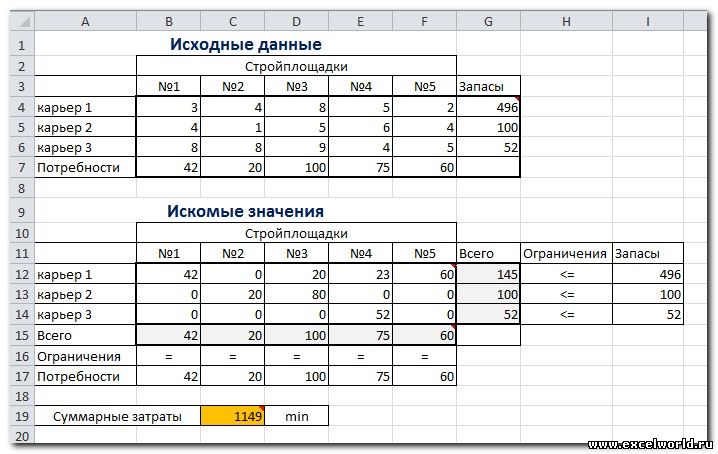
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке

В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.

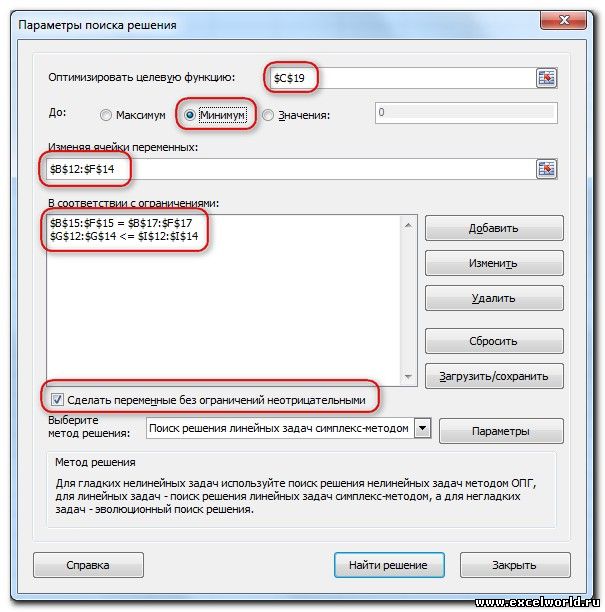
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)

Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже

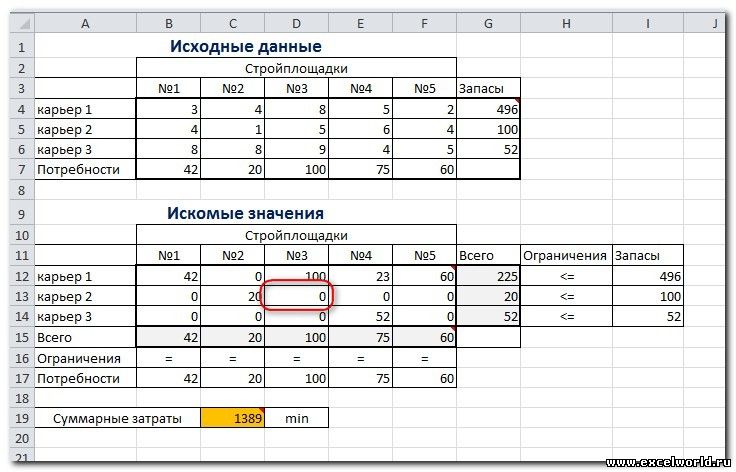
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат

И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения

Поиск решения EXCEL (1.3). Распределение ресурсов (ограничение по количеству оборудования, несколько периодов)

Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.

Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты. Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье Поиск решения MS EXCEL (1.2). Распределение ресурсов (ограничение по количеству оборудования) , и имеет смысл предварительно познакомиться с изложенным там материалом. В этой статье мы решим аналогичную задачу, но для случая работы оборудования в нескольких периодах (пример с сайта www.solver.com ).

Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .

Задача

Предприятие выпускает монопродукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. Выпуск продукции осуществляется в течение 5 дней. Отгрузка заказа ежедневная. На предприятии 3 типа оборудования. Каждый тип оборудования выпускает один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.

Создание модели

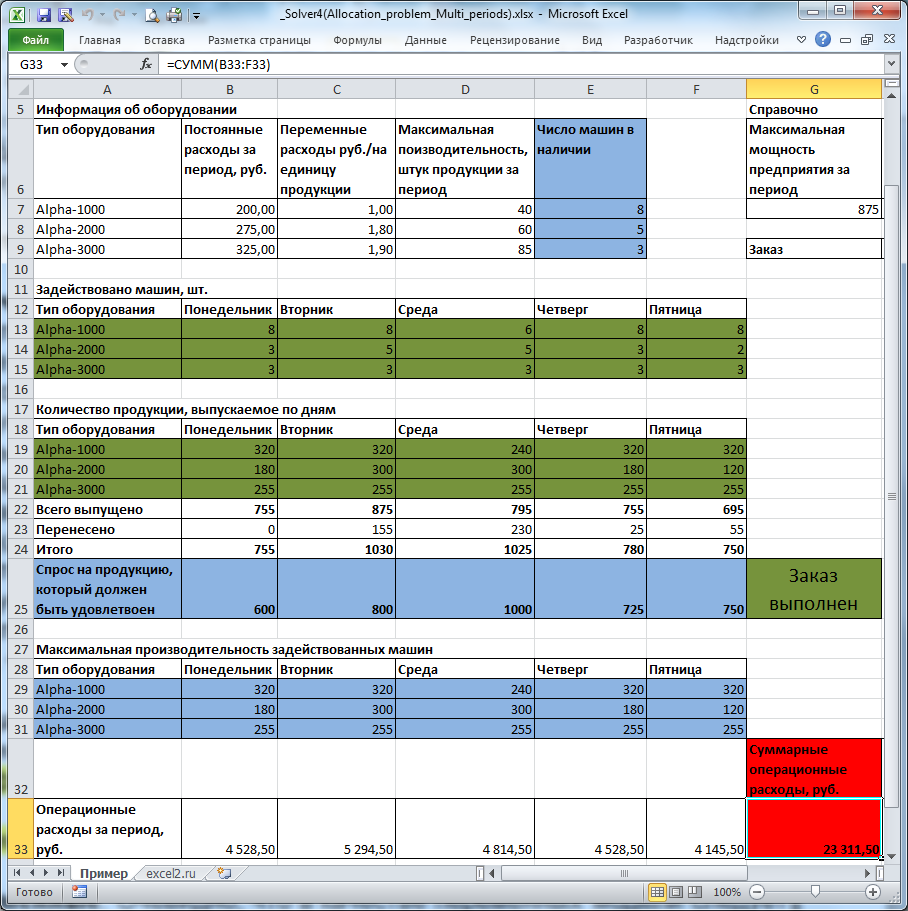
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).

Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача Поиска решения выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.

Переменные (выделено зеленым) . В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Для наглядности диапазонам ячеек, содержащих переменные, присвоены имена Машин_Задействовано и Продукции_выпущено.

Ограничения (выделено синим) . Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии (используются именованные диапазоны Alpha XXXX _Задействовано и Alpha XXXX _в_наличии ). Всего должно быть выпущено продукции не меньше чем величина заказа (используется именованный диапазон Продукции выпущено_Итого ). В день возможно производить больше продукции, чем требуется в день заказа, излишек переносится на следующий день. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом (используются именованные диапазоны Продукции выпущено и Макс_производительность_задейств_машин ).

Целевая функция (выделено красным) . Целевая функция – это сумма операционных расходов за 5 дней. Операционные расходы, понесенные за день, задается формулой =СУММПРОИЗВ(B19:B21; Расходы_переменные)+ СУММПРОИЗВ(B13:B15; Расходы_постоянные) B19:B21 – количество продукции, выпущенной в определенный день. B13:B15 — количество задействованных машин в определенный день.

Это суммарные операционные расходы (переменная и постоянные части). Сумма операционных расходов за 5 дней должна быть минимизирована.

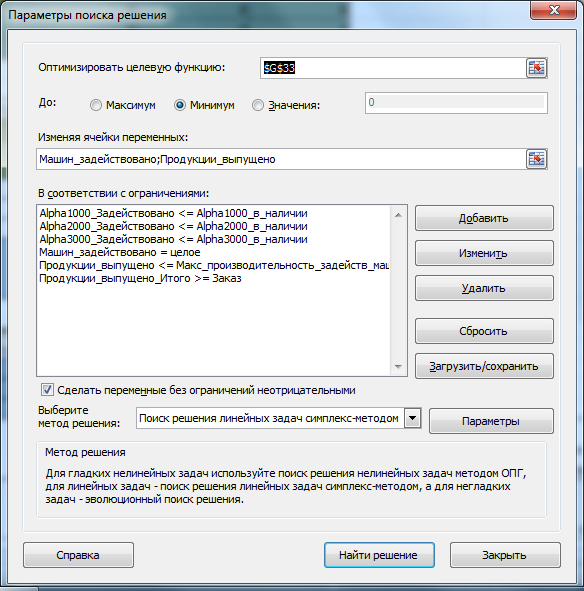
Убедитесь, что метод решения соответствует линейной задаче. Параметры Поиска решения были выбраны следующие:

Теперь в диалоговом окне можно нажать кнопку Найти решение .

Результаты расчетов

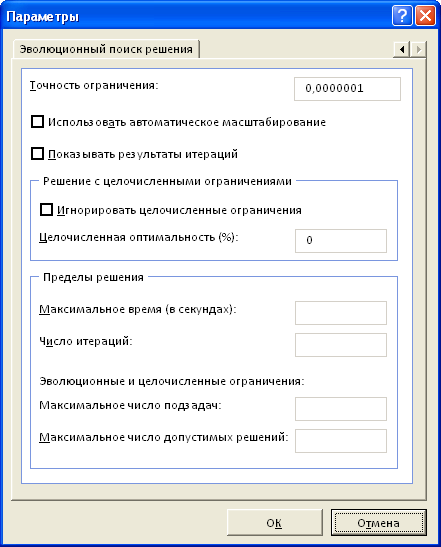
Поиск решения подберет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. В нашей задаче было установлено целочисленное ограничение, что существенно усложняет задачу поиска и, соответственно, сказывается на скорости расчета. Как показано на рисунке выше, Целочисленная оптимальность была выбрана 0% ( Целочисленная оптимальность (Integer Optimality) позволяет Поиску решения остановить поиск, в случае, если он найдет целочисленное решение, в пределах указанного процента от оптимального). В нашем случае (0%), требуется найти лучшее из известных Поиску решения решений. Поиск в этом случае занял 8 секунд, результат 23 311,50. Установив Целочисленную оптимальность 1%, поиск займет 0,2 сек, результат 23 370,50 (отличие на 0,3%). Это информация к размышлению: стоит ли увеличение точности на 0,3% уменьшения скорости расчетов более чем на порядок? Решать Вам. В любом случае, первые расчеты модели лучше проводить при Целочисленной оптимальности не равной 0%.

Распределение суммы по базе

Афиняне! Повсему вижу я, что Вы как-то по-особеному набожны, ибо проходя и осматривая Ваши святыни, я наткнулся и на жертвенник неведомому богу.

Где-то в библии в адрес древних греков.

Итак, классика!

Таким образом все сводится к такому вот методу:

Новое решение!

5 основ Excel (обучение): как написать формулу, как посчитать сумму, сложение с условием, счет строк и пр.

Многие кто не пользуются Excel — даже не представляют, какие возможности дает эта программа! ☝

Подумать только: складывать в автоматическом режиме значения из одних формул в другие, искать нужные строки в тексте, создавать собственные условия и т.д. — в общем-то, по сути мини-язык программирования для решения «узких» задач (признаться честно, я сам долгое время Excel не рассматривал за программу, и почти его не использовал) .

В этой статье хочу показать несколько примеров, как можно быстро решать повседневные офисные задачи: что-то сложить, вычесть, посчитать сумму (в том числе и с условием) , подставить значения из одной таблицы в другую и т.д.

То есть эта статья будет что-то мини гайда по обучению самому нужному для работы (точнее, чтобы начать пользоваться Excel и почувствовать всю мощь этого продукта!) .

Возможно, что прочти подобную статью лет 17-20 назад, я бы сам намного быстрее начал пользоваться Excel (и сэкономил бы кучу своего времени для решения «простых» задач. 👌

Обучение основам Excel: ячейки и числа

Примечание : все скриншоты ниже представлены из программы Excel 2016 (как одной из самой новой на сегодняшний день).

Многие начинающие пользователи, после запуска Excel — задают один странный вопрос: «ну и где тут таблица?». Между тем, все клеточки, что вы видите после запуска программы — это и есть одна большая таблица!

Теперь к главному : в любой клетке может быть текст, какое-нибудь число, или формула. Например, ниже на скриншоте показан один показательный пример:

слева : в ячейке (A1) написано простое число «6». Обратите внимание, когда вы выбираете эту ячейку, то в строке формулы (Fx) показывается просто число «6».
справа : в ячейке (C1) с виду тоже простое число «6», но если выбрать эту ячейку, то вы увидите формулу «=3+3» — это и есть важная фишка в Excel!

Просто число (слева) и посчитанная формула (справа)

👉 Суть в том, что Excel может считать как калькулятор, если выбрать какую нибудь ячейку, а потом написать формулу, например «=3+5+8» (без кавычек). Результат вам писать не нужно — Excel посчитает его сам и отобразит в ячейке (как в ячейке C1 в примере выше)!

Но писать в формулы и складывать можно не просто числа, но и числа, уже посчитанные в других ячейках. На скриншоте ниже в ячейке A1 и B1 числа 5 и 6 соответственно. В ячейке D1 я хочу получить их сумму — можно написать формулу двумя способами:

первый: «=5+6» (не совсем удобно, представьте, что в ячейке A1 — у нас число тоже считается по какой-нибудь другой формуле и оно меняется. Не будете же вы подставлять вместо 5 каждый раз заново число?!);
второй: «=A1+B1» — а вот это идеальный вариант, просто складываем значение ячеек A1 и B1 (несмотря даже какие числа в них!).

Сложение ячеек, в которых уже есть числа

Распространение формулы на другие ячейки

В примере выше мы сложили два числа в столбце A и B в первой строке. Но строк то у нас 6, и чаще всего в реальных задачах сложить числа нужно в каждой строке! Чтобы это сделать, можно:

в строке 2 написать формулу «=A2+B2» , в строке 3 — «=A3+B3» и т.д. (это долго и утомительно, этот вариант никогда не используют) ;
выбрать ячейку D1 (в которой уже есть формула) , затем подвести указатель мышки к правому уголку ячейки, чтобы появился черный крестик (см. скрин ниже) . Затем зажать левую кнопку и растянуть формулу на весь столбец. Удобно и быстро! ( Примечание : так же можно использовать для формул комбинации Ctrl+C и Ctrl+V (скопировать и вставить соответственно)) .

Кстати, обратите внимание на то, что Excel сам подставил формулы в каждую строку. То есть, если сейчас вы выберите ячейку, скажем, D2 — то увидите формулу «=A2+B2» (т.е. Excel автоматически подставляет формулы и сразу же выдает результат) .

Как задать константу (ячейку, которая не будет меняться при копировании формулы)

Довольно часто требуется в формулах (когда вы их копируете), чтобы какой-нибудь значение не менялось. Скажем простая задача: перевести цены в долларах в рубли. Стоимость рубля задается в одной ячейке, в моем примере ниже — это G2.

Далее в ячейке E2 пишется формула «=D2*G2» и получаем результат. Только вот если растянуть формулу, как мы это делали до этого, в других строках результата мы не увидим, т.к. Excel в строку 3 поставит формулу «D3*G3», в 4-ю строку: «D4*G4» и т.д. Надо же, чтобы G2 везде оставалась G2.

Чтобы это сделать — просто измените ячейку E2 — формула будет иметь вид «=D2*$G$2». Т.е. значок доллара $ — позволяет задавать ячейку, которая не будет меняться, когда вы будете копировать формулу (т.е. получаем константу, пример ниже) .

Константа / в формуле ячейка не изменяется

Как посчитать сумму (формулы СУММ и СУММЕСЛИМН)

Можно, конечно, составлять формулы в ручном режиме, печатая «=A1+B1+C1» и т.п. Но в Excel есть более быстрые и удобные инструменты.

Один из самых простых способов сложить все выделенные ячейки — это использовать опцию автосуммы (Excel сам напишет формулу и вставить ее в ячейку) .

Что нужно сделать, чтобы посчитать сумму определенных ячеек:

сначала выделяем ячейки (см. скрин ниже 👇) ;
далее открываем раздел «Формулы» ;
следующий шаг жмем кнопку «Автосумма» . Под выделенными вами ячейками появиться результат из сложения;
если выделить ячейку с результатом (в моем случае — это ячейка E8) — то вы увидите формулу «=СУММ(E2:E7)» .
таким образом, написав формулу «=СУММ(xx)» , где вместо xx поставить (или выделить) любые ячейки, можно считать самые разнообразные диапазоны ячеек, столбцов, строк.

Автосумма выделенных ячеек

Как посчитать сумму с каким-нибудь условием

Довольно часто при работе требуется не просто сумма всего столбца, а сумма определенных строк (т.е. выборочно). Предположим простую задачу: нужно получить сумму прибыли от какого-нибудь рабочего (утрировано, конечно, но пример более чем реальный) .

Я в своей таблицы буду использовать всего 7 строк (для наглядности) , реальная же таблица может быть намного больше. Предположим, нам нужно посчитать всю прибыль, которую сделал «Саша». Как будет выглядеть формула:

» =СУММЕСЛИМН( F2:F7 ; A2:A7 ;»Саша») » — ( прим .: обратите внимание на кавычки для условия — они должны быть как на скрине ниже, а не как у меня сейчас написано на блоге) . Так же обратите внимание, что Excel при вбивании начала формулы (к примеру «СУММ. «), сам подсказывает и подставляет возможные варианты — а формул в Excel’e сотни!;
F2:F7 — это диапазон, по которому будут складываться (суммироваться) числа из ячеек;
A2:A7 — это столбик, по которому будет проверяться наше условие;
«Саша» — это условие, те строки, в которых в столбце A будет «Саша» будут сложены (обратите внимание на показательный скриншот ниже) .

Сумма с условием

Примечание : условий может быть несколько и проверять их можно по разным столбцам.

Как посчитать количество строк (с одним, двумя и более условием)

Довольно типичная задача: посчитать не сумму в ячейках, а количество строк, удовлетворяющих какомe-либо условию.

Ну, например, сколько раз имя «Саша» встречается в таблице ниже (см. скриншот). Очевидно, что 2 раза (но это потому, что таблица слишком маленькая и взята в качестве наглядного примера). А как это посчитать формулой?

«=СЧЁТЕСЛИ( A2:A7 ; A2 )» — где:

A2:A7 — диапазон, в котором будут проверяться и считаться строки;
A2 — задается условие (обратите внимание, что можно было написать условие вида «Саша», а можно просто указать ячейку).

Результат показан в правой части на скрине ниже.

Количество строк с одним условием

Теперь представьте более расширенную задачу: нужно посчитать строки, где встречается имя «Саша», и где в столбце «B» будет стоять цифра «6». Забегая вперед, скажу, что такая строка всего лишь одна (скрин с примером ниже) .

Формула будет иметь вид:

=СЧЁТЕСЛИМН( A2:A7 ; A2 ; B2:B7 ;»6″) — (прим.: обратите внимание на кавычки — они должны быть как на скрине ниже, а не как у меня) , где:

A2:A7 ; A2 — первый диапазон и условие для поиска (аналогично примеру выше);

B2:B7 ;»6″ — второй диапазон и условие для поиска (обратите внимание, что условие можно задавать по разному: либо указывать ячейку, либо просто написано в кавычках текст/число).

Счет строк с двумя и более условиями

Как посчитать процент от суммы

Тоже довольно распространенный вопрос, с которым часто сталкиваюсь. Вообще, насколько я себе представляю, возникает он чаще всего — из-за того, что люди путаются и не знают, что от чего ищут процент (да и вообще, плохо понимают тему процентов (хотя я и сам не большой математик, и все таки. ☝) ).

👉 В помощь!

Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью Excel] — заметка для начинающих

Самый простой способ, в котором просто невозможно запутаться — это использовать правило «квадрата», или пропорции.

Вся суть приведена на скрине ниже: если у вас есть общая сумма, допустим в моем примере это число 3060 — ячейка F8 (т.е. это 100% прибыль, и какую то ее часть сделал «Саша», нужно найти какую. ).

По пропорции формула будет выглядеть так: =F10*G8/F8 (т.е. крест на крест: сначала перемножаем два известных числа по диагонали, а затем делим на оставшееся третье число).

В принципе, используя это правило, запутаться в процентах практически невозможно 👌.

Пример решения задач с процентами

Собственно, на этом я завершаю данную статью. Не побоюсь сказать, что освоив все, что написано выше (а приведено здесь всего лишь «пяток» формул) — Вы дальше сможете самостоятельно обучаться Excel, листать справку, смотреть, экспериментировать, и анализировать. 👌

Скажу даже больше, все что я описал выше, покроет многие задачи, и позволит решать всё самое распространенное, над которым часто ломаешь голову (если не знаешь возможности Excel) , и даже не догадывается как быстро это можно сделать. ✔

Источник

Gliridae

Пользователь

Сообщений: 4
Регистрация: 01.01.1970

Господа, встала проблема, есть данные продаж, которые необходимо пропорционально распределить по строкам и столбцам до заданных значений и в строках и в столбцах, у меня решение этой задачи требует «ручного доведения до ума», а предстоит считать бюджет на год, т.е. 12 месяцев*11 дистрибьюторов по каждой позиции, помогите идеями, как безболезненно это пережить.
закладка данные: даны продажи N13:X124
задача: пропорционально распределить продажи N13:X124, что бы значения по строкам были равны задачам от ШК( H13:H124) по каждой позиции, т.е.:
СУММ(N13:X13)=H13
СУММ(N14:X14)=H14
…
СУММ(N124:X124)=H124
И главное условие, что бы по столбцам суммы, в свою очередь были равны задачам поставленным НОП (N7: X7) по каждому дистрибьютору, т.е.:
СУММ(N13:N124)=N7
СУММ(O13:O124)=O7
…
СУММ(X13:X124)=X7
В итоге, в графах «не распределено»(N13:N124 и N8:X8) должны быть ноли.

Gliridae Пользователь Сообщений: 4 Регистрация: 01.01.1970	пардон, файл не прикрепился…

Jack Пользователь Сообщений: 352 Регистрация: 01.01.1970	непонятно. на основе какой пропорции должно быть распределение? N7=N7+ L7/СУММ(N7:X7)*N7

Gliridae

Пользователь

Сообщений: 4
Регистрация: 01.01.1970

{quote}{login=Jack}{date=13.12.2011 12:41}{thema=}{post}непонятно. на основе какой пропорции должно быть распределение?
N7=N7+ L7/СУММ(N7:X7)*N7{/post}{/quote}

когда обжимала файл удалила строки сверху, поэтому с описанием не совпадает((( тут при составлении пропорции нужно учитывать 2 фактора: «план НОП»(N1:X1) и «план ШК»(H7:H118) и сумма по строкам и по столбцам с этими данными должна биться 1:1

ps: Вашу формулу попробовала, не получилось…

Jack Пользователь Сообщений: 352 Регистрация: 01.01.1970	Это не формула)) это вопрос был такой

Jack Пользователь Сообщений: 352 Регистрация: 01.01.1970	тупой способ в два этапа. второй этап конечно несколько неуниверсален. но в общем цель достигнута <EM><STRONG>Файл удален</STRONG> — велик размер — [<STRONG>МОДЕРАТОРЫ</STRONG>]</EM>

Gliridae

Пользователь

Сообщений: 4
Регистрация: 01.01.1970

оригинальная идея исполнения, но возможно я не правильно выразила идею, в предложенном Вами решении(обычно я ставлю формулу =H7/K7, и умножаю получившийся коэффициент на каждое значение строки, и так по каждой строке, что в сочетании с округлением не идеально, но нельзя допускать отрицательных продаж, как получилось у Вас). В Вашем случае по строкам значения бьются вровень с заданными(H7:H118), но по столбцам они и приблизительно не сходятся с требуемыми(N1:X1), в чём и встаёт у меня основная загвоздка… если я подбиваю по столбцам, идут расхождения по строкам, и наоборот… а надо, что бы сходились с заданными значениями там и там…

Юрий М Модератор Сообщений: 60585 Регистрация: 14.09.2012 Контакты см. в профиле	#8 13.12.2011 21:03:58 {quote}{login=Jack}{date=13.12.2011 04:37}{thema=}{post}тупой способ в два этапа. {/post}{/quote}Каким бы не был способ, размер файла не должен превышать максимально допустимый.

Источник

Автор:
Robert Simon

Дата создания:
21 Июнь 2021

Дата обновления:
9 Апрель 2023

Видео: Сортировка данных в MS Excel

Содержание

Шаг 1
Шаг 2
Шаг 3
Шаг 4
Шаг 5
Шаг 6

Ячейки электронной таблицы Excel позволяют вводить числа и выполнять математические вычисления с этими числами, что делает его идеальным инструментом для пропорционального распределения чисел. Когда у вас есть стоимость, распределенная в течение определенного периода времени, например, ежемесячная арендная плата или двухнедельный платеж, если вам необходимо знать стоимость за долю этого периода времени, этот процесс называется пропорциональным распределением. Excel позволяет поместить каждый фактор в формуле пропорционального распределения в отдельную ячейку, что упрощает понимание математических расчетов, лежащих в основе процесса.

Шаг 1

Откройте новую электронную таблицу Excel 2010.

Шаг 2

Щелкните ячейку «A1», которая является верхней ячейкой в крайнем левом столбце. Введите общую сумму, которую вы собираетесь уменьшить до пропорциональной суммы. Если, например, вы распределяете ежемесячный счет пропорционально, это будет обычная ежемесячная стоимость счета.

Шаг 3

Щелкните ячейку «B1», которая находится справа от первой ячейки. Введите общее количество подпериодов в общем периоде. Например, если вы распределяете ежемесячный счет пропорционально на несколько дней, укажите количество дней в месяце в этой ячейке.

Шаг 4

Щелкните ячейку «C1». Введите количество подпериодов, которые вы хотите использовать для определения пропорциональной суммы. Продолжая примеры, это количество дней, прошедших в месяце на момент определения пропорциональной суммы.

Шаг 5

Щелкните ячейку «B2», которая находится чуть ниже общего количества подпериодов. Введите «= A1 / B1» без кавычек, чтобы получить стоимость для каждого подпериода.

Щелкните ячейку «C3» и введите «= B2 * C1» без кавычек, чтобы получить желаемую пропорциональную сумму.

Источник

Если вы боретесь с расчетом процентного увеличения или уменьшения в Microsoft Excel, это руководство расскажет вам об этом процессе.

Microsoft Excel отлично подходит как для базовых, так и для сложных расчетов, включая процентные различия. Если вам сложно рассчитать процентное увеличение или уменьшение на бумаге, Excel может сделать это за вас.

Если вы помните свою школьную математику, процесс вычисления процентов в Excel очень похож. Вот как использовать Excel для расчета процентного увеличения и уменьшения.

И выполнять другие процентные вычисления, такие как процентное отношение числа.

Процент увеличения включает в себя два числа. Основной математический подход для расчета процентного увеличения состоит в том, чтобы вычесть второе число из первого числа. Используя сумму этой цифры, разделите эту оставшуюся цифру на исходное число.

Пример, стоимость счета домашнего хозяйства стоит $ 100 в сентябре, но $ 125 в октябре. Чтобы рассчитать эту разницу, вы можете использовать формулу = СУММ (125-100) / 100 в Excel.

Если ваши цифры находятся в отдельных ячейках, вы можете заменить числа для ссылок на ячейки в своей формуле.

Например, если сумма счета за сентябрь находится в ячейке B4 и сумма счета за октябрь находится в камере B5, ваша альтернативная формула Excel будет = СУММ (B5-B4) / B4

Пример процентного увеличения в Microsoft Excel

Процентное увеличение в период с сентября по октябрь 25%с этой цифрой в виде десятичного числа (0,25) по умолчанию в Excel, используя формулу выше.

Если вы хотите отобразить этот показатель в процентах в Excel, вам нужно заменить форматирование для вашей ячейки. Выберите свою ячейку, затем нажмите Процент Стиль кнопка в Дом вкладка, под номер категория.

Установите для вашей ячейки тип числа в процентах, чтобы он отображался в процентах в Excel.

Вы также можете щелкнуть правой кнопкой мыши на вашей ячейке, нажмите Формат ячеек затем выберите Процентное соотношение от Категория -> Номер меню для достижения того же эффекта.

Расчет процентного снижения в Excel

Чтобы рассчитать процентное уменьшение между двумя числами, вы будете использовать расчет, идентичный процентному увеличению. Вы вычитаете второе число из первого, а затем делите его на первое число. Разница лишь в том, что первое число будет меньше второго.

Продолжая приведенный выше пример, если счет домохозяйства $ 125 в октябре, но возвращается $ 100 в ноябре вы использовали бы формулу = СУММ (100-125) / 125,

Использование ссылок на ячейки, если сумма счета за октябрь $ 125 находится в камере B4 и сумма счета за ноябрь $ 100 находится в камере B5, ваша формула Excel для процентного уменьшения будет = СУММ (В4-В5) / В5.

Пример процентного снижения в Microsoft Excel

Разница между показателями за октябрь и ноябрь 20%, Excel отображает это как отрицательное десятичное число (-0,2) в клетках B7 и B8 над.

Установка типа номера ячейки в Процентное соотношение с использованием Кнопка «Стили в процентах» изменит десятичную цифру (-0,2) в процентах (-20%).

Процент уменьшается в Excel, отформатированный в числовом формате Процент

Расчет процента как пропорция

Excel также может помочь вам рассчитать процент как пропорцию. В этом разница между одним числом, как вашей полной цифрой, и меньшим числом. Это требует еще более простого математического расчета, чем процентное изменение.

Например, если у вас есть долг $ 100, и вы уже заплатили $ 50, то доля долга, который вы заплатили (и по совпадению все еще должны) 50%, Чтобы рассчитать это, вы просто разделить 50 на 100,

В Excel формула для расчета этого примера будет = 50/100, Используя ссылки на ячейки, где $ 100 находится в камере B3 и $ 50 находится в камере B4требуется формула = B4 / B3.

Расчет процентов как пропорций с использованием Microsoft Excel

При этом используется только базовый оператор деления, чтобы получить результат в виде десятичного числа (0,5).

Преобразование этого типа номера ячейки в Процентное соотношение кликнув Домой> Кнопка Процент Стиль покажет правильную процентную цифру 50%.

Процентные показатели в виде пропорций в Excel с примененным форматом ячеек в процентах

Как рассчитать проценты числа

Расчет процента числа — это то, с чем вы столкнетесь в повседневной жизни. Хорошим примером будет предмет для продажи, где скидка составляет 20% применяется к первоначальной цене $ 200. Сотрудник магазина должен знать, что такое 20% от 200 долларов. Затем они могли бы вычесть это число из первоначальной цены, чтобы предоставить цену со скидкой.

Это требует еще одного простого математического вычисления в Excel. Знак умножения (*) и знак процента (%) используются здесь. Вычислить 20% от суммы $ 200, вы можете использовать либо = 20% * 200 или = 0,2 * 200 сделать расчет в Excel.

Использовать ссылки на ячейки, где 20% находится в клавише B4 и первоначальная цена $ 200 находится в клавише B5, вы можете использовать формулу = B4 * B5.

Проценты числа, показанные в Microsoft Excel

Результат тот же, используете ли вы 20%, 0.2 или отдельные ссылки на ячейки в вашей формуле.

20% от 200 долларов равно $ 40, как показано в ячейках От B6 до B8 над.

Использование Excel для сложных расчетов

Как показывает это руководство, Excel отлично подходит для простых вычислений, но он также обрабатывает и более сложные.

Расчеты с использованием таких функций, как функция VLOOKUP, упрощаются благодаря встроенному инструменту поиска функций.

Если вы новичок в Excel, воспользуйтесь советами Excel, которые должен знать каждый пользователь, для дальнейшего повышения производительности.

Источник

Есть довольно распространённая потребность в функции, которая могла бы распределять заданную сумму согласно весовым коэффициентам. На первый взгляд, не очень понятно, о чём речь. Приведу примеры.

Распределение скидки на заказ

Допустим, интернет-магазин предоставляет клиенту скидку на заказ (по бонусной карте, купону или ещё как-то). Скидка даётся на весь заказ, но её действие нужно пропорционально распределить по товарам, чтобы, например, правильно сформировать кассовый чек (в нём каждую позицию чека нужно расписать: цена до применения скидки и сумма с учётом скидки).

Пример:
1) Товар №1 — цена 1500 руб.
2) Товар №2 — цена 1700 руб.
Итого сумма заказа получается 3200 руб. Допустим, клиенту предоставляется скидка 10%. В данном случае легко посчитать, что скидка в процентах будет одинаковой для каждого товара:
1) Товар №1 — цена со скидкой 1500 — 10% = 1350 руб.
2) Товар №2 — цена со скидкой 1700 — 10% = 1530 руб.
Это лёгкий пример, где никакого распределения не потребовалось. Теперь изменим условия примера. Допустим, скидка на заказ предоставляется не в процентах, а в рублях, — например, 500 руб. Как её учесть в стоимостях товаров? Вот тут уже требуется распределение. Да, можно было бы скидку целиком вписать в один какой-то товар — но это было бы некрасиво; да к тому же не универсально, ведь все товары в заказе могли бы стоить меньше, чем сумма скидки — что ж теперь отрицательную цену делать?! Нет конечно.
Итак распределяем. Очевидно, что первый товар стоит дешевле, значит, и скидку не него надо сделать меньше, чем на второй товар. Считаем сумму заказа, а потом долю стоимости каждого товара в заказе. Полученную долю умножаем на скидку на заказ.
1) Товар №1 1500 * 100 / 3200 = 46,875% — такова доля стоимости первого товар в общем заказе
2) Товар №2 1700 * 100 / 3200 = 53,125%. Проверим, что мы не ошиблись в округлении и не потеряли какой-нибудь доли заказа: 46,875 + 53,125 = 100% — всё верно.
Скидка распределяется согласно полученным долям:
1) 500 * 46,875 / 100 = 234,375. Получилось не очень-то красивое число. Во-первых, суммы допустимо указывать с копейками, а копейки — это только сотые доли. А тут получились тысячных. Во-вторых, в интернет магазине вообще могут не захотеть иметь дела с копейками. Требуется округление. Приводим к скидке 234 руб. Т.е. цена товара с учётом скидки равна 1500 — 234 = 1266 руб.
2) 500 * 53,125 / 100 = 265,625 — аналогично математическим округлением получаем 266 руб. Цена с учётом скидки 1200 — 266 = 934 руб.
Проверим, все ли 500 рублей мы вписали в виде отдельных скидок по товарам: 234 + 266 = 500 — всё верно.
Это простой пример, который довольно легко поддаётся алгоритмизации и составлению функции. Подобные функции для различных языков мне попадались в интернете. Но есть тут и подвохи, не будь которых — не было бы и статьи.

Подводные камни

Подвоха два:
1. Округление — не всегда округление скидок по товарам в сумме даёт скидку заказа. С этим авторы многих функций решают путём проверки и учёта разницы в последнем или самом дорогом товаре. Алгоритм моей функции навеян функцией отсюда Распределение суммы прапорционально
2. Не все скидки вообще возможно распределить. Это справедливо, когда требуется учитывать ещё и количество товара — т.е. цена товара никогда не должна быть с точностью больше двух десятичных знаков (т.е. копеек), а в большинстве случаев реальных магазинов — вообще без копеек. Т.е. нужна заданная точность. Невозможно ведь иметь три штуки товара в сумме 1000 руб. — тогда каждый из товаров стоил бы 333,(3) (три в периоде) руб. Вот этот момент вообще нигде не нашёл в сети. Автоматическое распределение алгоритмом, как показан выше вполне может выдать такой неделимый результат. Значит алгоритм требует доработки.

Функция распределения

Мой вариант функции (для языка PHP 7) учитывает количество по каждой позиции и заданную точность. Возвращаемый результат — всегда массив с таким же порядком и количеством элементов, что и входящий массив. А все неразрешимые ситуации генерируют исключение. Таким образом функцию не безопасно использовать обычным образом, — требуется организация перехвата исключения и какая-то реакция на исключительное поведение.
Какие могут быть варианты реакций на неразрешимые распределения? Если распределяется некая скидка по купону, то можно пойти на встречу клиенту и в неразрешимой ситуации накинуть рубль или два к скидке — этого вполне может хватить чтобы подыскать ближайший возможный вариант распределения. Потребуется перебор возможных вариантов.
Если это применение бонусов с личного счёта клиента, то неправильно было бы применить больше, чем есть на счёте — тут наоборот нужно подыскать первый доступный вариант с уменьшением скидки (и не забыть пояснить клиенту, что скидка именно такая по математическим и бухгалтерским причинам).
А если, например, первоначальный взнос клиента по кредиту невозможно равномерно распределить по товарам (для печати чека, например), то тут уже надо запрашивать алгоритм действия у бухгалтерии и руководства.
Варианты всегда есть — нужно просто помнить об исключительных ситуациях и адекватно на них реагировать.
Вот сама функция:

/**
 * Метод выполняет пропорциональное распределение суммы в соответствии с заданными коэффициентами распределения.
 * Также может выполняться проверка полного деления суммы коэффициента на его количество. Например,
 * при нулевой точности для чётного количества штук товара было неправильно получить нечётную сумму
 * после распределения, - правильно немного увеличить сумму распределения (в ущерб пропорциональности),
 * чтобы добиться ровного распределения по количеству.
 * Используется, например, при распределении скидки равномерно по позициям корзины.
 * @param float $sum Распределяемая сумма
 * @param array $arCoefficients Массив коэффициентов распределения, где ключи - определённые значения,
 *    которые также будут возвращены в виде ключей результирующего массива. Значения - массив с ключами:
 *    "sum"   - величина коэффициента (сумма, а не цена)
 *    "count" - количество для коэффициента
 * @param int $precision Точность округления при распределении. Если передать 0,
 *    то все суммы после распределения будут целыми числами
 * @throws Exception Выбрасывается исключение в случае,
 *    если невозможно ровно распределить по заданным параметрам
 * @return array Массив, где сохранены ключи исходного массива $arCoefficients, а значения - массив с ключами:
 *    "init"  - начальная сумма, равная соответствующему входному коэффициенту
 *    "final" - сумма после распределения
 */
public static function getProportionalSums(float $sum, array $arCoefficients, int $precision) : array
{
    $arResult = [];

    /**
     * @var float Сумма значений всех коэффициентов
     */
    $sumCoefficients = 0.0;

    /**
     * @var float Значение максимального коэффициента по модулю
     */
    $maxCoefficient = 0.0;

    /**
     * @var mixed Ключ массива для максимального коэффициента по модулю
     */
    $maxCoefficientKey = null;

    /**
     * @var float Распределённая сумма
     */
    $allocatedAmount = 0;

    foreach ($arCoefficients as $keyCoefficient => $coefficient) {
        if (is_null($maxCoefficientKey)) {
            $maxCoefficientKey = $keyCoefficient;
        }

        $absCoefficient = abs($coefficient['sum']);
        if ($maxCoefficient < $absCoefficient) {
            $maxCoefficient = $absCoefficient;
            $maxCoefficientKey = $keyCoefficient;
        }
        $sumCoefficients += $coefficient['sum'];
    }
    if (!empty($sumCoefficients)) {
        /**
         * @var float Шаг, который прибавляем в попытках распределить сумму с учётом количества
         */
        $addStep = (0 === $precision) ? 1 : (1 / pow(10, $precision));

        foreach ($arCoefficients as $keyCoefficient => $coefficient) {
            /**
             * @var boolean Флаг, удалось ли подобрать сумму распределения для текущего коэффициента
             */
            $isOk = false;

            /**
             * @var integer Количество попыток подобрать сумму распределения
             */
            $i = 0;

            // Далее вычисляем сумму распределения с учётом заданного количества
            do {
                $result = round(($sum * $coefficient['sum'] / $sumCoefficients), $precision) + $i * $addStep;

                // Проверим распределённую сумму коэффициента относительно его количества
                if (isset($coefficient['count']) && $coefficient['count'] > 0) {
                    if (round($result / $coefficient['count'], $precision) != ($result / $coefficient['count'])) {
                        // Не прошли проверку по количеству - ровно по заданному количеству не распределяется

                    } else {
                        $isOk = true;
                    }
                } else {
                    // Количество не задано, значит не проверяем распределение по количеству
                    $isOk = true;
                }

                $i++;
                if ($i > 100) {
                    // Мы старались долго. Пора признать, что ничего не выйдет
                    throw new Exception(
                        'Не удалось распределить сумму для коэффициента ' . $keyCoefficient
                    );
                }
            } while (!$isOk);

            // Если сюда дошли, значит удалось вычислить сумму распределения
            $arResult[$keyCoefficient] = [
                'init'  => $coefficient['sum'],
                'final' => (0 === $precision) ? intval($result) : $result,
                'count' => $coefficient['count']
            ];

            $allocatedAmount += $result;
        }

        if ($allocatedAmount != $sum) {
            // Есть погрешности округления, которые надо куда-то впихнуть
            $tmpRes = $arResult[$maxCoefficientKey]['final'] + $sum - $allocatedAmount;
            if (!isset($arResult[$maxCoefficientKey]['count'])
                || (isset($arResult[$maxCoefficientKey]['count']) && 1 === $arResult[$maxCoefficientKey]['count'])
                || (isset($arResult[$maxCoefficientKey]['count'])
                    && $arResult[$maxCoefficientKey]['count'] > 0
                    && (round($tmpRes / $arResult[$maxCoefficientKey]['count'], $precision) == ($tmpRes / $arResult[$maxCoefficientKey]['count']))
                )
            ) {
                // Погрешности округления отнесём на коэффициент с максимальным весом
                $arResult[$maxCoefficientKey]['final'] = (0 === $precision) ? intval($tmpRes) : $tmpRes;
            } else {
                // Погрешности округления нельзя отнести на коэффициент с максимальным весом
                // Надо подыскать другой коэффициент
                $isOk = false;
                foreach ($arCoefficients as $keyCoefficient => $coefficient) {
                    if ($keyCoefficient != $maxCoefficientKey) {
                        // Пробуем погрешность округления впихнуть в текущий коэффициент
                        $tmpRes = $arResult[$keyCoefficient]['final'] + $sum - $allocatedAmount;
                        if (!isset($arResult[$keyCoefficient]['count'])
                            || (isset($arResult[$keyCoefficient]['count']) && 1 === $arResult[$keyCoefficient]['count'])
                            || (isset($arResult[$keyCoefficient]['count'])
                                && $arResult[$keyCoefficient]['count'] > 0
                                && (round($tmpRes / $arResult[$keyCoefficient]['count'], $precision) == ($tmpRes / $arResult[$keyCoefficient]['count']))
                            )
                        ) {
                            // Погрешности округления отнесём на коэффициент с максимальным весом
                            $arResult[$keyCoefficient]['final'] = (0 === $precision) ? intval($tmpRes) : $tmpRes;
                            $isOk = true;
                            break;
                        }
                    }
                }
                if (!$isOk) {
                    throw new Exception('Не удалось распределить погрешность округления');
                }
            }
        }
    }

    return $arResult;
}

Проверим на тестовых значениях:

Пример, где всё распределяется без дробной части:


$arProduct = [
    [
        'sum'   => 1000,
        'count' => 1 
    ],
    [
        'sum'   => 2000,
        'count' => 2
    ]
];
$arResult = getProportionalSums(1000, $arProduct, 0);
echo '<pre>';
print_r($arResult);
echo '</pre>';

Результат:

Array
(
    [0] => Array
        (
            [init] => 1000
            [final] => 332
            [count] => 1
        )

    [1] => Array
        (
            [init] => 2000
            [final] => 668
            [count] => 2
        )

)

Пример, где невозможно распределить без дробной части:


$arProduct = [
    [
        'sum'   => 1000,
        'count' => 3 
    ],
    [
        'sum'   => 2000,
        'count' => 3
    ]
];
$arResult = getProportionalSums(1111, $arProduct, 0);
echo '<pre>';
print_r($arResult);
echo '</pre>';

Результат:

Источник