Изучим графические
возможности пакета Excel по построению
графиков функций в трехмерном пространстве.
Пример 1. Построить
верхнюю часть эллипсоида:
Для построения
поверхности необходимо разрешить
заданное уравнение относительно
переменной z.

Так как в условии речь
идет о верхней части эллипсоида, то
рассмотрим ОДЗ положительной части
уравнения:
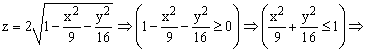
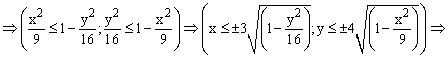
Приступим к построению
поверхности. В диапазон B1:J1 введем
последовательность значений переменной
y: -4, -3, …,4, а в диапазон ячеек А2:А14
последовательность значений переменой
x: -3, -2,5,…3.
В ячейку В2 введем
формулу = 2*(1-($A2^2)/9-(B$1^2)/16)^0,5.
Знак $, стоящий
перед буквой в имени ячейки, дает
абсолютную ссылку на столбец с данным
именем, а знак $, стоящий перед цифрой
— абсолютную ссылку на строку с этим
именем. Поэтому при копировании формулы
из ячейки В2 в ячейки диапазона
B2:J14 в них будет найдено значение z
при соответствующих значениях x, y.
Т.о. создается таблица значений z.
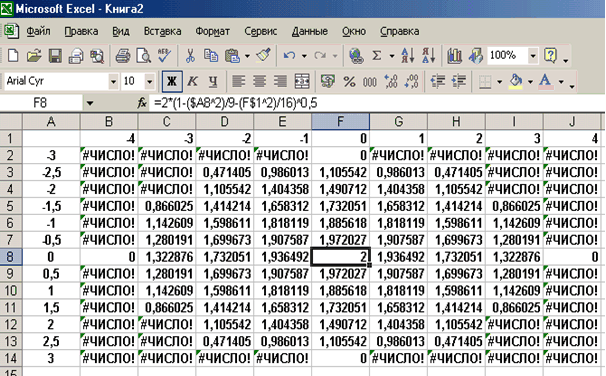
Рис. 2.19. Образцы
заполнения таблицы для построения
поверхности
Перейдем к построению
поверхности. Выделим диапазон ячеек
A1:J14, содержащий таблицу значений
функции и ее аргументов, вызовем Мастер
диаграмм и тип диаграммы Поверхность,
далее заполним диалоговые окна так как
было описано в лабораторной работе по
построению графиков функций. После
нажатия кнопки Готово получим
изображение заданной поверхности.
|
|
|
Рис. 2.20. Образцы
построения поверхностей
Пример
2. Построить поверхность z = x2-y2
при x, y [-1;1].
В диапазон B1:L1
введем последовательность значений
переменной x: -1, -0.8, …,1, а в диапазон
ячеек А2:А12 последовательность
значений переменой y. В ячейку В2
введем формулу = $A2^2-B$1^2 и скопируем
ее в ячейки диапазона B2:L12. На рисунке
2 изображена заданная поверхность.
Самостоятельная
работа
Задание 1. Построить
верхнюю (четные варианты) или нижнюю
(нечетные варианты) часть эллипсоида,
заданного уравнением:
Таблица 2.20
Варианты для самостоятельного выполнения
|
№ |
a |
b |
c |
№ |
a |
b |
c |
|
1 |
1 |
2 |
3 |
18 |
1.5 |
1.25 |
1.95 |
|
2 |
2 |
0.9 |
1.1 |
19 |
4 |
5 |
6 |
|
3 |
2 |
1 |
3 |
20 |
6 |
5 |
4 |
|
4 |
0.71 |
0.75 |
1.21 |
21 |
4 |
6 |
5 |
|
5 |
1.72 |
2.9 |
3.1 |
22 |
1 |
5 |
6 |
|
6 |
2 |
3 |
5 |
23 |
5 |
6 |
1 |
|
7 |
3 |
5 |
4 |
24 |
5 |
1 |
6 |
|
8 |
5 |
3 |
4 |
25 |
7.1 |
7.5 |
4.21 |
|
9 |
5 |
4 |
3 |
26 |
7.2 |
8.9 |
1 |
|
10 |
5.71 |
4.75 |
4.21 |
27 |
1 |
3 |
7 |
|
11 |
2.72 |
3.9 |
5.1 |
28 |
7 |
3 |
1 |
|
12 |
2 |
3 |
7 |
29 |
1 |
1 |
2 |
|
13 |
7 |
4 |
2 |
30 |
1.5 |
2.78 |
3.45 |
|
14 |
7 |
2 |
4 |
31 |
5.1 |
7.1 |
1.2 |
|
15 |
1.5 |
0.78 |
1.45 |
32 |
6.1 |
3.1 |
2.2 |
|
16 |
3.1 |
3.2 |
5.3 |
33 |
5 |
3 |
1.1 |
|
17 |
1.25 |
1.95 |
1.5 |
34 |
2.5 |
2.78 |
4.5 |
Задание
2. Построить однополостный (четные
варианты) или двуполостный (нечетные
варианты) гиперболоид, заданный
уравнением:
Таблица 2.21
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как построить эллипсоид по уравнению в excel
На этом шаге мы рассмотрим несколько примеров построения поверхностей в пространстве.
Задание 1. Построить часть плоскости, лежащей в I квадранте x [0;6] с шагом = 0,5; y [0;6] с шагом = 1. Плоскость задана уравнением 2x + 4y — 2z + 2 = 0.
Решение этого задания можно посмотреть здесь.
Задание 2. Построить эллипсоид, заданный уравнением
при x [-3;3], y [-2;2] с шагом = 0,5.
Решение этого задания можно увидеть здесь.
Задание 3. Построить эллипсоид, заданный уравнением
при x [-2;2] с шагом = 0,5, y [-3;3] с шагом = 1.
Решение этого задания можно посмотреть здесь.
Задание 4. Построить гиперболоид, заданный уравнением
при x [-3;3], y [-2;2] с шагом = 0,5.
Решение этого задания можно посмотреть здесь.
Задание 5. Построить гиперболоид, заданный уравнением
при x [-3;3] с шагом = 0,5, y [-4;4] с шагом = 1.
Решение этого задания можно посмотреть здесь.
Задание 6. Построить параболоид, заданный уравнением
при x [-2;2] с шагом = 0,5, y [-3;3] с шагом = 1.
Решение этого задания можно посмотреть здесь.
Задание 7. Построить параболоид, заданный уравнением
при x [-2;2] с шагом = 0,5, y [-3;3] с шагом = 1.
Решение этого задания можно посмотреть здесь.
Задание 8. Построить конус, заданный уравнением
при x [-2;2] с шагом = 0,5, y [-3;3] с шагом = 1.
Решение этого задания можно посмотреть здесь.
На следующем шаге мы познакомимся со списками.
Эллипс и окружность в EXCEL
history 29 марта 2015 г.
-
Группы статей
- Диаграммы и графики
Построим окружность и эллипс.
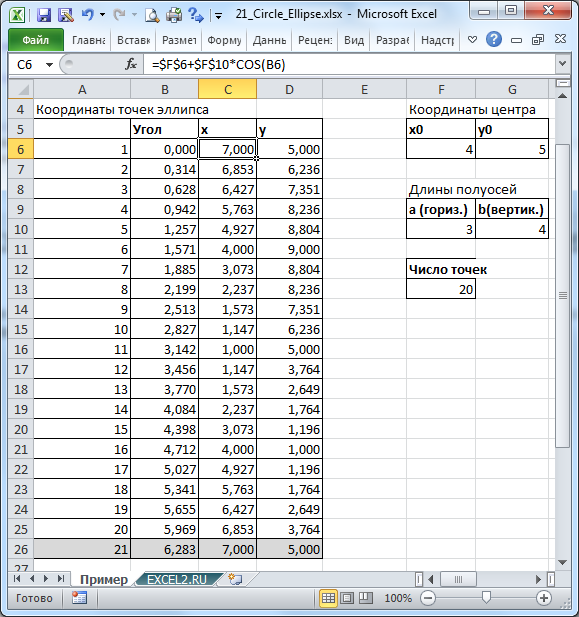
Вычислим х и y для эллипса из уравнения в параметрической форме: x=a*cos(t) и y=b*sin(t), где а и b — большая и малая полуось. При а=b получим окружность. Зададим угол от 0 до 2*ПИ() в 20 (21) точках.
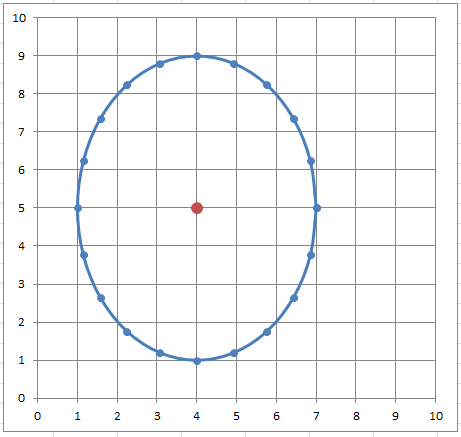
Выберем тип диаграммы Точечная с гладкими кривыми и маркерами.
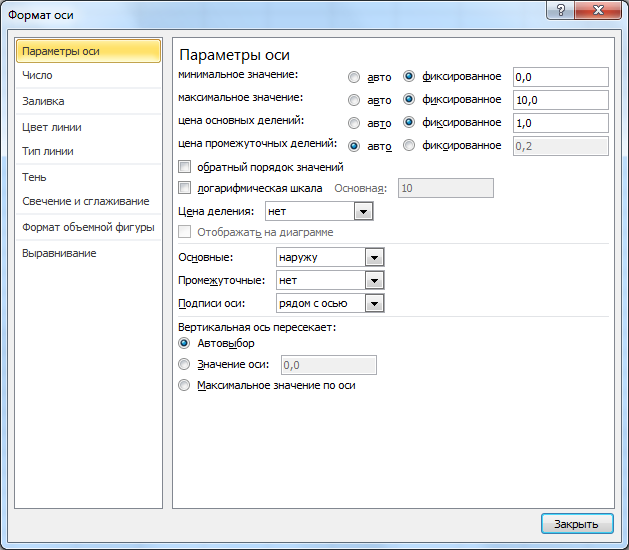
Т.к. MS EXCEL автоматически подбирает масштаб координатных осей, то для того чтобы форма эллипса и окружности соответствовала заданной, необходимо зафиксировать максимальное, минимальное значение и цену деления оси.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
ЛАБОРАТОРНАЯ РАБОТА №3
Дата добавления: 2014-11-28 ; просмотров: 4326 ; Нарушение авторских прав
Тема: Вычисление сложных функций в Excel
Цель занятия: получить практические навыки вычисления сложных функций от двух переменных z = f(x,у) и построения их графиков в Excel.
1.Создание формул для вычисления функций от двух переменных.
2.Построение графиков типа поверхностей в трехмерном пространстве.
Организационно – методические указания
В качестве примера рассмотрим построение поверхностей второго порядка таких как: эллипсоид, гиперболоид, параболоид и т.п.
1.Рассмотрим построение эллипсоида в Excel в соответствии с уравнением:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: хÎ[–3; 3], уÎ[–2; 2] с шагом D=0,5 для обеих переменных.
Решение данной задачи включает следующие этапы.
1.1.Вначале необходимо разрешить уравнение относительно переменной z:
1.2.Ввести значения переменных х(по вертикали), начиная с ячейки А2 иу(по горизонтали) , начиная с ячейки B1:
· в ячейку А2 вводится первое значение аргумента (х = –3), затем в ячейку A3 вводится второе значение аргумента (х= –2,5)и, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента х (за правый нижний угол блока протягиваем до ячейки А14).
· значения переменной увводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной (у = –2), в ячейку С1 вводится второе значение переменной ( у = –1,5) , а затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
1.3.Вычисление значений функции z. Для этого курсор необходимо поместить в ячейку В2 и вызвать Мастер функций. В появившемся диалоговом окне Мастер функций — шаг 1 из 2 слева в поле Категория выбираем Математические, в поле Функция выбираем функцию Корень инажимаем кнопку ОК. В диалоговом окне Кореньв рабочем поле вводим подкоренное выражение: 1 — $А2^2/9 — В$1^2/4. Обратите внимание, что символы $ предназначены для фиксации адреса столбца А — переменной хистроки 1 — переменной у. Нажимаем кнопку ОК и в ячейке В2 появляется « #ЧИСЛО!», так как при значениях х = –3 и у = –2 точек рассматриваемого эллипсоида не существует (рис 1.).
Рис.1. Построение эллипсоида
1.4.Копирование значений функции из ячейки В2, для чего автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, а затем протягиванием вниз копируем в диапазоне ВЗ:J14.
В результате должна быть получена таблица всех точек эллипсоида (рис.1).
1.5.Построение диаграммы. Выделяем полученную таблицу (A1: J14), вызываем вкладку Вставкаи в группе Диаграммывыбираем График®Все типы диаграмм®окноВставка диаграмм.В данном окне выбираем Поверхность®типПроволочная поверхностьи нажимаем ОК,в результате получаем поверхность эллипсоида (рис.2).Далее,используясредстваРабота с диаграммами ,оформляем полученную поверхность. Например, вкладки Стенка и Основание диаграммы позволяют определить их цвета. Для этого выберите опцию Дополнительные параметры стенок и вид заливки, название диаграммы и т.п. Выполните данные действия самостоятельно.
2.Рассмотрим построение гиперболоида следующего вида:
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[–3; 3], уÎ[–2; 2] с шагом D=0,5 для обеих переменных.
2.1.Вначале необходимо преобразовать уравнение относительно переменной Z:
Рис.2. Поверхность эллипсоида
2.2.Введем значения переменной хв столбец А. Для этого в ячейку А1 вводим символ x, в ячейку А2 вводится первое значение аргумента х = –3, а в ячейку A3 — второе значение аргумента х = –2,5. Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной увводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной у= –2, в ячейку С1 — второе значение переменной у = –1,5, а затем, выделив блок ячеек В1:С1,автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
2.3.Вычисление значения переменной Z. Для этого табличный курсор необходимо поместить в ячейку В2 , вызвать Мастер функций,в поле Категория выбрать Математические, в поле Функция выбираем функцию Кореньи нажимаем кнопку ОК. В рабочее поле вводим подкоренное выражение: 1 + $А2^2/9 + В$1^2/4инажимаем кнопку ОК. В ячейке В2появляется 1,732051. Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего протягиванием вниз — в диапазоне ВЗ:J14.
В результате должна быть получена таблица точек гиперболоида (рис.3.):
Рис.3. Построение гиперболоида
Построение диаграммы гиперболоида выполните самостоятельно по аналогии с эллипсоидом. Ниже на рис.4 приведен вариант диаграммы гиперболоида , построенного на основании данной таблицы.
источники:
http://excel2.ru/articles/ellips-i-okruzhnost-v-ms-excel
http://life-prog.ru/1_57303_laboratornaya-rabota-.html
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
3. .Уравнение плоскости, проходящей через три точки
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица (рис. 1).
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
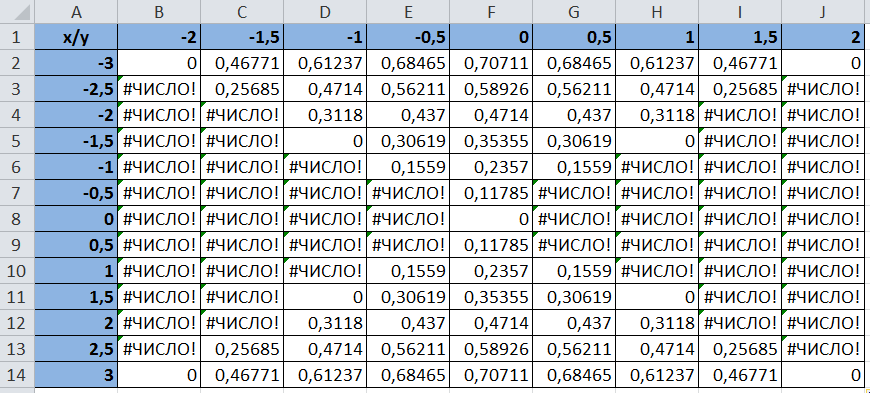
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
| | | следующая лекция ==> |
| | | Решите задачи с использованием диаграммы Эйлера-Венна. |
Дата добавления: 2017-02-25 ; просмотров: 2062 | Нарушение авторских прав
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
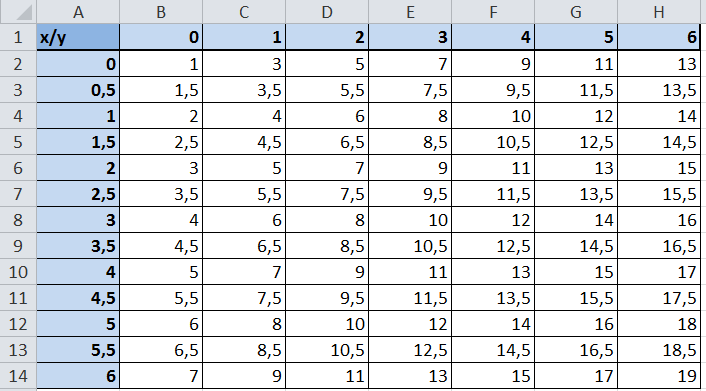
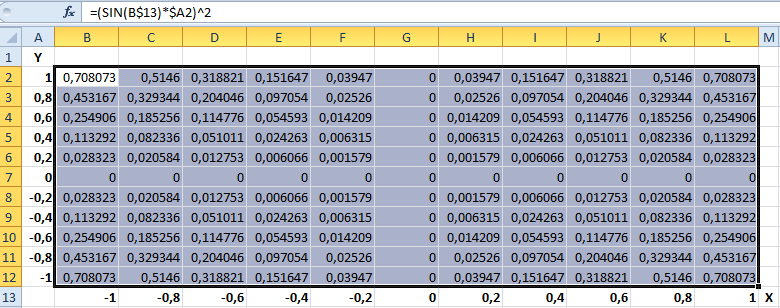
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
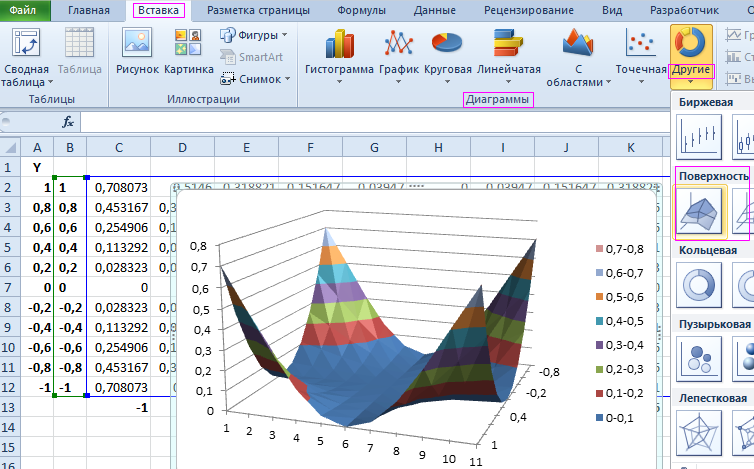
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
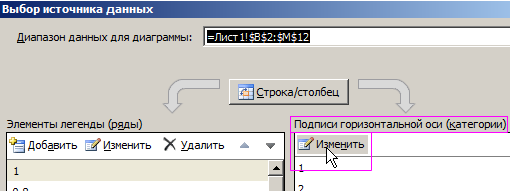
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
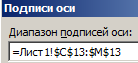
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
by Ирина Кяршис
ГЛАВА 1. Возможности табличного процессора Microsoft Excel
1.1.Ввод данных в Excel
Электронная таблица – это программа, позволяющая автоматизировать табличные расчеты. Документ Microsoft Ехсел является рабочей книгой, состоящей из листов. Таблица состоит из 65536 строк и 256 столбцов. Строки нумеруются числами, столбцы – буквами латинского алфавита (А, В …, Z, АА, АВ …). На пересечении строки и столбца расположена ячейка, которая имеет адрес, состоящий из имени столбца и номера строки (А4). Одна из ячеек всегда является активной.
Прямоугольная группа смежных ячеек называется диапазоном ячеек. Примеры диапазонов – А2: С4, В2: К40.
Ячейки могут содержать данные трех типов:
1) Текстовые данные – это строка текста произвольной длины.
2) Числовые данные – это отдельное число. Может быть целым, дробным (зап.). Если ширина ячейки мала, то число записывается в экспоненциальной форме, например 125 000 000 → 1,25Е + 8 или вместо числа ставятся символы ###. При этом число сохраняется.
3) Формула – это арифметическое выражение. Он представляет собой последовательность чисел, ссылок на ячейки и функций, объединенных знаками арифметических операций: +, -, /, *. Excel предлагает несколько сотен встроенных функций, которые разделены на категории.
Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.
Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.
Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).
1.2.Типы диаграмм
В зависимости от типа диаграммы данные отображаются на ней разным способом.
Можно отметить несколько стандартных типов:
1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.
2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.
3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.
4. С областями . Диаграмма с областями похожа на график.
5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.
Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.
6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)
7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.
8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.
Подробнее о типах диаграмм здесь
1.3 Основы построения диаграмм в Excel
Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.
Совокупность этих элементов определяет макет диаграммы.
Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).
Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.
Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.
6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.
Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).
Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.
ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2.1 Уравнения поверхностей второго порядка и их графики
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.
Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=1, где a и b – действительные полуоси, с – мнимая полуось.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=-1,где с – действительная полуось, a и b – мнимые полуоси.
x(в квадрате) /4 + y(в квадрате) /9+ z(в квадрате) /4=1
Диапазоны изменения переменных x и y: x [-2;2] с шагом 0,5 , y[-3;3] с шагом 1.
Вначале необходимо разрешить уравнение относительно переменной z!!!Правильно ли я ввёл выражение в рабочее поле?У меня везде вылазиет в полях ЧИСЛО!Где моя ошибка?Спасибо
http://s58.radikal.ru/i162/1001/79/0ce8a8d58946.jpg
Похоже подкоренное выражение <0.
samec, нарисовал верхнюю часть вашего… эллипсоида:
Эксель изощрён, но не злонамерен.
Цитата: samec от 09.01.2010, 15:41
объясните пожалуйста,куда девалась 4,когда вы перенесли все значения за знак равенства!!Я имею ввиду X^2/4+Y^2/9+Z^2/4=1, а после переноса получилось в ячейке B2 при решении =1-X^2/4-Y^2/9….а куда девалась 4?
Я
потом
извлёк из неё корень. Правда перепутал числитель с знаменателем 
Z = КОРНЕНЬ(1 — X^2/4 — Y^2/9)*2
Эксель изощрён, но не злонамерен.
|
1 / 1 / 1 Регистрация: 07.12.2014 Сообщений: 8 |
|
|
1 |
|
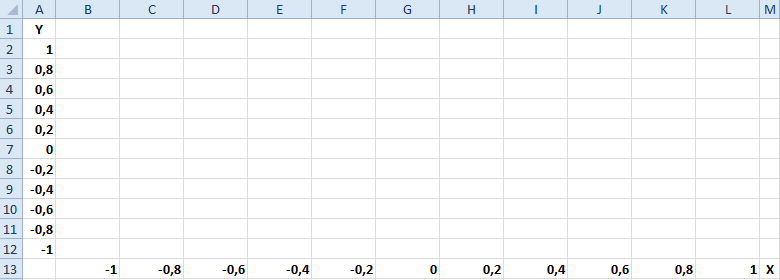
Построить верхнюю половину эллипса15.03.2015, 09:23. Показов 4305. Ответов 6
Помогите построить график. Что-то у меня все не получается: Постройте верхнюю половину эллипса x2/9 + y2/4 = 1 на интервале х– [-3.5;3.5] с шагом 0.25. Заранее благодарен господа!
0 |
|
6597 / 4708 / 1960 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
15.03.2015, 09:39 |
2 |
|
выразите у через х, далее стандартные 2 столбика: х — аргумент и у-функция…
0 |
|
1 / 1 / 1 Регистрация: 07.12.2014 Сообщений: 8 |
|
|
15.03.2015, 09:47 [ТС] |
3 |
|
я посчитал, построил, но эллипс не получается
0 |
|
6597 / 4708 / 1960 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
15.03.2015, 09:51 |
4 |
|
ваш excel-файл в студию!
0 |
|
1 / 1 / 1 Регистрация: 07.12.2014 Сообщений: 8 |
|
|
15.03.2015, 10:00 [ТС] |
5 |
|
0 |
|
6597 / 4708 / 1960 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
15.03.2015, 10:21 |
6 |
|
Решение формула неверна.. Кликните здесь для просмотра всего текста
2 |
|
1 / 1 / 1 Регистрация: 07.12.2014 Сообщений: 8 |
|
|
15.03.2015, 10:22 [ТС] |
7 |
|
аааа! спасибо вам огромное! +
0 |
Построим окружность и эллипс.
Вычислим х и y для эллипса из уравнения в параметрической форме: x=a*cos(t) и y=b*sin(t), где а и b — большая и малая полуось. При а=b получим окружность. Зададим угол от 0 до 2*ПИ() в 20 (21) точках.
Выберем тип диаграммы Точечная с гладкими кривыми и маркерами.
Т.к. MS EXCEL автоматически подбирает масштаб координатных осей, то для того чтобы форма эллипса и окружности соответствовала заданной, необходимо зафиксировать максимальное, минимальное значение и цену деления оси.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Поверхности второго порядка в пространстве
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
3. .Уравнение плоскости, проходящей через три точки
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица (рис. 1).
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
|
Поделиться с друзьями:
Лучшие изречения: Жизнь — это то, что с тобой происходит, пока ты строишь планы. © Джон Леннон Источник Adblock |
Обновлено: 15.04.2023
Цель работы. Изучение графических возможностей электронных таблиц MS Excel, приобретение навыков работы с Мастером диаграмм в электронных таблицах.
Задание.
1. Построить верхнюю (четные варианты) или нижнюю (нечетные варианты) часть эллипсоида, заданного уравнением . Варианты заданий представлены в табл. 9.
2. Построить однополостный (четные варианты) или двухполостный (нечетные варианты) гиперболоид, заданный уравнением . Знак плюс относится к уравнению однополостного гиперболоида, знак минус – к уравнению двухполостного гиперболоида. Варианты заданий представлены в табл. 10.
3. Построить эллиптический (четные варианты) или гиперболический (нечетные варианты) параболоид, заданного уравнением . Знак плюсотносится к уравнению эллиптического параболоида, знак минус – к уравнению гиперболического параболоида. Варианты заданий представлены в табл.11.
Таблица 9. Варианты заданий
| № | a | b | с | № | a | b | c |
| 3.1 | 3.2 | 5.3 | |||||
| 0.9 | 1.1 | 1.25 | 1.95 | 1.5 | |||
| 1.5 | 1.25 | 1.95 | |||||
| 0.71 | 0.75 | 1.21 | |||||
| 1.72 | 2.9 | 3.1 | |||||
| 5.71 | 4.75 | 4.21 | 7.1 | 7.5 | 4.21 | ||
| 2.72 | 3.9 | 5.1 | 7.2 | 8.9 | |||
| 1.5 | 0.78 | 1.45 | 1.5 | 2.78 | 3.45 |
Таблица 10. Варианты заданий
| № | a | b | с | № | a | b | c |
| 3.1 | 3.2 | 5.3 | |||||
| 0.9 | 1.1 | 1.25 | 1.95 | 1.5 | |||
| 1.5 | 1.25 | 1.95 | |||||
| 0.71 | 0.75 | 1.21 | |||||
| 1.72 | 2.9 | 3.1 | |||||
| 5.71 | 4.75 | 4.21 | 7.1 | 7.5 | 4.21 | ||
| 2.72 | 3.9 | 5.1 | 7.2 | 8.9 | |||
| 1.5 | 0.78 | 1.45 | 1.5 | 2.78 | 3.45 |
Таблица 11. Варианты заданий
| № | p | q | № | p | q |
| 1.5 | 2.5 | ||||
| 2.5 | 1/5 | ||||
| 1.4 | 3.4 | ||||
| 3.4 | 1.4 | ||||
| 2.5 | 5.6 | ||||
| 5.4 | 2/5 | ||||
| 1.1 | 4.1 | ||||
| 4.1 | 1.2 | ||||
| 1.5 | 5.1 | ||||
| 5.5 | 1.5 | ||||
| 3.3 | 5.3 | ||||
| 5.1 | 3.7 | ||||
| 4.1 | 5.1 | ||||
| 5.3 | 4.2 | ||||
| 6.05 | 1.9 |
Рекомендации к выполнению лабораторной работы. Рассмотрим пример построения поверхности z=x 2 -y 2 при x, y Î[-1;1]. В диапазон B1:L1 введем последовательность значений переменной x: -1, -0.8, …,1, а в диапазон ячеек А2:А12 последовательность значений переменой y. В ячейку В2 введем формулу =$A2^2-B$1^2. Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой – абсолютную ссылку на строку с этим именем. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:L12 в них будет найдено значение z для соответствующих значениях x, y. Таким образом, будет создана таблица значений z.
Для построения поверхности выделим диапазон ячеек A1:L12, содержащий таблицу значений функции. Далее обратимся к Мастеру диаграммивыберемтип диаграммы Поверхность. Затем заполним диалоговые окна в соответствии с вариантом задания и получим трехмерный график, показанный на рис 17.
Рис. 17. Поверхность вида z=x 2 -y 2
Лабораторная работа №6
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида.
Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии.
Для построения эллипсоида в Excel каноническое уравнение (7.7) необходимо разрешить относительно переменной z (представить в виде z=f(x, у)).
Упражнение 8.2.Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: хÎ[–3; 3], уÎ[–2; 2] с шагом D=0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (–3). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (–2,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (–2). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (–1,5). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
(при х=–3 и у=–2 точек рассматриваемого эллипсоида не существует).
Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего (протягиванием вниз) — в диапазон ВЗ:J14.
В результате должна быть получена следующая таблица точек эллипсоида.
Для построения диаграммы на панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы — Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне.
В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных B2:J14.
Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах.
Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей. Для этого щелкните в нем указателем мыши и введите диапазон подписей оси х — А2: A14.
Вводим значения подписей оси у. Для этого в рабочем поле Ряд указываем первую запись Ряд 1 иврабочее поле Имя, активизировав его указателем мыши, вводим первое значение переменной у: –2. Затем в поле Ряд указываем вторую запись Ряд 2 и в рабочее поле Имя вводим второе значение переменной у: –1,5. Повторяем таким образом до последней записи — Ряд 9.
После появления требуемых записей необходимо нажать кнопку Далее.
В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: Эллипсоид. Затем аналогичным образом ввести в рабочие поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: х, у и z.
Далее следует нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграммаэллипсоида.
Ячейки могут содержать данные трех типов:
Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.
Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.
Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).
1.2.Типы диаграмм
В зависимости от типа диаграммы данные отображаются на ней разным способом.
Можно отметить несколько стандартных типов:
1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.
2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.
3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.
4. С областями . Диаграмма с областями похожа на график.
5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.
Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.
6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)
7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.
8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.
Подробнее о типах диаграмм здесь
1.3 Основы построения диаграмм в Excel
Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.
Совокупность этих элементов определяет макет диаграммы.
Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).
Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.
Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.
6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.
Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).
Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.
ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2.1 Уравнения поверхностей второго порядка и их графики
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.
Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.
Эллиптическим параболоидом называется поверхность, которая в зависимости от типа канонического уравнения: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = z.
Гиперболическим параболоидом называется поверхность, которая определяется в каноническом соотношении: x ^ 2 / a ^ 2-y ^ 2 / b ^ 2 = z. Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».
2.2. Построение поверхностей второго порядка в Excel
Для построения шаблонов в Excel необходимо использовать диаграммы типа Поверхность и уметь работать с относительными и абсолютными адресами ячеек.
Для построения следующего порядка:
1. Из уравнения второй порядка выразить переменную z.
2. Подготовить изменения функций по двум координатам и другим направлениям, а также другим направлениям вдоль прилегающей строки вправо.
3. Ввести на пересечении геометрия для построения поверхности (и использовать марксист автозаполнения для ее копирования на всю область построения поверхности.
4. Выделить подготовленные данные и построить диаграмму типа Поверхность (вкладка Вставка, группа Диаграммы, Кнопка Другие).
4. Отформатировать полученную поверхность. Полученную фигуру можно вращать (кнопка Поворот объемной фигуры на вкладке Макет).
Для осуществления рассмотренного построения, заданной формулой:
x ^ 2 + y ^ 2 + z ^ 2 = 1
Для построения:
1. Выразим z: z = √ (x ^ 2 + y ^ 2-1)
2. Зададим диапазон С3: AR3 для x от -1 до 1 с шагом 0,1, причем каждое значение дублируется последовательно. Аналогично вводятся значения у для диапазона B4: B45.
3. Для расчёта z при изменяющихся x и y в ячейку С4 введем формулу:
= КОРЕНЬ (1-C $ 3 ^ 2- $ B4 ^ 2) * ЕСЛИ (ОСТАТ ($ A4; 2) = 0; 1; -1).
4. В диапазоне A4: A45 введем повторяющиеся числа 2 и 3 для определения знака в формуле.
5. Выделил подготовленные данные и построил диаграмму типа Поверхность.
6. Отформатируем полученную поверхность как показано на рисунке.
Для наиболее наглядного и полного отображения фигуры необходимо подбирать область и шаг изменения величины x и y.
Published: Oct 12, 2017
Latest Revision: Oct 12, 2017
Ourboox Unique Identifier: OB-373576
Copyright © 2017
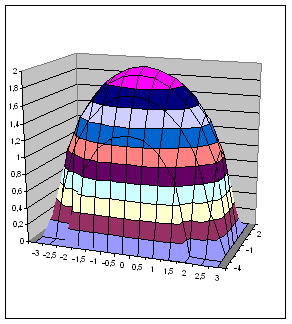
Изучим графические возможности пакета Excel по построению графиков функций в трехмерном пространстве.
Пример 1. Построить верхнюю часть эллипсоида:
Для построения поверхности необходимо разрешить заданное уравнение относительно переменной z.
Так как в условии речь идет о верхней части эллипсоида, то рассмотрим ОДЗ положительной части уравнения:
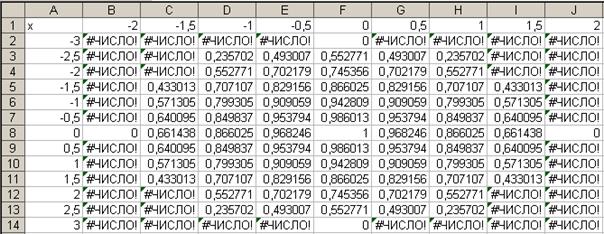
Приступим к построению поверхности. В диапазон B1:J1 введем последовательность значений переменной y: -4, -3, …,4, а в диапазон ячеек А2:А14 последовательность значений переменой x: -3, -2,5,…3.
В ячейку В2 введем формулу = 2*(1-($A2^2)/9-(B$1^2)/16)^0,5.
Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой — абсолютную ссылку на строку с этим именем. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:J14 в них будет найдено значение z при соответствующих значениях x, y. Т.о. создается таблица значений z.
Рис. 2.19. Образцы заполнения таблицы для построения поверхности
Перейдем к построению поверхности. Выделим диапазон ячеек A1:J14, содержащий таблицу значений функции и ее аргументов, вызовем Мастер диаграмм и тип диаграммы Поверхность, далее заполним диалоговые окна так как было описано в лабораторной работе по построению графиков функций. После нажатия кнопки Готово получим изображение заданной поверхности.
Рис. 2.20. Образцы построения поверхностей
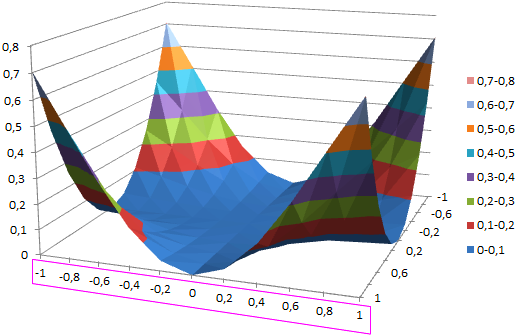
Пример 2. Построить поверхность z = x 2 -y 2 при x, y [-1;1].
В диапазон B1:L1 введем последовательность значений переменной x: -1, -0.8, …,1, а в диапазон ячеек А2:А12 последовательность значений переменой y. В ячейку В2 введем формулу = $A2^2-B$1^2 и скопируем ее в ячейки диапазона B2:L12. На рисунке 2 изображена заданная поверхность.
Самостоятельная работа
Задание 1. Построить верхнюю (четные варианты) или нижнюю (нечетные варианты) часть эллипсоида, заданного уравнением:
ПОСТРОЕНИЕ ПОВЕРХНОСТЕЙ В MS EXCEL Муниципальное автономное общеобразовательное учреждение «Начальная общеобразовательная школа № 1» Автор: Заслуженный учитель школы Российской Федерации Никифоров Юрий Васильевич Пермский край, г. Губаха, 2013 год
Данная разработка урока является исследованием таких возможностей MS Excel, которые нигде не рассматриваются, но которые позволяют взглянуть на MS Excel с непривычной для многих стороны. Этот слайд можно скрыть.
Ключом для создания поверхностей является прямоугольная таблица, состоящая из ячеек со смешанной адресацией. =$F$1*SIN(D$3/$I$1)*COS($A11/$L$1)
ПРИМЕРЫ Качество прорисовки Эффект «лесенки» Более 5 млн. Блики, тень Интерференция Логические функции ЕСЛИ/И
ФОРМУЛЫ В файле «Формулы.xlsx» представлена таблица с формулами и условными названиями поверхностей. Имеются графические примечания.
АССОЦИАЦИИ В презентации «Ассоциации.pptx» представлены поверхности, которые ассоциируются с конкретными объектами окружающего мира.
Выбранный для просмотра документ Ассоциации.pptx
Ищем студентов
для работы онлайн
в проекте «Инфоурок»
Описание презентации по отдельным слайдам:
Муниципальное автономное общеобразовательное учреждение «Начальная общеобразовательная школа № 1» Автор: Заслуженный учитель школы РФ Никифоров Юрий Васильевич Пермский край, г. Губаха, 2013 год «АССОЦИАЦИИ»
ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД ( С Е Д Л О )
МИТОХОНДРИЯ (Энергетический центр живой клетки организма)
ПИРАМИДЫ НАРОДНОСТИ МАЙЯ (Центральная Америка)
ЭПИТЕЛИЙ (внутренние стенки сосудов)
КУНГУРСКАЯ ЛЕДЯНАЯ ПЕЩЕРА СТАЛАКТИТЫ СТАЛАГМИТЫ
ЦВЕТЫ ТЮЛЬПАНЫ РОЗЫ
Выбранный для просмотра документ Библиотека поверхностей.docx
Выбранный для просмотра документ НикифоровЮВ_разработка_урока.docx
Название работы: построение поверхностей в MS Excel .
Номинация: сценарий медиаурока с компьютером.
Предмет: информатика + математика + воображение.
Участники: ученики 9-11 классов.
Цели и задачи: раскрыть графические возможности MS Excel при построении поверхностей, удивить их многообразием этих возможностей и научить строить их, обратить внимание учеников на красоту этих поверхностей.
Задачи:
— обучающие: повторение синтаксиса формулы логического условия, повторить понятие смешанной адресации, тюнинг поверхностей;
— развивающие: сформировать у учащихся ассоциации между графическими объектами и объектами окружающего мира;
— воспитательные: научить учащихся удивляться красоте поверхностей, находить «схожесть» с реальными объектами, развивать фантазию и воображение.
Данная разработка урока имеет своей целью раскрыть графические возможности табличного процессора MS Excel , которые в большинстве справочной и учебной литературы игнорируются или освещаются очень бедно.
Все эти возможности очень ярко проявляются при построении поверхностей.
Сформулируем предположение (гипотезу, догадку): используя богатый арсенал математических и логических функций, имеющихся в MS Excel , можно построить огромное количество поверхностей, которые являются моделями реальных объектов (явлений) окружающего мира. Этот урок является попыткой совместить несовместимое. С одной стороны, мы имеем строгие математические формулы, а с другой — изящные поверхности, которые и являются графическими интерпретациями этих формул.
При построении этих поверхностей не покидает чувство: неужели всё это возможно сделать в обычном и привычном табличном процессоре? Ничего подобного нигде не встречается. Самое первое чувство, которое испытываешь при работе над этой темой, это удивление. Учеников надо удивить многообразием самых фантастических форм. Вы словно открываете ящик Пандоры. Конечно, это эмоции. Но, зная, что за этой красотой и изяществом форм скрываются обычные математические формулы, ученики должны понять, что окружающий нас мир можно описать не только поэтическим языком, но и сухим языком формул.
Кому может пригодиться данная разработка? Наверное, творческим учителям, будущим художникам и дизайнерам, программистам. Всем тем, у
кого богатое воображение и абстрактное мышление тесно переплетены. Данная тема может стать основой для научно-исследовательской работы.
Автор: Никифоров Юрий Васильевич, педагог дополн. образования
Место работы: Пермский край, г. Губаха, Муниципальное автономное общеобразовательное учреждение «Начальная общеобразовательная школа № 1» (МАОУ «НОШ № 1»).
Читайте также:
- Современные компьютерные программы для исследования фонетики
- Как удалить теги в word
- Как сохранить из 1с прикрепленные файлы
- Фотошоп на паспорт можно ли
- Не удалось открыть excel файл wildberries




































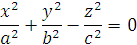






 Сообщение было отмечено Eraz как решение
Сообщение было отмечено Eraz как решение
 | 212 —
| 212 —