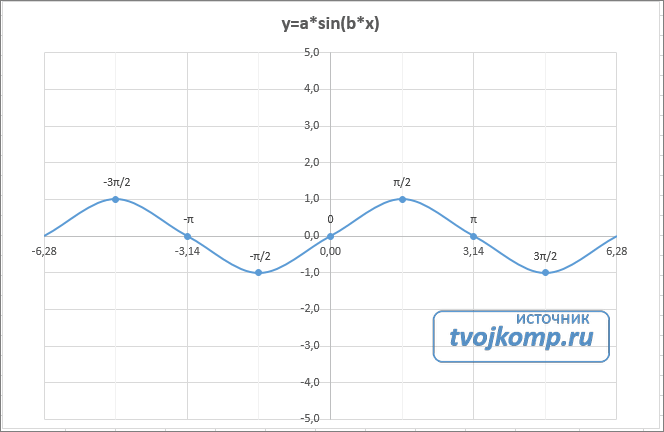
Построение графиков функций
1. Построить в разных системах координат при x [− 2, 2] графики функций
|
1 + x2 |
3 |
|||||||||||||||||
|
1 + x |
2 |
, x < 0 |
||||||||||||||||
|
, x ≤ 0 |
||||||||||||||||||
|
1 + x |
1 + x |
4 |
||||||||||||||||
|
2 |
−2x |
|||||||||||||||||
|
y = sin |
(x) + |
, |
g = |
, z |
= 2e |
, |
x [0;1] |
|||||||||||
|
1 + cos2 (x) |
||||||||||||||||||
|
2x |
x >1 |
|||||||||||||||||
|
1 + |
, x > 0 |
2sin(3x), |
||||||||||||||||
|
2 |
||||||||||||||||||
|
1 |
+ x |
|||||||||||||||||
|
В ячейки A1:D1 записываем заголовки |
||||||||||||||||||
|
таблицы x, y, g ,z. |
||||||||||||||||||
|
Графики нужно |
построить |
в пределах |
||||||||||||||||
|
x [− 2, 2], возьмём шаг 0,2. |
Тогда x будет принимать значения -2, -1,8, -1,6, -1,4 и так далее до 2
В ячейку A2 введем первое значение -2, в ячейку A3 введем следующее значение — 1,8. Выделим эти две ячейки и протянем их до значения 2.
Вячейку B2 введем формулу для вычисления y(x) =SIN(A2)^2+(1+A2)/(1+COS(A2)^2)
Вячейку C2 введем формулу для вычисления g(x) =ЕСЛИ(A2<=0;(1+A2^2)/(1+A2^4)^(1/2);(1+2*A2/(1+A2^2))^(1/2))
Вячейку D2 введем формулу для вычисления z(x) =ЕСЛИ(A2<0;(1+A2^2)^(1/3);ЕСЛИ(A2<=1;2*EXP(-2*A2);2*SIN(3*A2)))
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
1 |
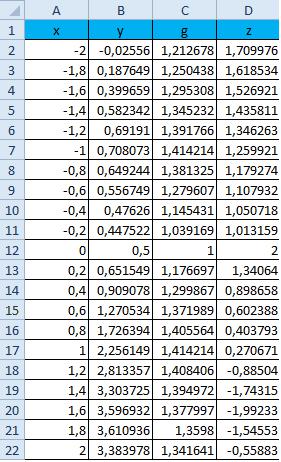
Ячейки B2, C2, D2 протянем вниз до значения x равного 2, в данном случае до 22 строчки. В результате, получим
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
2 |
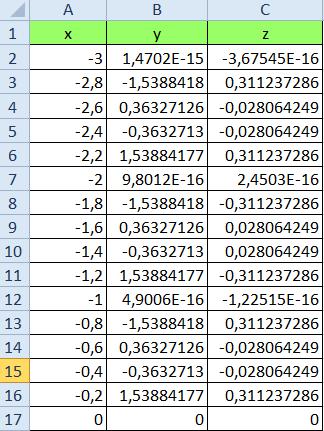
2. Построить в одной системе координат при x [− 3;0] графики функции
Y =2sin(2πx)cos(4πx) Z =cos3 (4πx)sin(πx)
На новом листе Excel в столбце A, протабулируем значения x в пределах от -3 до 0 с шагом 0,2.
В ячейку B2 введем формулу =2*SIN(2*ПИ()*A2)*COS(4*ПИ()*A2)
В ячейку C2 введем формулу =COS(4*ПИ()*A2)^3*SIN(ПИ()*A2)
Ячейки B2, C2 протянем вниз до значения x равного 0, в данном случае до 17 строчки.
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
3 |
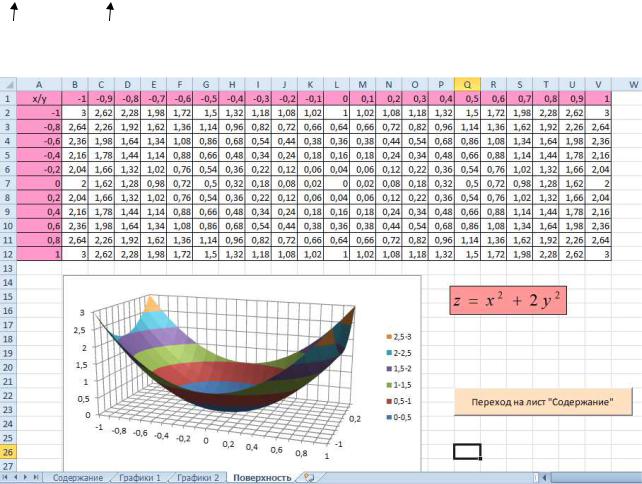
3. Построить поверхность z = x2 + 2y 2 при x [−1;1] В ячейку B2 введем формулу
=$A2^2+2*B$1^2
|
фиксируем |
фиксируем |
|
номер столбца |
номер строки |
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
4 |

Пользовательские функции.
Сохранить файл в формате *.xlsm (тип файла Книга Excel с поддержкой макросов)
Открыть редактор Visual Basic (Alt+F11) Добавить модуль Insert → Module
|
sin 2 (x) + |
1 + x |
||||||||||
|
1 + cos2 (x) |
|||||||||||
|
1 + x |
2 |
x ≤ 0 |
|||||||||
|
, |
|||||||||||
|
1 + x4 |
|||||||||||
|
1 + |
2x |
, x > 0 |
|||||||||
|
2 |
|||||||||||
|
1 + x |
|||||||||||
|
3 |
|||||||||||
|
1 + x |
2 , |
x < 0 |
|||||||||
|
2e−2x, |
x [0;1] |
||||||||||
|
x >1 |
|||||||||||
|
2sin(3x), |
|||||||||||
Y =2sin(2πx)cos(4πx)
Z =cos3 (4πx)sin(πx)
z = x2 + 2y 2
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
5 |
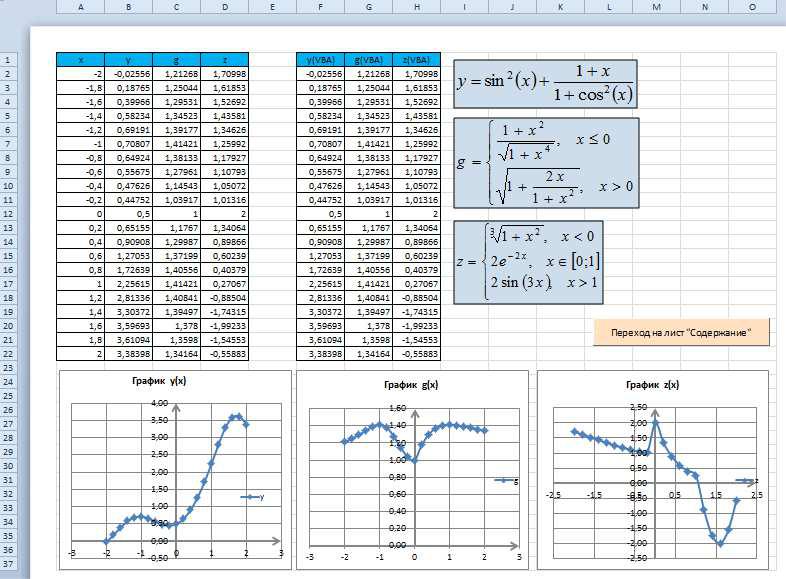
Построение графиков функций y(x), g(x), z(x) в разных системах координат
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
6 |
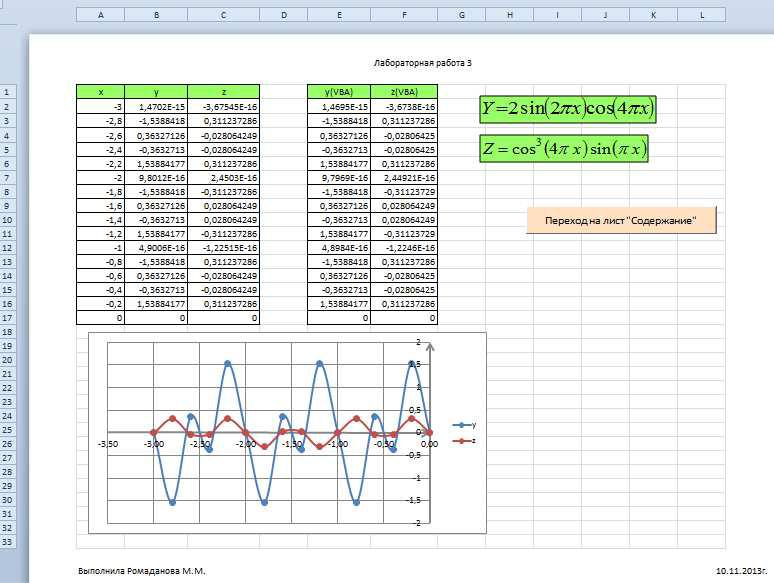
Построение графиков функций y(x), z(x) в одной системе координат
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
7 |
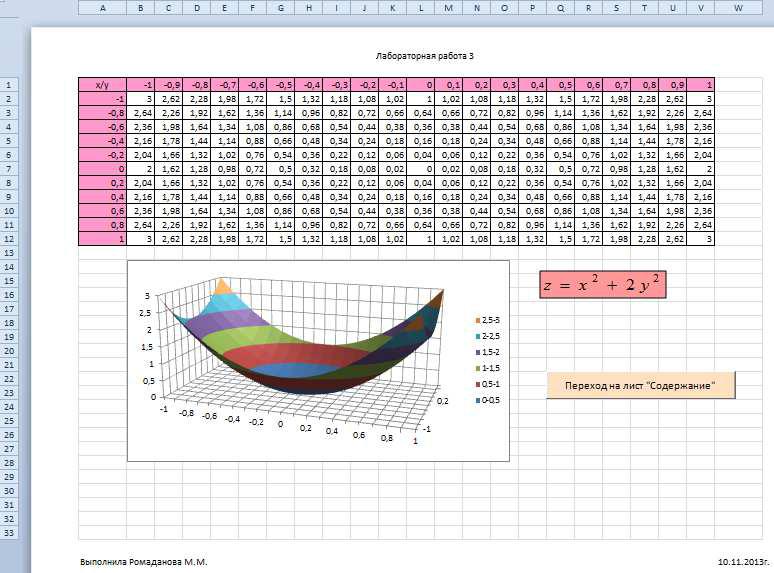
Построение поверхности z(x,y)
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
8 |
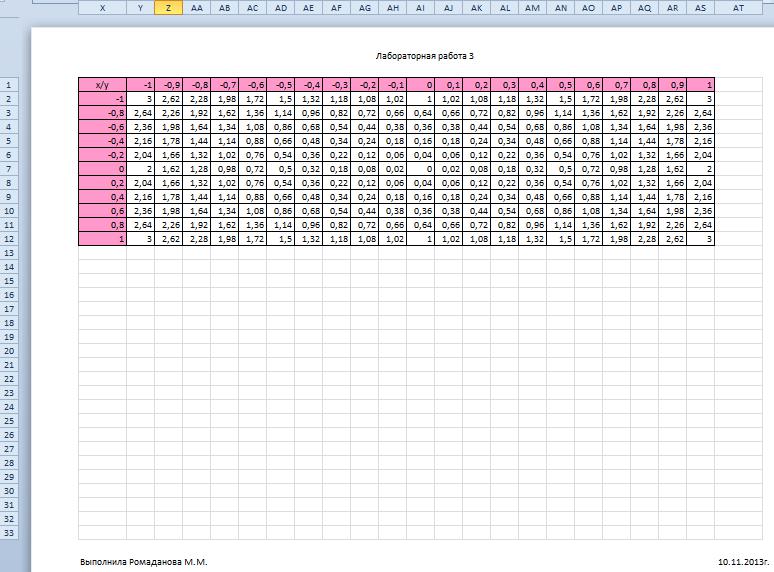
Поверхность z(x,y), построенная с помощью пользовательских функций. Должны получиться такие же значения, как и в предыдущей таблице.
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
9 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
29.03.2015511.29 Кб43.pdf
- #
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
|
1 / 1 / 1 Регистрация: 27.09.2016 Сообщений: 48 |
|
|
1 |
|
Построить в разных системах координат графики функций23.10.2016, 19:58. Показов 15013. Ответов 20
Построить в разных системах координат при х ϵ [-2; 2] графики функций. Помогите, заранее спасибо! Миниатюры
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
24.10.2016, 09:02 |
2 |
|
1. =(1+A2^2)/(1+2*A2^2)
2 |
|
2 / 2 / 0 Регистрация: 09.11.2015 Сообщений: 16 |
|
|
24.10.2016, 17:14 |
3 |
|
Почему бы не использовать маткад к примеру для построения графиков?) мне кажется что атм попроще это сделать. Хотя, кто как привык.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 10:49 |
4 |
|
Всем добрый день, уважаемые форумчане, со всеми новогодними праздниками! , может кто сталкивался, направьте на верный ход мыслей, пожалуйста.
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
08.01.2017, 11:34 |
5 |
|
Код y=(1+EXP(3*A2))^(1/4) g=ЕСЛИ(A2>0;2*A2^2*COS(A2)^2;(3+SIN(A2))/(1+A2^2)) с третим пробуем сами разобраться по аналогии второго. про построение смотрит похожие темы в форуме не раз обсуждалось. как вариант построение смотрим видео в теме в шапке (не полное совпадение).
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 13:05 |
6 |
|
нет, подобное не воспроизведу. .
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 13:43 |
7 |
|
графики построю сама, помощь нужна со значениями.
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
08.01.2017, 15:14 |
8 |
|
помощь нужна со значениями. для первых (задание «а») не дано значит берете произвольно. Добавлено через 5 минут Код 1,3 =ЕСЛИ(A2<0;ABS(A2)^(1/3);ЕСЛИ(A2<1;-2*A2+A2/(1+A2);ABS(3-A2)/(1+A2))) п.с. в 1,3 ошибка т.к. по условию получается 1 принадлежит двум условиям (второму и третьему). Добавлено через 3 минуты Код =2*SIN(ПИ()*A2)*COS(ПИ()*A2) =COS(ПИ()*A2)^2*SIN(3*ПИ()*A2) Добавлено через 3 минуты Код =2*$A6^2*COS($A6)^2-2*B$5^2
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 16:19 |
9 |
|
Огромное Вам спасибо.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
11.01.2017, 20:24 |
10 |
|
Vlad999, Вот что получилось, есть сомнения. Если не затруднит, посмотрите, пожалуйста.1.xls 2.xls 3
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
12.01.2017, 09:39 |
11 |
|
как то так. поверхность не настраивал.
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
12.01.2017, 19:08 |
12 |
|
Vlad999, спасибо Вам большое, очень помогли.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 22:43 |
13 |
|
Всем доброй ночи, уважаемые форумчане, как добавить вспомогательную ось в гистограмму в ексель 2003, смотрю, читаю примеры приведены в поисковике на более поздних версиях, у меня такого функционала нет.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 22:50 |
14 |
|
Вот как здесь, справа.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 22:52 |
15 |
|
И еще график, как добавит с данными, как на диаграмме.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 23:05 |
16 |
|
Вот что получилось у меня, нужно добавить график с данными и вспомогательную ось, затрудняюсь.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 23:07 |
17 |
|
Извините закачемтво фото.
0 |
|
0 / 0 / 0 Регистрация: 10.10.2019 Сообщений: 1 |
|
|
10.10.2019, 15:48 |
18 |
|
Буду благодарен, если решите) Миниатюры
0 |
|
2630 / 1636 / 744 Регистрация: 23.03.2015 Сообщений: 5,143 |
|
|
10.10.2019, 16:04 |
19 |
|
волололо, Вы хоть на верх этой темы заглядывали?
0 |
|
0 / 0 / 0 Регистрация: 28.01.2020 Сообщений: 4 |
|
|
30.11.2020, 12:47 |
20 |
|
Vlad999, Вы мне можете помочь с одним заданием?
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
30.11.2020, 12:47 |
|
Помогаю со студенческими работами здесь Построить в разных системах координат графики следующих функций Построить в разных системах координат при х ϵ [-1.8; 1.8] графики функций Построить в разных системах координат при x принадлежит [-1,7. 1,5] графики функций: построить в разных системах координат при x[-1,5;1,5] графики следующих функций с использо-ванием пользовательских функций
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 20 |
Содержание
- Задание 3.2
- Решение задач линейного программирования
- Задание 4.1
- Главная > Документ
Построить в разных системах счисления координат при х[-2; 2] графики следующих функций:
Данное задание выполняется в программе MC Excel. Для построения графика функции необходимо изначально задать значение аргумента х в заданном интервале с любым шагом. Для построения графиков функций y мы сначала вводим значения x-2; 2 в электронную таблицу. Затем в колонку со значением y пишем формулу y =(1+A2^2)/(1+2*A2^2). В результате получаем значение y (см. рисунок 3.1)
Рисунок 3.1 — Изображение значений x и y
Выделяем диапазон значения y, заходим в меню Вставка>график функции>вид графика. Строим график функции y. Жмём правой кнопкой на график, изменяем данные по вертикали, для этого выделяем диапазон x (см. рисунок 3.2).
Рисунок 3.2 — График функции y
Графики функций g, z строятся аналогично (см. рисунок 3.3 и рисунок 3.4), но в колонку со значением пишем формулы:
g =ЕСЛИ (A2 =1; (ABS (2-A2))^(1/3)))
Рисунок 3.3 — График функции g
Рисунок 3.4 — График функции z
Задание 3.2
Построить в одной системе координат при x [-2; 2] графики следующих функций:
y=2sin(x)-3cos(x), z=cos 2 (2x)-2sin(x).
Для построения в одной системе координат нескольких графиков функций (в нашем случае двух) нужно ввести значения x-2; 2 в электронную таблицу, (см. рисунок 3.5).Затем в колонку со значением y и z пишем формулы:
y = (2*SIN (ПИ()*A2) — 3*COS (ПИ()*A2))
z = (COS (2*ПИ()*A2)^2-2*SIN (ПИ()*A2)).
Затем выбираем столбцы y и z заходим в меню Вставка>графики> выбираем вид графика. Столбец x определяем по оси. Получаем график функций y и z (см. рисунок 3.5).
Рисунок 3.5 — График функций y и z
Решение задач линейного программирования
Задание 4.1
Графически и аналитически решить задачу максимизации целевой функции. Выполнить это задание, используя приложение MS EXCEL. Сравнить полученные результаты. Сделать выводы.
1 способ: Графически построить полигон допустимых значений
Для того чтобы решить графически данную систему, приравняем левую и правую части. Из последних двух условий выразим x2, это даст уравнения прямых, с помощью которых мы получим область определения. Из условия максимизации выразим x2:
В Excel построим в одной системе координат 3 графика функций, а именно , , . Для этого в первую колонку впишем координаты точек , а в три остальные формулы функций. После этого выделяем 3 столбца и вставляем график.
z=0, z — целевая функция, отсюда получаем
Полученные результаты представлены на рисунке 4.1
Рисунок 4.1 — Графики функций x2
На пересечении прямых и получаем точку максимума (1,5; 1) (см. рисунок 4.2)
Рисунок 4.2 — Графический способ
Аналитически решить задачу максимизации целевой функции
Для того чтобы решить задачу аналитически, нужно приравнять правую часть уравнений и
Теперь подставляем =1,5 в любое уравнение, например
>, отсюда получаем точку максимума (1,5; 1).
Решить задачу максимизации целевой функции, используя приложение MS EXCEL.
Необходимо создать таблицу в MS Excel. В ячейках В1 и В2 находятся исходные значения, эти числа могут быть любыми. В ячейку D1, D2, D3 записываем формулы данных функций. В ячейки С1 записываем ограничение. (см. рисунок 4.3)
Рисунок 4.3 — Данные, ограничение, целевая функция
Затем нажимаем Данные>Анализ>Поиск решения (см. рисунок 4.4)
В поле «Установить целевую ячейку» указываем целевую ячейку D3, содержащую функцию. Так как необходимо максимизировать ЦФ, то переключатель «Равной» следует установить в положение «Максимальное значение». В поле «Изменяя ячейки» указываем ячейки с начальными значениями х1 и х2. В поле ограничения заносим условия неотрицательности, также ячейки с ограничениями, нажимаем «Выполнить» и в появившемся окне затем «Сохранить найденное решение»
Рисунок 4.4 — Ограничение в поиске решения
И получаем результат (см. рисунок 4.5)
Рисунок 4.5 — Решение целевой функции
Проанализировав решение тремя способами, можно сделать вывод о том, что получается один и тот же результат, а именно =1,5 и
1. На листе Графики построить графики функций, приведенных ниже, используя диаграмму типа График и Точечную диаграмму. Результаты сравнить.
Результат сохранить в файле с именем Лабораторная работа №5.
2. Для таблицы, сформированной на листе «Преступность и судимость»в файле Лабораторная работа №2, по данным ее первого, второго, третьего и пятого столбцов построить графики, отражающие динамику основных криминологических показателей в России за 1985 – 1997 годы. Изменить на каждом графике маркеры значений данных и установить для каждого графика свою толщину линии.
3. Для таблицы, сформированной на листе «Торговля_и_Производство»в файле Лабораторная работа №2, выполнить следующие задания:
a) используя данные Год, Торговля, Производство за последние 10 лет, построить объемную гистограмму на отдельном листе с именем Развитие торговли;
b) отредактировать диаграмму:
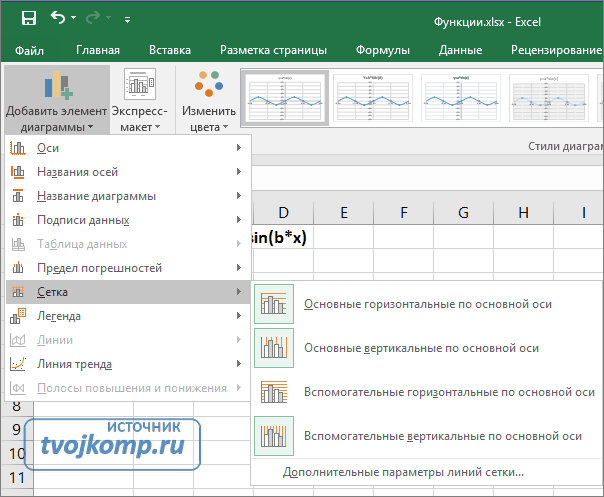
— изменить подтип гистограммы, чтобы ряды данных размещались один перед другим;
— вставить основную сетку по всем трем осям диаграммы;
— сместить легенду под область построения диаграммы;
— ввести заголовок «Развитие торговли по отношению к производству за последние 10 лет»;
— изменить данные в некоторой строке и посмотреть, что произойдет с диаграммой;
— вставить в таблицу новую строку и посмотреть, что произойдет с диаграммой;
c) по данным «Год» и «Доля» торговли построить круговую диаграмму на отдельном листе с именем «Доля_Торговли»;
d) отредактировать диаграмму:
— нанести на диаграмму показатели значений к каждому участку диаграммы;
— выдвинуть участок круговой диаграммы, соответствующий самому большому значению Доли торговли.
4. Для таблицы «Продажа видеофильмов», сохраненной в файле Лабораторная работа №2, выполнить следующие задания:
— построить объемную гистограмму с накоплением «Продажа видеофильмов за первые 3 дня по категориям» (по оси категорий – категории фильмов, по оси значений – число продаж по дням);
— построить круговую диаграмму «Продажи за 6 января 1998 года», отображающую итоги продажи видеофильмов за 6 января 1998 года;
Результат сохранить в файле с именем Лабораторная работа №5.
Следующие задания выполняются по вариантам.
Номер варианта выполняемого задания совпадает с номером по списку группы (если номер по списку >10, то отнять от номера число 10, если номер по списку >20, то отнять от номера число 20).
Вариант 1
1. Построить в разных системах координат при 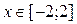

2. Построить в одной системе координат при 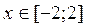
· 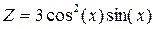
3. Построить поверхность 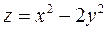

Вариант 2
1.Построить в разных системах координат при 
2.Построить в одной системе координат при 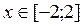
4.
5. 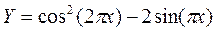
3.Построить поверхность 

Вариант 3
1. Простроить в разных системах координат при 

2. Построить в одной системе координат при 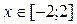
·
· 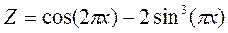
3. Построить поверхность 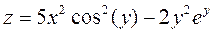
Вариант 4
1. Построить в разных системах координат при x 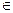


2. Построить в одной системе координат при x 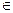
· Y = 3sin(2 πx) cos(πx) – cos 2 (3πx);
· Z = 2cos 2 (2πx) – 3sin(3πx).
3. Построить поверхность при x, y 
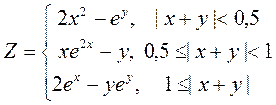
Вариант 5
1. Построить в разных системах координат при x 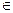
2. Построить в одной системе координат при x 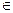
· Z = cos 
3. Построить поверхность 

Вариант 6
1. Построить в разных системах координат при x 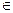

2. Построить в одной системе координат при x 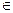
· Z = cos 3 (4πx)sin(πx).
3. Построить поверхность 

Вариант 7
1. Построить в разных системах координат при x 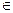
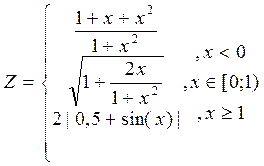

2. Построить в одной системе координат при x 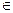
· Z = cos 2 (3πx) – cos(πx)sin(πx).
3. Построить поверхность 

Вариант 8
1. Построить в разных системах координат при 

2. Построить в одной системе координат при 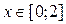
·
·
3. Построить поверхность при
Вариант 9
1. Построить в разных системах координат при xÎ[1,4;1,9] графики функций:

2. Построить в одной системе координат при хÎ[0;2] графики функций:
·
· 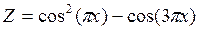
3. Построить поверхность при хÎ[-1;1]
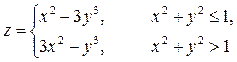
Вариант 10
1. Построить в разных системах координат при 
2. Построить в одной системе координат при 
·
·
3. Построить поверхность 
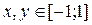
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9506 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Упражнения 1 в Excel.
Построить в разных системах координат при x[-2;2] графики следующих функций:
П
остроить в одной системе координат при x[-2;2] графики следующих двух функций:
Y=2sin(x)cos(x), Z=3cos 2 (2x)sin(x)
Построить поверхность z=x 2 -2y 2 , при x,y[-1;1]
Найти все корни уравнения x 3 2,92x 2 + 1,4355x + 0,791136=0
Упражнения 1 в Excel.
П
остроить в разных системах координат при x[-2;2] графики следующих функций:
Построить в одной системе координат при x[-2;2] графики следующих двух функций:
Y=2sin(x)-3cos(x), Z=cos 2 (2x)-2sin(x)
Построить поверхность z=3x 2 -2sin 2 (y)y 2 , при x,y[-1;1]
Найти все корни уравнения x 3 2,56x 2 1,3251x + 4,395006=0
Упражнения 1 в Excel.
Построить в разных системах координат при x[-2;1,5] графики следующих функций:
П
остроить в одной системе координат при x[-2;2] графики следующих двух функций:
Y=5sin(x)- cos(3x)sin(x), Z=cos(2x)-2sin 3 (x)
Построить поверхность z=5x 2 cos 2 (y)-2y 2 e y , при x,y[-1;1]
Найти все корни уравнения x 3 + 2,84x 2 5,6064x 14,766336=0
Упражнения 1 в Excel.
Построить в разных системах координат при x[-1,5;1,5] графики следующих функций:
Построить в одной системе координат при x[-2;2] графики следующих двух функций:
Y=3sin(2x)cos(x)- cos 2 (3x), Z=2cos 2 (2x)-3sin(3x)
Построить поверхность при x,y[-1;1]
Н
айти все корни уравнения x 3 + 1,41x 2 5,4724x 7,380384=0
Упражнения 1 в Excel.
Построить в разных системах координат при x[-1,8;1,8] графики следующих функций:
П
остроить в одной системе координат при x[0;3] графики следующих двух функций:
Y=2sin(x)cos(x), Z=cos 2 (x)sin(3x)
Построить поверхность z=2x 2 cos 2 (x) 2y 2 , при x,y[-1;1]
Найти все корни уравнения x 3 + 0,85x 2 0,4317x + 0,043911=0
Упражнения 1 в Excel.
Построить в разных системах координат при x[-2;1,8] графики следующих функций:
П
остроить в одной системе координат при x[-3;0] графики следующих двух функций:
Y=3sin(3x)cos(2x), Z=cos 2 (4x)sin(x)
Построить поверхность z=2e 0,2x x 2 2y 4 , при x,y[-1;1]
Найти все корни уравнения x 3 0,12x 2 1,4775x + 0,191906=0
Упражнения 1 в Excel.
П
остроить в разных системах координат при x[-1,7;1,5] графики следующих функций:
Построить в одной системе координат при x[-3;0] графики следующих двух функций:
Y=2sin(2x)cos(4x), Z=cos 2 (3x) cos(x)sin(x)
Построить поверхность z=x 2 2e 0,2 y y 2 , при x,y[-1;1]
Найти все корни уравнения x 3 + 0,77x 2 0,2513x + 0,016995=0
Упражнения 1 в Excel.
П
остроить в разных системах координат при x[-1,5;1,8] графики следующих функций:
Построить в одной системе координат при x[0;2] графики следующих двух функций:
Y=sin(3x) + 2sin(2x)cos(3x), Z= cos(x) cos (3x)sin 2 (x)
П
остроить поверхность при x,y[-1;1]
Найти все корни уравнения x 3 + 0,88x 2 0,3999x + 0,037638=0
Упражнения 1 в Excel.
П
остроить в разных системах координат при x[-1,4;1,9] графики следующих функций:
Построить в одной системе координат при x[0;2] графики следующих двух функций:
Y= cos(3x)sin(x) + 2sin(3x)cos(2x), Z=cos 2 (x) cos(3x)
Построить поверхность при x,y[-1;1]
Найти все корни уравнения x 3 + 0,78x 2 0,8569x + 0,146718=0
Упражнения 1 в Excel.
П
остроить в разных системах координат при x[-1,4;1,4] графики следующих функций:
Построить в одной системе координат при x[0;2] графики следующих двух функций:
Y=2sin(2x)cos(x) + sin(3x), Z=cos(2x)sin 2 (x) cos(4x)
Построить поверхность z=3x 2 sin 2 (x) 5e 2y y при x,y[-1;1]
Найти все корни уравнения x 3 + 2,28x 2 1,9347x 3,907574=0
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке . Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Поделитесь статьёй с друзьями:
Добрый день. А есть возможность в Excele создать график с тремя переменными, но на одном графике? 2 параметра как обычно, координаты х и у, а третий параметр чтоб отражался размером метки? Вот как пример, такой график —
Рубрика Excel
Также статьи о графиках в Экселе:
- Как сделать диаграмму в Эксель?
- Как сделать круговую диаграмму в Экселе?
- Как построить график в Экселе?
- Построение точечной диаграммы в Excel
В Экселе можно результаты расчетов отобразить в виде диаграммы или графика, придавая им большую наглядность, а для сравнения иногда нужно построить два графика рядом. Как построить два графика в Excel на одном поле мы далее и рассмотрим.
Начнем с того, что не каждый тип диаграмм в Экселе сможет отобразить именно тот результат, который мы ожидаем. К примеру, имеются результаты расчетов для нескольких функций на основе одинаковых исходных данных. Если по этим данным строить обычную гистограмму или график, то исходные данные не будут учитываться при построении, а лишь их количество, между которыми будут задаваться одинаковые интервалы.
Выделяем два столбца результатов расчетов и строим обычную гистограмму.
Теперь попробуем добавить еще одну гистограмму к имеющимся с таким же количеством результатов расчетов. Для добавления графика в Экселе делаем активным имеющийся график, выделив его, и на появившейся вкладке «Конструктор» выбираем «Выбрать данные». В появившемся окошке в разделе «Элементы легенды» нажимаем добавить, и указываем ячейки «Имя ряда:» и «Значения:» на листе, в качестве которых будут значения расчета функции «j».
Теперь посмотрим, как будет выглядеть наша диаграмма, если мы к имеющимся гистограммам добавим еще одну, у которой количество значений почти в два раза больше. Добавим к графику значения функции «k».
Как видно, последних добавленных значений гораздо больше, и они настолько малы, что их на гистограмме практически не видно.
Если изменить тип диаграммы с гистограммы на обычный график, результат получится в нашем случае более наглядным.
Если использовать для построения графиков в Экселе точечную диаграмму, то на полученных графиках будет учитываться не только результат расчетов, но и исходные данные, т.е. будет прослеживаться четкая зависимость между величинами.
Для создания точеного графика выделим столбец начальных значений, и пару столбцов результатов для двух разных функций. На вкладке «Вставка» выбираем точечную диаграмму с гладкими кривыми.
Для добавления еще одного графика выделяем имеющиеся, и на вкладке «Конструктор» нажимаем «Выбрать данные».
В новом окошке в графе «Элементы легенды» нажимаем «Добавить», и указываем ячейки для «Имя ряда:», «Значения X:» и «Значения Y:». Добавим таким образом функцию «j» на график.
Теперь добавим функцию «k», у которой совершенно другие исходные данные и их количество.
Как видно, на точечном графике функция «k» практически незаметна, но зато построена с учетом значений по обеим осям.
Построение графиков функций в Excel
Февраль 9th, 2014
Andrey K
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете
оставить комментарий
, или
ссылку
на Ваш сайт.
Душевые термостаты, лучшие модели на
http://tools-ricambi.ru/
изготавливаются из материалов высшего качества
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2× 2 -2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
В дополнение привожу видео — где показан порядок действий, описанный выше.
Как совместить два графика в excel с разными координатами
Построение графиков в Excel стало очень простым занятием в Excel 2010 и Excel 2013 – для этого достаточно сделать 3 движения мышкой. Но при построении двух графиков в одной координатной оси может возникнуть сложность, если значения для графиков сильно отличаются.
Для примера возьмем таблицу с показателями продаж и эффективностью и создадим для них график.
Как создать график в Excel?
Выделяете область, для которой хотите построить график, заходите в риббоне в закладку «Вставка», выбираете понравившийся график (Рис.1)
Рис.1. Как построить график в Excel
Если этим ограничиться, то результат вряд ли вас удовлетворит (Рис.2), т.к. график эффективности получился прямой линией. Это не удивительно, поскольку значения колонок «Продажи» и «Эффективность» отличаются на несколько порядков.
Рис.2. Неудовлетворительный вид графика
Чтобы в одной координатной плоскости Excel было отображено 2 графика с принципиально разными значениями, нужно добавить для одного из графиков так называемую «вспомогательную ось». Для этого нажмите правой кнопкой мыши на прямой график (на рисунке 2 – оранжевый график), в выпадающем меню выберите пункт «Формат ряда данных» и в открывшейся справа боковой колонке установите галочку около пункта «По вспомогательной оси» (см. анимацию ниже).
Совмещаем разные типы диаграмм в EXCEL
Иногда требуется на одной диаграмме совместить разные типы диаграмм, например гистограмму и обычную кривую:
Исходные данные для диаграммы представлены в таблице (см. файл примера ):
Для наглядности цвет строки в таблице совпадает с цветом соответствующей диаграммы. Например, строка 5 «Выручка от реализации» (выделена бордовым цветом) соответствует бордовой кривой на диаграмме (см. самый верхний рисунок).
Алгоритм построения совмещенных диаграмм следующий:
- выделяем все данные, которые должны попасть в диаграмму (ячейки A3:E6 );
- в меню Вставка/ Диаграммы/ Гистограммы выбираем, например, Гистограмма с группировкой; в Конструкторе диаграмм меняем местами столбцы и строки ( Работа с диаграммами/ Конструктор/ Данные/ Строка-Столбец );
- на диаграмме выделяем столбцы, которые соответствует Выручке от реализации (эти столбцы будут иметь другой тип графика — отличный от гистограммы);
- через меню Работа с диаграммами/ Конструктор/ Тип/ Изменить тип диаграммы выбрать нужный тип.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Другой пример. Пусть на диаграмме имеется 2 графика:
Требуется из зеленого графика сделать гистограмму. Для этого выделите зеленый график.
Через меню Работа с диаграммами/ Конструктор/ Тип/ Изменить тип диаграммы выберите тип Гистограмма с группировкой , нажмите ОК.
Некоторые типы диаграмм могут не сочетаться — EXCEL предупредит Вас об этом.
Более сложный вариант совмещения разных типов диаграмм содержится в файле примера и представлен на рисунке ниже:
Совет : Т.к. для совмещения различных типов диаграмм требуется несколько рядов данных, то для углубленного изучения диаграмм полезно прочитеть статью Построение диаграмм с несколькими рядами данных в MS EXCEL
Аннотация:
Цель работы: научиться определять значения функций и строить графики, а также использовать логические функции в табличном процессоре Excel.
Содержание работы:
Построение графика функции с одной переменной.
Построение графика функции с двумя условиями.
Построение графика функции с тремя условиями.
Построение двух графиков в одной системе координат.
Построение поверхности.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания.
Оформить отчет и ответить на контрольные вопросы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Построение графика функции
Процесс построения графика функции состоит из двух этапов:
- создание таблицы значений функции
- непосредственного построения ее графика.
Для построения графика функции необходимо первоначально построить таблицу ее значений при различных значениях аргумента, причем аргумент изменяют обычно с фиксированным шагом. Шаг выбирают небольшим, так чтобы таблица значений функции отражала ее поведение на интервале табуляции.
Рассмотрим технологию построения графика на примере функции 
![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
Создание таблицы значений функции
В нашем случае возьмем в качестве шага изменения аргумента, например, 0.1. Нам надо найти у(0), у(0.1), у(0.2), …, у(1). С этой целью в ячейки диапазона A1:А11 последовательно введем 0, 0.1, …, 1, т. е. значения переменной х. Отметим, что эта последовательность значений представляет собой арифметическую прогрессию.
Ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию, можно двумя способами.
Первый способ заключается в следующем:
- В ячейки А1 и А2 введите первый и второй члены арифметической прогрессии, т.е. 0 и 0,1
- Выделите диапазон ячеек А1:А2.
- Расположите указатель мыши на маркере заполнения выделенного диапазона (рис. 4.1
рис.
4.1) и протяните его вниз (в данном случае на диапазон A3:А11) до тех пор, пока не получится числовой ряд нужной длины (рис. 4.2
рис.
4.2).
Второй способ позволяет пользоваться диалоговым окном Прогрессия. Для этого:
- В ячейку А1 введите первый член арифметической профессии.
- Выберите команду Главная > Редактирование > Заполнить > Прогрессия.
- В появившемся диалоговом окне Прогрессия (рис. 4.3
рис.
4.3) в группе Расположение выбираем переключатель по столбцам, а в группе Тип – переключатель арифметическая. В поле Шаг введите значение 0,1, а в поле Предельное значение – 1. - Нажмите кнопку ОК.
Рис.
4.1.
Вид указателя мыши на маркере заполнения
Рис.
4.2.
Арифметическая последовательность, построенная по первым ее двум членам с помощью маркера заполнения
Рис.
4.3.
Диалоговое окно Прогрессия
Диалоговое окно Прогрессия закроется, а на рабочем листе автоматически будет построена требуемая прогрессия.
Примечание. Диалоговое окно Прогрессия, отображаемое на экране выбором команды Главная > Редактировать > Заполнить > Прогрессия, также позволяет создавать геометрические прогрессии.
В ячейку В1 введите формулу: =СОS(ПИ( )*А1)^2.
Ввод формул в ячейку можно производить либо с клавиатуры, либо с помощью диалогового окна Мастер функций, которое отображается на экране либо выбором команды Формулы > Вставить Функцию, либо нажатием кнопки Вставка функции
Продемонстрируем работу с мастером функций на примере ввода упомянутой выше формулы.
- Выберите ячейку В1.
- Нажмите кнопку Вставка функции
панели инструментов Стандартная, либо выберите команду Формулы > Вставить Функцию. На экране отобразится диалоговое окно Мастер функций – шаг 1 из 2 (рис. 4.4
рис.
4.4). Оно состоит из двух частей: - Категория – со списком двенадцати категорий функций;
- Функция – со списком имен функций, входящих в выбранную категорию.
Категория Полный алфавитный перечень содержит все встроенные функции и их имена упорядочены в алфавитном порядке, категория 10 недавно использовавшихся содержит имена десяти последних примененных функций. Эта категория ускоряет вызов функций, постоянно используемых пользователем.
- Функция cos относится к категории Математические. Выберите эту функцию и нажмите кнопку ОК. На экране отобразится панель формул (рис. 4.5
рис.
4.5).
Рис.
4.4.
Диалоговое окно Мастер функций – шаг 1 из 2
Рис.
4.5.
Панель формул
В поле Число вводится аргумент функции – в рассматриваемом примере это ПИ ()*А1. С помощью клавиатуры в это поле введите только ПИ ( )*, а ссылку на ячейку А1 в формулу добавьте, щелкнув по ячейке А1 на рабочем листе. Конечно, ее можно было также ввести с клавиатуры, но предложенный способ дает дополнительную проверку правильности ввода. После нажатия кнопки ОК в ячейку В1 будет введена формула:
Примечание. При использовании мастера функции перед вводом формулы в ячейку не надо вводить знак =, он вставляется в формулу автоматически.
- С помощью клавиатуры добавьте в формуле =COS(ПИ ())*А1 операцию возведения в квадрат функции cos. После всех описанных действий в ячейке В1 должна появиться формула =COS(ПИ()*Al)^2
Таким образом, пока найдено значение функции cos2(x) для значения х из ячейки A1. Теперь нам осталось найти значения этой функции для диапазона ячеек А2:А11.
Для этого:
- Выберите ячейку В1.
- Расположите указатель мыши на маркере заполнения выделенной ячейки и протяните его вниз на диапазон В2:В11.
Процесс создания таблицы значений функции завершен (рис. 4.6
рис.
4.6).
На рис. 4.6
рис.
4.6 на правом рабочем листе приведены формулы, введенные в ячейки рабочего листа. Для того чтобы в ячейках рабочего листа отображались не значения, а формулы, надо выбрать команду Формулы > Зависимости формул и Показать формулы.
Рис.
4.6.
Результат табуляции функции до и после форматирования данных
На среднем рабочем листе (рис. 4.6
рис.
4.6) приведен результат табуляции функции. Выглядит он не очень презентабельно: после десятичной точки отображается различное количество десятичных знаков. Кроме того, происходит перемешивание числового и экспоненциального форматов.
А именно, в ячейке В6 вместо 0 отображается 3.75Е-33, что приблизительно и равно нулю. Поэтому форматы надо привести к какому-то общему виду, например, как показано на левом рабочем листе: значения аргумента выводятся в числовом формате с точностью до одного знака после десятичной точки, а значения функции – с точностью до трех знаков после десятичной точки. Отформатируем, например, значения аргумента.
Для этого надо выбрать диапазон A1:A11. Это можно сделать, например, следующим способом. Выберите ячейку А1, а затем при нажатой клавише <Shift> выделите ячейку А11. Диапазон А1:А11 выбран.
Переходим к форматированию данных. Выберите команду Главная > Число. В появившемся диалоговом окне Формат ячеек: Число в списке Числовые форматы выберите Числовой, а в поле Число десятичных знаков введите 1. Нажмите кнопку ОК. Данные в Al:A11 будут отформатированы, как показано на левом рабочем листе (рис. 4.6
рис.
4.6). Аналогичным образом разберитесь с диапазоном В1:В11.
Построение графика
Перейдем теперь к конструированию графика cos2(xх) функции по существующей таблице значений аргументов и соответствующих значений функции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм на выберите вариант График, а в списке Вид укажите стандартный график (рис. 4.7
рис.
4.7). Нажмите кнопку Далее. - Чтобы изменить (шаг 2 из 4): источник данных диаграммы (которое позднее переименовывается в окно Исходные данные) необходимо нажать на график, затем выбрать вкладку Конструктор, затем вкладку Данные, Выбрать данные. В поле Диапазон автоматически будет введена ссылка на необходимый диапазон в абсолютном формате. Проверьте его, удалите 1 ряд. В итоге у вас должно получится, что Диапазон, =Лист1!$В1$:$В$11.
Обратите внимание на полученный график функции, отображаемый на вкладке Диапазон данных. В нем по оси ординат откладываются значения функции, а вот по оси абсцисс порядковые номера точек, а не значения аргумента.
Для того чтобы по оси абсцисс откладывались значения аргумента, надо выделить диаграмму и воспользоваться командой Конструктор > Данные > Выбрать данные, далее Подписи горизонтальной оси (категории) > Изменить и указать диапазон ячеек в которых расположен аргумент х функции.
Рис.
4.7.
Вкладка Стандартные диалогового окна Мастер диаграмм (шаг 1 из 4): тип диаграммы
Рис.
4.8.
Вкладка Диапазон данных диалогового окна Исходные данные
Создав диаграмму, можно изменить любой из ее элементов. Например, можно изменить вид осей, добавить название диаграммы, переместить или скрыть легенду, а также добавить дополнительные элементы.
Чтобы изменить диаграмму, выполните одно или несколько из указанных ниже действий.
- Изменение вида осей диаграммы. Можно указать масштаб осей и изменить промежутки между значениями или категориями. Для удобства чтения диаграммы можно добавить на оси деления указать величину промежутков между ними.
- Добавление к диаграмме названий и меток данных. Для пояснения отображенных на диаграмме данных можно добавить название диаграммы, названия осей и метки данных.
- Добавление легенды и таблицы данных Можно отобразить или скрыть легенду, изменить ее расположение или элементы. Для некоторых диаграмм также можно отобразить таблицу данных, в которой содержатся ключи легенды и значения, представленные на диаграмме.
- Применение специальных параметров для диаграмм разных типов Для различных типов диаграмм можно применять различные специальные линии (например, коридор колебания и линии тренда), полосы (например, полосы повышения и понижения и планки погрешностей), маркеры данных и т.д.
Вместо того чтобы добавлять или изменять элементы диаграммы и форматировать их вручную, можно быстро применить к данным готовый макет или стиль диаграммы. В приложении Excel существует множество полезных готовых макетов и стилей, которые можно адаптировать, изменив вручную макет или формат отдельных элементов диаграммы, таких как область диаграммы, область построения, ряды данных и легенда.
При использовании готового макета диаграммы на ней в определенном порядке отображается заданный набор элементов (например, названия, легенда, таблица данных или метки данных). Можно подобрать подходящий макет из предоставленных для диаграмм конкретного типа.
При использовании готового стиля диаграммы ее форматирование основано на примененной теме документа, поэтому внешний вид диаграммы будет соответствовать цветам темы (набору цветов), шрифтам темы (набору шрифтов заголовков и основного текста) и эффектам темы (набору границ и заливок), принятым в организации или заданным пользователем.
Собственные стили или макеты диаграмм создавать нельзя, но можно создать шаблоны диаграмм, содержащие нужный макет и форматирование.
Помимо применения готового стиля диаграммы можно легко изменить форматирование ее отдельных элементов, например маркеров данных, области диаграммы, области построения, чисел и текста в названиях и подписях, что привлечет внимание и сделает диаграмму оригинальной. Можно также применять стили фигур и стили WordArt или форматировать фигуры и текст в элементах диаграммы вручную.
Чтобы изменить форматирование диаграммы, выполните одно или несколько из указанных ниже действий:
- Заливка элементов диаграммы. Для привлечения внимания к определенным элементам диаграммы можно залить их цветом, текстурой, рисунком или применить градиентную заливку.
- Изменение контуров элементов диаграммы. Для выделения элементов диаграммы можно изменить цвет, стиль или толщину линий.
- Добавление специальных эффектов к элементам диаграммы. Для придания диаграмме завершенности к ее элементам можно применить специальные эффекты, например тень, отражение, свечение, сглаживание краев, рельеф или объемное вращение.
- Форматирование текста и чисел Текст и числа в названиях, подписях и надписях на диаграмме можно форматировать так же, как текст и числа на листе. Чтобы выделить текст или число, можно даже применять стили WordArt.
Рис.
4.9.
Вкладка Конструктор: параметры диаграммы
Рис.
4.10.
Диалоговое окно Макет: параметры диаграммы
Рис.
4.11.
Результат построения графика функции
Математические функции рабочего листа
Наиболее часто употребляемые стандартные математические функции рабочего листа приведены в табл. 4.1
таблица
4.1.
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| ABS (число) | ABS (number) | Возвращает абсолютную величину аргумента |
| ACOS (число) | ACOS (number) | Возвращает арккосинус аргумента |
| ASIN (число) | ASIN (number) | Возвращает арксинус аргумента |
| ATAN (число) | ATAN (number) | Возвращает арктангенс аргумента |
| COS (число) | COS (number) | Возвращает косинус аргумента |
| EXP (число) | EXP (number) | Возвращает экспоненту аргумента, т.е результат возведения основания натурального логарифма в степень, равную значению аргумента |
| LN (число) | LN (number) | Возвращает натуральный логарифм аргумента |
| LOG (число) | LOG (number) | Возвращает логарифм аргумента по данному основанию, если основание опущено, то оно полагается равным 10 |
| LOG10 (число; основание) | LOG10 (number; base) | Возвращает десятичный логарифм аргумента |
| SIN (число) | SIN (number) | Возвращает синус аргумента |
| TAN (число) | TAN (number) | Возвращает тангенс аргумента |
| ЗНАК (число) | SGN (number) | Возвращает знак аргумента |
| ОСТАТ (число; делитель) | MOD (number1; number1) | Возвращает остаток от деления числа на делитель |
| ПИ ( ) | PI ( ) | Возвращает значение числа ? с точностью до 15 знаков (в данном случае 3.14159265358979). обратите внимание на то, что функция ПИ ( ) не имеет аргумента |
| СЛЧИС ( ) | RND ( ) | Возвращает случайное число между 0 и 1. Чтобы получить случайное вещественное число между a и b, можно использовать следующую формулу: СЛЧИС ( )*(b-a)+a |
| ЦЕЛОЕ (число) | INT (number) | Округляет число до ближайшего меньшего целого |
График функции с двумя условиями
Рассмотрим пример построения графика функции при ![$хin[0;1]$$](https://intuit.ru/sites/default/files/tex_cache/5bbd057004769c8519124b98a54a24bf.png)
График строится по принципам, представленным в п. 4.1 «Построение графика функции»
«Построение графиков функций и использование логических формул»
, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.5;(1+ABS(0.2-А1))/(1+А1+А1^2);А1^ (1/3))
Примечание. Обратите внимание на то, что для возведения в степень в коде используется соответствующая операция, т.е. А1^(1/3), а не функция рабочего листа степень, т. е. степень (А1; 1/3). В обоих случаях получается один и тот же результат, но, применение операции возведения в степень здесь более разумно, т. к. делает код более очевидным.
В коде фигурирует функция логического ветвления Если (IF), которая имеет следующий синтаксис:
ЕСЛИ (лог выражение; значение_если_истина; значение_если_ложь)
Рассмотрим ее аргументы:
- лог выражение – это любое значение или выражение, принимающее значения истина или ложь. Например, А10=100 – это логическое выражение; если значение в ячейке А10 равно 100, то выражение принимает значение ИСТИНА. В противном случае – ЛОЖЬ. Данный аргумент может быть использован в любом операторе сравнения.
- значение_если_истина – это значение, которое возвращается, если лог выражение равно ИСТИНА. Например, если этот аргумент – строка «План реализации выполнен» и лог выражение равно ИСТИНА, тогда функция ЕСЛИ отобразит текст План реализации выполнен. Если лог выражение равно, ИСТИНА, а значение_если_истина пусто, то возвращается значение 0. Чтобы отобразить слово ИСТИНА, необходимо использовать логическое значение ИСТИНА для этого аргумента. значение_если_истина может быть формулой.
- значение_если_ложь – это значение, которое возвращается, если лог выражение равно ЛОЖЬ. Например, если этот аргумент – строка «План реализации перевыполнен» и лог выражение равно ЛОЖЬ, то функция ЕСЛИ отобразит текст План реализации перевыполнен. Если лог выражение равно ЛОЖЬ, а значение_если_ложь опущено (т. е. после значение_если_истина нет точки с запятой), то возвращается логическое значение ЛОЖЬ. Если лог выражение равно ЛОЖЬ, а значение_если_ложь пусто (т. е. после значение_если_истина стоит точка с запятой с последующей закрывающей скобкой), то возвращается значение 0. значение_если_ложь может быть формулой.
Логические функции
В MS Excel имеются функции логических условий, перечисленные в табл. 4.2.
таблица
4.2
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| И (лог знач1; лог знач2; …) | AND (arg1, arg2, …) | Логическое умножение. |
| Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=5) возвращает значение ИСТИНА. | ||
| Если ячейка В4содержит число из интервала от 1 до 100, то функция И (1<В4; В4<100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| ИЛИ (лог знач1; лог знач2; …) | OR (arg1, arg2, …) | Логическое сложение. |
| Возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=6) возвращает значение ИСТИНА. | ||
| Если ячейка В4 содержит число меньше 1 или больше 100, то ИЛИ (В4<1; В4>100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| НЕ (лог знач) | NOT (arg) | Логическое отрицание. Изменяет на противоположное значение логическое значение своего аргумента. Например, НЕ (2+5=5) возвращает значение ИСТИНА. |
| Если ячейка В4 содержит число меньше 1 или больше 100, то НЕ (ИЛИ(В4<1;В4>100)) возвращает ЛОЖЬ, а в противном случае – ЛОЖЬ. |
Примечание. Кроме функции ЕСЛИ в MS Excel имеются еще две функции, использующие логические условия. Это функции:
СЧЁТЕСЛИ (COUNTIF) – подсчитывает количество ячеек внутри диапазона, удовлетворяющих заданному критерию;
СУММЕСЛИ (SUMIF) – суммирует значения тех ячеек диапазона, удовлетворяющих заданному критерию.
График функции с тремя условиями
Рассмотрим пример построения графика функции у при ![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
График строится так, как описано в разд. «Построение графика функции» ранее в этой работе, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.2;1+ LN(1+A1); ЕСЛИ(И(А1>=0.2;А1<=0.8); (1+А1^(1/2))/(1+А1);2*ЕХР(-2*А1)))
Тот же самый результат можно получить, введя в ячейку В1 более простую формулу:
=ЕСЛИ (A1<0.2; 1+LN (1+A1); ЕСЛИ (А1<=0.8; (1+А1^(1/2))/(1+А1); 2*ЕХР(-2*А1)))
Два графика в одной системе координат
Рассмотрим пример построения в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
- y = 2sin(x)
- z = 3 cos(2x) – sin(x)
Итак, начнем процесс построений.
- В ячейки А1, В1 и С1 введите соответственно х, у и z.
- Выделите диапазон А1:С1. Выберите команду Главная. На вкладке
Выравнивание появившегося диалогового окна Формат ячеек в группе Выравнивание в списке по горизонтали укажите значение по правому краю. Нажмите кнопку ОК. Заголовки столбцов окажутся выровненными по правому краю.
- В диапазон ячеек А2:А17 введите значения аргумента х от -3 до 0 с шагом 0.2.
- В ячейки В2 и С2 введите формулы: =2*SIN(A2), =3*COS(2*A2)-SIN(A2)
- Выделите диапазон В2:С2, расположите указатель мыши на маркере заполнения этого диапазона и пробуксируйте его вниз так, чтобы заполнить диапазон В3:С17.
- Выделите диапазон В3:С17. Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы выберите значение График. Нажмите кнопку Далее.
- На вкладке Данные > выбрать данные диалогового окна Исходные данные в поле ввода Подписи оси X укажите ссылку на диапазон А2:А17, значения из которого откладываются по оси абсцисс (рис. 4.12
рис.
4.12). В списке Ряд приводятся ряды данных, откладываемых по оси ординат (в нашем случае имеется два ряда данных). Эти ряды автоматически определяются на основе ссылки, указанной в поле ввода Диапазон предыдущего шага алгоритма. В поле Значения автоматически выводится ссылка на диапазон, соответствующий выбранному ряду из списка Ряд. В поле ввода Имя отображается ссылка на ячейку, в которой содержится заголовок соответствующего ряда. Этот заголовок в дальнейшем используется мастером диаграмм для создания легенды.
Рис.
4.12.
Вкладка Ряд диалогового окна Исходные данные до задания имен рядов
- Выберите в списке Ряд элемент Ряд1. В поле ввода Имя укажите ссылку на ячейку В1, значение из которой будет использоваться в качестве идентификатора данного ряда. Вводить эту ссылку надо не с клавиатуры, а выбором с рабочего листа ячейки В1. Это приведет к тому, что в поле Имя автоматически будет введена ссылка на ячейку в абсолютном формате. В данном случае, =Лист1!$В$1. Теперь осталось только щелкнуть на элементе Ряд1 списка Ряд. Это приведет к тому, что элемент Ряд1 поменяется на у, т. е. на то значение, которое содержится в ячейке В1. Аналогично поступите с элементом Ряд2 списка Ряд. Сначала выберите его, затем в поле ввода Имя укажите ссылку на ячейку С1, а потом щелкните на элементе Ряд2. На рис. 4.13
рис.
4.13 показана вкладка Ряд диалогового окна Исходные данные после задания имен рядов. Теперь можно нажать кнопку Далее. - В появившемся диалоговом окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите График двух функций, в поле Ось X(категорий) введите х, в поле Ось Y(значений) введите у и z. На вкладке Легенда установите флажок Добавить легенду. Нажмите кнопку Далее.
- Нажмите кнопку Готово.
Результат проделанных шагов представлен на рисунке 4.14
рис.
4.14.
Рис.
4.13.
Вкладка Ряд диалогового окна Исходные данные после задания имен рядов
Для большей презентабельности построенной диаграммы в ней были произведены следующие изменения по сравнению с оригиналом:
- Изменена ориентация подписи оси ординат с вертикальной на горизонтальную. Для этого выберите подпись оси ординат. Нажмите правую кнопку мыши и в появившемся контекстном меню укажите команду Формат названия оси. На вкладке Выравнивание диалогового окна Формат названия оси в группе Ориентация установите горизонтальную ориентацию. Нажмите кнопку ОК.
- Для того чтобы пользователю было легче отличить, какая линия является графиком функции у, а какая – z, изменен вид графика функции z. С этой целью выделите график функции z. Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат рядов данных. На вкладке Вид диалогового окна Формат ряда данных, используя элементы управления групп Маркер и Линия, установите необходимый вид линии графика. Нажмите кнопку ОК.
- Изменен фон графика. С этой целью выделите диаграмму (но не область построения). Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат области диаграммы. На вкладке Вид диалогового окна Формат области диаграммы установите флажок скругленные углы, а используя элементы управления группы Заливка, установите цвет и вид заливки фона. Нажмите кнопку ОК.
Рис.
4.14.
Графики функций у(х) и z(x), построенные в одной системе координат
Построение поверхности
Продемонстрируем технологию построения поверхностей на примере следующей функции, зависящей от двух аргументов:
$z = x^{2}-y^{2}$ при ![$$хin [-2; 2], уin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/9ba0e461aae4f553cbb9279438619e6b.png)
Прежде чем воспользоваться мастером диаграмм, надо построить таблицу значений функции z по обоим ее аргументам, например, по аргументу х от -2 до 2 с шагом 0.2, а по у от -1 до 1 с шагом 0.2.
Для этого:
- Введите в ячейку А2 значение -2, а в ячейку А3 значение -1.8. Выберите диапазон ячеек А2:А3. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон А4:А22. Таким, образом, значения аргумента х протабулированы от -2 до 2 с шагом 0.2.
- Введите в ячейку В1 значение -1, а в ячейку С1 значение -0.8. Выберите диапазон ячеек В1:С1. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон D1:L1. Значения аргумента у протабулированы от -1 до 1 с шагом 0.2.
- В ячейку В2 введите формулу: =$А2^2 – В$1^2.
- Выберите ячейку В2, расположите указатель мыши на маркере ее заполнения и протяните его вниз на диапазон В2:L22.
На левом рабочем листе (рис. 4.15
рис.
4.15) показан результат табуляции функции, зависящей от двух аргументов, а на правом – часть формул, которые были введены в ячейке при копировании формулы, введенной в ячейку В2, перемещением маркера заполнения на диапазон В2:L22.
Рис.
4.15.
Таблица значений функции, зависящей от двух аргументов
Примечание. Использование в формуле абсолютной ссылки на строку и столбец существенно. Напомним, что знак $ в имени ячейки, стоящий перед номером строки, создает абсолютную ссылку на строку, а перед именем столбца – абсолютную ссылку на столбец. Поэтому при буксировке формулы из ячейки В2 на диапазоны B2:L22, в ячейках этого диапазона будут найдены значения функции z при соответствующих значениях аргументов х и у.
Перейдем к конструированию поверхности по результатам табуляции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы на вкладке Стандартные в списке Тип выберите значение Поверхность, а в списке Вид укажите стандартную поверхность. Нажмите кнопку Далее.
- В следующем диалоговом окне мастера диаграмм на вкладке Диапазон данных выберите переключатель Ряды в столбцах, т. к. данные располагаются в столбцах. В поле ввода Диапазон приведите ссылку на диапазон данных A1:L22, т. е. диапазон, который содержит в себе как значения аргументов, так и значения функции. Нажмите кнопку Далее.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): в параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите поверхность, в поле Ось X (категорий) укажите х, в поле Ось Y (рядов данных) задайте у, в поле Ось Z (значений) введите z. На вкладке Легенда сбросьте флажок Добавить легенду. Нажмите кнопку Готово.
- Поверхность построена, как показано на рисунке 4.16
рис.
4.16.
Рис.
4.16.
Построенная поверхность и диалоговое окно Формат трехмерной проекции
Примечание. MS Excel разрешает пользователю не только изменять размеры рабочей области диаграммы посредством маркеров изменения размеров, но и ориентацию поверхности в пространстве. Для этого достаточно выделить диаграмму, а затем выбрать команду Диаграмма > Объемный вид. На экране отобразится диалоговое окно Формат трехмерной проекции, элементы которого как раз и позволяют изменять ориентацию поверхности в пространстве.
ЗАДАНИЯ
Вариант 1.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 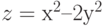
![$x,yin[-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/1dccee169ef8cd4747131b25d37db985.png)
Вариант 2.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 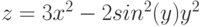
![$x, yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/53a8791dec1fce35a5f3ac0dd9605a3b.png)
Вариант 3.
1. Построить в разных системах координат при ![$xin[-2; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/075d390c8429b09a75c1effe8b21041a.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 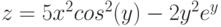
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 4.
1. Построить в разных системах координат при ![$хin [-1.5; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/f8ea986285591f482f6425385ca5802c.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность при мммх,yin [-1; 1]/ммм
Вариант 5.
1. Построить в разных системах координат при ![$хin [-1.8; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/78bc9ae987003e9c6801db7908c6bfbd.png)
2. Построить в одной системе координат при ![$хin [0; 3]$](https://intuit.ru/sites/default/files/tex_cache/153306b868b619790149dea95767b4f9.png)
3. Построить поверхность 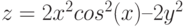
![$х,yin [-l; 1]$](https://intuit.ru/sites/default/files/tex_cache/f4f9de170788cb6bf2d9bec5dd801e0d.png)
Вариант 6.
1. Построить в разных системах координат при ![$хin [-2; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/0dbcf9e9bff0f78d00043ecdd4c74666.png)
2. Построить в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
3. Построить поверхность 
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 7.
1. Построить в разных системах координат при ![$хin [-1.7; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/68c9476760c3d9265176b82bcc296063.png)
2. Построить в одной системе координат при ![$хin [-3;0]$](https://intuit.ru/sites/default/files/tex_cache/625e1ce96d5bf506d83f626e5934b564.png)
3. Построить поверхность 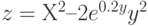
![$х,yin [-1;1]$](https://intuit.ru/sites/default/files/tex_cache/afd39bc8d16e67ea25b0fc35595fbb39.png)
Вариант 8.
1. Построить в разных системах координат при ![$хin [-1.5; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/2629a936172ba4ce71bd2c2e792ee4c2.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность при
Вариант 9.
1. Построить в разных системах координат при ![$хin [-1.4; 1.9]$](https://intuit.ru/sites/default/files/tex_cache/6c9405fb2d3d680c40a2b90ec8452bf2.png)
2. Построить в одной системе координат при ![$хin [0;2]$](https://intuit.ru/sites/default/files/tex_cache/adbba029f8747f8b59bce37c40dcc3a5.png)
3. Построить поверхность при
Вариант 10.
1. Построить в разных системах координат при ![$хin [-1.4; 1.4]$](https://intuit.ru/sites/default/files/tex_cache/077a3284889a9378e887806bcf4ea6f6.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность z = 3x2sin2(x) – 5e2yу при ![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Из каких этапов состоит процесс построения графика функции?
- Какими способами можно ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию?
- Как подписать ось X значениями аргумента?
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
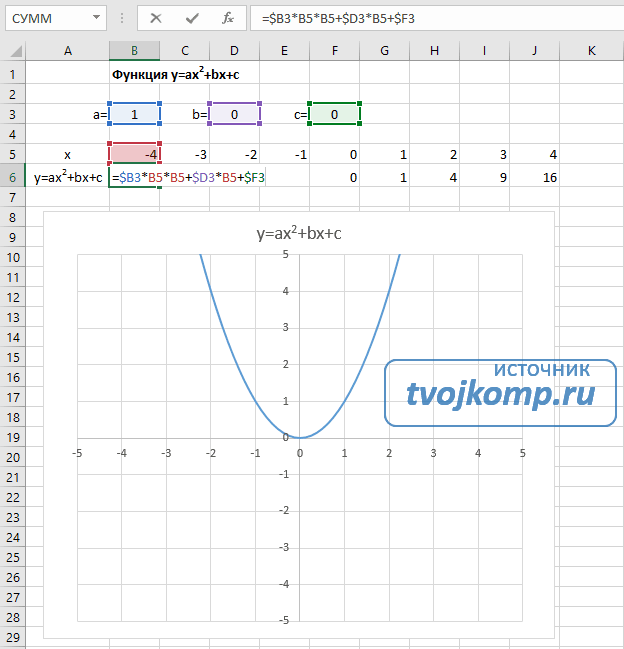
- Квадратичная функция y=ax2+bx+c
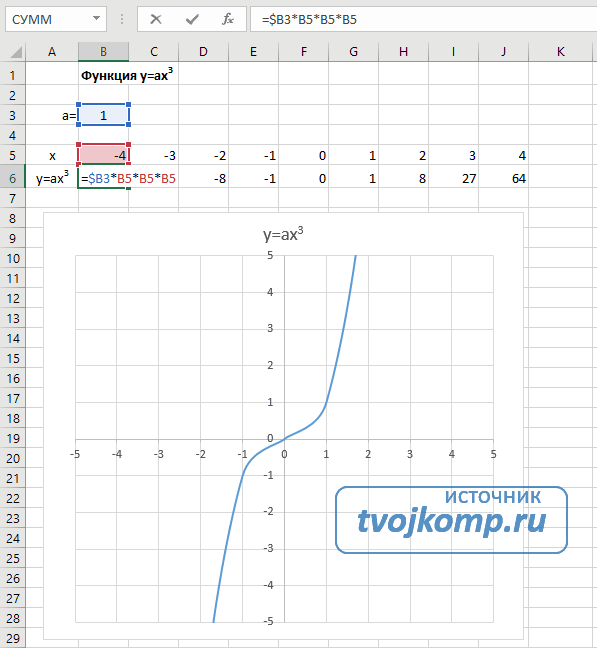
- Кубическая парабола y=ax3
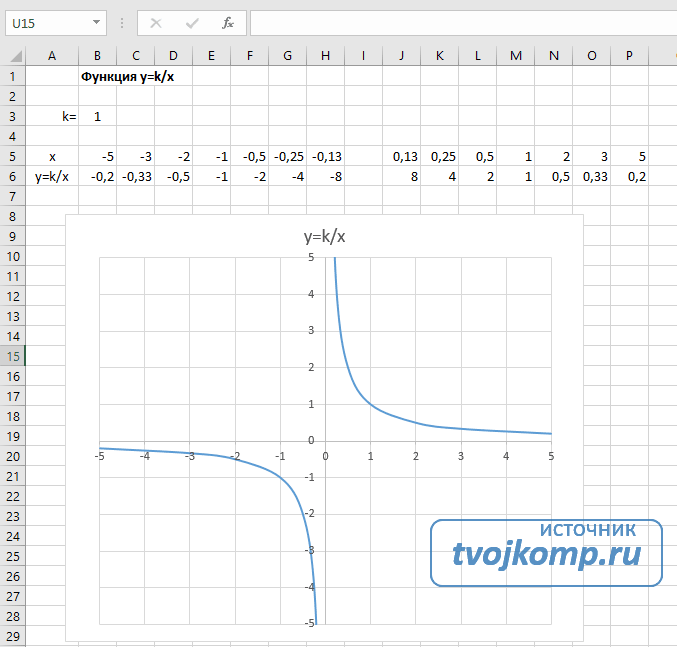
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
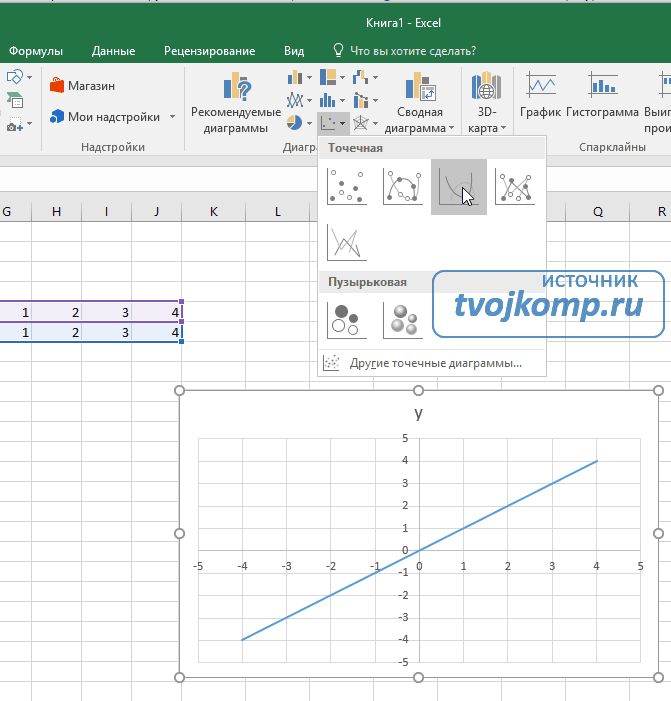
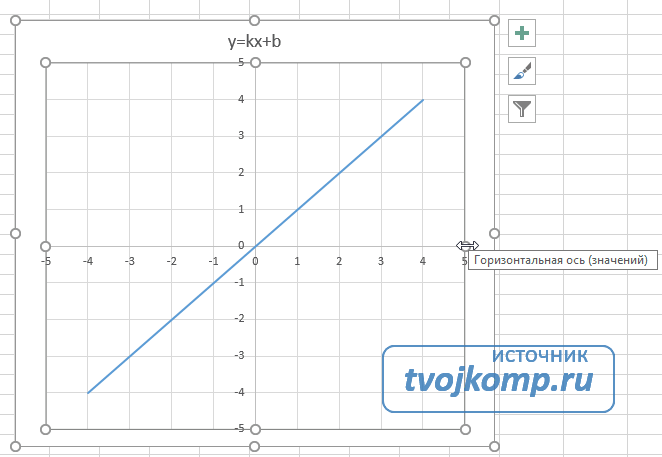
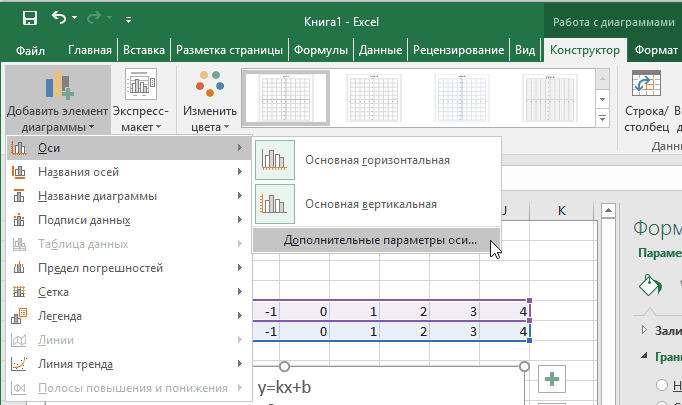
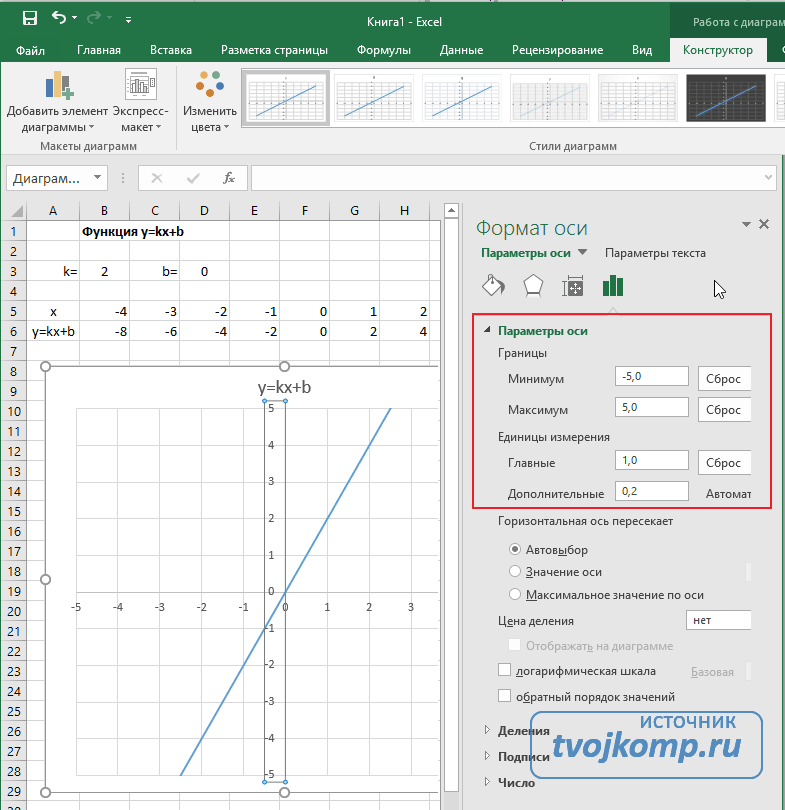
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
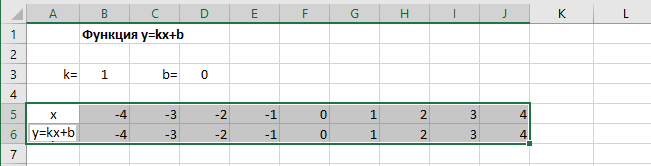
Подготовка расчетной таблицы
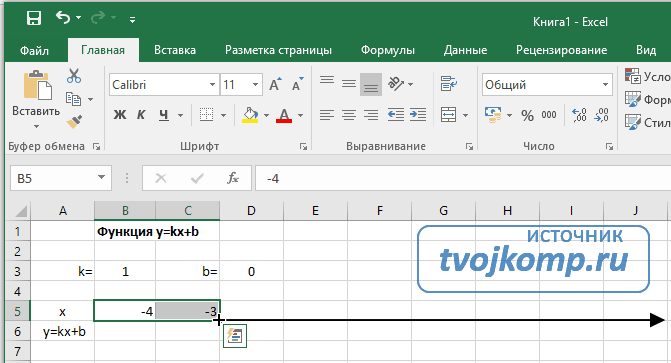
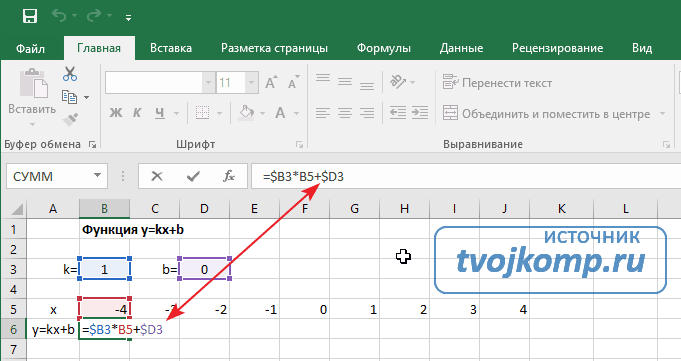
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
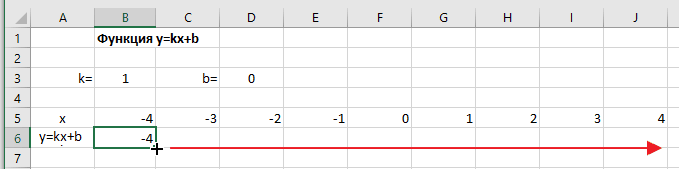
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
В итоге получим диаграмму.
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!














 Построить в разных системах координат при х ∈[-1,8,1,8] графики следующих функций
Построить в разных системах координат при х ∈[-1,8,1,8] графики следующих функций























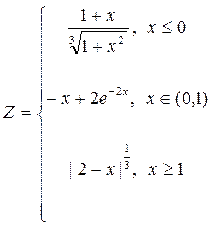
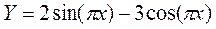


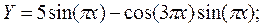
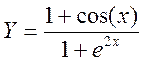
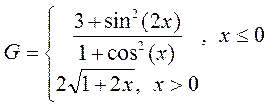


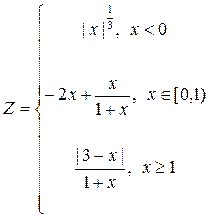

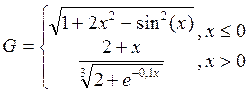
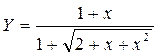
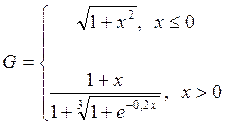

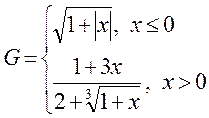




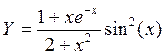


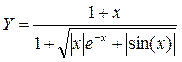






































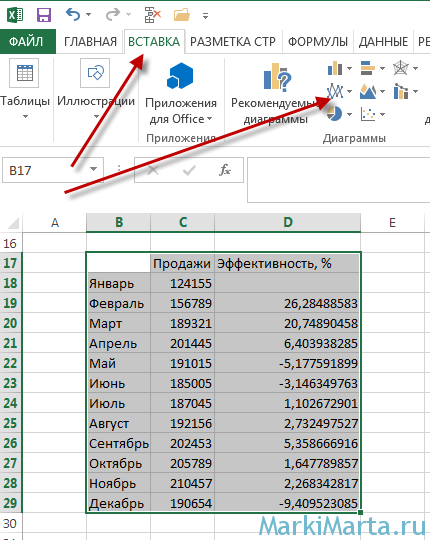
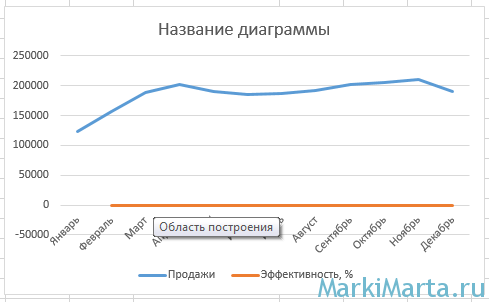
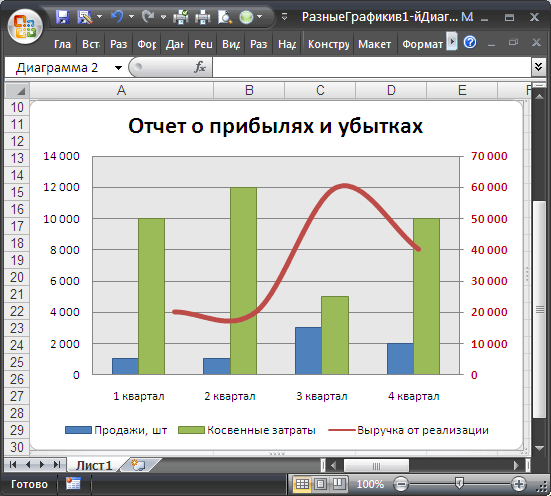
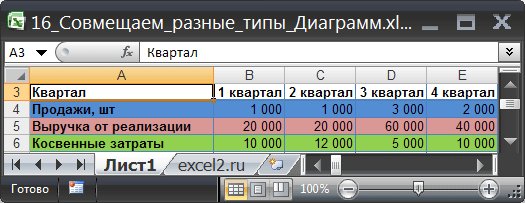
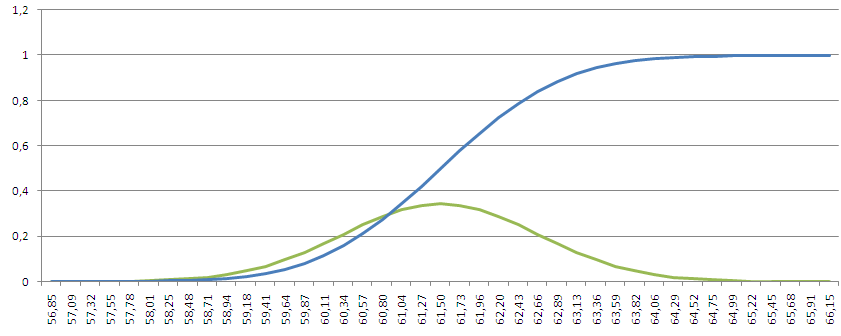
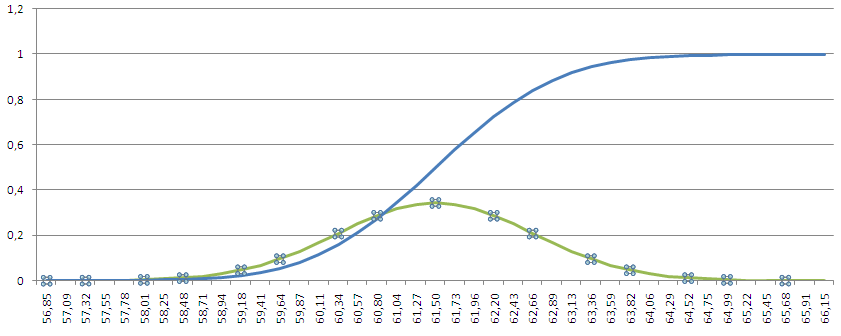
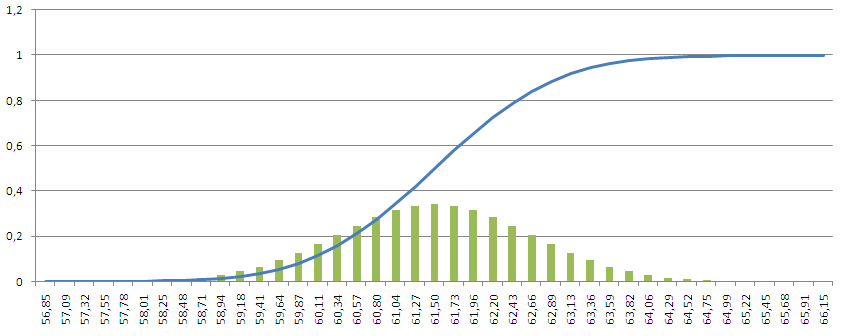
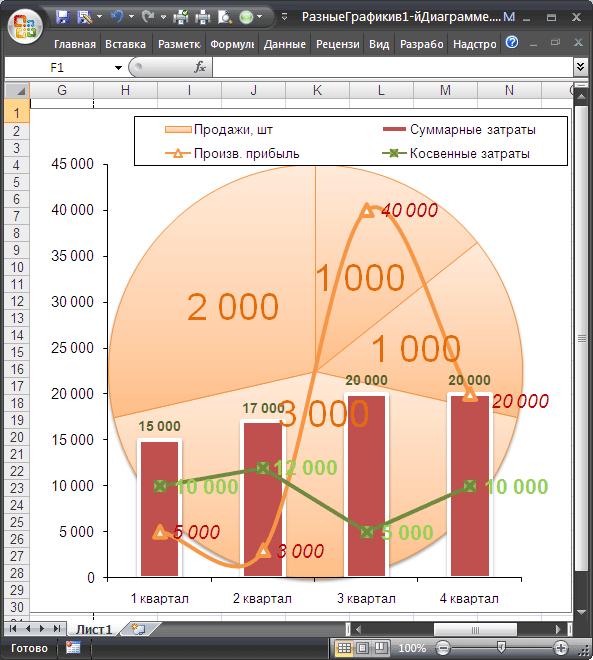











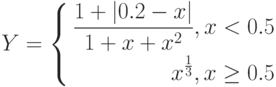
![$$
Y=left{
begin{aligned}
% nonumber to remove numbering (before each equation)
1+ln(1+x), x<0.2\
frac{1+x^{frac{1}{2}}}{1+x}, xin[0.2;0.8]\
2e^{-2x}, x>0.8
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/4205ce0704c58087ee2090c98d69defd.png)






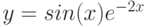
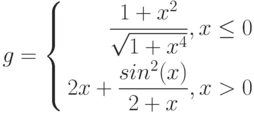
![$$
z=left{
begin{aligned}
frac{1+|x|}{sqrt[3]{1+x+x^{2}}},xleq-1\
2ln(1+x^{2}+frac{1+cos^{4}(x)}{2+x},xin [-1;0]\
(1+x)^{frac{3}{5}}, xgeq0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c4fbe6f0e5d1dfcbce7a704e471a929.png)
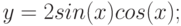
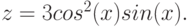
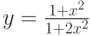
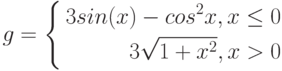
![$$
z=left{
begin{aligned}
frac{1+x}{sqrt[3]{1+x^{2}}},xleq0\
-x+2e^{-2x},xin(0,1)\
|2-x|^{frac{1}{3}},xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/b018b9edd908f216df636f345c6a0e0e.png)
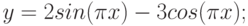
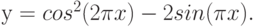
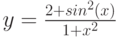
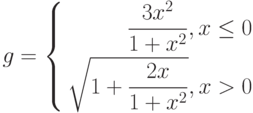
![$$
z=left{
begin{aligned}
3x+sqrt{1+x^{2}},x<0\
2cos(x)e^{-2x},xin[0,1]\
2sin(3x),x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/96eae18012c8cec7fa3195cb7cb16718.png)


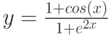
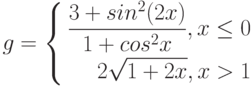
![$$
z=left{
begin{aligned}
sqrt{1+frac{x^{2}}{1+x^{2}}},x<0\
2cos^{2}(x),xin[0,1]\
sqrt{1+|2sin(3x)|^{frac{1}{3}}},x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0e0bd3f1b2b59b98e1d0aac6b9e4e060.png)

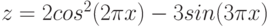
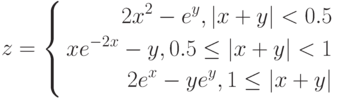
![$$y=sqrt[4]{1+e^{3x}}$$](https://intuit.ru/sites/default/files/tex_cache/38d26ef341d2e8b1539e5db30dd8d0fb.png)
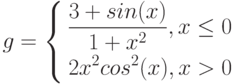
![$$
z=left{
begin{aligned}
|x|^{frac{1}{3}}, x<0\
-2x+frac{x}{1+x}, xin[0,1]\
frac{|3-x|}{1+x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/a336bbbfe739b8a27a42bc552dbba85d.png)
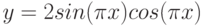

![$$
g=left{
begin{aligned}
sqrt{1+2x^{2}-sin(x)}, xleq0\
frac{2+x}{sqrt[3]{2+e^{-0.1x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/bf750a63e0bf1e99dcdc62a82b5ae8a1.png)
![$$
z=left{
begin{aligned}
frac{1+x}{1+x^{2}}, x<0\
sqrt{1+frac{x}{1+x}}, xin[0,1]\
2|sin(3x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0ba53b8c4d394ba14c7bea0640198a67.png)
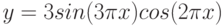
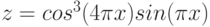
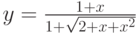
![$$
g=left{
begin{aligned}
sqrt{1+x^{2}}, x<0\
frac{1+x}{1+sqrt[3]{1+e^{-0.2x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c5f92dffe784f474d4780a60de478e2.png)
![$$
z=left{
begin{aligned}
frac{1+x+x^{2}}{1+x^{2}}, x<0\
sqrt{1+frac{2x}{1+x^{2}}}, xin[0,1]\
2|0.5+sin(x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/ea55ab481bac3e0b5e9e38e088173fa3.png)

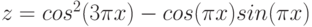
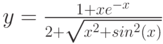
![$$
g=left{
begin{aligned}
sqrt{1+|x|}, xleq0\
frac{1+3x}{2+sqrt[3]{1+x}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5b2dfdc96ef1d57aec714b337234e6ad.png)
![$$
z=left{
begin{aligned}
1+frac{3+x}{1+x^{2}}, x<0\
sqrt{1+(1-x)^{2}},xin[0,1]\
frac{1+x}{1+cos^{2}(x)}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/d7447bf6d7e359d4eca3921d80e719a8.png)
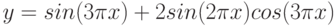

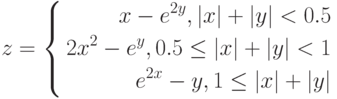
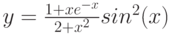
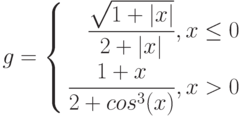
![$$
z=left{
begin{aligned}
frac{1+2x}{1+x^{2}}, x<0\
sin^{2}(x)sqrt{1+x},xin[0,1]\
sin^{2}(x)e^{0.2x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/12bdc437bdea736bdda75cef4a7e722c.png)
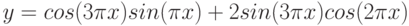
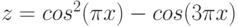
![$х,yin [-1; 1]$$](https://intuit.ru/sites/default/files/tex_cache/1398b5df6d8c02912de8ea030fafac71.png)
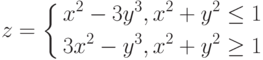
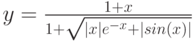
![$$
g=left{
begin{aligned}
sqrt[3]{1+x^{2}}, xleq0\
sin^{2}(x)+frac{1+x}{1+cos^{2}(x)}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5144de1617b0997002fd47d479761ecb.png)
![$$
z=left{
begin{aligned}
frac{|x|}{1+x^{2}}e^{-2x}, x<0\
sqrt{1+x^{2}},xin[0,1]\
frac{1+sin(x)}{1+x}+3x, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/fc2d46b4be846a82407b051315db3f0a.png)