Инфоурок
›
Информатика
›Другие методич. материалы›Практическая работа в MS EXCEL «Красивые графики»
Скачать материал
Скачать материал


- Сейчас обучается 30 человек из 17 регионов


- Сейчас обучается 82 человека из 37 регионов


- Сейчас обучается 21 человек из 13 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 211 007 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
-
Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 28.02.2017
- 1261
- 14
- 28.02.2017
- 701
- 4
- 28.02.2017
- 531
- 0
- 28.02.2017
- 476
- 0
- 28.02.2017
- 476
- 0
- 28.02.2017
- 1354
- 15
- 28.02.2017
- 434
- 6
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Скачать материал
-
28.02.2017
22403
-
DOCX
1.1 мбайт -
452
скачивания -
Рейтинг:
3 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Zilowski Max Jurievich. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 2 года и 6 месяцев
- Подписчики: 0
- Всего просмотров: 434925
-
Всего материалов:
49
Файлы
Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Был в сети 07.04.2023 09:00

Куликовский Максим Юрьевич
преподаватель
10 546
2 245
13.12.2018 08:46
Просмотр содержимого документа
«Практическая работа в MS Excel «Графики»»
Практическая работа «Красивые графики функций»
-
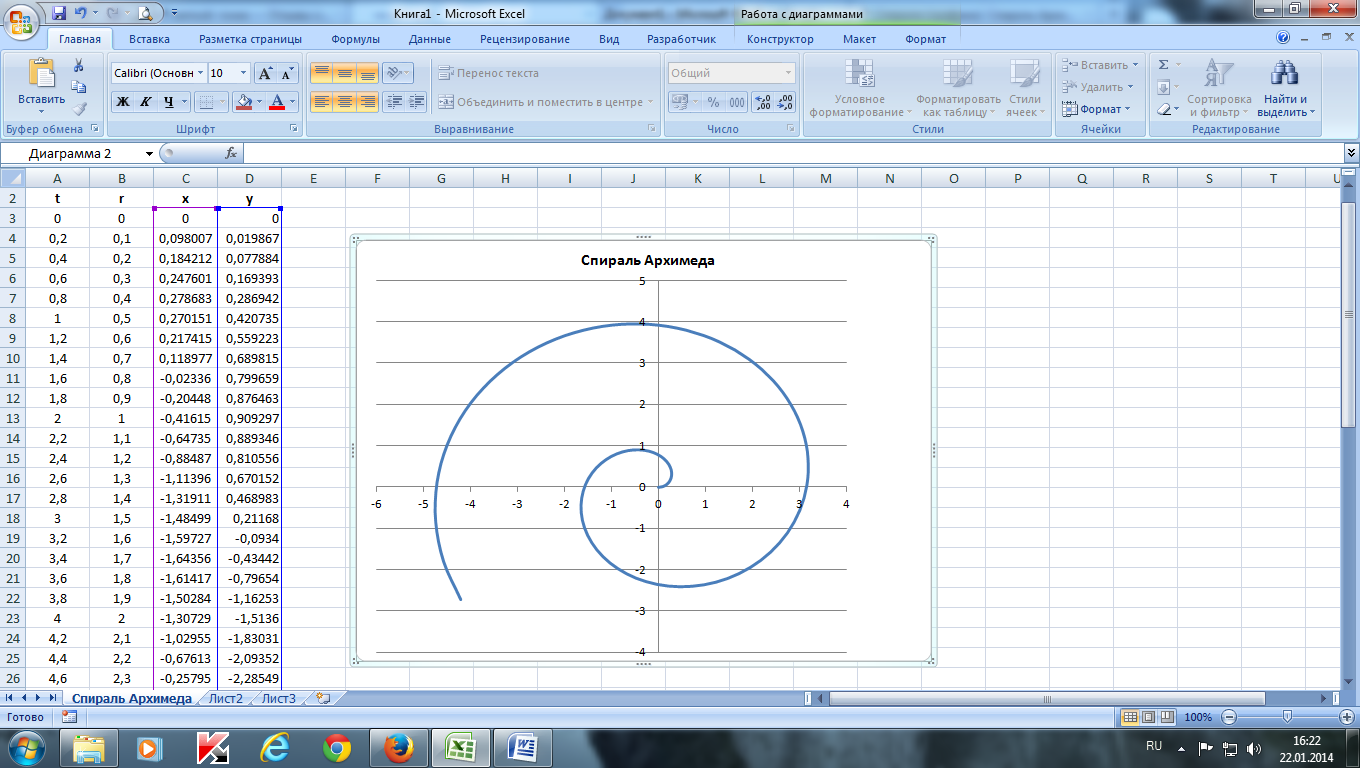
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5*t
— в столбце С – значения х = r*cos(t)
— в столбце D – значения y = r*sin(t)
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
-
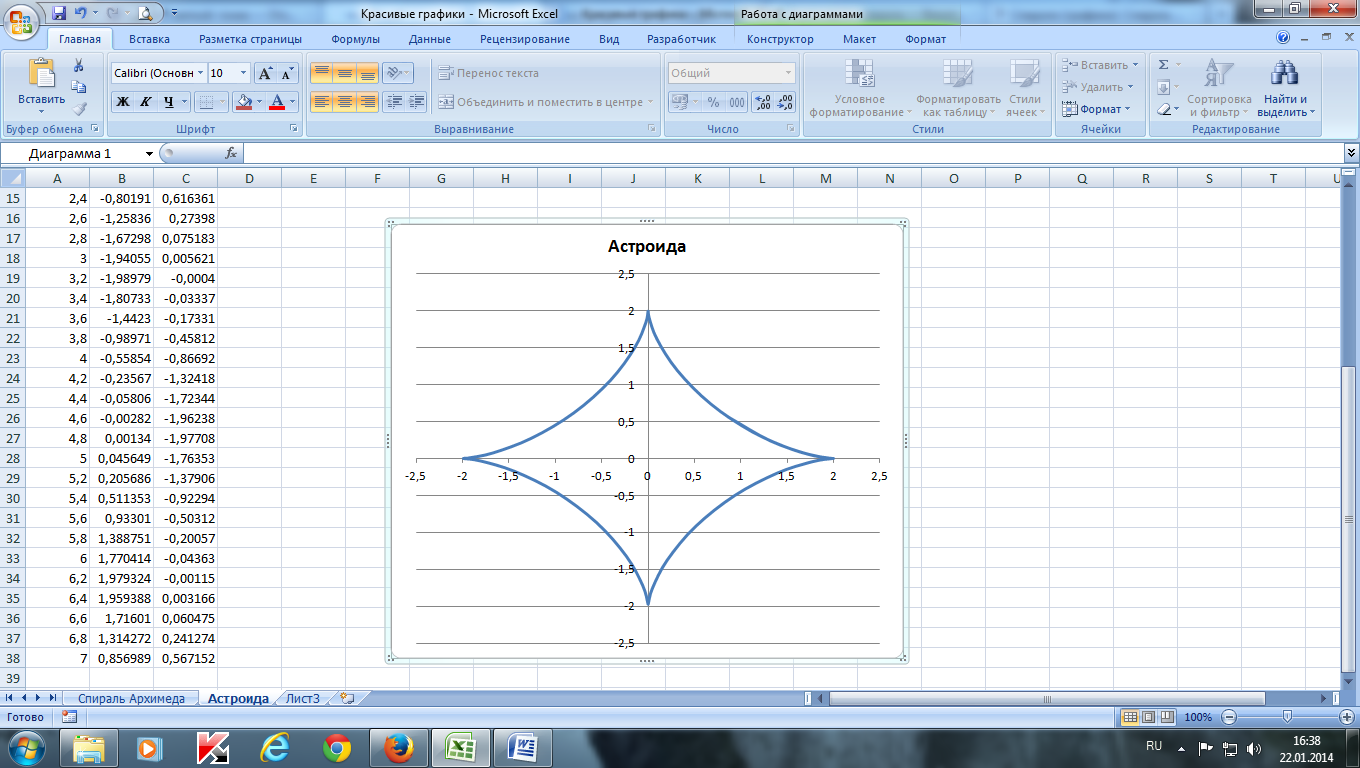
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*(cos (t))3
— в столбце С – значения y = 2*(sin (t))3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
-
Построить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения p = cos(t)–0,5
— в столбце D – значения x = p*cos(t)
— в столбце Е – значения у = p*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми) -
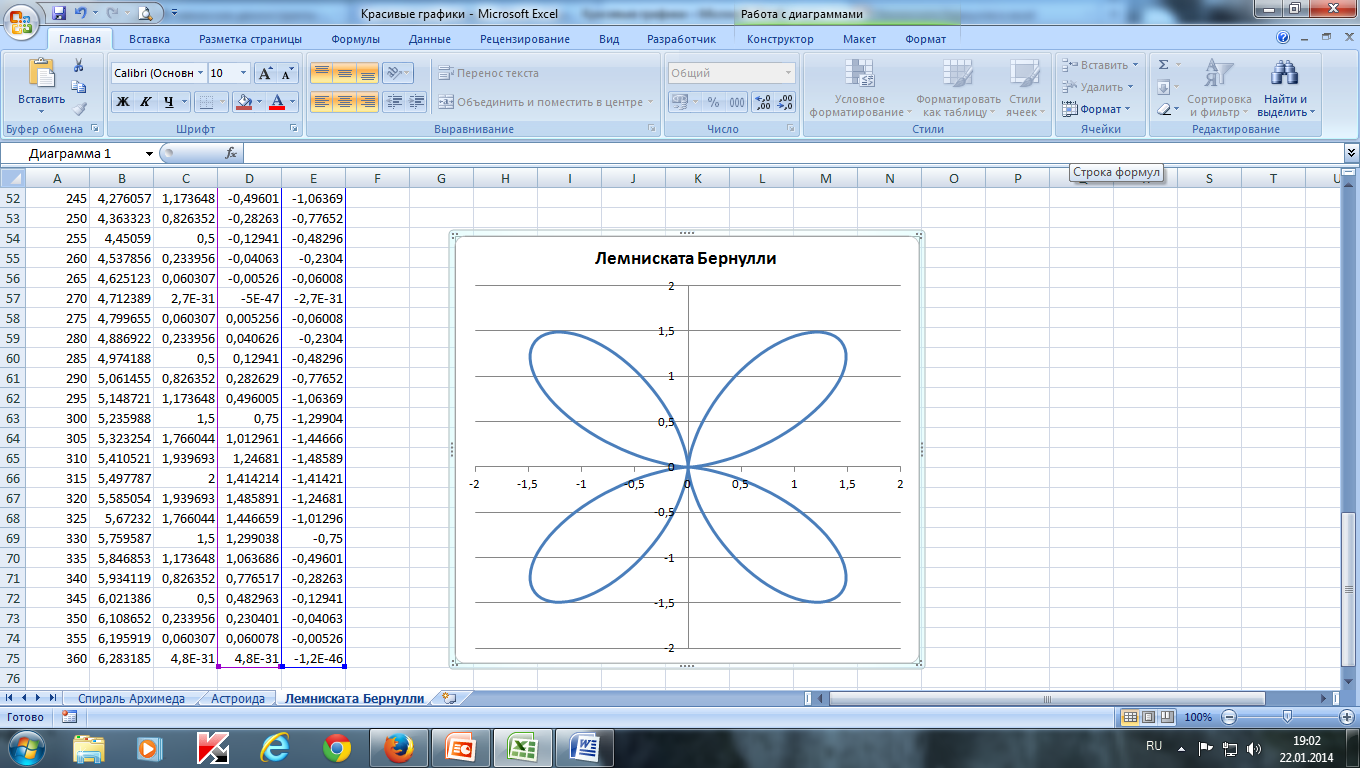
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения r = 2*sin(2*t)2
— в столбце D – значения x = r*cos(t)
— в столбце E – значения y = r*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
-
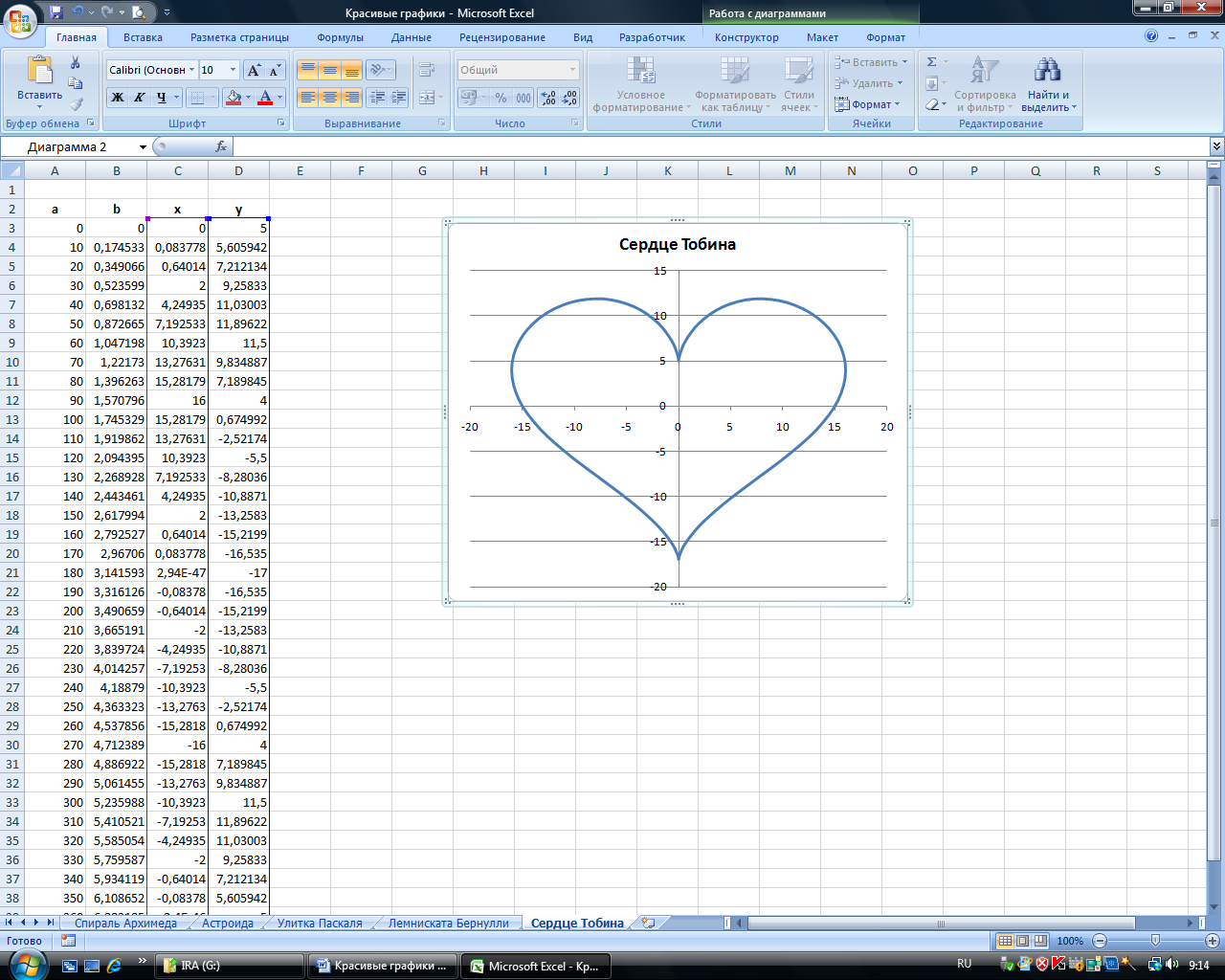
Построить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения x = 16*(sin(t))3
— в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
1 |
|
«Улитка» Паскаля12.11.2014, 15:52. Показов 13615. Ответов 9
Что то запутался в формулах, подскажите как правильно построить! Миниатюры
0 |
|
6597 / 4708 / 1960 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
12.11.2014, 16:14 |
2 |
|
Решениеулитка… Кликните здесь для просмотра всего текста
4 |
|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
12.11.2014, 16:31 [ТС] |
3 |
|
Все разобрался, спасибо!) Добавлено через 13 минут
0 |
|
6597 / 4708 / 1960 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
12.11.2014, 16:38 |
4 |
|
KNIGT, я желтым выделила правильную формулу для координаты y.
0 |
|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
12.11.2014, 16:48 [ТС] |
5 |
|
Это понятно, просто почему в задании одни формулы, у тебя свои, объясни этот момент пожалуйста!
0 |
|
6597 / 4708 / 1960 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
12.11.2014, 17:01 |
6 |
|
в задании ошибка
0 |
|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
12.11.2014, 17:07 [ТС] |
7 |
|
Все, вопрос исчерпан, спасибо еще раз!
0 |
|
0 / 0 / 0 Регистрация: 27.11.2014 Сообщений: 4 |
|
|
22.06.2015, 15:08 |
8 |
|
Krasme, как правильно вписать cos^2? Добавлено через 34 минуты
0 |
|
0 / 0 / 0 Регистрация: 12.12.2018 Сообщений: 1 |
|
|
12.12.2018, 08:49 |
9 |
|
Можете прислать этот файл в электроне? Заранее спасибо) Добавлено через 1 минуту
в задании ошибка Krasme, Можете прислать этот файл в электроне? Заранее спасибо)
0 |
|
Krasme |
|
12.12.2018, 11:04
|
|
Не по теме: druha97, теме более 4-х лет, какие файлы?
0 |
|
Улитка Паскаля |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Расчётно-графисечкие работы в MS Excel Стр. 1 из 13
|
MSExcel. Табулирование функции |
|||||||||
|
Задание: |
Протабулировать функцию y(x) на интервале |
||||||||
|
x [a |
x |
, b ], |
a |
x |
= −π |
2 |
, b = 2π c шагом h |
x |
= 0.1, варианты функций в |
|
x |
x |
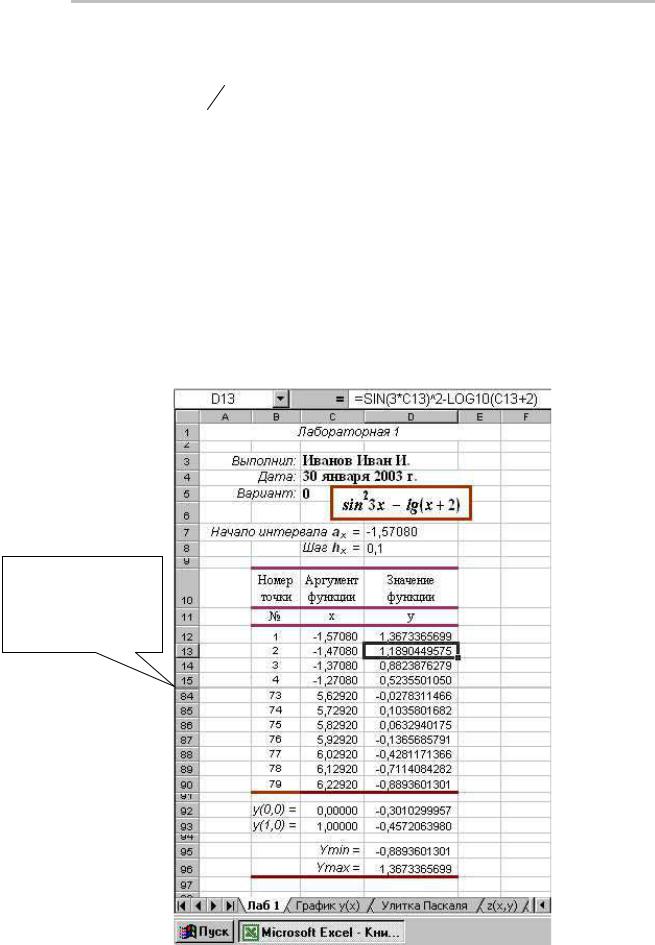
таблице 1 приложения. На защиту лабораторной подготовить лист электронной книги Excel по образцу на рисунке 1.
Ход работы:
1)Запустить программу Excel. Создать документ Книга1. Сохранить в свою папку на жестком диске под оригинальным именем, например, Книга Иванова, переименовать лист Лист1 на Лаб №.
2)Создать заголовок сверху по центру будущей таблицы, используя шрифты помельче, 12 пунктов, Аrial курсив и покрупнее, 14 пунктов, Times полужирный. Выделить название темы лабораторной цветом.
3)Сделать подпись Выполнил, Дата, Вариант. Дата должна пока-
Здесь скрыты строки с 16 по 83 для экономии места на рисунке.
Рисунок 1. Образец оформления лабораторной работы
на листе Excel (для 0-го варианта)
1
|
Расчётно-графисечкие работы в MS Excel |
Стр. 2 из 13 |
зывать текущую дату в заданном полном формате. Вставить свою функцию по варианту в математической нотации как объект MS Equation. Выделить формулу цветной рамкой.
4)Завести отдельные ячейки для начала интервала аx и шага табулирования hx, ячейки D7 и D8 на рисунке 1. Начало интервала определить через функцию ПИ(). Для заполнения диапазона ячеек со значениями аргумента функции использовать абсолютные адреса этих ячеек. В ячейки C7 и C8 вставьте пояснения Начало интервала аx =
иШаг hx =.
5)В строке 10 оформить шапку таблицы: Номер точки, Значение аргумента, Значение функции, и ниже, в строке 11 сокращенно: №, х, у.
6)Заполнение таблицы.
Создание столбца номеров точек. Набрать 1 в В12. Протащить маркер заполнения формул с нажатым Ctrl до 79 в всплывающем окне для получения арифметической прогрессии с приращением 1 в диапазоне ячеек B13:B90.
Создание столбца х. В первую сверху ячейку столбца, С12 набираем ссылку на начало интервала =$D$7 (абсолютный адрес). Под ней в ячейку C13 формулу для расчета следующего значения аргумента через предыдущее =C12+$D$8 (комбинация абсолютных и относительных адресов). Протаскиваем маркер заполнения через диапазон ячеек C14:C90 для получения в нем формул расчета значений аргумента.
Создание столбца y. В ячейку D12 набираем формулу расчета функции по варианту для первой строки таблицы. Для 0-го варианта =sin(3*C12)^2-log10(C12-2) (относительный адрес х). Далее используем технику протаскивания формулы для заполнения диапазона ячеек D13:D90 со значениями функции.
7)Форматирование таблицы. Вывести 5 значащих цифр для значений х и 10 для у. Выровнять по десятичной точке. Применяя условное форматирование, назначить холодный цвет (цвет шрифта, а не заливки), например, синий, отрицательным значениям и красный положительным. Навести рамки в таблице по образцу на рисунке 1.

9)Посчитать максимальное Ymax и минимальное Ymin значения функции в полученном диапазоне ячеек.
10)Сохранить книгу для использования в следующих лабораторных работах.
2
|
Расчётно-графисечкие работы в MS Excel |
Стр. 3 из 13 |
||
|
MS Excel. Построение графиков |
|||
|
Задание 1: Построить графики функции y(x) , |
x [ax , bx ] ломаной |
||
|
линией и сглаженной. |
Задание 2: Построить график кривой f (t) , заданной параметрически, и несколько вложенных в нее кривых.
Задание 3: Построить график трёхмерной поверхности z(x,y).
Вид функций и интервалы выбираются по варианту из таблиц 1, 3 Приложения.
Ход работы:
Построение на одних осях двух графиков функции y(x), x [ax,bx] ломаной линией и сглаженной.
1)График функции в Excel, как и все остальные диаграммы, строится по дискретным значениям. Исходные данные для графика получены в предыдущей лабораторной Лаб №[Книга Иванова].
2)Запускаем Мастера диаграмм. Выбираем тип диаграммы График. Во втором окне мастера указываем исходные данные для
первого ряда Значения: столбец y, Подписи оси Х: столбец x, Имя: набираем с клавиатуры Грубый график. Для второго ряда Значения и Подписи по оси Х те же, Имя: Сглаженный график. Лишние ряды удалить.
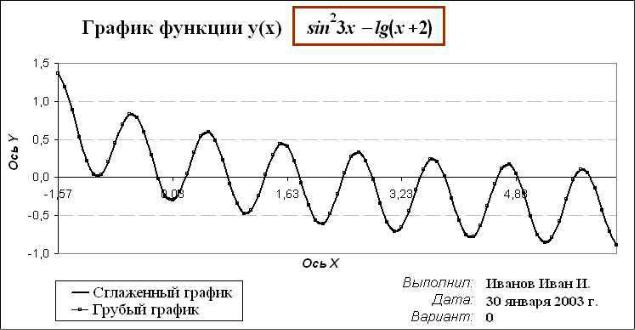
3) Отформатировать график по образцу рисунка 2.
На грубом графике соединить точки отрезками прямых сплошными, тонкими, синего цвета, в точках синие прозрачные квадратные маркеры 5 пунктов. На глаженном графике — соединяющие точки линии сплошные, толстые, красные, сглаженные, без маркеров. Настроить порядок рядов так, чтобы тонкие синие линии были видны на фоне красных. Оформить график заголовком, Equation скопировать с листа Лаб1 на график. Подписать оси как Ось Х и Ось Y. Ось Х провести че-
рез y=0. Проредить деления шкал, в подписях делений отобразить 2-3 цифры, чтобы не загромождали график. Настроить диапазон оси Y от ~Ymin до ~Ymax своей функции. Подпись Выполнил Дата Вариант подставить в шесть надписей из соответствующих ячеек листа. Выровнять и распределить надписи инструментами панели Рисование – Действия – Выровнять, Распределить, Группировка. Убрать серую заливку фона области построения. Линии сетки оставить только горизонтальные по основным делениям оси Y, уменьшить их яркость до штрих светло-серого цвета.
3
|
Расчётно-графисечкие работы в MS Excel |
Стр. 4 из 13 |
Рисунок 2. Образец оформления графика функции y(x)
4) Работа с книгой. Перенести диаграмму на отдельный лист под именем График y(x). Для обзора точности построения ломаной и сглаженной линий отобразить график в максимальном масштабе.
Построение графика кривой f(t), заданной параметрически, и
вложенных кривых при a=0.9, 0.8, 0.7,..
5)Задание выполняется на отдельном листе. Дать листу имя по названию кривой, Улитка Паскаля для 0-го варианта.
6)Предварительно перед построением графика рассчитать таб-
лицу значений x(t,a), y(t,a), комбинируя абсолютные и относительные
адреса ячеек со значениями t и а. Шаг по t подсчитать на этом же листе, чтобы можно было его изменить, если потребуется улучшить качество кривой. Достаточно взять 20 – 30 значений параметра t, диа-
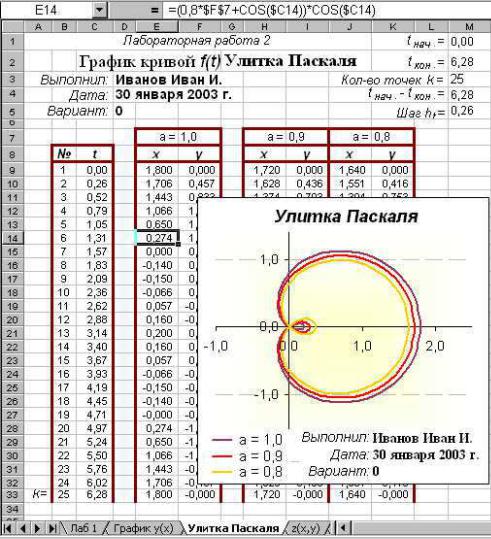
грамма не будет их использовать, они нужны для расчета x,y— координат точек кривой. Примерный вид таблицы рассчитанных для графика данных смотри на рисунке 3. В строке формул показана фор-
мула в выделенной ячейке Е14 для x-координаты шестой точки при
t=1.31 кривой а=1.0.
7) Неоднозначные или с неравномерным шагом по аргументу кривые строятся по точкам на диаграммах типа Точечная. Запускаем Мастера диаграмм, выбираем тип диаграммы Точечная, подтип сглаженные линии без маркеров. Точечная диаграмма — это составная диаграмма, одна точка данных составляется из двух ячеек со значе-
4
|
Расчётно-графисечкие работы в MS Excel |
Стр. 5 из 13 |
ниями её x, y координат. То есть исходными данными для одного ряда будет диапазон из двух столбцов. Обратите внимание, что диапазон ячеек для первой кривой окружен пустыми клетками, чтобы Excel автоматически распознал непрерывный диапазон исходных данных =’Улитка Паскаля’!$E$9:$F$33, необходимо только перед вызовом Мастера диаграмм установить курсор внутри этого диапазона. Тогда окно предварительного просмотра мастера дает удовлетворительную картинку уже на первом шаге. В качестве имени ряда взять значение
а=1.0. На остальных шагах Мастер диаграмм может сделать название диаграммы, заголовки осей, размещение легенды и самой диаграммы.

Рисунок 3. Вид таблицы значений x(t,a), y(t,a) и образец оформления графика f(t)
5
|
Расчётно-графисечкие работы в MS Excel |
Стр. 6 из 13 |
ний подобрать так, чтобы было 3 – 4 подписи на оси, в числовом формате подписей делений ограничиться одним знаком после запятой. Из формата выделенного ряда или ключа легенды настроить толщину и цвет линии – сглаженная, максимальной толщины, цвет красный, убрать маркеры точек.
9) Добавляем на диаграмму вложенные кривые. В окне Исходные данные на вкладке Ряд добавляем ряды, задавая диапазоны зна-
чений x и y. Например, для кривой а=0.9 Значения Х: =’Улитка Паска-
ля’!$H$9:$H$33, Значения Y: =’Улитка Паскаля’!$I$9:$I$33, Имя: =’Улитка Паскаля’!$H$7:$I$7. в окне предварительного просмотра сразу появляются кривые и их имена в легенде. Задать цвета кривым в
стиле Домна, плавно меняющиеся от красного для а=1.0 через оран-
жевые тона до желтого для последнего a.
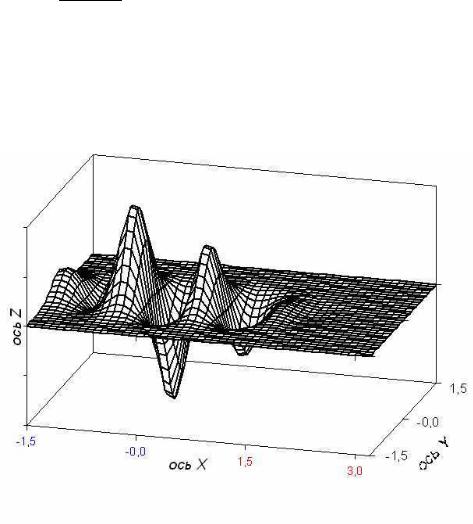
Построение проекции графика функции двух переменных
z( x , y ) = y( x ) , x [—π/2; π], y [—π/2; π/2],
e x 2 +2 y2
где y(x) выбирается по варианту из таблицы 1 приложения. Образец графика поверхности представлен на рисунке 4.
1)Заводим новый лист под именем z(x,y).
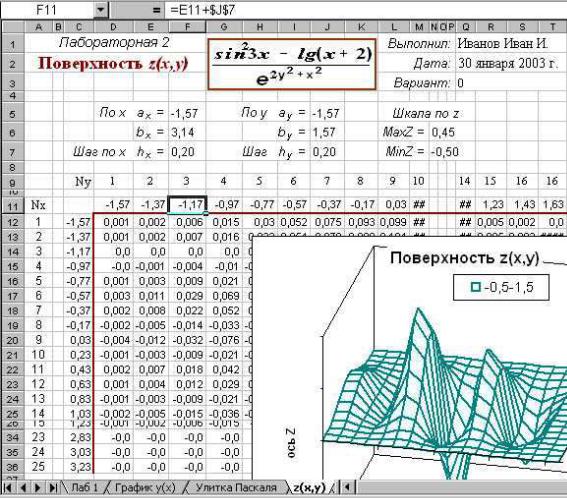
2)Строим таблицу значений x, y и z. Размещаем ее из сообра-
Рисунок 4. 3D-график функции z(x,y)
6
|
Расчётно-графисечкие работы в MS Excel |
Стр. 7 из 13 |
жений удобства работы на листе: чтоб она была компактная, то есть занимала меньше места на листе, чтобы направления роста х и у совпадали с направлением осей правосторонней системы координат. Образец на рисунке 5. Качество картинки зависит от шага, с которым посчитаны значения z(x,y). Поэтому рекомендуется разместить шаги изменения переменных на листе и использовать их адреса при расчете
xи y. Для начала возьмем hx=hy=0.2.
3)Устанавливаем курсор в диапазон значений z, запускаем Мастера диаграмм, заказываем тип Поверхность, единственный существенно трехмерный из стандартных автоформатов. Здесь каждая точка
данных составляется из трех ячеек с х, у и z значениями, где х и у задают равномерную сетку и расположены в первом столбце и первой строке прямоугольного диапазона.
4) Отказываемся от перспективного изображения Диаграмма – Объемный вид – Изометрия. Убираем серый фон стен и основания.
Рисунок 5. Образец расчёта данных для трёхмерного графика z(x,y)
7

|
Расчётно-графисечкие работы в MS Excel |
Стр. 8 из 13 |
Прореживаем деления и подписи осей. Формат оси категорий (оси X) – Шкала – Число категорий между делениями – увеличить — 8. И сразу убираем Пересечения с осью значений между категориями, это используется на гистограммах. Формат оси рядов (оси Y) – Число рядов между делениями – увеличить — 8. Формат оси значений (оси Z) – Вид
–Основные деления – Нет, Шкала – Цена основных делений >> ZmaxZmin, так как они задают не только деления оси значений, но и шкалу раскраски поверхности. И чтобы были деления на оси Z: Вид – Промежуточные деления – Наружу, Шкала — Цена промежуточных делений
–0.5.
5)Ключ легенды является ключом к раскраске поверхности. Выберите способ заливки поверхности посветлее или даже штриховым узором и в тон потемнее цвет линий сетки. Улучшает качество изображения подсветка: Формат ключа легенды — Параметры — Объемное заполнение.
Дополнительные задания
1)Улучшить внешний вид графика y(x) градиентной заливкой области построения.
2)Градиентная заливка центра фигуры, ограниченной замкнутой кривой f(t).
3)Построить поверхность z(x,y) с более мелким шагом по x и y. hx=hy=0.1. Образец на рисунке 4.
|
Приложение |
||||||||||||||||
|
Варианты функции y(x) |
||||||||||||||||
|
Таблица 1 |
||||||||||||||||
|
№ |
Функция |
y(x) |
Схематичный |
|||||||||||||
|
варианта |
график |
|||||||||||||||
|
0 |
sin2 3x |
− lg ( x + 2) |
||||||||||||||
|
2 |
x |
2 |
x |
|||||||||||||
|
1 |
sin |
+ 2 |
− |
|||||||||||||
|
5 |
||||||||||||||||
|
2 |
||||||||||||||||
|
2 |
sin (10 x −20 ) |
+ 0.25 x |
||||||||||||||
|
(x−2) 2 |
||||||||||||||||
|
e 5 |
||||||||||||||||
8

|
Расчётно-графисечкие работы в MS Excel |
Стр. 9 из 13 |
|||||||||||||||||||||||||||||||||||||
|
№ |
Функция y(x) |
Схематичный |
||||||||||||||||||||||||||||||||||||
|
варианта |
график |
|||||||||||||||||||||||||||||||||||||
|
3 |
1 cos |
x |
− sin2 3x |
|||||||||||||||||||||||||||||||||||
|
2 |
3 |
|||||||||||||||||||||||||||||||||||||
|
4 |
sin (10 x −20 ) |
− 0.25 x |
||||||||||||||||||||||||||||||||||||
|
( x−2) 2 |
||||||||||||||||||||||||||||||||||||||
|
e |
5 |
|||||||||||||||||||||||||||||||||||||
|
5 |
cos(x − 8)2 |
+ ln(x + 3)−1.5 |
||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||
|
6 |
cos (x − 8)2 − sin (x + 1) |
− 0.2 |
||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
7 |
1 |
( x + 5) |
2 |
x − 2 |
2 |
|||||||||||||||||||||||||||||||||
|
sin |
+ |
|||||||||||||||||||||||||||||||||||||
|
2 |
2 |
4 |
||||||||||||||||||||||||||||||||||||
|
8 |
sin ( x |
2+ 3) + |
sin 2 x |
|||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
9 |
2 sin 8 x |
+ |
3 cos x |
|||||||||||||||||||||||||||||||||||
|
3 |
4 |
|||||||||||||||||||||||||||||||||||||
|
10 |
cos 5x |
ln |
x + 3 |
|||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
11 |
3 |
2 x + 6 |
2 |
|||||||||||||||||||||||||||||||||||
|
sin |
||||||||||||||||||||||||||||||||||||||
|
x + 3 |
3 |
|||||||||||||||||||||||||||||||||||||
|
( x +2)2 |
+ |
3 |
||||||||||||||||||||||||||||||||||||
|
12 |
cos |
ln |
x |
|||||||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
13 |
cos ((x −5 )2 +1) |
ln(x +2.5 ) |
||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
14 |
sin(x −1)2 |
− 0.1 |
||||||||||||||||||||||||||||||||||||
|
x |
4 |
|||||||||||||||||||||||||||||||||||||
|
e |
||||||||||||||||||||||||||||||||||||||
|
( |
)2 |
|||||||||||||||||||||||||||||||||||||
|
15 |
1 sin |
x+3 |
ln (x +2 ) |
|||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
9

|
Расчётно-графисечкие работы в MS Excel |
Стр. 10 из 13 |
|||||||||||||||||||||||||||||||||||
|
№ |
Функция y(x) |
Схематичный |
||||||||||||||||||||||||||||||||||
|
варианта |
график |
|||||||||||||||||||||||||||||||||||
|
1 |
( |
)2 |
ln |
(x +2 ) |
||||||||||||||||||||||||||||||||
|
16 |
x+3 |
+ |
−1 |
|||||||||||||||||||||||||||||||||
|
2 sin |
2 |
2 |
||||||||||||||||||||||||||||||||||
|
17 |
sin(2(x − 2)2 ) |
− 0.1x |
||||||||||||||||||||||||||||||||||
|
e |
x |
|||||||||||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||||||||
|
18 |
sin10 x + 0.5 |
|||||||||||||||||||||||||||||||||||
|
(x−2) 2 |
||||||||||||||||||||||||||||||||||||
|
e |
5 |
|||||||||||||||||||||||||||||||||||
|
19 |
sin |
x |
− cos2 3x |
|||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||
|
20 |
cos (5 x +10) |
|||||||||||||||||||||||||||||||||||
|
ln (4 x |
+ 8) |
|||||||||||||||||||||||||||||||||||
|
21 |
2 cos 5x − |
x |
+ 1 |
|||||||||||||||||||||||||||||||||
|
3 |
6 |
3 |
||||||||||||||||||||||||||||||||||
|
22 |
2 2cos2( |
x |
+2)2 +2 |
− |
x |
−3 |
||||||||||||||||||||||||||||||
|
2 |
5 |
|||||||||||||||||||||||||||||||||||
|
sin(x − 8)2 |
x − 2 |
|||||||||||||||||||||||||||||||||||
|
23 |
− |
|||||||||||||||||||||||||||||||||||
|
3 |
5 |
|||||||||||||||||||||||||||||||||||
|
24 |
log (x+4) − 1 |
(sin ( |
x+6 )3+5) |
|||||||||||||||||||||||||||||||||
|
2 |
2 |
3 |
||||||||||||||||||||||||||||||||||
|
25 |
0.2 x − cos 2 3 x |
|||||||||||||||||||||||||||||||||||
Контрольные ответы
|
Таблица 2 |
||||
|
№ |
y(x=0.0) |
y(x=1.0) |
Ymin |
Ymax |
|
вари- |
||||
|
анта |
||||
|
0 |
-0,3010299957 |
-0,4572063980 |
-0,8893601301 |
1,3673365699 |
|
1 |
0,5727500169 |
-0,1988991396 |
-1,2056587561 |
1,3050593587 |
10
Соседние файлы в папке Лева_2.0
- #
14.03.201658.79 Кб23Kniga3.xlsx
- #
14.03.201641.89 Кб25Kniga_Dukhovny.xlsx
- #
- #
- #
14.03.201615.48 Кб18Суперплоховсе.xlsm
Содержание
- Как построить улитку паскаля в excel
- «Улитка» Паскаля
- Решение
- Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
- Практическая работа в MS Excel «Графики»
- Просмотр содержимого документа «Практическая работа в MS Excel «Графики»»
- Практическая работа в MS EXCEL «Красивые графики»
- Лемниската бернулли уравнение и график в excel
- Формула Бернулли в Excel
- Схема независимых испытаний
- Формула Бернулли в Эксель
- Примеры решений задач
- Плоские алгебраические кривые в EXCEL
- Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Как построить улитку паскаля в excel
«Улитка» Паскаля
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Улитка паскаля
Люди добрые помогите построить улитку паскаля. Улитка Паскаля, 0 «»;O4:R4=0;O4:R4<>«»)> — которая в ячейках H4:K4, O4:R4 — выбирает.
Как сделать: если во всех ячейках диапазона знач.=»выполнено», то в данной ячейке тоже «выполнено» иначе «в работе»
Прилагаю файл. В ячейке G17 формула, в которой надо упростить условие: Если в диапазоне ячеек.
Сообщение было отмечено chumich как решение
Решение
Все разобрался, спасибо!)
Добавлено через 13 минут
У тебя какая то другая формула!
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Источник
Практическая работа в MS Excel «Графики»

Работа в формате .docx
Просмотр содержимого документа
«Практическая работа в MS Excel «Графики»»
Практическая работа «Красивые графики функций»

Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5*t
— в столбце С – значения х = r*cos(t)
— в столбце D – значения y = r*sin(t)
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)

Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*(cos (t)) 3
— в столбце С – значения y = 2*(sin (t)) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
Построить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения p = cos(t)–0,5
— в столбце D – значения x = p*cos(t)
— в столбце Е – значения у = p*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)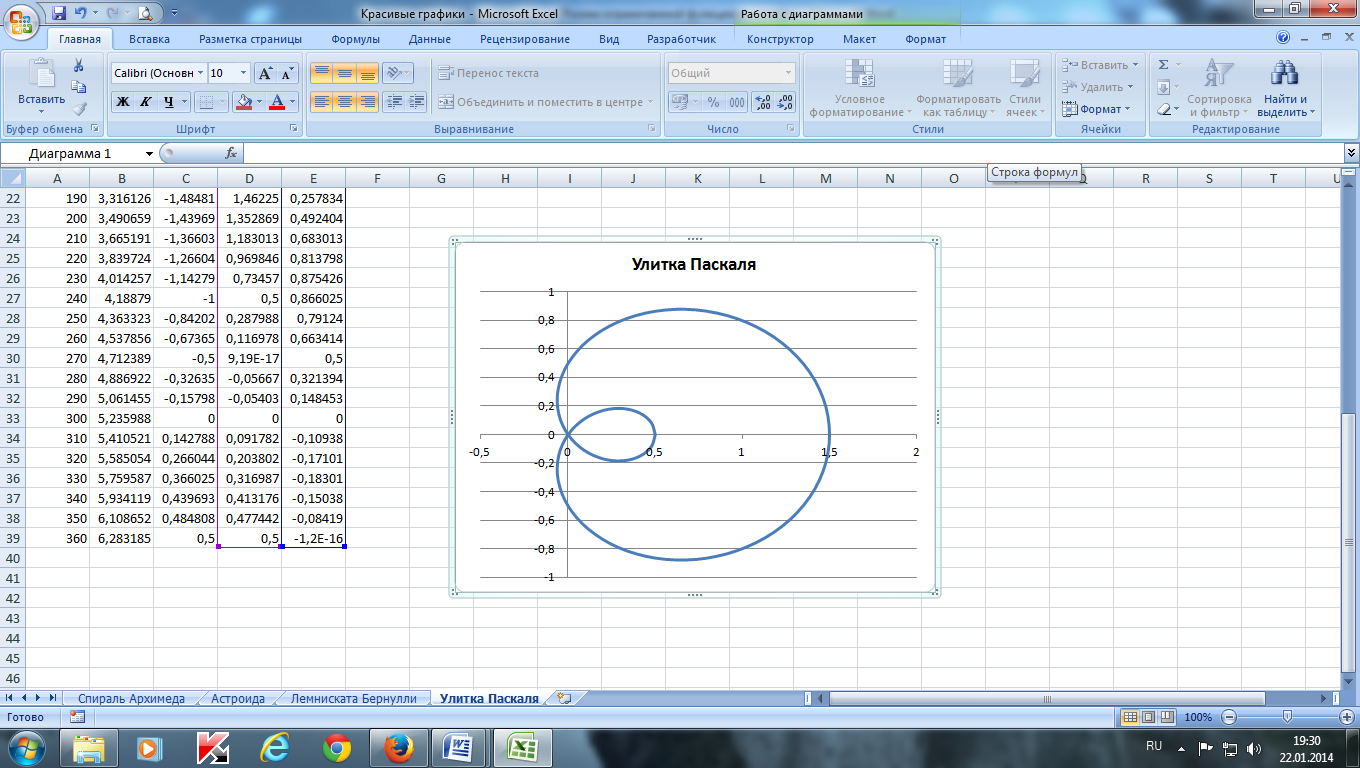
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения r = 2*sin(2*t) 2
— в столбце D – значения x = r*cos(t)
— в столбце E – значения y = r*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
Построить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения x = 16*(sin(t)) 3
— в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Источник
Практическая работа в MS EXCEL «Красивые графики»
Практическая работа «Красивые графики функций»
1) Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
2) Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
3) 

— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
4) Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
5) 
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Источник
Лемниската бернулли уравнение и график в excel
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^ =C_n^k cdot p^k cdot q^ . qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^ $$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_ ^ C_n^i cdot p^i cdot q^ $$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_ ^ C_n^i cdot p^i cdot q^ $$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_ ^ C_n^i cdot p^i cdot q^ $$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^ $$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_ ^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_ ^6 cdot 0,75^6 cdot 0,25^1+C_ ^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_ (k)=C_ ^k cdot 0,5^kcdot 0,5^ =C_ ^k cdot 0,5^ $$ Приступим к вычислениям:
$$1. P_ (2)=C_ ^2 cdot 0,5^ = frac cdot 0,5^ approx 0,044.$$ $$2. P_ (4)+P_ (5)=C_ ^4 cdot 0,5^ + C_ ^5 cdot 0,5^ =left( frac + frac right)cdot 0,5^ approx 0,451.$$ $$3. P_ (0)+P_ (1)+P_ (2)=C_ ^0 cdot 0,5^ + C_ ^1 cdot 0,5^ + C_ ^2 cdot 0,5^ =left( 1+10+ frac right)cdot 0,5^ approx 0,055.$$ $$4. P_ (7)+P_ (8)+P_ (9)+P_ (10)=\ = C_ ^7 cdot 0,5^ + C_ ^8 cdot 0,5^ + C_ ^9 cdot 0,5^ + C_ ^10 cdot 0,5^ =\=left(frac + frac + 10 +1right)cdot 0,5^ approx 0,172.$$ $$5. P_ (ge 1)=1-P_ (0)=1-C_ ^0 cdot 0,5^ = 1- 0,5^ approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:
Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.
Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
- Группы статей
- Диаграммы и графики
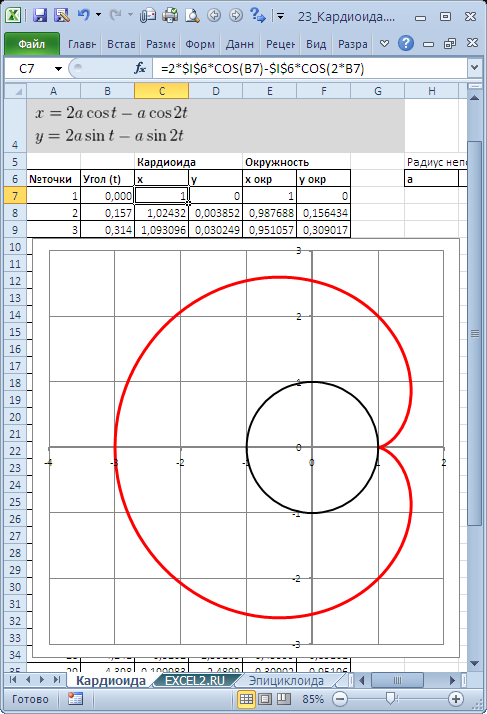
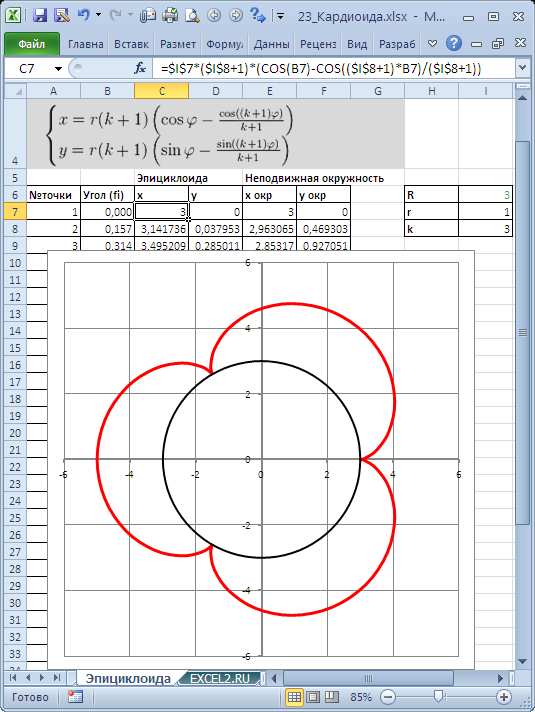
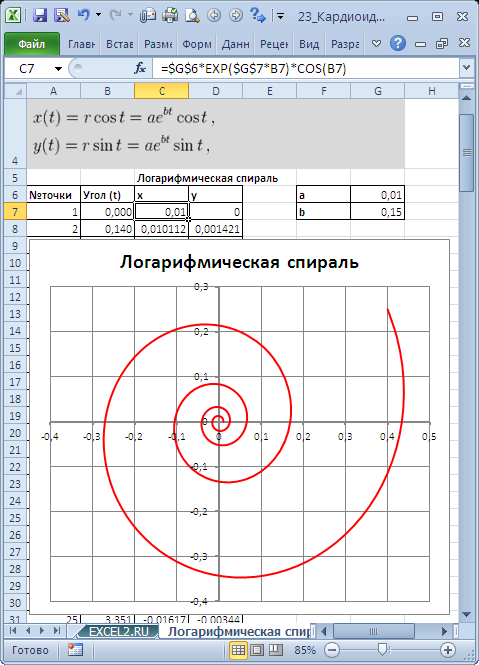
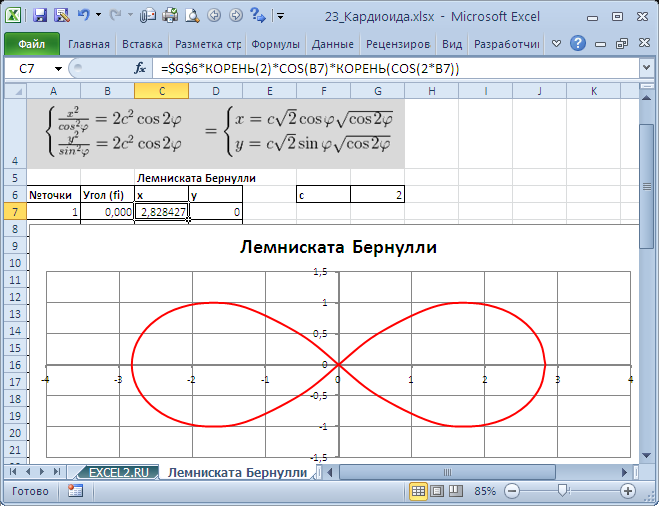
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Источник
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
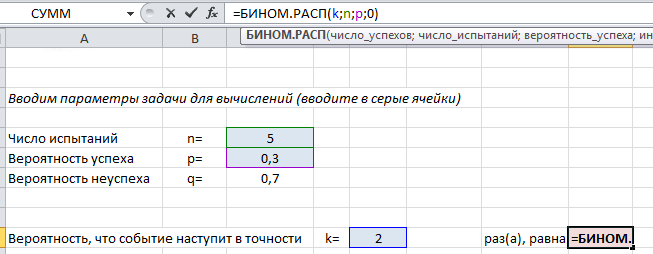
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
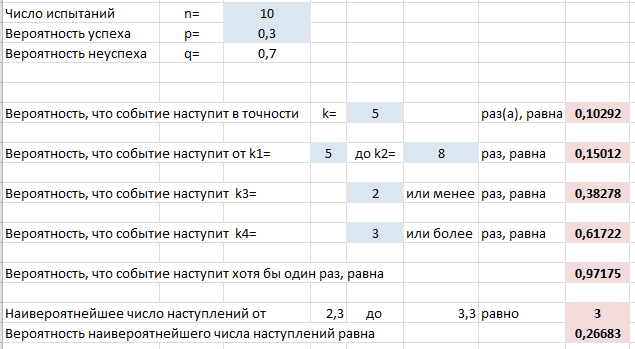
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
-
Группы статей
- Диаграммы и графики
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
источники:
http://excel2.ru/articles/ploskie-algebraicheskie-krivye-v-ms-excel
http://pedsovet.su/excel/48255_krasivye_grafiki_v_excel




 Сообщение было отмечено chumich как решение
Сообщение было отмечено chumich как решение



 _xlfn ……
_xlfn ……