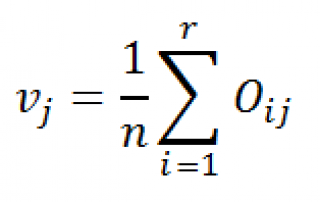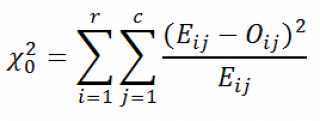Для решения действительно важных исследовательских задач нужно пользоваться специализированными статистическими пакетами, но временами под рукой оказываются только офисные приложения. Табличный редактор Excel включает в себя ряд полезных инструментов, при помощи которых можно удовлетворительно решать простые задачи, стоящие перед социологом. Например, сводные таблицы дают возможность построить таблицу сопряженности с учетом взвешивания массива. Предположим, на одном из листов рабочей книги размещены данные опроса, причем в первой строке указаны имена переменных (В1, В2, И3 и т.д.). Добавьте к данным еще один столбец, в котором будут храниться весовые коэффициенты для наблюдений (если все респонденты имеют одинаковый вес, в нем будут находиться единицы). Пусть этот столбец имеет имя ВЕС. Теперь выберите ленту Вставка, Сводная таблица, Сводная таблица. В появившемся диалоговом окне выберите, если необходимо, таблицу или диапазон, в которых находятся данные, а также лист, на который будет помещена созданная таблица сопряженности, затем щелкните кнопку ОК. В появившемся списке полей сводной таблицы перетащите строковую переменную (например, В1) в поле Названия строк, столбцовую переменную (скажем, В2) в список Названия столбцов, а имя весовой переменной в поле Значения. На листе появится таблица с частотами и итогами. Чтобы заказать проценты, щелкните по элементу Сумма по полю ВЕС и в меню выберите пункт Параметры полей значений. Перейдите на вкладку Дополнительные вычисления и в выпадающем списке дополнительных вычислений установите Доля от суммы по строке, столбцу или Доля от общей суммы
Добавил:
Вуз:
Предмет:
Файл:
Старый материал / Лабораторная работа №8 — Анализ качественных признаков.doc
Скачиваний:
41
Добавлен:
21.08.2018
Размер:
1.95 Mб
Скачать
Ход выполнения работы
-
Для решения поставленной задачи
необходимо сформировать таблицу
сопряженности (в нашем случае это
таблица 2х2). Для этого воспользуемся
возможностями сводной таблицы MS
Excel. -
Скопируем исходную таблицу
на лист 1 программы
MS Excel
-
Выделите всю таблицу.
-
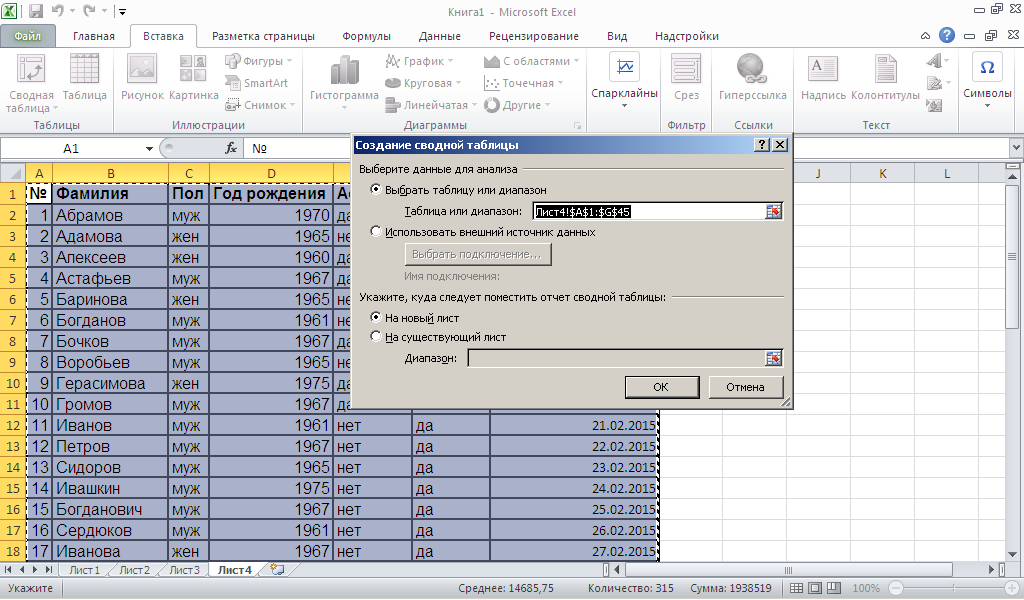
Далее: вкладка
Вставка-Сводная таблица- Сводная
таблица-Ok
-
В появившемся макете сводной
таблице укажите название строк,
столбцов и значений
так, как показано на иллюстрациях ниже.
-
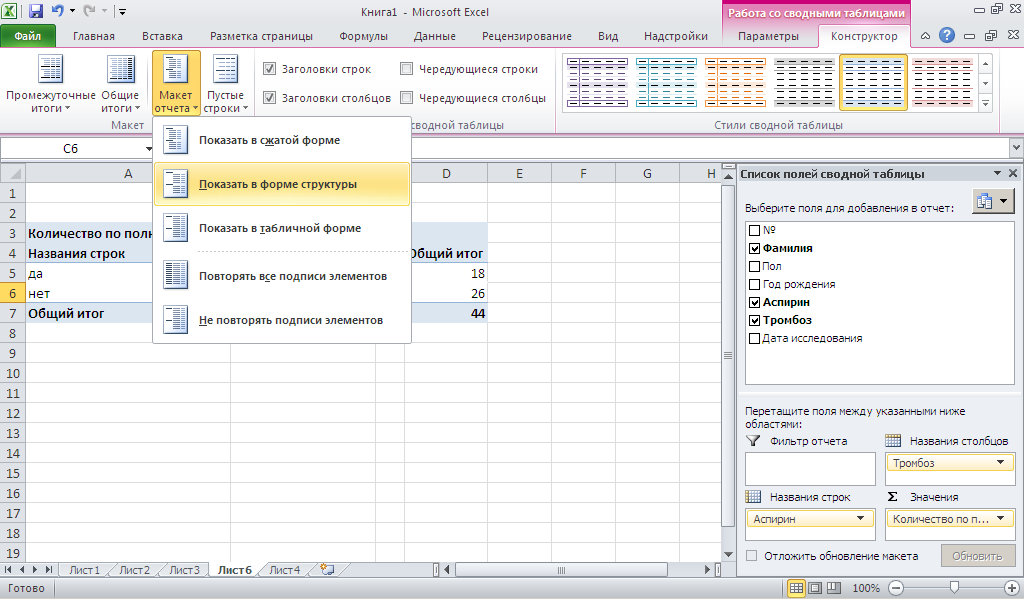
Для большей наглядности
сводной таблицы во вкладке Конструктор
укажите Макет отчета
как Показать в форме
структуры.
-
Получившуюся сводную таблицу
(таблица сопряженности) скопируйте в
отдельный документ Word
и при необходимости доофйормите ее.
-
В результате предыдущих
действий вы получили таблицу сопряженности
2х2, впринципе ее можно было бы получить
и вручную, но возможности сводной
таблицы Excel
значительно упрощают процесс построения.
Таблица сопряженности показывает
количество человек с тромбозом, которым
был введен аспирин и количество больных
тромбозом, которым вместо аспирина
давали плацебо. Как видно из таблицы
налицо явные преимущества аспирина.
Теперь видя только нужные для анализа
цифры необходимо оценить статистическую
значимость видимых различий. Воспользуемся
критерием хи-квадрат. -
Откройте программу Statistica,
создайте новый документ. -
Далее: Анализ-Непараметрическая
статистика-Таблицы 2х2…..
-
В появившемся окне введите
значения из полученной таблицы
сопряженности
-
Полученная таблица результата
анализа. Так как в нашем случае анализ
проводился таблицы сопряженности 2х2,
то необходимо учитывать поправку
Йейтса. Исходя из полученных значений
критерия хи-квадрат и вероятности p,
следует заключить, что видимые различия
в клетках таблицы сопряженности значимы.
Поэтому нулевая гипотеза отвергается.
Аспирин действительно положительно
влияет на снижение вероятности
возникновения тромбоза шунта.
Результат скопируйте в
документ Word.
Сделайте ваш собственный вывод.
-
Так как в подобного рода
анализе часто возникает потребность
в указании процентного соотношения в
таблице сопряженности, то вновь вернемся
к сводной таблице Excel.
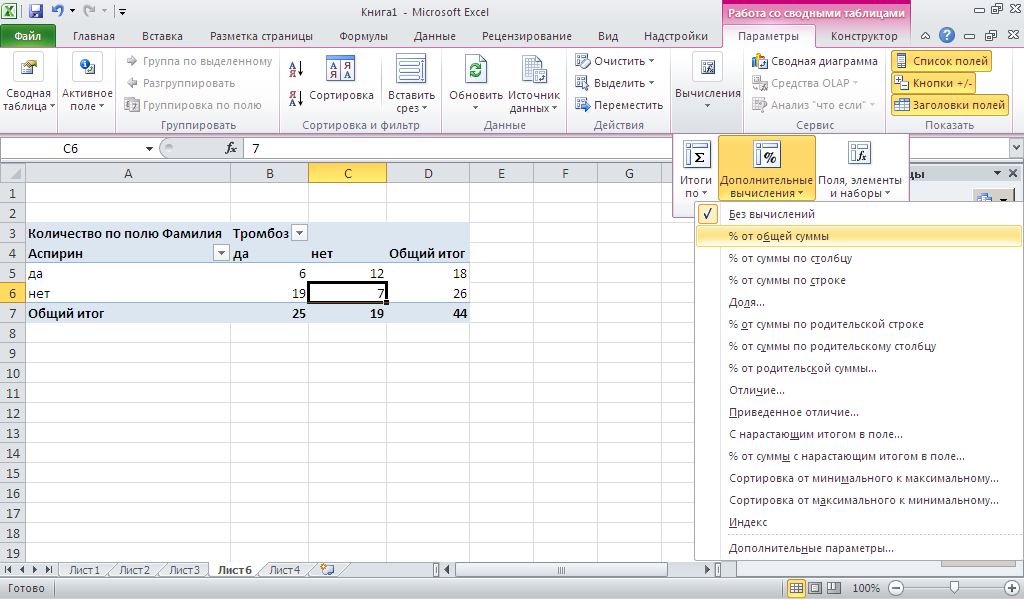
И во вкладке Параметры
выберите Вычисления-Дополнительные
вычисления-%от общей суммы.
-
Полученный результат
скопируйте в документ Word
-
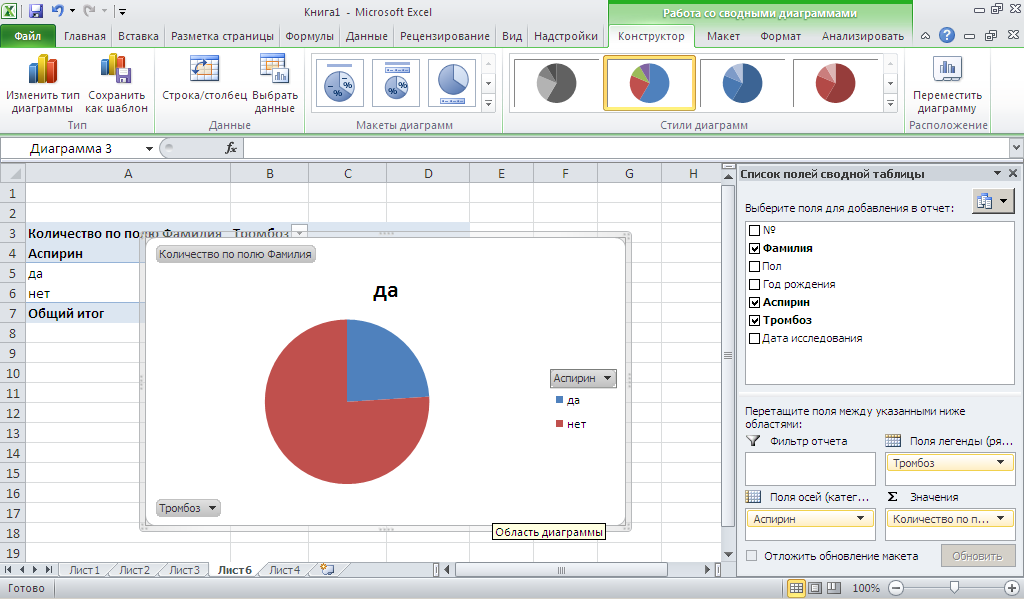
Постройте три типа сводных
диаграмм как указано ниже. Параметры-Сводная
диаграмма. Скопируйте
в отчет.
-
Сделайте выводы о проделанном анализе.
14
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
- #
В предыдущей заметке таблицы и диаграммы применялись для представления числовых данных. Однако часто данные носят не числовой, а категориальный характер. В этой заметке изучаются способы организации и представления категорийных данных в виде таблиц и диаграмм. [1]
Вернемся к анализу доходности взаимных фондов. Кроме среднегодовой доходности фонды характеризуются риском, связанном с инвестированием в эти фонды. Взаимные фонды могут иметь очень низкий, низкий, средний, высокий и очень высокий риск. При работе с категорийными переменными данные сначала заносятся в сводную таблицу, а затем графически представляются в виде гистограмм, круговых диаграмм или диаграмм Парето.
Сводная таблица
По внешнему виду сводная таблица для категорийных данных напоминает распределение частот для числовых данных. Чтобы проиллюстрировать процесс ее построения, рассмотрим данные о классификации взаимных фондов по уровню риска (рис. 1).
Рис. 1. Уровень риска 259 взаимных фондов. Частоты и процентные доли
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Линейчатая диаграмма
Информацию, содержащуюся в таблице (рис. 1), можно представить в виде линейчатой диаграммы (рис. 2), в которой каждая категория элементов изображается в виде столбца. Высота столбца равна частоте или процентной доле элементов выборки, относящихся к данной категории.
Рис. 2. Линейчатая диаграмма, отображающая уровень риска фондов
Круговая диаграмма
Существует еще один весьма популярный способ отображения информации, содержащейся в сводной таблице, — круговая диаграмма (рис. 3). При построении круговых диаграмм используется тот факт, что угол окружности равен 360°. Круг разделяется на секторы, углы которых соответствуют процентным долям каждой категории. Например, на рис. 3 показан сектор, соответствующий доле взаимных фондов с низким риском, которая равна 29,3%. При построении круговой диаграммы величина 360° умножается на 0,293. В результате образуется сектор, угол которого равен 105,6°. Как видим, круговая диаграмма позволяет отразить долю каждой категории в общем «пироге».
Рис. 3. Круговая диаграмма, отображающая уровень риска фондов
Цель графического представления данных — точность и ясность. Например, рис. 2 и 3 отображают одинаковую информацию. Какой из двух видов диаграмм предпочесть — дело вкуса. В частности, некоторые исследования показывают, что люди труднее воспринимают круговые диаграммы. Оказывается, человеку намного проще интерпретировать разницу между высотами столбцов в линейчатых диаграммах, чем углы секторов в круговых диаграммах. Обратите внимание на то, что по рис. 3 нелегко определить, какая из категорий фондов больше — с низким, средним или высоким уровнем риска. В то же время по линейчатой диаграмме легко определить, что доля фондов со средним уровнем риска больше, чем доли фондов с высоким и низким уровнями риска.
С другой стороны, круговые диаграммы четко демонстрируют, что сумма долей всех категорий равна 100%. Таким образом, выбор диаграммы является субъективным и часто зависит от предпочтений пользователя. Если необходимо сравнивать доли категорий, лучше применять линейчатые диаграммы. Если важно продемонстрировать вклад долей отдельных категорий в общий «пирог», лучше использовать круговые диаграммы.
Диаграмма Парето
Существует более информативный способ графического изображения категорийных данных — диаграмма Парето. Она особенно полезна, если количество категорий велико. Диаграмма Парето — это особая разновидность вертикальной диаграммы, в которой категории приводятся в порядке убывания их частот одновременно с полигоном накопленных частот. Это позволяет выделить наиболее важные категории из большого количества менее значимых групп. Диаграмма Парето получила широкое распространение при анализе производственных процессов и контроле качества (см., например, АВС-анализ и принцип Парето для бизнеса).
Например, для построения Диаграммы Парето на основе данных рис. 1, необходимо отсортировать строки по убыванию, и одновременно отобразить как количество фондов в каждой категории, так и интегральный процент (рис. 4).
Рис. 4. Диаграмма Парето, отображающая специфику фондов
Надо отметить, что в Excel2013 предоставляется стандартная возможность построения таких комбинированных диаграмм (рис. 5). Если же у вас Excel2007, то вам придется помучиться (см., например, Диаграмма Excel с двумя осями ординат).
Рис. 5. Построение комбинированной диаграммы
Представление двумерных категорийных данных
Довольно часто необходимо анализировать пары категорийных переменных. Для этого используют таблицы сопряженности признаков и нормированные диаграммы.
Таблица сопряженности признаков. Чтобы можно было одновременно анализировать две категорийные переменные, образующие пару, используются таблицы перекрестной классификации с двумя входами, или таблицы сопряженности признаков (их также называют факторными таблицами). Например, может возникнуть вопрос: существует ли зависимость между уровнем риска и платой, взимаемой фондами за осуществление продаж своих акций (рис. 6)?
Рис. 6. Таблица сопряженности признаков, содержащая данные об уровне риска и плате, взимаемой фондами за осуществление продаж своих акций
Чтобы выявить возможную зависимость между специализацией фонда и прейскурантом его комиссионных сборов, эти результаты сначала преобразуют в процентные доли, используя следующие три базиса:
- общую сумму (259 взаимных фондов);
- сумму по строкам (фонды, взимающие плату за продажу своих акций, и фонды без брокерской комиссии);
- сумму по столбцам (пять уровней риска).
Удобную возможность построения таблиц сопряжения дает опция Excel Сводные таблицы. Для начала нужно представить исходные данные в виде строк, в каждой из которых содержатся все исследуемые параметры (рис. 7). Далее выделяем область В3:D13, и проходим по меню Вставка → Сводная таблица. В открывшемся окне Создание сводной таблицы указываем на существующий лист и в поле Диапазон кликаем на ячейку, где мы хотели расположить левый верхний угол сводной таблицы, кликаем Ok. (Если вы хотите разместить сводную таблицу на отдельном листе, сразу после открытия окна Создание сводной таблицы, кликните Ok.)
Рис. 7. Построение сводной таблицы
Для настройки сводной таблицы просто перетащите строки из верхней части области Поля сводной таблицы в нижнюю, как указано на рис. 8.
Рис. 8. Настройка полей сводной таблицы
Логично расположить строки в сводной таблицы в порядке возрастания (или убывания) степени риска. Для этого надо по очереди выбрать каждую строку, выбрав ячейку в области Название строк (например, Очень высокий), кликнуть правой кнопкой мыши, и выбрать в контекстном меню Переместить, указав, куда именно переместить выбранную строку (рис. 9).
Рис. 9. Перетаскивание строк сводной таблицы
И, наконец, мы можем выбрать базис для анализа процентных долей. Встаньет в любую ячейку в области значений (рис. 10), кликните правой кнопкой мыши, и в открывшемся контекстном меню выберите Параметры полей значений.
Рис. 10. Параметр поля значений
В окне Параметры полей значений перейдите на закладку Дополнительные вычисления, и выберите одну из опций (рис. 11):
- % от общей суммы
- % от суммы по столбцу
- % от суммы по строке
Рис. 11. Выбор базиса процентной доли
Поскольку нас интересует корреляция между степенью риска и наличием комиссии, уместно выбрать опцию % от суммы по строке. Мы увидим, подчиняется ли закономерности доля фондов, взимающих комиссию, при переходе от фондов с очень высоким риском к фондам с очень низким риском (рис. 12). Явной тенденции обнаружить не удалось. [2]
Рис. 12. Доля фондов, взимающих комиссию по уровням риска
Нормированные диаграммы
Для визуализации двумерных категорийных данных часто строят нормированные диаграммы, то есть диаграммы, в которых высота столбиков равна 1 (100%) вне зависимости от общего числа случаев в той или иной категории. На рис. 13 представлен пример такой диаграммы (ось ординат охватывает значения от 0% до 100%, просто, масштаб диаграммы выбран таким образом, что отражается лишь часть этой области). Четко видна закономерность: доля трафика google выросла летом – осенью 2012 г. с 40 до 55%, а затем вновь упала до 40% (для меня остается загадкой, с чем это связано :)).
Рис. 13. Соотношение вклада google и yandex в поисковый трафик сайта baguzin.ru
Предыдущая заметка Представление категорийных данных в виде таблиц и диаграмм
Следующая заметка Искусство графического представления данных
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 124–138
[2] Любопытно, что авторы книги такую закономерность (на тех же исходных данных) увидели 🙂
Критерий независимости хи-квадрат используется для определения связи между двумя категориальными переменными. Примерами пар категориальных переменных являются: Семейное положение vs. Уровень занятости респондента; Порода собак vs. Профессия хозяина, Уровень з/п vs. Специализация инженера и др. При вычислении критерия независимости проверяется гипотеза о том, что между переменными связи нет. Вычисления будем производить с помощью функции MS EXCEL 2010
ХИ2.ТЕСТ()
и обычными формулами.
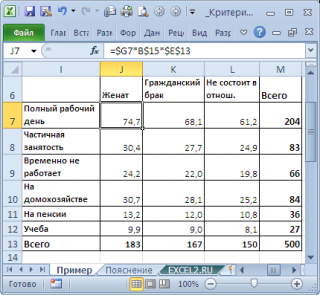
Предположим у нас есть
выборка
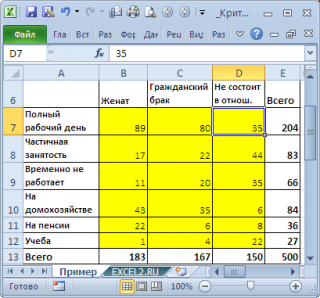
данных, представляющая результат опроса 500 человек. Людям задавалось 2 вопроса: про их семейное положение (женаты, гражданский брак, не состоят в отношениях) и их уровень занятости (полный рабочий день, частичная занятость, временно не работает, на домохозяйстве, на пенсии, учеба). Все ответы поместили в таблицу:
Данная таблица называется
таблицей сопряжённости признаков
(или факторной таблицей, англ. Contingency table). Элементы на пересечении строк и столбцов таблицы обычно обозначают O
ij
(от англ. Observed, т.е. наблюденные, фактические частоты).
Нас интересует вопрос «Влияет ли Семейное положение на Занятость?», т.е. существует ли зависимость между двумя методами классификации
выборки
?
При
проверке гипотез
такого вида обычно принимают, что
нулевая гипотеза
утверждает об отсутствии зависимости способов классификации.
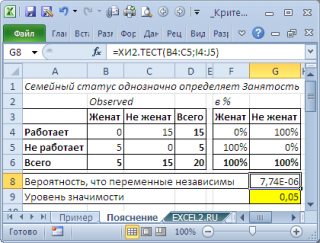
Рассмотрим предельные случаи. Примером полной зависимости двух категориальных переменных является вот такой результат опроса:
В этом случае семейное положение однозначно определяет занятость (см.
файл примера лист Пояснение
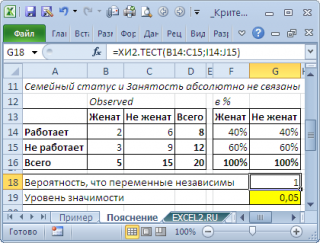
). И наоборот, примером полной независимости является другой результат опроса:
Обратите внимание, что процент занятости в этом случае не зависит от семейного положения (одинаков для женатых и не женатых). Это как раз совпадает с формулировкой
нулевой гипотезы
. Если
нулевая гипотеза
справедлива, то результаты опроса должны были бы так распределиться в таблице, что процент занятых был бы одинаковым независимо от семейного положения. Используя это, вычислим результаты опроса, которые соответствуют
нулевой гипотезе
(см.
файл примера лист Пример
).
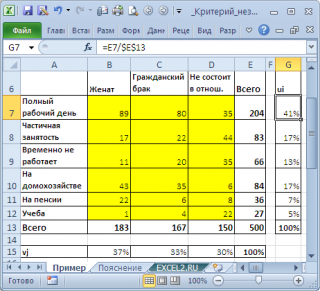
Сначала вычислим оценку вероятности, того, что элемент
выборки
будет иметь определенную занятость (см. столбец u
i
):
где
с
– количество столбцов (columns), равное количеству уровней переменной «Семейное положение».
Затем вычислим оценку вероятности, того, что элемент
выборки
будет иметь определенное семейное положение (см. строку v
j
).
где
r
– количество строк (rows), равное количеству уровней переменной «Занятость».
Теоретическая частота для каждой ячейки E
ij
(от англ. Expected, т.е. ожидаемая частота) в случае независимости переменных вычисляется по формуле: E
ij
=n* u
i
* v
j
Известно, что статистика Х
2
0
при больших n имеет приблизительно
ХИ2-распределение
с (r-1)(c-1) степенями свободы (df – degrees of freedom):
Примечание
: Вышеуказанная статистика при с=1 используется для вычисления
критерия согласия Пирсона ХИ-квадрат
(см. статью
Проверка гипотез критерием хи-квадрат Пирсона в MS EXCEL
).
Если вычисленное на основе
выборки
значение этой статистики «слишком большое» (больше порогового), то
нулевая гипотеза
отвергается. Пороговое значение вычисляется на основании
уровня значимости
, например с помощью формулы
=ХИ2.ОБР.ПХ(0,05; df)
.
Примечание
:
Уровень значимости
обычно принимается равным 0,1; 0,05; 0,01.
При
проверке гипотезы
также удобно вычислять
p-значение
, которое мы сравниваем с
уровнем значимости
.
p
-значение
рассчитывается с использованием
ХИ2-распределения
с (r-1)*(c-1)=df степеней свободы.
Если вероятность, того что случайная величина имеющая
ХИ2-распределение
с (r-1)(c-1)
степенями свободы
примет значение больше вычисленной статистики Х
2
0
, т.е. P{Х
2
(r-1)*(c-1)
>Х
2
0
}, меньше
уровня значимости
, то
нулевая гипотеза
отклоняется.
В MS EXCEL
p-значение
можно вычислить с помощью формулы
=ХИ2.РАСП.ПХ(Х
2
0
;df)
, конечно, вычислив непосредственно перед этим значение статистики Х
2
0
(это сделано в
файле примера
). Однако, удобнее всего воспользоваться функцией
ХИ2.ТЕСТ()
. В качестве аргументов этой функции указываются ссылки на диапазоны содержащие фактические (Observed) и вычисленные теоретические частоты (Expected).
Если
уровень значимости
>
p
-значения
, то означает это фактические и теоретические частоты, вычисленные из предположения справедливости
нулевой гипотезы
, серьезно отличаются. Поэтому,
нулевую гипотезу
нужно отклонить.
Использование функции
ХИ2.ТЕСТ()
позволяет ускорить процедуру
проверки гипотез
, т.к. не нужно вычислять значение
статистики
. Теперь достаточно сравнить результат функции
ХИ2.ТЕСТ()
с заданным
уровнем значимости
.
Примечание
: Функция
ХИ2.ТЕСТ()
, английское название CHISQ.TEST, появилась в MS EXCEL 2010. Ее более ранняя версия
ХИ2ТЕСТ()
, доступная в MS EXCEL 2007 имеет тот же функционал. Но, как и для
ХИ2.ТЕСТ()
, теоретические частоты нужно вычислить самостоятельно.
СОВЕТ
: О проверке других видов гипотез см. статью
Проверка статистических гипотез в MS EXCEL
.
На этом шаге мы рассмотрим создание таблиц подстановки.
При работе с моделью «что-если» в определенный момент времени можно использовать только один сценарий (только один набор данных). Но что если необходимо сравнить результаты нескольких сценариев? Вот несколько вариантов решения подобной проблемы:
- Отпечатать несколько копий рабочего листа с разными сценариями на каждом.
- Скопировать модель на другие листы и расположить их окна на экране так, чтобы были видны все сценарии.
- Вручную создать формулу, которая бы подытоживала значения из ключевых ячеек для каждого сценария.
- Использовать команду Excel Данные | Таблица подстановки для автоматического создания итоговой таблицы.
- Имеется один набор данных для одной ячейки (одной переменной), на которую ссылаются несколько формул. В этом случае создается так называемая таблица подстановки с одним входом .
- Имеются два набора данных для двух ячеек (две переменные), на которые ссылается одна формула. Создаваемая в этом случае таблица называется таблицей подстановки с двумя входами .
Создать таблицу подстановки очень просто, но на ее использование наложены некоторые ограничения. Самое главное ограничение — это то, что она может временно оперировать только с одной или двумя ячейками исходных данных. Другими словами, нельзя создать таблицу подстановки, которая бы использовала комбинацию трех или более ячеек с исходными данными.
В таблице подстановки с одним входом приводятся результаты расчетов по одной или нескольким формулам при различных значениях одного входного параметра. На рисунке 1 показан общий макет таблицы подстановки с одним входом.
В приведенном ниже примере используется рабочий лист, по которому рассчитывается ипотечная ссуда (рис. 2).
Рассмотрим пример создания таблицы подстановки, в которой бы отражались значения, рассчитанные по формулам, находящимся в ячейках Размер ссуды, Месячная плата, Общая сумма, Общая сумма комиссионных , при изменении ставок от 7% до 9% с шагом 0,25%. На рисунке 3 показана заготовка таблицы подстановки для описанного примера. Строка 2 состоит из ссылок на соответствующие ячейки с формулами.
Рис.3. Подготовка к созданию таблицы подстановки с одним входом
Чтобы создать таблицу подстановки, выделите диапазон ячеек (для рассматриваемого примера G2:K11 ), а затем выберите команду Данные | Таблица подстановки . Появится диалоговое окно, показанное на рисунке 4.
Вам необходимо определить ячейку листа, в которую должны подставляться исходные данные. Поскольку все исходные данные находятся в столбце, то адрес следует поместить в поле Подставлять значения по строкам в (для нашего примера следует ввести $D$7 ). Щелкните на кнопке OK , и Excel заполнит таблицу соответствующими результатами (рис. 5).
Рис.5. Результат анализа, проведенного с помощью таблицы подстановки с одним входом
Таблица подстановки с одним входом может быть организована вертикально или горизонтально. Если значения исходных данных, которые должны подставляться во входную ячейку, расположены в строке, введите ссылку на эту ячейку в поле Подставлять значения по столбцам в , которое находится в диалоговом окне Таблица подстановки .
Таблица подстановки с двумя входами позволяет отобразить на экране результаты расчетов при изменении двух входных параметров. Макет для этого типа таблицы показан на рисунке 6.
Приведем пример таблицы подстановки с двумя входами. Это пример расчета эффективности проведения рекламной компании с помощью рассылки материалов по почте путем вычисления чистой прибыли после продажи (рис. 7).
Рис.7. Пример расчета чистой прибыли после проведения рекламной акции
В этой модели используются две ячейки для ввода информации: количество разосланных рекламных материалов и предполагаемый процент ответов. Область результата включает следующее:
- Стоимость печатных материалов . Стоимость печати одного рекламного буклета. Цена изменяется в зависимости от количества: 0,20 — если количество экземпляров не превышает 200000; 0,15 — от 200001 до 300000 экземпляров; 0,10 — если больше 300000. Стоимость отпечатаннх материалов (в зависимости от их количества) определяется по фомуле:
=ЕСЛИ(Разослано_материалов . - Почтовые расходы . Их стоимость фиксирована и составляет 0,32 за одно почтовое отправление.
- Число респондентов . Количество ответов, которое предполагается получить. Оно определяется в зависимости от процента предполагаемых ответов и количества разосланных материалов. Формула для этой ячейки следующая:
=Процент_ответевших*Разослано_материалов . - Доход на одного респондента . Это фиксированное значение. Компании известно, что за каждый заказ она получит прибыль 22.
- Суммарный доход . Суммарный доход вычисляется по простой формуле, в которой величина дохода, полученного от одного заказа, умножается на количество заказов:
=Доход_на_одного_респондента*Число_респондентов . - Суммарные расходы . По формуле, находящейся в этой ячейке, вычисляются суммарные расходы на рекламу, в которую входит стоимость печатных материалов и почтовых услуг:
=(Стоимость_печатных_материалов+Почтовые_расходы)*Разослано_материалов . - Чистая прибыль . Определяется как разность суммарных доходов и суммарных расходов.
Рис.8. Результат анализа, проведенного с помощью таблицы подстановки с двумя входами
По данным таблицы подстановки с двумя входами можно построить трехмерные диаграммы (рис. 9).
На следующем шаге мы рассмотрим анализ данных с помощью средства Диспетчер сценариев .
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Хотя Excel может подсказать вам, когда необходима связь, он не может подсказать, какие таблицы и столбцы использовать, а также возможна ли связь между таблицами. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Кстати, еще фишка (по-моему уже слишком много фишек для одной статьи), если вдруг вам нужно быстро посмотреть сумму или даже среднее значение, а нажимать вы ничего не хотите (например, вас одолела лень), то можно просто выделить то что необходимо и посмотреть вправо вниз, там всё будет написано.
Создание связи между двумя таблицами в Excel
Значения данных в столбце подстановки должны быть уникальными. Другими словами, столбец не может содержать дубликаты. В модели данных нули и пустые строки эквивалентны пустому полю, которое является самостоятельным значением данных. Это означает, что не может быть несколько нулей в столбце подстановок.
Дополнительные сведения о связях между таблицами в Excel
Вы узнаете, существуют ли связи, при перетаскивании полей из разных таблиц в список полей сводной таблицы. Если вам не будет предложено создать связь, то в Excel уже есть сведения, необходимые для связи данных.
Создание связей аналогично использованию VLOOKUP: вам нужны столбцы, содержащие совпадающие данные, чтобы Excel могли ссылаться на строки в одной таблице с строками из другой таблицы. В примере со временем в таблице Customer должны быть значения дат, которые также существуют в таблице аналитики времени.
Типы данных в двух столбцах должны быть совместимы. Подробные сведения см. в статье Типы данных в моделях данных.
Другие способы создания связей могут оказаться более понятными, особенно если неизвестно, какие столбцы использовать. Дополнительные сведения см. в статье Создание связи в представлении диаграммы в Power Pivot.
Создание сводной таблицы для анализа данных листа
Выбираем в меню Вставка пункт Сводная таблица . В указанном диалоговом окне мы видим опцию Добавить эти данные в модель данных . Мы могли бы её выбрать, но я рекомендую другой, более удобный способ. Просто нажмите OK .
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Примечание Выбранные поля добавляются в области по умолчанию не числовые поля добавляются в строки , иерархии дат и времени в столбцы , а числовые в значения. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
В списке полей разверните таблицу On_Time_Performance и нажмите ArrDelayMinutes, чтобы добавить их в область значений. В сводной таблице вы увидите общее время задержанных рейсов в минутах.
Сводная таблица на основе двух и более связанных таблиц — Сводные таблицы — Excel — Каталог статей — Perfect Excel
Чтобы импортировать данные, выберите BasicCalendarUS и нажмите Готово. При быстром подключении к Интернету импорт займет около минуты. После выполнения вы увидите отчет о состоянии перемещения 73 414 строк. Нажмите Закрыть.