Построение
графиков 3-х видов в электронной таблице
Excel
1.
Построить несколько графиков параметрически
заданной функции при разных значениях
конcтант
а, b,
.
Оси графика – х и y,
которые зависят от аргумента t
или .
|
№ |
Название кривой |
Вид |
Параметрические |
Диапазон аргумента |
Кол-во граф. |
Значения |
|
1 |
Циклоида |
|
x = a(t — sin
y = a(1 — cos |
t 0 6
шаг |
5 |
a = 1; |
|
2 |
Циклоида |
|
x = a(t — sin
y = a(1 — cos |
t 0 6
шаг |
6 |
a = 2
= 0.4; |
|
3 |
Трохоида |
|
x = at — bsin
y = a — bcos |
t 0 10
шаг |
5 |
a = -1
b |
|
4 |
Эпитрохоида |
|
x = acos
y = asin |
t 0 10
шаг |
6 |
a = 0;
b = 2 |
|
5 |
Гипотрохоида |
|
x = acos
y = asin |
t 0 10
шаг |
6 |
a = 0;
b = 2 |
|
6 |
Декартов лист |
|
x = at / (1 + t3)
y = a |
t -6 6
шаг |
6 |
a = 1; |
|
7 |
Циссоида |
|
x = a
y = a |
t -6 6
шаг |
6 |
a = 1; |
|
8 |
Строфоида |
|
x = a y = at(t2 — 1) / (t2 + 1) |
t -6 6
шаг |
6 |
a = 1; |
|
9 |
Конхоида Никомеда |
|
x = a + bcos
y = atg |
t 0
шаг |
5 |
a = 2
b |
|
10 |
Улитка Паскаля |
|
x = acos2
y = a |
t 0 2
шаг |
6 |
a = 1; b |
|
11 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a
b = 1; |
|
12 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 10
Шаг |
6 |
a = 3;
= 0.5; |
|
13 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a = 1;
= 0.5; |
|
14 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a = 7;
= 0.5; |
|
15 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 2
Шаг |
6 |
a
b = 1.5; |
|
16 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 6
Шаг |
6 |
a b = 1 |
|
17 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 2
Шаг |
6 |
a = 1;
= 0.5; |
|
18 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 10
Шаг |
6 |
a = 5;
= 0.2; |
|
19 |
Спираль |
|
x = atcos
y = btsin |
t 0 10
Шаг |
6 |
a
b = -2; |
|
20 |
Гиперболич. спираль |
|
x = (acos
y = (b |
t -6 6
Шаг |
5 |
a = 2
b = 1; |
|
21 |
Гиперболич. спираль |
|
x = (acos
y = (b |
t 0.5 20
Шаг |
5 |
a = 3
b = 1; |
|
22 |
Астроида |
|
x = acos3
y = b |
t 0 8
Шаг |
5 |
a
b = 1; |
|
23 |
Астроида |
|
x = acos3
y = a |
t 0 8
Шаг |
5 |
a
b = 0; |
|
24 |
Астроида |
|
x = acos3
y = a |
t 0 8
Шаг |
5 |
a
b = 0.5; |
|
25 |
Эвольвента |
|
x = acos
y = a |
t -10 10
Шаг |
4 |
a |
|
26 |
Эвольвента |
|
x = acos
y = a |
t 0 20
Шаг |
4 |
a |
|
27 |
Эллипс |
|
x = acos
y = b |
t 0 2
Шаг |
5 |
a
b = 1; |
|
28 |
Эллипс |
|
x = acos(c
y = b |
t 0 2
Шаг |
5 |
a
b = 1; |
|
29 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
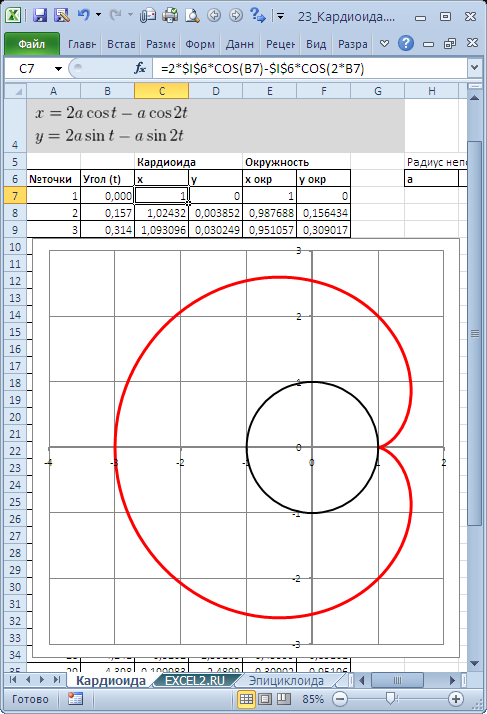
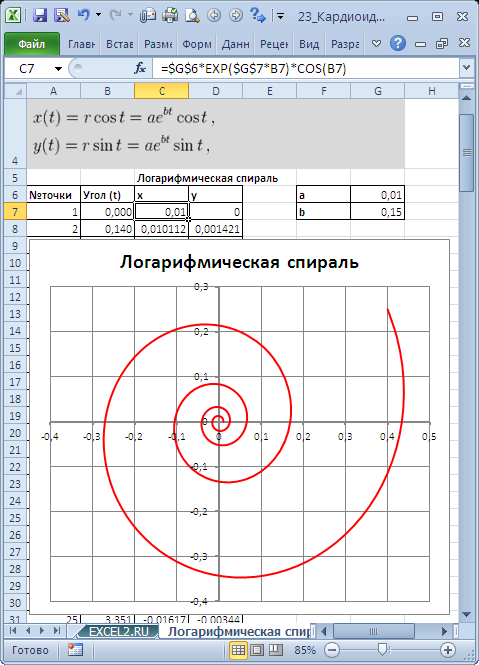
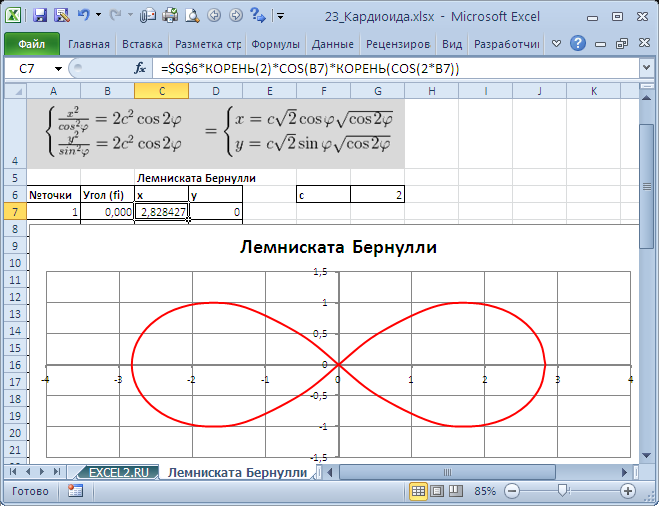
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см.
файл примера
):
х=2*а*cos(t)-а*cos(2*t)
y=2*а*sin(t)-а*sin(2*t)
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье
Эллипс и окружность в MS EXCEL
построены окружность и эллипс.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Слайд 1
Исследование алгебраических, геометрических моделей
учитель информатики
МБОУ «Средняя школа № 36»
Новикова
Ирина Васильевна
г. Дзержинск
Нижегородская область
Слайд 2
Построение графиков функций
Слайд 3
Проверка домашнего задания
Слайд 4
Логарифмическая функция
Лист Excel
Слайд 5
SINx
Лист Excel
Слайд 6
Экспонента
Лист Excel
Слайд 7
Тригонометрические функции
sinx, cosx
Лист Excel
Слайд 8
Повторение темы
«Абсолютные и относительные ссылки»
Слайд 9
Составить кластеры по теме «Абсолютные и относительные ссылки»
Слайд 10
Примеры кластеров
Какие бывают ссылки
абсолютные
относительные
смешанные
Слайд 11
Кластеры-вопросы-ответы
Если значение не меняется в ходе решения задачи
Ссылка, которая не
меняется при протягивании или копировании
$A$1

Слайд 12
Кластеры-вопросы-ответы
Если значение меняется в ходе решения задачи
Ссылка, которая изменяется при
протягивании или копировании
A1

Слайд 13
Кластеры-вопросы-ответы
Ссылка, в которой не меняется имя столбца при протягивании или
копировании
$A1
Ссылка, в которой не меняется номер строки при протягивании или копировании
A$1

Слайд 14
Задание по группам:
Найти, используя ресурсы Интернета, уравнения кривых:
1 – улитка
Паскаля
2 – строфоида
3 – кардиоида
4 – циклоида
Слайд 15
Строфоида
Построить 2 графика строфоиды
для а=2 и
а=-5.
Х=a(t2-1)/(t2+1),
Y= at(t2-1)/(t2+1),
t изменяется от -50 до 50 с шагом 10.
Слайд 16
Кардиоида
Построить 2 графика кардиоиды
для а=2 и а=-2.
Х=acost(1+cost),
Y=asint(1+cost),
t изменяется от 00 до 3600 с шагом 200
( t – перевести в радианы).
Слайд 17
Циклоида
Построить 2 графика циклоиды
для а=2
L=3
L=1.
x=a(t-Lsint)
y=a(1-Lcost)
t – изменяется 0 до 900 с шагом 50
(t перевести в радианы)
Слайд 18
Улитка Паскаля
Построить 2 графика улитки Паскаля для L=3 и
L=-2.
Х=a(2cosf-cos2f),
Y=a(2sinf-Lsin2f),
f изменятся от 00 до 3600 с шагом 200
(f – перевести в радианы, a=2).
Слайд 19
Результаты практической работы
Слайд 20
Улитка Паскаля
Лист Excel
L=-2
L=3
Слайд 21
Кардиоида
Лист Excel
а=-2
а=2
Слайд 22
Строфоида
Лист Excel
а=2
а=-5
Слайд 23
Циклоида
Лист Excel
L=1
L=3
Введение
 |
Вы
видели когда-нибудь красивые графики? Чтобы хотелось на них смотреть и
смотреть…. Как-то наткнулся на график, о котором говорилось, что его когда-то
астроном — математик подарил своей
невесте траекторию движения планеты
Венеры, которую можно наблюдать в течение 8 лет только с Земли:
Увидев
такую красоту, мне тоже захотелось поэкспериментировать. Решил более подробно
изучить тему построения графиков. И чем больше занимался этим вопросом, тем
больше хотелось сделать своими руками.
Представление
данных на компьютере в графическом виде впервые было реализовано в середине
50-х годов. Сначала, графика применялась в научно-военных целях.
Сейчас эта
область детально изучается в высших технических учебных заведениях.
Занимаясь
проектом, вывел для себя, что построение графических изображений, исследование
графиков функций, одна из интересных тем программирования.
Создание
программы для построения графиков функций
Цель моего
проекта, средствами языка Delphi разработать действующую программу для
построения графиков функций.
Задачи,
поставленные в проекте, это: разработать пользовательский интерфейс программы,
с которой легко работать и получать различные варианты одной и той же функции.
Продумать инструментарий. Разрабатываемая программа должна строить по заданному
параметрическому представлению графиков функций: эпициклоиды, кардиоиды,
астроиды, улитки Паскаля, строфоиды.
Этапы проведения моделирования
Ø математическое представление
исследования графиков,
Ø разработка структурограммы,
Ø составление алгоритма работы,
Ø написание программы,
Ø отладка и получение результатов на
компьютере в среде Delphi.
Разработка форм проекта
Чтобы
удобно было работать с нужной функцией, расположим на основной форме кнопки,
вызывающие выбранную функцию:
Для
перехода на выбранную форму, создадим функцию:
procedure
TForm1.Button1Click(Sender: TObject);
begin
Form2.Show;
end;
Структура проекта
 |
Рассмотрим, как работает форма с квадратичной
функцией
Система координат
Для того чтобы нарисовать график y:=
a*sqr(x+b)+c, нужна система координат.
Начало
координат на форме находится в левом верхнем углу, а начало координат для
графика устанавливается в точке с координатами (X0,Y0). Значения X и Y
вычисляются с учетом смещения: x+x0;y-y0.
 |
Построение графика функции
Система координат строится черным
цветом:
x0:=400;
y0:=300;
x:=-x0;
pen.Color:= clblack;
moveto (x0,30); lineto (x0, 500);
moveto (30,y0); lineto (1000, y0);
Коэффициенты
функции задаются с помощью объекта Edit, а для использования значений
коэффициентов при вычислении координат графика, преобразуем показания объекта Edit в числовые:
a:=strtofloat(edit1.Text);
b:=strtofloat(edit2.Text);
c:=strtofloat(edit3.Text);
Координатами
точек при изображении их на форме могут быть только целые числа. Единица
измерения – пиксель. Если значения функции очень маленькие, то изображение
графика нужно увеличивать в несколько раз
Построение графика функции
m:=50;
x:=-x0;
repeat
y:= a*sqr(x)+bх+c;
Pixels [x0+Trunc(x*m),
y0-Trunc(y*m)]:=clgreen;
x:=x+0.001 ;
until (x>=x0);
m –
масштаб — целое число, подбирается в зависимости от вида графика.
x —
изменяется в цикле. Шаг изменения тоже зависит от вида графика.
Графики
функций строятся зеленым цветом.
Работа формы, которая строит график функции
Следующий
график также из школьного курса – это кубическая функция. Порядок построения
аналогичен предыдущему.
Другие
графики не входят в школьный курс, но исследовать их очень интересно.
Астроида
Астро́ида(от греч.
αστρον — звезда и ειδος — вид, то есть звездообразная) — плоская кривая,
описываемая точкой окружности радиуса r , катящейся по внутренней стороне
окружности радиуса R=4r.

y:=R*Sin(t)*sin(t)*sin(t)
Улитка Паскаля
Улитка Паскаля ― плоская
алгебраическая кривая 4-го
порядка.
x
:= a*cos( 2* t) + b* cos( t);
y
:= a* cos( t)* sin (t) +b* sin (t);

диаметр исходной окружности
b -расстояние, на которое смещается точка вдоль радиус-вектора
Три улитки
Паскаля: зелёнаяa>b, красная
(кардиоида)a = b и синяя a<b
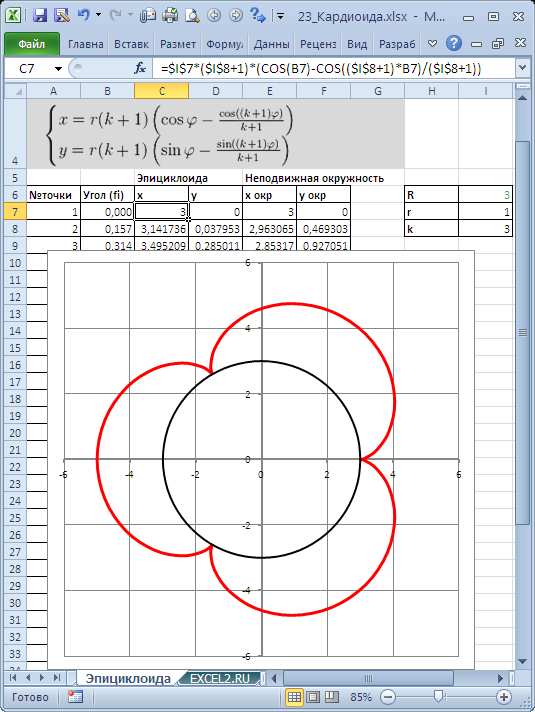
Эпициклоида
Эпицикло́ида —
плоская кривая, образуемая фиксированной точкой окружности, катящейся по
внешней стороне другой окружности без скольжения.
x
:= ( a+b)*cos(t) — a* cos((a+b)* t/a);
y
:= (a+b)* sin( t)- a*sin ((a+b)*t/a);
a – радиус
окружности, центр которой находится в начале координат;
b
– радиус
малой окружности
Кардиоида
Кардио́ида— плоская
линия, которая описывается фиксированной точкой окружности, катящейся по
неподвижной окружности с таким же радиусом. Получила своё название из-за
схожести своих очертаний со стилизованным изображением сердца
Пусть —
радиус окружностей, начало координат находится в конечной точке горизонтального
диаметра неподвижной окружности. Тогда уравнения кардиоиды можно записать в
следующих формах.
x := 2*a*cos(t)*(1+ cos( t));
y := 2*a* sin( t)*(1+cos(t))
Строфоида
Строфоида — алгебраическая кривая 3-го
порядка.
Считается,
что строфоида впервые была рассмотрена французским математиком ЖилемРобервалем в 1645 году. Роберваль называл эту кривую
— «птероида» (от греч. πτερον— крыло).
x := a*(t*2-1)/(t*2+1);
y := a*
t*(t*2-1)/(t*2+1)
Гипоциклоида
Гипоцикло́ида— плоская
кривая, образуемая точкой окружности,
катящейся по внутренней стороне другой окружности без скольжения.
где , где
—
радиус неподвижной окружности, — радиус
катящейся окружности.
К
сожалению, у меня гипоциклоида пока что не получается, но, то что получается,
мне очень нравится, думаю, и вам понравится.
Заключение
Проект
можно использовать на уроках математики при изучении функций гиперболы и параболы.
А также можно работать над продолжением проекта – добавлять функции, изучаемые
в школе. Конечно, мне очень хочется продолжить работу над проектом и создать
проект построения функций в полярных координатах. И, как говорилось в начале
проекта, может быть я смогу вывести формулу любви и построить её график.
Пример построения графика астроиды (кубоциклоида/звездообразной кривой) в Excel.
Для построения графика использованы параметрические уравнения x = R*cos3t и y = R*sin3t.
Также посчитана площадь фигуры.
Скачать пример — Astroida.xlsx
То же в Python:
import matplotlib.pyplot as plt
import math
x=[]
y=[]
for i in range (1,1000):
x.append((math.sin(i))**3)
y.append((math.cos(i))**3)
plt.scatter(x,y)
plt.show()