МНК: Степенная зависимость в EXCEL
history 11 ноября 2018 г.
-
Группы статей
- Статистический анализ
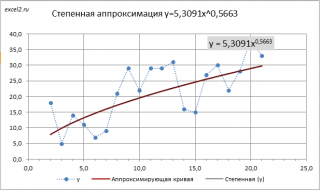
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью степенной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL .
Степенную зависимость y=a*x m для x, y, a также можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
После замены переменных Х=ln(x), Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=m*X+A. Для нахождения параметра а необходимо выполнить обратное преобразование а= EXP(А) .
Примечание : Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда ( Степенная линия тренда ). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL .
Примечание : Степенную функцию y=a*x m (переменная х – в основании степени, показатель степени m — const) не следует путать с показательной функцией y=a*m x (переменная х – в показателе степени, основание степени m — const). Как аппроксимировать показательную функцию показано в статье МНК: Экспоненциальная зависимость в MS EXCEL .
Функция СТЕПЕНЬ
Предположим, что вам нужно вычислить очень маленький допуск для детали механизма или огромное расстояние между двумя галактиками. Для возведения числа в степень используйте функцию СТЕПЕНЬ.
Описание
Возвращает результат возведения числа в степень.
Синтаксис
Аргументы функции СТЕПЕНЬ описаны ниже.
Число — обязательный аргумент. Базовое число. Это может быть любое настоящее число.
Степень Обязательный. Показатель степени, в которую возводится основание.
Замечание
Вместо функции СТЕПЕНЬ для возведения в степень можно использовать оператор ^, например: 5^2.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Примеры использования функции СТЕПЕНЬ в Excel
Функция СТЕПЕНЬ в Excel используется для возведения чисел в степень, значение которой может являться сложным выражением, и возвращает полученное в результате числовое значение.
Функция СТЕПЕНЬ в Excel для возведения числа в указанную степень
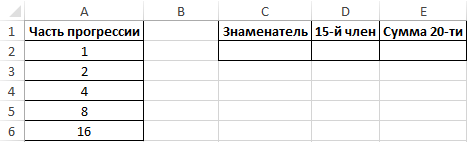
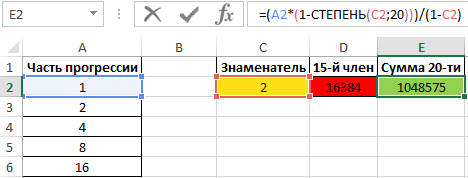
Пример 1. В таблице записана последовательность, которая представляет собой часть геометрической прогрессии. Необходимо определить: знаменатель геометрической прогрессии, значение 15-го ее члена, а также сумму первых 20 членов.
Таблица исходных данных:
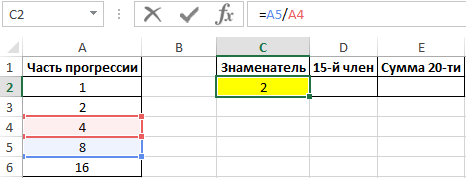
Определим знаменатель из условия, что он равен частному от деления любых последующего и предыдущего соседних членов:
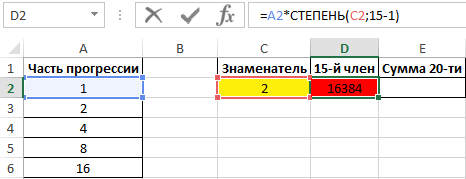
Для нахождения 15-го члена используем формулу:
- A2 – ячейка, содержащая значение первого члена;
- СТЕПЕНЬ(C2;15-1) – формула, принимающая на вход значение знаменателя прогрессии, который возводится в степень, равную номеру позиции искомого члена -1.
Для нахождения суммы первых 20 вхождений в последовательности введем формулу:
Примечание: в данном примере использовались известные из математики формулы, а применение функция СТЕПЕНЬ позволило упростить расчеты.
Как построить график функций используя СТЕПЕНЬ в Excel
Пример 2. Построить график функции y=2^(x^2+2x).
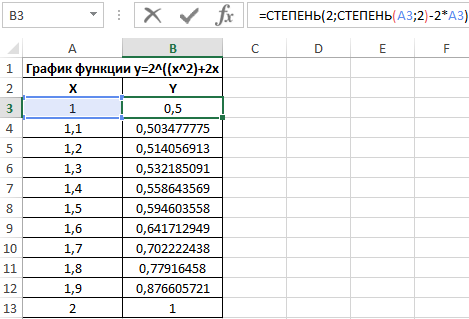
Для построения графика будем использовать несколько точек, полученных в результате расчета значения зависимой координаты y на основе известных произвольных значениях независимой координаты x. Внесем исходные данные в таблицу:
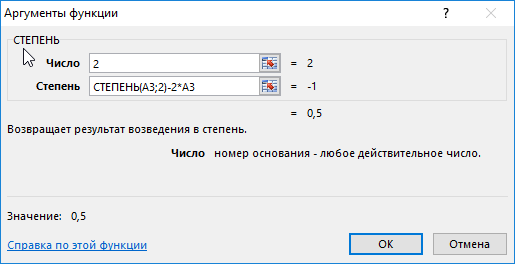
Определим первое значение зависимой переменной:
- 2 – число, которое необходимо возвести в степень;
- СТЕПЕНЬ(A3;2)-2*A3 – степень, полученная в результате вычисления данного выражения.
Аналогично определим второе значение для Y, выделим ячейки B3 и B4, автоматически заполним остальные ячейки растягиванием выделенной области:
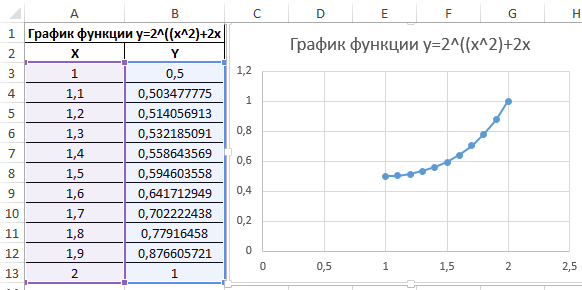
Для построения графика используем точечную диаграмму с маркерами. Готовый график функций имеет следующий вид:
Депозитный калькулятор в Excel
Пример 3. В таблице Excel создан калькулятор для расчета суммы процентов прибыли по депозитным вкладам в банковскую организацию. Рассмотрим его реализацию.
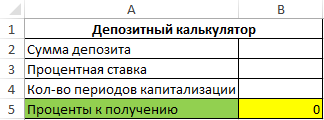
Калькулятор имеет следующий вид:
Заполним шаблон депозитного калькулятора исходными данными для расчетов:
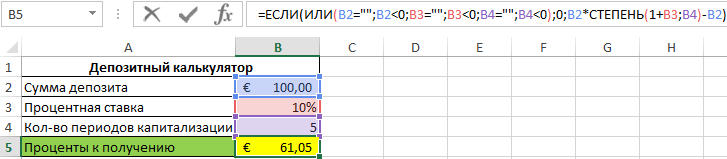
В ячейке B5 содержится следующая формула:
-
ИЛИ(B2=»»;B2 Примечание: для корректной работы данного калькулятора значение процентной ставки должно являться десятичной дробью (например, значение 10% — 0,1 указано в процентном формате ячеек).
Функция СТЕПЕНЬ в Excel и особенности ее использования
Рассматриваемая функция принадлежит к классу математических функций Excel и имеет следующую синтаксическую запись:
- число – обязательный аргумент, характеризующий число, которое необходимо возвести в степень.
- степень – обязательный аргумент, характеризующий степень, в которую требуется возвести число.
- Функция СТЕПЕНЬ вернет код ошибки #ЗНАЧ!, если один из параметров содержит текстовые данные.
- Записи типа =СТЕПЕНЬ(2;ЛОЖЬ) или =СТЕПЕНЬ(5;ИСТИНА) являются допустимыми, поскольку Excel выполняет автоматическое преобразование типов данных там, где это возможно. В первом случае будет возвращено значение 1 (ЛОЖЬ соответствует числовому значению 0), а во втором – 5 (ИСТИНА соответствует числовому значению 1).
- Запись типа =СТЕПЕНЬ(2;СТЕПЕНЬ(2;3)) является допустимой, в данном случае будет возвращено значение 256.
- Аргумент степень принимает также значения из диапазона отрицательных чисел. Запись типа =СТЕПЕНЬ(4;-2) эквивалентна записи =1/СТЕПЕНЬ(4;2).
- Для возведения чисел в степень можно также использовать запись типа «a^b», где a – число, возводимое в степень, b – степень, в которую требуется возвести значение, «^» — символ возведения в степень. Однако запись типа =СТЕПЕНЬ(a;b) является более наглядной.
- С помощью рассматриваемой функции можно извлечь корень любой степени из числа. Для реализации необходимо в качестве степени ввести выражение типа (1/b), где b – корень степени b.
источники:
http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D1%81%D1%82%D0%B5%D0%BF%D0%B5%D0%BD%D1%8C-d3f2908b-56f4-4c3f-895a-07fb519c362a
http://exceltable.com/funkcii-excel/primery-funkcii-stepen
Функция СТЕПЕНЬ в Excel используется для возведения чисел в степень, значение которой может являться сложным выражением, и возвращает полученное в результате числовое значение.
Функция СТЕПЕНЬ в Excel для возведения числа в указанную степень
Пример 1. В таблице записана последовательность, которая представляет собой часть геометрической прогрессии. Необходимо определить: знаменатель геометрической прогрессии, значение 15-го ее члена, а также сумму первых 20 членов.
Таблица исходных данных:
Определим знаменатель из условия, что он равен частному от деления любых последующего и предыдущего соседних членов:
Для нахождения 15-го члена используем формулу:
=A2*СТЕПЕНЬ(C2;15-1)
Описание аргументов:
- A2 – ячейка, содержащая значение первого члена;
- СТЕПЕНЬ(C2;15-1) – формула, принимающая на вход значение знаменателя прогрессии, который возводится в степень, равную номеру позиции искомого члена -1.
Для нахождения суммы первых 20 вхождений в последовательности введем формулу:
Примечание: в данном примере использовались известные из математики формулы, а применение функция СТЕПЕНЬ позволило упростить расчеты.
Как построить график функций используя СТЕПЕНЬ в Excel
Пример 2. Построить график функции y=2^(x^2+2x).
Для построения графика будем использовать несколько точек, полученных в результате расчета значения зависимой координаты y на основе известных произвольных значениях независимой координаты x. Внесем исходные данные в таблицу:
Определим первое значение зависимой переменной:
Описание аргументов:
- 2 – число, которое необходимо возвести в степень;
- СТЕПЕНЬ(A3;2)-2*A3 – степень, полученная в результате вычисления данного выражения.
Аналогично определим второе значение для Y, выделим ячейки B3 и B4, автоматически заполним остальные ячейки растягиванием выделенной области:
Для построения графика используем точечную диаграмму с маркерами. Готовый график функций имеет следующий вид:
Депозитный калькулятор в Excel
Пример 3. В таблице Excel создан калькулятор для расчета суммы процентов прибыли по депозитным вкладам в банковскую организацию. Рассмотрим его реализацию.
Калькулятор имеет следующий вид:
Заполним шаблон депозитного калькулятора исходными данными для расчетов:
В ячейке B5 содержится следующая формула:
Описание аргументов:
- ИЛИ(B2=»»;B2<0;B3=»»;B3<0;B4=»»;B4<0) – условия для проверки, чтобы в ячейке B5 не выводилась ошибка #ЗНАЧ!, если предыдущие ячейки не заполнены или введены неверные значения.
- 0 – значение, которое выводится по умолчанию, если расчет не производится.
- B2*СТЕПЕНЬ(1+B3;B4)-B2 – формула расчета суммы процентов. Для возведения в степень используется функция СТЕПЕНЬ.
Пример использования:
Примечание: для корректной работы данного калькулятора значение процентной ставки должно являться десятичной дробью (например, значение 10% — 0,1 указано в процентном формате ячеек).
Функция СТЕПЕНЬ в Excel и особенности ее использования
Рассматриваемая функция принадлежит к классу математических функций Excel и имеет следующую синтаксическую запись:
=СТЕПЕНЬ(число; степень)
Описание аргументов:
- число – обязательный аргумент, характеризующий число, которое необходимо возвести в степень.
- степень – обязательный аргумент, характеризующий степень, в которую требуется возвести число.
Примечания:
- Функция СТЕПЕНЬ вернет код ошибки #ЗНАЧ!, если один из параметров содержит текстовые данные.
- Записи типа =СТЕПЕНЬ(2;ЛОЖЬ) или =СТЕПЕНЬ(5;ИСТИНА) являются допустимыми, поскольку Excel выполняет автоматическое преобразование типов данных там, где это возможно. В первом случае будет возвращено значение 1 (ЛОЖЬ соответствует числовому значению 0), а во втором – 5 (ИСТИНА соответствует числовому значению 1).
- Запись типа =СТЕПЕНЬ(2;СТЕПЕНЬ(2;3)) является допустимой, в данном случае будет возвращено значение 256.
- Аргумент степень принимает также значения из диапазона отрицательных чисел. Запись типа =СТЕПЕНЬ(4;-2) эквивалентна записи =1/СТЕПЕНЬ(4;2).
- Для возведения чисел в степень можно также использовать запись типа «a^b», где a – число, возводимое в степень, b – степень, в которую требуется возвести значение, «^» — символ возведения в степень. Однако запись типа =СТЕПЕНЬ(a;b) является более наглядной.
- С помощью рассматриваемой функции можно извлечь корень любой степени из числа. Для реализации необходимо в качестве степени ввести выражение типа (1/b), где b – корень степени b.
Содержание
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- Вопросы и ответы
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
f(x) = e^n,
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
=EXP(число)
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
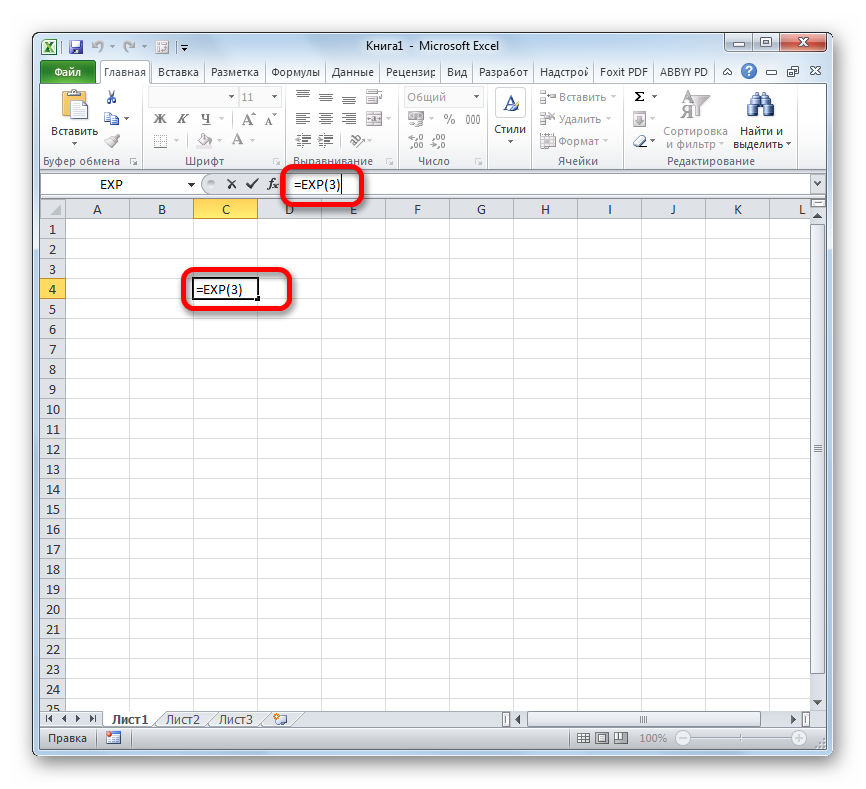
- Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
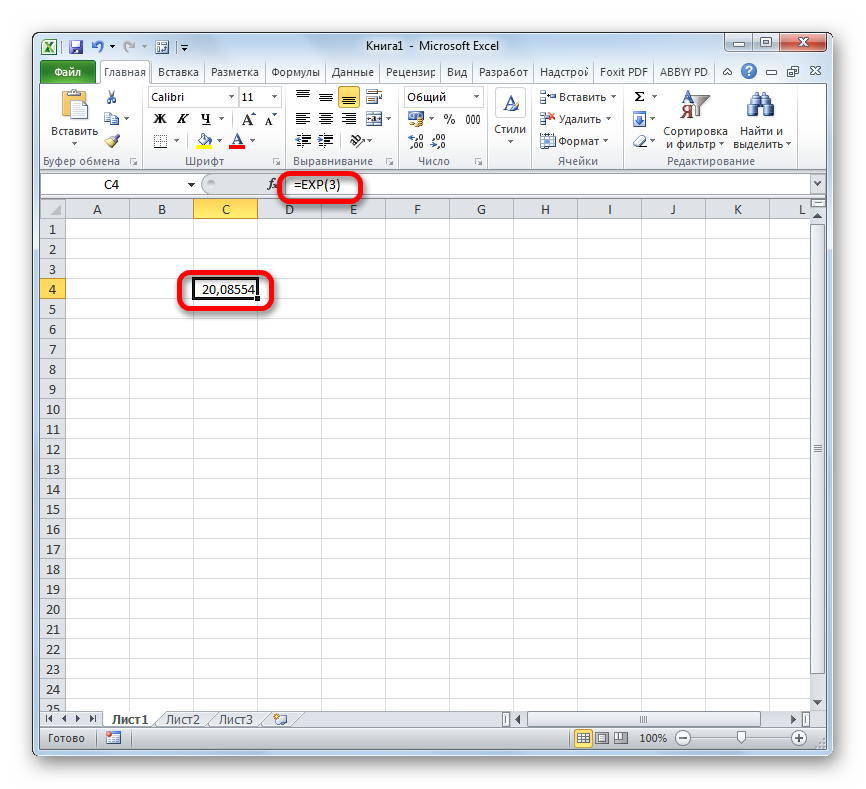
=EXP(3) - Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.
Урок: Другие математические функции в Эксель
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
- Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
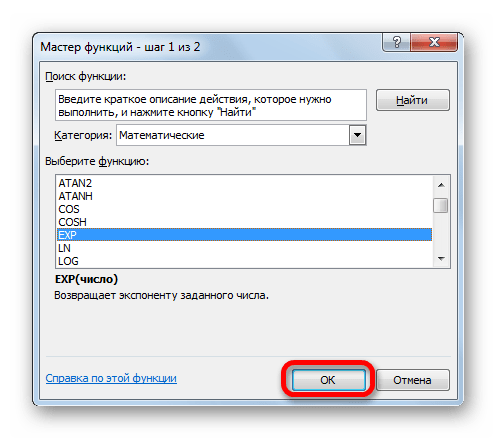
- Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
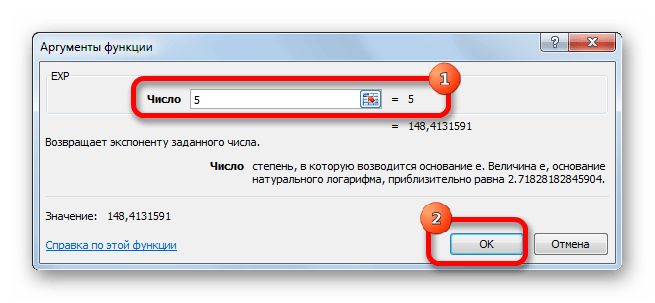
- Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
- После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.
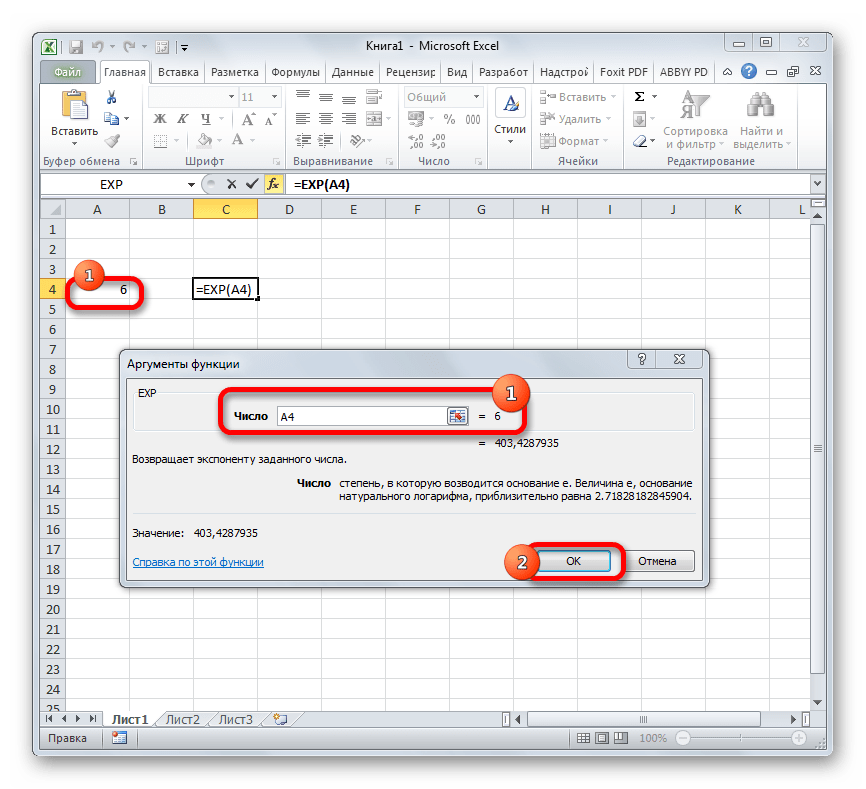
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Урок: Мастер функций в Microsoft Excel
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
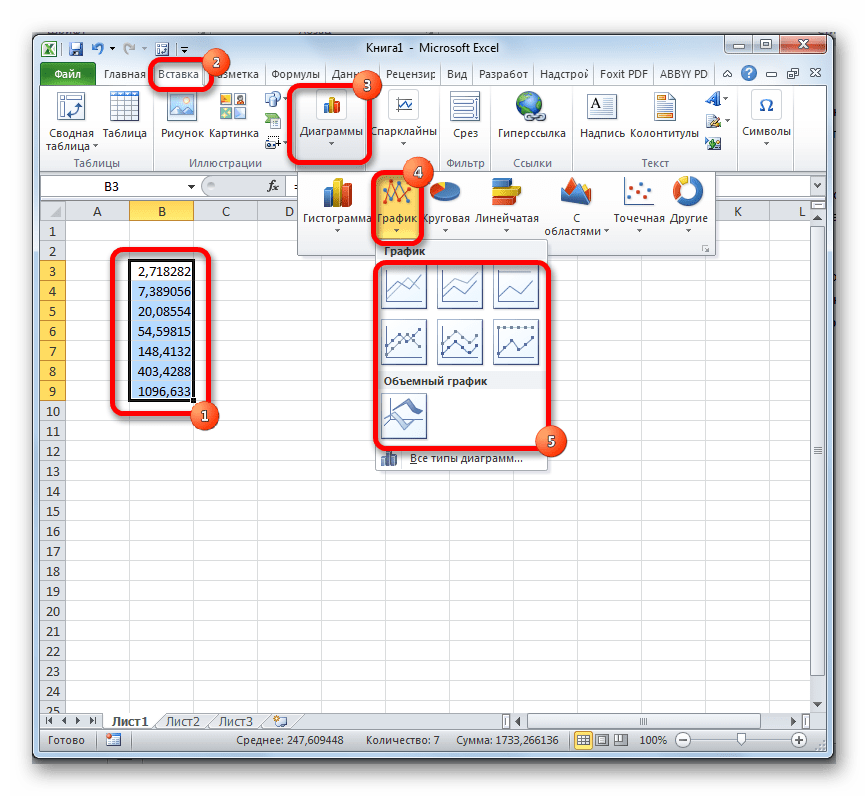
- Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
- После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.
Урок: Как сделать график в Excel
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Еще статьи по данной теме:
Помогла ли Вам статья?
По теме: методические разработки, презентации и конспекты
Бинарный урок «Использование возможностей табличного редактора Excel для построения графиков целых функций. Описание свойств целых функций, заданных графическим способом.»
Конспект бинарного урока по алгебре и информатике.. Данный урок позволяет проверить знания учащихся по теме»Функция. График функции. Описание свойств функции, заданной графически». По информатике на у…
Урок Информатика и ИКТ Тема: Деловая графика. Построение графиков и диаграмм средствами редактора электронных таблиц Microsoft Excel
Разработка урока и презентация по информатике и ИКТ в 9 кл. по теме: Деловая графика. Построение графиков и диаграмм средствами редактора электронных таблиц Microsoft Excel…
Метод. разработка по теме «Выпуклость и вогнутость функции. Исследование функции с помощью производной и построение графиков этих функций».
Метод. разработка по теме «Выпуклость и вогнутость функции. Исследование функции с помощью производной и построение графиков этих функций»….
Использование возможностей Excel для построения графиков показательной функции и решения задач. /2 курс СПО/
Открытый урок «Иформатика — Математика»…
Практическая работа «Построение графиков математических функций в Excel»
Excel позволяет строить не только обычные графики, но и даже графики различных математических функций. Вот шаги, которые необходимо предпринять для построения графика функции в Excel: &bull…
Построение графиков и рисунков средствами MS Excel
Практическая работа «Построение графиков и рисунков средствами MS Excel»…
Технологическая карта интегрированного урока точных наук (математики и информатики) по теме Построение графиков элементарных функций в Excel с применением технологии «перевернутого класса».
Технологическая карта интегрированного урока точных наук (математики и информатики) по теме Построение графиков элементарных функций в Excel с применением технологии «перевернутого класса»…
Плоский график подразумевает две оси – вертикальную и горизонтальную. Они могут быть подписаны совершенно произвольно, но всегда смысл один – каждой точке на горизонтальной оси соответствует значение по вертикали. Или как привыкли из школы: каждому иксу – свой игрек. А вот это соответствие может сразу задаваться некой уже имеющейся таблицей или даётся формулой.
Простой график
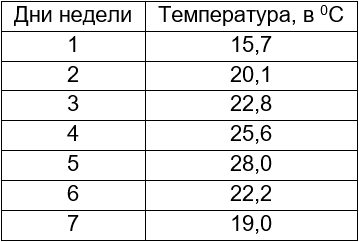
Самая простая таблица – из двух столбцов.
Уже с ней могут возникнуть проблемы. Например, выделяем эту таблицу в excel, нажимаем на Вставка в верней строке и попадаем в:
Нажимаем на График (что под Данные), открывается оконце:
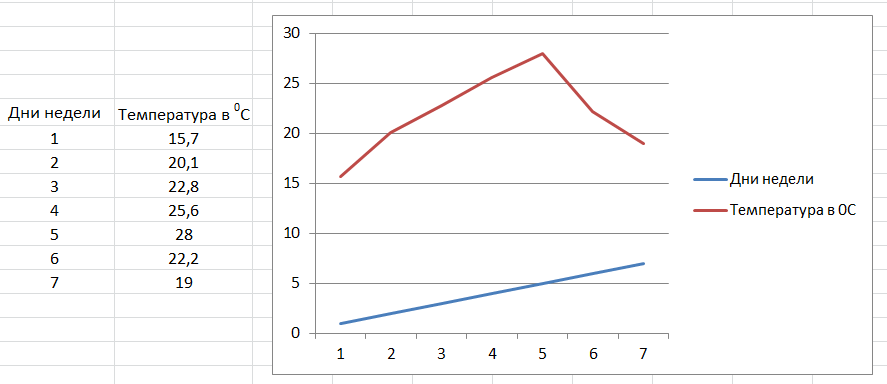
Нажимаем на первый (верхний слева) и получаем график:
Разве это мы хотели? Думали, что дни недели образуют нижнюю ось, а они выстроились второй линией на графике. Как быть?
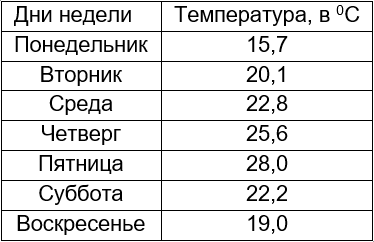
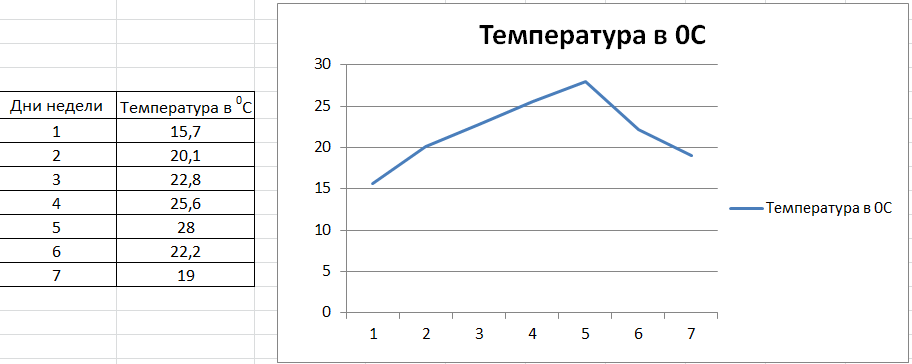
Вариант 1 – поменять цифры на названия:
Выделяем эту табличку в excel и повторяем действия по рисованию графика, получаем:
Дни недели расположились на горизонтальной оси, как и хотелось. Как же вернуть на горизонталь дни недели в цифрах? Очень просто – выделять в excel только столбец с Температурой, тогда получится:
Это важно: если первый столбец цифровой и есть желание расположить его на горизонтальной оси, не надо выделять его при рисовании графика.
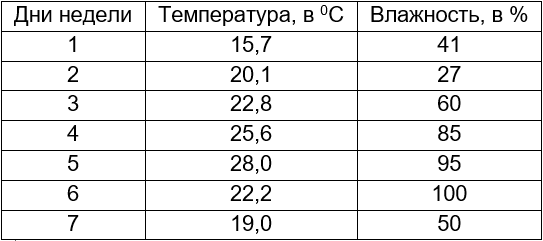
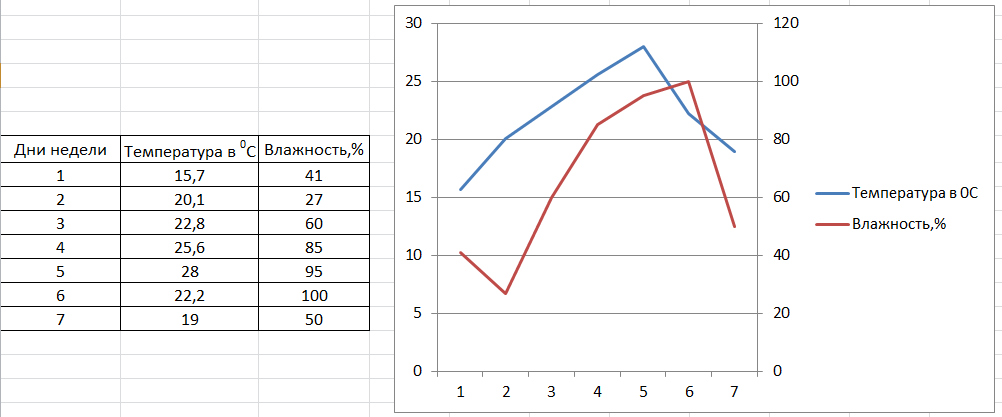
Из приведённого примера уже понятно, что если в таблице будет больше двух столбцов, то это приведёт просто к дополнительным линиям на графике. Например:
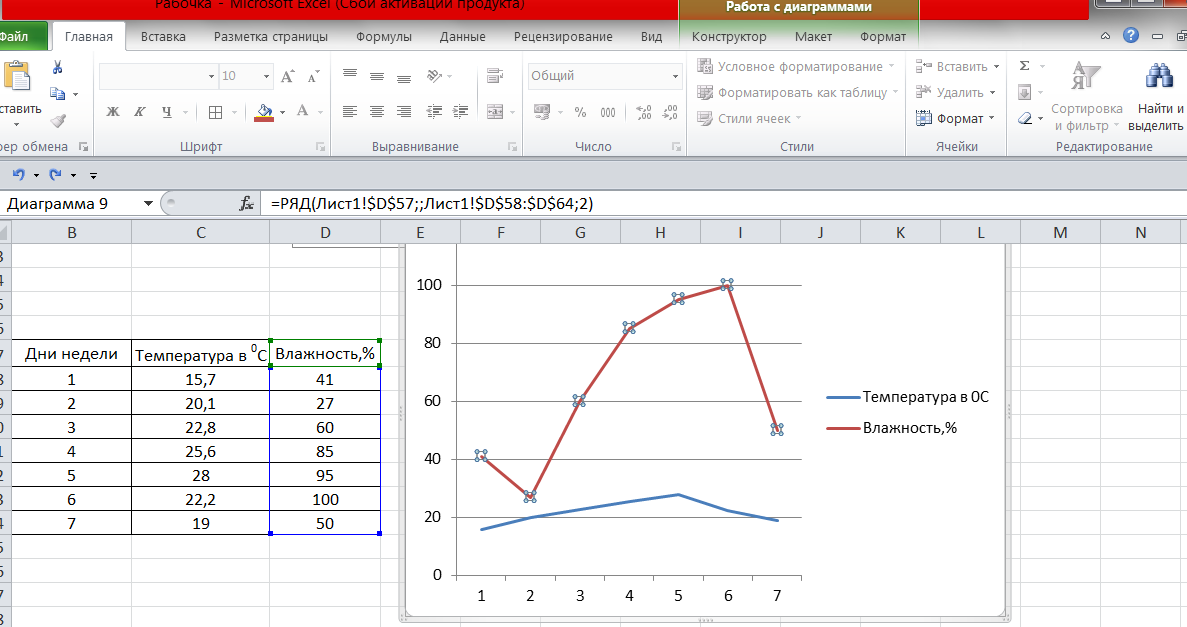
Видно неудобство: на одной вертикальной оси отражены и шкала температуры, и шкала влажности. Проблема решается вводом дополнительной вертикальной оси справа. Пусть справа будет шкала по влажности. Тогда наводим курсор на красную кривую влажности и кликаем по ней. Наверху страницы активировалось окно Работа с диаграммами:
В окне активированы Конструктор, Макет и Формат. Нажимаем на Формат:
И в левом столбце нажимаем на фрагмент выделенного. Открывается окно Формат ряда данных:
В правом столбце осталось поставить крыжик в строке По вспомогательной оси. И нажать на Закрыть. Появляется ось справа:
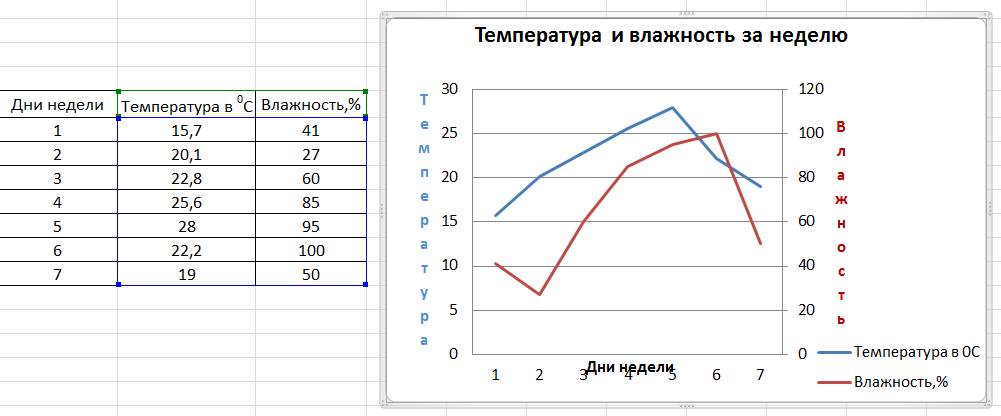
Осталось улучшить оформление: подписать оси, сделать заголовок.
Оформление простого графика
Кликая левой кнопкой по графику (в excel), активируем сверху блок Работа с диаграммами. В нём – Макет, открывается:
Входя в Названия осей, по очереди даём названия горизонтальной оси и двум вертикальным. При этом правой кнопкой можно менять размер шрифта, цвет. Также выбираем написание вертикальных осей – горизонтальное или вертикальное.
Входя в Название диаграммы, пишем название графика, также правой мышкой выбирая размер, цвет, выравнивание.
Можно также задать сеть (нажимая Сетка) и заливку (правой мышкой):
Построение графика функции
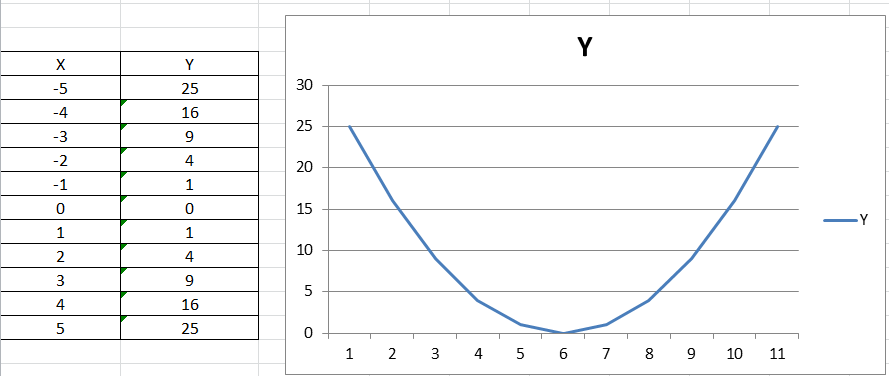
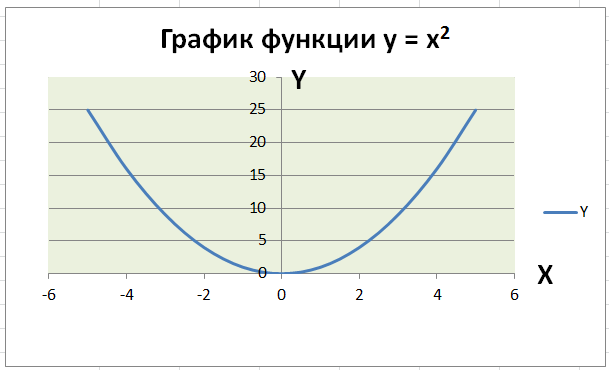
Для начала – график простой функции, например, квадратной y=x2. Поскольку построение графика по таблице не вызывает уже проблем, то и надо этим воспользоваться, создать таблицу. В excel это очень просто:
В столбце Y напротив -5 ставится = и нажимается значок функции fx. В появившемся окне Мастер функций выбирается категория Математические и находится (по алфавиту) СТЕПЕНЬ. Курсор на неё и нажать ОК. В появившемся окне Аргументы функции вставить курсор в строку Число, а потом в таблице выделить значения Х. В строке Число введётся диапазон. В строке окошка Степень поставить 2, раз функция квадратичная. В столбце Y таблицы напротив -5 появится цифра 25. Курсор в нижний правый угол ячейки с 25 и протащить вниз до конца таблицы. В каждой ячейке появится цифра.
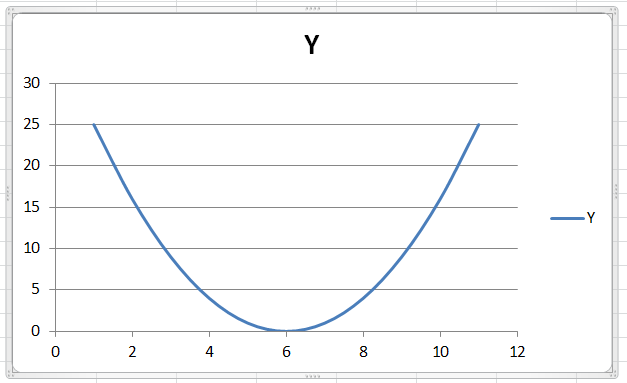
Далее – по отработанной схеме: выделяем столбец Y, потом – Вставка-График-первый из появившегося окна. Получаем:
Кривая построена по точкам, её надо сгладить. Для этого наводим курсор на график, правой кнопкой выбираем Изменить тип диаграммы, переходим на Точечную диаграмму, а в ней на ту, что без точек и жмём ОК. Получается:
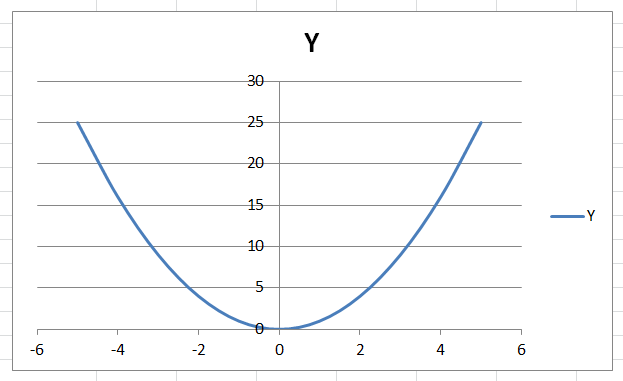
Но это ещё не график функции y=x2, (при х=0, у=6). Для корректировки горизонтальной оси наводим курсор на эту ось, правой кнопкой нажимаем на Выбрать данные и в левом столбце появившегося окошка жмём Изменить. Появляется окошко Изменение ряда. В нём в строку Х вносим столбец Х из нашей таблицы (только значения), два раза – ОК и получаем:
После нескольких завершающих штрихов:
Несколько общих советов:
• когда график нарисован, то с помощью правой кнопки можно выбрать нужный шрифт, его размеры – для всех названий;
• все названия можно перетаскивать по графику в нужное место;
• можно также в разных стилях размещать подписи, используя Метки данных из окошка Элементы диаграммы;
• можно поиграть с видами графиков из вкладки Конструктор, выбирая шаблоны в Стилях диаграмм.
График сложной функции
Как в excel построить график любой сложной функции?
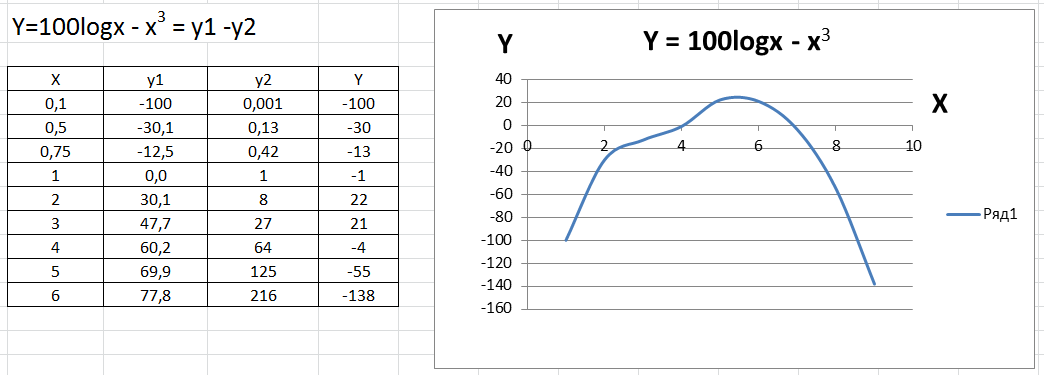
Зная, как построить график простой функции, то есть функции из Математических функций Мастера функций, можно легко построить любую сложную функцию – из произвольного сочетания тригонометрических, степенных, показательных, логарифмических функций, просто надо искомую функцию представить как сумму (алгебраическую) функций: Y = y1 + y2 +y3 +… И таблицу делать из аргументов и этих функций. Далее – всё, как было описано для графика простой функции.
Например, Y=100logx — х3 = y1 -y2
Возможности Excel гораздо шире описанных в статье, и знакомство с ними расцветит красками оформление графиков, их подачу. Но основной подход построения – через составление (или изначальное наличие) предварительной таблицы – описан и позволит любому пользователю построить график любой зависимости.