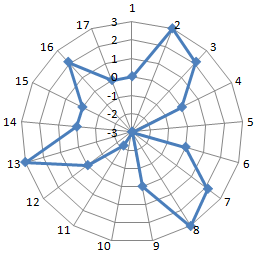
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
Как построить лепестковую диаграмму в Excel
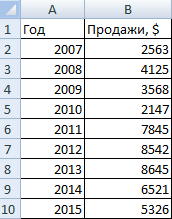
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
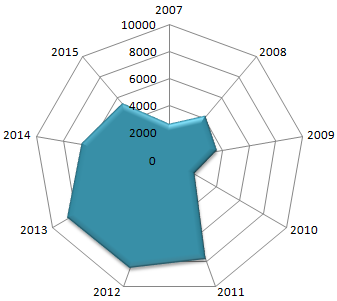
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
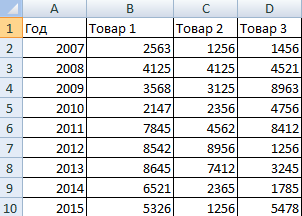
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
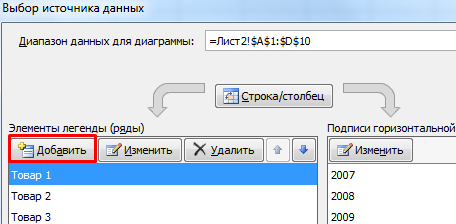
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
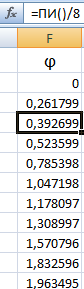
Формулы для заполнения первого столбца берем из таблицы значений точек:
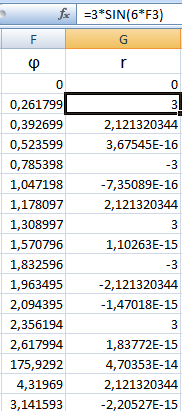
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
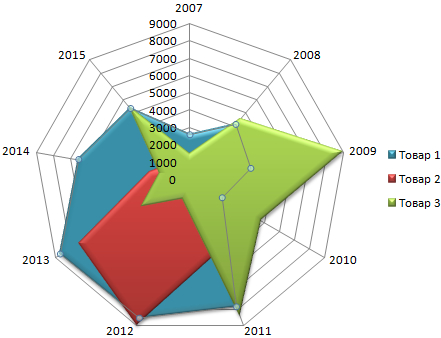
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Архимедова спираль
Архимедова спираль Архимедова спираль – это кривая, задаваемая так: X(T)=T*COS(T), Y(T)=T*SIN(T) T – задается в радианах и изменяется от 0 до бесконечности. Кривая, заданная параметрически, — это множество точек плоскости вида (X(T);Y(T)), где T – это независимая переменная, называемая в данном случае параметром. Таких кривых очень много. Мы познакомимся с некоторыми из них. Давайте построим эту кривую. Запустим Excel. В данном случае нам нужно табулировать не одну, а две функции – X(T) и Y(T).
Слайд 17 из презентации «Построение графиков в Excel». Размер архива с презентацией 381 КБ.
Excel
«Работа в Excel» — Форматирование. Команды на ленте. Улучшение Excel. Столбцы листа. Начало работы. Операции. Подробные сведения. Форматы файлов. Обучение работе с Microsoft. Верхний колонтитул. Работа с файлами предыдущих версий. Отличия. Столбец. Шаблон Excel. Заголовки. Доступ к командам. Резюме практических заданий. Панель быстрого доступа. Откройте нужный файл. Формат файлов. Что изменилось и почему. Формат файлов Excel.
«Знакомство с Excel» — Формулы. Табличный процессор. Адреса ячеек. Строка. Принцип относительной адресации. Отрицательное значение. Основной элемент. Данные электронной таблицы. Текстовые данные. Функции обработки диапазона. Операции манипулирования. Ячейка. Cтолбцы. Знакомство с Excel. Числовой формат. Назначение. Тип даты. Запуск электронных таблиц. Имя файла.
«Программа Excel» — Маркер заполнения. Абсолютная ссылка. Цель урока. Результат в данной ячейке. План урока. Функция. Арифметические действия. Ссылка на ячейку, то есть на адрес. Ситуация. Некоторые форматы находятся на панели инструментов. Закрепим основные понятия. Сортировка. Смешанные ссылки. Ярлык. Решение расчётной задачи. Возможности программы. Диаграмма. У каждой ячейки есть свой адрес. Виды ссылок. Тест. Когда курсор попадает в ячейку, она становится активной.
«Таблица данных в Excel» — Статистические данные. Регрессионная модель. Постановка задачи и гипотезы. Построим таблицу. Познакомить с понятием «статистика». Графики. График квадратичной функции. Исходная информация. Метод наименьших квадратов. Таблица «Excel». Запишите функции. График регрессионной модели. Математическая модель. Данные медицинской статистики. Сумма квадратов отклонений. Практическое использование. Продолжите предложения.
«Электронные таблицы Microsoft Excel» — Группировка данных. Диаграммы на основе сводных таблиц. Изменение области данных. Описание частей сводной таблицы. Добавление области данных. Анализ электронных таблиц. Консолидация. Обновление исходных данных. Сводная таблица. Внешние источники данных. Поля страницы. Части сводной таблицы. Структура сводной таблицы. Создание связей итоговой таблицы. Переключатель. Мастера сводных таблиц. Методы консолидации данных.
«Microsoft Office Excel» — Ячейка. Овладение практическими способами работы с информацией. MS Excel. Форматирование ячеек. Практическая работа. Объекты программы MS Excel. Элементы диаграммы. Правильный адрес ячейки. Диаграмма. Смешанной ссылкой. Назначение. Что такое ЭТ. Выдающийся, превосходящий другие. Электронные таблицы. Идеальный режим. Ссылка. Порядок создания диаграммы. Обработка числовых данных.
history 16 апреля 2015 г.
- Группы статей
- Диаграммы и графики
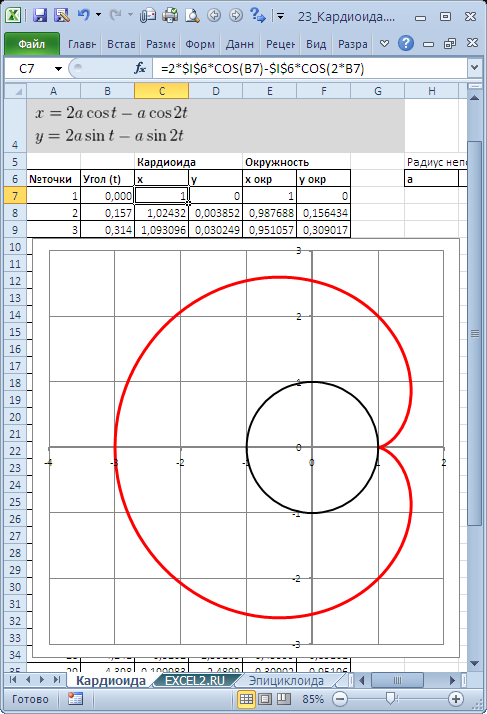
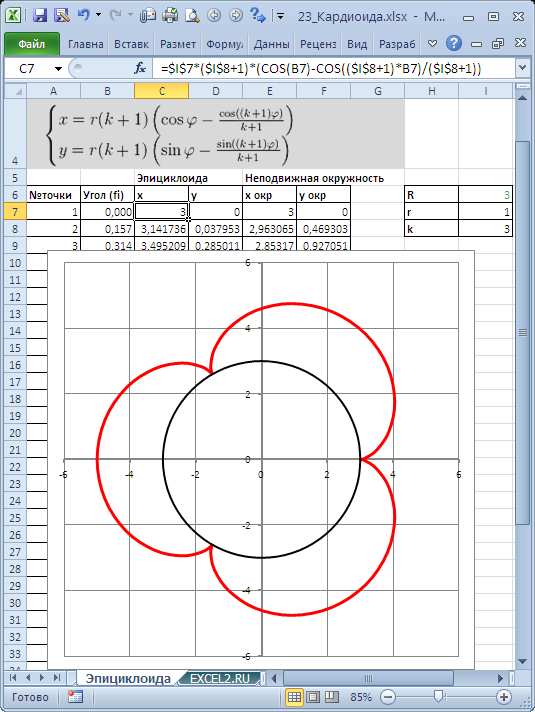
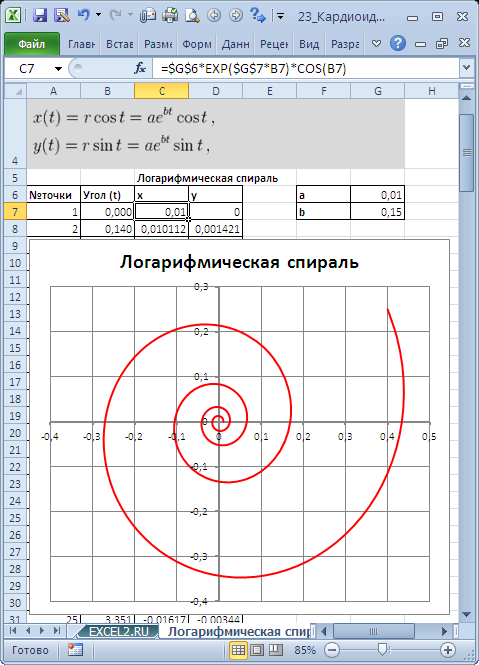
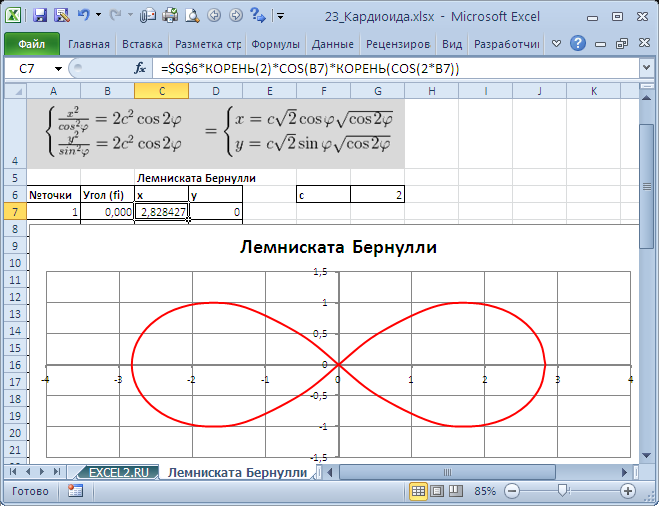
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Инфоурок
›
Информатика
›Другие методич. материалы›Практическая работа в MS EXCEL «Красивые графики»
Скачать материал
Скачать материал


- Сейчас обучается 30 человек из 17 регионов


- Сейчас обучается 82 человека из 37 регионов


- Сейчас обучается 21 человек из 13 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 211 007 материалов в базе
-
Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 28.02.2017
- 1261
- 14
- 28.02.2017
- 701
- 4
- 28.02.2017
- 531
- 0
- 28.02.2017
- 476
- 0
- 28.02.2017
- 476
- 0
- 28.02.2017
- 1354
- 15
- 28.02.2017
- 434
- 6
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Скачать материал
-
28.02.2017
22401
-
DOCX
1.1 мбайт -
452
скачивания -
Рейтинг:
3 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Zilowski Max Jurievich. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 2 года и 6 месяцев
- Подписчики: 0
- Всего просмотров: 434924
-
Всего материалов:
49
Файлы
Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Был в сети 07.04.2023 09:00

Куликовский Максим Юрьевич
преподаватель
10 546
2 245
13.12.2018 08:46
Просмотр содержимого документа
«Практическая работа в MS Excel «Графики»»
Практическая работа «Красивые графики функций»
-
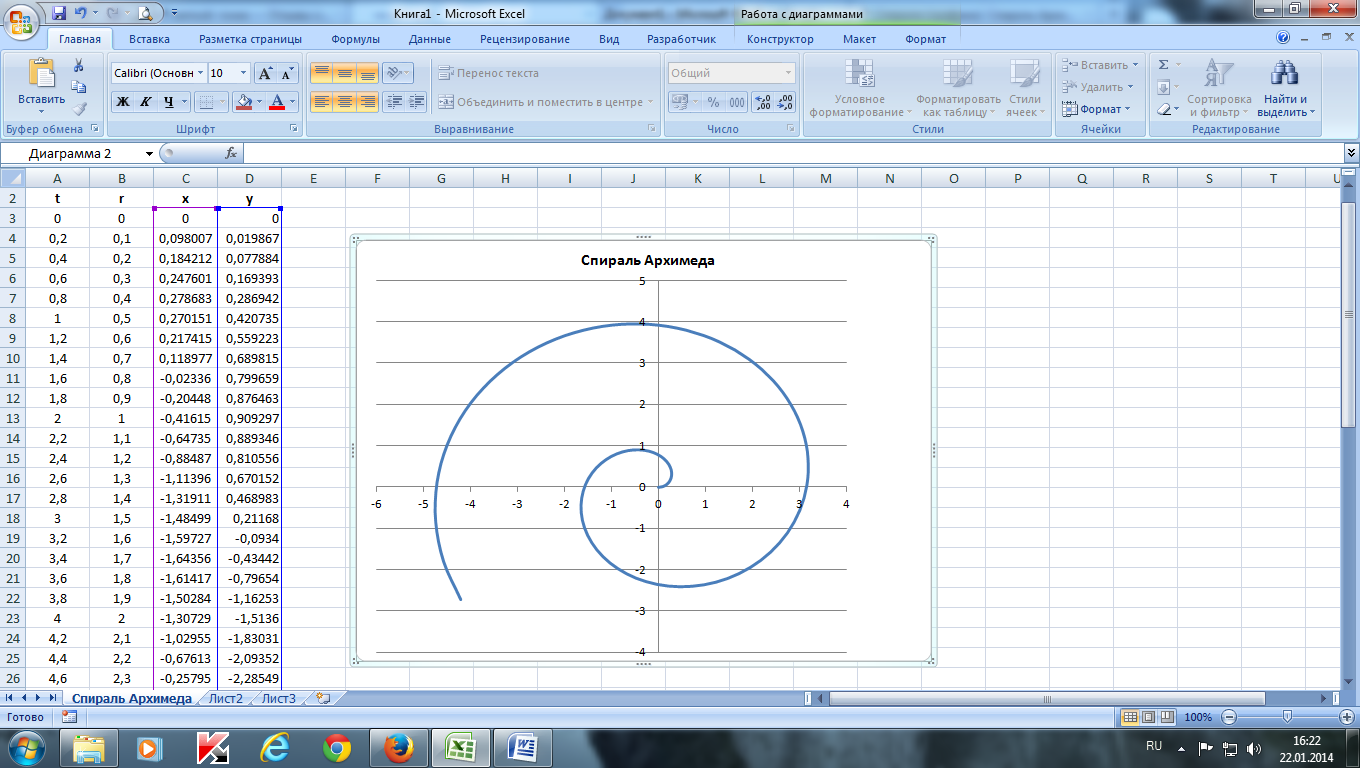
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5*t
— в столбце С – значения х = r*cos(t)
— в столбце D – значения y = r*sin(t)
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
-
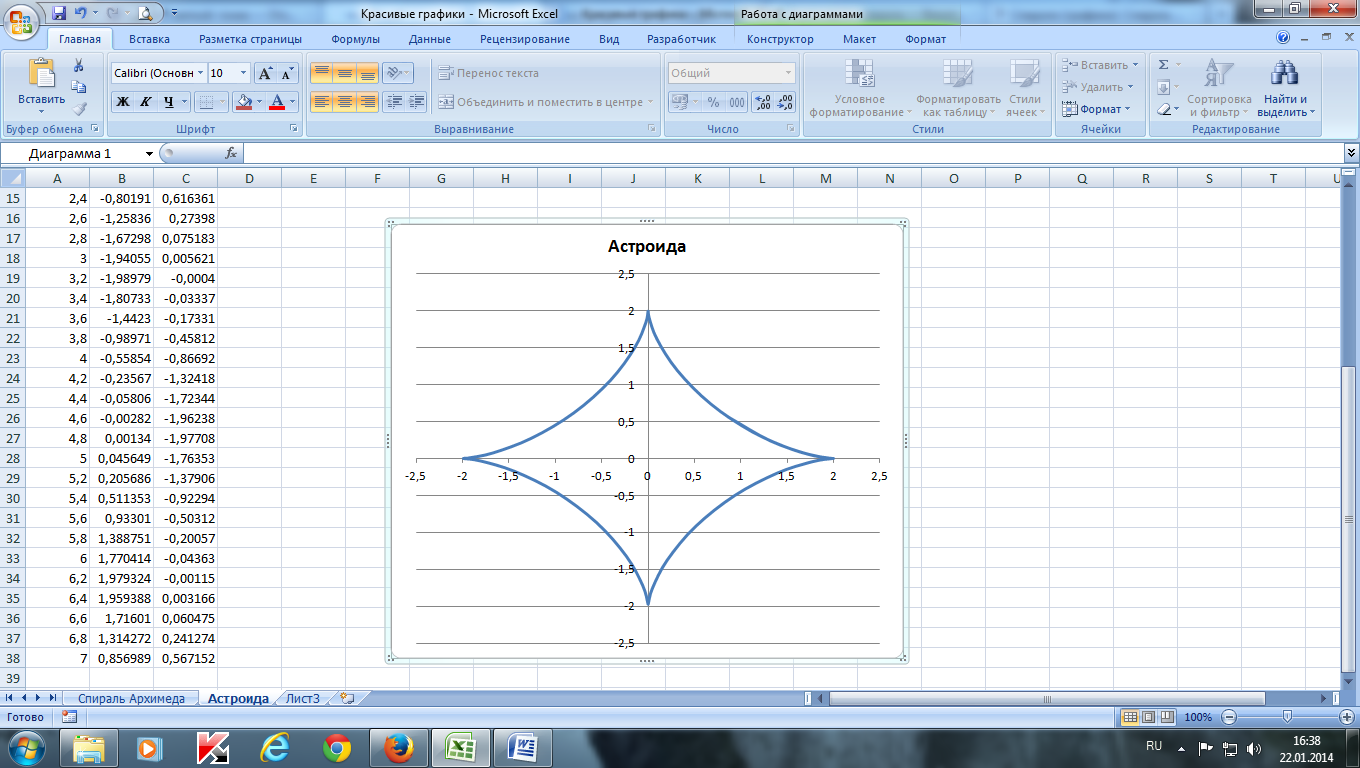
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*(cos (t))3
— в столбце С – значения y = 2*(sin (t))3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
-
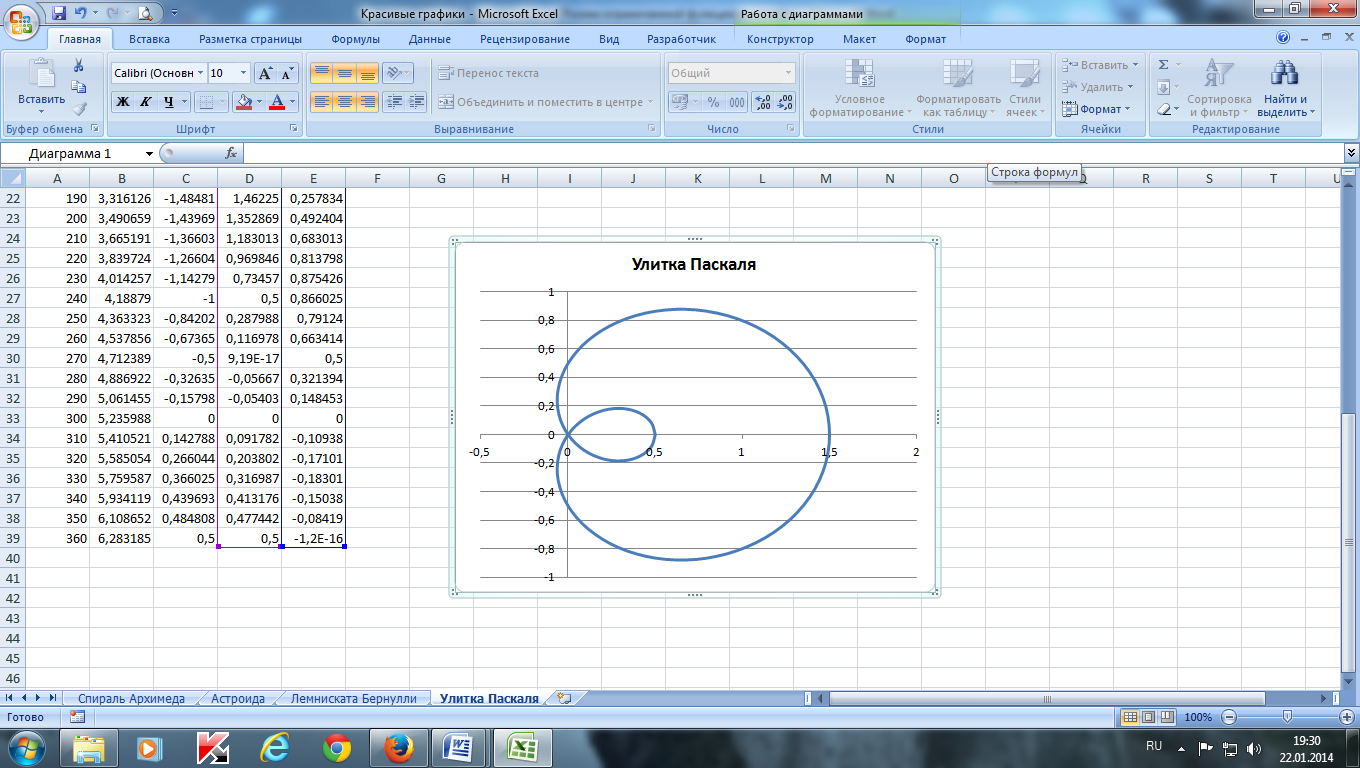
Построить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения p = cos(t)–0,5
— в столбце D – значения x = p*cos(t)
— в столбце Е – значения у = p*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми) -
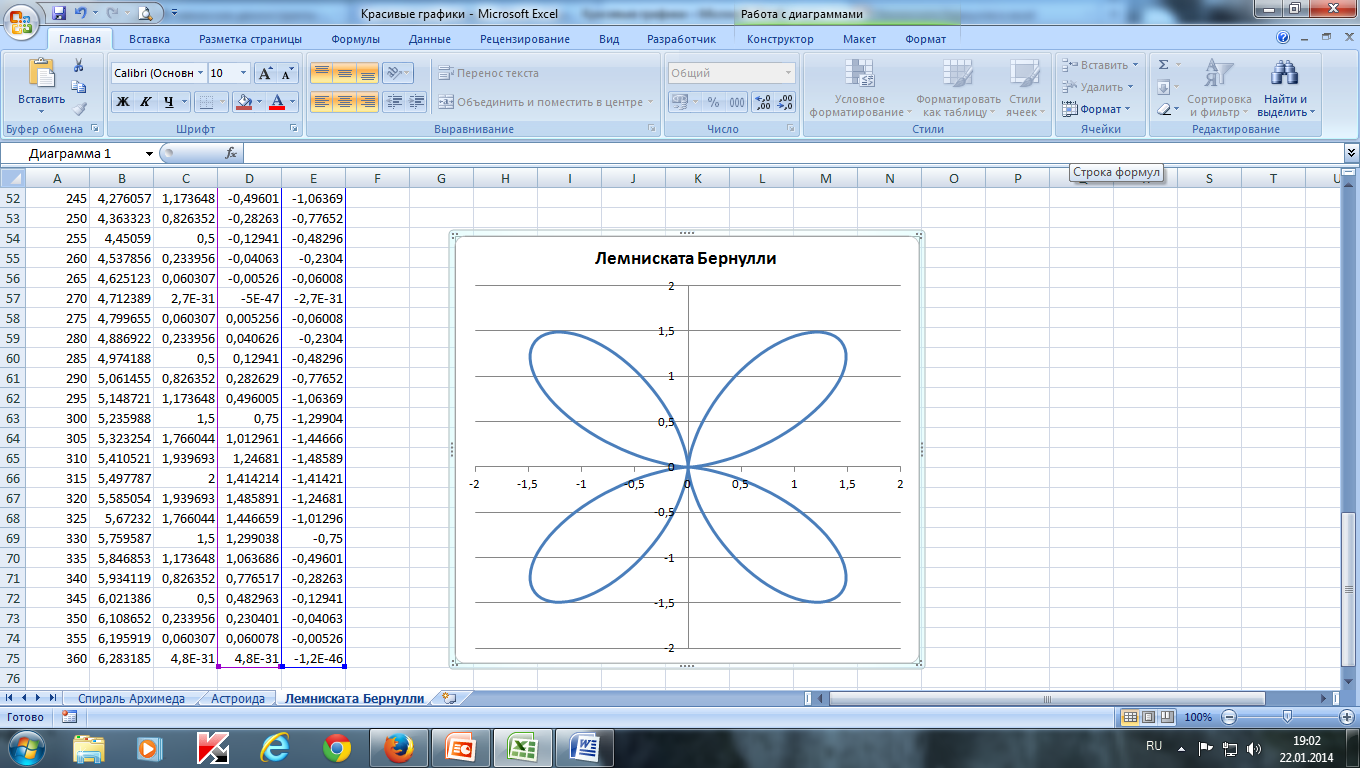
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения r = 2*sin(2*t)2
— в столбце D – значения x = r*cos(t)
— в столбце E – значения y = r*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
-
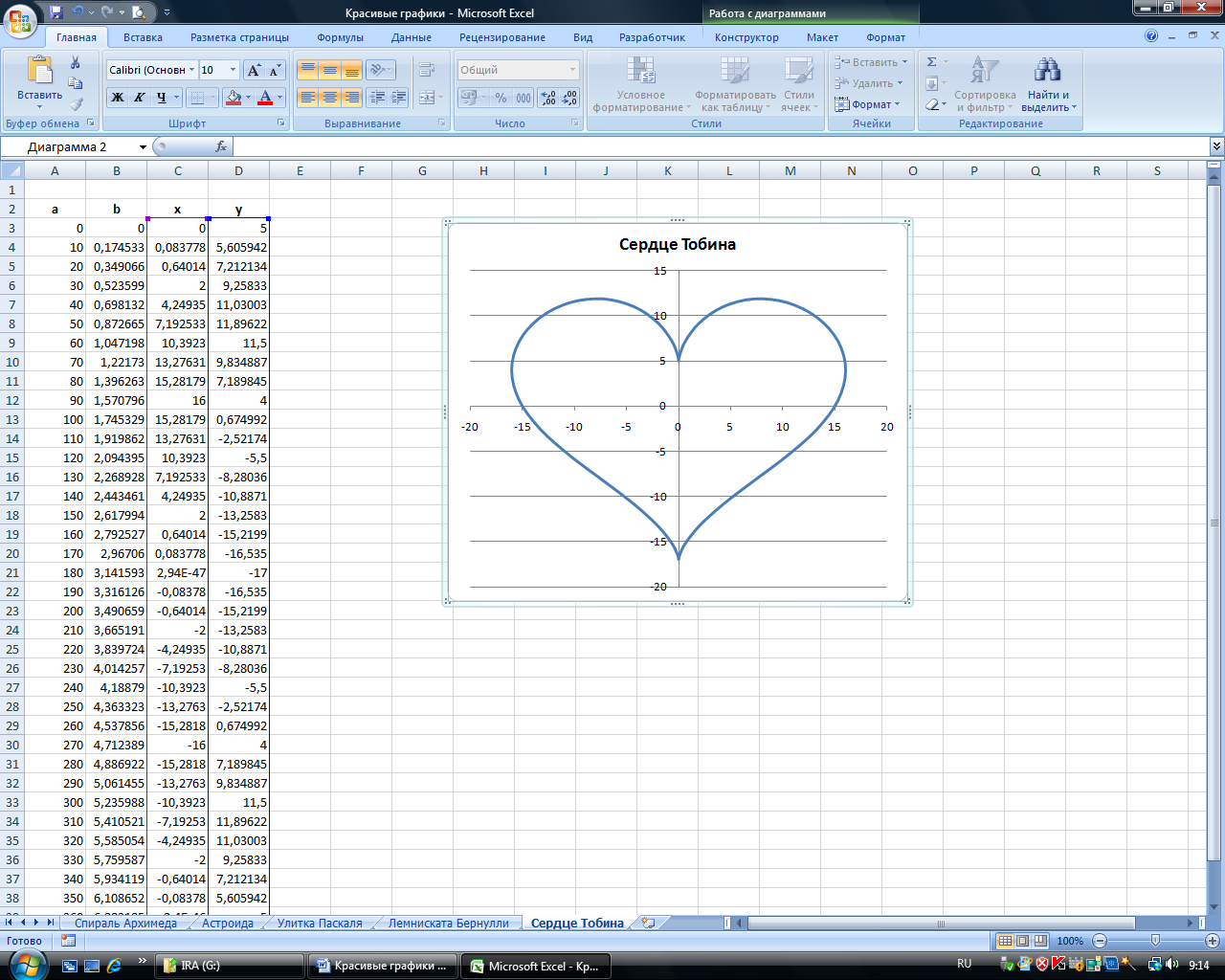
Построить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения x = 16*(sin(t))3
— в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Егорова Елена 
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.
Наговицина Ольга Витальевна 
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования
занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз
разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио.
Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь
полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и
особенно радует, что есть варианты с сочинением, без сочинения, только анализ
сочинения! Превосходно!
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см.
файл примера
):
х=2*а*cos(t)-а*cos(2*t)
y=2*а*sin(t)-а*sin(2*t)
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье
Эллипс и окружность в MS EXCEL
построены окружность и эллипс.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
|
Как построить график спирали Архимеда в Excel? |
||||||||
Ответить |
||||||||
Ответить |
Содержание
- Как сделать спираль архимеда в excel
- Архимедова спираль
- Excel
- Плоские алгебраические кривые в EXCEL
- Как Построить Спираль Архимеда в Excel Пошагово • Построение окружности
- СОДЕРЖАНИЕ
- Вывод общего уравнения спирали [ править ]
- Длина дуги, кривизна [ править ]
- Характеристики [ править ]
- Общая архимедова спираль [ править ]
- Приложения [ править ]
- Спираль в SOLIDWORKS | Спираль Архимеда © Студия Vertex
- Спираль в SOLIDWORKS
- Видеокурс по этой теме
- Видеокурс «Моделирование в SOLIDWORKS. Полное руководство»
- Спираль по траектории
- Построение логарифмической спирали
- Архимедова спираль
- Как Построить Спираль Архимеда в Excel по Данным • Построение гороскопа
- Содержание
- Вывод общего уравнения спирали.
- Характеристики
- Общая архимедова спираль
- Приложения
Как сделать спираль архимеда в excel
Архимедова спираль
Архимедова спираль Архимедова спираль – это кривая, задаваемая так: X(T)=T*COS(T), Y(T)=T*SIN(T) T – задается в радианах и изменяется от 0 до бесконечности. Кривая, заданная параметрически, — это множество точек плоскости вида (X(T);Y(T)), где T – это независимая переменная, называемая в данном случае параметром. Таких кривых очень много. Мы познакомимся с некоторыми из них. Давайте построим эту кривую. Запустим Excel. В данном случае нам нужно табулировать не одну, а две функции – X(T) и Y(T).
Слайд 17 из презентации «Построение графиков в Excel». Размер архива с презентацией 381 КБ.
Excel
«Работа в Excel» — Форматирование. Команды на ленте. Улучшение Excel. Столбцы листа. Начало работы. Операции. Подробные сведения. Форматы файлов. Обучение работе с Microsoft. Верхний колонтитул. Работа с файлами предыдущих версий. Отличия. Столбец. Шаблон Excel. Заголовки. Доступ к командам. Резюме практических заданий. Панель быстрого доступа. Откройте нужный файл. Формат файлов. Что изменилось и почему. Формат файлов Excel.
«Знакомство с Excel» — Формулы. Табличный процессор. Адреса ячеек. Строка. Принцип относительной адресации. Отрицательное значение. Основной элемент. Данные электронной таблицы. Текстовые данные. Функции обработки диапазона. Операции манипулирования. Ячейка. Cтолбцы. Знакомство с Excel. Числовой формат. Назначение. Тип даты. Запуск электронных таблиц. Имя файла.
«Программа Excel» — Маркер заполнения. Абсолютная ссылка. Цель урока. Результат в данной ячейке. План урока. Функция. Арифметические действия. Ссылка на ячейку, то есть на адрес. Ситуация. Некоторые форматы находятся на панели инструментов. Закрепим основные понятия. Сортировка. Смешанные ссылки. Ярлык. Решение расчётной задачи. Возможности программы. Диаграмма. У каждой ячейки есть свой адрес. Виды ссылок. Тест. Когда курсор попадает в ячейку, она становится активной.
«Таблица данных в Excel» — Статистические данные. Регрессионная модель. Постановка задачи и гипотезы. Построим таблицу. Познакомить с понятием «статистика». Графики. График квадратичной функции. Исходная информация. Метод наименьших квадратов. Таблица «Excel». Запишите функции. График регрессионной модели. Математическая модель. Данные медицинской статистики. Сумма квадратов отклонений. Практическое использование. Продолжите предложения.
«Электронные таблицы Microsoft Excel» — Группировка данных. Диаграммы на основе сводных таблиц. Изменение области данных. Описание частей сводной таблицы. Добавление области данных. Анализ электронных таблиц. Консолидация. Обновление исходных данных. Сводная таблица. Внешние источники данных. Поля страницы. Части сводной таблицы. Структура сводной таблицы. Создание связей итоговой таблицы. Переключатель. Мастера сводных таблиц. Методы консолидации данных.
«Microsoft Office Excel» — Ячейка. Овладение практическими способами работы с информацией. MS Excel. Форматирование ячеек. Практическая работа. Объекты программы MS Excel. Элементы диаграммы. Правильный адрес ячейки. Диаграмма. Смешанной ссылкой. Назначение. Что такое ЭТ. Выдающийся, превосходящий другие. Электронные таблицы. Идеальный режим. Ссылка. Порядок создания диаграммы. Обработка числовых данных.
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
- Группы статей
- Диаграммы и графики
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Источник
Как Построить Спираль Архимеда в Excel Пошагово • Построение окружности
Резьб (также известный как арифметическая спираль ) представляет собой спираль , названной в честь третьего века до нашей эры греческого математика Архимеда . Это геометрическое место, соответствующее местоположениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью . Эквивалентно в полярных координатах ( r , θ ) его можно описать уравнением
с действительными числами a и b . Изменение параметра a перемещает центральную точку спирали наружу от начала координат (положительное значение a в направлении θ = 0 и отрицательное значение a в сторону θ = π ), в то время как b контролирует расстояние между петлями.
Таким образом, из приведенного выше уравнения можно утверждать: положение частицы от точки старта пропорционально углу θ с течением времени.
Архимед описал такую спираль в своей книге « О спиралях» . Конон Самосский был его другом, и Папп утверждает, что эту спираль открыл Конон. [1]
СОДЕРЖАНИЕ
Вывод общего уравнения спирали [ править ]
Ниже используется физический подход для понимания понятия спиралей Архимеда.
Предположим, что точечный объект движется в декартовой системе с постоянной скоростью v, направленной параллельно оси x относительно плоскости xy . Пусть в момент времени t = 0 объект находился в произвольной точке ( c , 0, 0) . Если плоскость xy вращается с постоянной угловой скоростью ω вокруг оси z , то скорость точки относительно оси z может быть записана как:
В ху плоскость поворачивается на угол ωt (против часовой стрелки) вокруг начала координат в времени т . ( c , 0) — положение объекта при t = 0 . P — это положение объекта в момент времени t на расстоянии R = vt + c .
Здесь vt + c — модуль вектора положения частицы в любой момент времени t , v x — составляющая скорости вдоль оси x, а v y — составляющая вдоль оси y . Рисунок, показанный рядом, объясняет это.
Вышеупомянутые уравнения можно интегрировать, применяя интегрирование по частям , что приводит к следующим параметрическим уравнениям:
Возведение двух уравнений в квадрат с последующим сложением (и некоторыми небольшими изменениями) приводит к декартову уравнению
(используя тот факт, что ωt = θ и θ = arctg y / Икс ) или же
Длина дуги, кривизна [ править ]
Характеристики [ править ]
Архимедова спираль обладает тем свойством, что любой луч из начала координат пересекает последовательные повороты спирали в точках с постоянным разделительным расстоянием (равным 2 πb, если θ измеряется в радианах ), отсюда и название «арифметическая спираль». В отличие от этого, в логарифмической спирали эти расстояния, а также расстояния до точек пересечения, измеренные от начала координат, образуют геометрическую прогрессию .
Оскулирующие круги спирали Архимеда. Сама спираль не рисуется: мы видим ее как геометрическое место точек, где окружности особенно близки друг к другу.
Для больших θ точка движется с хорошо аппроксимированным равномерным ускорением по спирали Архимеда, в то время как спираль соответствует положениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью [2] (см. вклад Михаила Гайченкова).
Общая архимедова спираль [ править ]
Иногда термин спираль Архимеда используется для более общей группы спиралей.
Приложения [ править ]
В одном из методов квадрата круга , предложенном Архимедом, используется архимедова спираль. Архимед также показал, как спиралью можно разрезать угол пополам . Оба подхода ослабляют традиционные ограничения на использование линейки и циркуля в древнегреческих геометрических доказательствах. [3] [expert_bq использованием инструментов Основание по траектории и Геликоид и спираль , в SolidWorks можно создавать на первый взгляд сложные, но на практике простые и разнообразные вещи. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq] Всеобъемлющий видеокурс направленный на максимально полное освоение и профессиональное применение инструментов и приемов конструирования в программном комплексе SOLIDWORKS. Обучение на примере создания цифровых прототипов сложных изделий и сборок, разбор…
Спираль в SOLIDWORKS | Спираль Архимеда © Студия Vertex
Спираль Архимеда и закон октав Искусство – и я имею в виду подлинное, доброе искусство – зиждется, помимо всего прочего, на принципах баланса, динамики, местоположения и композиции. Эти элементы должны находиться в гармонии, взаимодействовать друг с другом, чтобы
Спираль в SOLIDWORKS
Рассмотрим как можно сделать спираль в SolidWorks и какие операции можно проводить используя инструмент Геликод и спираль.
Видеокурс по этой теме
Видеокурс «Моделирование в SOLIDWORKS. Полное руководство»
Всеобъемлющий видеокурс направленный на максимально полное освоение и профессиональное применение инструментов и приемов конструирования в программном комплексе SOLIDWORKS. Обучение на примере создания цифровых прототипов сложных изделий и сборок, разбор…
Спираль по траектории
Запустим SolidWorks и создадим новый документ Деталь.
Построим эскиз на плоскости Спереди.
Чертим окружность с диаметром 5 мм и расстоянием от центра координат 50 мм.
Выходим из эскиза и создаем еще один эскиз на этой же плоскости.
От центра координат, чертим вертикальную линию с высотой в 100 мм. Нажимаем ОК и выходим из эскиза.
Итого имеем два эскиза на плоскости Спереди. Во вкладке Элементы нажимаем на Бобышка/основание по траектории. Построим спираль по траектории.
На панели параметров для синей области указываем Эскиз 1 который будет являться сечением для спирали, а для красной области выбираем Эскиз 2, который будет как центр вращением траектории спирали.
Далее открываем вкладку Параметры>Указать величину скручивания и в Контроль скручивания выбираем Вращения (указываем значение 10). То есть задавая эти параметры, мы неким образом накладываем массив по спирали. При этом можем видеть как предварительно будет выглядеть спираль. Нажимаем ОК.
Спираль по траектории готова. Таким образом мы построили пружину.
Построение логарифмической спирали
Рассмотрим как можно построить так называемую спираль Архимеда в SolidWorks.
Откроем новый документ и создадим Эскиз на плоскости Спереди.
Переходим во вкладку Элементы > Кривые > Геликоид и спираль.
Кликаем на построенную окружность и в панели параметров указываем нужные параметры для построения логарифмической спирали (Шаг, количество оборотов, угол, направление по стрелке). Нажимаем ОК.
Спираль Архимеда готова! Если указать для нее сечение, как в предыдущем блоке и построить эскиз, можно создать так же основание по траектории и получим твердотельную спираль.
С использованием инструментов Основание по траектории и Геликоид и спираль, в SolidWorks можно создавать на первый взгляд сложные, но на практике простые и разнообразные вещи.
[expert_bq спираль обладает тем свойством, что любой луч из начала координат пересекает последовательные повороты спирали в точках с постоянным разделительным расстоянием равным 2 πb, если θ измеряется в радианах , отсюда и название арифметическая спираль. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq] Здесь vt + c — модуль вектора положения частицы в любой момент времени t , v x — составляющая скорости вдоль оси x, а v y — составляющая вдоль оси y . Рисунок, показанный рядом, объясняет это.
Архимедова спираль
Глава 11. Конец спирали, ведущей вниз Следующие семь лет моя карьера и семейная жизнь продолжали испытывать кризис. Долгое время окружающие меня люди — даже самые близкие — не могли понять, каковы мои проблемы. Но постепенно, наблюдая за мной, Холли и сестры догадались, в
Источник
Как Построить Спираль Архимеда в Excel по Данным • Построение гороскопа
В Архимедова спираль (также известный как арифметическая спираль) это спираль назван в честь III века до нашей эры Греческий математик Архимед. Это локус точек, соответствующих местоположениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловая скорость. Эквивалентно в полярные координаты (р, θ) его можно описать уравнением
с действительные числа а и б . Изменение параметра а перемещает центральную точку спирали наружу от начала координат (положительный а к θ = 0 и отрицательный а к θ = π ), пока б контролирует расстояние между петлями.
Таким образом, из приведенного выше уравнения можно утверждать: положение частицы от начальной точки пропорционально углу θ по прошествии времени.
Архимед описал такую спираль в своей книге. На спиралях. Конон Самосский был его другом и Паппус заявляет, что эта спираль была открыта Кононом. [1]
Содержание
Вывод общего уравнения спирали.
А физический подход используется ниже для понимания понятия спиралей Архимеда.
Предположим, что точечный объект движется в Декартова система с постоянным скорость v направлен параллельно Икс -оси относительно ху -самолет. Пусть на время т = 0 , объект находился в произвольной точке (c, 0, 0) . Если ху самолет вращается с постоянной угловая скорость ω о z -оси, то скорость точки относительно z -axis можно записать как:
В ху плоскость поворачивается на угол ωt (против часовой стрелки) о происхождении во времени т . (c, 0) положение объекта в т = 0 . п положение объекта во время т , на расстоянии р = vt + c .
Здесь vt + c модуль вектор положения частицы в любое время т , vИкс — компонента скорости вдоль Икс ось и vу компонент вдоль у -ось. Рисунок, показанный рядом, объясняет это.
Приведенные выше уравнения можно интегрировать, применяя интеграция по частям, что приводит к следующим параметрическим уравнениям:
Возведение двух уравнений в квадрат с последующим сложением (и некоторыми небольшими изменениями) приводит к декартову уравнению
(используя тот факт, что ωt = θ и θ = arctan у / Икс ) или же
Характеристики
Архимедова спираль обладает тем свойством, что любой луч из начала координат пересекает последовательные повороты спирали в точках с постоянным разделительным расстоянием (равным 2πb если θ измеряется в радианы), отсюда и название «арифметическая спираль». В отличие от этого, в логарифмическая спираль эти расстояния, а также расстояния до точек пересечения, измеренные от начала координат, образуют геометрическая прогрессия.
Оскулирующие круги архимедовой спирали. Сама спираль не рисуется: мы видим ее как геометрическое место точек, в которых круги особенно близки друг к другу.
Для больших θ точка движется с хорошо приближенным равномерным ускорением по спирали Архимеда, в то время как спираль соответствует положениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью [2] (см. вклад Михаила Гайченкова).
Общая архимедова спираль
Иногда термин Архимедова спираль используется для более общей группы спиралей
Нормальная архимедова спираль возникает, когда c = 1 . К другим спиралям, попадающим в эту группу, относятся: гиперболическая спираль ( c = −1 ), Спираль Ферма ( c = 2 ), а литуус ( c = −2 ). Практически все статические спирали, встречающиеся в природе, являются логарифмические спиралиа не архимедовы. Многие динамические спирали (например, Спираль Паркера из Солнечный ветер, или узор, сделанный Екатерининское колесо) архимедовы.
Приложения
Один метод квадрат круга, согласно Архимеду, использует спираль Архимеда. Архимед также показал, как можно использовать спираль для разрезать угол. Оба подхода ослабляют традиционные ограничения на использование линейки и циркуля в древнегреческих геометрических доказательствах. [3]
Источник
Разберем интересную интерпретацию радиальной гистограммы в Excel позволяющая сравнивать несколько показателей и эффектно визуализировать данные.
Приветствую всех, дорогие читатели блога TutorExcel.Ru!
Практически бесконечно долго можно обсуждать и придумывать как можно тот или иной тип данных визуализировать в Excel. Сегодня тоже не пройдем мимо этой темы, поговорим про визуализацию данных и рассмотрим построение радиальной гистограммы в Excel.
Чем же особенна эта радиальная гистограмма?
В общем и целом это гистограмма построенная в радиальной системе координат (всем нам привычная классическая линейная гистограмма использует евклидову геометрию), грубо говоря мы берем обычную гистограмму и сворачиваем ее в круг:

Ее отличительной особенностью и одновременно недостатком является то, что иногда ее интерпретируют некорректно, так как каждая полоса радиальной гистограммы становится длиннее (чем дальше полоса от центра), даже если им соответствуют одни и те же числа. Нашему глазу более привычен классический вид диаграммы с прямыми столбцами/строками, поэтому этот вариант применяется скорее для эффектного представления данных.
В общем мы в какой-то степени жертвуем функциональностью ради внешнего вида, но в некоторых случаях это того стоит.
Начнем.
Для построения графика в исходной таблице не должно быть очень большого количества данных, так как чем их больше, тем сложнее их будет уместить.
Давайте для примера рассмотрим выручку компании по итогам года в разбивке по кварталам и перед нами стоит задача сравнить периоды друг с другом:

Идем по стандартной схеме построения любого графика, выделим диапазон $A$1:$E$2 и построим кольцевую диаграмму, в панели вкладок выбираем Вставка -> Диаграммы -> Круговая -> Кольцевая:

Получили вот такой своеобразный бублик. Давайте сразу поменяем строки и столбцы местами, чтобы каждое значение из нашей таблицы откладывалось по новому ряду и, условно говоря, из одного кольца получить несколько, в данном случае 4, по числу кварталов в таблице:
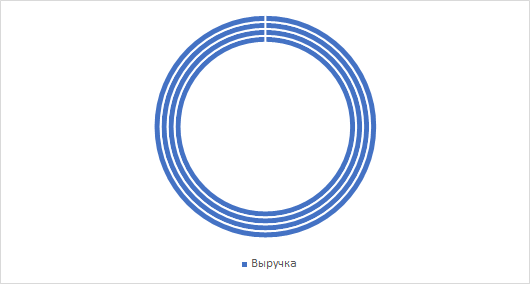
Как мы видим все ряды на диаграмме выглядят абсолютно одинаково, хотя на самом деле соответствуют разным значениям. Это происходит из-за того, что радиальная диаграмма по построению заполняет данными всю длину кольца. Поэтому чтобы значения из нашей таблицы показывались действительно по-разному нам нужно добавить вспомогательный ряд, который бы уравновесил величину столбцов на диаграмме.
На первый взгляд может показаться несколько сложно, но на самом деле мы сейчас на примере все подробно разберем.
Давайте введем параметр, отвечающий какой процент от величины круга занимает столбец с максимальным значением, установим его равным 75%.
Теперь перейдем к заданию дополнительного ряда, найдем максимальное значение в таблице (с помощью функции МАКС, в английской версии MAX) и с учетом заданного параметра пропишем каждое значение из дополнительного ряда как дополнение до максимума значения из основной таблицы:

Теперь расширяем диапазон построения гистограммы до $A$1:$E$3, чтобы на диаграмму добавился дополнительный ряд и в результате получаем:

Как мы видим картинка уже внешне стала напоминать желаемый вид. Также обратите внимание, что столбец с максимальным значением занимает ровно 3/4 круга, т.е 75%, именно эту величину мы и задавали в качестве параметра. Можете поиграться со значением и выбрать именно тот вариант который подойдет для вашей задачи.
Затем скроем ненужные на диаграмме столбцы вспомогательного ряда, по очереди выделим каждый из них на гистограмме и поставим прозрачную заливку, чтобы оранжевые столбцы пропали с графика:

Пока на графике остается достаточно много свободного и неиспользованного места, поэтому можем также настроить, чтобы столбцы стали толще и пространство внутри диаграммы уменьшилось, для этого щелкаем правой кнопкой мыши по любому из рядов на диаграмме и в формате ряда данных настраиваем параметр Диаметр отверстия, в % от общего диаметра (в моем случаем установлено 75%, уменьшим его, к примеру, до 30%):

Остались небольшие детали, нам нужно добавить подписи данных на диаграмму.
Однако если мы это сделаем стандартным способом (щелкаем правой кнопкой мыши по ряду и выбираем Добавить подпись данных), то подпись добавится в середину каждого из столбцов, что визуально выглядит не лучшим образом:
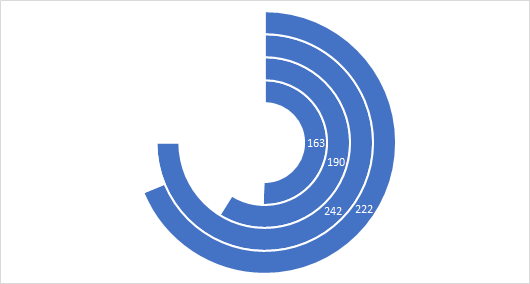
Поэтому предложу немного схитрить и добавить слева от начала каждого столбца текстовое поле, где мы пропишем числовое значение соответствующее каждому столбцу.
При этом чтобы каждый раз не менять руками значения пропишем в текстовом поле формулу в виде ссылки на значение из таблицы:

Теперь покрасим столбцы в подходящие цвета и диаграмма будет полностью готова:
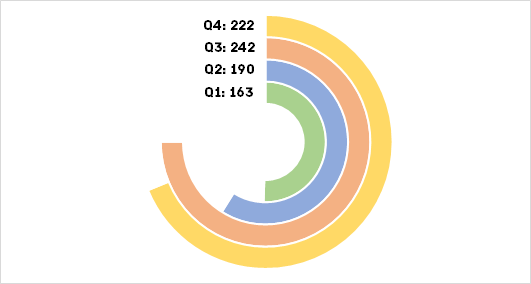
Также можно изменить точку начала отсчета гистограммы и повернуть ее на произвольный угол, иногда это может пригодиться. Щелкаем правой кнопкой мыши по ряду с данными, выбираем Формат ряда данных и устанавливаем параметр Угол поворота первого сектора. По умолчанию он задан равным 0 градусов, мы можем выставить любое значение от 0 до 360 градусов, например, тоже достаточно интересным вариантом будет значение 180 градусов:

В итоге мы получили весьма интересный формат диаграммы, который может пригодиться и как отдельный тип графика, так и, к примеру, в составе дэшборда для отображения KPI.
На этом все!
Скачать файл с примером.
Спасибо за внимание!
Если у вас есть какие-либо вопросы или мысли по теме — добро пожаловать в комментарии, не стесняйтесь спрашивать.
Удачи вам и до скорых встреч на страницах блога TutorExcel.Ru!