- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН();
- 3-й способ с помощью Forecast4AC PRO;
Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.
Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).
Что такое полином? Полином — это степенная функция y=ax2+bx+c (полином второй степени) и y=ax3+bx2+cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.
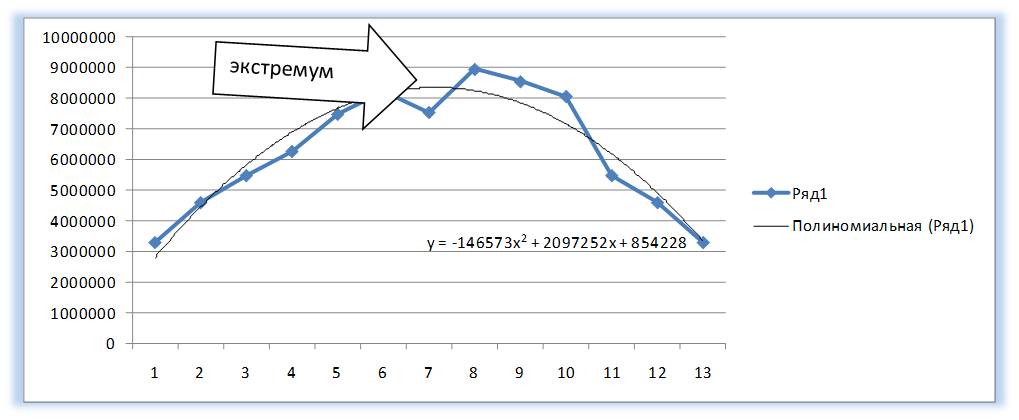
У полинома второй степени y=ax2+bx+c один экстремум (на графике ниже 1 максимум).
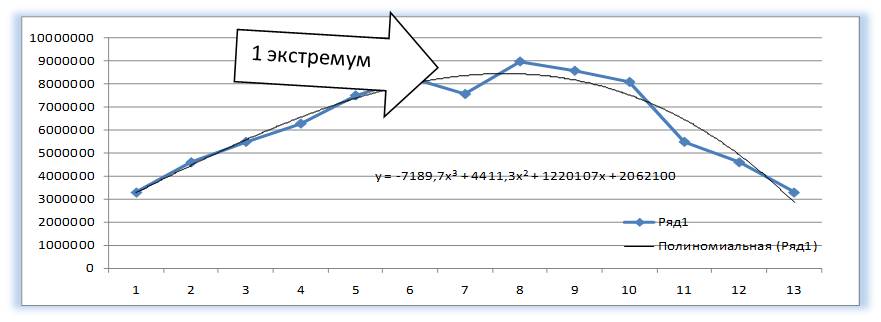
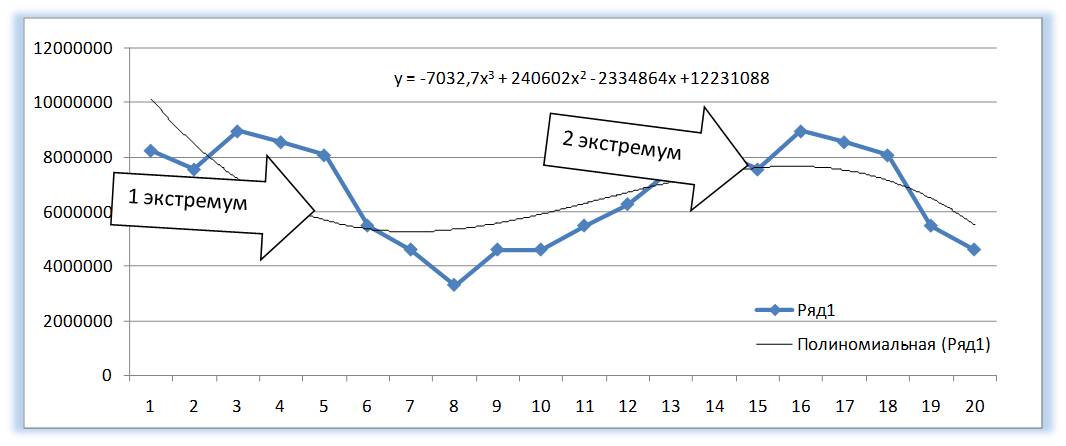
У Полинома третьей степени y=ax3+bx2+cx+d может быть один или два экстремума.
Один экстремум
Два экстремума
У Полинома четвертой степени не более трех экстремумов и т.д.
Как рассчитать значения полинома в Excel?
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН;
- 3-й способ с помощью Forecast4AC PRO;
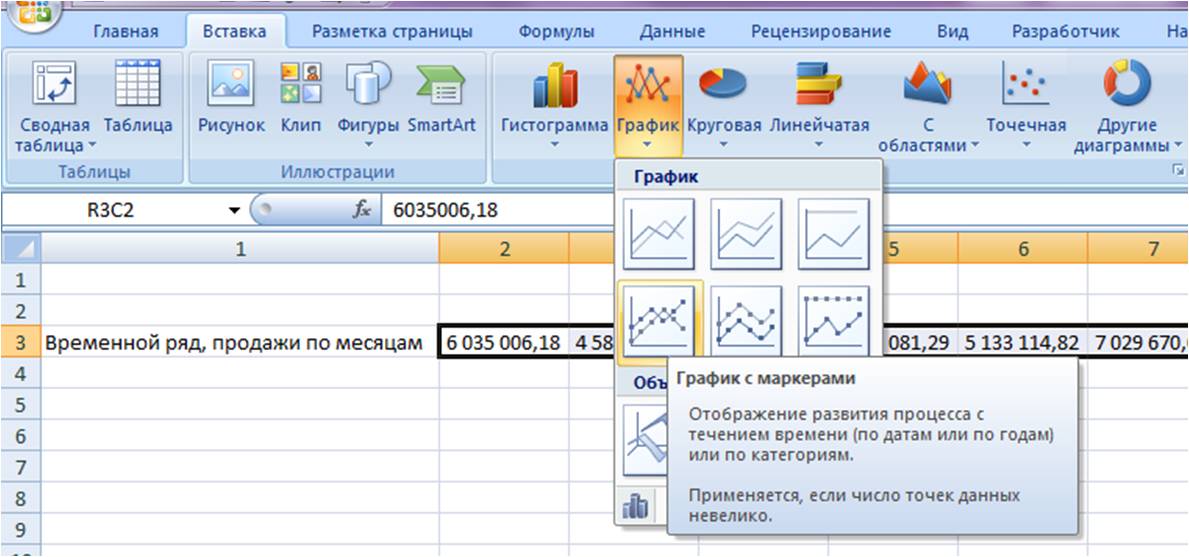
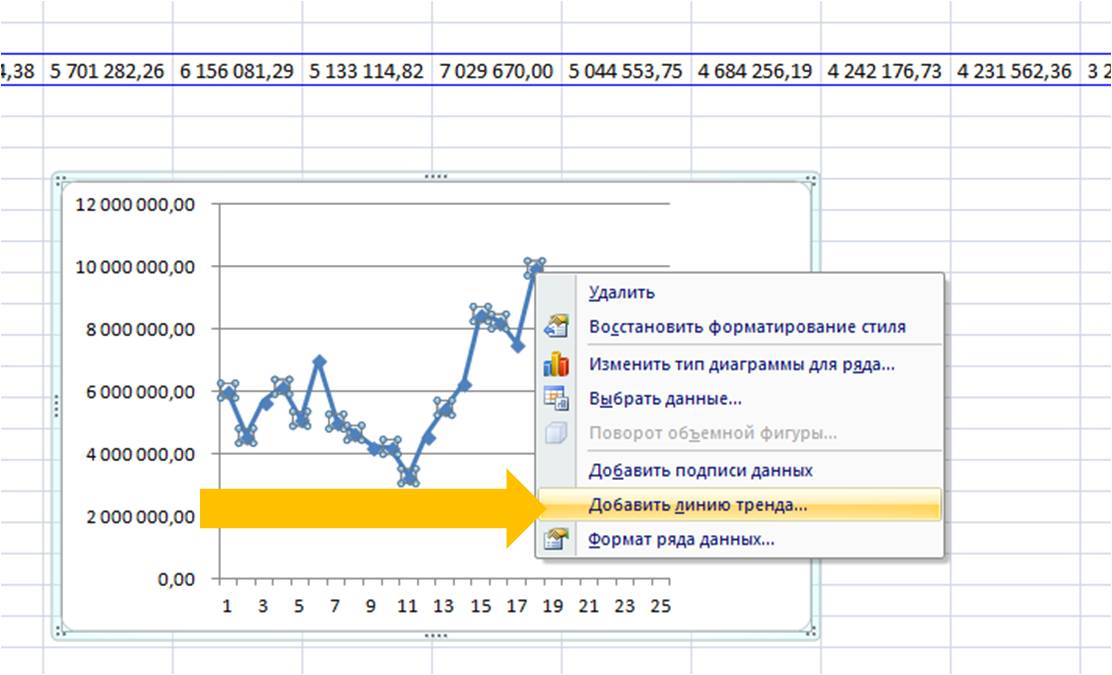
1-й способ расчета полинома — с помощью графика
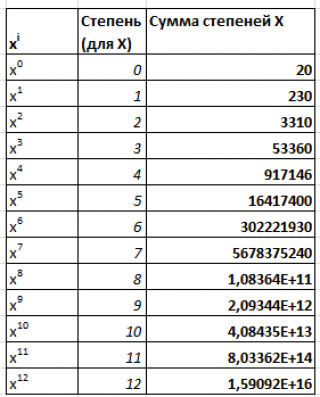
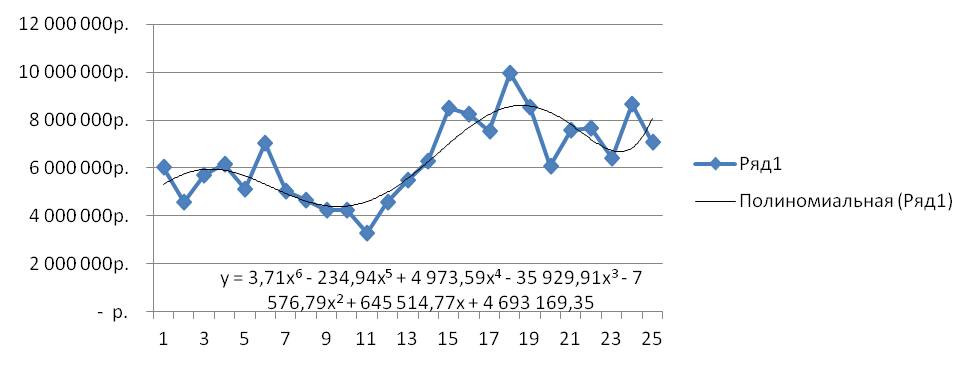
Выделяем ряд со значениями и строим график временного ряда.
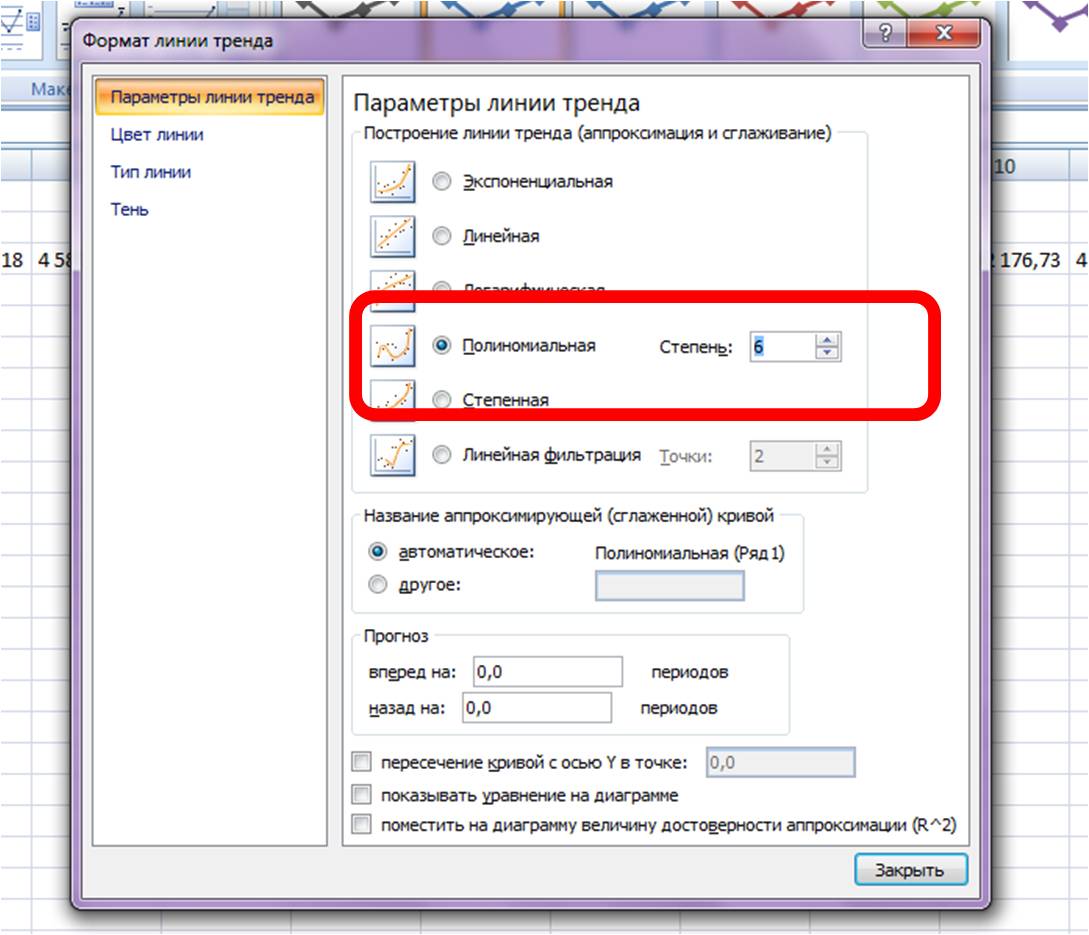
На график добавляем полином 6-й степени.
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»
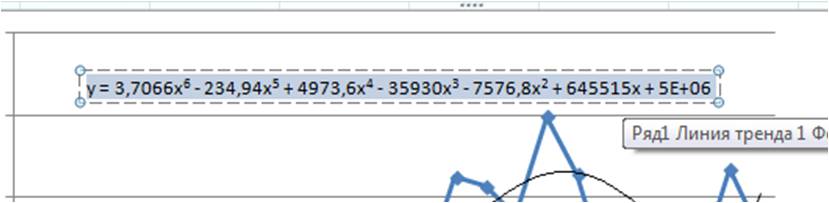
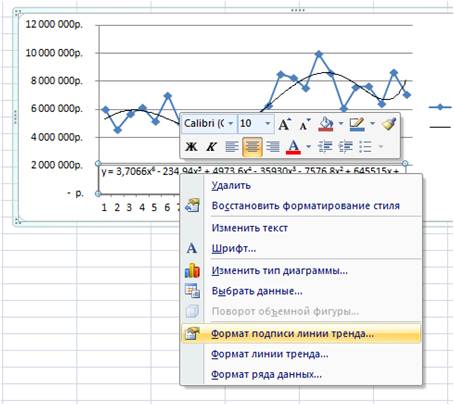
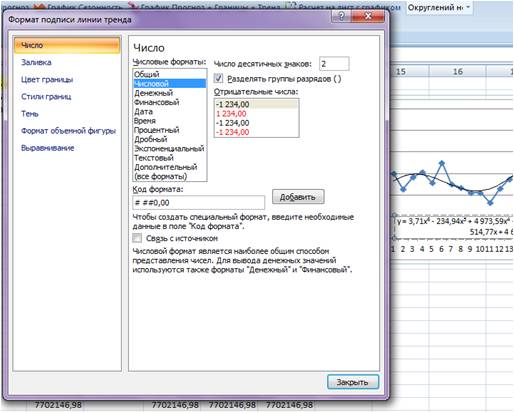
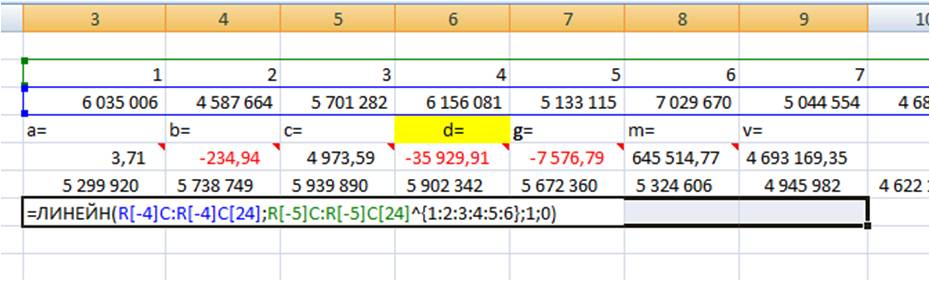
После этого уравнение выводится на график y = 3,7066x6 — 234,94x5 + 4973,6x4 — 35930x3 — 7576,8x2 + 645515x + 5E+06. Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».
Получаем уравнение полинома в читаемом формате:
y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35
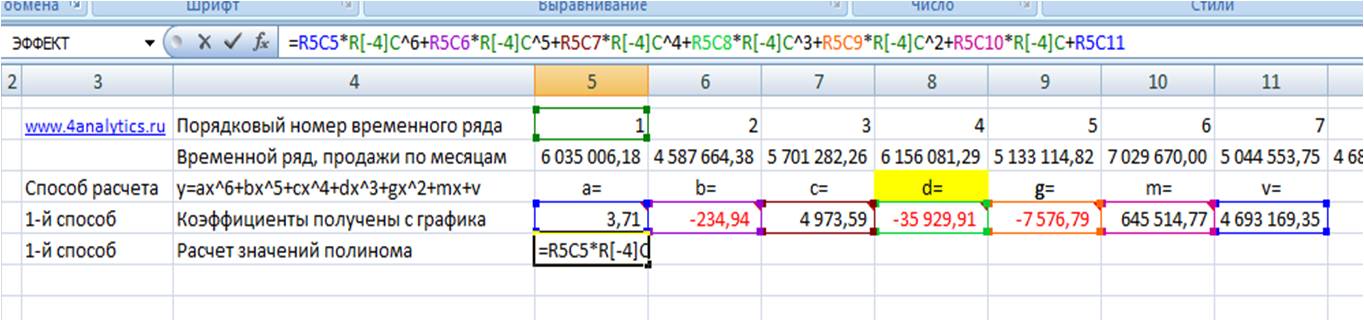
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.
Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()
Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:
- «известные значения y» (объёмы продаж за периоды),
- «известные значения x» (порядковый номер временного ряда),
- в константу ставим «1»,
- в статистику «0»
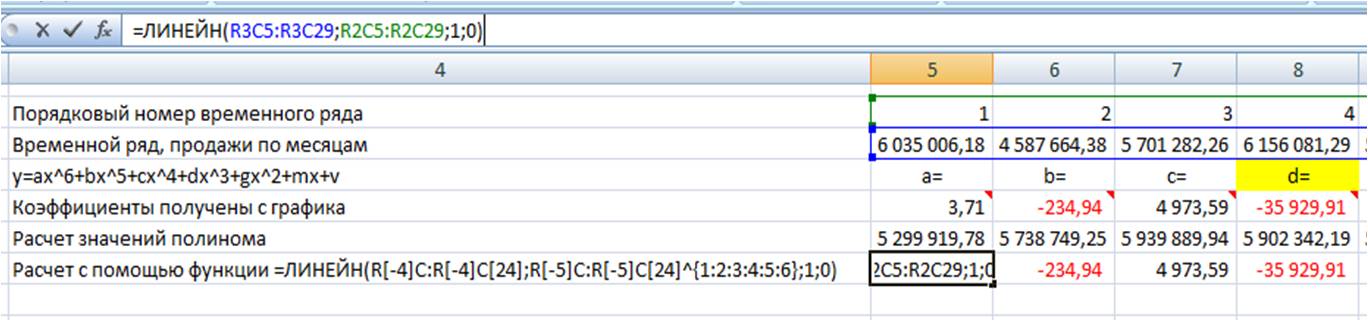
Получаем следующего вида формулу:
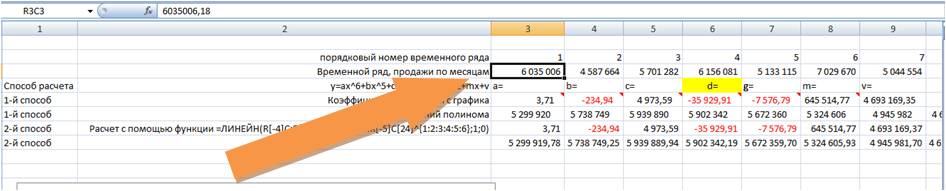
=ЛИНЕЙН(R[-4]C:R[-4]C[24];R[-5]C:R[-5]C[24];1;0),
Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.
Для этого в часть формулы с «известными значениями x» вписываем степень полинома:
- ^{1:2:3:4:5:6} — для расчета коэффициентов полинома 6-й степени
- ^{1:2:3:4:5} — для расчета коэффициентов полинома 5-й степени
- ^{1:2} — для расчета коэффициентов полинома 2-й степени
Получаем формулу следующего вида:
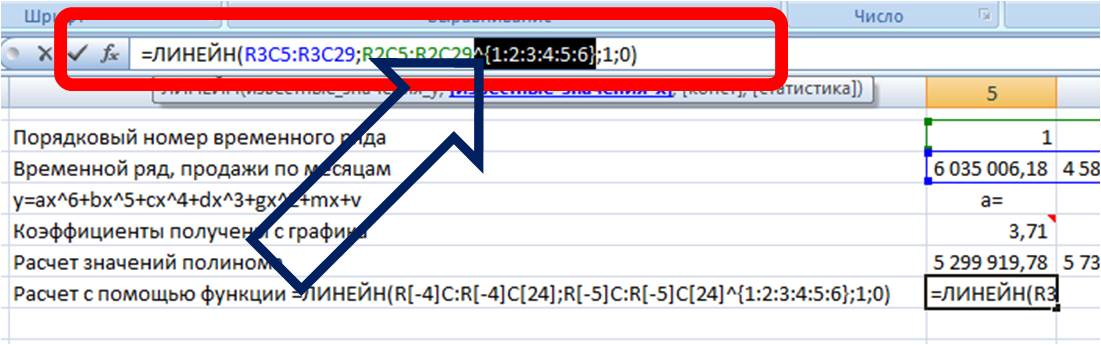
=ЛИНЕЙН(R[-4]C:R[-4]C[24]; R[-5]C:R[-5]C[24]^{1:2:3:4:5:6}; 1; 0)
Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v
Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:
1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:
2. Нажать на клавишу F2
3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)
Получаем 7 коэффициентов полиномиального тренда 6-й степени.
Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.
Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Устанавливаем курсор в начало временного ряда
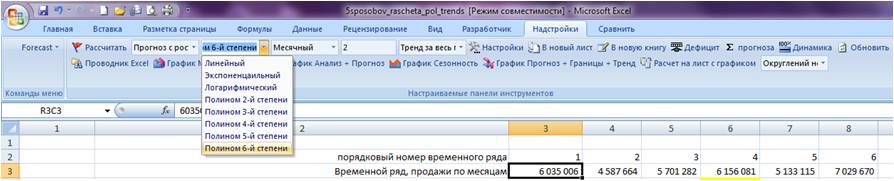
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».
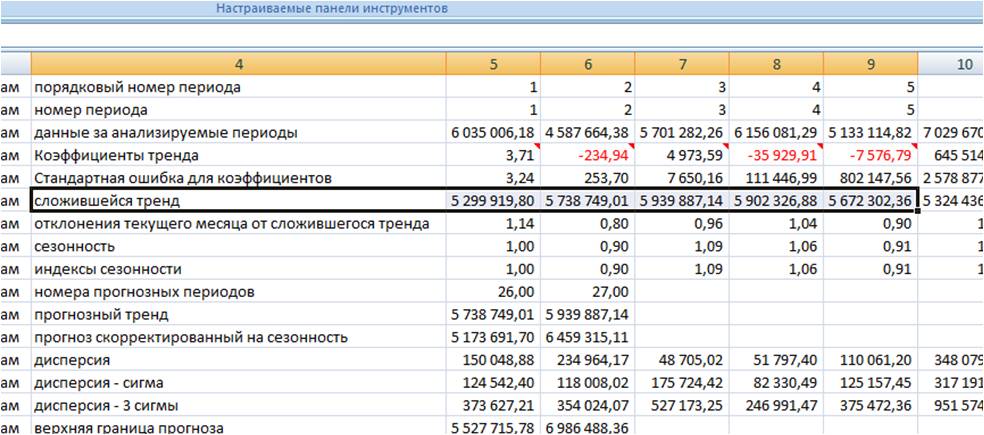
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:
Копируем значения в наш лист.
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:
Скачать файл с примером расчета значений полинома.
- Коэффициентов полиномиального тренда выведенных на график;
- Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
- и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
17 авг. 2022 г.
читать 1 мин
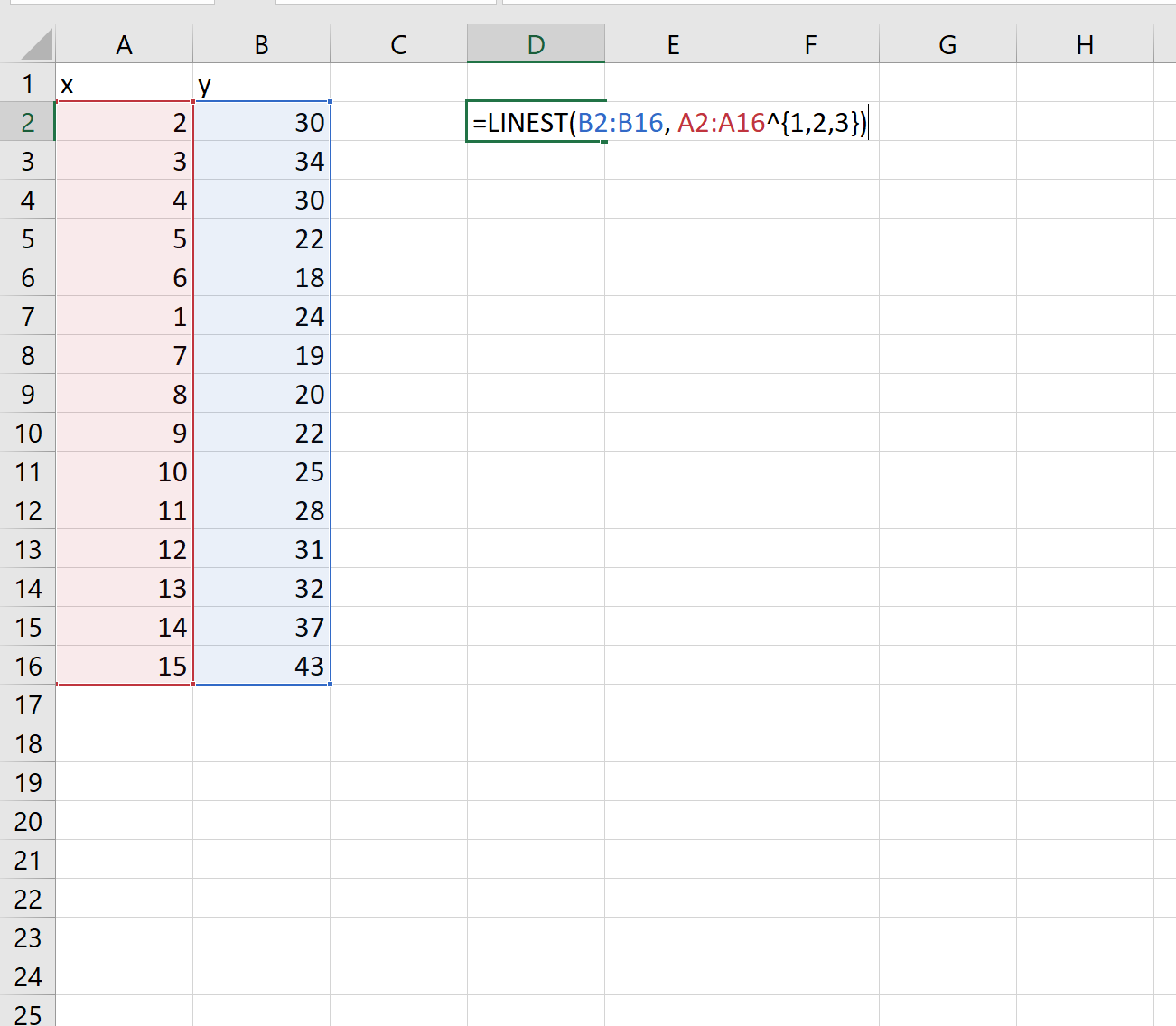
Вы можете использовать функцию ЛИНЕЙН() в Excel, чтобы подобрать полиномиальную кривую с определенной степенью.
Например, вы можете использовать следующий базовый синтаксис, чтобы подогнать полиномиальную кривую со степенью 3:
=LINEST( known_ys , known_xs ^{1, 2, 3})
Функция возвращает массив коэффициентов, описывающих полиномиальную подгонку.
В следующем пошаговом примере показано, как использовать эту функцию для подбора полиномиальной кривой в Excel.
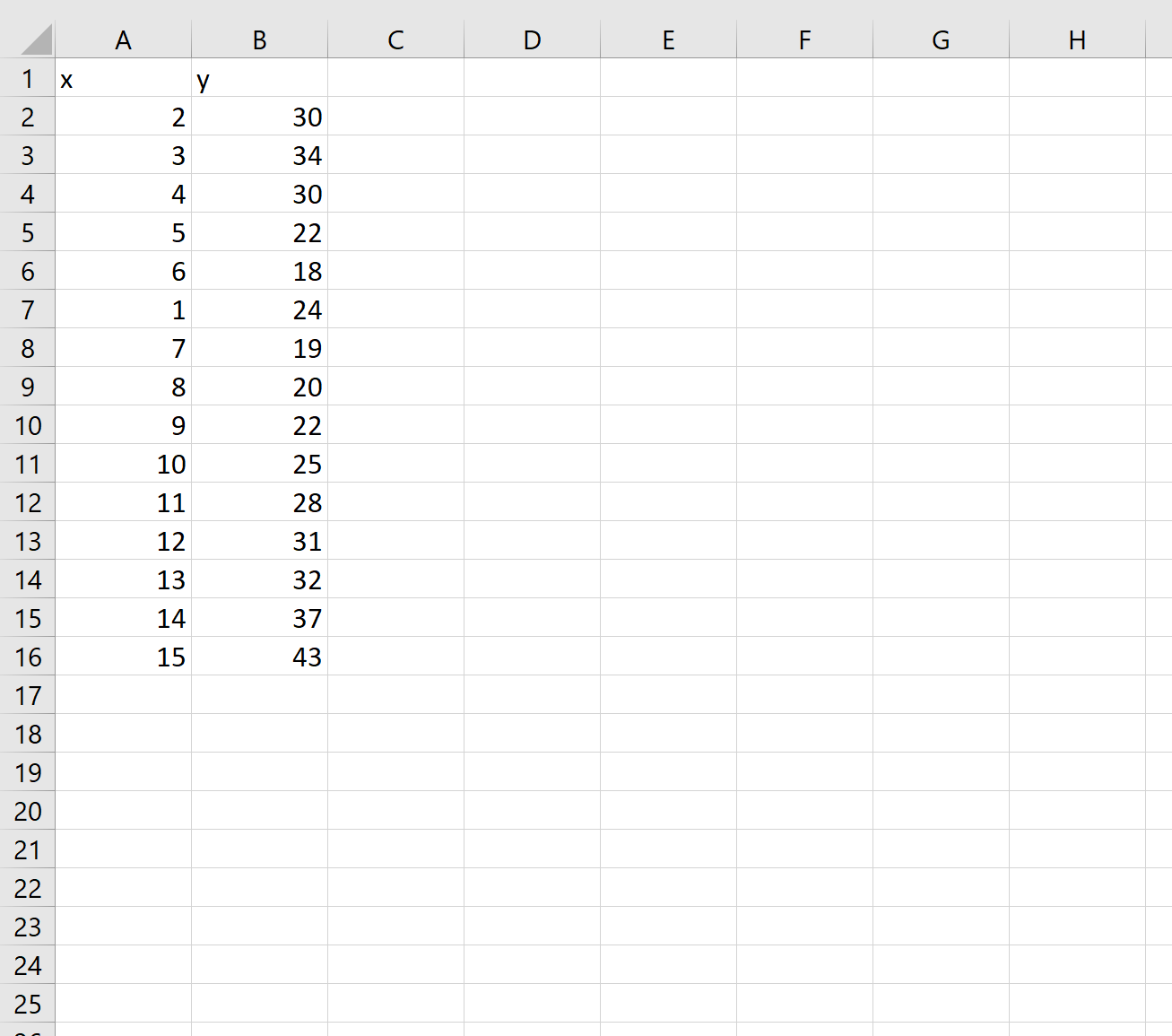
Шаг 1: Создайте данные
Во-первых, давайте создадим некоторые данные для работы:
Шаг 2: Подберите полиномиальную кривую
Далее воспользуемся функцией ЛИНЕЙН() , чтобы подобрать полиномиальную кривую степени 3 к набору данных:
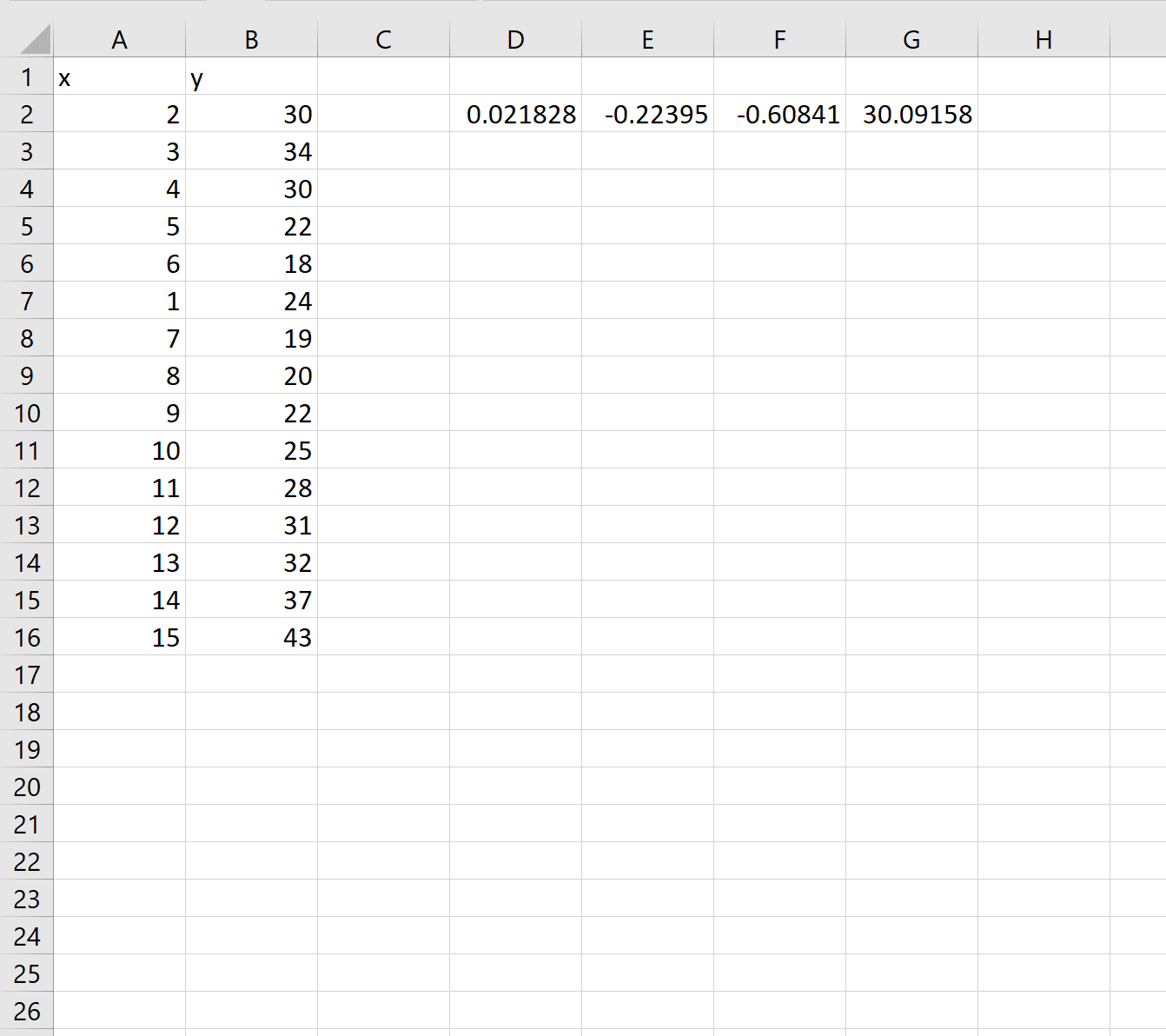
Шаг 3: Интерпретация полиномиальной кривой
Как только мы нажмем ENTER , появится массив коэффициентов:
Используя эти коэффициенты, мы можем построить следующее уравнение, описывающее взаимосвязь между x и y:
у = 0,0218x 3 – 0,2239x 2 – 0,6084x + 30,0915
Мы также можем использовать это уравнение для вычисления ожидаемого значения y на основе значения x.
Например, предположим, что x = 4. Ожидаемое значение y будет следующим:
у = 0,0218(4) 3 – 0,2239(4) 2 – 0,6084(4) + 30,0915 = 25,47
Дополнительные ресурсы
Как выполнить полиномиальную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как добавить квадратную линию тренда в Excel
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью полинома (до 6-й степени включительно).
В
основной статье про МНК
было рассмотрено приближение линейной функцией. В этой статье рассмотрим приближение полиномиальной функцией (с 3-й до 6-й степени) следующего вида: y=b
0
+b
1
x+b
2
x
2
+b
3
x
3
+…+b
6
x
6
Примечание
: В инструменте MS EXCEL
Линия тренда
, который доступен для диаграмм типа
Точечная и График
, можно построить
линию тренда
на основе полинома с максимальной степенью 6. В
файле примера
продемонстрировано полное совпадение
линии тренда
диаграммы и линии, вычисленной с помощью формул.
Покажем, как вычислить коэффициенты
b
линии тренда, заданной полиномом.
Как известно,
квадратичная зависимость y=b
0
+b
1
x+b
2
x
2
,
подробно рассмотренная в статье
МНК: Квадратичная зависимость в MS EXCEL
, является частным случаем полиномиальной y=b
0
+b
1
x+b
2
x
2
+b
3
x
3
+… зависимости (в этом случае степень полинома равна 2). Соответственно, используя тот же подход (приравнивание к 0 частных производных), можно вычислить коэффициенты любого полинома.
Примечание
: Существует еще один метод вычисления коэффициентов – замена переменных, который рассмотрен в конце статьи.
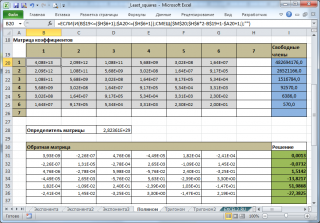
Для нахождения m+1 коэффициента полинома m-й степени составим систему из m+1 уравнения и решим ее
методом обратной матрицы
. Для квадратного уравнения (m=2) нам потребовалось вычислить сумму значений
х
с 1-й до 4-й степени, а для полинома m-й степени необходимо вычислить значения
х
с 1-й до 2*m степени.
Примечание
: Для удобства суммы степеней значений
х
можно вычислить в отдельном диапазоне (
файл примера
столбцы К:М).
В
файле примера
создана универсальная форма для вычисления коэффициентов полиномов.
Выбрав с помощью
элемента управления Счетчик
нужную степень полинома, автоматически получим аппроксимацию наших данных выбранным полиномом (будет построен соответствующий график).
Примечание:
При использовании полиномов высокой степени необходимо следить за тем, чтобы количество пар значений (х
i
; y
i
) превышало степень полинома хотя бы на несколько значений (для обеспечения точности аппроксимации). Кроме того, график функции полинома степени m имеет m-1 точку перегиба. Понятно, что точек данных должно быть гораздо больше, чем точек перегиба, чтобы такой изменчивый тренд стал очевидным (если утрировать, то бессмысленно строить по двум точкам параболу, логичнее построить прямую).
Как видно из расчетов, в MS EXCEL этот путь является достаточно трудоемким. Гораздо проще в MS EXCEL реализовать другой подход для вычисления коэффициентов полинома — с помощью замены переменных.
С помощью замены переменных x
i
=x
i
полиномиальную зависимость y=b
0
+b
1
x+b
2
x
2
+b
3
x
3
+… можно свести к линейной. Теперь переменная
y
зависит не от одной переменной
х
в
m
разных степенях, а от m независимых переменных x
i
. Поэтому для нахождения коэффициентов полинома мы можем использовать функцию
ЛИНЕЙН()
. Этот подход также продемонстрирован в
файле примера
.
Excel: как построить степенной полином функцией ЛИНЕЙН
Мы уже строили аналогичный интерполирующий полином в Excel, и в Mathcad «вручную», и стандартными функциями Mathcad тоже можно это сделать.
Сейчас мы хотим, во-первых, построить в Excel интерполирующий полином тоже стандартной функцией, во-вторых, не вдаваясь в детали теории, понять смысл этой простой задачи — как построить кривую, проходящую через несколько известных точек на плоскости.
Итак, по известному набору из N значений функции f(xi)=yi, заданному парой векторов xi, yi=f(xi), i=1, 2, ..., N, нужно построить кривую, проходящую через все точки.
Через N различных между собой по оси x точек всегда можно построить кривую, зависящую от xN-1, её уравнение будет иметь общий вид
f(x)=c0+c1*x+c2*x2+…+сN-1*xN-1 (1)
В этом уравнении нам неизвестны коэффициенты сi. Из условия, что кривая проходит через все заданные в постановке задачи точки, можно записать систему линейных алгебраических уравнений:
c0 +c1x1 +c2x12 +...+cN-1x1N-1 =y1
c0 +c1x2 +c2x22 +...+cN-1x2N-1 =y2
...
c0 +c1xN +c2xN2 +...+cN-1xNN-1 =yN
или, в матричном виде
Система линейных алгебраических уравнений, записанная в матричном виде
Решив эту систему уравнений, то есть, найдя обратную к матрице Вандермонда матрицу и умножив её на вектор y, найдём коэффициенты сi. Теперь, подставив их в уравнение (1), мы можем аналитически оценить значение функции в произвольной точке x.
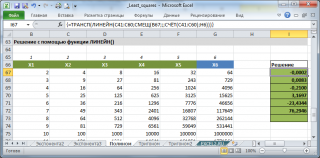
Ниже показано «ручное» решение в Excel и решение с помощью стандартной функции ЛИНЕЙН.
Скриншот файла Excel с решением
Вот пояснения к формулам:
C2— формируем матрицу из степеней значенийx; избегаем при этом возведения нуля в нулевую степень, заменяя любое число, возводимое в нулевую степень, единицей; ввести формулу в ячейкуC2; затем растягиваем формулу на ячейкиC2:C5, отпускаем левую кнопку мыши и, не снимая выделения, растягиваем на столбцыD:F(см. Пояснение 1 ниже);G2:G5— вычисляем коэффициенты полиномаci«вручную», обратив матрицу и умножив её на вектор значенийyi; выделить диапазонG2:G5; не снимая выделения, ввести формулу в ячейкуG2; не снимая выделения, нажать комбинацию клавишCrl+Shift+Enter(см. Пояснение 2 ниже);I2— вычисляем полином третьей степени в точках, не обязательно совпадающих с исходными; по выделенным жирным шрифтом значениям полинома видно, что он прошёл через исходные точки; ввести формулу в ячейкуI2, растянуть за уголок доI8;J2:J5— вычисляем коэффициенты полинома ci с помощью функцииЛИНЕЙН, пример в справке (пример 2), к сожалению, прямо ошибочен, плюс не показывает вычисление нескольких коэффициентов полинома; выделить диапазонJ2:J5; не снимая выделения, ввести формулу в ячейкуG2; не снимая выделения, нажать комбинацию клавишCrl+Shift+Enter; коэффициенты возвращаются в «перевёрнутом» по отношению к нашему ручному расчёту виде;K2— для единообразия расчёта переворачиваем массив коэффициентов, готовой функции для этого нет, показан образец, как перевернуть диапазон в Excel; ввести формулу в ячейкуK2, растянуть за уголок доK5;L2— вычисляем полином третьей степени в тех же точкахH2:H8, в которых вычисляли его значения первым способом; ввести формулу в ячейкуL2, растянуть за уголок доL8; видно, что кривая также прошла через исходные точки данных.
Скачать файл Excel (2007 и выше, делался в Excel 2016) в архиве .zip (13 Кб)
Пояснение 1. Как растянуть формулу на матрицу значений
1. Введите требуемую формулу и нажмите Enter, на рисунке показан вид экрана перед нажатием:
Ввод «матричной» формулы со смешанными ссылками
2. Подведите курсор мыши к нижнему правому уголку ячейки C2, уголок превратился в чёрный крестик, зажмите левую кнопку мыши и растяните формулу вниз до ячейки C5.
Курсор для растягивания в Excel, «чёрный крестик»
Формула растянута вниз
3. Отпустите кнопку мыши, снова так же подведите курсор к уголку ячейки C5 (опять чёрный крестик) и при зажатой левой кнопке мыши растяните выделение вправо до столбца F.
Заполнение таблицы формулой в Excel
Пояснение 2. Как ввести формулу массива
1. Выделить диапазон ячеек, в которые будет помещён результат матричной или векторной операции (мышкой при зажатой левой кнопке за любое место, на котором курсор имеет вид по умолчанию или при зажатой Shift клавишами со стрелками):
Вид курсора по умолчанию в Excel
Мы сами отвечаем за правильность выделения ячеек диапазона результата, например, Excel не обязан знать, что в результате обращения матрицы размерностью 3x3 получится тоже матрица размерностью 3x3:
Выделение диапазона ячеек результата в Excel
2. Не снимая выделения, ввести формулу массива в первую ячейку выделенного диапазона, это можно сделать «вручную», просто нажав клавишу F2 и начав набирать формулу со знака «=«, или с помощью Мастера Функций (см. п.3 документа по Excel здесь).
Ввод формулы массива в первую ячейку выделенного диапазона
3. При зажатых клавишах Ctrl и Shift, нажать клавишу Enter, то есть, ввести комбинацию клавиш Ctrl+Shift+Enter.
22.02.2020, 18:58 [4255 просмотров]
К этой статье пока нет комментариев, Ваш будет первым
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Любому бизнесу интересно заглянуть в будущее и правильно ответить на вопрос: «А сколько денег мы заработаем за следующий период?» Ответить на такого рода вопросы позволяют различные методики прогнозирования. В данной статье мы с вами рассмотрим несколько таких методик и произведем все необходимые расчеты в Excel. Еще больше про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Постановка задачи
Исходные данные
Для начала, давайте определимся, какие у нас есть исходные данные и что нам нужно получить на выходе. Фактически, все что у нас есть, это некоторые исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут продажи за предыдущие периоды.
Примечание. Собранные в разные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такого временного ряда называется измерением. Например: данные о продажах за последние 5 лет по месяцам — временной ряд; продажи за январь прошлого года — измерение.
Составляющие прогноза
Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:
- Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
- Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.
Эти три пункта в совокупность образуют регулярную составляющую временного ряда.
Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.
Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно – продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.
Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Виды моделей
Следующий вопрос, на который нужно ответить при построении прогноза: “А какие модели временного ряда бывают?”
Обычно выделяют два основных вида:
- Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отклонения
- Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отклонения
Иногда также выделают смешанную модель в отдельную группу:
- Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отклонения
С моделями мы определились, но теперь возникает еще один вопрос: «А когда какую модель лучше использовать?»
Классический вариант такой:
— Аддитивная модель используется, если амплитуда колебаний более-менее постоянная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной компоненты.
Пример:

Решение задачи с помощью Excel
Итак, необходимые теоретические знания мы с вами получили, пришло время применить их на практике. Мы будем с вами использовать классическую аддитивную модель для построения прогноза. Однако, мы построим с вами два прогноза:
- с использованием линейного тренда
- с использованием полиномиального тренда
Во всех руководствах, как правило, разбирается только линейный тренд, поэтому полиномиальная модель будет крайне полезна для вас и вашей работы!
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Модель с линейным трендом
Пусть у нас есть исходная информация по продажам за 2 года:

Учитывая, что мы используем линейный тренд, то нам необходимо найти коэффициенты уравнения
y = ax + b
где:
- y – значения продаж
- x – номер периода
- a – коэффициент наклона прямой тренда
- b – свободный член тренда
Рассчитать коэффициенты данного уравнения можно с помощью формулы массива и функции ЛИНЕЙН. Нам необходимо будет сделать следующую последовательность действий:
- Выделяем две ячейки рядом
- Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
- Нажимаем Ctrl+Shift+Enter, чтобы активировать формулу массива
На выходе мы получили 2 числа: первое — коэффициент a, второе – свободный член b.

Теперь нам нужно рассчитать для каждого периода значение линейного тренда. Сделать это крайне просто — достаточно в полученное уравнение подставить известные номера периодов. Например, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.

Нам осталось рассчитать коэффициент сезонности для каждого периода. Учитывая, что у нас есть исторические данные за два года, разумно будет учесть это при расчете. Можем сделать следующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).

Что нам это дало? Мы посчитали, сколько суммарно продавалось каждый январь/каждый февраль и так далее, а потом разделили это на среднее значение продаж за все два периода.
То есть мы выяснили, как продажи двух январей отклонялись от средних продаж за два года, как продажи двух февралей отклонялись и так далее. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.
Примечание. Рассчитали только 12 коэффициентов, т.к. один коэффициент учитывает продажи сразу за 2 аналогичных периода.
Итак, теперь мы на финишной прямой. Нам осталось рассчитать тренд для будущих периодов и учесть коэффициент сезонности для них. Давайте амбициозно построим прогноз на год вперед.
Сначала создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.
Далее, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 прогнозируемых периодов.
И последний штрих — умножаем полученное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!
Модель с полиномиальным трендом
Конструкция, которую мы только что с вами построили, достаточно проста. Но у нее есть один большой минус — далеко не всегда она дает достоверные результаты.
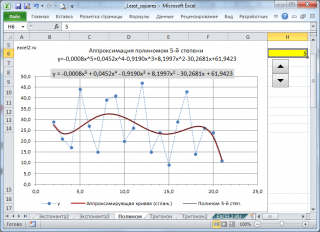
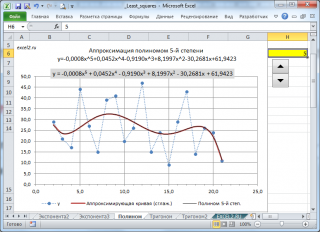
Посмотрите сами, какая модель более точно аппроксимирует наши точки — линейный тренд (прямая зеленая линия) или полиномиальный тренд (красная кривая)? Ответ очевиден. Поэтому сейчас мы с вами и разберем, как построить полиномиальную модель в Excel.
Пусть все исходные данные у нас будут такими же. Для простоты модели будем учитывать только тренд, без сезонной составляющей.
Для начала давайте определимся, чем полиномиальный тренд отличается от обычного линейного. Правильно — формой уравнения. У линейного тренда мы разбирали обычный график прямой:

У полиномиального тренда же уравнение выглядит иначе:

где конечная степень определяется степенью полинома.
Т.е. для полинома 4 степени необходимо найти коэффициенты уравнения:

Согласитесь, выглядит немного страшно. Однако, ничего страшного нет, и мы с легкостью можем решить эту задачку с помощью уже известных нам методов.
- Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;1). Функция ЛИНЕЙН позволяет произвести расчет коэффициентов, а с помощью функции ИНДЕКС мы вытаскиваем нужный нам коэффициент. В данном случае за выбор коэффициента отвечает самый последний аргумент. У нас стоит 1 — это коэффициент при самой высокой степени (т.е. при 4 степени, коэффициент). Кстати, узнать о самых полезных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
- Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;2) в ячейке ниже.
- Делаем такие же действия, пока не найдем все коэффициенты.
Кстати говоря, мы можем легко сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.
- Выделяем столбец с продажами
- Выбираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
- Нажимаем на любую точку графика правой кнопкой мыши и выбираем «Добавить линию тренда»
- В открывшемся справа меню выбираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Показывать уравнение на диаграмме»
Теперь вы наглядно можете видеть, как рассчитанный тренд аппроксимирует исходные данные и как выглядит само уравнение. Можно сравнить уравнение на графике с вашими коэффициентами. Сходится? Значит сделали все верно!
Помимо всего прочего, вы можете сразу оценить точность аппроксимации (не полностью, но хотя бы первично). Это делается с помощью коэффициента R^2. Тут у вас снова есть два пути:
- Вы можете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
- Вы можете рассчитать коэффициент R^2 самостоятельно по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4};;1);3;1)
Заключение
Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.
Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.
Автор: Алексанян Андрон, эксперт SF Education
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Data Science
5 примеров экономии времени в Excel
Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на наш взгляд,…