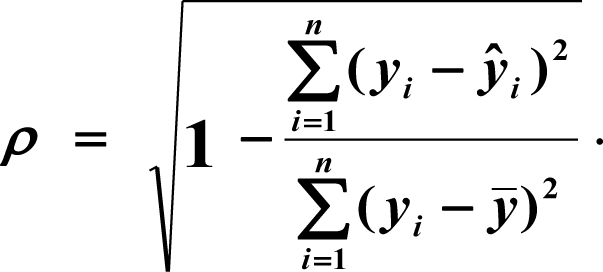Нелинейная регрессия в Excel
Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ.
Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.
Основными типами нелинейных регрессий являются:
- полиномиальные (квадратичная, кубическая);
- гиперболическая;
- степенная;
- показательная;
- логарифмическая.
Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.
В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А), если она находится в промежутке <8…10%, значит модель достаточно точна.
На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.
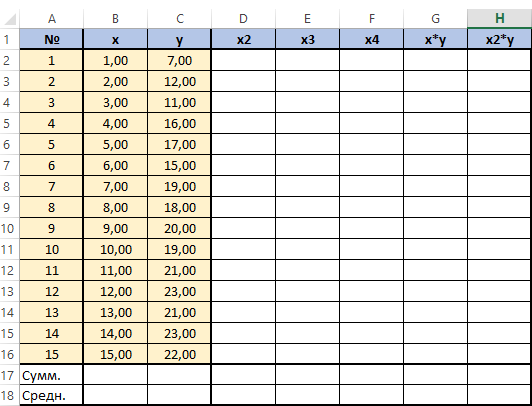
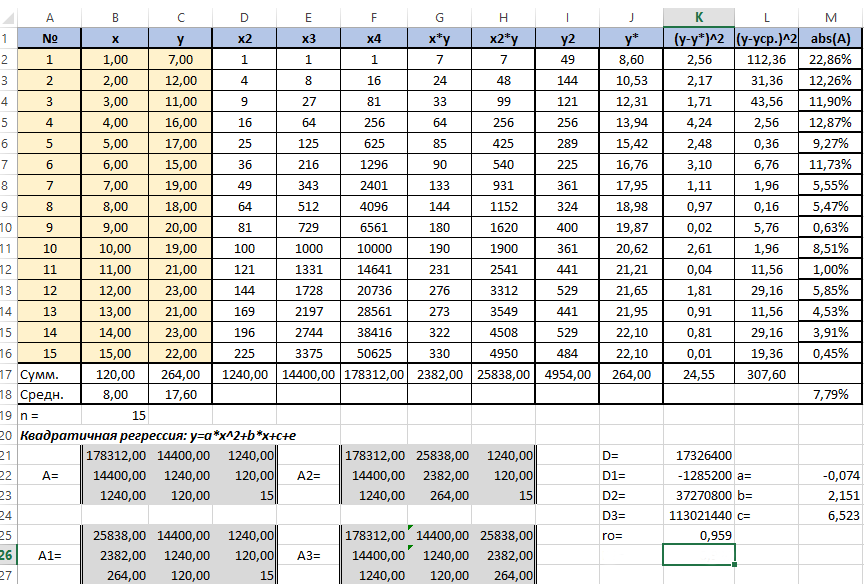
У нас имеется таблица продаж автомобилей за промежуток 15 лет (обозначим его X), количество шагов измерений будет аргумент n, также имеется выручка за эти периоды (обозначим её Y), нам нужно спрогнозировать какова будет выручка в дальнейшем. Построим следующую таблицу:
Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax2+bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов — a, b, c. Он приведёт к системе алгебраических уравнений вида:
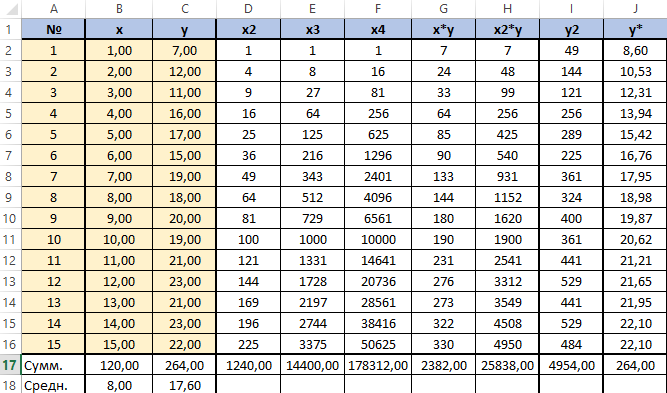
Для решения этой системы воспользуемся, к примеру, методом Крамера. Видим, что входящие в систему суммы являются коэффициентами при неизвестных. Для их вычисления добавим в таблицу несколько столбцов (D,E,F,G,H) и подпишем соответственно смыслу вычислений — в столбце D возведём x в квадрат, в E в куб, в F в 4 степень, в G перемножим показатели x и y, в H возведём x в квадрат и перемножим с y.
Получится заполненная нужными для решения уравнения таблица вида.
Далее посчитаем суммы по каждому столбцу — воспользуемся ∑ в программе Excel.
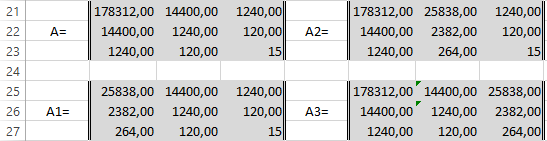
Сформируем матрицу A системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём «А=«. Следуем той системе уравнений, которую мы избрали для решения регрессии.
То есть, в ячейку B21 мы должны поместить сумму столбца, где возводили показатель X в четвёртую степень — F17. Просто сошлёмся на ячейку — «=F17». Далее нам необходима сумма столбца где возводили X в куб — E17, далее идём строго по системе. Таким образом, нам необходимо будет заполнить всю матрицу.
В соответствии с алгоритмом Крамера наберём матрицу А1, подобную А, в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. То есть сумма столбца X в квадрате умноженная на Y, сумма столбца XY и сумма столбца Y.
Также нам понадобятся ещё две матрицы — назовём их А2 и А3 в которых второй и третий столбцы будут состоять из коэффициентов правых частей уравнений. Картина будет такова.
Следуя избранному алгоритму, нам нужно будет вычислить значения определителей (детерминантов, D) полученных матриц. Воспользуемся формулой МОПРЕД. Результаты разместим в ячейках J21:K24.
Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a (в ячейке M22) — «=K22/K21»; b (в ячейке M23) — «=K23/K21»; с (в ячейке M24) — «=K24/K21».
Получим наше искомое уравнение парной квадратичной регрессии:
y=-0,074x2+2,151x+6,523
Оценим тесноту линейной связи индексом корреляции.
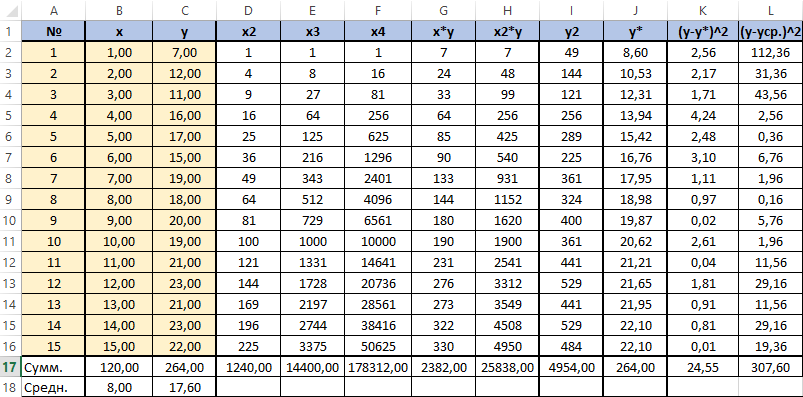
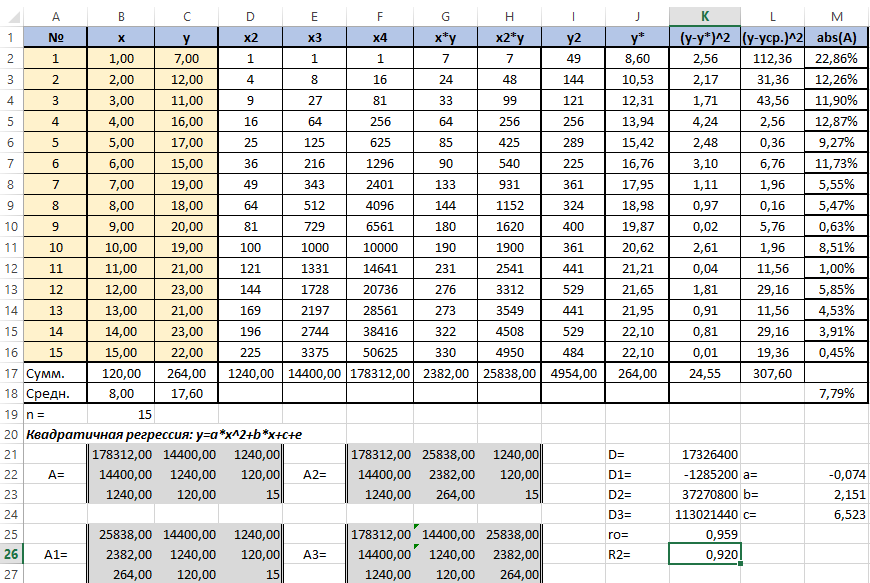
Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) — «=$m$22*B2*B2+$M$23*B2+$M$24». Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.
Для вычисления сумм (Y-Y усредненное)2 добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.
В ячейке K25 разместим формулу подсчёта индекса корреляции — «=КОРЕНЬ(1-(K17/L17))».
Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь.
Осталось оценить качество подгонки полученного квадратичного уравнения регрессии (индекс детерминации). Он рассчитывается по формуле квадрата индекса корреляции. То есть формула в ячейке K26 будет очень проста — «=K25*K25».
Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.
Последним действием будет вычисление относительной ошибки. Добавим столбец и внесём туда формулу: «=ABS((C2-J2)/C2), ABS — модуль, абсолютное значение. Протянем маркером вниз и в ячейке M18 выведем среднее значение (СРЗНАЧ), назначим ячейкам процентный формат. Полученный результат — 7,79% находится в пределах допустимых значений ошибки <8…10%. Значит вычисления достаточно точны.
Если возникнет необходимость, по полученным значениям мы можем построить график.
Файл с примером прилагается — ССЫЛКА!
Nonlinear regression is a regression technique that is used when the relationship between a predictor variable and a response variable does not follow a linear pattern.
The following step-by-step example shows how to perform nonlinear regression in Excel.
Step 1: Create the Data
First, let’s create a dataset to work with:
Step 2: Create a Scatterplot
Next, let’s create a scatterplot to visualize the data.
First, highlight the cells in the range A1:B21. Next, click the Insert tab along the top ribbon, and then click the first plot option under Scatter:
The following scatterplot will appear:
Step 3: Add a Trendline
Next, click anywhere on the scatterplot. Then click the + sign in the top right corner. In the dropdown menu, click the arrow next to Trendline and then click More Options:
In the window that appears to the right, click the button next to Polynomial. Then check the boxes next to Display Equation on chart and Display R-squared value on chart.
This produces the following curve on the scatterplot:
Note that you may need to experiment with the value for the Order of the polynomial until you find the curve that best fits the data.
Step 4: Write the Regression Equation
From the plot we can see that the equation of the regression line is as follows:
y = -0.0048x4 + 0.2259x3 – 3.2132x2 + 15.613x – 6.2654
The R-squared tells us the percentage of the variation in the response variable that can be explained by the predictor variables.
The R-squared for this particular curve is 0.9651. This means that 96.51% of the variation in the response variable can be explained by the predictor variables in the model.
Additional Resources
How to Perform Simple Linear Regression in Excel
How to Perform Multiple Linear Regression in Excel
How to Perform Logarithmic Regression in Excel
How to Perform Exponential Regression in Excel
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
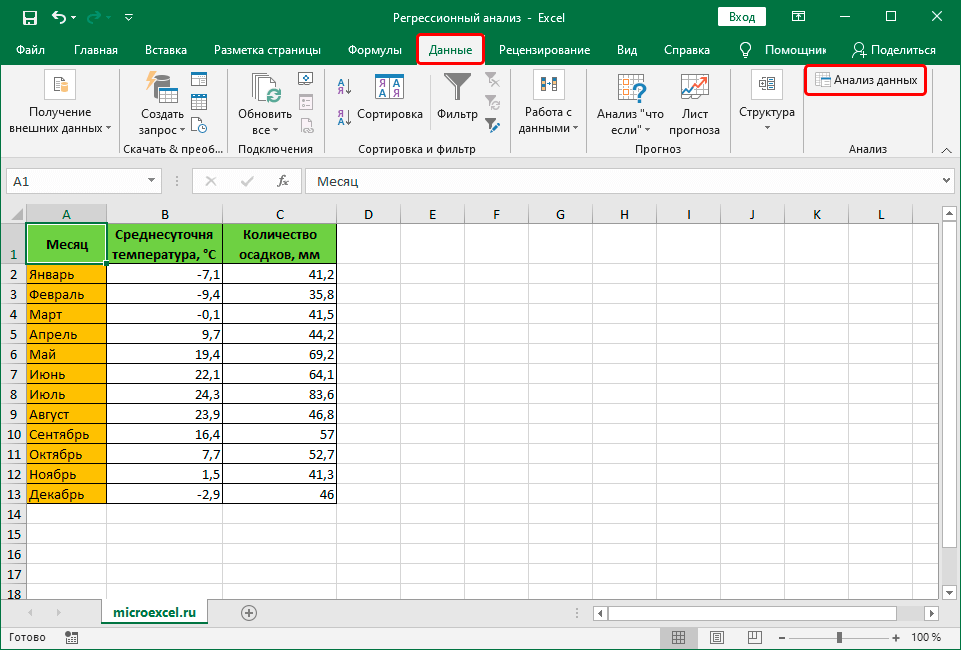
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
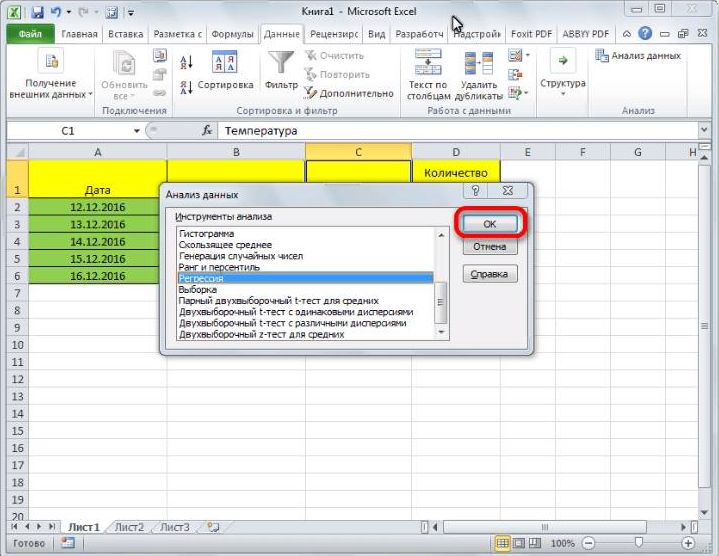
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
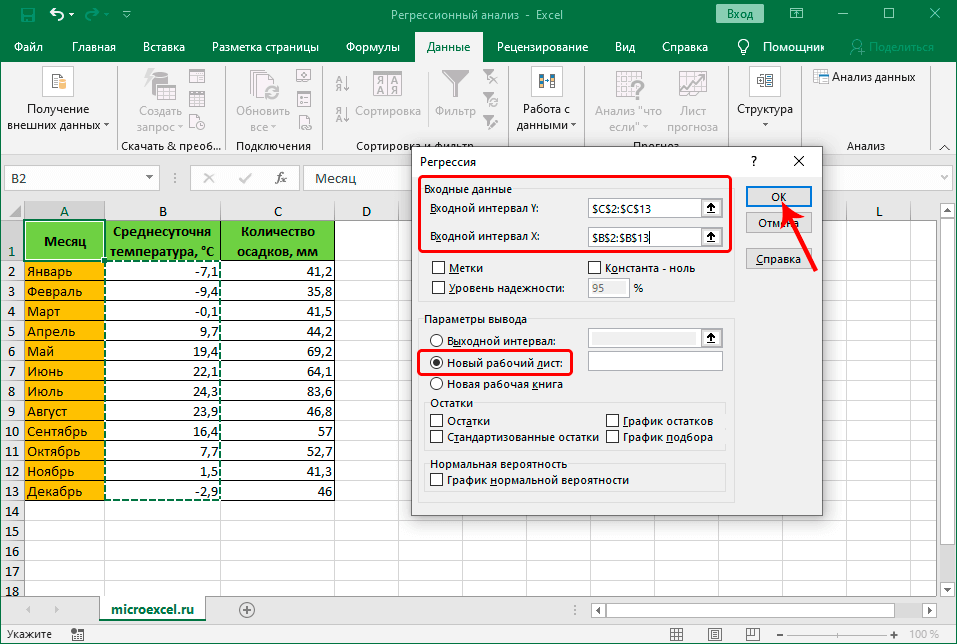
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
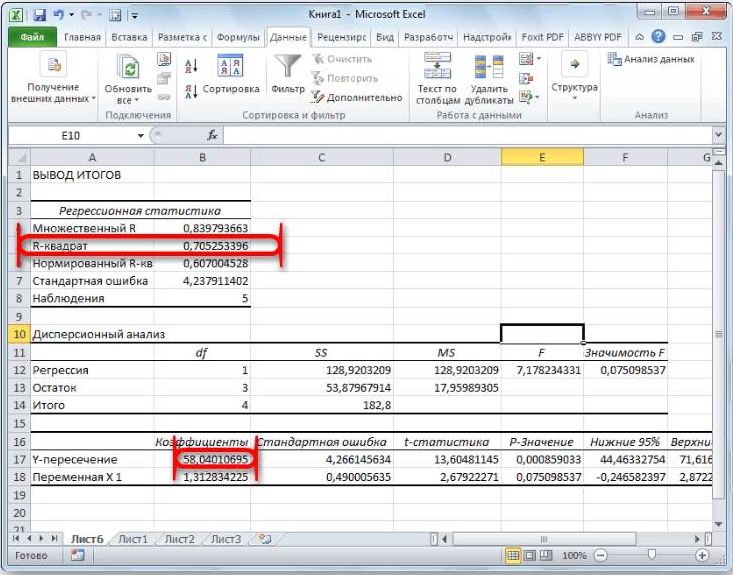
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Нелинейная регрессия в Excel
Нелинейная регрессия в Excel
Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ.
Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.
Основными типами нелинейных регрессий являются:
- полиномиальные (квадратичная, кубическая);
- гиперболическая;
- степенная;
- показательная;
- логарифмическая.
Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.
В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А), если она находится в промежутке
На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.
У нас имеется таблица продаж автомобилей за промежуток 15 лет (обозначим его X), количество шагов измерений будет аргумент n, также имеется выручка за эти периоды (обозначим её Y), нам нужно спрогнозировать какова будет выручка в дальнейшем. Построим следующую таблицу:
Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax 2 +bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов — a, b, c. Он приведёт к системе алгебраических уравнений вида:
Для решения этой системы воспользуемся, к примеру, методом Крамера. Видим, что входящие в систему суммы являются коэффициентами при неизвестных. Для их вычисления добавим в таблицу несколько столбцов (D,E,F,G,H) и подпишем соответственно смыслу вычислений — в столбце D возведём x в квадрат, в E в куб, в F в 4 степень, в G перемножим показатели x и y, в H возведём x в квадрат и перемножим с y.
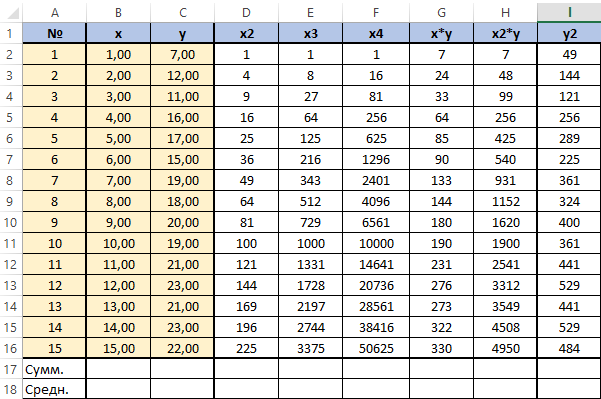
Получится заполненная нужными для решения уравнения таблица вида.
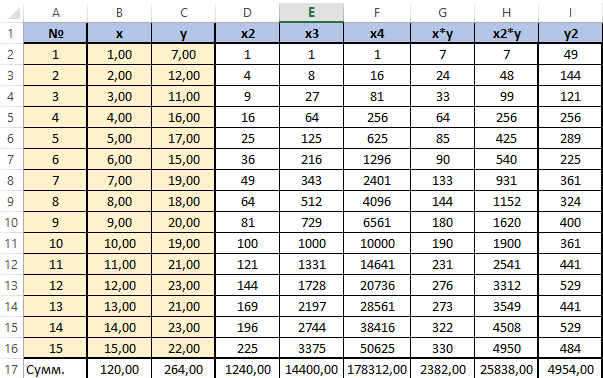
Далее посчитаем суммы по каждому столбцу — воспользуемся ∑ в программе Excel.
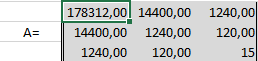
Сформируем матрицу A системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём «А=«. Следуем той системе уравнений, которую мы избрали для решения регрессии.
То есть, в ячейку B21 мы должны поместить сумму столбца, где возводили показатель X в четвёртую степень — F17. Просто сошлёмся на ячейку — «=F17». Далее нам необходима сумма столбца где возводили X в куб — E17, далее идём строго по системе. Таким образом, нам необходимо будет заполнить всю матрицу.
В соответствии с алгоритмом Крамера наберём матрицу А1, подобную А, в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. То есть сумма столбца X в квадрате умноженная на Y, сумма столбца XY и сумма столбца Y.
Также нам понадобятся ещё две матрицы — назовём их А2 и А3 в которых второй и третий столбцы будут состоять из коэффициентов правых частей уравнений. Картина будет такова.
Следуя избранному алгоритму, нам нужно будет вычислить значения определителей (детерминантов, D) полученных матриц. Воспользуемся формулой МОПРЕД. Результаты разместим в ячейках J21:K24.
Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a (в ячейке M22) — «=K22/K21»; b (в ячейке M23) — «=K23/K21»; с (в ячейке M24) — «=K24/K21».
Получим наше искомое уравнение парной квадратичной регрессии:
y=-0,074x 2 +2,151x+6,523
Оценим тесноту линейной связи индексом корреляции.
Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) — «=$m$22*B2*B2+$M$23*B2+$M$24». Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.
Для вычисления сумм (Y-Y усредненное) 2 добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.
В ячейке K25 разместим формулу подсчёта индекса корреляции — «=КОРЕНЬ(1-(K17/L17))».
Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь.
Осталось оценить качество подгонки полученного квадратичного уравнения регрессии (индекс детерминации). Он рассчитывается по формуле квадрата индекса корреляции. То есть формула в ячейке K26 будет очень проста — «=K25*K25».
Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.
Последним действием будет вычисление относительной ошибки. Добавим столбец и внесём туда формулу: «=ABS((C2-J2)/C2), ABS — модуль, абсолютное значение. Протянем маркером вниз и в ячейке M18 выведем среднее значение (СРЗНАЧ), назначим ячейкам процентный формат. Полученный результат — 7,79% находится в пределах допустимых значений ошибки
Если возникнет необходимость, по полученным значениям мы можем построить график.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
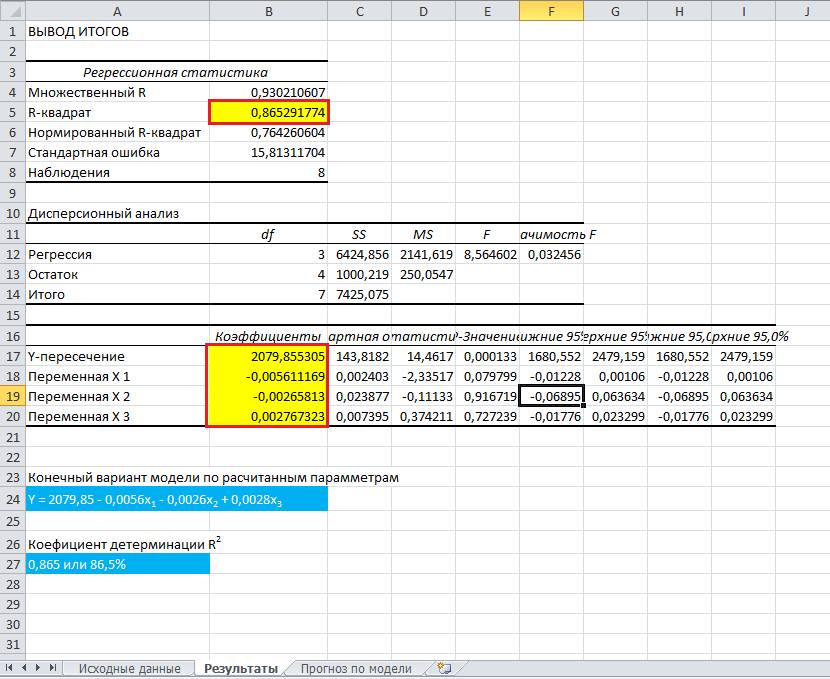
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Регрессионный анализ данных в Excel
Регрессионный анализ – это набор статистических методов, позволяющих изучить влияние одной или нескольких независимых переменных на зависимую. Давайте разберемся, каким образом можно выполнить данный анализ в программе Excel.
Включение функции анализа в программе
Для начала нужно активировать функцию программы, с помощью которой мы будем проводить анализ. Для этого делаем следующее:
- Открываем меню “Файл”.
- Щелкаем по пункту “Параметры”.
- В нижней части содержимого подраздела “Надстройки” выбираем значение “Надстройки Excel” для параметра “Управление”, после чего кликаем “Перейти”.
Линейный регрессионный анализ
Выделяют несколько разновидностей регрессий: линейная, гиперболическая, множественная, логарифмически линейная, нелинейная, обратная, парная.
В рамках данной статьи мы рассмотрим линейную регрессию. В общем виде ее функция выглядит так:
В данном уравнении:
- Y – переменная, влияние на которую нужно найти;
- X – факторы, влияющие на переменную;
- A – коэффициенты регрессии, определяющие значимости факторов;
- N – общее количество факторов.
Чтобы было понятнее, давайте разберем конкретный практический пример. Допустим, у нас есть таблица, в которой представлена информация по среднесуточной температуре и количеству осадков с разбивкой по месяцам.
Наша задача – выяснить, как температура влияет на осадки. Приступи к ее выполнению.
- Щелкаем по кнопке “Анализ данных”.
- В открывшемся окошке отмечаем пункт “Регрессия”, после чего щелкаем OK.
- Перед нами появится окно, в котором нужно настроить параметры регрессии:
- в поле “Входной интервал_Y” пишем координаты диапазона ячеек, в которых находятся переменные, влияние на которые нам нужно выяснить. У нас это столбец “Количество осадков, мм”. Координаты диапазона можно указать как вручную, используя клавиши на клавиатуре, так и выделив его в самой таблице с помощью зажатой левой кнопки мыши.
- в поле “Входной интервал_X” указываем координаты диапазона ячеек с данными, влияние которых нам нужно найти. В нашем случае – это столбец “Среднесуточная температура”.
- Остальные параметры не являются обязательными и, чаще всего, остаются незаполненными. У нас есть возможность установить метки, значения уровня надежности в процентах, константу-ноль, график нормальной вероятности и т.д. Пожалуй, самым важным здесь является способ вывода результатов анализа. Доступны следующие варианты: на новом листе (по умолчанию), в новой книге или в указанном диапазоне на этом же листе. Мы оставим все как есть и жмем кнопку OK.
Анализ полученных результатов
После корректного заполнения всех параметров и нажатия кнопки OK отобразятся результаты анализа (в зависимости от выбранного способа). В нашем случае – на отдельном листе.
Ключевым показателем здесь является R-квадрат (коэффициент детерминации), значение которого характеризует качество модели. Приемлемым считается значение не менее 0,5 (или 50%).
Также следует обратить внимание на ячейку, расположенную на пересечении строки “Y-пересечение” и столбца “Коэффициенты”. Здесь показывается, каким будет значение Y (количество осадков), если все остальные факторы будут равны нулю.
Ячейка на пересечении строки “Переменная X 1” и столбца “Коэффициенты” содержит значение, характеризующее степень зависимости Y от X. Коэф. 0,89 в нашем случае говорит о достаточно сильной связи между переменными.
Заключение
Регрессионный анализ – сложная и трудоемкая задача, которая требует определенных математических и статистических знаний. Но с помощью стандартных инструментов Эксель ее выполнение можно значительно облегчить.
источники:
http://lumpics.ru/regression-analysis-in-excel/
http://microexcel.ru/regressionnyj-analiz/
Рассмотрим
теперь, как в MS EXCEL можно быстро построить
модели парных нелинейных регрессий.
Покажем это на данных примера 1.
Шаг
1. Сначала построим диаграмму (например,
точечную или график) зависимости между
Y и X.
Рис.
4.1. Построение диаграммы (точечной)
зависимости между Y и X
Шаг
2. Устанавливаем точку мыши на одну из
помеченных точек диаграммы, чтобы все
точки зажглись жёлтым цветом. И тут же
нажимаем на правую кнопку мыши. Возникнет
окно диалога, в котором четвёртой строкой
является фраза «Добавить линию тренда»
(см. рис.4.2.). Левой кнопкой мыши выбираем
эту четвёртую строку.
Рис.
4.2. Окно диалога при построении разных
видов регрессии
Шаг
3. В появившемся окне диалога выберите
тип зависимости между Y и X, например,
логарифмический (см. рис. 4.3).
Рис.
4.3. Выбор нужной зависимости
Шаг
6. Выбираем закладку «Параметры» и
устанавливаем левой кнопкой мыши флажки
«Показывать уравнение на диаграмме»,
а также «Поместить на диаграмму величину
достоверности аппроксимации (R^2)» (см.
рис. 4.4).
Рис.
4.4. Установление флажков на закладке
«Параметры»
Шаг
5. Нажмите «ОК». Получите диаграмму
выбранной зависимости, изображённой
на рисунке 4.5.
Рис.
4.5. Построение логарифмической зависимости
между факторами Y и X
Замечание
1. Для аппроксимации исходных данных
другой зависимостью между Y и X, начните
с шага 1. Не забудьте после построения
очередной зависимости перетащить
полученную диаграмму на другое место,
потому что MS EXCEL будет помещать диаграммы
на одно и то же место на листе EXCELа.
4.4. Задание к лабораторной работе №2 «Парная нелинейная регрессия»
Задание.
Построить нелинейную модель связи между
указанными факторами. Исходные данные
находятся в таблицах 1 — 2 лабораторной
работы №1. Номера вариантов — в таблицах
3. Для выбора индивидуального варианта
используйте последние две цифры зачётки.
Например, если последние цифры 1 и 9, то
в таблице 1 и 2 надо выбрать 6-ю и 9-ю строки
соответственно.
Методические
указания к решению задачи.
1.
Вначале расположите исходные данные
по факторам X и Y в столбцы. По этим
исходным данным постройте диаграмму в
MS EXCEL и сделайте предварительное
заключение о наличии связи между
факторами X и Y, а также о её виде
(логарифмическая, обратная или другая)
и форме (линейная или нелинейная) на
основании графика.
2.
Полагая, что связь между факторами X и
Y может быть описана нелинейной функцией,
запишите соответствующее уравнение
этой зависимости. Используя процедуру
метода наименьших квадратов, получите
систему нормальных уравнений относительно
коэффициентов линейного уравнения
регрессии. Любым способом решите ее.
Проверьте полученные оценки a* и b* двумя
описанными выше способами в MS EXCEL.
3.
Выполните точечный прогноз на прогнозное
значение переменной x по полученной
модели. Выберите прогнозную точку хп
в стороне от основного массива данных.
Используя уравнение регрессии, выполните
точечный прогноз величины Y в точке хп.
6.
Для полученной модели связи между
факторами X и Y рассчитайте коэффициент
детерминации R2.
Сделайте предварительное заключение
о приемлемости полученной модели.
5.
Постройте логарифмическую, полиномиальную,
степенную и экспоненциальную зависимости.
Выберите лучшую зависимость из критерия
близости коэффициента детерминации R2
к единице. Запишите на листе EXCELа отчёт
по лабораторной работе.
Соседние файлы в папке Эконометрика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17 авг. 2022 г.
читать 2 мин
Вы можете использовать функцию ЛИНЕЙН , чтобы быстро найти уравнение регрессии в Excel.
Эта функция использует следующий базовый синтаксис:
LINEST(known_y's, known_x's)
куда:
- known_y’s : столбец значений для переменной ответа.
- known_x’s : один или несколько столбцов значений для переменных-предикторов.
В следующих примерах показано, как использовать эту функцию для поиска уравнения регрессии для простой модели линейной регрессии и модели множественной линейной регрессии .
Пример 1: Найдите уравнение для простой линейной регрессии
Предположим, у нас есть следующий набор данных, который содержит одну предикторную переменную (x) и одну переменную ответа (y):
Мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить простое уравнение линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:B15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для простой модели линейной регрессии:
Вот как интерпретировать вывод:
- Коэффициент на перехват 3,115589.
- Коэффициент наклона равен 0,479072.
Используя эти значения, мы можем написать уравнение для этой простой модели регрессии:
у = 3,115589 + 0,478072 (х)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
Пример 2: найти уравнение для множественной линейной регрессии
Предположим, у нас есть следующий набор данных, который содержит две переменные-предикторы (x1 и x2) и одну переменную ответа (y):
Мы можем ввести следующую формулу в ячейку E1 , чтобы вычислить уравнение множественной линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:C15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для модели множественной линейной регрессии:
Вот как интерпретировать вывод:
- Коэффициент на перехват 1.471205
- Коэффициент для x1 равен 0,047243.
- Коэффициент для x2 равен 0,406344.
Используя эти значения, мы можем написать уравнение для этой модели множественной регрессии:
у = 1,471205 + 0,047243 (х1) + 0,406344 (х2)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели для модели множественной линейной регрессии в Excel, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о регрессии в Excel:
Как интерпретировать вывод регрессии в Excel
Как добавить линию регрессии на диаграмму рассеяния в Excel
Как выполнить полиномиальную регрессию в Excel
Регрессионный метод – это способ статистического исследования. Для проведения регрессионного анализа часто используют Excel – табличный процессор компании Microsoft, позволяющие быстро систематизировать и просчитывать данные. Программа имеет список определенных инструментов и техник, которые нужно активировать и изучить заранее для проведения подобных расчетов.
Что такое регрессионный анализ?
Исследование данного типа позволяет находить взаимосвязь или зависимость между независимой и постоянной переменной. Используется, например, для поиска различий между социальными группами (мужчинами и женщинами), температурными показателями. С точки зрения геометрии целью процесса является построение прямой или графика. Различают следующие типы регрессионного анализа:
- степенной;
- логарифмический;
- параболический;
- показательный;
- линейный;
- гиперболический;
- экспоненциальный.
Каждый из методов имеет собственное назначение и результаты. Дополнительные варианты – однофакторная и многофакторная технологии регрессионного анализа.
Как подключить пакет анализа?
Excel содержит технику регрессионного анализа внутри программы. Но чтобы начать использование, необходимо произвести активацию пакета функций. После этого требуемые инструменты начнут отображаться на общей панели доступа (в верхней части файла). Этапы действий:
Кнопка появится во вкладке «Данные», справа – «Анализ данных». Перезагрузка программы не требуется.
Линейная регрессия
Чтобы подробно объяснить схему работы, в Excel была создана таблица с указанием определенных данных. Цель – попытка обнаружить связь между температурой и числом посетителей торговой точки. Запустить процесс подсчета и регрессии необходимо с помощью кнопки «Анализ данных».
Откроется диалоговое окошко, из представленного списка выбирают пункт «Регрессия», клавиша «Ок». В полях «Входной интервал Y» и «Входной интервал X» – для первого указывают список ячеек переменного параметра (в примере – покупатели), для второго диапазон по температуре.
Внимание! Пункт «Параметры вывода» осуществляет сохранение результата разными способами – на новом листе, книге и т.д. Удобнее будет переставить значок и получить ответы на той же странице, что и начальная таблица.
Запуска процесса – кнопка «Ок». После необходимо правильно прочитать результат.
Расшифровка результата – анализ данных
Ответы по анализу помещаются в небольшую таблицу «Вывод итогов». Качество показывает R-квадрат – в данном примере 0,70, что является приемлемым. Y-пересечение указывает на уровень переменной, при остальных данных равных «0». Остальные характеристики указывают на взаимосвязь исходников.
Другие виды регрессии
В примере, который представлен выше, используется только две переменных. Такая ситуация является скорее редкостью. Для расчета нескольких или разных показателей используют иные методы регрессии.
Множественная
Техника применяется в случае, когда параметров Х больше одного. Чтобы корректно рассчитать характеристики можно использовать дополнительные инструменты: заданный тренд, коэффициент детерминации, проверка гипотез и иные. Выполнить расчеты может только подготовленный специалист.
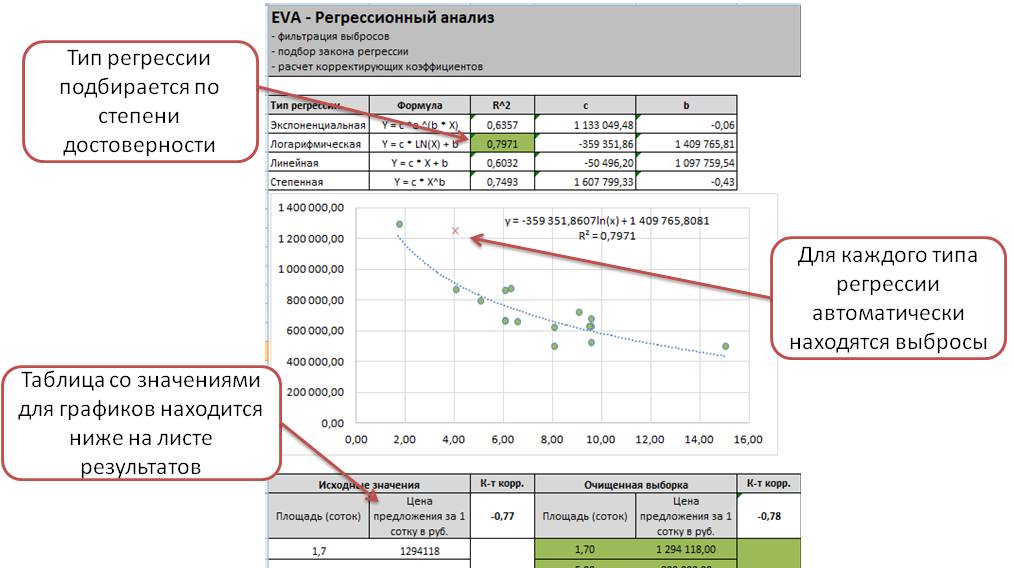
Степенная
Для этой модели формула расчета выглядит так: y = a*x˄b. Выбросы для данного метода вычисляются автоматически. Используется, если уровень достоверности техники выше остальных – графа R˄2.
Нелинейная
Для нелинейной методики важно рассчитать коэффициент корреляции. Характеристика указывает на наличие взаимосвязи различных показателей. Как правило, если параметр близок к единице, то взаимодействие есть, а анализ достаточно точный.
Дополнительным элементом является относительная ошибка. Характеристика должна находиться в пределах от 8% до 10% – значит, что расчеты точные и результаты можно использовать дальше.
Кроме основных типов регрессионного анализа в Excel используют различные сочетания техник. К примеру, для исследования данных в банковской сфере, колебаний демографических показателей и других. Чтобы корректно пользоваться результатами, важно детально изучить механизм работы подобного исследования. Чаще всего обращаются к специалистам соответствующего профиля.