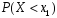«Многоугольник конкурентоспособности» — метод, позволяющий достаточно быстро провести анализ конкурентоспособности товара компании в сравнении с ключевыми конкурентами и разработать эффективные мероприятия по повышению уровня конкурентоспособности продукции.
В статье мы предлагаем на готовом примере разобрать построение многоугольника конкурентоспособности предприятия. У статье также прилагается удобный шаблон, с помощью которого вы можете построить многоугольник конкурентоспособности для продукта вашей компании.
Описание метода
Суть данного метода заключается в сравнительной оценке ключевых свойств товара компании и товаров конкурентов, и в последующей визуализации результатов сравнения в форме многоугольника:
Каждая грань такого многоугольника представляет отдельную характеристику товара, по которой проводится сравнительная оценка.
Пример построения и использования многоугольника конкурентоспособности
Использовать метод построения многоугольника конкурентоспособности на практике очень просто! Для этого достаточно пройти три последовательных этапа анализа.
Сперва определите ключевые критерии товара компании, которые влияют на приверженность и удовлетворенность товаром, прибыль от продажи товара и привлекательность товара для целевой аудитории. Затем оцените конкурентоспособность вашего товара и товара конкурентов по 10-ти бальной шкале, где 1 — самый низкий балл, а 10 — максимальный балл. И в заключении составьте план действий по улучшению конкурентоспособности товара по тем критериям, которые ниже конкурентов.
На практике этот процесс выглядит следующим образом:
Готовые решения
Вы можете скачать шаблон для построения многоугольника конкурентоспособности в разделе Готовые шаблоны по маркетингу
comments powered by
Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки М1 (Х1; Р1), M2(X2; Р2). • • • Mn(Хn; Рn) (Xi—-возможные значения X, Pi—соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют
многоугольником распределения. Задача 164. Дискретная случайная величина X задана законом распределения:
X 1 3 6 8
р 0,2 0,1 0,4 0,3
Построить многоугольник распределения.
Как построить многоугольник распределения в Excel
В Excel имеются средства для создания графиков и диаграмм, с помощью которых вы сможете в наглядной форме представить зависимости и тенденции, отраженные в числовых данных. Кнопки построения графиков и диаграмм находятся в группе Диаграммы на вкладке Вставка (Рис.1).
Для того чтобы построить многоугольник распределения сначала нужно сформировать таблицу, например так (Рис.2).
Далее просто выделяем нужные нам ячейки и выбираем тип графика который надо построить (Рис.3).
В результате мы получи многоугольник распределения с которым сможем производить дальнейшие действия Рис.4.
Для тех кому облом учить Excel, даем готовый шаблон (калькулятор) для построения многоугольника распределения, скачать шаблон бесплатно.
Задания на тему: «Многоугольник распределения» для самостоятельного решения.
165. Дискретная случайная величина X задана законом распределения:
а) X 2 4 5 6 б) X 10 15 20
р 0,3 0,1 0,2 0,4 р 0,1 0,7 0,2
Построить многоугольник распределения
16
Лабораторная
работа №1.
Дискретные
случайные величины.
Лабораторная
работа выполняется в Excel
2007.
Цель
работы – дать навыки построения законов
распределения дискретных случайных
величин и вычисления числовых характеристик
средствами Excel.
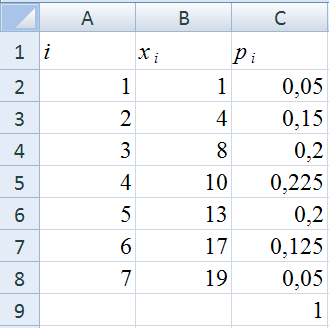
Задание.
Дискретная случайная величина X
задана рядом распределения.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
xi |
1 |
4 |
8 |
10 |
13 |
17 |
19 |
|
pi |
0,05 |
0,15 |
0,2 |
0,225 |
0,2 |
0,125 |
0,05 |
Построить
многоугольник распределения и функцию
распределения. Найти математическое
ожидание, дисперсию, среднее квадратическое
отклонение.
Найти
вероятности
,
,
.
1.
Представьте заданный ряд распределения
в Excel
в виде таблицы, как это показано на рис.
1.
Рис.
1. Таблица исходных данных (ряд
распределения)
2.
Постройте многоугольник
распределения.
Для этого выделите оба столбца исходных
данных вместе с метками xi
и pi.
В главном меню выберите закладку
Вставка
→ График → Все типы диаграмм…→Точечная,
и далее — график с точками, соединенными
прямыми линиями. ОК.
Отформатируйте
график как показано на рис. 2 (название
диаграммы, подписи осей, линии сеток).
Рис.
2. Многоугольник распределения.
3.
Постройте функцию
распределения.
Выделите ячейку D2.
В главном
меню Excel
выберите закладку Формулы
→ Вставить функцию → в
диалоговом окне
Мастер функций – шаг 1 из 2 в
категории
Статистические → ВЕРОЯТНОСТЬ.
ОК.
Рис.
3. Диалоговое окно
для выбора
функции ВЕРОЯТНОСТЬ.
В
открывшемся диалоговом окне Аргументы
функции ВЕРОЯТНОСТЬ
заполните поля ввода как показано на
рис. 3:
X_интервал
– $B$2:
$B$8,
столбец адресов ячеек переменной x;
Интервал_вероятностей
— $C$2:
$C$8,
столбец адресов ячеек переменной p;
Нижний_предел
— $B$2,
адрес ячейки переменной x1;
Верхний_предел
– B2,
адрес ячейки переменной x1.
ОК.
Рис.
4. Диалоговое окно
функции
ВЕРОЯТНОСТЬ с заполненными полями
ввода.
В
ячейке D2
будет размещена формула
и
результат ее вычислений как показано
на рис. 5.
Рис.
5. Результат
вычисления функции ВЕРОЯТНОСТЬ значений
функции распределения
в ячейке D2.
Размножьте
результат вычислений в ячейки D2:D8,
обозначив предварительно этот столбец
меткой F(x)
= P(X
≤ x)
– функция распределения.
Рис.
6.
Таблица значений функции распределения
.
В
нашей учебной литературе (контент, тема
4, с. 2, определение 4.1.2.) функцией
распределения случайной величины X
называется функция действительной
переменной x,
значение которой при каждом x
равно вероятности выполнения неравенства
,
то
есть
.
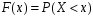
В
Excel,
как и во всей англоязычной литературе,
функцией распределения случайной
величины X
называется функция действительной
переменной x,
значение которой при каждом x
равно вероятности выполнения неравенства
,
то
есть
С
учетом определения, данного в нашей
учебной литературе, можно записать
функцию распределения и построить ее
график.
К
сожалению Excel
не располагает процедурой построения
функции распределения, поэтому в отчете
ее придется строить вручную, как показано
на рис.7.
p
1
0,9
0,9
0,8
0,825
0,7
0,6
0,625
0,5
0,4
0,4
0,3
0,2
0,2 
0,1
0,05
x
0
1 4 8 10
13 17 19
Рис.
7. График
функции распределения
.
Кончики
стрелок обозначают те точки, которые
не принадлежат графику функции
распределения
4.
Математическое
ожидание
,
дисперсия
и среднее квадратическое отклонение
вычисляются по формулам:
—
математическое ожидание
—
дисперсия
,
где
.
—
среднее квадратическое отклонение
.
Для
вычисления математического ожидания
необходимо воспользоваться формулой
СУММПРОИЗВ. Выберите курсором ячейку,
например A12,
в которой будет вычислено математическое
ожидание, и пометьте ее M(X).
В
главном меню Excel
следует выбрать последовательно
закладки Формулы
→ Вставить функцию → в
диалоговом окне
Мастер функций – шаг 1 из 2 в
категории
Математические → СУММПРОИЗВ →
ОК (рис.
8).
Рис.
8. Диалоговое окно выбора функции
СУММПРОИЗВ
Заполните
поля ввода диалогового окна СУММПРОИЗВ
как показано на рис. 9.
Рис.
9. Диалоговое окно функции СУММПРОИЗВ
с заполненными полями ввода
Рис.
10. Результат вычисления математического
ожидания
Для
вычисления дисперсии
в ячейку B12
поместите формулу
Для
этого вновь воспользуйтесь функцией
СУММПРОИЗВ.
Рис.
11. В поле
ввода Массив1
введен массив A2:A8^2.
В
ячейке B12
появится результат вычисления дисперсии:
Для
вычисления среднего квадратического
отклонения в ячейку C12
поместите формулу КОРЕНЬ(B12).
Результат
вычислений даст значение среднего
квадратического отклонения.
Рис.
12. Результаты вычисления
,
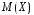
и
.
5.
Вероятности
,
,
вычисляются с использованием формулы
СУММ.
,
,
.
Рис.
13. Результаты вычисления
,
и
.
Результаты
вычислений в Excel
показаны в приложении.
Приложение
1.
Приложение
2.
Отчет
по
лабораторной работе №1
“Дискретные случайные величины”
Группа
190-1. Мельников Иван Л. Вариант №5.
Задание.
Дискретная случайная величина X
задана рядом распределения. Построить
многоугольник распределения и функцию
распределения. Найти математическое
ожидание, дисперсию, среднее квадратическое
отклонение.
Найти
вероятности
,
,
.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
xi |
1 |
4 |
8 |
10 |
13 |
17 |
19 |
|
pi |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,15 |
0,1 |
Рис.
1. Результаты вычислений в Excel
Функция
распределения дискретной случайной
величины и ее график.
pi
1
0,9
0,9
0,8
0,825
0,7
0,6
0,625
0,5
0,4
0,4
0,3
0,2
0,2 
0,1
0,05
xi
0
1 4 8 10
13 17 19
Рис.
2. График
функции распределения
.
Дата
сдачи работы:
Проверил:
Приложение
3.
Варианты
лабораторной работы №1
Вариант
1.
|
X |
-4 |
-2 |
-1 |
1 |
3 |
5 |
6 |
8 |
|
p |
0,03 |
0,22 |
0,2 |
0,05 |
0,05 |
0,1 |
0,15 |
0.2 |
Вариант
2.
|
X |
-3 |
-2 |
1 |
3 |
5 |
6 |
8 |
9 |
|
p |
0,2 |
0,15 |
0,05 |
0,05 |
0,1 |
0,2 |
0.24 |
0,01 |
Вариант
3.
|
X |
-4 |
-2 |
1 |
3 |
5 |
7 |
8 |
|
p |
0,05 |
0,15 |
0,2 |
0,2 |
0,25 |
0,1 |
0.05 |
Вариант
4.
|
X |
2 |
3 |
5 |
7 |
8 |
9 |
9.5 |
|
p |
0,05 |
0,1 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
5.
|
X |
-6 |
-5 |
-4.6 |
-1.3 |
1 |
3 |
4.7 |
8 |
|
p |
0,02 |
0,08 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
6.
|
X |
-4 |
-3.5 |
-1.2 |
0 |
3.7 |
5.8 |
6.1 |
7.0 |
|
p |
0,02 |
0,08 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
7.
|
X |
1 |
2 |
5 |
7 |
8 |
9 |
10 |
|
p |
0,05 |
0,1 |
0,2 |
0,3 |
0,2 |
0,1 |
0.05 |
Вариант
8.
|
X |
-5 |
-3 |
-1 |
1 |
3 |
5 |
6 |
7 |
|
p |
0,01 |
0,09 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
9.
|
X |
-2 |
-1 |
1 |
3 |
5 |
6 |
8 |
|
p |
0,05 |
0,1 |
0,35 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
10.
|
X |
-3 |
-2 |
1 |
3 |
5 |
6 |
8 |
|
p |
0,05 |
0,15 |
0,2 |
0,3 |
0,15 |
0,1 |
0.05 |
Вариант
11.
|
X |
-1 |
0 |
1 |
3 |
5 |
6 |
8 |
|
p |
0,05 |
0,15 |
0,2 |
0,2 |
0,25 |
0,1 |
0.05 |
Вариант
12.
|
X |
2 |
3 |
5 |
7 |
8 |
9 |
9.5 |
|
p |
0,05 |
0,1 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
13.
|
X |
-5 |
-4.6 |
-1.3 |
1 |
3 |
4.7 |
8 |
|
p |
0,1 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
14.
|
X |
-3.5 |
-1.2 |
0 |
3.7 |
5.8 |
6.1 |
7.0 |
|
p |
0,1 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
15.
|
X |
1 |
2 |
5 |
7 |
8 |
9 |
10 |
|
p |
0,1 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
16.
|
X |
-3,5 |
-1 |
1 |
3 |
5,5 |
6 |
7,5 |
|
p |
0,1 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
17.
|
X |
-5 |
-4.6 |
-1.3 |
1 |
3 |
4.7 |
8 |
|
p |
0,1 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Вариант
18.
|
X |
-3.5 |
-1.2 |
0 |
3.7 |
5.8 |
6.1 |
7.0 |
|
p |
0,1 |
0,15 |
0,25 |
0,2 |
0,15 |
0,1 |
0.05 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- 2.1.1. Полигон распределения
- Как сделать полигон частот в Excel
- Пример: полигон частот в Excel
- Как построить полигон в excel
- Инструменты Excel для построения гистограмм, полигонов
- Постройка полигона и гистограммы частот
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
- Использование Excel для расчета статистических характеристик случайной величины
2.1.1. Полигон распределения
Полигон частот – это ломаная, соединяющая соседние точки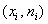 
: 
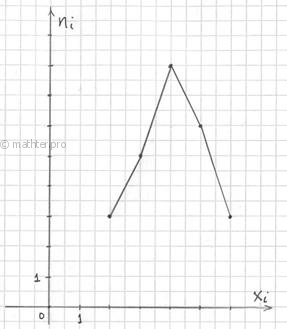
Кстати, с помощью полигона можно не только изобразить, но ещё и однозначно задать дискретный вариационный ряд (вместо таблицы с вариантами и частотами).
Теперь программный способ решения:
Задание
Самостоятельно решить данную задачу в Экселе (прямо в открывшемся файле).
Решаем! – все исходные данные с пошаговыми инструкциями прилагаются.
После чего переходим ко второй части задачи, в которой требуется найти относительные частоты и построить эмпирическую функцию распределения.
Относительные частоты рассчитываем по формуле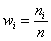 
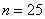
– для этого каждую частоту 
делим на объём выборки 
и результаты заносим в дополнительный столбец, далее я перехожу к электронной версии оформления: 
Обязательно проверяем, что сумма всех относительных частот равна единице: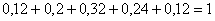 
, ОК.
Иногда требуется построить полигон относительных частот. Как вы правильно догадались – это ломаная, соединяющая соседние точки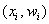 
. Но такое задание больше характерно для интервального вариационного ряда, до которого мы доберёмся в самом близком будущем.
А теперь посмотрим на относительные частоты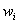 
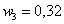
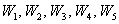
и задумаемся: на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что 
– есть примерная вероятность того, что наугад выбранный рабочий цеха будет иметь 4-й разряд. «Примерная» – по той причине, что перед нами выборка. А вот учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты 
– в точности и есть эти вероятности.
Полигон относительных частот – это статистический аналог многоугольника распределения из теории вероятностей. Следует заметить, что он уже не задаёт вариационный ряд, так как относительные частоты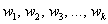 
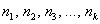
(сами по себе) ничего не говорят нам о частотах 
и объеме совокупности.
Но не полигоном единым жив дискретный вариационный ряд, существует и другой подход к его заданию и изображению:
Источник
Как сделать полигон частот в Excel
Частотный полигон — это тип диаграммы, которая помогает нам визуализировать распределение значений.
В этом руководстве объясняется, как создать полигон частот в Excel.
Пример: полигон частот в Excel
Используйте следующие шаги для создания полигона частот.
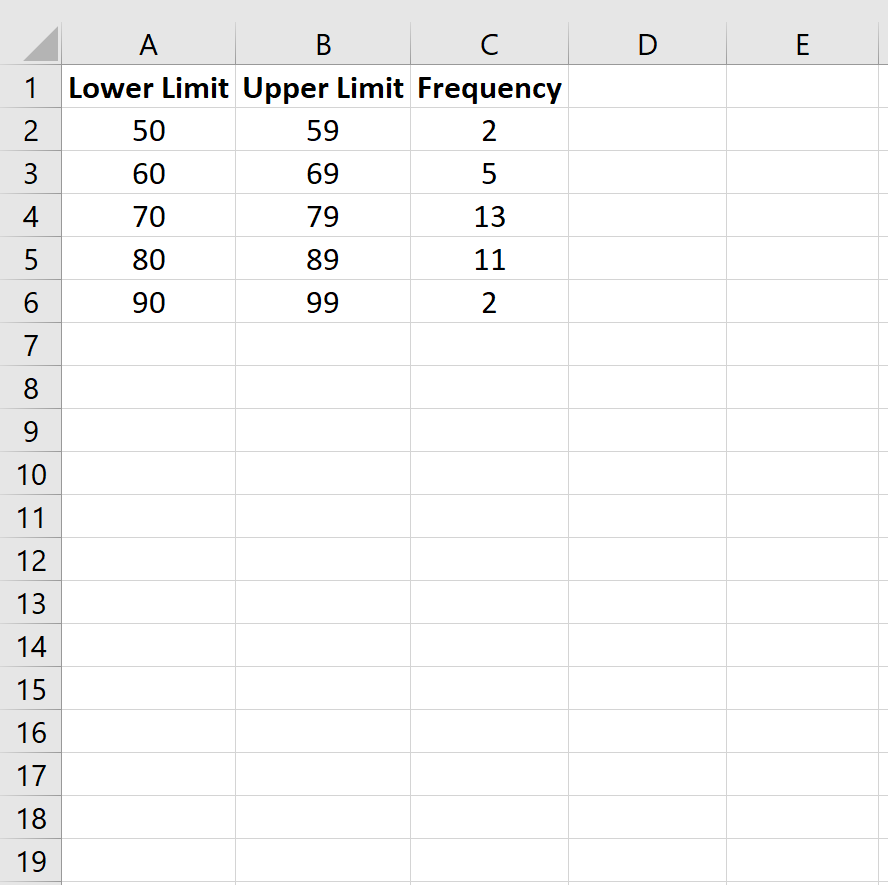
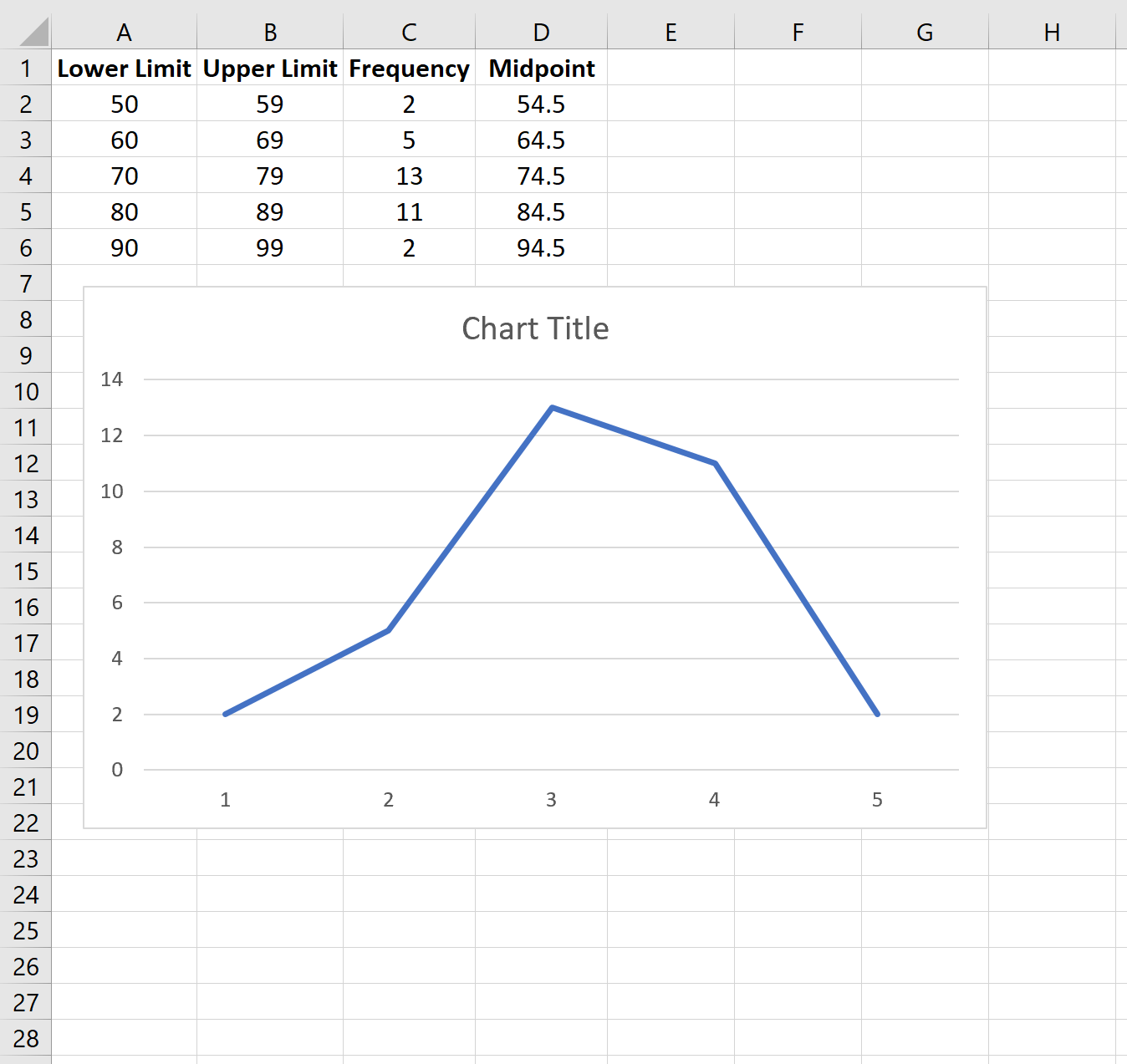
Шаг 1: Введите данные для таблицы частот.
Введите следующие данные для таблицы частоты, которая показывает количество студентов, получивших определенный балл на экзамене:
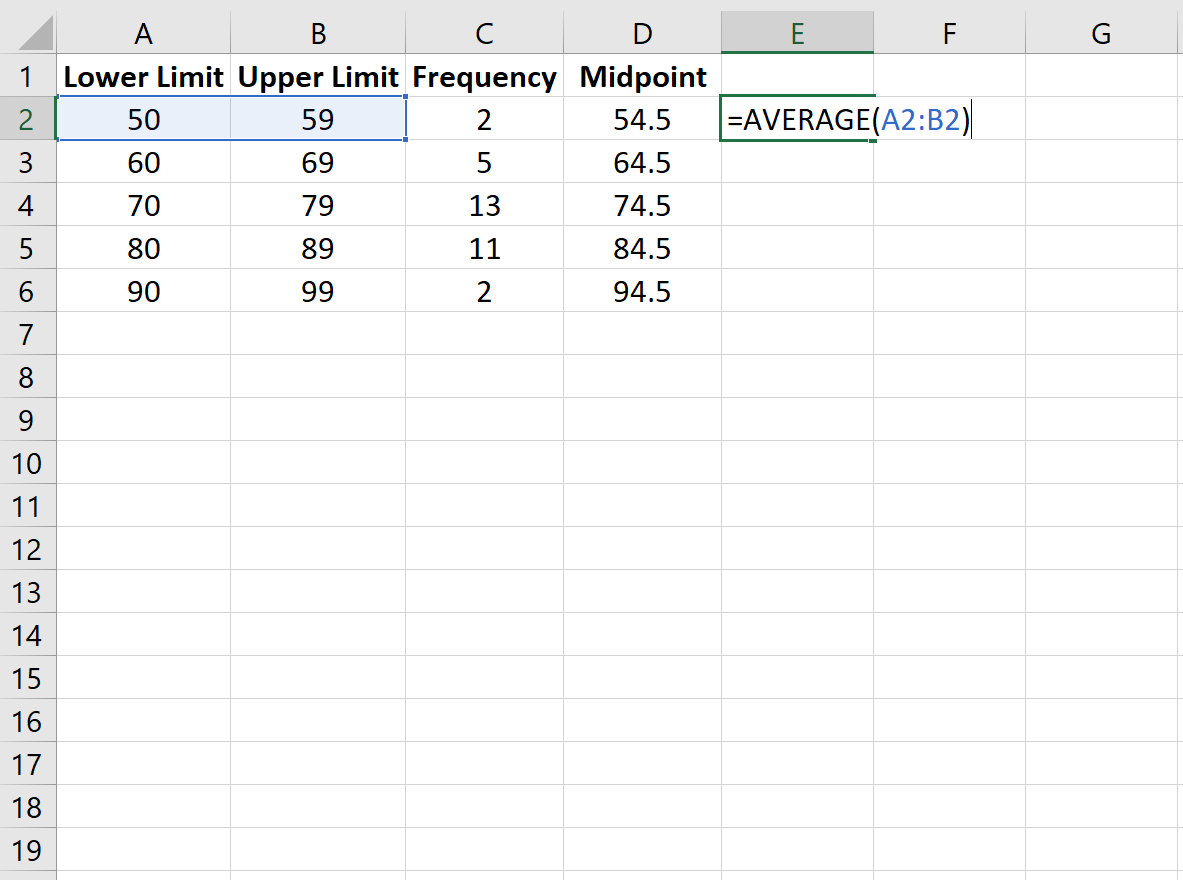
Шаг 2: Найдите среднюю точку каждого класса.
Затем используйте функцию = СРЗНАЧ() в Excel, чтобы найти среднюю точку каждого класса, которая представляет среднее число в каждом классе:
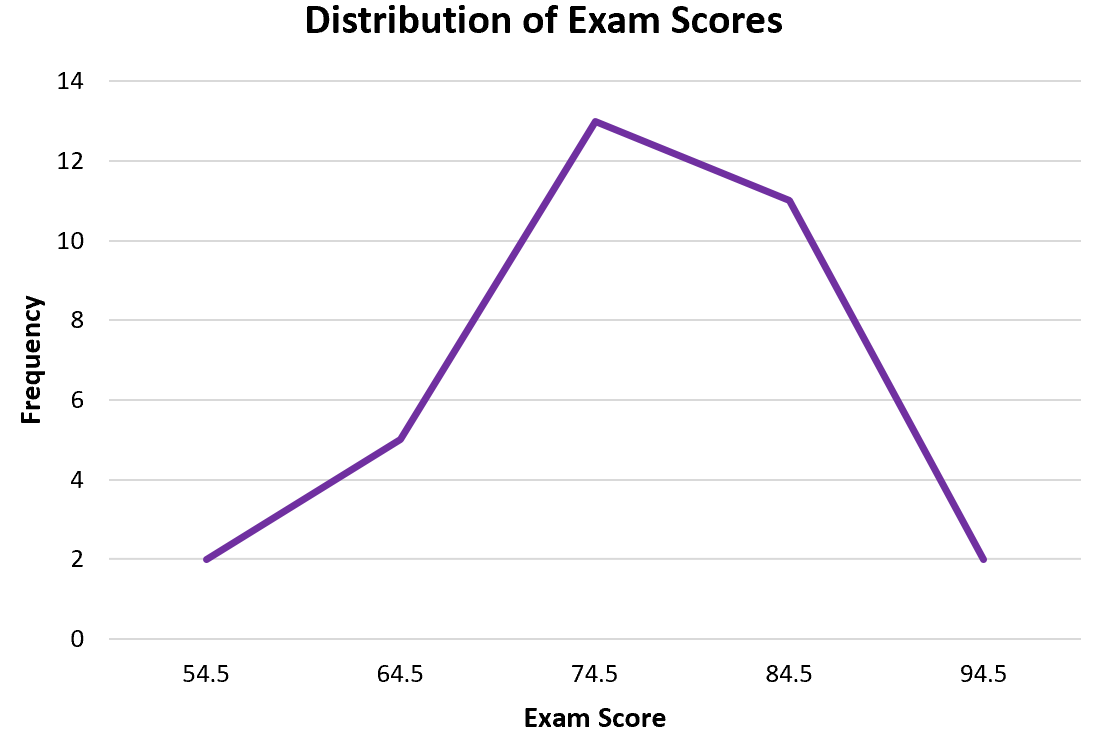
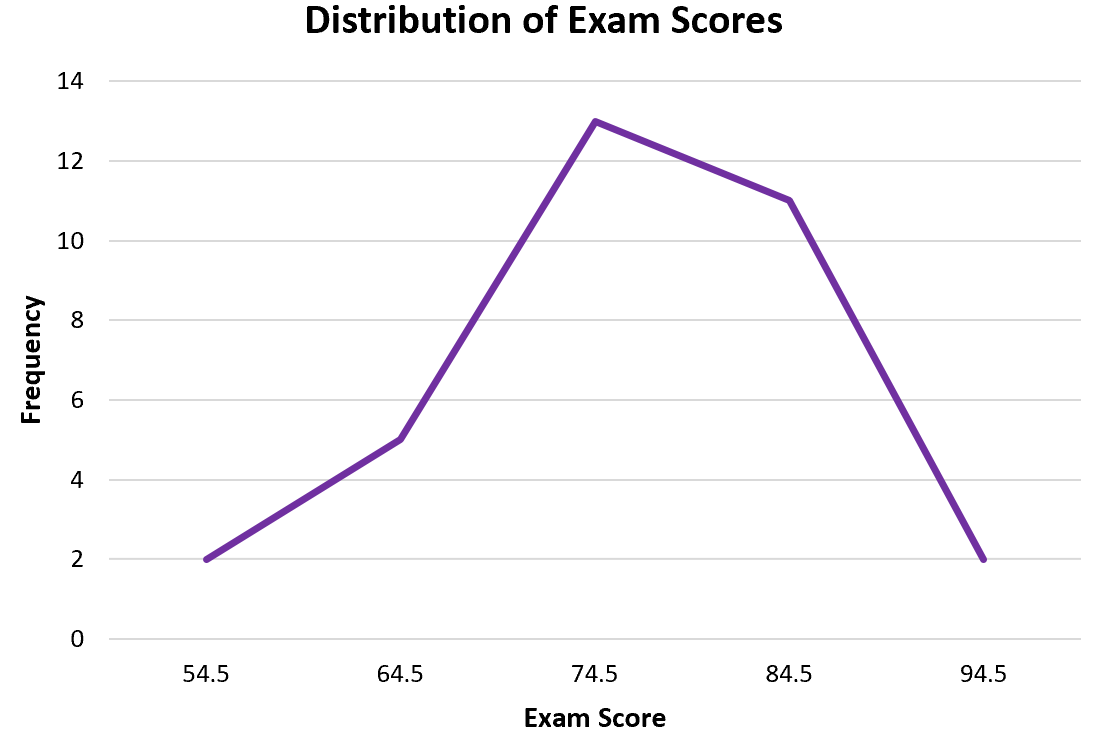
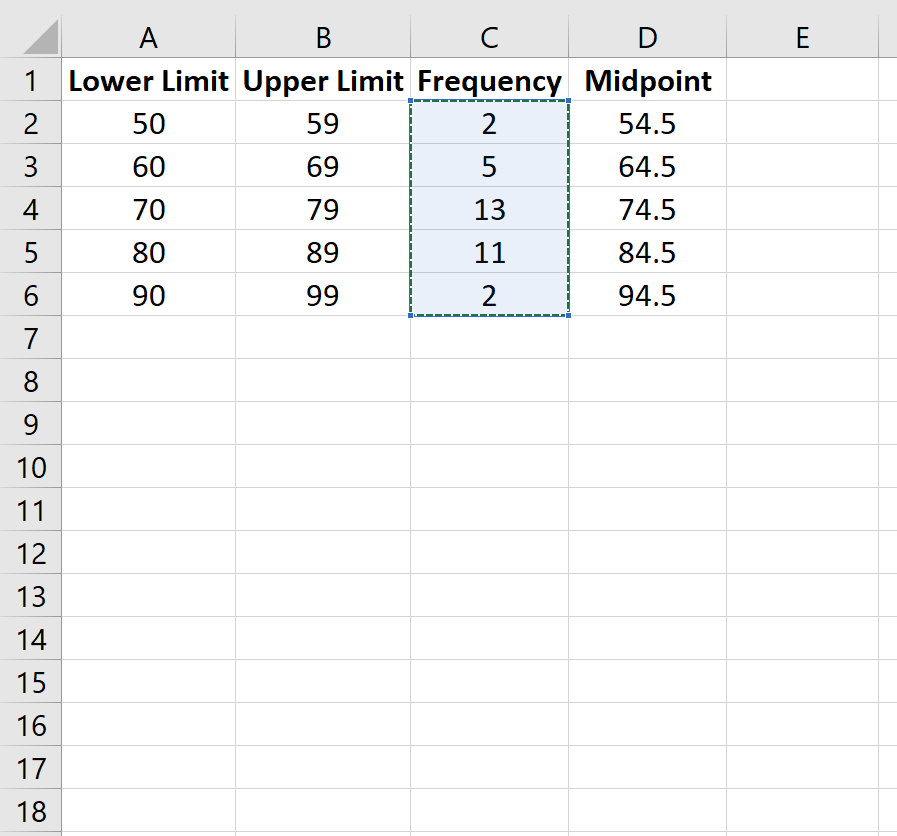
Шаг 3: Создайте полигон частот.
Далее мы создадим полигон частот. Выделите значения частоты в столбце C:
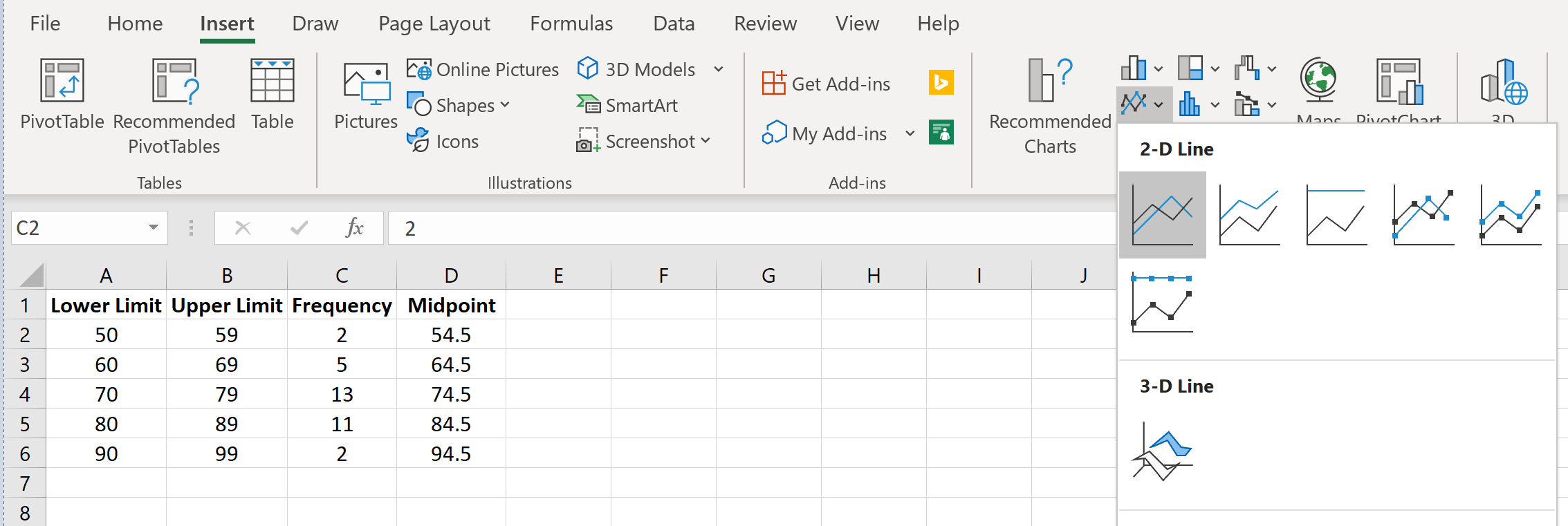
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить линию или диаграмму с областями» :
Автоматически появится полигон частот:
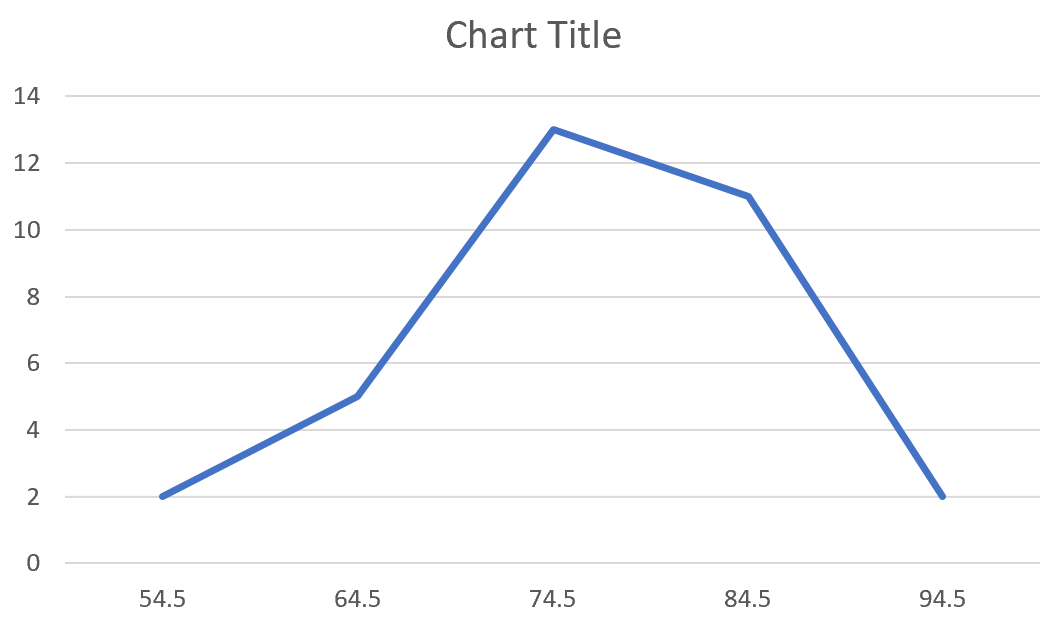
Чтобы изменить метки оси X, щелкните правой кнопкой мыши в любом месте диаграммы и выберите « Выбрать данные ». Появится новое окно. В разделе « Метки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий значения средней точки. Нажмите OK , и новые метки осей появятся автоматически:
Не стесняйтесь изменять заголовок диаграммы, добавлять метки осей и изменять цвет графика, чтобы сделать его более эстетичным.
Из полигона частот легко увидеть, что большинство учащихся набрали 70-е и 80-е баллы, несколько — 60-е и еще меньше — 50-е и 90-е.
Источник
Как построить полигон в excel
Инструменты Excel для построения гистограмм, полигонов
Процедура «Гистограмма» пакета «Анализ данных. Вычисление частот и накопленных частот. Построение гистограмм.
В процедуре автоматически выполняются следующие вычисления:
выбирается число m интервалов группировки (7 £ m £ 20);
вычисляются середины интервалов группировки , , ;
для каждого интервала вычисляются частоты nj — количество выборочных значений, которые попали в j -й интервал;
для каждого интервала вычисляются накопленные частоты — количество выборочных значений, не превышающих верхней границы j -го интервала;
Строится гистограмма – график ступенчатой функции , , , D j = ( aj , bj ) , .
Для того чтобы вычислять накопленные частоты и отобразить гистограмму в листе в листе Excel , в окне процедуры следует пометить соответствующие поля.
Результаты вычислений процедуры представлены в виде таблицы (ниже приведены две таблицы, первая – когда поле «Интегральный процент» не помечено, вторая – когда помечено)
Постройка полигона и гистограммы частот
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2). (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2). (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
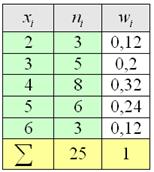
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Источник
Использование Excel для расчета статистических характеристик случайной величины
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Источник
17 авг. 2022 г.
читать 2 мин
Частотный полигон — это тип диаграммы, которая помогает нам визуализировать распределение значений.
В этом руководстве объясняется, как создать полигон частот в Excel.
Пример: полигон частот в Excel
Используйте следующие шаги для создания полигона частот.
Шаг 1: Введите данные для таблицы частот.
Введите следующие данные для таблицы частоты, которая показывает количество студентов, получивших определенный балл на экзамене:
Шаг 2: Найдите среднюю точку каждого класса.
Затем используйте функцию = СРЗНАЧ() в Excel, чтобы найти среднюю точку каждого класса, которая представляет среднее число в каждом классе:
Шаг 3: Создайте полигон частот.
Далее мы создадим полигон частот. Выделите значения частоты в столбце C:
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить линию или диаграмму с областями» :
Автоматически появится полигон частот:
Чтобы изменить метки оси X, щелкните правой кнопкой мыши в любом месте диаграммы и выберите « Выбрать данные ». Появится новое окно. В разделе « Метки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий значения средней точки. Нажмите OK , и новые метки осей появятся автоматически:
Не стесняйтесь изменять заголовок диаграммы, добавлять метки осей и изменять цвет графика, чтобы сделать его более эстетичным.
Из полигона частот легко увидеть, что большинство учащихся набрали 70-е и 80-е баллы, несколько — 60-е и еще меньше — 50-е и 90-е.
Написано
Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
|
12:56 Построить многоугольник распределения |
|
Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки М1 (Х1; Р1), M2(X2; Р2). • • • Mn(Хn; Рn) (Xi—-возможные значения X, Pi—соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. Задача 164. Дискретная случайная величина X задана законом распределения: X 1 3 6 8 Построить многоугольник распределения.
Как построить многоугольник распределения в Excel В Excel имеются средства для создания графиков и диаграмм, с помощью которых вы сможете в наглядной форме представить зависимости и тенденции, отраженные в числовых данных. Кнопки построения графиков и диаграмм находятся в группе Диаграммы на вкладке Вставка (Рис.1).
Для того чтобы построить многоугольник распределения сначала нужно сформировать таблицу, например так (Рис.2).
Далее просто выделяем нужные нам ячейки и выбираем тип графика который надо построить (Рис.3). В результате мы получи многоугольник распределения с которым сможем производить дальнейшие действия Рис.4. Для тех кому облом учить Excel, даем готовый шаблон (калькулятор) для построения многоугольника распределения, скачать шаблон бесплатно. Задания на тему: «Многоугольник распределения» для самостоятельного решения.
165. Дискретная случайная величина X задана законом распределения: |
Категория: Теория вероятности | Просмотров: 22065 | | Теги: закон распределения, многоугольник распределения, Дискретная случайная величина | Рейтинг: 5.0/1 |
