Содержание
- Создание параболы
- Создание таблицы
- Построение графика
- Редактирование диаграммы
- Вопросы и ответы
Построение параболы является одной из известных математических операций. Довольно часто она применяется не только в научных целях, но и в чисто практических. Давайте узнаем, как совершить данную процедуру при помощи инструментария приложения Excel.
Создание параболы
Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.
Создание таблицы
Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.
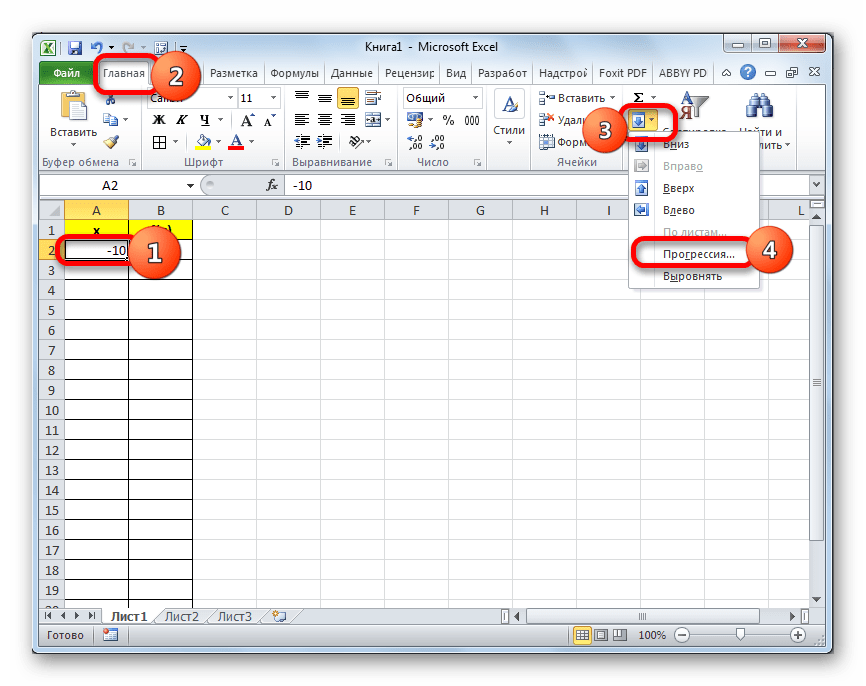
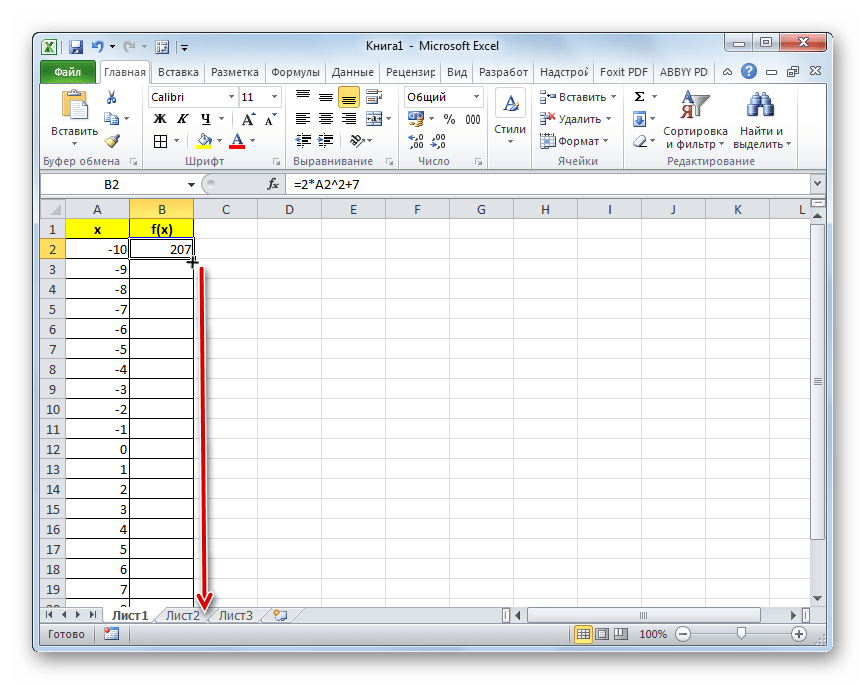
- Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».
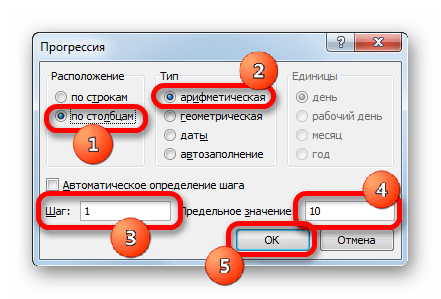
- Выполняется активация окна регулировки прогрессии. В блоке «Расположение» следует переставить кнопку в позицию «По столбцам», так как ряд «X» размещается именно в столбце, хотя в других случаях, возможно, нужно будет выставить переключатель в позицию «По строкам». В блоке «Тип» оставляем переключатель в позиции «Арифметическая».
В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».
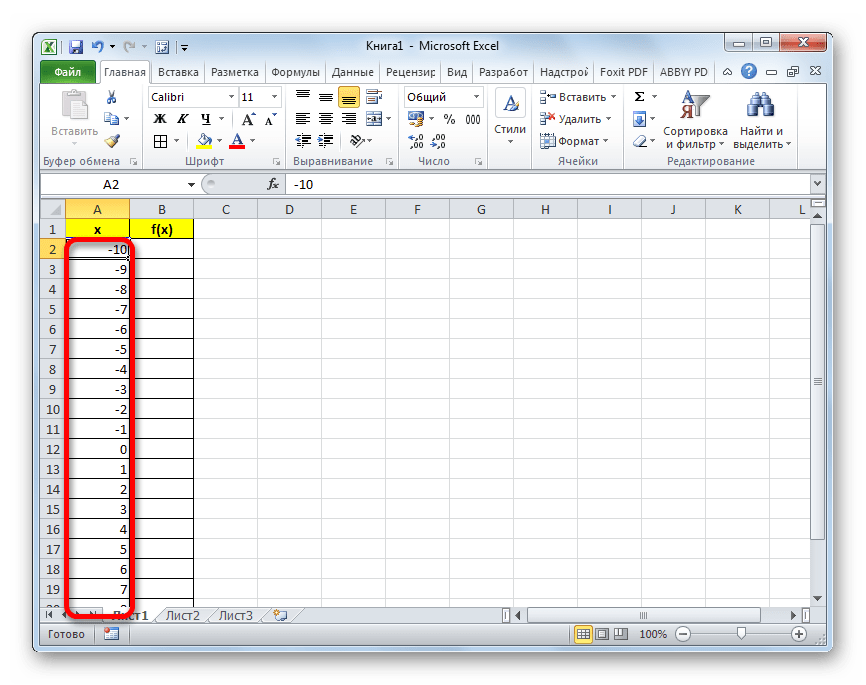
- После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.
- Теперь нам предстоит заполнить данными столбец «f(x)». Для этого, исходя из уравнения (f(x)=2x^2+7), нам нужно вписать в первую ячейку данного столбца выражение по следующему макету:
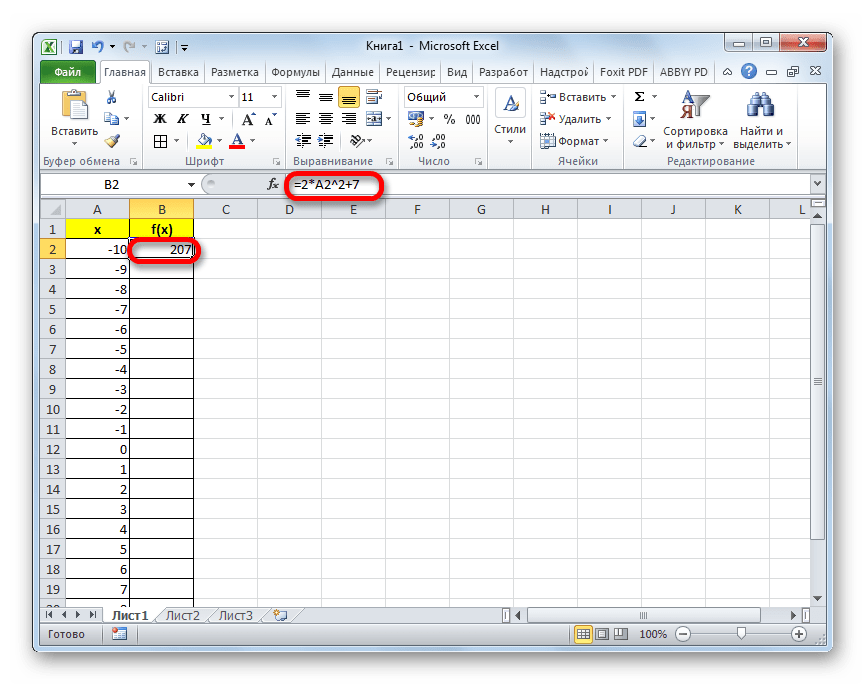
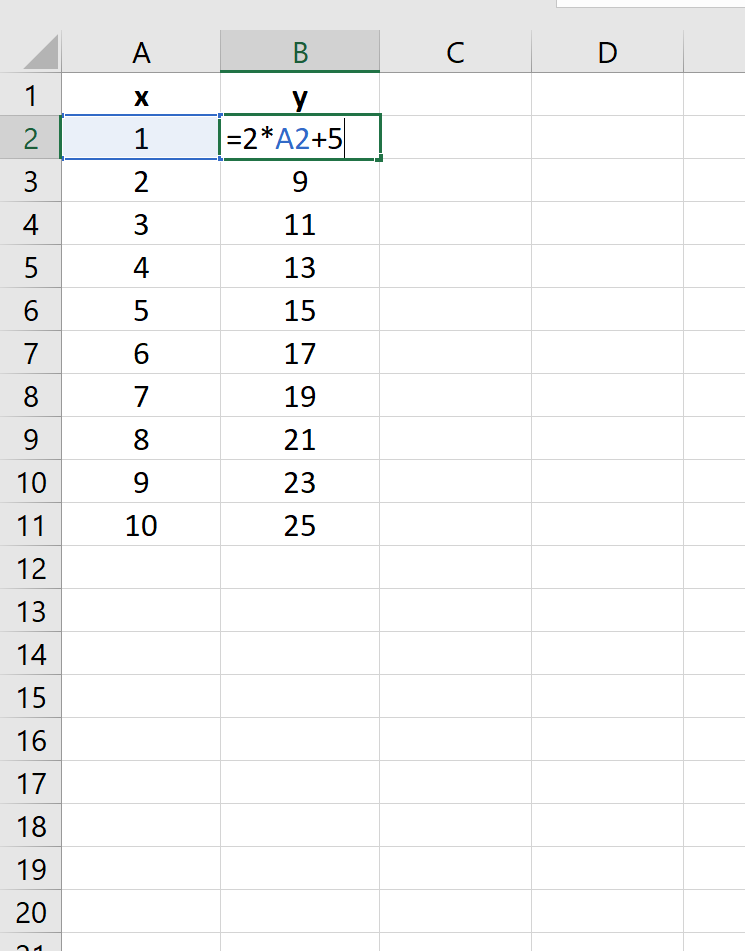
=2*x^2+7Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:
=2*A2^2+7 - Теперь нам нужно скопировать формулу и на весь нижний диапазон данного столбца. Учитывая основные свойства Excel, при копировании все значения x будут поставлены в соответствующие ячейки столбца «f(x)» автоматически. Для этого ставим курсор в правый нижний угол ячейки, в которой уже размещена формула, записанная нами чуть ранее. Курсор должен преобразоваться в маркер заполнения, имеющий вид маленького крестика. После того, как преобразование произошло, зажимаем левую кнопку мыши и тянем курсор вниз до конца таблицы, после чего отпускаем кнопку.
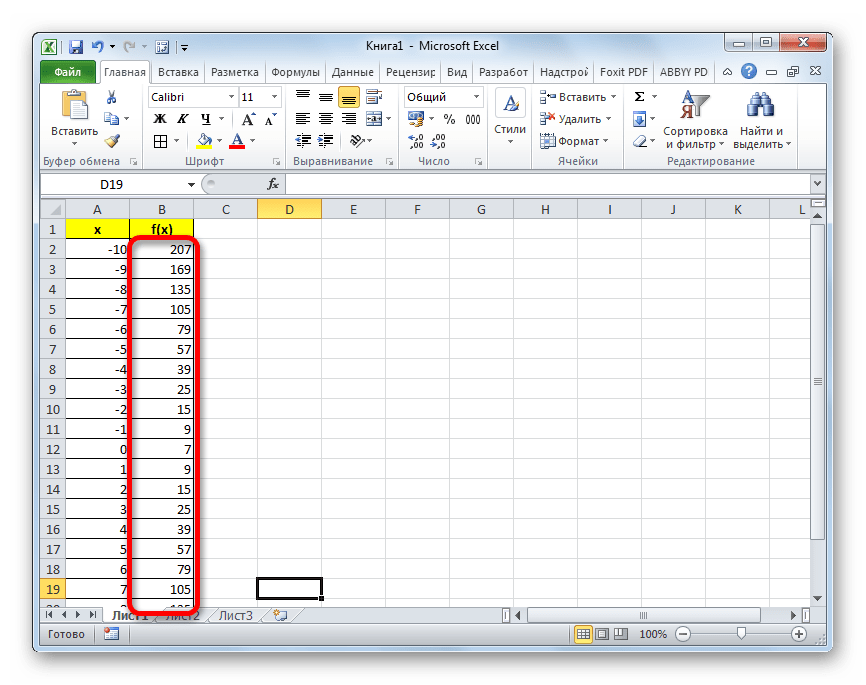
- Как видим, после этого действия столбец «f(x)» тоже будет заполнен.
На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.
Урок: Как сделать автозаполнение в Экселе
Построение графика
Как уже было сказано выше, теперь нам предстоит построить сам график.
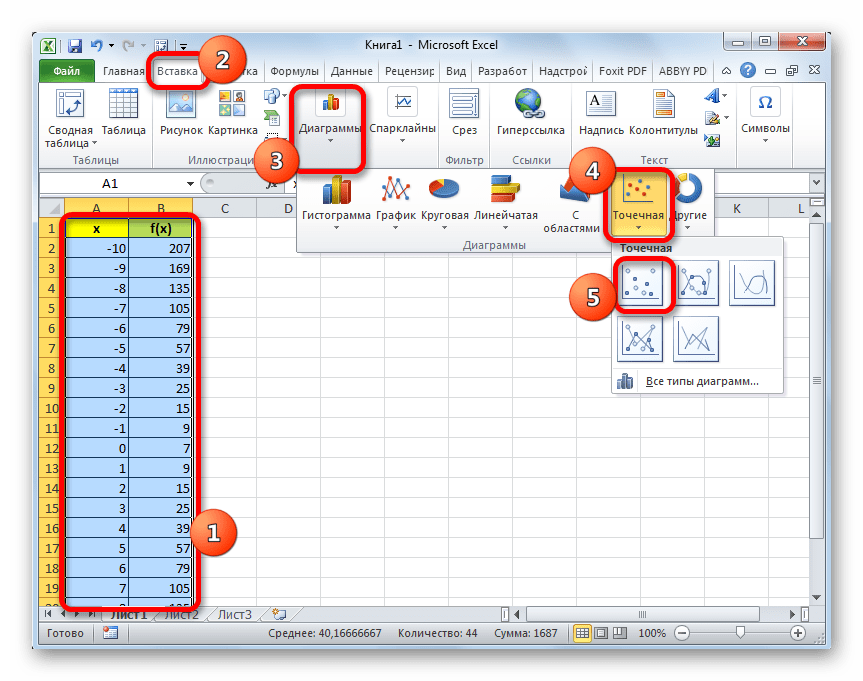
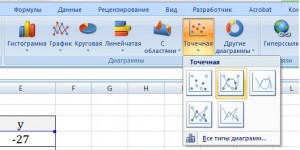
- Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.
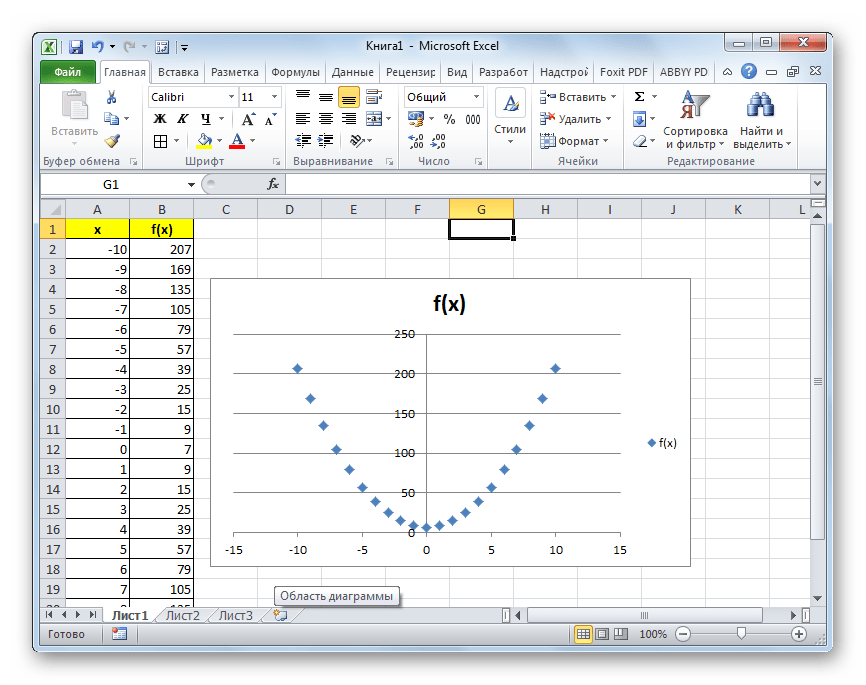
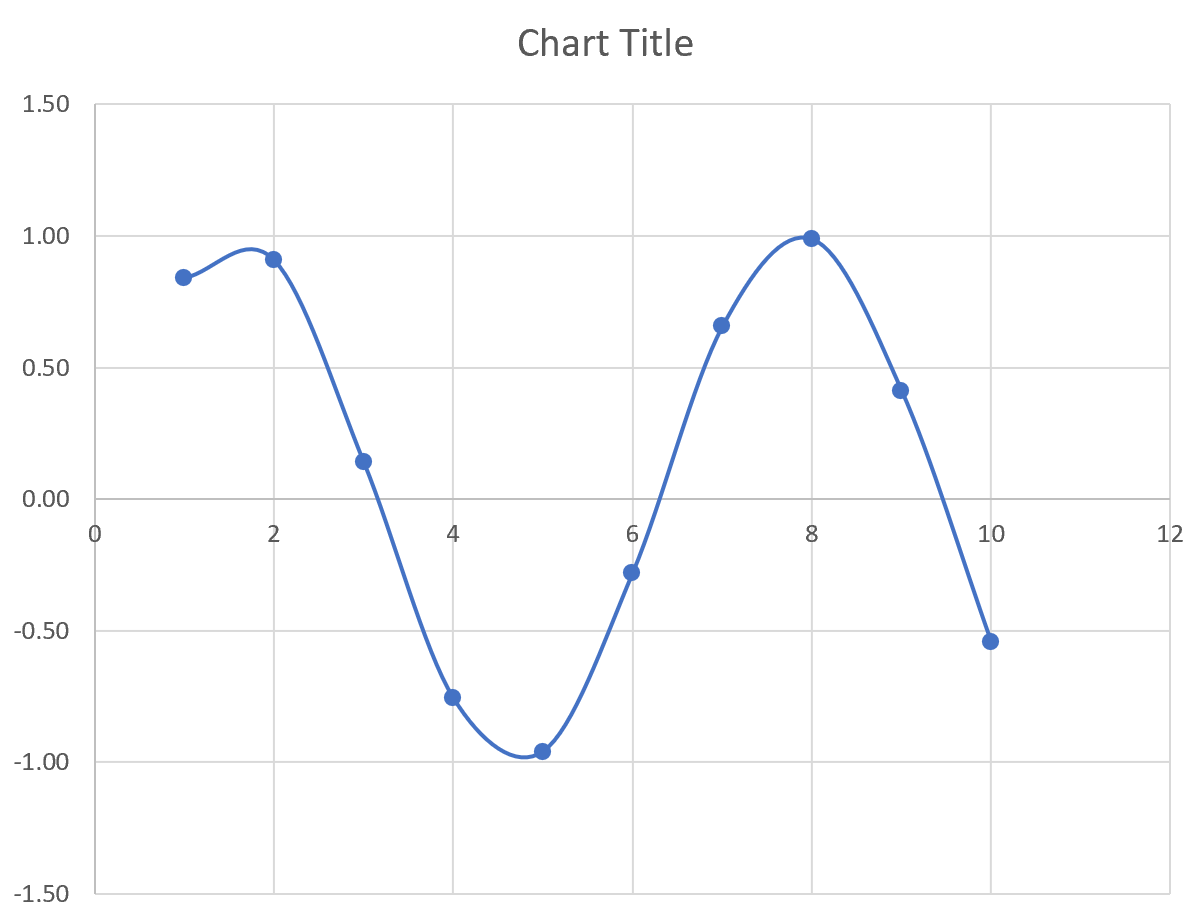
- Как видим, после этих действий, парабола построена.
Урок: Как сделать диаграмму в Экселе
Редактирование диаграммы
Теперь можно немного отредактировать полученный график.
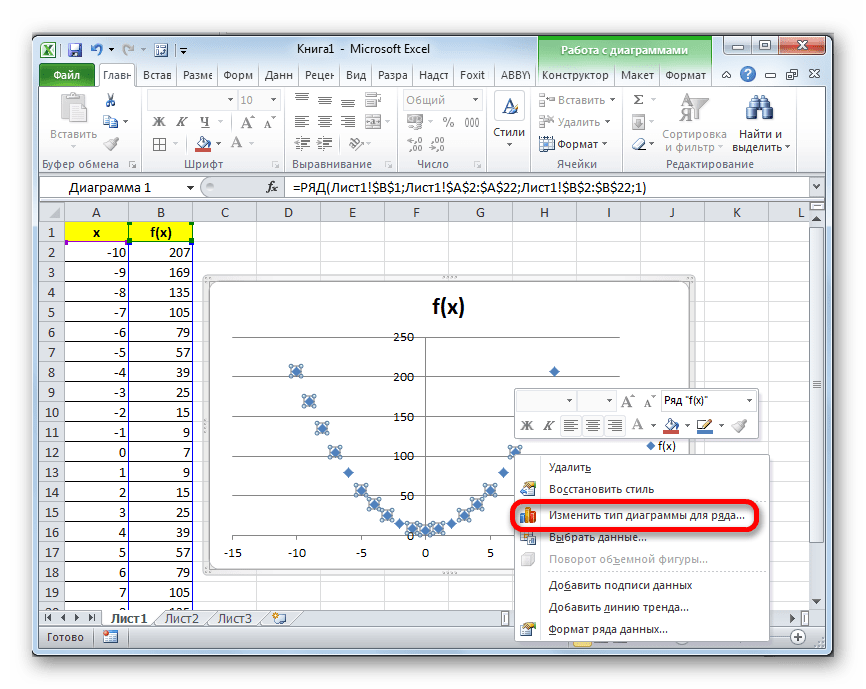
- Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».
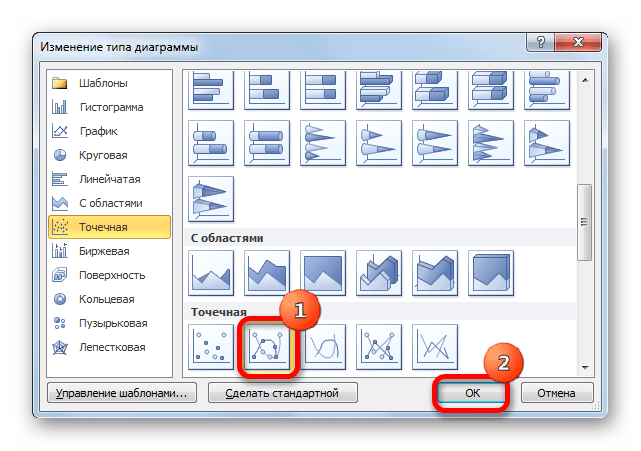
- Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».
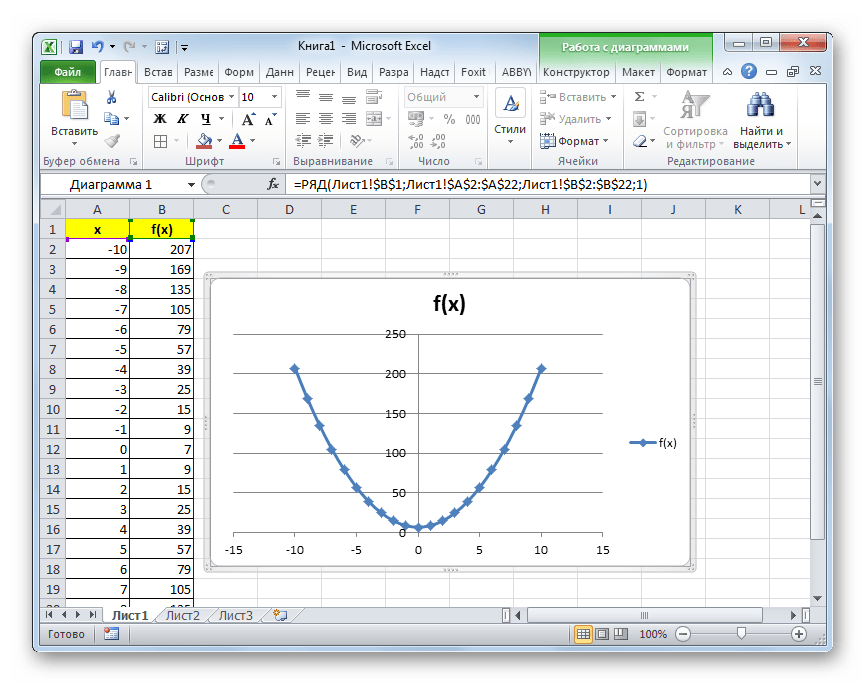
- Теперь график параболы имеет более привычный вид.
Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.
Урок: Как подписать оси диаграммы в Excel
Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.
Еще статьи по данной теме:
Помогла ли Вам статья?
Построение параболы в Microsoft Excel
Построение параболы является одной из известных математических операций. Довольно часто она применяется не только в научных целях, но и в чисто практических. Давайте узнаем, как совершить данную процедуру при помощи инструментария приложения Excel.
Создание параболы
Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.
Создание таблицы
Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.
- Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».
Выполняется активация окна регулировки прогрессии. В блоке «Расположение» следует переставить кнопку в позицию «По столбцам», так как ряд «X» размещается именно в столбце, хотя в других случаях, возможно, нужно будет выставить переключатель в позицию «По строкам». В блоке «Тип» оставляем переключатель в позиции «Арифметическая».
В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».
После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.
Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:
На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.
Построение графика
Как уже было сказано выше, теперь нам предстоит построить сам график.
-
Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.
Редактирование диаграммы
Теперь можно немного отредактировать полученный график.
-
Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».
Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».
Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.
Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Квадратное уравнение (строим график функции в EXCEL)
history 1 апреля 2015 г.
-
Группы статей
- Диаграммы и графики
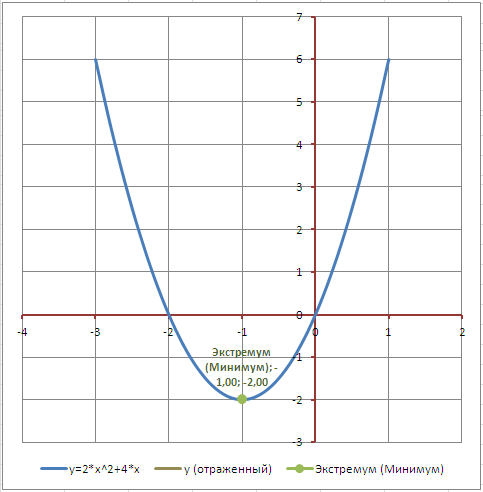
Построим график функции y=a*x^2+b*x+с (квадратное уравнение). Также рассчитаем дискриминант, найдем корни уравнения, координаты точки экстремума (максимума или минимума). Сделаем форму для сдвига и отражения графика с помощью элементов управления формы.
Построим график функции y=a*x^2+b*x+с в диаграмме типа Точечная с гладкими кривыми. (см. файл примера лист График).
Укажем на графике точку экстремума (для этого в диаграмме создан дополнительный ряд, состоящий из 1 точки).
Коэффициенты а, b, с введем в отдельные ячейки, чтобы можно было быстро построить нужный график.
Строить график в диаграмме типа Точечная с гладкими кривыми проще, чем строить его в диаграмме типа График (см. статью График vs Точечная диаграмма в MS EXCEL ), т.к. точку пересечения вертикальной осью горизонтальной оси можно настроить только по номеру категории (порядковый номер точки), а не по значению x (получается, что вертикальная ось y не проходит через х=0, что не удобно).
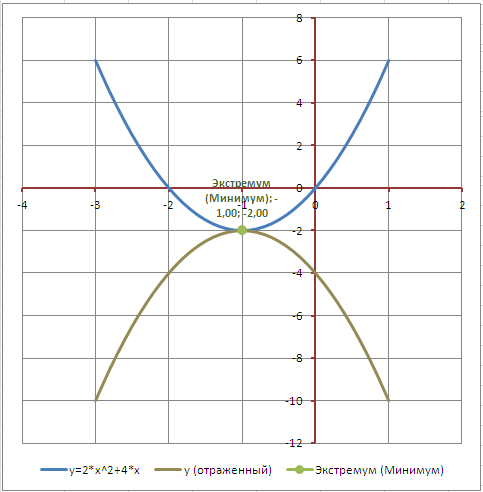
Диаграмма также может построить график, отраженный относительно горизонтальной оси (проходящей через точку экстремума).
Сдвиг графика
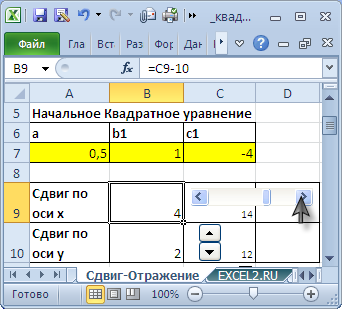
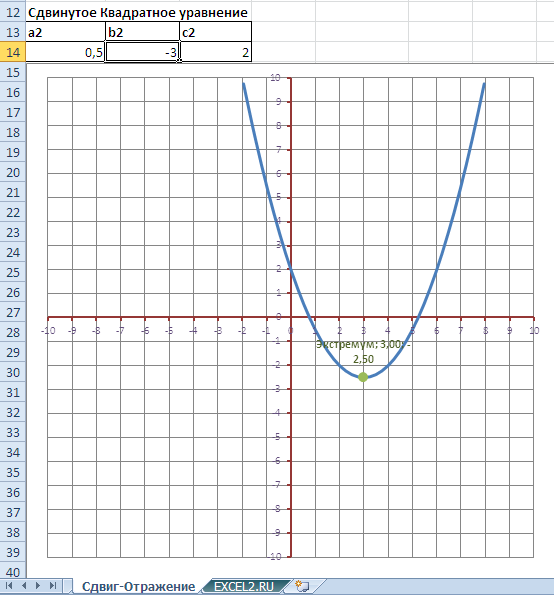
В файле примера на листе Сдвиг-Отражение сделана форма для сдвига графика по координатам х и y с помощью Элементов управления формы .
Эта форма позволяет быстро рассчитывать коэффициенты нового квадратного уравнения, полученного при сдвиге.
Форма также позволяет рассчитывать коэффициенты квадратного уравнения, полученного при горизонтальном отражении ранее сдвинутого графика (с его построением на диаграмме).
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://excel2.ru/articles/kvadratnoe-uravnenie-stroim-grafik-funkcii-v-ms-excel
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
history 8 января 2023 г.
- Группы статей
- Диаграммы и графики
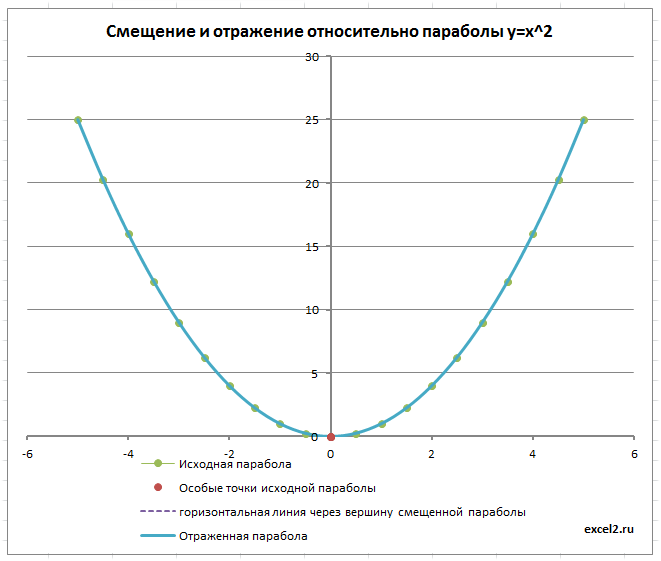
Построим параболу, используя стандартную диаграмму MS EXCEL. C помощью элементов управления построим удобную форму для смещения вершины параболы вверх/низ, отражения ее относительно осей координат.
Задача
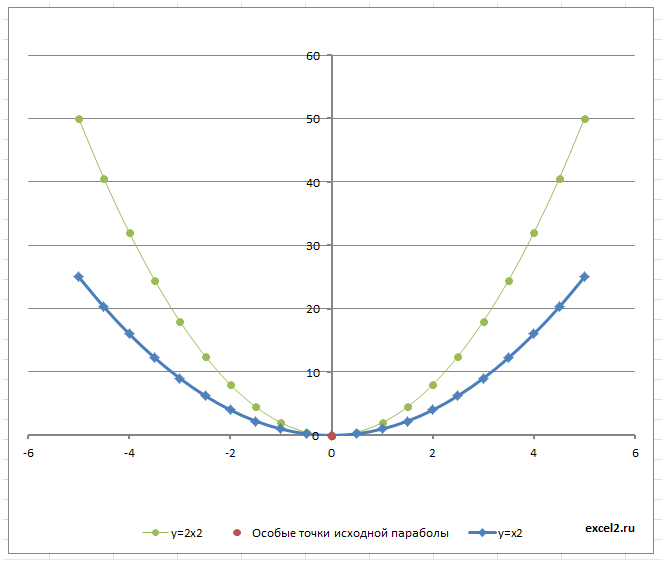
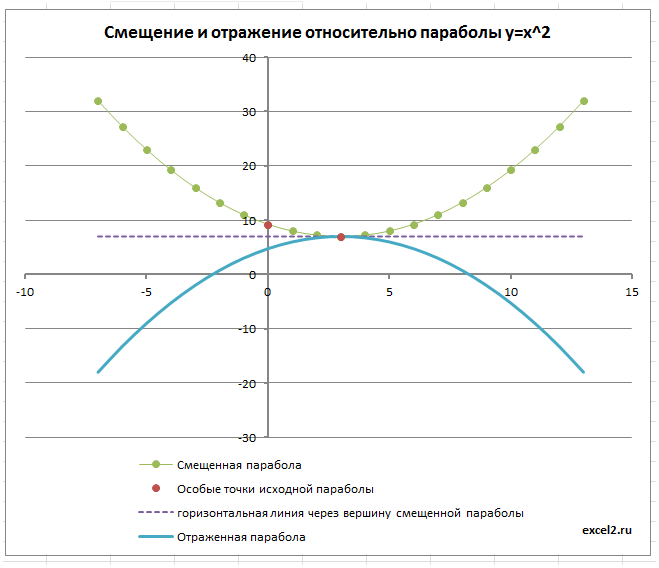
- Построим Параболу имеющую уравнение y=x2.
- Отметим на диаграмме ее особые точки: пересечения с осями (осью) и вершину.
- Создадим на листе кнопки для смещения вершины параболы в произвольном направлении
- Выберем такой шаг по оси Х и диапазон изменения переменной Х, чтобы после смещения параболы на диаграмме обе ее ветви отображались одинаковой длины и присутствовали все особые точки
- Вычислим новые значения параметров параболы y=ax2 + bx + с
Построение исходной параболы
С помощью точечной диаграммы построим Параболу имеющую уравнение y=x2, назовем ее исходной параболой.
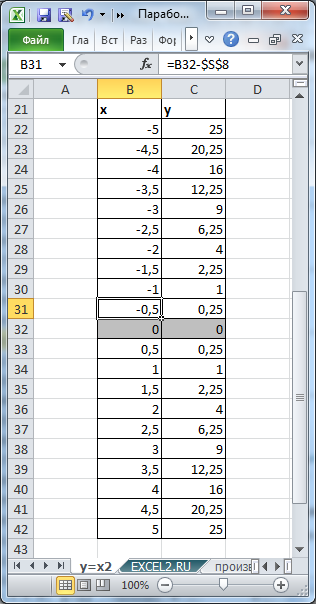
Для этого на листе в файле примера подготовлена таблица исходных значений по Х и Y.
Особенностью этого набора данных является то, что значения Х отсчитываются от координат вершины параболы с определенным шагом.
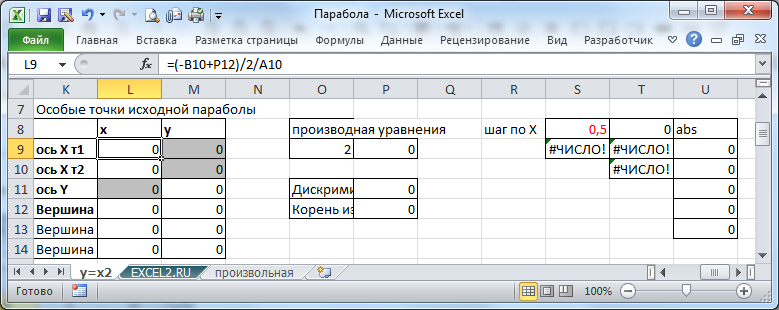
Для определения вершины параболы можно использовать различные формулы, например через производную или по формуле х0=-b/2a. Для этого в файле примера делаются соответствующие вычисления (при изменении местоположения параболы эти вычисления производятся автоматически).
Для определения масштаба изменения переменной Х, вычисляются точки пересечения, а затем вычисляется такой шаг по Х, чтобы все эти точки пересечения гарантированно были отражены на диаграмме.
Чтобы шаг по Х не был равен значениям с длинной десятичной частью, используется округление до первой значащей цифры.
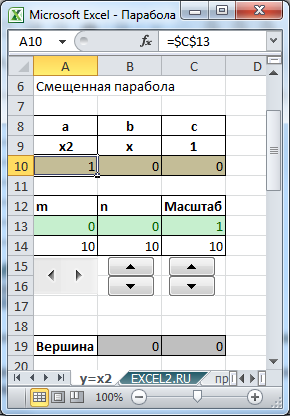
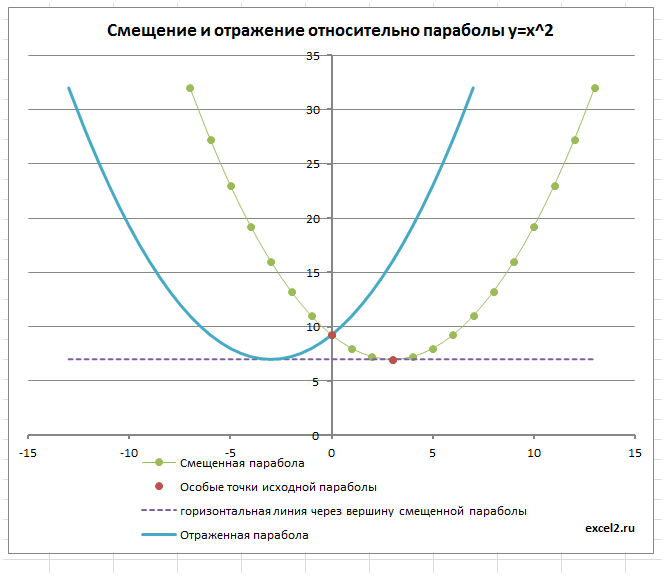
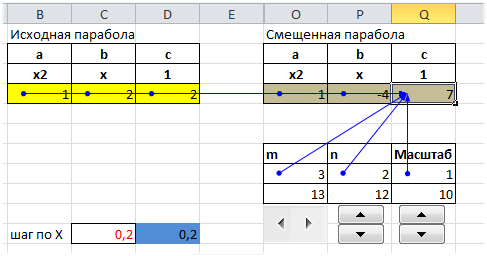
Смещение исходной параболы
Смещение вершины параболы будем производить с помощью Полосы прокрутки и Элемента управления Счетчик.
Смещение по оси Х будем обозначать m, а по Y обозначим n. Значения m и n являются новыми координатами вершины смещенной параболы.
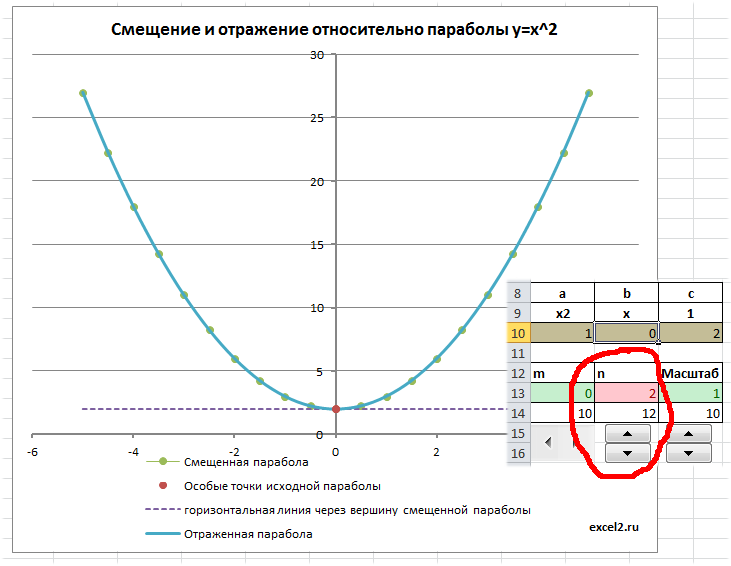
Изменив, например, с помощью Счетчика значение n на 2, автоматически пересчитаются значения параметров параболы в строке 10: y=ax2 + bx + с, а следовательно и координаты вершины вместе со всеми значениями исходной таблицы — парабола сместится на величину 2 по Y.
Примечание: альтернативная запись параболы через координаты вершины: y=a(x-m)2+n
Изменение масштаба параболы (параметр а)
Параметр а отвечает за масштаб параболы. Например, парабола с уравнением y=2x2 будет вытянута по оси Х в 2 раза по отношению к y=x2.
В файле примера изменение масштаба параболы реализовано с помощью элемента Счетчик, аналогичным образом, как и смещение.
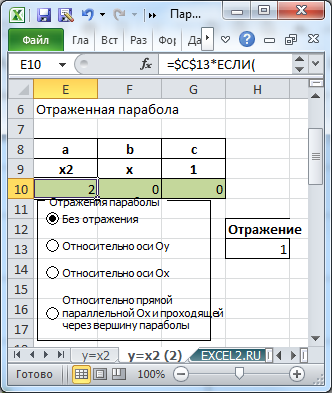
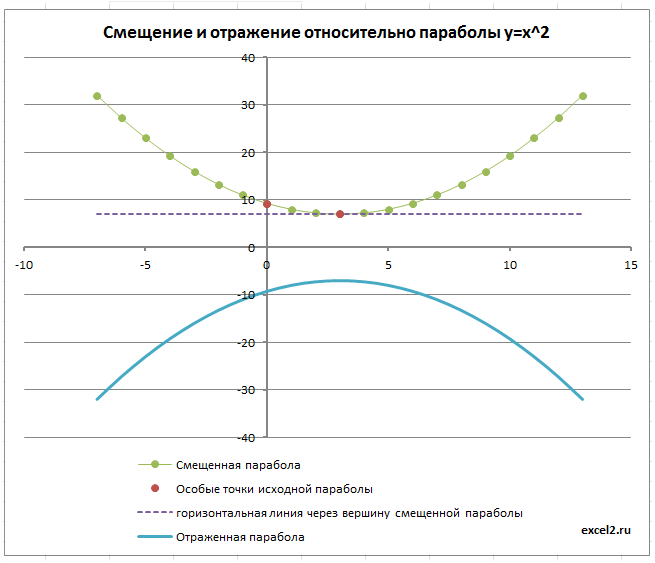
Отражение параболы
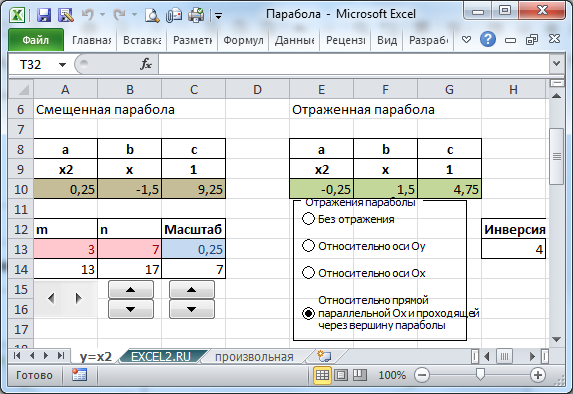
Смещенную параболу можно отразить относительно оси Х, относительно оси Y и относительно прямой параллельной Ох и проходящей через вершину параболы. Все эти манипуляции реализованы с помощью формул и элементов управления Переключатель.
Выбирая нужный тип отражения параболы, диаграмма отобразит нужный график.
Вычисления параметров параболы
Построить параболу не сложно, сложнее вычислить значения параболы (a, b, с), которая была смещена, у которой также был изменен масштаб и, наконец, она была отражена.
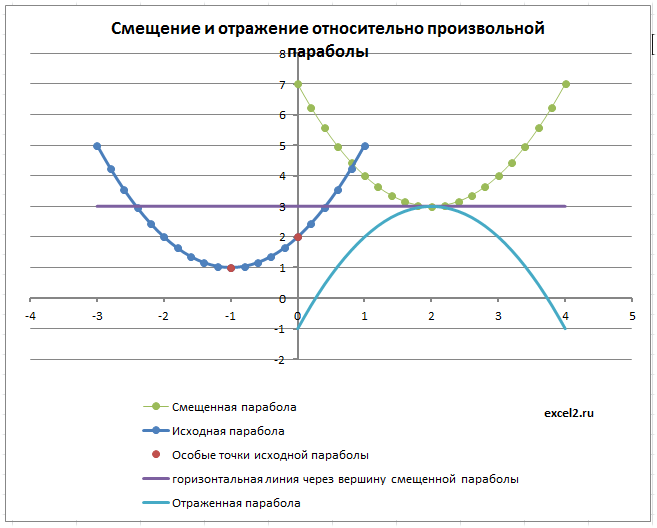
Все эти вычисления приведены в формулах строки 10 в файле примера. На листе «произвольная» расчеты параметров сделаны относительно исходной параболы с произвольными значениями параметров. Формулы получаются в этом случае достаточно громоздкими, т.к. параметры смещенной параболы зависят как от параметров исходной параболы, так и от значений m, n и масштаба.
Автор: Пенский Владимир Константинович
Предмет: алгебра, информатика.
Тема урока: Квадратичная функция в MS EXCEL.
Класс: 9.
Продолжительность: 45 минут.
Цель урока: применение
электронных таблиц для построения графика и изучения основных свойств квадратичной
функции.
Задачи урока:
Образовательные:
·
систематизация знаний о свойствах квадратичной
функции;
·
закрепить умение строить графики квадратичной
функции и по графику определять ее основные свойства;
·
закрепление умения работать с электронными
таблицами.
Развивающие:
·
формирование умения сравнивать, обобщать изучаемые
факты;
·
повышение уровня учебной мотивации с использованием
компьютерных технологий, развитие логического мышления;
·
развитие умения грамотно
излагать свои мысли, обосновывать свои действия.
Воспитательные:
·
развитие коммуникативных умений, формирование адекватной
оценки собственной деятельности;
·
развитие чувства
товарищества, взаимопомощи, деликатности,
дисциплинированности.
Оборудование: компьютерный класс, мультимедийный проектор, экран.
Ход урока
1. Организационный момент.
2. Постановка
цели урока.
Сегодня на уроке мы повторим свойства квадратичной функции и научимся
строить соответствующие графики функций с помощью прикладного программного
обеспечения компьютера и, используя полученный график, определим свойства этой
функции.
3. Актуализация
знаний. Фронтальный опрос.
Вспомним определение и
основные свойства квадратичной функции. Для этого ответьте на вопросы.
1.
Как называется функция вида у = aх2 +
bx + c (а ≠ 0), где а, b, c – действительные
числа?
- Что является графиком
квадратичной функции? - При каких
значениях х квадратичная функция у = х2 возрастает?
убывает? - Как называются
значения переменной х, при которых значение функции равно нулю. - При а >
0 ветви параболы у = ах2 направлены … . - Если а
< 0 и х < 0, то квадратичная функция у = ах2
принимает …(положительные, отрицательные) значения.
3. Повторение
изученного материала.
1. Обоснуйте, что областью определения функции у
= aх2 + bx + c является множество всех
действительных чисел.
2. Выясните, какие из следующих квадратичных функций являются: чётными;
нечётными; не являются ни чётными, ни нечётными.
а) y = x2; б)
y = 3 − 2x
+ x2.
3. Найдите нули квадратичной функции:
а) y = 2x2 + x − 3; б)
y = x2 − 8x + 15.
4. Найдите координаты вершины параболы у = х2
– 4х + 4.
5. Укажите наибольшее (наименьшее) значение
функции:
а) y = x2; б) y = 3x2 + 1.
4. Изложение нового
материала.
Можно ли, не проводя
аналитических рассуждений определить свойства квадратичной функции?
Действительно, по графику квадратичной функции можно определить все ее основные
свойства.
Как построить график
квадратичной функции? На помощь приходят современные компьютерные технологии.
Сегодня существует множество программ, которые позволяют строить графики различных
функций. Одним из простейших способов построения графика (в нашем случае
графика квадратичной функции) является использование электронных таблиц Microsoft
Excel.
Вспомним, каким образом
можно построить график функции в данной программе.
Построим, например,
график квадратичной функции у =
х2 + 2х – 3 и исследуем ее свойства.
1) Составим таблицу
значений зависимости переменной у от х:
–
в ячейку А1 введите заголовок столбца «х»;
–
в ячейку А2 введите значение –5, а в ячейку А3 – –4,5;
–
выделите содержимое ячеек А2 и А3, далее с помощью функции автозаполнения скопируйте
до ячейки А18 (получим соответствующие значения х от –5 до 3);
–
в ячейку В1 введите заголовок столбца у = х2 + 2х
– 3;
–
в ячейку В2 введите формулу = В1^2 + 2*B1 – 3;
–
скопируйте формулу из ячейки В2 (используя функцию автозаполнения) до ячейки В19.
2) Построение
графика с помощью мастера диаграмм:
– выделите
подготовленные данные, начиная с заголовка В1:В18.
– вызовите
мастер диаграмм (Вставка – график – график);
– при
задании параметров название диаграммы оставить;
– нажмите
«ОК» и график автоматически вставится.
3) Работа с
графиком:
–
вставьте названия осей (Макет – названия осей – название основной горизонтальной
оси – название под осью; Макет – названия осей – название основной вертикальной
оси – горизонтальное название) и перенесите (х справа от оси, у
выше оси);
– щелчком
мыши в готовой диаграмме по каждой из осей, вызовите контекстное меню и установите:
«горизонтальная ось пересекает значение оси 0», «вертикальная ось пересекает в
категории с номером 11»;
–
добавьте сетку (Макет – сетка – вертикальные линии сетки по основной оси –
основные линии сетки).
Задание. С помощью построенного графика квадратичной
функции у = х2 +
2х – 3 определите:
а) четность-нечетность
функции;
б) нули функции;
в) промежутки
монотонности;
г) наибольшее и
наименьшее значение функции.
5. Проверка усвоения нового материала.
Класс делится на две
группы. Каждой группе предлагается решить определенное задание. После того как
все обучающиеся в группе решили это задание, происходит взаимопроверка
полученных решений.
1 группа.
1. Найдите координаты
точек пересечения параболы у = х2 + х – 12 с
осями координат.
2. Постройте график квадратичной функции y =
−3x2 в программе Microsoft Excel и определите по графику значения этой функции в точках x1 = 5, x2 = −3.
2 группа.
1. Найдите значения квадратичной функции y =
−3x2 в точках x1 = 5, x2 = −3.
2. Постройте график квадратичной функции у = х2 +
х – 12 в программе Microsoft Excel и по графику
определите координаты точек пересечения параболы с осями координат.
6. Подведение итогов.
Итак, мы повторили
материал, касающийся свойств квадратичной функции, решали задачи.
Что нового вы
узнали сегодня?
Довольны
ли вы своей работой?
7. Домашнее задание.
Задайте аналитически квадратичную функцию, которая:
а) имеет два нуля −3 и 0;
б) имеет только один нуль −3;
в) не имеет нулей.
Однозначно ли можно выполнить задание во всех случаях?
Список использованной литературы:
1. Алгебра: учебник для 9 класса / Гельфман Э.Г., Демидова Л.Н., Терре
А.И. и др. – М: БИНОМ. Лаборатория знаний, 2013. – 272 с.
2. Семакин И.Г. Информатика и ИКТ: учебник для 9 класса / И.Г. Семакин,
Л.А. Залогова, и др. – М: БИНОМ. Лаборатория знаний, 2012. – 341 с.
3. Социальная сеть работников образования «Наша сеть». – Режим доступа: http://nsportal.ru/shkola/informatika-i-ikt/library/2013/11/02/integrirovannyy-urok-po-algebre-i-informatike
17 авг. 2022 г.
читать 3 мин
Часто вас может заинтересовать построение уравнения или функции в Excel. К счастью, это легко сделать с помощью встроенных формул Excel.
В этом руководстве представлено несколько примеров того, как строить уравнения/функции в Excel.
Пример 1: построение линейного уравнения
Предположим, вы хотите построить следующее уравнение:
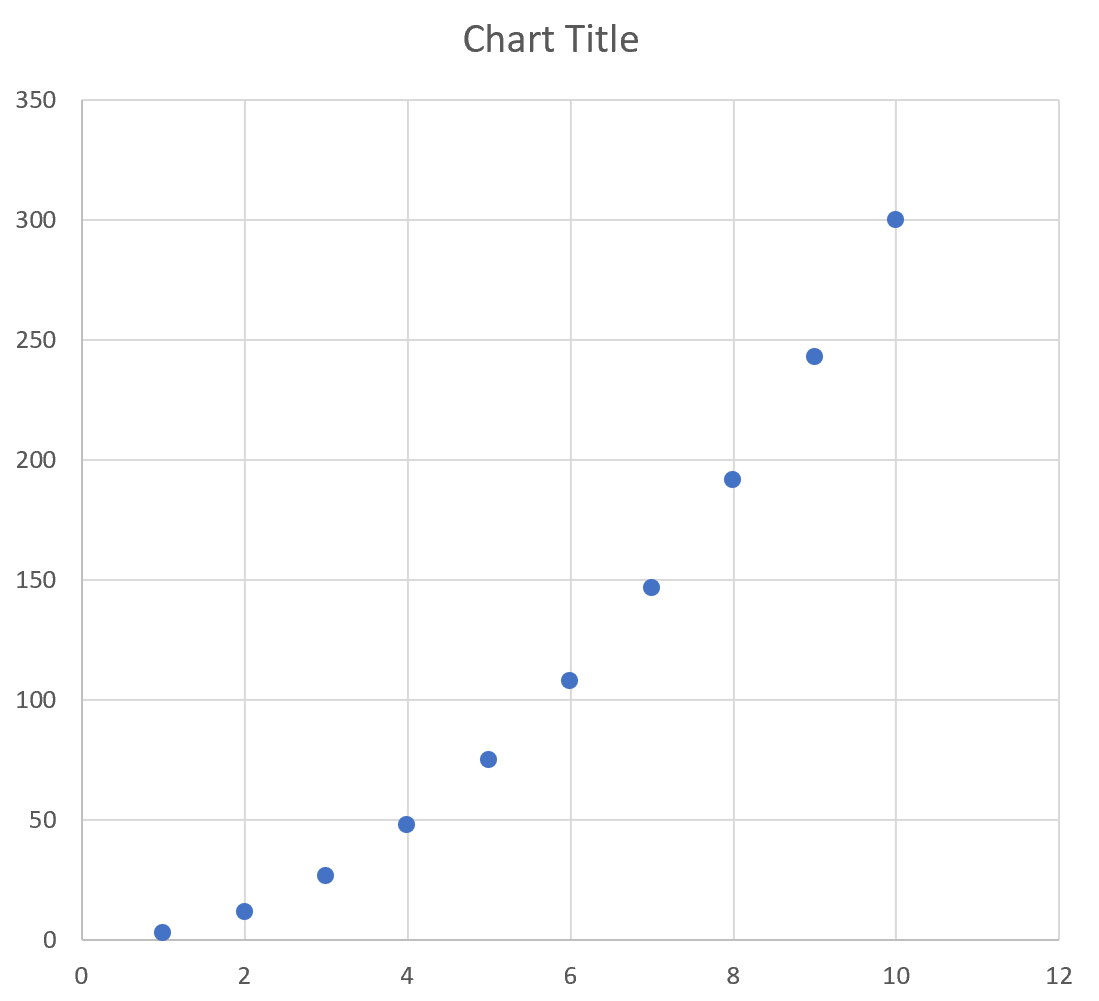
у = 2х + 5
На следующем изображении показано, как создать значения y для этого линейного уравнения в Excel, используя диапазон от 1 до 10 для значений x:
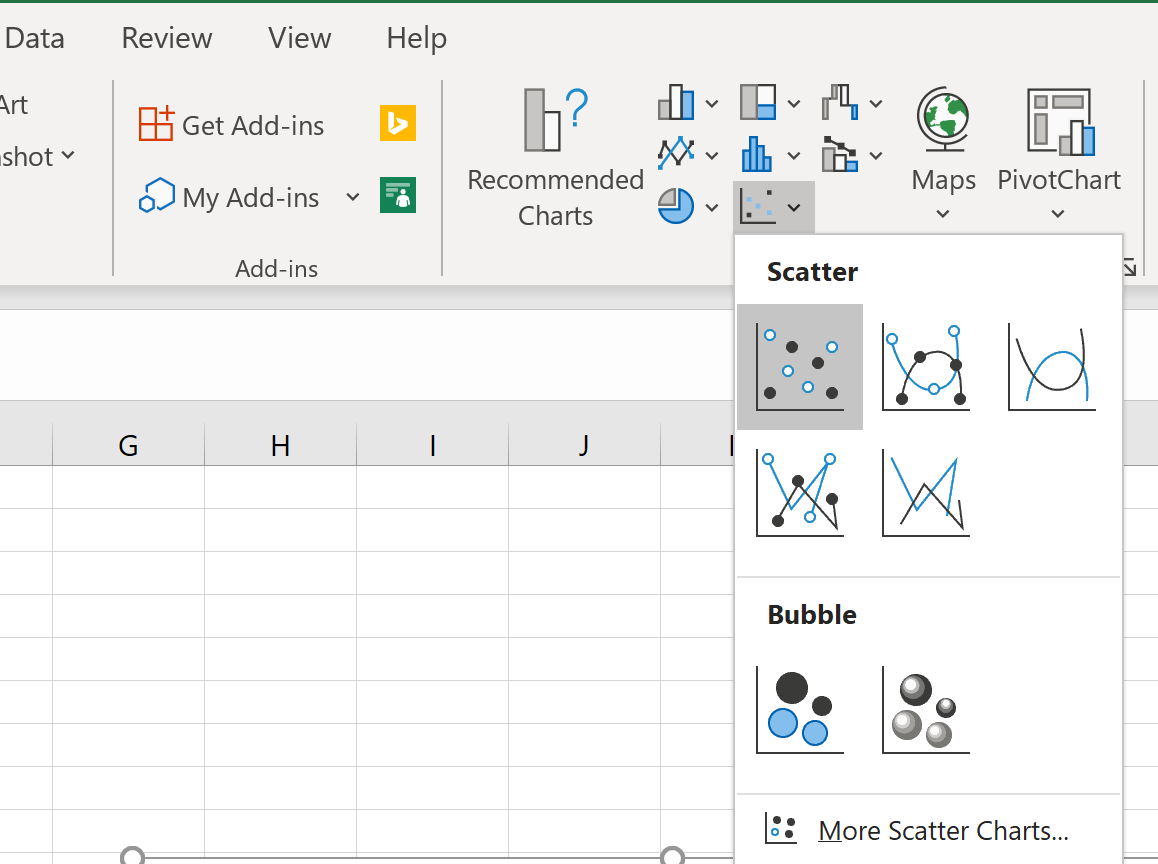
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
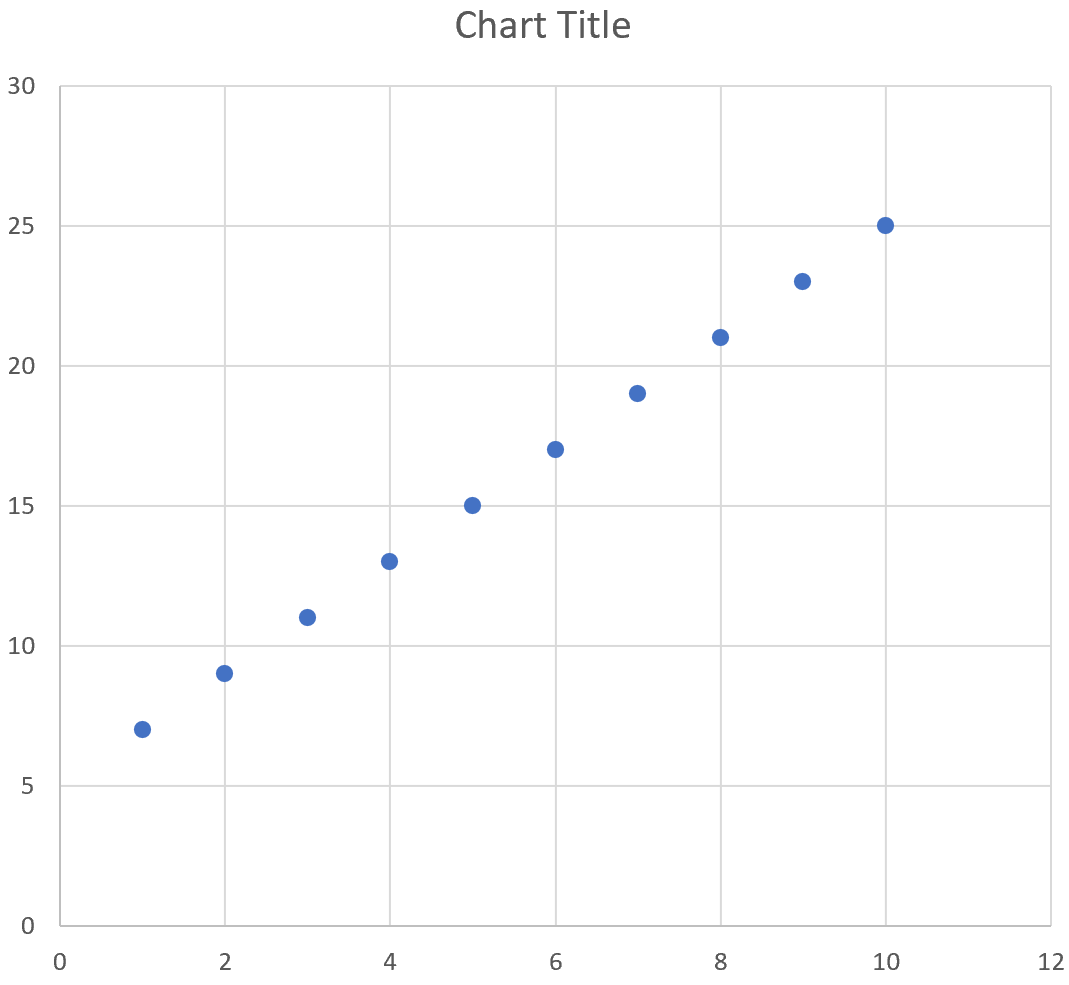
Автоматически появится следующий график:
Мы видим, что график следует прямой линии, поскольку уравнение, которое мы использовали, было линейным по своей природе.
Пример 2. Построение квадратного уравнения
Предположим, вы хотите построить следующее уравнение:
у = 3x 2
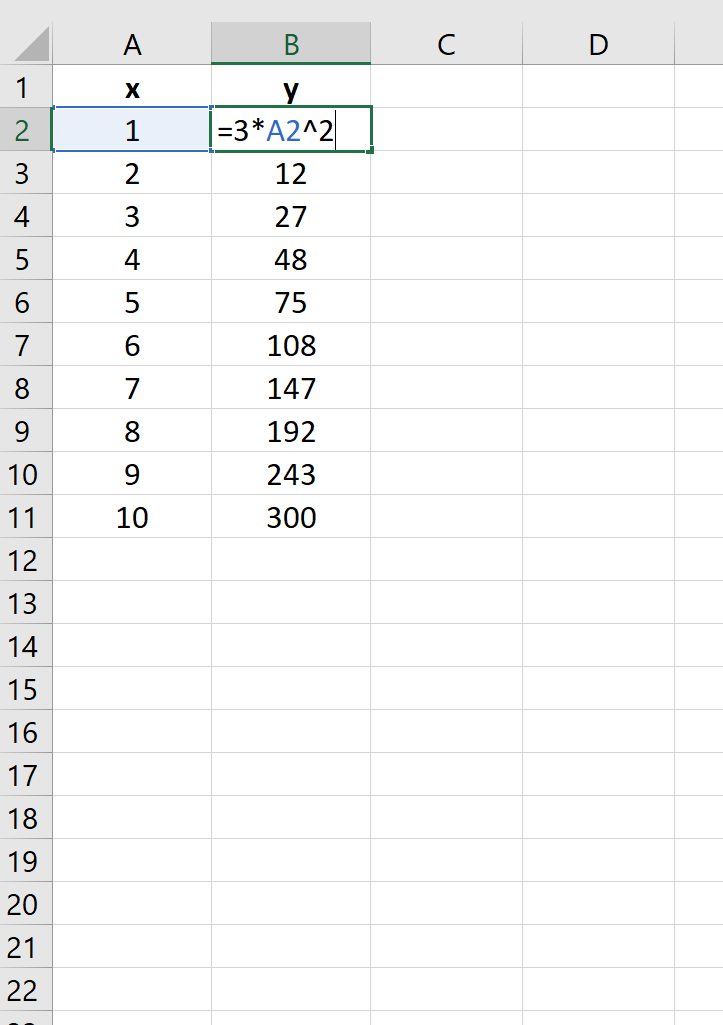
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует изогнутой линии, поскольку уравнение, которое мы использовали, было квадратным.
Пример 3: построение уравнения обратной связи
Предположим, вы хотите построить следующее уравнение:
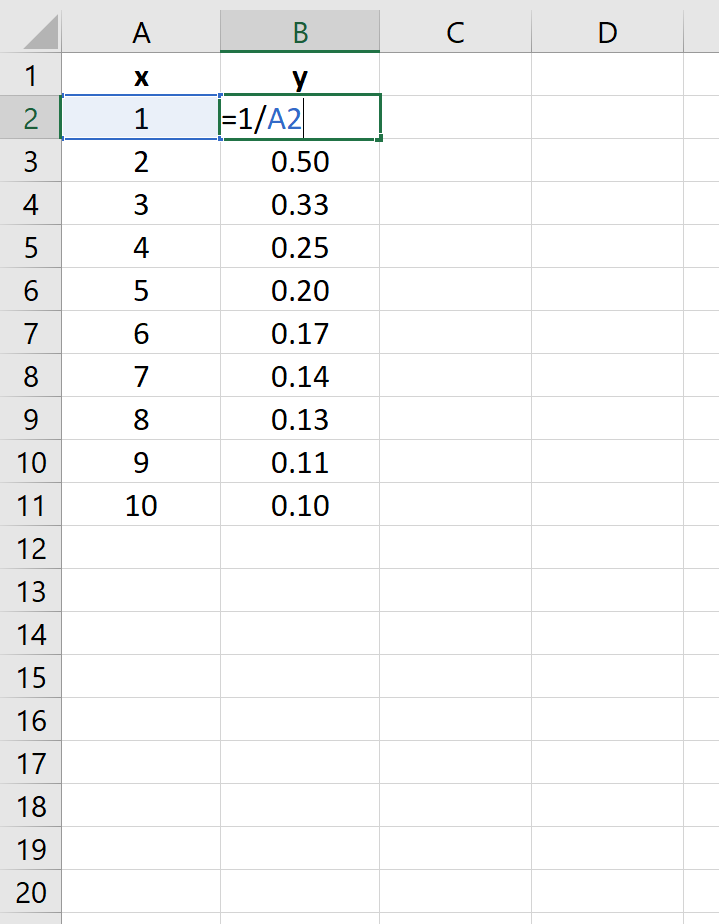
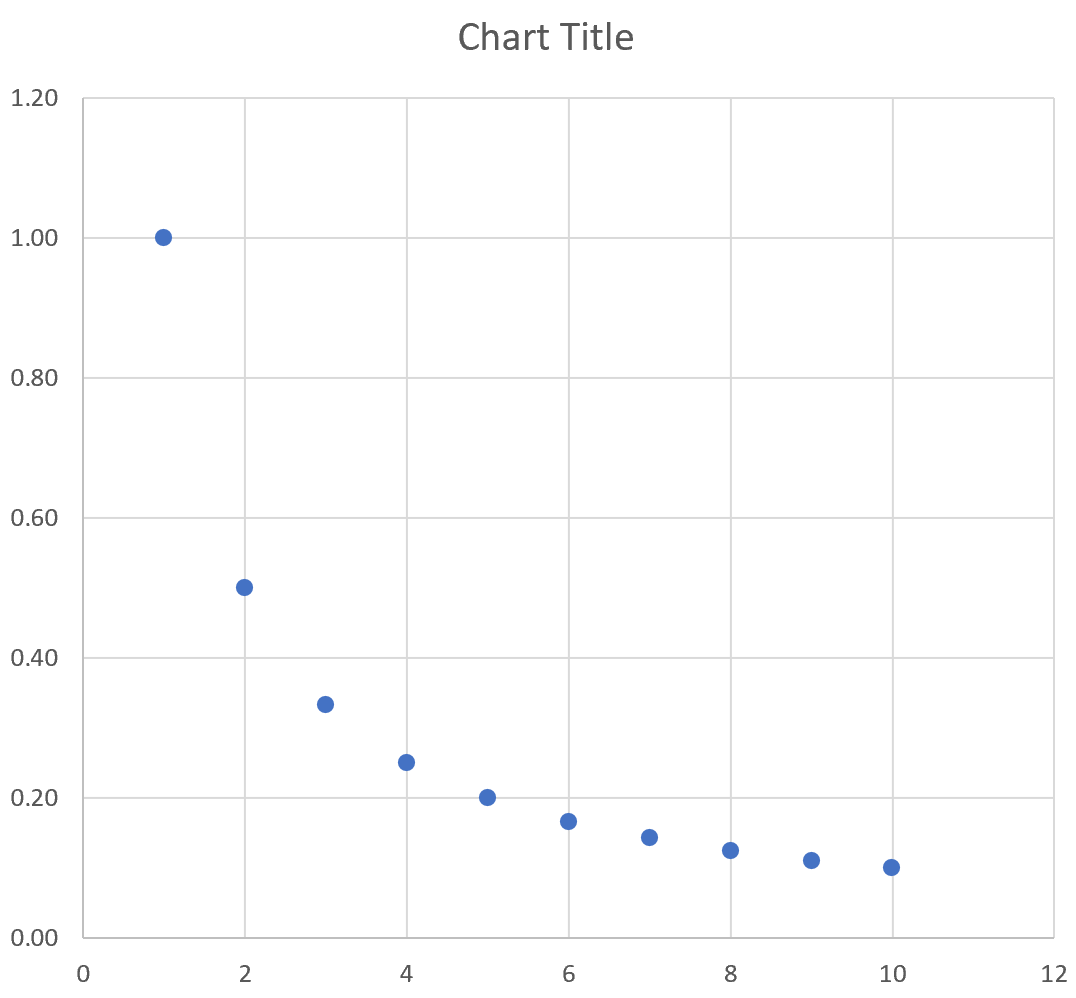
у = 1/х
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует по изогнутой линии вниз, поскольку это представляет уравнение y = 1/x.
Пример 4. Построение уравнения синуса
Предположим, вы хотите построить следующее уравнение:
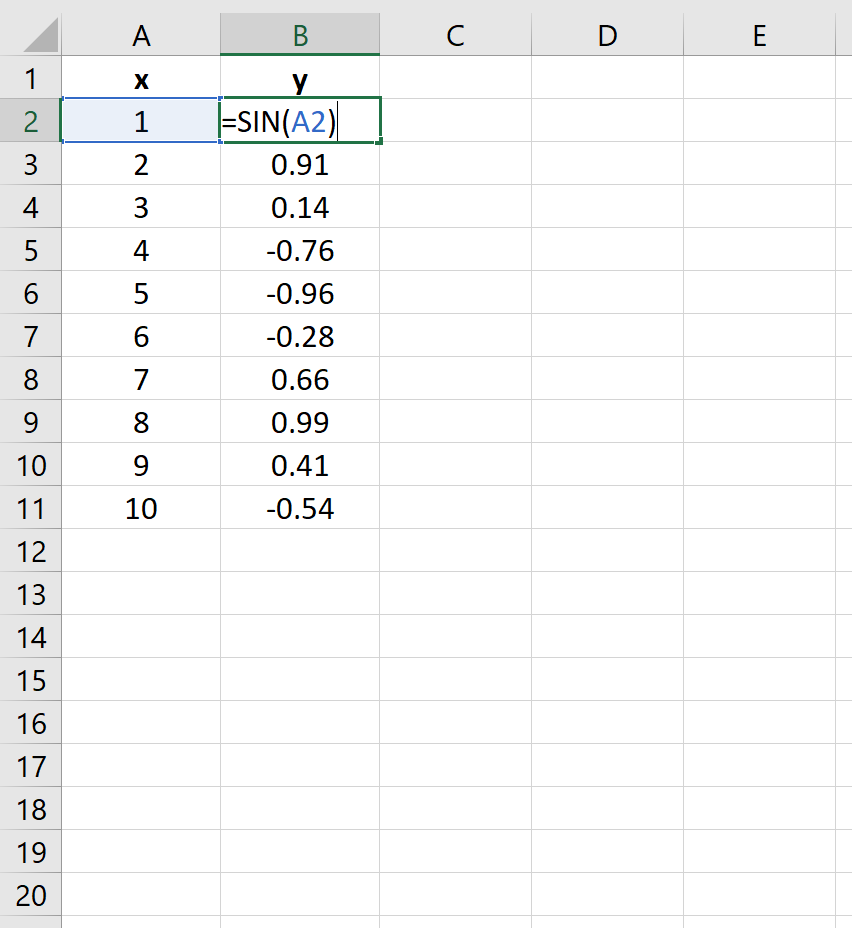
у = грех (х)
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика « Разброс с плавными линиями и маркерами» .
Автоматически появится следующий график:
Вывод
Вы можете использовать аналогичную технику для построения графика любой функции или уравнения в Excel. Просто выберите диапазон значений x для использования в одном столбце, затем используйте уравнение в отдельном столбце, чтобы определить значения y на основе значений x.


Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
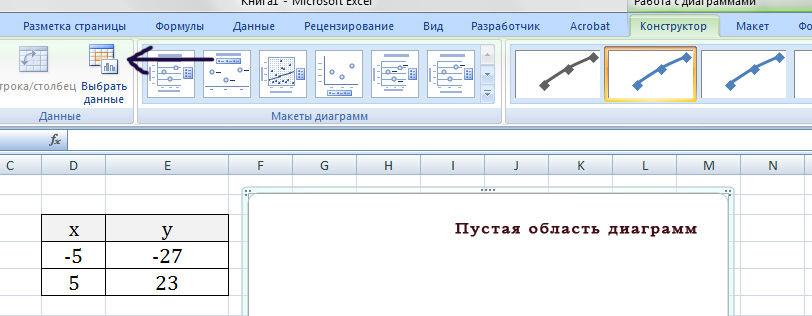
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
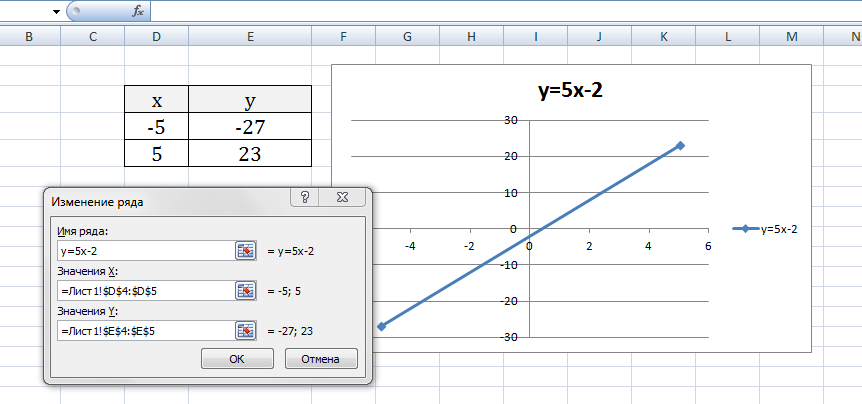
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
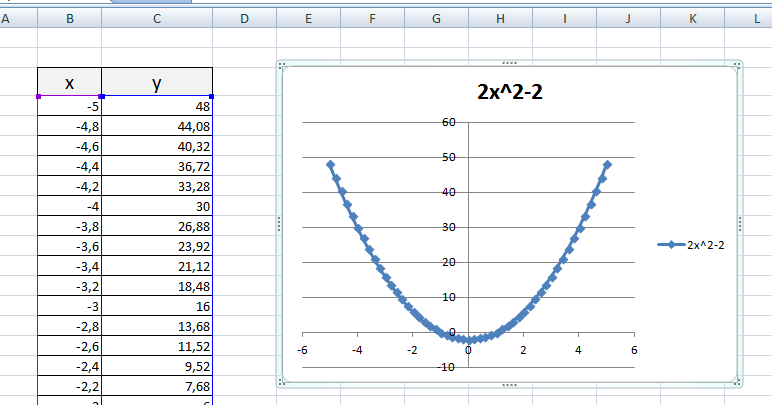
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
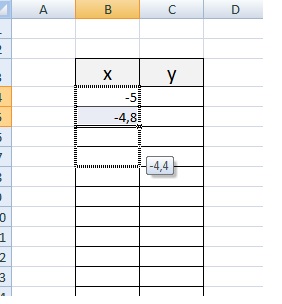
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
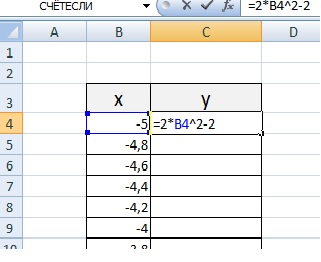
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
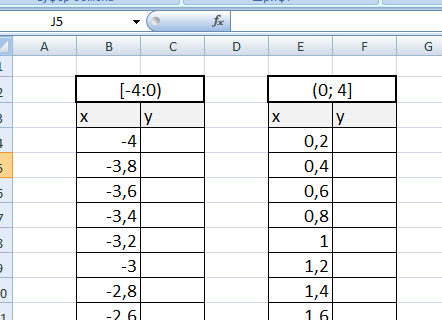
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
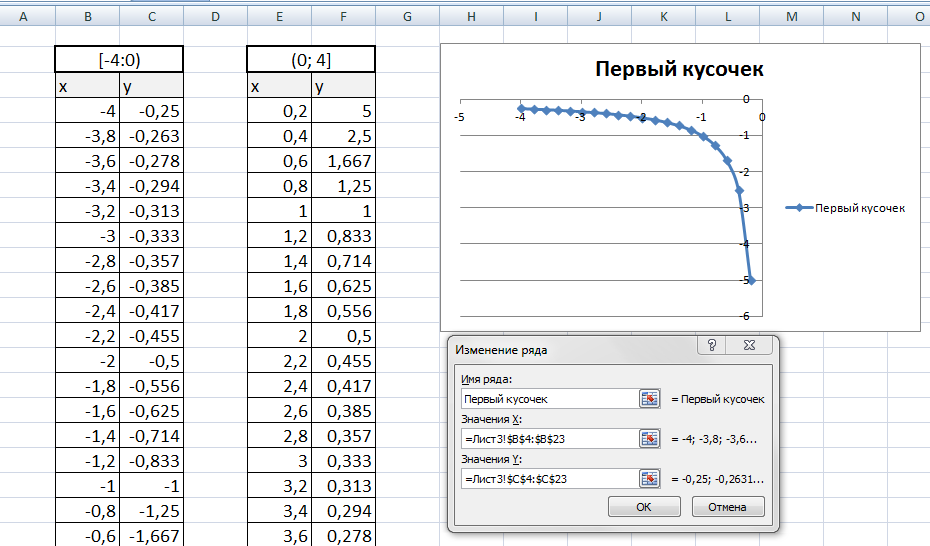
Находим значения функции от каждого аргумента х аналогично примерам выше.
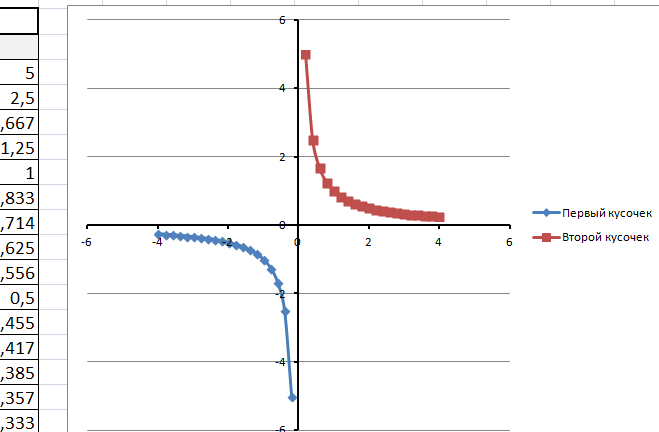
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете оставить комментарий, или ссылку на Ваш сайт.
Душевые термостаты, лучшие модели на http://tools-ricambi.ru/ изготавливаются из материалов высшего качества
Оставить комментарий
График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.
Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.
График функции F(x) = X^2
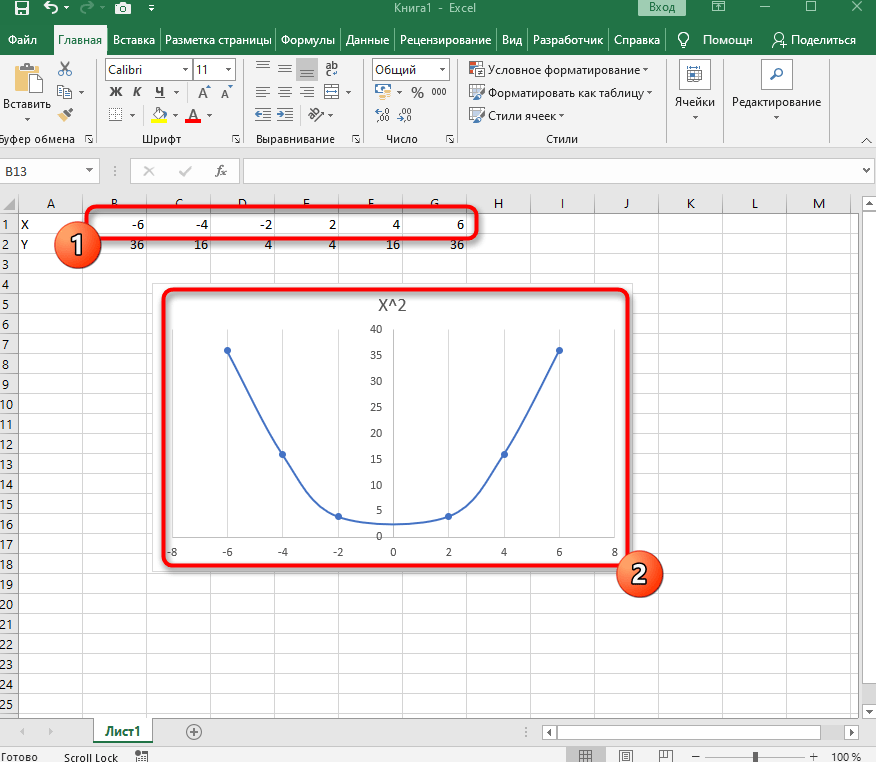
Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:
-
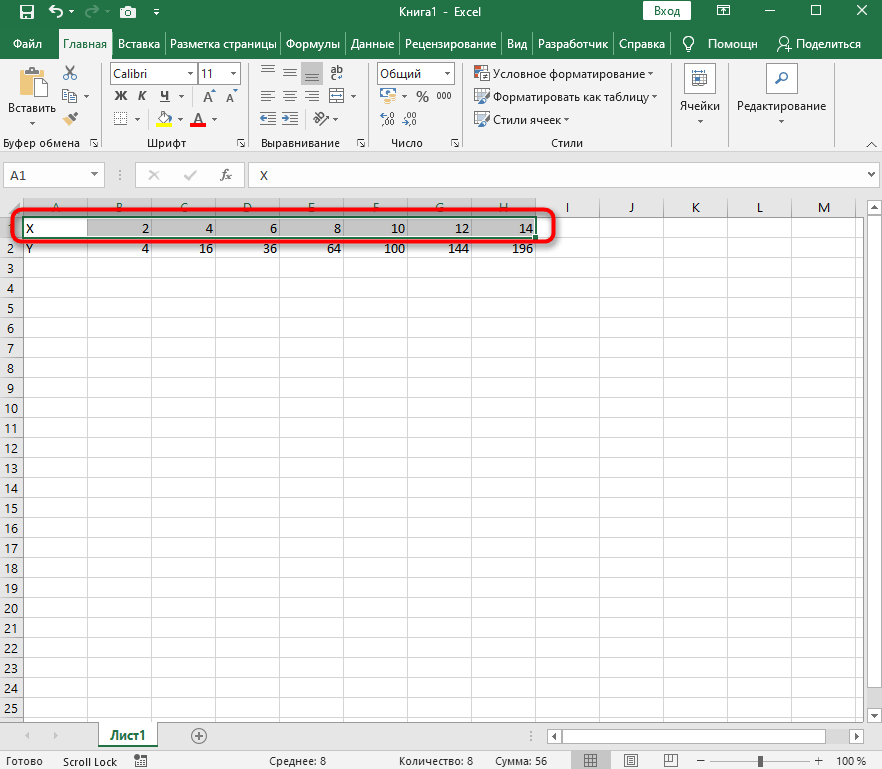
Создайте строку на листе в программе, вписав туда известные значения X.
-
Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.
-
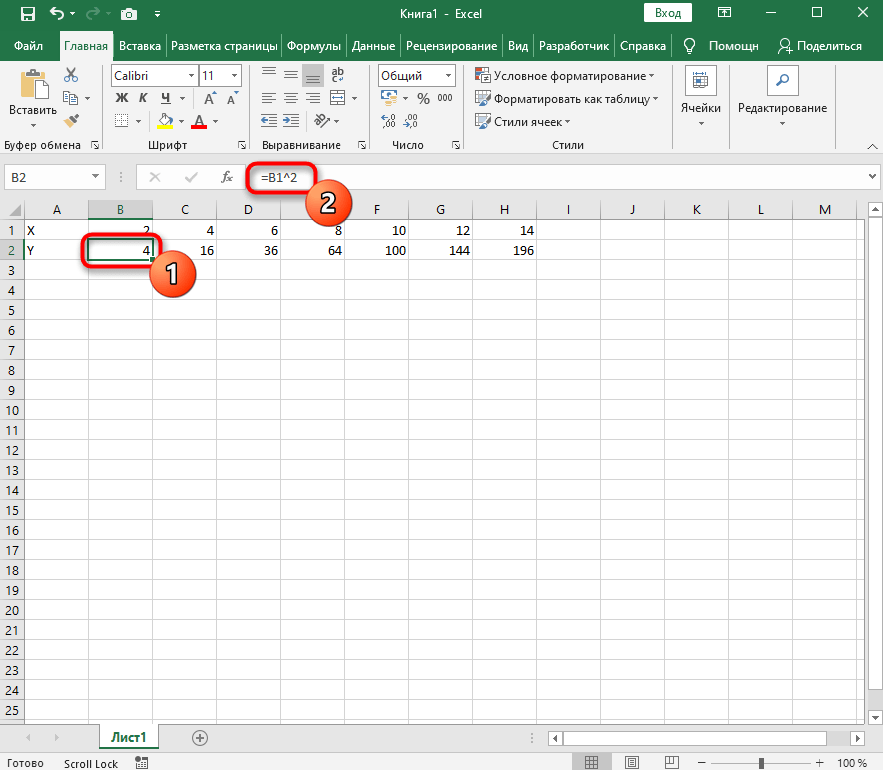
Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.
-
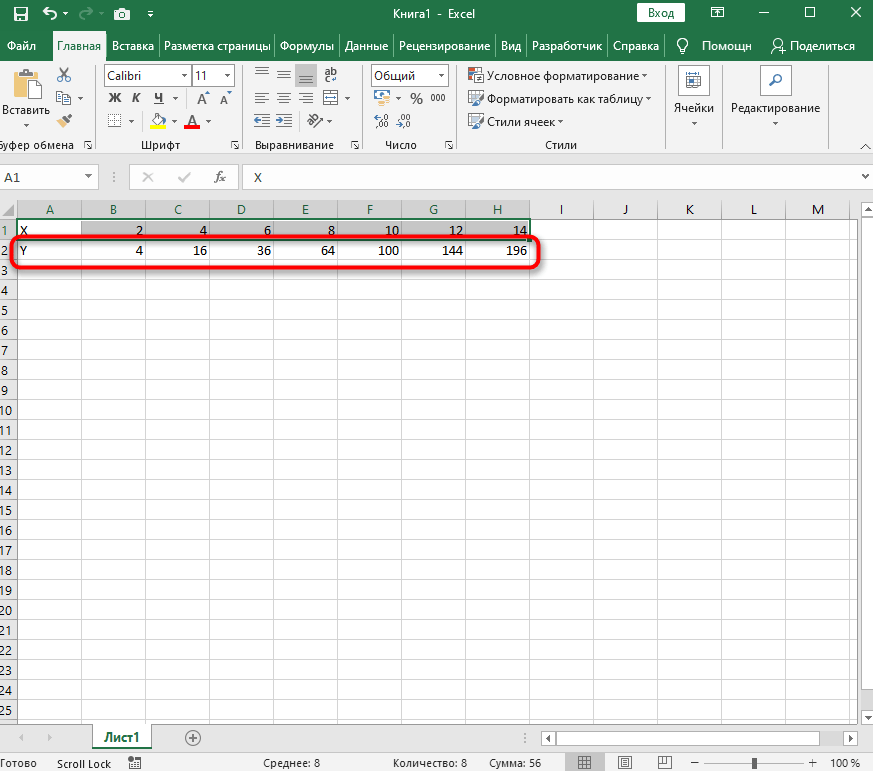
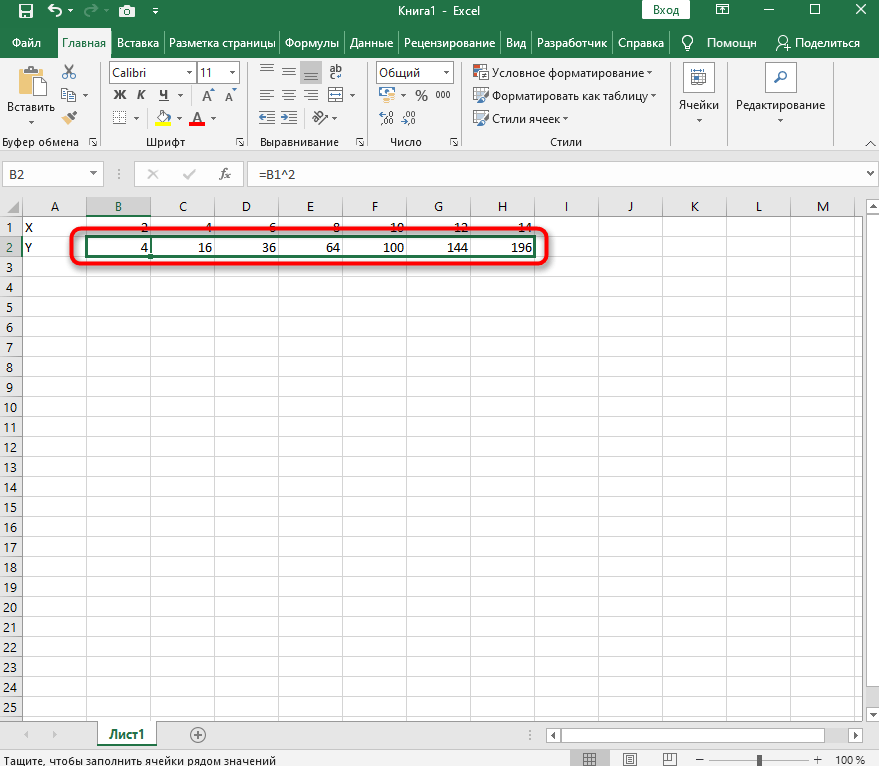
Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.
-
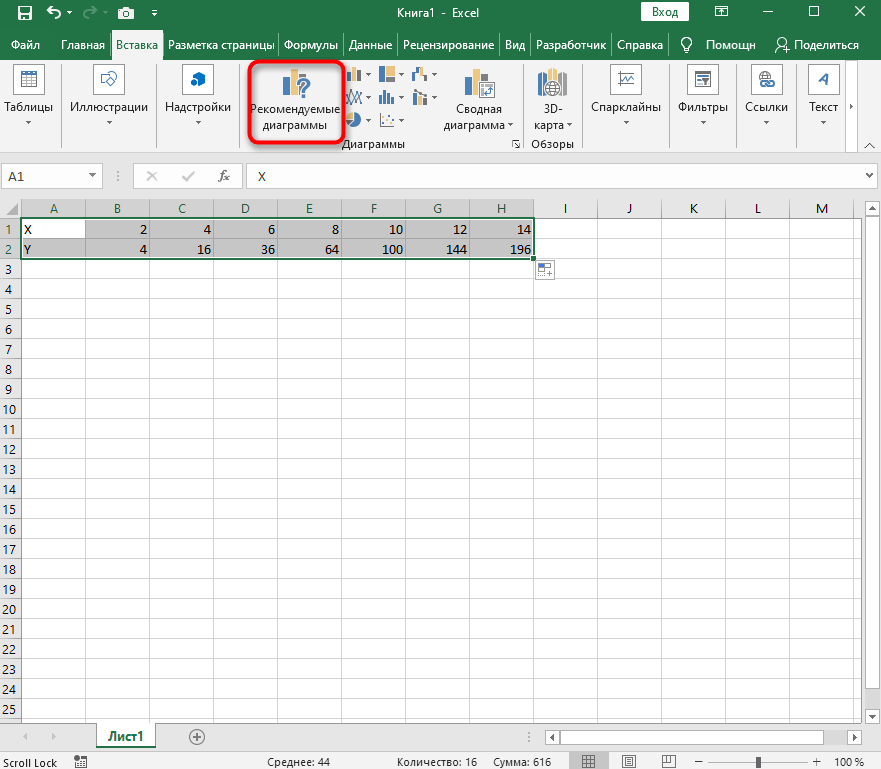
Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.
-
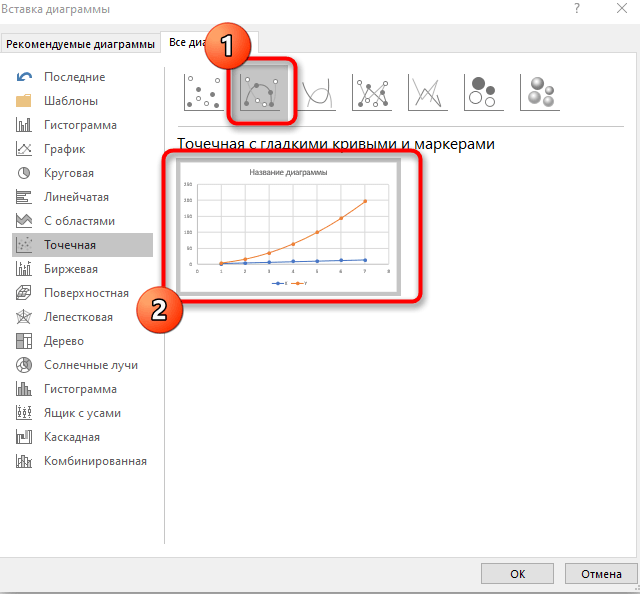
В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.
-
Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).
Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
График функции y=sin(x)
y=sin(x) – вторая функция, которую мы возьмем за пример. Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.
-
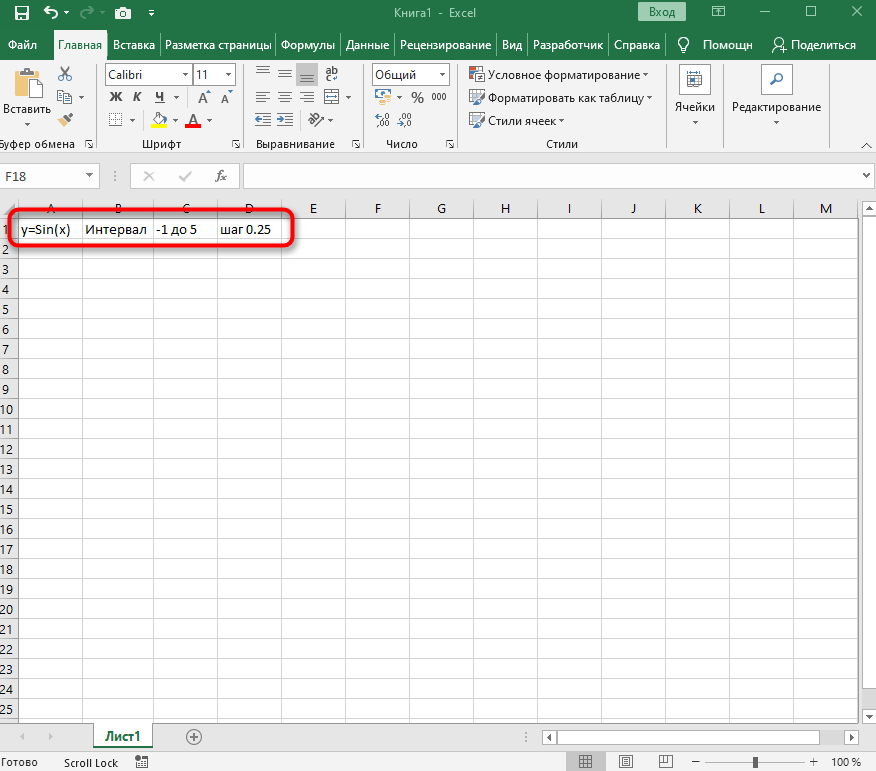
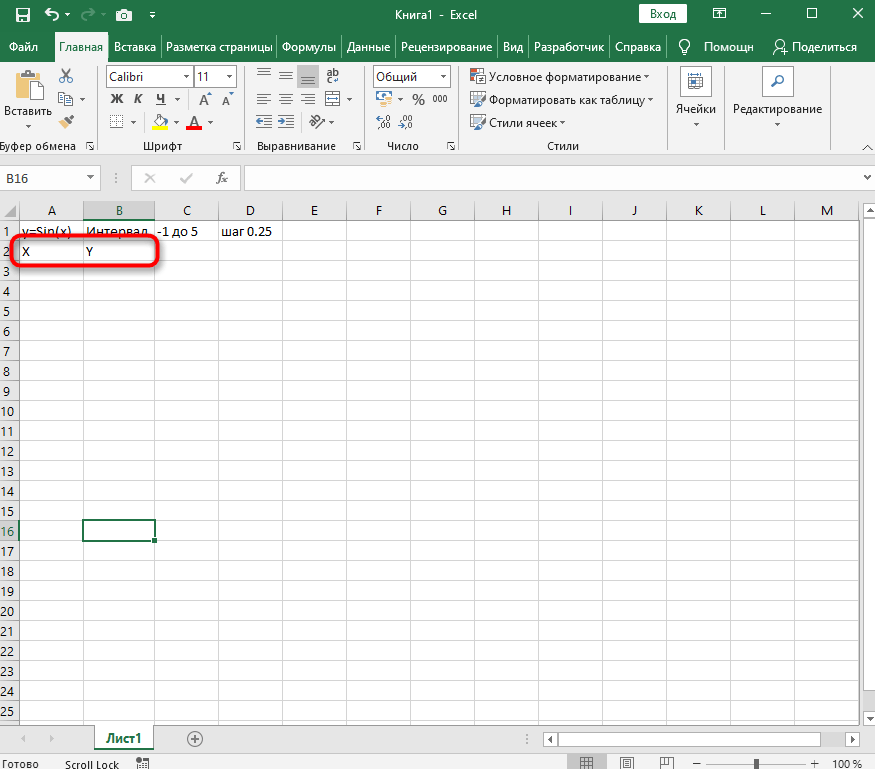
Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.
-
Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.
-
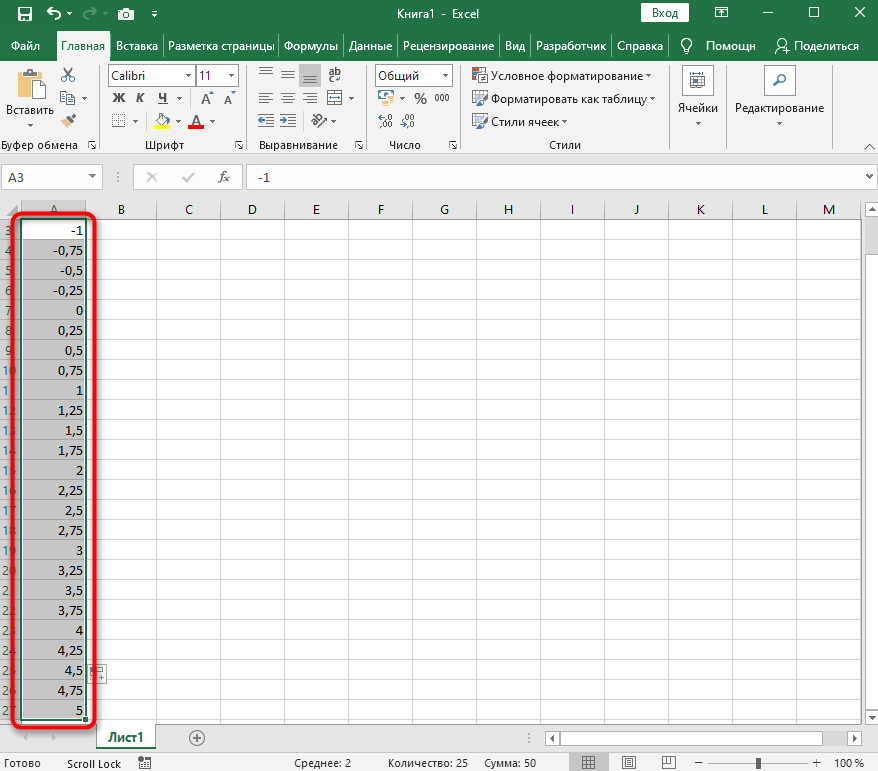
Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.
-
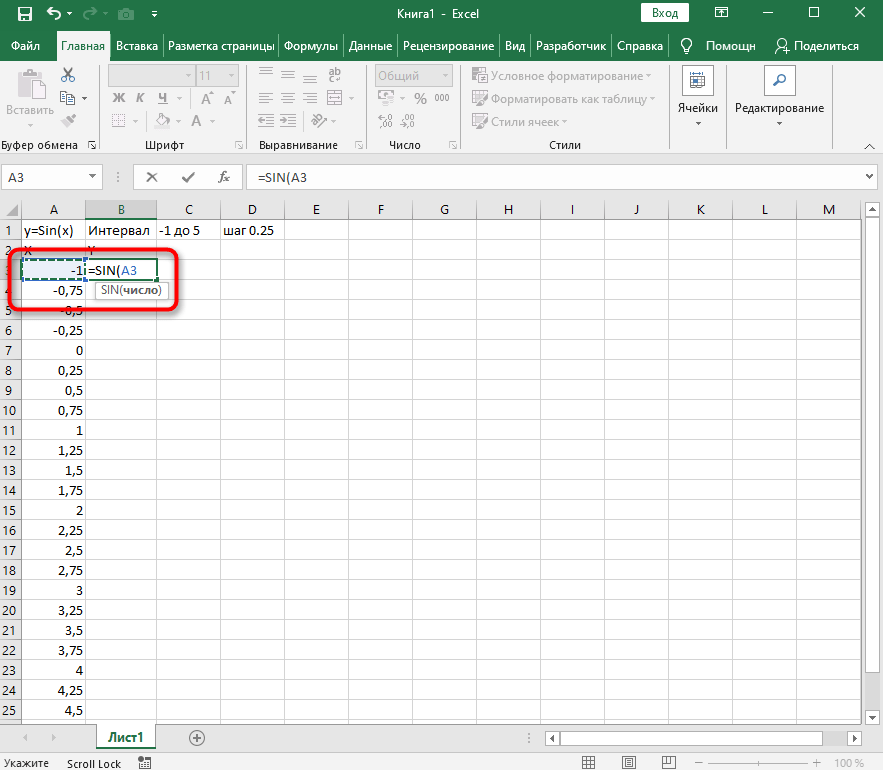
Теперь более сложное, но не страшное действие – определение значения Y. Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.
-
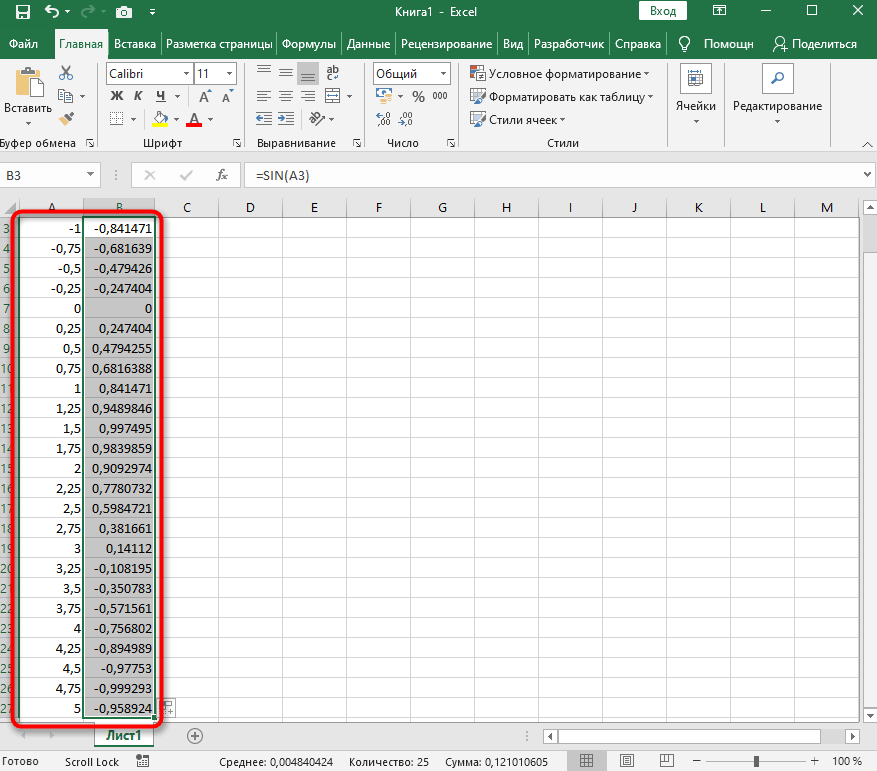
На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.
-
Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.
На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.