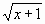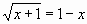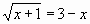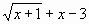Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Содержание
- Что это такое
- А нужно ли это
- Как построить график уравнения регрессии в Excel
- Подготовительные работы
- Как пользоваться
- Анализ
- Как построить график квадратного уравнения в Excel
- Как построить график линейного уравнения
- Вывод
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите:
Выберите раздел:
Далее:
Прокрутите окно вниз, выберите:
Отметьте пункт:
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
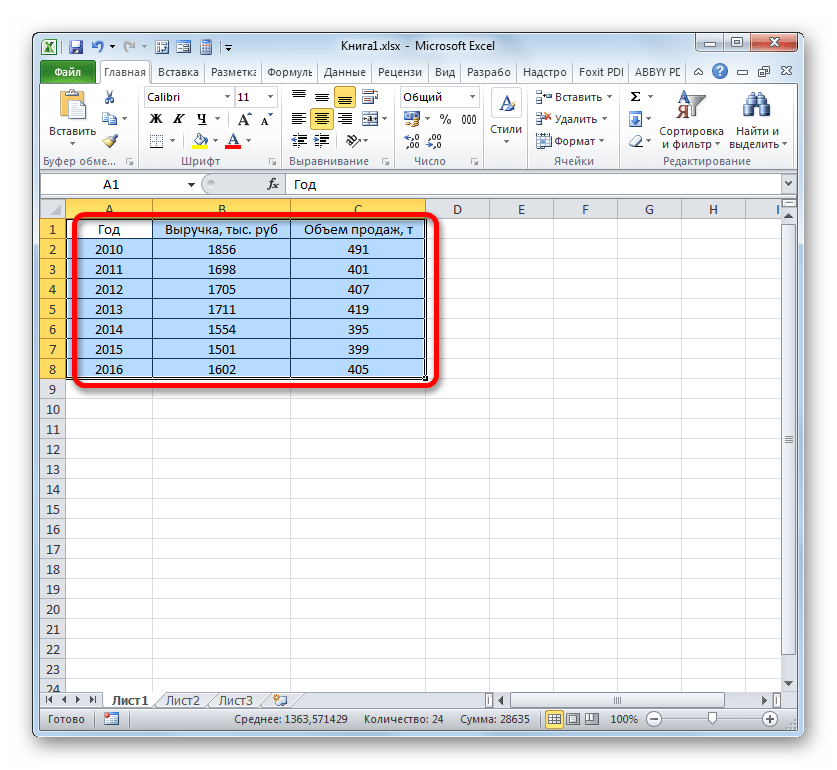
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите:
Выберите:
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат.
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
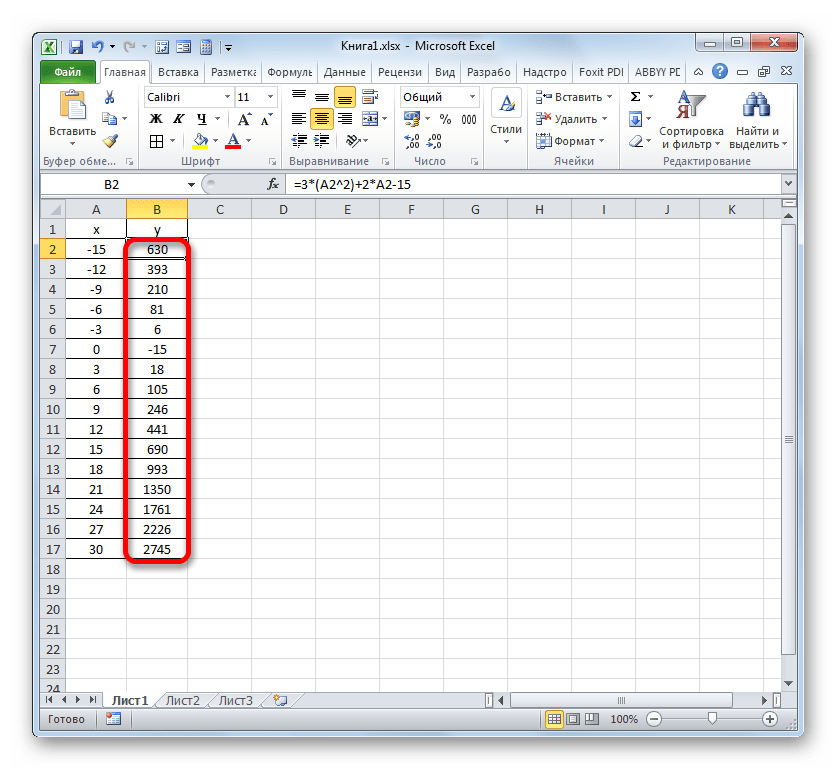
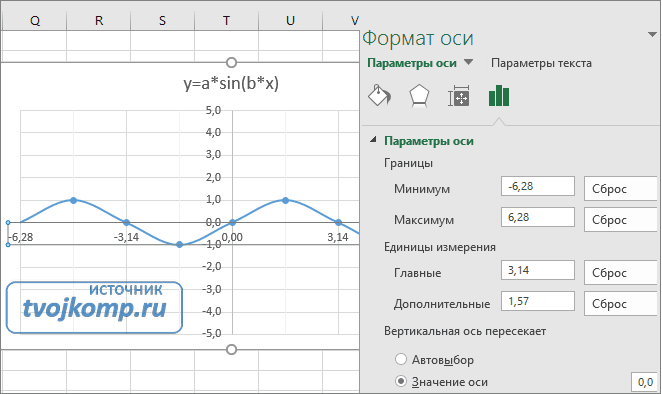
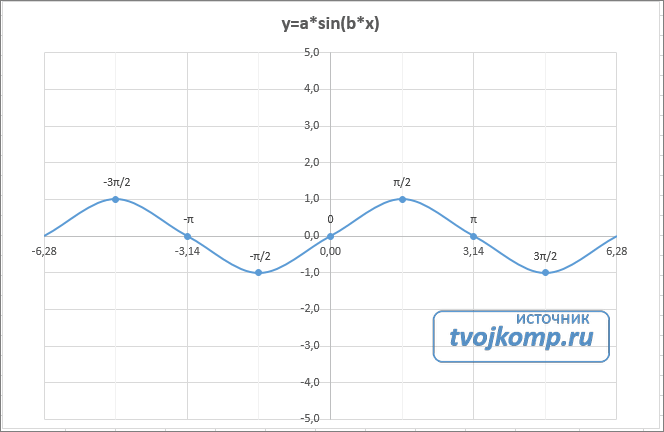
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;

При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
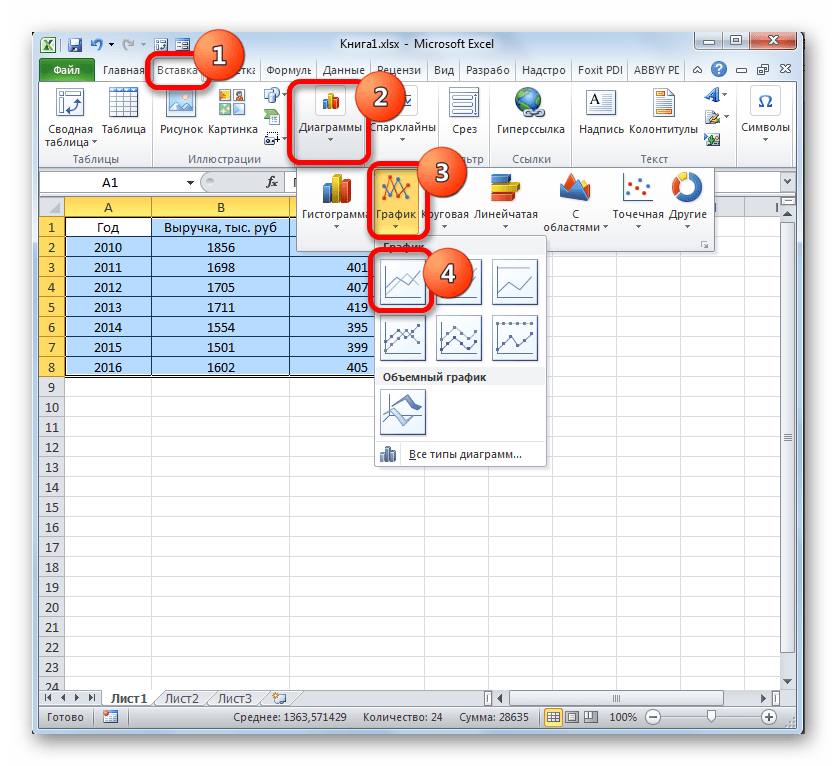
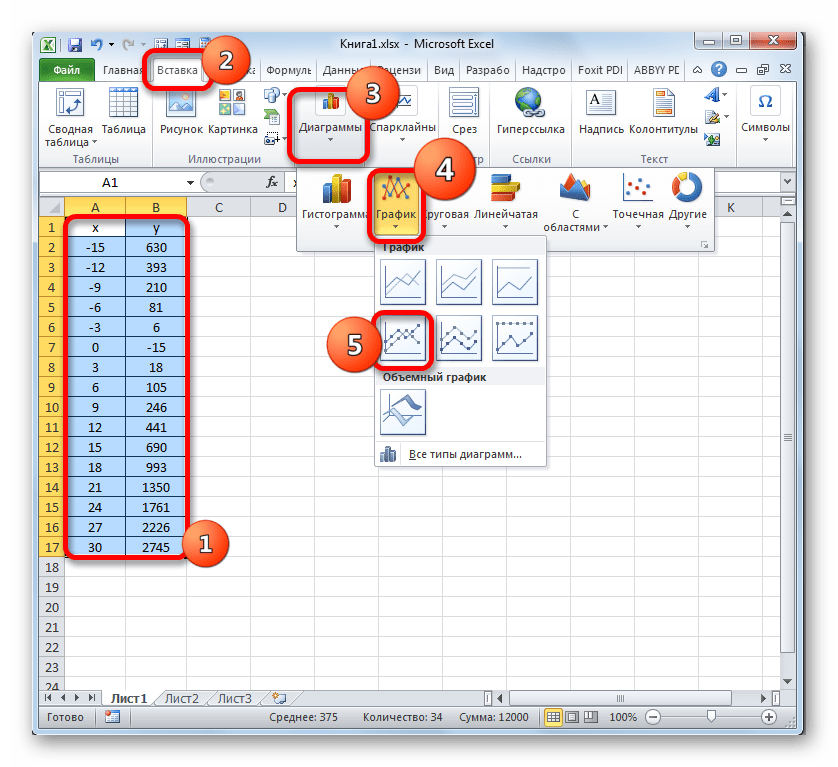
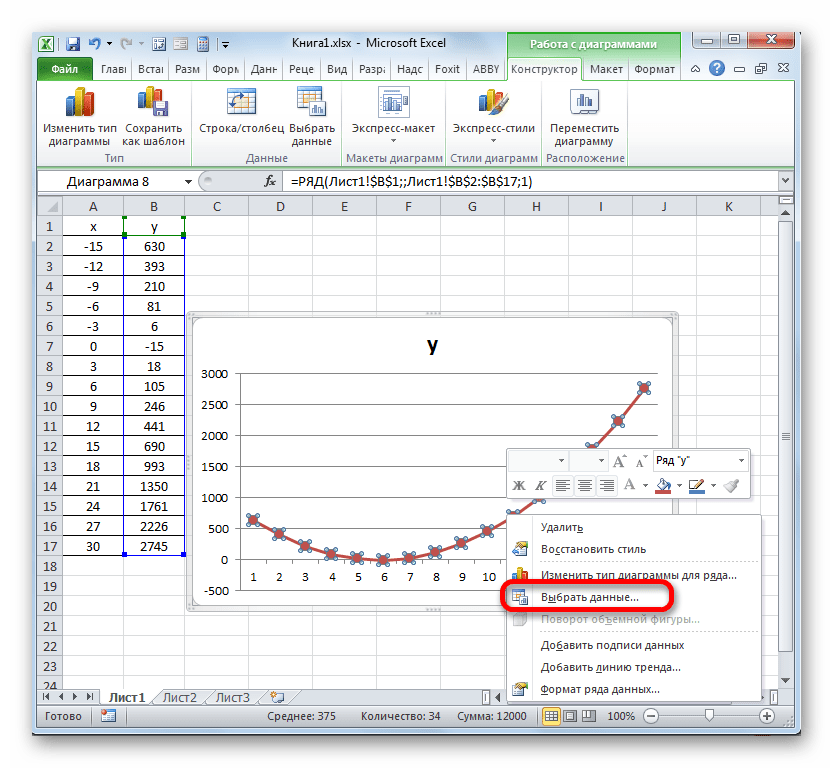
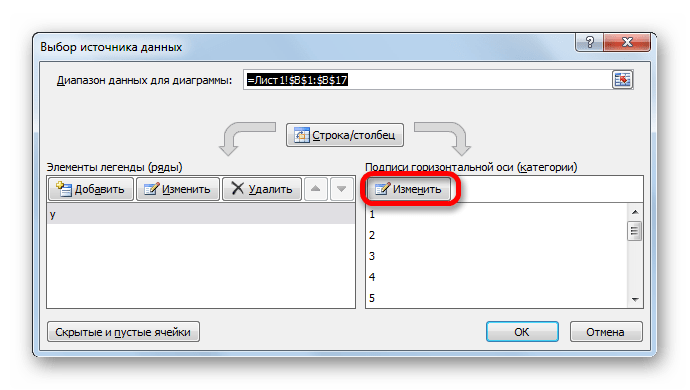
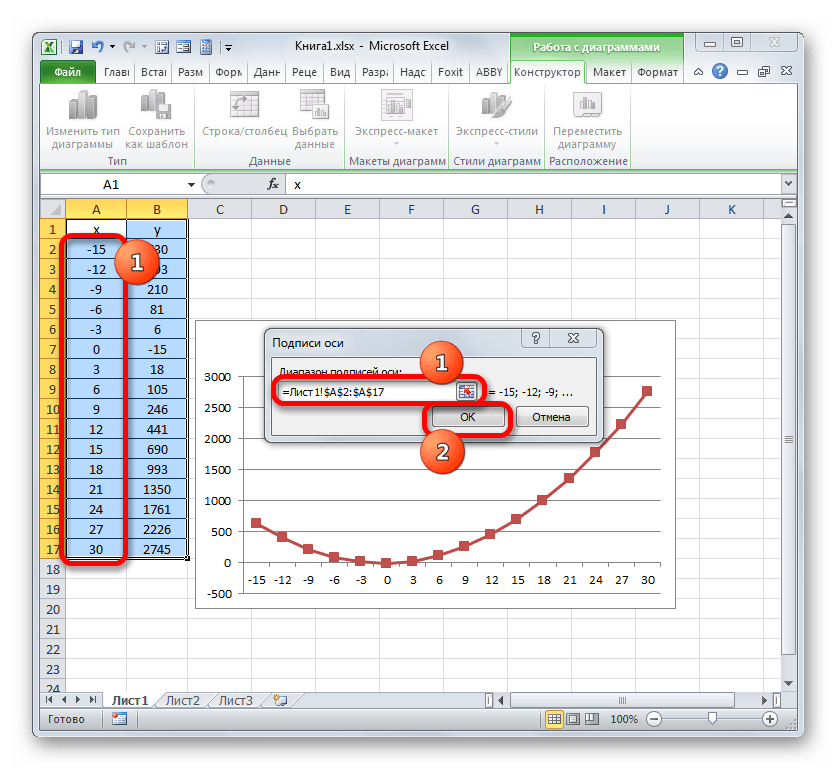
Выделите диапазон значений по ним будем строить график. Перейдите:
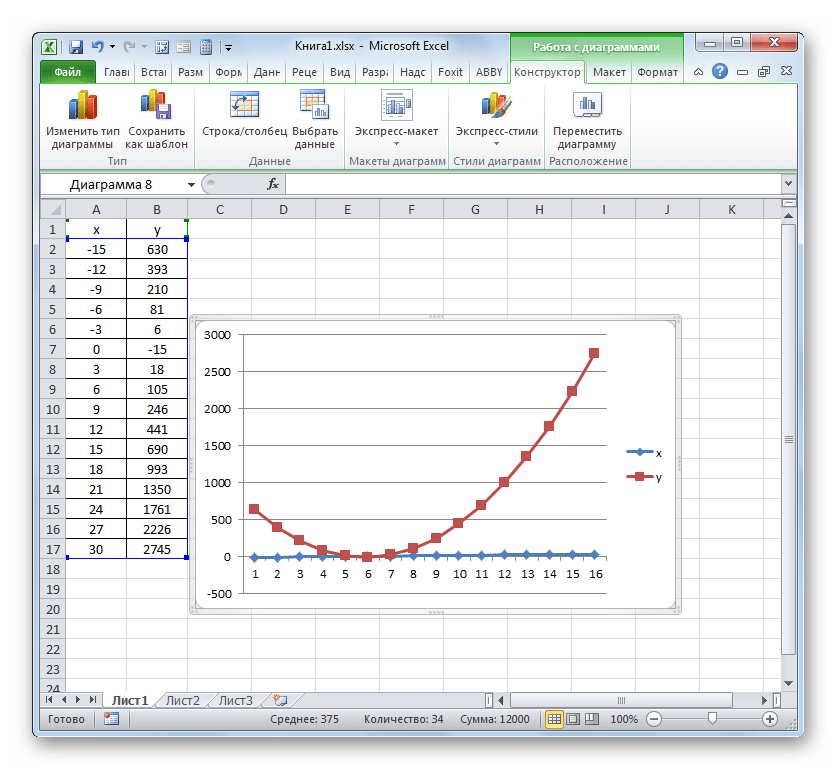
Поместите график в свободное место на листе.
Как построить график линейного уравнения
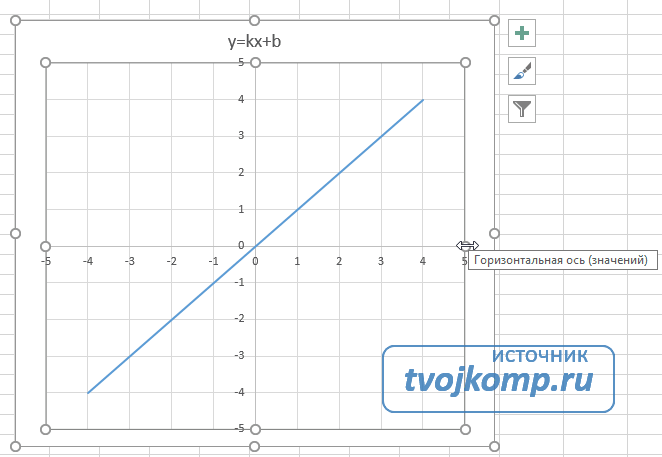
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
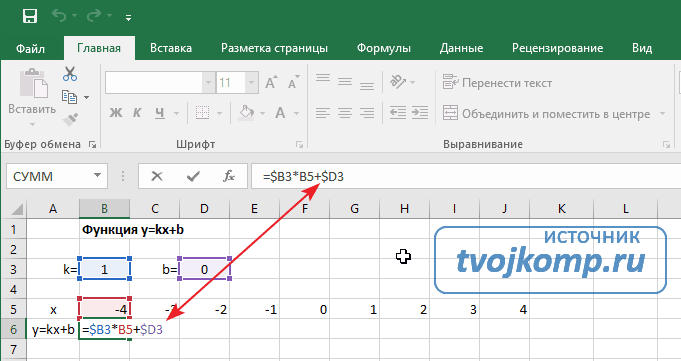
- Ячейка В6. Прописываем формулу.

График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
Метод аппроксимации в Microsoft Excel
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
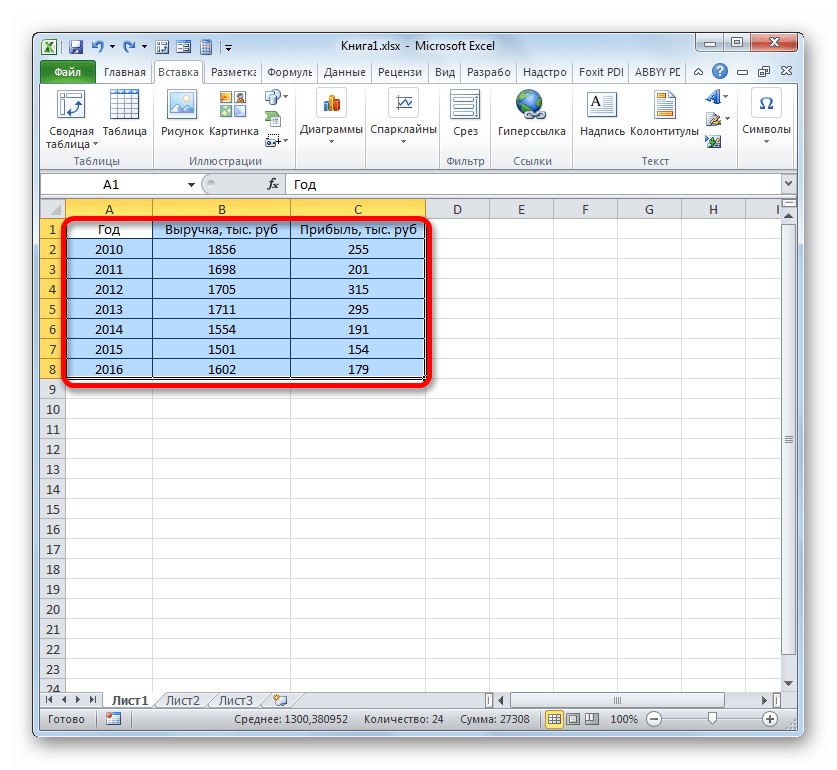
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
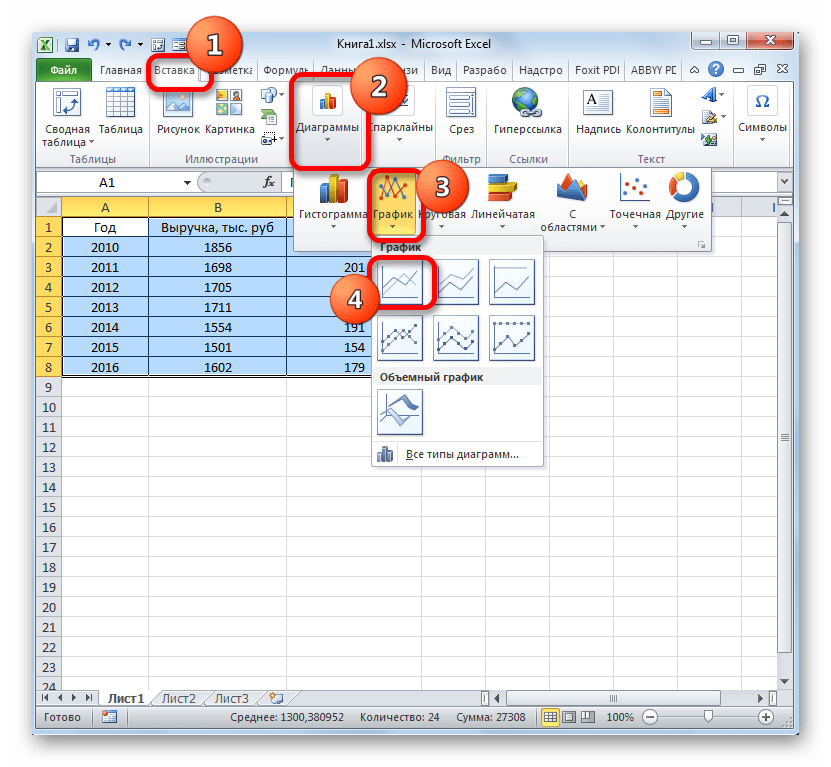
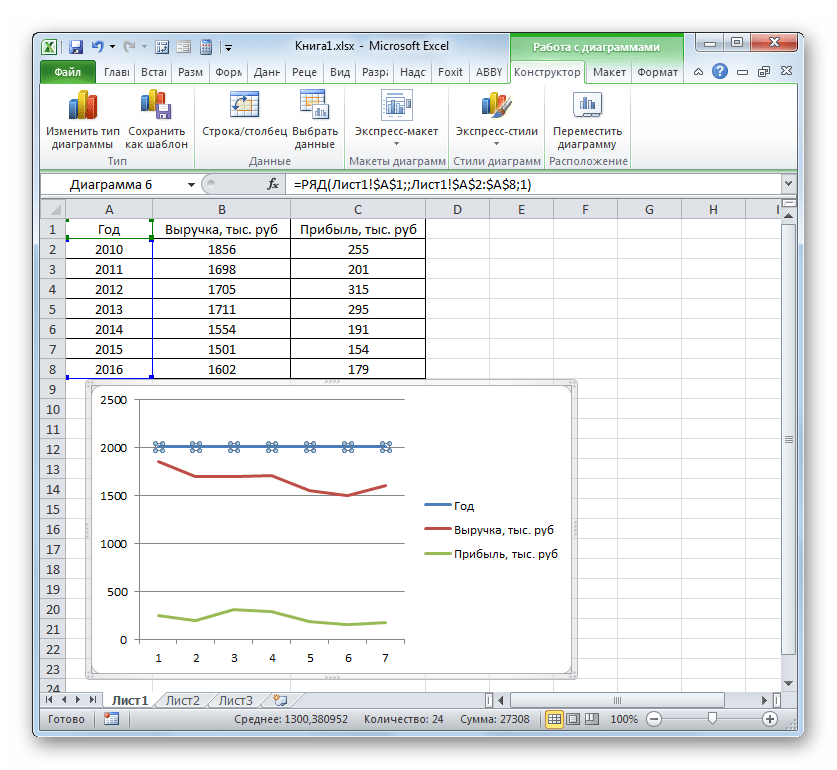
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.
Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
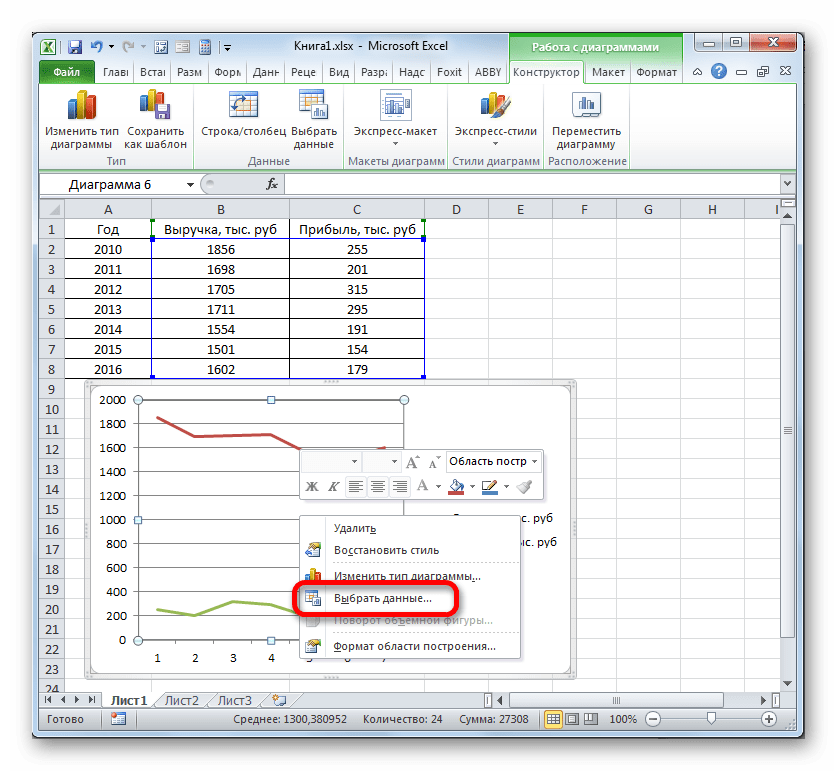
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
В нашем случае формула приняла такой вид:
y=0,0015*x^2-1,7202*x+507,01
Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Как сделать линейную калибровочную кривую в Excel
В Excel есть встроенные функции, которые вы можете использовать для отображения ваших данных калибровки и расчета линии наилучшего соответствия. Это может быть полезно, когда вы пишете отчет химической лаборатории или программируете поправочный коэффициент на единицу оборудования.
В этой статье мы рассмотрим, как использовать Excel для создания диаграммы, построить линейную калибровочную кривую, отобразить формулу калибровочной кривой, а затем настроить простые формулы с помощью функций НАКЛОН и ПЕРЕКЛЮЧИТЬ, чтобы использовать уравнение калибровки в Excel.
Что такое калибровочная кривая и как Excel полезен при ее создании?
Чтобы выполнить калибровку, вы сравниваете показания устройства (например, температуру, отображаемую термометром) с известными значениями, называемыми стандартами (например, точки замерзания и кипения воды). Это позволяет вам создать серию пар данных, которые вы затем будете использовать для построения калибровочной кривой.
Двухточечная калибровка термометра с использованием точек замерзания и кипения воды будет иметь две пары данных: одну с момента, когда термометр помещают в ледяную воду (32 ° F или 0 ° C), и одну в кипящую воду (212 ° F). или 100 ° С). Когда вы построите эти две пары данных в виде точек и проведете линию между ними (калибровочную кривую), а затем, предполагая, что реакция термометра является линейной, вы можете выбрать любую точку на линии, которая соответствует значению, которое отображает термометр, и вы мог найти соответствующую «истинную» температуру.
Таким образом, линия, по сути, заполняет информацию между двумя известными для вас точками, так что вы можете быть достаточно уверенными при оценке фактической температуры, когда термометр показывает 57,2 градуса, но когда вы никогда не измеряли «стандарт», который соответствует это чтение.
В Excel есть функции, которые позволяют графически отображать пары данных на графике, добавлять линию тренда (калибровочную кривую) и отображать уравнение калибровочной кривой на графике. Это полезно для визуального отображения, но вы также можете рассчитать формулу линии, используя функции Excel SLOPE и INTERCEPT. Когда вы введете эти значения в простые формулы, вы сможете автоматически рассчитать «истинное» значение на основе любого измерения.
Давайте посмотрим на пример
Для этого примера мы разработаем калибровочную кривую из серии из десяти пар данных, каждая из которых состоит из значения X и значения Y. Значения Х будут нашими «стандартами», и они могут представлять что угодно, от концентрации химического раствора, который мы измеряем с помощью научного прибора, до входной переменной программы, которая управляет пусковой машиной для мрамора.
Значения Y будут «откликами», и они будут представлять собой показания прибора, полученные при измерении каждого химического раствора, или измеренное расстояние, на котором расстояние от пусковой установки, на которую упал мрамор, используя каждое входное значение.
После того, как мы графически изобразим калибровочную кривую, мы будем использовать функции SLOPE и INTERCEPT, чтобы вычислить формулу калибровочной линии и определить концентрацию «неизвестного» химического раствора на основании показаний прибора или решить, какой ввод мы должны дать программе, чтобы мрамор приземляется на определенном расстоянии от пусковой установки.
Шаг первый: создайте свою диаграмму
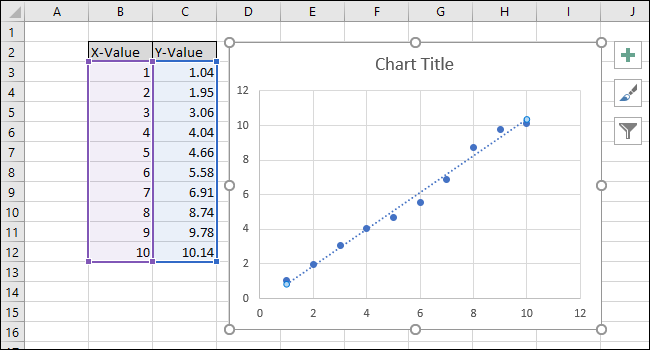
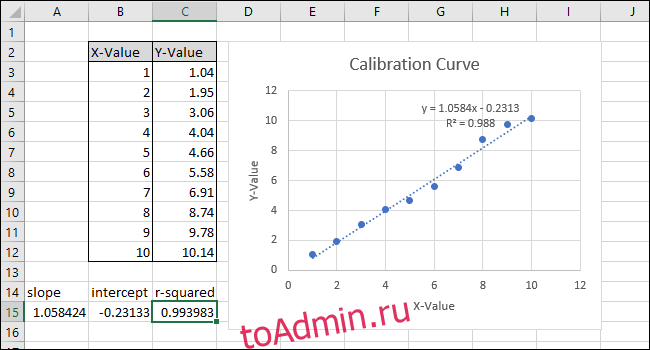
Наш простой пример электронной таблицы состоит из двух столбцов: X-Value и Y-Value.
Начнем с выбора данных для построения графика.
Сначала выберите ячейки столбца «X-значение».
Теперь нажмите клавишу Ctrl и затем щелкните ячейки столбца Y-значения.
Перейдите на вкладку «Вставить».
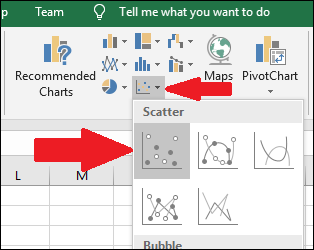
Перейдите в меню «Графики» и выберите первый вариант в раскрывающемся меню «Разброс».
разброс» width=»314″ height=»250″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20314%20250’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-05.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.zXPKQgYC7-.png»/>
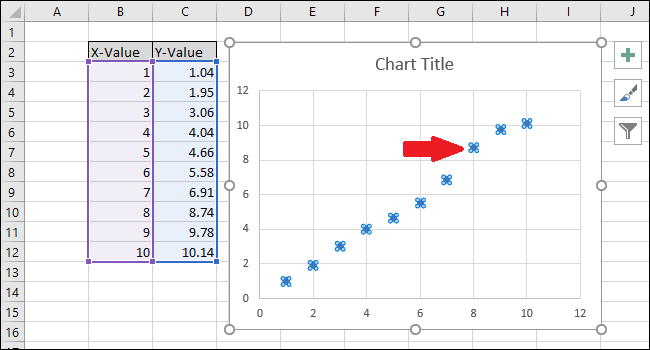
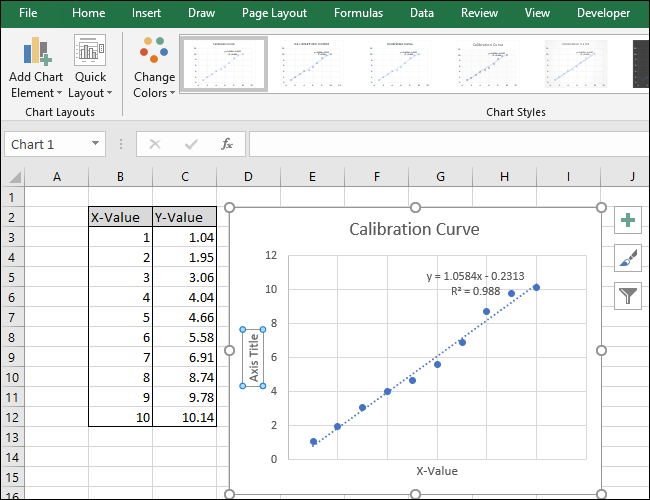
Появится диаграмма, содержащая точки данных из двух столбцов.
Выберите серию, нажав на одну из синих точек. После выбора Excel обрисовывает в общих чертах точки.
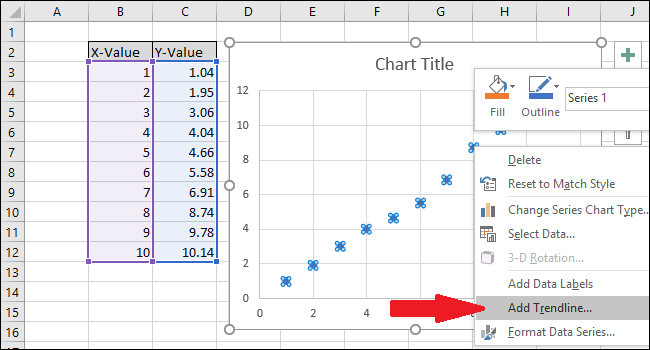
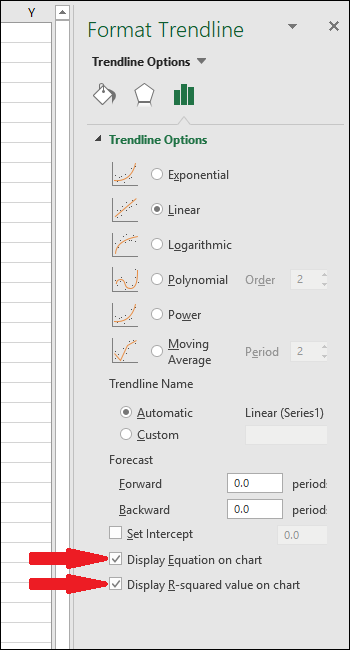
Щелкните правой кнопкой мыши одну из точек и выберите опцию «Добавить линию тренда».
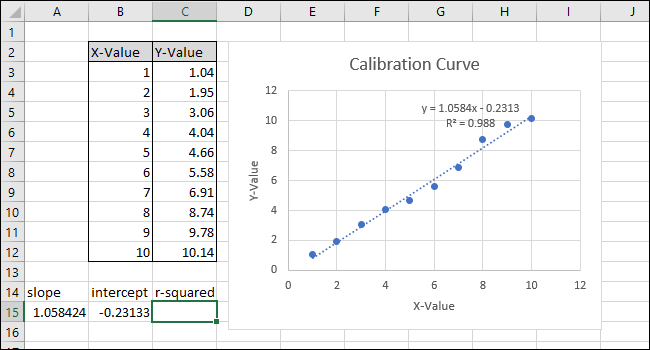
На графике появится прямая линия.
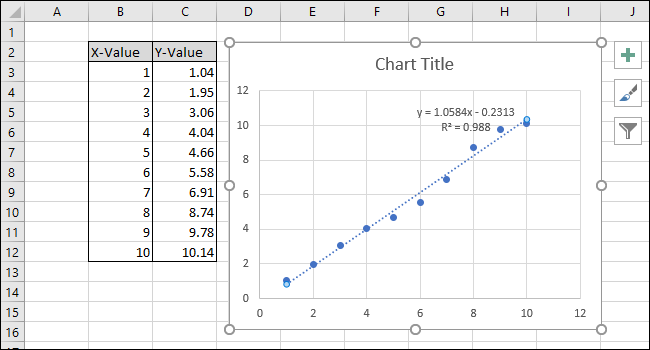
В правой части экрана появится меню «Format Trendline». Установите флажки рядом с «Показать уравнение на графике» и «Показать значение R-квадрат на графике». Значение R-квадрат является статистикой, которая говорит вам, насколько точно линия соответствует данным. Наилучшее значение R-квадрата равно 1.000, что означает, что каждая точка данных касается линии. По мере роста различий между точками данных и линией значение r-квадрата уменьшается, причем 0,000 является наименьшим возможным значением.
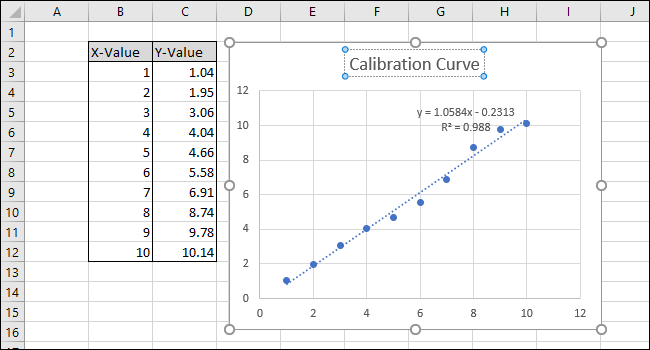
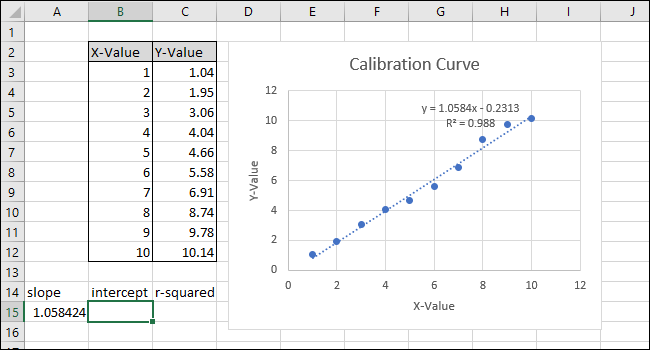
Уравнение и R-квадрат статистики трендовой линии появятся на графике. Обратите внимание, что в нашем примере корреляция данных очень хорошая, значение R-квадрата равно 0,988.
Уравнение имеет вид «Y = Mx + B», где M — наклон, а B — пересечение оси y прямой.
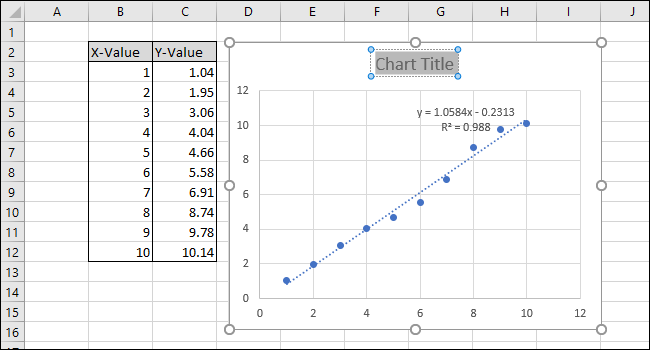
Теперь, когда калибровка завершена, давайте поработаем над настройкой диаграммы, отредактировав заголовок и добавив заголовки осей.
Чтобы изменить заголовок диаграммы, щелкните по нему, чтобы выделить текст.
Теперь введите новый заголовок, который описывает диаграмму.
Чтобы добавить заголовки к осям X и Y, сначала перейдите к «Инструменты диаграммы»> «Дизайн».
дизайн» width=»650″ height=»225″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20225’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-14.png»/>
Нажмите «Добавить элемент диаграммы».
Теперь перейдите к Названия осей> Первичная горизонтальная.
первичная горизонтальная» width=»650″ height=»500″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20500’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-16.png»/>
Появится название оси.
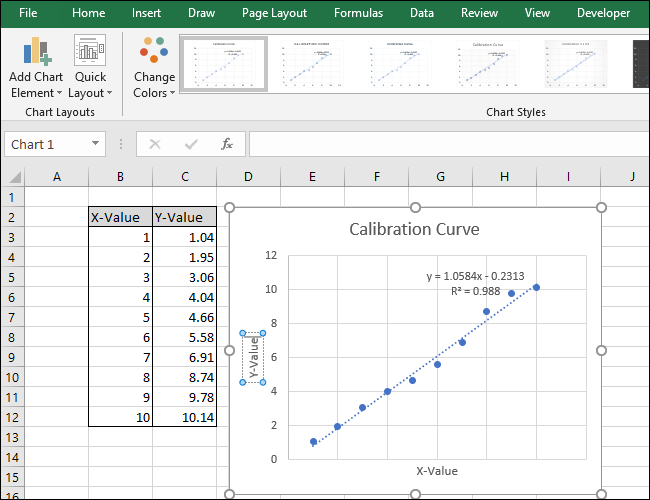
Чтобы переименовать заголовок оси, сначала выделите текст, а затем введите новый заголовок.
Теперь перейдите к Названию осей> Первичная вертикаль.
Появится название оси.
Переименуйте этот заголовок, выделив текст и введя новый заголовок.
Ваша диаграмма теперь завершена.
Шаг второй: Рассчитать линейное уравнение и R-квадрат
Теперь давайте вычислим линейное уравнение и R-квадрат, используя встроенные в Excel функции SLOPE, INTERCEPT и CORREL.
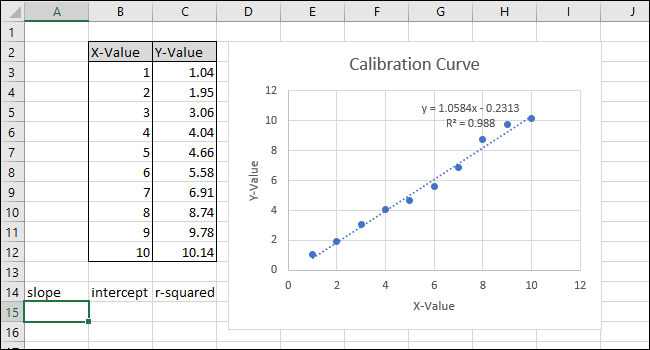
К нашему листу (в строке 14) мы добавили заголовки для этих трех функций. Мы выполним фактические вычисления в ячейках под этими заголовками.
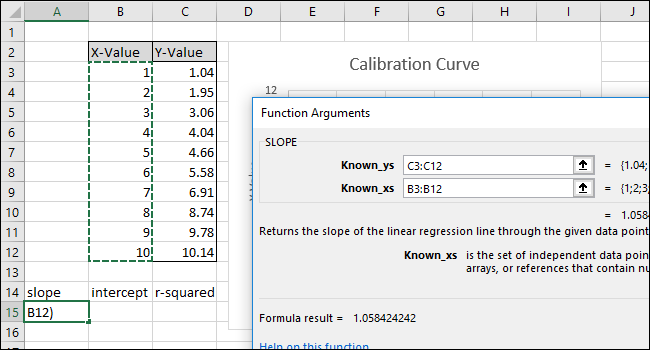
Сначала рассчитаем НАКЛОН. Выберите ячейку A15.
Перейдите к формулам> Дополнительные функции> Статистические> НАКЛОН.
Дополнительные функции> Статистические> НАКЛОН» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-24.png»/>
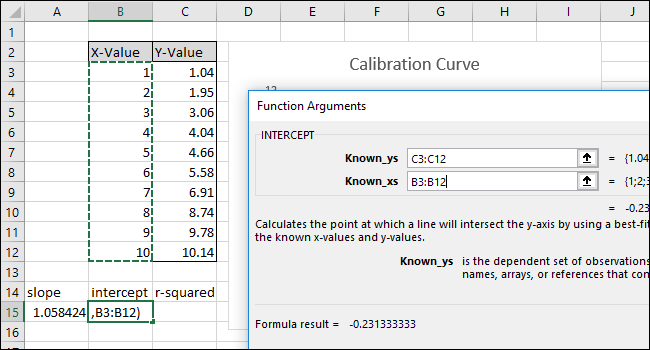
Откроется окно «Аргументы функции». В поле «Known_ys» выберите или введите ячейки столбца Y-значения.
В поле «Known_xs» выберите или введите ячейки столбца X-Value. Порядок полей ‘Known_ys’ и ‘Known_xs’ имеет значение в функции SLOPE.
Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:
Обратите внимание, что значение, возвращаемое функцией SLOPE в ячейке A15, соответствует значению, отображенному на графике.
Затем выберите ячейку B15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «ПЕРЕКРЫТЬ».
Дополнительные функции> Статистические> INTERCEPT» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-28.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.6UWCgXDsRt.png»/>
Откроется окно «Аргументы функции». Выберите или введите в ячейки столбца Y-значение для поля «Known_ys».
Выберите или введите в ячейки столбца X-Value поле «Known_xs». Порядок полей «Known_ys» и «Known_xs» также имеет значение в функции INTERCEPT.
Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:
Обратите внимание, что значение, возвращаемое функцией INTERCEPT, соответствует точке пересечения y, отображаемой на диаграмме.
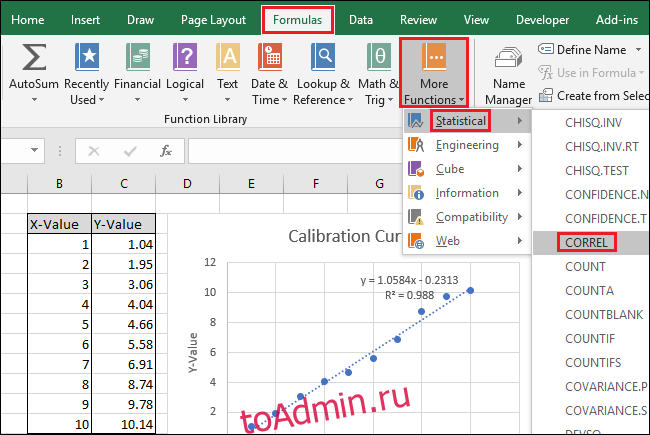
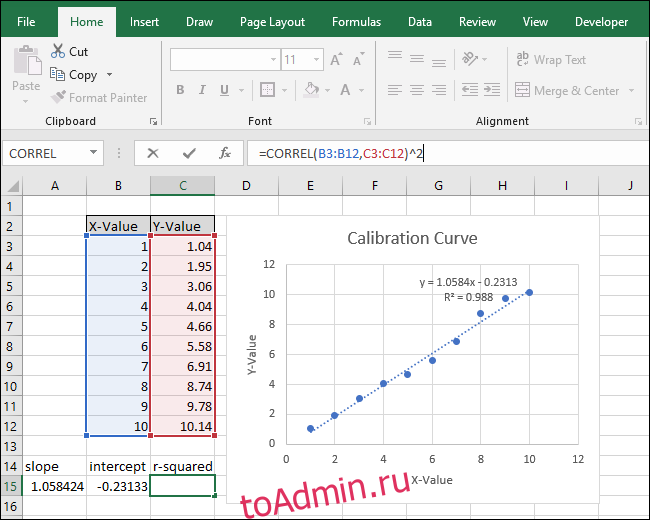
Затем выберите ячейку C15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «CORREL».
дополнительные функции> статистические> CORREL» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-32.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.n7KBBl00Uj.png»/>
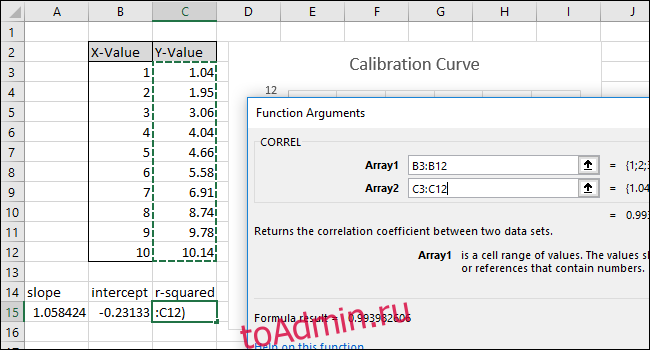
Откроется окно «Аргументы функции». Выберите или введите любой из двух диапазонов ячеек для поля «Массив1». В отличие от SLOPE и INTERCEPT, порядок не влияет на результат функции CORREL.
Выберите или введите другой из двух диапазонов ячеек для поля «Array2».
Нажмите «ОК». Формула должна выглядеть следующим образом на панели формул:
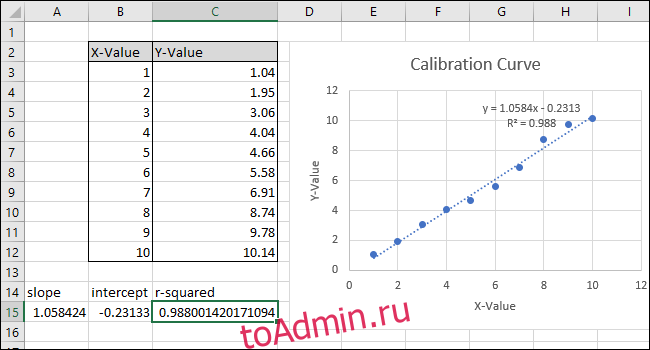
Обратите внимание, что значение, возвращаемое функцией CORREL, не соответствует значению «r-квадрат» на графике. Функция CORREL возвращает «R», поэтому мы должны возвести ее в квадрат, чтобы вычислить «R-квадрат».
Щелкните внутри панели функций и добавьте «^ 2» в конец формулы, чтобы возвести в квадрат значение, возвращаемое функцией CORREL. Заполненная формула теперь должна выглядеть так:
После изменения формулы значение «R-квадрат» теперь соответствует значению, отображенному на графике.
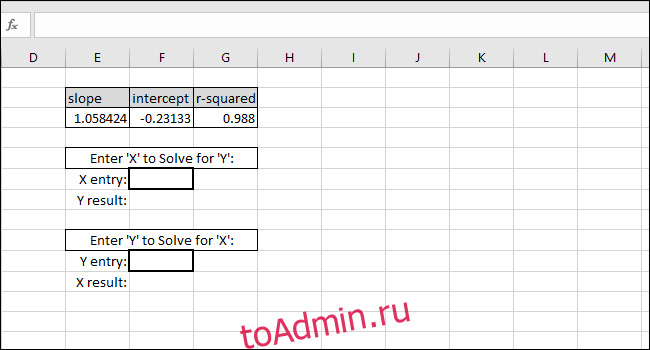
Шаг третий: настройка формул для быстрого расчета значений
Теперь мы можем использовать эти значения в простых формулах, чтобы определить концентрацию этого «неизвестного» раствора или то, что мы должны ввести в код, чтобы шарик пролетел определенное расстояние.
Эти шаги настроят формулы, необходимые для того, чтобы вы могли ввести значение X или значение Y и получить соответствующее значение на основе калибровочной кривой.
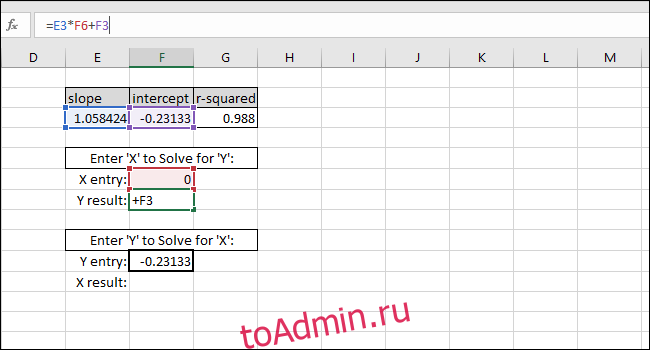
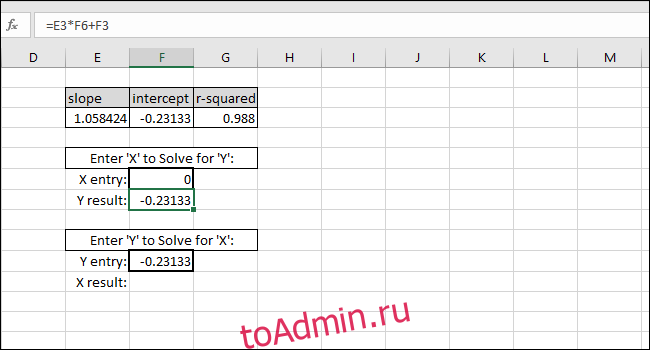
Уравнение линии наилучшего соответствия имеет вид «Y-значение = НАКЛОН * X-значение + INTERCEPT», поэтому решение для «Y-значения» выполняется путем умножения значения X и SLOPE, а затем добавив ИНТЕРЦЕПТ.
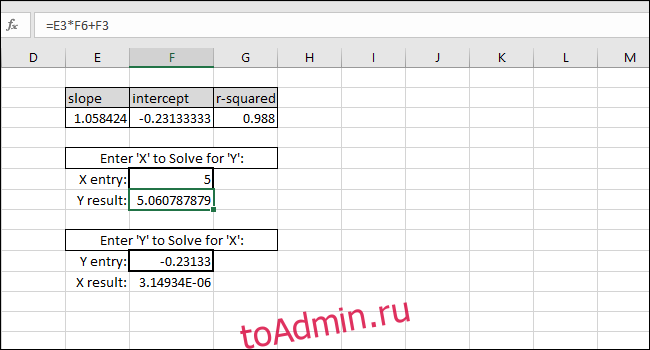
В качестве примера мы вводим ноль в качестве значения X. Возвращаемое значение Y должно быть равно ПЕРЕКЛЮЧЕНИЮ линии наилучшего соответствия. Это соответствует, поэтому мы знаем, что формула работает правильно.
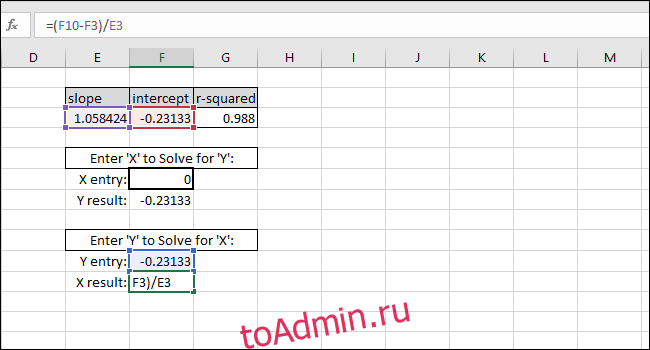
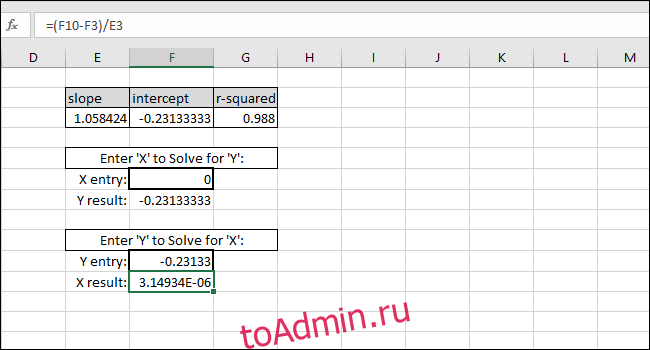
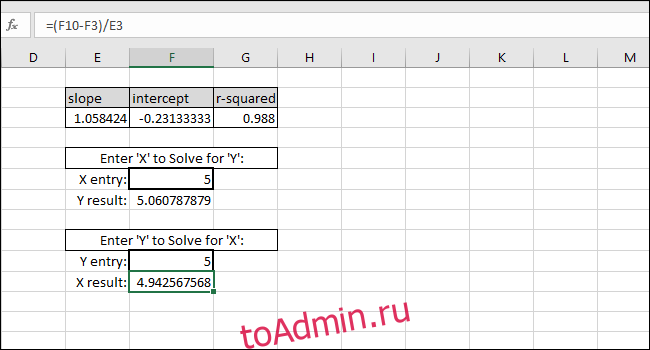
Решение для значения X на основе значения Y выполняется путем вычитания INTERCEPT из значения Y и деления результата на НАКЛОН:
В качестве примера мы использовали INTERCEPT в качестве значения Y. Возвращаемое значение Х должно быть равно нулю, но возвращаемое значение равно 3.14934E-06. Возвращаемое значение не равно нулю, потому что мы непреднамеренно обрезали результат INTERCEPT при вводе значения. Однако формула работает правильно, потому что результат формулы равен 0,00000314934, что по существу равно нулю.
Вы можете ввести любое значение X в первую ячейку с толстыми границами, и Excel автоматически вычислит соответствующее значение Y.
Ввод любого значения Y во вторую ячейку с толстой рамкой даст соответствующее значение X. Эта формула используется для расчета концентрации этого раствора или того, что необходимо для запуска мрамора на определенном расстоянии.
В этом случае прибор показывает «5», поэтому при калибровке будет предложена концентрация 4,94, или мы хотим, чтобы шарик прошел пять единиц расстояния, поэтому при калибровке предлагается ввести 4,94 в качестве входной переменной для программы, управляющей пусковой установкой мрамора. Мы можем быть достаточно уверены в этих результатах из-за высокого значения R-квадрата в этом примере.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
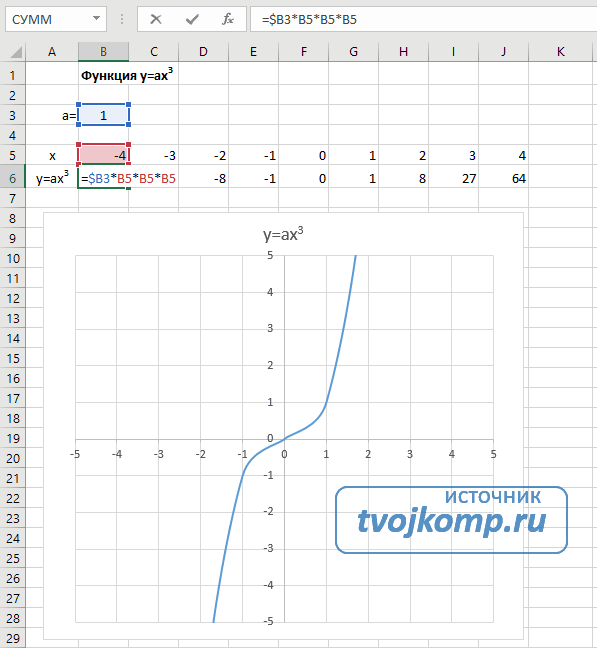
Как построить график квадратного уравнения в Excel
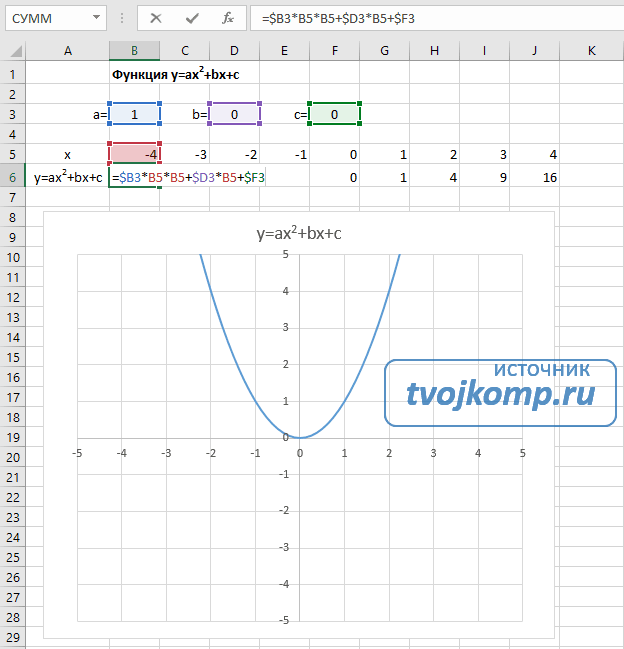
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
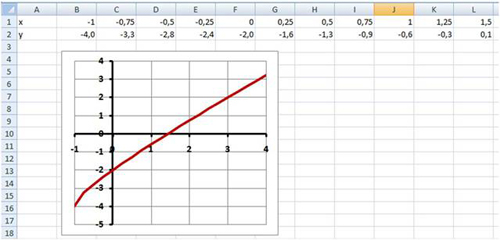
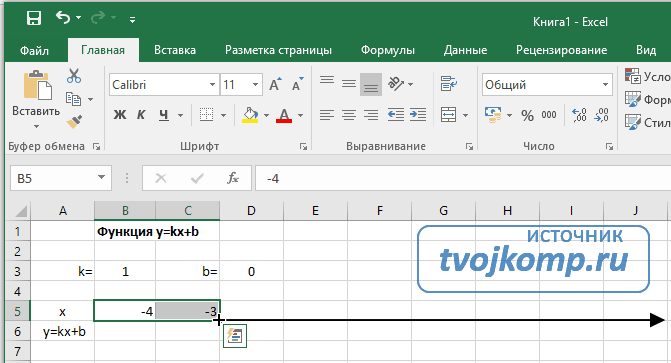
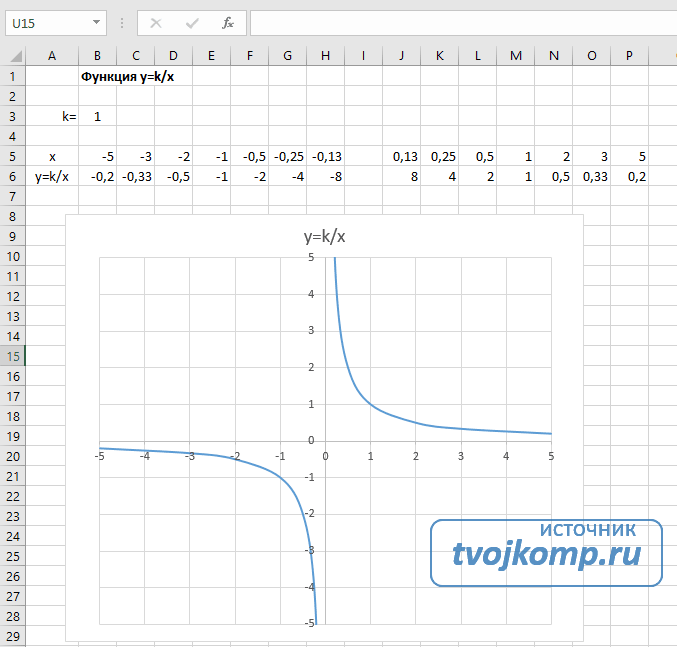
Как построить график линейного уравнения
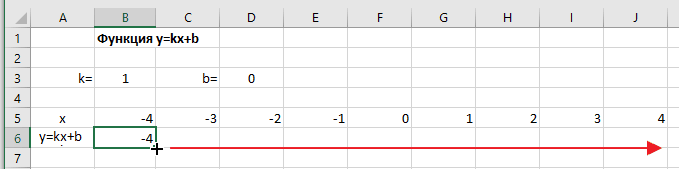
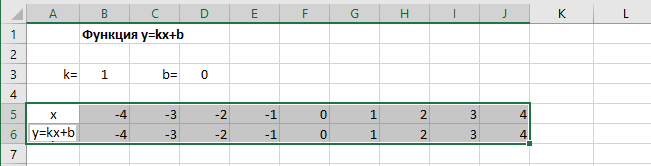
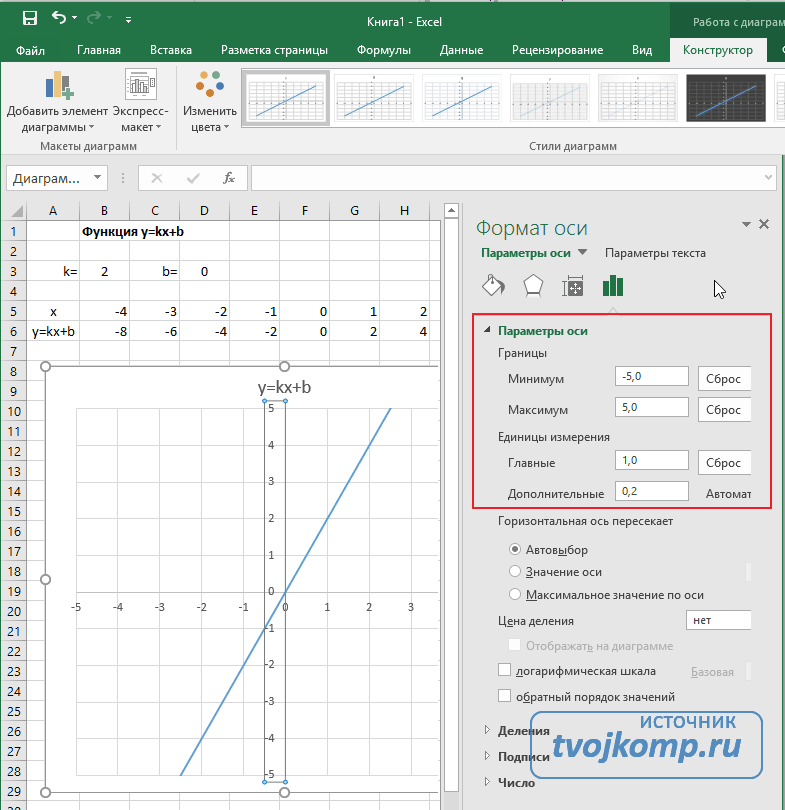
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


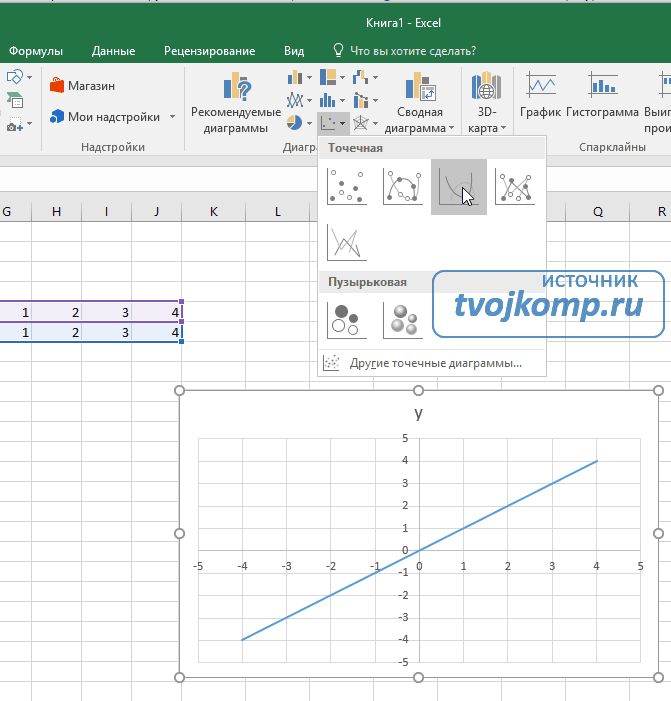
График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://gadgetshelp.com/how-to/kak-sdelat-lineinuiu-kalibrovochnuiu-krivuiu-v-excel/
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
Варианты построения графика функции в Microsoft Excel
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
-
Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
Подойдет вариант «Точечная с гладкими кривыми и маркерами».
После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
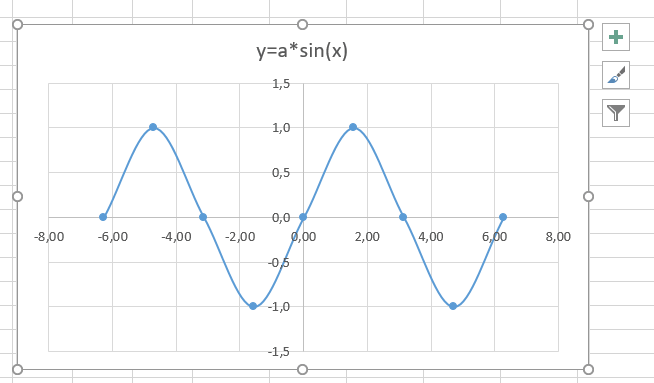
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
-
Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
Создайте сразу два столбца — X и Y, куда будете записывать данные.
Запишите самостоятельно первые два или три значения с указанным шагом.
Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
Перейдите к столбцу Y и объявите функцию =SIN( , а в качестве числа укажите первое значение X.
Сама функция автоматически высчитает синус заданного числа.
Растяните столбец точно так же, как это было показано ранее.
Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
Выделите столбец с Y и перейдите на вкладку «Вставка».
Создайте стандартный график, развернув выпадающее меню.
График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
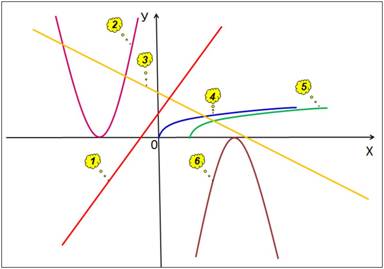
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
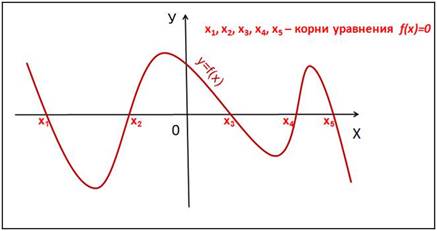
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
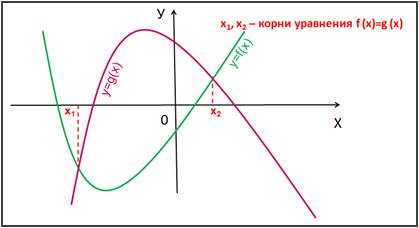
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
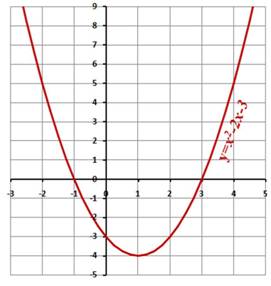
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
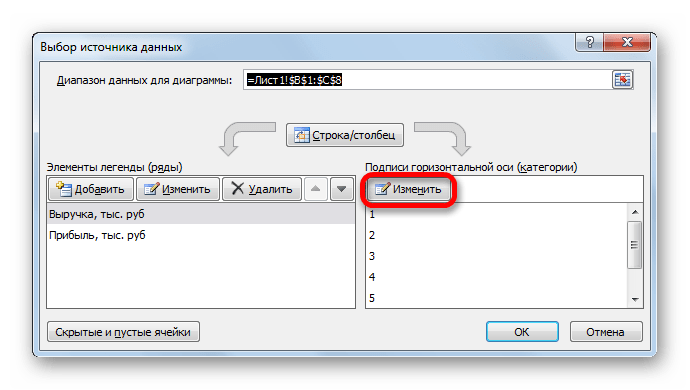
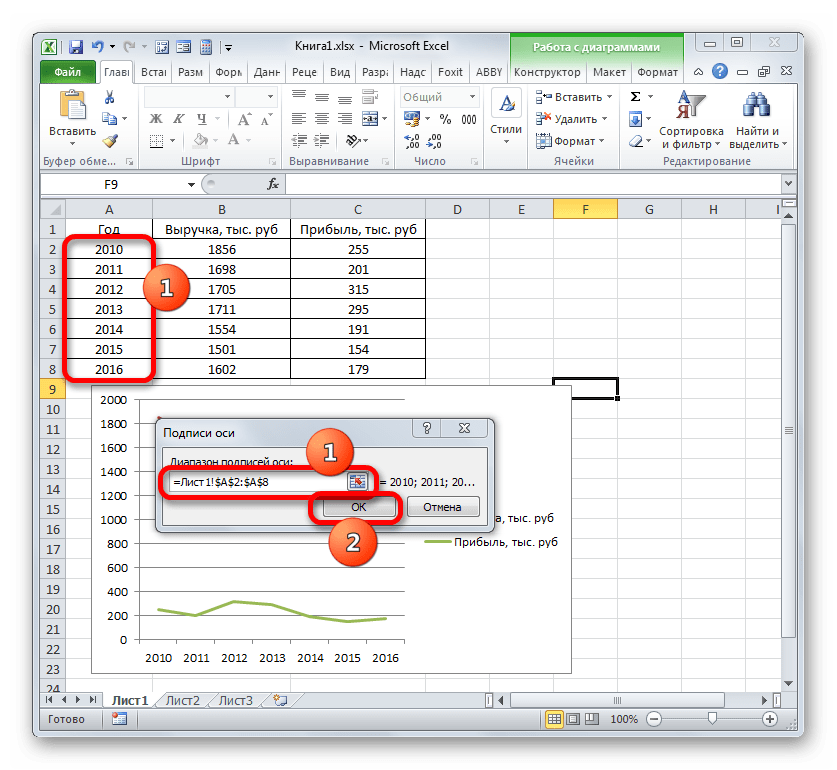
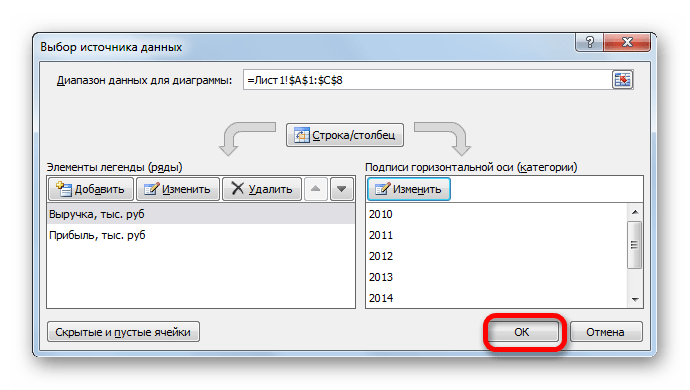
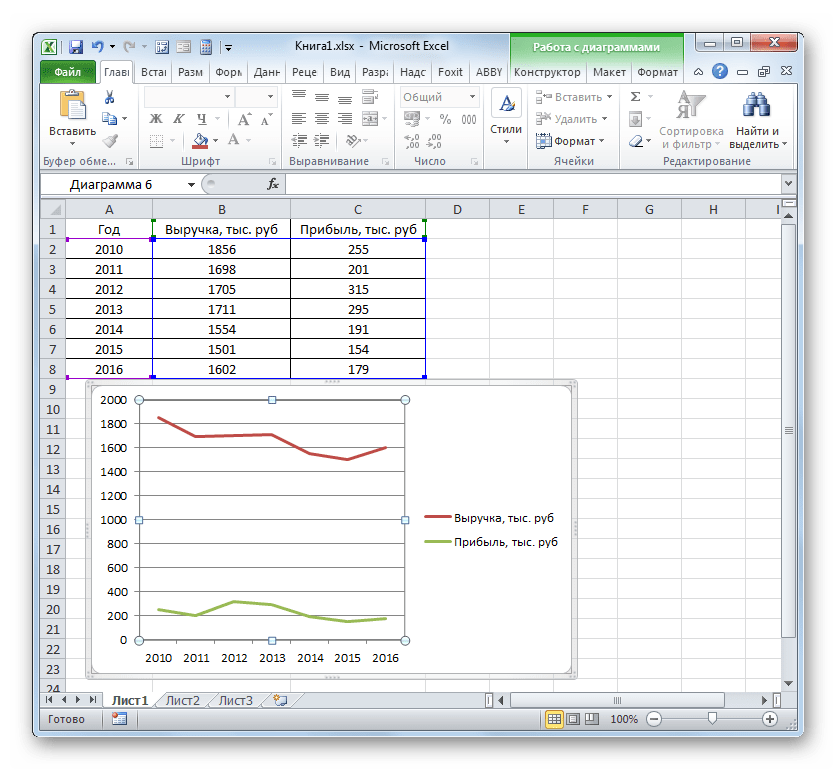
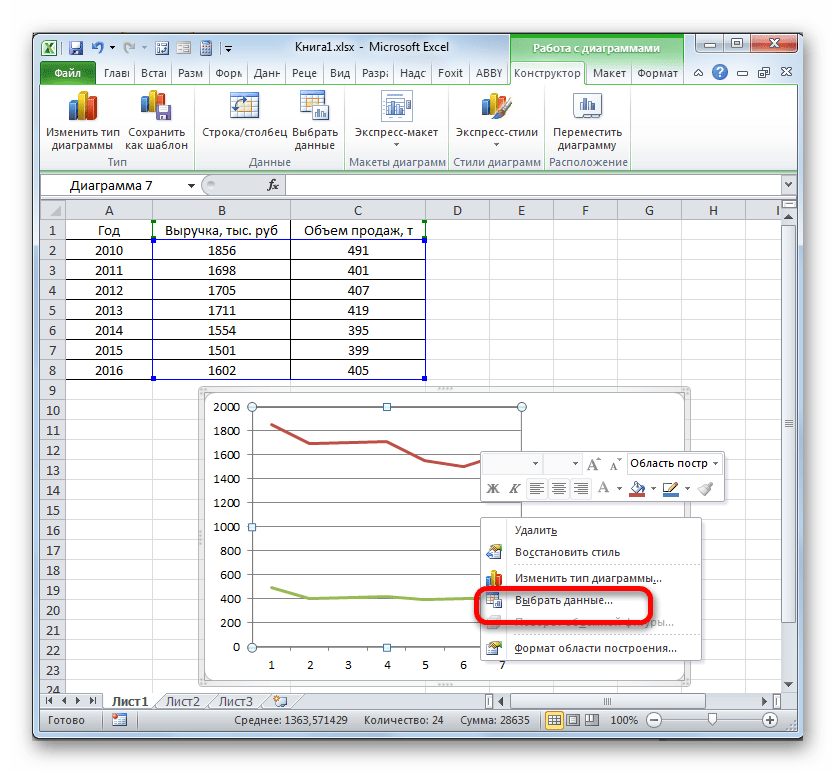
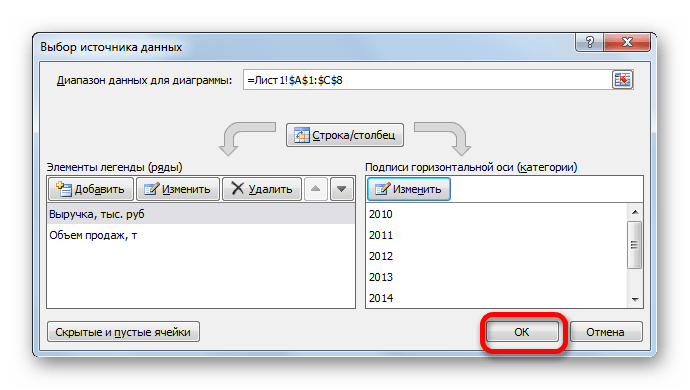
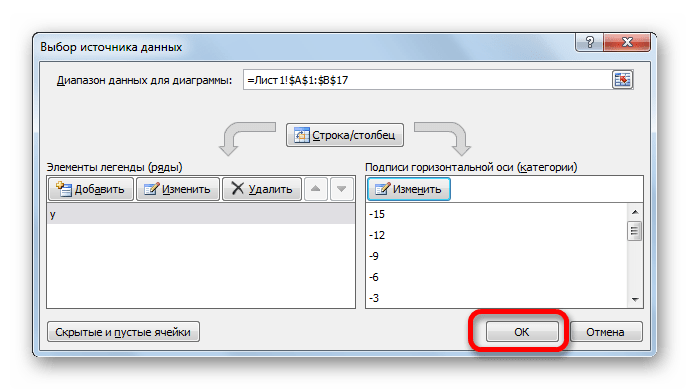
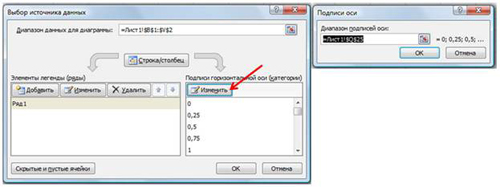
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
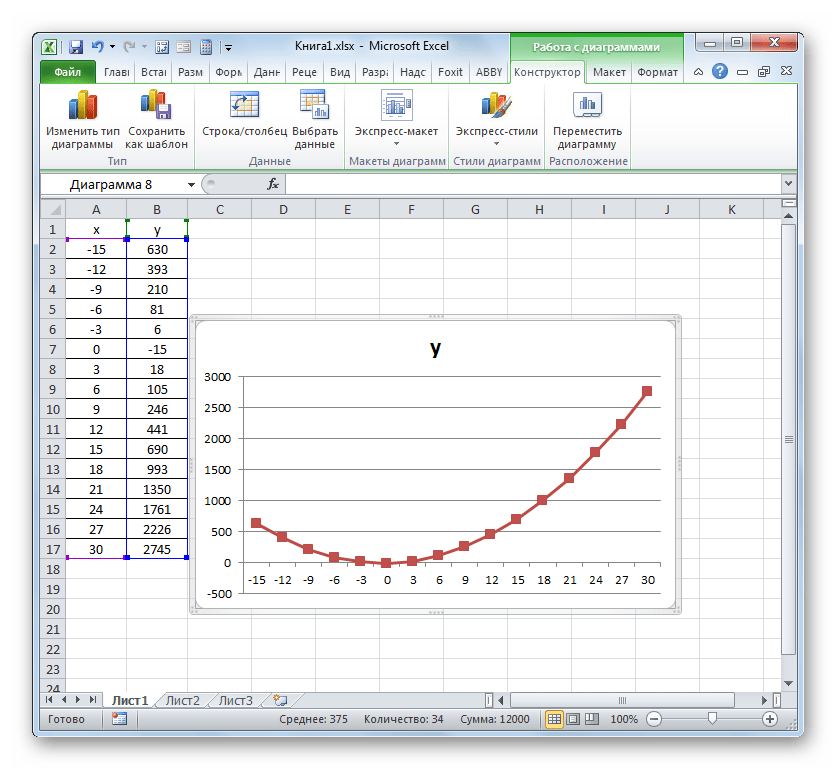
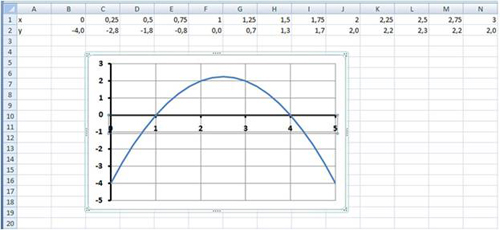
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
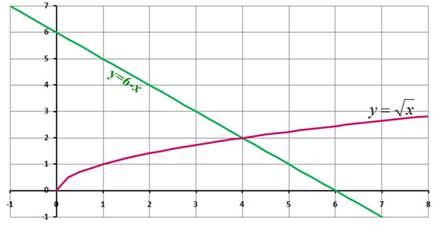
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
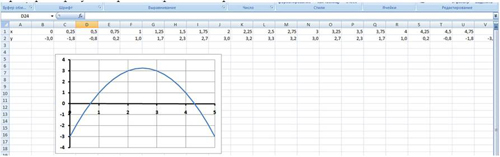
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
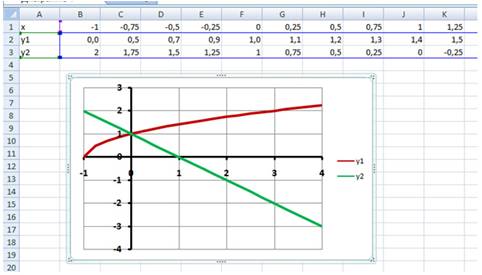
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
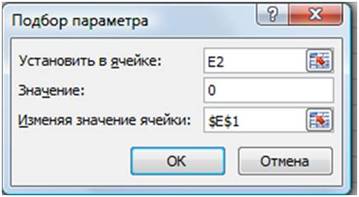
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
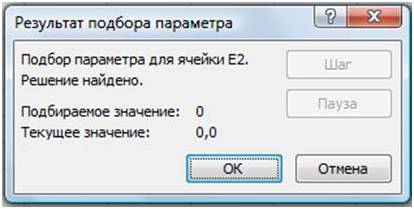
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://urok.1sept.ru/articles/564361
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
17 авг. 2022 г.
читать 3 мин
Часто вам может понадобиться найти уравнение, которое лучше всего соответствует некоторой кривой для набора данных в Excel.
К счастью, это довольно легко сделать с помощью функции Trendline в Excel.
В этом руководстве представлен пошаговый пример того, как подогнать уравнение к кривой в Excel.
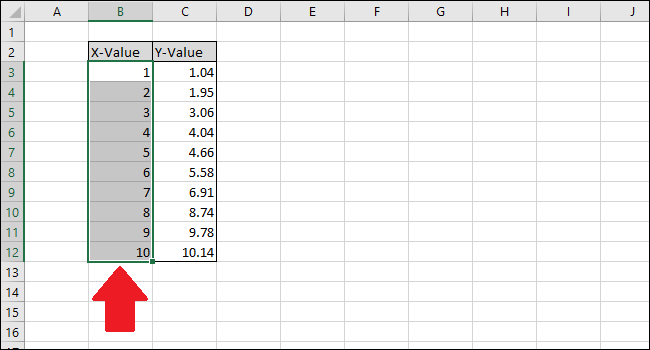
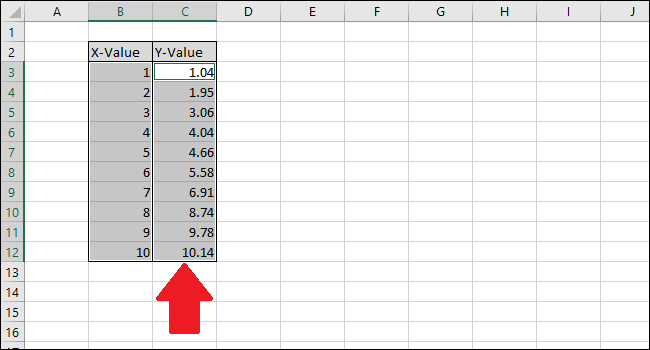
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных для работы:
Шаг 2: Создайте диаграмму рассеивания
Затем давайте создадим диаграмму рассеяния для визуализации набора данных.
Сначала выделите ячейки A2: B16 следующим образом:
Затем щелкните вкладку « Вставка » на верхней ленте, а затем щелкните первый параметр графика в разделе « Разброс »:
Получается следующая диаграмма рассеяния:
Шаг 3: Добавьте линию тренда
Затем щелкните в любом месте диаграммы рассеяния. Затем нажмите знак + в правом верхнем углу. В раскрывающемся меню щелкните стрелку рядом с линией тренда , а затем выберите « Дополнительные параметры »:
В появившемся справа окне нажмите кнопку рядом с Polynomial.Затем установите флажки рядом с Отображать уравнение на диаграмме и Отображать значение R-квадрата на диаграмме .
Это дает следующую кривую на диаграмме рассеяния:
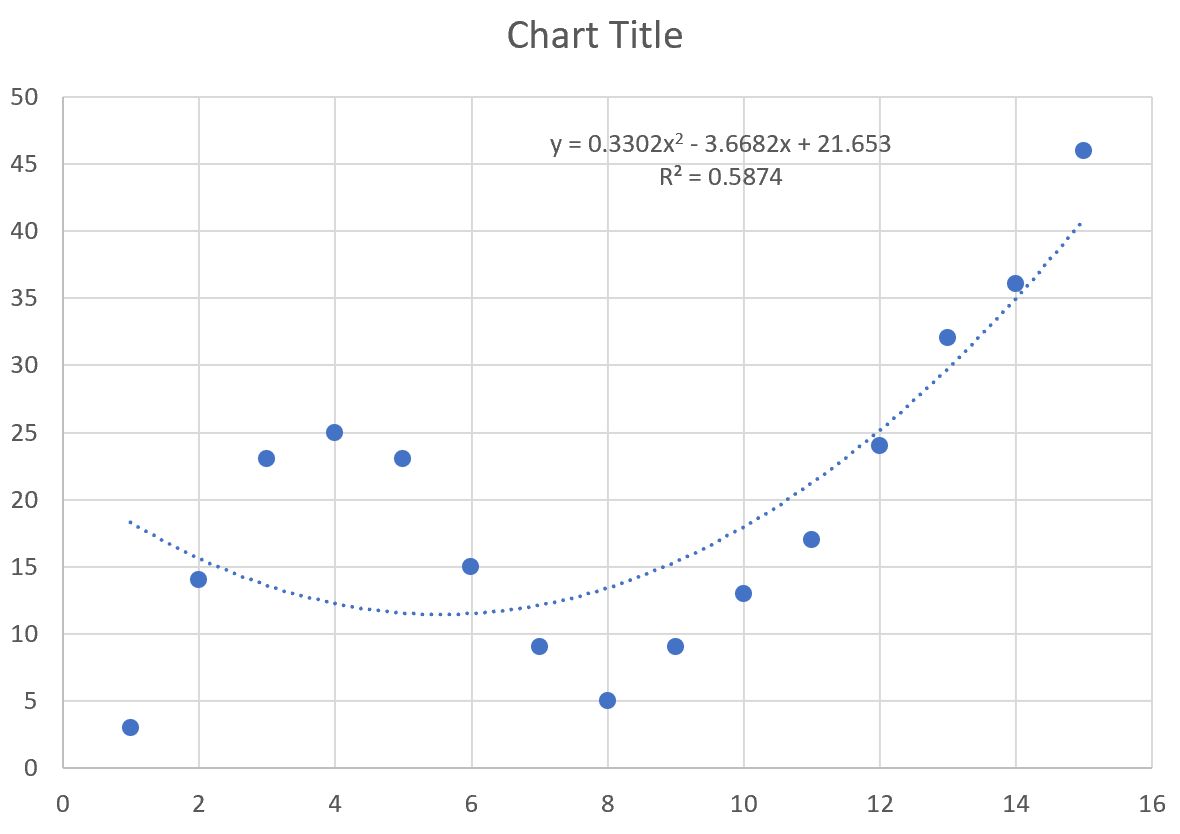
Уравнение кривой выглядит следующим образом:
у = 0,3302 х 2 – 3,6682 х + 21,653
R-квадрат говорит нам о проценте вариации переменной отклика , которая может быть объяснена переменными-предикторами. R-квадрат для этой конкретной кривой равен 0,5874 .
Шаг 4: Выберите лучшую линию тренда
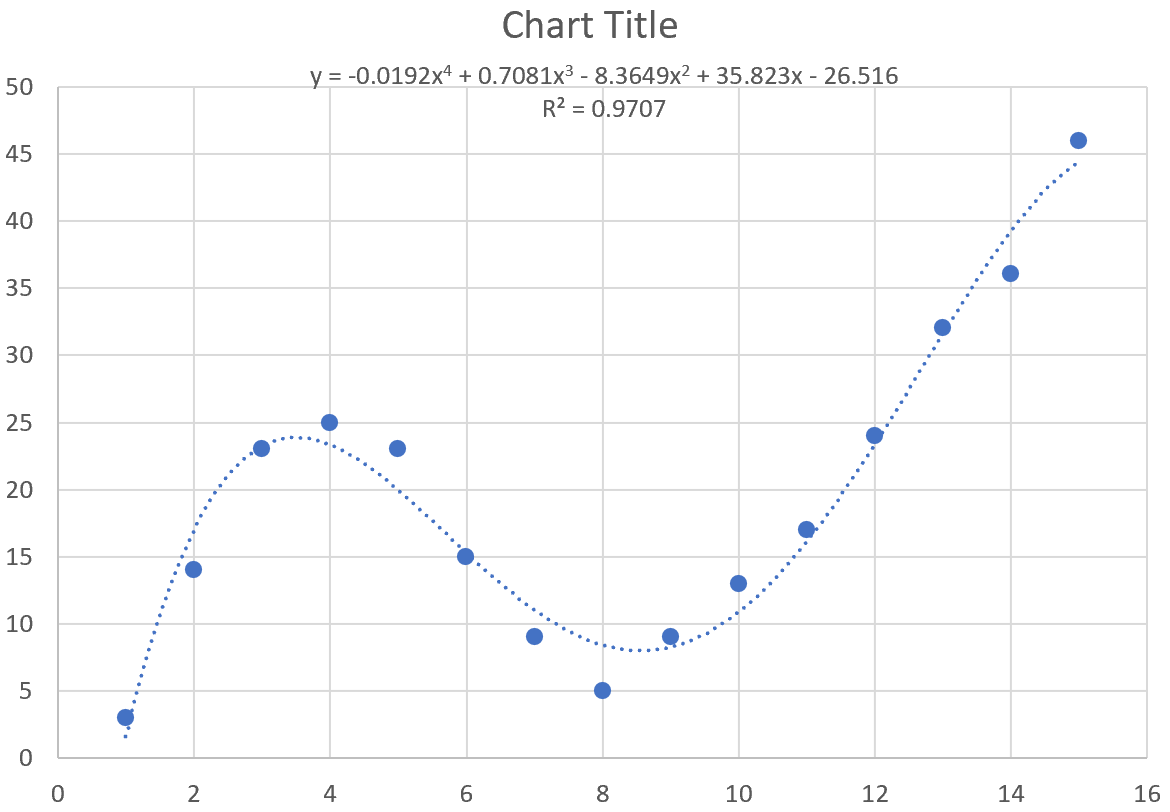
Мы также можем увеличить порядок полинома, который мы используем, чтобы увидеть, лучше ли более гибкая кривая подходит для набора данных.
Например, мы могли бы установить полиномиальный порядок равным 4:
В результате получается следующая кривая:
Уравнение кривой выглядит следующим образом:
у = -0,0192 х 4 + 0,7081 х 3 – 8,3649 х 2 + 35,823 х – 26,516
R-квадрат для этой конкретной кривой равен 0,9707 .
Этот R-квадрат значительно выше, чем у предыдущей кривой, что указывает на то, что он гораздо лучше соответствует набору данных.
Мы также можем использовать это уравнение кривой, чтобы предсказать значение переменной ответа на основе переменной-предиктора. Например, если x = 4, то мы можем предсказать, что y = 23,34 :
у = -0,0192(4) 4 + 0,7081(4) 3 – 8,3649(4) 2 + 35,823(4) – 26,516 = 23,34
Вы можете найти больше руководств по Excel на этой странице .
В Excel есть встроенные функции, которые можно использовать для отображения данных калибровки и расчета линии наилучшего соответствия. Это может быть полезно, когда вы пишете отчет о химической лаборатории или программируете поправочный коэффициент для единицы оборудования.
В этой статье мы рассмотрим, как с помощью Excel создать диаграмму, построить линейную калибровочную кривую, отобразить формулу калибровочной кривой, а затем настроить простые формулы с функциями НАКЛОН и ПЕРЕСЕЧЕНИЕ, чтобы использовать уравнение калибровки в Excel.
Чтобы выполнить калибровку, вы сравниваете показания устройства (например, температуру, отображаемую термометром) с известными значениями, называемыми стандартами (например, точки замерзания и кипения воды). Это позволяет вам создать серию пар данных, которые затем вы будете использовать для построения калибровочной кривой.
Двухточечная калибровка термометра с использованием точек замерзания и кипения воды будет иметь две пары данных: одну, когда термометр помещают в ледяную воду (32 ° F или 0 ° C), и одну в кипящую воду (212 ° F). или 100 ° C). Когда вы наносите эти две пары данных в виде точек и проводите линию между ними (калибровочная кривая), а затем, предполагая, что реакция термометра является линейной, вы можете выбрать любую точку на линии, которая соответствует значению, отображаемому термометром, и вы смог найти соответствующую «истинную» температуру.
Таким образом, линия по существу заполняет информацию между двумя известными точками для вас, чтобы вы могли быть достаточно уверены при оценке фактической температуры, когда термометр показывает 57,2 градуса, но когда вы никогда не измеряли «стандарт», который соответствует это чтение.
В Excel есть функции, которые позволяют графически отображать пары данных на диаграмме, добавлять линию тренда (калибровочную кривую) и отображать уравнение калибровочной кривой на диаграмме. Это полезно для визуального отображения, но вы также можете вычислить формулу линии, используя функции НАКЛОН и ПЕРЕСЕЧЕНИЕ Excel. Когда вы вводите эти значения в простые формулы, вы сможете автоматически рассчитать «истинное» значение на основе любого измерения.
Давайте посмотрим на пример
В этом примере мы построим калибровочную кривую из серии из десяти пар данных, каждая из которых состоит из значения X и значения Y. Значения X будут нашими «стандартами», и они могут представлять что угодно, от концентрации химического раствора, который мы измеряем с помощью научного инструмента, до входной переменной программы, которая управляет машиной для запуска мрамора.
Значения Y будут «откликами», и они будут представлять показания прибора, предоставленные при измерении каждого химического раствора, или измеренное расстояние, на котором от пусковой установки приземлился шарик с использованием каждого входного значения.
После того, как мы графически изобразим калибровочную кривую, мы будем использовать функции НАКЛОН и ПЕРЕСЕЧЕНИЕ, чтобы вычислить формулу калибровочной линии и определить концентрацию «неизвестного» химического раствора на основе показаний прибора или решить, какие входные данные мы должны дать программе, чтобы мрамор приземляется на определенном расстоянии от пусковой установки.
Шаг первый: создайте свою диаграмму
Наша простая таблица-пример состоит из двух столбцов: X-Value и Y-Value.
Начнем с выбора данных для отображения на диаграмме.
Сначала выберите ячейки столбца «X-Value».
Теперь нажмите клавишу Ctrl и щелкните ячейки столбца Y-Value.
Перейдите на вкладку «Вставка».
Перейдите в меню «Графики» и выберите первую опцию в раскрывающемся списке «Точечный».
Выберите серию, щелкнув одну из синих точек. После выбора Excel обрисовывает в общих чертах точки.
Щелкните правой кнопкой мыши одну из точек и выберите параметр «Добавить линию тренда».
На графике появится прямая линия.
В правой части экрана появится меню «Форматировать линию тренда». Установите флажки рядом с «Отображать уравнение на диаграмме» и «Отображать значение R-квадрата на диаграмме». Значение R-квадрата — это статистика, которая показывает, насколько точно линия соответствует данным. Наилучшее значение R-квадрата составляет 1.000, что означает, что каждая точка данных касается линии. По мере того, как разница между точками данных и линией увеличивается, значение r-квадрата уменьшается, при этом 0,000 является наименьшим возможным значением.
Уравнение и статистика R-квадрата линии тренда появятся на графике. Обратите внимание, что корреляция данных в нашем примере очень хорошая, со значением R-квадрат 0,988.
Уравнение имеет вид «Y = Mx + B», где M — наклон, а B — точка пересечения прямой линии с осью Y.
Теперь, когда калибровка завершена, давайте поработаем над настройкой диаграммы, отредактировав заголовок и добавив заголовки осей.
Чтобы изменить заголовок диаграммы, щелкните по нему, чтобы выделить текст.
Теперь введите новый заголовок, описывающий диаграмму.
Чтобы добавить заголовки к осям x и y, сначала перейдите в Инструменты диаграммы> Дизайн.
Теперь перейдите к Названиям осей> Первичный горизонтальный.
Появится заголовок оси.
Чтобы переименовать заголовок оси, сначала выберите текст, а затем введите новый заголовок.
Теперь перейдите в Названия осей> Основная вертикаль.
Появится название оси.
Переименуйте этот заголовок, выделив текст и введя новый заголовок.
Теперь ваша диаграмма завершена.
Шаг второй: вычислить линейное уравнение и статистику R-квадрат
Теперь давайте рассчитаем линейное уравнение и статистику R-квадрата, используя встроенные в Excel функции НАКЛОН, ПЕРЕСЕЧЕНИЕ и КОРРЕЛЬ.
К нашему листу (в строке 14) мы добавили заголовки для этих трех функций. Мы выполним фактические вычисления в ячейках под этими заголовками.
Сначала мы рассчитаем НАКЛОН. Выберите ячейку A15.
Перейдите к формулам> Дополнительные функции> Статистические данные> НАКЛОН.
В поле «Known_xs» выберите или введите значения в ячейках столбца X-Value. Порядок полей Known_ys и Known_xs имеет значение в функции SLOPE.
Нажмите «ОК». Окончательная формула в строке формул должна выглядеть так:
= НАКЛОН (C3: C12; B3: B12)
Обратите внимание, что значение, возвращаемое функцией НАКЛОН в ячейке A15, соответствует значению, отображаемому на диаграмме.
Затем выберите ячейку B15 и перейдите в раздел Формулы> Дополнительные функции> Статистические данные> ПЕРЕСЕЧЕНИЕ.
Выберите или введите ячейки столбца X-Value для поля «Known_xs». Порядок полей «Known_ys» и «Known_xs» также имеет значение в функции INTERCEPT.
Нажмите «ОК». Окончательная формула в строке формул должна выглядеть так:
= ПЕРЕСЕЧЕНИЕ (C3: C12; B3: B12)
Обратите внимание, что значение, возвращаемое функцией ПЕРЕСЕЧЕНИЕ, совпадает с точкой пересечения оси Y, отображаемой на диаграмме.
Затем выберите ячейку C15 и перейдите в раздел Формулы> Дополнительные функции> Статистические данные> CORREL.
Выберите или введите другой из двух диапазонов ячеек для поля «Массив2».
Нажмите «ОК». Формула в строке формул должна выглядеть так:
= КОРРЕЛ (B3: B12; C3: C12)
Обратите внимание, что значение, возвращаемое функцией CORREL, не соответствует значению «r-квадрат» на диаграмме. Функция КОРРЕЛ возвращает «R», поэтому мы должны возвести его в квадрат, чтобы вычислить «R-квадрат».
Щелкните внутри функциональной панели и добавьте «^ 2» в конец формулы, чтобы возвести в квадрат значение, возвращаемое функцией CORREL. Заполненная формула должна теперь выглядеть так:
= КОРРЕЛ (B3: B12; C3: C12) ^ 2
Нажмите Ввод.
После изменения формулы значение «R-квадрат» теперь соответствует значению, отображаемому на диаграмме.
Шаг третий: настройте формулы для быстрого расчета значений
Теперь мы можем использовать эти значения в простых формулах, чтобы определить концентрацию этого «неизвестного» раствора или какие входные данные мы должны ввести в код, чтобы шарик пролетел определенное расстояние.
На этих этапах будут созданы формулы, необходимые для того, чтобы вы могли ввести значение X или Y и получить соответствующее значение на основе калибровочной кривой.
Уравнение линии наилучшего соответствия имеет форму «Значение Y = НАКЛОН * значение X + ПЕРЕСЕЧЕНИЕ», поэтому решение для «значения Y» выполняется путем умножения значения X и НАКЛОНА, а затем добавление ПЕРЕСЕЧЕНИЯ.
В качестве примера мы добавляем ноль в качестве значения X. Возвращаемое значение Y должно быть равно ПЕРЕСЕЧЕНИЮ линии наилучшего соответствия. Он совпадает, поэтому мы знаем, что формула работает правильно.
Решение для значения X на основе значения Y выполняется путем вычитания ПЕРЕСЕЧЕНИЯ из значения Y и деления результата на НАКЛОН:
X-value=(Y-value-INTERCEPT)/SLOPE
В качестве примера мы использовали ПЕРЕСЕЧЕНИЕ как Y-значение. Возвращаемое значение X должно быть равно нулю, но возвращаемое значение — 3.14934E-06. Возвращенное значение не равно нулю, потому что мы непреднамеренно усекли результат INTERCEPT при вводе значения. Однако формула работает правильно, потому что результат формулы равен 0,00000314934, что по существу равно нулю.
Вы можете ввести любое желаемое значение X в первую ячейку с толстой рамкой, и Excel автоматически вычислит соответствующее значение Y.
Ввод любого значения Y во вторую ячейку с толстой рамкой даст соответствующее значение X. Эта формула — то, что вы использовали бы для расчета концентрации этого раствора или того, какие входные данные необходимы для запуска шарика на определенное расстояние.
В этом случае прибор показывает «5», поэтому калибровка предполагает концентрацию 4,94, или мы хотим, чтобы шарик прошел пять единиц расстояния, поэтому калибровка предлагает ввести 4,94 в качестве входной переменной для программы, управляющей гранатометом. Мы можем быть достаточно уверены в этих результатах из-за высокого значения R-квадрата в этом примере.
Для оценки уровня неравенства между различными слоями населения общества часто используют кривую Лоренца и производный от неё показатель — коэффициент Джинни. С помощью них можно определить, насколько велик социальный разрыв в обществе между самыми богатыми и наиболее бедными слоями населения. С помощью инструментов приложения Excel можно значительно облегчить процедуру построения кривой Лоренца. Давайте, разберемся, как в среде Эксель это можно осуществить на практике.
Содержание
Использование кривой Лоренца
Кривая Лоренца представляет собой типичную функцию распределения, отображенную графически. По оси X данной функции располагается количество населения в процентном соотношении по нарастающей, а по оси Y — общее количество национального дохода. Собственно, сама кривая Лоренца состоит из точек, каждая из которых соответствует процентному соотношению уровня дохода определенной части общества. Чем больше изогнута линия Лоренца, тем больше в обществе уровень неравенства.
В идеальной ситуации, при которой отсутствует общественное неравенство, каждая группа населения имеет уровень дохода прямо пропорциональный её численности. Линия, характеризующая такую ситуацию, называется кривой равенства, хотя она и представляет собой прямую. Чем больше площадь фигуры, ограниченной кривой Лоренца и кривой равенства, тем выше уровень неравенства в обществе.
Кривая Лоренца может использоваться не только для определения ситуации имущественного расслоения в мире, в конкретной стране или в обществе, но и для сравнения в данном аспекте отдельных домохозяйств.
Вертикальная прямая, которая соединяет линию равенства и наиболее удаленную от неё точку кривой Лоренца, называется индексом Гувера или Робин Гуда. Данный отрезок показывает, какую величину дохода нужно перераспределить в обществе, чтобы достичь полного равенства.
Уровень неравенства в обществе определяется с помощью индекса Джинни, который может варьироваться от 0 до 1. Он ещё называется коэффициентом концентрации доходов.
Построение линии равенства
Теперь давайте на конкретном примере посмотрим, как создать линию равенства и кривую Лоренца в Экселе. Для этого используем таблицу количества населения разбитого на пять равных групп (по 20%), которые суммируются в таблице по нарастающей. Во второй колонке этой таблицы представлена величина национального дохода в процентном соотношении, которая соответствует определенной группе населения.
Для начала построим линию абсолютного равенства. Она будет состоять из двух точек — нулевой и точки суммарного национального дохода для 100% населения.
- Переходим во вкладку «Вставка». На линии в блоке инструментов «Диаграммы» жмем на кнопку «Точечная». Именно данный тип диаграмм подойдет для нашей задачи. Далее открывается список подвидов диаграмм. Выбираем «Точечная с гладкими кривыми и маркерами».
- После выполнения данного действия открывается пустая область для диаграммы. Это случилось потому, что мы не выбрали данные. Для того, чтобы внести данные и построить график, кликаем правой кнопкой мыши по пустой области. В активировавшемся контекстном меню выбираем пункт «Выбрать данные…».
- Открывается окно выбора источника данных. В левой его части, которая называется «Элементы легенды (ряды)» жмем на кнопку «Добавить».
- Запускается окно изменения ряда. В поле «Имя ряда» записываем то наименование диаграммы, которое хотим ей присвоить. Оно может также располагаться на листе и в этом случае нужно указать адрес ячейки его нахождения. Но в нашем случае легче просто вписать название вручную. Дадим диаграмме наименование «Линия равенства».
В поле «Значения X» следует указать координаты точек диаграммы по оси X. Как мы помним, их будет всего две: 0 и 100. Записываем данные значения через точку с запятой в данном поле.
В поле «Значения Y» следует записать координаты точек по оси Y. Их тоже будет две: 0 и 35,9. Последняя точка, как мы можем видеть по графику, соответствует совокупному национальному доходу 100% населения. Итак, записываем значения «0;35,9» без кавычек.
После того, как все указанные данные внесены, жмем на кнопку «OK».
- После этого мы возвращаемся к окну выбора источника данных. В нем тоже следует нажать на кнопку «OK».
- Как видим, после вышеуказанных действий линия равенства будет построена и отобразится на листе.
Урок: Как сделать диаграмму в Экселе
Создание кривой Лоренца
Теперь нам предстоит непосредственно построить кривую Лоренца, опираясь на табличные данные.
- Кликаем правой кнопкой мыши по области диаграммы, на которой уже расположена линия равенства. В запустившемся меню снова останавливаем выбор на пункте «Выбрать данные…».
- Опять открывается окно выбора данных. Как видим, среди элементов уже представлено наименование «Линия равенства», но нам нужно внести ещё одну диаграмму. Поэтому жмем на кнопку «Добавить».
- Снова открывается окно изменения ряда. Поле «Имя ряда», как и в прошлый раз, заполняем вручную. Сюда можно вписать наименование «Кривая Лоренца».
В поле «Значения X» следует занести все данные столбца «% населения» нашей таблицы. Для этого устанавливаем курсор в область поля. Далее зажимаем левую кнопку мыши и выделяем соответствующий столбец на листе. Координаты тут же будут отображены в окне изменения ряда.
В поле «Значения Y» заносим координаты ячеек столбца «Сумма национального дохода». Делаем это по той же методике, по которой вносили данные в предыдущее поле.
После того, как все вышеуказанные данные внесены, жмем на кнопку «OK».
- После возврата к окну выбора источника опять жмем на кнопку «OK».
- Как видим, после выполнения вышеуказанных действий кривая Лоренца также отобразится на листе Excel.
Построение кривой Лоренца и линии равенства в Экселе производится на тех же принципах, что и построение любого другого вида диаграмм в этой программе. Поэтому для пользователей, которые овладели умением строить диаграммы и графики в Excel, данная задача не должна вызвать больших проблем.
Содержание
- Процедура создания графика
- Способ 1: создание графика зависимости на основе данных таблицы
- Способ 2: создание графика зависимости с несколькими линиями
- Способ 3: построение графика при использовании различных единиц измерения
- Способ 4: создание графика зависимости на основе алгебраической функции
- Вопросы и ответы
Одной из типичных математических задач является построение графика зависимости. В нем отображается зависимость функции от изменения аргумента. На бумаге выполнить данную процедуру не всегда просто. Но инструменты Excel, если в должной мере овладеть ими, позволяют выполнить данную задачу точно и относительно быстро. Давайте выясним, как это можно сделать, используя различные исходные данные.
Процедура создания графика
Зависимость функции от аргумента является типичной алгебраической зависимостью. Чаще всего аргумент и значение функции принято отображать символами: соответственно «x» и «y». Нередко нужно произвести графическое отображение зависимости аргумента и функции, которые записаны в таблицу, или представлены в составе формулы. Давайте разберем конкретные примеры построения подобного графика (диаграммы) при различных заданных условиях.
Способ 1: создание графика зависимости на основе данных таблицы
Прежде всего, разберем, как создать график зависимости на основе данных, предварительно внесенных в табличный массив. Используем таблицу зависимости пройденного пути (y) от времени (x).
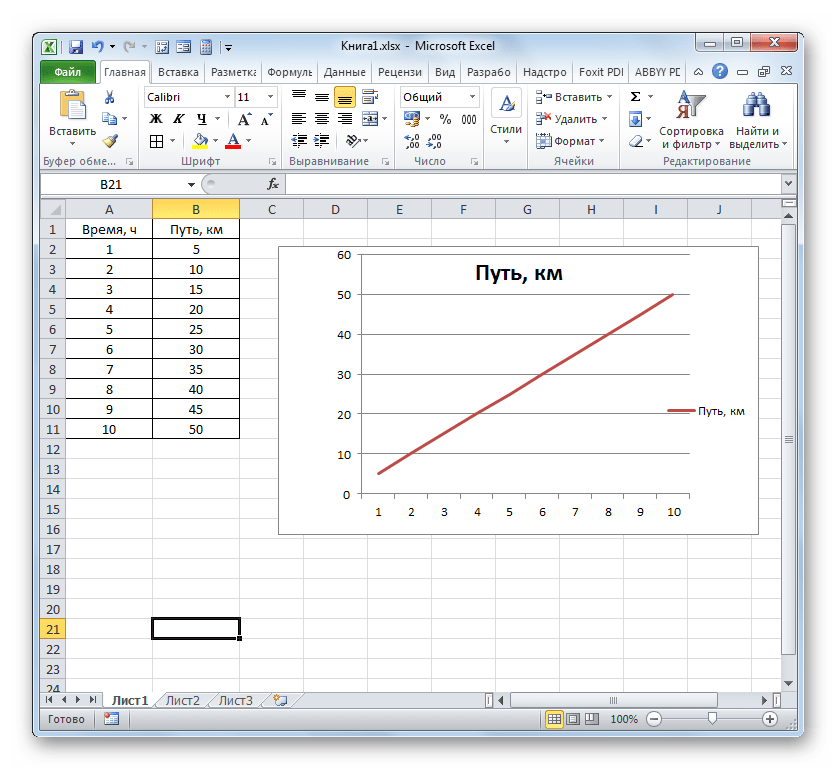
- Выделяем таблицу и переходим во вкладку «Вставка». Кликаем по кнопке «График», которая имеет локализацию в группе «Диаграммы» на ленте. Открывается выбор различных типов графиков. Для наших целей выбираем самый простой. Он располагается первым в перечне. Клацаем по нему.
- Программа производит построение диаграммы. Но, как видим, на области построения отображается две линии, в то время, как нам нужна только одна: отображающая зависимость пути от времени. Поэтому выделяем кликом левой кнопки мыши синюю линию («Время»), так как она не соответствует поставленной задаче, и щелкаем по клавише Delete.
- Выделенная линия будет удалена.
Собственно на этом построение простейшего графика зависимости можно считать завершенным. При желании также можно отредактировать наименования диаграммы, её осей, удалить легенду и произвести некоторые другие изменения. Об этом подробнее рассказывается в отдельном уроке.
Урок: Как сделать график в Экселе
Способ 2: создание графика зависимости с несколькими линиями
Более сложный вариант построения графика зависимости представляет собой случай, когда одному аргументу соответствуют сразу две функции. В этом случае потребуется построить две линии. Для примера возьмем таблицу, в которой по годам расписана общая выручка предприятия и его чистая прибыль.
- Выделяем всю таблицу вместе с шапкой.
- Как и в предыдущем случае, жмем на кнопку «График» в разделе диаграмм. Опять выбираем самый первый вариант, представленный в открывшемся списке.
- Программа производит графическое построение согласно полученным данным. Но, как видим, в данном случае у нас имеется не только лишняя третья линия, но ещё и обозначения на горизонтальной оси координат не соответствуют тем, которые требуются, а именно порядку годов.
Сразу удалим лишнюю линию. Ею является единственная прямая на данной диаграмме — «Год». Как и в предыдущем способе, выделяем линию кликом по ней мышкой и жмем на кнопку Delete.
- Линия удалена и вместе с ней, как вы можете заметить, преобразовались значения на вертикальной панели координат. Они стали более точными. Но проблема с неправильным отображением горизонтальной оси координат все-таки остается. Для решения данной проблемы кликаем по области построения правой кнопкой мыши. В меню следует остановить выбор на позиции «Выбрать данные…».
- Открывается окошко выбора источника. В блоке «Подписи горизонтальной оси» кликаем по кнопке «Изменить».
- Открывается окошко ещё меньше предыдущего. В нём нужно указать координаты в таблице тех значений, которые должны отображаться на оси. С этой целью устанавливаем курсор в единственное поле данного окна. Затем зажимаем левую кнопку мыши и выделяем всё содержимое столбца «Год», кроме его наименования. Адрес тотчас отразится в поле, жмем «OK».
- Вернувшись в окно выбора источника данных, тоже щелкаем «OK».
- После этого оба графика, размещенные на листе, отображаются корректно.
Способ 3: построение графика при использовании различных единиц измерения
В предыдущем способе мы рассмотрели построение диаграммы с несколькими линиями на одной плоскости, но при этом все функции имели одинаковые единицы измерения (тыс. руб.). Что же делать, если нужно создать графики зависимости на основе одной таблицы, у которых единицы измерения функции отличаются? В Экселе существует выход и из этого положения.
Имеем таблицу, в которой представлены данные по объему продаж определенного товара в тоннах и по выручке от его реализации в тысячах рублей.
- Как и в предыдущих случаях выделяем все данные табличного массива вместе с шапкой.
- Клацаем по кнопке «График». Снова выбираем первый вариант построения из перечня.
- Набор графических элементов сформирован на области построения. Тем же способом, который был описан в предыдущих вариантах, убираем лишнюю линию «Год».
- Как и в предыдущем способе, нам следует на горизонтальной панели координат отобразить года. Кликаем по области построения и в списке действий выбираем вариант «Выбрать данные…».
- В новом окне совершаем щелчок по кнопке «Изменить» в блоке «Подписи» горизонтальной оси.
- В следующем окне, производя те же действия, которые были подробно описаны в предыдущем способе, вносим координаты столбца «Год» в область «Диапазон подписей оси». Щелкаем по «OK».
- При возврате в предыдущее окно также выполняем щелчок по кнопке «OK».
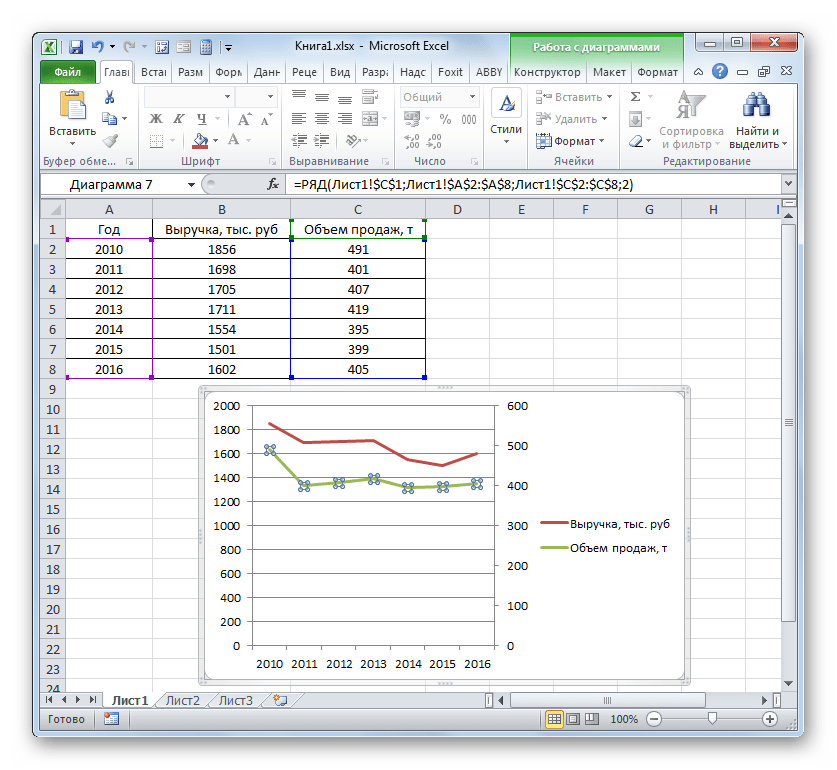
- Теперь нам следует решить проблему, с которой ещё не встречались в предыдущих случаях построения, а именно, проблему несоответствия единиц величин. Ведь, согласитесь, не могут располагаться на одной панели координат деления, которые одновременно обозначают и денежную сумму (тыс. рублей) и массу (тонны). Для решения данной проблемы нам потребуется произвести построение дополнительной вертикальной оси координат.
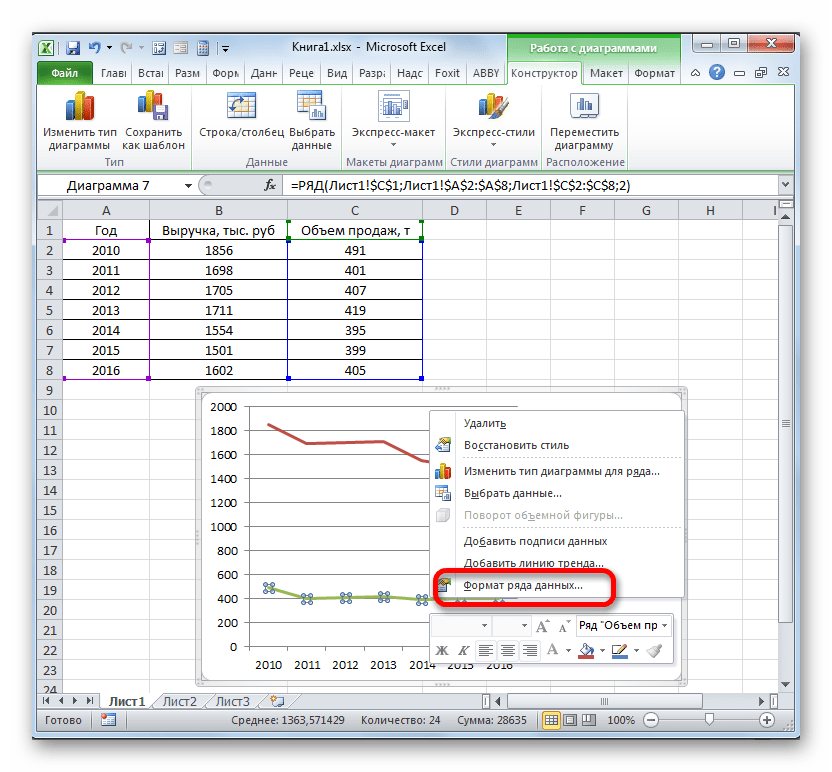
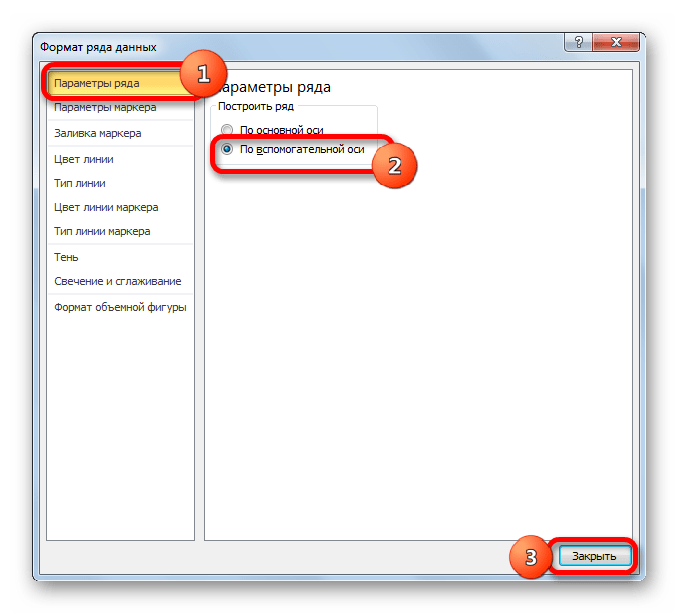
В нашем случае для обозначения выручки оставим ту вертикальную ось, которая уже имеется, а для линии «Объём продаж» создадим вспомогательную. Клацаем по данной линии правой кнопкой мышки и выбираем из перечня вариант «Формат ряда данных…».
- Запускается окно формата ряда данных. Нам нужно переместиться в раздел «Параметры ряда», если оно было открыто в другом разделе. В правой части окна расположен блок «Построить ряд». Требуется установить переключатель в позицию «По вспомогательной оси». Клацаем по наименованию «Закрыть».
- После этого вспомогательная вертикальная ось будет построена, а линия «Объём продаж» переориентируется на её координаты. Таким образом, работа над поставленной задачей успешно окончена.
Способ 4: создание графика зависимости на основе алгебраической функции
Теперь давайте рассмотрим вариант построения графика зависимости, который будет задан алгебраической функцией.
У нас имеется следующая функция: y=3x^2+2x-15. На её основе следует построить график зависимости значений y от x.
- Прежде, чем приступить к построению диаграммы, нам нужно будет составить таблицу на основе указанной функции. Значения аргумента (x) в нашей таблице будут указаны в диапазоне от -15 до +30 с шагом 3. Чтобы ускорить процедуру введения данных, прибегнем к использованию инструмента автозаполнения «Прогрессия».
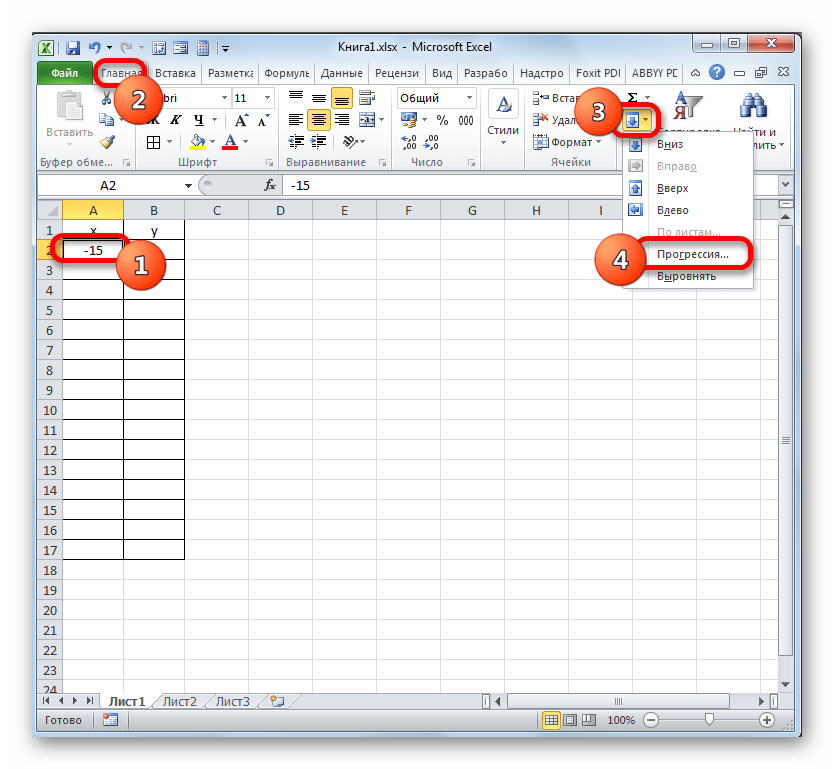
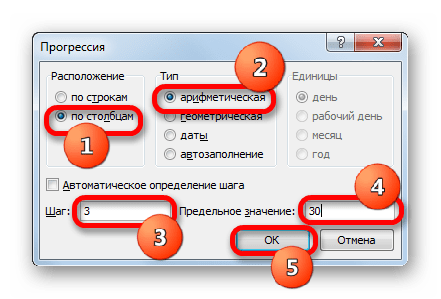
Указываем в первой ячейке столбца «X» значение «-15» и выделяем её. Во вкладке «Главная» клацаем по кнопке «Заполнить», размещенной в блоке «Редактирование». В списке выбираем вариант «Прогрессия…».
- Выполняется активация окна «Прогрессия». В блоке «Расположение» отмечаем наименование «По столбцам», так как нам необходимо заполнить именно столбец. В группе «Тип» оставляем значение «Арифметическая», которое установлено по умолчанию. В области «Шаг» следует установить значение «3». В области «Предельное значение» ставим цифру «30». Выполняем щелчок по «OK».
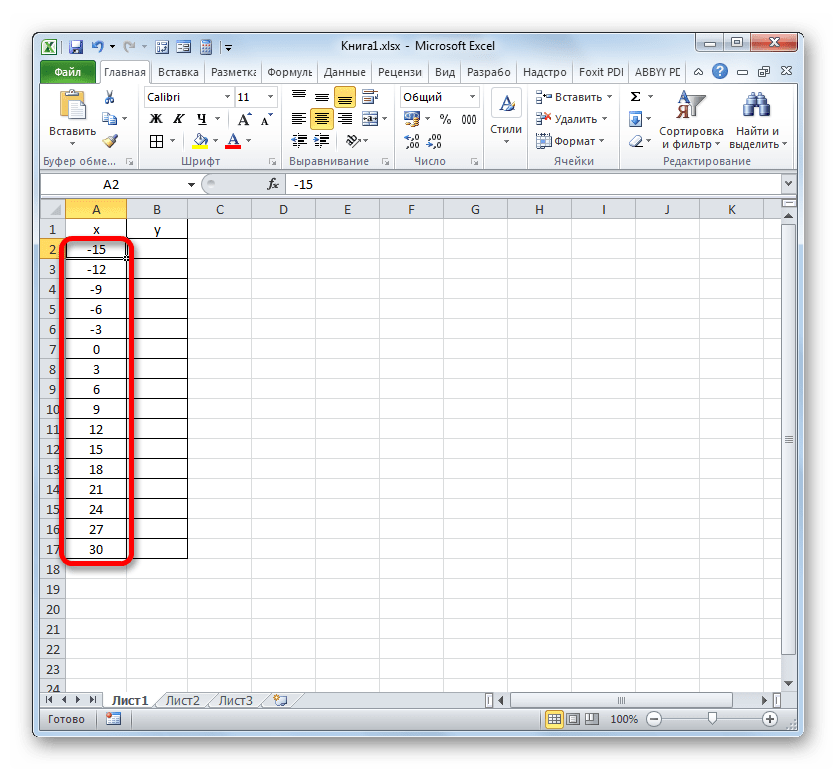
- После выполнения данного алгоритма действий весь столбец «X» будет заполнен значениями в соответствии с заданной схемой.
- Теперь нам нужно задать значения Y, которые бы соответствовали определенным значениям X. Итак, напомним, что мы имеем формулу y=3x^2+2x-15. Нужно её преобразовать в формулу Excel, в которой значения X будут заменены ссылками на ячейки таблицы, содержащие соответствующие аргументы.
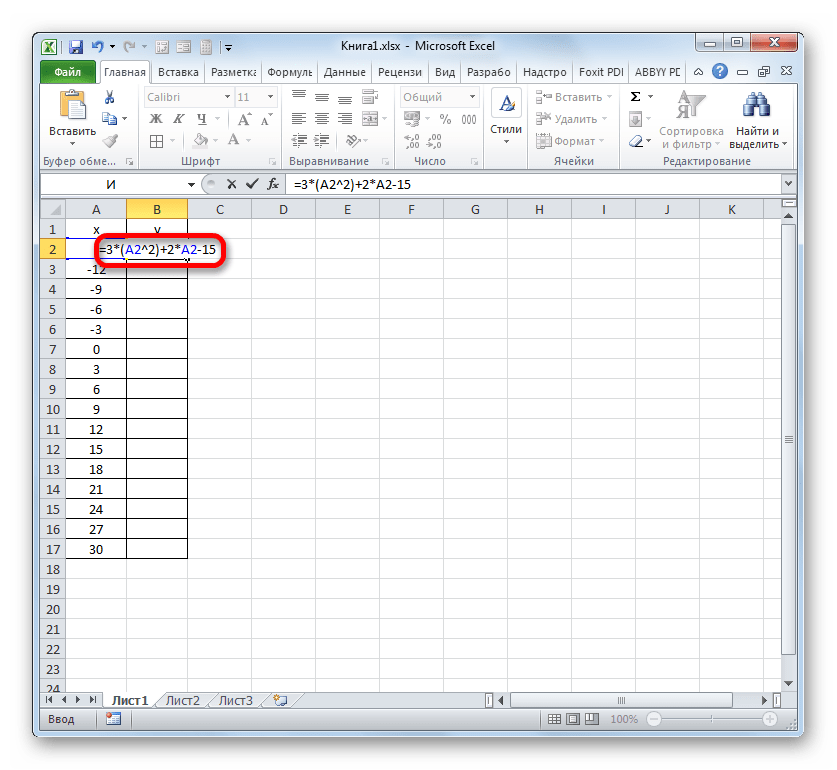
Выделяем первую ячейку в столбце «Y». Учитывая, что в нашем случае адрес первого аргумента X представлен координатами A2, то вместо представленной выше формулы получаем такое выражение:
=3*(A2^2)+2*A2-15Записываем это выражение в первую ячейку столбца «Y». Для получения результата расчета щелкаем по клавише Enter.
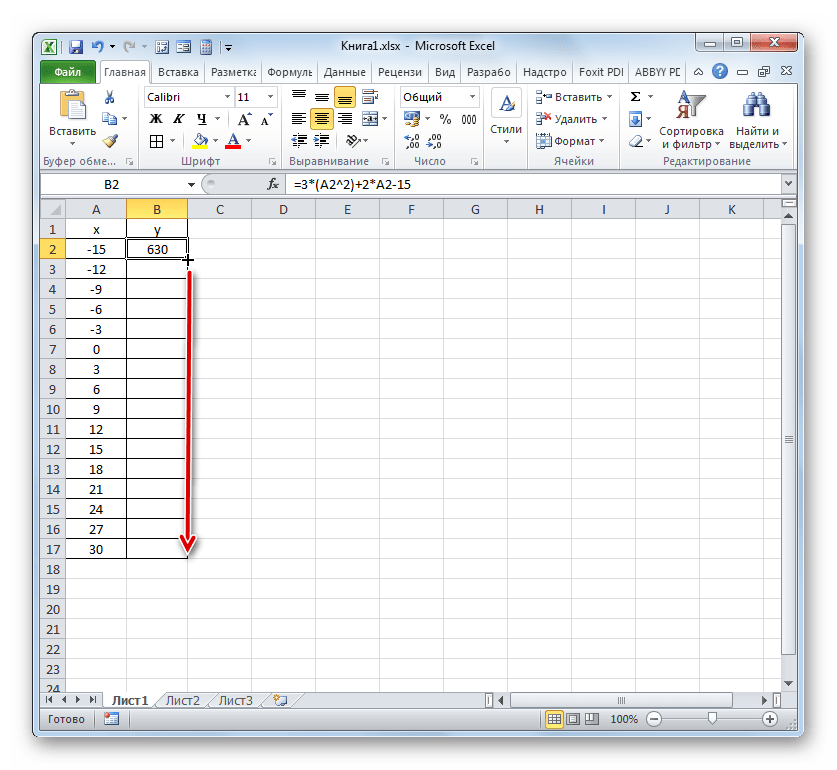
- Результат функции для первого аргумента формулы рассчитан. Но нам нужно рассчитать её значения и для других аргументов таблицы. Вводить формулу для каждого значения Y очень долгое и утомительное занятие. Намного быстрее и проще её скопировать. Эту задачу можно решить с помощью маркера заполнения и благодаря такому свойству ссылок в Excel, как их относительность. При копировании формулы на другие диапазоны Y значения X в формуле будут автоматически изменяться относительно своих первичных координат.
Наводим курсор на нижний правый край элемента, в который ранее была записана формула. При этом с курсором должно произойти преображение. Он станет черным крестиком, который носит наименование маркера заполнения. Зажимаем левую кнопку мыши и тащим этот маркер до нижних границ таблицы в столбце «Y».
- Вышеуказанное действие привело к тому, что столбец «Y» был полностью заполнен результатами расчета формулы y=3x^2+2x-15.
- Теперь настало время для построения непосредственно самой диаграммы. Выделяем все табличные данные. Снова во вкладке «Вставка» жмем на кнопку «График» группы «Диаграммы». В этом случае давайте из перечня вариантов выберем «График с маркерами».
- Диаграмма с маркерами отобразится на области построения. Но, как и в предшествующих случаях, нам потребуется произвести некоторые изменения для того, чтобы она приобрела корректный вид.
- Прежде всего, удалим линию «X», которая разместилась горизонтально на отметке 0 координат. Выделяем данный объект и жмем на кнопку Delete.
- Легенда нам тоже не нужна, так как мы имеем только одну линию («Y»). Поэтому выделяем легенду и снова жмем по клавише Delete.
- Теперь нам нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «X» в таблице.
Кликом правой кнопки мыши выделяем линию диаграммы. В меню перемещаемся по значению «Выбрать данные…».
- В активировавшемся окне выбора источника клацаем по уже хорошо знакомой нам кнопке «Изменить», располагающейся в блоке «Подписи горизонтальной оси».
- Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «X». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».
- Вернувшись к окну выбора источника данных, клацаем по кнопке «OK» в нём, как до этого сделали в предыдущем окне.
- После этого программа произведет редактирование ранее построенной диаграммы согласно тем изменениям, которые были произведены в настройках. График зависимости на основе алгебраической функции можно считать окончательно готовым.
Урок: Как сделать автозаполнение в Майкрософт Эксель
Как видим, с помощью программы Excel процедура построения графика зависимости значительно упрощается в сравнении с созданием его на бумаге. Результат построения можно использовать как для обучающих работ, так и непосредственно в практических целей. Конкретный вариант построения зависит от того, на основе чего строится диаграмма: табличные значения или функция. Во втором случае перед построением диаграммы придется ещё создавать таблицу с аргументами и значениями функций. Кроме того, график может быть построен, как на основе одной функции, так и нескольких.
Еще статьи по данной теме:
Помогла ли Вам статья?
Тип урока: Обобщение, закрепление
пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического
способа решения уравнений; - закрепление навыков записи и
копирования формул, построения графиков
функций в электронных таблицах Excel 2007; - формирование и первичное закрепление
знаний о решении уравнений с
использованием возможностей электронных
таблиц Excel 2007; - формирование мышления, направленного на
выбор оптимального решения; - формирование информационной культуры
школьников.
Оборудование: персональные
компьютеры, мультимедиапроектор,
проекционный экран.
Материалы к уроку: презентация Power Point
на компьютере учителя (Приложение 1).
Ход урока
Организационный момент.
Слайд 1 из Приложения1 ( далее
ссылки на слайды идут без указания
Приложения1).
Объявление темы урока.
1. Устная работа (актуализация
знаний).
Слайд 2 — Соотнесите перечисленные
ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3)2; у = -(х — 4)2;
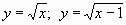
Рис. 1.
Слайд 3 Графический способ решения
уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются
значения х1, х2, … точек
пересечения графика функции y=f(x) с осью
абсцисс (Рис. 2).
Рис. 2.
Слайд 4
Найдите корни уравнения х2-2х-3=0,
используя графический способ решения
уравнений (Рис.3).
Ответ: -1; 3.
Рис. 3.
Слайд 5 Графический способ решения
уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются
значения х1, х2, … точек
пересечения графиков функций y=f(x) и у=g(x).
(Рис. 4):
Рис. 4.
Слайд 6 Найдите корни уравнения 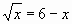
используя графический способ решения
уравнений (Рис. 5).
Ответ: 4.
Рис. 5.
2. Объяснение нового материала.
Практическая работа.
Решение уравнений графическим способом
требует больших временных затрат на
построение графиков функций и в
большинстве случаев дает грубо
приближенные решения. При использовании
электронных таблиц, в данном случае – Microsoft
Excel 2007, существенно экономится время на
построение графиков функций, и появляются
дополнительные возможности нахождения
корней уравнения с заданной точностью (метод
Подбор параметра).
I. Графический способ решения
уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в
Excel одновременно с учениками с подробными (при
необходимости) инструкциями и выводом
результатов на проекционный экран. Слайды
Приложения 1 используются для формулировки
задач и подведения промежуточных итогов.
Слайд 7
Пример1: Используя средства построения
диаграмм в Excel, решить графическим способом
уравнение —х2+5х-4=0.
Для этого: построить график функции у=-х2+5х-4
на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения
графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в
табличной форме (рис. 6):
Рис. 6.
Для этого:
- в ячейку А1 ввести текст Х, в
ячейку A2 — Y; - в ячейку В1 ввести число 0, в ячейку С1
– число 0,25; - выделить ячейки В1:С1, подвести
указатель мыши к маркеру выделения, и в
тот момент, когда указатель мыши примет
форму черного крестика, протянуть маркер
выделения вправо до ячейки V1 (Рис. 7).
Рис. 7.
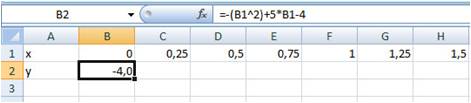
- в ячейку B2 ввести формулу =-(B1^2)+5*B1-4;
При вводе формулы можно
вводить адрес ячейки с клавиатуры (не
забыть переключиться на латиницу), а
можно просто щелкнуть мышью на ячейке с
нужным адресом.
После ввода формулы в ячейке
окажется результат вычисления по
формуле, а в поле ввода строки формул —
сама формула (Рис. 8):
Рис. 8.
- скопировать содержимое ячейки B2 в
ячейки C2:V2 за маркер выделения. Весь
ряд выделенных ячеек заполнится
содержимым первой ячейки. При этом ссылки
на ячейки в формулах изменятся
относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
Для этого:
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График
выбрать вид График; - на вкладке Конструктор|Выбрать данные
(Рис. 9) в открывшемся окне «Выбор
источника данных» щелкнуть по кнопке Изменить
в поле Подписи горизонтальной оси —
откроется окно «Подписи оси». Выделить в
таблице диапазон ячеек B1:V1 (значения
переменной х). В обоих окнах щелкнуть
по кнопкам ОК;
Рис. 9.
- на вкладке Макет|Оси|Основная
горизонтальная ось|Дополнительные
параметры основной горизонтальной оси
выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица
измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки
Тип
линии и Цвет линии);
- самостоятельно изменить ширину и цвет
линии для вертикальной оси; - на вкладке Макет|Сетка|Вертикальные
линии сетки по основной оси выбрать Основные
линии сетки.
Примерный результат работы приведен на
рис. 10:
Рис. 10.
3 этап: Определение корней уравнения.
График функции у=-х2+5х-4
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня: х1=1; х2=4.
II. Графический способ решения уравнений
вида f(x)=g(x) в Excel.
Слайд 8
Пример 2: Решить графическим способом
уравнение 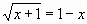
Для этого: в одной системе координат
построить графики функций у1=
и у2=1-х
на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки
пересечения графиков функций.
1 этап: Представление функций в
табличной форме (рис. 1):
- Перейти на Лист2.
- Аналогично Примеру 1, применив
приемы копирования, заполнить таблицу.
При табулировании функции у1=
воспользоваться встроенной функцией Корень
(Рис. 11).
Рис. 11.
2 этап: Построение диаграммы типа График.
- Выделить диапазон ячеек (А2:V3);
- Аналогично Примеру 1 вставить и
отформатировать диаграмму типа График,
выбрав дополнительно в настройках
горизонтальной оси: вертикальная ось
пересекает в категории с номером 5.
Примерный результат работы приведен на
Рис. 12:
Рис. 12.
3 этап: Определение корней уравнения.
Графики функций у1=
и у2=1-х пересекаются в одной
точке (0;1) и, следовательно, уравнение
имеет один корень – абсцисса этой точки: х=0.
III. Метод Подбор параметра.
Слайд 9
Графический способ решения уравнений
красив, но далеко не всегда точки
пересечения могут быть такими «хорошими»,
как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц
позволяют находить приближенные значения
коней уравнения с заданной точностью. Для
этого используется метод Подбор
параметра.
Слайд 10
Пример 3: Разберем метод Подбор
параметра на примере решения уравнения —х2+5х-3=0.
1 этап: Построение диаграммы типа График
для приближенного определения корней
уравнения.
Построить график функции у=—х2+5х-3,
отредактировав полученные в Примере 1
формулы.
Для этого:
- выполнить двойной щелчок по ячейке B2,
внести необходимые изменения; - с помощью маркера выделения
скопировать формулу во все ячейки
диапазона C2:V2.
Все изменения сразу отобразятся на
графике.
Примерный результат работы приведен на
Рис. 13:
Рис. 13.
2 этап: Определение приближенных
значений корней уравнения.
График функции у=-х2+5х-3
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня.
По графику приближенно можно
определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения
уравнения с заданной точностью методом Подбор
параметра.
1) Начать с поиска более точного
значения меньшего корня.
По графику видно, что ближайший
аргумент к точке пересечения графика с
осью абсцисс равен 0,75. В таблице
значений функции этот аргумент
размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор
параметра…;
В открывшемся диалоговом окне Подбор
параметра (Рис. 14) в поле Значение
ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки:
ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
Рис. 14.
Рис. 15.
- В окне Результат подбора (Рис. 15)
выводится информация о величине
подбираемого и подобранного значения
функции: - В ячейке E1 выводится подобранное
значение аргумента 0,6972 с требуемой
точностью (0,0001).
Установить точность можно путем
установки в ячейках таблицы точности
представления чисел – числа знаков
после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения
определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение
большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для
решения уравнений вида f(x)=g(x).
При использовании метода Подбор
параметров для решения уравнений вида f(x)=g(x)
вводят вспомогательную функцию y(x)=f(x)-g(x)
и находят с требуемой точностью значения х
точек пересечения графика функции y(x) с
осью абсцисс.
3. Закрепление изученного материала. Самостоятельная
работа.
Слайд 11
Задание: Используя метода Подбор
параметров, найти корни уравнения
с точностью до 0,001.
Для этого:
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с
шагом 0,25 (Рис. 16):
Рис. 16.
- найти приближенное значение х
точки пересечения графика функции с
осью абсцисс (х≈1,4); - найти приближенное решение уравнения с
точностью до 0,001 методом Подбор
параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной
работы.
Слайд 13 Повторение графического
способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического
способа решения уравнения вида f(x)=g(x).
Выставление оценок.
5. Домашнее задание.
Слайд 15 .
Используя средства построения диаграмм
в Excel и метод Подбор параметра, определите
корни уравнения х2-5х+2=0 с
точностью до 0,01.
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
В итоге получим диаграмму.
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!







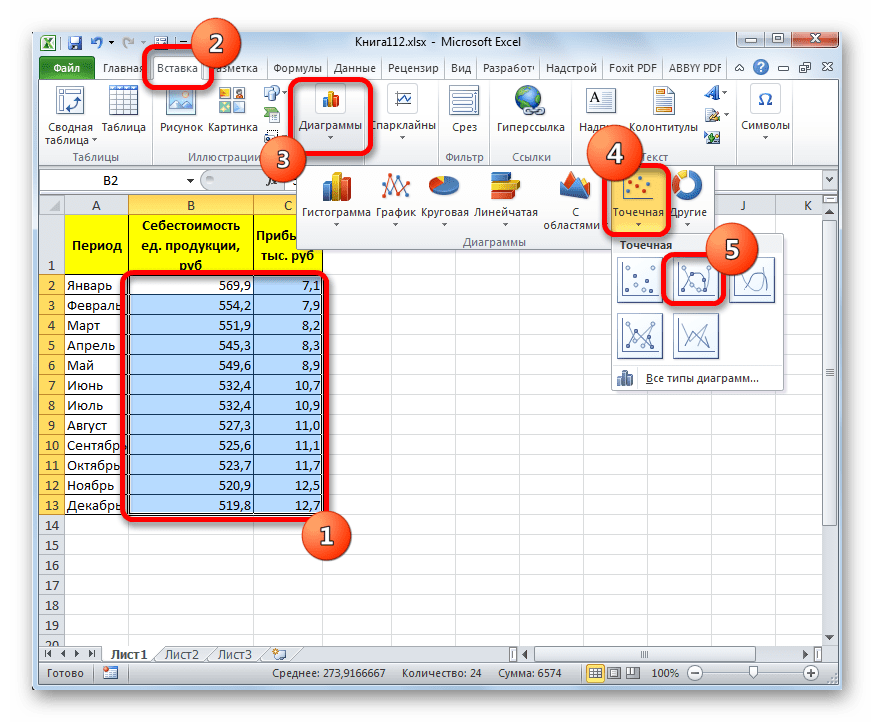
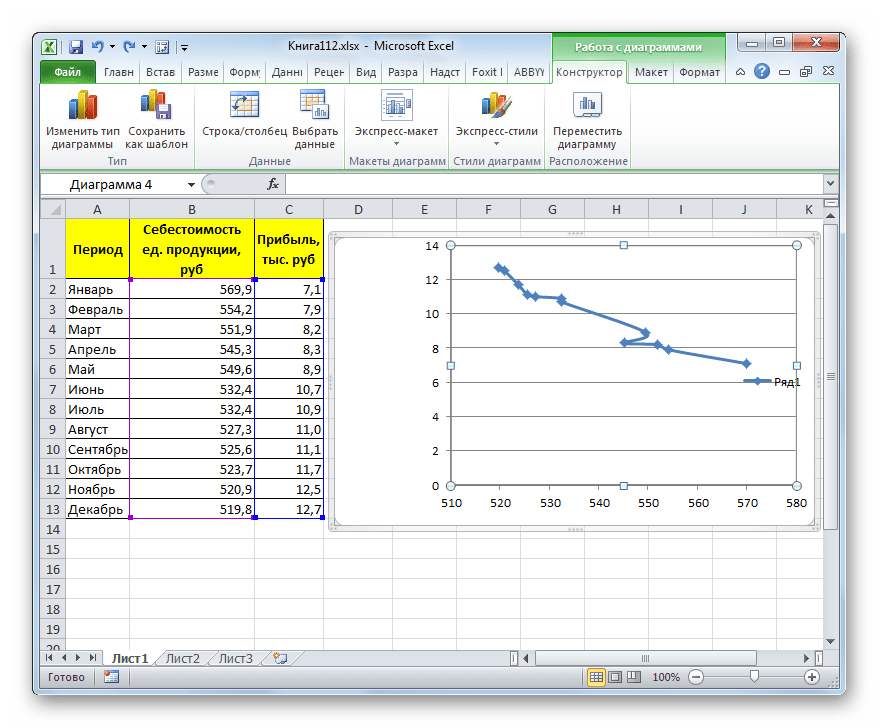
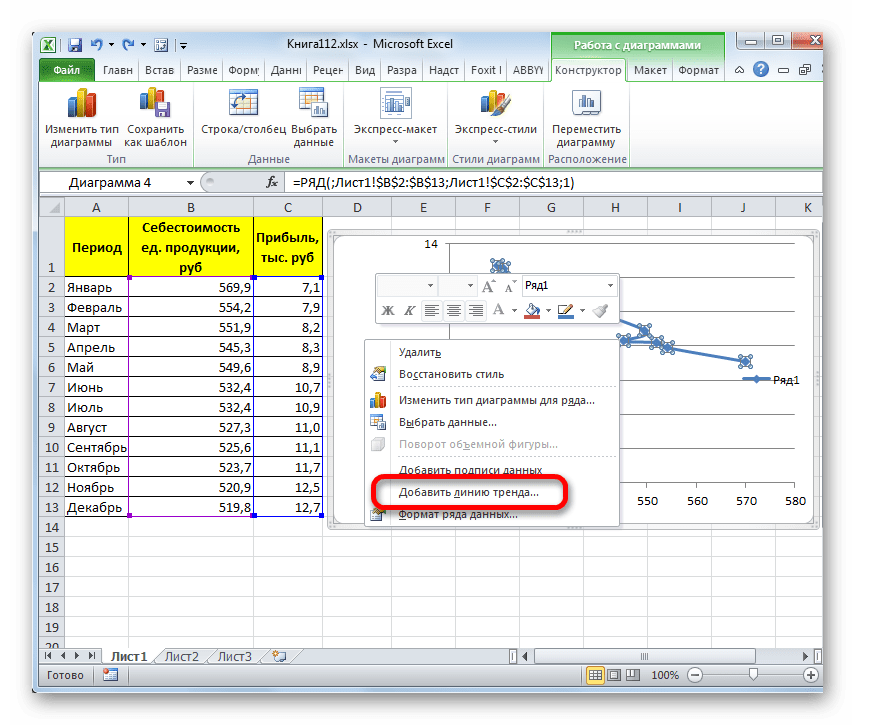
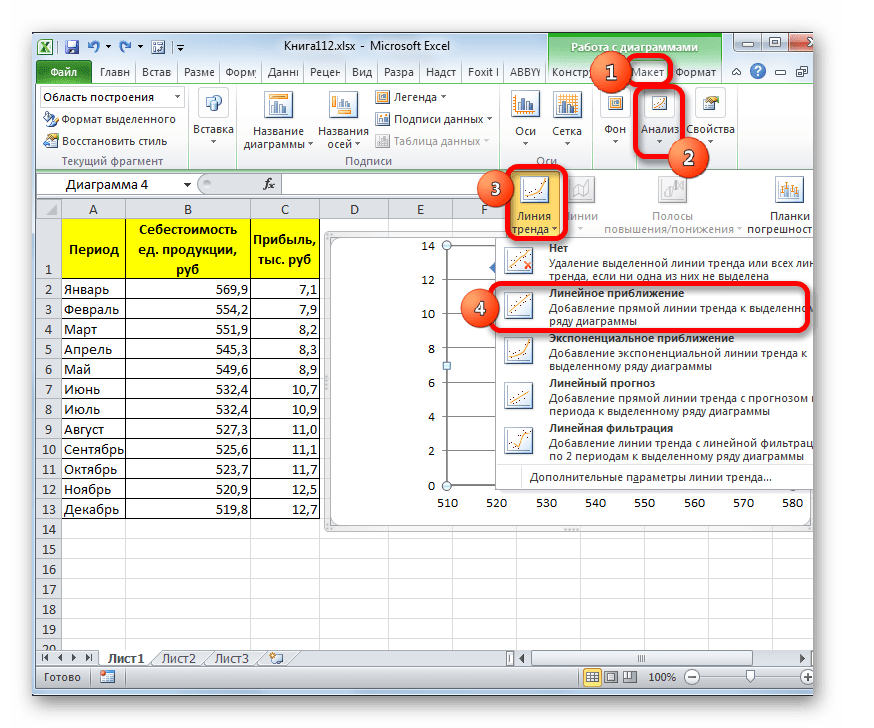
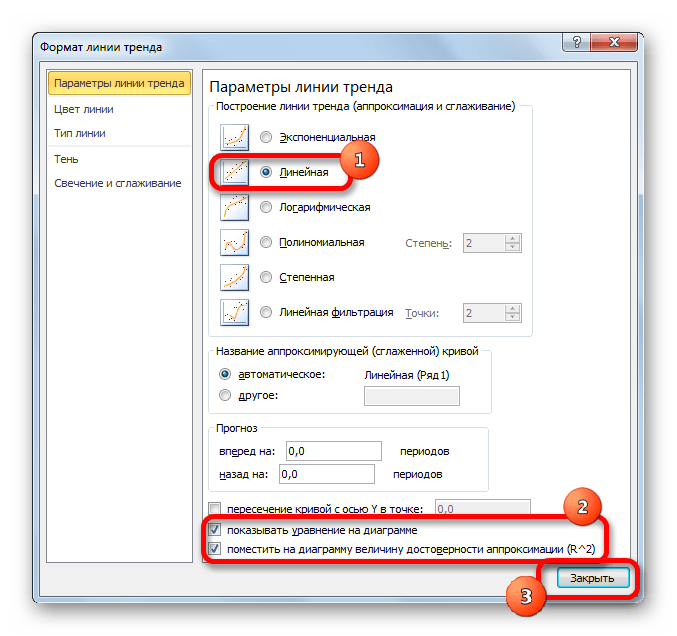
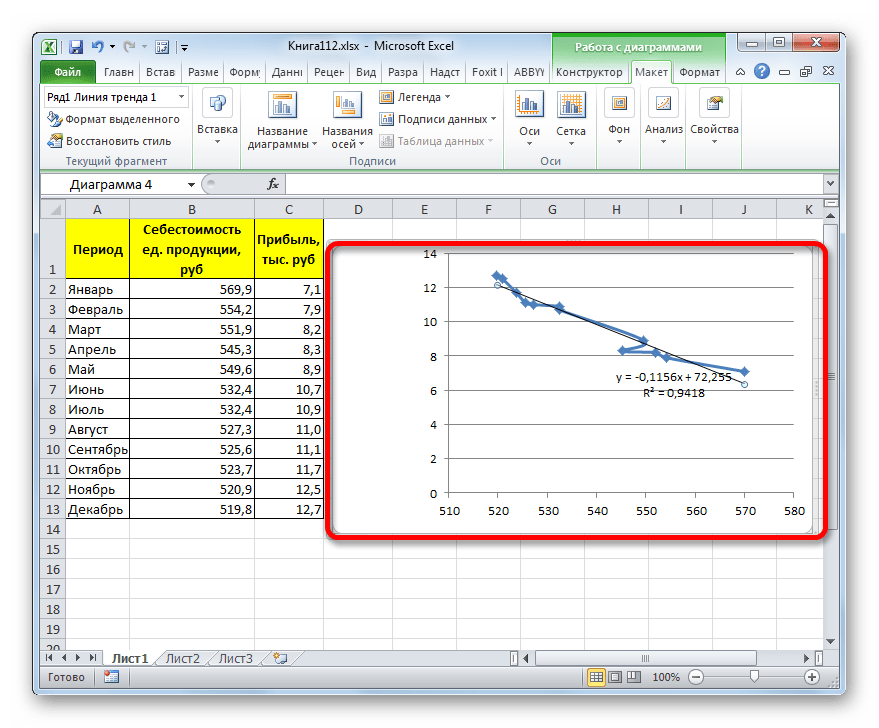
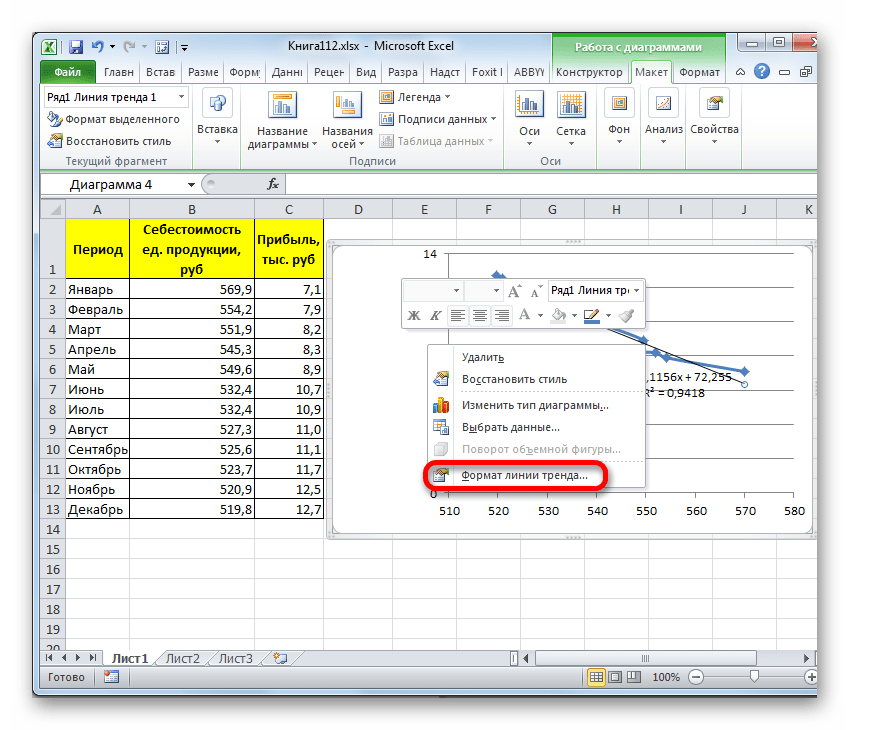
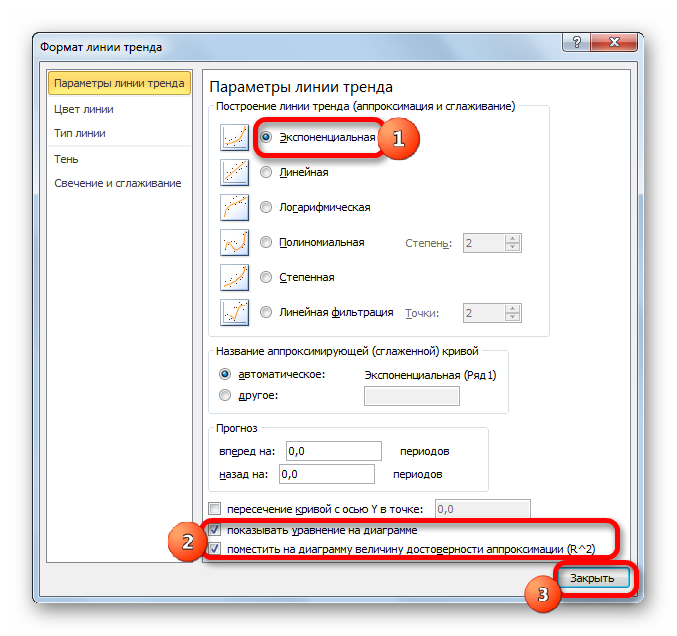
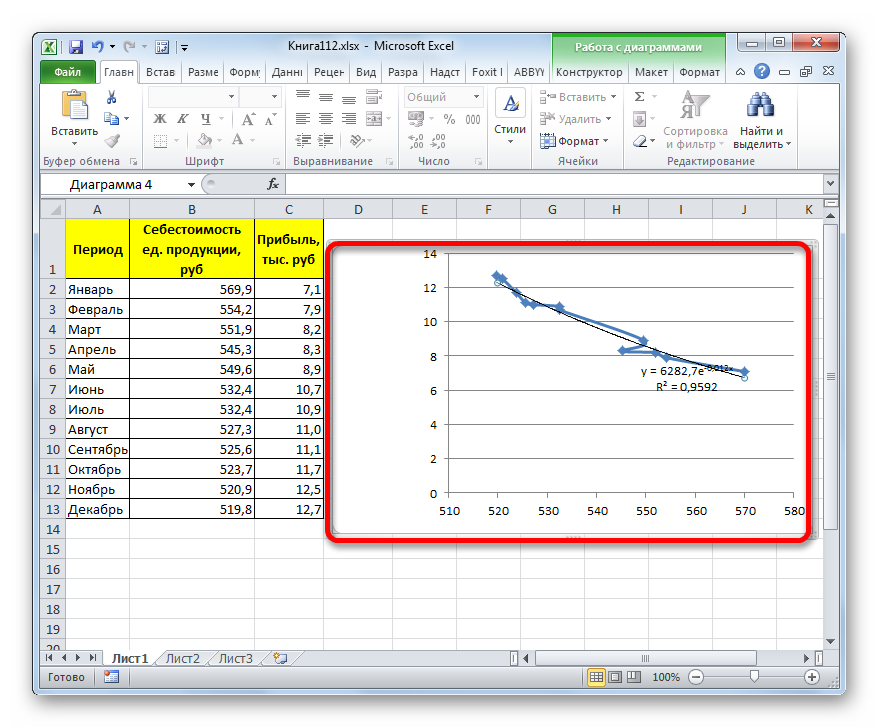
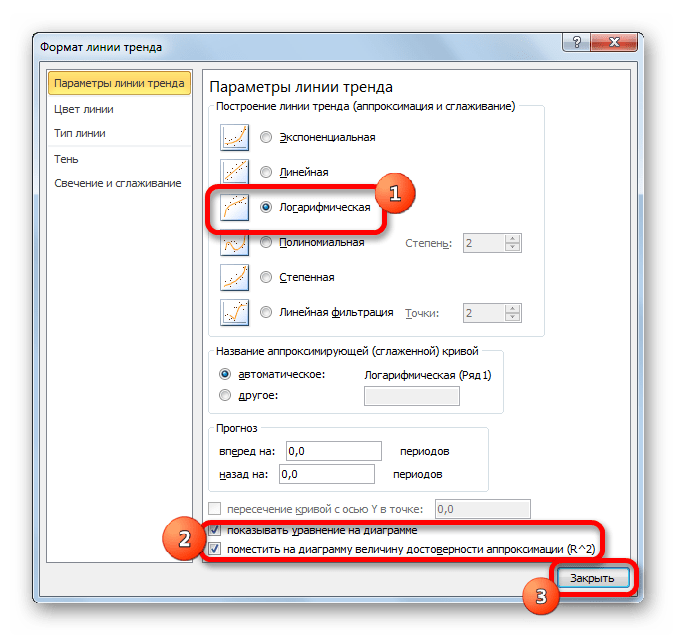
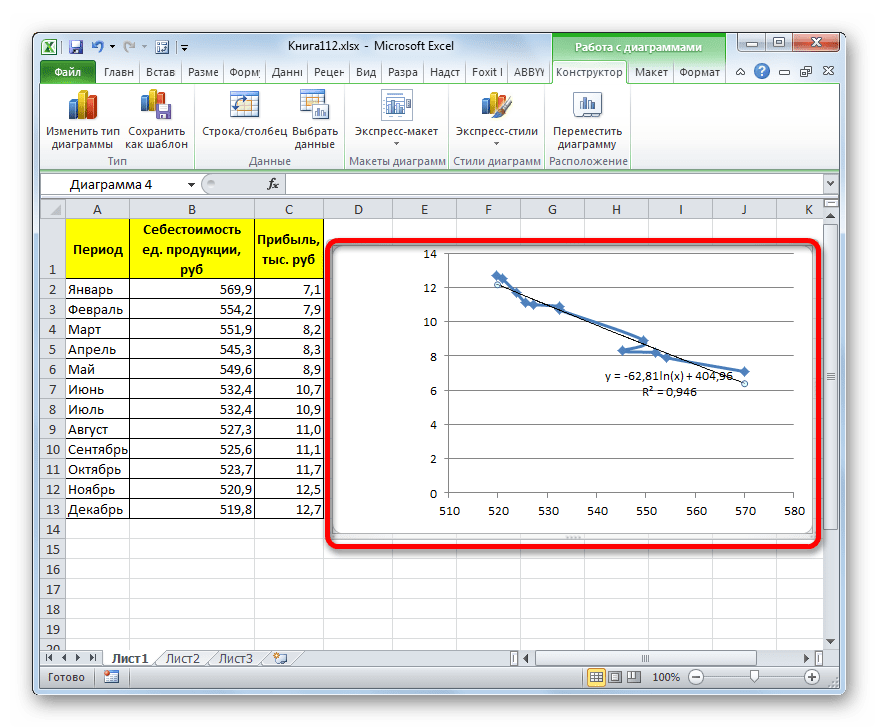
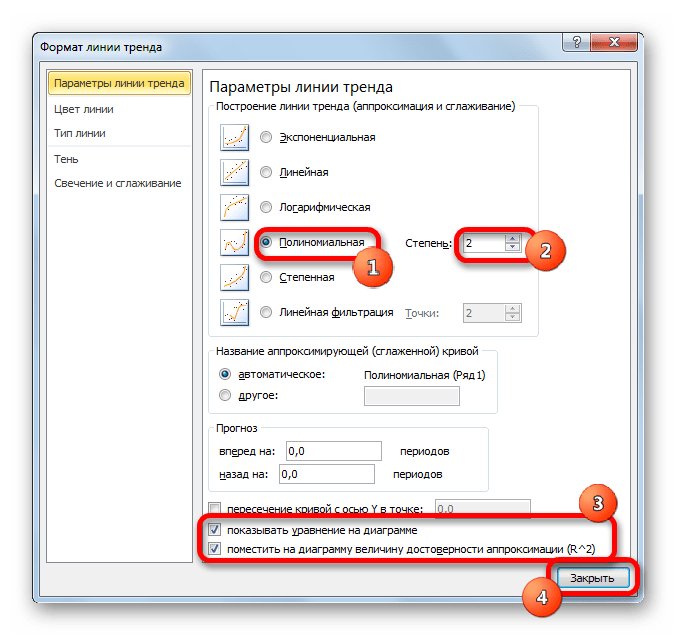
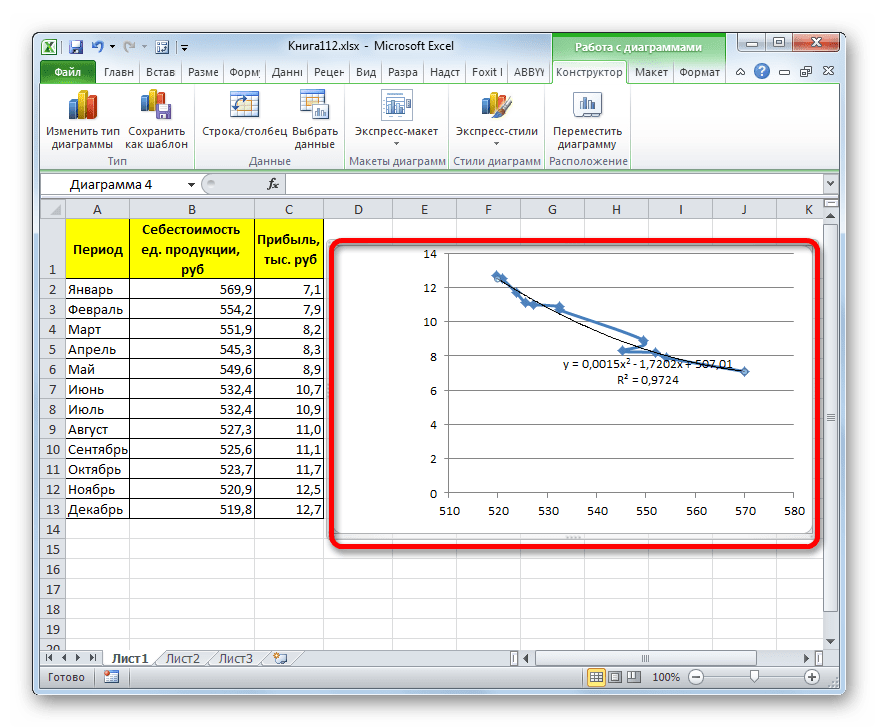
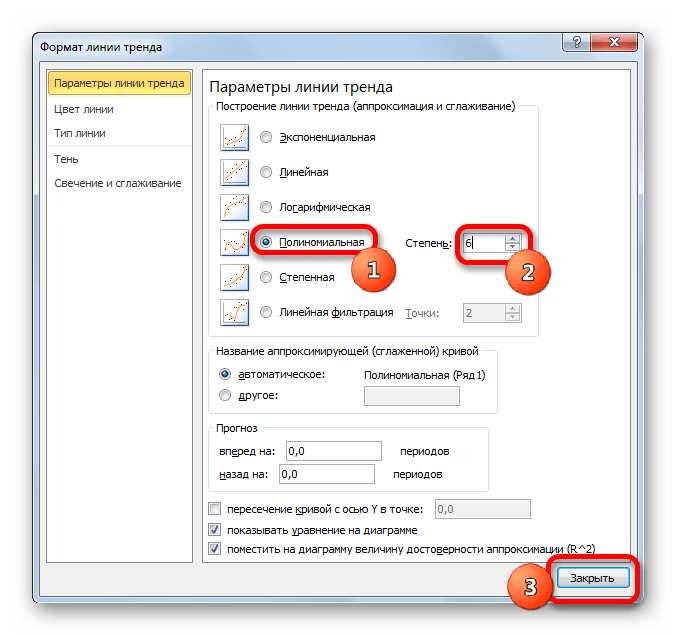
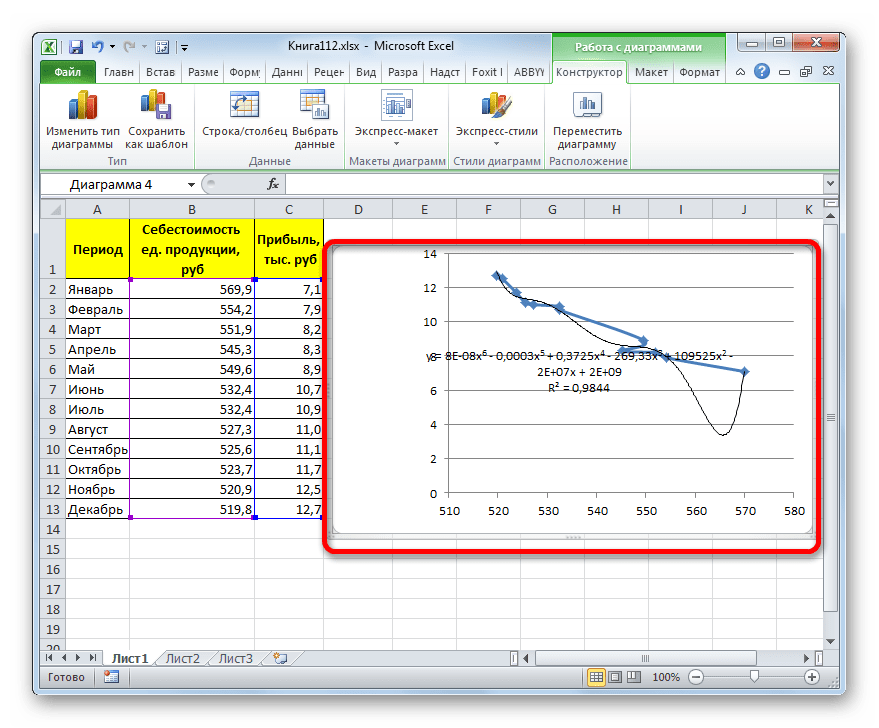
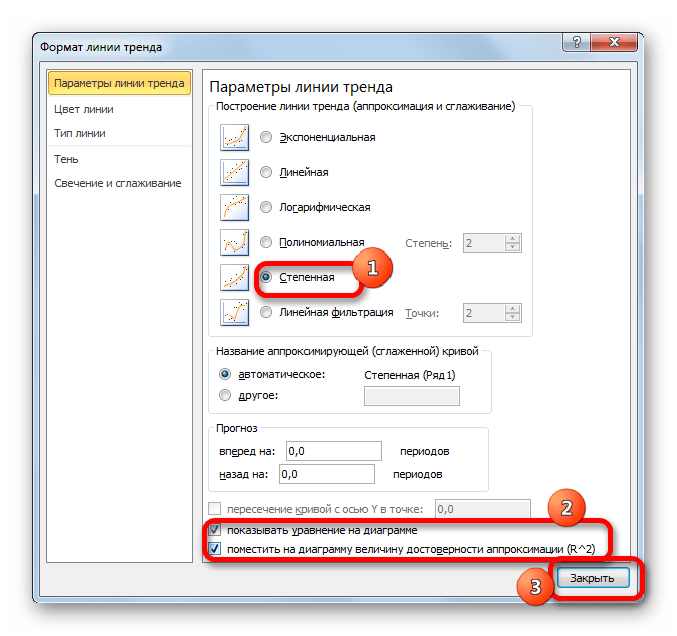
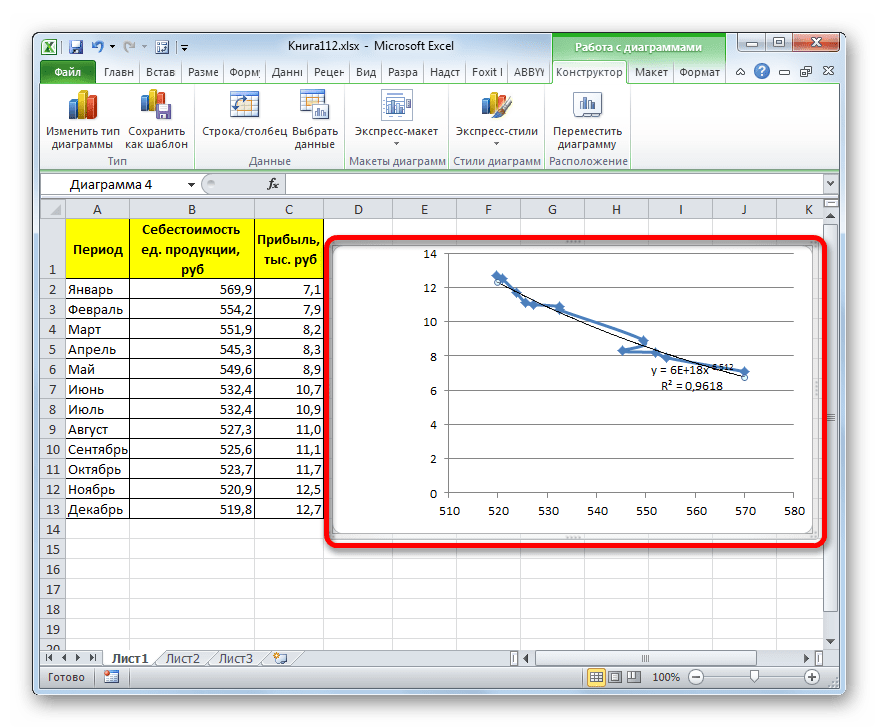








































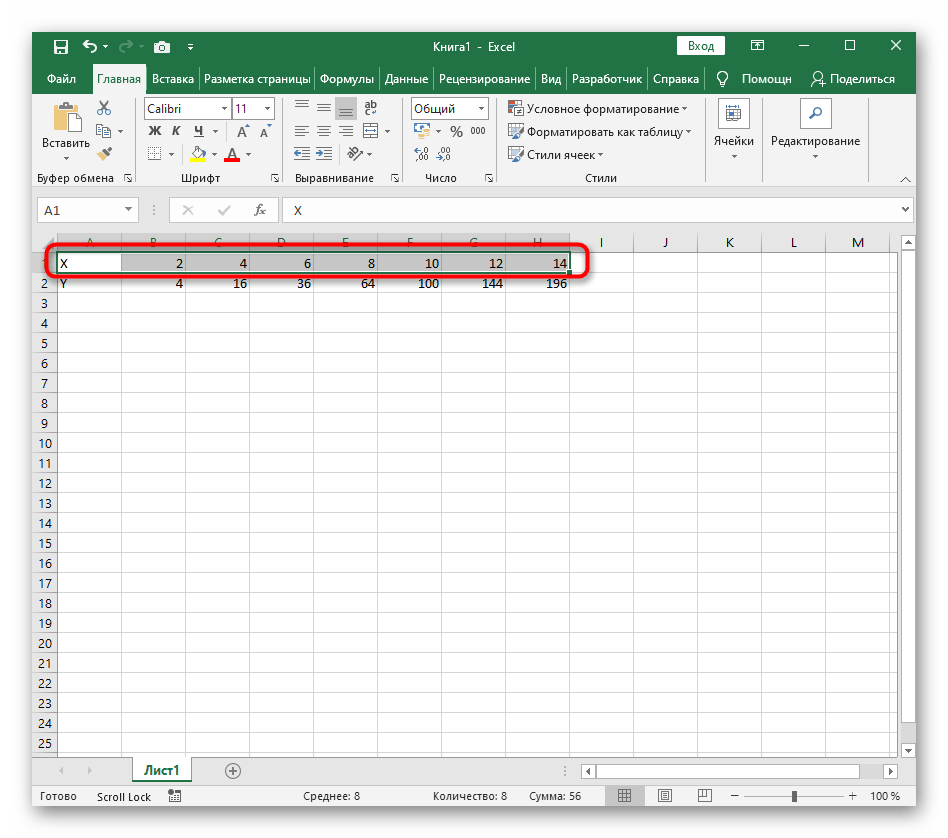

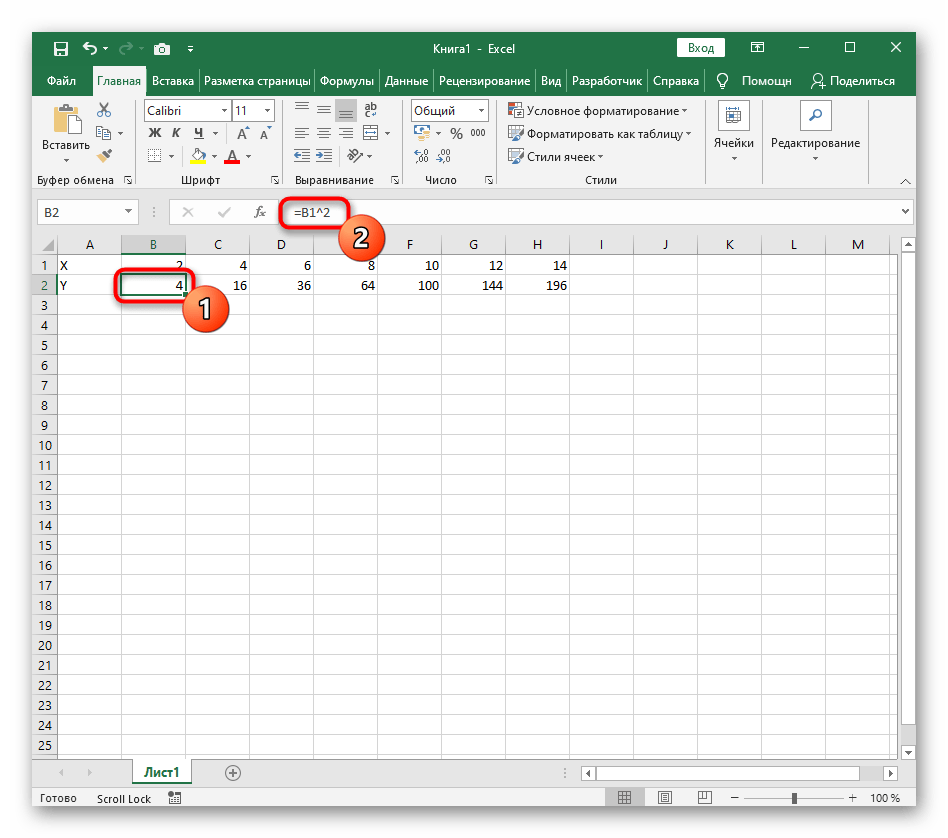
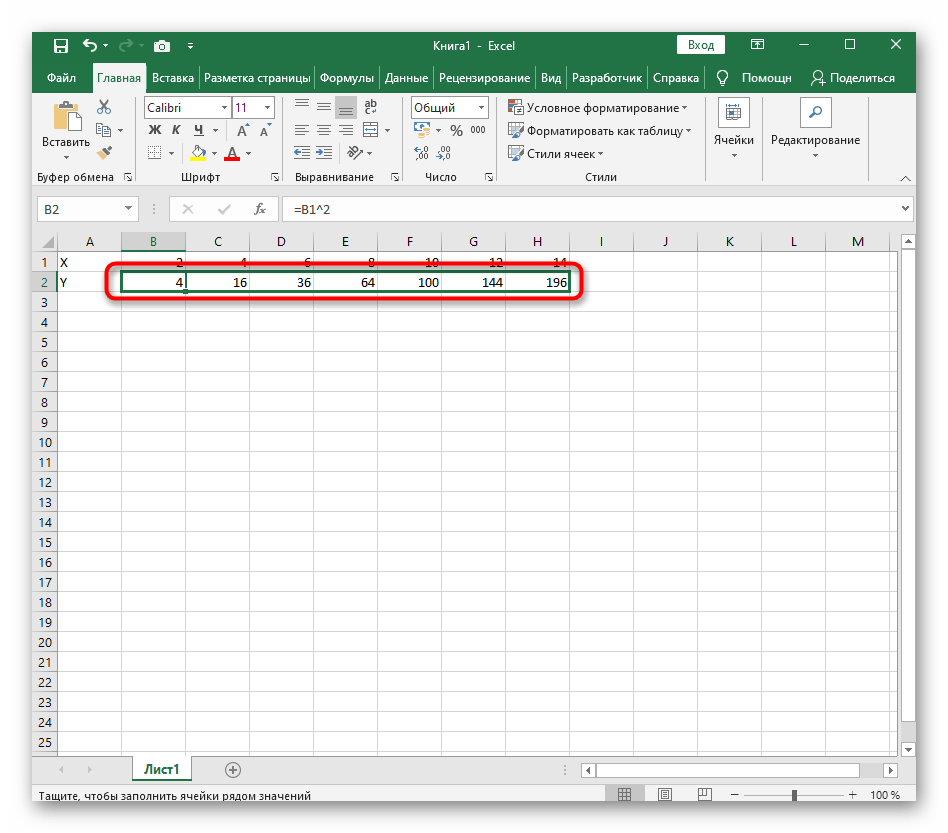




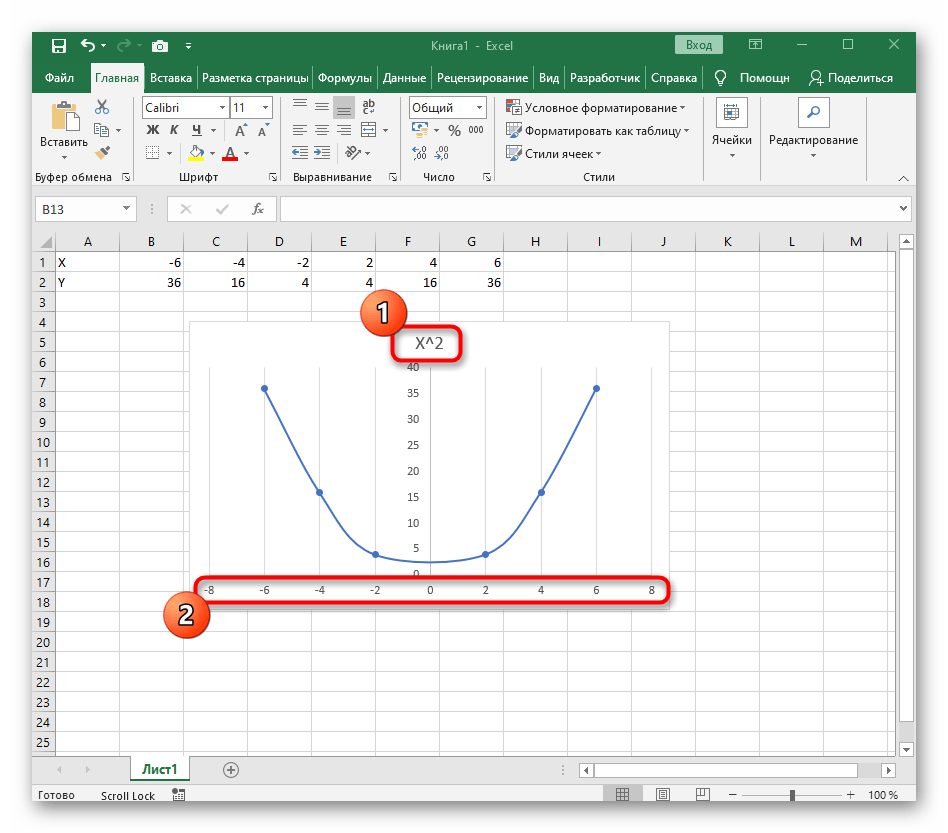
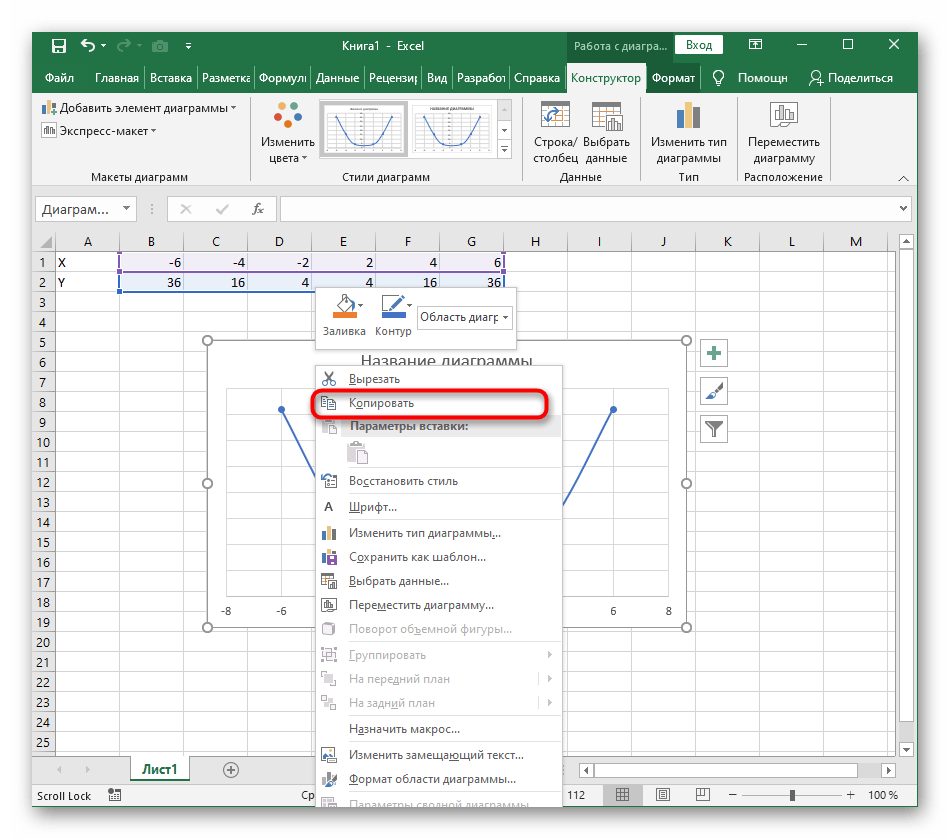
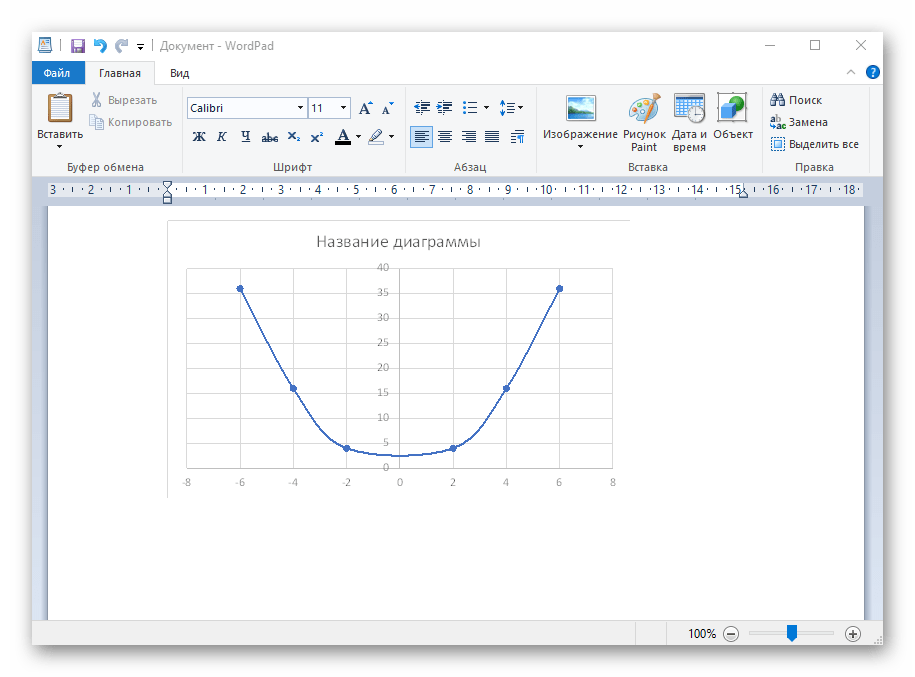

























 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):