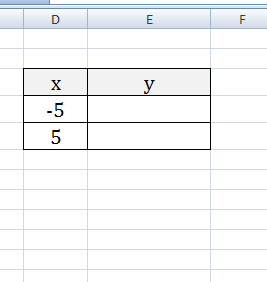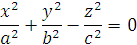Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
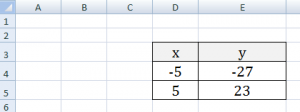
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке . Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
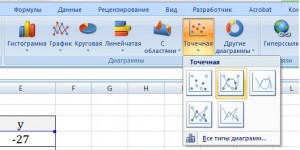
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
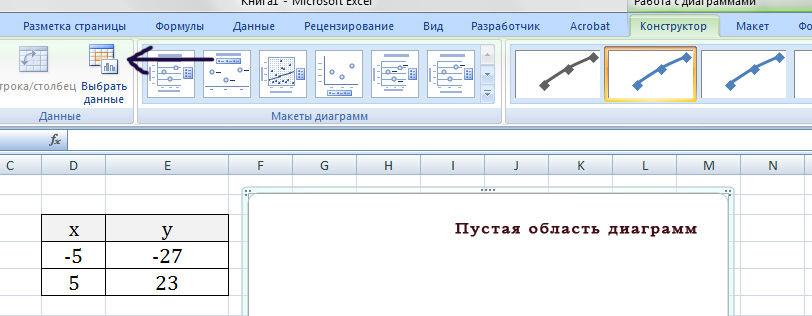
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Поделитесь статьёй с друзьями:
Добрый день. А есть возможность в Excele создать график с тремя переменными, но на одном графике? 2 параметра как обычно, координаты х и у, а третий параметр чтоб отражался размером метки? Вот как пример, такой график —
Рубрика Excel
Также статьи о графиках в Экселе:
- Как сделать диаграмму в Эксель?
- Как сделать круговую диаграмму в Экселе?
- Как построить график в Экселе?
- Построение точечной диаграммы в Excel
В Экселе можно результаты расчетов отобразить в виде диаграммы или графика, придавая им большую наглядность, а для сравнения иногда нужно построить два графика рядом. Как построить два графика в Excel на одном поле мы далее и рассмотрим.
Начнем с того, что не каждый тип диаграмм в Экселе сможет отобразить именно тот результат, который мы ожидаем. К примеру, имеются результаты расчетов для нескольких функций на основе одинаковых исходных данных. Если по этим данным строить обычную гистограмму или график, то исходные данные не будут учитываться при построении, а лишь их количество, между которыми будут задаваться одинаковые интервалы.
Выделяем два столбца результатов расчетов и строим обычную гистограмму.
Теперь попробуем добавить еще одну гистограмму к имеющимся с таким же количеством результатов расчетов. Для добавления графика в Экселе делаем активным имеющийся график, выделив его, и на появившейся вкладке «Конструктор» выбираем «Выбрать данные». В появившемся окошке в разделе «Элементы легенды» нажимаем добавить, и указываем ячейки «Имя ряда:» и «Значения:» на листе, в качестве которых будут значения расчета функции «j».
Теперь посмотрим, как будет выглядеть наша диаграмма, если мы к имеющимся гистограммам добавим еще одну, у которой количество значений почти в два раза больше. Добавим к графику значения функции «k».
Как видно, последних добавленных значений гораздо больше, и они настолько малы, что их на гистограмме практически не видно.
Если изменить тип диаграммы с гистограммы на обычный график, результат получится в нашем случае более наглядным.
Если использовать для построения графиков в Экселе точечную диаграмму, то на полученных графиках будет учитываться не только результат расчетов, но и исходные данные, т.е. будет прослеживаться четкая зависимость между величинами.
Для создания точеного графика выделим столбец начальных значений, и пару столбцов результатов для двух разных функций. На вкладке «Вставка» выбираем точечную диаграмму с гладкими кривыми.
Для добавления еще одного графика выделяем имеющиеся, и на вкладке «Конструктор» нажимаем «Выбрать данные».
В новом окошке в графе «Элементы легенды» нажимаем «Добавить», и указываем ячейки для «Имя ряда:», «Значения X:» и «Значения Y:». Добавим таким образом функцию «j» на график.
Теперь добавим функцию «k», у которой совершенно другие исходные данные и их количество.
Как видно, на точечном графике функция «k» практически незаметна, но зато построена с учетом значений по обеим осям.
Построение графиков функций в Excel
Февраль 9th, 2014
Andrey K
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
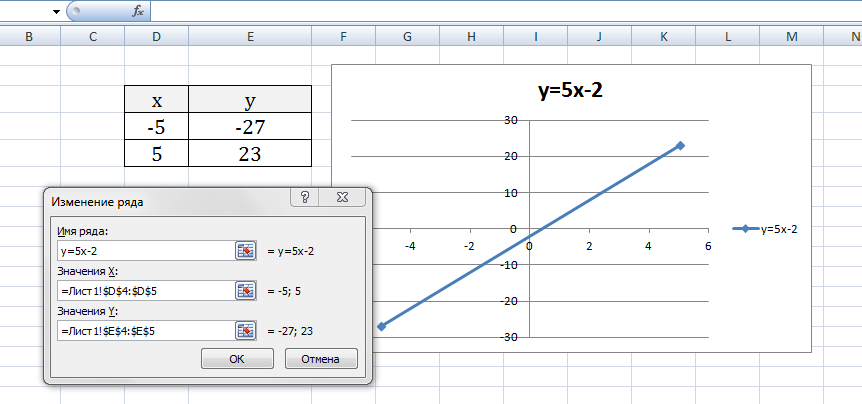
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
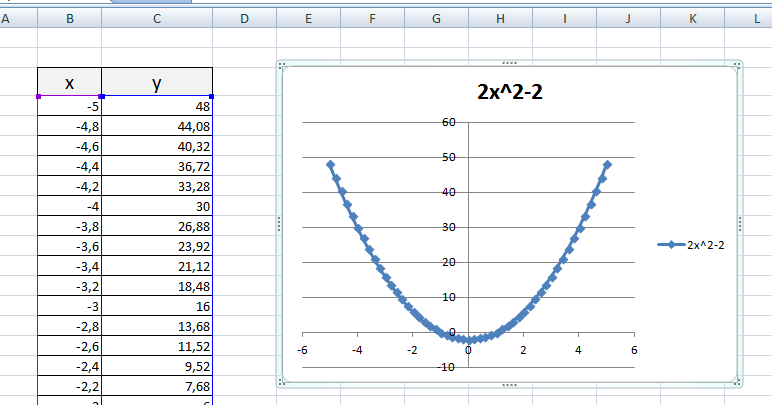
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
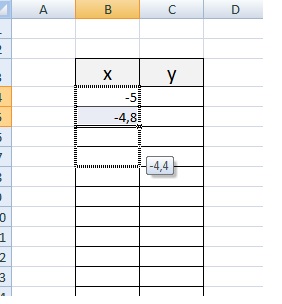
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
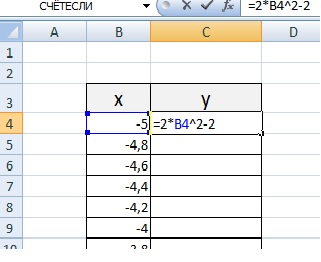
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете
оставить комментарий
, или
ссылку
на Ваш сайт.
Душевые термостаты, лучшие модели на
http://tools-ricambi.ru/
изготавливаются из материалов высшего качества
Чтобы правильно построить линейный график функций в Excel необходимо выбрать точечную диаграмму с прямыми отрезками и маркерами. Естественно это не единственный, но весьма быстрый и удобный способ.
Для разного рода данных нужно использовать разные типы графиков. Убедимся в этом, разобрав практический пример с построением математического графика функций в Excel.
Построение графиков функций в Excel
Начнем из анализа и создания графика функций в Excel. Мы убедимся в том, что линейный график в Excel существенно отличается от графика линейной функции, который преподают в школе.
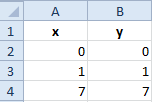
Линейная функция x=y имеет следующие значения: x1=0, x2=1, x3=7. Заполните таблицу этими значениями как показано на рисунке:
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«График»-«График с маркерами».
В результате у нас созданы 2 линии на графике, которые наложены одна сверх другой. Так же мы видим, что линии сломаны, а значит, они не соответствуют презентации школьному графику линейной функции. Излом линий, получается, по причине того, что на оси X у нас после значений: 0, 1 сразу идет значение 7 (упущены 2,3,4,5,6).
Вывод один: данный способ графического построения данных нам не подходит. А значит щелкните по нему левой кнопкой мышки (чтобы сделать его активным) и нажмите клавишу DELETE на клавиатуре, чтобы удалить его.
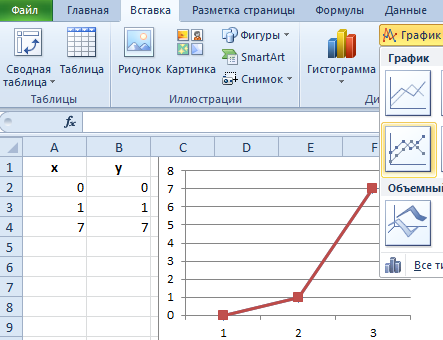
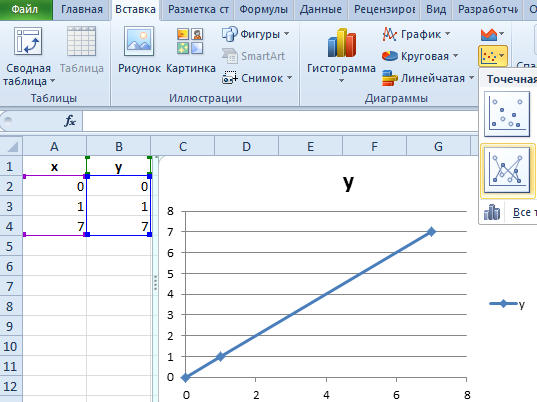
Как построить график линейной функции в Excel
Чтобы создать правильный график функций в Excel выберите подходящий график.
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с прямыми отрезками и маркерами».
Как видно на рисунке данный график содержит одинаковое количество значений на осях X и Y. По умолчанию в шаблоне данного графика цена делений оси X равна 2. При необходимости ее можно изменить. Для этого:
Теперь у нас отображается одинаковое количество значений по всем осям.
Очень важно понимать разницу в предназначениях графиков Excel. В данном примере мы видим, что далеко не все графики подходят для презентации математических функций.
Примечание. В принципе первый способ можно было-бы оптимизировать под отображение линейной функции, если таблицу заполнить всеми значениями 0-7. Но это не всегда работающее решение, особенно в том случае если вместо значений будут формулы изменяющие данные. Одним словом если нужно забить гвоздь лучше взять молоток, чем микроскоп. Несмотря на то, что теоретически гвозди можно забивать и микроскопом.
Не существует универсальных графиков и диаграмм, которыми можно отобразить любой отчет. Для каждого типа отчета наиболее подходящее то или иное графическое представление данных. Выбор зависит от того что и как мы хотим презентовать. На следующих примерах вы убедитесь, что выбор имеет большое значение. Существует даже целая наука «Инфографика», которая учит лаконично презентовать информацию с максимальным использованием графики вместо текста, насколько это только возможно.
Как сделать систему координат в excel?
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
Как построить лепестковую диаграмму в Excel
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке . Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Поделитесь статьёй с друзьями:
Добрый день. А есть возможность в Excele создать график с тремя переменными, но на одном графике? 2 параметра как обычно, координаты х и у, а третий параметр чтоб отражался размером метки? Вот как пример, такой график —
Также статьи о графиках в Экселе:
- Как сделать диаграмму в Эксель?
- Как сделать круговую диаграмму в Экселе?
- Как построить график в Экселе?
- Построение точечной диаграммы в Excel
В Экселе можно результаты расчетов отобразить в виде диаграммы или графика, придавая им большую наглядность, а для сравнения иногда нужно построить два графика рядом. Как построить два графика в Excel на одном поле мы далее и рассмотрим.
Начнем с того, что не каждый тип диаграмм в Экселе сможет отобразить именно тот результат, который мы ожидаем. К примеру, имеются результаты расчетов для нескольких функций на основе одинаковых исходных данных. Если по этим данным строить обычную гистограмму или график, то исходные данные не будут учитываться при построении, а лишь их количество, между которыми будут задаваться одинаковые интервалы.
Выделяем два столбца результатов расчетов и строим обычную гистограмму.
Теперь попробуем добавить еще одну гистограмму к имеющимся с таким же количеством результатов расчетов. Для добавления графика в Экселе делаем активным имеющийся график, выделив его, и на появившейся вкладке «Конструктор» выбираем «Выбрать данные». В появившемся окошке в разделе «Элементы легенды» нажимаем добавить, и указываем ячейки «Имя ряда:» и «Значения:» на листе, в качестве которых будут значения расчета функции «j».
Теперь посмотрим, как будет выглядеть наша диаграмма, если мы к имеющимся гистограммам добавим еще одну, у которой количество значений почти в два раза больше. Добавим к графику значения функции «k».
Как видно, последних добавленных значений гораздо больше, и они настолько малы, что их на гистограмме практически не видно.
Если изменить тип диаграммы с гистограммы на обычный график, результат получится в нашем случае более наглядным.
Если использовать для построения графиков в Экселе точечную диаграмму, то на полученных графиках будет учитываться не только результат расчетов, но и исходные данные, т.е. будет прослеживаться четкая зависимость между величинами.
Для создания точеного графика выделим столбец начальных значений, и пару столбцов результатов для двух разных функций. На вкладке «Вставка» выбираем точечную диаграмму с гладкими кривыми.
Для добавления еще одного графика выделяем имеющиеся, и на вкладке «Конструктор» нажимаем «Выбрать данные».
В новом окошке в графе «Элементы легенды» нажимаем «Добавить», и указываем ячейки для «Имя ряда:», «Значения X:» и «Значения Y:». Добавим таким образом функцию «j» на график.
Теперь добавим функцию «k», у которой совершенно другие исходные данные и их количество.
Как видно, на точечном графике функция «k» практически незаметна, но зато построена с учетом значений по обеим осям.
Построение графиков функций в Excel
Февраль 9th, 2014
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
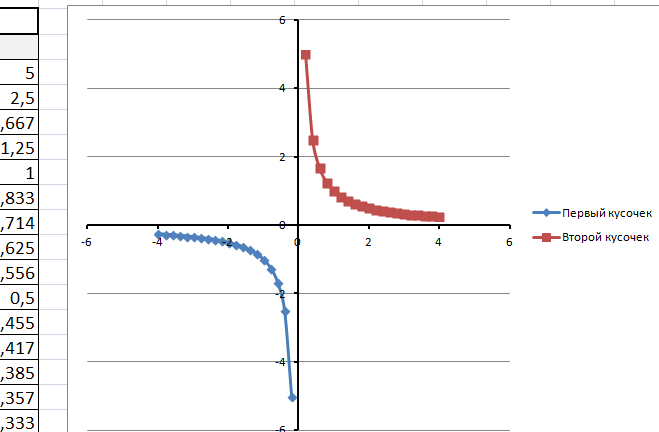
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
Как сделать координатную плоскость в MS Excel — Наука — 2022
Координатная плоскость образована двумя линиями, которые пересекаются под прямым углом, создавая четыре секции, называемые квадрантами. Координатные плоскости используются для построения графика упорядоченных пар и уравнений или построения диаграмм рассеяния. Вы можете создать координатную плоскость в Microsoft Excel, используя инструменты форматирования и рисования ячеек.
Откройте новый пустой документ Excel. Нажмите «Прямоугольник» в верхнем левом углу электронной таблицы, расположенной на пересечении столбца A и строки 1. Это выберет всю электронную таблицу. Нажмите на вкладку «Вид». В группе «Показать / Скрыть» отмените выбор «Линии сетки».
Поместите курсор на линию между любыми двумя заголовками столбцов. Ваш курсор изменится на вертикальную линию, пересекаемую горизонтальной стрелкой. Перетащите линию влево, пока ширина столбца не станет ровно 20 пикселей. Когда вы отпустите кнопку мыши, все клетки будут квадратными. Нажмите в ячейке «А1», чтобы убрать выделение.
Щелкните ячейку «C3» и перетащите и выделите область из 400 ячеек в ячейку V22. В группе «Шрифт» на вкладке «Главная» нажмите «Стрелка» на инструменте границы. Выберите «Границу», которая напоминает окно с четырьмя панелями.
Нажмите вкладку «Вставить». В группе «Иллюстрации» нажмите стрелку «Фигуры». Выберите линию с двумя стрелками.
Нарисуйте ось X между строкой 12 и строкой 13. Чтобы сделать прямую линию, удерживайте нажатой клавишу «Shift», удерживая ее нажатой и перетаскивая. Нарисуйте ось Y между столбцами L и M.
Как винт похож на наклонную плоскость?
Наклонные плоскости облегчают работу, увеличивая расстояние, которое должен пройти объект, но это приводит к уменьшению количества силы, необходимой для перемещения этого объекта. Толкание мяча вверх по рампе требует меньшего усилия, чем его выброс в воздух.
Как использовать координатную плоскость в реальной жизни
Использование координатных плоскостей в реальной жизни является полезным навыком для составления карты местности, проведения экспериментов или даже планирования повседневных нужд, таких как расстановка мебели в комнате.
Кто изобрел наклонную плоскость?
Наклонная плоскость — это не то, о чем думают люди, когда они думают о машине, потому что наклонные плоскости присутствуют в природе. Посмотрите на склон холма, и вы смотрите на наклонную плоскость. Тем не менее, как механическая концепция, это один из самых фундаментальных принципов в технике, и один из .
A coordinate plane is formed by two lines that intersect at right angles, creating four sections called quadrants. Coordinate planes are used to graph ordered pairs and equations or to construct scatter plots. You can make a coordinate plane in Microsoft Excel, using cell formatting and drawing tools.
Open a new, blank Excel document. Click the «Rectangle» in the upper-left corner of the spreadsheet located at the intersection of column A and row 1. This will select the entire spreadsheet. Click the «View» tab. In the Show/Hide group, deselect «Gridlines.»
Place your cursor on a line between any two column headers. Your cursor will change to a vertical line crossed by a horizontal arrow. Drag the line left until the column width is exactly 20 pixels. When you release the mouse, all cells will be square. Click in cell «A1» to remove the highlighting.
Click cell «C3» and drag and highlight the 400-cell area to cell V22. In the Font group on the Home tab, click the «Arrow» on the border tool. Select the «Border» that resembles a window with four panes.
Click the «Insert» tab. In the Illustrations group, click the arrow on «Shapes.» Select the line with two arrow heads.
Draw the x-axis between row 12 and row 13. To make a straight line, hold the «Shift» key while you click and drag. Draw the y-axis between columns L and M.
Диаграммы Excel – точечная диаграмма (XY)
Точечные (XY) диаграммы обычно используются для отображения и сравнения числовых значений, таких как научные, статистические и технические данные.
Он объединяет значения x и y в отдельные точки данных и отображает их с нерегулярными интервалами или кластерами.
Рассмотрите возможность использования точечной диаграммы, когда –
Значения для горизонтальной оси распределены неравномерно.
Вы хотите настроить шкалы независимых осей точечной диаграммы, чтобы получить больше информации о данных, которые включают пары или сгруппированные наборы значений.
Вы хотите показать сходство между большими наборами данных вместо различий между точками данных.
Вы хотите сравнить множество точек данных независимо от времени.
Чем больше данных вы включите в точечную диаграмму, тем лучше будет сравнение.
Значения для горизонтальной оси распределены неравномерно.
Вы хотите настроить шкалы независимых осей точечной диаграммы, чтобы получить больше информации о данных, которые включают пары или сгруппированные наборы значений.
Вы хотите показать сходство между большими наборами данных вместо различий между точками данных.
Вы хотите сравнить множество точек данных независимо от времени.
Чем больше данных вы включите в точечную диаграмму, тем лучше будет сравнение.
Следуйте приведенным ниже инструкциям, чтобы вставить точечную диаграмму в свой рабочий лист.
Шаг 1 – Расположите данные в столбцах или строках на листе.
Шаг 2. Поместите значения x в одну строку или столбец, а затем введите соответствующие значения y в соседние строки или столбцы.
Шаг 4 – На вкладке ВСТАВИТЬ в группе Диаграммы щелкните значок точечной диаграммы на ленте.
Вы увидите различные типы доступных точечных диаграмм.
Шаг 5 – Наведите указатель мыши на каждый из значков. Предварительный просмотр этого типа диаграммы будет показан на листе.
Шаг 6 – Дважды щелкните тип диаграммы, который соответствует вашим данным.
В этой главе вы поймете, когда каждая из диаграмм разброса полезна.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
По условию уравнение не нужно приводить к каноническому виду , а значит, требуемые вещи проще найти напрямую с учётом параллельного переноса гиперболы , к тому же, она не повёрнута. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Можно также скопировать диаграмму из Excel в Office Word 2007. При копировании диаграммы она может быть внедрена как статический объект или связана с книгой. Для связанной диаграммы, к которой пользователь имеет доступ, можно задать автоматическую проверку изменений в связанной книге при каждом открытии диаграммы.
Как построить линию в полярной системе координат?
И скажите, зачем столько трудностей, когда нужен всего-то рисунок этого графика для иллюстрации функции. Следовательно, проще взять и нарисовать этот график средствами векторного редактора, встроенного в Word.
Вставка и построение
Для примера используем таблицу выручки и затрат за год, на основании которой построим простой график:
| янв.13 | фев.13 | мар.13 | апр.13 | май.13 | июн.13 | июл.13 | авг.13 | сен.13 | окт.13 | ноя.13 | дек.13 | |
| Выручка | 150 598р. | 140 232р. | 158 983р. | 170 339р. | 190 168р. | 210 203р. | 208 902р. | 219 266р. | 225 474р. | 230 926р. | 245 388р. | 260 350р. |
| Затраты | 45 179р. | 46 276р. | 54 054р. | 59 618р. | 68 460р. | 77 775р. | 79 382р. | 85 513р. | 89 062р. | 92 370р. | 110 424р. | 130 175р. |
Вне зависимости от используемого типа, будь это гистограмма, поверхность и т.п., принцип создания в основе не меняется. На вкладке «Вставка» в приложении Excel необходимо выбрать раздел «Диаграммы» и кликнуть по требуемой пиктограмме.
Выделите созданную пустую область, чтобы появились дополнительные вкладки лент. Одна из них называется «Конструктор» и содержит область «Данные», на которой расположен пункт «Выбрать данные». Клик по нему вызовет окно выбора источника:
Обратите внимание на самое первое поле «Диапазон данных для диаграммы:». С его помощью можно быстро создать график, но приложение не всегда может понять, как именно хочет видеть это пользователь. Поэтому рассмотрим простой способ добавления рядов и осей.
На упомянутом выше окне нажмите кнопку «Добавить» в поле «Элементы легенды». Появится форма «Изменение ряда», где нужно задать ссылку на имя ряда (не является обязательным) и значения. Можно указать все показатели вручную.
После занесения требуемой информации и нажатия кнопки «OK», новый ряд отобразиться на диаграмме. Таким же образом добавим еще один элемент легенды из нашей таблицы.
Теперь заменим автоматически добавленные подписи по горизонтальной оси. В окне выбора данных имеется область категорий, а в ней кнопка «Изменить». Кликните по ней и в форме добавьте ссылку на диапазон этих подписей:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Используйте Scatter с прямыми линиями и маркерами и Scatter с прямыми линиями, когда данные представляют отдельные измерения. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Для изменения внешнего вида диаграммы можно воспользоваться предоставленными по умолчанию стилями. Для этого выделите ее и выберите появившуюся вкладку «Конструктор», на которой расположена область «Стили диаграмм».
Диаграммы Excel — точечная диаграмма (XY).
- Ряды данных – представляют главную ценность, т.к. визуализируют данные;
- Легенда – содержит названия рядов и пример их оформления;
- Оси – шкала с определенной ценой промежуточных делений;
- Область построения – является фоном для рядов данных;
- Линии сетки.
Иногда, из-за сильных различий значений рядов диаграммы, использование единой шкалы невозможно. Но можно добавить альтернативную шкалу. Перейдите в меню «Формат ряда данных…» и в разделе «Параметры ряда» переместите флажок на пункт «По вспомогательной оси».
| янв.13 | фев.13 | мар.13 | апр.13 | май.13 | июн.13 | июл.13 | авг.13 | сен.13 | окт.13 | ноя.13 | дек.13 | |
| Выручка | 150 598р. | 140 232р. | 158 983р. | 170 339р. | 190 168р. | 210 203р. | 208 902р. | 219 266р. | 225 474р. | 230 926р. | 245 388р. | 260 350р. |
| Затраты | 45 179р. | 46 276р. | 54 054р. | 59 618р. | 68 460р. | 77 775р. | 79 382р. | 85 513р. | 89 062р. | 92 370р. | 110 424р. | 130 175р. |
Меняем тип графического объекта
Если после построения диаграммы Вы решили, что она недостаточно наглядна, можно изменить тип объекта всего в пару кликов. Рассмотрим этот процесс на примере построенной выше гистограммы движения финансовых средств. Предположим, что она должна стать графиком.
-
В меню «Конструктор» вкладки «Работа с диаграммами» выберите пункт «Изменить тип диаграммы».
Учтите, что не удастся заменить сложную диаграмму на более простую без потери части данных. Так, одной круговой диаграммы не хватит для отражения информации из гистограммы с двумя рядами.
Видео — Как построить график и диаграмму в Excel?
Автор блога, занимаюсь программированием, делаю обзоры бытовой техники веду свой Youtube канал. Консультирую по вопросам IT
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Кликнув по требуемому ряду правой кнопкой мыши, из списка выберите пункт Изменить тип диаграммы для ряда , затем Гистограмма. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Иногда, из-за сильных различий значений рядов диаграммы, использование единой шкалы невозможно. Но можно добавить альтернативную шкалу. Перейдите в меню «Формат ряда данных…» и в разделе «Параметры ряда» переместите флажок на пункт «По вспомогательной оси».
На ниже приведенной диаграмме представлено сравнение 3-х организаций по 4-ем направлениям: Доступность; Ценовая политика; Качество продукции; Клиентоориентированность. Видно, что компания X лидирует по первому и последнему направлению, компания Y по качеству продукции, а компания Z предоставляет лучшие цены.
Автор:
John Pratt
Дата создания:
17 Февраль 2021
Дата обновления:
13 Апрель 2023
Содержание
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
Координатная плоскость состоит из двух линий, которые пересекаются под прямым углом, образуя четыре секции, называемые квадрантами. Они используются для построения графиков упорядоченных пар и уравнений или для построения диаграмм рассеяния. Вы можете создать координатную плоскость в Microsoft Excel, используя формат ячейки и инструменты рисования.
Шаг 1
Откройте новый пустой документ Excel. Щелкните прямоугольник в верхнем левом углу рабочего листа на пересечении столбца и строки 1. Будет выбран весь рабочий лист. Щелкните вкладку «Просмотр». В группе «Показать / скрыть» снимите флажок «Линии сетки».
Шаг 2
Помещает курсор на строку между заголовками двух столбцов. Это изменится на вертикальную линию, пересеченную горизонтальной стрелкой. Перетащите линию влево, пока ширина столбца не станет ровно 20 пикселей. Когда вы отпустите кнопку мыши, все ячейки станут квадратными. Щелкните ячейку A1, чтобы удалить выделение.
Шаг 3
Щелкните ячейку C3 и перетащите и выделите область из ячейки 400 в ячейку V22. В группе Шрифт на вкладке Главная щелкните стрелку на инструменте границы. Выберите границу, которая напоминает окно с четырьмя панелями.
Шаг 4
Щелкните вкладку Вставка. В группе Иллюстрации щелкните стрелку Фигуры. Выберите линию с двумя стрелками.
Нарисуйте ось x между строками 12 и 13. Чтобы построить прямую линию, удерживайте клавишу «Shift», щелкая и перетаскивая. Проведите ось между столбцами L и M.


Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
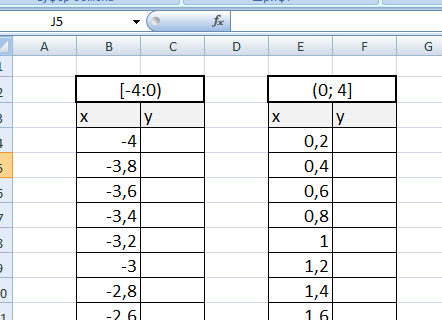
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
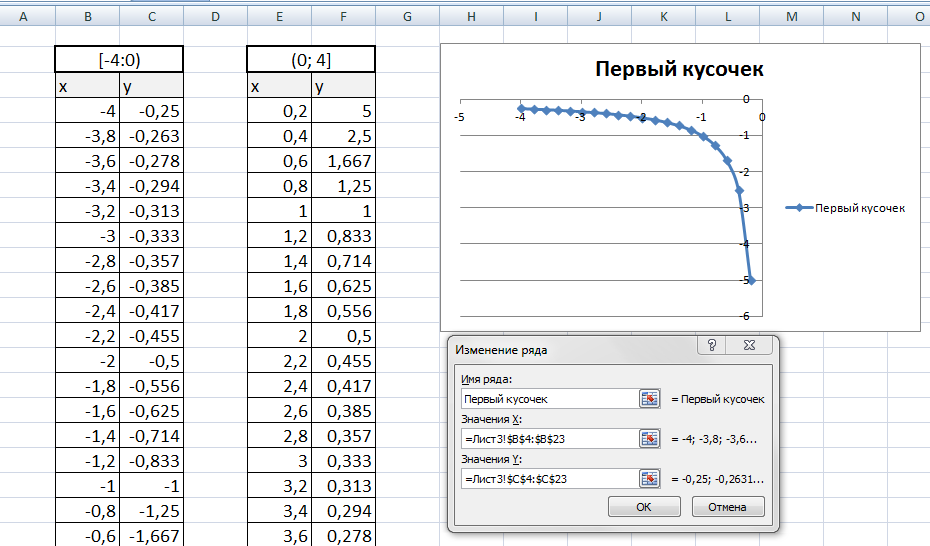
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете оставить комментарий, или ссылку на Ваш сайт.
Душевые термостаты, лучшие модели на http://tools-ricambi.ru/ изготавливаются из материалов высшего качества
Оставить комментарий
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Трехмерные диаграммы (поверхности и изолинии) в EXCEL
history 16 мая 2015 г.
-
Группы статей
- Диаграммы и графики
Рассмотрим трехмерные диаграммы в MS EXCEL 2010. С помощью трехмерных диаграмм отображают поверхности объемных фигур (гиперболоид, эллипсоид и др.) и изолинии.
Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
При попытке построить диаграмму типа Поверхность на основе одного ряда данных, MS EXCEL может сказать, что ему требуется как минимум 2 ряда. На самом деле, для более или менее наглядной поверхности потребуется как минимум 10 рядов (лучше 20 – для сложных поверхностей). К счастью, ряды не нужно создавать в ручную – достаточно правильно сформировать таблицу с исходными данными.
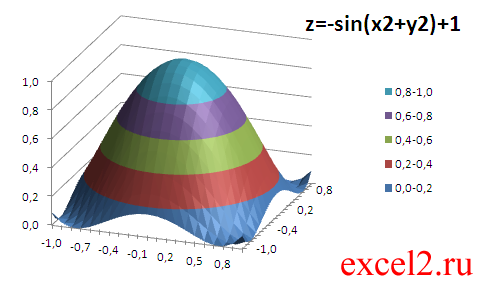
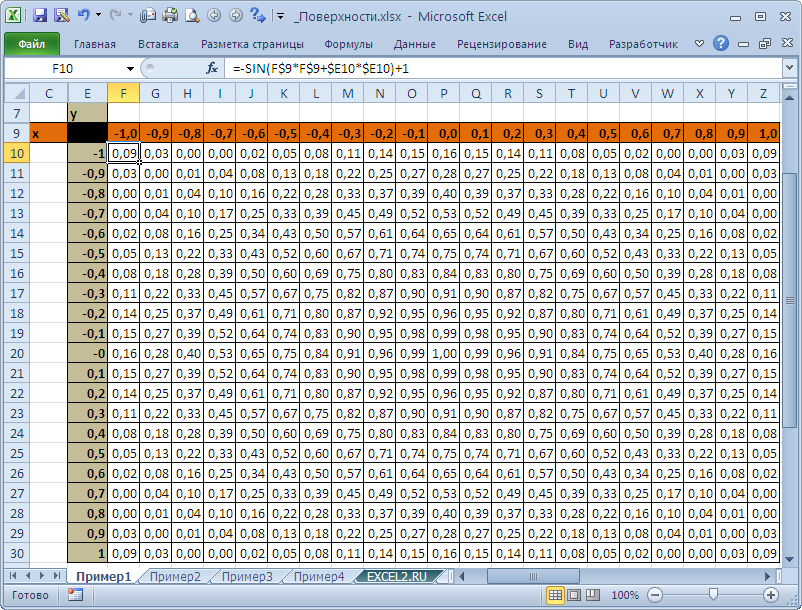
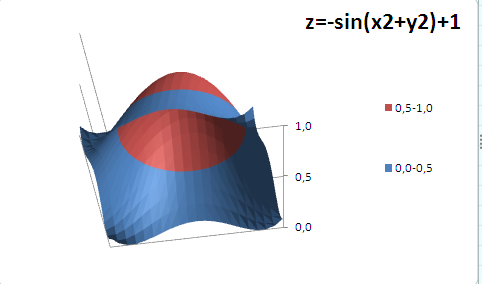
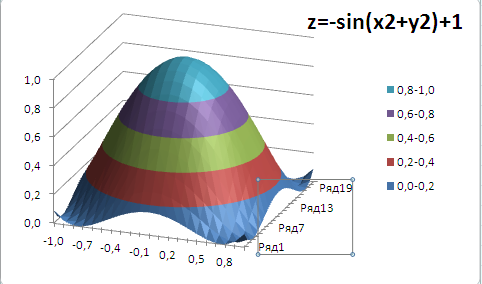
Построим график функции z=-sin(x*х+y*y)+1 (см. файл примера ).
В качестве источника данных используем таблицу, в которой в верхней строке указаны значения Х, а в левом столбце Y. В остальных ячейках – значения Z для всех пар (Х,Y)
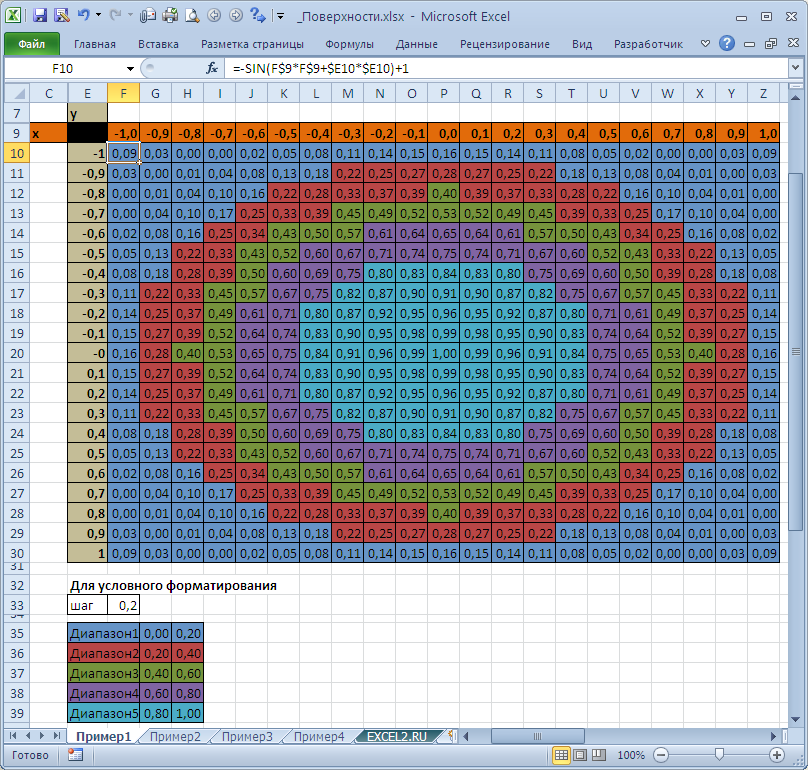
Чтобы значения Z были более информативны — можно использовать Условное форматирование .
Условное форматирование показывает некий вариант изолиний (см. ниже): близкие значения Z выделены одним цветом. Это также позволяет предварительно оценить вид создаваемой диаграммы.
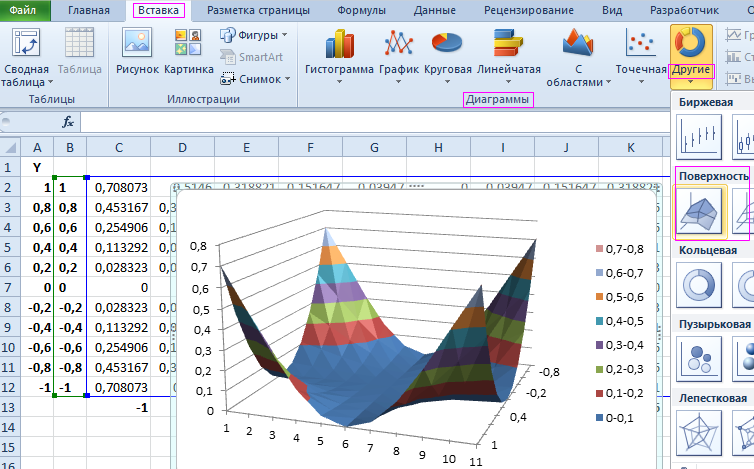
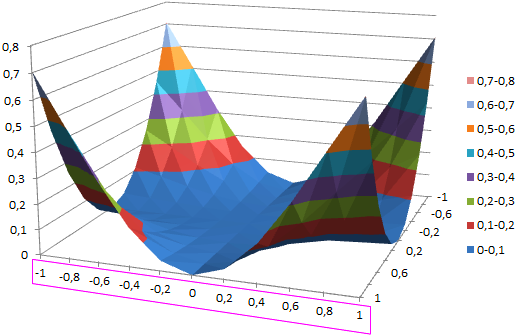
Теперь выделите любую ячейку таблицы и постройте диаграмму типа Поверхность (вкладка Вставка , группа Диаграммы , Кнопка Другие ).
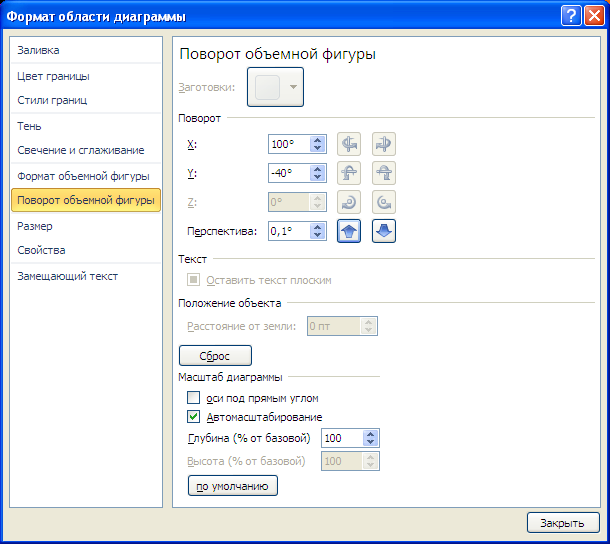
Полученную фигуру можно повращать (кнопка Поворот объемной фигуры на вкладке Макет ).
Для построения диаграммы используется 3 оси: горизонтальная ось (категорий), вертикальная ось (значений), ось Z (рядов значений). Все 3 названия осей требуют пояснения.
Во-первых, ось Z на самом деле является нашей осью Х и отображает имена рядов. Если имена рядов убрать, то изменятся и подписи оси (убрать имена рядов можно нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор ).
Этот факт роднит диаграмму Поверхность с Диаграммой График , где по Х отображаются лишь подписи. Т.е. при попытке построить поверхность с неравномерным шагом по Х (например, 1, 2, 5, 9, 77, 103, ..) получим искажения масштаба: значения по Х будут откладываться последовательно 1, 2, 3, … (конечно, Z будет рассчитаны правильно). Интересно, что формат подписей по оси Z можно настроить только изменяя формат ячеек, на которые ссылаются имена рядов (изменение формата на вкладке Число (в окне Формат Оси) ни к чему не приводит).
Во-вторых, по вертикальной оси (значений) на самом деле откладываются значения Z (это очевидно из рисунка).
И, наконец, в-третьих, горизонтальная ось (категорий) – это значения Y (на самом деле опять только подписи). Подписи, как и для Графика можно удалить или изменить нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор (на этот раз нужно нажать кнопку расположенную справа).
Так как диаграмма Поверхность – это по сути трехмерный График , в котором одному Х соответствует один Y, то некоторые объемные фигуры отобразить на диаграмме Поверхность не удастся. Например, не удастся отобразить гиперболоид, т.к. каждой паре (Х;Y) на диаграмме Поверхность соответствует только один Z, а для гиперболоида это не так (каждой паре соответствует 2 значения Z). Поэтому, в MS EXCEL придется довольствоваться только половиной гиперболоида.
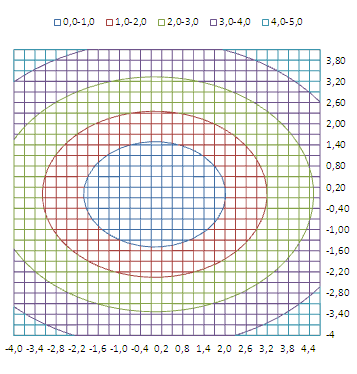
Как видно из диаграммы, близкие значения Z выделены одним цветом, которые указаны в Легенде. К сожалению, в MS EXCEL невозможно управлять этими уровнями (даже при повороте фигуры количество уровней и диапазоны значений существенно изменяются). Это приводит к тому, что построение изолиний ( линии уровня, контурный график, англ. Contour plot ) реализовано в MS EXCEL в достаточно ограниченном виде: невозможно указать на диаграмме значение изолинии (диапазоны цветов указаны на Легенде), разбиение на диапазоны по Z производится MS EXCEL автоматически и нет возможности на это повлиять. Ниже приведены изолинии для упомянутого выше гиперболоида. Это особый вид диаграммы – Проволочная контурная .
Практически такой же картинки можно добиться простым поворотом фигуры на диаграмме Поверхность .
Построение поверхностей второго порядка в excel
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
3. .Уравнение плоскости, проходящей через три точки
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица (рис. 1).
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
| | | следующая лекция ==> |
| | | Решите задачи с использованием диаграммы Эйлера-Венна. |
Дата добавления: 2017-02-25 ; просмотров: 2062 | Нарушение авторских прав
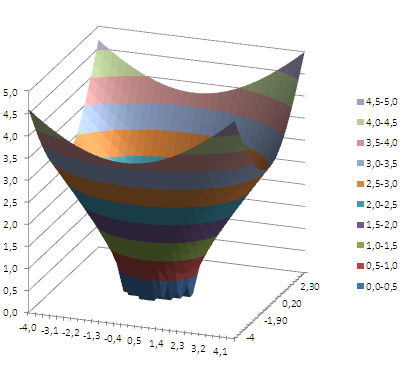
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
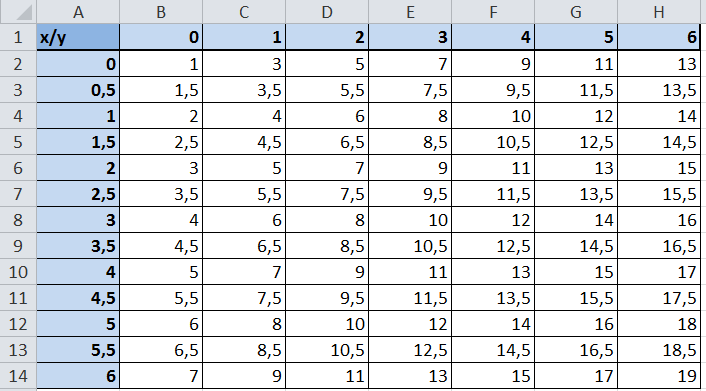
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
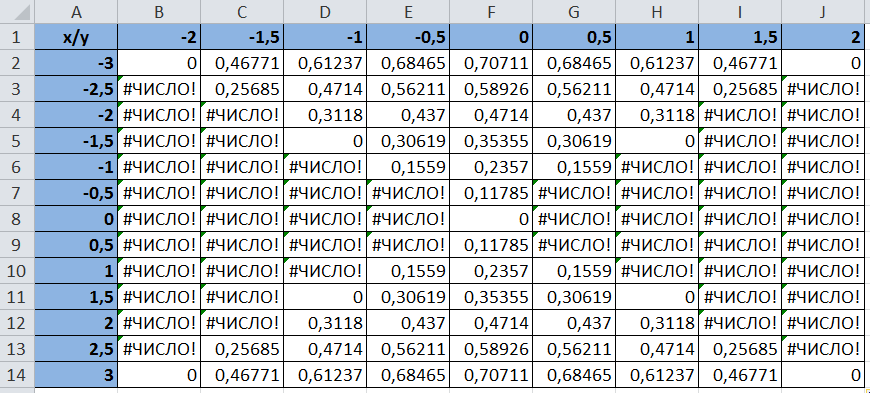
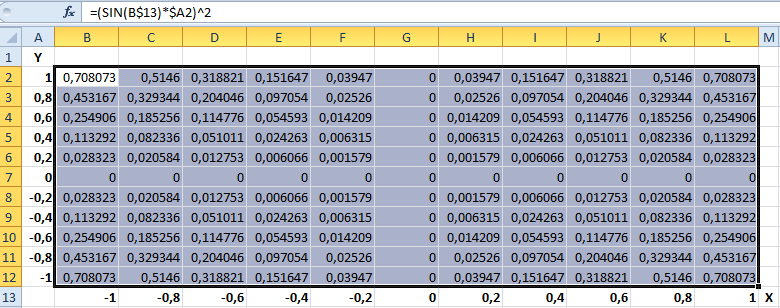
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
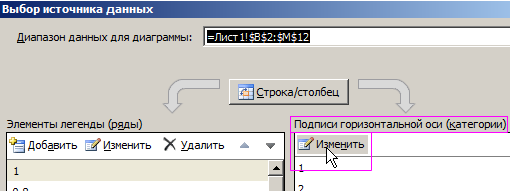
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
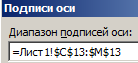
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
by Ирина Кяршис
ГЛАВА 1. Возможности табличного процессора Microsoft Excel
1.1.Ввод данных в Excel
Электронная таблица – это программа, позволяющая автоматизировать табличные расчеты. Документ Microsoft Ехсел является рабочей книгой, состоящей из листов. Таблица состоит из 65536 строк и 256 столбцов. Строки нумеруются числами, столбцы – буквами латинского алфавита (А, В …, Z, АА, АВ …). На пересечении строки и столбца расположена ячейка, которая имеет адрес, состоящий из имени столбца и номера строки (А4). Одна из ячеек всегда является активной.
Прямоугольная группа смежных ячеек называется диапазоном ячеек. Примеры диапазонов – А2: С4, В2: К40.
Ячейки могут содержать данные трех типов:
1) Текстовые данные – это строка текста произвольной длины.
2) Числовые данные – это отдельное число. Может быть целым, дробным (зап.). Если ширина ячейки мала, то число записывается в экспоненциальной форме, например 125 000 000 → 1,25Е + 8 или вместо числа ставятся символы ###. При этом число сохраняется.
3) Формула – это арифметическое выражение. Он представляет собой последовательность чисел, ссылок на ячейки и функций, объединенных знаками арифметических операций: +, -, /, *. Excel предлагает несколько сотен встроенных функций, которые разделены на категории.
Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.
Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.
Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).
1.2.Типы диаграмм
В зависимости от типа диаграммы данные отображаются на ней разным способом.
Можно отметить несколько стандартных типов:
1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.
2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.
3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.
4. С областями . Диаграмма с областями похожа на график.
5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.
Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.
6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)
7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.
8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.
Подробнее о типах диаграмм здесь
1.3 Основы построения диаграмм в Excel
Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.
Совокупность этих элементов определяет макет диаграммы.
Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).
Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.
Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.
6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.
Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).
Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.
ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2.1 Уравнения поверхностей второго порядка и их графики
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.
Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=1, где a и b – действительные полуоси, с – мнимая полуось.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=-1,где с – действительная полуось, a и b – мнимые полуоси.
Поверхностная диаграмма в Excel и пример ее построения
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
источники:
http://4systems.ru/inf/postroenie-poverhnostej-vtorogo-porjadka-v-excel/
http://exceltable.com/grafiki/poverhnostnaya-diagramma