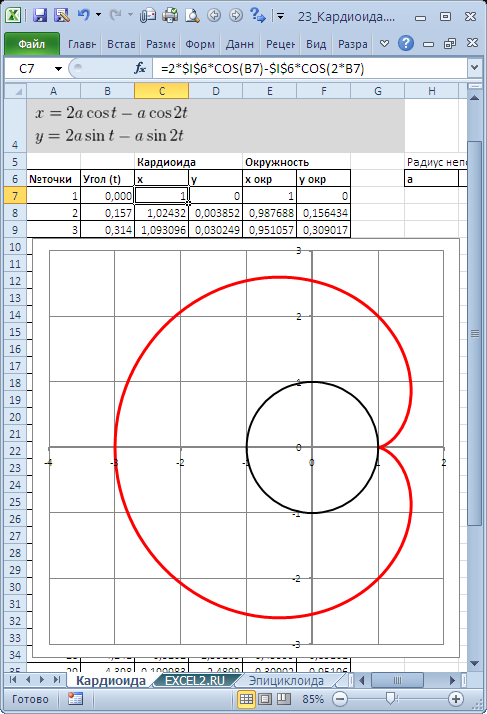
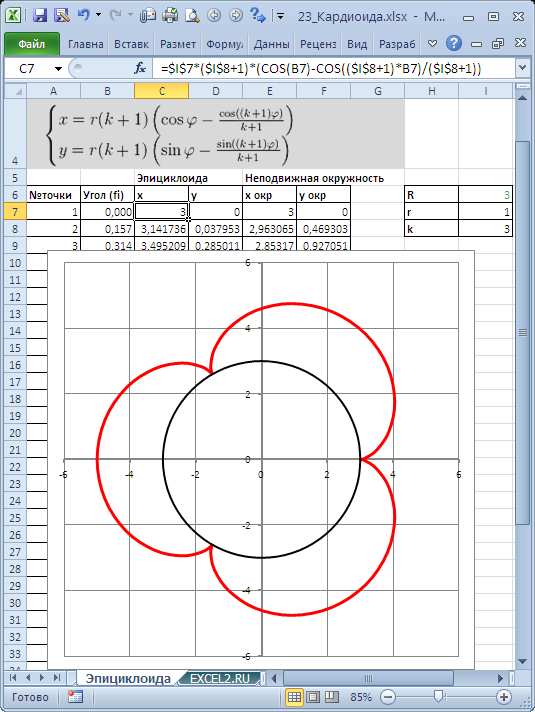
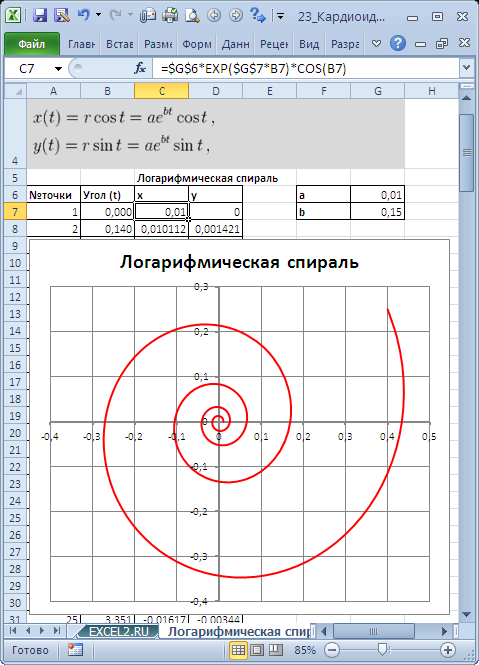
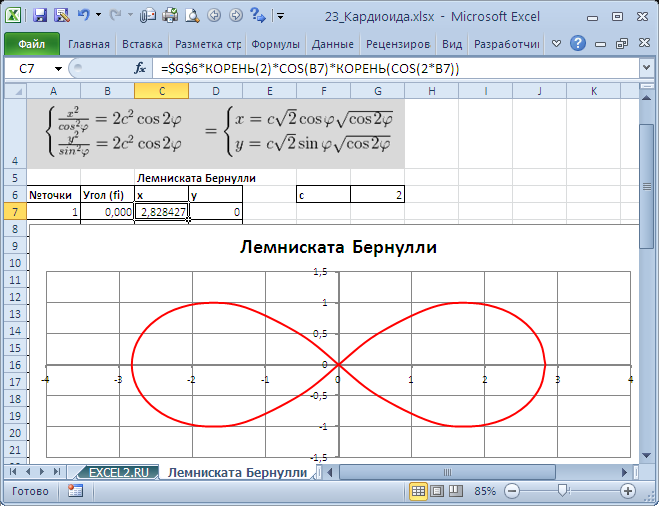
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см.
файл примера
):
х=2*а*cos(t)-а*cos(2*t)
y=2*а*sin(t)-а*sin(2*t)
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье
Эллипс и окружность в MS EXCEL
построены окружность и эллипс.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Подборка по базе: Учебник по EXCEL.doc, Работа с программой Excel.pdf, Методическая разработка открытого урока по теме «Microsoft Excel, Отсеивание грубых погрешностей результатов измерений с помощью р, Автоматты есептеулер. Excel бағдарламасындағы функциялар.docx, Excel_5_Работа с базами данных в EXCEL 2007.doc, ВШМ — 8. Решение задач линейной алгебры с помощью пакета Ms Exce, 2.2.2 Выделение ячеек в Excel и Проверка орфографии в Excel.docx, Решение в EXCEL задачи об инвестициях(1).doc, Диаграммы в Microsoft Excel.docx
Как строится Кардиоида в Excel.
1.Нам понадобятся два уравнения в прямоугольных координатах (в параметрической записи):
Для начала создаём точки от 1 до 41
2.Создаём столбец Угол(t) с шагом 0.157 и растягиваем до конца.
3.Создаём таблицу с радиусом неподвижной окружности. В нашем случае он будет равен 1.
4.Создаём два столбца рядом и выделяем их как x и y,они будут координатами кардиоиды.
В столбец x вставляем формулу которую я выделил в самом начале
И растягиваем все значения до конца.
В столбец y вставляем уже другую формулу
5.В конечном итоге у нас получается два таких столбца
6.Теперь добавляем два столбца и выделяем их как “x окр” и “y окр”
В x окр вставляем формулу с косинусом
В y окр вставляем формулу с синусом
И растягиваем до конца.
7.В конечном итоге мы получаем такую таблицу
8.Создаём сначало диаграмму кардиоиды из столбцов x и y
Затем создаём вторую диаграмму окружности из столбцов “x окр” и у “окр”
Теперь берем диаграмму окружности,копируем её и вставляем в диаграмму кардиоиды.
Получается диаграмма Кардиоида
Делаем её красивой
Работа сделана.
Слайд 2Полярная система координат
Полярная система координат ставит в соответствие каждой точке
на плоскости пару чисел .
Основными понятиями этой системы являются
точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось.
Фигуры в полярных координатах
образуются как след конца
бегающего по кругу полярного
радиуса переменной длины.
Длина радиуса определяется
величиной угла, который он
образует с полярной осью.
Знак «+», если угол против
часовой стрелки, и знак «-»
если угол по часовой стрелки.

Слайд 3Пусть (x; y) – координаты точки в декартовой системе координат, –
в полярной. Тогда очевидно, что:
Формулы обратного перехода:
Замечание:
число в полярной системе
определено не однозначно:
парам чисел соответствует
одна и та же точка при любых
натуральных n.
Переход от ДСК к ПСК

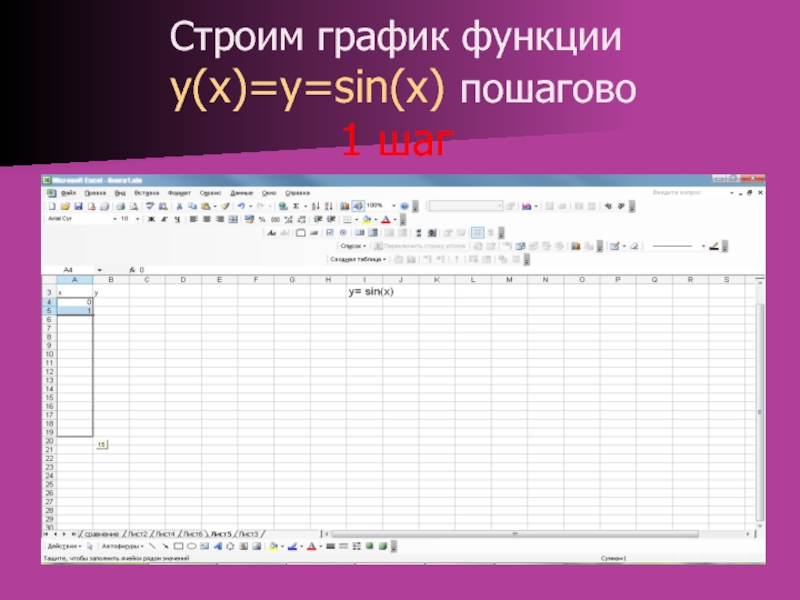
Слайд 4Строим график функции
y(x)=y=sin(x) пошагово
1 шаг
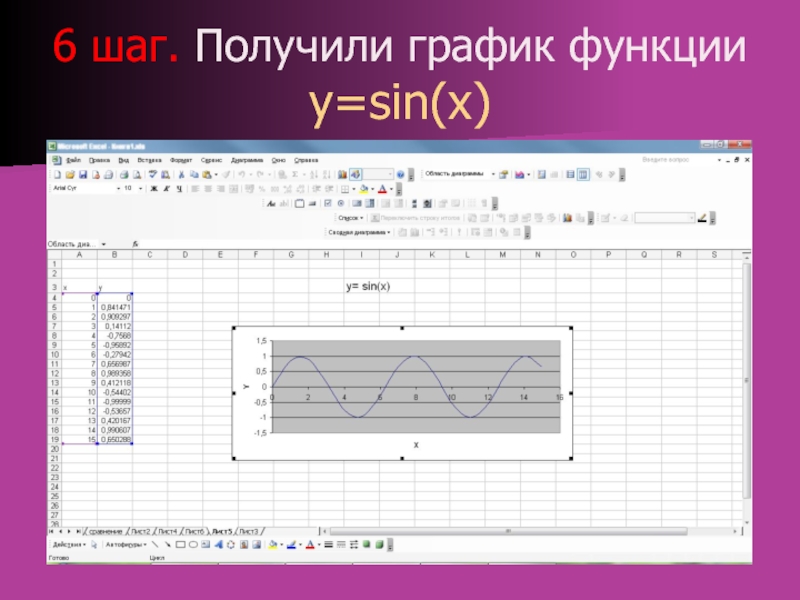
Слайд 106 шаг. Получили график функции y=sin(x)
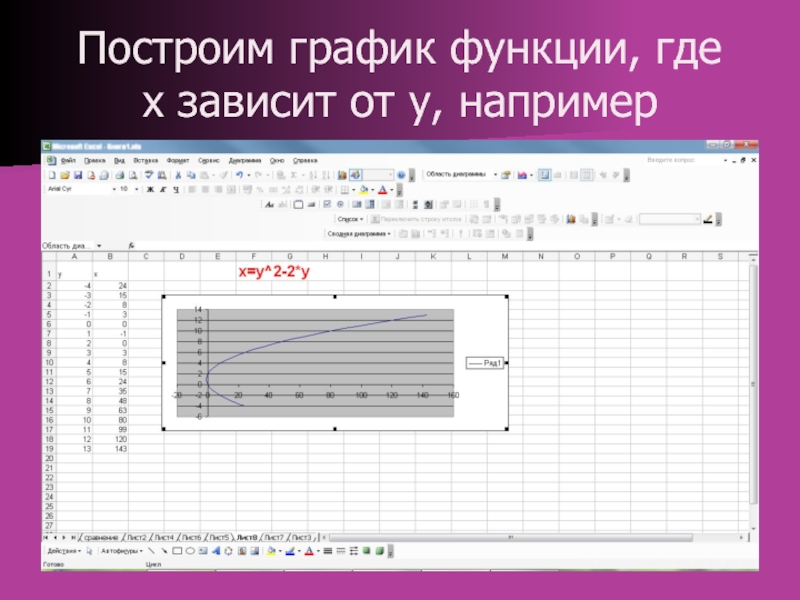
Слайд 11Построим график функции, где
x зависит от y, например
Слайд 12Инструкция по построению кривых
с помощью программы Microsoft Excel
Переведем уравнение
из декартовых координат в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F).
Задача.
Построить
кривую, заданную уравнением
Решение. Найдем уравнение линии в полярных координатах
Для программы Microsoft Excel:
R=4*COS(3*F)
Пусть угол
Выберем шаг изменения 0,1
Построим компьютерную модель исследования

Слайд 13Внесем данные и получим следующее распре-
деление по столбцам электронной таблицы:
А2
=0,1
А3 =А2+0,1
B2 =4*COS(3*F)
C2 =SIN(А2)
D2 =COS(А2)
E2 =B2*D2
F2 =В2*C2
Для построения графика выделим
информационный блок E2..F63, так как аргумент
F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д.

Слайд 15Спирали
Спираль Архимеда может быть определена как траектория точки, участвующей одновременно
в двух равномерных движениях, одно из которых совершается вдоль прямой,
а другое – по окружности.
Гиперболическая спираль
По мере роста спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.

Слайд 22
Кривая Хабеннихта
R=1+7 cos8F+ 4(sin8F)^2 + 3 (sin8F)^4

Слайд 23
Лист клевера
R=1+1/3(2 cos3F — cos6F)

Слайд 25І Вариант. (x ̸ 7)² + (y ̸ 12)² +
(z ̸ 9)² =1 на интервале х,y ∊ [-7;7] с
шагом 0.5 ;
ІІ Вариант. x² ̸ 9 + y² ̸ 4 =2z на интервале х,y ∊ [-5;5] с шагом 0.5 ;
ІІІ Вариант. x² ̸ (1 ̸ 3)² + y² ̸ (1 ̸ 6)² — z² ̸ (1 ̸ 2)² = 1 на интервале х,y ∊ [-5;4,5] с шагом 0.5 ;
ІV Вариант. x² ̸ 9 + y² ̸ 4 — z² = -1 на интервале х ∊ [-3;3] с шагом 0.5, y∊[-2;2] с шагом 1.
Самостоятельная работа

Изображение слайда
2
Слайд 2: Полярная система координат
Полярная система координат ставит в соответствие каждой точке на плоскости пару чисел.
Основными понятиями этой системы являются точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось.
Фигуры в полярных координатах
образуются как след конца
бегающего по кругу полярного
радиуса переменной длины.
Длина радиуса определяется
величиной угла, который он
образует с полярной осью.
Знак «+», если угол против
часовой стрелки, и знак «-»
если угол по часовой стрелки.
Изображение слайда
3
Слайд 3: Переход от ДСК к ПСК
Пусть ( x ; y ) – координаты точки в декартовой системе координат, – в полярной. Тогда очевидно, что:
Формулы обратного перехода:
Замечание:
число в полярной системе
определено не однозначно:
парам чисел соответствует
одна и та же точка при любых
натуральных n.
Переход от ДСК к ПСК
Изображение слайда
4
Слайд 4: Строим график функции y(x)=y=sin(x) пошагово 1 шаг
Изображение слайда
Изображение слайда
Изображение слайда
Изображение слайда
8
Слайд 8: 5 шаг. Мастер диаграммы
Изображение слайда
9
Слайд 9: Мастер диаграммы
Изображение слайда
10
Слайд 10: 6 шаг. Получили график функции y=sin(x)
Изображение слайда
11
Слайд 11: Построим график функции, где x зависит от y, например
Изображение слайда
12
Слайд 12: Инструкция по построению кривых с помощью программы Microsoft Excel
Переведем уравнение из декартовых координат в полярные, используя формулы: X = R * COS ( F ), Y = R * SIN ( F ).
Задача.
Построить кривую, заданную уравнением
Решение. Найдем уравнение линии в полярных координатах
Для программы Microsoft Excel :
R=4*COS(3*F)
Пусть угол
Выберем шаг изменения 0,1
Построим компьютерную модель исследования
Изображение слайда
Внесем данные и получим следующее распре-
деление по столбцам электронной таблицы:
А2 =0,1
А3 =А2+0,1
B2 =4*COS(3*F)
C2 =SIN(А2)
D2 =COS(А2)
E2 =B2*D2
F2 =В2*C2
Для построения графика выделим
информационный блок E2..F63, так как аргумент
F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д.
Изображение слайда
14
Слайд 14: Получим следующую кривую
Изображение слайда
Спираль Архимеда может быть определена как траектория точки, участвующей одновременно в двух равномерных движениях, одно из которых совершается вдоль прямой, а другое – по окружности.
Гиперболическая спираль
По мере роста спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.
Изображение слайда
16
Слайд 16: Получим следующие кривые
Изображение слайда
17
Слайд 17: Построение кардиоиды
Изображение слайда
18
Слайд 18: График астроиды
Изображение слайда
19
Слайд 19: Поверхность 1
Изображение слайда
20
Слайд 20: Поверхность 2
Изображение слайда
Изображение слайда
22
Слайд 22: Кривая Хабеннихта R =1+7 cos8F+ 4(sin8F)^2 + 3 (sin8F)^4
Изображение слайда
23
Слайд 23: Лист клевера R=1+1/3(2 cos3F — cos6F)
Изображение слайда
24
Слайд 24: Пируэты роз»
Изображение слайда
25
Слайд 25: Самостоятельная работа
І Вариант. (x ̸ 7)² + (y ̸ 12)² + (z ̸ 9)² =1 на интервале х,y ∊ [-7;7] с шагом 0.5 ;
ІІ Вариант. x ² ̸ 9 + y² ̸ 4 =2z на интервале х,y ∊ [- 5 ; 5 ] с шагом 0.5 ;
ІІІ Вариант. x ² ̸ (1 ̸ 3)² + y² ̸ (1 ̸ 6)² — z² ̸ (1 ̸ 2)² = 1 на интервале х,y ∊ [- 5 ; 4,5 ] с шагом 0.5 ;
І V Вариант. x ² ̸ 9 + y² ̸ 4 — z² = -1 на интервале х ∊ [- 3 ; 3 ] с шагом 0.5, y ∊[ — 2;2] с шагом 1.
Самостоятельная работа
Изображение слайда
26
Слайд 26: І Вариант. ІІ Вариант
Изображение слайда
27
Последний слайд презентации: ПОСТРОЕНИЕ КРИВЫХ В EXCEL: ІІІ Вариант. І V Вариант
Изображение слайда
Егорова Елена 
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.
Наговицина Ольга Витальевна 
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования
занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз
разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио.
Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь
полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и
особенно радует, что есть варианты с сочинением, без сочинения, только анализ
сочинения! Превосходно!
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
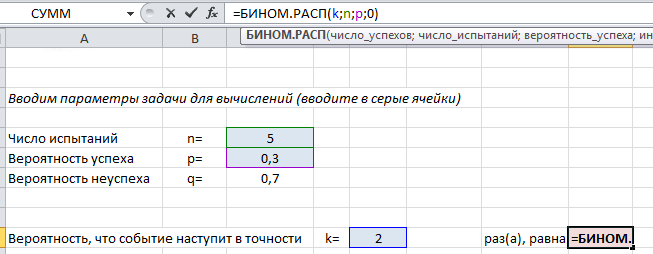
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
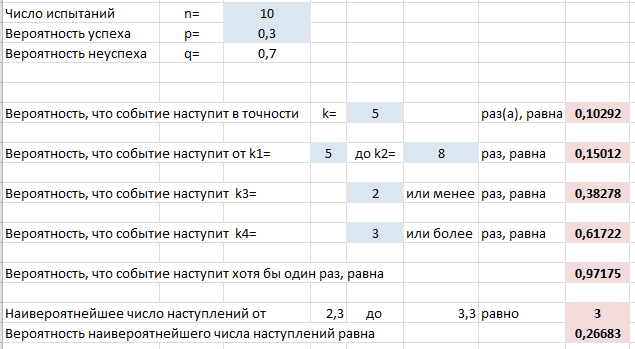
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
-
Группы статей
- Диаграммы и графики
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
источники:
http://excel2.ru/articles/ploskie-algebraicheskie-krivye-v-ms-excel
http://pedsovet.su/excel/48255_krasivye_grafiki_v_excel
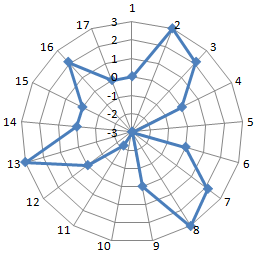
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
Как построить лепестковую диаграмму в Excel
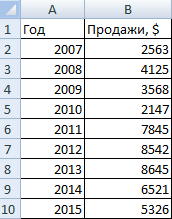
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
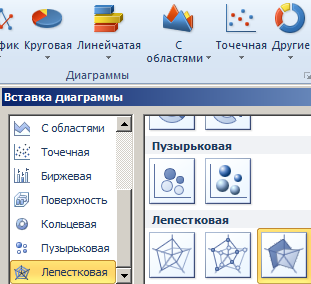
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
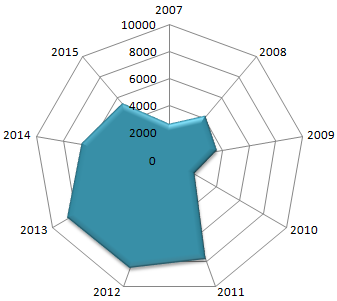
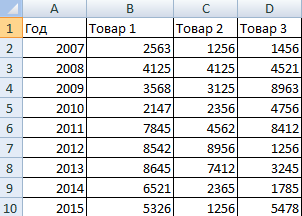
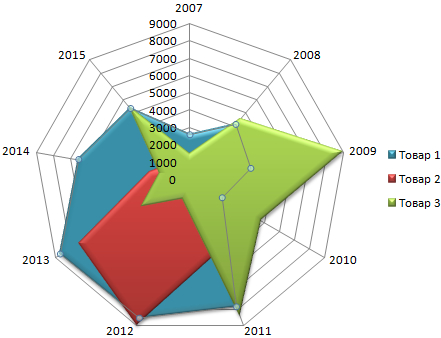
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
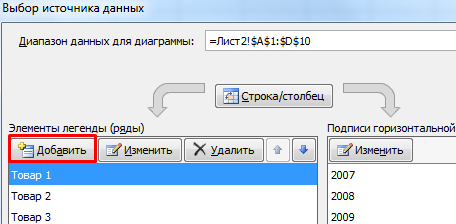
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
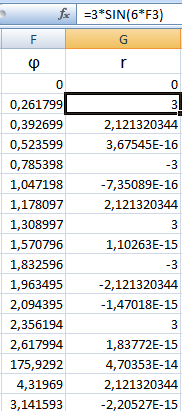
r = 3 * sin (6 * φ)/
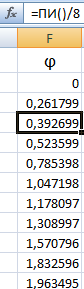
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.