Построим дискретный вариационный ряд
по затратам труда на 1 ц зерна.
Открываем лист Excel,
в ячейку А1 записываем условное обозначение
результативного признака – у, а в ячейки
А2:А31 значения затрат труда на 1 ц зерна.
В ячейки В2:В3 введём наименьшее и
следующее за ним значения признака 0,7
и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем
мышью правый нижний угол выделительной
рамки и потянем вниз до значения 1,5
(наибольшее значение признака). В ячейках
В2:В10 получим варианты признака в
ранжированном порядке. Для определения
частот проделаем следующие шаги:
1.Поставим курсор в ячейку С2.
2.Выберем Вставка,
Функция.
Выберем в категории
Статистические функции
функцию Частота и
нажмём ОК.
3.В поле данных
укажем ячейки А2:А31, а в поле интервалов
В2:В10.
4.Нажмём кнопку ОК.
5.Выделим ячейки
С2:С10.
6.Нажмём F2,
а затем комбинацию клавиш Shift+Ctrl+Enter.
В ячейках С2:С10 появятся
частоты.
Вычислим накопленные
частоты, которые потребуются для
дальнейших расчётов, путём последовательного
суммирования локальных частот (нарастающим
итогом). Так, первая плюс вторая частоты
дают накопленную частоту второго
варианта (1+2=3); прибавляя к ней третью
частоту, получим накопленную частоту
третьего варианта (3+4=7) и т.д.
Скопируем полученный
в Excel
вариационный ряд и построим таблицу.
Таблица 2
Дискретный вариационный ряд распределения
затрат труда на 1 ц зерна
|
Варианты |
Частоты |
Накопленные |
|
0,7 |
1 |
1 |
|
0,8 |
2 |
3 |
|
0,9 |
4 |
7 |
|
1,0 |
5 |
12 |
|
1,1 |
6 |
18 |
|
1,2 |
4 |
22 |
|
1,3 |
3 |
25 |
|
1,4 |
3 |
28 |
|
1,5 |
2 |
30 |
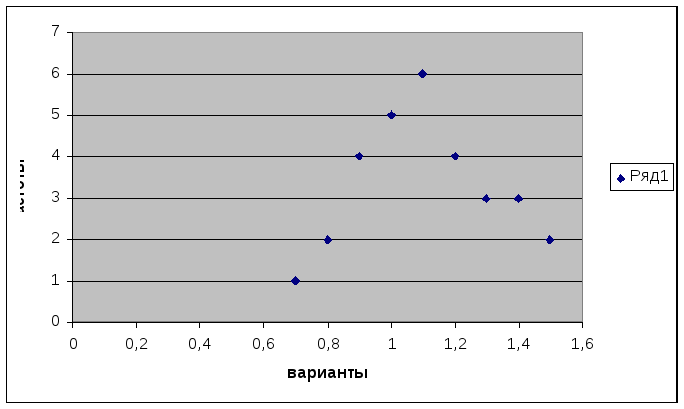
Построим
полигон распределения частот с помощью
Мастера
диаграмм.
Выберем точечную диаграмму, соединим
полученные точки отрезками, а крайние
точки с осью абсцисс в точках, отстоящих
от крайних на расстоянии шага.
Р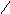
1. Полигон распределения сельскохозяйственных
предприятий по затратам труда на 1 ц
зерна
Рассмотрим
построение интервального вариационного
ряда.
Рис. 2. Построение интервального
вариационного ряда
На
листе Excel в ячейку А1 записываем условное
обозначение факторного признака – х,
в ячейки А2:А31 – значения факторного
признака – урожайности озимой пшеницы.
Произведём сортировку данных, для чего
выделяем диапазон данных, выбираем
Данные – Сортировка и в появившемся
окне «Сортировка диапазона» указываем
«по возрастанию», нажимаем ОК. Данные
в ячейках А2:А31 расположатся в ранжированном
порядке по возрастанию признака. По
формуле Стерджесса определяем количество
групп (интервалов). Для вычисления
десятичного логарифма lg30 выбираем
Мастер функций – Математические –
LOG10. В появившемся окне в поле Число
записываем число 30, десятичный логарифм
которого необходимо найти. Нажатием ОК
получаем этот логарифм 1,477121. . Подставляя
числовые данные в формулу (1), получим
число групп (интервалов) 5,9, округляем
до 6. По формуле (2) определяем величину
интервалов – шаг с такой же точностью,
с которой даны исходные данные (в данном
случае с точностью до десятых:
(30-20)/6≈1,7. Следовательно, совокупность
надо разбить на 6 интервалов. Получаем
шаг 1,7. Озаглавим следующие столбцы в
Excel словами «Интервалы», «Частоты»,
«Накопленные частоты», «Середины
интервалов». В ячейку В2 вписываем
минимальное значение признака Хmin=20,
в ячейку В3 формулу =В2+1,7, т.е. минимальное
значение плюс шаг. Копируем эту формулу
на 5 строк вниз. В результате в этих шести
строках (В3:В8) получим верхние границы
всех интервалов. Нижними границами
интервалов будут данные в соседних
верхних ячейках, т.е. для первого интервала
нижней границей будет содержание ячейки
В2, для второго В3 и для шестого В7.
Для
расчёта частот выберем Сервис — Анализ
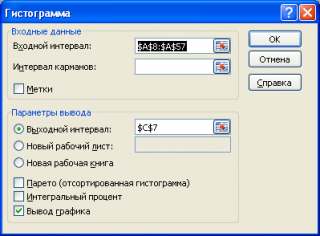
данных – Гистограмма и нажмём ОК. В
появившемся окне «Гистограмма» в поле
«Входной интервал» копируем исходные
данные (ячейки А2:А31), в поле «Интервал
карманов» — верхние границы интервалов
(ячейки В3:В8), в поле «Выходной интервал»
ячейки частот (С3:С8), нажимаем ОК. В ячейки
D3:D8 будут записаны частоты для всех
шести интервалов. Накопленные частоты
подсчитываем нарастающим итогом.
Для
построения диаграммы необходимо найти
середины интервалов. Для этого вводим
формулу расчёта середины интервала:
,
рассчитаем середину первого интервала.
Копируем формулу для остальных пяти
групп.
Для
построения диаграммы выделяем массив
частот и середин интервалов.
Далее в
Мастере диаграмм выбираем вид диаграммы
— гистограмму определённого вида.
Нажимаем кнопку Далее. В появившемся
окне выбираем вкладку Ряд, удаляем ряд
1, а в поле «Подписи оси х» копируем
середины интервалов. Нажимаем далее, в
появившемся окне выбираем вкладку
Заголовки. В поле «ось х (категорий)»
вписываем название факторного признака
(в данном случае урожайность, ц/га), в
поле «Ось у (значений)» вписываем частоты.
Нажимаем Далее, Готово. Появится
диаграмма, состоящая из столбиков,
отделённых друг от друга некоторым
зазором. Щёлкаем правой кнопкой мыши
на одном из столбиков диаграммы. В
раскрывающемся списке элементов щёлкаем
по кнопке Формат рядов данных. В
появившемся диалоговом окне активизируем
вкладку Параметры и в поле Ширина зазора
устанавливаем значение 0. Нажимаем ОК,
в результате чего гистограмма принимает
стандартный вид.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение рядов распределения
Любой ряд распределения характеризуется двумя элементами:
— варианта(хi) – это отдельные значения признака единиц выборочной совокупности. Для вариационного ряда варианта принимает числовые значения, для атрибутивного – качественные (например, х=«государственный служащий»);
— частота (ni) – число, показывающее, сколько раз встречается то или иное значение признака. Если частота выражена относительным числом (т.е. долей элементов совокупности, соответствующих данному значению варианты, в общем объеме совокупности), то она называется относительной частотойили частостью.
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Интервальный ряд может строиться как с интервалами равной длины (равноинтервальный ряд) так и с неодинаковыми интервалами, если это диктуется условиями статистического исследования. Например, может рассматриваться ряд распределения доходов населения со следующими интервалами:
где k – число интервалов, n – объем выборки. (Конечно, формула обычно дает число дробное, а в качестве числа интервалов выбирается ближайшее целое к полученному число.) Длина интервала в таком случае определяется по формуле
При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:
— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.
Проиллюстрируем процесс первичной обработки данных на следующих примерах.
Пример 1.1. имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Теперь построим полигон: выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Пример 1.2. Имеются данные о выбросах загрязняющих веществ из 50 источников:
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Составить равноинтервальный ряд, построить гистограмму
Внесем массив данных в лист Excel, он займет диапазон А1:J5 Как и в предыдущей задаче, определим объем выборки n, минимальное и максимальное значения в выборке. Поскольку теперь требуется не дискретный, а интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу =1+3,322*LOG10(B7).
Рис.1.4. Пример 2. Построение равноинтервального ряда
Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(В9-В8)/С10.
Рис.1.5. Пример 2. Построение равноинтервального ряда
Теперь заполним массив «карманов» при помощи функции ЧАСТОТА, как это было сделано в примере 1.
Рис.1.6. Пример 2. Построение равноинтервального ряда
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
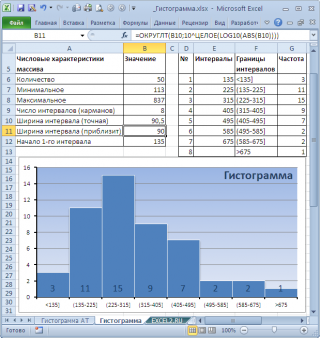
Расчет ширины интервала и таблица интервалов приведены в файле примера на листе Гистограмма . Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() . О вводе этой функции см. статью Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL .
Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Стиль и внешний вид гистограммы
После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:
- добавить заголовок и другие дополнительные данные для отображения. Для того, чтобы добавить данные на график, кликните на пункт “Добавить элемент диаграммы”, затем, выберите нужный пункт из выпадающего списка:
Вы также можете использовать кнопки быстрого доступа к редактированию элементов гистограммы, стиля и фильтров:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Например:
Для распределения учеников по росту получаем: begin S^2=fraccdot 104,1approx 105,1\ sapprox 10,3 end Коэффициент вариации: $ V=fraccdot 100textapprox 6,0textlt 33text $ Выборка однородна. Найденное значение среднего роста (X_)=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
- если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
1. Построение вариационного ряда
Нужно выделить ячейки содержащие результаты эксперимента, и воспользоваться операцией сортировка по возрастанию (либо с панели инструментов, либо через главное меню Данные>Сортировка), и в появившемся окне сообщения – «обнаружены данные выходящие за пределы выделенного диапазона» выбрать действие – «сортировать в пределах указанного выделения»
2. Построение группировочного статистического ряда
Для вычисления абсолютной частоты нужна статистическая функция ЧАСТОТА. При её использовании нужно выполнить следующие действия:
а) выделить весь диапазон ячеек, в которых будет располагаться результат подсчёта частот (т.е. это ячейки под заголовком Абсолютная частота в количестве равном числу промежутков)
b) не снимая выделения, поставить курсор в строку формул и нажать на кнопку вставка функции (чуть левее курсора) или Главное меню – вставка – формула.
с) выбрать функцию ЧАСТОТА
d) ввести Массив_данных – диапазон, содержащий элементы выборки (в файле 2.xls это ячейки) B2:B101
e) ввести Массив_интервалов – диапазон ячеек под заголовком Начало промежутка начиная со строчки, соответствующей промежутку под номером 2 до строчки, соответствующей последнему промежутку.
f) нажмите на кнопку ОК и после закрытия окна для ввода аргументов функции ЧАСТОТА поставьте курсор обратно в строку формул.
g) Нажмите на три кнопки Ctrl+Shift+Enter (сначала на первые две, а потом, не отпуская их, нажмите на Enter).
Примечание. Формулу вычисления абсолютной частоты необходимо ввести как формулу массива. Нажатие комбинации клавиш CTRL+SHIFT+ENTER позволяет определить формулу как формулу массива. Если формула не будет введена как формула массива, единственное значение будет равно 1.
В результате изначально выделенный диапазон будет содержать абсолютные частоты попадания во все промежутка. Проверьте, что сумма всех абсолютных частот равна общему числу элементов выборки (100).
3. Построение гистограммы группировочного статистического ряда
Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
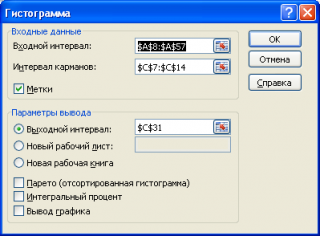
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
Перед тем как анализировать полученный результат —
отсортируйте исходный массив данных
.
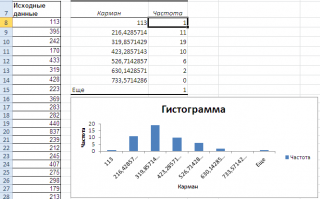
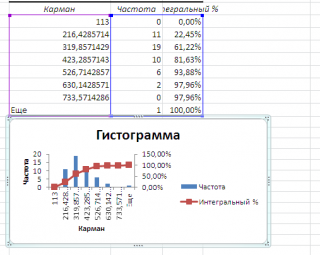
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
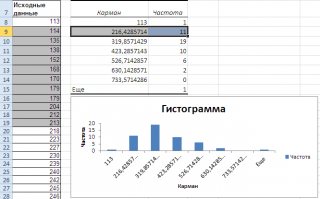
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
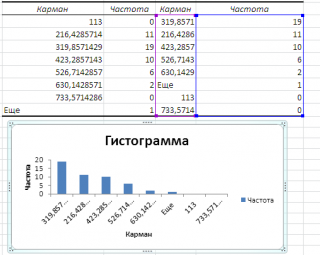
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
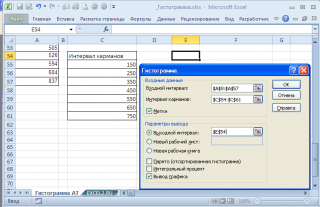
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
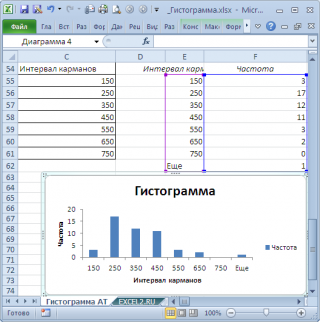
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
В итоге можно добиться вот такого результата.
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
Одной из разновидностей гистограмм является
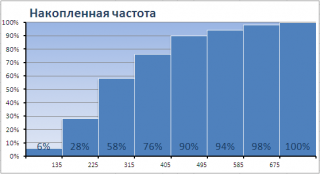
график накопленной частоты
(cumulative frequency plot).
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).