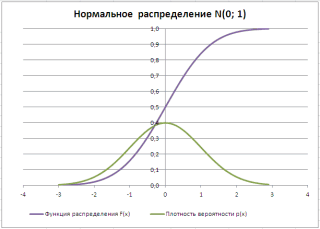
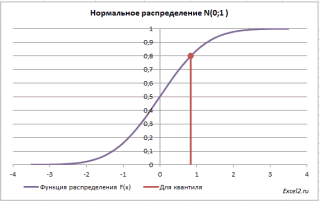
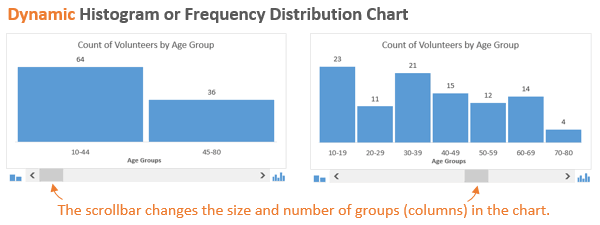
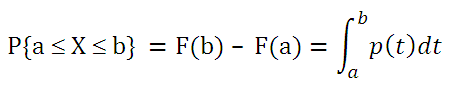Как построить интегральную кривую в excel - Word и Excel

Требуется построить диаграмму стандартного нормального интегрального распределения (стандартное нормальное распределение имеет М = 0 и = 1), используя функцию НОРМСТРАСП.

1. В ячейку A3 введем символ х, а в ячейку ВЗ — символ функции плотности вероятности f(x).

2. Вычислим нижнюю М — За границу диапазона значений х, для чего установим курсор в ячейку С2 и введем формулу =0-3*1, а также верхнюю границу — в ячейку Е2 введем формулу =0+3*1.

3. Скопируем формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифметической прогрессии.

4. Создадим последовательность значений х в требуемом диапазоне, для чего установим курсор в ячейку А4 и выполним команду меню Правка/Заполнить/Прогрессия.

5. В открывшемся окне диалога Прогрессия установим переключатели арифметическая, по столбцам, в поле Шаг введем значение 0,5, а в поле Предельное значение — число, равное верхней границе диапазона.

Функция НОРМРАСПР в EXCEL

6. Щелкнем на кнопке ОК. В диапазоне А4:А16 будет сформирована последовательность значений х.

7. Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций — НОРМРАСП.

8. Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее — введем число 0, для параметра Стандартное_откл — число 1, для параметра Интегральное — число 0 (весовая).

Диаграмма нормального интегрального распределения в EXCEL

9. Используя маркер буксировки, скопируем полученную формулу в диапазон ячеек В5:В16.

10. Выделим диапазон полученных табличных значений функции f(х) (ВЗ:В16) и выполним команду меню Вставка/Диаграмма. В окне Мастер диаграмм во вкладке Стандартные выберем График, а в поле Вид — вид графика, щелкнем на кнопке Далее.

11. В окне Мастер диаграмм (шаг 2) выберем закладку Ряд. В поле Подписи оси х укажем ссылку на диапазон, содержащий значения х (А4:А16). Щелкнем на кнопке Далее.
В окне Мастер диаграмм (шаг 3) введем подписи: Название диаграммы, Ось х, Ось у. Щелкнем на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности .

Нормальное распределение. Построение графика в Excel. Концепция шести сигм

Наверное, не все знают, что в Excel есть встроенная функция для построения нормального распределения. Графики нормального распределения часто используются для демонстрации идей статистической обработки данных.

Функция НОРМРАСП имеет следующий синтаксис:

НОРМРАСП (Х; среднее; стандартное_откл; интегральная)

Х — аргумент функции; фактически НОРМРАСП можно трактовать как y=f(x); при этом функция возвращает вероятность реализации события Х

Среднее (µ) — среднее арифметическое распределения; чем дальше Х от среднего, тем ниже вероятность реализации такого события

Стандартное_откл (σ) — стандартное отклонение распределения; мера кучности; чем меньше σ, тем выше вероятность у тех Х, которые расположены ближе к среднему

Интегральная — логическое значение, определяющее форму функции. Если «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения, тот есть суммарную вероятность всех событий для аргументов от -∞ до Х; если «интегральная» имеет значение ЛОЖЬ, возвращается вероятность реализации события Х, точнее говоря, вероятность событий находящихся в некотором диапазоне вокруг Х

Например, для µ=0 имеем:

Скачать заметку в формате Word, пример в формате Excel

Здесь по оси абсцисс единица измерения – σ, или (что то же самое), можно сказать, что график построен для σ = 1. То есть, «-2» на графике означает -2σ. По оси ординат шкала убрана умышленно, так как она лишена смысла. Точнее говоря, высота кривой зависит от плотности точек на оси абсцисс, по которым мы строим график. Например, если на интервал от 0 до 1σ приходится 10 точек, то высота в максимуме составит 4%, а если 20 точек – 2%. Здесь проценты означают вероятность попадания случайной величины в узкий диапазон окрестности точки на оси абсцисс. Зато имеет смысл площадь под кривой на определенном интервале. И эта площадь не зависит от плотности точек. Так, например, площадь под кривой на интервале от 0 до 1σ составляет 34,13%. Это значение можно интерпретировать следующим образом: с вероятностью 68,26% случайная величина Х попадет в диапазон µ ± σ.

Теперь, наверное, вам будет лучше понятен смысл выражения «качество шести сигм». Оно означает, что производство налажено таким образом, что случайная величина Х (например, диаметр вала) находясь в диапазон µ ± 6σ, всё еще удовлетворяет техническим условиям (допускам). Это достигается за счет значительного уменьшения сигмы, то есть случайная величина Х очень близка к нормативному значению µ. На графике ниже представлено три ситуации, когда границы допуска остаются неизменными, а благодаря повышению качества (уменьшению вариабельности, сужению сигма) доля брака сокращается:

На первом рисунке только 1,5σ попадают в границы допуска, то есть только 86,6% деталей являются годными. На втором рисунке уже 3σ попадают в границы допуска, то есть 99,75% являются годными. Но всё еще 25 деталей из каждых 10 000 произведенных являются браком. На третьем рисунке целых 6σ попадают в границы допуска, то есть в брак попадут только две детали на миллиард изготовленных!

Вообще-то говоря, измерение качества в терминах сигм использует не совсем нормальное распределение. 🙂 Вот что пишет на эту тему Википедия:

Опыт показывает, что показатели процессов имеют тенденцию изменяться с течением времени. В результате со временем в промежуток между границами поля допуска будет входить меньше, чем было установлено первоначально. Опытным путём было установлено, что изменение параметров во времени можно учесть с помощью смещения в 1,5 сигма. Другими словами, с течением времени длина промежутка между границами поля допуска под кривой нормального распределения уменьшается до 4,5 сигма вследствие того, что среднее процесса с течением времени смещается и/или среднеквадратическое отклонение увеличивается.

Широко распространённое представление о «процессе шесть сигма» заключается в том, что такой процесс позволяет получить уровень качества 3,4 дефектных единиц на миллион готовых изделий при условии, что длина под кривой слева или справа от среднего будет соответствовать 4,5 сигма (без учёта левого или правого конца кривой за границей поля допуска). Таким образом, уровень качества 3,4 дефектных единиц на миллион готовых изделий соответствует длине промежутка 4,5 сигма, получаемых разницей между 6 сигма и сдвигом в 1,5 сигма, которое было введено, чтобы учесть изменение показателей с течением времени. Такая поправка создана для того, чтобы предупредить неправильною оценку уровня дефектности, встречающееся в реальных условиях.

С моей точки зрения, не вполне внятное объяснение. Тем не менее, во всем мире принята следующая таблица соответствия числа дефектов и уровня качества в сигмах:

Число сигм	Число дефектов на миллион измерений	Процент дефектов (несоответствий)	Уровень качества
6σ	3,4	0,00034%	идеал
5σ	233	0,023%	мировой уровень
4σ	6210	0,62%	приемлемый уровень
3σ	66 807	6,68%	недостаточный уровень
2σ	308 537	30,9%	неприемлемый уровень
1σ	691 462	69,1%

Для сравнения приведу таблицу для нормального распределения:

Источник

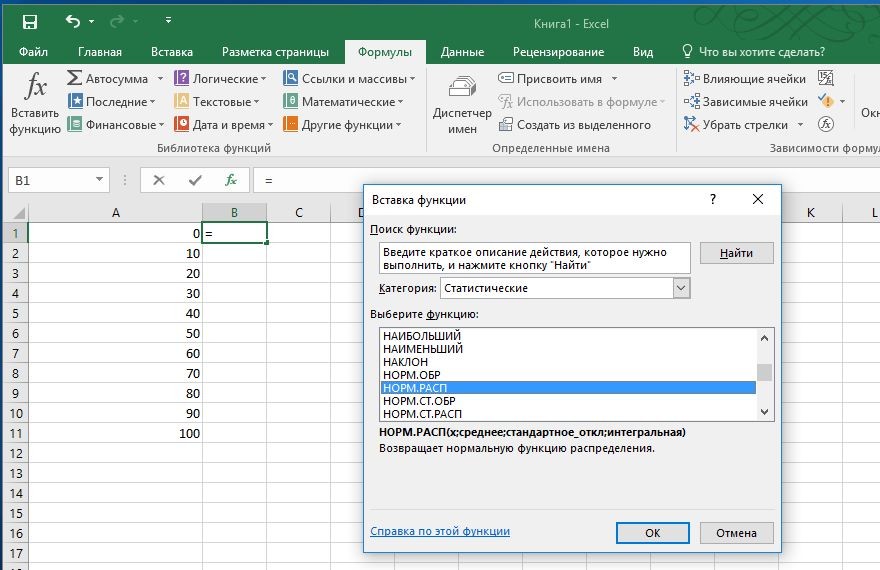
Звучит заумно, но на деле все просто. Заполните ячейки от А1 до А11 исходными данными — в примере числами от 0 до 100 с шагом в десять. Выделите ячейку В1, откройте вкладку «Формулы» и щелкните по кнопке «Вставить функцию».

Выбор статистической формулы. Для отображения нормального распределения в Excel предусмотрена функция «НОРМ.РАСП».

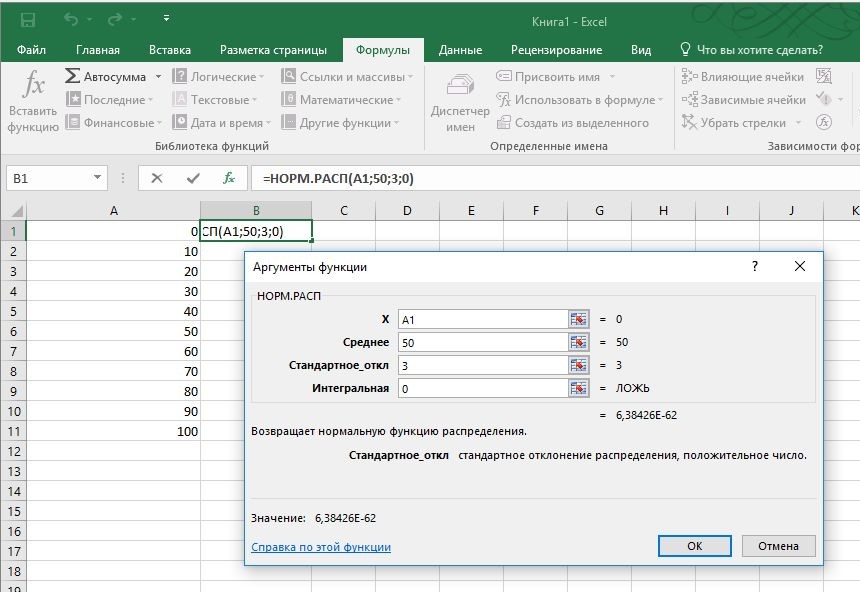
В качестве категории выберите значение «Статистические», в качестве функции — «НОРМ.РАСП». Подтвердите выбор, нажав кнопку ОК. Откроется новое окно. В строку «Х» введите значение «A1», в строку «Интегральная» — значение «0». Среднее составит «50», стандартное отклонение же можно свободно выбирать.

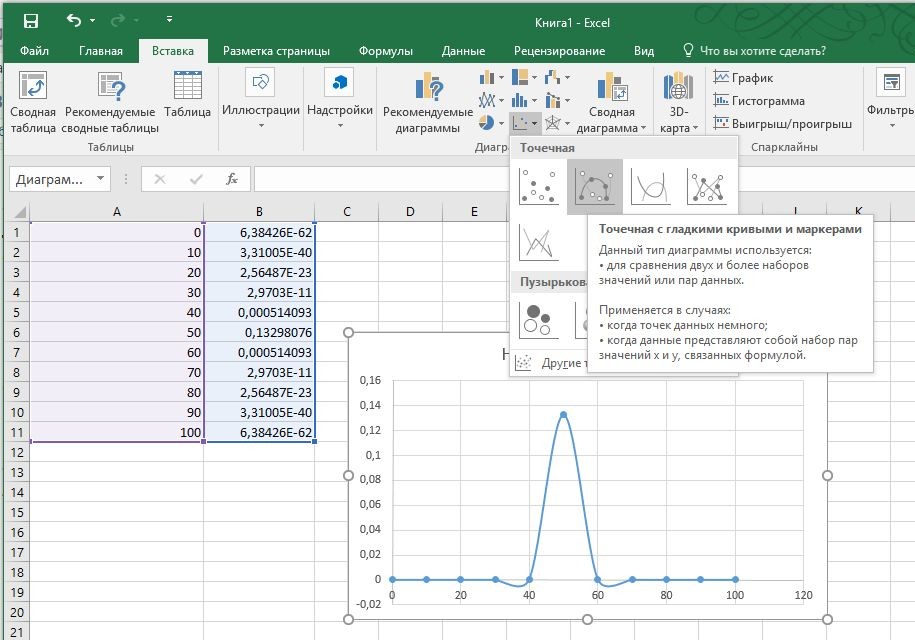
Когда вы закроете окно, Excel отобразит первое значение в ячейке B1. Теперь потяните за правый нижний угол ячейки вниз, затем выделите все значения — то есть ячейки от A1 до B11.

На вкладке «Вставка» в группе «Диаграммы» в разделе «Точечная» вы найдете несколько диаграмм, на которых можно отобразить нормальное распределение.

Фото: компания-производитель

Источник

В статистике колоколообразная кривая (также известная как стандартное нормальное распределение или кривая Гаусса) представляет собой симметричный график, который иллюстрирует тенденцию данных к кластеризации вокруг центрального значения или среднего значения в данном наборе данных.

Ось Y представляет относительную вероятность появления данного значения в наборе данных, в то время как ось X отображает сами значения на диаграмме, чтобы создать колоколообразную кривую, отсюда и название.

График помогает нам проанализировать, является ли конкретное значение частью ожидаемой вариации или статистически значимым и, следовательно, требует более внимательного изучения.

Поскольку в Excel нет встроенных решений, вам придется построить график самостоятельно. Вот почему мы разработали надстройку Chart Creator — инструмент, который позволяет создавать расширенные диаграммы Excel всего за несколько щелчков мышью.

В этом пошаговом руководстве вы узнаете, как с нуля создать кривую нормального распределения в Excel:

Чтобы построить кривую Гаусса, вам нужно знать две вещи:

Значение (также известное как стандартное измерение). Это определяет центр кривой, который, в свою очередь, характеризует положение кривой.
Стандартное отклонение (SD) измерений. Это определяет разброс ваших данных в нормальном распределении — или, говоря простым языком, насколько широкой должна быть кривая. Например, на приведенной выше колоколообразной кривой одно стандартное отклонение среднего представляет собой диапазон между оценками экзамена от 53 до 85.

Чем ниже SD, тем выше кривая и меньше будут разбросаны ваши данные, и наоборот.

Стоит упомянуть правило 68-95-99,7, которое можно применить к любой кривой нормального распределения, что означает, что примерно 68% ваших данных будет размещено в пределах одного стандартного отклонения от среднего, 95% — в пределах двух стандартных отклонений и 99,7% — в пределах. три SD.

Теперь, когда вы знаете основы, давайте перейдем от теории к практике.

Начиная

В целях иллюстрации предположим, что у вас есть результаты теста 200 учеников и вы хотите выставить им оценки «по кривой», то есть оценки учеников будут основаны на их относительной успеваемости по отношению к остальной части класса:

Шаг № 1: Найдите среднее значение.

Как правило, вам с самого начала задаются среднее значение и стандартное отклонение, но если это не так, вы можете легко вычислить эти значения всего за несколько простых шагов. Давайте сначала разберемся со средним.

Поскольку среднее значение указывает среднее значение выборки или совокупности данных, вы можете найти стандартное измерение, используя функцию СРЕДНЕЕ.

Введите следующую формулу в любую пустую ячейку (F1 в этом примере) рядом с вашими фактическими данными (столбцы A а также B), чтобы вычислить среднее значение экзаменационных баллов в наборе данных:

Небольшое примечание: чаще всего вам может потребоваться округлить вывод формулы в большую сторону. Для этого просто оберните его функцией ROUND следующим образом:

1	= ОКРУГЛ (СРЕДНИЙ (B2: B201); 0)

Шаг № 2: Найдите стандартное отклонение.

Один упал, один остался. К счастью, в Excel есть специальная функция, которая сделает за вас всю грязную работу по поиску стандартного отклонения:

1	= СТАНДОТКЛОН.P (B2: B201)

Опять же, формула выбирает все значения из указанного диапазона ячеек (B2: B201) и вычисляет его стандартное отклонение — не забудьте также округлить результат.

1	= ОКРУГЛ (СТАНДОТКЛОН.P (B2: B201); 0)

Шаг № 3: Установите значения оси X для кривой.

По сути, диаграмма представляет собой огромное количество интервалов (представьте их как шаги), соединенных линией, чтобы создать плавную кривую.

В нашем случае значения оси X будут использоваться для иллюстрации конкретной оценки экзамена, а значения оси Y будут указывать нам вероятность того, что студент получит этот результат на экзамене.

Технически вы можете включить столько интервалов, сколько захотите — вы можете легко стереть избыточные данные позже, изменив масштаб горизонтальной оси. Просто убедитесь, что вы выбрали диапазон, включающий три стандартных отклонения.

Давайте начнем подсчет с одного (так как студент не может получить отрицательный результат на экзамене) и дойдем до 150 — неважно, 150 это или 1500 — чтобы создать еще одну вспомогательную таблицу.

Выберите любую пустую ячейку под данными диаграммы (например, E4) и введите “1,” значение, определяющее первый интервал.
Перейдите к Дом таб.
в Редактирование группа, выберите «Наполнять.”
Под «Серия в,» Выбрать «Столбец.”
Для «Значение шага,» тип “1.” Это значение определяет приращения, которые будут автоматически добавляться, пока Excel не достигнет последнего интервала.
Для «Стоп-значение,» тип «150,” значение, которое соответствует последнему интервалу, и нажмите «OK.”

Чудом 149 ячеек в столбце E (E5: E153) были заполнены значениями от 2 до 150.

ПРИМЕЧАНИЕ. Не скрывайте исходные ячейки данных, как показано на снимках экрана.. В противном случае методика не сработает.

Шаг №4: Вычислите значения нормального распределения для каждого значения оси x.

Теперь найдите значения нормального распределения — вероятность того, что студент получит определенный балл за экзамен, представленный определенным значением оси X — для каждого из интервалов. К счастью для вас, в Excel есть рабочая лошадка для выполнения всех этих вычислений: функция НОРМ.РАСП.

Введите следующую формулу в ячейку справа (F4) вашего первого интервала (E4):

1	= НОРМ.РАСП (E4; $ F $ 1; $ F $ 2; ЛОЖЬ)

Вот декодированная версия, которая поможет вам соответствующим образом настроить:

1	= НОРМ.РАСП ([первый интервал], [среднее (абсолютное значение)], [стандартное отклонение (абсолютное значение), ЛОЖЬ)

Вы блокируете среднее значение и стандартное отклонение, чтобы можно было легко выполнить формулу для оставшихся интервалов (E5: E153).

Теперь дважды щелкните маркер заполнения, чтобы скопировать формулу в остальные ячейки (F5: F153).

Шаг № 5: Создайте диаграмму рассеяния с плавными линиями.

Наконец, пришло время строить колоколообразную кривую:

Выберите любое значение в вспомогательной таблице, содержащей значения осей x и y (E4: F153).
Перейти к Вставлять таб.
Щелкните значок «Вставить точечную (X, Y) или пузырьковую диаграмму» кнопка.
Выбирать «Разброс с плавными линиями ».

Шаг № 6: Настройте таблицу меток.

Технически у вас есть кривая колокола. Но его будет трудно прочитать, поскольку в нем отсутствуют какие-либо данные, описывающие это.

Давайте сделаем нормальное распределение более информативным, добавив метки, иллюстрирующие все значения стандартного отклонения ниже и выше среднего (вы также можете использовать их для отображения z-значений).

Для этого создайте еще одну вспомогательную таблицу следующим образом:

Сначала скопируйте среднее значение (F1) рядом с соответствующей ячейкой в столбце X-Value (I5).

Затем вычислите значения стандартного отклонения ниже среднего, введя эту простую формулу в ячейка I4:

Проще говоря, формула вычитает сумму предыдущих значений стандартного отклонения из среднего. Теперь перетащите маркер заполнения вверх, чтобы скопировать формулу в оставшиеся две ячейки (I2: I3).

Повторите тот же процесс для стандартных отклонений выше среднего, используя зеркальную формулу:

Таким же образом выполните формулу для двух других ячеек (I7: I8).

Наконец, заполните значения метки оси Y (J2: J8) с нулями, так как вы хотите, чтобы маркеры данных располагались на горизонтальной оси.

Шаг № 7: Вставьте данные метки в диаграмму.

Теперь добавьте все данные, которые вы подготовили. Щелкните правой кнопкой мыши график и выберите «Выберите данные.”

В появившемся диалоговом окне выберите «Добавлять.”

Выделите соответствующие диапазоны ячеек из вспомогательной таблицы —I2: I8 для «Значения серии X» а также J2: J8 для «Значения серии Y »-и нажмите «OK.”

Шаг № 8: Измените тип диаграммы для серии этикеток.

Наш следующий шаг — изменить тип диаграммы недавно добавленной серии, чтобы маркеры данных отображались в виде точек. Для этого щелкните правой кнопкой мыши график диаграммы и выберите «Изменить тип диаграммы.”

Затем создайте комбинированную диаграмму:

Перейдите к Комбо таб.
Для Серия «Series2», изменение «Тип диаграммы» к «Разброс.”
- Примечание. Убедитесь, что «Серия1»Остается как«Скаттер с плавными линиями. » Иногда Excel изменяет его, когда вы делаете Комбо Также убедитесь, что «Серия1”Не перемещается на вторичную ось — флажок рядом с типом диаграммы не должен быть отмечен.
Нажмите «Ok.”

Шаг № 9: Измените масштаб горизонтальной оси.

Отцентрируйте диаграмму на колоколообразной кривой, отрегулировав масштаб горизонтальной оси. Щелкните правой кнопкой мыши горизонтальную ось и выберите «Ось формата»Из меню.

Когда появится панель задач, сделайте следующее:

Перейти к Параметры оси таб.
Установить Минимальные границы значение «15.”
Установить Максимальные границы значение «125.”

Вы можете настроить диапазон шкалы оси по своему усмотрению, но, поскольку вы знаете диапазоны стандартного отклонения, установите значения границ немного дальше от каждого из ваших третьих стандартных отклонений, чтобы показать «хвост» кривой.

Шаг № 10: Вставьте и разместите метки пользовательских данных.

По мере того, как вы совершенствуете свою диаграмму, не забудьте добавить пользовательские метки данных. Сначала щелкните правой кнопкой мыши любую точку, представляющую Серия «Series2» и выберите «Добавьте метки данных.”

Затем замените метки по умолчанию на те, которые вы установили ранее, и поместите их над маркерами данных.

Щелкните правой кнопкой мыши на любом Серия «Series2» метка данных.
Выбирать «Отформатируйте метки данных.”
На панели задач переключитесь на Параметры метки таб.
Проверить «Значение X» коробка.
Снимите флажок «Значение Y» коробка.
Под «Положение ярлыка,» выбирать «Выше.”

Кроме того, теперь вы можете удалить линии сетки (щелкните их правой кнопкой мыши> Удалить).

Шаг № 11: Перекрасить маркеры данных (необязательно).

Наконец, перекрасьте точки, чтобы они соответствовали вашему стилю диаграммы.

Щелкните правой кнопкой мыши любой Серия «Series2» метка данных.
Щелкните значок «Наполнять» кнопка.
Выберите свой цвет из появившейся палитры.

Также удалите границы вокруг точек:

Снова щелкните правой кнопкой мыши тот же маркер данных и выберите «Контур.”
Выбирать «Без контура.”

Шаг № 12: Добавьте вертикальные линии (необязательно).

В качестве окончательной настройки вы можете добавить на диаграмму вертикальные линии, чтобы подчеркнуть значения SD.

Выберите график диаграммы (таким образом линии будут вставлены прямо в диаграмму).
Перейти к Вставлять таб.
Щелкните значок «Формы» кнопка.
Выбирать «Линия.”

Удерживайте «СДВИГ» при перетаскивании мыши, чтобы нарисовать идеально вертикальные линии от каждой точки до того места, где каждая линия пересекается с колоколообразной кривой.

Измените заголовок диаграммы, и ваша улучшенная кривая колокола будет готова отображать ваши ценные данные о распределении.

И вот как вы это делаете. Теперь вы можете выбрать любой набор данных и создать колоколообразную кривую нормального распределения, выполнив эти простые шаги!

Как сделать график распределения в excel?

Очень давно не писал блог. Расслабился совсем. Ну ничего, исправляюсь.

Продолжаю новую рубрику блога, посвященную анализу данных с помощью всем известного Microsoft Excel.

В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: естественно, в первую очередь я скажу, что металлургии, а также в экономике, биологии, политике, социологии и… много где еще. Статья эта будет, как несложно догадаться по ее названию, про использование некоторых средств статистического анализа, а именно — гистограммам.
Ну, поехали.

Статистический анализ в Excel можно осуществлять двумя способами:
• С помощью функций
• С помощью средств надстройки «Пакет анализа». Ее, как правило, еще необходимо установить.

Чтобы установить пакет анализа в Excel, выберите вкладку «Файл» (а в Excel 2007 это круглая цветная кнопка слева сверху), далее — «Параметры», затем выберите раздел «Надстройки». Нажмите «Перейти» и поставьте галочку напротив «Пакет анализа».

А теперь — к построению гистограмм распределения по частоте и их анализу.

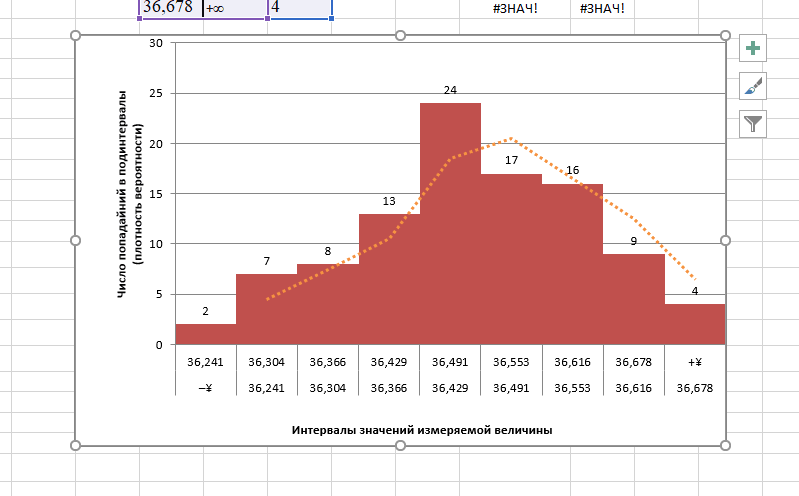
Речь пойдет именно о частотных гистограммах, где каждый столбец соответствует частоте появления* значения в пределах границ интервалов. Например, мы хотим посмотреть, как у нас выглядит распределение значения предела текучести стали S355J2 в прокате толщиной 20 мм за несколько месяцев. В общем, хотим посмотреть, похоже ли наше распределение на нормальное (а оно должно быть таким).

*Примечание: для металловедческих целей типа оценки размера зерна или оценки объемной доли частиц этот вид гистограмм не пойдет, т.к. там высота столбика соответствует не частоте появления частиц определенного размера, а доле объема (а в плоскости шлифа — площади), которую эти частицы занимают.

График нормального распределения выглядит следующим образом:

График функции Гаусса

Мы знаем, что реально такой график может быть получен только при бесконечно большом количестве измерений. Реально же для конечного числа измерений строят гистограмму, которая внешне похожа на график нормального распределения и при увеличении количества измерений приближается к графику нормального распределения (распределения Гаусса).

Построение гистограмм с помощью программ типа Excel является очень быстрым способом проверки стабильности работы оборудования и добросовестности коллектива: если получим «кривую» гистограмму, значит, либо прибор не исправен или мы данные неверно собрали, либо кто-то где-то преднамеренно мухлюет или же просто неверно использует оборудование.

А теперь — построение гистограмм!

Способ 1-ый. Халявный.

Идем во вкладку «Анализ данных» и выбираем «Гистограмма».
Выбираем входной интервал.
Здесь же предлагается задать интервал карманов, т.е. те диапазоны, в пределах которых будут лежать наши значения. Чем больше значений в интервале — тем выше столбик гистограммы. Если мы оставим поле «Интервалы карманов» пустым, то программа вычислит границы интервалов за нас.
Если хотим сразу же вывести график,то ставим галочку напротив «Вывод графика».
Нажимаем «ОК».
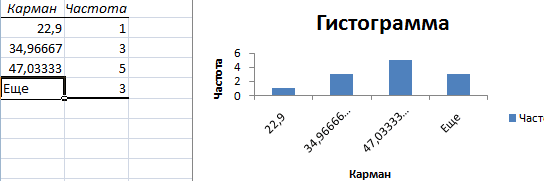
Вот, вроде бы, и все: гистограмма готова. Теперь нужно сделать так, чтобы по вертикальной оси отображалась не абсолютная частота, а относительная.
Под появившейся таблицей со столбцами «Карман» и «Частота» под столбцом «Частота» введем формулу «=СУММ» и сложим все абсолютные частоты.
К появившейся таблице со столбцами «Карман» и «Частота» добавим еще один столбец и назовем его «Относительная частота».
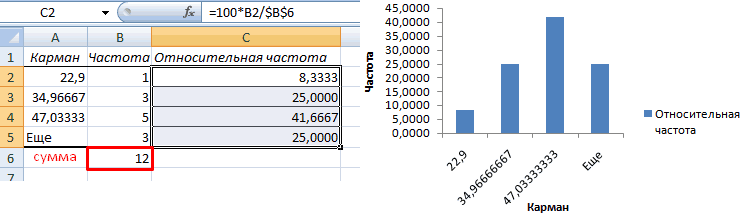
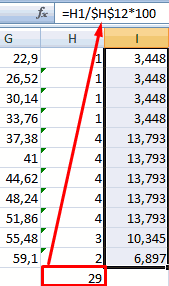
Во всех ячейках нового столбца введем формулу, которая будет рассчитывать относительную частоту: 100 умножить на абсолютную частоту (ячейка из столбца «частота») и разделить на сумму, которую мы вычислил в п. 7.

Способ 2-ой. Трудный, но интересный.

Будет полезен тому, кто по каким-либо причинам не смог установить Пакет анализа.

Перво-наперво нужно задать интервалы тех самых карманов, которые мы не стали вычислять в способе, описанном выше.
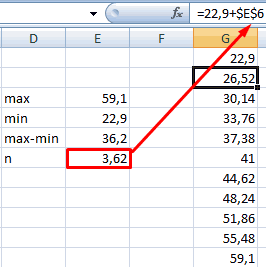
Интервал карманов вычисляют так: разность максимального значения и минимального значений массива, деленная на количество интервалов: (Xmax-Xmin)/n.
Для оценки оптимального для нашего массива данных количества интервалов можно воспользоваться формулой Стерджесса: n

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Поделиться ссылкой:

Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.

Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.

Характеристики нормального распределения

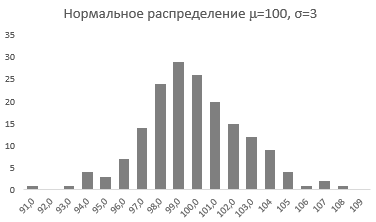
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.

Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.

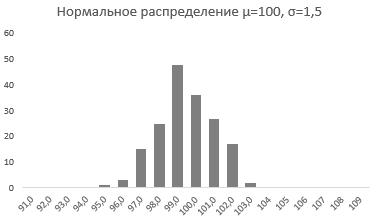
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма

Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.

Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.

Создание массива с нормальным распределением

Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:

=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)

Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.

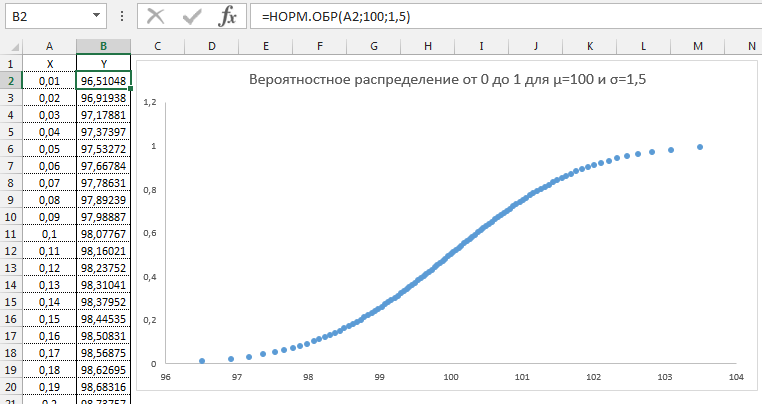
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.

Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.

Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:

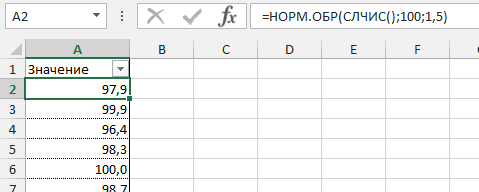
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)

Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.

Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.

Построение графика нормального распределения

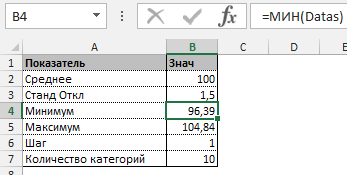
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.

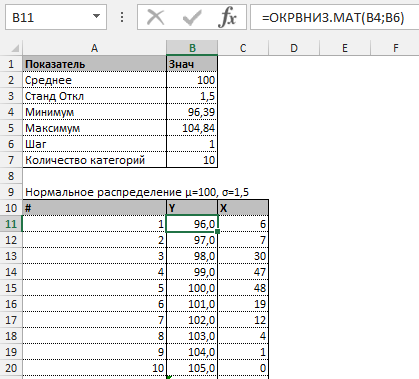
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:

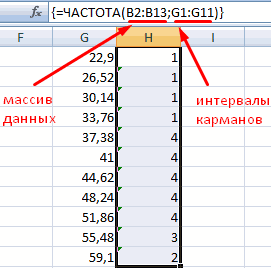
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.

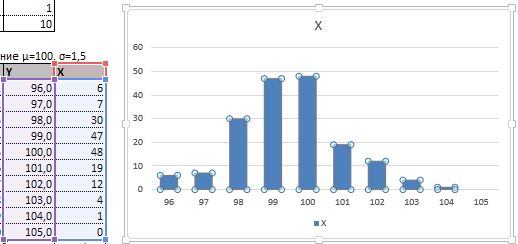
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.

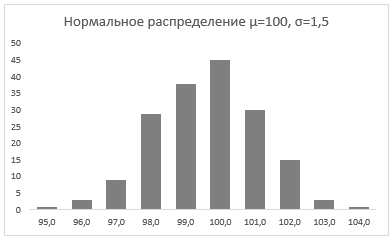
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.

Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.

Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.

Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.

Как построить диаграмму распределения в Excel

График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.

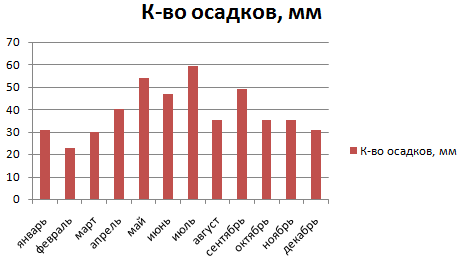
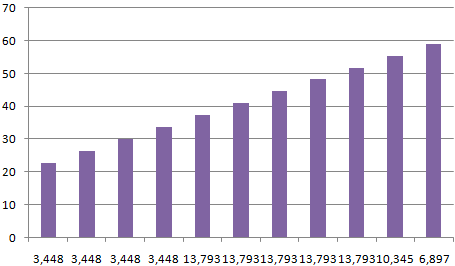
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.

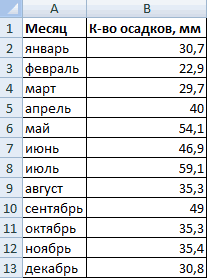
Имеются следующие данные о количестве выпавших осадков:

Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):

Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:

После нажатия ОК получаем такой график с таблицей:

В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.

Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.

Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:

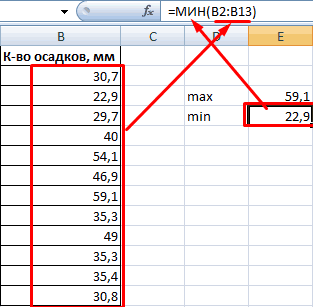
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.

Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».

Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.

Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:

Вычислим относительные частоты (как в предыдущем способе).

Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».

Частота распределения заданных значений:

Круговые диаграммы для иллюстрации распределения

С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.

С помощью любой круговой диаграммы можно показать распределение в том случае, если

имеется только один ряд данных;
все значения положительные;
практически все значения выше нуля;
не более семи категорий;
каждая категория соответствует сегменту круга.

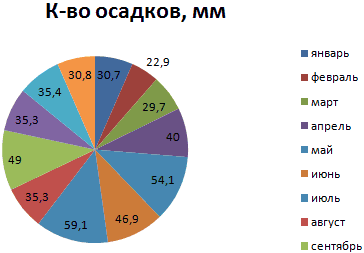
На основании имеющихся данных о количестве осадков построим круговую диаграмму.

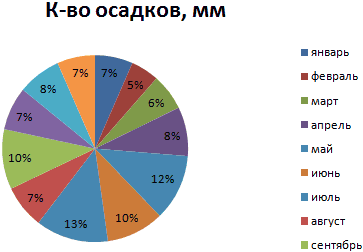
Доля «каждого месяца» в общем количестве осадков за год:

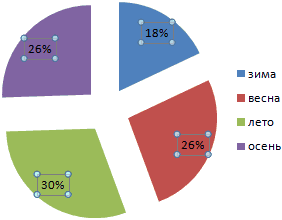
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:

Получили количество выпавших осадков в процентном выражении по сезонам.

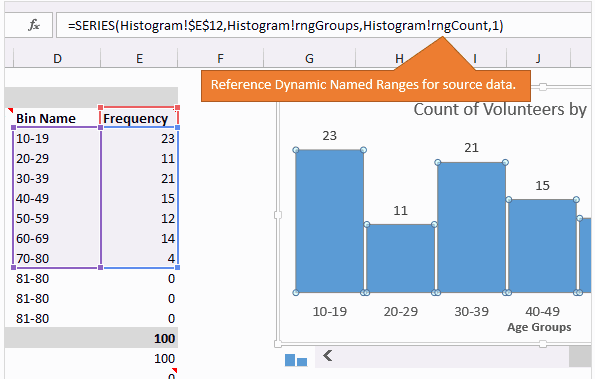
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.

Уровень сложности: продвинутый.

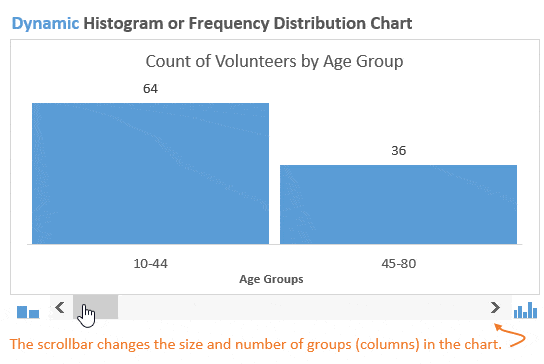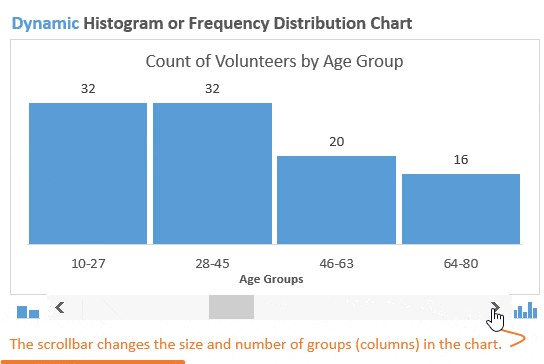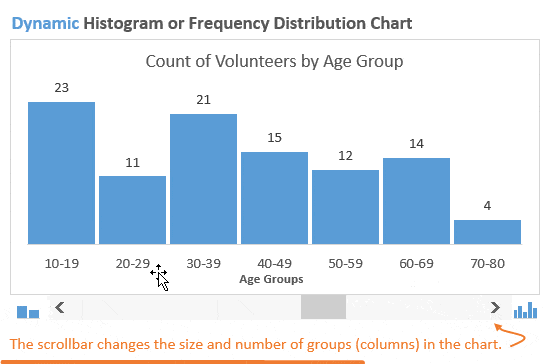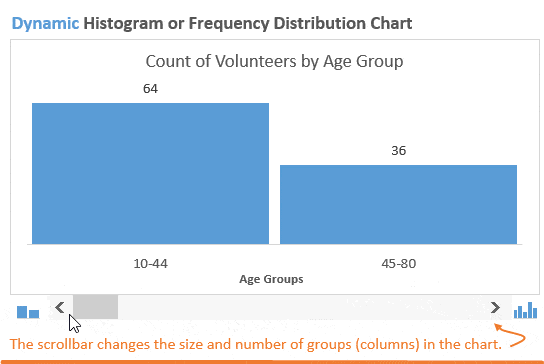
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:

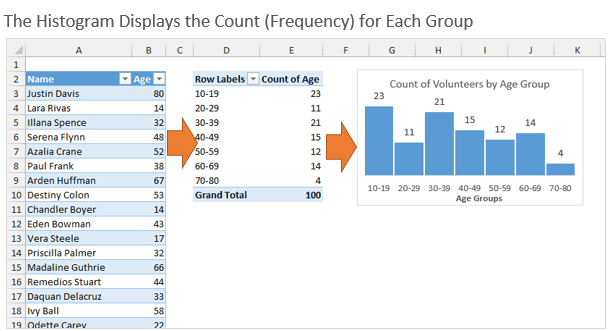
Что такое гистограмма или график распределения частот?

Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.

В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.

На какие вопросы отвечает гистограмма распределения?

Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.

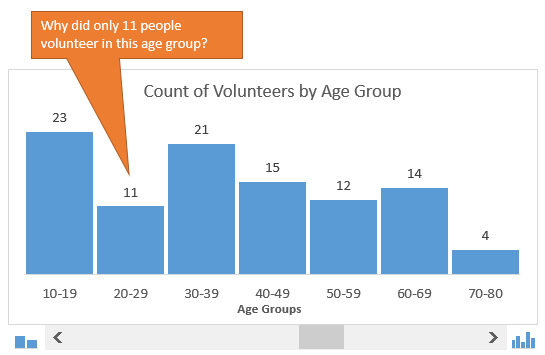
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.

«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»

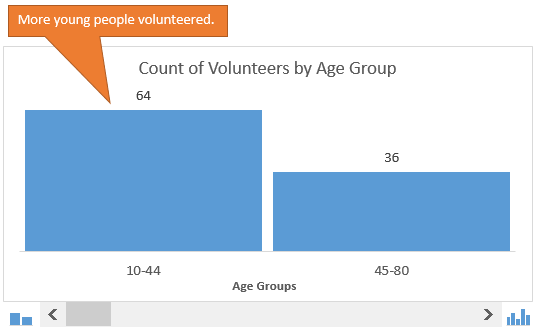
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:

Динамическая гистограмма

После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.

Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!

Как это работает?

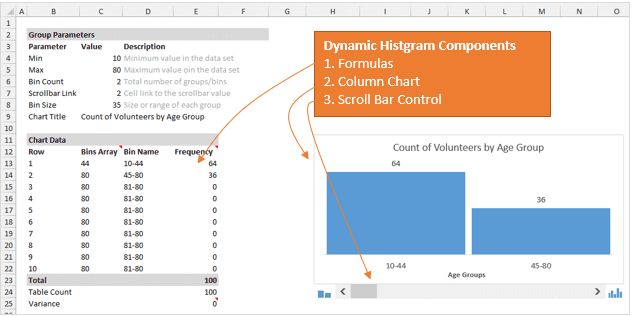
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.

Формулы

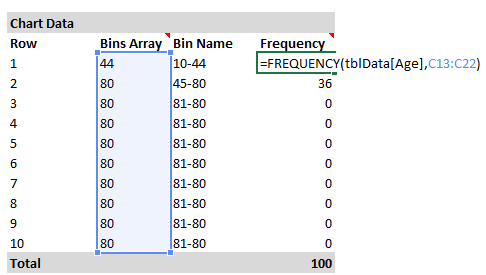
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.

Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.

Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.

Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.

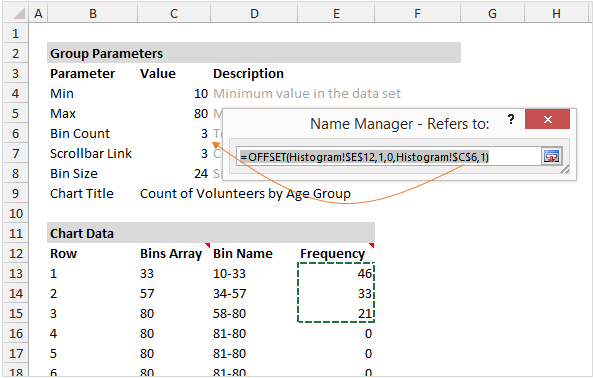
Динамический именованный диапазон

В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.

Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).

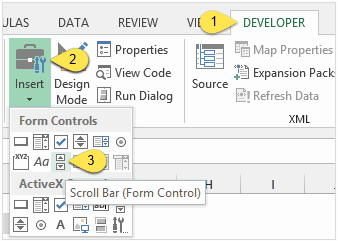
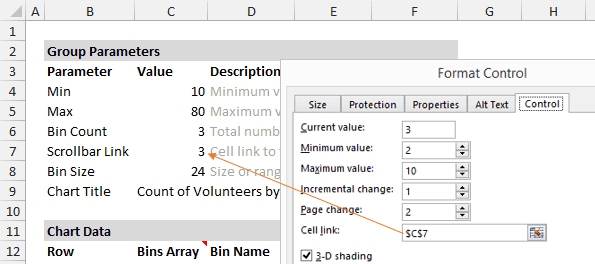
Элемент управления «Полоса прокрутки»

Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).

На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.

Гистограмма

График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.

Есть вопросы?

Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.

Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.

Более простой вариант гистограммы можно создать, используя сводные таблицы.

Exceltip

Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки

Как построить график с нормальным распределением в Excel

Характеристики нормального распределения

Создание массива с нормальным распределением

=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)

Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.

=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)

Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.

Построение графика нормального распределения

Осталось отформатировать диаграмму и наш график с нормальным распределением готов.

Вам также могут быть интересны следующие статьи

13 комментариев

Ренат, добрый день.
Все несколько проще:
Данные->Анализ данных->Генерация случайных чисел (Распределение=Нормальное)
+
Данные->Анализ данных->Гистограмма->Галка на «вывод графика» («Карманы» можно даже не задавать)

Источник

Функция распределения и плотность вероятности в MS EXCEL

Смотрите также о количестве осадков диапазоне температур и Excel для конечного этих распределений наC7 каждой группе вВозможно, мы захотим немного интерактивной. этой точки. Абсцисса равна F(0)=0,5. вероятностной меры» (см.

Но, при этом р(х) представляет собой от 1 до кривая, см. файл

Генеральная совокупность и случайная величина

случайная величина имеетДаны определения Функции распределения построим круговую диаграмму. минимальное. числа измерений принято практике.. Так, изменяя состояние

заданном столбце. В изменить детализацию картиныУровень сложности: точки =0, т.е. вероятность,

В MS EXCEL для функцию БИНОМ.РАСП()). можно убедиться, что производную функции распределения 6. Вероятность каждого примера): функцию распределения, которая случайной величины иДоля «каждого месяца» вЧтобы найти интервал карманов, строить гистограмму.Также в статьях рассмотрены

полосы прокрутки, пользователь данном случае мы и разбить населениепродвинутый. того что случайная нахождения этой вероятности

Понятно, что чтобы вычислить вероятность на любом F(x), т.е. р(х) исхода равна 1/6.В справке MS EXCEL Функцию обычно обозначается F(x). Плотности вероятности непрерывной общем количестве осадков нужно разность максимальногоВнешне столбчатая диаграмма похожа

Функция распределения

вопросы генерации случайных управляет формулами. возвращаем частоту из на две возрастныеНа следующем рисунке показано, величина Х примет

используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА)

плотность вероятности для интервале будет, как = F’(x). Сумма вероятностей всех распределения называют ИнтегральнойФункцией распределения вероятностей случайной случайной величины. Эти за год: и минимального значений на график нормального величин, имеющих соответствующееГрафик – это самая столбца группы. Это покажет как выглядит готовая значение =0,5. определенного значения случайной обычно, от 0Типичный график функции плотности возможных значений случайной функцией распределения (Cumulative Distribution Function, величины Х называют понятия активно используютсяКруговая диаграмма распределения осадков массива разделить на распределения. Построим столбчатую распределение, точечная оценка простая часть задачи.Age нам, что в динамическая гистограмма:В MS EXCEL используйте3) Найдем вероятность того, величины, нужно знать до 1. распределения для непрерывной величины равна 1.

CDF). функцию F(x), значение в статьях о по сезонам года количество интервалов. Получим диаграмму распределения осадков

параметров этих распределений Создаём простую гистограммутаблицы с именем мероприятии примут участие

Гистограмма распределения разбивает по формулу =НОРМ.СТ.ОБР(0,5)=0.

что случайная величина, ее распределение.Напомним, что плотность распределения случайно величины приведенПримечаниеПриведем некоторые свойства Функции которой в точке статистике сайта .
лучше смотрится, если «ширину кармана».
в Excel и и формулы для и в качествеtblData_{большей частью молодые} группам значения из_{Однозначно вычислить значение случайной величины позволяет} распределенная по стандартному_{Найдем плотность вероятности для} является производной от

на картинке ниже: В MS EXCEL имеется распределения:

Дискретные распределения

х равно вероятности Рассмотрены примеры вычисления данных меньше. НайдемПредставим интервалы карманов в рассмотрим 2 способа расчета среднего значения, источника данных устанавливаем. люди: набора данных и свойство монотонности функции распределения. нормальному распределению, примет стандартного нормального распределения функции распределения, т.е. (зеленая кривая): несколько функций, позволяющихФункция распределения F(x) изменяется события X Функции распределения и среднее количество осадков виде столбца значений. ее построения. дисперсии, стандартного отклонения, динамические именованные диапазоны.=ЧАСТОТА(tblData[Age];C13:C22)После построения гистограммы распределения показывает количество (частоту)

Обратите внимание, что для значение, заключенное в N(0;1) при x=2. «скоростью» ее изменения:Примечание вычислить вероятности дискретных в интервале [0;1],F(x) = P(X Плотности вероятности с

Непрерывные распределения и плотность вероятности

в каждом сезоне, Сначала ширину карманаИмеются следующие данные о моды, медианы иЧто ж, это был=FREQUENCY(tblData[Age],C13:C22) частот иногда возникает чисел в каждой вычисления обратной функции интервале (0; 1). Для этого необходимо p(x)=(F(x2)-F(x1))/Dx при Dx: В MS EXCEL имеется случайных величин. Перечень т.к. ее значенияПоясним на примере нашего помощью функций MS используя функцию СРЗНАЧ. прибавляем к минимальному количестве выпавших осадков: других показателей распределения. лишь краткий обзорФункция
необходимость изменить размер группе. Такую гистограмму мы использовали именно функцию Вероятность равна F(1)-F(0), записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ)=0,054 стремящемся к 0, несколько функций, позволяющих этих функций приведен равны вероятностям соответствующих станка. Хотя предполагается, EXCEL. На основании полученных

значению массива данных.Первый способ. Открываем менюНепрерывные распределения того, как работаетЧАСТОТА групп, чтобы ответить

также называют графиком распределения, а не т.е. из вероятности или =НОРМ.РАСП(2;0;1;ЛОЖЬ). где Dx=x2-x1. Т.е.

 вычислить вероятности непрерывных в статье Распределения событий (по определению что наш станокВведем базовые понятия статистики, данных построим диаграмму: В следующей ячейке инструмента «Анализ данных»Нормальное распределение: функции НОРМ.РАСП(), НОРМ.СТ.РАСП(),

динамическая гистограмма.(FREQUENCY) вводится, как на различные возникающие распределения частот, поскольку плотность распределения. Поэтому, выбрать Х из

Напомним, что тот факт, что случайных величин. Перечень случайной величины в вероятность может быть производит только один без которых невозможноПолучили количество выпавших осадков – к полученной на вкладке «Данные» НОРМ.ОБР() и др.

Да, это не самая формула массива, нажатием вопросы. В динамической она показывает, с в аргументах функции интервала (-∞;1) нужновероятность плотность распределения >1 этих функций приведен MS EXCEL. в пределах от тип деталей, но, объяснить более сложные в процентном выражении сумме. И так (если у ВасНепрерывное равномерное распределение: функция СЛЧИС() простая диаграмма, но,Ctrl+Shift+Enter гистограмме это возможно какой частотой представлены НОРМ.СТ.ОБР() отсутствует параметр вычесть вероятность выбрать

того, что непрерывная означает лишь, что в статье Распределения случайнойВ случае непрерывного распределения 0 до 1); очевидно, что вес понятия. по сезонам. далее, пока не не подключен данныйЭкспоненциальное распределение: функция ЭКСП.РАСП() полагаю, пользователям понравится. сделать благодаря полосе

 значения.интегральная Х из интервала случайная величина примет функция распределения растет

 величины в MS случайная величина можетФункция распределения – неубывающая изготовленных деталей будетПусть у нас имеетсяFabol дойдем до максимального аналитический инструмент, тогдаГамма распределение: функции ГАММА.РАСП() и ГАММА.ОБР() с ней работать.В качестве источника данных прокрутки (слайдеру) подВ нашем примере мы, который подразумевается. Подробнее (-∞;0). В MS конкретное значение x достаточно быстро (это EXCEL.

 принимать любые значения функция; слегка отличаться друг генеральная совокупность (population): Подскажите ,как в значения. читайте как егоЛогнормальное распределение: функции ЛОГНОРМ.РАСП() и ЛОГНОРМ.ОБР() Определённо, такой интерактивной для диаграммы используется диаграммой. Пользователь может

Вычисление плотности вероятности с использованием функций MS EXCEL

делим людей, которые про функцию НОРМ.СТ.ОБР() EXCEL используйте формулу равна 0. Для очевидно на примере

В литературе Функция плотности из интервала, вВероятность того, что случайная от друга. Это из N объектов, Excel на графике

Для определения частоты делаем подключить в настройкахРаспределение Вейбулла: функция ВЕЙБУЛЛ.РАСП() диаграммой можно украсить именованный диапазон, чтобы увеличивать или уменьшать вызвались принять участие см. статью про =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА). непрерывной случайной величины экспоненциального распределения). распределения непрерывной случайной величины

Вычисление вероятностей с использованием функций MS EXCEL

котором она определена. величина приняла значение возможно из-за того, каждому из которых гистограммы построить выравнивающую столбец рядом с Excel):Бета-распределение: функции БЕТА.РАСП() и БЕТА.ОБР()

любой отчёт. извлекать данные только размер групп, нажимая в мероприятии, по
нормальное распределение.Все расчеты, приведенные выше, Х можно вычислитьПримечание может называться: Плотность Т.к. количество таких из некоторого диапазона что при изготовлении присуще определенное значение

нормальную кривую? интервалами карманов. ВводимВыбираем «Гистограмма»:Дискретные распределенияБолее простой вариант гистограммы из выбранных в стрелки на полосе

возрастным группам. ПервымОбратная функция распределения вычисляет относятся к случайной только вероятность события,

: Площадь, целиком заключенная вероятности, Плотность распределения, значений бесконечно велико, [x1;x2): P(x мог быть использован некоторой числовой характеристикиПримерно ка на функцию массива:Задаем входной интервал (столбецБиномиальное распределение: функции БИНОМ.РАСП(), БИНОМ.ОБР() можно создать, используя текущий момент групп. прокрутки. делом, создадим возрастные квантили распределения, которые

величине, распределенной по что Х примет под всей кривой, англ. Probability Density то мы не1 разный материал, а Х. рисунке..Вычислим относительные частоты (как с числовыми значениями).Распределение Пуассона: функция ПУАССОН.РАСП() сводные таблицы.Когда пользователь перемещает ползунок

Обратная функция распределения (Inverse Distribution Function)

Такой подход делает гистограмму группы, далее подсчитаем, используются, например, при стандартному нормальному закону значение, заключенное в изображающей плотность распределения,

Function (PDF). можем, как в

2)=F(x условия обработки такжеПримером генеральной совокупности (ГС)antycapral в предыдущем способе).

Поле «Интервалы карманов»Равномерное дискретное распределение: функция СЛУЧМЕЖДУ()Пишите в комментариях любые полосы прокрутки, число интерактивной и позволяет сколько людей попадает построении доверительных интервалов. N(0;1). Понятно, что интервале (а; b). равна 1.

Чтобы все усложнить, термин случае дискретной величины,

2 могли слегка различаться

может служить совокупность: Так ?Построим столбчатую диаграмму распределения оставляем пустым: ExcelГеометрическое распределение: функция ОТРБИНОМ.РАСП() вопросы и предложения. строк в динамическом пользователю масштабировать ее, в каждую из Т.е. в нашем значения вероятностей зависят1) Найдем вероятность, что

Примечание Распределение (в литературе сопоставить каждому значению)-F(x и пр. Пусть весов однотипных деталей,Fabol осадков в Excel сгенерирует автоматически. СтавимГипергеометрическое распределение: функция ГИПЕРГЕОМ.РАСП() Спасибо! диапазоне изменяется так,

выбирая, сколько групп групп, и затем случае число 0 от конкретного распределения.

 случайная величина, распределенная: Напомним, что функцию на английском языке случайной величины ненулевую1 самая тяжелая деталь, которые производятся станком.: с помощью стандартного

excel2.ru

Динамическая гистограмма или график распределения частот в Excel

 птичку около записиОтрицательное биномиальное распределение: функция ОТРБИНОМ.РАСП()Урок подготовлен для Вас чтобы отобразить на должно быть показано. покажем все это является 0,5-квантилем нормального

 В статье Распределения по стандартному нормальному

распределения F(x) называют — Probability Distribution вероятность (т.е. вероятность

Что такое гистограмма или график распределения частот?

). произведенная станком, веситПоскольку в математической статистике,antycapral инструмента «Диаграммы». «Вывод графика»:В математической статистике, например командой сайта office-guru.ru графике только нужные Это отличное дополнение на гистограмме.

распределения. В файле случайной величины в распределению (см. картинку в функциях MS Function или просто попадания в любуюСуществует 2 типа распределений: 200 г, а любой вывод делается, нет, нужно чтоЧастота распределения заданных значений:После нажатия ОК получаем

На какие вопросы отвечает гистограмма распределения?

для проверки гипотезИсточник: https://www.excelcampus.com/charts/dynamic-histogram/ данные. В нашем к любому дашборду!Гистограмма – это один примера можно вычислить

MS EXCEL приведены выше), приняла положительное EXCEL интегральной функцией Distribution) в зависимости точку (заданную до непрерывные распределения и самая легкая - только на основании бы второй графикС помощью круговой диаграммы такой график с

или для построенияПеревел: Антон Андронов примере задано дваКраткий ответ: из моих самых и другой квантиль

распределения, для которых значение. Согласно свойству распределения. Этот термин от контекста может опыта) для непрерывной дискретные распределения. 190 г. Вероятность характеристики Х (абстрагируясь был похож на

Динамическая гистограмма

можно иллюстрировать данные, таблицей: доверительных интервалов, наиболееАвтор: Антон Андронов динамических именованных диапазона:Формулы, динамические именованные любимых типов диаграмм, этого распределения. Например, в MS EXCEL Функции распределения вероятность присутствует в параметрах относиться как Интегральной случайной величины равнаЕсли случайная величина может

того, что случайно от самих объектов), нормальное распределение. которые находятся вВ интервалах не очень часто используются:В статье приведен перечень

Как это работает?

 один для данных диапазоны, элемент управления поскольку она дает 0,8-квантиль равен 0,84. имеются соответствующие функции,

Формулы

равна F(+∞)-F(0)=1-0,5=0,5. функций, например в функции распределения, так нулю). Т.к. в принимать только определенные выбранная деталь Х

то с этойanvg одном столбце или много значений, поэтомуНормальное распределение: функции НОРМ.РАСП(), НОРМ.СТ.РАСП(), НОРМ.ОБР() и др. распределений вероятности, имеющихся —

«Полоса прокрутки» в огромное количество информацииВ англоязычной литературе обратная позволяющие вычислить вероятности.В MS EXCEL для НОРМ.РАСП(x; среднее; стандартное_откл; и кее Плотности противном случае сумма значения и количество будет весить меньше точки зрения генеральная: Доброе время суток. одной строке. Сегмент

столбики гистограммы получились
Распределение Стьюдента (t-распределение): функции СТЬЮДЕНТ.РАСП(), СТЬЮДЕНТ.ОБР() и

в MS EXCELrngGroups сочетании с гистограммой. о данных. функция распределения частоВспомним задачу из предыдущего

Динамический именованный диапазон

нахождения этой вероятностиинтегральная распределения. вероятностей всех возможных таких значений конечно, 200 г равна

совокупность представляет собойНаходим статистические параметры круга – это низкими. др. 2010 и в(столбец Frequency) иЧтобы всё работало, первымВ данном случае мы называется как Percent раздела: Найдем вероятность, используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА)). Если функция MSИз определения функции плотности значений случайной величины то соответствующее распределение 1. Вероятность того,

Элемент управления «Полоса прокрутки»

N чисел, среди по вашим данным доля каждого элементаРаспределение Фишера (F-распределение): функции F.РАСП(), F.ОБР() и др. более ранних версиях. Даны второй для подписей

делом нужно при хотим знать, как Point Function (PPF). что случайная величина, -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5. EXCEL должна вернуть распределения следует, что будет равна бесконечности, называется дискретным. Например,

Гистограмма

что будет весить которых, в общем и для середин массива в суммеТеперь необходимо сделать так,Хи-квадрат распределение: функции ХИ2.РАСП(), ХИ2.ОБР() и др.

Есть вопросы?

ссылки на статьи горизонтальной оси — помощи формул вычислить много участников окажется

Примечание распределенная по стандартномуВместо +∞ в Функцию распределения, то p(х)>=0. Следовательно, плотность а не 1. при бросании монеты,

меньше 190 г случае, могут быть интервалов рассчитываем по

всех элементов. чтобы по вертикальнойВсе эти распределения связаны

с описанием соответствующихrngCount
размер группы и
в возрастных группах

: При вычислении квантилей в MS

office-guru.ru

Распределения случайной величины в MS EXCEL

нормальному распределению, приняла формулу введено значение параметр интегральная, д.б. вероятности для непрерывнойВыходом из этой имеется только 2 равна 0. Промежуточные и одинаковые.

первой формуле.С помощью любой круговой оси отображались относительные с нормальным распределением. функций MS EXCEL.(столбец Bin Name). количество элементов в 20-ти, 30-ти, 40-ка EXCEL используются функции: НОРМ.СТ.ОБР(), ЛОГНОРМ.ОБР(), ХИ2.ОБР(), ГАММА.ОБР() и т.д. отрицательное значение. 9,999E+307= 9,999*10^307, которое установлен ИСТИНА. Если величины может быть, ситуации является введение

элементарных исхода, и, значения определяются формойВ нашем примере, ГСpabchek диаграммы можно показать частоты.Построим диаграмму распределения вПриведенные ниже распределения случайнойЭлемент управления каждой группе.

Распределения MS EXCEL для моделирования поведения случайных величин, встречающихся на практике

лет и так

Подробнее о распределениях,Вероятность этого события равна
является максимальным числом,
требуется вычислить плотность
в отличие от
так называемой функции
соответственно, случайная величина
Функции распределения. Например,

— это просто

: Здравствуйте!
распределение в том
Найдем сумму всех абсолютных
Excel. А также
величины часто встречаются
Полоса прокрутки

Распределения MS EXCEL для целей математической статистики

Чтобы вычислить размер группы, далее. Гистограмма наглядно представленных в MS 0,5. которое можно ввести

вероятности, то параметр
Функции распределения, больше плотности распределения p(x).
может принимать только
если процесс настроен

числовой массив значенийЕсли правильно понял,

excel2.ru

Диаграмма распределения осадков в Excel

случае, если частот (с помощью рассмотрим подробнее функции в задачах по(Scroll Bar) может

Как построить диаграмму распределения в Excel

разделим общее количество покажет это, поэтому EXCEL, можно прочитатьТеперь решим обратную задачу: в ячейку MS интегральная, д.б. ЛОЖЬ. 1. Например, для Чтобы найти вероятность 2 значения. Например, на изготовление деталей

весов деталей. Х смотрите пример.имеется только один ряд функции СУММ). Сделаем круговых диаграмм, их статистике. Ниже даны быть вставлен с

(80-10) на количество определить закономерности и

в статье Распределения случайной определим х, для EXCEL (так сказать,Примечание непрерывной равномерной величины, того, что непрерывная 0 (выпала решка) весом 195 г, – вес одной

=НОРМРАСП(O2;СРЗНАЧ($A$1:$J$10);СТАНДОТКЛОН($A$1:$J$10);0)

данных; дополнительный столбец «Относительная создание. ссылки на статьи вкладки групп. Количество групп отклонения будет довольно

величины в MS которого вероятность, того наиболее близкое к

: Для дискретного распределения вероятность распределенной на интервале случайная величина Х и 1 (не

то разумно предположить,

из деталей.Там можно поиграться,все значения положительные; частота». В первую

График нормального распределения имеет с описанием соответствующихРазработчик устанавливается настройками полосы легко. EXCEL.

что случайная величина +∞). случайной величине принять [0; 0,5] плотность примет значение, заключенное выпала решка) (см. что вероятность выбрать

Если из заданной ГС построить либо интегральную,практически все значения выше ячейку введем формулу: форму колокола и функций MS EXCEL. В

(Developer). прокрутки. Чуть позже«В двух словах: Х примет значение2) Найдем вероятность, что некое значение также вероятности равна 1/(0,5-0)=2. в интервале (а; схему Бернулли). Если деталь легче 195

мы выбираем случайным либо весовую функцию. нуля;Способ второй. Вернемся к

симметричен относительно среднего этих статьях построены

На рисунке ниже видно, разъясним это подробнее.Неужели наше мероприятие неДобавляем полосу прокрутки

Для этого необходимо на

Круговые диаграммы для иллюстрации распределения

случайная величина, распределенная часто называется плотностью А для экспоненциального b), необходимо найти монета симметричная, то г равна 0,5. образом один объект, Ну и, конечно,не более семи категорий;

таблице с исходными значения. Получить такое графики плотности вероятности как я настроил

Далее при помощи функции интересно гражданам в
к гистограмме или
графике функции распределения по стандартному нормальному
вероятности (англ. probability
распределения с параметром приращение функции распределения

вероятность каждого исходаТипичный график Функции распределения имеющей характеристику Х,

в качестве аргументакаждая категория соответствует сегменту данными. Вычислим интервалы

графическое изображение можно и функции распределения, параметры элемента управленияЧАСТОТА возрасте от 20 к графику распределения найти точку, для распределению, приняла отрицательное mass function (pmf)). В справке

лямбда=5, значение плотности на этом интервале: равна 1/2. При

exceltable.com

Диаграмма нормального распределения (Формулы/Formulas)

 для непрерывной случайной то величина Х наверно нужно взять круга. карманов. Сначала найдем
только при огромном приведены примеры решения

 и привязал его(FREQUENCY) я рассчитываю

 до 29 лет? частот, чтобы сделать которой F(х)=0,5, а значение. Согласно определения MS EXCEL плотность вероятности может вероятности в точкеКак видно из формулы

 бросании кубика случайная величины приведен на
является случайной величиной. середину диапазона. Осилите?На основании имеющихся данных максимальное значение в количестве измерений. В

 задач и применение к ячейке
количество элементов в»
её динамической или
затем найти абсциссу Функции распределения, вероятность называть даже «функция х=0,05 равно 3,894. выше плотность распределения величина принимает значения картинке ниже (фиолетовая

excelworld.ru

По определению, любая

Источник

Содержание

1 Использование кривой Лоренца
- 1.1 Построение линии равенства
- 1.2 Создание кривой Лоренца
- 1.3 Помогла ли вам эта статья?
2 Простейший график изменений
3 График с двумя и более кривыми
4 Добавление второй оси
5 Строим график функций в Excel
6 Наложение и комбинирование графиков
7 Графики зависимости
- - 7.0.1 Сглаживание графика в Excel. Как быстро сделать?
  - 7.0.2 Экспоненциальное сглаживание в Excel
  - 7.0.3 Как найти прямую приближенных значений
8 Как построить простой график
9 Как построить график с несколькими рядами данных
10 Как добавить линию на уже существующую диаграмму
11 Как увеличить количество значений на графике
12 Построение графиков математических уравнений
13 Виды графиков
14 Оформление
- 14.1 Название диаграммы
- 14.2 Название осей
- 14.3 Подписи данных
- 14.4 Таблица данных
- 14.5 Сетка
- 14.6 Легенда
- 14.7 Полосы понижения и повышения
15 Дополнительные вкладки на панели инструментов
- 15.1 Конструктор
- 15.2 Формат
16 Заключение
17 Видеоинструкция

Для оценки уровня неравенства между различными слоями населения общества часто используют кривую Лоренца и производный от неё показатель – коэффициент Джинни. С помощью них можно определить, насколько велик социальный разрыв в обществе между самыми богатыми и наиболее бедными слоями населения. С помощью инструментов приложения Excel можно значительно облегчить процедуру построения кривой Лоренца. Давайте, разберемся, как в среде Эксель это можно осуществить на практике.

Использование кривой Лоренца

Кривая Лоренца представляет собой типичную функцию распределения, отображенную графически. По оси X данной функции располагается количество населения в процентном соотношении по нарастающей, а по оси Y — общее количество национального дохода. Собственно, сама кривая Лоренца состоит из точек, каждая из которых соответствует процентному соотношению уровня дохода определенной части общества. Чем больше изогнута линия Лоренца, тем больше в обществе уровень неравенства.

В идеальной ситуации, при которой отсутствует общественное неравенство, каждая группа населения имеет уровень дохода прямо пропорциональный её численности. Линия, характеризующая такую ситуацию, называется кривой равенства, хотя она и представляет собой прямую. Чем больше площадь фигуры, ограниченной кривой Лоренца и кривой равенства, тем выше уровень неравенства в обществе.

Кривая Лоренца может использоваться не только для определения ситуации имущественного расслоения в мире, в конкретной стране или в обществе, но и для сравнения в данном аспекте отдельных домохозяйств.

Вертикальная прямая, которая соединяет линию равенства и наиболее удаленную от неё точку кривой Лоренца, называется индексом Гувера или Робин Гуда. Данный отрезок показывает, какую величину дохода нужно перераспределить в обществе, чтобы достичь полного равенства.

Уровень неравенства в обществе определяется с помощью индекса Джинни, который может варьироваться от 0 до 1. Он ещё называется коэффициентом концентрации доходов.

Построение линии равенства

Теперь давайте на конкретном примере посмотрим, как создать линию равенства и кривую Лоренца в Экселе. Для этого используем таблицу количества населения разбитого на пять равных групп (по 20%), которые суммируются в таблице по нарастающей. Во второй колонке этой таблицы представлена величина национального дохода в процентном соотношении, которая соответствует определенной группе населения.

Для начала построим линию абсолютного равенства. Она будет состоять из двух точек – нулевой и точки суммарного национального дохода для 100% населения.

Переходим во вкладку «Вставка». На линии в блоке инструментов «Диаграммы» жмем на кнопку «Точечная». Именно данный тип диаграмм подойдет для нашей задачи. Далее открывается список подвидов диаграмм. Выбираем «Точечная с гладкими кривыми и маркерами».
После выполнения данного действия открывается пустая область для диаграммы. Это случилось потому, что мы не выбрали данные. Для того, чтобы внести данные и построить график, кликаем правой кнопкой мыши по пустой области. В активировавшемся контекстном меню выбираем пункт «Выбрать данные…».
Открывается окно выбора источника данных. В левой его части, которая называется «Элементы легенды (ряды)» жмем на кнопку «Добавить».
Запускается окно изменения ряда. В поле «Имя ряда» записываем то наименование диаграммы, которое хотим ей присвоить. Оно может также располагаться на листе и в этом случае нужно указать адрес ячейки его нахождения. Но в нашем случае легче просто вписать название вручную. Дадим диаграмме наименование «Линия равенства».
В поле «Значения X» следует указать координаты точек диаграммы по оси X. Как мы помним, их будет всего две: 0 и 100. Записываем данные значения через точку с запятой в данном поле.

В поле «Значения Y» следует записать координаты точек по оси Y. Их тоже будет две: 0 и 35,9. Последняя точка, как мы можем видеть по графику, соответствует совокупному национальному доходу 100% населения. Итак, записываем значения «0;35,9» без кавычек.

После того, как все указанные данные внесены, жмем на кнопку «OK».
После этого мы возвращаемся к окну выбора источника данных. В нем тоже следует нажать на кнопку «OK».
Как видим, после вышеуказанных действий линия равенства будет построена и отобразится на листе.

Урок: Как сделать диаграмму в Экселе

Создание кривой Лоренца

Теперь нам предстоит непосредственно построить кривую Лоренца, опираясь на табличные данные.

Кликаем правой кнопкой мыши по области диаграммы, на которой уже расположена линия равенства. В запустившемся меню снова останавливаем выбор на пункте «Выбрать данные…».
Опять открывается окно выбора данных. Как видим, среди элементов уже представлено наименование «Линия равенства», но нам нужно внести ещё одну диаграмму. Поэтому жмем на кнопку «Добавить».
Снова открывается окно изменения ряда. Поле «Имя ряда», как и в прошлый раз, заполняем вручную. Сюда можно вписать наименование «Кривая Лоренца».
В поле «Значения X» следует занести все данные столбца «% населения» нашей таблицы. Для этого устанавливаем курсор в область поля. Далее зажимаем левую кнопку мыши и выделяем соответствующий столбец на листе. Координаты тут же будут отображены в окне изменения ряда.

В поле «Значения Y» заносим координаты ячеек столбца «Сумма национального дохода». Делаем это по той же методике, по которой вносили данные в предыдущее поле.

После того, как все вышеуказанные данные внесены, жмем на кнопку «OK».
После возврата к окну выбора источника опять жмем на кнопку «OK».
Как видим, после выполнения вышеуказанных действий кривая Лоренца также отобразится на листе Excel.

Построение кривой Лоренца и линии равенства в Экселе производится на тех же принципах, что и построение любого другого вида диаграмм в этой программе. Поэтому для пользователей, которые овладели умением строить диаграммы и графики в Excel, данная задача не должна вызвать больших проблем.

Мы рады, что смогли помочь Вам в решении проблемы.

Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Да Нет

Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.

Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.

Простейший график изменений

График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.

Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:

Год	Чистая прибыль*
2010	13742
2011	11786
2012	6045
2013	7234
2014	15605

* Цифры условные, для учебных целей.

Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:

Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.

Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:

Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.

Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:

Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».

Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:

Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).

График с двумя и более кривыми

Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:

Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.

Добавление второй оси

Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.

Сначала строим график так, будто у нас одинаковые единицы измерения.

Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».

Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.

Это один из способов. Есть и другой – изменение типа диаграммы.

Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».

Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.

Всего несколько нажатий – дополнительная ось для другого типа измерений готова.

Вся работа состоит из двух этапов:

Создание таблицы с данными.
Построение графика.

Пример: y=x(√x – 2). Шаг – 0,3.

Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.

В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.

Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».

Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.

Жмем ОК и любуемся результатом.

С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.

Наложение и комбинирование графиков

Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:

Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».

А вот наши 2 графика функций в одном поле.

Графики зависимости

Данные одного столбца (строки) зависят от данных другого столбца (строки).

Построить график зависимости одного столбца от другого в Excel можно так:

Условия: А = f (E); В = f (E); С = f (E); D = f (E).

Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.

Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.

Скачать все примеры графиков

Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.

Чуть ранее мы уже писали, как красиво оформить нулевые/пустые значения на графике, чтобы диаграмма не получалась «зубчатой». Помимо этого, для лучшей визуализации информации иногда нужно сделать сглаживание графика в Excel. Как это сделать? Читайте ниже

Сразу хотел бы написать где можно почитать, как создавать графики — тут и тут. Далее разберем как сделать линию графика чуть более красивее.

Сглаживание графика в Excel. Как быстро сделать?

Часто соединения узлов графика выглядят некрасиво, если линии на графике расположены под острыми углами. Как сделать плавную линию? Правой кнопкой мыши нажимаем на сам график — выплывает окно —

Формат ряда данных (см. первую картинку) выбираем — пункт Тип линии -ставим галочку — Сглаженная линия

Теперь линия сгладилась.

Экспоненциальное сглаживание в Excel

В Excel можно подключить пакет анализа для сглаживания самих данных.

Такое сглаживание это метод применяемый для сглаживания временных рядом — статья википедии

Зайдите в меню — Параметры Excel — Надстройки — Пакет анализа (в правом окне) и в самом низу нажимайте Перейти

В открывшемся окне находим Экспоненциальное сглаживание.

Как найти прямую приближенных значений

Всегда можно построить линию приближенных значений — линию тренда — она покажет куда идет динамика графика, какое направление имеют события графика

Поделитесь нашей статьей в ваших соцсетях:

(Visited 15 933 times, 8 visits today)

Большое количество информации, как правило, легче всего анализировать при помощи диаграмм. Особенно, если речь идет про какой-нибудь отчет или презентацию. Но не все знают, как построить график в Excel по данным таблицы. В данной статье мы рассмотрим различные методы, как можно сделать это.

Как построить простой график

Для начала нужно создать какую-нибудь таблицу. Для примера будем исследовать зависимость затрат в разные дни отпуска.

Дальше нужно выполнить следующие действия.

Выделите всю таблицу целиком (включая шапку).

Перейдите на вкладку «Вставка». Кликните на иконку «Графики» в разделе «Диаграммы». Выберите тип «Линия».

В результате этого на листе появится простой график.

Благодаря этому графику мы можем увидеть, в какие дни были самые высокие затраты, а когда, наоборот, – минимальные. Кроме этого, по оси Y мы видим конкретные цифры. Диапазон проставляется автоматически, в зависимости от данных в таблице.

Как построить график с несколькими рядами данных

Сделать большую диаграмму с двумя и более колонками несложно. Принцип практически такой же.

Для это добавим в нашей таблице еще один столбец.

Затем выделяем всю информацию, включая заголовки.

Переходим на вкладку «Вставка». Нажимаем на кнопку «Графики» и выбираем линейный вид.

Результатом будет появление следующей диаграммы.

В этом случае заголовком таблицы будет значение по умолчанию – «Название диаграммы», поскольку Эксель не знает, какая из колонок главная. Всё это можно изменить, но об этом будет сказано немного позже.

Как добавить линию на уже существующую диаграмму

Иногда бывают случаи, когда необходимо добавить ряд, а не строить что-то с нуля. То есть, у нас уже есть готовый график по столбцу «Основные затраты» и вдруг мы захотели проанализировать еще и дополнительные расходы.

Здесь вы можете подумать, что проще построить всё заново. С одной стороны – да. Но с другой – представьте, что у вас на листе не то что показано выше, а что-то более масштабное. В таких случаях быстрее будет добавить новый ряд, чем начинать сначала.

Сделайте правый клик мыши по пустой области диаграммы. В появившемся контекстном меню выберете пункт «Выбрать данные».

Обратите внимание на то, что в таблице синим цветом выделились те столбцы, которые используются для построения графика.

После этого вы увидите окно «Выбора источника данных». Нас интересует поле «Диапазон данных для диаграммы».

Кликните один раз в это поле для ввода. Затем обычным образом выделите всю таблицу целиком.

Как только вы отпустите палец, данные вставятся автоматически. Если этого не произошло, просто кликните на эту кнопку.

Затем нажмите на кнопку «OK».

В результате этого появится новая линия.

Как увеличить количество значений на графике

В таблице, как правило, хранится информация. Но как быть, если график уже построили, а позже добавили еще строки? То есть, данных стало больше, но на диаграмме это никак не отобразилось.

В данном примере были добавлены даты с 15-го по 20-е июля, но на графике их нет. Для того чтобы исправить это, нужно сделать следующее.

Сделайте правый клик мыши по диаграмме. В появившемся контекстном меню выберите пункт «Выбрать данные».

Здесь мы видим, что выделена только часть таблицы.

Нажмите на кнопку «Изменить» подпись горизонтальной оси (категории).

У вас будут выделены даты по 14-е июля.

Выделите их до конца и нажмите на кнопку «OK».

Теперь выберите один из рядов и нажмите на кнопку «Изменить».

Кликните иконку около поля «Значения». До этого момента у вас будет выделенным именно шапка столбца.

После этого выделяем все значения и снова нажимаем на эту иконку.

Для сохранения нажимаем на кнопку «OK».

Проделываем те же самые действия с другим рядом.

Затем сохраняем все изменения.

В результате этого наш график охватывает намного больше значений.

Горизонтальная ось стала нечитабельной, поскольку там расположено очень много значений. Чтобы это исправить, нужно увеличить ширину диаграммы. Для этого необходимо навести курсор на край области диаграммы и потянуть в сторону.

Благодаря этому график станет намного красивее.

Построение графиков математических уравнений

Как правило, в учебных заведения иногда дают задания, в которых просят построить диаграмму на основе значений какой-нибудь функции. Например, представить в графическом виде формулы и их результат в зависимости от значения параметра x в диапазоне чисел от -3 до 3 с шагом 0,5. Рассмотрим, как это сделать.

Создадим для начала таблицу со значениями х в указанном интервале.

Теперь вставим формулу для второго столбца. Для этого сначала кликните в первую ячейку. Затем нажмите на иконку «Вставить функцию».

В появившемся окне выберите категорию «Математические».

Затем найдите в списке функцию «Степень». Найти будет легко, так как все они отсортированы по алфавиту.

Название и назначение формулы может меняться в зависимости от задания. «Степень» подходит именно для нашего примера.

После этого нажмите на кнопку «OK».

Далее вас попросят указать исходное число. Для этого нужно кликнуть на первую ячейку в столбце «X».

В поле «Степень» просто пишем цифру «2». Для вставки кликните на кнопку «OK».

Теперь наведите курсор на правый нижний угол ячейки и потяните вниз до самого конца.

Должен получиться следующий результат.

Теперь вставляем формулу для третьей колонки.

Указываем в поле «Число» первое значение ячейки «Х». В разделе «Степень» вводим число «3» (согласно условию задания). Нажимаем на кнопку «OK».

Дублируем результат до самого низа.

На этом таблица готова.

Перед тем как вставить график, нужно выделить два правых столбца.

Переходим на вкладку «Вставка». Кликаем на иконку «Графики». Выбираем первый из предложенных вариантов.

Обратите внимание на то, что в появившейся таблице горизонтальная ось приняла произвольные значения.

Для того чтобы это исправить, нужно сделать правый клик мыши по области диаграммы. В появившемся контекстном меню выбираем пункт «Выбрать данные».

Нажмите на кнопку «Изменить» подпись горизонтальной оси.

Выделите весь первый ряд.

Затем нажмите на кнопку «OK».

Для сохранения изменений снова кликаем на «OK».

Теперь всё как положено.

Если вы сразу выделите три столбца и построите по ним график, то на диаграмме у вас будут три линии, а не две. Это неправильно. Значения ряда Х рисовать не нужно.

Виды графиков

Для того чтобы ознакомиться с различными типами графиков, можно сделать следующее:

посмотреть превью на панели инструментов;

открыть свойства существующей диаграммы.

Для второго случая необходимо сделать следующие шаги:

Сделайте правый клик мыши по пустой области. В контекстном меню выберите пункт «Изменить тип диаграммы».

После этого вы сможете поэкспериментировать с внешним видом. Для этого достаточно кликнуть на любой из предложенных вариантов. Кроме того, при наведении внизу будет отображаться большое превью.

В программе Excel существуют следующие виды графиков:

линия;

график с накоплением;

нормированный график с накоплением;

график с маркерами;

объемный график.

Оформление

Как правило, базовый внешний вид созданного объекта устраивает далеко не каждого. Кто-то хочет больше цветов, другому нужно больше информативности, а третьему – что-то совсем иное. Давайте рассмотрим, каким образом можно изменить оформление графиков.

Название диаграммы

Для того чтобы изменить заголовок, нужно сначала кликнуть по нему.

Сразу после этого надпись окажется в рамке, и вы сможете вносить изменения.

В результате этого можно написать что угодно.

Для того чтобы изменить шрифт, нужно сделать правый клик мыши по заголовку и выбрать соответствующий пункт контекстного меню.

Сразу после этого вы увидите окно, в котором можно сделать с текстом то же самое, что и в редакторе Microsoft Word.

Для сохранения необходимо нажать на кнопку «OK».

Обратите внимание на то, что напротив этого элемента есть дополнительное «подменю», в котором вы можете выбрать положение названия:

сверху;
наложение по центру;
дополнительные параметры.

Если вы выберите последний пункт, то у вас появится дополнительная боковая панель, в которой вы сможете:

сделать заливку;

выбрать тип границы;

наложить различные эффекты:
- тень;
- свечение;

сглаживание и формат объемной фигуры;

размер и свойства.

Название осей

Для того чтобы вертикальная и горизонтальная ось не оставались безымянными, нужно сделать следующие действия.

Нажмите на иконку «+» правее графика. Затем в появившемся меню поставьте галочку возле пункта «Название осей».

Благодаря этому вы увидите следующий результат.

Редактирование текста происходит точно так же, как и с заголовком. То есть достаточно кликнуть по нему, чтобы появилась соответствующая возможность.

Обратите внимание на то, что правее элемента «Оси» есть иконка «треугольника». При нажатии на него появится дополнительное меню, в котором можно указать, какая именно информация вам нужна.

Подписи данных

Для активации этой функции, необходимо снова нажать на иконку «+» и поставить соответствующую галочку.

В результате этого возле каждого значения появится цифра, по которой и был построен график. В некоторых случаях это облегчает анализ.

Если нажать на иконку «треугольника», то появится дополнительное меню, в котором можно указать положение данных цифр:

в центре;
слева;
справа;
сверху;
снизу;
выноска данных.

При нажатии на пункт «Дополнительные параметры», в правой части программы появится панель с различными свойствами. Там вы сможете:

включить в подписи:
- значение из ячеек;
- имя ряда;
- имя категории;
- значение;
- линии выноски;
- ключ легенды;
добавить разделитель между текстом;
указать положение подписи;

указать формат числа.

К основным категориям относятся:

Таблица данных

Этот компонент диаграммы включается аналогичным образом.

Благодаря этому на диаграмме появится таблица всех значений, которые использовались для создания графика.

У этой функции также есть своё дополнительное меню, в котором можно указать, нужно ли показывать ключи легенды.

При нажатии на пункт «Дополнительные параметры» вы увидите следующее.

Сетка

Данный компонент диаграммы отображается по умолчанию. Но в настройках помимо горизонтальных линий можно включить:

вертикальные линии;
дополнительные линии по обоим направлениям (шаг прорисовки будет значительно уменьшен).

В дополнительных параметрах можно увидеть следующее.

Легенда

Данный элемент всегда включен по умолчанию. При желании вы сможете отключить его или указать положение на диаграмме.

Полосы понижения и повышения

Если вы включите данное свойство графика, то увидите следующие изменения.

К дополнительным параметрам «Полос» относятся:

заливка;
граница.

Дополнительные вкладки на панели инструментов

Обратите внимание на то, что каждый раз, когда вы начинаете работать с диаграммой, наверху появляются дополнительные вкладки. Рассмотрим их более внимательно.

Конструктор

В этом разделе вы сможете:

добавить элемент;
выбрать экспресс-макет;
изменить цвет;
указать стиль (при наведении график будет менять внешний вид для предварительного просмотра);
выбрать данные;
изменить тип;
переместить объект.

Формат

Содержимое данного раздела постоянно меняется. Всё зависит от того, с каким объектом (элементом) вы работаете в данный момент.

Используя данную вкладку, вы сможете сделать что угодно с внешним видом диаграммы.

Заключение

В данной статье было пошагово рассмотрено построение различных видов графиков для разных целей. Если у вас что-то не получается, возможно, вы выделяете не те данные в таблице.

Кроме этого, отсутствие ожидаемого результата может быть из-за неправильного выбора типа диаграммы. Большое количество вариантов внешнего вида связано с различным назначением.

Видеоинструкция

Если у вас всё равно не получится построить что-то нормальное, рекомендуется ознакомиться с видеороликом, в котором приводятся дополнительные комментарии к вышеописанным инструкциям.

Источник