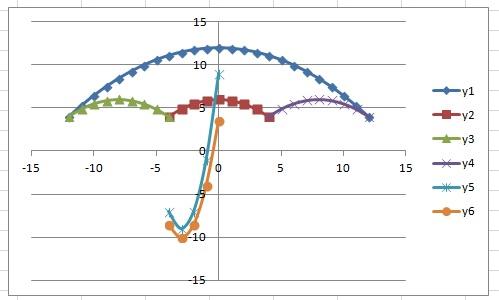
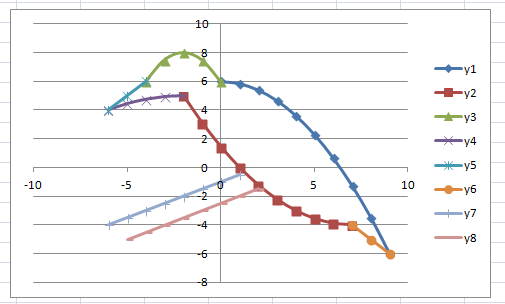
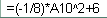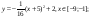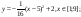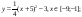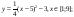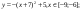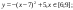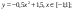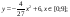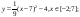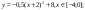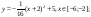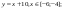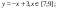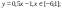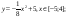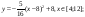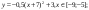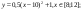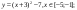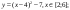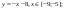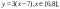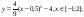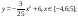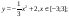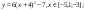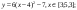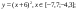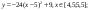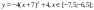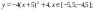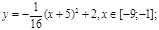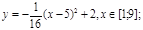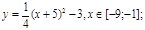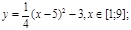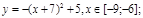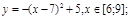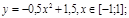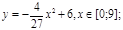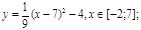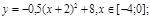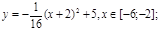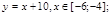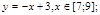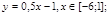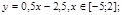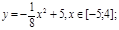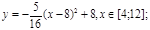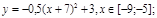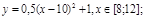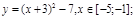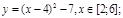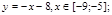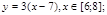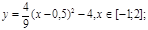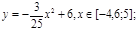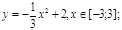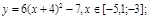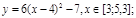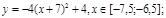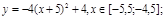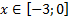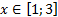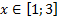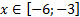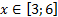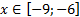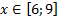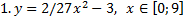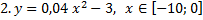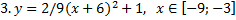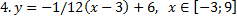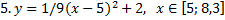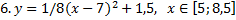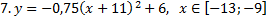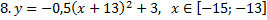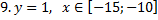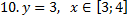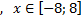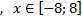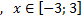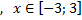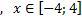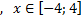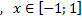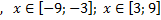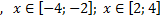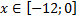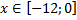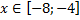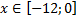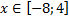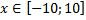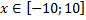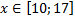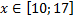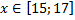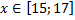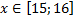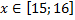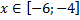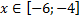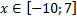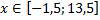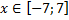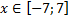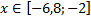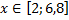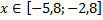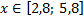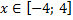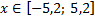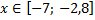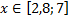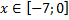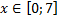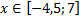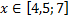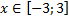Практическая работа «Создание диаграмм средствами MS Excel», “зонтик” и другое
Содержимое разработки
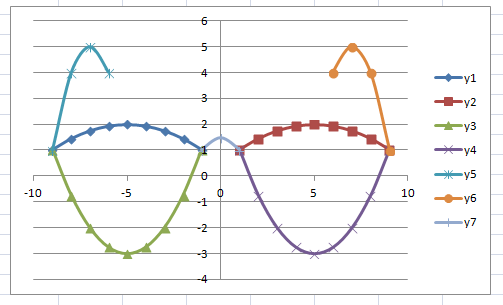
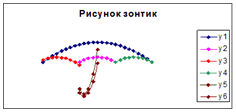
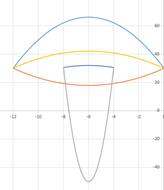
Задание: Построение рисунка «ЗОНТИК»
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х[-12;12]
y 2= -1/8х 2 +6, х[-4;4]
y 3= -1/8( x +8) 2 + 6, х[-12; -4]
y 4= -1/8( x- 
y5= 2 ( x+3 ) 2 – 9, х[-4; 0 ]
y 6=1. 5 ( x +3) 2 – 10 , х[-4;0]
Запустить MS EXCEL
В ячейке А1 внести обозначение переменной х
Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х 2 + 12, х[-12;12]
Порядок выполнения действий:
Устанавливаем курсор в ячейку В1 и вводим у1
В ячейку В2 вводим формулу
Нажимаем Enter на клавиатуре
Автоматически происходит подсчет значения функции.
Растягиваем формулу до ячейки В26
Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х[-4;4]) вводим формулу для графика функции y 2= -1/8х 2 +6.
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций.
Выделяем диапазон ячеек А1: G26
На панели инструментов выбираем меню Вставка → Диаграмма.
В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok . 

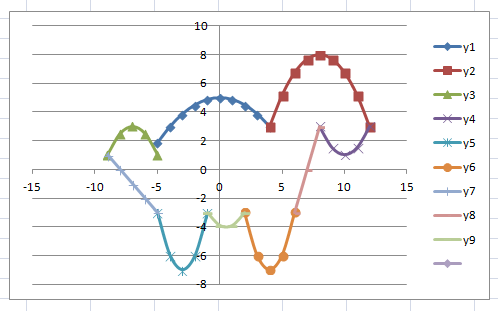
В результате должен получиться следующий рисунок:
Построить графики функций в одной системе координат. Получить рисунок.
1)
2)
3)
4)
5)
6)
7)
1)
2)
3)
4)
5)
6)
7)
1)
2)
3)
4)
5)
6)
7)
9)
1)
2)
3)
4)
5)
6)
7)
Предварительный просмотр:
Практическая работа: Построение рисунка «ЗОНТИК» в электронных таблицах MS Excel
Цель работы: закрепление практических навыков по теме: «Построение графиков».
Задание. Построение рисунка «ЗОНТИК»
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х ∈ [-12;12]
y2= -1/8х 2 +6, х ∈ [-4;4]
y3= -1/8(x+8) 2 + 6, х ∈ [-12; -4]
y4= -1/8(x-8) 2 + 6, х ∈ [4; 12]
y5= 2(x+3) 2 – 9, х ∈ [-4;0]
y6=1.5(x+3) 2 – 10, х ∈ [-4;0]
- Запустить MS EXCEL
- В ячейке А1 внести обозначение переменной х
- Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х 2 + 12, х ∈ [-12;12]
Порядок выполнения действий:
- Устанавливаем курсор в ячейку В1 и вводим у1
- В ячейку В2 вводим формулу
- Нажимаем Enter на клавиатуре
- Автоматически происходит подсчет значения функции.
- Растягиваем формулу до ячейки В26
- Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х ∈ [-4;4]) вводим формулу для графика функции y2= -1/8х 2 +6
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций .
- Выделяем диапазон ячеек А1:G26
- На панели инструментов выбираем меню Вставка → Диаграмма.
- В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok.
Помогите с Excel
Что такое стили WordArt
Чтобы оформить текст внутри фигуры, используйте блок команд Средства рисования – Формат – WordArt. По аналогии со стилями фигур, здесь есть выпадающее меню с готовыми стилями и кнопки ручной настройки: Заливка, Контур, Эффекты. Поэкспериментируйте с форматами фигур и текста, здесь можно получить настоящее эстетическое удовольствие!
Когда Вы вставляете на лист несколько фигур, при наложении одна на другую, они перекрывают друг друга. При этом объекты, созданные раньше, будут в самом низу, а последние – вверху.
Для изменения порядка следования фигур, на ленте есть группа команд: Средства рисования – Формат – Упорядочение. Чтобы фигура располагалась выше – нажмите «Переместить вперед». В выпадающем меню выберите:
- Переместит вперед – поднять фигуру на один уровень вверх;
- На передний план – сделать фигуру самой верхней;
Аналогично можно понижать уровень фигуры.
Если у Вас на листе несколько фигур, которые нужно выровнять относительно какой-то базовой линии, выделите все выравниваемы фигуры (кликайте по ним с зажатой клавишей Ctrl). После этого выполните на ленте Средства рисования – Формат – Упорядочение – Выровнять. В выпадающем меню будет несколько вариантов выравнивания, выберите тот, который подходит Вам. Благодаря миниатюрам возле каждого пункта, проще сориентироваться, что делает каждая из команд.
В этом же меню есть две важные опции: «Распределить по вертиали» и «Распределить по горизонтали». Они выстраивают объекты так, чтобы между ними было одинаковое расстояние.
Комбинируйте команды выравнивания и распределения, тогда Ваши фигуры будут не просто набросаны на лист, а будут выстроены в строгом порядке, что важно для любого уважающего себя эксперта Эксель.
Любая фигура будет выглядеть гармоничнее, если назначить для нее подходящий стиль. Для этого, на ленте найдите выпадающий список Средства рисования – Формат – Стили фигур. Кликнув на кнопке «Дополнительные параметры», Вы увидите сразу весь список предустановленных стилей, вероятно, что там будет подходящий вариант.
Если же не будет, можно воспользоваться дополнительными меню в этой группе команд:
- Заливка фигуры – задайте здесь цвет и способ заливки:
- Сплошным цветом;
- Вашим рисунком;
- Градиентом;
- Текстурой;
- Контур фигуры:
- Цвет контура;
- Толщина линии контура;
- Штрихи (сплошной контур или прерывистый)
- Вид стрелки (для объектов из группы «Линия»)
- Эффекты фигуры – различные визуальные эффекты для более «продвинутых» решений:
- Заготовка – несколько уже сгруппированных эффектов, готовые решения;
- Тень;
- Подсветка;
- Отражение;
- Сглаживание;
- Рельеф;
- Поворот объемной фигуры
Назначайте стили фигур, чтобы получить самый выразительные визуальные эффекты на своих графических объектах.
Если нужно получить объект строго заданных размеров, на ленте есть блок: Средства рисования – Формат – Размер. Задайте здесь точные размеры Вашего изображения искусства. Учтите, изменяя масштаб печати, вы измените и размеры напечатанной фигуры.
Интегрированный урок (алгебра + информатика) по теме «Рисуем графиками функций». 8-й класс
Класс: 8
Тема (математика): Преобразования графиков функций.
Тема (информатика): Построение графиков в MS Excel.
Цели урока:
- Образовательные:
- повторение знаний по преобразованию графиков функций,
- применение приобретенных умений и навыков графического изображения в процессе решения задач по математике и информатике;
- формирование практических навыков построения графиков в программе Excel.
- Развивающие:
- развитие умений выделять главное,
- развитие речи, эмоций, логического мышления учащихся,
- активизация познавательной и творческой активности учащихся.
- Воспитательные:
- формирование интереса к предмету, навыков контроля и самоконтроля, чувства ответственности, самостоятельности, деловых и коммуникативных качеств учащихся.
Задачи урока:
- Повторить виды преобразований графика функции y = f(x):
- y = – f(x) ;
- y = kf(x);
- y = f(x) + а;
- y = f(x – b);
- y = f(x – b) + а.
- Использовать изученные виды преобразований для построения рисунка с помощью графиков.
- Использовать умения построения графиков в одной системе координат с помощью программы Excel для получения некоторого изображения.
- Продолжить формирование у учащихся потребности использования информационных технологий в решении графических заданий по математике.
- Продемонстрировать применение полученных знаний на практике и для решения задач из смежных дисциплин.
Структура урока:
- Организационный момент (объявление темы, цели и задач урока).
- Актуализация знаний (повторение видов преобразований графиков функций)
- Повторение темы «Преобразования графиков функций»:
- выполнение задания на построение графиков функций с помощью различных видов преобразований;
- построение рисунка в тетради с помощью графиков функций на заданной области определения.
- Повторение темы «Построение графиков функций с помощью программы Excel:
- повторение особенностей ввода формул и построения графиков в программе Excel.
- практическая работа «Рисуем графиками функций в программе Excel».
- проверка практической работы, анализ ошибок и выставление оценок.
- Постановка домашнего задания.
- Подведение итогов урока, рефлексия.
1. Организационный момент
Сегодня мы проводим интегрированный урок, в ходе которого попробуем совместить два предмета: математику и информатику. Нам предстоит повторить преобразования графиков функций и использовать эти знания для выполнения заданий по математике и информатике на построение различных изображений.
2. Актуализация знаний
Для повторения изученных видов преобразований графиков необходимо выполнить предложенное задание.
Задание для фронтальной работы: установите соответствие между предложенными графиками и формулами функций, дайте характеристику данному виду преобразований (рис.1, 2).
3. Повторение темы «Преобразования графиков функций»
Применение рассмотренных видов преобразований осуществляется при выполнении двух следующих заданий, которые учащиеся выполняют в тетрадях. Один ученик выполняет задание на интерактивной (либо обычной) доске. Графики обозначаются разными цветами.
Задание 1: постройте графики функций с помощью изученных видов преобразований
Первый график должен быть построен обязательно на доске, второй рассчитан на учеников, быстро выполнивших задание, либо может быть использован как резервный в конце урока для самостоятельной работы учащихся, быстро справившихся с практической работой.
Задание 2: Постройте рисунок с помощью графиков функций (рис.3):
Графики 4),5),6),7) до пересечения с графиком 
А теперь попробуем получить рисунки в программе Excel.
4. Повторение темы «Построение графиков функций с помощью программы Excel:
Для повторения темы на данном этапе урока необходимо провести фронтальный опрос учащихся с целью актуализации знаний по информатике, необходимых для выполнения практической работы.
Вопросы для устной фронтальной работы:
- Как задать диапазон значений для переменной Х?
- Как задать диапазон значений для переменной У?
- Как показать, что в ячейку будет введена формула?
- Какие правила ввода формул вы знаете?
- Какими символами обозначаются действия умножения, деления, возведения в степень?
- Может ли формула в программе Excel содержать переменную Х? А что вместо Х она должна содержать?
- Как построить несколько графиков в одной системе координат?
- Какой тип диаграмм надо выбрать для построения графика функции?
- Как изменить цвет графика?
Практическая работа «Рисуем графиками функций в программе Excel».
Все ученики получают карточки с заданиями. Задания (зонтик, очки, кит) берутся из источника [6]. В одной системе координат необходимо построить графики всех функций на указанных промежутках. Если все будет выполнено верно, то получится картинка. За работу каждому будет выставлена отметка с учетом объема выполненной работы и допущенных ошибок. Работу сохранить на Рабочий стол и не закрывать.
На данном этапе учащиеся осуществляют самоконтроль:
- определяют, какие элементы рисунка «не вписываются» в общую картину,
- чем это было вызвано (ошибки при вводе формулы, при задании диапазона значений и т.п.), опираясь на полученные на уроках математики знания о различных видах преобразований, вносят изменения и оценивают, как они повлияют на вид рисунка. Во время работы учитель проходит по классу и оценивает работу учащихся.
На следующем этапе учитель показывает с помощью проектора, какие рисунки должны получиться у учащихся, объявляет оценки за выполненную работу, проводит с помощью учеников анализ типичных неточностей и ошибок.
5 . Постановка домашнего задания
По алгебре (творческое задание): придумать рисунок с помощью графиков 7-8 функций. Изобразить его в координатной плоскости, записать используемые функции на заданной области определения.
По информатике: построить с помощью программы Excel рисунок по заданным формулам функций из того же источника [6] (бабочка и лягушка).
6. Подведение итогов урока, рефлексия
Подведение итогов урока осуществляется в форме беседы, в ходе которой обсуждается вопрос: в каких сферах человеческой деятельности могут применяться графики функций.
На этапе рефлексии ученикам предоставляется возможность оценить свою работу, а также ответить на вопросы: получилось ли достигнуть цели урока, достаточно ли было знаний для выполнения предложенных заданий, какие задания требуют дополнительного внимания.
Список использованной литературы
- Алгебра,8 класс: учеб. для учащихся общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е.Феоктистов.–10-е изд., испр. – М.: Мнемозина, 2010.–384с.
- Босова Л.Л. Информатика и ИКТ: учебник для 7 класса / Л.Л. Босова. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2010. – 229 с.
- Цукарь А.Я. Рисуем графиками функций // Математика в школе. – 1999. – №4. – с. 80-81
Научно — практическая работа» Первые шаги в науку»: «Рисуем графиками линейных функций»
Цель работы: научиться создавать простые рисунки и сюжеты с помощью графиков линейных функций с заданными ограничениями в сервисе DESMOS-графический калькулятор.
Скачать:
| Вложение | Размер |
|---|---|
| 67_nesmina_a.l_matematika.docx | 111.27 КБ |
Предварительный просмотр:
ХIV городская научно-практическая конференция школьников «Первые шаги в науку»
Возрастная категория: «Юниор»
«Рисуем графиками линейных функций»
Несмина Анастасия Леонидовна
г.о. Тольятти, МБУ «Лицей № 67», 7 класс
Столярчук Лилия Геннадьевна,
учитель математики первой категории, МБУ «Лицей № 67»
2.1. Элементарные функции и их графики………………5
2.2. Линейная функция и ее график………………………6
2.3. Рисование графиками линейных функций………….7
Каждый год счастливые родители ведут своих детей в школу. И далее дорога для большего числа учащихся составляет 11 лет упорного труда в получении знаний. Математика сопровождает нас на всем пути, но, к сожалению, не у всех ребят есть прирожденная склонность к ней. Возникает необходимость для поиска методов воздействия на учащихся, которые могли бы повысить стимул приобретения и расширения знаний. Как заставить ученика работать с удовольствием, а не из-под палки? Как сделать так, чтобы он захотел чему то научиться? Математика – одна из важнейших наук на земле и именно поэтому есть необходимость развивать у детей интерес к этой науке. А это означает, что задания в математике должны быть такими, чтобы постоянно была пища для размышлений и, даже, для творческого полета.
Тема исследовательской работы : « Рисуем графиками линейных функций ».
Гипотеза : « графиками линейных функций можно рисовать отдельные объекты и даже целые сюжеты».
Цель : научиться создавать простые рисунки и сюжеты с помощью графиков линейных функций с заданными ограничениями в сервисе DESMOS-графический калькулятор.
Объект исследования : линейная функция и ее график.
Предмет исследования : рисование графиками линейной функции.
1. Изучить разнообразную литературу по теме: «Линейная функция и ее график»
2. Создать авторские рисунки графиками линейных функций в сервисе DESMOS-графический калькулятор;
3. Предложить одноклассникам построить рисунки по заданным функциям с ограничениями;
4. Предложить одноклассникам создать авторские рисунки графиками линейных функций в сервисе DESMOS-графический калькулятор;
6. Выполнить оценку результатов своей работы и сделать выводы.
- поиск, анализ и синтез литературы и программного обеспечения;
- практическое применение знаний, умений и навыков;
- обобщение;
Понятие «функция» одно из важнейших в математике. С помощью функции описываются различные процессы и явления: химические, статистические, физические, природные и т.д.
Актуальность работы заключается в том, что при выполнении творческих заданий на создание изображений графиками линейных функций, развиваются художественные способности учащихся, которые лежат в основе различных профессий: дизайнер, архитектор, скульптор и т.д., кроме того, повышается интерес к изучению темы: «Линейная функция и ее график». Красота и эстетика математики в школе в особой мере проявляется именно в «красивых» и творческих заданиях.
Рисование графиками линейных функций заставляет воочию увидеть неразрывную связь красоты и математики, непосредственно соприкоснуться с миром прекрасного. Вместо однообразных упражнений по изучаемой теме можно предложить ребятам творческий подход и тогда математика становится интересной, удивительной и красивой.
Относительная «новизна» заданий, неожиданная фабула интригует, а положительные эмоции включают второе дыхание в получении знаний. Такие нестандартные упражнения послужат достаточно хорошей школой для приобретения необходимых основ мышления, владея которыми можно решать любые задачи. Кроме того, чтобы облегчить дальнейшее изучение специальных функций в школе, нужно научиться свободно оперировать графиками элементарных функций.
2. Основное содержание.
2.1 Элементарные функции и их графики
Знакомство и изучение свойств различных функций и их графиков занимает важное место и в школьной математике, и в следующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве предметов узкого профиля. Например в экономике – это функции издержек, полезности, функции спроса, предложения и потребления, в радиотехнике – функции управления и функции отклика, в статистике – функции распределения и т.д.
Определение: зависимость переменной у от переменной х, при которой каждому значению переменной х из определенного множества D соответствует единственное значение переменной у, называется функцией. у = f(х), где х – независимая переменная (аргумент), у – зависимая переменная (функция).
Область определения функции D(f)- множество, на котором задаётся функция. Иначе: множество значений, которые может принимать аргумент.
Область значений функции E(f)- множество, состоящее из всех значений, которые принимает функция.
График функции – множество точек на координатной плоскости, координатами которых являются пары чисел (х; у), где х – значение аргумента, у – соответствующее ему значение функции.
1. Линейная функция y = kx + m
График функции – прямая.
2. Функция y = kx² (k ≠ 0)
График функции – парабола.
3. Квадратичная функция y = ax² + bx + c
График функции – парабола
4. Функция обратной пропорциональности y =
График функции – гипербола.
График функции – ветвь параболы, перевернутая «набок».
График функции – объединение двух лучей
3. y = xⁿ (n = 3, 5, 7, 9…)
График функции – кубическая парабола (при n=3)
2.2. Линейная функция и ее график.
Линейная функция y = kx + m, график функции – прямая.
Коэффициент k отвечает за угол наклона (k>0 – угол острый, k 0 – вверх, m
у = kx – частный случай линейной функции при m=0 (прямая пропорциональность)
В этом случае график функции обязательно проходит через начало координат.
Свойства линейной функции y = kx + m
2) Возрастает, если k > 0; убывает, если k
3) Не ограничена ни снизу, ни сверху
4) Нет ни наибольшего, ни наименьшего значений
Чтобы составить уравнение линейной функции надо:
- взять координаты двух точек, через которые проходит прямая ( x 1 ,y 1 ) ( x 2 ,y 2 );
- подставить эти координаты в уравнение линейной функции и получить систему двух уравнений:
- выразить из первого уравнения m = у 1 — k х 1 ;
- подставить во второе у 2 = k х 2 + у 1 — k х 1 ;
- найти значение k = ;
- подставить значение k в формулу m = у 1 — k х 1 .
Например, мы выяснили, что график линейной функции (прямая) проходит через точки с координатами (5;2) и (4:1). Действуем по плану: составим систему уравнений
Из первого уравнения выразим m : m=2-5k, подставим значение m во второе уравнение и найдем k : 1=4k+2-5k, k =1. Далее в уравнение линейной функции подставляем значения коэффициентов k и m и получаем искомое уравнение прямой: у=х-3 .
2.3. Рисование графиками линейных функций на уроке математики
источники:
http://urok.1sept.ru/articles/646551
http://nsportal.ru/ap/library/drugoe/2018/10/31/nauchno-prakticheskaya-rabota-pervye-shagi-v-nauku-risuem-grafikami
Содержание
- Практическая работа построение графиков в MS Excel
- Содержимое разработки
- Как сделать очки в эксель
- Практическая работа «Создание диаграмм средствами MS Excel», “зонтик” и другое
- Предварительный просмотр:
- Помогите с Excel
- Что такое стили WordArt
- Практическая работа построение графиков в MS Excel
- П_ПОСТРОЕНИЕ ДИАГРАММ И ГРАФИКОВ СРЕДСТВАМИ MSEXCEL
Практическая работа построение графиков в MS Excel
В работе показано как с помощью графиков в Excel можно выполнить интересные рисунки
Шестакова Марина Васильевна , 21.02.2019
Содержимое разработки
Практическая работа в MS Excel по теме
ПОСТРОЕНИЕ ДИГРАММ И ГРАФИКОВ
Задание: Построение рисунка «ЗОНТИК»
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х[-12;12]
y 2= -1/8х 2 +6, х[-4;4]
y 3= -1/8( x +8) 2 + 6, х[-12; -4]
y 4= -1/8( x- 
y5= 2 ( x+3 ) 2 – 9, х[-4; 0 ]
y 6=1. 5 ( x +3) 2 – 10 , х[-4;0]
Запустить MS EXCEL
В ячейке А1 внести обозначение переменной х
Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х 2 + 12, х[-12;12]
Порядок выполнения действий:
Устанавливаем курсор в ячейку В1 и вводим у1
В ячейку В2 вводим формулу

Нажимаем Enter на клавиатуре
Автоматически происходит подсчет значения функции.
Растягиваем формулу до ячейки В26
Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х[-4;4]) вводим формулу для графика функции y 2= -1/8х 2 +6.
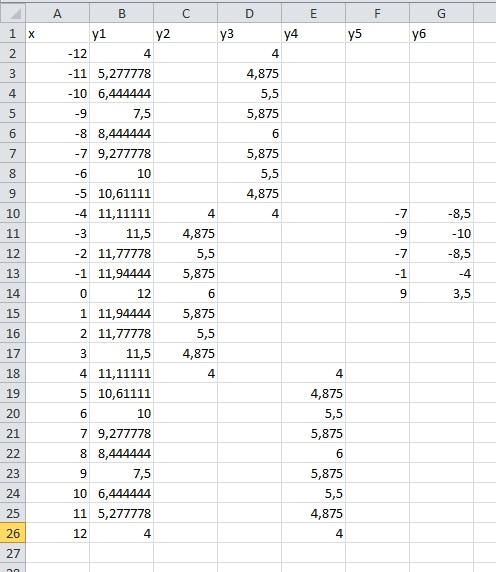
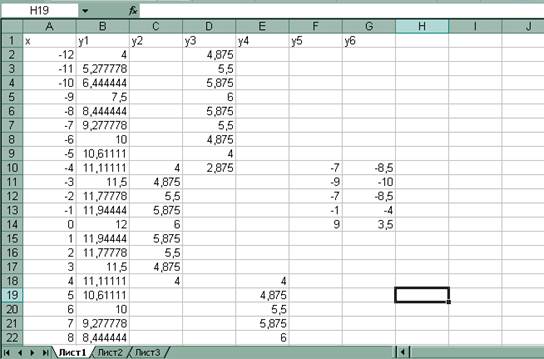
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций.
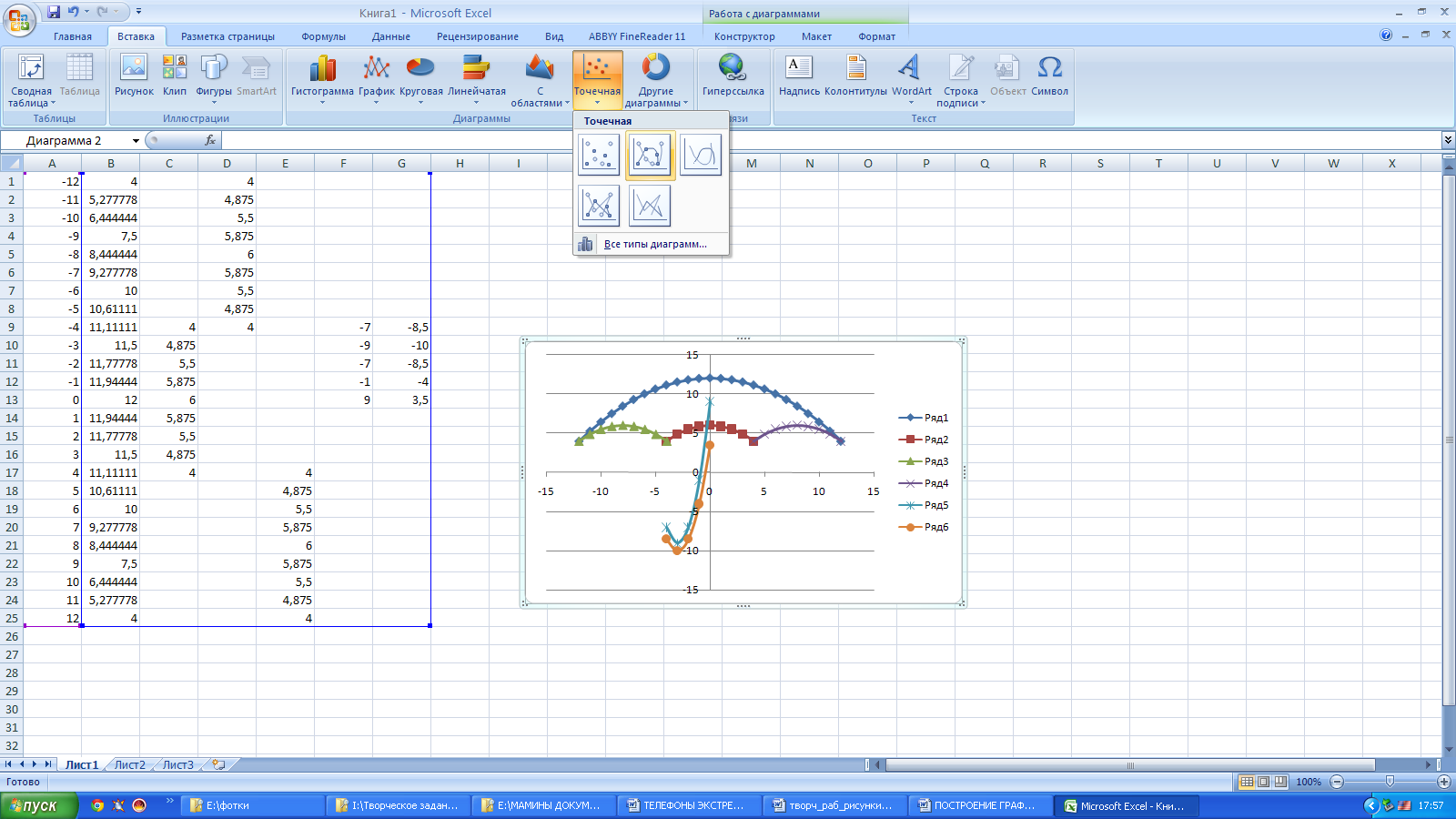
Выделяем диапазон ячеек А1: G26
На панели инструментов выбираем меню Вставка → Диаграмма.
В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok .
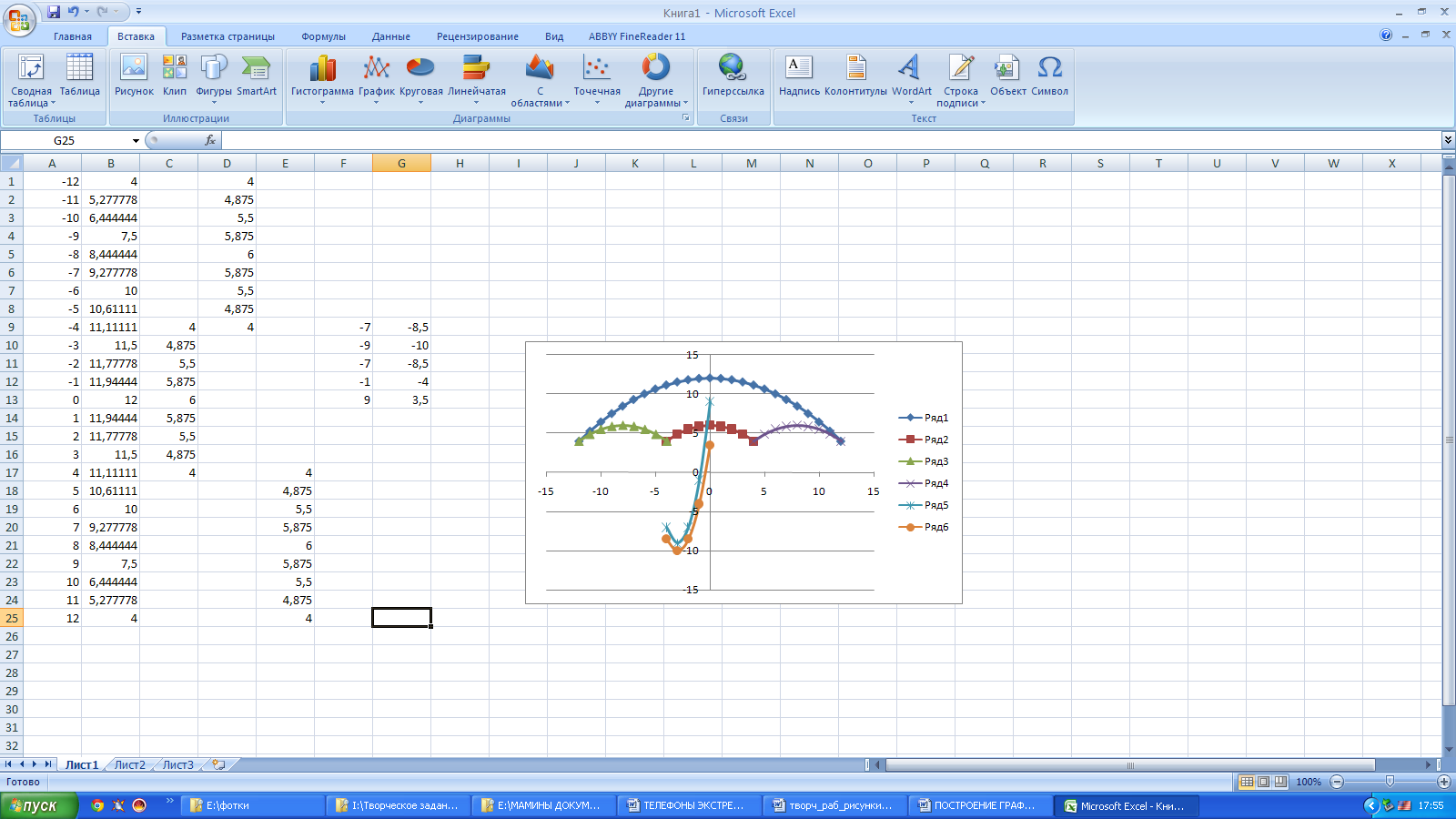
В результате должен получиться следующий рисунок:
Построить графики функций в одной системе координат. Получить рисунок.
1)
2)
3)
4)
5)
6)
7)
1)
2)
3)
4)
5)
6)
7)

1)
2)
3)
4)
5)
6)
7)

9)
1)
2)
3)
4)
5)
6)
7)

Источник
Как сделать очки в эксель
Практическая работа «Создание диаграмм средствами MS Excel», “зонтик” и другое
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х[-12;12]
y 2= -1/8х 2 +6, х[-4;4]
y 3= -1/8( x +8) 2 + 6, х[-12; -4]
y 4= -1/8( x- 
y5= 2 ( x+3 ) 2 – 9, х[-4; 0 ]
y 6=1. 5 ( x +3) 2 – 10 , х[-4;0]
Запустить MS EXCEL
В ячейке А1 внести обозначение переменной х
Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х 2 + 12, х[-12;12]
Порядок выполнения действий:
Устанавливаем курсор в ячейку В1 и вводим у1
В ячейку В2 вводим формулу
Нажимаем Enter на клавиатуре
Автоматически происходит подсчет значения функции.
Растягиваем формулу до ячейки В26
Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х[-4;4]) вводим формулу для графика функции y 2= -1/8х 2 +6.
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций.
Выделяем диапазон ячеек А1: G26
На панели инструментов выбираем меню Вставка → Диаграмма.
В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok .
В результате должен получиться следующий рисунок:
Построить графики функций в одной системе координат. Получить рисунок.
1)
2)
3)
4)
5)
6)
7)
1)
2)
3)
4)
5)
6)
7)
1)
2)
3)
4)
5)
6)
7)
9)
1)
2)
3)
4)
5)
6)
7)
Предварительный просмотр:
Практическая работа: Построение рисунка «ЗОНТИК» в электронных таблицах MS Excel
Цель работы: закрепление практических навыков по теме: «Построение графиков».
Задание. Построение рисунка «ЗОНТИК»
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х ∈ [-12;12]
y2= -1/8х 2 +6, х ∈ [-4;4]
y3= -1/8(x+8) 2 + 6, х ∈ [-12; -4]
y5= 2(x+3) 2 – 9, х ∈ [-4;0]
y6=1.5(x+3) 2 – 10, х ∈ [-4;0]
- Запустить MS EXCEL
- В ячейке А1 внести обозначение переменной х
- Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х 2 + 12, х ∈ [-12;12]
Порядок выполнения действий:
- Устанавливаем курсор в ячейку В1 и вводим у1
- В ячейку В2 вводим формулу
- Нажимаем Enter на клавиатуре
- Автоматически происходит подсчет значения функции.
- Растягиваем формулу до ячейки В26
- Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х ∈ [-4;4]) вводим формулу для графика функции y2= -1/8х 2 +6
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций .
- Выделяем диапазон ячеек А1:G26
- На панели инструментов выбираем меню Вставка → Диаграмма.
- В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok.
Помогите с Excel
Тип диаграммы: точечная (Точечная диаграмма со значениями, соединенными сглаживающими пиниями) , добавить 5 рядов, указав соотвтствующие данные
Что такое стили WordArt
Чтобы оформить текст внутри фигуры, используйте блок команд Средства рисования – Формат – WordArt. По аналогии со стилями фигур, здесь есть выпадающее меню с готовыми стилями и кнопки ручной настройки: Заливка, Контур, Эффекты. Поэкспериментируйте с форматами фигур и текста, здесь можно получить настоящее эстетическое удовольствие!
Когда Вы вставляете на лист несколько фигур, при наложении одна на другую, они перекрывают друг друга. При этом объекты, созданные раньше, будут в самом низу, а последние – вверху.
Для изменения порядка следования фигур, на ленте есть группа команд: Средства рисования – Формат – Упорядочение. Чтобы фигура располагалась выше – нажмите «Переместить вперед». В выпадающем меню выберите:
- Переместит вперед – поднять фигуру на один уровень вверх;
- На передний план – сделать фигуру самой верхней;
Аналогично можно понижать уровень фигуры.
Если у Вас на листе несколько фигур, которые нужно выровнять относительно какой-то базовой линии, выделите все выравниваемы фигуры (кликайте по ним с зажатой клавишей Ctrl). После этого выполните на ленте Средства рисования – Формат – Упорядочение – Выровнять. В выпадающем меню будет несколько вариантов выравнивания, выберите тот, который подходит Вам. Благодаря миниатюрам возле каждого пункта, проще сориентироваться, что делает каждая из команд.
В этом же меню есть две важные опции: «Распределить по вертиали» и «Распределить по горизонтали». Они выстраивают объекты так, чтобы между ними было одинаковое расстояние.
Комбинируйте команды выравнивания и распределения, тогда Ваши фигуры будут не просто набросаны на лист, а будут выстроены в строгом порядке, что важно для любого уважающего себя эксперта Эксель.
Любая фигура будет выглядеть гармоничнее, если назначить для нее подходящий стиль. Для этого, на ленте найдите выпадающий список Средства рисования – Формат – Стили фигур. Кликнув на кнопке «Дополнительные параметры», Вы увидите сразу весь список предустановленных стилей, вероятно, что там будет подходящий вариант.
Если же не будет, можно воспользоваться дополнительными меню в этой группе команд:
- Заливка фигуры – задайте здесь цвет и способ заливки:
- Сплошным цветом;
- Вашим рисунком;
- Градиентом;
- Текстурой;
- Контур фигуры:
- Цвет контура;
- Толщина линии контура;
- Штрихи (сплошной контур или прерывистый)
- Вид стрелки (для объектов из группы «Линия»)
- Эффекты фигуры – различные визуальные эффекты для более «продвинутых» решений:
- Заготовка – несколько уже сгруппированных эффектов, готовые решения;
- Тень;
- Подсветка;
- Отражение;
- Сглаживание;
- Рельеф;
- Поворот объемной фигуры
Назначайте стили фигур, чтобы получить самый выразительные визуальные эффекты на своих графических объектах.
Если нужно получить объект строго заданных размеров, на ленте есть блок: Средства рисования – Формат – Размер. Задайте здесь точные размеры Вашего изображения искусства. Учтите, изменяя масштаб печати, вы измените и размеры напечатанной фигуры.
Практическая работа построение графиков в MS Excel
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х[-12;12]
y 2= -1/8х 2 +6, х[-4;4]
y 3= -1/8( x +8) 2 + 6, х[-12; -4]
y 4= -1/8( x- 
y5= 2 ( x+3 ) 2 – 9, х[-4; 0 ]
y 6=1. 5 ( x +3) 2 – 10 , х[-4;0]
Запустить MS EXCEL
В ячейке А1 внести обозначение переменной х
Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
Последовательно для каждого графика функции будем вводить формулы.
Для у1= -1/18х 2 + 12, х[-12;12]
Порядок выполнения действий:
Устанавливаем курсор в ячейку В1 и вводим у1
В ячейку В2 вводим формулу
Нажимаем Enter на клавиатуре
Автоматически происходит подсчет значения функции.
Растягиваем формулу до ячейки В26
Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х[-4;4]) вводим формулу для графика функции y 2= -1/8х 2 +6.
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций.
Выделяем диапазон ячеек А1: G26
На панели инструментов выбираем меню Вставка → Диаграмма.
В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok .
В результате должен получиться следующий рисунок:
Построить графики функций в одной системе координат. Получить рисунок.
1)
2)
3)
4)
5)
6)
7)
1)
2)
3)
4)
5)
6)
7)

1)
2)
3)
4)
5)
6)
7)

9)
1)
2)
3)
4)
5)
6)
7)

П_ПОСТРОЕНИЕ ДИАГРАММ И ГРАФИКОВ СРЕДСТВАМИ MSEXCEL
1. В электронной таблице построить на листе с данными линейчатую диаграмму с вертикальными столбцами (гистограмму), позволяющую отобразить рост количества серверов Интернета по годам.
2. В электронных таблицах построить графики кубической функции у=х 3 и линейной функции у=2*х.
3. Построение рисунка «ЗОНТИК»
Приведены функции, графики которых участвуют в этом изображении:
у1= -1/18х 2 + 12, х Î [-12;12]
y2= -1/8х 2 +6, х Î [-4;4]
y3= -1/8(x+8) 2 + 6, х Î [-12; -4]
y4= -1/8(x-8) 2 + 6, х Î [4; 12]
y5= 2(x+3) 2 – 9, х Î [-4;0]
y6=1,5(x+3) 2 – 10, х Î [-4;0]
· Запустить MS EXCEL
· В ячейке А1внести обозначение переменной х
· Заполнить диапазон ячеек А2:А26 числами с -12 до 12.
· Последовательно для каждого графика функции будем вводить формулы.Для у1= -1/18х 2 + 12, х Î [-12;12]
Порядок выполнения действий:
1. Устанавливаем курсор в ячейку В1 и вводим у1
2. В ячейку В2вводим формулу= (-1/18)*А2^2+12
3. НажимаемEnterна клавиатуре
4. Автоматически происходит подсчет значения функции.
5. Растягиваем формулу до ячейки В26
6. Аналогично в ячейку С10 (т.к значение функции находим только на отрезке х Î [-4;4]) вводим формулу для графика функции y2= -1/8х 2 +6: = (-1/8)*А10^2+6
В результате должна получиться следующая ЭТ
После того, как все значения функций подсчитаны, можно строить графики этих функций.
2. На панели инструментов выбираем меню Вставка→ Диаграмма.
3. В окне Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok.
В результате должен получиться следующий рисунок:
Задания для индивидуальной работы
Построить графики функций в одной системе координат. Получить рисунок.
1. «Очки» х от -9 до 9, шаг 1
1)
3)
4)
5)
6)
7)
2. «Птица» x от -6 до 9 с шагом 1
2)
3)
4)
5)
6)
7)

3. «Динозаврик» х от -9 до 13 с шагом 0,2
2)
3)
4)
5)
6)
7)

9)
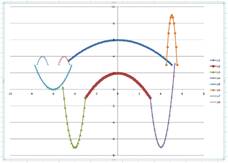
1)
2)
3)
4)
5) 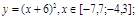
6) 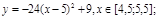

Задачи повышенного уровня, для углубленного изучения
Диапазон и шаг определите сами (на разных отрезках они могут быть различны)
1. Построить бабочку
1. y = – ( x +2) 2 + 6,
y = – ( x – 2) 2 + 6,
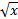
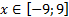
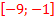
3. y = 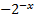
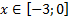
4. y = 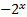
5. y = – ( x +5) 3 ,
y = ( x – 5) 3 ,
6. y = – 4/3 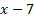
y = 4/3 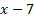
· Для 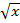
· Для 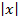
· Степенные функции можно также вводить, используя ^. Пример: x 3 будет выглядеть так =(ячейка)^3
· C возведением числа в степень х можно использовать тот же прием, либо применить функцию =СТЕПЕНЬ(число; степень). Например: 3 x будет выглядеть так: = СТЕПЕНЬ (3; ячейка)
2. Построить кита
3. Построить лицо человека
1. у =1/8 x 2 – 8
2. у =–1/8 x 2 + 8
3. у =–1/3 x 2
4. у =1/3 x 2 – 6
5. у =1/16 x 2 + 6
6. у =–1/4 x 2 +11,
7. у =1/2 x 2 – 7
8. у =–1/9 x 2 – 6
9. у =( 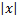
1. y = – (x + 6) 2 + 66 ,
2. y = (x + 6) 2 /3 + 18 ,
3. y = 20(x + 6) 2 – 50 ,
4. y = – (x + 6) 2 /3 + 42 ,
5. y = – (x + 6) 2 /3 + 32 ,
5. Построить рыбу с шагом 0,5
1. y = –0,05x 2 + 5,
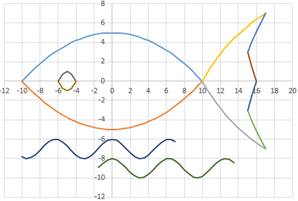
3. y = 170/x – 17,
4. y = –170/x+ 17,
5. y = –510/x+ 37,
6. y = 510/x –37,
7. y = 3x – 48,
8. y = –3x + 48,
9. y = –x 2 – 10x – 24,
10. y = x 2 +10x + 24,
11. y = cos x – 7,
12. y = cos x – 9,
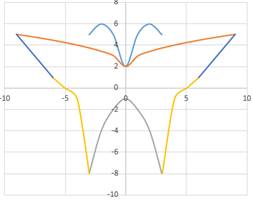
6. Построить лягушку
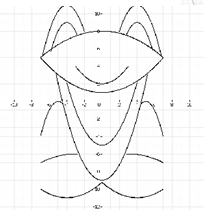
2. y = 4/49 x 2 + 1,
3. y = –0,75( x +4) 2 + 11,
4. y = –0,75(x – 4) 2 + 11,
5. y = –(x+ 4) 2 + 9,
6. y = –(x – 4) 2 + 9,
7. y = 4/9x 2 – 5,
8. y= 4/9x 2 – 9,
9. y = –1/16(x+3) 2 – 6,
10. y = –1/16(x – 3) 2 – 6 ,
11. y = 1/9(x+ 4) 2 –11,
12. y = –1/9(x – 4) 2 –11,
13. y = –(x+5) 2 ,
13. y = –(x – 5) 2 ,
14.y = 2/9 x 2 ,
Источник
ПРАКТИЧЕСКАЯ РАБОТА
ПОСТРОЕНИЕ ДИАГРАММ И ГРАФИКОВ СРЕДСТВАМИ MSEXCEL
1. В электронной
таблице построить на листе с данными линейчатую диаграмму с вертикальными
столбцами (гистограмму), позволяющую отобразить рост количества серверов
Интернета по годам.
|
Годы |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
|
Кол-во серверов |
16 |
30 |
43 |
72 |
110 |
147 |
172 |
233 |
318 |
395 |
433 |
2. В электронных
таблицах построить графики кубической функции у=х3 и линейной
функции у=2*х.
3. Построение
рисунка «ЗОНТИК»
Приведены функции,
графики которых участвуют в этом изображении:
у1= -1/18х2 +
12, хÎ[-12;12]
y2= -1/8х2 +6,
хÎ[-4;4]
y3= -1/8(x+8)2 +
6, хÎ[-12; -4]
y4= -1/8(x-8)2 +
6, хÎ[4; 12]
y5= 2(x+3)2 –
9, хÎ[-4;0]
y6=1,5(x+3)2 –
10, хÎ[-4;0]
·
Запустить
MS EXCEL
·
В
ячейке А1внести обозначение переменной х
·
Заполнить
диапазон ячеек А2:А26 числами с -12 до 12.
·
Последовательно
для каждого графика функции будем вводить формулы.Для у1= -1/18х2 +
12, хÎ[-12;12]
Порядок выполнения
действий:
1. Устанавливаем
курсор в ячейку В1 и вводим у1
2.В
ячейку В2вводим формулу= (-1/18)*А2^2+12
3. НажимаемEnterна
клавиатуре
4. Автоматически
происходит подсчет значения функции.
5.Растягиваем
формулу до ячейки В26
6. Аналогично в
ячейку С10 (т.к значение функции находим только на отрезке хÎ[-4;4]) вводим
формулу для графика функции y2= -1/8х2 +6: =
(-1/8)*А10^2+6
И.Т.Д.
В результате
должна получиться следующая ЭТ
После того, как
все значения функций подсчитаны, можно строить графики этих функций.

Выделяем диапазон ячеек А1:G26
2.
На панели инструментов выбираем меню Вставка→ Диаграмма.
3. В окне Мастера диаграмм
выберите Точечная → Выбрать нужный вид→ Нажать Ok.
В
результате должен получиться следующий рисунок:
Задания для индивидуальной
работы
Построить графики
функций в одной системе координат. Получить рисунок.
1.
«Очки» х от -9 до 9, шаг 1
1)

3)
4)
5)
6)
7)
2.
«Птица»x от -6 до 9 с шагом 1

2)
3)
4)
5)
6)
7)

3.
«Динозаврик» х от -9 до 13 с шагом 0,2

2)
3)
4)
5)
6)
7)

9)

«Кошка» х от -7,7 до 5,5 с шагом 0,1
1)
2)
3)
4)
5)
7)
6)

Задачи
повышенного уровня, для углубленного изучения
Диапазон
и шаг определите сами (на разных отрезках они могут быть различны)
1.
Построить бабочку
1. y = – (x+2)2 + 6,
y
= – (x – 2)2 + 6,

+
2, обратите внимание, что к отрицательным значениямx нужно применить
функцию еще МОДУЛЬ, иначе значения на отрезке не посчитаются.
3. y =,
обратите внимание, что в степень возводится 2, а не -2.
4.
y = ,
5.
y = – (x +5)3,
y
= (x – 5)3,
6.
y = – 4/3,
y
= 4/3,
Примечание:
· Для
применяют функцию =КОРЕНЬ(число)
— возвращает значение квадратного корня.
· Для
применяют функцию =МОДУЛЬ(число)
— возвращает модуль (абсолютную) величину числа.
· Степенные
функции можно также вводить, используя ^. Пример: x3
будет выглядеть так =(ячейка)^3
· C
возведением числа в степень х можно использовать тот же прием, либо
применить функцию =СТЕПЕНЬ(число; степень). Например: 3xбудет
выглядеть так: = СТЕПЕНЬ (3; ячейка)

Построить гриб с шагом 0,2
1.
y = – (x + 6)2 + 66,
2.
y = (x + 6)2/3 + 18,
3.
y = 20(x + 6)2 – 50,
4.
y = – (x + 6)2/3 + 42,
5. y = – (x + 6)2/3 + 32,
5. Построить рыбу с шагом 0,5
1.
y = –0,05x2 + 5,

3.
y = 170/x – 17,
4.y = –170/x+ 17,
5.y = –510/x+ 37,
6.y = 510/x –37,
7.y = 3x – 48,
8.y = –3x + 48,
9.y = –x2 – 10x – 24,
10.y = x2 +10x + 24,
11.y = cos x – 7,
12.y = cos x – 9,
6. Построить лягушку

2. y = 4/49x2 + 1,
3. y = –0,75(x+4)2+ 11,
4.
y = –0,75(x – 4)2+ 11,
5.
y = –(x+ 4)2+ 9,
6.
y = –(x – 4)2+ 9,
7.
y = 4/9x2 – 5,
8.
y= 4/9x2– 9,
9.
y = –1/16(x+3)2 – 6,
10.
y = –1/16(x – 3)2 – 6 ,
11.
y = 1/9(x+ 4)2–11,
12.y = –1/9(x – 4)2–11,
13. y = –(x+5)2,
13. y = –(x – 5)2,
14.y = 2/9 x2,
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
ПРАКТИЧЕСКАЯ РАБОТА
ПОСТРОЕНИЕ ДИАГРАММ И ГРАФИКОВ
СРЕДСТВАМИ MSEXCEL
1. В
электронной таблице построить на листе с данными линейчатую диаграмму с
вертикальными столбцами (гистограмму), позволяющую отобразить рост количества
серверов Интернета по годам.
|
Годы |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
|
Кол-во |
16 |
30 |
43 |
72 |
110 |
147 |
172 |
233 |
318 |
395 |
433 |
2. В
электронных таблицах построить графики кубической функции у=х3 и
линейной функции у=2*х.
3. Построение рисунка «ЗОНТИК»
Приведены функции, графики которых
участвуют в этом изображении:
у1= -1/18х2 + 12, хÎ[-12;12]
y2= -1/8х2 +6, хÎ[-4;4]
y3= -1/8(x+8)2 + 6, хÎ[-12; -4]
y4= -1/8(x-8)2 + 6, хÎ[4; 12]
y5= 2(x+3)2 – 9, хÎ[-4;0]
y6=1,5(x+3)2 – 10, хÎ[-4;0]
·
Запустить
MS EXCEL
·
В
ячейке А1внести обозначение переменной х
·
Заполнить
диапазон ячеек А2:А26 числами с -12 до 12.
·
Последовательно
для каждого графика функции будем вводить формулы.Для у1= -1/18х2 +
12, хÎ[-12;12]
Порядок выполнения действий:
1. Устанавливаем курсор в
ячейку В1 и вводим у1
2.В ячейку В2вводим
формулу= (-1/18)*А2^2+12
3. НажимаемEnterна клавиатуре
4. Автоматически происходит подсчет
значения функции.
5.Растягиваем формулу до ячейки В26
6. Аналогично в ячейку С10 (т.к значение
функции находим только на отрезке хÎ[-4;4]) вводим формулу для графика функции y2= -1/8х2 +6:
= (-1/8)*А10^2+6
И.Т.Д.
В результате должна получиться следующая
ЭТ
После того, как все значения функций
подсчитаны, можно строить графики этих функций.

диапазон ячеек А1:G26
2.
На панели инструментов выбираем меню Вставка→ Диаграмма.
3. В окне
Мастера диаграмм выберите Точечная → Выбрать нужный вид→
Нажать Ok.
В
результате должен получиться следующий рисунок:
Задания
для индивидуальной работы
Построить
графики функций в одной системе координат. Получить рисунок.
1.
«Очки» х от -9 до 9, шаг 1
1)

3)
4)
5)
6)
7)
2.
«Птица»x от -6 до 9 с
шагом 1

2)
3)
4)
5)
6)
7)

3.
«Динозаврик» х от -9 до 13 с шагом 0,2

2)
3)
4)
5)
6)
7)

9)

0,1
1)
2)
3)
4)
5)
7)
6)

Задачи
повышенного уровня, для углубленного изучения
Диапазон
и шаг определите сами (на разных отрезках они могут быть различны)
1.
Построить бабочку
1.
y = – (x+2)2 + 6,
y = – (x – 2)2 + 6,

+
2, обратите внимание, что к отрицательным значениямx нужно применить функцию
еще МОДУЛЬ, иначе значения на отрезке не посчитаются.
3.
y =,
обратите внимание, что в степень возводится 2, а не -2.
4.
y = ,
5.
y = – (x +5)3,
y = (x – 5)3,
6.
y = – 4/3,
y = 4/3,
Примечание:
· Для
применяют функцию =КОРЕНЬ(число)
— возвращает значение квадратного корня.
·
Для
применяют функцию =МОДУЛЬ(число)
— возвращает модуль (абсолютную) величину числа.
· Степенные
функции можно также вводить, используя ^. Пример: x3
будет
выглядеть так =(ячейка)^3
· C
возведением числа в степень х можно использовать тот же прием, либо
применить функцию =СТЕПЕНЬ(число; степень). Например: 3xбудет
выглядеть так: = СТЕПЕНЬ (3; ячейка)

1. y = – (x + 6)2
+ 66,
2. y = (x + 6)2/3
+ 18,
3. y = 20(x + 6)2
– 50,
4. y = – (x + 6)2/3
+ 42,
5. y = – (x + 6)2/3
+ 32,
5.
Построить рыбу с шагом 0,5
1. y = –0,05x2 +
5,

– 5,
3. y = 170/x – 17,
4.y = –170/x+ 17,
5.y = –510/x+ 37,
6.y = 510/x –37,
7.y = 3x – 48,
8.y = –3x + 48,
9.y = –x2 – 10x –
24,
10.y = x2 +10x + 24,
11.y = cos x – 7,
12.y = cos x – 9,
6. Построить лягушку

+ 8,
2.
y = 4/49x2 + 1,
3.
y = –0,75(x+4)2+ 11,
4. y = –0,75(x – 4)2+
11,
5. y = –(x+ 4)2+
9,
6. y = –(x – 4)2+
9,
7. y = 4/9x2
– 5,
8. y= 4/9x2–
9,
9. y = –1/16(x+3)2
– 6,
10. y = –1/16(x – 3)2
– 6 ,
11. y = 1/9(x+ 4)2–11,
12.y = –1/9(x – 4)2–11,
13. y = –(x+5)2,
13. y = –(x – 5)2,
14.y = 2/9 x2,