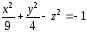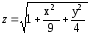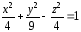Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
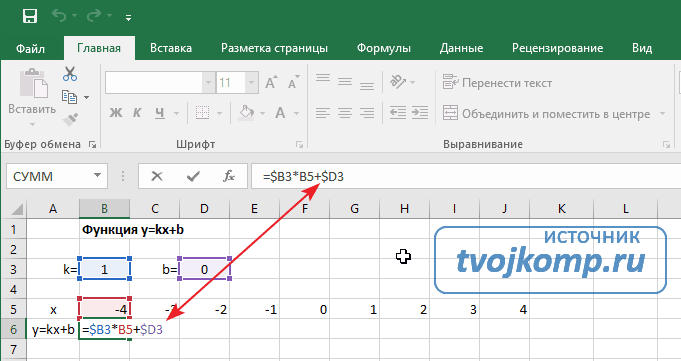
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
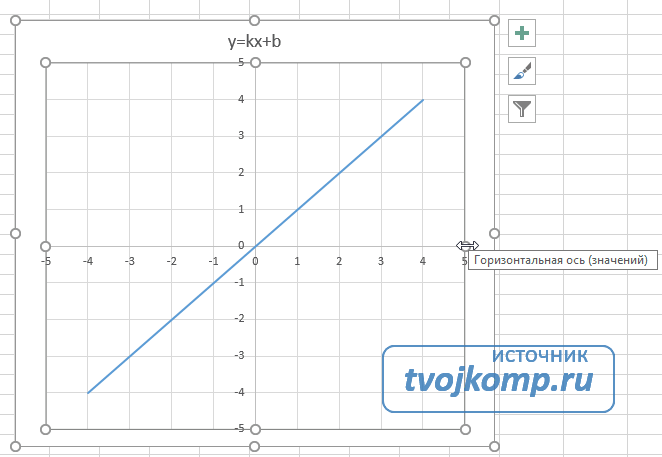
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
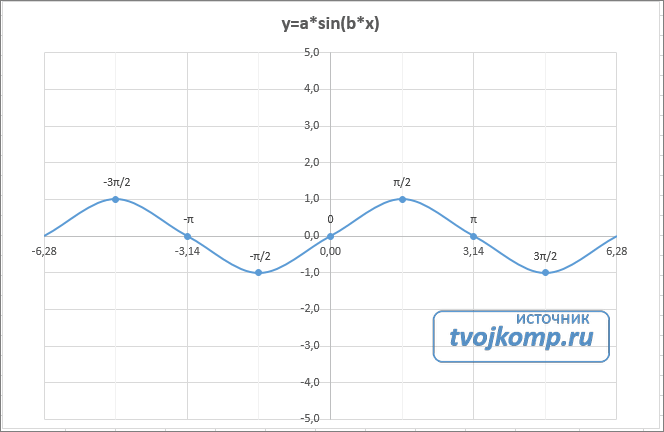
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
В итоге получим диаграмму.
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
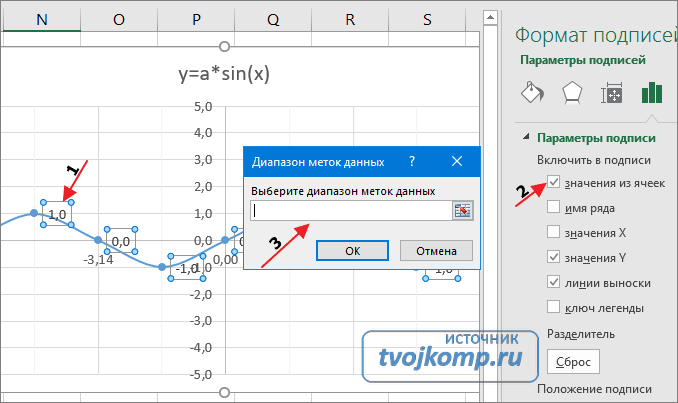
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

Лабораторная работа
№2
Тема:
«Вычисление
функций одной переменной в Excel»
Цель
занятия:
получить практические навыки вычисления
функций одной переменной у=f(x)
и построения их графиков в Excel
Отрабатываемые
вопросы:
1.Создание
формул для вычисления функций одной
переменной.
2.Построение
графиков функций.
Организационно
– методические указания
В Excel
удобно осуществлять построение различных
функций на плоскости и поверхностей в
пространстве.
1.Построение
прямой.
Рассмотрим построение данной функции
в Excel
на примере уравнения у=2х+1
в диапазоне
: х[0; 3]
с шагом х=0,25. Решение
задачи
включает следующие этапы.
1.1. Ввод данных.
Для этого
значения аргумента Х
и функции У
следует
представить в таблице, первый
столбец
которой будет заполнен значениями Х ,
а второй
– функцией У.
Для этого в
ячейку А1 вводим заголовок Аргумент,
а в ячейку В1
– заголовок Прямая.
В ячейку А2 вводится
первое значение аргумента 0,
а в ячейку A3
вводится второе значение аргумента с
учетом шага построения (0,25).
Затем, выделив
блок ячеек А2:АЗ, автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки А14).
Далее вводим
уравнение прямой: в ячейку В2 вводим
формулу: =2*A2+1,
затем копируем
эту формулу в ячейки В2:В14. В результате
должна быть получена следующая таблица
исходных данных и результатов (рис.1.) .
Рис.1.Построение
прямой
1.2. Построение
графика функции. Выделите диаграмму и,
используя вкладку Вставка
График, постройте
график
функции у=2х+1
(рис.2.).
Рис.2. График прямой
1.3.
Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).
2.Решение
уравнения второго порядка.
Примерами уравнений второго порядка
являются: парабола,
гипербола, окружность,
эллипс и другие.
В качестве
примера рассмотрим построение параболы
вида: у =х2
в диапазоне
х[–3;
+3] с шагом х=0,5.
2.1. Ввод данных.
В ячейку А2
вводится первое значение аргумента
(-3), в
ячейку A3 вводится второе значение
аргумента (–2,5),
а затем, выделив
блок ячеек А2:АЗ,
автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки А14).
Далее в ячейку В2
вводим уравнение =А2*А2,
а затем копируем
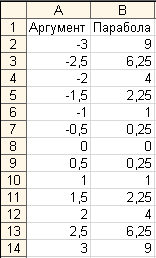
эту формулу в диапазон В2:В14. В результате
должна быть получена следующая таблица
исходных данных.
2.2.Построение
графика функции. Используя вкладку
Вставка
ДИАГРАММА, постройте
график
функции у=х^2
(РИС.4).
Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).
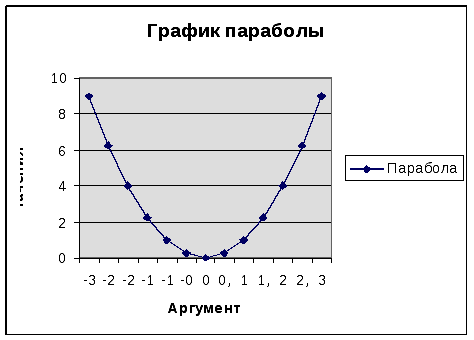
Рис.3. Построение
параболы
Рис.4.График параболы
Рис.5. График
гиперболы
3.Построение
гиперболы.
В простейшем
случае уравнение гиперболы имеет вид
y=k/x.
Задача построения гиперболы аналогична
построению параболы.
Рассмотрим
построение гиперболы y=1/x
в диапазоне х[0,1:
10,1] с шагом х=0,5. Выполните
все вышеуказанные действия самостоятельно
(рис.5).
Задания для
самостоятельного выполнения
-
Построить график
функции Зх+2у–4=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции Зх–5у+15=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции У=е2х в диапазоне х[0.1;
2] с шагом =0,2. -
Построить график
функции У=2х в диапазоне х[–2;
2] с шагом =0,5. -
Построить график
функции У=lnx в диапазоне х[0.5;
10] с шагом =0,5. -
Построить график
функции Зх+2у–4=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции y=2cos3x в диапазоне х[0.1;
1.8] с шагом =0,1. -
Построить график
функции y=x2 в диапазоне х[–3;
3] с шагом =0,25. -
Построить график
функции y=1/2x в диапазоне х[0.1;
10] с шагом =0,25. -
Построить верхнюю
часть параболы у2=х в диапазоне x[0;
4] с шагом =0,25. -
Построить гиперболу
y =1/2х в диапазоне х
[0,1; 5,1] с шагом =0,25 -
Построить верхнюю
полуокружность эллипса x4/4+у2=1 в диапазоне
х
[–2,25; 2,25] с шагом =0,25. -
Постройте параболу:
у2=6х в диапазоне х
[0; 4] с шагом =0,25.
Найдите координаты фокуса и уравнение
директрисы. -
Постройте параболу:
х2=8у в диапазоне x
[–2,25; 2,25] с шагом =0,25.
Найдите координаты фокуса и уравнение
директрисы.
ЛАБОРАТОРНАЯ
РАБОТА №3
Тема:
Вычисление сложных функций в Excel
Цель
занятия:
получить практические навыки вычисления
сложных функций от двух переменных z
= f(x,у)
и построения их графиков в Excel.
Отрабатываемые
вопросы.
1.Создание
формул для вычисления функций от двух
переменных.
2.Построение
графиков типа поверхностей в трехмерном
пространстве.
Организационно
– методические указания
В качестве примера
рассмотрим построение поверхностей
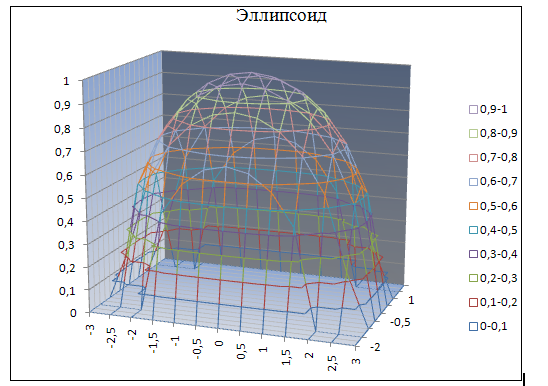
второго порядка таких как: эллипсоид,
гиперболоид, параболоид и т.п.
1.
Рассмотрим
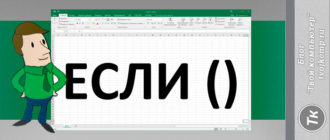
построение эллипсоида в Excel
в соответствии с уравнением:
Пусть необходимо
построить верхнюю часть эллипсоида,
лежащую в диапазонах: х[–3;
3], у[–2;
2] с шагом =0,5
для обеих переменных.
Решение данной
задачи включает следующие этапы.
1.1.Вначале необходимо
разрешить уравнение относительно
переменной z:
1.2.Ввести значения
переменных х
(по вертикали)
, начиная с
ячейки А2
и у (по
горизонтали) , начиная с ячейки B1:
-
в ячейку А2
вводится первое значение аргумента (х
= –3),
затем в ячейку A3
вводится второе значение аргумента (х
= –2,5)
и,
выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения
аргумента х
(за правый нижний угол блока протягиваем
до ячейки А14). -
значения переменной
у
вводим в
строку 1.
Для этого в ячейку В1
вводится первое значение переменной
(у = –2),
в ячейку С1
вводится второе значение переменной
( у = –1,5)
, а затем,
выделив блок ячеек В1:С1,
автозаполнением получаем все значения
аргумента (за правый нижний угол блока
протягиваем до ячейки J1).
1.3.Вычисление
значений функции z.
Для этого
курсор необходимо поместить в ячейку
В2
и вызвать Мастер
функций. В
появившемся диалоговом окне Мастер
функций — шаг 1 из 2
слева в поле Категория
выбираем Математические,
в поле Функция
выбираем функцию Корень
и нажимаем
кнопку ОК.
В диалоговом окне Корень
в рабочем
поле вводим подкоренное выражение: 1
— $А2^2/9 — В$1^2/4.
Обратите
внимание, что символы $
предназначены для фиксации адреса
столбца А
— переменной х
и
строки 1
— переменной у.
Нажимаем
кнопку ОК
и в ячейке В2
появляется « #ЧИСЛО!»,
так как при значениях х
= –3 и у
= –2 точек
рассматриваемого эллипсоида не существует
(рис 1.).
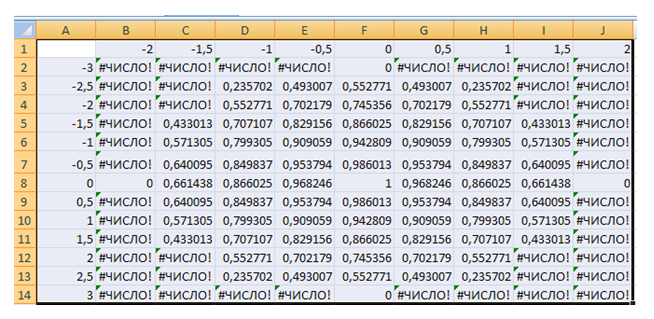
Рис.1. Построение
эллипсоида
1.4.Копирование
значений функции из ячейки В2,
для чего автозаполнением (протягиванием
вправо) копируем эту формулу вначале в
диапазон B2:J2,
а затем протягиванием вниз копируем в
диапазоне ВЗ:J14.
В результате должна
быть получена таблица всех точек
эллипсоида (рис.1).
1.5.Построение
диаграммы. Выделяем полученную таблицу
(A1:
J14),
вызываем вкладку Вставка
и в группе
Диаграммы
выбираем
График
Все типы диаграмм
окно
Вставка диаграмм. В
данном окне выбираем Поверхность
тип
Проволочная поверхность и
нажимаем ОК,
в результате
получаем поверхность эллипсоида (рис.2).
Далее,
используя
средства
Работа с диаграммами , оформляем
полученную поверхность. Например,
вкладки Стенка
и Основание диаграммы
позволяют определить их цвета. Для этого
выберите опцию Дополнительные параметры
стенок и вид заливки, название диаграммы
и т.п. Выполните данные действия
самостоятельно.
2.
Рассмотрим
построение гиперболоида следующего
вида:
Пусть необходимо
построить верхнюю часть гиперболоида,
лежащую в диапазонах:
х[–3;
3], у[–2;
2] с шагом
=0,5
для обеих переменных.
2.1.Вначале необходимо
преобразовать уравнение относительно
переменной Z:
Рис.2. Поверхность
эллипсоида
2.2.Введем значения
переменной х
в столбец
А.
Для этого в ячейку А1
вводим символ x,
в ячейку А2
вводится первое значение аргумента х
= –3, а в
ячейку A3
— второе значение аргумента х = –2,5
. Затем,
выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения
аргумента (за правый нижний угол блока
протягиваем до ячейки А14).
Значения переменной
у
вводим в
строку 1.
Для этого в ячейку В1
вводится первое значение переменной
у= –2,
в ячейку С1
— второе значение переменной у
= –1,5,
а затем, выделив
блок ячеек В1:С1,
автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки J1).
2.3.Вычисление
значения переменной Z.
Для этого
табличный курсор необходимо поместить
в ячейку В2
, вызвать Мастер
функций, в
поле Категория
выбрать Математические,
в поле Функция
выбираем функцию Корень
и нажимаем
кнопку ОК.
В рабочее поле вводим подкоренное
выражение: 1
+ $А2^2/9 + В$1^2/4 и
нажимаем
кнопку ОК.
В ячейке В2
появляется
1,732051.
Теперь необходимо
скопировать функцию из ячейки В2.
Для этого автозаполнением (протягиванием
вправо) копируем эту формулу вначале в
диапазон B2:J2,
после чего протягиванием вниз — в
диапазоне ВЗ:J14.
В результате должна
быть получена таблица точек гиперболоида
(рис.3.):
Рис.3. Построение
гиперболоида
Построение диаграммы
гиперболоида выполните самостоятельно
по аналогии с эллипсоидом. Ниже на рис.4
приведен вариант диаграммы гиперболоида
, построенного на основании данной
таблицы.
Рис.4.
Диаграмма гиперболоида
Задания для
самостоятельного выполнения
1.Построить верхнюю
часть эллипсоида:
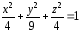
Диапазоны изменения
переменных х
и у: х[–2;
2] с шагом =0,5,
у[–3;
3] с шагом =1.
2.Построить верхнюю
часть однополостного гиперболоида:
Диапазоны изменения
переменных х
и у:
х[–3;
3] с шагом =0,5,
у[–4;
4] с шагом =1.
3.Построить
эллиптический параболоид:

Диапазоны изменения
переменных х
и у:
х[–2;
2] с шагом =0,5,
у[–3;
3] с шагом =1.
4.Построить верхнюю
часть конуса
Диапазоны изменения
переменных х
и у:
х[–2;
2] с шагом =0,5,
у [–3;
3] с шагом =1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- y = x (при k > 0)
- y = -x (при k < 0)
Смещение асимптот
Допустим у нас есть функция, заданная формулой:
- x = a – это вертикальная асимптота графика вместо оси Oy;
- y = b – горизонтальная асимптота вместо оси Ox.
Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):
Алгоритм построения гиперболы
Пример 1
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
См. ответ на вопрос про параболу в Эксель. Единственная разница — в функции, по которой определяется значение У. Для гиперболы формула имеет общий вид У = к / Х, и, соответственно, эта функция будет иметь разрыв при Х = 0, что нужно учитывать при задании диапазона для Х. Диапазонов может быть два — например, от -10 до -1 и от 1 до 10 с шагом 0,1 каждый. Формула, например, =3/A2.
График нужно будет построить сначала для одного из диапазонов, потом — щелкнуть правой кнопкой на линии графика, выбрать пункт «Выбрать данные» и нажать кнопку «Добавить», выбрав второй диапазон данных, после чего щелкнуть уже на второй линии, выбрав для нее тот же цвет и толщину, что и для первой линии, чтобы казалось, что график один.
Впрочем, можно поступить и проще — построить график сразу для всего диапазона, после чего удалить значения в ячейках из его середины (для Х = -1 и Х = 1). Внешне результат не изменится.
Построение гиперболы, на самом деле, очень простое занятие, если знать как, ведь для этого нужно построить массив значений гиперболы.
Для этого приходится брать произвольные значения Х, кроме того, когда знаменатель стремится к нулю, но не слишком близко к нулю. Затем, с помощью формулы установите значения У и растяните их, скопировав эту нужную формулу и получив, таким образом, значения У. Затем остаётся выделить получившийся диапазон значений Х и У, а затем выбрать во вкладке графика соответствующий вашим потребностям график. Мне лично нравится точечная диаграмма, но можно выбрать и график. Затем остаётся посмотреть на получившуюся диаграмму и добавить или убрать x-значения или заменить их другими.
Получите точки, согласно которым график будет построен. Обозначьте два столбца, у одного должно быть значение Х, у второго у. В первый столбец введите данные от -7 до 7, с шагом 1, но исключите ноль. Там где должен быть 0 следует оставить ячейку пустой.
После в ячейке В2 следует прописать формулу: «=1/A2». После, ее скопируйте на оставшиеся ячейке, пустую строку не трогайте. Получатся готовые данные для построения гиперболы.
После, следует выделить область со значением, также пустую строку. Зайдите на верхней панели во вкладку Вставка, выберите Точечная среди возможных графиков. Выберите второй график.
Получился график гиперболы, который можно оформить, прописав оси и функцию.
Для прописания осей, на панели Вставка найдите с правой стороны блок Текст. Нажмите на иконку с надписью — Надпись. При помощи курсора нажмите на любую область на графике и пропишите название оси, после перетащите в место, которое нужно для получение обоих оси.
Следует выделить надпись Ряд1 и нажать при помощи правой кнопки мыши для появления меню. В нем нужно выбрать Выбрать данные, а на экране будет новое меню. В левой части нужно выделить Ряд1, которое вы увидите и нажать на кнопку Изменить. В меню, которое появится вы сможете отредактировать название, а после можно закрыть таблицы, которые являются дополнительными.
Как в экселе построить гиперболу?
В программе эксель можно построить многие функции, которые проходят в школе на уроках математики. Давайте рассмотрим подробную инструкцию, как в программе эксель построить гиперболу.
Первый этап. Построим гиперболу следующей функции: Y=1/X. Сначала нужно получить точки, по которым можно построить данный график. Для этого обозначим два столбца: «Значение X» и «Значение Y». В первый столбец введем данный от -7 до 7 с шагом 1, но при этом исключим ноль. При этом в месте, где должен быть ноль, оставим просто пустые ячейки.
Второй этап. В ячейке «В2» пропишем следующую формулу: «=1/A2». После необходимо её скопировать на остальные ячейки, кроме пустой строки. В итоге данные для построения гиперболы готовы.
Третий этап. Выделим область со значением, в т.ч. пустую строку. После на верхней панели зайдем во вкладку «Вставка», где среди возможных графиков, выберем «Точечная». В появившемся меню выберем второй график.
Четвертый этап. График гиперболы готов, но его стоить оформить: подписать оси и функцию.
Пятый этап. Чтобы подписать оси, вам нужно на панели «Вставка», справа отыскать блок «Текст», в котором нажать на иконку с надписью «Надпись». Появившимся курсором, нажимаете на любую область графика, прописываете название оси и потом перетаскиваете в нужное место, чтобы получилось в итоге обе подписи:
Шестой этап. Выделите надпись «Ряд1», нажмите на правую клавишу, чтобы появилось меню, в котором выберете «Выбрать данные», на экране появиться новое меню, в его левой части вы увидите название «Ряд1», выделите его и нажмите на кнопку «Изменить», в появившемся меню можете отредактировать название, после закрывайте все дополнительные таблицы. Сверху может тоже появиться название функции, его можно удалить.
Содержание
- Как в экселе построить гиперболу?
- Видео как постоить гиперболу в excele
- Как в экселе построить гиперболу?
- Видео как постоить гиперболу в excele
- Как построить график функции в Microsoft Excel
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax 2 +bx+c
- Кубическая парабола y=ax 3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Как в экселе построить гиперболу?
В программе эксель можно построить многие функции, которые проходят в школе на уроках математики. Давайте рассмотрим подробную инструкцию, как в программе эксель построить гиперболу.
Первый этап. Построим гиперболу следующей функции: Y=1/X. Сначала нужно получить точки, по которым можно построить данный график. Для этого обозначим два столбца: «Значение X» и «Значение Y». В первый столбец введем данный от -7 до 7 с шагом 1, но при этом исключим ноль. При этом в месте, где должен быть ноль, оставим просто пустые ячейки.
Второй этап. В ячейке «В2» пропишем следующую формулу: «=1/A2». После необходимо её скопировать на остальные ячейки, кроме пустой строки. В итоге данные для построения гиперболы готовы.
Третий этап. Выделим область со значением, в т.ч. пустую строку. После на верхней панели зайдем во вкладку «Вставка», где среди возможных графиков, выберем «Точечная». В появившемся меню выберем второй график.
Четвертый этап. График гиперболы готов, но его стоить оформить: подписать оси и функцию.
Пятый этап. Чтобы подписать оси, вам нужно на панели «Вставка», справа отыскать блок «Текст», в котором нажать на иконку с надписью «Надпись». Появившимся курсором, нажимаете на любую область графика, прописываете название оси и потом перетаскиваете в нужное место, чтобы получилось в итоге обе подписи:
Шестой этап. Выделите надпись «Ряд1», нажмите на правую клавишу, чтобы появилось меню, в котором выберете «Выбрать данные», на экране появиться новое меню, в его левой части вы увидите название «Ряд1», выделите его и нажмите на кнопку «Изменить», в появившемся меню можете отредактировать название, после закрывайте все дополнительные таблицы. Сверху может тоже появиться название функции, его можно удалить.
Видео как постоить гиперболу в excele
Источник
Как в экселе построить гиперболу?
В программе эксель можно построить многие функции, которые проходят в школе на уроках математики. Давайте рассмотрим подробную инструкцию, как в программе эксель построить гиперболу.
Первый этап. Построим гиперболу следующей функции: Y=1/X. Сначала нужно получить точки, по которым можно построить данный график. Для этого обозначим два столбца: «Значение X» и «Значение Y». В первый столбец введем данный от -7 до 7 с шагом 1, но при этом исключим ноль. При этом в месте, где должен быть ноль, оставим просто пустые ячейки.
Второй этап. В ячейке «В2» пропишем следующую формулу: «=1/A2». После необходимо её скопировать на остальные ячейки, кроме пустой строки. В итоге данные для построения гиперболы готовы.
Третий этап. Выделим область со значением, в т.ч. пустую строку. После на верхней панели зайдем во вкладку «Вставка», где среди возможных графиков, выберем «Точечная». В появившемся меню выберем второй график.
Четвертый этап. График гиперболы готов, но его стоить оформить: подписать оси и функцию.
Пятый этап. Чтобы подписать оси, вам нужно на панели «Вставка», справа отыскать блок «Текст», в котором нажать на иконку с надписью «Надпись». Появившимся курсором, нажимаете на любую область графика, прописываете название оси и потом перетаскиваете в нужное место, чтобы получилось в итоге обе подписи:
Шестой этап. Выделите надпись «Ряд1», нажмите на правую клавишу, чтобы появилось меню, в котором выберете «Выбрать данные», на экране появиться новое меню, в его левой части вы увидите название «Ряд1», выделите его и нажмите на кнопку «Изменить», в появившемся меню можете отредактировать название, после закрывайте все дополнительные таблицы. Сверху может тоже появиться название функции, его можно удалить.
Видео как постоить гиперболу в excele
Источник
Как построить график функции в Microsoft Excel
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графика линейной функции в Excel
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
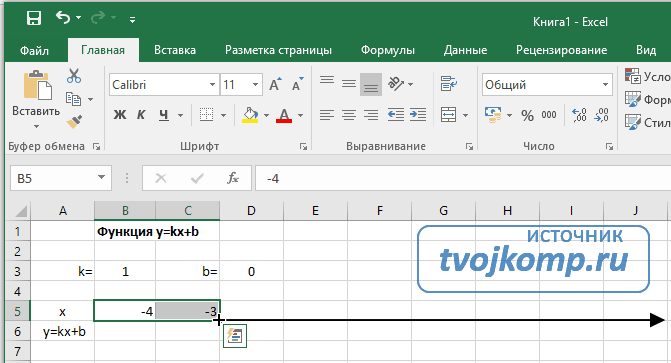
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

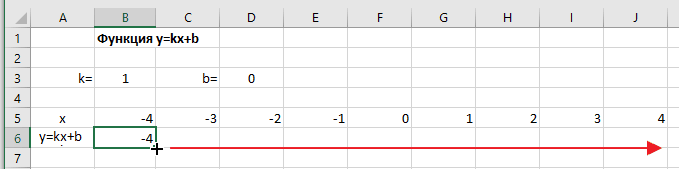
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
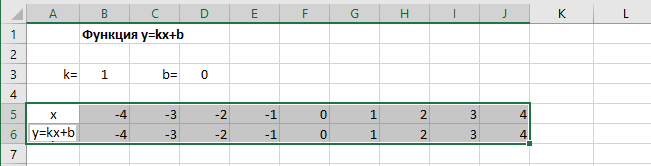
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
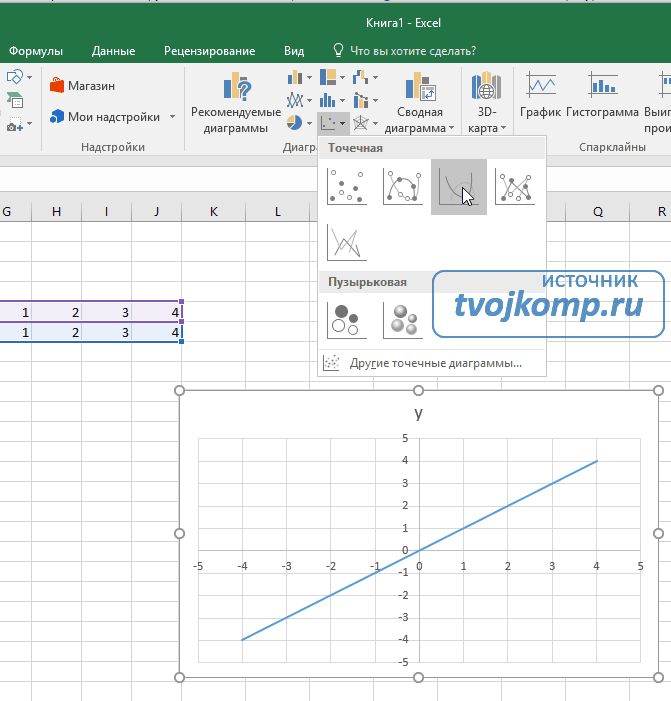
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
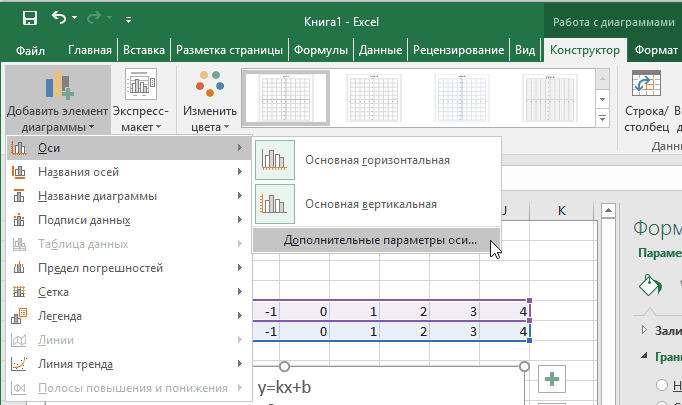
В правой части окна появиться боковая панель настроек Формат оси.
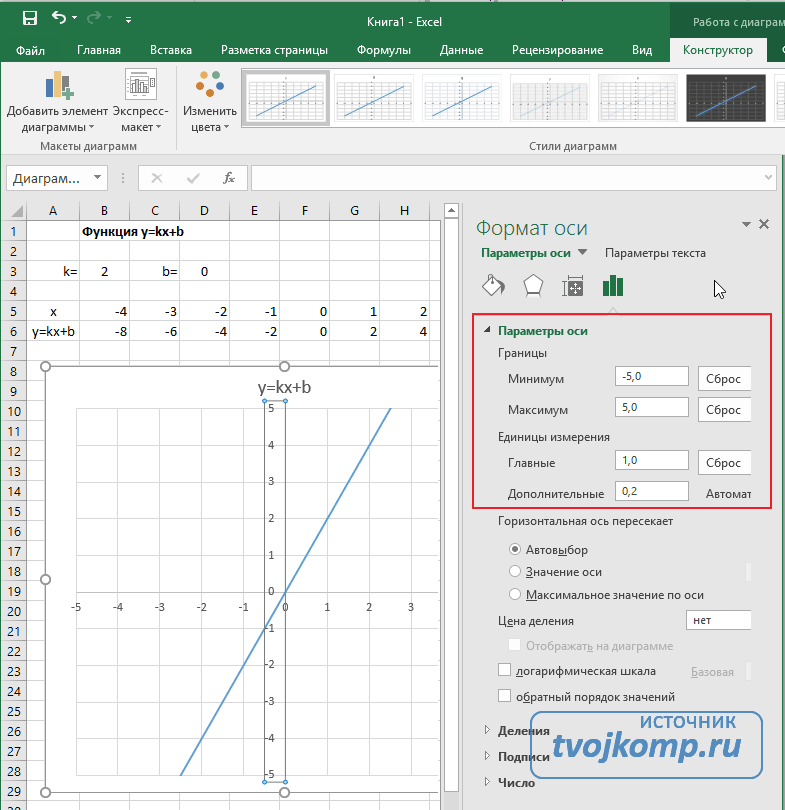
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax 2 +bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
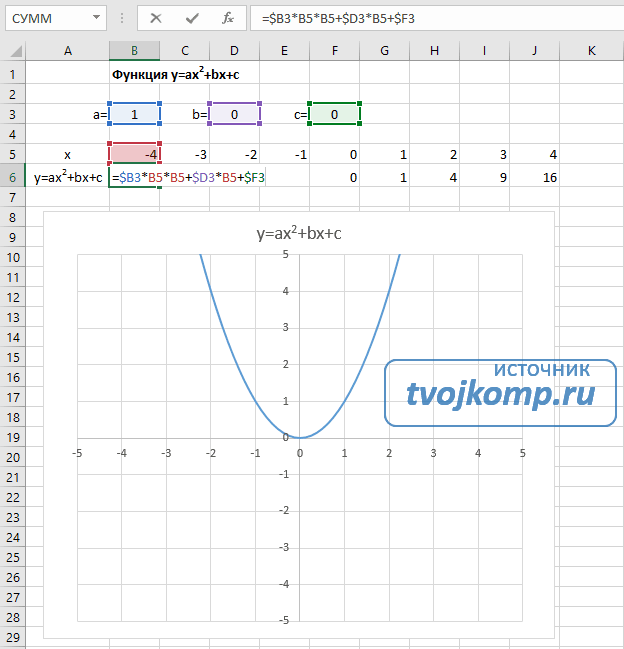
Кубическая парабола y=ax 3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
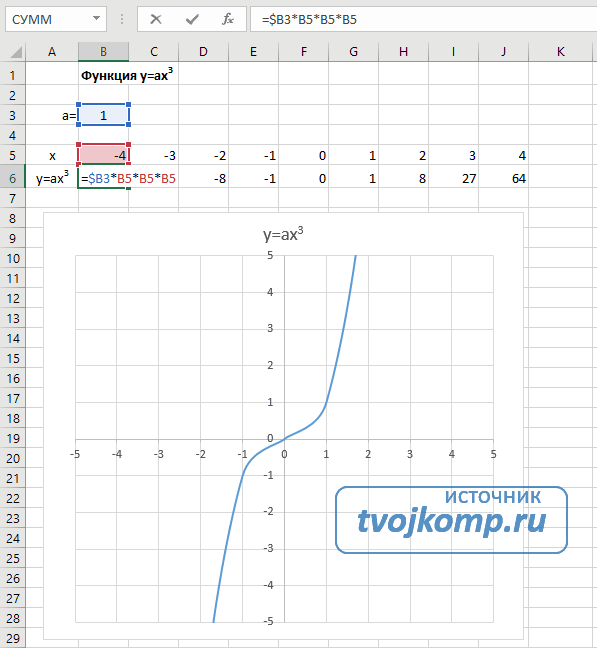
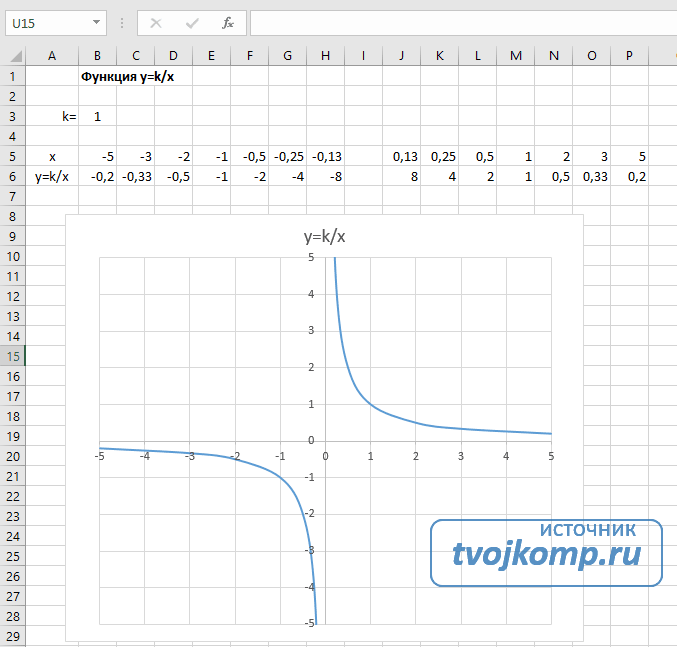
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
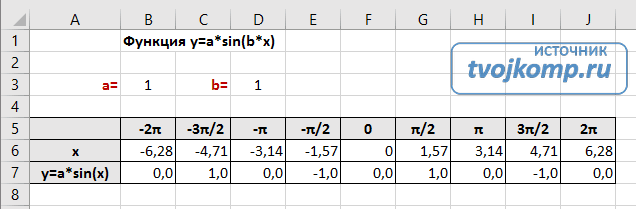
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
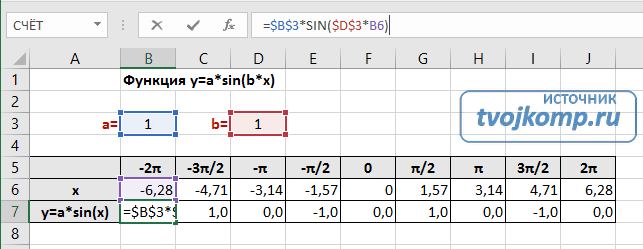
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
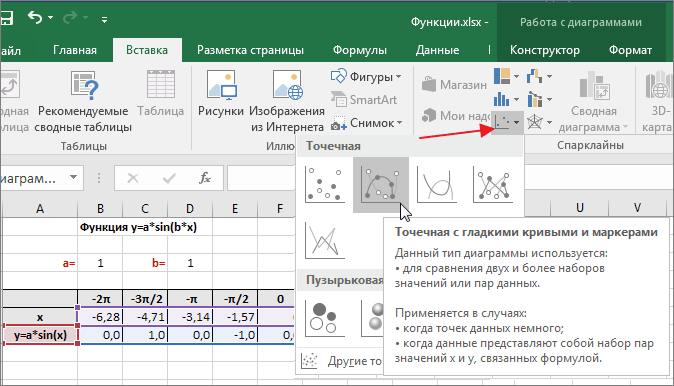
В итоге получим диаграмму.
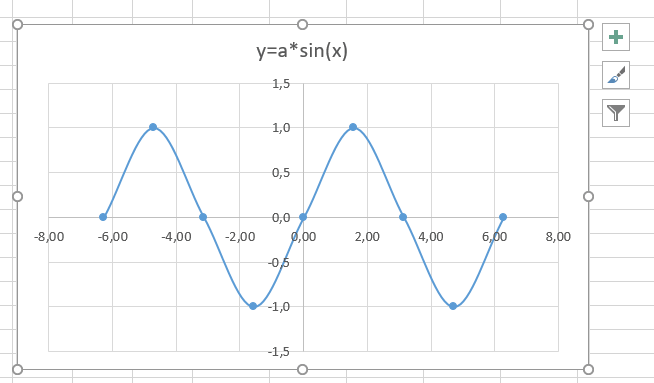
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
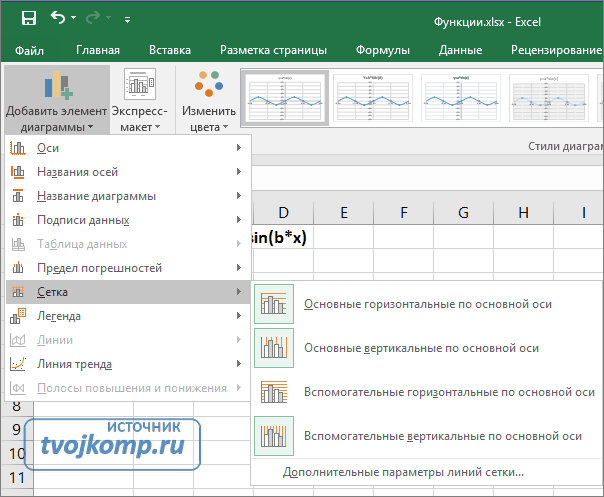
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
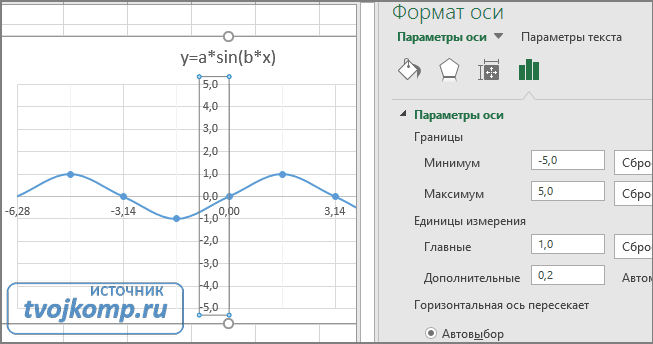
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
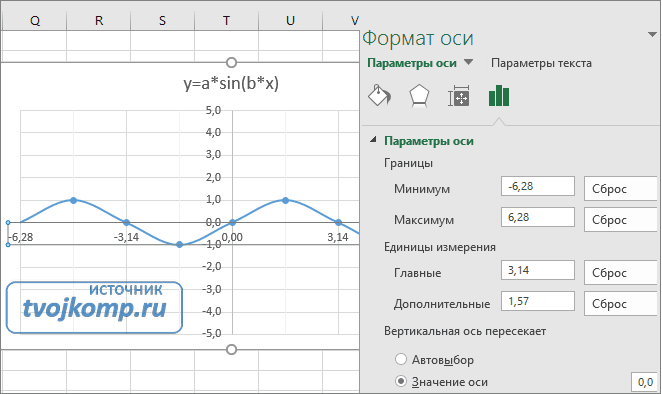
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
Дорогой читатель! Вы посмотрели статью до конца. Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью! 

Подскажите, пожалуйста, на какой версии Excel у вас основаны скриншоты? Спасибо за статью, и у вас и тут похоже одинаковая версия, но на мою не похоже.
Илья, скриншоты сделаны для версии Excel2016, в начале статьи это упоминается. Предыдущие версии имеют отличия в интерфейсе, но следуя описанной последовательности действий, можно уловить логику и других интерфейсов.
Источник