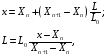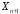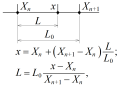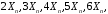Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке . Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
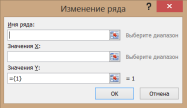
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Поделитесь статьёй с друзьями:
Добрый день. А есть возможность в Excele создать график с тремя переменными, но на одном графике? 2 параметра как обычно, координаты х и у, а третий параметр чтоб отражался размером метки? Вот как пример, такой график —
Рубрика Excel
Также статьи о графиках в Экселе:
- Как сделать диаграмму в Эксель?
- Как сделать круговую диаграмму в Экселе?
- Как построить график в Экселе?
- Построение точечной диаграммы в Excel
В Экселе можно результаты расчетов отобразить в виде диаграммы или графика, придавая им большую наглядность, а для сравнения иногда нужно построить два графика рядом. Как построить два графика в Excel на одном поле мы далее и рассмотрим.
Начнем с того, что не каждый тип диаграмм в Экселе сможет отобразить именно тот результат, который мы ожидаем. К примеру, имеются результаты расчетов для нескольких функций на основе одинаковых исходных данных. Если по этим данным строить обычную гистограмму или график, то исходные данные не будут учитываться при построении, а лишь их количество, между которыми будут задаваться одинаковые интервалы.
Выделяем два столбца результатов расчетов и строим обычную гистограмму.
Теперь попробуем добавить еще одну гистограмму к имеющимся с таким же количеством результатов расчетов. Для добавления графика в Экселе делаем активным имеющийся график, выделив его, и на появившейся вкладке «Конструктор» выбираем «Выбрать данные». В появившемся окошке в разделе «Элементы легенды» нажимаем добавить, и указываем ячейки «Имя ряда:» и «Значения:» на листе, в качестве которых будут значения расчета функции «j».
Теперь посмотрим, как будет выглядеть наша диаграмма, если мы к имеющимся гистограммам добавим еще одну, у которой количество значений почти в два раза больше. Добавим к графику значения функции «k».
Как видно, последних добавленных значений гораздо больше, и они настолько малы, что их на гистограмме практически не видно.
Если изменить тип диаграммы с гистограммы на обычный график, результат получится в нашем случае более наглядным.
Если использовать для построения графиков в Экселе точечную диаграмму, то на полученных графиках будет учитываться не только результат расчетов, но и исходные данные, т.е. будет прослеживаться четкая зависимость между величинами.
Для создания точеного графика выделим столбец начальных значений, и пару столбцов результатов для двух разных функций. На вкладке «Вставка» выбираем точечную диаграмму с гладкими кривыми.
Для добавления еще одного графика выделяем имеющиеся, и на вкладке «Конструктор» нажимаем «Выбрать данные».
В новом окошке в графе «Элементы легенды» нажимаем «Добавить», и указываем ячейки для «Имя ряда:», «Значения X:» и «Значения Y:». Добавим таким образом функцию «j» на график.
Теперь добавим функцию «k», у которой совершенно другие исходные данные и их количество.
Как видно, на точечном графике функция «k» практически незаметна, но зато построена с учетом значений по обеим осям.
Построение графиков функций в Excel
Февраль 9th, 2014
Andrey K
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете
оставить комментарий
, или
ссылку
на Ваш сайт.
Душевые термостаты, лучшие модели на
http://tools-ricambi.ru/
изготавливаются из материалов высшего качества
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:
Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
|
karter171  Пользователь Сообщений: 47 |
Всем привет! пол дня промучался так и не нашел, как построить такой график как в ссылке. никак не могу такие координаты выбрать в диаграммах. Кто подскажет буду очень благодарен! http://s020.radikal.ru/i718/1506/6e/8480feb89075.jpg |
|
ikki  Пользователь Сообщений: 9709 |
файл с примером Ваших данных тоже за Вас рисовать? Изменено: ikki — 22.06.2015 20:18:39 фрилансер Excel, VBA — контакты в профиле |
|
karter171 Пользователь Сообщений: 47 |
Прикрепить бы его както всегда более 100 кб( вот файл на файлообменнике http://файлообменник.рф/09d8zrkuvh4b.html Изменено: karter171 — 22.06.2015 21:03:07 |
|
vikttur Пользователь Сообщений: 47199 |
Примера нет, название никудышнее… Прав ikki. |
|
karter171 Пользователь Сообщений: 47 |
Вот мои данные, которые надо в график внести, как его построить я не знаю
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
vikttur Пользователь Сообщений: 47199 |
Вы Правила читали?! Что там о примере пишут? |
|
karter171 Пользователь Сообщений: 47 |
Я данные прикрепил постом выше. мне б хотелось не только решение а и алгоритм действий что и как делать, что б самому научиться и глупых вопросов потом не задавать |
|
JeyCi  Пользователь Сообщений: 3357 |
#8 22.06.2015 20:39:42
1 — внести данные в файл чтобы не гадать на кофейной гуще, кто вам отвечает и после этого не совершать кучу ошибок — обратитесь к собеседнику на ВЫ — ответ на ваш вопрос получите — а остальное вас не касается (п.п.п. на форумах) |
||
|
karter171 Пользователь Сообщений: 47 |
#9 22.06.2015 20:50:22
Не могу понять как выставить, все равно у меня получается только так. http://s020.radikal.ru/i702/1506/53/7ba18927d41b.jpg |
||
|
ikki Пользователь Сообщений: 9709 |
ну и что осталось? только вертикальную ось на 0 передвинуть? фрилансер Excel, VBA — контакты в профиле |
|
karter171 Пользователь Сообщений: 47 |
да и именно над этим я бьюсь как рыба об лед, ничего не выходит((( |
|
ikki Пользователь Сообщений: 9709 |
формат горизонтальной оси — Параметры оси — Вертикальная ось пересекает: — Значение оси: ввести в поле 0 фрилансер Excel, VBA — контакты в профиле |
|
karter171 Пользователь Сообщений: 47 |
Всем спасибо за помощь! Тема закрыта. Изменено: karter171 — 22.06.2015 21:55:16 |
|
ikki Пользователь Сообщений: 9709 |
тип диаграммы какой выбрали? фрилансер Excel, VBA — контакты в профиле |
|
karter171 Пользователь Сообщений: 47 |
#15 22.06.2015 22:02:47 у меня такая же |
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
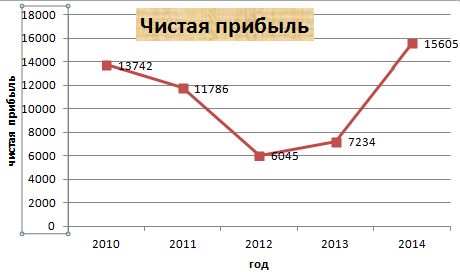
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
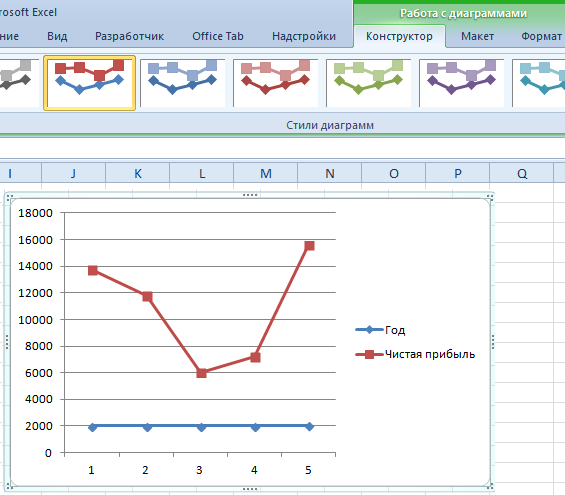
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
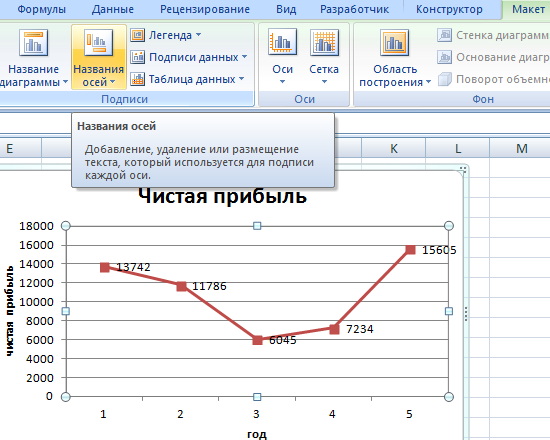
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
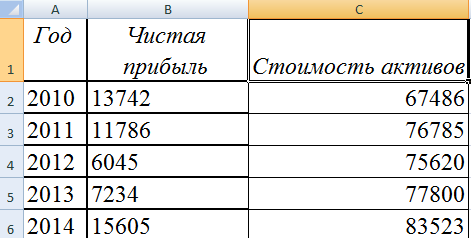
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
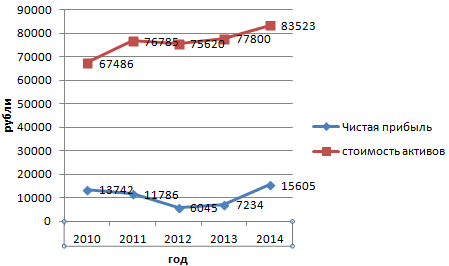
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
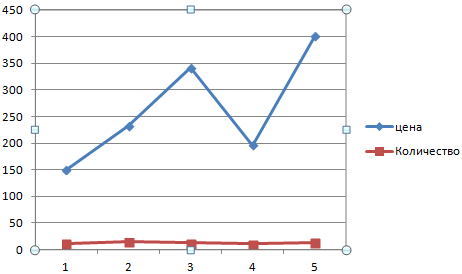
Сначала строим график так, будто у нас одинаковые единицы измерения.
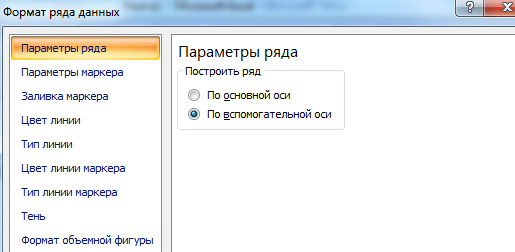
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
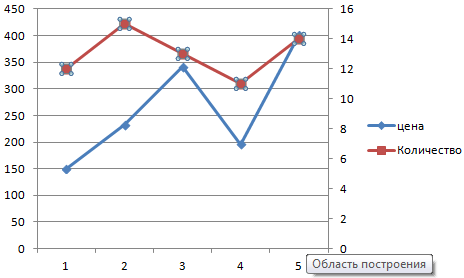
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
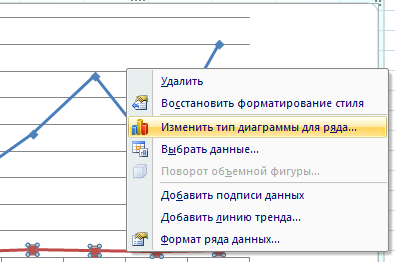
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
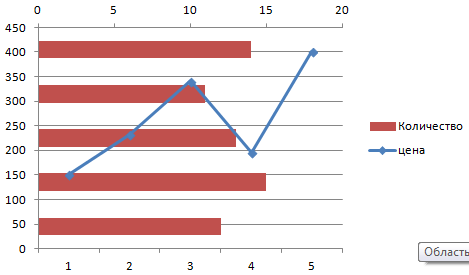
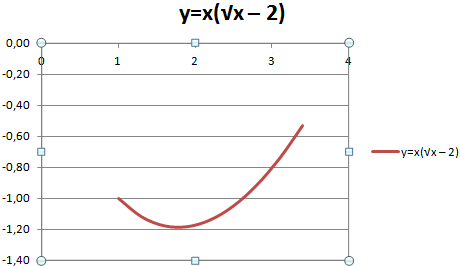
Пример: y=x(√x – 2). Шаг – 0,3.
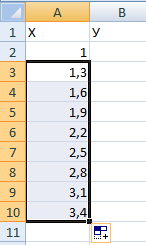
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
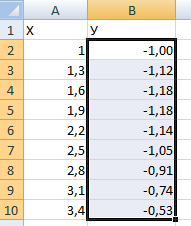
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
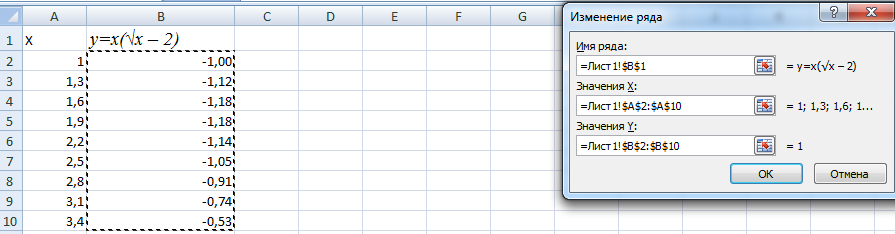
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
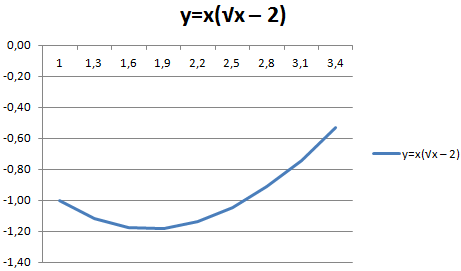
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
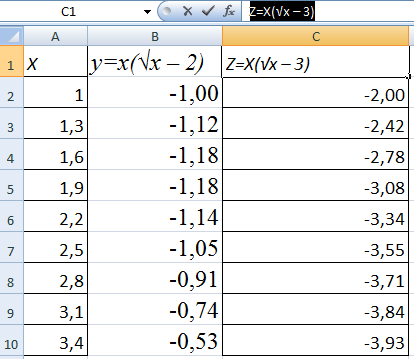
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
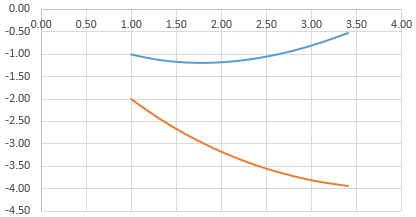
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
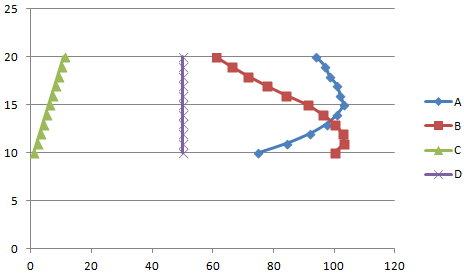
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
Скачать шаблоны и дашборды с диаграммами для отчетов в Excel.
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Содержание
- Создание параболы
- Создание таблицы
- Построение графика
- Редактирование диаграммы
- Вопросы и ответы
Построение параболы является одной из известных математических операций. Довольно часто она применяется не только в научных целях, но и в чисто практических. Давайте узнаем, как совершить данную процедуру при помощи инструментария приложения Excel.
Создание параболы
Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.
Создание таблицы
Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.
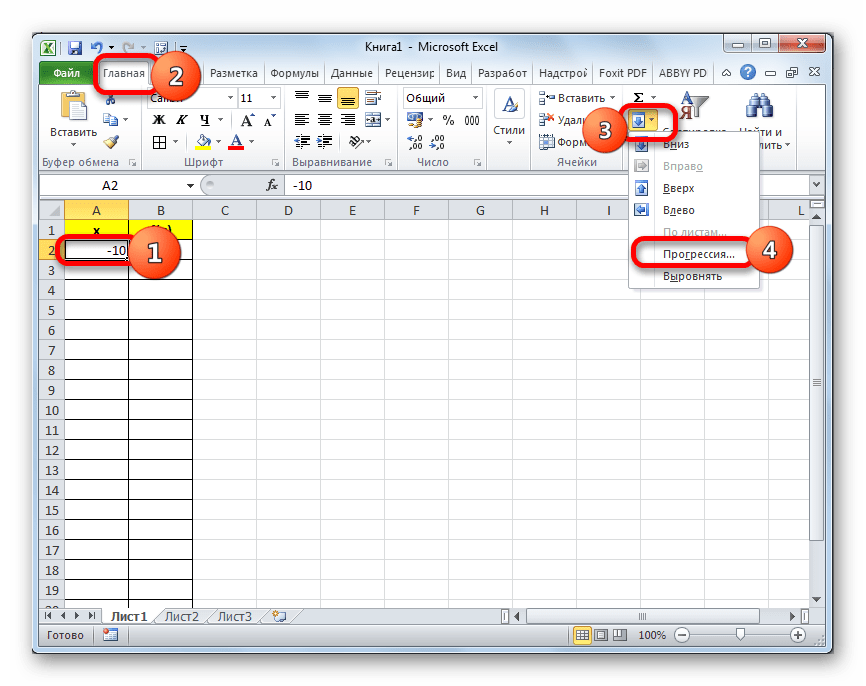
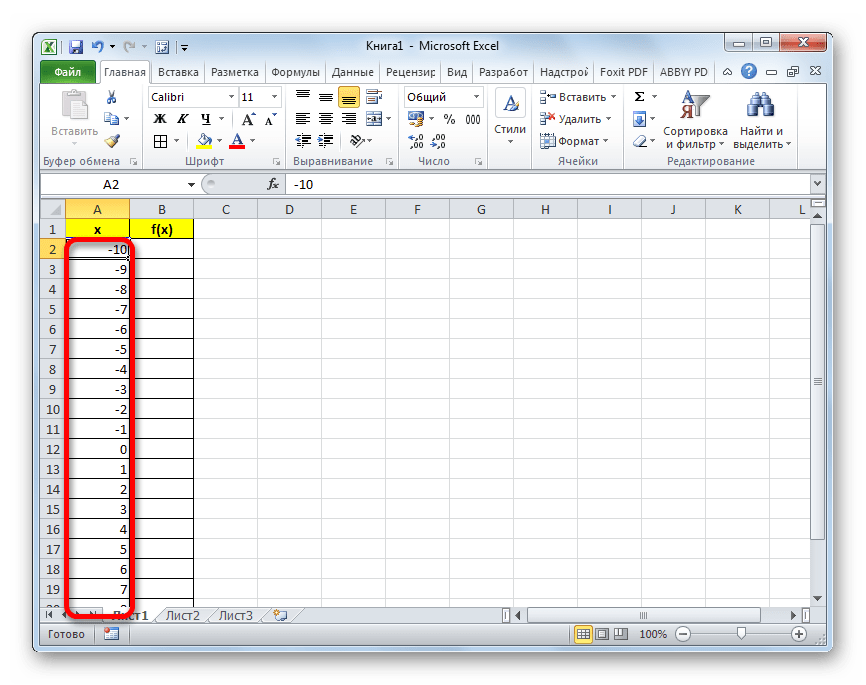
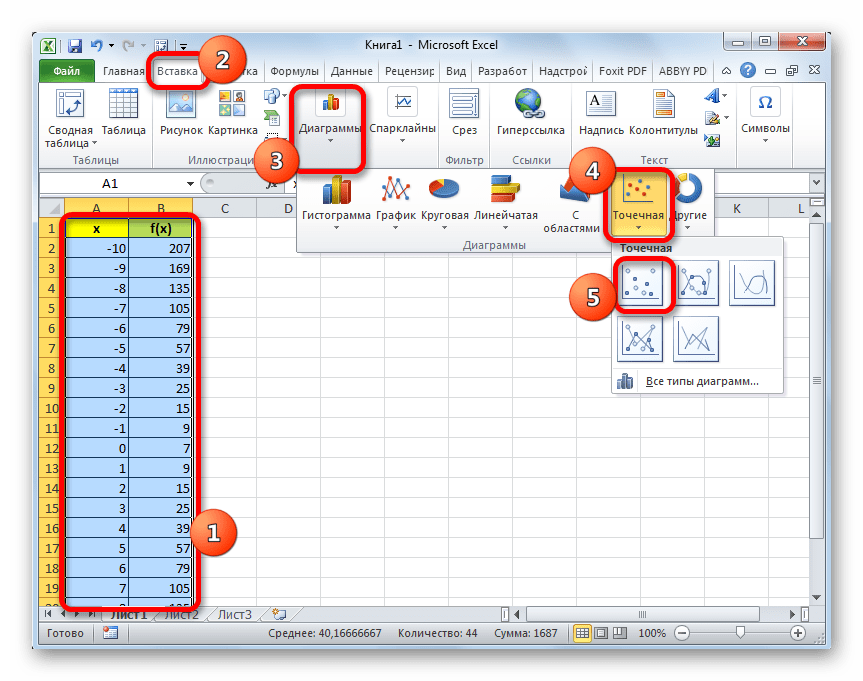
- Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».
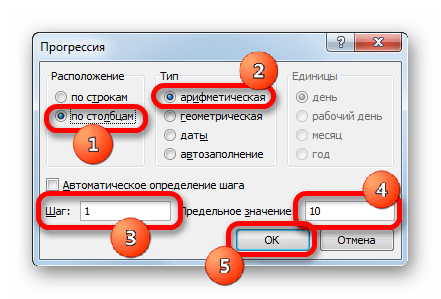
- Выполняется активация окна регулировки прогрессии. В блоке «Расположение» следует переставить кнопку в позицию «По столбцам», так как ряд «X» размещается именно в столбце, хотя в других случаях, возможно, нужно будет выставить переключатель в позицию «По строкам». В блоке «Тип» оставляем переключатель в позиции «Арифметическая».
В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».
- После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.
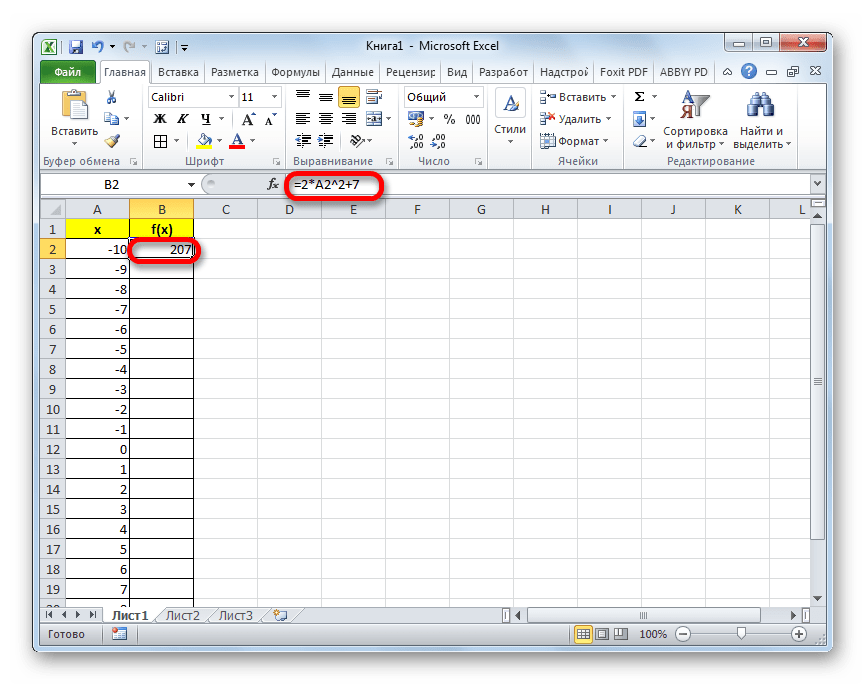
- Теперь нам предстоит заполнить данными столбец «f(x)». Для этого, исходя из уравнения (f(x)=2x^2+7), нам нужно вписать в первую ячейку данного столбца выражение по следующему макету:
=2*x^2+7Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:
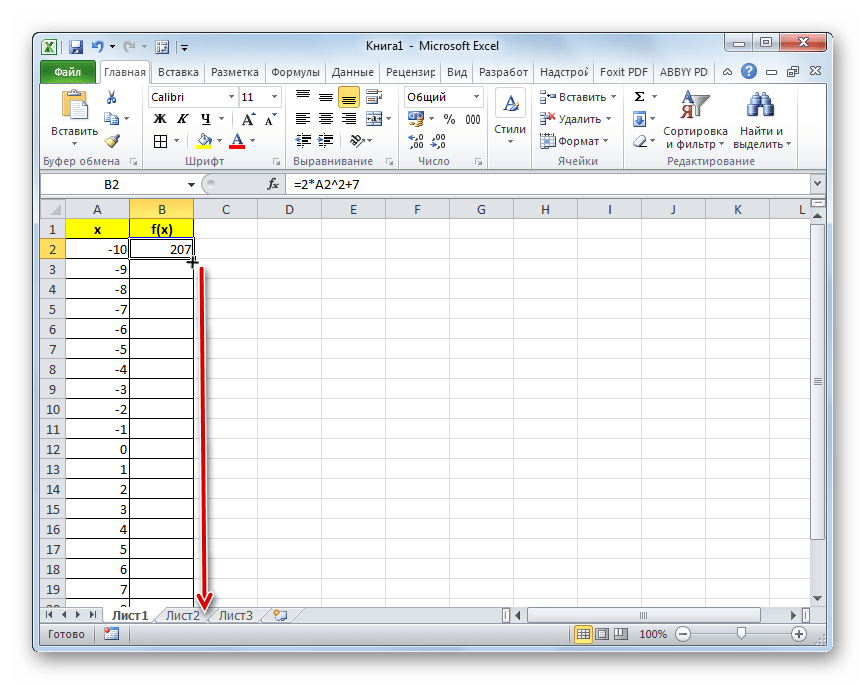
=2*A2^2+7 - Теперь нам нужно скопировать формулу и на весь нижний диапазон данного столбца. Учитывая основные свойства Excel, при копировании все значения x будут поставлены в соответствующие ячейки столбца «f(x)» автоматически. Для этого ставим курсор в правый нижний угол ячейки, в которой уже размещена формула, записанная нами чуть ранее. Курсор должен преобразоваться в маркер заполнения, имеющий вид маленького крестика. После того, как преобразование произошло, зажимаем левую кнопку мыши и тянем курсор вниз до конца таблицы, после чего отпускаем кнопку.
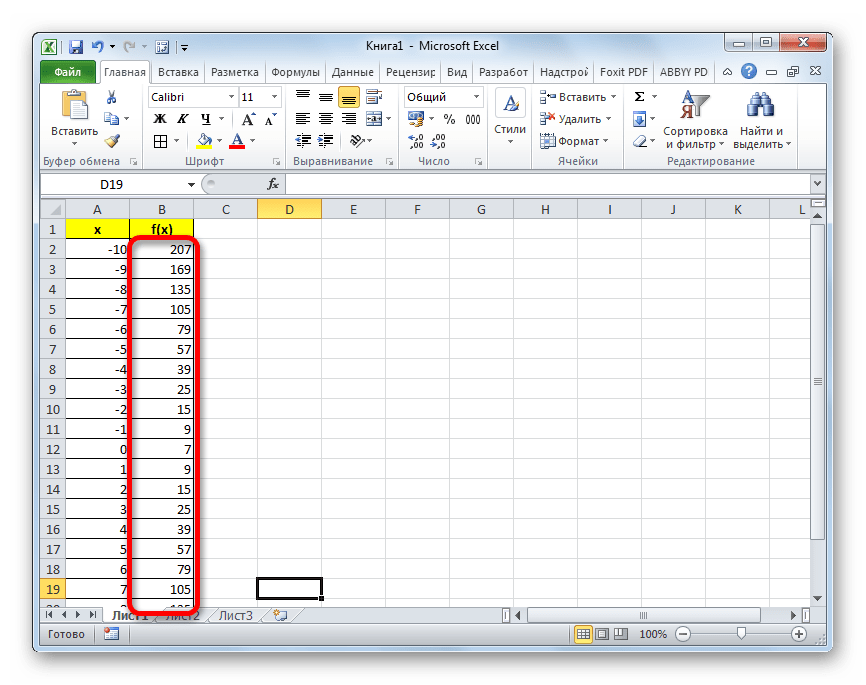
- Как видим, после этого действия столбец «f(x)» тоже будет заполнен.
На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.
Урок: Как сделать автозаполнение в Экселе
Построение графика
Как уже было сказано выше, теперь нам предстоит построить сам график.
- Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.
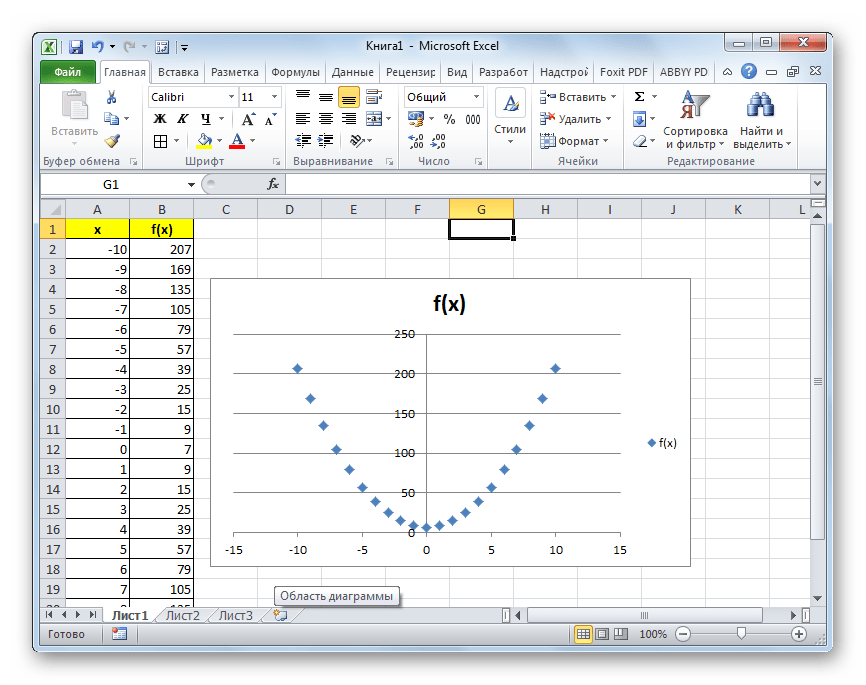
- Как видим, после этих действий, парабола построена.
Урок: Как сделать диаграмму в Экселе
Редактирование диаграммы
Теперь можно немного отредактировать полученный график.
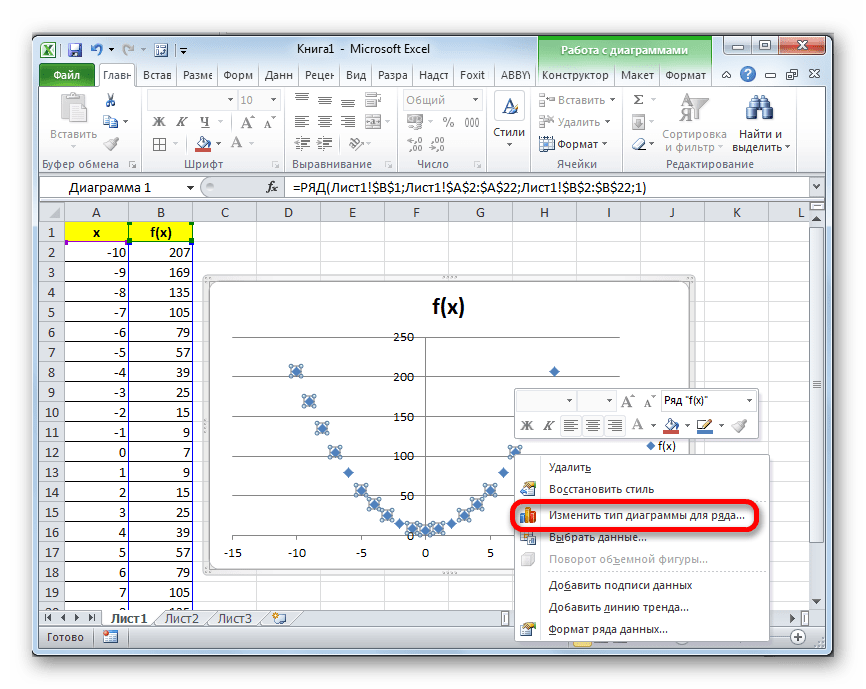
- Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».
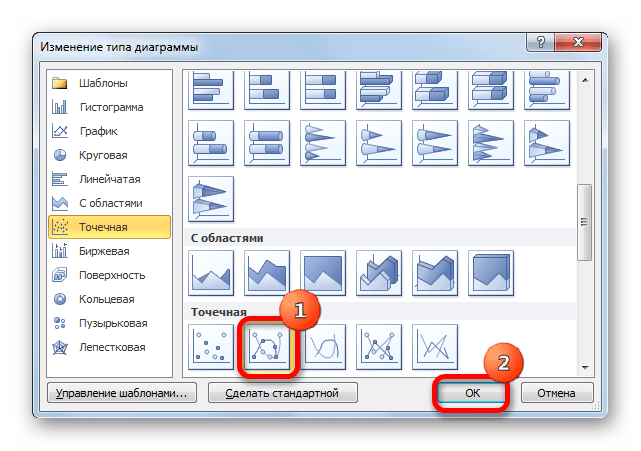
- Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».
- Теперь график параболы имеет более привычный вид.
Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.
Урок: Как подписать оси диаграммы в Excel
Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.
Еще статьи по данной теме:
Помогла ли Вам статья?
При подготовке научно-технических
текстов практически у каждого автора
возникает потребность графически
представить ту или иную зависимость. В
подавляющем большинстве случаев
изображается зависимость значения
некоторой функции (действительное
число) от аргумента этой функции
(действительное число). В естественно-научной
среде принято представлять зависимости
в виде графиков.
График – это изображение на плоскости
(обычно – на листе бумаги или на экране
компьютера) множества точек (возможно,
бесконечного множества точек), физические
координаты которых несут информацию о
значениях аргумента функции (то, от чего
зависит) и значениях функции (то, что
зависит). Физические координаты точек
принято считывать в большинстве случаев
– в декартовой системе координат,
значительно реже – в полярной системе
координат, практически никогда – в
других специальных системах координат.
В декартовой системе координат, как
правило, рисуют две оси – горизонтальную
(ось X, ось аргумента
функции) и вертикальную (ось Y,
ось значений функции). По оси X
откладывают возможные значения аргумента
функции. Эти значения откладываются в
порядке возрастания слева направо.
По оси Y откладывают
возможные значения функции. Эти значения
откладываются в порядке возрастания
снизу вверх (иногда, в порядке исключения,
допускается – в порядке возрастания
сверху вниз).
Соответствие между значением аргумента
x и физической
координатой деления оси l
теоретически может быть любым. Однако
«в рамках приличия» использовать два
типа соответствия:
1. Линейная шкала.
Физические координаты делений шкалы l
связаны со значениями делений шкалы
x линейной зависимостью:
.
Значения шкалы выбираются равномерно
– например, 0, 10, 20, 30, 40, …, или 1150, 1200,
1250, 1300, …, то есть каждое последующее
деление превышает предыдущее на одно
и то же значение. Это значение носит
название «цена делений шкалы» и в
приведённых примерах оно равно 10 и 50.
Через каждое деление горизонтальной
оси проводится вертикальная линия,
набор этих линий составляет вертикальную
сетку. Каждое деление шкалы имеет подпись
– значение этого деления. Принято
деления горизонтальной оси и цену
деления выбирать круглыми значениями,
как это сделано в приведённых примерах.
Деления типа 312, 315, 318, 321, …– это дурной
тон.
Соседние деления линейной шкалы Xn
и Xn+1,
разность значений которых составляет
цену деления, физически отстоят на
графике на одинаковое расстояние.
Помимо основных делений шкалы, описанных
выше, иногда выполняется вертикальная
сетка промежуточных делений. В этом
случае промежуток между двумя соседними
основными делениями равномерно
разбивается на несколько интервалов
(обычно – 2, 4, 5 или 10) и эти интервалы
разделяются вертикальными линиями.
Сетка промежуточных делений помогает
точнее определить положение точки на
графике.
При использовании линейной шкалы связь
между значением величины x
и его физической координатой выглядит
как
|
где |
|
По вертикальной оси графика в линейном
масштабе точно так же откладываются
основные и промежуточные деления и
точно так же рисуется горизонтальная
сетка графика.
2. Логарифмическая шкала.
Физические координаты делений шкалы l
связаны со значениями делений шкалы
x линейной зависимостью:
.
Основание логарифма значения не имеет
– оно влияет только на величину
коэффициента A в
приведённой формуле, поэтому в дальнейшем
будем использовать десятичный логарифм.
В отличие от линейной шкалы, у которой
одинаковое расстояние разделяют соседние
деления шкалы Xn
и Xn+1
с одинаковой разностью
,
в логарифмической шкале соседние деления
шкалы, расстояние между которыми
постоянно, имеют значениями Xn
и Xn+1,
отношение которых постоянно:
.
Наиболее часто это отношение
выбирают равным 10. В этом случае в
логарифмической шкале связь меж-
|
ду значением
как это показано на рисунке. |
|
Как и в случае линейной шкалы, при
применении логарифмической шкалы на
графике иногда допускаются промежуточные
деления, причём их значения, как правило,
обычно выбираются равными
Следует отметить, что, в отличие от
линейной шкалы, где промежуточные
деления располагаются равномерно, в
логарифмической шкале промежуточные
деления располагаются сильно неравномерно.
Подписи значений промежуточных значений
шкалы ставить н принято ни при использовании
линейной, ни при использовании
логарифмической шкалы.
Примеры осей с линейной шкалой и с
логарифмической шкалой:
|
|
При построении графиков экспериментальных
или теоретических зависимостей следует
придерживаться равномерного ряда
значений аргумента. В случае линейного
масштаба это пожелание проблем не
вызывает, в случае логарифмического
масштаба равномерный ряд значений
аргумента выглядит как 1, 10, 100, 1000, …
(одна точка на декаду), либо 1, 3, 10, 30, 100,
300, … (две точки на декаду), либо 1, 2, 5, 10,
20, 50, 100, 200, 500, 1000, … (три точки на декаду.
Возможно также логарифмически-равномерный
выбор значений из рядов:
1, 1,5, 2,2, 3,2, 4,5, 6,8, 10, 15, 22, 32,
45, 68, 100, … (ряд Е6),
1, 1,2, 1,5, 1,8, 2,2, 2,6, 3,2,
3,8, 4,6, 5,6, 6,8, 8,3, 10, 12, 15, 18, … (ряд Е12),
и
т.д. Каждое последующее значение ряда
получается домножением предыдущего на
101/6 (ряд Е6), либо на 101/12 (ряд
Е12), либо на 101/24 (ряд Е24), и т.д.
Каждая ось должна быть подписана. Подпись
располагается в самом конце оси (крайняя
правая точка для горизонтальной оси и
крайняя верхняя – для вертикальной) и
должна содержать название величины,
значения которой откладываются на шкале
оси, и единицу измерения. Примеры подписей
осей:
f, кГц;
K, дБ;
з/пл., млн.руб.;
U, 10-12 В.
При этом подписи делений шкалы единицу
измерения содержать не должны – только
значение.
Количество точек для построения не
регламентируется. Точек должно быть,
во-первых, столько, чтобы отразить все
особенности графика, и, во-вторых, график
не должен претерпевать резких изломов
в своих точках. Если при построении
графика обнаруживается излом в точках
со значениями аргумента xn–1,
xn,
xn+1,
следует добавить на график точки со
значениями аргумента
и
.
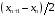
И поступать подобным образом следует
до тех пор, пока резкие изломы на графике
не исчезнут.
При построении графиков экспериментальных
зависимостей следует отмечать каждую
экспериментально полученную (измеренную)
точку зависимости, после чего соединять
эти точки отрезками прямых линий, без
сглаживания.
При построении графиков теоретических
зависимостей следует вычислить значения
как можно большего количества точек
(вплоть до нескольких тысяч. После этого
нужно каждую пару точек соединить
отрезком прямой линии, не отмечая
специально рассчитанные точки графика.
Примеры выбора точек для построения
графиков:
|
|
|
|
неправильно |
правильно |
При графическом сравнении теоретической
зависимости с результатами измерений
на графике строится теоретическая
зависимость (максимальное количество
рассчитанных точек, точки не рисуются
и соединяются отрезками прямых линий)
и отдельно наносятся точки, соответствующие
результатам измерений. На профессионально
построенных графиках при этом принято
отмечать погрешности измерений, как
это показано на рисунке:
|
|
|
|
сравнение с |
указание |
Рекомендуется на графиках линии
различного назначения изображать
различной яркости (толщины). Например,
линия графика – наиболее ярко, оси –
менее ярко, основная сетка – ещё менее
ярко, дополнительная сетка – с наименьшей
яркостью.
На графике можно располагать текстовую
информацию, как то: название графика,
название отдельных зависимости, значения
параметров, относящихся к разным
зависимостям, и т.д.
Сформулируем в итоге требования к
графикам, выполняемым в ходе лабораторных
работ:
1. График должен иметь две оси –
горизонтальную (ось значений аргумента)
и вертикальную (ось значений функции).
2. Каждая ось должна быть подписана.
Подпись к оси должна располагаться в
конце оси и должна содержать наименование
величины и единицу её измерения.
3. На каждой оси должны быть основные
деления с подписями их значений. Основные
деления определяют основную сетку (по
вертикали и по горизонтали), которая
также должна быть на графике.
Дополнительное требование к графикам,
оформляемым к отчётам к лабораторным
работам:
График может быть выполнен в одном из
двух вариантов:
1. На миллиметровой бумаге. Все линии и
надписи выполняются от руки. Пишущий
инструмент не регламентируется. Готовый
график вклеивается в отчёт по лабораторной
работе.
2. В виде компьютерной распечатки. Все
линии и надписи выполняются при распечатке
одновременно с выводом графика.
Дописывания от руки не допускаются.
Готовый график вставляется в текст
отчёта по лабораторной работе. Программа,
используемая для построения графика,
не регла-ментируется.
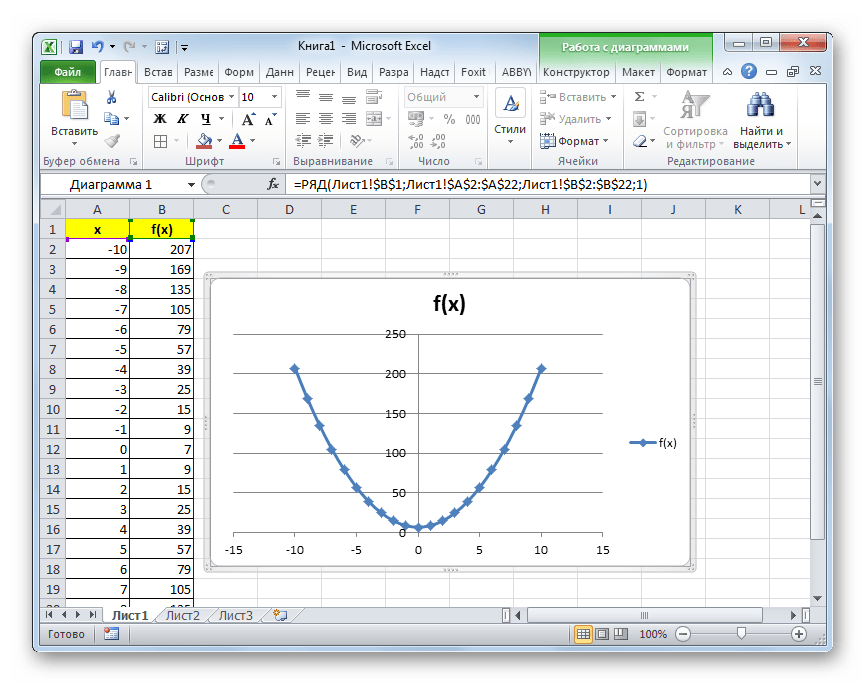
Построение графиков в программе MS
Excel 7/10.
В программе Excel предусмотрена
возможность построения графиков. Графики
в программе строятся по точкам. Координаты
точек удобнее всего задавать в столбцах
листа Excel.
Если в одном столбце листа последовательно
сверху вниз поместить значение аргумента
точек графика, а в соседнем (справа)
столбце – последовательно сверху вниз
значения функции, то по этим координатам
можно построить график. Для этого нужно
выделить все введённые числа и выбрать
действия Вставить/Диаграмма/Точечная.
Полезное мнемоническое правило: Если
Вы хотите построить график, ни в коем
случае не выбирайте подпункт со словом
«График»! При построении точечной
диаграммы Excel предлагает
варианты построения:
|
|
– выделение маркерами |
|
|
– выделение маркерами |
|
|
– выделение маркерами |
|
|
– соединение точек графика |
|
|
– соединение точек графика |
|
После |
|
изменении
размера области диаграммы деления осей
и сетка автоматически изменяются, размер
шрифта подписи делений остаётся
неизменным.
На графике обязательно должна
присутствовать вертикальная сетка,
которой нет по умолчанию. Чтобы её
построить, достаточно выполнить правый
клик по подписи любого деления оси и
«Добавить основные линии сетки». Точно
так же можно «Добавить промежуточные
линии сетки».
Легенда графика (… Ряд1) для графика,
показывающего одну зависимость, является
излишней, и её лучше удалить (правый
клик/Удалить).
Параметры построенной линии зависимости
можно изменять. Для этого следует
выполнить правый клик по маркеру или
линии зависимости/Формат ряда данных.
После этого в открывшемся диалоговом
окне можно выбрать значения всех
актуальных параметров: тип и цвет линии,
тип и размер маркера, цвет границы
маркера, цвет заливки маркера и многое
другое.
Очень часто в построенном графике нужно
изменить параметры построения –
минимальное и максимальное значения
аргумента либо функции, шаг делений
оси, наличие/отсутствие основных и
промежуточных линий сетки,
линейный/логарифмический масштаб
построения и многое другое. Все эти
настройки можно изменить, сделав правый
клик по линии/маркеру и выбрав Формат
ряда данных.
Иногда возникает необходимость изобразить
на одном графике несколько зависимостей.
Это можно сделать двумя способами:
1. Зависимости содержат одинаковые
количества точек с одинаковыми значениями
аргумента. В этом случае следует в одном
столбце расположить значения аргумента
точек, в столбце справа – значения
первой зависимости, в следующем справа
столбце – значения второй зависимости,
и т.д. При построении графика нужно
выделить все заполненные столбцы и
нажать пункт «Вставка» главного меню.
2. Зависимости содержат абсолютно
независимые значения. В этом случае
следует построить сначала одну зависимость
стандартным методом, затем выполнить
на диаграмме правый клик/Выбрать данные,
в открывшемся окне нажать на «Добавить»,
и в новом диалоговом окне указать
столбец, содержащий значения аргумента
(X) и значения зависимости
(Y). Кроме того, можно
указать имя ряда, которое, например,
будет использоваться, например, в легенде
графика. Наименование и расположение
данных каждого ряда можно редактировать
с помощью кнопки «Изменить» справа от
кнопки «Добавить». Можно также удалить
зависимость кнопкой «Удалить» справа
от кнопки «Изменить»:
|
|
При нажатии на кнопку «Добавить» будет
открыто окно «Изменение ряда», в которое
необходимо внести имя нового ряда (оно
будет использоваться
|
|
в легенде графика), колонку со
значениями аргумента графика («Значения
X», можно указать диапазон,
можно выделить ячейки на листе вручную),
и колонку со значениями функции графика
(«Значения Y», можно указать
диапазон, можно выделить ячейки на листе
вручную). После нажатия кнопки «ОК» ряд
будет добавлен к графику.
Все параметры всех элементов построенного
графика можно редактировать. Доступ к
ним открывается (при «фокусировке» на
диаграмме) на вкладках «Конструктор»,
«Макет» и «Формат», названия всех
элементов и действий с ними интуитивно
понятно. Некоторую проблему иногда
вызывает доступ к конкретному ряду
значений на построенном графике (с
целью, например, изменить цвет линии).
Доступ у конкретному ряду можно получить,
выполнив действия Макет/Текущий фрагмент:
|
|
и выбрав вместо «Область диаграммы»
имя соответствующего ряда:
|
|
Примеры построения графиков:
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Практическая работа: Построение графиков функций
Практическая работа: Построение графиков функций
ЦЕЛЬ: научиться строить, корректировать различные графики функций с использованием возможностей программы МS Excel.
ОСНАЩЕНИЕ: ПК, ИК, мультимедиа.
(время выполнения 3 часа)
Работа по построению графиков функций предполагает использование следующей методики:
1. Подготовить диапазон области определения функции (или функций) с помощью маркера автозаполнения.
2. Рассчитать значение функции (функций) на данном диапазоне, используя формулы и функции рабочего листа MS Excel и маркера автозаполнения.
3. Выделить диапазон области определения и области значения функции (функций) и воспользоваться Мастером построения диаграмм. Для построения графиков использовать типы диаграмм График и Точечная.
4. Отформатировать полученный график (графики)
Часто различные линии на плоскости задаются в полярных координатах, общее уравнение которых можно записать в f
, где 
– полярные координаты.
Если линия задана уравнением 
в полярных координатах, то ее уравнение в декартовых координатах можно записать в виде:
X=p (
)cos,
Y= p ()sin.
Для построения графика в декартовой системе координат надо:
Ø Подготовить диапазон изменения координаты.
Ø Рассчитать значение функции на данном диапазоне в полярных координатах.
Ø Рассчитать значение x и y в декартовой системе координат по формулам:
X=p()cos(); Y=p ()sin ().
Ø Выделить диапазон значений x и y и воспользоваться Мастером диаграмм. Откорректировать график.
Упражнение 1. Построение простого графика функции.
График линейной зависимости типа y = kx (y = 2x).
1. Создайте список значений аргумента в диапазоне (-10:10), используя прогрессию.
2. Для создания значений функций выберите следующий столбец. Активизируйте ячейку В1. Введите в строку формул следующее: = 2*А1.
3. 
Заполните значениями диапазон ячеек В1. В21
( этот диапазон включает то же количество строк, что и диапазон аргументов в столбце А). Выберите команду Правка – Заполнить — Вниз.
4. Активизируйте кнопку Мастер диаграмм. Перейдите на вкладку Нестандартные и в списке Тип выберите пункт Гладкие графики.
5. Во втором окне мастера перейдите на вкладку Ряд и в поле Подписи оси Х задайте диапазон значений из столбца А.
6. В третьем и четвертых окнах можно ничего не настраивать. Результат приведен на рис.1.
УПРАЖНЕНИЕ 2. Построить функцию, заданную уравнением в полярных координатах: p= asin(3)
Построение графиков в Excel. Практическая работа
Цель работы:
- научиться строить графики в Excel;
- развить самостоятельность;
- развить навыки мыслительной деятельности, включая каждого учащегося в учебно – познавательный процесс и создавая условия для работы каждого в индивидуальном темпе;
Оборудование:
- ПЭВМ, сеть, проектор;
- опорный конспект, план практической работы, варианты для самостоятельной работы учащихся.
| Этапы | План урока + опорный конспект | Средства обучения |
| I | Подготовительный. Постановка учебных задач. Устное разъяснение порядка работы на уроке, тема урока. |
— |
| II | Повторение.
Фронтальный опрос изученного материала.
|
проектор |
| III | Объяснение нового материала и подготовка к практической работе:
|
Проектор, раздаточный материал |
| IV | Выполнение проектной практической работы:
|
Компьютер |
| V | Итоги:
|
Проектор, раздаточный материал, компьютер |
Опорный конспект
Построение совмещенных графиков в Microsoft Office Excel -2007.
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:
Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя переменными, при проведении сравнения анализа значений y при одних и тех же значениях x.
ПРИМЕР.
(Используется при объяснении материала через проектор.)
Построить графики функций y1= x 2 и y2= x 3 на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:
2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y
5. Должен получиться график:
P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.
Раздаточный материал
Варианты
ВАРИАНТ 1
Построить графики функций y1= x 2 -1, y2= x 2 +1 и y=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.
ВАРИАНТ 2
Построить графики функций y1= 
и y2= 2 х на интервале [- 3 ; 3] с шагом 0,5.
ВАРИАНТ 3
Построить графики функций y1= 
, y2= 
на интервале [- 0,5 ; 9] с шагом 0,5.
ВАРИАНТ 4
Построить графики функций y1=
, y2= 
на интервале [- 5 ; -0,5] с шагом 0,5.
ВАРИАНТ 5
Построить графики функций y1= 
, y2= 
на интервале [0,5 ; 5] с шагом 0,5.
Практическая работа на тему:»Построение графиков функций»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Практическая работа: Построение графиков функций
ЦЕЛЬ: научиться строить, корректировать различные графики функций с использованием возможностей программы М S Excel .
ОСНАЩЕНИЕ: ПК, ИК, мультимедиа.
(время выполнения 3 часа)
Работа по построению графиков функций предполагает использование следующей методики:
Подготовить диапазон области определения функции (или функций) с помощью маркера автозаполнения.
Рассчитать значение функции (функций) на данном диапазоне, используя формулы и функции рабочего листа MS Excel и маркера автозаполнения.
Выделить диапазон области определения и области значения функции (функций) и воспользоваться Мастером построения диаграмм. Для построения графиков использовать типы диаграмм График и Точечная.
Отформатировать полученный график (графики)
Часто различные линии на плоскости задаются в полярных координатах, общее уравнение которых можно записать в f 
, где 
– полярные координаты.
Если линия задана уравнением 
в полярных координатах, то ее уравнение в декартовых координатах можно записать в виде:
X= p (
)cos,
Y= p ()sin.
Для построения графика в декартовой системе координат надо:
Подготовить диапазон изменения координаты.
Рассчитать значение функции на данном диапазоне в полярных координатах.
Рассчитать значение x и y в декартовой системе координат по формулам:
X= p() cos(); Y= p () sin ( ).
Выделить диапазон значений x и y и воспользоваться Мастером диаграмм. Откорректировать график.
пражнение 1. Построение простого графика функции.
График линейной зависимости типа y = kx ( y = 2 x ).
Создайте список значений аргумента в диапазоне (-10:10), используя прогрессию.
Для создания значений функций выберите следующий столбец. Активизируйте ячейку В1. Введите в строку формул следующее: = 2*А1.
З
аполните значениями диапазон ячеек В1. В21
( 
этот диапазон включает то же количество строк, что и диапазон аргументов в столбце А). Выберите команду Правка – Заполнить — Вниз.
Активизируйте кнопку Мастер диаграмм . Перейдите на вкладку Нестандартные и в списке Тип выберите пункт Гладкие графики .
Во втором окне мастера перейдите на вкладку Ряд и в поле Подписи оси Х задайте диапазон значений из столбца А.
В третьем и четвертых окнах можно ничего не настраивать. Результат приведен на рис.1.
УПРАЖНЕНИЕ 2. Построить функцию, заданную уравнением в полярных координатах: p = asin (3)
источники:
http://urok.1sept.ru/articles/525206
http://infourok.ru/prakticheskaya-rabota-na-temupostroenie-grafikov-funkciy-1907384.html
Помогаю со студенческими работами здесь
Построить в одной системе координат при x принадлежит [0.2] графики следующих функций:
y=sin(3pi chi )+2sin(2pi chi )cos(3pi chi ) ,
z=cos(pi chi )-cos(3pi chi ){sin}^{2}(pi…
Построить в декартовой системе координат
построить в декартовой системе координат, используя тип диаграммы "точечная с гладкими кривыми и…
Построить графики функций в декартовой системе координат
Построить графики функций
1. В декартовой системе координат
1-
2. В полярной системе…
Построение графика функций в декартовой системе координат
Составьте программу построения графика функций в декартовой системе координат:
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму: