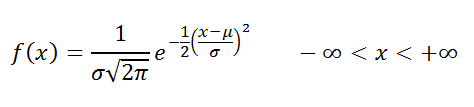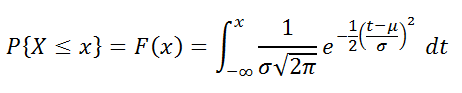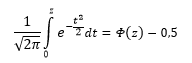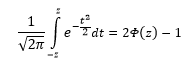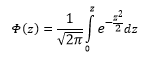У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами. Рассмотрим только лучше из них.
Функция случайного числа в Excel
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
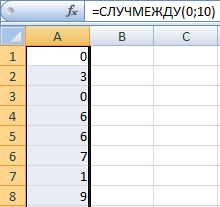
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Рассмотрим их использование на примерах.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.
Возвращаемое случайное число распределено равномерно на интервале [1,10].
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
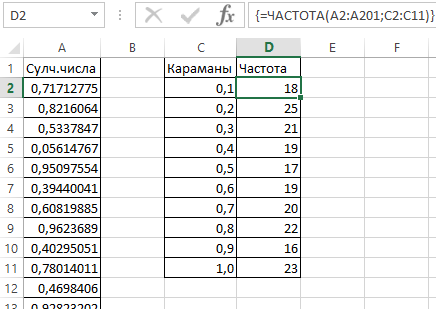
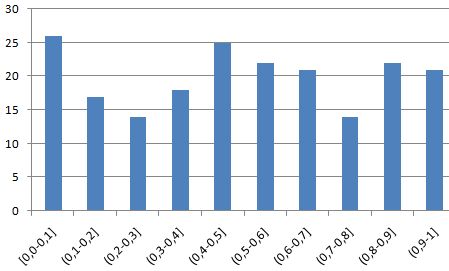
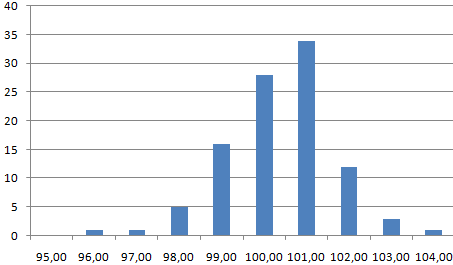
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
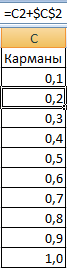
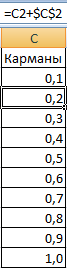
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
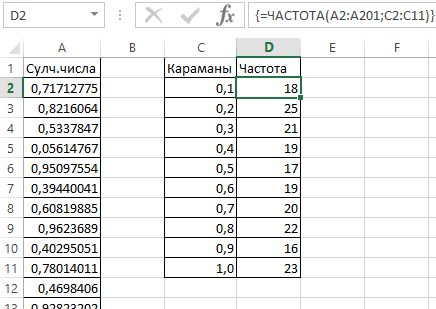
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива {=ЧАСТОТА(A2:A201;C2:C11)}.
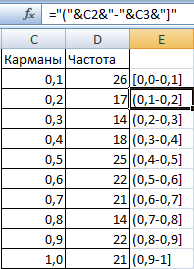
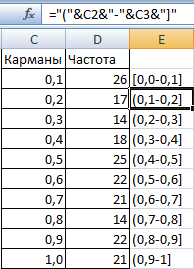
- Сформируем диапазоны с помощью знака «сцепления» (=»[0,0-«&C2&»]»).
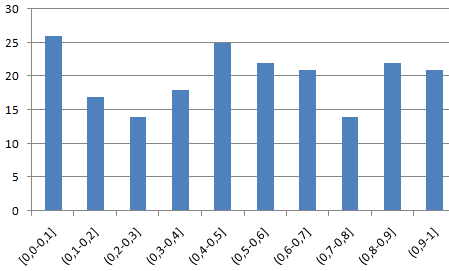
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
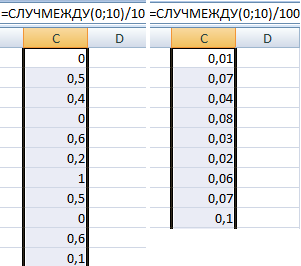
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
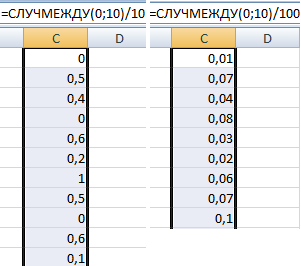
Случайные числа с точностью 0,1 и 0,01:
Как сделать генератор случайных чисел в Excel
Сделаем генератор случайных чисел с генерацией значения из определенного диапазона. Используем формулу вида: =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
Сделаем генератор случайных чисел в диапазоне от 0 до 100 с шагом 10.
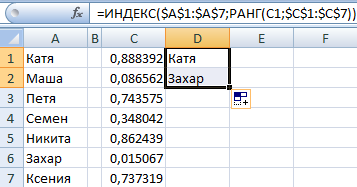
Из списка текстовых значений нужно выбрать 2 случайных. С помощью функции СЛЧИС сопоставим текстовые значения в диапазоне А1:А7 со случайными числами.
Воспользуемся функцией ИНДЕКС для выбора двух случайных текстовых значений из исходного списка.
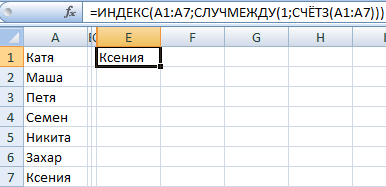
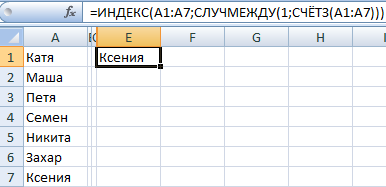
Чтобы выбрать одно случайное значение из списка, применим такую формулу: =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))).
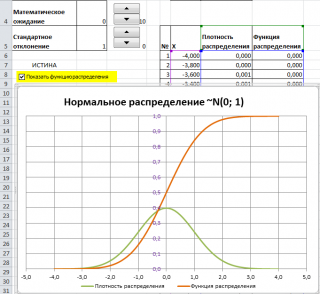
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
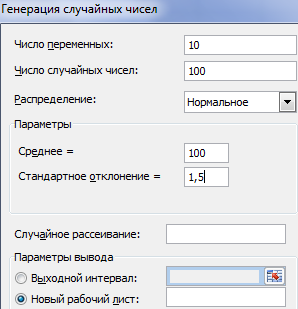
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.
Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).
Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
- Нижняя граница таблицы с категориями – округленное вниз ближайшее кратное число. В ячейку Н1 вводим формулу =ОКРВНИЗ(E1;E5).
- В ячейке Н2 и последующих формула будет выглядеть следующим образом: =ЕСЛИ(G2;H1+$E$5;»»). То есть каждое последующее значение будет увеличено на величину шага.
- Посчитаем количество переменных в заданном промежутке. Используем функцию ЧАСТОТА. Формула будет выглядеть так:
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.
График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».
О том как подключить стандартную настройку «Анализ данных» читайте здесь.
Заполняем параметры для генерации. Распределение – «нормальное».
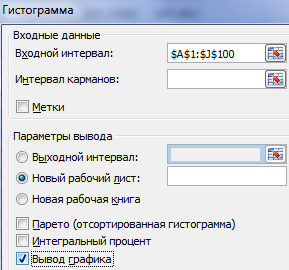
Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».
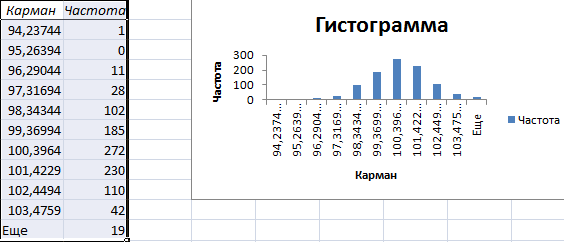
Получаем результат:
Скачать генератор случайных чисел в Excel
График с нормальным распределением в Excel построен.
Рассмотрим Нормальное распределение. С помощью функции
MS EXCEL
НОРМ.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения
.
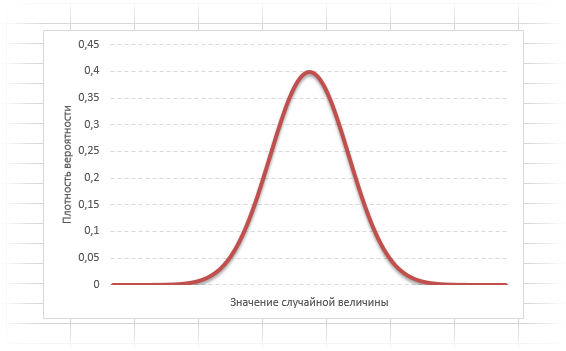
Нормальное распределение
(также называется распределением Гаусса) является самым важным как в теории, так в приложениях системы контроля качества. Важность значения
Нормального распределения
(англ.
Normal
distribution
)
во многих областях науки вытекает из
Центральной предельной теоремы
теории вероятностей.
Определение
: Случайная величина
x
распределена по
нормальному закону
, если она имеет
плотность распределения
:
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Нормальное распределение
зависит от двух параметров: μ
(мю)
— является
математическим ожиданием (средним значением случайной величины)
, и σ (
сигма)
— является
стандартным отклонением
(среднеквадратичным отклонением). Параметр μ определяет положение центра
плотности вероятности
нормального распределения
, а σ — разброс относительно центра (среднего).
Примечание
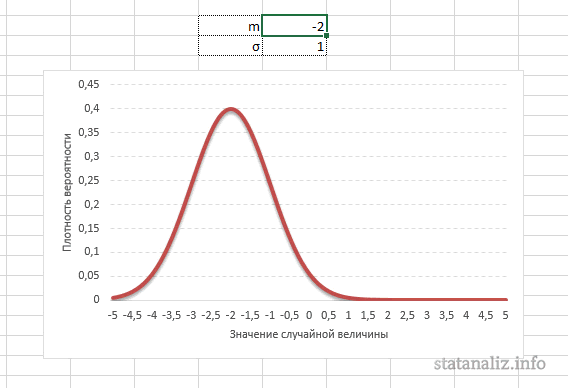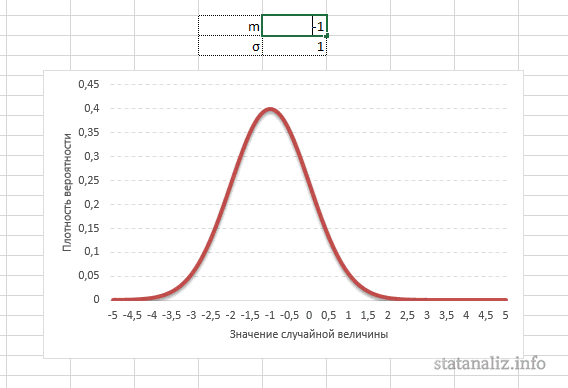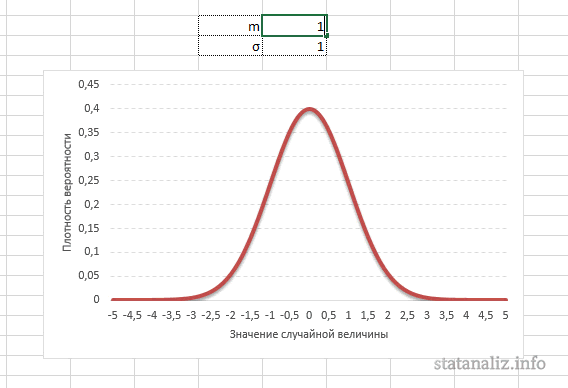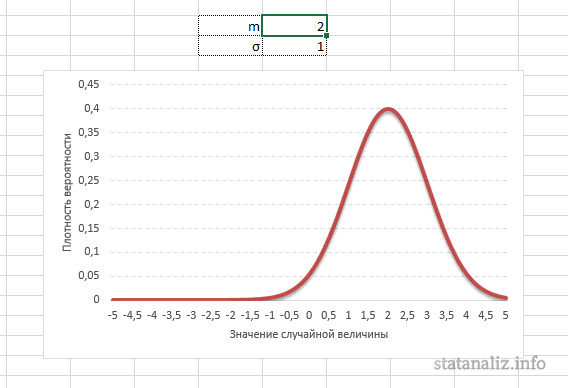
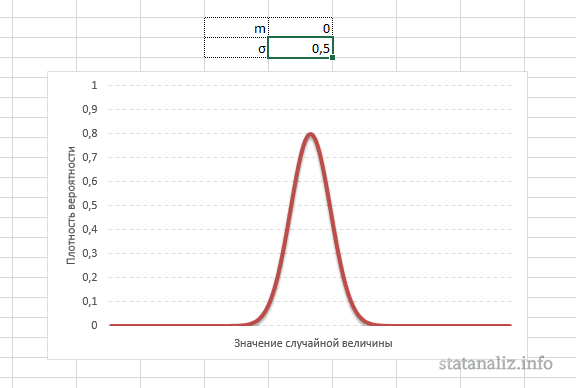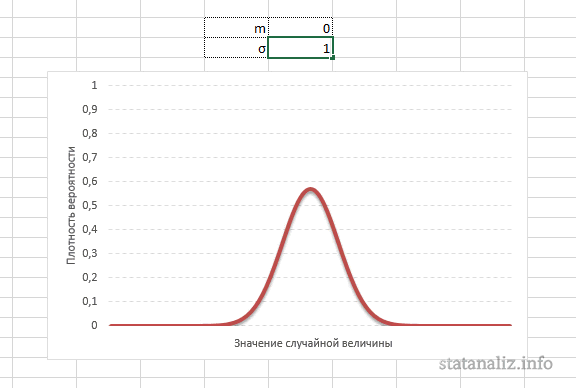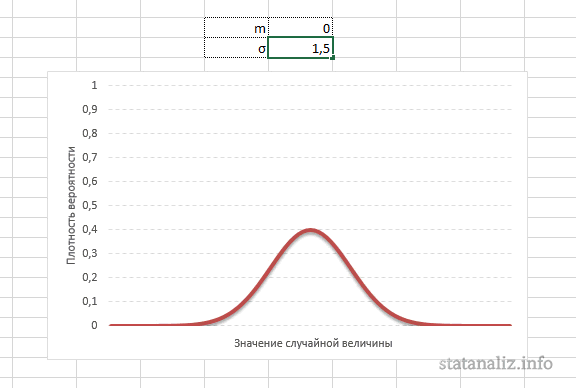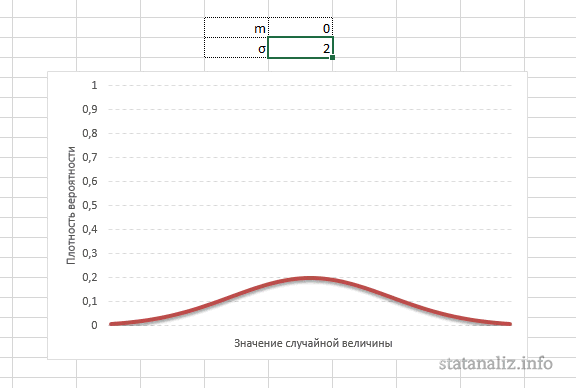
: О влиянии параметров μ и σ на форму распределения изложено в статье про
Гауссову кривую
, а в
файле примера на листе Влияние параметров
можно с помощью
элементов управления Счетчик
понаблюдать за изменением формы кривой.
Нормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Нормального распределения
имеется функция
НОРМ.РАСП()
, английское название — NORM.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина X, распределенная по
нормальному закону
, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Вышеуказанное распределение имеет обозначение
N
(μ; σ).
Так же часто используют обозначение через
дисперсию
N
(μ; σ
2
).
Примечание
: До MS EXCEL 2010 в EXCEL была только функция
НОРМРАСП()
, которая также позволяет вычислить функцию распределения и плотность вероятности.
НОРМРАСП()
оставлена в MS EXCEL 2010 для совместимости.
Стандартное нормальное распределение
Стандартным нормальным распределением
называется
нормальное распределение
с
математическим ожиданием
μ=0 и
дисперсией
σ=1. Вышеуказанное распределение имеет обозначение
N
(0;1).
Примечание
: В литературе для случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение z.
Любое
нормальное распределение
можно преобразовать в стандартное через замену переменной
z
=(
x
-μ)/σ
. Этот процесс преобразования называется
стандартизацией
.
Примечание
: В MS EXCEL имеется функция
НОРМАЛИЗАЦИЯ()
, которая выполняет вышеуказанное преобразование. Хотя в MS EXCEL это преобразование называется почему-то
нормализацией
. Формулы
=(x-μ)/σ
и
=НОРМАЛИЗАЦИЯ(х;μ;σ)
вернут одинаковый результат.
В MS EXCEL 2010 для
стандартного нормального распределения
имеется специальная функция
НОРМ.СТ.РАСП()
и ее устаревший вариант
НОРМСТРАСП()
, выполняющий аналогичные вычисления.
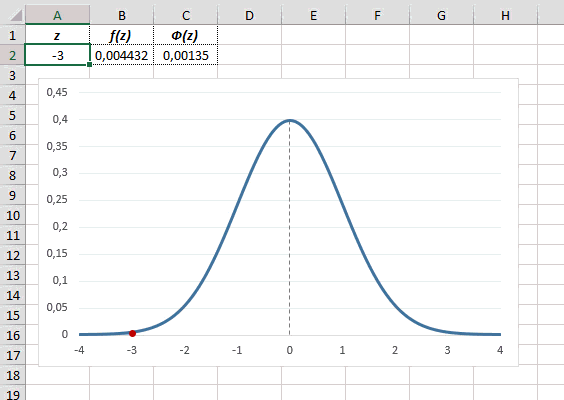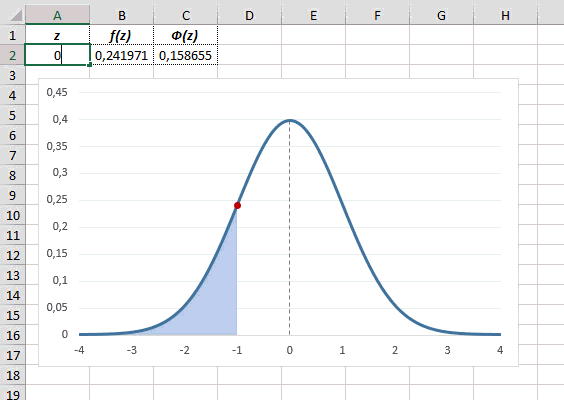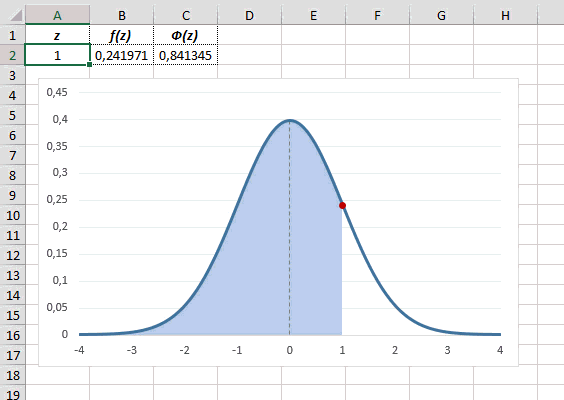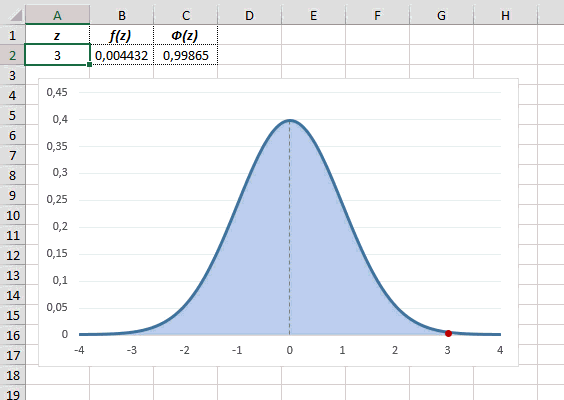
Продемонстрируем, как в MS EXCEL осуществляется процесс стандартизации
нормального распределения
N
(1,5; 2).
Для этого вычислим вероятность, что случайная величина, распределенная по
нормальному закону
N(1,5; 2)
, меньше или равна 2,5. Формула выглядит так:
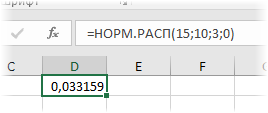
=НОРМ.РАСП(2,5; 1,5; 2; ИСТИНА)
=0,691462. Сделав замену переменной
z
=(2,5-1,5)/2=0,5
, запишем формулу для вычисления
Стандартного нормального распределения:
=НОРМ.СТ.РАСП(0,5; ИСТИНА)
=0,691462.
Естественно, обе формулы дают одинаковые результаты (см.
файл примера лист Пример
).
Обратите внимание, что
стандартизация
относится только к
интегральной функции распределения
(аргумент
интегральная
равен ИСТИНА), а не к
плотности вероятности
.
Примечание
: В литературе для функции, вычисляющей вероятности случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение Ф(z). В MS EXCEL эта функция вычисляется по формуле
=НОРМ.СТ.РАСП(z;ИСТИНА)
. Вычисления производятся по формуле
В силу четности функции
плотности стандартного нормального
распределения f(x), а именно f(x)=f(-х), функция
стандартного нормального распределения
обладает свойством Ф(-x)=1-Ф(x).
Обратные функции
Функция
НОРМ.СТ.РАСП(x;ИСТИНА)
вычисляет вероятность P, что случайная величина Х примет значение меньше или равное х. Но часто требуется провести обратное вычисление: зная вероятность P, требуется вычислить значение х. Вычисленное значение х называется
квантилем
стандартного
нормального распределения
.
В MS EXCEL для вычисления
квантилей
используют функцию
НОРМ.СТ.ОБР()
и
НОРМ.ОБР()
.
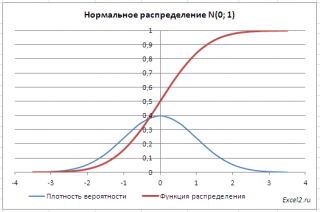
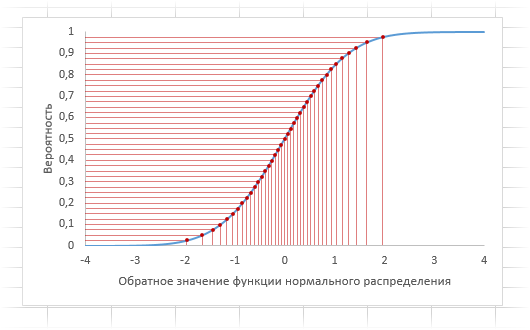
Графики функций
В
файле примера
приведены
графики плотности распределения
вероятности и
интегральной функции распределения
.
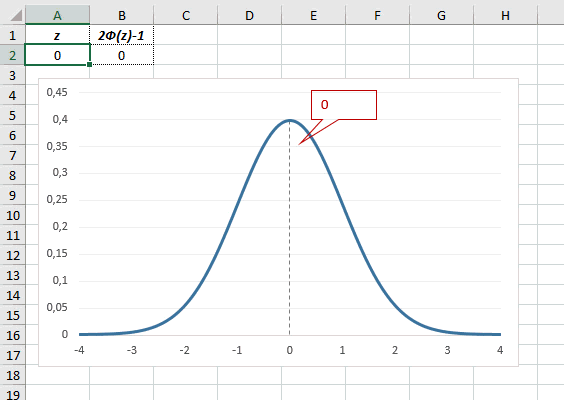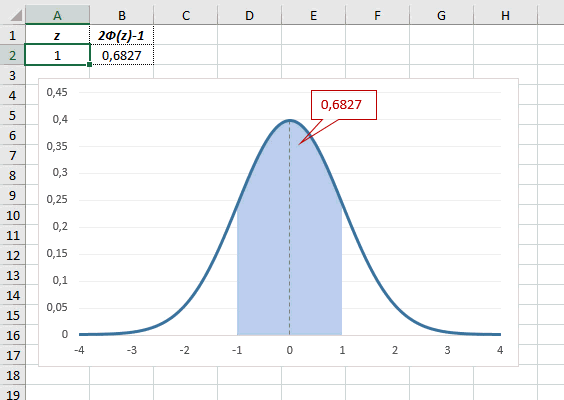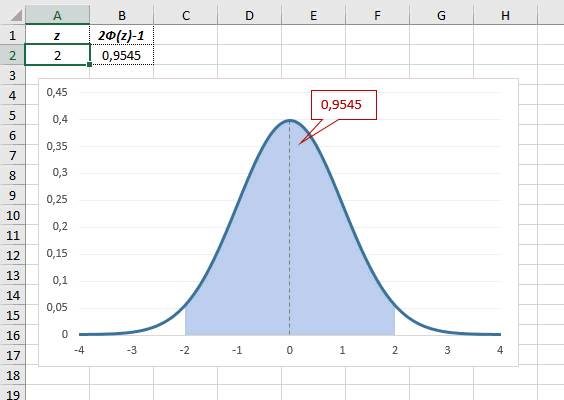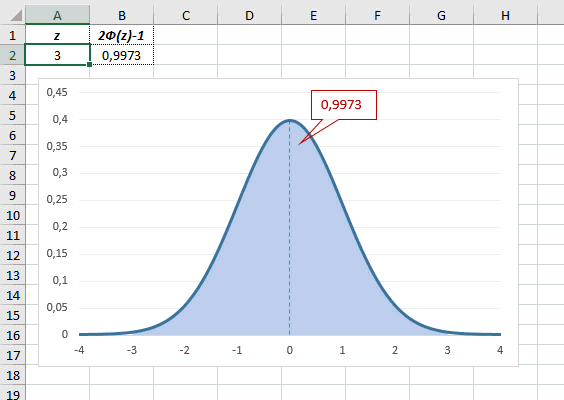
Как известно, около 68% значений, выбранных из совокупности, имеющей
нормальное распределение
, находятся в пределах 1 стандартного отклонения (σ) от μ(среднего или математического ожидания); около 95% — в пределах 2-х σ, а в пределах 3-х σ находятся уже 99% значений. Убедиться в этом для
стандартного нормального распределения
можно записав формулу:
=
НОРМ.СТ.РАСП(1;ИСТИНА)-НОРМ.СТ.РАСП(-1;ИСТИНА)
которая вернет значение 68,2689% — именно такой процент значений находятся в пределах +/-1 стандартного отклонения от
среднего
(см.
лист График в файле примера
).
В силу четности функции
плотности стандартного нормального
распределения:
f
(
x
)=
f
(-х)
, функция
стандартного нормального распределения
обладает свойством F(-x)=1-F(x). Поэтому, вышеуказанную формулу можно упростить:
=
2*НОРМ.СТ.РАСП(1;ИСТИНА)-1
Для произвольной
функции нормального распределения
N(μ; σ) аналогичные вычисления нужно производить по формуле:
=2* НОРМ.РАСП(μ+1*σ;μ;σ;ИСТИНА)-1
Вышеуказанные расчеты вероятности требуются для
построения доверительных интервалов
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении
диаграмм
читайте статью
Основные типы диаграмм
.
Примечание
: Для удобства написания формул в
файле примера
созданы
Имена
для параметров распределения: μ и σ.
Генерация случайных чисел
С помощью надстройки
Пакет анализа
можно сгенерировать случайные числа, распределенные по
нормальному закону
.
СОВЕТ
: О надстройке
Пакет анализа
можно прочитать в статье
Надстройка Пакет анализа MS EXCEL
.
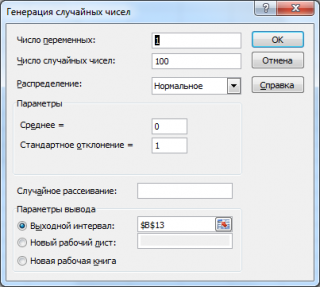
Сгенерируем 3 массива по 100 чисел с различными μ и σ. Для этого в окне
Генерация
случайных чисел
установим следующие значения для каждой пары параметров:
Примечание
: Если установить опцию
Случайное рассеивание
(
Random Seed
), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию равной 25, можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции
Случайное рассеивание
может запутать. Лучше было бы ее перевести как
Номер набора со случайными числами
.
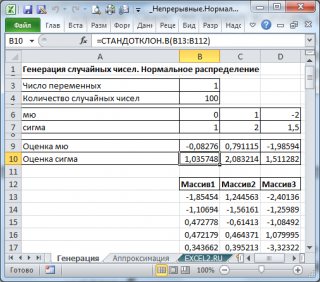
В итоге будем иметь 3 столбца чисел, на основании которых можно, оценить параметры распределения, из которого была произведена выборка: μ и σ
.
Оценку для μ можно сделать с использованием функции
СРЗНАЧ()
, а для σ – с использованием функции
СТАНДОТКЛОН.В()
, см.
файл примера лист Генерация
.
Примечание
: Для генерирования массива чисел, распределенных по
нормальному закону
, можно использовать формулу
=НОРМ.ОБР(СЛЧИС();μ;σ)
. Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Задачи
Задача1
. Компания изготавливает нейлоновые нити со средней прочностью 41 МПа и стандартным отклонением 2 МПа. Потребитель хочет приобрести нити с прочностью не менее 36 МПа. Рассчитайте вероятность, что партии нити, изготовленные компанией для потребителя, будут соответствовать требованиям или превышать их.
Решение1
: =
1-НОРМ.РАСП(36;41;2;ИСТИНА)
Задача2
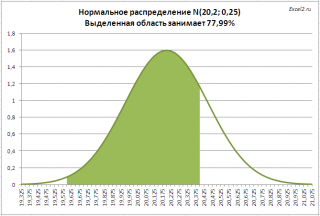
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Согласно техническим условиям, трубы признаются годными, если диаметр находится в пределах 20,00+/- 0,40 мм. Какая доля изготовленных труб соответствует ТУ?
Решение2
: =
НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25)
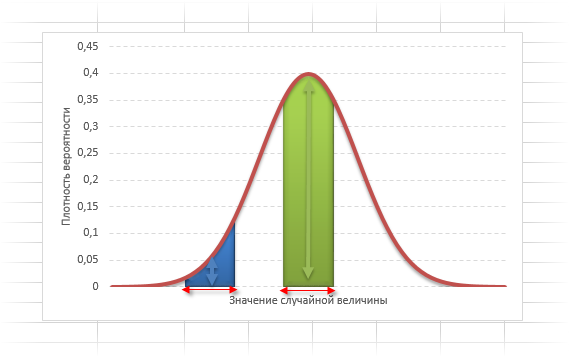
На рисунке ниже, выделена область значений диаметров, которая удовлетворяет требованиям спецификации.
Решение приведено в
файле примера лист Задачи
.
Задача3
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Внешний диаметр не должен превышать определенное значение (предполагается, что нижняя граница не важна). Какую верхнюю границу в технических условиях необходимо установить, чтобы ей соответствовало 97,5% всех изготавливаемых изделий?
Решение3
: =
НОРМ.ОБР(0,975; 20,20; 0,25)
=20,6899 или =
НОРМ.СТ.ОБР(0,975)*0,25+20,2
(произведена «дестандартизация», см. выше)
Задача 4
. Нахождение параметров
нормального распределения
по значениям 2-х
квантилей
(или
процентилей
). Предположим, известно, что случайная величина имеет нормальное распределение, но не известны его параметры, а только 2-я
процентиля
(например, 0,5-
процентиль
, т.е. медиана и 0,95-я
процентиль
). Т.к. известна
медиана
, то мы знаем
среднее
, т.е. μ. Чтобы найти
стандартное отклонение
нужно использовать
Поиск решения
. Решение приведено в
файле примера лист Задачи
.
Примечание
: До MS EXCEL 2010 в EXCEL были функции
НОРМОБР()
и
НОРМСТОБР()
, которые эквивалентны
НОРМ.ОБР()
и
НОРМ.СТ.ОБР()
.
НОРМОБР()
и
НОРМСТОБР()
оставлены в MS EXCEL 2010 и выше только для совместимости.
Линейные комбинации нормально распределенных случайных величин
Известно, что линейная комбинация нормально распределённых случайных величин
x
(
i
)
с параметрами μ
(
i
)
и σ
(
i
)
также распределена нормально. Например, если случайная величина Y=x(1)+x(2), то Y будет иметь распределение с параметрами μ
(1)+ μ(2)
и
КОРЕНЬ(σ(1)^2+ σ(2)^2).
Убедимся в этом с помощью MS EXCEL.
С помощью надстройки
Пакет анализа
сгенерируем 2 массива по 100 чисел с различными μ и σ.
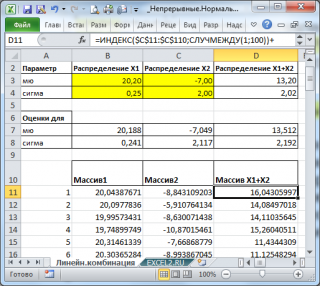
Теперь сформируем массив, каждый элемент которого является суммой 2-х значений, взятых из каждого массива.
С помощью функций
СРЗНАЧ()
и
СТАНДОТКЛОН.В()
вычислим
среднее
и
дисперсию
получившейся
выборки
и сравним их с расчетными.
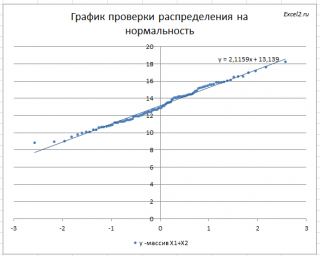
Кроме того, построим
График проверки распределения на нормальность
(
Normal
Probability
Plot
), чтобы убедиться, что наш массив соответствует выборке из
нормального распределения
.
Прямая линия, аппроксимирующая полученный график, имеет уравнение y=ax+b. Наклон кривой (параметр а) может служить оценкой
стандартного отклонения
, а пересечение с осью y (параметр b) –
среднего
значения.
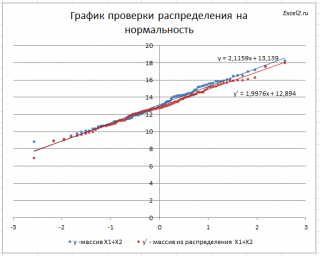
Для сравнения сгенерируем массив напрямую из распределения
N
(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ σ(2)^2)
).
Как видно на рисунке ниже, обе аппроксимирующие кривые достаточно близки.
В качестве примера можно провести следующую задачу.
Задача
. Завод изготавливает болты и гайки, которые упаковываются в ящики парами. Пусть известно, что вес каждого из изделий является нормальной случайной величиной. Для болтов средний вес составляет 50г, стандартное отклонение 1,5г, а для гаек 20г и 1,2г. В ящик фасуется 100 пар болтов и гаек. Вычислить какой процент ящиков будет тяжелее 7,2 кг.
Решение
. Сначала переформулируем вопрос задачи: Вычислить какой процент пар болт-гайка будет тяжелее 7,2кг/100=72г. Учитывая, что вес пары представляет собой случайную величину = Вес(болта) + Вес(гайки) со средним весом (50+20)г, и
стандартным отклонением
=КОРЕНЬ(СУММКВ(1,5;1,2))
, запишем решение =
1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА)
Ответ
: 15% (см.
файл примера лист Линейн.комбинация
)
Аппроксимация Биномиального распределения Нормальным распределением
Если параметры
Биномиального распределения
B(n;p) находятся в пределах 0,1<=p<=0,9 и n*p>10, то
Биномиальное распределение
можно аппроксимировать
Нормальным распределением
.
При значениях
λ
>15
,
Распределение Пуассона
хорошо аппроксимируется
Нормальным распределением
с параметрами: μ
=λ
, σ
2
=
λ
.
Подробнее о связи этих распределений, можно прочитать в статье
Взаимосвязь некоторых распределений друг с другом в MS EXCEL
. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Содержание
- Создаём генератор случайных чисел с помощью функции СЛЧИС
- Генерация случайной величины, распределенной по равномерному закону
- Способ применения функции «СЛУЧМЕЖДУ( ; )»:
- Способ применения функции «СЛЧИС()»:
- Функция случайного числа в Excel
- Выборка случайных чисел с помощью СЛЧИС
- Функция СЛУЧМЕЖДУ
- Выбор рандом чисел в заданном диапазоне
- Дробные числа больше единицы
- Как сделать генератор чисел в экселе. Генератор случайных чисел в Excel
- Случайное число в определенном диапазоне. Функция
- Случайное число с определенным шагом
- Как применять рандом для проверки модели?
- Использование надстройки Analysis ToolPack
- Произвольное дискретное распределение
- Генератор случайных чисел нормального распределения
- Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
Создаём генератор случайных чисел с помощью функции СЛЧИС
С помощью функции СЛЧИС, мы имеем возможность генерировать любое случайное число в диапазоне от 0 до 1 и эта функция будет выглядеть так:
=СЛЧИС();

=СЛЧИС()*100;
=ОКРУГЛ((СЛЧИС()*100);0);
=ОТБР((СЛЧИС()*100);0)
=СЛЧИС()*(b-а)+а, где,
- a – представляет нижнюю границу,
- b – верхний предел
и полная формула будет выглядеть: =СЛЧИС()*(6-1)+1, а без дробных частей вам нужно написать: =ОТБР(СЛЧИС()*(6-1)+1;0)
Генерация случайной величины, распределенной по равномерному закону
Дискретное равномерное распределение – это такое распределение, для которого вероятность каждого из значений случайной величины одна и та же, то есть
Р(ч)=1/N,
где N – количество возможных значений случайной величины
Для получения случайной величины, распределенной по равномерному закону, в библиотеке Мастера функций табличного процессора в категории Математические есть специальная функция СЛЧИС(), которая генерирует случайные вещественные числа в диапазоне 0 -1. Функция не имеет параметров
Если необходимо сгенерировать случайные числа в другом диапазоне, то для этого нужно использовать формулу:
= СЛЧИС() * (b – a) +a, где
a – число, устанавливающее нижнюю границу диапазона;
b – число, устанавливающее верхнюю границу диапазона.
Например, для генерации чисел распределенных по равномерному закону в диапазоне 10 – 20, нужно в ячейку рабочего листа ввести формулу:
=СЛЧИС()*(20-10)+10.
Для генерации целых случайных чисел, равномерно распределенных в диапазоне между двумя заданными числами в библиотеке табличного процессора есть специальная функция СЛУЧМЕЖДУ. Функция имеет параметры:
СЛУЧМЕЖДУ(Нижн_гран; Верхн_гран), где
Нижн_гран – число, устанавливающее нижнюю границу диапазона;
Верхн_гран – число, устанавливающее верхнюю границу диапазона. Применение функций СЛЧИС и СЛУЧМЕЖДУ рассмотрим на примере.
Пример 1. Требуется создать массив из 10 чисел, распределенных равномерно в диапазоне 50 – 100.
Решение
1. Выделим диапазон, включающий десять ячеек рабочего листа, например B2:B11 (рис. 1).
2. На ленте Формулы в группе Библиотека функций кликнем на пиктограмме Вставить функцию.
3. В открывшемся окне диалога Мастер функций выберем категорию Математические, в списке функций – СЛЧИС, кликнем на ОК – появится окно диалога Аргументы функции.
4. Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter> – в выделенном диапазоне будут помещены числа, распределенные по равномерному закону в диапазоне 0 – 1 (рис. 1).
5. Щелкнем указателем мыши в строке формул и изменим имеющуюся там формулу, приведя ее к виду: =СЛЧИС()*(100-50)+50.
6. Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter> – в выделенном диапазоне будут размещены числа, распределенные по равномерному закону в диапазоне 50 – 100 (рис. 2).
Способ применения функции «СЛУЧМЕЖДУ( ; )»:
- Установить курсор в ячейку, которой присваиваете значение;
- Выбрать функцию «СЛУЧМЕЖДУ( ; )»;
- В меню указать начальное и конечное число диапазона или ячейки, содержащие эти числа;
- Нажать «ОК»
Наряду с функцией «СЛУЧМЕЖДУ» существует «СЛЧИС()», эта функция в отличие от «СЛУЧМЕЖДУ» выбирает случайное число из диапазона от 0 до 1. То есть присваивает ячейке случайное дробное число до единицы.
Способ применения функции «СЛЧИС()»:
- Установить курсор в ячейку, которой присваиваете значение;
- Выбрать функцию «СЛЧИС()»;
- Нажать «ОК»
У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами.
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.
Возвращаемое случайное число распределено равномерно на интервале .
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива {=ЧАСТОТА(A2:A201;C2:C11)}.
- Сформируем диапазоны с помощью знака «сцепления» (=»»).
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
Случайные числа с точностью 0,1 и 0,01:
Выбор рандом чисел в заданном диапазоне
Вы можете получить случайное целое число в нужном диапазоне. Для этого используем функцию =СЛУЧМЕЖДУ(мин макс). Первым аргументом функции будет минимальное допустимое число, вторым – максимальное.
Например, так можно получить число в промежутке от -100 до 100:
Функции СЛЧИС и СЛУЧМЕЖДУ изменяют свой результат при каждом пересчёте листа. Если Вам нужно этого избежать – замените формулы на значения с помощью специальной вставки.
А теперь немного примеров использования приведенных функций.
Дробные числа больше единицы
Как вы уже поняли, функция СЛЧИС всегда возвращает дробное число от 0 до 1, а СЛУЧМЕЖДУ – целое в указанном диапазоне. А как выбрать число рандомно, дробное и больше единицы? К примеру, нам нужно случайное дробное число в пределах от 10 до 90. Поможет такая формула:
Как сделать генератор чисел в экселе. Генератор случайных чисел в Excel
В Excel есть функция нахождения случайных чисел =СЛЧИС(). Возможность же найти случайное число в Excel, важная составляющая планирования или анализа, т.к. вы можете спрогнозировать результаты вашей модели на большом количестве данных или просто найти одно рандомное число для проверки своей формулы или опыта.
Чаще всего эта функция применяется для получения большого количества случайных чисел. Т.е. 2-3 числа всегда можно придумать самому, для большого количества проще всего применить функцию.
В большинстве языков программирования подобная функция известная как Random (от англ. случайный), поэтому часто можно встретить обрусевшее выражение «в рандомном порядке» и т.п.
В английском Excel функция СЛЧИС числится как RAND
Начнем с описания функции =СЛЧИС(). Для этой функции не нужны аргументы.
А работает она следующим образом — выводит случайное число от 0 до 1. Число будет вещественное, т.е. по большому счету любое, как правило это десятичные дроби, например 0,0006.
При каждом сохранении число будет меняться, чтобы обновить число без обновления нажмите F9.
Случайное число в определенном диапазоне. Функция
Что делать если вам не подходит имеющийся диапазон случайных чисел, и нужно набор случайных чисел от 20 до 135. Как это можно сделать?
Нужно записать следующую формулу.
СЛЧИС()*115+20
Т.е. к 20 будет случайным образом прибавляться число от 0 до 115, что позволит получать каждый раз число в нужном диапазоне (см. первую картинку).
- Кстати, если вам необходимо найти целое число в таком же диапазоне, для этого существует специальная функция, где мы указываем верхнюю и нижнюю границу значений
- СЛУЧМЕЖДУ(20;135)
- Просто, но очень удобно!
- Если нужно множество ячеек случайных чисел просто протяните ячейку ниже.
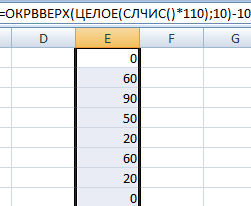
Случайное число с определенным шагом
Если нам нужно получить рандомное число с шагом, к примеру пять, то мы воспользуемся одной из . Это будет ОКРВВЕРХ()
ОКРВВЕРХ(СЛЧИС()*50;5)
Где мы находим случайное число от 0 до 50, а затем округляем его до ближайшего сверху значения кратного 5. Удобно, когда вы делаете расчет для комплектов по 5 штук.
Как применять рандом для проверки модели?
Проверить придуманную модель можно при помощи большого количества случайных чисел. Например проверить будет ли прибыльным бизнес-план
Использование надстройки Analysis ToolPack
Другой способ получения случайных чисел в листе состоит в использовании надстройки Analysis ToolPack (которая поставлялась вместе с Excel). Этот инструмент может генерировать неравномерные случайные числа. Они генерируются не формулами, поэтому, если вам нужен новый набор случайных чисел, необходимо перезапустить процедуру.
Получите доступ к пакету Analysis ToolPack, выбрав Данные Анализ Анализ данных.
Если эта команда отсутствует, установите пакет Analysis ToolPack с помощью диалогового окна Надстройки . Самый простой способ вызвать его — нажать Atl+TI.
В диалоговом окне Анализ данныхвыберите Генерация случайных чисели нажмите ОК. Появится окно, показанное на рис. 130.1.
Выберите тип распределения в раскрывающемся списке Распределение, а затем задайте дополнительные параметры (они изменяются в зависимости от распределения). Не забудьте указать параметр Выходной интервал, в котором хранятся случайные числа.
Чтобы выбрать из таблицы случайные данные, нужно воспользоваться функцией в Excel «Случайные числа». Это готовый генератор случайных чисел в Excel.
Эта функция пригодится при проведении выборочной проверки или при проведении лотереи, т.д. Итак, нам нужно провести розыгрыш призов для покупателей.
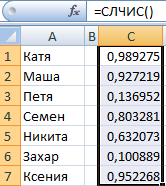
В столбце А стоит любая информация о покупателях – имя, или фамилия, или номер, т.д. В столбце в устанавливаем функцию случайных чисел. Выделяем ячейку В1. На закладке «Формулы» в разделе «Библиотека функций» нажимаем на кнопку «Математические» и выбираем из списка функцию «СЛЧИС». Заполнять в появившемся окне ничего не нужно. Просто нажимаем на кнопку «ОК».
Копируем формулу по столбцу. Получилось так.
Эта формула ставит случайные числа меньше нуля. Чтобы случайные числа были больше нуля, нужно написать такую формулу. =СЛЧИС()*100
При нажатии клавиши F9, происходит смена случайных чисел. Можно выбирать каждый раз из списка первого покупателя, но менять случайные числа клавишей F9.
Случайное число из диапазона Excel.
Чтобы получить случайные числа в определенном диапазоне, установим функцию «СЛУЧМЕЖДУ» в математических формулах. Установим формулы в столбце С. Диалоговое окно заполнили так.

Внимание!
В таблице случайные числа располагаем в первом столбце. У нас такая таблица.
=НАИМЕНЬШИЙ($A$1:$A$6;E1)
Копируем формулу на ячейки F2 и F3 – мы выбираем трех призеров.
В ячейке G1 пишем такую формулу. Она выберет имена призеров по случайным числам из столбца F. =ВПР(F1;$A$1:$B$6;2;0)
Получилась такая таблица победителей.
=НАИМЕНЬШИЙ($A$1:$A$6;E1)
Копируем формулу на ячейки F2 и F3 – мы выбираем трех призеров.
В ячейке G1 пишем такую формулу. Она выберет имена призеров по случайным числам из столбца F. =ВПР(F1;$A$1:$B$6;2;0)
Получилась такая таблица победителей.
Если нужно выбрать призеров по нескольким номинациям, то нажимаем на клавишу F9 и произойдет не только замена случайных чисел, но и связанных с ними имен победителей.
Как отключить обновление случайных чисел в Excel.
Чтобы случайное число не менялось в ячейке, нужно написать формулу вручную и нажать клавишу F9 вместо клавиши «Enter», чтобы формула заменилась на значение.
В Excel есть несколько способов, как копировать формулы, чтобы ссылки в них не менялись. Смотрите описание простых способов такого копирования в статье »
Доброго времени суток, уважаемый, читатель!
Недавно, возникла необходимость создать своеобразный генератор случайных чисел в Excel в границах нужной задачи, а она была простая, с учётом количества человек выбрать случайного пользователя, всё очень просто и даже банально. Но меня заинтересовало, а что же ещё можно делать с помощью такого генератора, какие они бывают, каковые их функции для этого используются и в каком виде. Вопросом много, так что постепенно буду и отвечать на них.
Итак, для чего же собственно мы можем использовать этом механизм:
- во-первых: мы можем для тестировки формул, заполнить нужный нам диапазон случайными числами;
- во-вторых: для формирования вопросов различных тестов;
- в-третьих: для любого случайно распределения заранее задач между вашими сотрудниками;
- в-четвёртых: для симуляции разнообразнейших процессов.
Произвольное дискретное распределение
С помощью надстройки Пакет Анализа можно сгенерировать числа, имеющие произвольное дискретное распределение , т.е. распределение, где пользователь сам задает значения случайной величины и соответствующие вероятности.
В поле Входной интервал значений и вероятностей необходимо ввести ссылку на двухстолбцовый диапазон (см. файл примера ).
Необходимо следить, чтобы сумма вероятностей модельного распределения была равна 1. Для этого в MS EXCEL имеется специальная функция ВЕРОЯТНОСТЬ() .
СОВЕТ : О генерации чисел, имеющих произвольное дискретное распределение , см. статью Генерация дискретного случайного числа с произвольной функцией распределения в MS EXCEL . В этой статье также рассмотрена функция ВЕРОЯТНОСТЬ() .
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
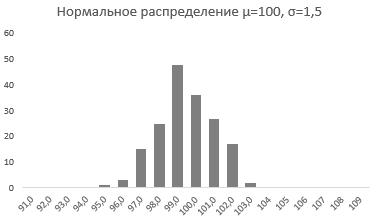
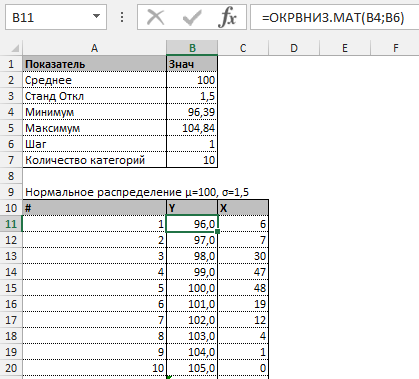
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.
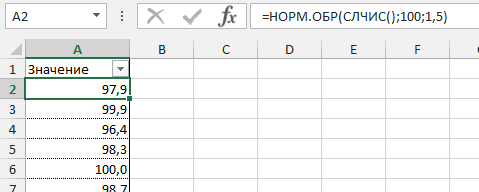
Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).

Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
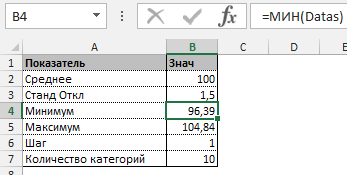
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
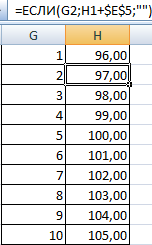
- Нижняя граница таблицы с категориями – округленное вниз ближайшее кратное число. В ячейку Н1 вводим формулу =ОКРВНИЗ(E1;E5).
- В ячейке Н2 и последующих формула будет выглядеть следующим образом: =ЕСЛИ(G2;H1+$E$5;””). То есть каждое последующее значение будет увеличено на величину шага.
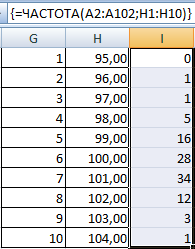
- Посчитаем количество переменных в заданном промежутке. Используем функцию ЧАСТОТА. Формула будет выглядеть так:



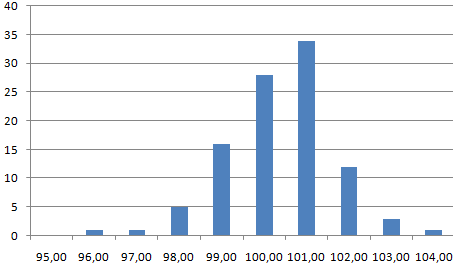
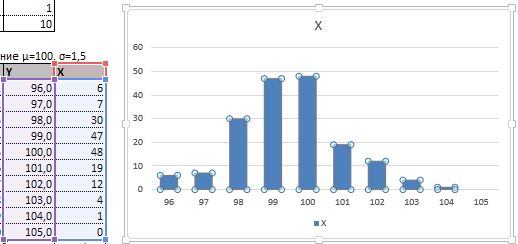
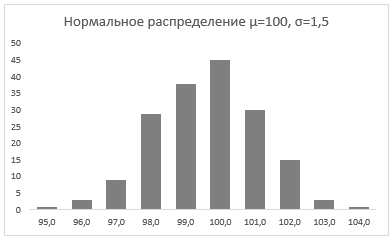
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.

График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».

О том как подключить стандартную настройку «Анализ данных» читайте здесь.
Заполняем параметры для генерации. Распределение – «нормальное».

Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».

Получаем результат:
Скачать генератор случайных чисел в Excel

График с нормальным распределением в Excel построен.
Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
Если вы хотите получить постоянный набор случайных чисел, дат или текстовых строк, которые не будут меняться каждый раз, то есть зафиксировать случайные числа, когда лист пересчитывается, используйте один из следующих способов:
- Чтобы остановить функции СЛЧИС или СЛУЧМЕЖДУ от пересчета в одной ячейке, выберите эту ячейку, переключитесь на панель формул и нажмите F9, чтобы заменить формулу на ее значение.
- Чтобы предотвратить функцию случайных чисел в Excel от автоматического обновления значений в нескольких ячейках, используйте функцию Вставить. Выберите все ячейки с формулой генерации случайных значений, нажмите Ctrl+C, чтобы скопировать их, затем щелкните правой кнопкой мыши выбранный диапазон и нажмите «Вставить специальные»–> «Значения».
Источники
- https://topexcel.ru/sozdaem-generator-sluchajnyx-chisel-v-excel/
- https://zen.yandex.ru/media/id/5d4d8e658da1ce00ad5ece61/5dbadd11e6e8ef00ad7c0e34
- http://word-office.ru/kak-sdelat-random-v-excel.html
- https://officelegko.com/2019/09/09/randomizator-chisel-v-excel/
- https://iiorao.ru/prochee/kak-sdelat-random-v-excel.html
- https://excel2.ru/articles/generaciya-sluchaynyh-chisel-v-ms-excel
- https://exceltable.com/funkcii-excel/generator-sluchaynyh-chisel
- https://naprimerax.org/posts/63/generator-sluchainykh-chisel-v-excel
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
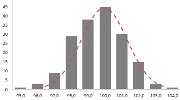
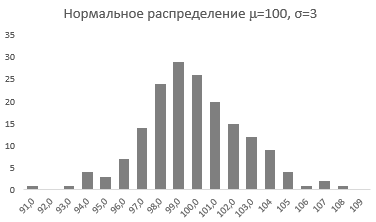
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
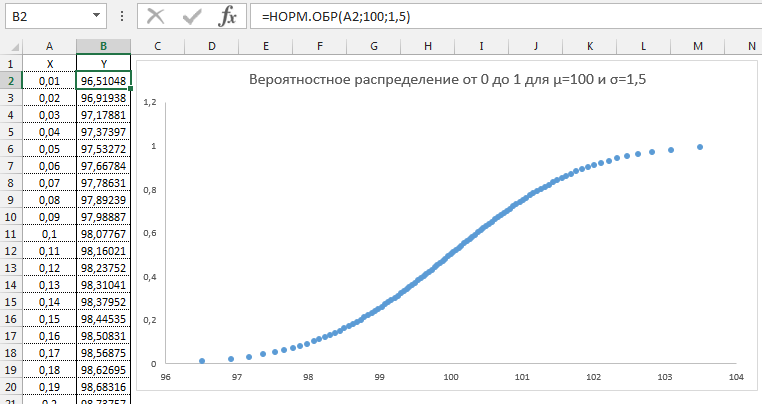
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Skip to content
В статье объясняются особенности алгоритма получения случайных чисел Excel и показано, как использовать функции СЛЧИС и СЛУЧМЕЖДУ для чисел, дат, паролей и других текстовых выражений.
Прежде чем мы углубимся в различные методы производства случайных чисел в Excel, давайте определимся, что они собой представляют. Говоря простым языком, случайные данные – это последовательность цифр, букв или других символов, в которой отсутствуют какой-либо шаблон или закономерность.
Случайность имеет множество различных приложений в криптографии, статистике, лотерее, азартных играх и многих других областях. И поскольку она всегда была востребована, с древних времен существовали различные методы создания случайных чисел, такие как подбрасывание монет, бросание кубиков, тасование игральных карт и так далее. Конечно, мы не будем полагаться на такие «экзотические» техники в этом руководстве и сосредоточимся на том, что может предложить генератор случайных чисел Excel.
- Как работает алгоритм случайных чисел
- Функция СЛЧИС
- Случайные числа в указанном диапазоне при помощи функции СЛУЧМЕЖДУ
- Случайные числа с нужным количеством десятичных знаков
- Случайные даты в Excel
- Как вставить случайное время в Excel
- Случайные дата и время
- Как получить случайные буквы
- Создание текстовых строк и паролей
- Как предотвратить постоянный пересчет формул СЛЧИС и СЛУЧМЕЖДУ
- Как создать уникальные случайные числа в Excel
Создание случайных чисел в Excel – основы.
Случайные числа — это без всякой закономерности выбранная последовательность чисел. Но в жизни практически всегда применяются псевдослучайные числа. Их получают по заранее определенному сложному алгоритму. Для постороннего человека они выглядят случайными, но все же их можно предсказать, если узнать этот сложный алгоритм. Псевдослучайные числа применяются во всех компьютерных программах.
Хотя функции случайных чисел Excel удовлетворяют всем стандартным тестам на случайность, они все же не выдают истинные случайные числа. Но это не значит, что Excel для этих целей не годится. Псевдослучайные числа, создаваемые функциями Excel, прекрасно подходят для многих целей.
Давайте подробнее рассмотрим, как это происходит, чтобы вы знали, чего от стандартных функций Excel можно ожидать, а чего нельзя.
Как и большинство компьютерных программ, генератор случайных чисел Excel производит псевдослучайные числа с помощью некоторых математических формул. Для вас это означает, что теоретически эти числа, создаваемые Excel, предсказуемы. Но только при условии, что кто-то знает все детали алгоритма. Это причина того, что это никогда не было задокументировано и вряд ли когда-либо будет сделано.
Итак, как можно создавать случайные числа в Excel?
- Функции Excel СЛЧИС и СЛУЧМЕЖДУ (RAND и RANDBETWEEN в английской версии) возвращают псевдослучайные числа из равномерного распределения, также известного как прямоугольное распределение, где существует равная вероятность для всех значений, которые величина может принимать. Хороший пример равномерного распределения — бросок одной игральной кости. Итогом такой жеребьевки являются шесть возможных значений (1, 2, 3, 4, 5, 6), и каждое из них имеет одинаковую вероятность.
- Функции Excel СЛЧИС и СЛУЧМЕЖДУ, по слухам, инициализируются из системного времени компьютера. Технически начальное число является отправной точкой для создания последовательности чисел. И каждый раз, когда вызывается случайная функция Excel, используется новое начальное число, которое возвращает уникальную последовательность. Другими словами, при использовании генератора случайных чисел в Excel вы не можете получить повторяемую комбинацию ни с помощью функции СЛЧИС и СЛУЧМЕЖДУ, ни с помощью VBA, ни какими-либо другими способами.
- В ранних версиях Excel, до Excel 2003, алгоритм случайных чисел имел относительно небольшой диапазон (менее 1 миллиона неповторяющихся последовательностей чисел) и не прошел несколько стандартных тестов на случайность для длинных последовательностей. По этой причине, если кто-то все еще работает со старой версией Excel, вам лучше не использовать функцию СЛЧИС с большими имитационными моделями.
Это довольно длинное техническое введение закончено, и мы переходим к более практическим и более полезным вещам.
Функция случайного числа — СЛЧИС.
Функция СЛЧИС в Excel — одна из двух функций, специально разработанных для случайных чисел. Она возвращает произвольное десятичное число (действительное число) от 0 до 1.
СЛЧИС – это непостоянная функция, означающая, что новое случайное число возникает каждый раз при вычислении рабочего листа. А это происходит часто — когда вы выполняете какое-либо действие, например, редактируете формулу (не обязательно СЛЧИС, даже любую другую формулу на листе), редактируете ячейку или вводите новые данные.
Функция СЛЧИС доступна во всех версиях Excel, начиная с самых ранних.
Поскольку она не имеет аргументов, вы просто записываете её в ячейку, а затем копируете куда это необходимо:
А теперь давайте составим несколько формул СЛЧИС для создания случайных чисел в соответствии с вашими условиями.
Ограничение верхней границы диапазона случайных чисел.
Чтобы создать массив от нуля до любого значения N, вы умножаете функцию СЛЧИС на N:
СЛЧИС() * N
Например, чтобы создать последовательность чисел, больше или равных 0, но меньше 50, используйте следующую формулу:
=СЛЧИС()*50
Примечание. Значение верхней границы никогда не включается в возвращаемую последовательность. Например, если вы хотите получить случайные числа от 0 до 10, включая 10, правильная формула будет =СЛЧИС()*11.
Обратите также внимание, что количество отображаемых десятичных знаков определяется форматом ячеек. В данном случае установлено 2 знака после запятой, хотя на самом деле их гораздо больше. Об округлении их мы поговорим чуть ниже.
Случайные числа в интервале «от-до».
Чтобы создать случайное число между любыми двумя указанными вами величинами, используйте следующую формулу СЛЧИС:
СЛЧИС() * ( B — A ) + A
Где A — значение нижней границы (наименьшее число), а B — значение верхней границы (наибольшее).
Например, чтобы записать на ваш лист случайные числа от 10 до 50, вы можете использовать следующую формулу:
=СЛЧИС()*(50-10)+10
Примечание. Эта формула никогда не вернет число, равное максимальному значению указанного диапазона (то есть, B).
Случайные целые числа.
Чтобы функция Excel СЛЧИС выдавала целые числа, возьмите любую из вышеупомянутых формул и оберните ее в функцию ЦЕЛОЕ().
Чтобы создать случайные целые числа от 0 до 50:
=ЦЕЛОЕ(СЛЧИС()*50)
Чтобы получить их в интервале от 10 до 50:
=ЦЕЛОЕ(СЛЧИС()*(50-10)+10)
А теперь рассмотрим более новую функцию — СЛУЧМЕЖДУ().
Функция Excel СЛУЧМЕЖДУ — как получить случайные целые числа в указанном диапазоне
СЛУЧМЕЖДУ — еще одна функция, предоставляемая Excel для случайных чисел. Она возвращает их в указанном вами диапазоне:
СЛУЧМЕЖДУ(нижнее_значение; верхнее_значение)
Как и СЛЧИС, СЛУЧМЕЖДУ в Excel – это непостоянная функция, которая возвращает новый результат каждый раз, когда ваша электронная таблица пересчитывается. А происходит это при любом изменении на листе.
Например, чтобы решить ту же задачу, которую мы рассматривали чуть выше: получить случайные целые числа от 10 до 50 (включая 10 и 50), используйте следующую формулу:
=СЛУЧМЕЖДУ(10; 50)
Функция СЛУЧМЕЖДУ в Excel может создавать как положительные, так и отрицательные числа. Например, чтобы получить список целых чисел от -10 до 10, введите следующую формулу:
=СЛУЧМЕЖДУ(-10; 10)
Функция СЛУЧМЕЖДУ доступна в Excel 2019 — 2007. В более ранних версиях вы можете использовать формулу СЛЧИС, рассмотренную нами выше.
Далее в этом руководстве вы найдете еще несколько примеров формул, демонстрирующих, как использовать функцию СЛУЧМЕЖДУ для записи случайных значений, отличных от целых.
Как создавать случайные числа с нужным количеством десятичных знаков.
Хотя функция СЛУЧМЕЖДУ в Excel была разработана для возврата целых чисел, вы можете заставить ее возвращать случайные десятичные числа с любым количеством знаков после запятой.
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
СЛУЧМЕЖДУ( нижнее значение * 10; верхнее значение * 10) / 10
Следующая формула СЛУЧМЕЖДУ() возвращает случайные десятичные числа от 1 до 50:
=СЛУЧМЕЖДУ(1*10; 50*10)/10
Однако, обратите внимание, что среди полученных результатов встречаются и значения без десятых, то есть десятичный знак может быть равен нулю.
Аналогичным образом, чтобы выдать случайные числа от 1 до 50 с двумя десятичными знаками, вы умножаете аргументы функции СЛУЧМЕЖДУ на 100, а затем также делите результат на 100:
=СЛУЧМЕЖДУ(1*100; 50*100) / 100
Как получить случайные даты в Excel
Как вы знаете, даты в Excel представляют собой числа. Поэтому рассматриваемые нами подходы вполне применимы и к ним.
Чтобы вернуть список произвольных дат в каком-то временном интервале, используйте функцию СЛУЧМЕЖДУ в сочетании с ДАТАЗНАЧ:
СЛУЧМЕЖДУ(ДАТАЗНАЧ( дата начала ), ДАТАЗНАЧ( дата окончания ))
Например, чтобы получить список дат с 1 июня 2015 года по 30 июня 2015 года включительно, введите следующую формулу в свой рабочий лист:
=СЛУЧМЕЖДУ(ДАТАЗНАЧ(«1-Июл-2021»); ДАТАЗНАЧ(«31-Авг-2021»))
В качестве альтернативы вы можете использовать функцию ДАТА:
=СЛУЧМЕЖДУ(ДАТА(2021,7,1),ДАТА(2021,8,31))
Не забудьте применить формат даты, и вы получите список случайных дат, подобный этому:
Для некоторых дополнительных опций, таких как получение списка будних или выходных дней, можно использовать расширенный генератор случайных чисел и дат .
Как вставить случайное время в Excel
Учитывая, что во внутренней системе Excel время хранится как десятичное число от 0 до 1, вы можете использовать стандартную функцию Excel СЛЧИС для вставки случайных действительных чисел, а затем просто применить формат времени к этим ячейкам:
Чтобы вернуть случайное время в соответствии с вашими критериями, требуются более сложные формулы, как показано ниже.
Случайное время в указанном интервале.
Чтобы вставить случайное время между любыми двумя указанными вами значениями времени, используйте функцию ВРЕМЯ() или ВРЕМЗНАЧ() вместе с СЛЧИС():
ВРЕМЯ( время начала ) + СЛЧИС() * (ВРЕМЯ( время начала ) — ВРЕМЯ( время окончания ))
или
ВРЕМЗНАЧ ( время начала ) + СЛЧИС () * (ВРЕМЗНАЧ ( время начала ) — ВРЕМЗНАЧ ( время окончания ))
Например, чтобы вставить время между 6:00 и 20:30, вы можете использовать любую из следующих формул:
=ВРЕМЯ(6;0;0) + СЛЧИС() * (ВРЕМЯ(20;30;0) — ВРЕМЯ(6;0;0))
=ВРЕМЗНАЧ(«6:00:00») + СЛЧИС() * (ВРЕМЗНАЧ(«20:30:00») — ВРЕМЗНАЧ(«6:00:00»))
Случайные дата и время.
Чтобы создать список случайных дат и времени, используйте комбинации функций СЛУЧМЕЖДУ и ДАТАЗНАЧ:
СЛУЧМЕЖДУ(ДАТАЗНАЧ( начальная дата) ; ДАТАЗНАЧ( конечная дата )) + СЛУЧМЕЖДУ(ВРЕМЗНАЧ( время начала ) * 10000; ВРЕМЗНАЧ( время окончания ) * 10000) / 10000
Предположим, вы хотите вставить произвольные даты между 1 июня 2021 года и 31 августа того же года со временем между 8:30 и 17:00. Следующая формула подойдет для вас:
=СЛУЧМЕЖДУ(ДАТАЗНАЧ(«1-июн-2021»); ДАТАЗНАЧ(«31-авг-2021»)) + СЛУЧМЕЖДУ(ВРЕМЗНАЧ(«8:30») * 10000; ВРЕМЗНАЧ(«17:00») * 10000) / 10000
Вы также можете указать дату и время, используя функции ДАТА и ВРЕМЯ соответственно:
=СЛУЧМЕЖДУ(ДАТА(2021;6;1); ДАТА(2021;8;31)) + СЛУЧМЕЖДУ(ВРЕМЯ(8;30;0) * 10000; ВРЕМЯ(17;0;0) * 10000) / 10000
Выбирайте тот вариант, который больше подходит для вашей задачи.
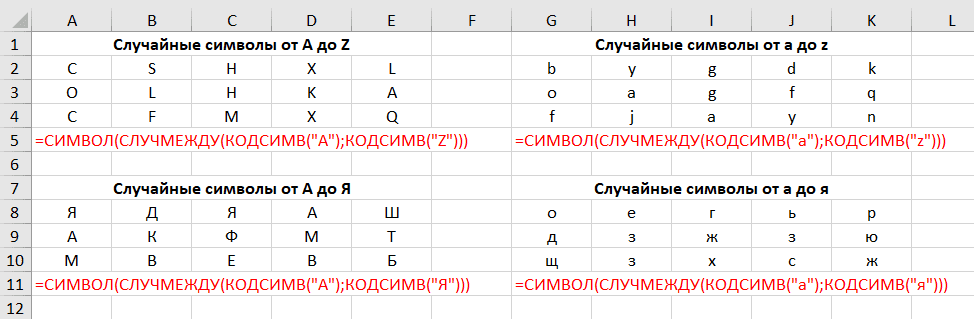
Как получить случайные буквы в Excel
Чтобы вернуть случайную букву, требуется комбинация трех разных функций:
=СИМВОЛ(СЛУЧМЕЖДУ(КОДСИМВ(«А»);КОДСИМВ(«Я»)))
Где A — первый символ, а Я — последний символ в диапазоне букв, который вы хотите использовать (в алфавитном порядке).
В приведенной выше формуле:
- КОДСИМВ() возвращает коды ANSI для указанных букв.
- СЛУЧМЕЖДУ() принимает код, возвращаемый функцией КОДСИМВ, как нижнее и верхнее значения диапазона.
- СИМВОЛ() преобразует коды ANSI, возвращаемые СЛУЧМЕЖДУ, в соответствующие буквы.
Примечание. Так как код ANSI различный для прописных и строчных букв, эта формула чувствительна к регистру.
Если кто-то помнит таблицу кодов символов ANSI, ничто не мешает вам передать коды букв непосредственно в функцию СЛУЧМЕЖДУ.
Например, чтобы получить заглавные буквы между A (код ANSI 192) и Я (код ANSI 223), вы пишете:
=СИМВОЛ(СЛУЧМЕЖДУ(192;223))
Чтобы получить строчные буквы от а (код ANSI 224) до я (код ANSI 255), используйте следующую формулу:
=СИМВОЛ(СЛУЧМЕЖДУ(224;255))
Коды символов:
- 192-223 — прописные буквы А-Я
- 224-255 — строчные буквы а-я
Чтобы вставить случайный специальный символ, например, ! «# $% & ‘() * +, -. /, используйте функцию СЛУЧМЕЖДУ с первым параметром, установленным на 33 (код ANSI для «!’), и вторым параметром 47 (код ANSI для «/»).
=СИМВОЛ(СЛУЧМЕЖДУ(33;47))
Создание текстовых строк и паролей в Excel
Чтобы создать произвольную текстовую строку в Excel, вам просто нужно объединить несколько функций СИМВОЛ и СЛУЧМЕЖДУ.
Например, чтобы получить список паролей, состоящих из 4 символов, вы можете использовать формулу, подобную этой:
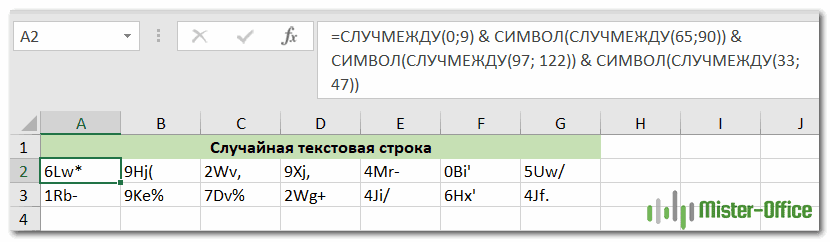
=СЛУЧМЕЖДУ(0;9) & СИМВОЛ(СЛУЧМЕЖДУ(65;90)) & СИМВОЛ(СЛУЧМЕЖДУ(97; 122)) & СИМВОЛ(СЛУЧМЕЖДУ(33;47))
Чтобы сделать запись более компактной, я ввел коды ANSI непосредственно в формулу. Четыре функции возвращают следующие случайные значения:
- СЛУЧМЕЖДУ(0;9) — возвращает числа от 0 до 9.
- СИМВОЛ(СЛУЧМЕЖДУ(65;90)) —прописные буквы от A до Z.
- СИМВОЛ(СЛУЧМЕЖДУ(97; 122)) — получаем строчные буквы от a до z.
- СИМВОЛ(СЛУЧМЕЖДУ(33;47)) — добавляем специальные символы.
Текстовые строки, полученные с помощью приведенной выше формулы, будут иметь вид « 4Np# » или « 2Yu& ».
Внимание! Если вы используете аналогичную формулу для создания случайных паролей, они не будут слишком надежными. Конечно, вы можете создавать более длинные текстовые строки, связывая больше функций. Однако невозможно изменить порядок следования, т.е. первая по счёту функция всегда возвращает цифру, вторая функция возвращает заглавную букву и так далее.
Если вы ищете расширенный генератор случайных паролей в Excel, способный создавать текстовые строки любой длины и шаблона, вы можете проверить возможности Advanced Random Generator для тестовых строк.
Кроме того, имейте в виду, что текстовые строки, созданные с помощью приведенной выше формулы, будут изменяться каждый раз, когда ваш рабочий лист пересчитывается. А это автоматически происходит после ввода либо корректировки любого значения либо формулы на листе.
Чтобы гарантировать, что ваши строки или пароли остаются неизменными после их создания, вам нужно будет заблокировать функцию СЛУЧМЕЖДУ от обновления значений, что подводит нас непосредственно к следующему разделу.
Как предотвратить постоянный пересчет формул СЛЧИС и СЛУЧМЕЖДУ.
Если вы хотите получить постоянный набор чисел, дат или текстовых строк, который не будет меняться каждый раз при пересчете таблицы, используйте один из следующих методов:
- Чтобы функции СЛЧИС или СЛУЧМЕЖДУ не пересчитывались в одной определённой ячейке, выберите её, переключитесь на строку формул и нажмите клавишу
F9, чтобы заменить формулу ее значением. - Чтобы предотвратить пересчет, используйте инструмент Специальная вставка. Выделите все ячейки с формулой, нажмите
Ctrl + C, чтобы скопировать их в буфер обмена. Затем щелкните правой кнопкой мыши выбранный диапазон и выберите Специальная вставка > Значения. Или же можете нажатьShift + F10 а потом V, что также позволит вставить ранее скопированные значения вместо формул. - Можно использовать специальный инструмент преобразования формул в значения, который является составной частью надстройки Ultimate Suite.
Как создать уникальные случайные числа в Excel
Ни одна из случайных функций Excel не умеет создавать уникальные случайные значения. Совпадения всегда возможны, особенно если вы получаете целые числа, используя округление. Если вы хотите создать список без дубликатов , выполните следующие действия:
- Используйте функцию СЛЧИС или СЛУЧМЕЖДУ для создания списка чисел. Создайте больше значений, чем вам действительно нужно, потому что некоторые из них будут дублироваться и будут удалены позже.
- Преобразуйте формулы в значения, как описано выше.
- Удалите повторяющиеся значения с помощью встроенного инструмента Excel (см. Как удалить дубликаты в Excel) или специального инструмента для удаления дубликатов в Excel.
Также вы можете воспользоваться специальным генератором случайных значений в Excel, в котором есть опция получения случайных цифровых и текстовых значений. Более подробно читайте о нем по этой ссылке.
 Расширенный генератор случайных чисел для Excel — Теперь, когда вы знаете, как использовать случайные функции в Excel, позвольте мне продемонстрировать вам более быстрый, простой и не требующий формул способ создания списка случайных чисел, дат или текстовых строк…
Расширенный генератор случайных чисел для Excel — Теперь, когда вы знаете, как использовать случайные функции в Excel, позвольте мне продемонстрировать вам более быстрый, простой и не требующий формул способ создания списка случайных чисел, дат или текстовых строк…
Время от времени у пользователей Excel появляется необходимость генерировать случайные числа для того, чтобы использовать их в формулах или же для других целей. Для этого в программе предусмотрен целый арсенал возможностей. Есть возможность сгенерировать случайные числа самыми различными способами. Мы же приведем только те, которые показали себя на практике самым лучшим образом.
Содержание
- Функция случайного числа в Excel
- Выборка случайных чисел с помощью СЛЧИС
- Функция СЛУЧМЕЖДУ
- Как сделать генератор случайных чисел в Excel
- Генератор случайных чисел нормального распределения
Функция случайного числа в Excel
Предположим, у нас есть набор данных, который должен содержать элементы, которые абсолютно не связаны друг с другом между собой. В идеале, чтобы они были сформированы по закону нормального распределения. Для этого нужно использовать функцию случайного числа. Есть две функции, с помощью которых можно достичь поставленной задачи: СЛЧИСЛ и СЛУЧМЕЖДУ. Давайте детально рассмотрим, как их можно использовать на практике.
Выборка случайных чисел с помощью СЛЧИС
Эта функция не предусматривает наличия каких-либо аргументов. Но несмотря на это она дает возможность настраивать диапазон значений, в рамках которых она должна генерировать случайное число. Например, чтобы получить его в рамках от единицы до пяти, нам необходимо использовать такую формулу: =СЛЧИС()*(5-1)+1.
Если эту функцию распределить на другие ячейки с помощью маркера автозаполнения, то мы увидим, что распределение осуществляется равномерно.
В ходе каждого расчета случайного значения, если в любом месте листа изменить какую-угодно ячейку, числа будут автоматически сгенерированы заново. Поэтому сохраняться эта информация не будет. Чтобы сделать так, чтобы они остались, необходимо вручную написать это значение в числовом формате или же воспользовавшись этой инструкцией.
- Делаем клик по ячейке, содержащей случайное число.
- Делаем клик по строке формул, после чего выделяем ее.
- Нажимаем на кнопку F9 на клавиатуре.
- Заканчиваем эту последовательность действий нажатием клавиши Enter.
Проверим то, насколько равномерно распределены случайные числа. Для этого нам нужно воспользоваться гистограммой распределения. Чтобы ее сделать, выполняем следующие шаги:
- Создадим колонку с карманами, то есть, теми ячейками, в которых мы будем держать наши диапазоны. Первый такой – 0-0,1. Формируем следующие с помощью такой формулы: =C2+$C$2.
- После этого нам надо определить, насколько часто встречаются случайные числа, относящиеся к каждому конкретному диапазону. Для этого мы можем использовать формулу массива {=ЧАСТОТА(A2:A201;C2:C11)}.
- Далее, с использованием знака «сцепления» делаем наши следующие диапазоны. Формула простая =»[0,0-«&C2&»]».
- Теперь мы делаем диаграмму, описывающую то, как распределяются эти 200 значений.
В описанном нами примере частота соответствует оси Y, а «карманы» – оси X.
Функция СЛУЧМЕЖДУ
Если говорить про функцию СЛУЧМЕЖДУ, то согласно ее синтаксису, у нее есть два аргумента: нижняя граница и верхняя граница. Важно, чтобы величина первого параметра была меньше, чем второго. Допускается, что границами могут быть целые числа, а дробные формулой не учитываются. Давайте посмотрим, как эта функция работает, на этом скриншоте.
Видим, что точность можно регулировать с помощью деления. Можно получать случайные числа с любой разрядностью после запятой.
Видим, что эта функция гораздо более органична и понятна для обычного человека, чем предыдущая. Поэтому в большинстве случаев можно использовать только ее.
Как сделать генератор случайных чисел в Excel
А теперь давайте сделаем небольшой генератор чисел, который будет получать значения, основываясь на определенном диапазоне данных. Для этого применяется формула =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
Создадим генератор случайных чисел, которые будут создаваться от нуля до 10. С помощью этой формулы мы можем регулировать шаг, с которым они будут создаваться. Например, можно создать генератор, который будет создавать только значения, заканчивающиеся на ноль.
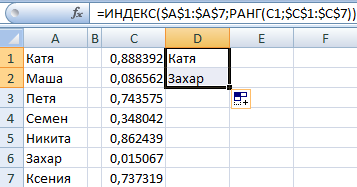
Или же такой вариант. Давайте предположим, что нам надо выделить два случайных значения из перечня текстовых ячеек.
А чтобы выбрать два случайных числа, необходимо применить функцию ИНДЕКС.
Формула, с помощью которой мы это сделали, приведена на скриншоте выше. =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))) – с помощью этой формулы мы можем создать генератор для одного текстового значения. Видим, что мы спрятали вспомогательную колонку. Так можете сделать и вы.
Генератор случайных чисел нормального распределения
Проблема функций СЛЧИС и СЛУЧМЕЖДУ в том, что они формируют набор чисел, которые находятся очень далеко от целевого показателя. Вероятность того, что появится число, близкое к нижней границе, середине или верхней границе, одинаковая.
Нормальное распределение в статистике – это такой набор данных, в которых по мере большей отдаленности от центра на графике частота, с которой встречается значение в определенном коридоре, уменьшается. То есть, большая часть значений скапливается вокруг центрального. Давайте с помощью функции СЛУЧМЕЖДУ попробуем создать набор чисел, распределение которых относится к разряду нормального.
Итак, у нас есть товар, производство которого стоит 100 рублей. Следовательно, числа должны генерироваться приблизительно такие же. В этом случае средним значением должно быть 100 рублей. Создадим массив данных, и создадим график, в котором стандартное отклонение составит 1,5 рубля, а распределение значений – нормальное.
Для этого нужно использовать функцию =НОРМОБР(СЛЧИС();100;1,5). Далее программа автоматически меняет вероятности, исходя из того, что самый высокий шанс имеют числа, приближенные к сотне.
Теперь нам осталось лишь построить график стандартным способом, выбрав в качестве диапазона набор сгенерированных значений. В результате, мы видим, что распределение действительно является нормальным.
Вот так все просто. Успехов.
Оцените качество статьи. Нам важно ваше мнение:
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
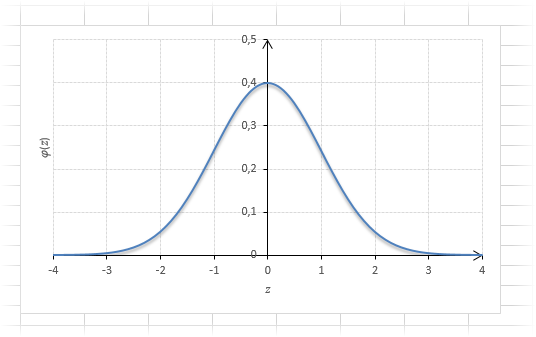
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
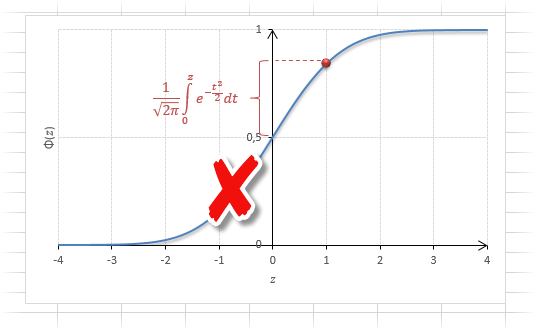
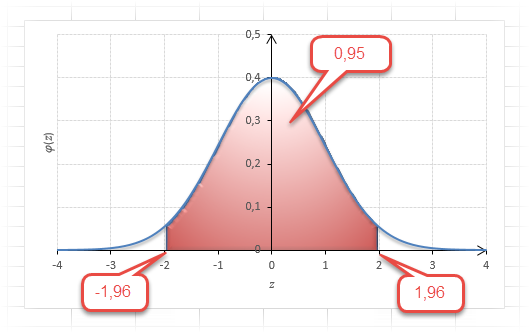
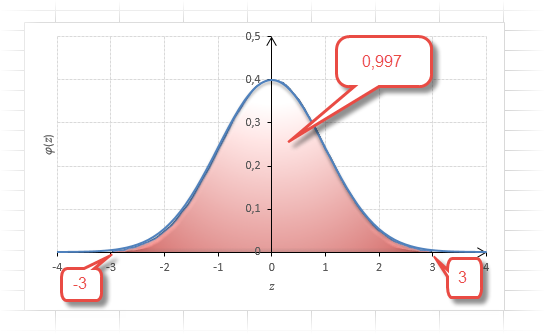
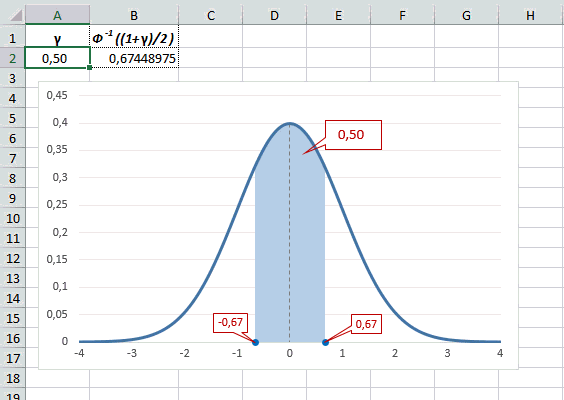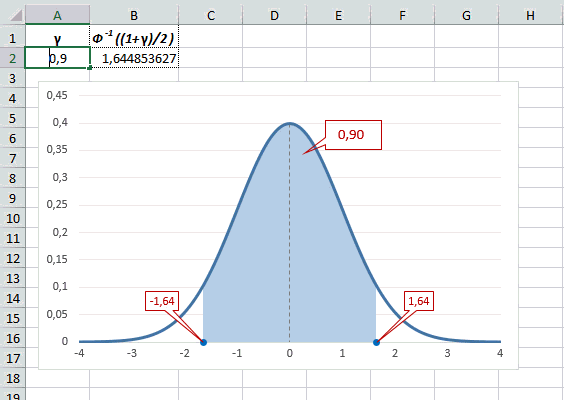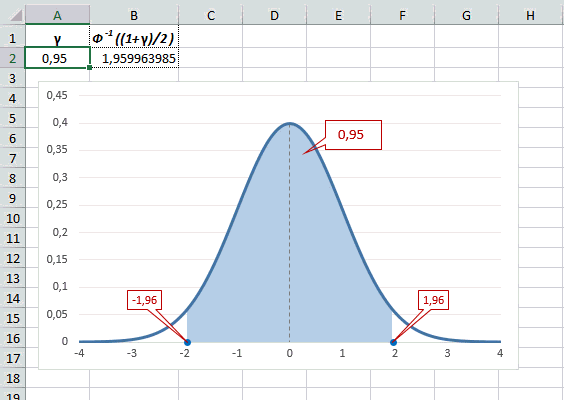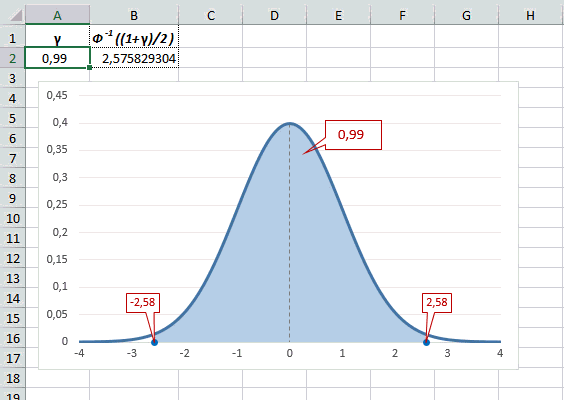
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
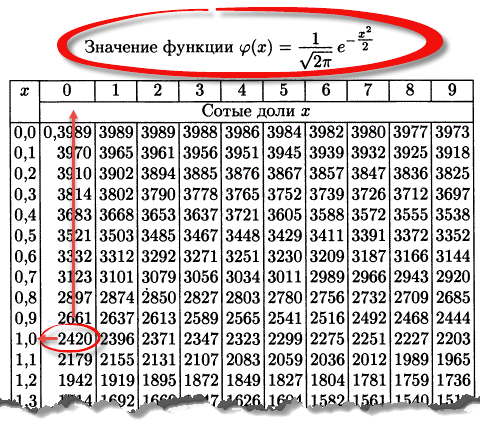
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
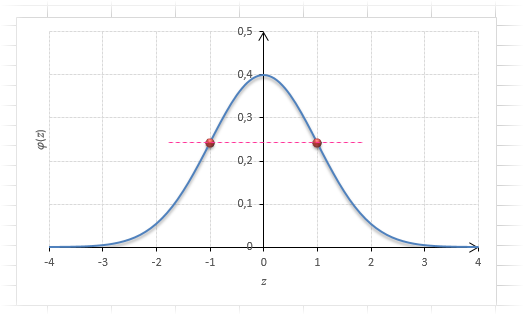
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
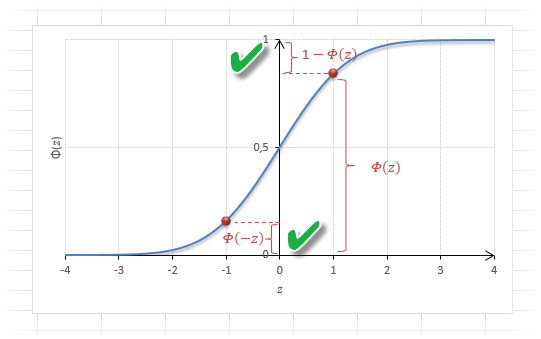
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
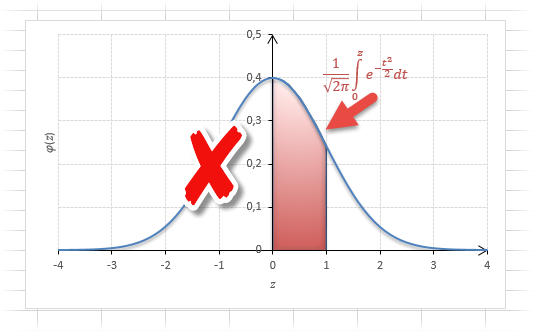
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
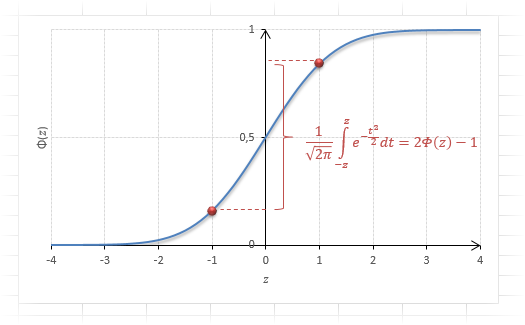
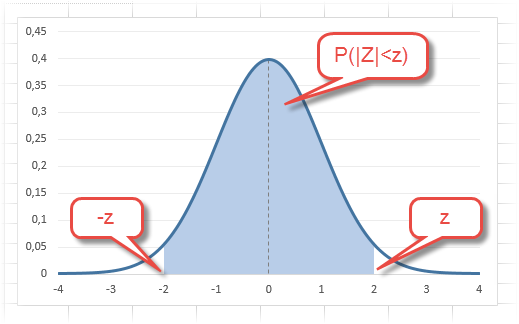
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
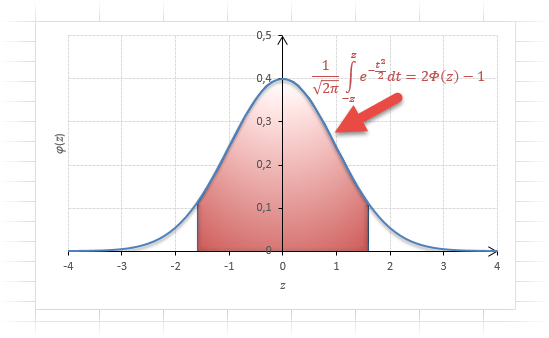
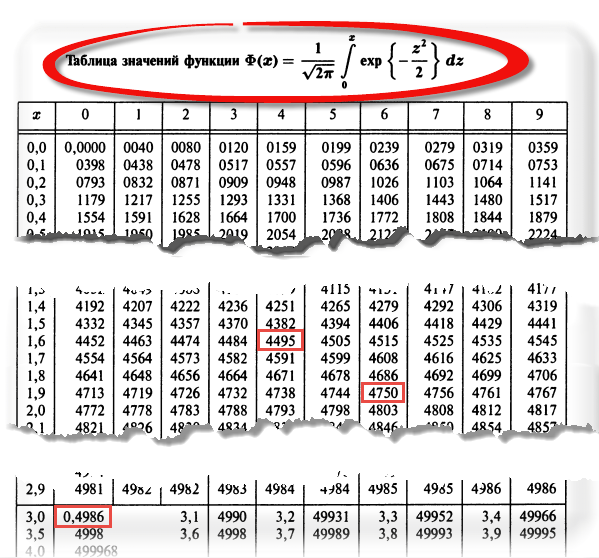
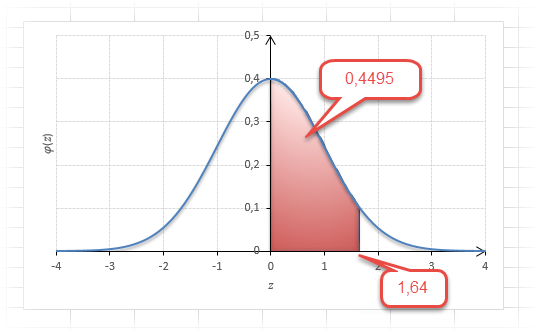
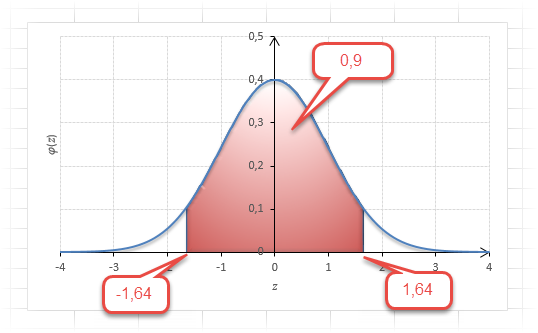
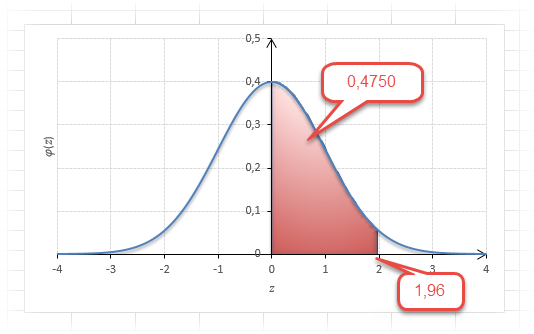
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях:
Лотерея — это не охота за удачей,
это охота за неудачниками.
С завидной регулярностью (а в последнее время — всё чаще) мне пишут люди с просьбами помочь в различных вычислениях, связанных с лотереями. Кто-то хочет реализовать в Excel свой секретный алгоритм подбора выигрышных чисел, кто-то — найти закономерности в выпавших номерах прошедших тиражей, кто-то — подловить организаторов лотереи на нечестной игре.
В этой статье мне хотелось бы ответить на часть этих вопросов. Благо, в Excel для решения таких задач достаточно инструментов, многие из которых, кстати, могут пригодиться и в более прозаических рабочих ситуациях.
Задача 1. Вероятность выигрыша
Возьмем для примера классическую лотерею «Столото 6 из 45». По правилам суперприз (10 млн. рублей или больше, если накопился остаток призового фонда с прошлых тиражей) получают только те, кто угадал все 6 чисел из 45. Если вы угадали 5, то получите 150 тыс. рублей, если 4 — 1500 р., если 3 числа из 6, то 150 р., если 2 числа — вернете 50 р., потраченных на билет. Угадаете только одно или ни одного — получите только эндорфины от процесса игры.
Математическую вероятность выигрыша можно легко рассчитать с помощью стандартной функции ЧИСЛКОМБ (COMBIN), которая имеется в Microsoft Excel на такой случай. Эта функция вычисляет количество комбинаций N чисел из M. Так для нашей лотереи «6 из 45» это будет:
=ЧИСЛКОМБ(45;6)
… что равно 8 145 060 — общее число всех возможных комбинаций в этой лотерее.
Если же хочется рассчитать вероятность для частичного выигрыша (2-5 чисел из 6), то придётся сначала вычислить количество таких вариантов, которое равно произведению числа комбинаций угаданных чисел из 6 на количество не угаданных чисел из оставшихся (45-6)=39 чисел. Затем общее количество всех возможных комбинаций (8 145 060) мы делим на полученное количество выигрышей по каждому варианту — и получим вероятности выигрыша для каждого случая:
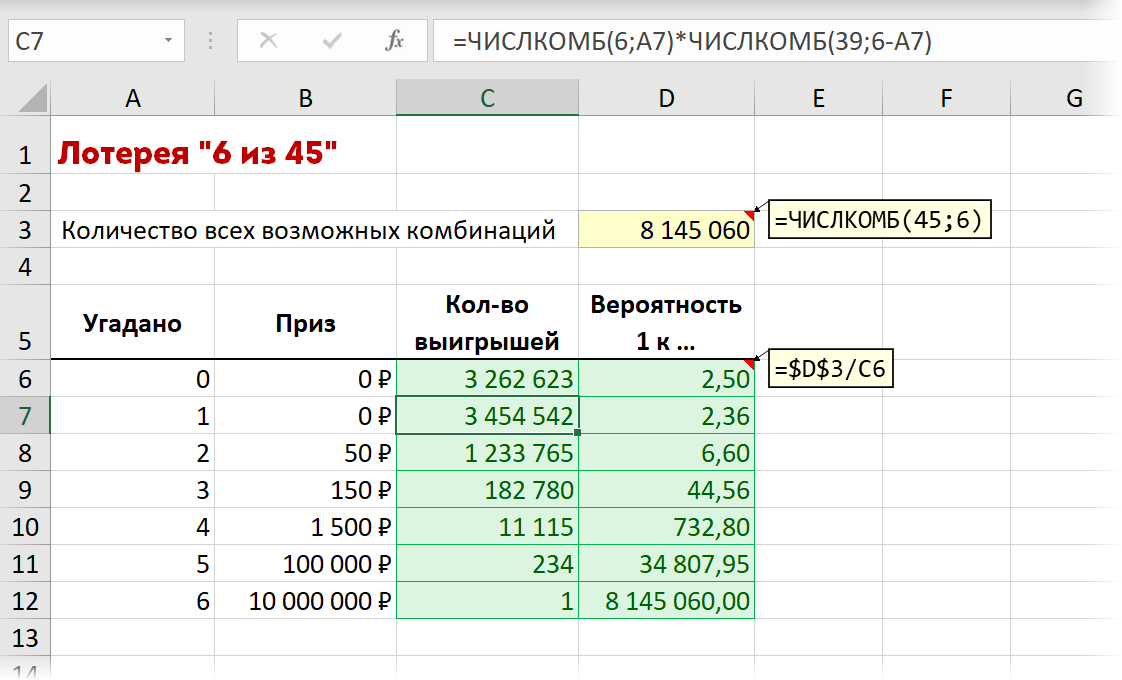
К слову, вероятность, например, погибнуть в авиакатастрофе в России оценивается примерно как 1 к миллиону. А вероятность выиграть в казино в рулетку, поставив всё на один номер — 1 к 37.
Если всё вышеперечисленное вас не остановило и вы по-прежнему готовы играть дальше — продолжаем.
Задача 2. Частота выпадения каждого числа
Для начала давайте определим с какой частотой выпадают те или иные числа. В идеальной лотерее, если брать для анализа достаточно большой временной интервал, у всех шаров должна быть одинаковая вероятность попадания в победную выборку. В реальности же особенности конструкции лототрона и вес-форма шаров могут вносить искажения в эту картину и для каких-то шаров вероятность выпадения вполне может оказаться выше/ниже, чем для других. Давайте проверим эту гипотезу на практике.
Возьмём для примера данные по всем прошедшим в 2020-21 году тиражам лотереи 6 из 45 с сайта их организатора Столото, оформленные в виде вот такой удобной для анализа «умной» таблицы с именем таблАрхивТиражей. Розыгрыши проходят два раза в день (в 11 утра и в 11 вечера), т.е. в этой таблице у нас полторы тысячи тиражей-строк — вполне достаточная для начала выборка для анализа:
Для подсчёта частоты выпадения каждого числа используем функцию СЧЁТЕСЛИ (COUNTIF) и дополнительно вложим в неё функцию ТЕКСТ (TEXT), чтобы добавить к одноразрядным числам начальные нули и звёздочки перед и после, чтобы СЧЁТЕСЛИ искала вхождение числа в любом месте комбинации в столбце В. Также для пущей наглядности построим диаграмму по результатам и отсортируем частоты по убыванию:
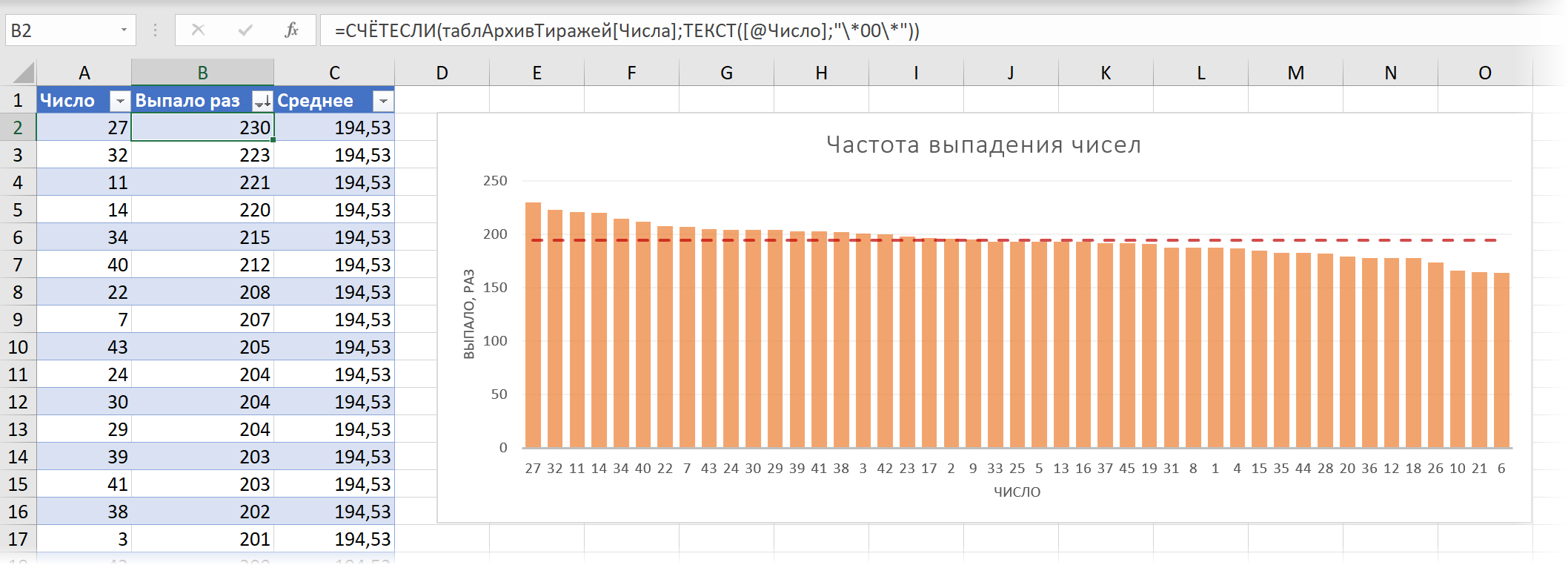
В среднем любой шар должен выпадать 1459 тиражей * 6 шаров / 45 номеров = 194,53 раз (это как раз то, что называется в статистике математическим ожиданием), но хорошо видно, что некоторые числа (27, 32, 11…) выпадали заметно чаще (+18%), а некоторые (10, 21, 6…) наоборот заметно реже (-15%), чем основная масса. Соответственно, можно попробовать использовать эту информацию для стратегии выигрыша, т.е. либо ставить на те шары, что выпадают чаще, либо наоборот — делать ставку на редко выпадающие шары в надежде, что они должны нагнать отставание.
Задача 3. Какие числа давно не выпадали?
Ещё одна стратегия базируется на идее, что при достаточно большом количестве тиражей рано или поздно должно выпасть каждое число из всех имеющихся от 1 до 45. Так что если какие-то числа давно не появлялись среди выигравших («холодные шары»), то логично попробовать сделать на них ставку в будущем.
Можно легко найти все давно не выпадавшие номера, если отсортировать наш архив тиражей за 2020-21 год по убыванию даты и использовать функцию ПОИСКПОЗ (MATCH). Она будет сверху-вниз (т.е. от новых к старым тиражам) искать каждое число и выдавать порядковый номер тиража (считая от конца года к началу), где последний раз это число выпало:
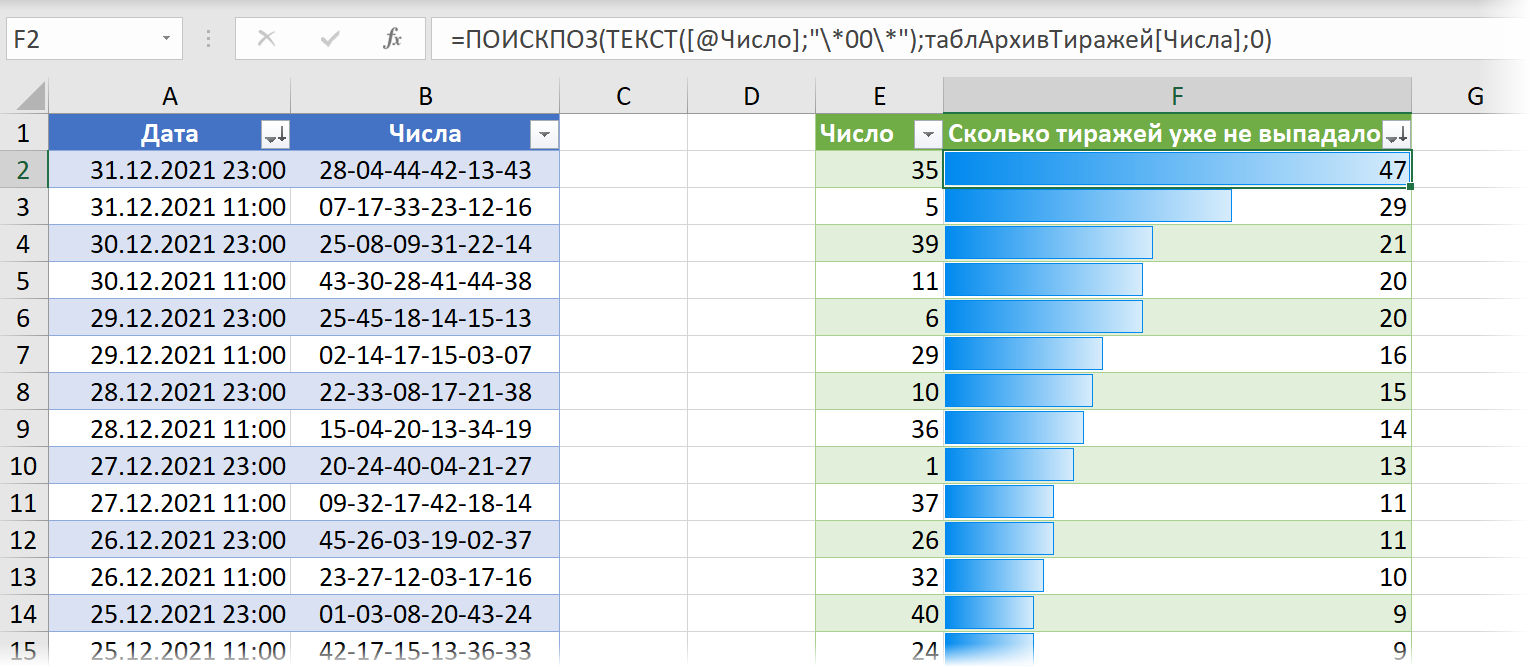
Задача 4. Генератор случайных чисел
Ещё одна стратегия игры основана на том, чтобы исключить психологический фактор при угадывании номеров. Когда игрок выбирает числа, делая свою ставку, то подсознательно делает это не совсем рационально. По статистике, например, числа от 1 до 31 выбирают на 70 % чаще, чем остальные (любимые даты), реже выбирают 13 (чертова дюжина), чаще выбирают числа содержащие «счастливую» семерку и т.д. Но играем мы против машины (лототрона), для которой все числа одинаковы, так что имеет смысл выбирать их с такой же математической беспристрастностью, чтобы уравнять наши шансы. Для этого нам потребуется создать в Excel генератор случайных и — что особенно важно — неповторяющихся чисел:
Для этого:
- Создадим «умную» таблицу с именем таблГенератор, где в первом столбце будут наши числа от 1 до 45.
- Во втором столбце введём вес для каждого числа (он потребуется нам чуть позднее). Если все числа для нас одинаково ценны и мы хотим выбирать их с равной вероятностью, то вес везде можно поставить равным 1.
- В третьем столбце используем функцию СЛЧИС (RAND), которая в Excel генерирует случайное дробное число от 0 до 1, добавив к нему вес из предыдущего столбца. Таким образом каждый раз при пересчёте листа (нажатии на клавишу F9) будет генерироваться новый набор из 45 случайных чисел с учётом веса для каждого из них.
- Добавим четвертый столбец, где с помощью функции РАНГ (RANK) вычислим ранг (позицию в топе) для каждого из чисел.
Теперь останется сделать выборку первых шести по рангу 6 чисел с помощью функции ПОИСКПОЗ (MATCH):
При нажатии на клавишу F9 формулы на листе Excel будут пересчитываться и мы будем каждый раз получать новый набор из 6 чисел в зеленых ячейках. Причём числа, для которых был задан в столбце B больший вес, будут получать пропорционально больший ранг и, таким образом, чаще оказываться в результатах нашей случайной выборки. Если же вес для всех чисел задать одинаковым, то все они будут выбираться с одинаковой вероятностью. Таким образом мы получаем справедливый и беспристрастный генератор случайных чисел 6 из 45, но с возможностью внести корректировки в случайность распределения при необходимости.
Если же мы решим играть в каждом тираже не одним, а, например, двумя билетами сразу, в каждом из которых будем выбирать неповторяющиеся числа, то можно просто добавить к зелёному диапазону дополнительные строки снизу, прибавив к рангу 6, 12, 18 и т.д. соответственно:
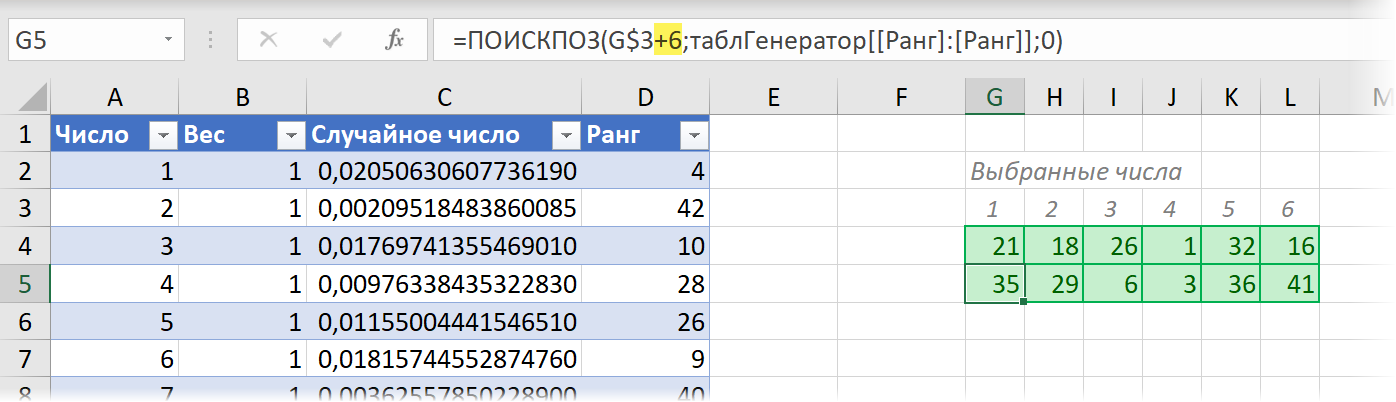
Задача 5. Симулятор лотереи в Excel
В качестве апофеоза всей этой темы давайте создадим в Excel полноценный симулятор лотереи, на котором можно будет опробовать любые стратегии и сравнить результаты (в теории оптимизации что-то похожее ещё называют методом Монте-Карло, но у нас будет попроще).
Чтобы все было максимально приближено к реальности, представим на минуту, что сейчас 1 января 2022 года и впереди у нас тиражи этого года, в которых мы планируем играть. Реальные выпавшие числа я занёс в таблицу таблТиражи2022, отделив дополнительно выпавшие числа друг от друга в отдельные столбцы для удобства последующих вычислений:
На отдельном листе Игра создадим заготовку для моделирования в виде «умной» таблицы с именем таблИгра следующего вида:
Здесь:
- В желтых ячейках сверху будем задавать для макроса количество тиражей 2022 года, в которых мы хотим участвовать (1-82) и количество билетов, которыми мы играем в каждом тираже.
- Данные для первых 11 столбцов (A-J) макрос будет копировать с листа тиражей 2022 года.
- Данные для следующих шести столбцов (K-P) макрос будет брать с листа Генератор, где мы реализовали генератор случайных чисел (см. задачу 4 выше).
- В столбце Q мы считаем количество совпадений выпавших чисел и сгенерированных с помощью функции СУММПРОИЗВ (SUMPRODUCT).
- В столбце R вычисляем финансовый результат (если не выиграли, то минус 50 рублей за билет, если выиграли, то приз — 50 р. за билет)
- В последнем столбце S считаем общий результат всей игры нарастающим итогом, чтобы видеть динамику в процессе.
И чтобы оживить всю эту конструкцию нам потребуется небольшой макрос. На вкладке Разработчик (Developer) выберем команду Visual Basic или воспользуемся сочетанием клавиш Alt+F11. Затем добавим новый пустой модуль через меню Insert — Module и введем туда следующий код:
Sub Lottery()
Dim iGames As Integer, iTickets As Integer, i As Long, t As Integer, b As Integer
'объявляем переменные для ссылки на листы
Set wsGame = Worksheets("Игра")
Set wsNumbers = Worksheets("Генератор")
Set wsArchive = Worksheets("Тиражи 2022")
iGames = wsGame.Range("C1") 'количество тиражей
iTickets = wsGame.Range("C2") 'количество билетов в каждом тираже
i = 5 'первая строка в таблице таблИгра
wsGame.Rows("6:1048576").Delete 'очищаем старые данные
For t = 1 To iGames
For b = 1 To iTickets
'копируем выигравшие номера с листа Тиражи 2022 и вставляем на лист Игра
wsArchive.Cells(t + 1, 1).Resize(1, 10).Copy Destination:=wsGame.Cells(i, 1)
'копируем и вставляем специальной вставкой значений сгенерированные номера с листа Генератор
wsNumbers.Range("G4:L4").Copy
wsGame.Cells(i, 11).PasteSpecial Paste:=xlPasteValues
i = i + 1
Next b
Next t
End Sub
Останется ввести желаемые исходные параметры в жёлтые ячейки и запустить макрос через Разработчик — Макросы (Developer — Macros) или сочетанием клавиш Alt+F8.
Для наглядности можно ещё построить диаграмму по последнему столбцу с нарастающим итогом, отражающую изменение денежного баланса в процессе игры:
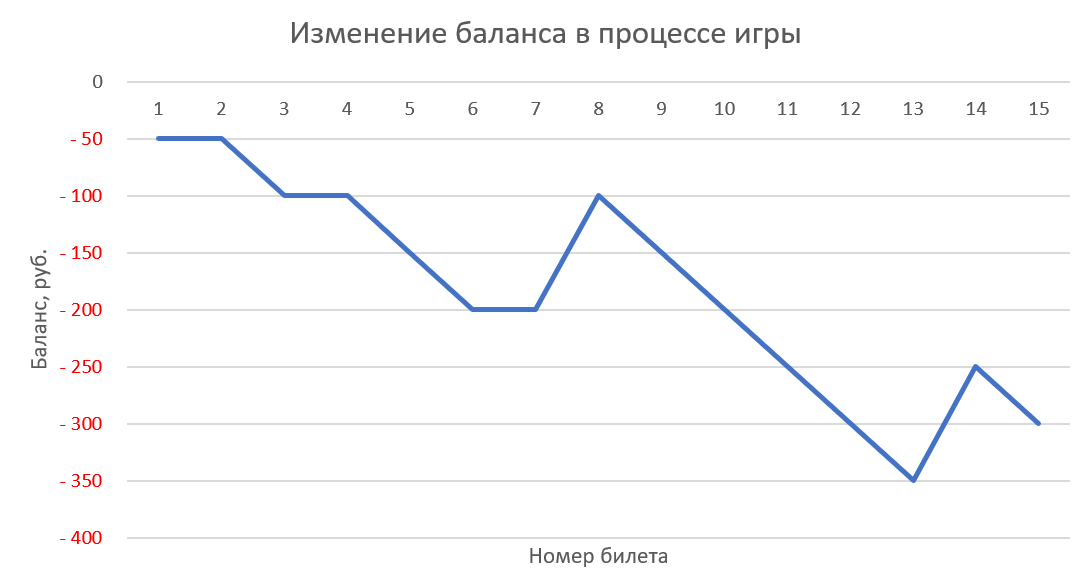
Сравнение разных стратегий
Теперь, используя созданный симулятор, можно протестировать на реальных тиражах 2022 года любую стратегию игры и посмотреть на результаты, которые бы она принесла. Если играть 1 билетом в каждом тираже, то общая картина «слива» выглядит примерно так:
Здесь:
- Генератор — игра, где в каждом тираже мы выбираем случайные числа, созданные нашим генератором (с одинаковым весом).
- Любимчики — игра, где в каждом тираже мы используем одни и те же числа — те, что чаще всего выпадали в тиражах за последние два года (27, 32, 11, 14, 34, 40).
- Аутсайдеры — то же самое, но используем самые редко выпадающие числа (12, 18, 26, 10, 21, 6).
- Холодные — в всех тиражах используем числа, которые давно не выпадали (35, 5, 39, 11, 6, 29).
Как видите, разницы большой нет, но генератор случайных чисел ведёт себя чуть лучше остальных «стратегий».
Можно также попробовать играть большим количеством билетов в каждом тираже, чтобы перекрыть большее количество вариантов (иногда для этого несколько игроков объединяются в группу).
Игра в каждом тираже одним билетом со случайно сгенерированными числами (с одинаковым весом):
Игра 10 билетами в каждом тираже со случайно сгенерированными числами (с одинаковым весом):
Игра 100 билетами в каждом тираже со случайными числами (с одинаковым весом):
Комментарии, как говорится, излишни — слив депозита неизбежен во всех случаях 
Интервальный вариационный ряд и его характеристики
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Здесь k — число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $ F=x_-x_ $
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $ k=1+lfloorlog_2 Nrfloor $ или, через десятичный логарифм: $ k=1+lfloor 3,322cdotlg Nrfloor $
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_).
Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Частота интервалов – число, показывающее сколько раз значения, относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти числа на общее количество наблюдений (n), находят относительную частоту (частость) попадания случайной величины X в заданные интервалы.
Эмпирические распределения — Мегаобучалка
Существует также теоретическая функция распределения (функция распределения генеральной совокупности). Ее отличие от выборочной функции распределения состоит в определении объективной возможности или вероятности события X
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Все несколько проще Данные- Анализ данных- Генерация случайных чисел Распределение Нормальное Данные- Анализ данных- Гистограмма- Галка на вывод графика Карманы можно даже не задавать. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:
8. Постройте диаграмму относительных и накопленных частот. Щелчком указателя мыши по кнопке Анализ данных вкладки Данные вызовите Пакет анализа, выберите в нем опцию Гистограмма и постройте график абсолютных и накопленных частот. После редактирования диаграмма будет иметь такой вид, как на рис. 2.
Как сменить строки и столбцы в гистограмме
Для того чтобы сменить порядок строк и столбцов в гистограмме проделайте следующие шаги:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Построить эмпирическое распределение веса студентов в килограммах для следующей выборки 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
8. Постройте диаграмму относительных и накопленных частот. Щелчком указателя мыши по кнопке Анализ данных вкладки Данные вызовите Пакет анализа, выберите в нем опцию Гистограмма и постройте график абсолютных и накопленных частот. После редактирования диаграмма будет иметь такой вид, как на рис. 2.
Эмпирическая функция распределения
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
- если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так: =(МАКС( Исходные_данные )-МИН( Исходные_данные ))/7 где Исходные_данные – именованный диапазон , содержащий наши данные.
Как построить график
Построение графика эмпирической функции распределения возможно после вычисления ее значений на всей числовой оси. Для рассмотренного примера схематическое изображение будет выглядеть так:
Эмпирическая функция распределения
Гистограмма распределения – это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции ЧАСТОТА() и диаграммы.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Характеристики нормального распределения
- Значения рассматриваемой функции F * (x) располагаются на отрезке [0; 1].
- Функция имеет неубывающий характер.
- При минимальной варианте x1 верно равенство F * (x)=0 при условии, что х1. При максимальной варианте хkверно равенство F * (x)=1 при условии х>xk.
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка ).
Распределение вероятностей – одно из центральных понятий теории
вероятности и математической статистики. Определение распределения вероятности
равносильно заданию вероятностей всех СВ, описывающих некоторое случайное
событие. Распределение вероятностей некоторой СВ, возможные значения которой x1, x2, … xn образуют
выборку, задается указанием этих значений и соответствующих им вероятностей p1, p2,… pn. (pn должны быть
положительны и в сумме давать единицу).
В данной лабораторной работе будут рассмотрены и построены с помощью MS Excel наиболее
распространенные распределения вероятности: биномиальное и нормальное.
1 Биномиальное распределение
Представляет собой распределение вероятностей числа наступлений
некоторого события («удачи») в n повторных
независимых испытаниях, если при каждом испытании вероятность наступления этого
события равна p. При этом
распределении разброс вариант (есть или нет события) является следствием
влияния ряда независимых и случайных факторов.
Примером практического использования биномиального распределения
может являться контроль качества партии фармакологического препарата. Здесь
требуется подсчитать число изделий (упаковок), не соответствующих требованиям.
Все причины, влияющие на качество препарата, принимаются одинаково вероятными и
не зависящими друг от друга. Сплошная проверка качества в этой ситуации не
возможна, поскольку изделие, прошедшее испытание, не подлежит дальнейшему
использованию. Поэтому для контроля из партии наудачу выбирают определенное
количество образцов изделий (n). Эти образцы всестороннее
проверяют и регистрируют число бракованных изделий (k). Теоретически число
бракованных изделий может быть любым, от 0 до n.
В Excel функция БИНОМРАСП
применяется для вычисления вероятности в задачах с фиксированным числом тестов
или испытаний, когда результатом любого испытания может быть только успех или
неудача.
Функция использует следующие
параметры:
БИНОМРАСП (число_успехов;
число_испытаний; вероятностъ_успеха; интегральная), где
число_успехов — это количество успешных
испытаний;
число_испытаний — это число независимых
испытаний (число успехов и число испытаний должны быть целыми числами);
вероятность_ успеха — это вероятность успеха
каждого испытания;
интегральный — это логическое значение,
определяющее форму функции.
Если данный параметр имеет
значение ИСТИНА (=1), то считается интегральная функция распределения
(вероятность того, что число успешных испытаний не менее значения число_
успехов);
если этот параметр имеет
значение ЛОЖЬ (=0), то вычисляется значение функции плотности
распределения (вероятность того, что число успешных испытаний в точности равно
значению аргумента число_ успехов).
Пример 1. Какова вероятность того,
что трое из четырех новорожденных будут мальчиками?
Решение:
1. Устанавливаем табличный курсор в свободную
ячейку, например в А1. Здесь должно оказаться значение искомой
вероятности.
2. Для получения значения вероятности
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка
функции (fx).
3. В появившемся диалоговом окне Мастер
функций — шаг 1 из 2 слева в поле Категория указаны виды функций.
Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.
Появляется диалоговое окно
функции. В поле Число_s вводим с клавиатуры
количество успешных испытаний (3). В поле Испытания вводим с клавиатуры
общее количество испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха в отдельном испытании (0,5). В поле Интегральный
вводим с клавиатуры вид функции распределения — интегральная или весовая (0).
Нажимаем на кнопку ОК.
В ячейке А1 появляется
искомое значение вероятности р = 0,25. Ровно 3 мальчика из 4
новорожденных могут появиться с вероятностью 0,25.
Если изменить формулировку
условия задачи и выяснить вероятность того, что появится не более трех
мальчиков, то в этом случае в рабочее поле Интегральный вводим 1 (вид
функции распределения интегральный). Вероятность этого события будет равна
0,9375.
Задания для самостоятельной работы
1. Какова вероятность того, что восемь из десяти студентов,
сдающих зачет, получат «незачет». (0,04)
2.
Нормальное распределение
Нормальное распределение — это совокупность объектов, в которой крайние значения
некоторого признака — наименьшее и наибольшее — появляются редко; чем ближе значение признака к математическому ожиданию,
тем чаще оно встречается. Например, распределение студентов по их весу приближается
к нормальному распределению. Это распределение имеет очень широкий круг приложений в
статистике, включая проверку гипотез.
Диаграмма нормального
распределения симметрична относительно точки а (математического
ожидания). Медиана нормального распределения равна тоже а. При этом в
точке а функция f(x) достигает своего максимума, который равен
.
В Excel для вычисления значений
нормального распределения используются функция НОРМРАСП, которая
вычисляет значения вероятности нормальной функции распределения для указанного
среднего и стандартного отклонения.
Функция имеет параметры:
НОРМРАСП (х; среднее;
стандартное_откл; интегральная), где:
х — значения выборки, для
которых строится распределение;
среднее — среднее арифметическое
выборки;
стандартное_откл — стандартное отклонение
распределения;
интегральный — логическое значение,
определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то
функция НОРМРАСП возвращает интегральную функцию распределения; если это
аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности
распределения.
Если среднее = 0 и
стандартное_откл = 1, то функция НОРМРАСП возвращает стандартное
нормальное распределение.
Пример 2. Построить график
нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8
с шагом 0,5, a=24,3 и
=1,5.
Решение
1. В ячейку А1 вводим символ
случайной величины х, а в ячейку B1 — символ функции
плотности вероятности — f(x).
2. Вводим в диапазон А2:А21
значения х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся
маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в
ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).
3. Устанавливаем табличный курсор в ячейку В2 и
для получения значения вероятности воспользуемся специальной функцией —
нажимаем на панели инструментов кнопку Вставка функции (fx). В появившемся диалоговом
окне Мастер функций — шаг 1 из 2 слева в поле Категория указаны виды
функций. Выбираем Статистическая. Справа в поле Функция выбираем
функцию НОРМРАСП. Нажимаем на кнопку ОК.
4. Появляется диалоговое
окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2
щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры
значение математического ожидания (24,3). В рабочее поле Стандартное_откл
вводим с клавиатуры значение среднеквадратического отклонения (1,5). В рабочее
поле Интегральная вводим с клавиатуры вид функции распределения (0).
Нажимаем на кнопку ОК.
5. В ячейке В2 появляется
вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного
курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21
копируем функцию НОРМРАСП в диапазон В3:В21.
6. По полученным данным строим искомую диаграмму
нормальной функции распределения. Щелчком указателя мыши на кнопке на панели
инструментов вызываем Мастер диаграмм. В появившемся диалоговом окне
выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки
Далее указываем диапазон данных — В1:В21 (с помощью мыши). Проверяем,
положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с
помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее,
вводим названия осей Х и У и нажимаем на кнопку Готово.
Рис. 1 График нормальной функции распределения
Получен приближенный график
нормальной функции плотности распределения (см. рис.1).
Задания для самостоятельной работы
1. Построить график нормальной
функции плотности распределения f(x) при x, меняющемся от 20 до 40 с
шагом 1 при
= 3.
3. Генерация случайных величин
Еще одним аспектом
использования законов распределения вероятностей является генерация случайных величин. Бывают ситуации, когда необходимо
получить последовательность случайных чисел. Это, в частности, требуется для
моделирования объектов, имеющих случайную природу, по известному распределению
вероятностей.
Процедура генерации
случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из
одного или нескольких распределений.
В MS Excel для генерации СВ используются функции из категории Математические:
СЛЧИС () – выводит на экран равномерно
распределенные случайные числа больше или равные 0 и меньшие 1;
СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран
случайное число, лежащее между произвольными заданными
значениями.
В случае использования
процедуры Генерация случайных чисел из пакета Анализа необходимо
заполнить следующие поля:
— число переменных
вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все
столбцы в выходном диапазоне будут заполнены;
— число случайных чисел
вводится число случайных значений, которое необходимо вывести для
каждой переменной, если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены;
— в поле распределение необходимо выбрать тип распределения,
которое следует использовать для генерации случайных переменных:
1. равномерное — характеризуется
верxней и нижней границами. Переменные извлекаются с одной и
той же вероятностью для всех значений интервала.
2. нормальное
— характеризуется средним значением и стандартным отклонением. Обычно для
этого распределения используют среднее значение
0 и стандартное отклонение 1.
3. биномиальное
— характеризуется вероятностью успеха (величина р) для некоторого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной
переменной;
4. дискретное
— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,
содержащего значения, и правого, содержащего
вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть
равна 1;
5. распределения Бернулли, Пуассона
и Модельное.
— в поле случайное рассеивание
вводится произвольное значение, для которого необходимо
генерировать случайные числа. Впоследствии можно снова использовать это
значение для получения тех же самых случайных чисел.
— выходной диапазон
вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и
на экран будет выведено сообщение в случае
возможного наложения выходного диапазона на исходные
данные.
Рассмотрим пример.
Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы
первые блюда чередовались в случайном порядке.
Решение
1.
Пронумеруем первые
блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.
2.
Укажем желаемую вероятность появления
каждого первого блюда. Пусть все блюда будут
равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.
3.
В меню Сервис
выбираем пункт Анализ данных и далее указываем строку Генерация
случайных чисел. В появившемся диалоговом окне указываем Число
переменных — 1, Число случайных чисел — 30 (количество
дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной
интервал значений и вероятностей
вводим (мышью) диапазон, содержащий номера супов и их
вероятности. – А2:В5.
4.
Указываем выходной
диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,
4.
Задание для
самостоятельной работы
1. Сформировать
выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.
2. Сформировать
выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.
3. Пусть
спортсмену необходимо составить график тренировок на 10 дней, так чтобы
дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.
4. Составить
расписание внеклассных мероприятий на неделю для случайного проведения:
семинаров, интеллектуальных игр, КВН и спец. курса.
5. Составить
расписание на месяц для случайной демонстрации на телевидении одного из четырех
рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1
должна быть в два раза выше, чем остальных рекламных роликов.