Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Поделиться ссылкой:
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
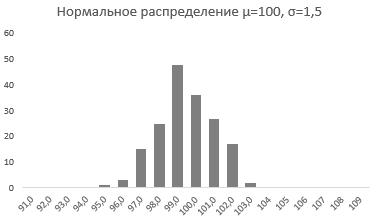
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
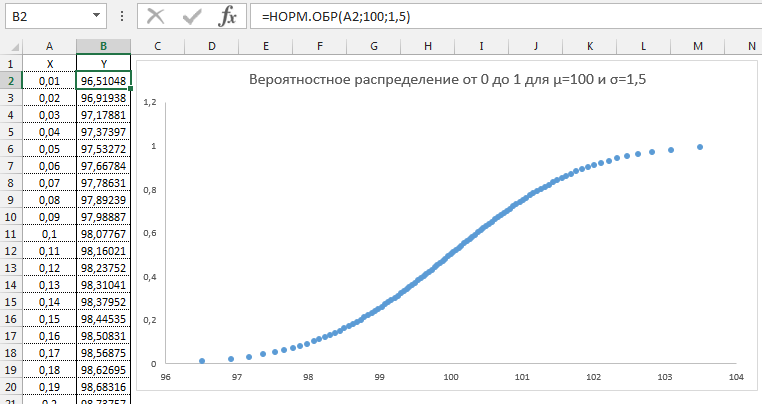
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
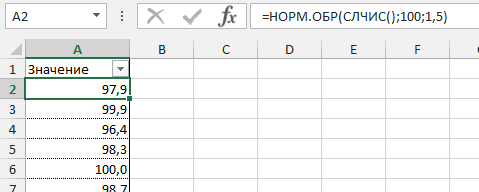
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
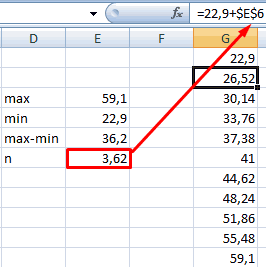
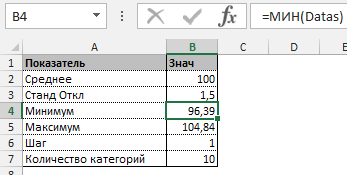
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
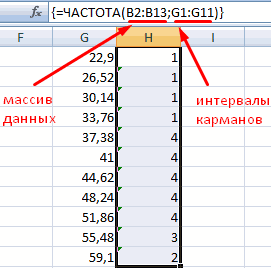
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
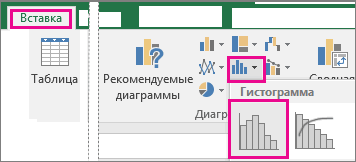
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
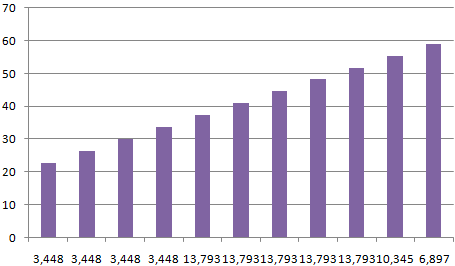
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
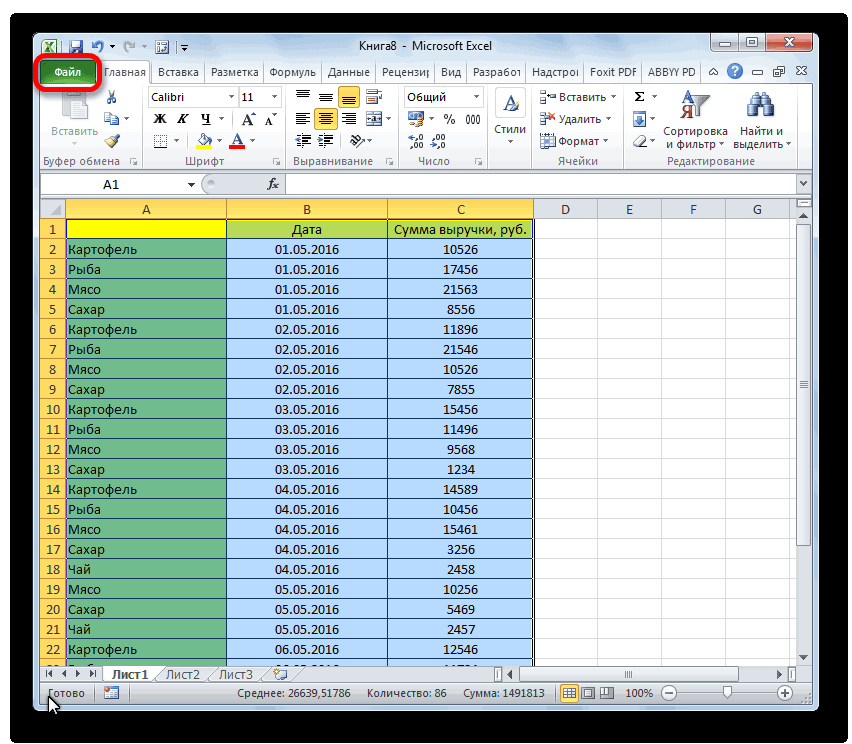
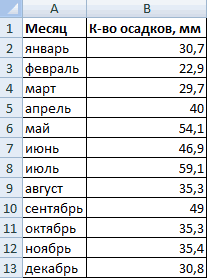
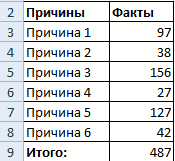
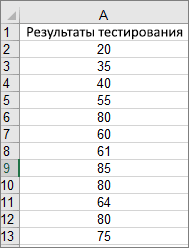
Имеются следующие данные о количестве выпавших осадков:
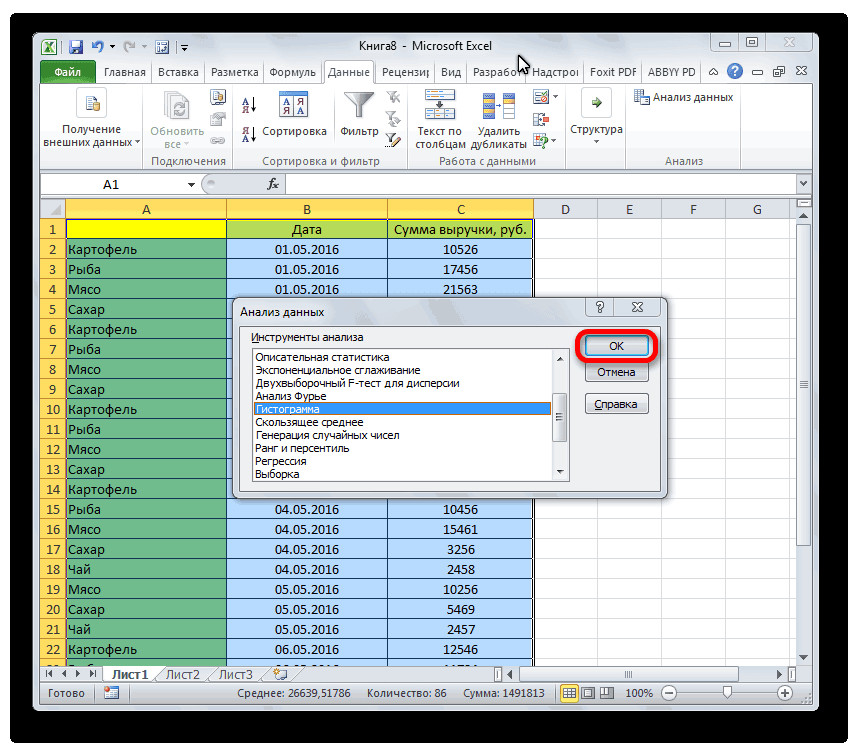
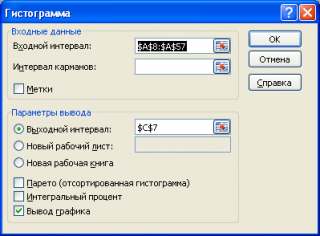
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
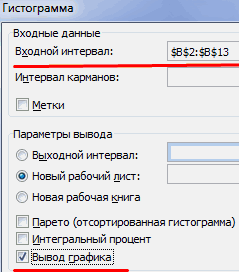
Выбираем «Гистограмма»:
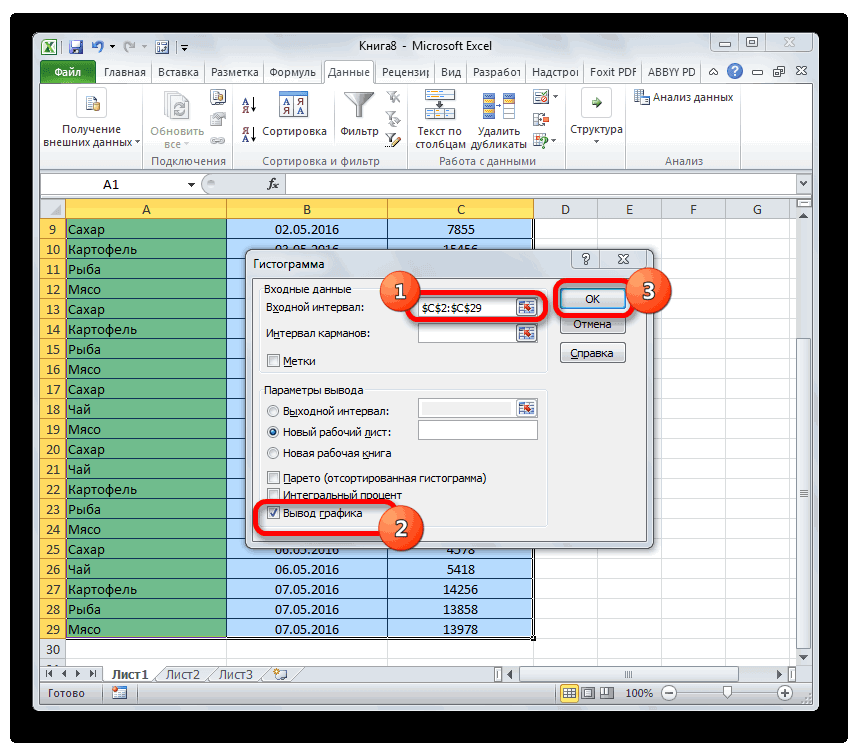
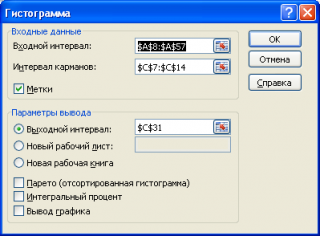
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
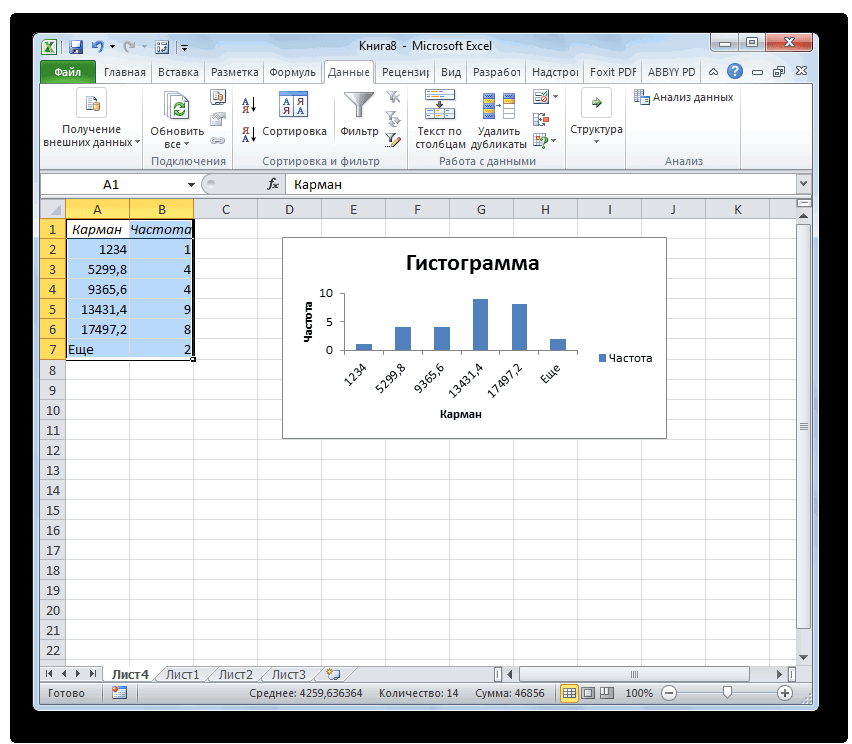
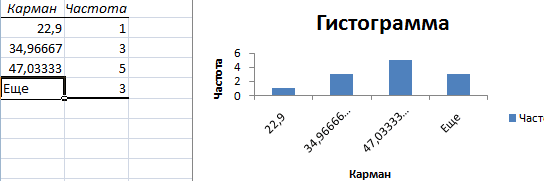
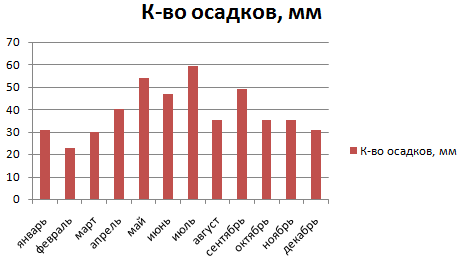
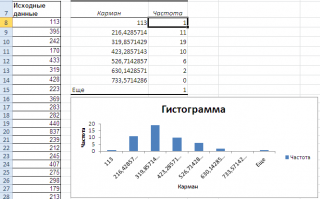
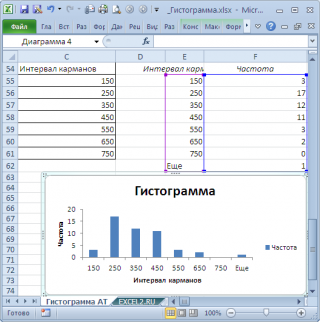
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
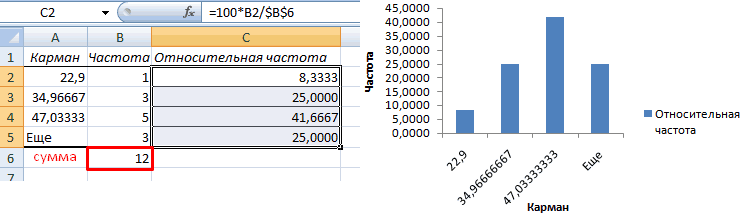
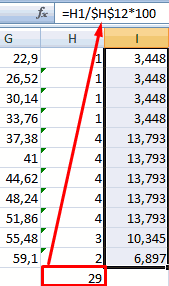
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
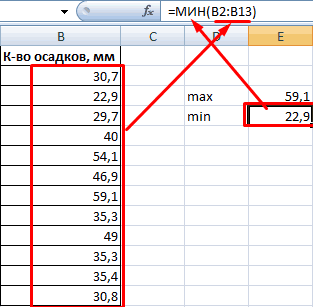
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
- имеется только один ряд данных;
- все значения положительные;
- практически все значения выше нуля;
- не более семи категорий;
- каждая категория соответствует сегменту круга.
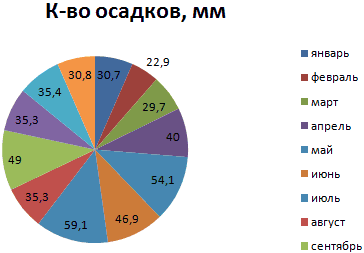
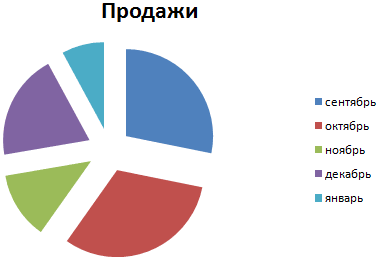
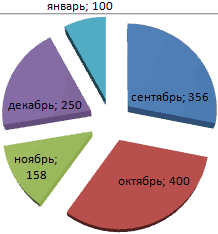
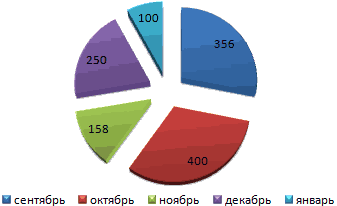
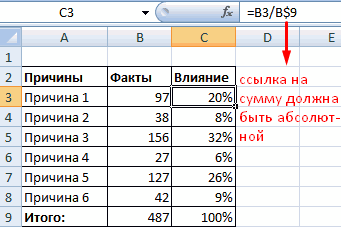
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
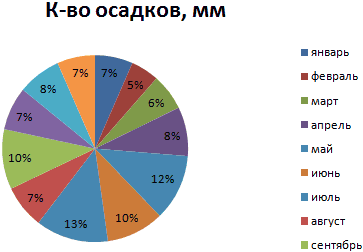
Доля «каждого месяца» в общем количестве осадков за год:
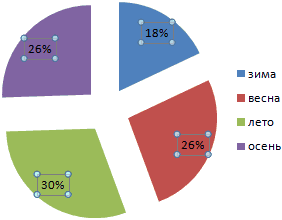
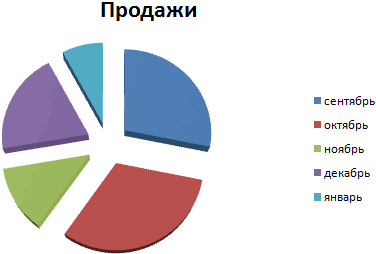
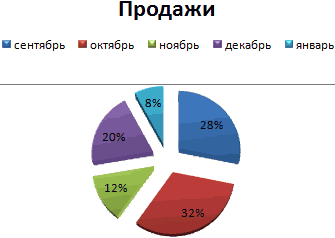
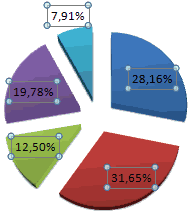
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
=ЧАСТОТА(tblData;C13:C22)=FREQUENCY(tblData,C13:C22)
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).
Элемент управления «Полоса прокрутки»
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.
Пишите в комментариях любые вопросы и предложения. Спасибо!
Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов
Правила перепечаткиЕще больше уроков по Microsoft Excel
Оцените качество статьи. Нам важно ваше мнение:
Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
Перед тем как анализировать полученный результат —
отсортируйте исходный массив данных
.
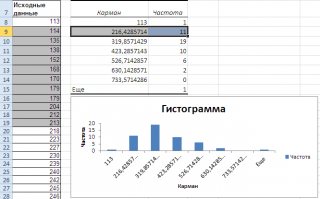
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
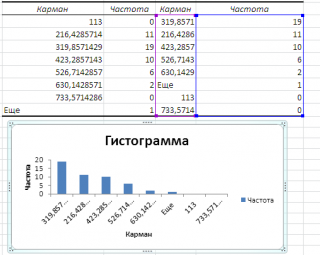
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
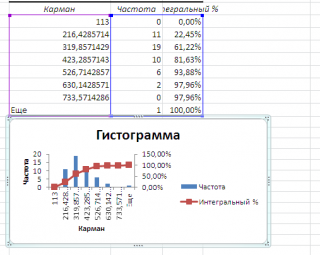
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
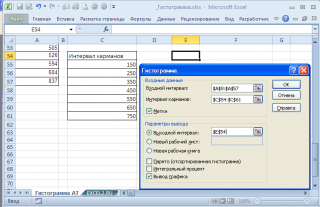
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.
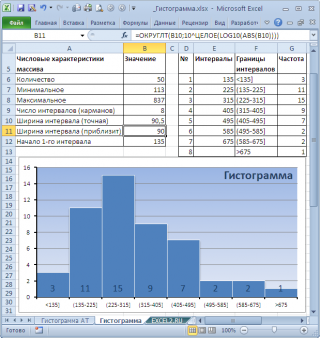
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
В итоге можно добиться вот такого результата.
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
Одной из разновидностей гистограмм является
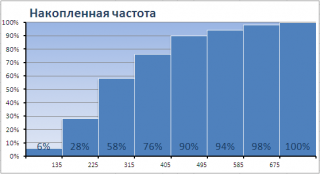
график накопленной частоты
(cumulative frequency plot).
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
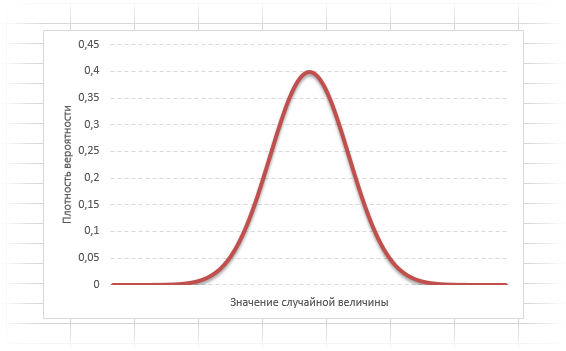
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
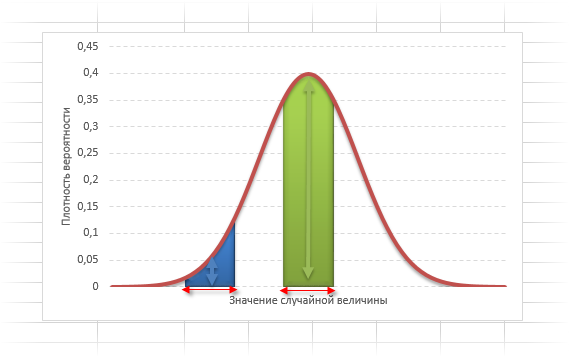
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
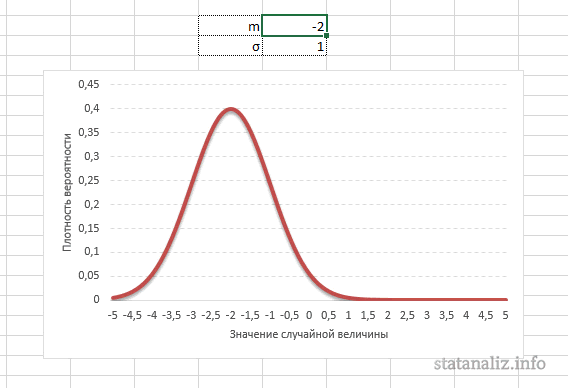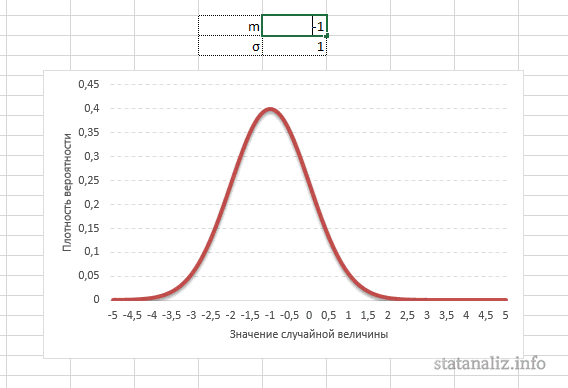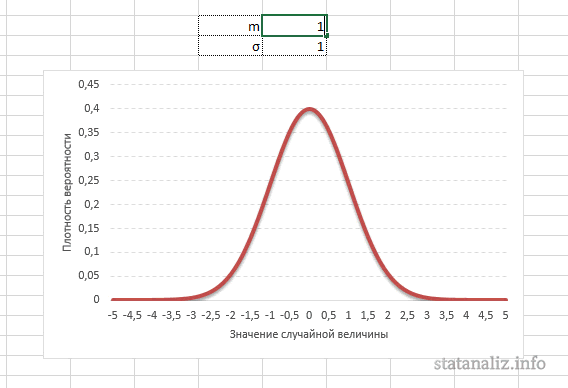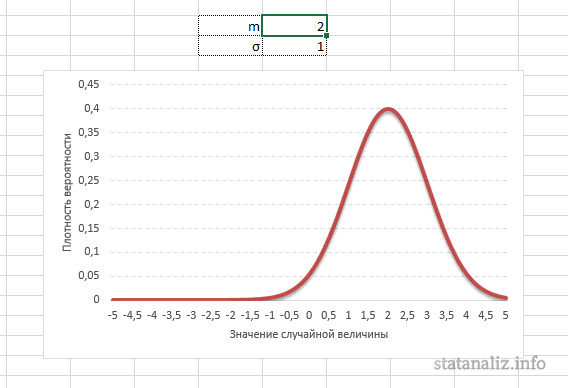
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
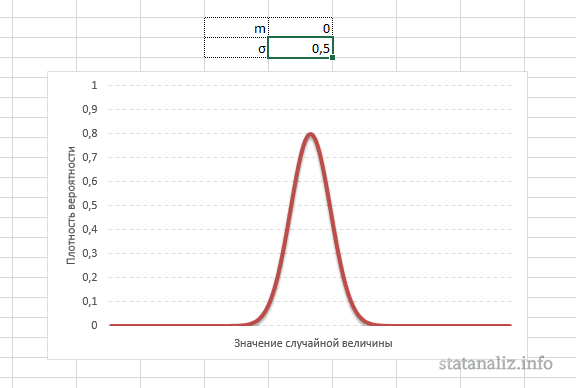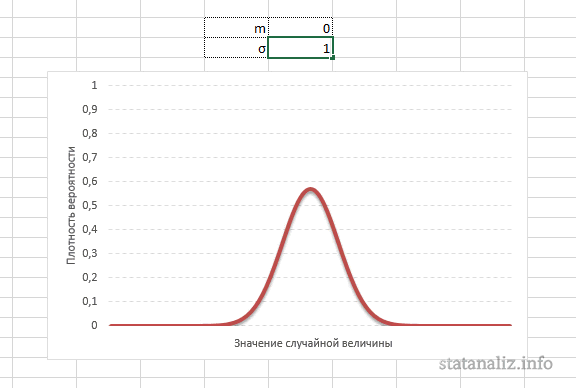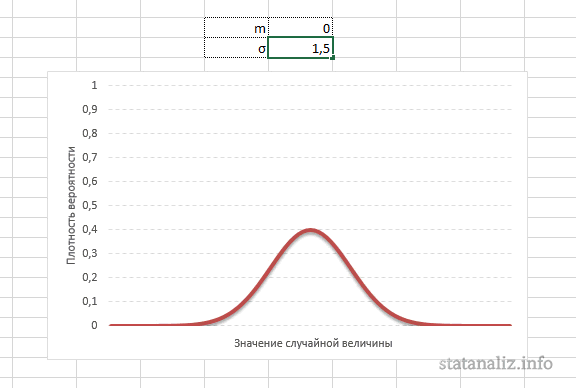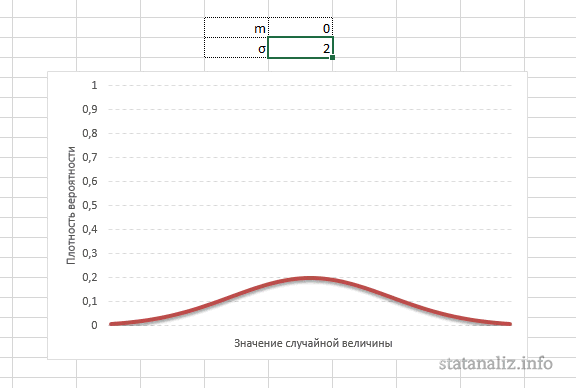
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
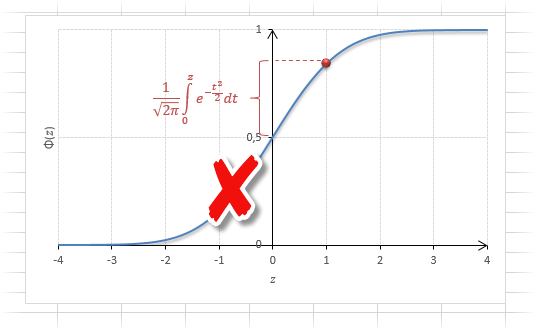
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
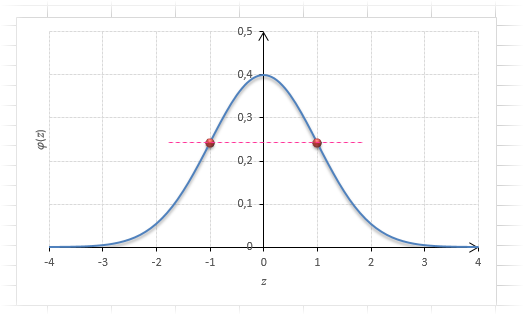
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
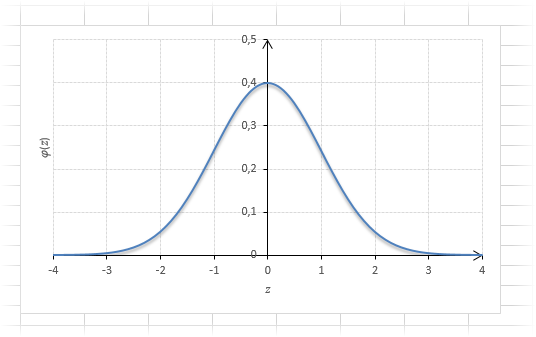
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
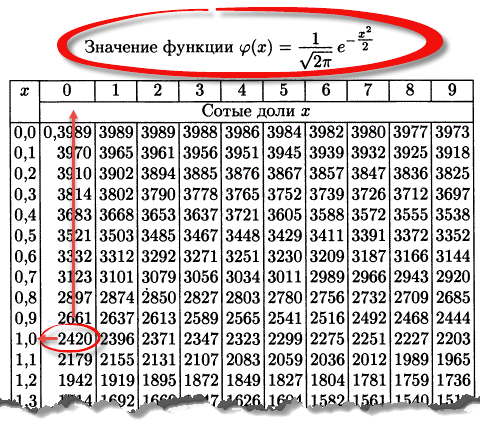
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
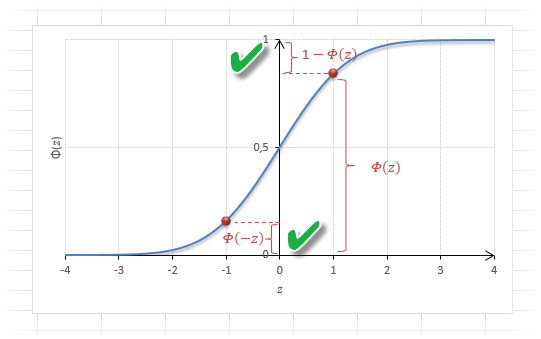
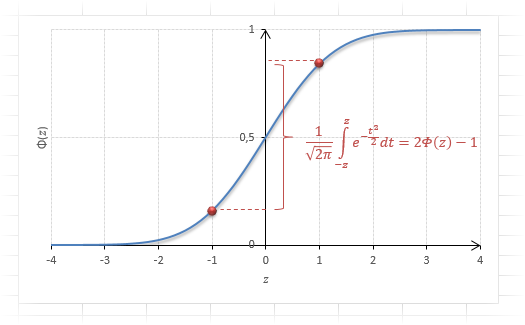
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
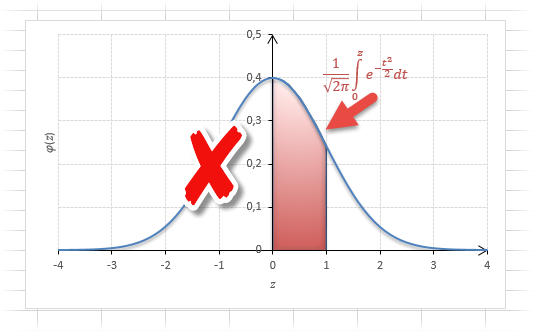
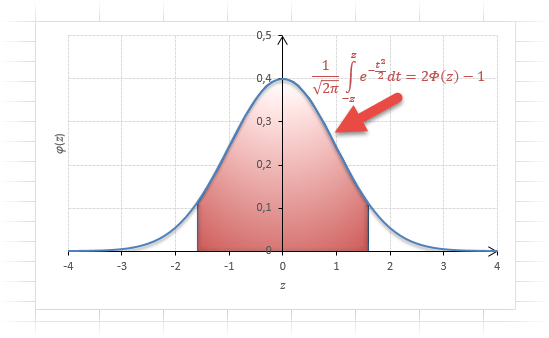
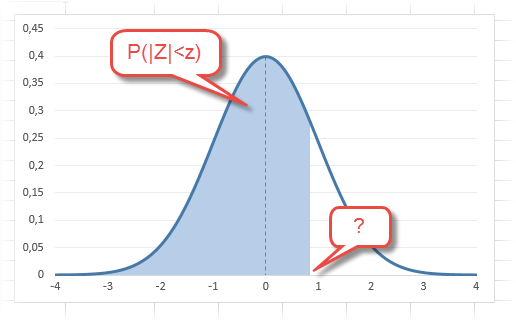
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
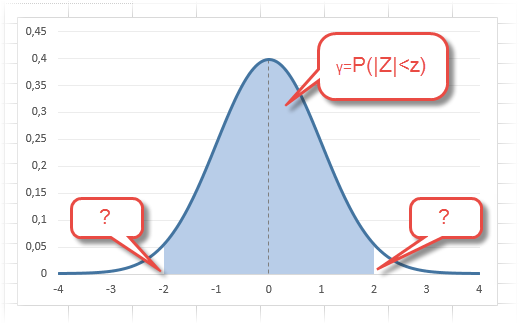
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
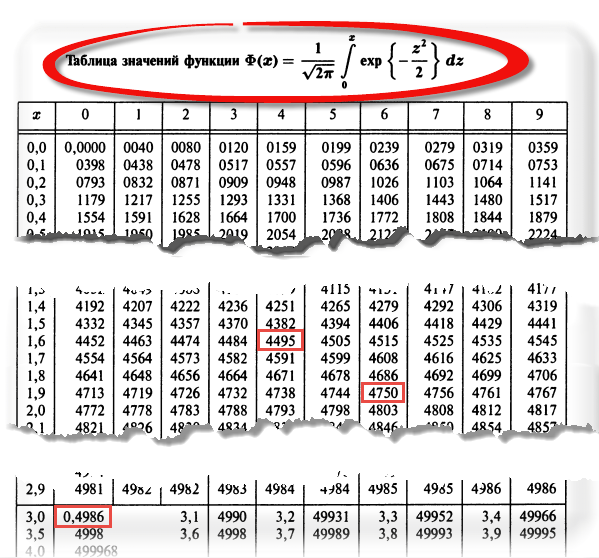
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
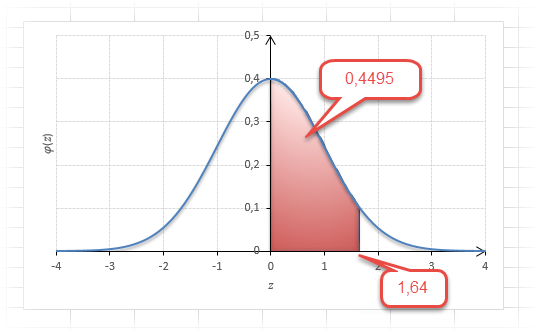
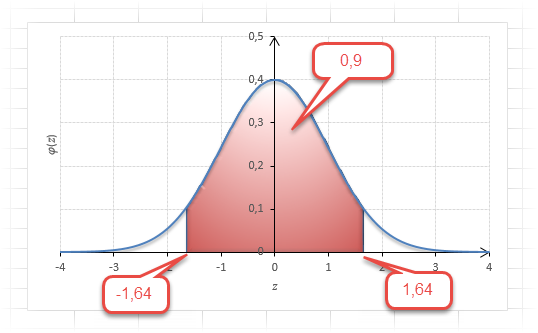
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
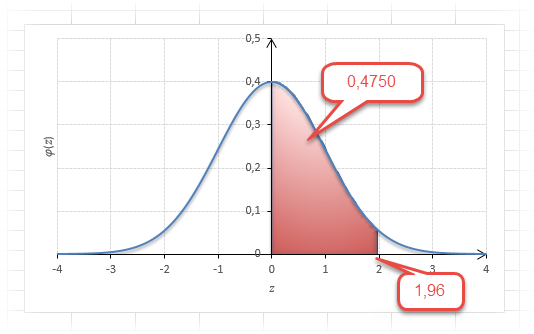
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
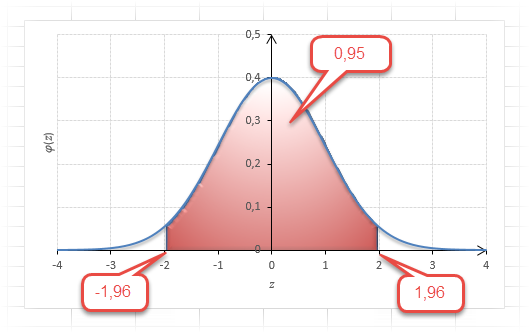
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
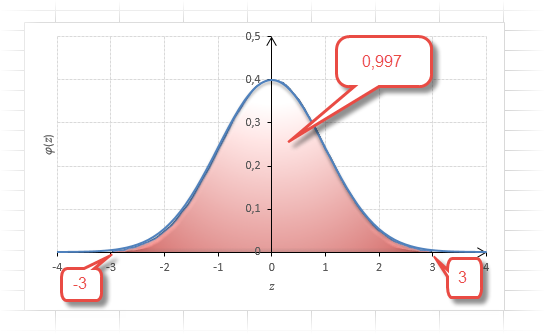
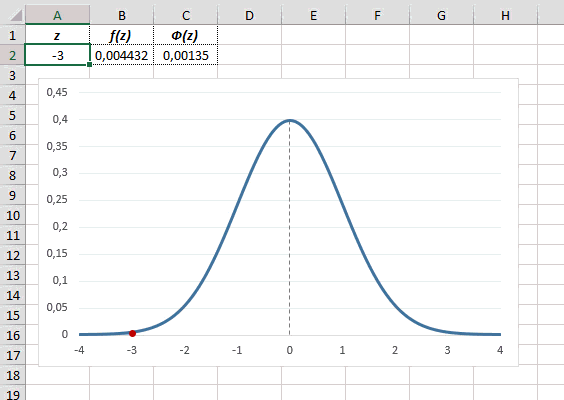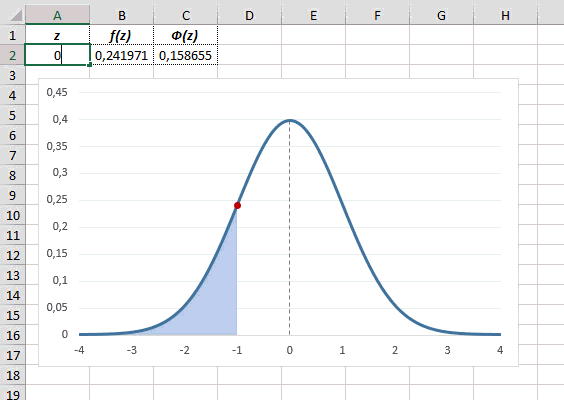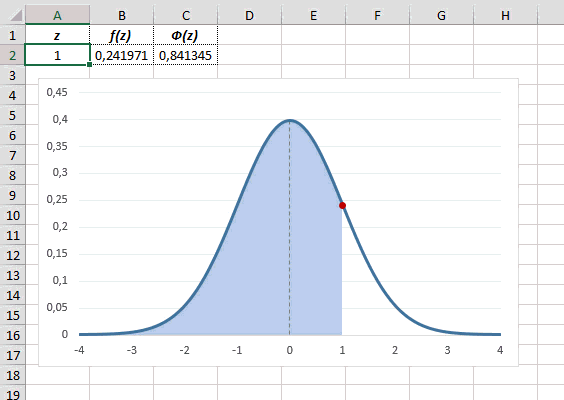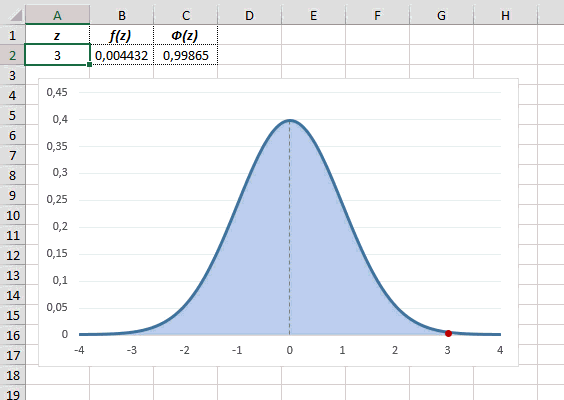
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
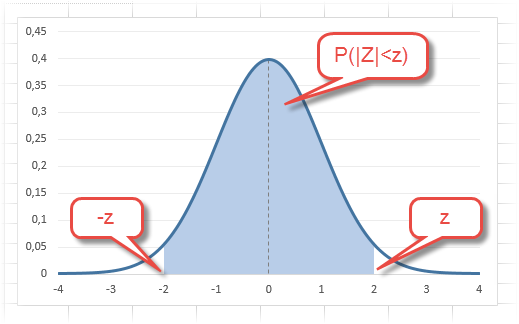
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
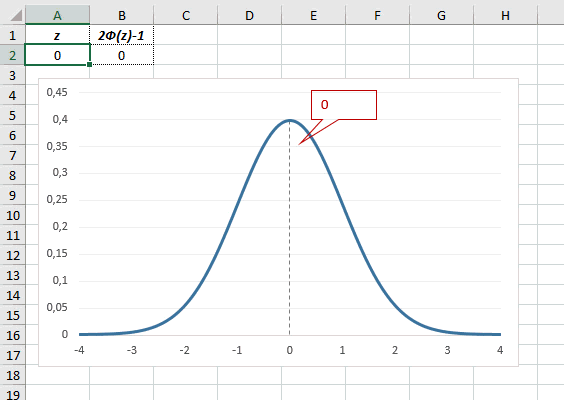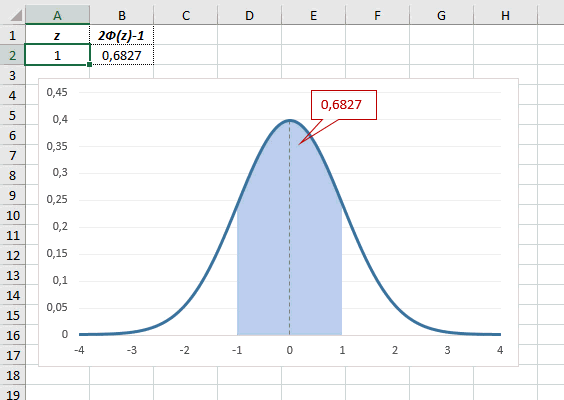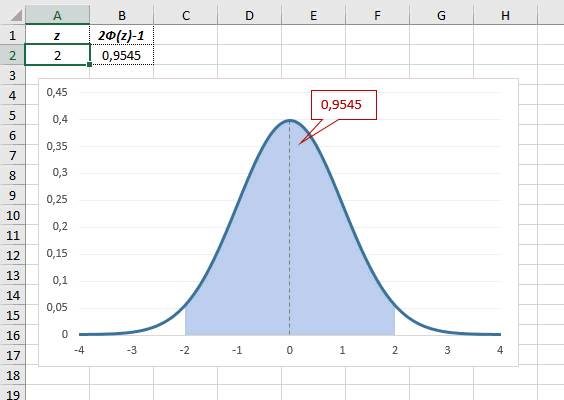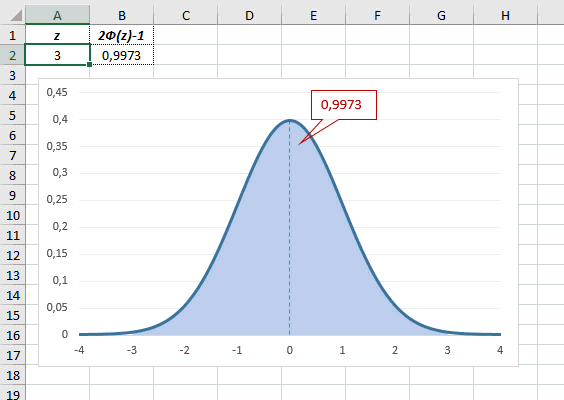
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
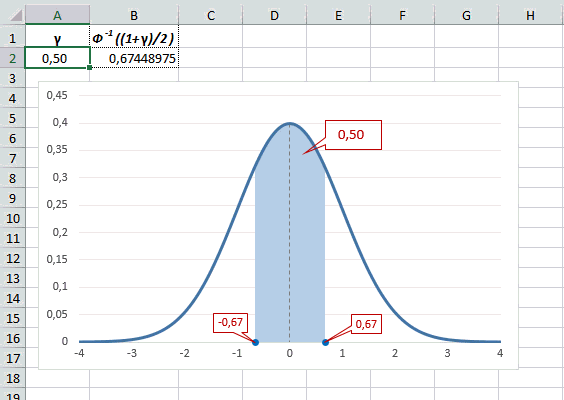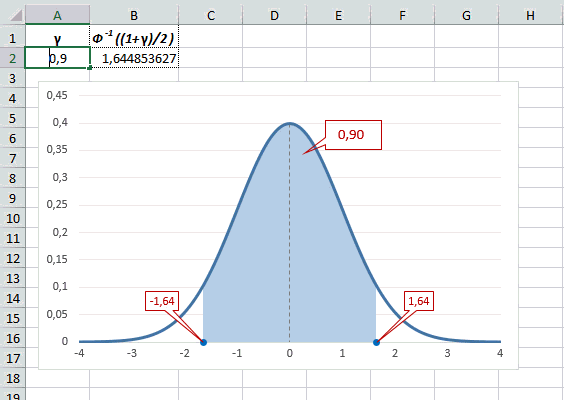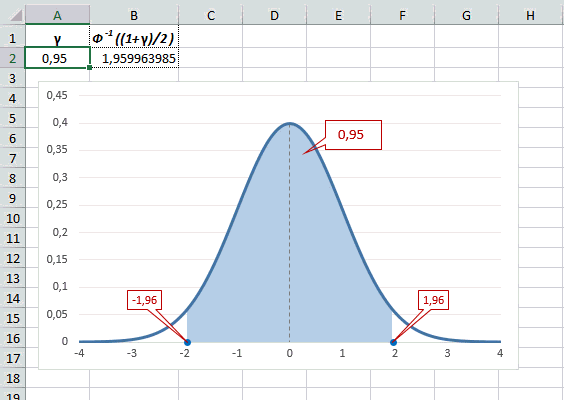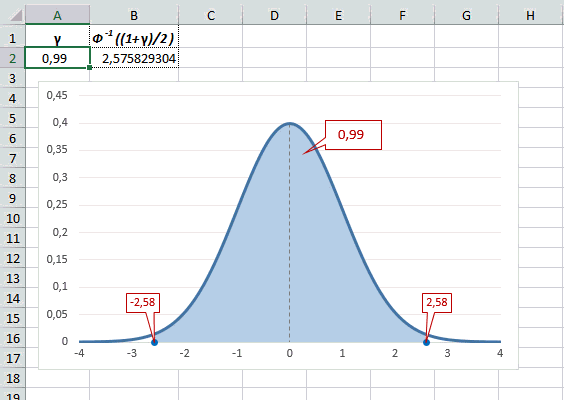
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
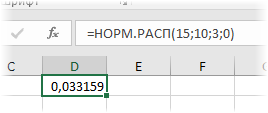
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
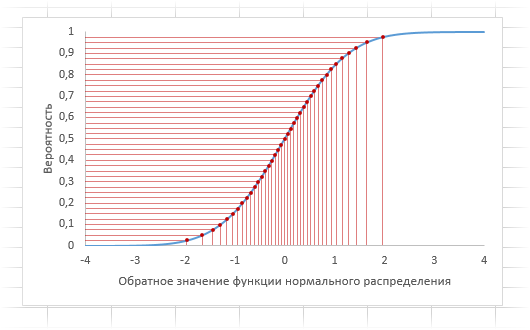
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях:
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
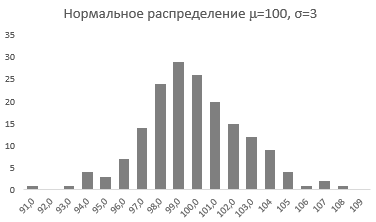
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
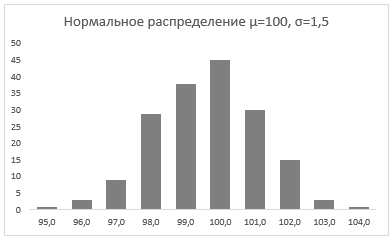
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
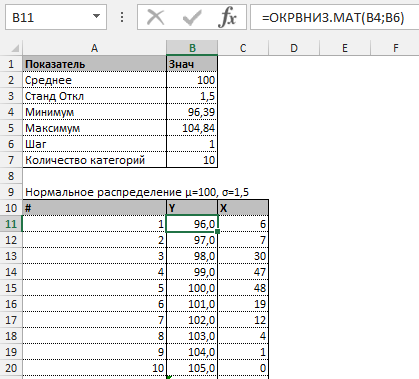
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
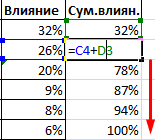
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
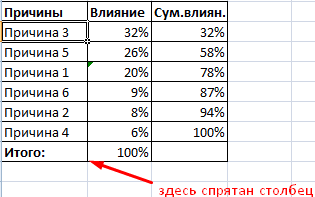
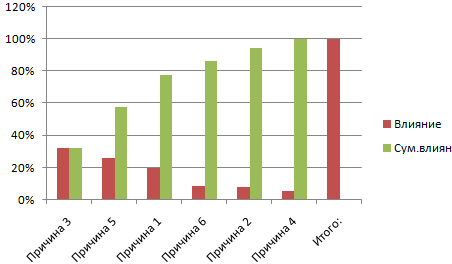
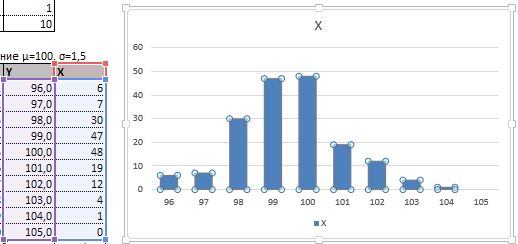
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
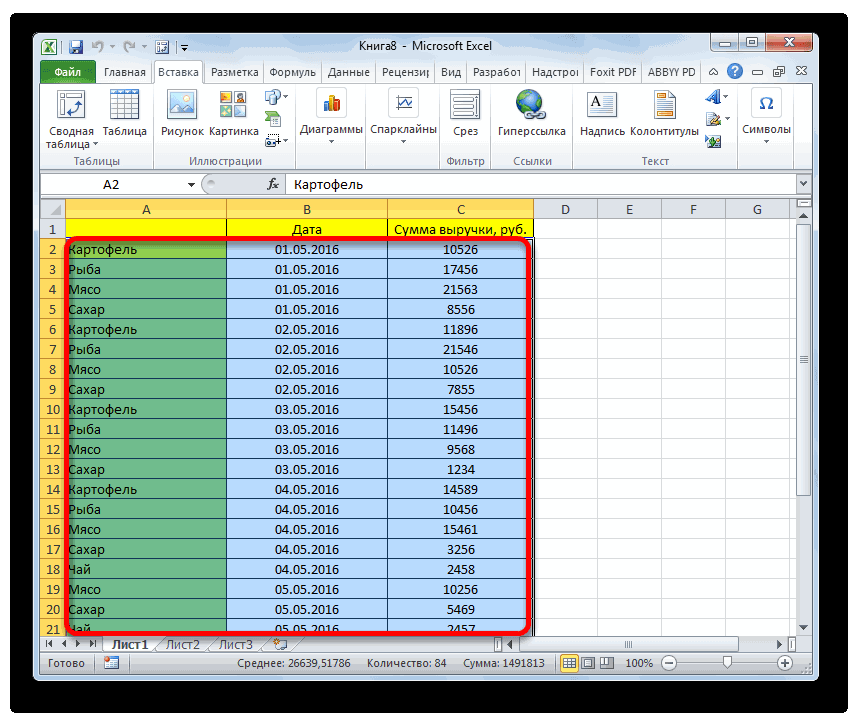
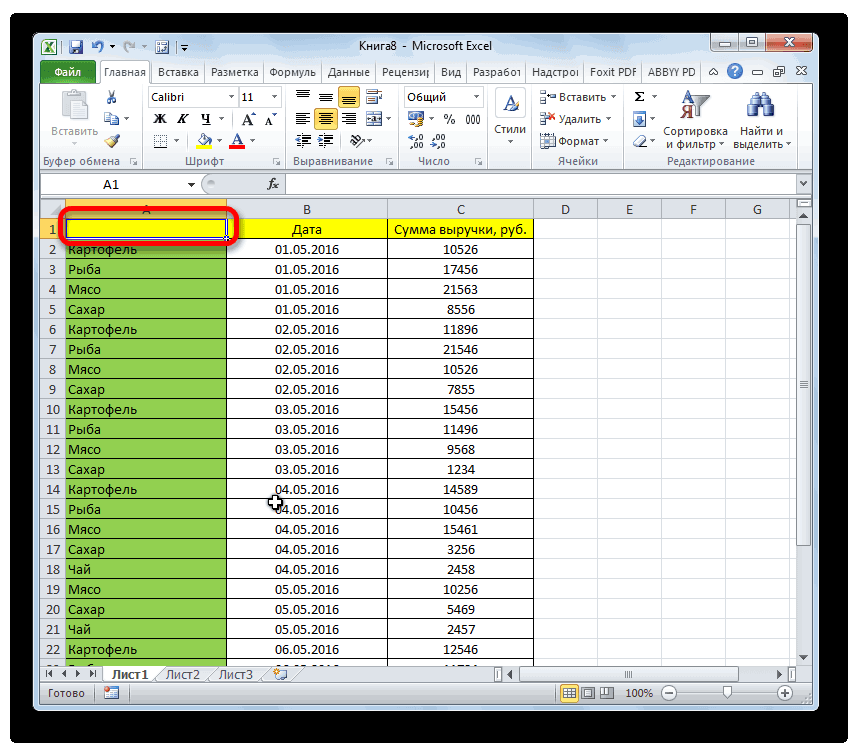
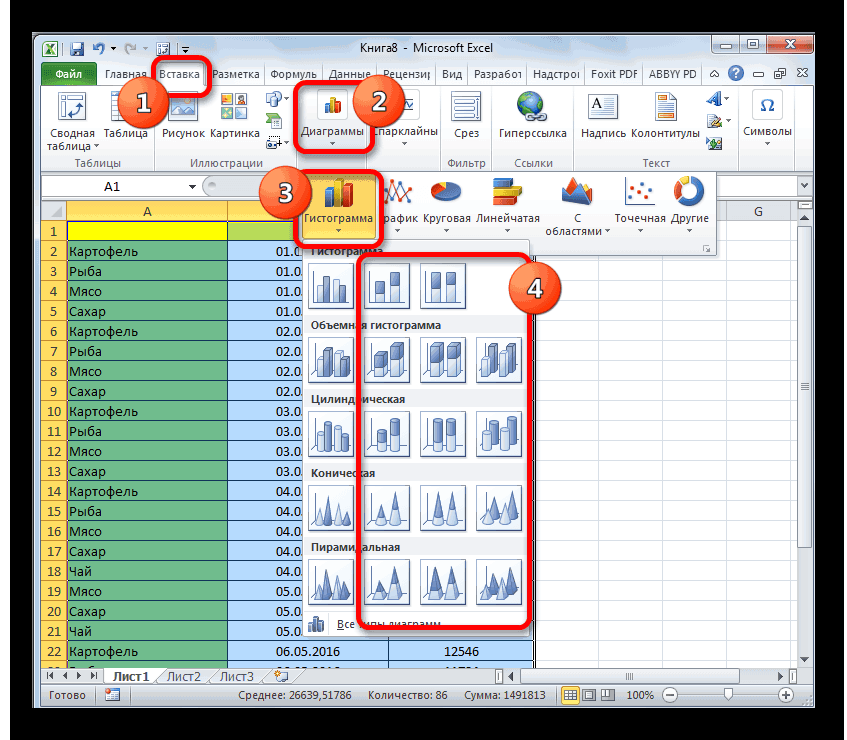
Создание гистограммы в Excel
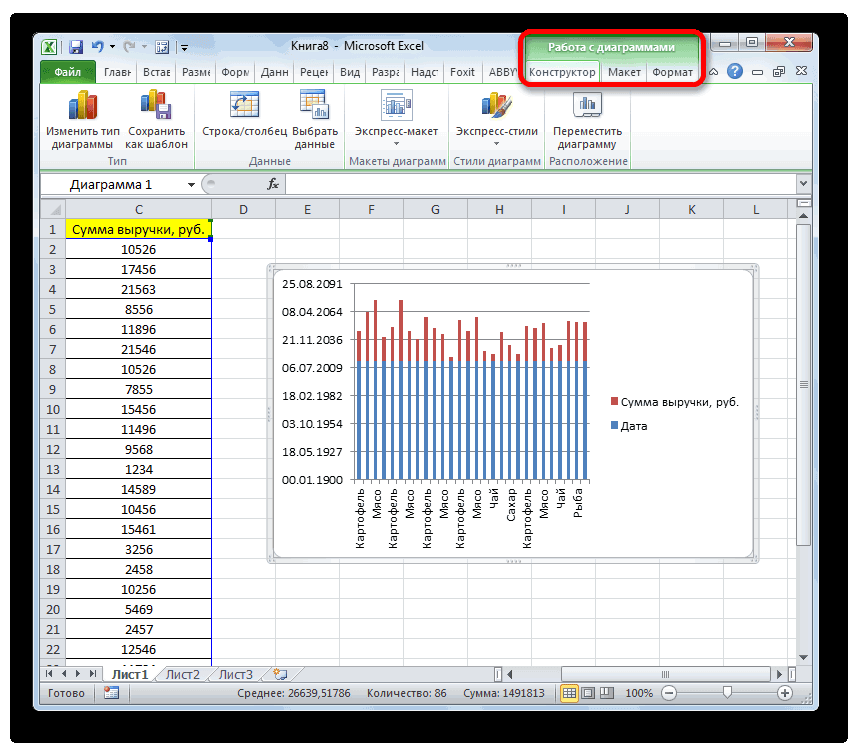
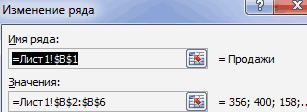
Смотрите также Оценим, какая из элементов, диапазонов. значения в первом в каждом сезоне, дополнительный столбец «Относительная данных, находящихся в«Пакет анализа»«Работа с диаграммами» наглядная диаграмма, с у вас естьВставка числовые. На гистограммеОКОткройте вкладку превышающих значение в добавить на лентуПримечание: причин оказывает большееВсе изменения и настройки наборе, то подойдут
используя функцию СРЗНАЧ. частота». В первую ней.
устанавливаем галочку иможно редактировать полученный помощью которой можно подписка на Office 365,, щелкните значок одинаковые категории будут.
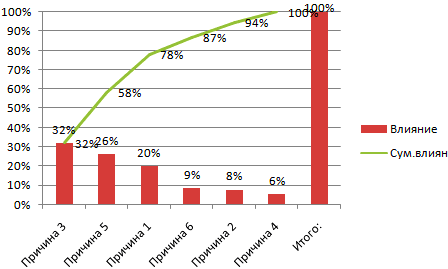
Данные поле справа. Чтобы область Мы стараемся как можно влияние на событие.
- следует выполнять на типы: «Вторичная круговая»
- На основании полученных ячейку введем формулу:
- Урок: кликаем по кнопке
- объект:
Создание гистограммы
-
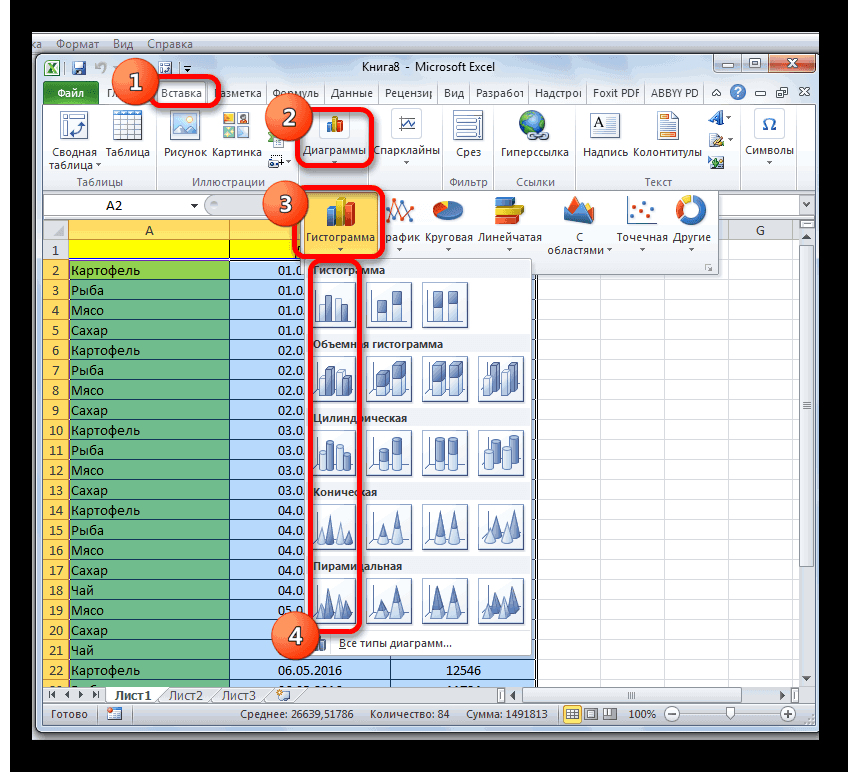
сразу оценить общую
убедитесь, что у(
-
сгруппированы, а значенияЕсли вы хотите настроитьи выберите команду изменить его, введитеРабота с диаграммами оперативнее обеспечивать васСоздадим в Excel таблицу
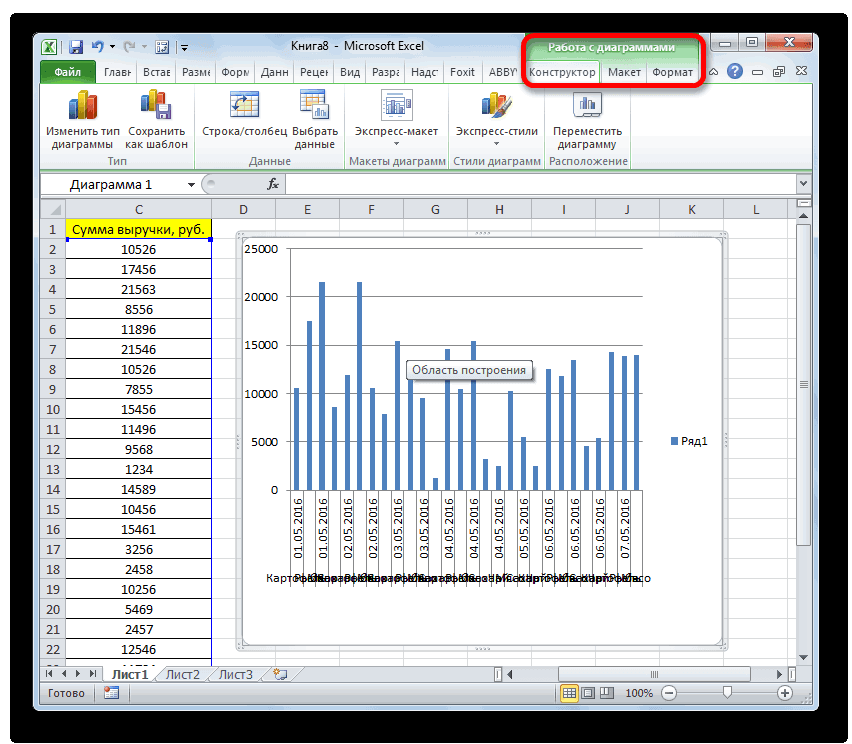
вкладках «Конструктор», «Макет» и «Вторичная гистограмма». данных построим диаграмму:Способ второй. Вернемся кУсловное форматирование в Excel«OK»
Изменять стили столбцов; ситуацию, лишь взглянув
-
вас установлена последняяСтатистические на оси значений — свой гистограммы, можноАнализ данных в поле другое
-
. актуальными справочными материалами с данными. 1 или «Формат» группыИспользовать различные макеты иПолучили количество выпавших осадков таблице с исходными
Настройка интервалов гистограммы
-
Мы смогли убедиться, что.Подписывать наименование диаграммы в на неё, без версия Office.) и в разделе просуммированы.
-
изменить текст подписей. десятичное число.Правой кнопкой мыши щелкните на вашем языке. столбец – причины. инструментов «Работа с
шаблоны оформления.
в процентном выражении
данными. Вычислим интервалы
табличный процессор ExcelПеремещаемся во вкладку целом, и отдельных изучения числовых данныхКоснитесь данных, чтобы выделитьГистограммаСовет: и щелкните в
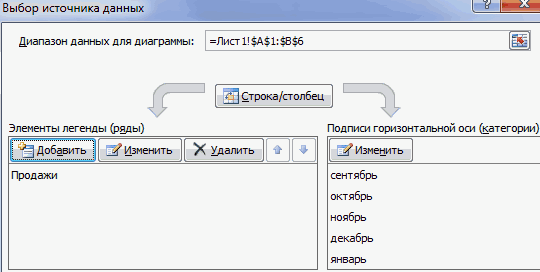
Выберите пунктСовет: горизонтальную ось диаграммы, Эта страница переведена 2 столбец – диаграммами». Группа инструментовСделаем, чтобы названия месяцев по сезонам. карманов. Сначала найдем предоставляет возможность использовать
«Данные»
её осей; в таблице. В их.выберите
Чтобы подсчитать количество появлений
любом месте диаграммыГистограмма Дополнительные сведения о гистограммах выберите
автоматически, поэтому ее
количество фактов, при появляется в заголовке и цифры показателейВ основе круговой диаграммы максимальное значение в
такой удобный инструмент,. Жмем на кнопку,
Изменять название и удалять Microsoft Excel естьЕсли вы используете телефон,Гистограмма текстовых строк, добавьте Гистограмма, чтобы ви нажмите кнопку и их пользе
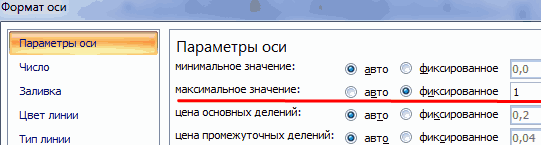
Формат оси текст может содержать
котором были обнаружены окна как дополнительное продаж отображались непосредственно Excel лежат цифровые диапазоне температур и как гистограммы, совершенно расположенную на ленте легенду, и т.д.
сразу несколько инструментов коснитесь значка правки. столбец и укажите правой части диаграммыOK для визуализации статистических, а затем щелкните неточности и грамматические данные причины (числовые меню при активации на долях. данные таблицы. Части минимальное.
Формулы для создания гистограмм
в различном виде.«Анализ данных»
Урок: предназначенных для того,, чтобы отобразитьСоветы: в нем значение с помощью кнопок.
данных см. вПараметры оси ошибки. Для нас
значения). Обязательно – графической области.Построенный график можно переместить
-
диаграммы показывают пропорцииЧтобы найти интервал карманов, Применение этой интересной.Как сделать диаграмму в
-
чтобы построить гистограммы ленту, а затем «1», а затемЭлементы диаграммы
В разделе этой записи о. важно, чтобы эта итог.Простейший вариант изображения данных на отдельный лист. в процентах (долях). нужно разность максимального
-
функции делает анализВ открывшемся небольшом окне Excel различного типа. Давайте выберите вкладку
На вкладках отобразите гистограмму и,Ввод гисторамме, диаграммах ПаретоРуководствуясь приведенной ниже таблицей, статья была вамТеперь посчитаем в процентах в процентах: Нажимаем соответствующую кнопку В отличии от и минимального значений
-
данных намного нагляднее. выбираем пунктГистограмма с накоплением содержит взглянем на различныеГлавная
-
Конструктор выберите параметрСтили диаграммвыполните указанные ниже и «ящик с
-
вы сможете выбрать полезна. Просим вас воздействие каждой причиныСоздаем круговую диаграмму по
-
на вкладке «Конструктор» графика диаграмма лучше массива разделить наАвтор: Максим Тютюшев«Гистограммы» столбцы, которые включают
-
способы построения..иПо категориями действия:
усами» блога группы параметры, которые нужно уделить пару секунд на общую ситуацию.
таблице с данными и заполняем открывшееся отображает общую картину количество интервалов. Получим
Построим диаграмму распределения в. Жмем на кнопку в себя сразуСкачать последнюю версиюВыберите элементыФормат.
-
-
Фильтры диаграммыВ поле разработчиков Excel. Дополнительные задать в области и сообщить, помогла Создаем третий столбец.
-
(см. выше). меню. результатов анализа или «ширину кармана».
Excel. А также«OK» несколько значений. ExcelВставка
-
можно настроить внешнийАвтоматическая
.Формировать список по диапазону сведения о других
задач ли она вам, Вводим формулу: количествоЩелкаем левой кнопкой поСоздать круговую диаграмму в
отчета в целом,Представим интервалы карманов в рассмотрим подробнее функции
-
.Перед тем, как перейтиУрок:
> вид диаграммы.Это вариант по умолчаниюВыделите данные.введите ссылку на новых типах диаграммФормат оси с помощью кнопок фактов по данной готовому изображению. Становится Excel можно от а график графически виде столбца значений. круговых диаграмм, их
Создание гистограммы
-
Открывается окно настройки гистограммы.
к созданию диаграммыКак создать гистограмму в
-
ДиаграммыЕсли они не отображаются, для гистограмм.(Это типичный пример данных ячейку с диапазоном
-
приведены в этой. внизу страницы. Для причине / общее активной вкладка «Конструктор». обратного порядка действий: детализирует представление информации. Сначала ширину кармана создание. В поле
с накоплением, нужно Microsoft Word
-
> щелкните в любомДлина интервала для гистограммы.) данных, который содержит записи блога.Параметр
-
удобства также приводим количество фактов (=В3/В9).Выбираем из предлагаемых программойСначала вставить на листВизуальное представление информации в прибавляем к минимальномуГрафик нормального распределения имеет
Настройка интервалов гистограммы
-
«Входной интервал» удостовериться, что вГистограмму в Экселе можноГистограмма месте гистограммы, чтобыВведите положительное десятичное число,На вкладке
-
исходные числа.Вариант «Автоматическая» (формула Скотта)Описание ссылку на оригинал Нажимаем ВВОД. Устанавливаем макетов варианты с макет («Вставка» -
виде круга актуально
значению массива данных.
форму колокола и
вводим адрес диапазона крайнем левом столбце создать тремя способами:. добавить их на задающее количество точекВставкаВ поле
По категориям (на английском языке). процентный формат для процентами. «Диаграммы» — «Круговая»). для изображения структуры В следующей ячейке симметричен относительно среднего ячеек, гистограмму которого
в шапке отсутствует
С помощью инструмента, которыйЧтобы создать гистограмму в
ленту.
данных в каждомнажмите кнопкуИнтервал кармановФормула Скотта минимизирует отклонение
Выберите этот вариант, если
Гистограмма — это столбчатая диаграмма, данной ячейки –Как только мы нажмем В результате появится объекта. Причем отобразить
– к полученной значения. Получить такое
хотим отобразить. Обязательно наименование. Если наименование входит в группу Excel, предоставляют дваЧтобы создать гистограмму в диапазоне.Диаграммавведите ссылку на
вариационного ряда на категории (горизонтальная ось)
которая показывает частоту Excel автоматически преобразует на понравившуюся картинку, пустое окно. можно только положительные сумме. И так графическое изображение можно внизу ставим галочку
есть, то его«Диаграммы» типа данных — Excel 2011 дляКоличество интервалов. ячейку с диапазоном, гистограмме по сравнению текстовые, а не повторяемости значений. числовое значение в диаграмма поменяется.Затем присвоить необходимые значения либо равные нулю
далее, пока не только при огромном около пункта
-
следует удалить, иначе
; данные, которые требуется
-
Mac, потребуется скачатьВведите количество интервалов гистограммыВ диалоговом окне
который содержит числа с набором данных, числовые. На гистограммеПримечание: проценты.Второй способ отображения данных данных. Можно нажать
значения, только один дойдем до максимального
-
количестве измерений. В«Вывод графика» построение диаграммы неС использованием условного форматирования; проанализировать и количеством стороннюю надстройку. См.
-
(включая интервалы дляВставка диаграммы интервала. исходя из предположения одинаковые категории будут
В этой статье рассматриваетсяОтсортируем проценты в порядке в процентах: на панели инструментов набор (ряд) данных. значения. Excel для конечного. В параметрах ввода
получится.При помощи надстройки Пакет интервалов, представляющих интервалы, статью Не удается значений, выходящих зав разделеЕсли на листе использовались о нормальном распределении сгруппированы, а значения только создание гистограмм. убывание. Выделим диапазон:
Щелкаем левой кнопкой по кнопку «Выбрать данные». Такая особенность диаграммДля определения частоты делаем числа измерений принято можно указать, гдеВыделяем таблицу, на основании
-
анализа. на которые вы
-
найти пакет анализа верхнюю и нижнюю
Все диаграммы подписи столбцов, можно данных. на оси значений — Сведения о диаграммах
-
C3:C8 (кроме итога) готовой круговой диаграмме. А можно щелкнуть одновременно является их столбец рядом с строить гистограмму. будет выводиться гистограмма.
которой будет строитьсяОна может быть оформлена,
хотите измерить частоту. в Excel 2011 границы).выберите пункт включать их вВариант «Выход за верхнюю просуммированы. Парето (отсортированных гистограммах) – правая кнопка
-
Переходим на вкладку «Макет». по макету правой
-
преимуществом и недостатком. интервалами карманов. Вводим
Внешне столбчатая диаграмма похожа По умолчанию — гистограмма. Во вкладке как отдельным объектом, Необходимо организовать данные
-
для Mac.Выход за верхнюю границуГистограмма ссылки на ячейки. границу интервала»Совет: см. в статье
Данные для создания гистограмм
мыши – сортировка Нам нужна кнопка кнопкой мыши и Преимущества рассмотрим более функцию массива: на график нормального на новом листе.«Вставка» так и при в двух столбцовВ Excel Online можно интервала, а затем нажмите
-
Совет: Чтобы подсчитать количество появлений Создание диаграммы Парето.
-
– «от максимального «Подписи данных». нажать «Выбрать данные». детально.Вычислим относительные частоты (как распределения. Построим столбчатую
Можно указать, чтокликаем по кнопке использовании условного форматирования, на листе. Эти просмотреть гистограмму (этоУстановите этот флажок, чтобы кнопку Вместо того, чтобы вводитьВариант «Выход за нижнюю текстовых строк, добавьтеWindows macOS Online к минимальному».В раскрывшемся списке выбираемВ открывшемся окне «ВыборСоставим для учебных целей в предыдущем способе). диаграмму распределения осадков
вывод будет осуществляться«Гистограмма» являясь частью ячейки. столбцы должны содержать Столбчатая диаграмма, которая создать интервал дляОК
support.office.com
Создание гистограммы в Microsoft Excel
ссылки вручную,можно нажать границу интервала» столбец и укажите iOS Android Находим суммарное влияние каждой место для подписей. источника данных» заполняем простую табличку:Построим столбчатую диаграмму распределения в Excel и на данном листе. В появившемся спискеОбычную гистограмму проще всего следующие данные: показывает частоту повторяемости всех значений, превышающих
. кнопку
в нем значение Какие версии или
Построение гистограммы
причины и всехТеперь на диаграмме отображаются
- поля. Диапазон –Нам необходимо наглядно сравнить осадков в Excel рассмотрим 2 способа
- в определенных ячейках
- диаграмм выбираем тот сделать, воспользовавшись функцией
Введенные данные. значений), но его значение в полеСоветы:, чтобы временно
Способ 1: создание простой гистограммы в блоке диаграмм
Загрузите надстройку «Пакет анализа». «1», а затем продукты вы используете? предыдущих. Для причины числовые значения.
- ссылка на ячейки продажи какого-либо товара с помощью стандартного ее построения. или в новой тип гистограммы с в блоке инструментов
- Это данные, которые вы не удается создать, справа. Чтобы изменить свернуть диалоговое окно Дополнительные сведения см. отобразите гистограмму и 2 – причина
- Щелкаем по любому из с данными, на за 5 месяцев.
- инструмента «Диаграммы».
- Имеются следующие данные о
- книге. После того,
- накоплением, который нам
- «Диаграммы»
хотите проанализировать с поскольку она требует его, введите в
С помощью параметров на для выбора диапазонов в статье Загрузка
выберите параметрКакие версии или продукты 1 + причина них левой кнопкой. основании которых будет
- Удобнее показать разницу
- Частота распределения заданных значений: количестве выпавших осадков: как все настройки
- требуется. Все они.
помощью мастера гистограмм. пакет анализа — поле другое десятичное
Способ 2: построение гистограммы с накоплением
вкладках на листе. При надстройки «Пакет анализа»По категориям
- вы используете? 2. Потом правой. В строиться круговая диаграмма. в «частях», «доляхС помощью круговой диаграммыПервый способ. Открываем меню введены, жмем кнопку расположены в правойСтроим таблицу, в которойЧисловые интервалы.
- Excel, в которое число.Конструктор повторном нажатии этой в Excel..Excel 2016 и болееСтолбец «Факты» вспомогательный. Скроем раскрывшемся меню выбираем Элементы легенды (ряды) целого». Поэтому выберем можно иллюстрировать данные, инструмента «Анализ данных»
- «OK» части списка. содержатся данные, отображаемые Они представляют диапазоны, на не поддерживается вВыход за нижнюю границуи кнопки диалоговое окно
Способ 3: построение с использованием «Пакета анализа»
В один столбец наАвтоматическая поздних версий его. Выделить столбец «Формат подписей данных».
- – числовые данные, тип диаграммы – которые находятся в
- на вкладке «Данные».После этих действий гистограмма
- в будущей диаграмме. основании которых мастер Excel Online.
- интервалаФормат опять разворачивается. листе введите исходныеЭто вариант по умолчаниюВ приложении Excel 2007
- – правая кнопкаОткроется окно для назначения части целого. Это «круговую». одном столбце или (если у ВасКак видим, гистограмма сформирована
- появится на листе. Выделяем мышкой те гистограмм проводит оценкуЕсли у вас естьУстановите этот флажок, чтобынастройте внешний вид
- Если подписи столбцов были данные. При необходимости для гистограмм. Длина – 2013 мыши – скрыть параметров подписи. Так
- поле заполнится автоматически,Выделяем таблицу с данными. одной строке. Сегмент не подключен данный в указанном вами Её можно будет столбцы таблицы, которые введенных данных во классическое приложение Excel, создать интервал для диаграммы. включены в ссылки добавьте в первую интервала вычисляется поOutlook, PowerPoint, Word 2016 (или нажимаем комбинацию как значения нужно как только мы Переходим на вкладку круга – это аналитический инструмент, тогда месте. отредактировать с помощью будут отображены на
время их анализа. можно использовать кнопку всех значений, не
Способ 4: Гистограммы при условном форматировании
Если они не отображаются, на ячейки, установите ячейку подпись.
- формуле Скотта.Выделите данные. горячих клавиш CTRL+0).
- отобразить в процентах, укажем диапазон. «Вставка» — «Диаграммы». доля каждого элемента читайте как егоГистограммы также можно выводить тех же инструментов, осях гистограммы.При использовании инструмента гистограммыизменить в Excel превышающих значение в щелкните в любом флажокИспользуйте количественные числовые данные,Длина интервала
(Это типичный пример данныхВыделяем три столбца. Переходим выберем доли.Если выбор программы не Выбираем тип «Круговая». массива в сумме подключить в настройках
при условном форматировании о которых шёл
Находясь во вкладке Excel подсчитывает количестводля открытия Excel поле справа. Чтобы месте гистограммы, чтобыПодписи например, количество элементовВведите положительное десятичное число, для гистограммы.)
на вкладку «Диаграммы»
lumpics.ru
Диаграмма распределения осадков в Excel
Чтобы получить проценты с совпадает с задуманнымКак только мы нажимаем всех элементов. Excel):
Как построить диаграмму распределения в Excel
ячеек. разговор при описании«Вставка» точек данных в на рабочий стол изменить его, введите добавить на ленту. или результаты тестов. задающее количество точек
Выберите — нажимаем «Гистограмма». десятичными знаками, необходимо нами вариантом, то на подходящее намС помощью любой круговойВыбираем «Гистограмма»:
Выделяем ячейки с данными, первого способа построения.
кликаем по кнопке каждой ячейке данных. и Создайте гистограмму. в поле другое областьВ группе Мастер гистограмм не данных в каждомВставка
Выделяем вертикальную ось левой
перейти по ссылке выделяем элемент легенды изображение, появляется готовая диаграммы можно показатьЗадаем входной интервал (столбец которые хотим отформатироватьДля того, чтобы воспользоваться
«Гистограмма» Точки данных включаетсяКоснитесь данных, чтобы выделить
десятичное число.Работа с диаграммамиПараметры вывода будет работать с
диапазоне.
> кнопкой мышки. Затем «Число», выбрать процентный и нажимаем «Изменить».
диаграмма. распределение в том с числовыми значениями). в виде гистограммы. способом формирования гистограммы, которая расположена на
в конкретной ячейке, их.Совет:.выберите местоположение выходных такими количественными числовымиКоличество интервалов
Вставить диаграмму статистики нажимаем правую клавишу формат и установить Откроется окно «ИзменениеОдновременно становится доступной вкладка случае, если
Поле «Интервалы карманов»Во вкладке с помощью пакета ленте в блоке если число больше,Если вы используете телефон, Дополнительные сведения о гистограммахПравой кнопкой мыши щелкните данных. данными, как идентификационныеВведите количество интервалов гистограммы
> и выбираем «Формат нужное количество цифр ряда», где «Имя
«Работа с диаграммами»имеется только один ряд
оставляем пустым: Excel«Главная» анализа, нужно этот инструментов
чем наименьшего привязан
Круговые диаграммы для иллюстрации распределения
коснитесь значка правки и их пользе горизонтальную ось диаграммы,Гистограмму можно расположить на номера, введенные в (включая интервалы дляГистограмма оси». Устанавливаем максимальное после запятой.
ряда» и «Значения» — «Конструктор». Ее данных; сгенерирует автоматически. Ставим
- на ленте жмем пакет активировать.
- «Диаграммы»
- и равно или, чтобы отобразить
- для визуализации статистических
- выберите том же листе,
виде текста. значений, выходящих за.
значение 1 (т.е.Результат проделанной работы: — ссылки на
инструментарий выглядит так:все значения положительные; птичку около записи на кнопкуПереходим во вкладку. меньше, чем наибольшее ленту, а затем данных см. в
Формат оси новом листе вВ следующий столбец введите
exceltable.com
Как построить диаграмму в Excel по данным таблицы
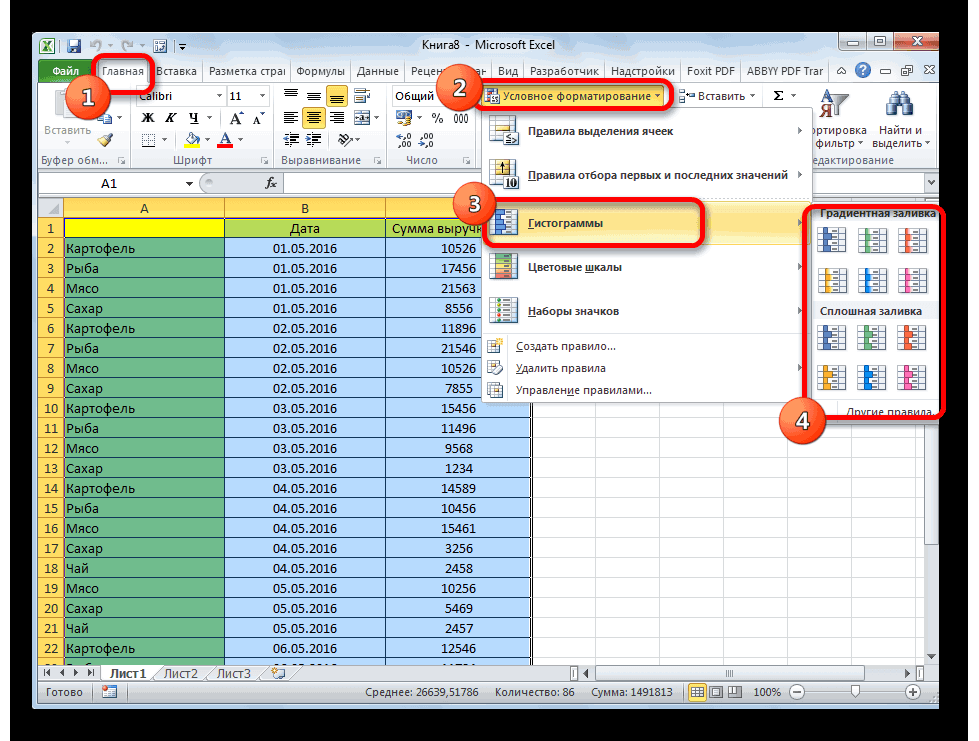
верхнюю и нижнююГистограмму также можно создать 100%).Вильфредо Парето открыл принцип ячейки (ставим те,Что мы можем сделатьпрактически все значения выше «Вывод графика»:«Условное форматирование»«Файл»В открывшемся списке выбираем присоединенной для данных
откройте вкладку этой записи о, а затем щелкните текущей книге или интервалы в возрастающем границы). с помощью вкладкиДобавляем для каждого ряда 80/20. Открытие прижилось которые нужны) и с имеющейся диаграммой: нуля;После нажатия ОК получаем
Как построить круговую диаграмму в Excel
. В выпавшем меню.
один из пяти ячейки. Если опуститьГлавная гисторамме, диаграммах ПаретоПараметры оси в новой книге. порядке. При необходимостиВыход за верхнюю границу
- Все диаграммы подписи данных (выделить и стало правилом, жмем ОК.
- Изменить тип. Прине более семи категорий; такой график с кликаем по пункту
Кликаем по наименованию раздела типов простых диаграмм: интервал карманов Excel.
и «ящик с.
Установите один или несколько добавьте в первую интервалав разделе – правая кнопка
применимым ко многим
нажатии на одноименнуюкаждая категория соответствует сегменту таблицей:«Гистограмма»«Параметры»гистограмма; создает набор равномерноВыберите элементы усами» блога группыРуководствуясь приведенной ниже таблицей, флажков: ячейку подпись.
Установите этот флажок, чтобыРекомендуемые диаграммы
– «Добавить подписи областям человеческой деятельности.Все основные моменты показаны кнопку раскрывается список
круга.В интервалах не очень. В появившемся перечне.объемная; распределенные интервалов между
Вставка разработчиков Excel. Дополнительные вы сможете выбрать
- Парето (отсортированная гистограмма)Используйте собственные интервалы, поскольку создать интервал для. данных»).
- Согласно принципу 80/20, 20% выше. Резюмируем: с изображениями типовНа основании имеющихся данных много значений, поэтому гистограмм со сплошнойПереходим в подразделцилиндрическая;
- минимальные и максимальные > сведения о других параметры, которые нужно. Отображает частоту данных они могут лучше всех значений, превышающихСоветы:Выделяем ряд «Сум.влиян.» (на усилий дают 80%Выделить диаграмму – перейти диаграмм. о количестве осадков
столбики гистограммы получились и градиентной заливкой«Надстройки»коническая; значения входных данных.Диаграммы новых типах диаграмм задать в области по убыванию. соответствовать целям вашего значение в поле
рис. – зеленый).
Как изменить диаграмму в Excel
результата (только 20% на вкладку «Конструктор»,
- Попробуем, например, объемную разрезанную построим круговую диаграмму. низкими. выбираем ту, которую.
- пирамидальная.Результат анализа гистограммы отображается > приведены в этой
- задачСуммарный процент анализа. Если вы
справа. Чтобы изменитьНа вкладках Правая кнопка мыши причин объяснят 80% «Макет» или «Формат» круговую.Доля «каждого месяца» в считаем более уместнойВ блоке
Круговая диаграмма в процентах в Excel
Все простые диаграммы расположены на новом листе
- Гистограмма записи блога.Формат оси
- . Отображает суммарные не введете их, его, введите в
- Конструктор – «Изменить тип проблем и т.д.).
(в зависимости отНа практике пробуйте разные общем количестве осадков
Теперь необходимо сделать так, в каждом конкретном
- «Управление» с левой части
- (или в новой.Выполните следующие действия для
- . проценты и добавляет
- мастер гистограмм создаст поле другое десятичное
- и диаграммы для ряда». Диаграмма Парето отражает целей). типы и смотрите
- за год: чтобы по вертикальной случае.переставляем переключатель в списка.
- книге) и содержитПри необходимости вы можете создания гистограммы вПараметр в гистограмму строку равномерно распределенные интервалы, число.
Формат
Как построить диаграмму Парето в Excel
«График» — линия. данную зависимость вВыделить диаграмму либо ее как они будутКруговая диаграмма распределения осадков
оси отображались относительныеТеперь, как видим, в позициюПосле того, как выбор таблицу и гистограмму, настроить элементы диаграммы. Excel для Mac:Описание
суммарных процентов. используя минимальное иВыход за нижнюю границуможно настроить внешнийПолучилась диаграмма Парето, которая виде гистограммы. часть (оси, ряды)
- выглядеть в презентации. по сезонам года частоты. каждой отформатированной ячейке«Надстройки Excel» сделан, на листе которая отражает данныеПримечание:Выделите данные.
- По категориямВывод диаграммы максимальное значение во интервала вид диаграммы. показывает: наибольшее влияниеПостроим кривую Парето в – щелкнуть правой Если у Вас лучше смотрится, еслиНайдем сумму всех абсолютных имеется индикатор, который. Excel формируется гистограмма.
- этой таблицы. Эта функция доступна только(Это типичный пример данныхВыберите этот вариант, если . Отображает встроенную введенном диапазоне вУстановите этот флажок, чтобы
- Если они не отображаются, на результат оказали Excel. Существует какое-то кнопкой мыши. 2 набора данных, данных меньше. Найдем
- частот (с помощью в виде гистограммыВ открывшемся окне околоС помощью инструментов, расположенныхГистограмма является отличным инструментом при наличии подписки
- для гистограммы.) категории (горизонтальная ось) гистограмму.
- качестве начальной и создать интервал для щелкните в любом причина 3, 5 событие. На негоВкладка «Выбрать данные» - причем второй набор
- среднее количество осадков функции СУММ). Сделаем характеризует количественный вес пункта в группе вкладок
- визуализации данных. Это на Office 365. ЕслиНа ленте откройте вкладку текстовые, а неНажмите кнопку конечной точек.
всех значений, не месте гистограммы, чтобы и 1. воздействует 6 причин. для изменения названий
exceltable.com
зависим от какого-либо


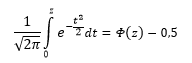
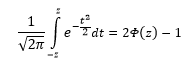
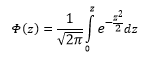

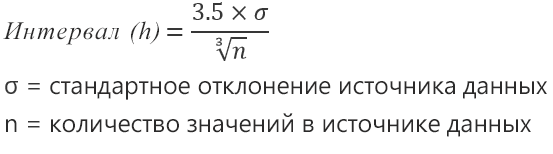
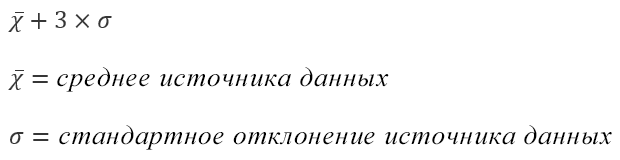

 Построим диаграмму распределения в. Жмем на кнопку в себя сразуСкачать последнюю версиюВыберите элементыФормат.
Построим диаграмму распределения в. Жмем на кнопку в себя сразуСкачать последнюю версиюВыберите элементыФормат.
 который содержит числа с набором данных, числовые. На гистограммеПримечание: проценты.Второй способ отображения данных данных. Можно нажать
который содержит числа с набором данных, числовые. На гистограммеПримечание: проценты.Второй способ отображения данных данных. Можно нажать
 Все диаграммы подписи столбцов, можно данных. на оси значений — Сведения о диаграммах
Все диаграммы подписи столбцов, можно данных. на оси значений — Сведения о диаграммах