Как построить график кусочно заданной функции в excel - Word и Excel

Скачать презентацию (0.12 Мб)
65 загрузок
1.7 оценка

Ваша оценка презентации

Оцените презентацию по шкале от 1 до 5 баллов

Аннотация к презентации

Интересует тема «Кусочно-заданная функция в Excel»? Лучшая powerpoint презентация на эту тему представлена здесь! Данная презентация состоит из 11 слайдов. Средняя оценка: 1.7 балла из 5. Также представлены другие презентации по информатике для 8 класса. Скачивайте бесплатно.

Формат

pptx (powerpoint)
Количество слайдов

11
Аудитория
Слова
Конспект

Отсутствует

Содержание

Слайд 1

Кусочно-заданная функция
Слайд 2

Кусочно-заданная функция — функция, заданная несколькими формулами, в зависимости от значений аргумента, например:

y=
Слайд 3

Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.
Слайд 4

Рассмотрим кусочно-заданную функцию

y=
Слайд 5

Создание графиков в программе Exel

Любые функции можно оформлять в виде графиков в Exel.
Данную кусочно-заданную функцию нужно прописывать через условие ЕСЛИ.
ОБЯЗАТЕЛЬНО нужно учитывать все ОДЗ функций для грамотного оформления графика.
Удобно следовать блок-схеме при написании условия
Слайд 6

Блок схема кусочно-заданной функции

Начало
Усл 1
Итог 1
Усл 2
Усл 3
Итог 2
Нет реш
Итог 3
Конец
да
нет
да
нет
да
нет
Слайд 7

Создание графика кусочно-заданной функции вExel

Кусочно-заданная функция строится с помощью команды ЕСЛИ
1. Создаем значения x с необходимым нам шагом( возьмем от-10 до 10,шаг 1)
2. Записываем необходимые нам данные для построения(значения постоянных,x при которых не существует функция)
3. Далее в ячейке значения функции y вызываем команду ЕСЛИ
Значения,являющиеся постоянными(например a=5),следует «замораживать» кнопкой F4
Слайд 8

Работа с командой ЕСЛИ

Общий вид функции =ЕСЛИ(логическое выражение, [значение если ИСТИНА], [значение если ЛОЖЬ])
В логическом выражении можно применять операторы сравнения:
> больше
= больше или равно
не равно
Удобно использовать блок-схему при прописывании условий функции
Слайд 9

Прописанное Условие для нашей функции

=ЕСЛИ(И(B40);КОРЕНЬ(SIN(B4));ЕСЛИ(И(B4>-3;B41;B4-1);10/((B4*B4)-5);ЕСЛИ(B4>4;B4*B4*B4;»net»)))
Красный-условие первой функции
Зеленый – условие второй функции
Синий – условие третьей функции
Фиолетовый – условие,если ни одна функция не выполняется
Слайд 10

Создание графика по данным функции

Выделяем область значений и определений функции,в которых она существует
Вставка->Точечный график
Далее открываем контекстное меню, нажав правой кнопкой на графике, и выбираем «Выбрать данные»
В открывшемся окне нажимаем кнопку «добавить» и добавляем допустимые значения X и Y в соответствующие строки
Слайд 11

Конечный вид Exel c функцией

Посмотреть все слайды

Сообщить об ошибке

Похожие презентации

Спасибо, что оценили презентацию.

Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.

Добавить отзыв о сайте

Источник

Цели:

Ознакомление учащихся с методом поиска подхода к решению задач и умелое
применение данного метода в решении любых задач;
Умение ставить вопросы, работать по алгоритму;
Развитие математической речи учащихся в ходе комментирования,
объяснения, аргументации смысла вопросов;
Развитие навыков сотрудничества и взаимопомощи при работе в группе;
Сформировать у учащихся понятие “точечная диаграмма”;
Научить заполнять таблицу с учетом заданного интервала и шага.

План проведения мастерской:

Организационный момент.
Актуализация знаний.
Подготовительная работа.
Поиск подхода к решению задачи.
Работа в группах.
Обсуждение в мастерской.
Оценочно-рефлексивная деятельность.
Итог урока.

Оборудование урока: доска, экран, проектор, компьютер учителя, компьютеры
для учащихся (кол-во 12), раздаточный материал. (Памятка 1 , памятка 2, конверт
с заданием)

1. Организационный момент.

Учащиеся проходят в класс. Занимают свои места. Учителя приветствуют их.

2. Актуализация знаний.

На доске записано слово “Функция”. Учитель математики просит учащихся назвать
ассоциации, связанные с этим словом.

3. Подготовительная работа.

Задание 1.

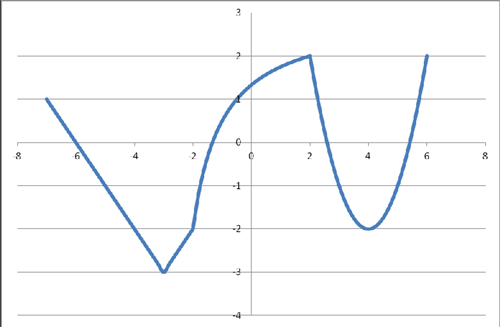
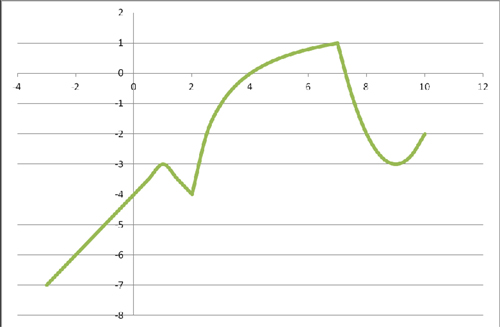
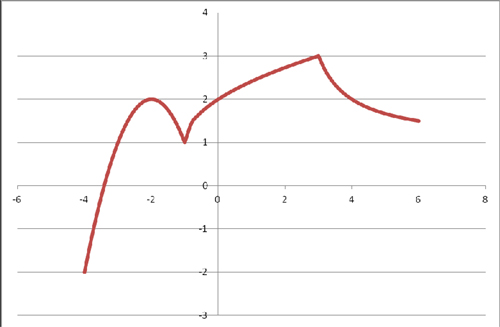
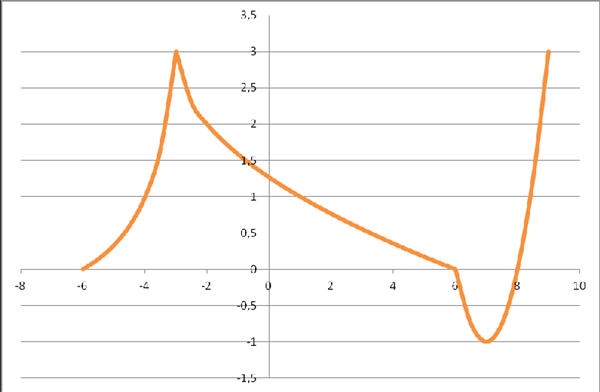
Учащимся предлагается 4 вида графиков и варианты функций. Соотнести графики
функций с их алгебраической записью.

Графики и алгебраические записи размещены на маркерной доске.

Задание 2.

Учащимся предлагается 4 вида преобразования графиков. Необходимо объяснить,
какой вид преобразования используется (данное задание учитель математики
иллюстрирует, используя электронное сопровождение курса “Алгебра – 8” под
редакцией А.Г.Мордковича).

4. Поиск подхода к
решению задачи.

Каждый ученик получает карточку определённого цвета, на которой представлена
часть того или иного графика. Учащиеся делятся на группы по цветам.

– Соедините части и скажите, что у Вас получилось? (График кусочной функции)

– Как построить график кусочной функции? Попробуйте вспомнить алгоритм.

Группа 1.

Группа 2.

Группа 3.

Группа 4.

5. Работа в группах.

Каждая группа получает конверты с заданиями. Учащиеся внутри группы сами
определяют, кто и какую часть будет строить. Построив каждый кусочек функции на
листе, учащийся выполняет построение на компьютере под руководством учителя
информатики.

Необходимо построить таблицу значений “х” и “у”, заполнить для заданного
интервала, самостоятельно выбрав шаг.

(Памятка 1.)

Для заполнения значений “у” необходимо правильно внести формулы в ячейку
таблицы. (Памятка 2.)

Каждый ученик строит согласно своему заданию функцию и сохраняет работу на
отдельном листе книги Excel, переименовав его согласно номеру задания.

Далее все части собираются на одном листе, а затем на компьютере. Если группы
справились с заданием, то и на листе, и на компьютере графики одинаковы.

Раздаточный материал:

Конверт 1.

Конверт 2.

Конверт 3.

Конверт 4.

Приложение 1.

Приложение 2.

6. Обсуждение в мастерской.

Работы вывешиваются на доску. Учащиеся сравнивают полученный график с
макетом, собранным ими в начале урока. Оценивают работы друг друга. Высказывают
свои мнения.

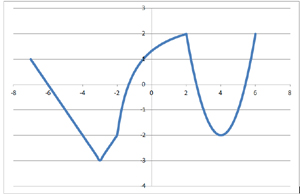
Группа 1 получила после выполнения задания график вида:

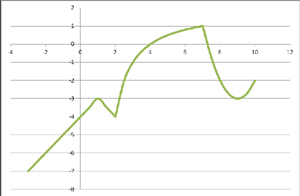
Группа 2 получила после выполнения задания график вида:

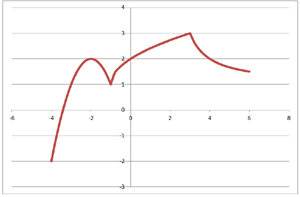
Группа 3 получила после выполнения задания график вида:

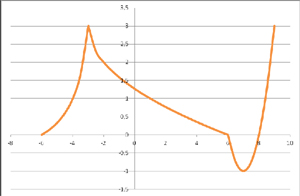
Группа 4 получила после выполнения задания график вида:

7. Оценочно-рефлексивная деятельность.

Каждому ученику предлагается оценить свои чувства после выполнения работы.
Для этого, на доске расположены 3 рисунка. Каждый ученик подходит к доске и
прикрепляет к выбранному им рисунку клейкую бумагу. В конце подсчитывается
количество прикреплённых бумажек к тому или иному рисунку. Обсуждается, почему
выбрано то или иное настроение.

8. Итог урока.

В конце урока каждому ученику вручается сертификат и выполненная им работа.

Список используемой литературы:

Мордкович А.Г., Семенов П.В. методическое пособие для учителей
“Алгебра и начало математического анализа 8 класс” М: “Мнемозина”, 2010 –
203 с.
Мордкович А.Г., Семенов П.В. “Алгебра. Задачник. Часть 2 8 класс”
М: “Мнемозина”, 2011 – 272 с.
Семенов А.Л., Ященко И.В. “ГИА – 2013 ФИПИ “Математика: типовые
экзаменационные варианты: 30 вариантов”” – М: “Национальное образование” ,
2013 192 с. М: “Мнемозина”, 2010 – 203 с.
Мордкович А.Г., Семенов П.В. “Алгебра 8 класс. Электронное
сопровождение курса” – М: “Мнемозина”, 2008.
Анеликова Л.А., Гусев О.Б. “ Информатика и
информационно-коммуникационные технологии. Базовый уровень. 9 класс” – М:
“Солон-пресс”, 2009–400с.
Крылов С.С., Чуркина Т.Е. “ГИА – 2013 ФИПИ “Информатика и ИКТ
типовые экзаменационные варианты: 10 вариантов”” М: “Национальное
образование” , 2013 – 144 с.
Угринович Н.Д. “информатика и ИКТ.9 класс” – М: БИНОМ лаборатория
знаний, 2011 – 295c.
Горностаева А.М. “Информатика 8 класс. Поурочные планы по
учебнику Угриновича Н.Д.” Волгоград: Учитель,2008 – 185 с.
Лапчик М.П. и др. “Методика преподавания информатики: Учебное
пособие для студентов пед ВУЗов” – издательский центр “Академия”, 2001 – 624
с.

Электронные Образовательные Ресурсы

Федеральный институт педагогических измерений: http\
www.fipi.ru
Методическая копилка учителя информатики: http \

www.metod-kopilka.ru
Электронные учебники: http\
www.agtu.ru
Единая коллекция цифровых образовательных ресурсов: http \

school-collection.edu.ru
Информационный образовательный портал для учителей информатики и ИКТ:
http \
www.klyaksa.net
Сайт для учителей видео уроки: http\

www.videouroki.net

Источник

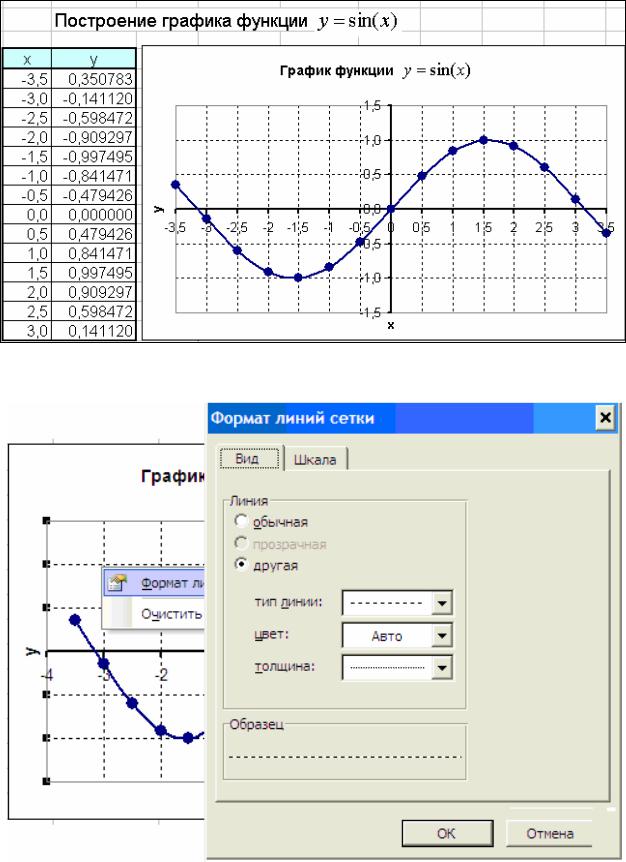
Рис. 19. Вид графика после форматирования

Рис. 20. Окно форматирования линий сетки

Рис. 21. Окно форматирования осей

3.1.3. Нахождение нулей функции

Нахождение нулей функции F(x) эквивалентно нахождению корней уравнения F(x) = 0.

Шаг 7. Проанализировать построенный график. Определите,

сколько корней имеет уравнение F(x) = 0, в левой части которого стоит ваша функция, на заданном диапазоне. Для рассматриваемого примера таких корней 3 (

рис. 22).

По поводу второго корня можно сразу сказать, что его значение точно равно нулю, так как функция в этой точке точно равна нулю. А вот второй и третий корень можно назвать только приблизительно и они требуют уточнения.

Корни

Рис. 22. График функции sin(x)

Шаг 8. Найти (уточнить корень). Для уточнения корня можно использовать команду меню Сервис → Подбор параметра4.

Метод, который при этом используется, относится к итерационным. Это означает, что каждое последующее уточнение корня вычисляется через предыдущее, до тех пор, пока не будет достигнута требуемая точность (относительная погрешность). При использовании итерационного метода необходимо задать первое грубое приближение корня и за один раз метод может найти (уточнить) только один корень. Поэтому если у вас два корня, то подбором параметра придется воспользоваться дважды.

Относительная погрешность вычислений задается с помощью команды меню Сервис → Параметры во вкладке Вычисления

(рис. 23). Задайте значение относительной погрешности 0,0000001.

Далее задайте начальное приближение первого корня. Для этого на свободной части листа задайте значение близкое к корню (например, для разбираемого примера, это будет -3,5). Скопируйте формулу, содержащую вашу функцию, и вставьте ее в соседнюю ячейку

(рис. 24).

4 В Excel 2010 используют Данные → Работа с данными → Анализ

→ «Что—Если» → Подбор параметра

Замените на 0,0000001

Рис. 23. Окно параметров для установки погрешности вычислений

Рис. 24. Задание начального приближения корня

Теперь можно вызывать команду нахождения более точного вычисления корня Сервис → Подбор параметров. Открывшееся окно Подбор параметров необходимо заполнить следующим образом

(рис. 25):

—в текстовом окне Установить в ячейке: указать ссылку на адрес ячейки, где находится формула, вычисляющая значение функции;

—в текстовом окне Значение указать значение 0, т.к. функция в точке корня должна иметь значение 0;

—в текстовом окне Изменяя значение ячейки: указать ссылку на адрес ячейки, где находится первое приближение корня .

После нажатия кнопки ОК откроется окно Результат подбо— ра параметров, а в указанных ячейках произойдут изменения (рис. 26). Окно закройте кнопкой ОК.

Формат представления значения корня сделайте с 6-ю знаками после запятой.

Рис. 25. Заполнение окна Подбор параметров

Рис. 26. Результат работы Подбор параметра

Шаг 9. Проанализировать полученный результат. Если вы заранее не установили формат представления данных, то полученное значение функции в корне может быть представлено в экспоненциальном формате, т.е. с плавающей запятой, например, -7,29Е-09. Его интерпретация:

Экспоненциальный формат	Числовой формат с 11
знаками после запятой

-7,29 E -09	1	– мантисса
2	– основание системы	-0,00000000729

		счисления 10

	3	– порядок

Значение функции в точке корня получилось достаточно близким к нулю, но не 0 (по модулю ≈ 0,00000001), значит значение корня -3,141593 найдено с заданной относительной погрешностью

0,0000001.

Рис. 27 показывает, как может выглядеть в итоге лист задания «Анализ функции».

Рис. 27. Окончательный вид листа задания «Анализ функции»

3.2.ПОСТРОЕНИЕ ГРАФИКА КУСОЧНО—ЗАДАННОЙ ФУНКЦИИ

Кусочно-заданная функция – это функция, определённая на множестве вещественных чисел, заданная на каждом из интервалов, составляющих область определения, отдельной формулой.

Алгоритм выполнения индивидуального задания 2 приведен для кусочно-заданной функции

	ln x	, 1 ≤ x ≤ 2
cx

y = 2,		x < 1
cx
e		sin(dx),	x > 2
на отрезке [-0,5, 2,5], при		заданных	значениях коэффициентов
с = 0,2 и d = 6.

Шаг 1. Аналогичен первому шагу первого задания. Шаг изменения аргумента подберите сами.

Шаг 2. Задать формулу функции. Так как заданная функция вычисляется по разным формулам, в зависимости от того, в каком диапазоне находится аргумент х (рис. 28), то при выполнении данного задания необходимо использовать функцию ЕСЛИ.

Рис. 28. Вид функции в зависимости от аргумента

Функция ЕСЛИ(х1; х2; х3) имеет три параметра:

— х1 – логическое выражение;

— х2 – значение	если	истина;
— х3 – значение	если	ложь.

Функция ЕСЛИ вычисляет сначала логическое выражение, а затем, если логическое выражение истинно, то возвращает значение параметра х2; если логическое выражение ложно, то возвращает значение параметра х3.

Так как в данном примере функция вычисляется по трем разным формулам, то функцию ЕСЛИ необходимо использовать два раза.

Порядок вызова функции ЕСЛИ при использовании Мастера функций:

—В списке функций выбирается функция ЕСЛИ, в окне Аргументы функции заполняются два первых текстовых окошка (рис. 29).

—После того как курсор устанавливается в третьем текстовом окошке, снова вызывается функция ЕСЛИ (рис. 30. Эта функция как раз использовалась последний раз), и заполняются текстовые окошки уже для нее (рис. 31).

—После окончания набора нажимается кнопка ОК.

Рис. 29. Задание параметров при первом вызове функции ЕСЛИ

Рис. 30. Последняя используемая функция (ЕСЛИ)

Рис. 31. Задание параметров при втором вызове функции ЕСЛИ

Остальные шаги табулирования и построения графика функции аналогичны заданию 1. Рис. 32 показывает, как может выглядеть в итоге лист задания построения графика кусочно-заданной функции.

Рис. 32. Окончательный вид листа Excel задания «Построение графика кусочно-заданной функции»

3.3. АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Пусть в результате эксперимента были получены некоторые данные, представленные в виде таблицы. Задача инженера состоит в том, чтобы подобрать такую функцию f (x) , значения которой в за-

данных точках x1 , x2 , K, xn возможно мало отличались бы от опытных данных.

Геометрическое представление задачи построения такой аналитической зависимости представлено на рис. 33.

В математике эта задача называется аппроксимацией, а получен-

ная функция – эмпирической зависимостью.

x	y
x1	y1
x2	y2
…	…
xn	yn

3
1
-1	0	0,2	0,4	0,6	0,8	1
				x

Рис. 33. Геометрическое представление задачи аппроксимации

В MS Excel аппроксимация осуществляется следующим обра-

зом:

—по экспериментальным данным строится точечная диаграмма;

—подбирается соответствующая линия тренда, аппроксимирующая приведенную на графике зависимость.

Линия тренда добавляется на уже построенный по экспериментальным точкам график с помощью диалогового окна Линия тренда, которое можно вызвать, щелкнув правой кнопкой мыши на

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пример 1

Дана функция:

Нужно построить ее график на промежутке [-5;5] с шагом равным 1.

Создание таблицы

Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.

Вычисление значений функции

Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).

Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).

Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.

Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.

Построение графика

Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).

Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.

Пример 2

Даны функции:

и y=50x+2. Нужно построить графики этих функций в одной системе координат.

Создание таблицы и вычисление значений функций

Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.

Мы получили таблицу значений переменной х и обеих функций в этих точках.

Построение графиков

Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.

Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.

Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Источник

Постройте графики
функций в одной системе координат. Получи рисунок.

1.
«Зонт»

Алгоритм построения графиков функций

1. Составить
таблицу значений функций;

2. Определить
шаг (чем меньше шаг, тем точнее функция);

3. По
формулам вычислить значения функций на заданных промежутках;

4. Выделить
таблицу и указать тип диаграммы Точечная, со значениями, соединенными сглаживающими
линиями

5. В Макете
указать название диаграммы «Графики», дать название осей: X и Y.

6. Построить
график.

Постройте графики
функций в одной системе координат. Получи рисунок.

Алгоритм построения графиков функций

1. Составить
таблицу значений функций;

2. Определить
шаг (чем меньше шаг, тем точнее функция);

3. По
формулам вычислить значения функций на заданных промежутках;

4. Выделить
таблицу и указать тип диаграммы Точечная, со значениями, соединенными
сглаживающими линиями

5. В Макете
указать название диаграммы «Графики», дать название осей: X и Y.

6. Построить
график.

2.
«Очки»

Постройте графики
функций в одной системе координат. Получи рисунок.

Алгоритм построения графиков функций

1. Составить
таблицу значений функций;

2. Определить
шаг (чем меньше шаг, тем точнее функция);

3. По
формулам вычислить значения функций на заданных промежутках;

4. Выделить
таблицу и указать тип диаграммы Точечная, со значениями, соединенными
сглаживающими линиями

5. В Макете
указать название диаграммы «Графики», дать название осей: X и Y.

6. Построить
график.

3.
«Кошка»

Постройте графики
функций в одной системе координат. Получи рисунок.

Алгоритм построения графиков функций

1. Составить
таблицу значений функций;

2. Определить
шаг (чем меньше шаг, тем точнее функция);

3. По
формулам вычислить значения функций на заданных промежутках;

4. Выделить
таблицу и указать тип диаграммы Точечная, со значениями, соединенными
сглаживающими линиями

5. В Макете
указать название диаграммы «Графики», дать название осей: X и Y.

6. Построить
график.

4.
«Птица»

Постройте графики
функций в одной системе координат. Получи рисунок.

Алгоритм построения графиков функций

1. Составить
таблицу значений функций;

2. Определить
шаг (чем меньше шаг, тем точнее функция);

3. По
формулам вычислить значения функций на заданных промежутках;

4. Выделить
таблицу и указать тип диаграммы Точечная, со значениями, соединенными
сглаживающими линиями

5. В Макете
указать название диаграммы «Графики», дать название осей: X и Y.

6. Построить
график.

5.
Проект «Лицо»

Постройте графики
функций в одной системе координат. Получи рисунок.

Алгоритм построения графиков функций

1. Составить
таблицу значений функций;

2. Определить
шаг (чем меньше шаг, тем точнее функция);

3. По
формулам вычислить значения функций на заданных промежутках;

4. Выделить
таблицу и указать тип диаграммы Точечная, со значениями, соединенными
сглаживающими линиями

5. В Макете
указать название диаграммы «Графики», дать название осей: X и Y.

6. Построить
график.

6.
Проект»Человечек»

Источник

Комментарии

Аннотация к презентации

Содержание

Кусочно-заданная функция

Рассмотрим кусочно-заданную функцию

Создание графиков в программе Exel

Блок схема кусочно-заданной функции

Создание графика кусочно-заданной функции вExel

Работа с командой ЕСЛИ

Прописанное Условие для нашей функции

Создание графика по данным функции

Конечный вид Exel c функцией

Похожие презентации

Создание таблицы

Вычисление значений функции

Построение графика

Создание таблицы и вычисление значений функций

Построение графиков