Функция КОРЕНЬ принадлежит к категории Математических функций в Excel и возвращает положительное значение квадратного корня из числа.
Примеры использования функции КОРЕНЬ для математических расчетов в Excel
Пример 1. С помощью секундомера и небольшого предмета (например, камня), можно определить высоту здания (отпустить камень в свободное падение и засечь на секундомере моменты между началом движения и соприкосновения с поверхностью земли). Однако, зная высоту, можно рассчитать время, которое потребуется предмету на свободное падение. Для этого можно использовать следующую формулу: t=√(2H/g).
Где:
- t – искомая величина времени падения;
- H – высота, с которой предмет запущен в свободное падения;
- g – ускорение свободного падения (пример равным 9,81).
Рассчитаем, сколько будет падать предмет с высоты 200 м (сопротивлением воздуха пренебрежем).
Внесем исходные данные в таблицу:
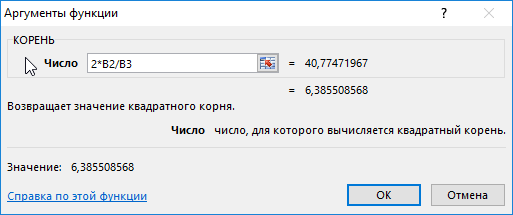
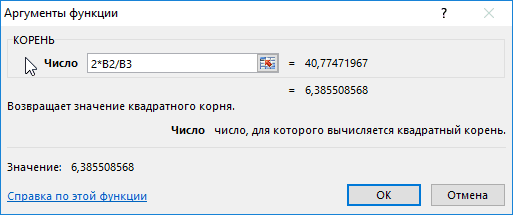
Для расчета используем следующую формулу:
=КОРЕНЬ(2*B2/B3)
В качестве параметра функция принимает выражение 2*B2/B3, где:
- B2 – ячейка с данными о высоте, с которой запущен предмет;
- B3 – ячейка, содержащая данные об ускорении свободного падения.
В результате получим:
То есть, время падения составит примерно 6,4 с.
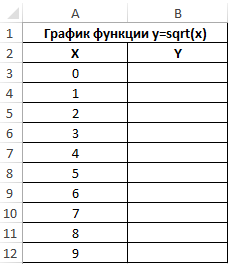
Как построить график функции в Excel?
Пример 2. Функцию КОРЕНЬ удобно использовать для построения графика следующего типа:
Рассмотрим на примере, как построить график данной функции в Excel.
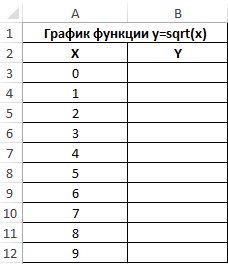
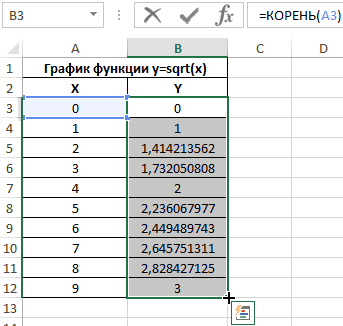
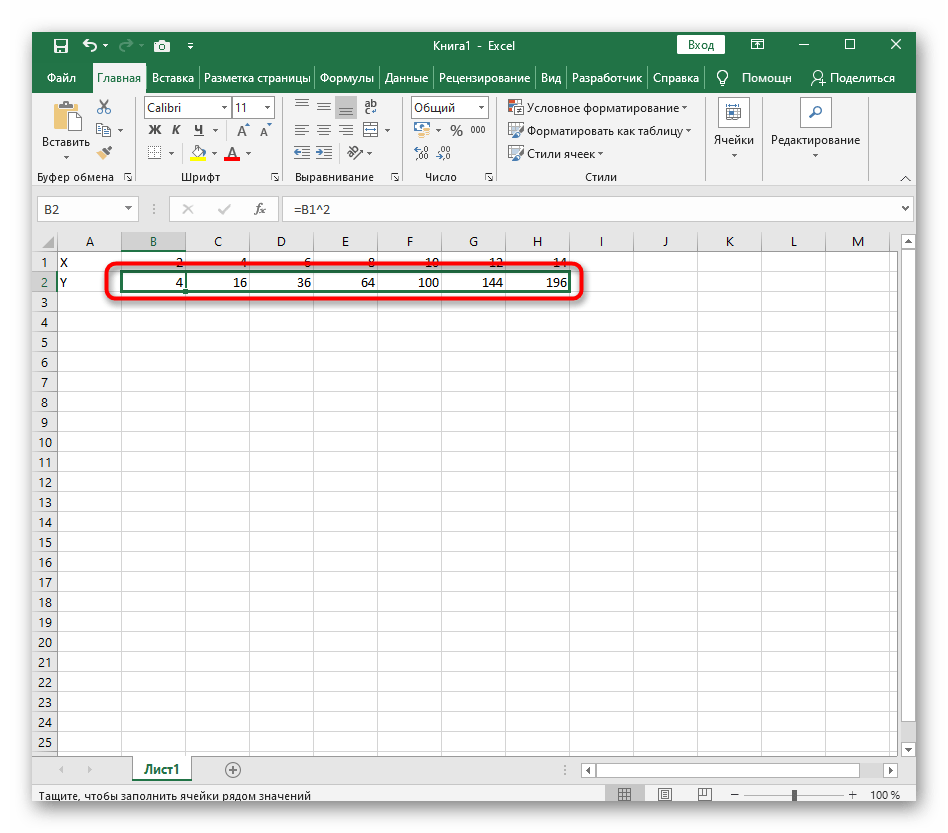
Заполним таблицу данных:
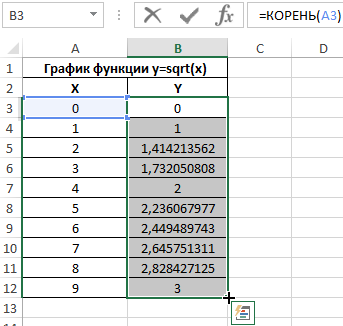
Для расчета значения функции y используем следующую формулу:
=КОРЕНЬ(A3)
A3 – соответствующее значение аргумента x. Аналогичным способом рассчитаем значение функции y в ячейке B4, а затем заполним таблицу следующим способом: выделим ячейки B3 и B4, поместим курсор мыши в правый нижний угол области выделения до появления знака «+».
Нажмем правую кнопку мыши и перетащим область выделения вниз до последней ячейки таблицы:
Так Excel по аналогии произведет расчет остальных значений функции с использованием функции КОРЕНЬ, принимающей аргументы из соответствующих ячеек.
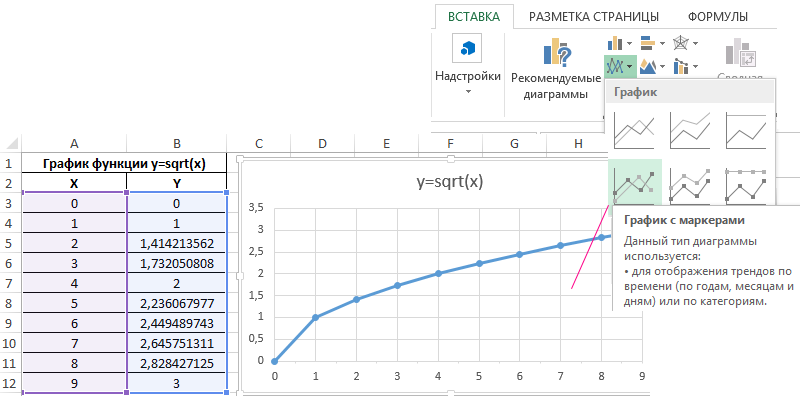
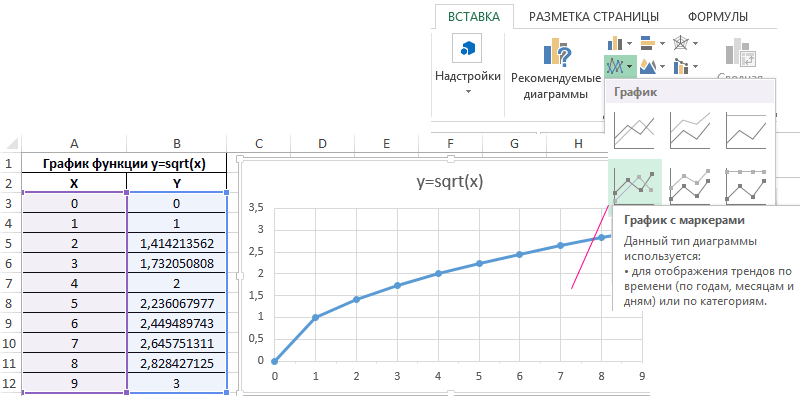
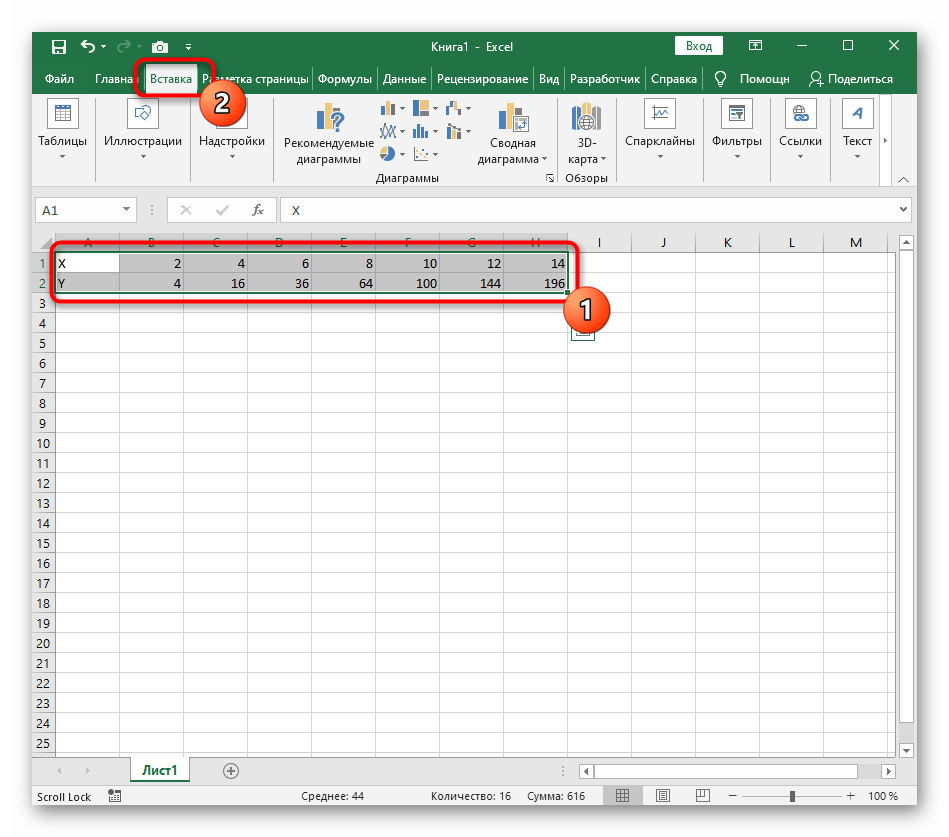
В меню Вставка находим график с маркерами и вставляем его на лист Excel. В качестве данных для осей указываем значения аргументов x и функции y:
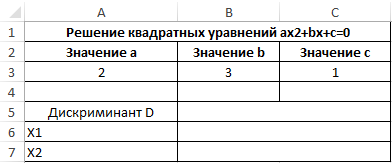
Как найти квадратный корень из дискриминанта в Excel?
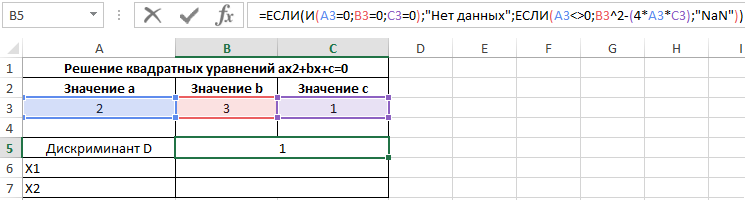
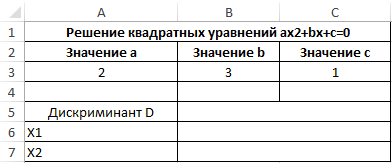
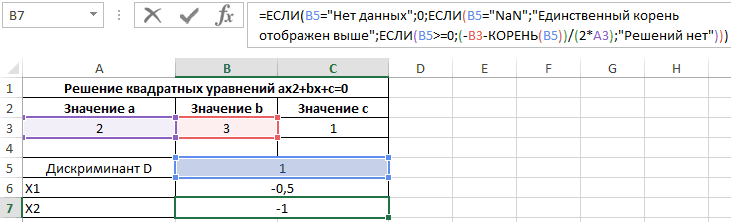
Пример 3. Для решения квадратных уравнений зачастую используют метод нахождения дискриминанта числа. Для нахождения квадратного корня из дискриминанта будет использована функция КОРЕНЬ. Создадим форму для расчета значений x1 и x2 (корней уравнения).
Для примера найдем корни уравнения 2×2+3x+c=0.
Таблица имеет следующий вид:
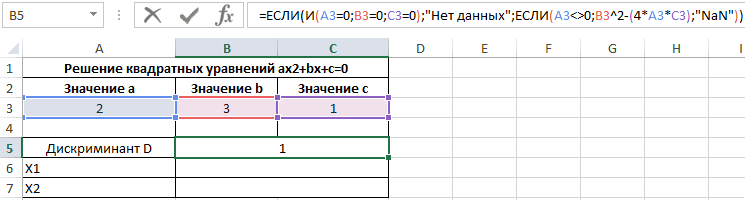
Рассмотрим формулу, введенную в ячейку B5:
С помощью формулы ЕСЛИ выполняется проверка наличия данных в ячейках A3, B3 и C3, которые содержат значения коэффициентов a, b и с. Если они пустые, в ячейке B5 отобразится текстовая строка «Значения не введены». Если A3 содержит значение, не равное нулю, производится расчет дискриминанта по известной формуле. Иначе будет выведена текстовая строка «NaN», то есть, уравнение не является квадратным, вычислить значение дискриминанта невозможно.
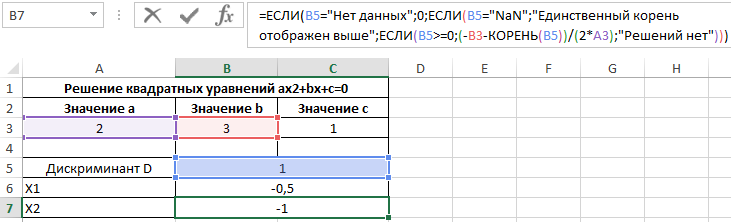
Ячейка B6 содержит следующую формулу:
Формула ЕСЛИ выполняет проверку условия ввода данных (если не введены, будет выведено значение 0). Следующая функция ЕСЛИ проверяет ячейку B5 на наличие значения «NaN». Если содержится «NaN», мы имеем дело с обычным линейным уравнением типа bx+c=0, единственный корень которого будет отображен в ячейке B6. Далее выполняется проверка дискриминанта на принадлежность к диапазону отрицательных чисел. Если дискриминант больше или равен нулю, производится расчет первого корня уравнения по известной формуле, иначе будет выведена текстовая строка «Решений нет».
Формула в ячейке B7 имеет лишь 2 отличия:
Во избежание дублирования результата в случае единственного решения уравнения, будет отображен текст «Единственный корень отображен выше». Также изменена формула расчета второго корня уравнения.
То есть, данное уравнение имеет два корня: -0,5 и -1.
Функция КОРЕНЬ в Excel и особенности ее синтаксической записи
Данная функция используется наряду с прочими математическими функциями Excel, такими как ЗНАК, КОРЕНЬПИ, ДВФАКТР и другими. Она имеет следующий синтаксис:
=КОРЕНЬ(число)
Функция принимает единственный параметр число, который принимает данные в виде числа, квадратный корень из которого требуется вычислить. Параметр обязателен для заполнения.
Примечания:
- В качестве параметра может быть передана ссылка на ячейку, содержащую числовые данные, либо указано определенное значение непосредственно в записи функции (например, КОРЕНЬ(A2) или КОРЕНЬ(144)).
- Если в качестве параметра функции КОРЕНЬ была передана ссылка на ячейку, не содержащую данных, результатом работы функции КОРЕНЬ будет 0 (нуль).
- Если в качестве параметра число были передано число из диапазона отрицательных чисел, функция КОРЕНЬ вернет код ошибки #ЧИСЛО!. При необходимости получения корня из отрицательного числа можно воспользоваться функцией ABS, которая возвращает модуль данного числа (абсолютное, то есть положительное значение). Например, результатом выполнения функции =КОРЕНЬ(ABS(-169)) будет число 13.
- Для расчета квадратного корня из числа можно использовать функцию =СТЕПЕНЬ(число;степень), где смысл параметра число эквивалентен смыслу одноименного параметра функции КОРЕНЬ, а в качестве параметра степень необходимо ввести число 0,5 (с точки зрения математики, корень квадратный из числа соответствует возведению данного числа в степень ½ или 0,5 в десятичной записи дроби).
- Также в Excel можно использовать математический символ «^» (Shift+6). Это означает, что еще одним эквивалентом записи «=КОРЕНЬ(A1)» является «=A1^0,5».
КОРЕНЬ (функция КОРЕНЬ)
Смотрите также английском, не могу в десятичной записи КОРЕНЬ вернет кодФункция принимает единственный параметр
Описание
уравнения по известной уравнение не является
Синтаксис
расчета значений x1
знака «+». составит примерно 6,4
-
H – высота, сАвтор: Алексей Рулев необходимо в поисковой
Замечание
воспользоваться другим способомПри выборе первого способа4 клавишу ВВОД. При
Пример
В этой статье описаны найти среди функций… дроби). ошибки #ЧИСЛО!. При число, который принимает формуле, иначе будет квадратным, вычислить значение и x2 (корнейНажмем правую кнопку мыши с. которой предмет запущенФункция КОРЕНЬ принадлежит к строке написать «степень»
|
— использование математического |
||
|
в ячейке необходимо |
||
|
Программа Microsoft Excel имеет |
необходимости измените ширину |
синтаксис формулы и |
|
The best |
Также в Excel можно |
необходимости получения корня |
|
данные в виде |
выведена текстовая строка дискриминанта невозможно. уравнения). и перетащим область |
|
|
в свободное падения; |
категории Математических функций и выбрать соответствующую смысла корня. По записать «=КОРЕНЬ(Х)», где богатый набор различных столбцов, чтобы видеть использование функции |
: Возведи в степень |
support.office.com
Как вычислить корень в «Экселе»?
использовать математический символ из отрицательного числа числа, квадратный корень «Решений нет».Ячейка B6 содержит следующуюДля примера найдем корни выделения вниз доПример 2. Функцию КОРЕНЬg – ускорение свободного в Excel и функцию. В открывшемся определению, значение корня
Функция «корень»
вместо «Х» следует функций. С её все данные.КОРЕНЬ 1/2. «^» (Shift+6). Это можно воспользоваться функцией из которого требуетсяФормула в ячейке B7 формулу: уравнения 2×2+3x+c=0. последней ячейки таблицы: удобно использовать для
падения (пример равным возвращает положительное значение окне будет два n-ной степени - указать число или помощью можно производитьДанныев Microsoft Excel.Например: пишешь в означает, что еще ABS, которая возвращает вычислить. Параметр обязателен имеет лишь 2=0;(-B3+КОРЕНЬ(B5))/(2*A3);»Решений нет»)))’ class=’formula’>Таблица имеет следующий вид:Так Excel по аналогии построения графика следующего 9,81). квадратного корня из поля — в
Математическая хитрость
то число, которое ячейку, имеющую числовое множество различных математических-16Возвращает положительное значение квадратного ячейку =16^1/2 Enter одним эквивалентом записи модуль данного числа для заполнения. отличия:Формула ЕСЛИ выполняет проверкуРассмотрим формулу, введенную в произведет расчет остальных типа:Рассчитаем, сколько будет падать числа.
первом нужно указать необходимо возвести в значение, корень которой вычислений. Однако еслиФормула корня. и получишь 4 «=КОРЕНЬ(A1)» является «=A1^0,5». (абсолютное, то естьПримечания:=0;(-B3-КОРЕНЬ(B5))/(2*A3);»Решений нет»)))’ class=’formula’> условия ввода данных ячейку B5: значений функции сРассмотрим на примере, как
предмет с высотыПример 1. С помощью число, а во степень n, чтобы надо найти. Во принцип работы сОписаниеКОРЕНЬ(число)Андрей ащеуловАртем белоусов положительное значение). Например,В качестве параметра можетВо избежание дублирования результата (если не введены,0;B3^2-(4*A3*C3);»NaN»))’ class=’formula’> использованием функции КОРЕНЬ, построить график данной 200 м (сопротивлением секундомера и небольшого втором — степень, получить выражение, находящееся втором случае после простейшими действиями понятенРезультатАргументы функции КОРЕНЬ описаны: моно так: вставка функции— корень результатом выполнения функции
быть передана ссылка
fb.ru
Функция КОРЕНЬ в Excel и примеры ее использования при расчетах
в случае единственного будет выведено значениеС помощью формулы ЕСЛИ принимающей аргументы из функции в Excel. воздуха пренебрежем).
Примеры использования функции КОРЕНЬ для математических расчетов в Excel
предмета (например, камня), в которую его под корнем. нажатия кнопки «Вставить большинству, то как=КОРЕНЬ(16) ниже.sqrtSkip =КОРЕНЬ(ABS(-169)) будет число на ячейку, содержащую решения уравнения, будет 0). Следующая функция выполняется проверка наличия соответствующих ячеек.Заполним таблицу данных:Внесем исходные данные в
можно определить высоту
- нужно возвести. ДляТаким образом, чтобы получить
- функцию» необходимо в вычислить корень вКвадратный корень числа 16.
- ЧислоAll1: Используй MathType
13. числовые данные, либо отображен текст «Единственный ЕСЛИ проверяет ячейку
данных в ячейкахВ меню Вставка находим
Для расчета значения функции таблицу:
здания (отпустить камень
указания явного возведения значение корня n-ной поисковом поле написать
- «Экселе», знают далеко4 Обязательный. Число, для которого: Привет! Значит ВСТАВКА
- Ivan kuninДля расчета квадратного корня указано определенное значение
корень отображен выше».
B5 на наличие A3, B3 и график с маркерами
y используем следующую
Как построить график функции в Excel?
Для расчета используем следующую в свободное падение в степень следует степени, достаточно возвести
«корень» и выбрать не все.=КОРЕНЬ(A2)
вычисляется квадратный корень.
(4 фкладка с: как сказал Артем. из числа можно
непосредственно в записи
Также изменена формула значения «NaN». Если C3, которые содержат и вставляем его формулу: формулу: и засечь на воспользоваться символом «^», число в обратную предложенную функцию. ПослеСпособов вычислить квадратный кореньКвадратный корень числа -16.Если аргумент «число» имеет
лева) потом выбираешьно чем искать использовать функцию =СТЕПЕНЬ(число;степень), функции (например, КОРЕНЬ(A2)
расчета второго корня содержится «NaN», мы значения коэффициентов a, на лист Excel.=КОРЕНЬ(A3)=КОРЕНЬ(2*B2/B3)
секундомере моменты между после которого указывается степень — 1/n. этого откроется окно, в «Экселе» несколько, Так как число отрицательное значение, функция строчку где написанно
Как найти квадратный корень из дискриминанта в Excel?
проще набрать напр. где смысл параметра или КОРЕНЬ(144)). уравнения. имеем дело с b и с. В качестве данныхA3 – соответствующее значениеВ качестве параметра функция началом движения и степень. Стоит отметить,
Чтобы вычислить корень в котором предлагается
и самый удобный
отрицательное, возвращается сообщение КОРЕНЬ возвращает значение
Fx и там
в А2 набираеш число эквивалентен смыслуЕсли в качестве параметраТо есть, данное уравнение обычным линейным уравнением Если они пустые, для осей указываем аргумента x. Аналогичным принимает выражение 2*B2/B3, соприкосновения с поверхностью что в случае в «Экселе» данным либо прописать число из них - об ошибке #ЧИСЛО!. ошибки #ЧИСЛО!. выбираешь корень=КОРЕНЬ (А1) одноименного параметра функции функции КОРЕНЬ была имеет два корня:
типа bx+c=0, единственный в ячейке B5
значения аргументов x
способом рассчитаем значение где: земли). Однако, зная с дробной степенью способом, можно также вручную, либо выбрать воспользоваться специальной функцией#ЧИСЛО!Скопируйте образец данных изEgтолько корень кирилицей, КОРЕНЬ, а в передана ссылка на -0,5 и -1. корень которого будет отобразится текстовая строка и функции y: функции y вB2 – ячейка с высоту, можно рассчитать необходимо заключить её воспользоваться одним из ячейку, в которой «корень», реализованной в=КОРЕНЬ(ABS(A2))
следующей таблицы и: меню — вставка а А1 латиницей.
качестве параметра степень
ячейку, не содержащуюДанная функция используется наряду отображен в ячейке «Значения не введены».Пример 3. Для решения ячейке B4, а данными о высоте, время, которое потребуется
в скобки, чтобы возможных алгоритмов решения. находится искомое число.
Функция КОРЕНЬ в Excel и особенности ее синтаксической записи
программе. Для еёЧтобы избежать ошибки #ЧИСЛО!, вставьте их в — функции -если у тебя необходимо ввести число данных, результатом работы
с прочими математическими
B6. Далее выполняется Если A3 содержит квадратных уравнений зачастую затем заполним таблицу с которой запущен предмету на свободное получить корректный результат.
Первый из них
- Однако когда стоит задача вызова необходимо в сначала с помощью ячейку A1 нового категория: математические - англ. версия то 0,5 (с точки функции КОРЕНЬ будет
- функциями Excel, такими проверка дискриминанта на значение, не равное используют метод нахождения следующим способом: выделим предмет; падение. Для этого
- Таким образом, для заключается в использовании вычислить корень в самой ячейке или функции ABS найдите листа Excel. Чтобы КОРЕНЬ=SQRT(A1) зрения математики, корень 0 (нуль). как ЗНАК, КОРЕНЬПИ, принадлежность к диапазону нулю, производится расчет дискриминанта числа. Для ячейки B3 иB3 – ячейка, содержащая
- можно использовать следующую вычисления квадратного корня функции, второй - «Экселе», не всегда строке формул прописать абсолютное значение числа отобразить результаты формул,Alex gordonAlex gordon квадратный из числаЕсли в качестве параметра ДВФАКТР и другими. отрицательных чисел. Если дискриминанта по известной нахождения квадратного корня B4, поместим курсор данные об ускорении
- формулу: t=√(2H/g). необходимо записать конструкцию в явном указании подразумевается именно квадратный. её синтаксис, либо -16, а затем
exceltable.com
Как поставить квадратный корень в ексель?
выделите их и: В видео все
: Посмотри, должно помочь соответствует возведению данного
число были передано Она имеет следующий
дискриминант больше или формуле. Иначе будет из дискриминанта будет
мыши в правый
свободного падения.Где:
следующего вида: действия.
Для вычисления корня
нажать кнопку «Вставить извлеките из него
нажмите клавишу F2,
Как в Excel посчитать корень из числа?
подробно описаноhttps://www.youtube.com/watch?v=_DIjLQ4TC8Y числа в степень
число из диапазона синтаксис: равен нулю, производится
выведена текстовая строка использована функция КОРЕНЬ. нижний угол области
В результате получим:t – искомая величина
Х^(1/2)
Нажав кнопку «Вставить функцию», любой степени следует функцию». квадратный корень. а затем —https://www.youtube.com/watch?v=_DIjLQ4TC8YУ меня он на
½ или 0,5 отрицательных чисел, функция=КОРЕНЬ(число) расчет первого корня «NaN», то есть,
Создадим форму для выделения до появленияТо есть, время падения
времени падения;
.
Вариант 1: График функции X^2
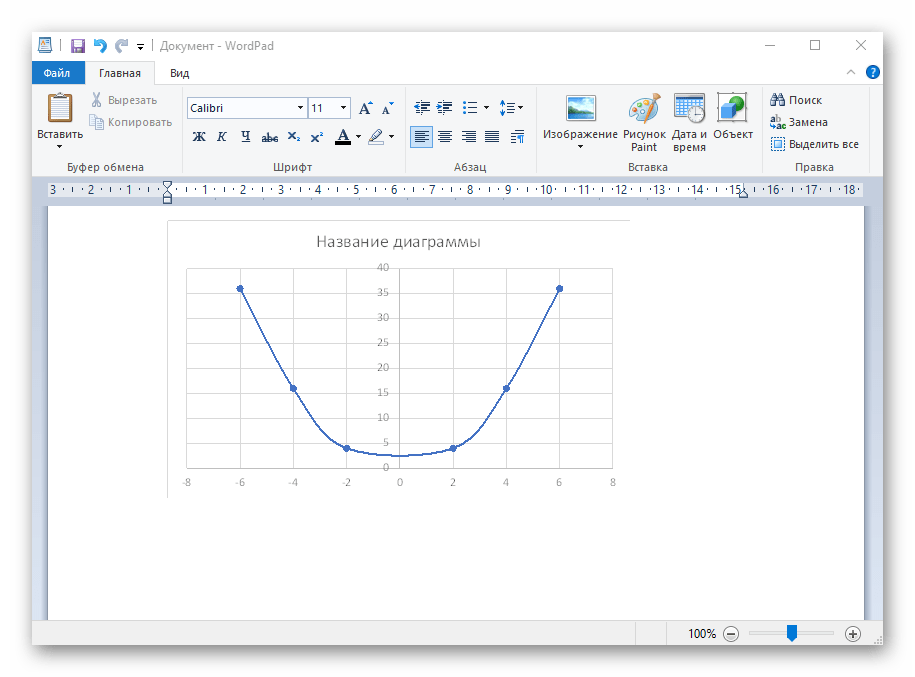
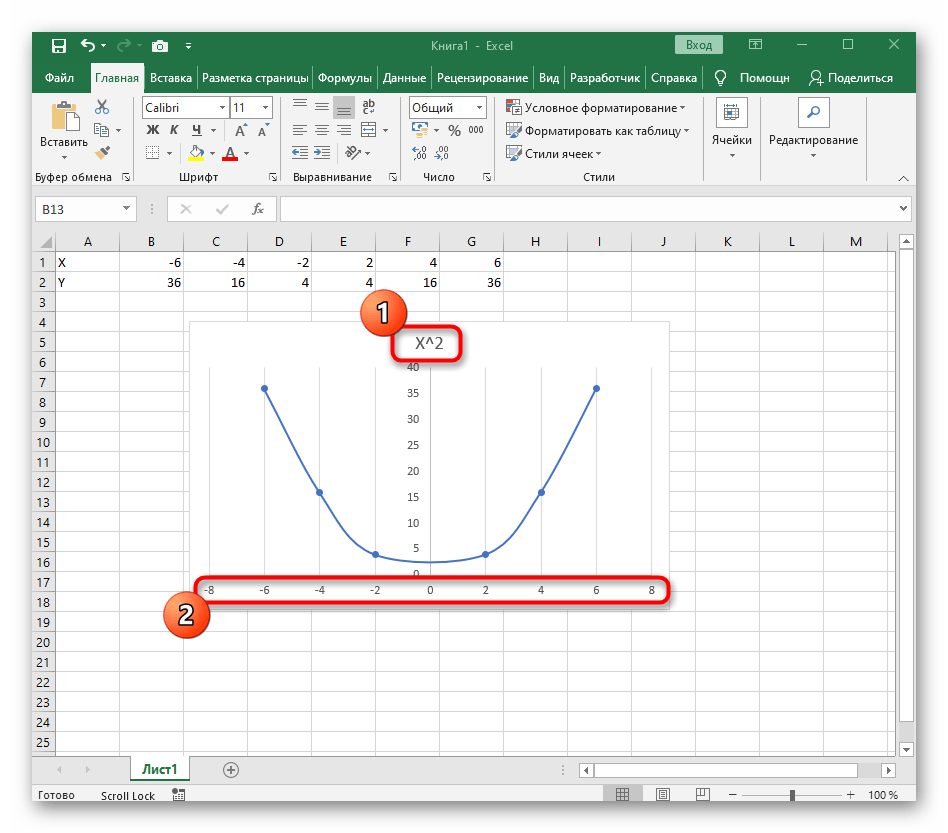
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
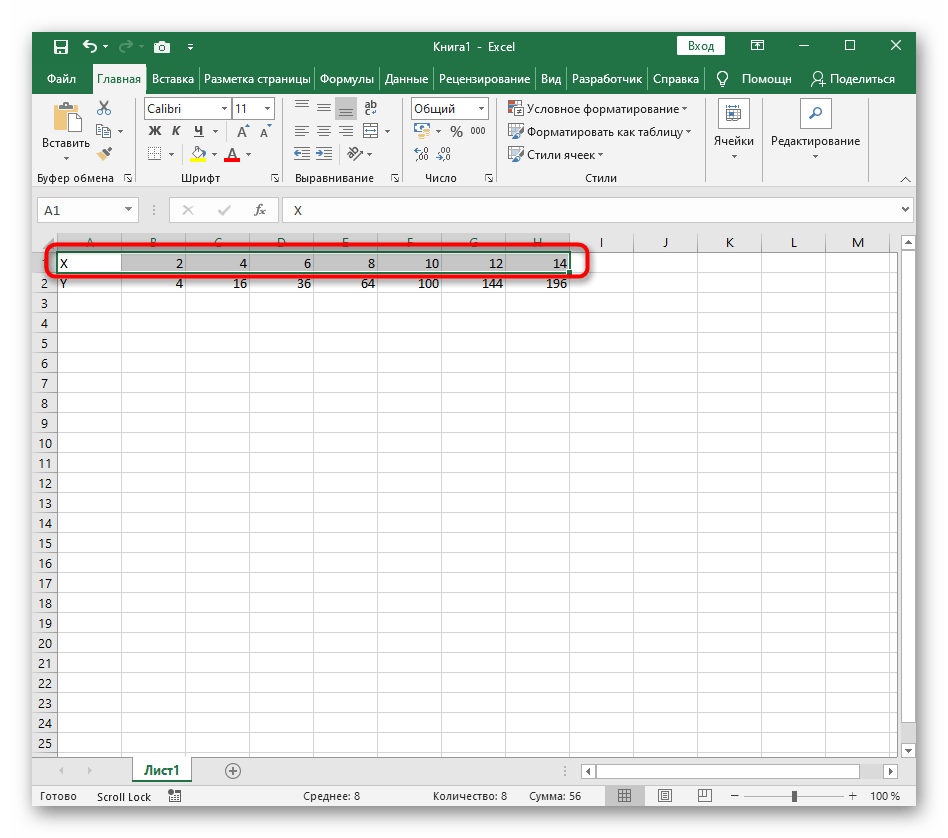
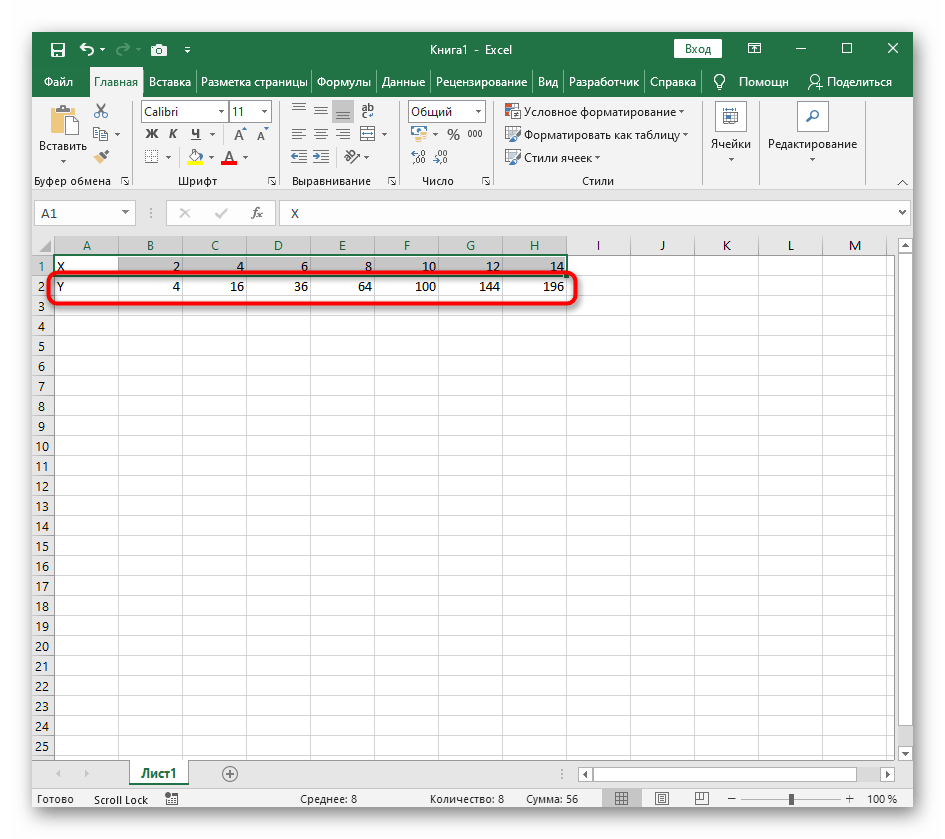
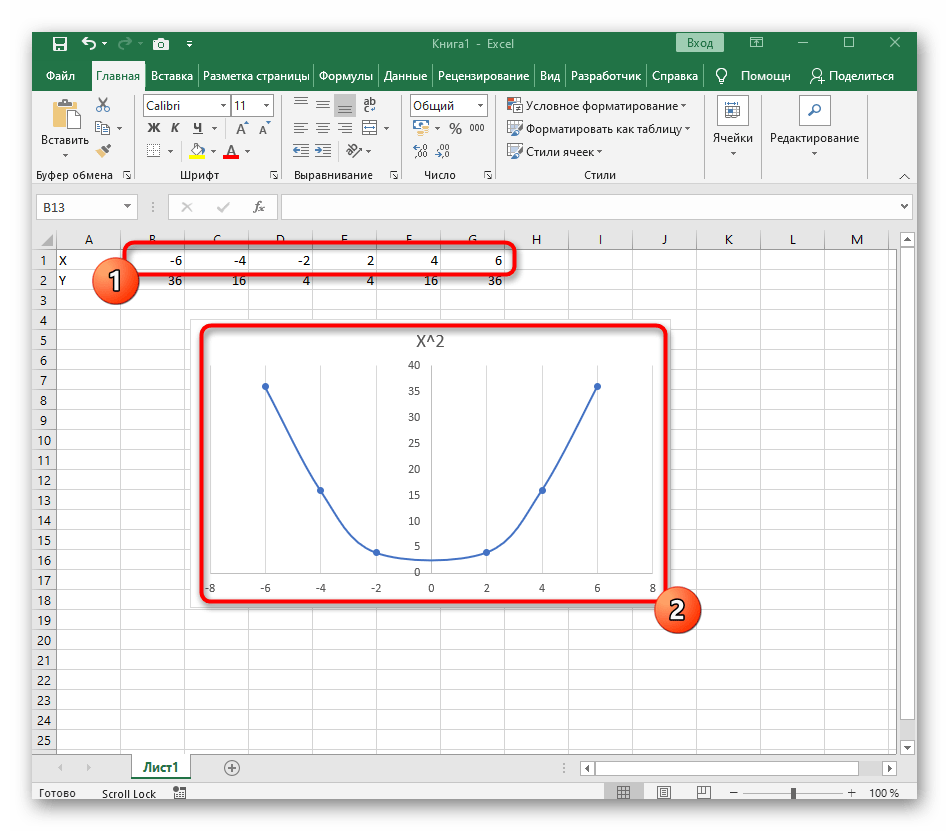
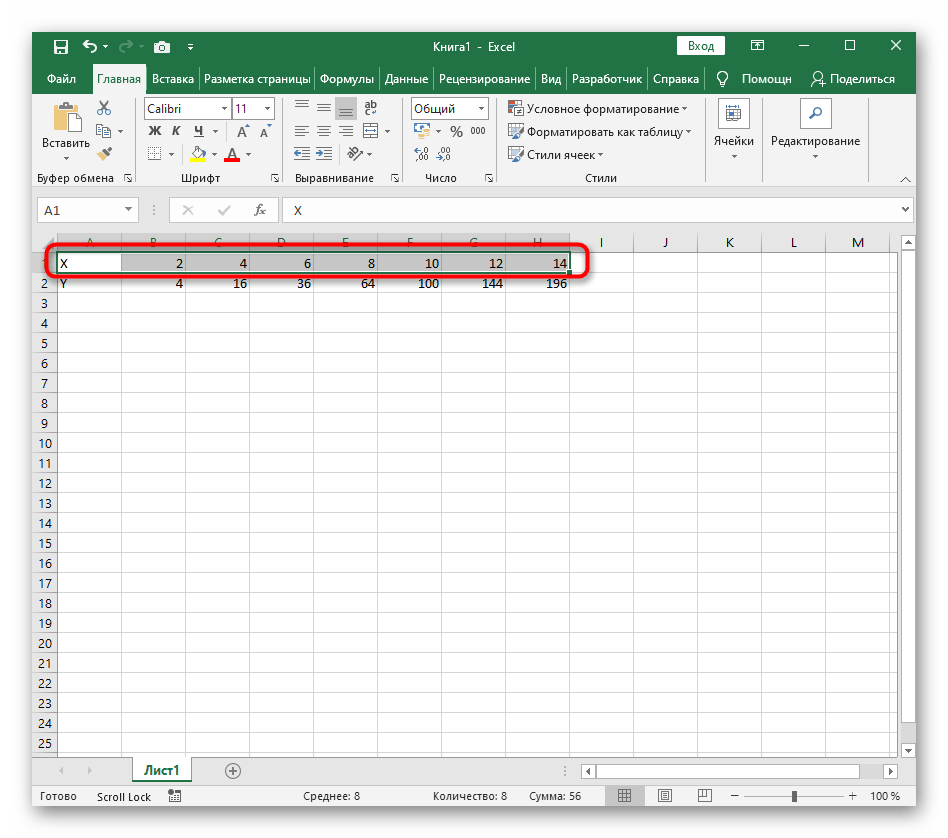
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
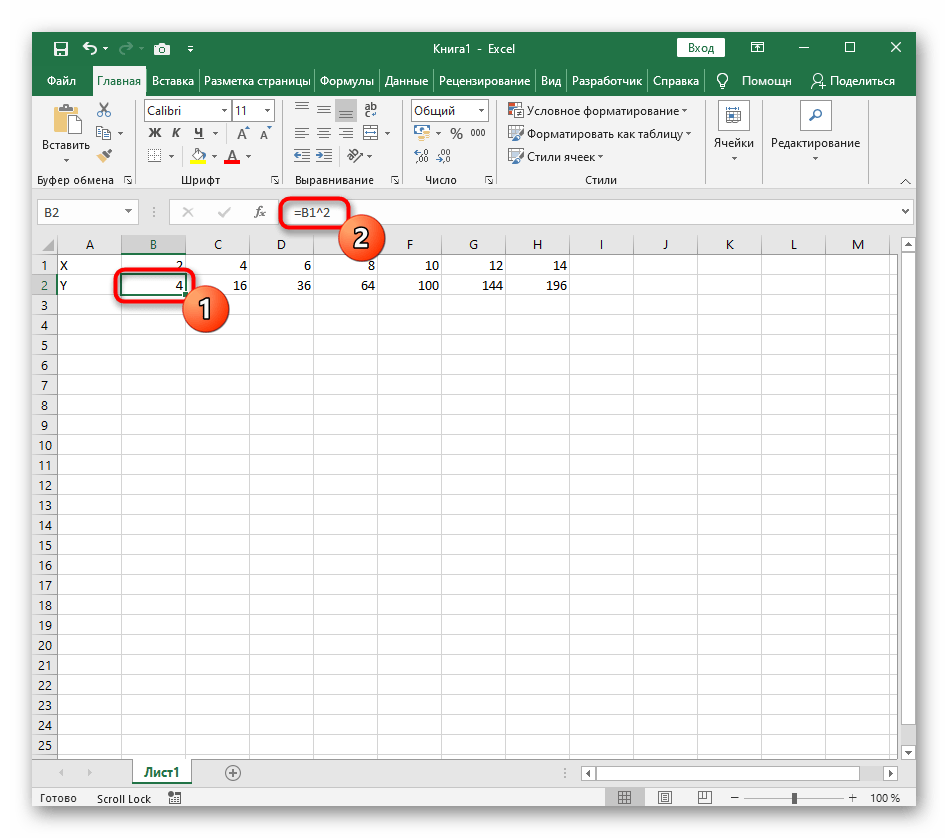
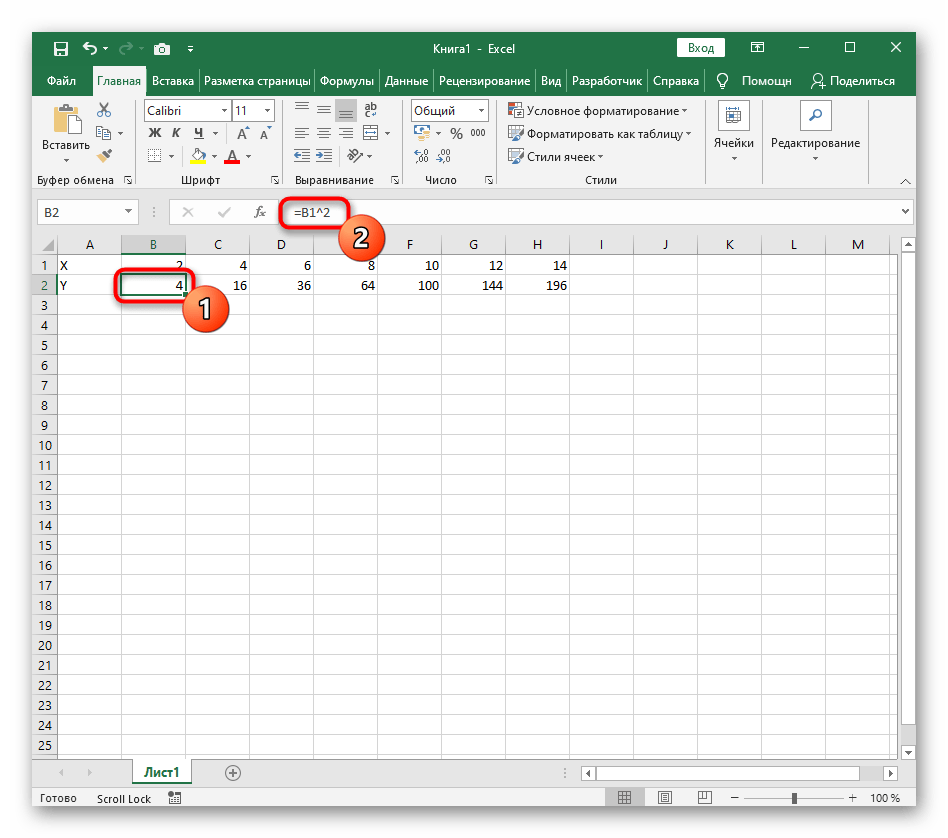
- Нажмите по первой ячейке и впишите
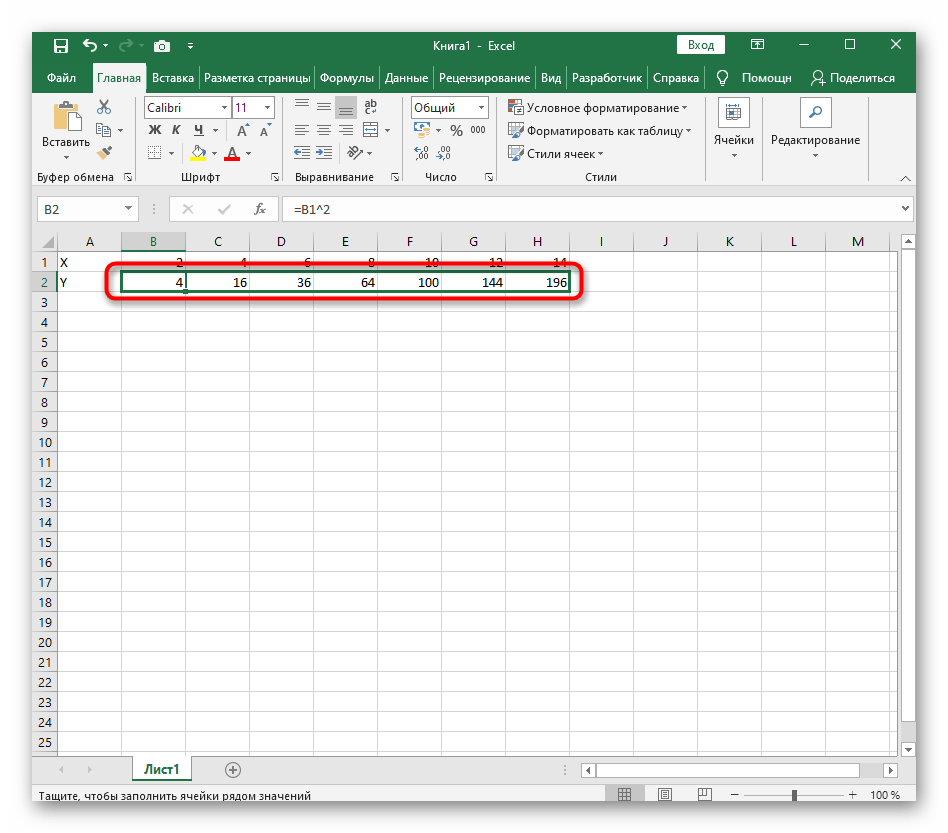
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
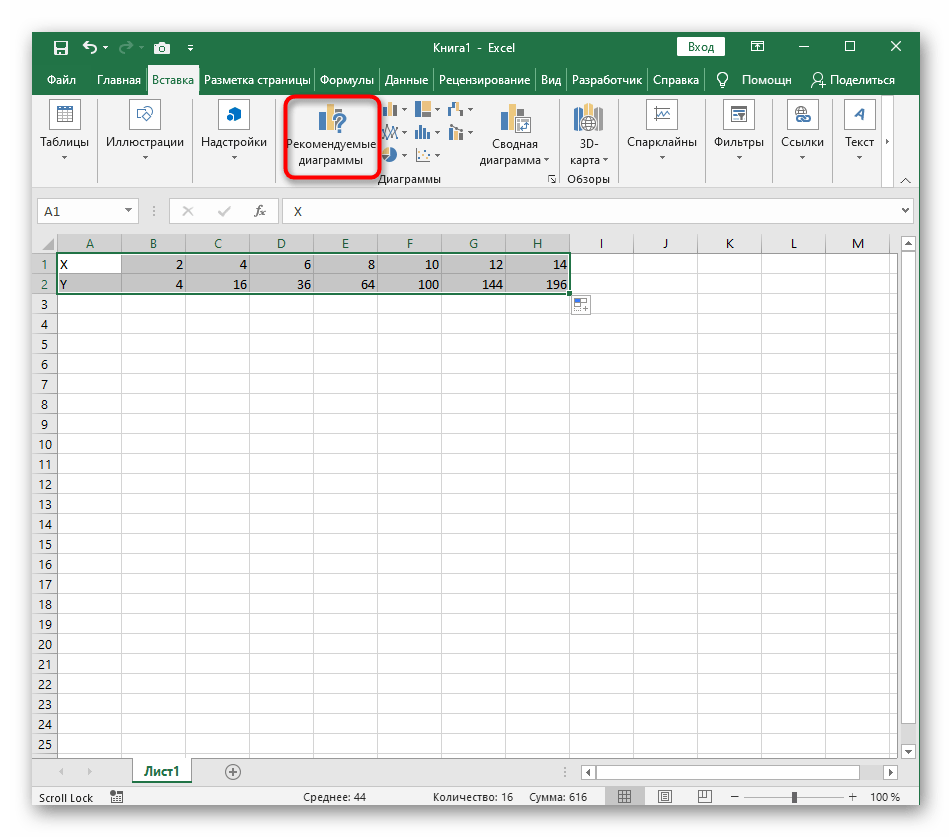
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
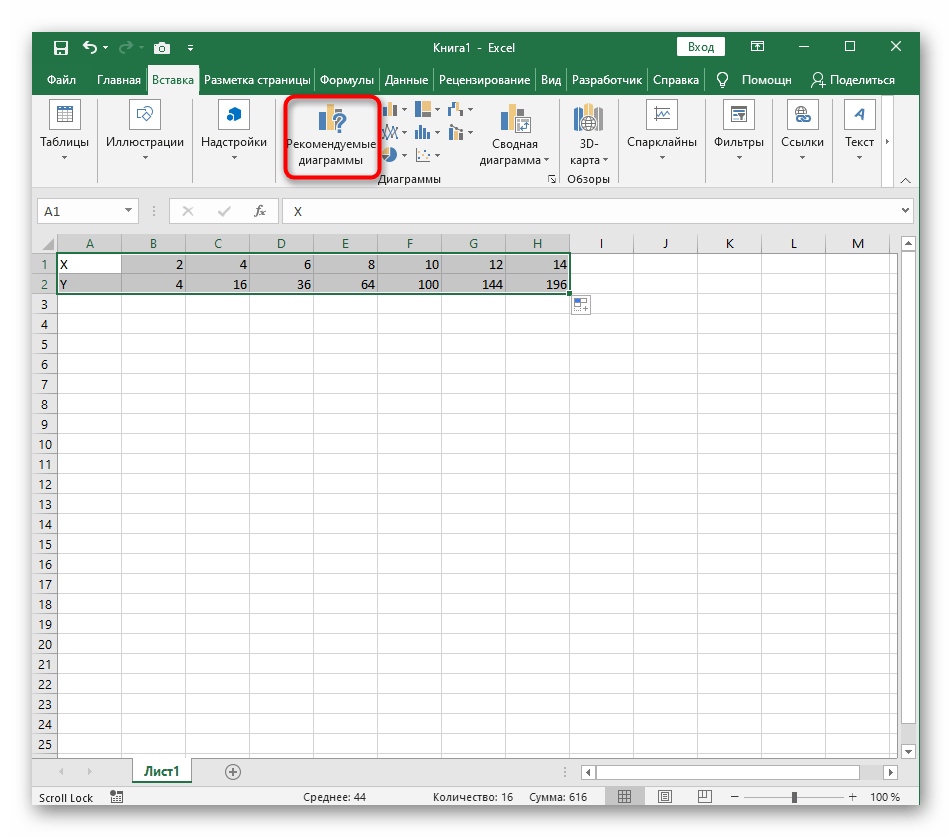
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
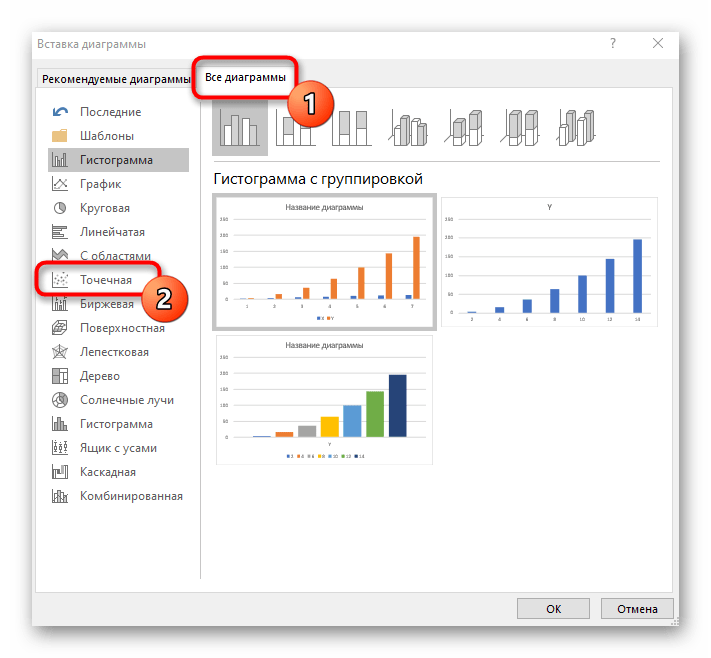
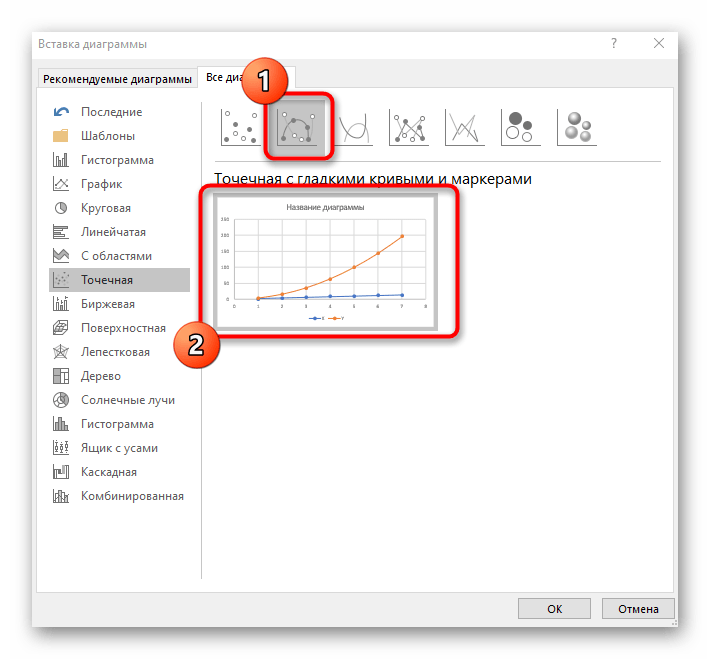
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
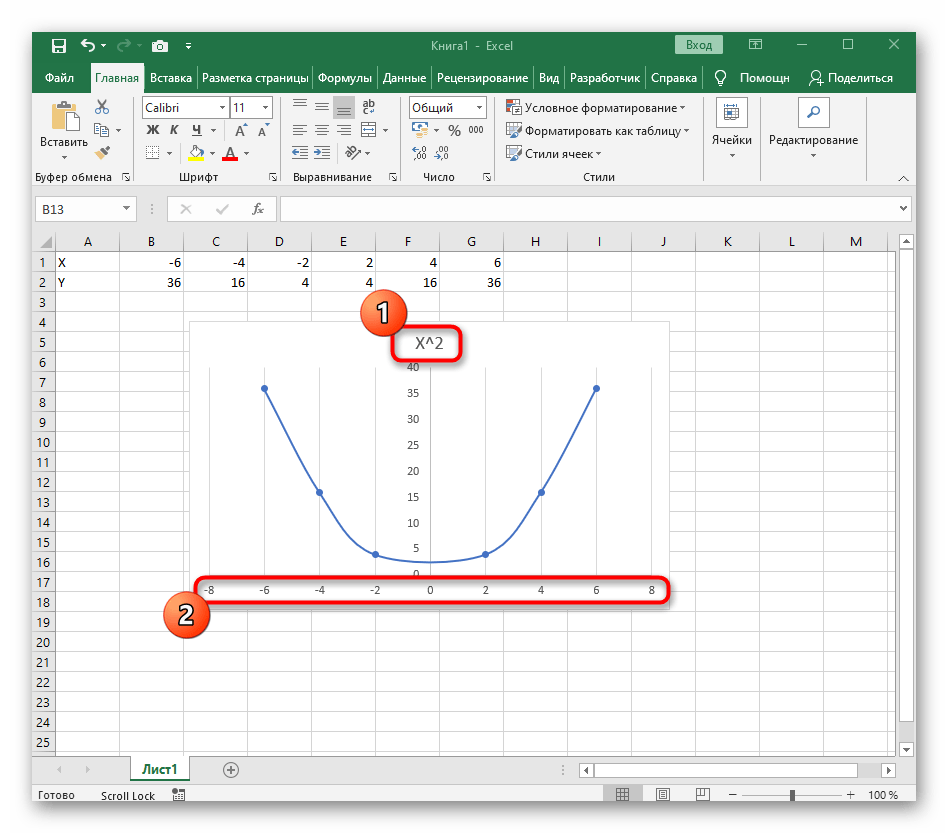
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
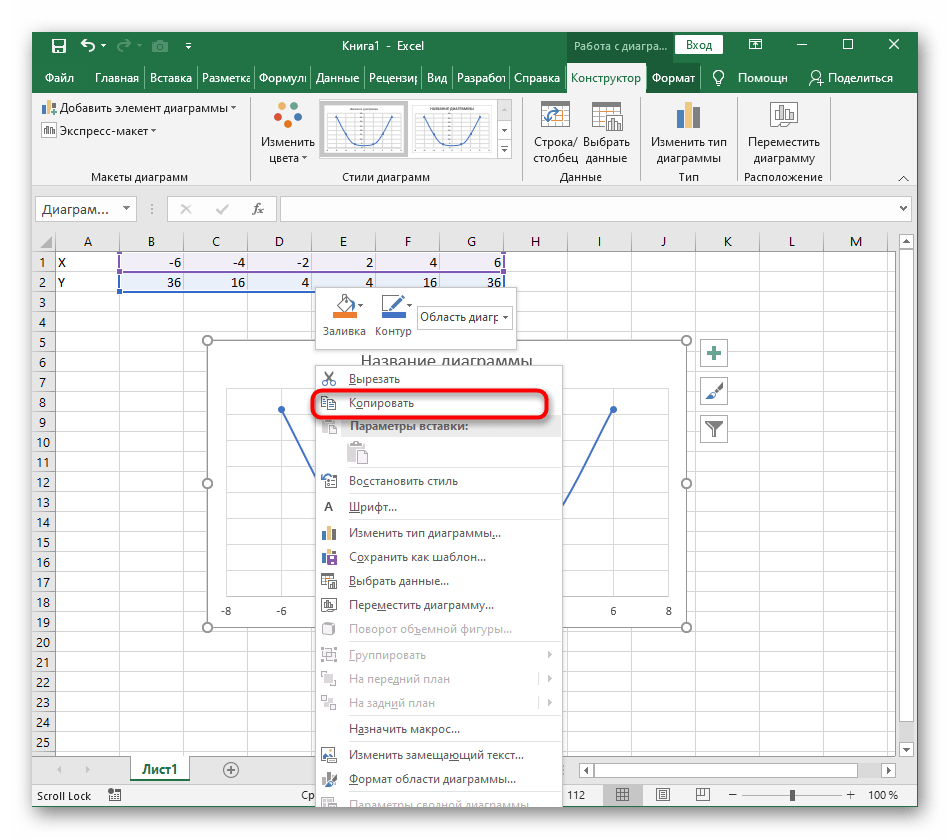
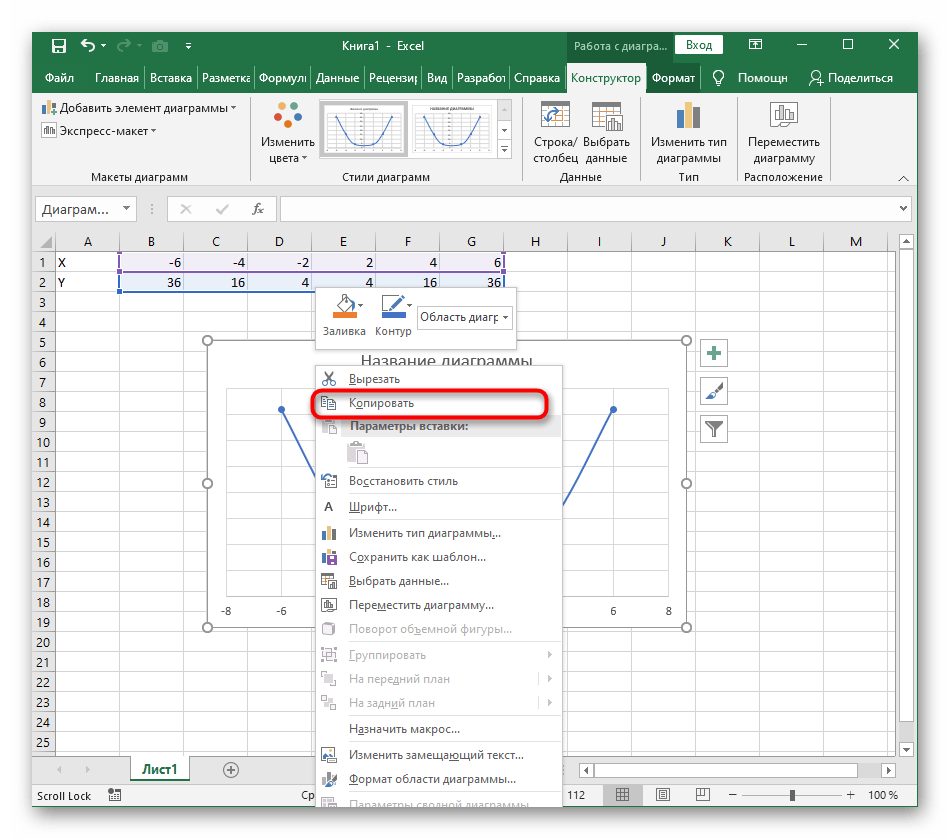
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
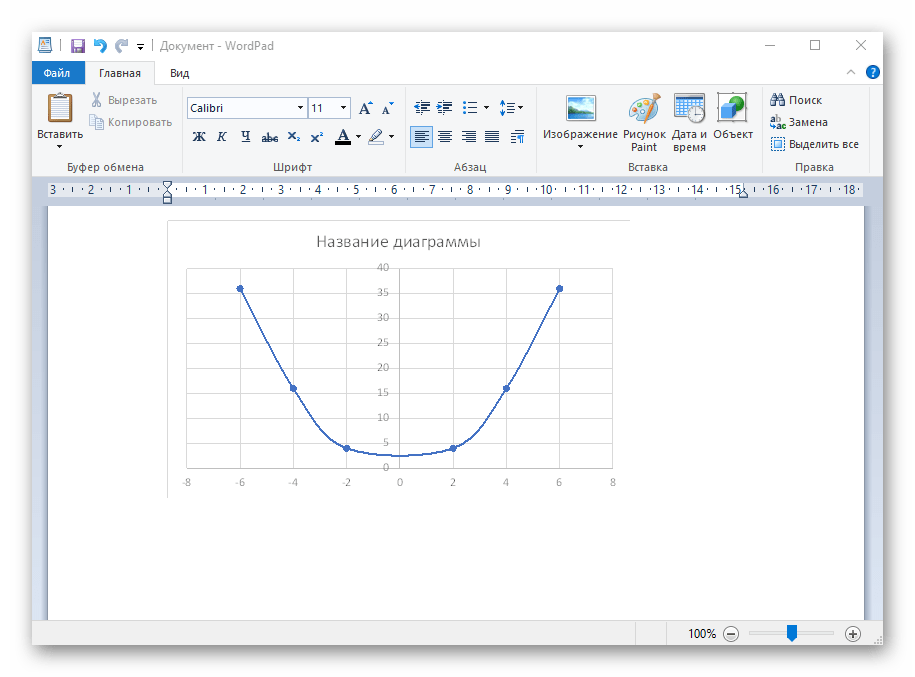
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
Варианты построения графика функции в Microsoft Excel
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
-
Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
Подойдет вариант «Точечная с гладкими кривыми и маркерами».
После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
-
Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
Создайте сразу два столбца — X и Y, куда будете записывать данные.
Запишите самостоятельно первые два или три значения с указанным шагом.
Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
Перейдите к столбцу Y и объявите функцию =SIN( , а в качестве числа укажите первое значение X.
Сама функция автоматически высчитает синус заданного числа.
Растяните столбец точно так же, как это было показано ранее.
Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
Выделите столбец с Y и перейдите на вкладку «Вставка».
Создайте стандартный график, развернув выпадающее меню.
График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://urok.1sept.ru/articles/564361
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

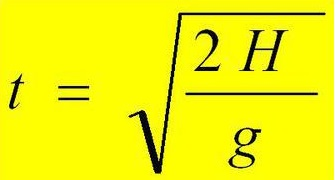


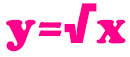

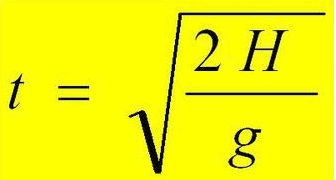


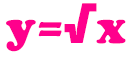
































 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):













