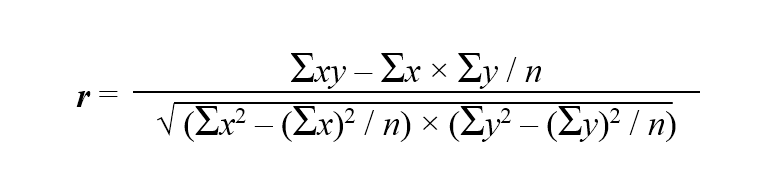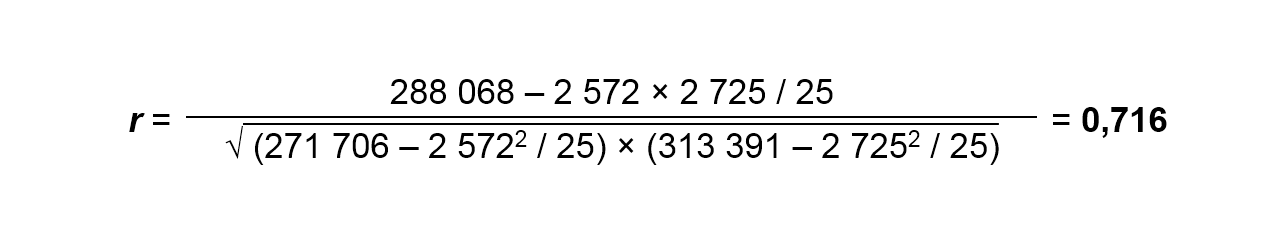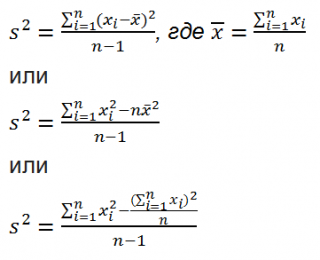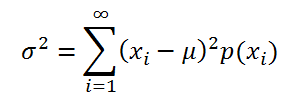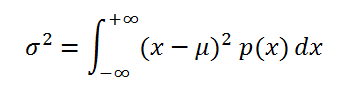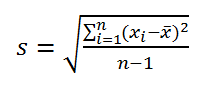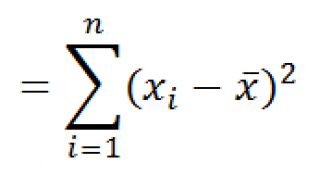В окружающем мире очень много взаимосвязей между объектами, предметами, событиями, отношениями и т.д. Например, между количеством заключенных контрактов и трудовыми затратами, между сбытом и доходами населения, между образованием и уровнем заработной платы, вмешательством государства и состоянием экономики. Каждое из измерений в этих парах можно изучать по отдельности. Как одномерную совокупность. Но реальный результат получается лишь при изучении обоих измерений, взаимосвязи между ними.
При работе с двумерными данными обычно рисуют диаграммы рассеяния. Другие названия – «диаграммы разброса», «точечные диаграммы». Подобные графики показывают значения двух переменных в виде точек. Если в двумерных данных содержатся какие-либо проблемы (выбросы), то их легко будет обнаружить с помощью соответствующей диаграммы разброса.
Что показывает диаграмма рассеяния
Диаграмма рассеяния – один из инструментов статистического контроля, анализа. С ее помощью выявляется зависимость и характер связи между двумя разными параметрами экономического явления, производственного процесса. Диаграмма разброса показывает вид и тесноту взаимосвязи между парами данных. К примеру, между:
- качеством продукта и влияющим фактором;
- двумя разными характеристиками качества;
- двумя обстоятельствами, влияющими на качество, и т.п.
Диаграммы рассеяния применяются для обнаружения корреляции между данными. Если корреляционная зависимость присутствует, то установить контроль над наблюдаемым явлением значительно проще.
Построение диаграммы рассеяния в Excel
Диаграмма разброса представляет наблюдаемое явление в пространстве двух измерений. Если одну величину рассматривать как «причину», влияющую на другую величину, то ей будет соответствовать ось Х (горизонтальная ось). Реагирующей на это влияние величине соответствует ось Y (вертикальная ось). Когда четко классифицировать переменные невозможно, распределение производится пользователем.
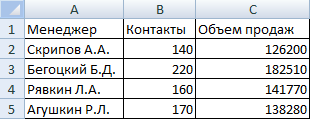
Построим диаграмму рассеяния для небольшой двумерной совокупности данных:
Предположим, что затраченные усилия каждого менеджера повлияли на результат его работы (так принято считать). Следовательно, число контактов необходимо показать на горизонтальной оси, а продажи (результат затраченных усилий) – на вертикальной.
Для построения диаграммы рассеяния в Excel выделим столбцы «Контакты», «Объем продаж» (включая заголовки). Перейдем на вкладку «Вставка» в группу «Диаграммы». Использование данного инструмента анализа возможно с помощью точечных диаграмм:
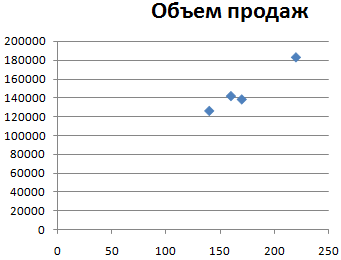
По умолчанию программа построила диаграмму разброса такого вида:
Изменим параметры горизонтальной и вертикальной оси, чтобы четыре пары показателей расположились более равномерно в области построения. Щелкнем сначала правой кнопкой мыши по вертикальной оси. Выберем «Формат оси»:
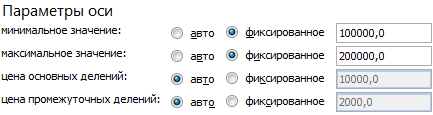
На вкладке «Параметры оси» установим минимальное значение 100 000, а максимальное – 200 000. Показатели объема продаж находятся в этих пределах:
Минимальное значение для горизонтальной оси Х – 100, т.к. ниже этого показателя данных в таблице нет.
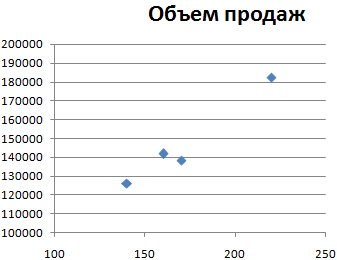
Диаграмма разброса приобрела следующий вид:
Какие можно сделать выводы по данной диаграмме рассеяния:
- Каждая точка дает представление об объеме продаж и контактах (как об одномерных совокупностях) и о взаимосвязи между этими параметрами.
- Количество контактов (горизонтальная ось) распределилось в диапазоне 140-220. Типичное значение равно примерно 170.
- Объемы продаж за анализируемый период (вертикальная ось) находятся в диапазоне примерно от 130 000 до 190 000. Типичное значение равняется приблизительно 150 000.
- Взаимосвязь между числом контактов и объемом сбыта является положительной, т.к. точки выстроились слева направо снизу вверх. Следовательно, чем больше у менеджера было контактов с клиентами (точки правее), тем больше прибыли организации он дал (точки выше).
«СЕМЬ ОСНОВНЫХ ИНСТРУМЕНТОВ КОНТРОЛЯ КАЧЕСТВА»
Диаграмма рассеяния
Что такое диаграмма рассеяния?
Очень часто в производственной, маркетинговой и иных видах деятельности необходимо понять, связаны ли между собой какие-либо явления, и если связаны, то насколько тесно.
Если вы, например, заметили увеличение объёма брака в какую-либо смену, вы вправе предположить, что это связано с трудовой деятельностью того или иного работника. Но как понять, так ли это на самом деле? Или вы считаете, что на тот или иной показатель качества выпускаемого изделия влияет некая технологическая операция, но хотите убедиться в этом и понять, насколько сильно данная операция оказывает влияние на интересующий вас показатель качества. А ваш маркетолог хочет выявить наличие и силу взаимосвязи между типом упаковки и её привлекательностью для потребителя. Директор же по информационным технологиям желает убедиться в том, что переход вашего предприятия на облачные технологии напрямую повлиял на снижение затрат в сфере ИТ, для чего хотел бы выявить связь между таким переходом и затратами, а также силу этой связи.
Практически любую такую связь или, более научно, корреляцию позволяет установить диаграмма рассеяния (другие названия – диаграмма разброса, диаграмма рассеивания, поле корреляции).
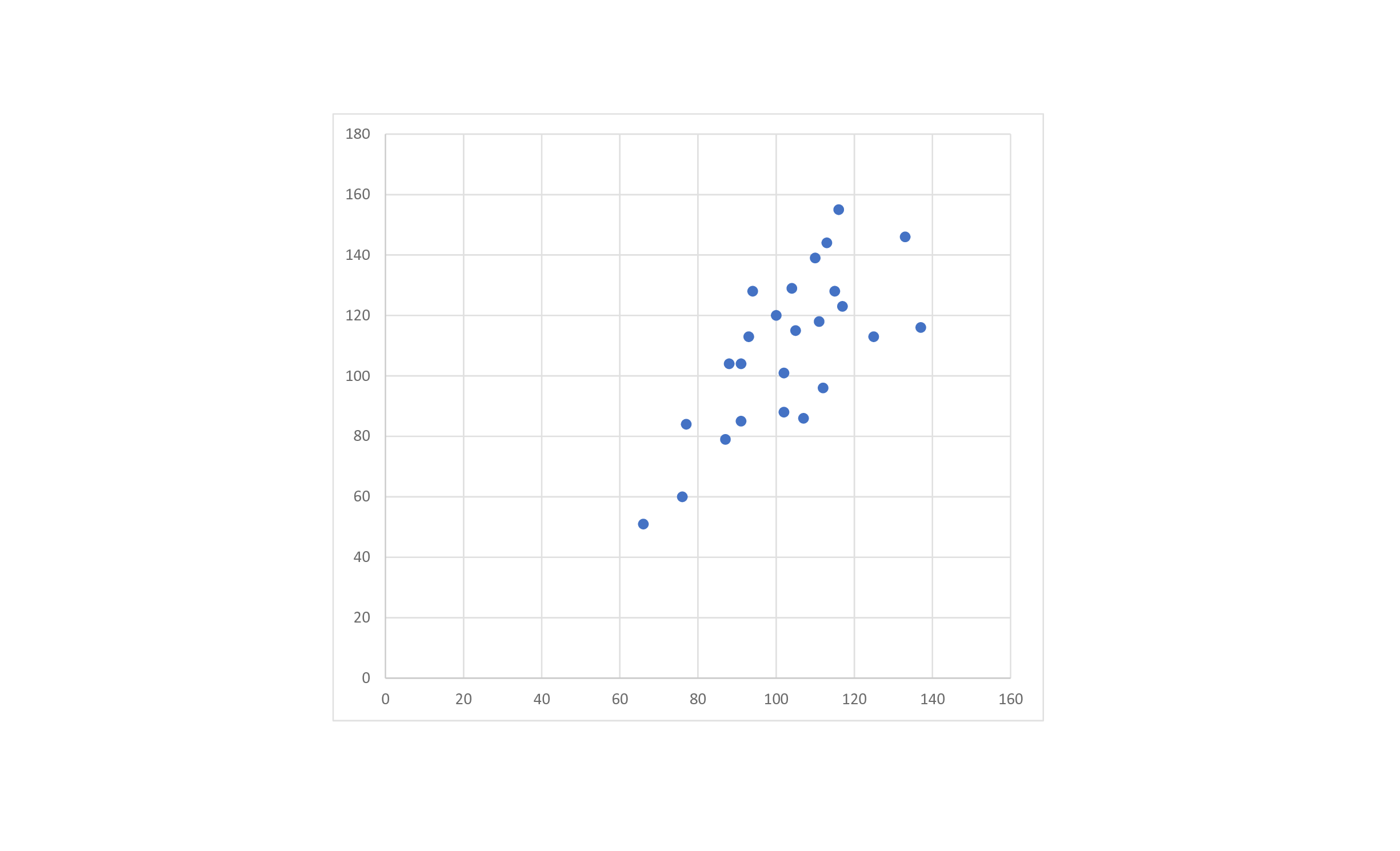
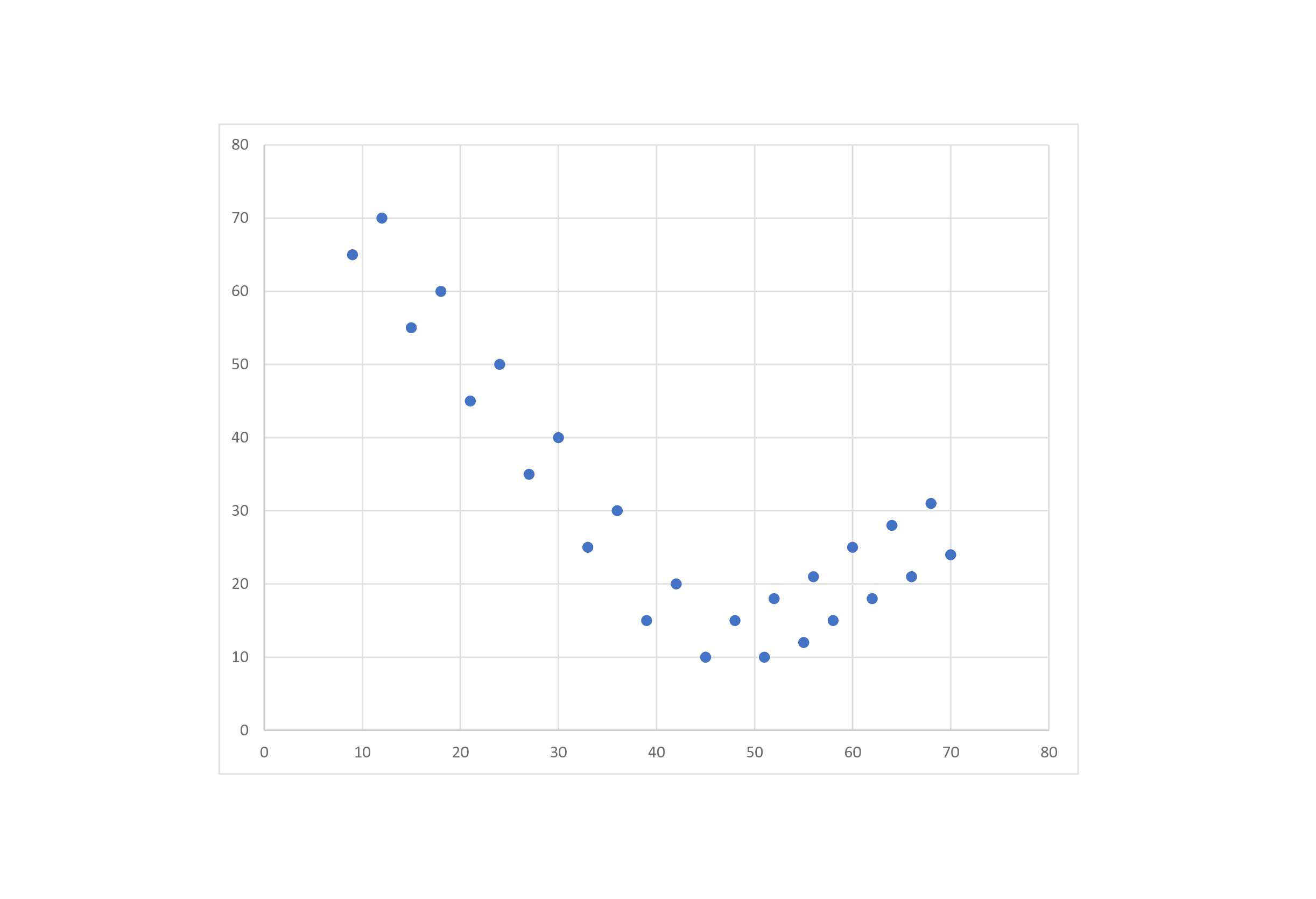
Типичный вид диаграммы рассеяния представлен на рисунке 1.
Диаграмма рассеяния – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.
В зависимости от наличия или отсутствия предполагаемых причинно-следственных связей при помощи диаграммы рассеяния можно анализировать зависимость:
- между влияющим фактором (причиной) и характеристикой (следствием);
- между двумя характеристиками;
- между двумя факторами.
Влияющий фактор (причину) иногда называют также факторным признаком, а характеристику (следствие) – результативным признаком.
Если говорить конкретно о качестве, то такие пары переменных чаще всего относятся [1, с. 144; 2, с. 125]:
- к характеристике качества и влияющему на неё фактору;
- к двум различным характеристикам качества;
- к двум факторам, влияющим на одну характеристику качества.
Все три категории анализа крайне важны, поскольку [4]:
- в первом случае, при наличии корреляционной зависимости, причинный фактор оказывает значительное влияние на характеристику качества, а потому если причинный фактор удерживать под контролем, то можно, во-первых, достичь стабильности характеристики качества, а во-вторых, определить уровень контроля, необходимый для требуемого показателя качества;
- во втором случае, при наличии корреляционной зависимости между двумя различными характеристиками качества, можно, например, осуществлять контроль только одной из них;
- в третьем случае наличие корреляционной зависимости между отдельными факторами значительно облегчает контроль процесса с технологической, временнóй и экономической точек зрения.
Если между сопоставляемыми парами переменных предполагается наличие причинно-следственной связи, то при построении диаграммы рассеяния причинные факторы, как правило, обозначаются переменной х и откладываются по горизонтальной оси (оси абсцисс); характеристики же, как правило, обозначаются переменной y и откладываются по вертикальной оси (оси ординат).
Построение диаграммы выполняется в следующей последовательности [1, с. 145–146; 2, с. 126]:
- Собираются парные данные (х, у), между которыми мы хотим исследовать зависимость, и заполняется таблица. Желательно собрать не менее 25–30 пар данных.
- Определяются максимальные и минимальные значения для х и y. Исходя из разницы между их максимальными и минимальными значениями устанавливаются размеры и шкалы осей, причём их лучше делать примерно одинаковыми, чтобы диаграмма легче читалась.
- Строится график, на который наносятся данные. Если на одну и ту же точку графика попадает несколько одинаковых значений, то соответствующие точки обозначаются при помощи концентрических кругов (точка в круге, в двух, трёх кругах) либо рядом с первой точкой наносится вторая, третья точка.
- На график наносятся все необходимые обозначения: название диаграммы, её составитель, дата, интервал времени, число пар данных, единицы измерения для каждой оси и т.д.
В зависимости от значений x и y графики могут иметь различный вид, при этом построенные графики надо уметь читать. Посмотрим, как это делается.
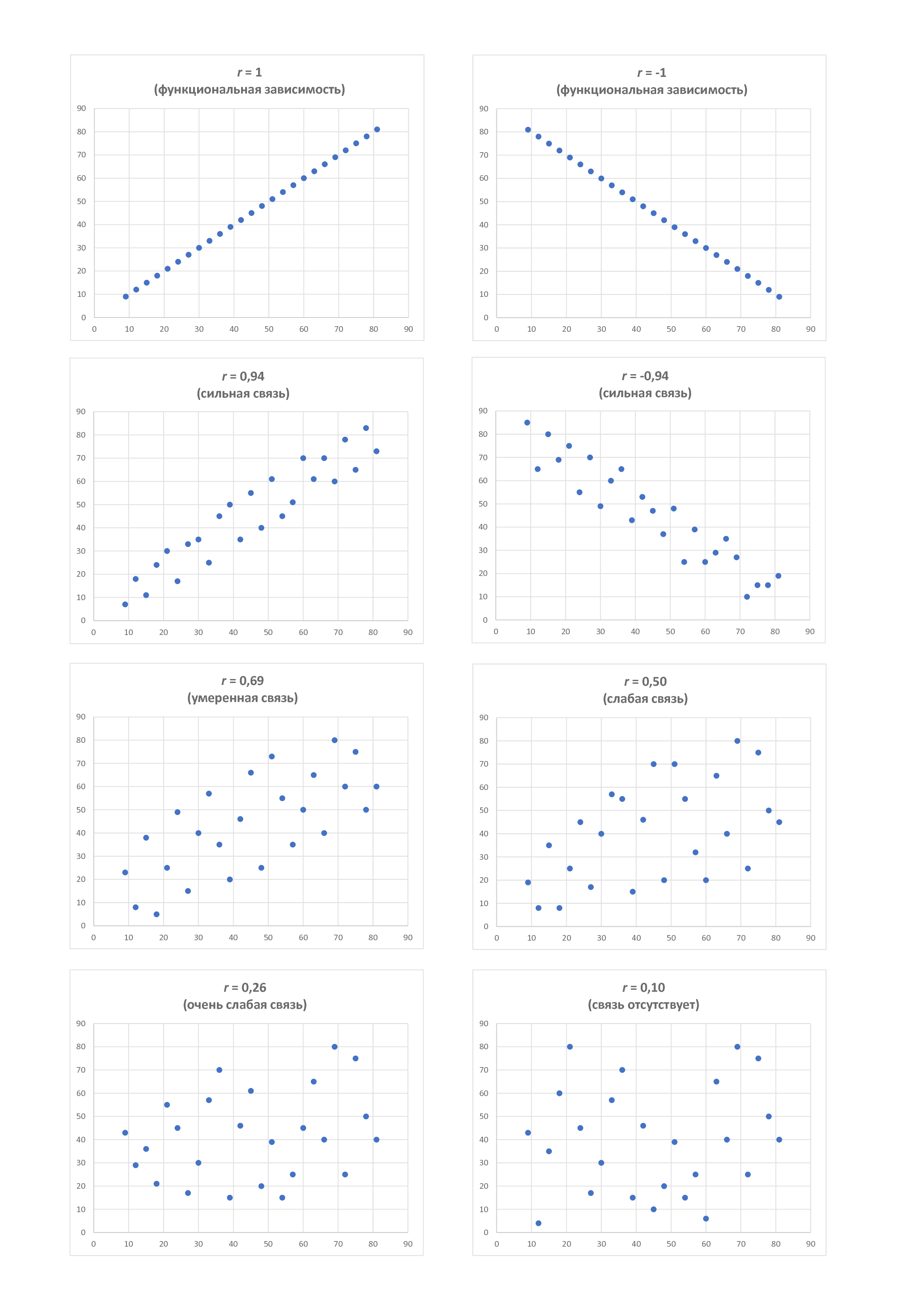
Ниже, на рисунке 2, представлены различные виды графиков. График позволяет нам воочию увидеть характер и тесноту связи между соответствующими переменными x и y. Ниже мы также научимся определять степень этой тесноты, называемую коэффициентом корреляции.
Коэффициент корреляции r может принимать значения от -1 до +1, т.е. -1 ≤ r ≤ 1. При этом чем ближе значение коэффициента к ±1, тем теснее связь. Чем ближе оно к нулю, тем связь меньше. В ±1 связь полная (её также называют функциональной, поскольку каждому значению x соответствует строго определённое значение y). В нуле связь отсутствует вообще.
Знак «плюс» или «минус» говорит о направлении связи – прямой или обратной: при плюсе значение y возрастает с возрастанием значения х; при минусе, наоборот, уменьшается.
Что касается оценки тесноты связи, то в разных источниках встречаются разные классификации (градации). Например, в источнике [3, с. 105] даётся следующая классификация:
- от ±0,81 до ±1,0 – сильная сила связи;
- от ±0,61 до ±0,8 – умеренная сила связи;
- от ±0,41 до ±0,6 – слабая сила связи;
- от ±0,21 до ±0,4 – очень слабая сила связи;
- от 0 до ±0,2 – связь отсутствует.
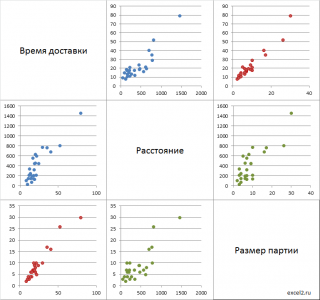
А теперь посмотрим на рисунок 2, на котором представлены различные виды диаграммы рассеяния, при этом сверху указаны соответствующие значения коэффициента корреляции r.
При отсутствии связи (корреляции) между исследуемыми параметрами точки на диаграмме расположены хаотично. Практически ту же самую картину мы видим и при слабой силе связи. Умеренная сила связи характеризуется большей степенью упорядоченности и достаточно равномерной удалённостью нанесённых точек от воображаемой средней линии. Сильная связь в большей степени стремится к такой воображаемой линии, а при r=1 график, собственно говоря, и представляет собой линию.
В случаях, представленных на рис. 2, корреляция носит линейный характер (воображаемая средняя линия – прямая), но в реальной жизни график может иметь иную, нелинейную (криволинейную) форму, например такую, как представлена на рис. 3.
Далее мы научимся рассчитывать коэффициент корреляции. Проще всего его рассчитать в программе MS Excel, и ниже мы покажем, как это делается, но прежде представим математическую формулу расчёта коэффициента корреляции и научимся рассчитывать его самостоятельно – без MS Excel или иной аналогичной программы. Все соответствующие расчёты делаются в рамках так называемого корреляционного анализа.
Корреляционный анализ
Коэффициент корреляции вычисляется по формуле:
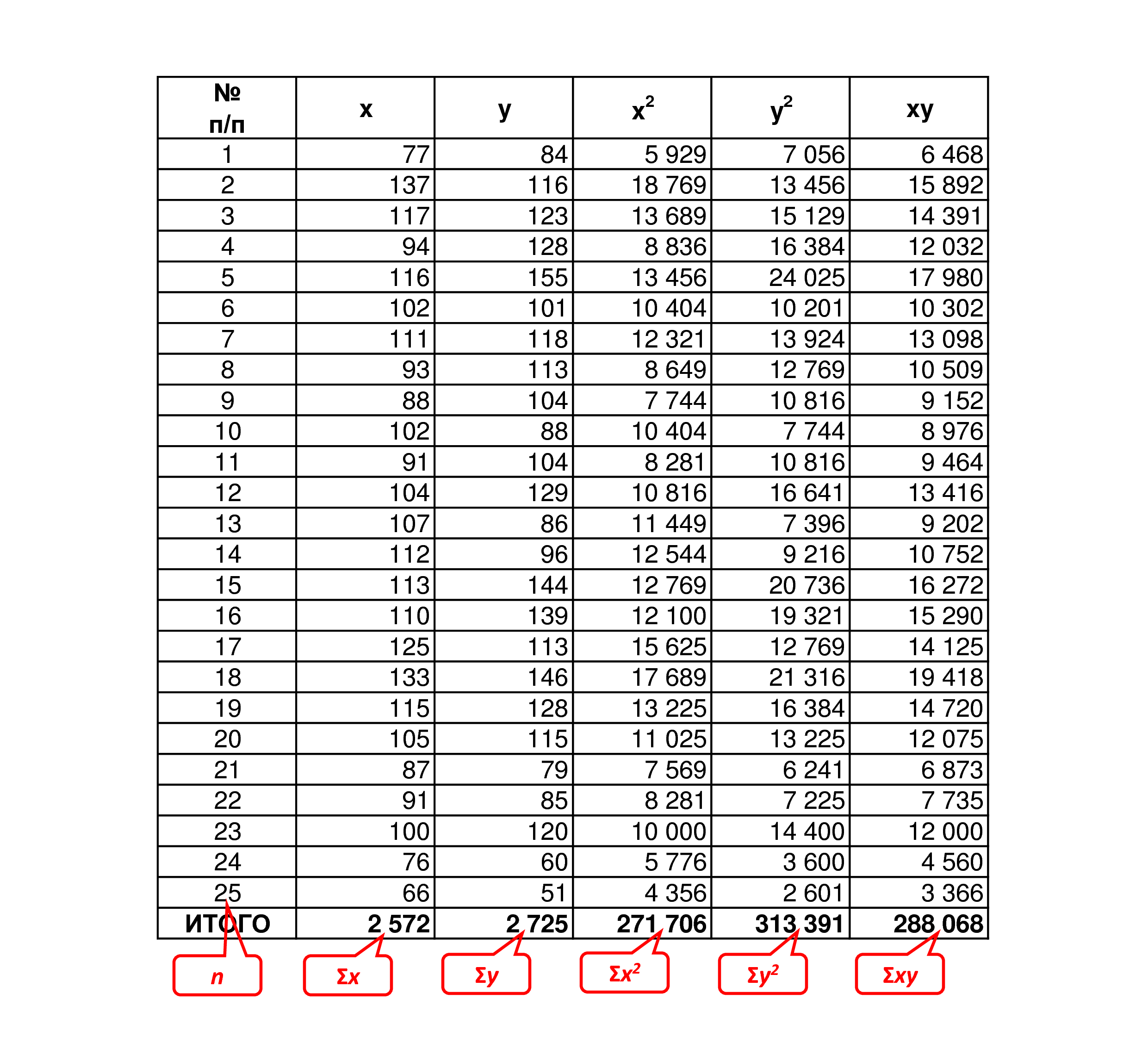
Допустим, мы собрали 25 (n=25) пар данных x и y и хотим определить коэффициент корреляции между ними. Разместим их в таблице и для удобства расчётов сразу определим значения x2, у2 и xy, чтобы затем просто подставить их в формулу:
Подставляем значения в указанную выше формулу и получаем коэффициент корреляции:
Диаграмма рассеяния, соответствующая этому массиву пар данных, была представлена выше – на рисунке 1.
Воспользуемся программой MS Excel
Всё сказанное выше, по сути, было теорией, призванной объяснить, что такое диаграмма рассеяния, как её читать и как рассчитать коэффициент корреляции.
В реальной жизни коэффициент корреляции рассчитывается, а диаграмма рассеяния – строится значительно проще и быстрее. Для наглядности будем использовать те же самые значения, что и выше.
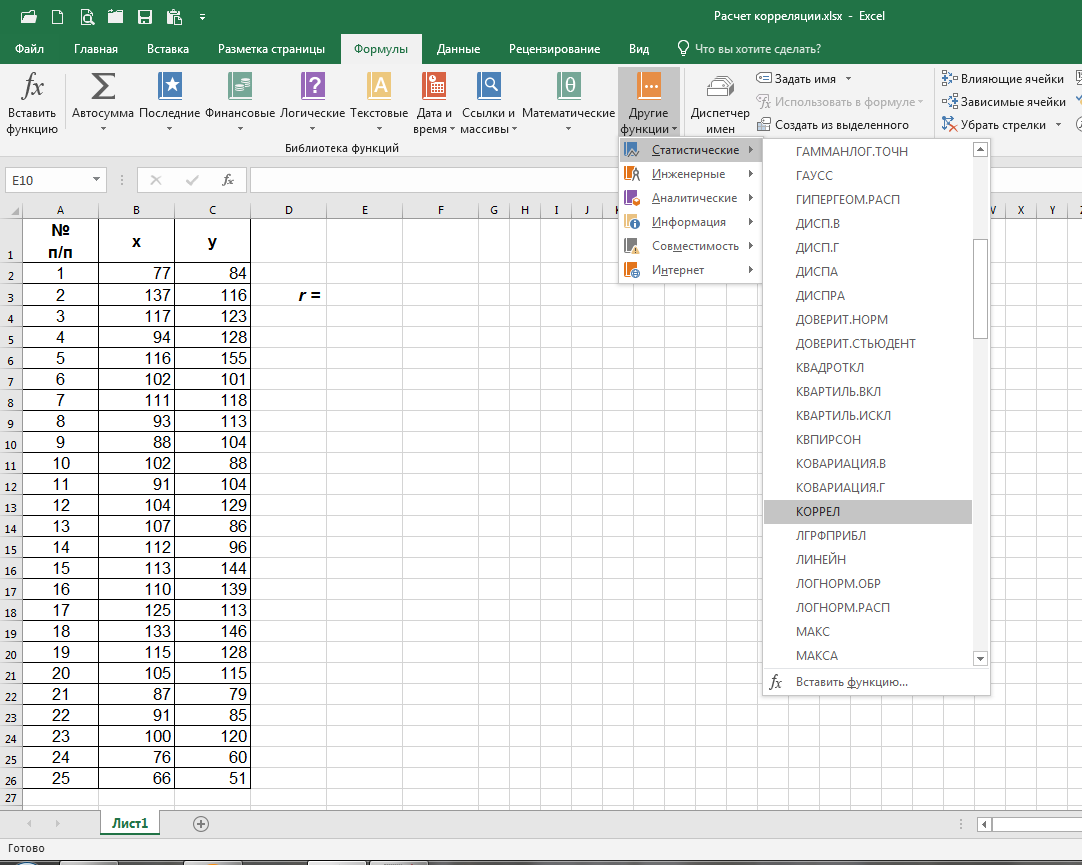
Шаг 1 – Составление таблицы и расчёт коэффициента корреляции
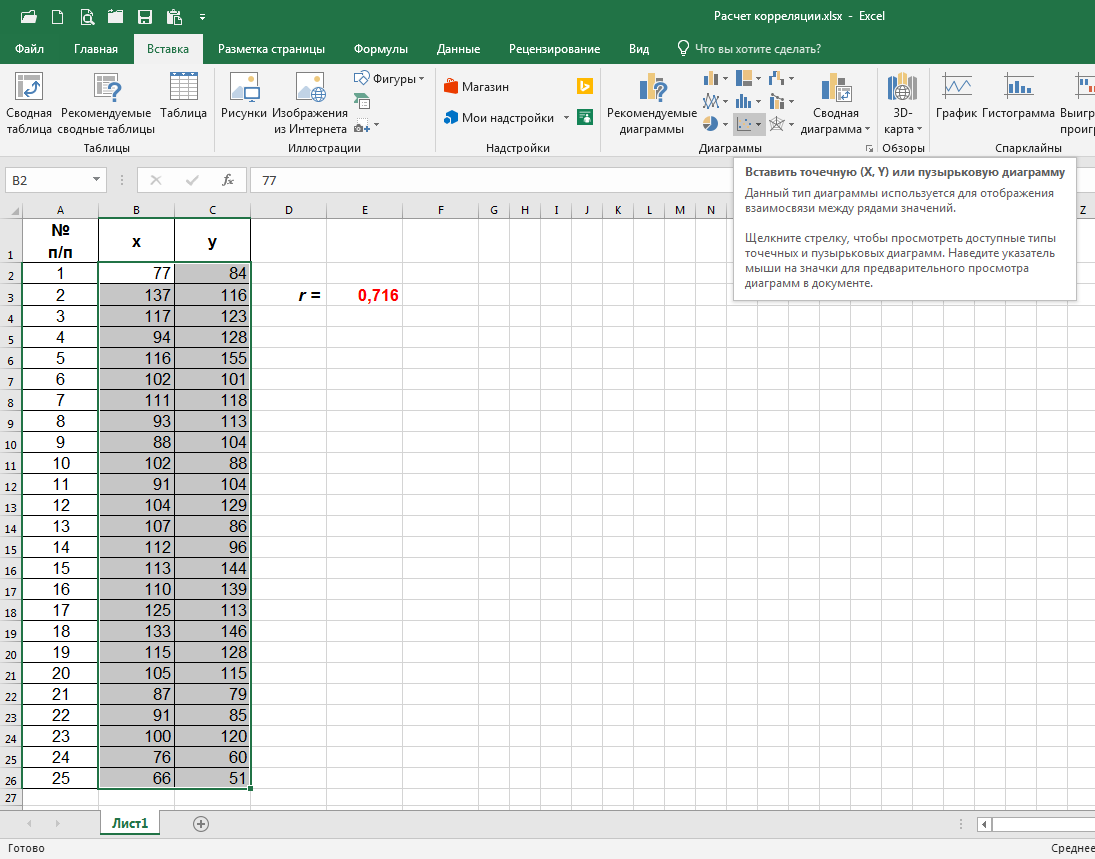
В программе Excel составляем таблицу и в любой удобной нам ячейке за пределами таблицы вводим формулу расчёта коэффициента корреляции (Формулы => Другие функции => Статистические => КОРРЕЛ):
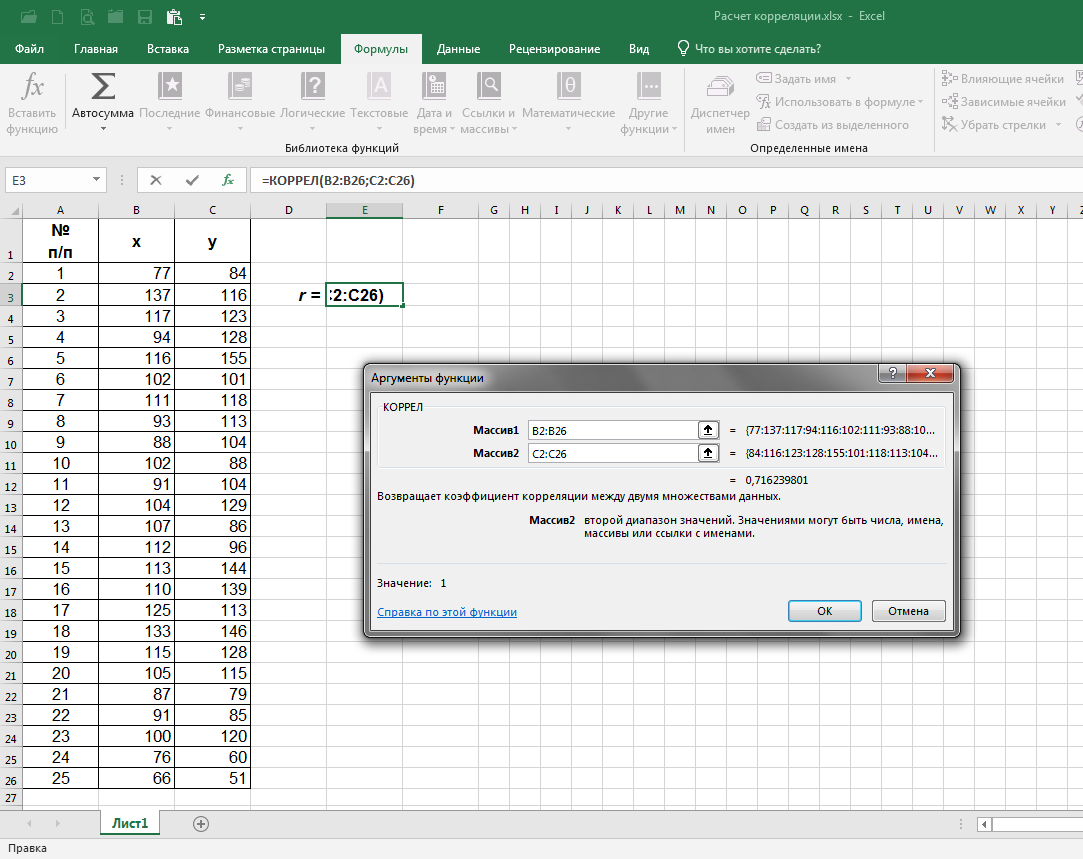
При нажатии на «КОРРЕЛ» в открывающемся окне в качестве значений «Массив1» и «Массив2» через двоеточие ставим верхнюю и нижнюю ячейки соответствующих колонок х и y (в нашем случае – B2:B26 и C2:C26) и нажимаем на ОК:
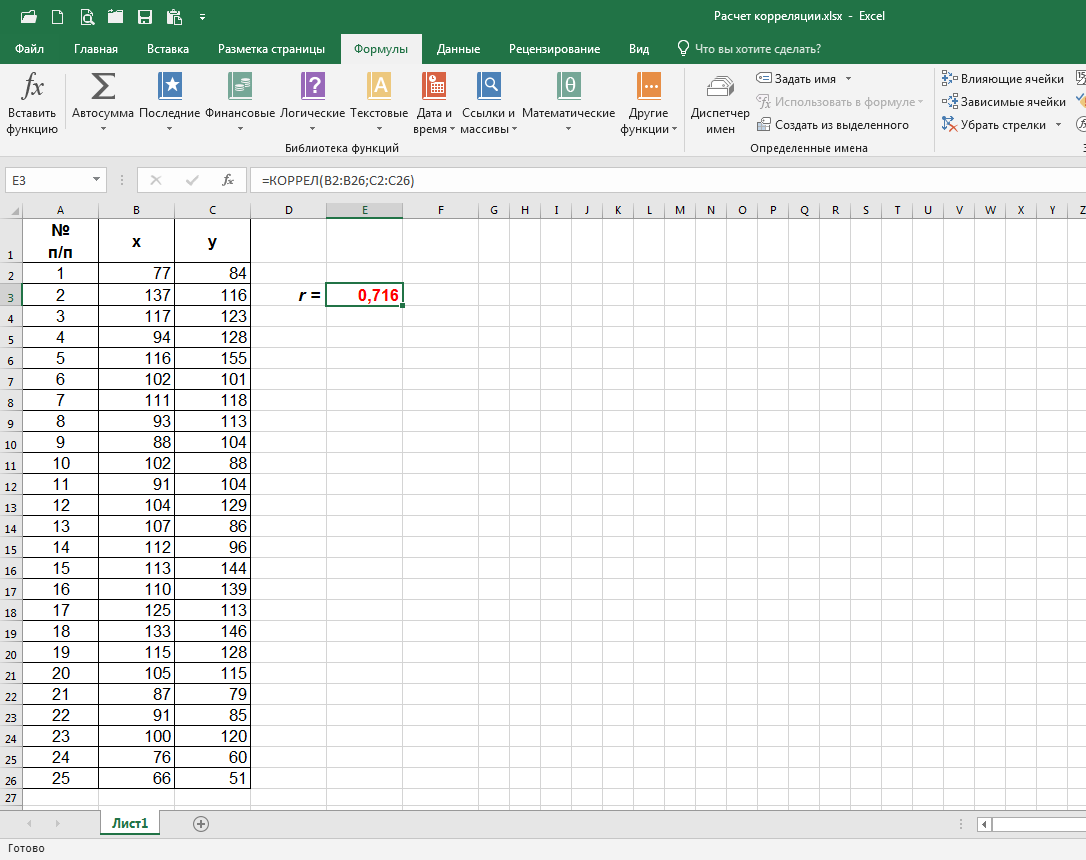
Итак, коэффициент корреляции рассчитан! Как и при расчётах выше, он равен 0,716. (Если необходимо, измените числовой формат в соответствующей ячейке, а иначе коэффициент может быть округлён до единицы.)
В принципе, коль скоро коэффициент корреляции нам уже известен, диаграмма рассеяния не очень-то и нужна. И всё же её иногда полезно построить, чтобы воочию увидеть, как соответствующие точки располагаются.
Шаг 2 – Построение диаграммы рассеяния
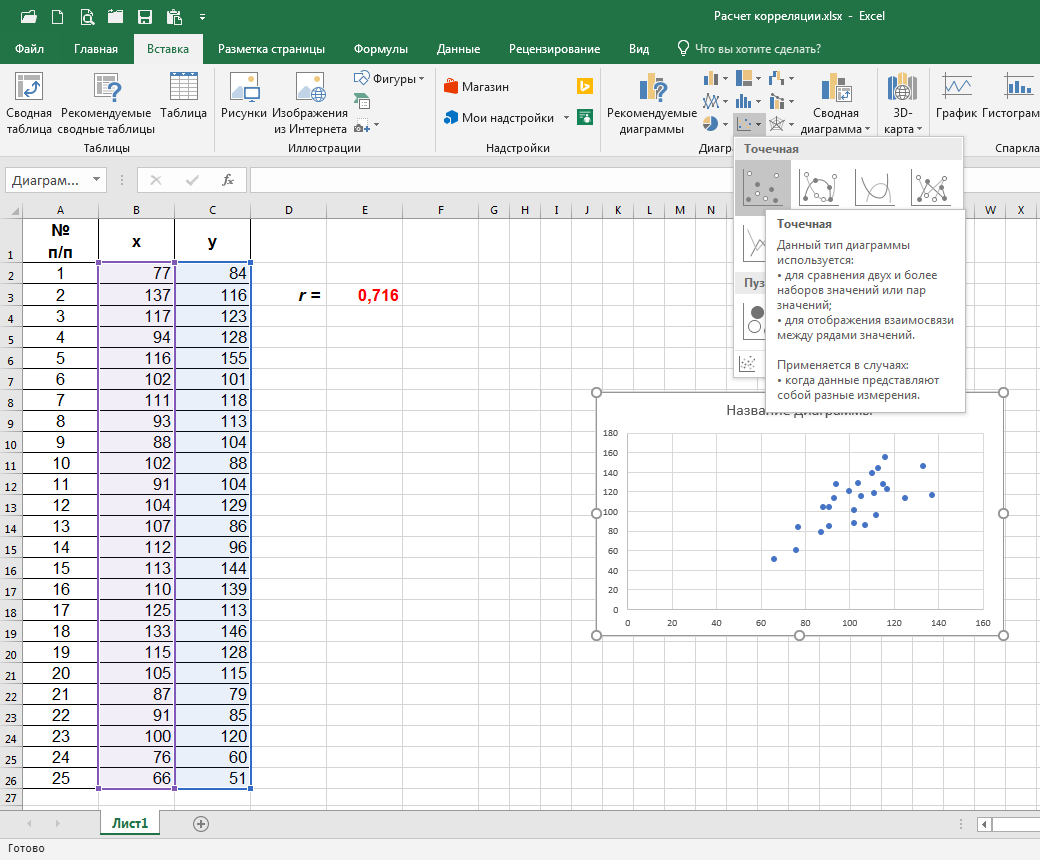
Чтобы построить диаграмму рассеяния, открываем вкладку «Вставка», выделяем мышкой ячейки от B2 до С26 в нашем случае (т.е. от верхней ячейки столбца x до нижней столбца y) и нажимаем на значок «Точечная» в разделе «Диаграммы»:
Далее, при нажатии на верхний левый значок в выпадающем окне, мы получаем необходимую нам диаграмму рассеяния:
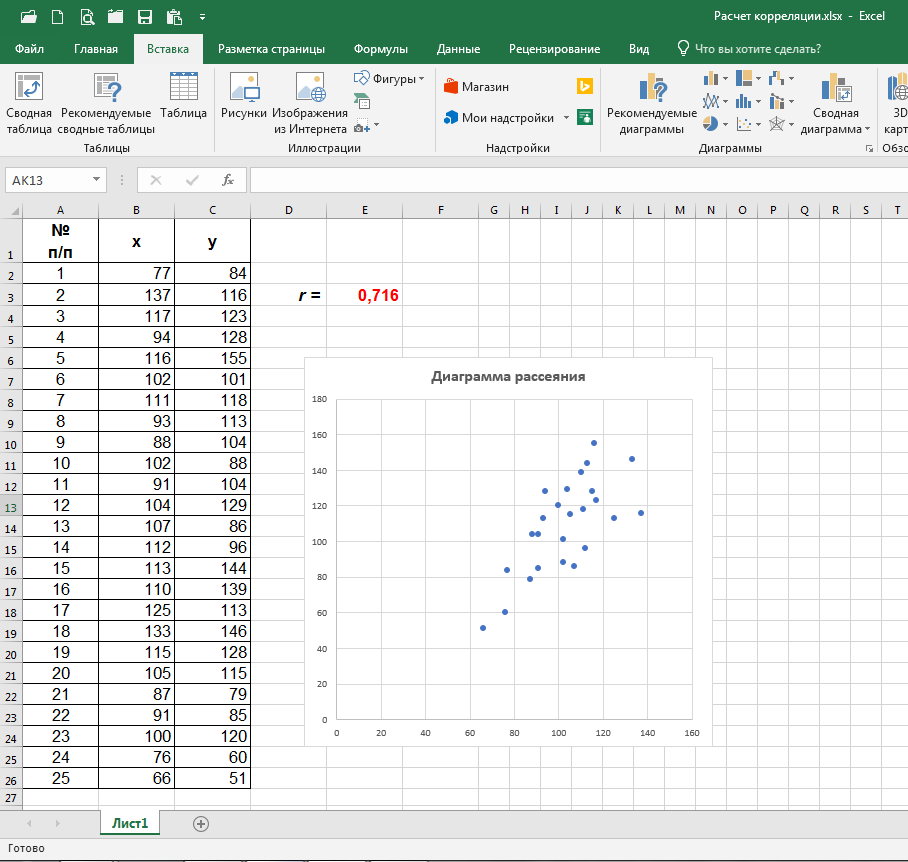
Если необходимо, мышкой выравниваем диаграмму (меняем размеры её сторон), перемещаем в нужное нам место на листе и вставляем название диаграммы:
Итак, коэффициент корреляции определён, диаграмма рассеяния построена. Поставленная задача нами выполнена.
Что ещё важно знать
Следует учесть, что данный инструмент (диаграмма рассеяния и расчёт коэффициента корреляции) не является стопроцентной гарантией того, что две переменные, имеющие высокий коэффициент корреляции, действительно связаны между собой: существуют так называемые ложные корреляции, при которых расчётное значение коэффициента корреляции высоко, но при этом зависимости одного признака от другого нет. Причины возникновения ложных корреляций могут быть самыми разнообразными, например наличие какого-либо другого, скрытого от нас признака, который влияет одновременно на оба исследуемых нами признака. Так, цена продуктов питания и стоимость жилья могут показывать высокий коэффициент корреляции, но на самом деле эти величины связаны не между собой, а с инфляцией или с ростом стоимости производства. Подобные ситуации – ловушка для исследователей [2, с. 128].
Возможны и обратные ситуации: связь реально существует, но установить её данным инструментом не удалось. Причины этого опять-таки могут быть самыми разными – от недостаточного числа собранных данных до чрезмерно большой ошибки измерения [2, с. 128–129].
Но это не значит, что данным инструментом нельзя пользоваться! Наоборот, это достаточно простое, но эффективное средство статистического анализа. Необходимо всего лишь учитывать, что, во-первых, правильно диаграмму рассеяния и коэффициент корреляции могут оценить только те, кто хорошо знаком с исследуемым процессом; во-вторых, полученный таким образом коэффициент корреляции – это величина случайная и физической константой не является [2, с. 129].
Иными словами, применение данного инструмента требует известной доли осторожности, внимания к деталям и знания сути вопроса.
А что дальше?
Ещё одним важным моментом является то, что коэффициент корреляции позволяет оценить степень тесноты связи между результативным признаком (y) и воздействующим на него фактором (х), но не даёт ответа на вопрос: на сколько единиц изменится результативный признак при изменении фактора на одну единицу? [3, с. 108].
Ответ на этот вопрос можно получить при помощи другого инструмента – регрессионного анализа. Объяснение сути данного анализа выходит за рамки настоящей темы, но с ней можно самостоятельно ознакомиться по различным источникам, например по источнику [3, с. 108].
Вместе с тем один сугубо практический совет на этот счёт мы дадим.
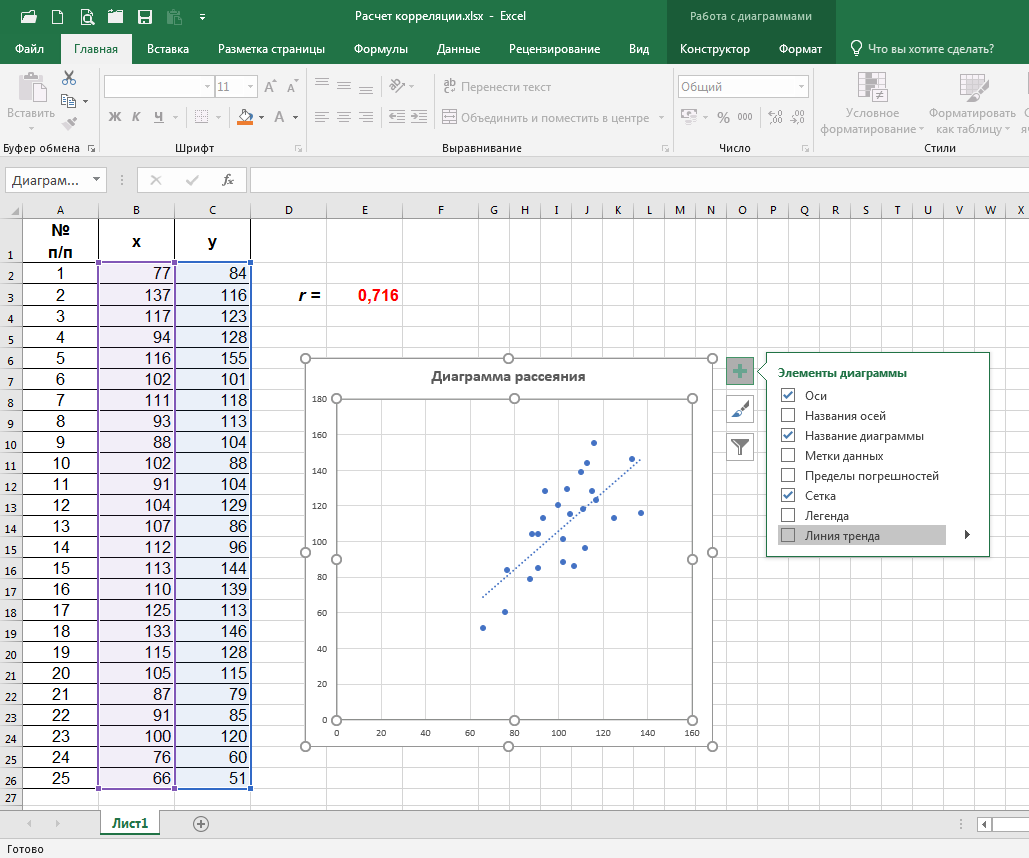
В любой диаграмме рассеяния, построенной в последних версиях программы Excel, можно мгновенно, путём нажатия мышкой на соответствующее поле, как показано на рисунке ниже, построить «линию тренда», т.е. ту самую воображаемую среднюю линию, о который мы говорили выше. Она и даст нам общее представление о характере и величине изменения результативного признака y при изменении воздействующего на него фактора х:
Описание представленного инструмента контроля качества мы постарались изложить в максимально простой и доступной форме – в расчёте на то, что его будут читать и, надеемся, применять в работе в том числе и далёкие от математики люди.
Источники:
- Васин С.Г. Управление качеством. Всеобщий подход : учебник для бакалавриата и магистратуры / С.Г. Васин. – М. : Издательство Юрайт, 2016.
- Гродзенский С.Я. Управление качеством : учебник. – Москва : Проспект, 2017.
- Маркетинг: теория и практика : учеб. пособие для бакалавров / под общ. ред. С.В. Карповой. – М. : Издательство Юрайт, 2016.
- Диаграмма разброса. / Сайт studfiles.net [Электронный ресурс]. Режим доступа: https://studfiles.net/preview/4499997 (дата обращения: 25.12.2018).
Если вы считаете, что при публикации настоящего материала нарушены ваши авторские права, напишите нам.
If you believe that the publication of this material infringes your copyright, please let us know.
Построим диаграмму рассеяния для различных видов взаимосвязей двух переменных. Сгенерируем различные варианты трендов: линейный, квадратичный и затухающий синусоидальный.
Диаграмма рассеяния
(
scatter
plot
) используется для отображения возможной взаимосвязи между двумя переменными.
Диаграмма рассеяния
незаменима при проведении корреляционного и регрессионного анализа.
Возьмем 2 переменные
Х
и
Y
и, соответственно,
выборку
состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности зададим различные типы зависимости между переменными: линейную, квадратичную и затухающую синусоидальную. Для этого сгенерируем соответствующие тренды и настроим случайный разброс переменной Y (по
нормальному закону
).
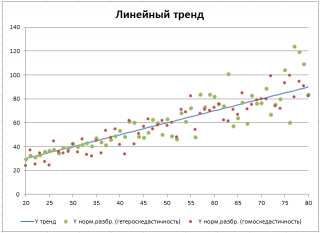
Сначала рассмотрим
линейный тренд
Y
=
aX
+
b
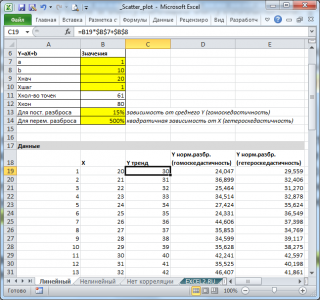
(см. Файл примера, лист Линейный ). Параметры тренда (прямой линии)
a
и
b
зададим в отдельной табличке, там же зададим параметры отвечающие за величину
дисперсии
переменной Y.
Величину постоянного разброса (отвечающую за
гомоскедастичность
модели) будем задавать в % от
среднего значения
Y. Иногда,
дисперсия
переменной Y не постоянна (имеется неоднородность наблюдений —
гетероскедастичность
). Поэтому, при построении формул учтем и такую возможность.
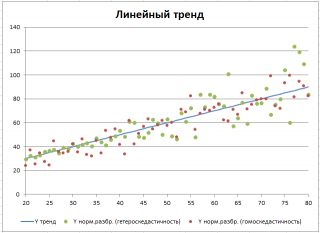
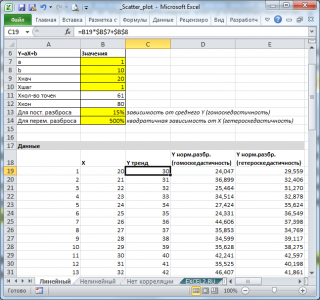
Для построения
диаграммы рассеяния
в файле примера использована
диаграмма График
, т.к. шаг по Х у нас задан постоянным. В случае реальных данных (переменная Х является случайной величиной, а не жестко заданной, как в нашем примере) используйте диаграмму типа Точечная. В файле примера реализовано оба варианта.
Примечание
: Подробнее о построении диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
Отображение информации о 3-х переменных на двухмерной диаграмме
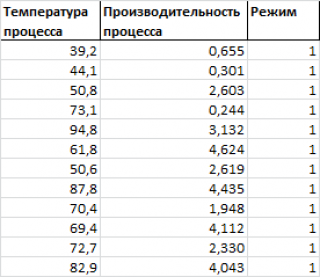
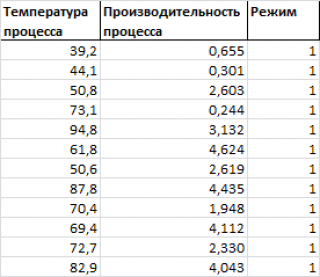
Предположим, что у нас имеются результаты измерения производительности некого непрерывного производственного процесса. Измерения проводились при различных рабочих температурах протекания процесса и в двух режимах.
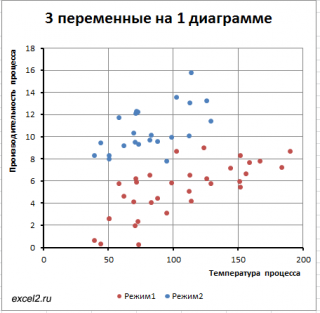
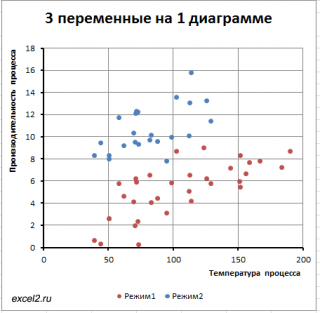
Нам требуется построить двумерную
диаграмму рассеяния
(на плоскости), хотя у нас имеется 3 переменных:
производительность, температура
и
режим
.
Обратим внимание, что третья переменная
Режим
является категориальной (принимает только значения из ограниченного набора значений). В нашем случае переменная
Режим
принимает 2 значения:
Режим №1
и
Режим №2
(значения 1 и 2 присвоены номинально).
Пары значений (
производительность; температура
), относящиеся к
Режиму №1
будем на
диаграмме рассеяния
выводить красным цветом, а относящиеся к
Режиму №2
будем выводить синим ( файл примера лист 3-переменных ).
Такой же подход можно использовать для
дискретных переменных
, когда они принимают небольшое количество значений: 2-5.
Категоризованные диаграммы
Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые
категоризованные диаграммы
(coplot = conditioning plot).
Теперь вместо категориальной переменной
Режим
у нас имеется
непрерывная переменная
Давление
, которая принимает значения от 10 до 20. Предположим, что значение переменной
Давление
= 15, является неким пороговым и протекание процесса значительно отличается, если оно протекает при давлении от 10 до 15 и от 15 до 20. Используя этот факт строят 2 диаграммы:
-
Пары значений (
производительность; температура
) при давлении от 10 до 15: -
Пары значений (
производительность; температура
) при давлении от 15 до 20.
Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.
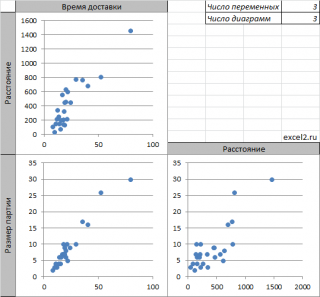
Матрица диаграмм рассеивания
Для множественной регрессии, когда имеется 3 или более переменных, часто строят
Матрицу диаграмм рассеивания
(Matrix Scatter Plot, Scatter Plot Matrix — SPM).
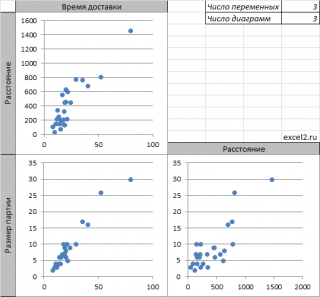
Если имеется 3 переменных (x 1 , x 2 , y), то строятся 3 обычные
диаграммы рассеяния
отображающие парные взаимосвязи переменных: (x 1 , x 2 ); (x 1 , y); (x 2 , y).
Примечание
: Чтобы найти количество
диаграмм рассеяния
в матрице, необходимо вычислить
число сочетаний
из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ЧИСЛКОМБ(4;2) =6.
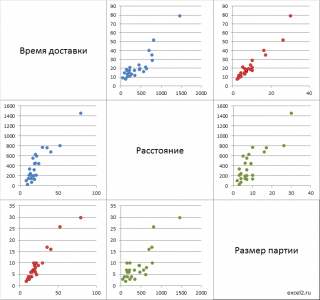
Иногда строят не только диаграмму (x 1 , x 2 ), но и (x 2 , x 1 ). В этом случае матрица будет содержать в 2 раза больше диаграмм рассеяния (см. файл примера лист Matrix ).
Примечание
: Чтобы найти количество
диаграмм рассеяния
в такой (полной) матрице, необходимо вычислить
число перестановок
из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ПЕРЕСТ(4;2) =12.
Содержание
- Дисперсия и стандартное отклонение в EXCEL
- Дисперсия выборки
- Дисперсия случайной величины
- Стандартное отклонение выборки
- Другие меры разброса
- Как рассчитать объединенную дисперсию в Excel (шаг за шагом)
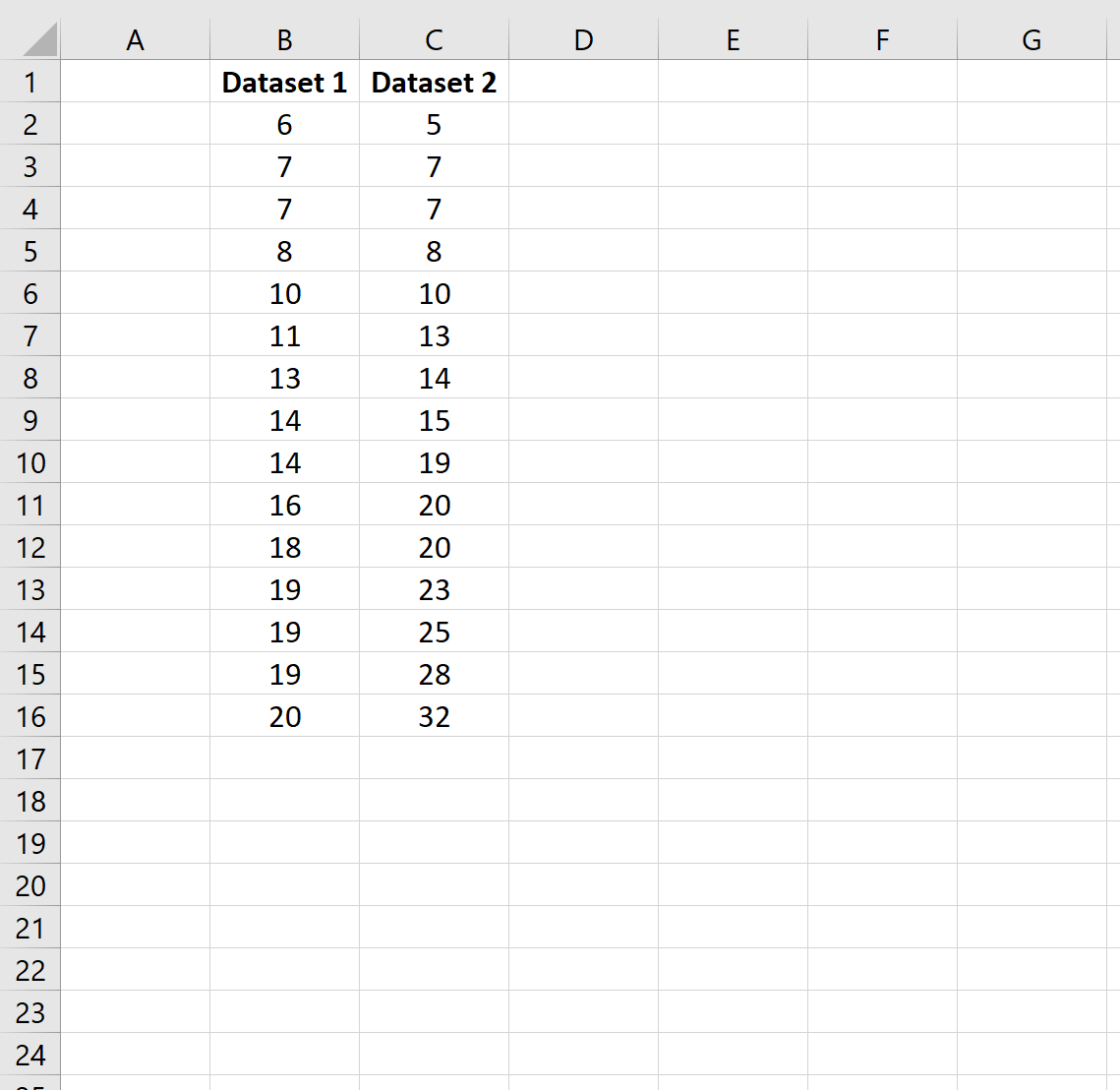
- Шаг 1: Создайте данные
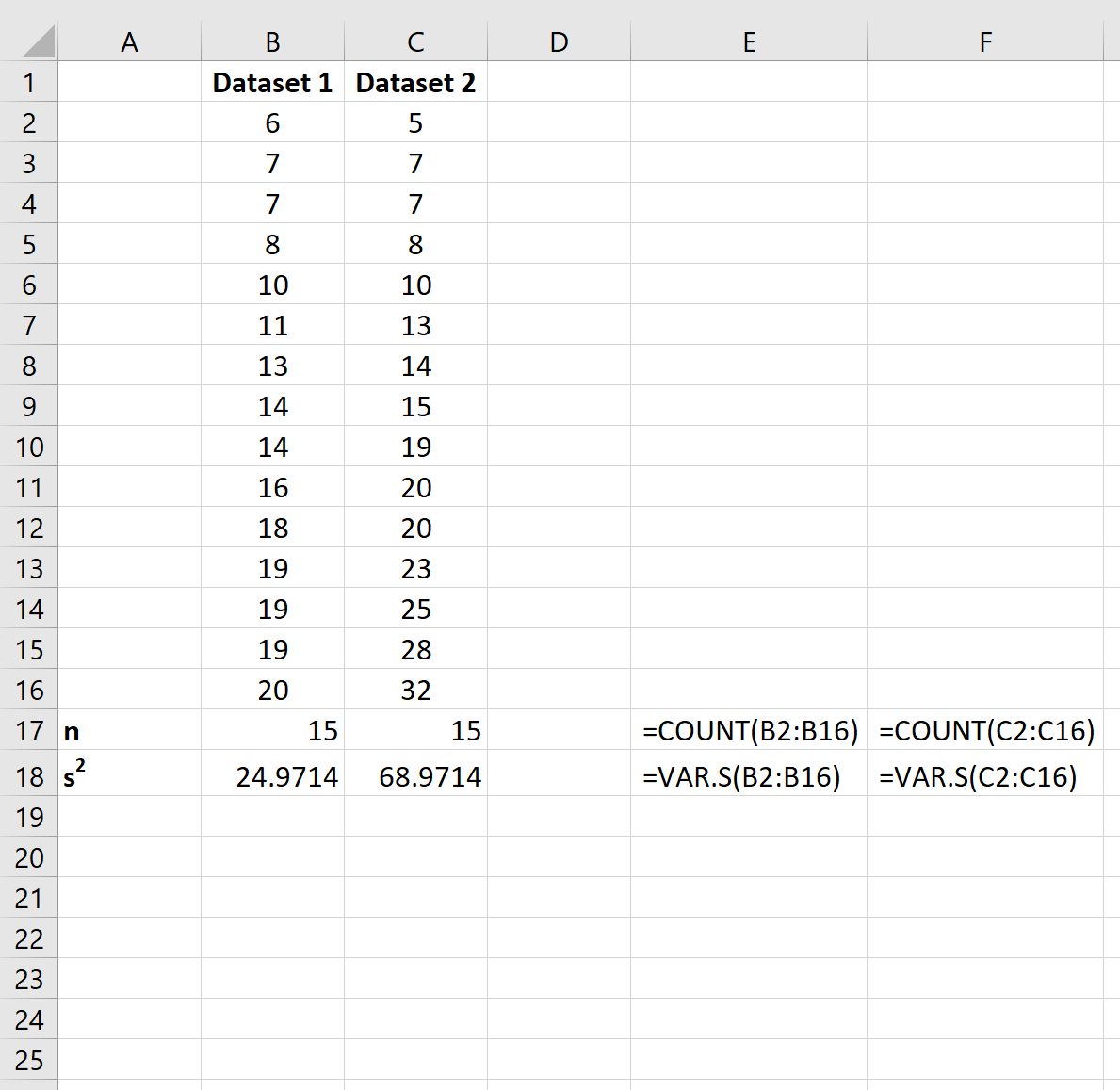
- Шаг 2: Рассчитайте размер выборки и дисперсию выборки
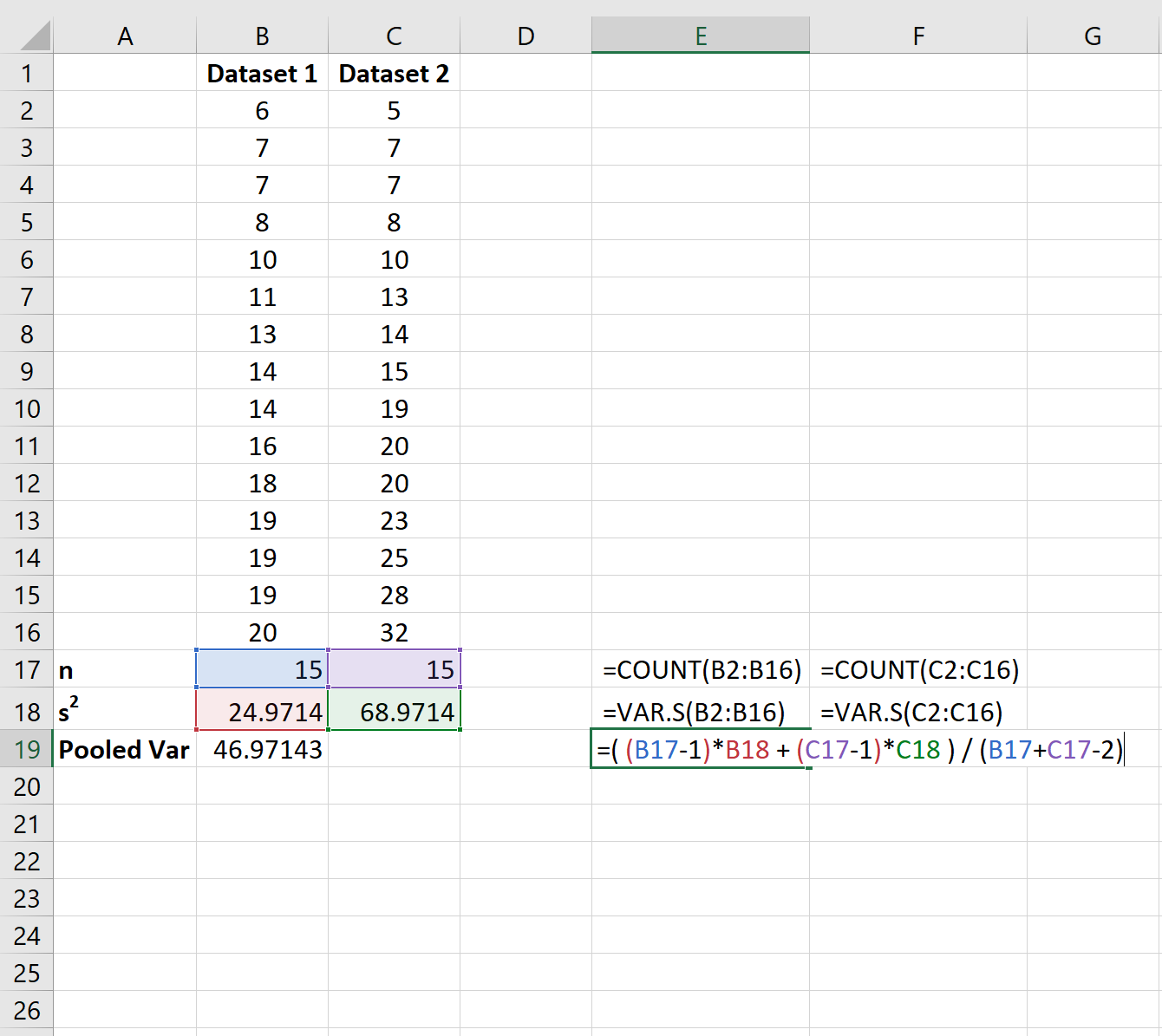
- Шаг 3: Рассчитайте объединенную дисперсию
- Диаграмма рассеяния в EXCEL
- Отображение информации о 3-х переменных на двухмерной диаграмме
- Категоризованные диаграммы
- Матрица диаграмм рассеивания
Дисперсия и стандартное отклонение в EXCEL
history 4 октября 2016 г.
Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим дисперсию , затем стандартное отклонение .
Дисперсия выборки
Дисперсия выборки ( выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно среднего .
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() , англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог ДИСП.В() , англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция ДИСП.Г(), англ. название VARP, т.е. Population VARiance, которая вычисляет дисперсию для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у ДИСП.В() , у ДИСП.Г() в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР() .
Дисперсию выборки можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула =СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1 ) – формула массива
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.
Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .
Дисперсия случайной величины
Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения .
Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]
Если случайная величина имеет дискретное распределение , то дисперсия вычисляется по формуле:
где x i – значение, которое может принимать случайная величина, а μ – среднее значение ( математическое ожидание случайной величины ), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет непрерывное распределение , то дисперсия вычисляется по формуле:
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.
Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .
Примечание : О распределениях в MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Некоторые свойства дисперсии :
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(Х)=E[(X-E(X)) 2 ]=E[X 2 -2*X*E(X)+(E(X)) 2 ]=E(X 2 )-E(2*X*E(X))+(E(X)) 2 =E(X 2 )-2*E(X)*E(X)+(E(X)) 2 =E(X 2 )-(E(X)) 2
Это свойство дисперсии используется в статье про линейную регрессию .
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего .
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних .
Примечание : квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их среднего .
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция =СТАНДОТКЛОН() , англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог =СТАНДОТКЛОН.В() , англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция СТАНДОТКЛОН.Г() , англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет стандартное отклонение для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у СТАНДОТКЛОН.В() , у СТАНДОТКЛОН.Г() в знаменателе просто n.
Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция КВАДРОТКЛ() вычисляет с умму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г( Выборка )*СЧЁТ( Выборка ) , где Выборка — ссылка на диапазон, содержащий массив значений выборки ( именованный диапазон ). Вычисления в функции КВАДРОТКЛ() производятся по формуле:
Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка — ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции СРОТКЛ () производятся по формуле:
Источник
Как рассчитать объединенную дисперсию в Excel (шаг за шагом)
В статистике объединенная дисперсия относится к среднему значению двух или более групповых дисперсий.
Мы используем слово «объединенные», чтобы указать, что мы «объединяем» две или более групповые дисперсии, чтобы получить единое число для общей дисперсии между группами.
На практике объединенная дисперсия чаще всего используется в двухвыборочном t-тесте , который используется для определения того, равны ли две средние значения совокупности.
Объединенная дисперсия между двумя выборками обычно обозначается как s p 2 и рассчитывается как:
s p 2 = ( (n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
В этом руководстве представлен пошаговый пример того, как рассчитать объединенную дисперсию между двумя группами в Excel.
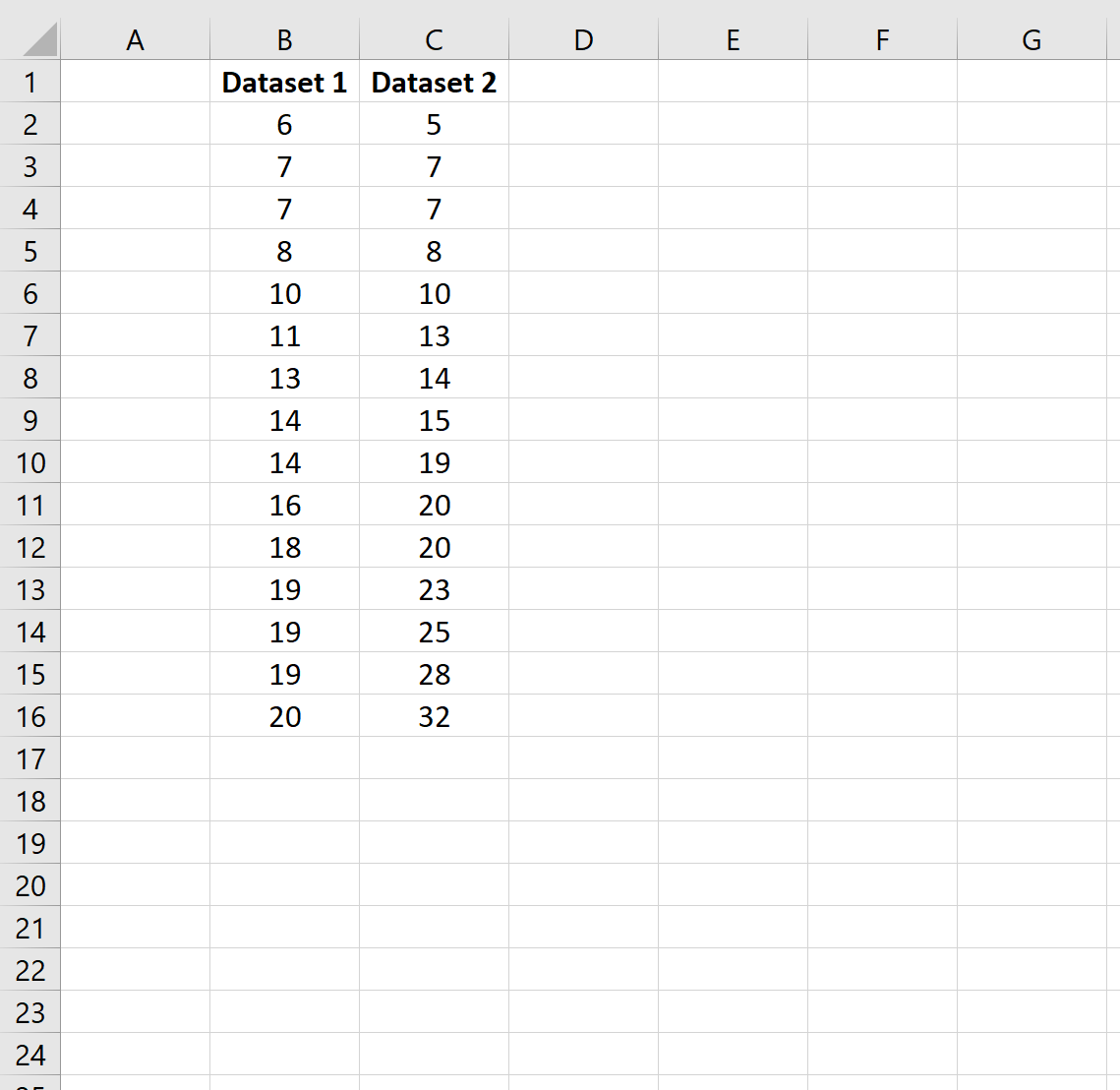
Шаг 1: Создайте данные
Во-первых, давайте создадим два набора данных:
Шаг 2: Рассчитайте размер выборки и дисперсию выборки
Далее давайте рассчитаем размер выборки и дисперсию выборки для каждого набора данных.
В ячейках E17:F18 показаны формулы, которые мы использовали:
Шаг 3: Рассчитайте объединенную дисперсию
Наконец, мы можем использовать следующую формулу для расчета объединенной дисперсии:
Суммарная дисперсия между этими двумя группами оказывается равной 46,97 .
Бонус: вы можете использовать этот Калькулятор объединенной дисперсии для автоматического расчета объединенной дисперсии между двумя группами.
Источник
Диаграмма рассеяния в EXCEL
history 25 ноября 2018 г.
Построим диаграмму рассеяния для различных видов взаимосвязей двух переменных. Сгенерируем различные варианты трендов: линейный, квадратичный и затухающий синусоидальный.
Диаграмма рассеяния ( scatter plot ) используется для отображения возможной взаимосвязи между двумя переменными. Диаграмма рассеяния незаменима при проведении корреляционного и регрессионного анализа.
Возьмем 2 переменные Х и Y и, соответственно, выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности зададим различные типы зависимости между переменными: линейную, квадратичную и затухающую синусоидальную. Для этого сгенерируем соответствующие тренды и настроим случайный разброс переменной Y (по нормальному закону ).
Сначала рассмотрим линейный тренд Y = aX + b (см. Файл примера, лист Линейный ). Параметры тренда (прямой линии) a и b зададим в отдельной табличке, там же зададим параметры отвечающие за величину дисперсии переменной Y.
Величину постоянного разброса (отвечающую за гомоскедастичность модели) будем задавать в % от среднего значения Y. Иногда, дисперсия переменной Y не постоянна (имеется неоднородность наблюдений — гетероскедастичность ). Поэтому, при построении формул учтем и такую возможность.
Для построения диаграммы рассеяния в файле примера использована диаграмма График , т.к. шаг по Х у нас задан постоянным. В случае реальных данных (переменная Х является случайной величиной, а не жестко заданной, как в нашем примере) используйте диаграмму типа Точечная. В файле примера реализовано оба варианта.
Примечание : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Отображение информации о 3-х переменных на двухмерной диаграмме
Предположим, что у нас имеются результаты измерения производительности некого непрерывного производственного процесса. Измерения проводились при различных рабочих температурах протекания процесса и в двух режимах.
Нам требуется построить двумерную диаграмму рассеяния (на плоскости), хотя у нас имеется 3 переменных: производительность, температура и режим .
Обратим внимание, что третья переменная Режим является категориальной (принимает только значения из ограниченного набора значений). В нашем случае переменная Режим принимает 2 значения: Режим №1 и Режим №2 (значения 1 и 2 присвоены номинально).
Пары значений ( производительность; температура ), относящиеся к Режиму №1 будем на диаграмме рассеяния выводить красным цветом, а относящиеся к Режиму №2 будем выводить синим ( файл примера лист 3-переменных ).
Такой же подход можно использовать для дискретных переменных , когда они принимают небольшое количество значений: 2-5.
Категоризованные диаграммы
Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые категоризованные диаграммы (coplot = conditioning plot).
Теперь вместо категориальной переменной Режим у нас имеется непрерывная переменная Давление , которая принимает значения от 10 до 20. Предположим, что значение переменной Давление = 15, является неким пороговым и протекание процесса значительно отличается, если оно протекает при давлении от 10 до 15 и от 15 до 20. Используя этот факт строят 2 диаграммы:
- Пары значений ( производительность; температура ) при давлении от 10 до 15:
- Пары значений ( производительность; температура ) при давлении от 15 до 20.
Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.
Матрица диаграмм рассеивания
Для множественной регрессии, когда имеется 3 или более переменных, часто строят Матрицу диаграмм рассеивания (Matrix Scatter Plot, Scatter Plot Matrix — SPM).
Если имеется 3 переменных (x 1 , x 2 , y), то строятся 3 обычные диаграммы рассеяния отображающие парные взаимосвязи переменных: (x 1 , x 2 ); (x 1 , y); (x 2 , y).
Примечание : Чтобы найти количество диаграмм рассеяния в матрице, необходимо вычислить число сочетаний из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ЧИСЛКОМБ(4;2) =6.
Иногда строят не только диаграмму (x 1 , x 2 ), но и (x 2 , x 1 ). В этом случае матрица будет содержать в 2 раза больше диаграмм рассеяния (см. файл примера лист Matrix ).
Примечание : Чтобы найти количество диаграмм рассеяния в такой (полной) матрице, необходимо вычислить число перестановок из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ПЕРЕСТ(4;2) =12.
Источник
17 авг. 2022 г.
читать 2 мин
Матрица диаграммы рассеяния — это матрица диаграмм рассеяния, которая позволяет понять попарные отношения между различными переменными в наборе данных.
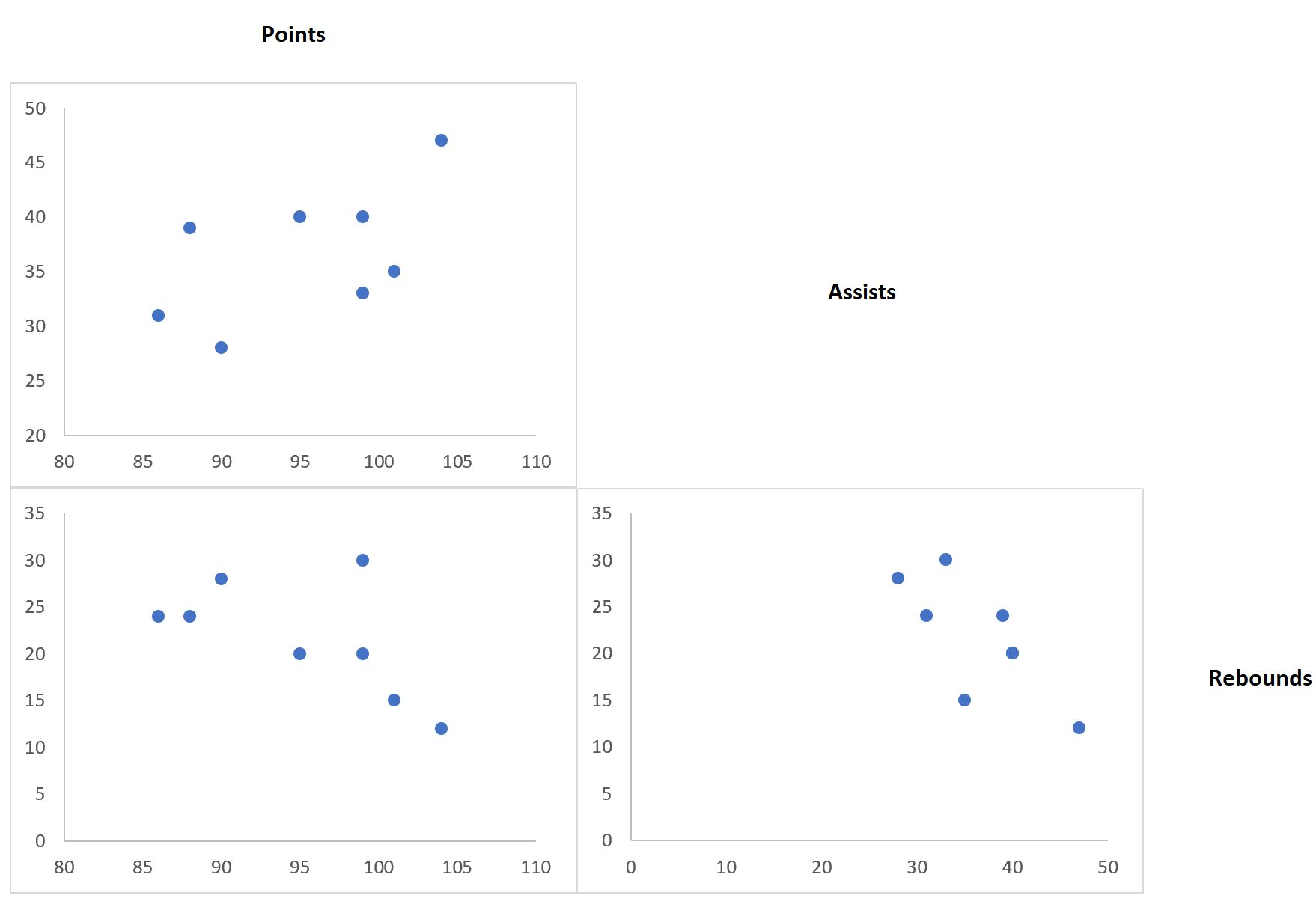
В этом руководстве объясняется, как создать следующую матрицу диаграммы рассеяния в Excel:
Давайте прыгать!
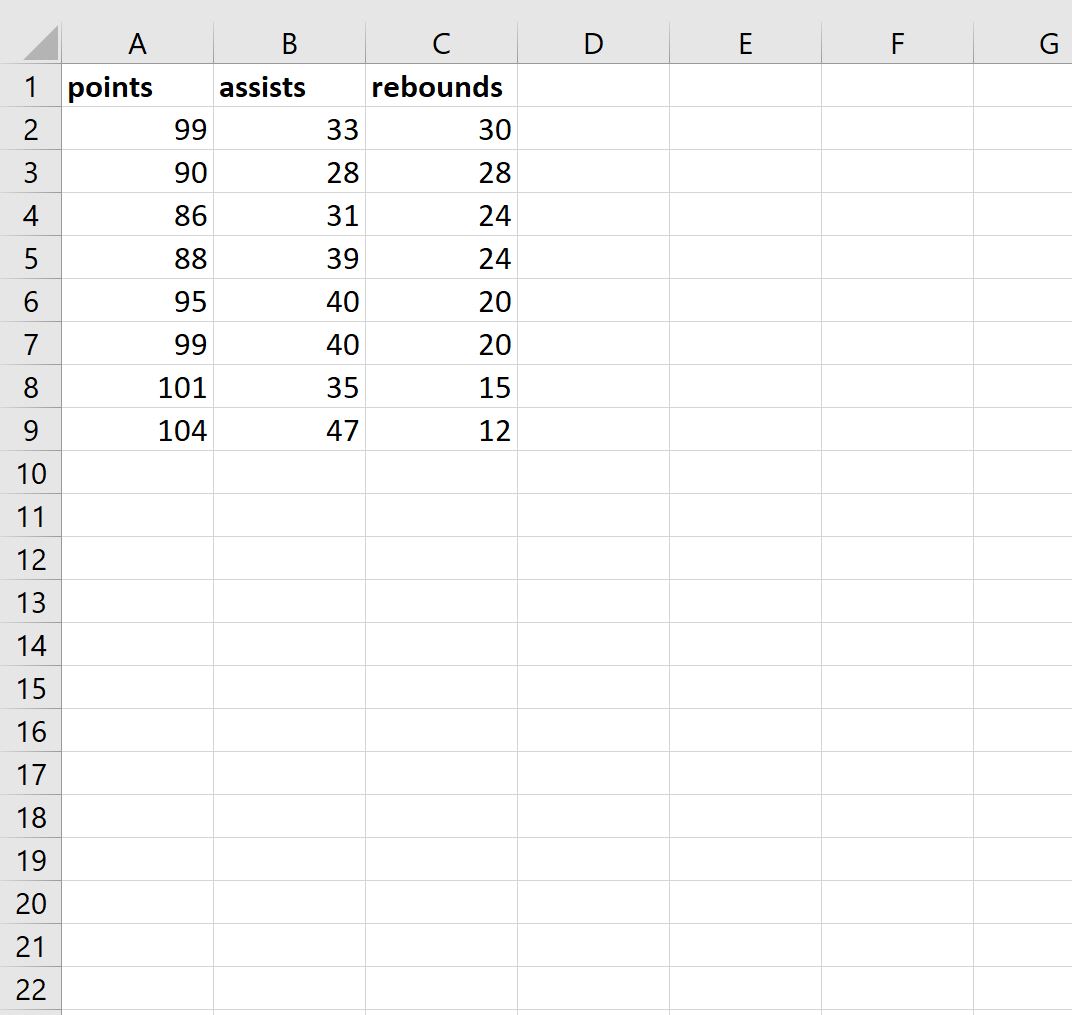
Шаг 1: введите данные
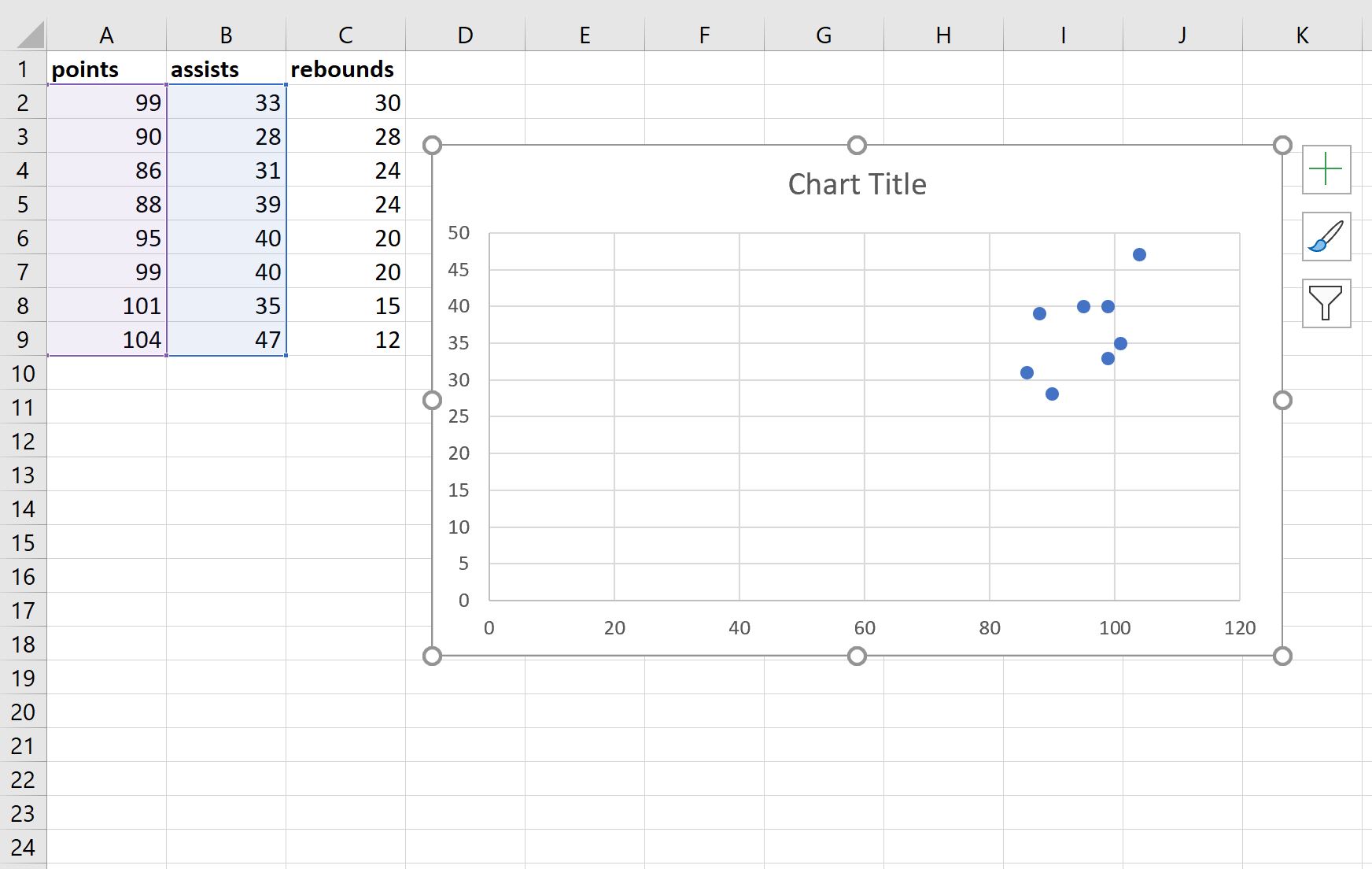
Во-первых, давайте введем следующие значения для набора данных, который содержит три переменные: очки, передачи и подборы.
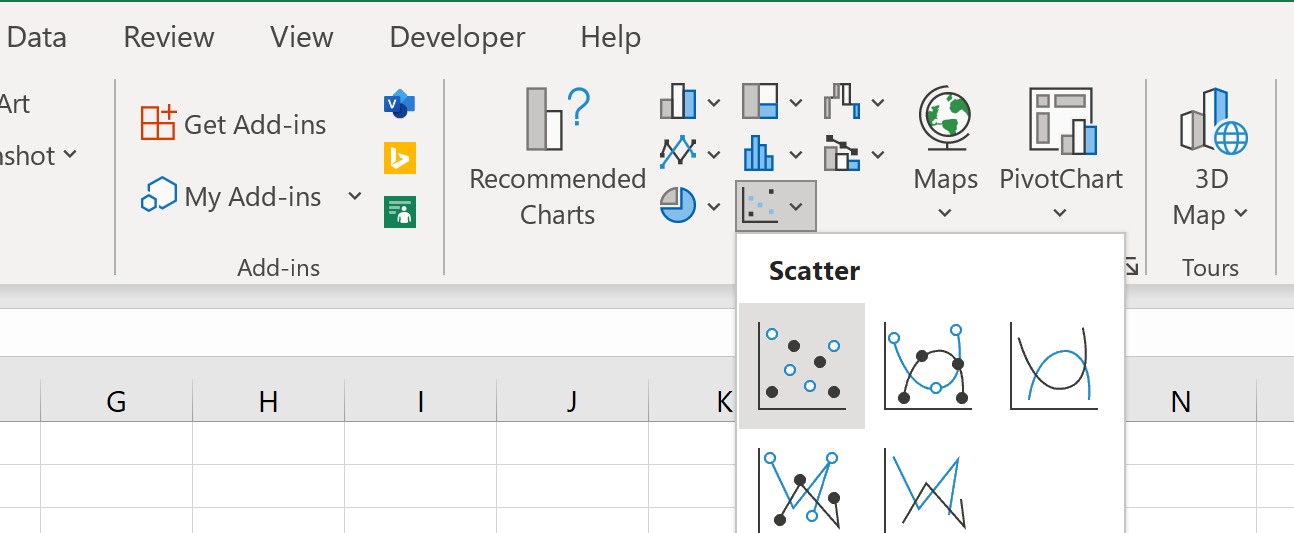
Шаг 2: Создайте диаграммы рассеяния
Затем выделим диапазон ячеек A2:B9 , затем щелкните вкладку « Вставка », затем нажмите кнопку « Разброс » в группе « Диаграммы ».
Автоматически будет создана следующая диаграмма рассеяния очков и передач:
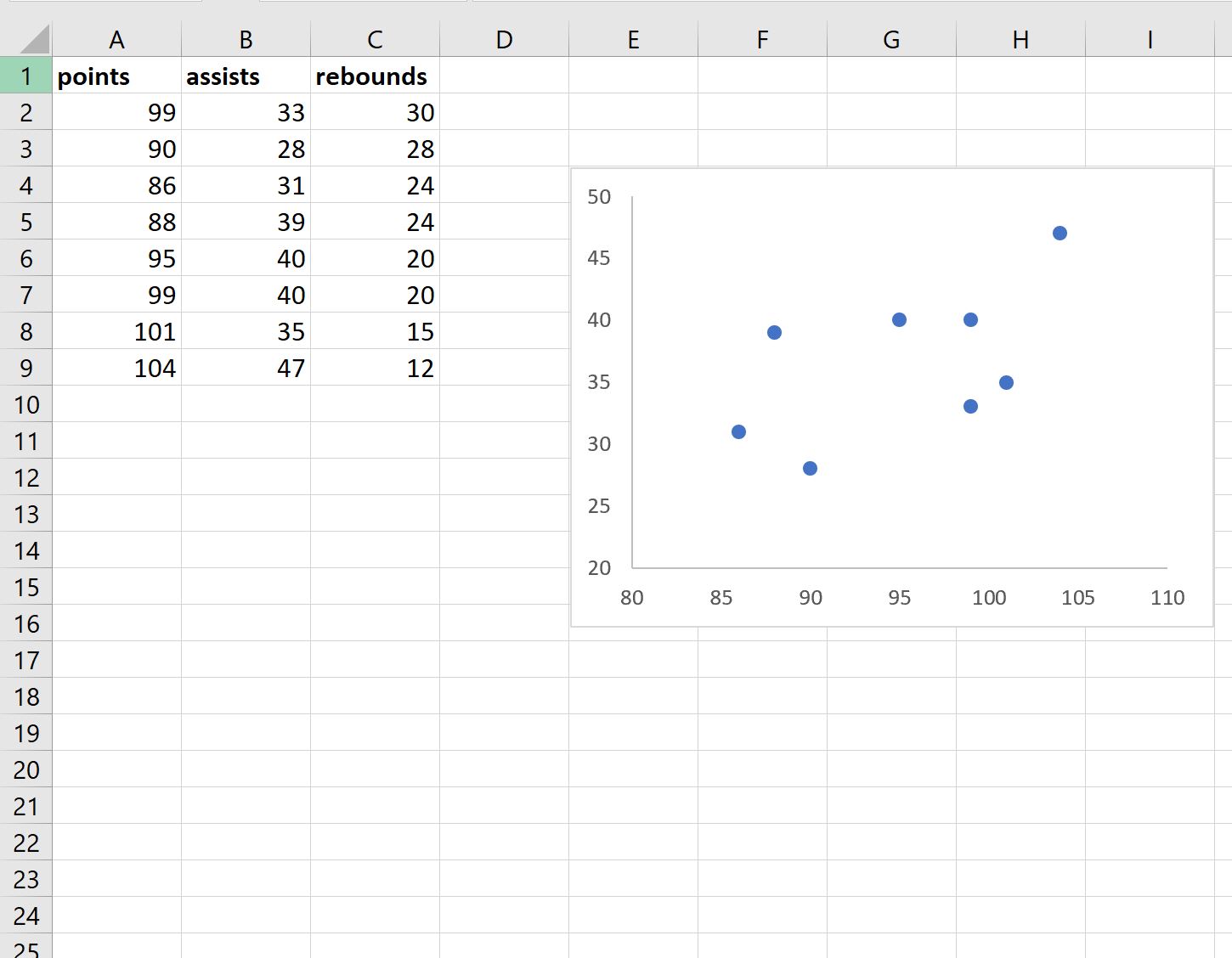
Далее выполните следующие шаги:
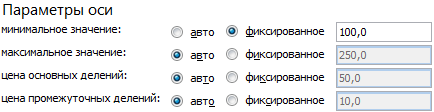
- Нажмите на значения на оси X и измените минимальную ось, привязанную к 80.
- Щелкните ось Y и измените минимальное значение оси на 20.
- Щелкните заголовок диаграммы и удалите его.
- Нажмите на линии сетки на диаграмме и удалите их.
- Наконец, измените размер диаграммы, чтобы сделать ее меньше.
Конечный результат должен выглядеть примерно так:
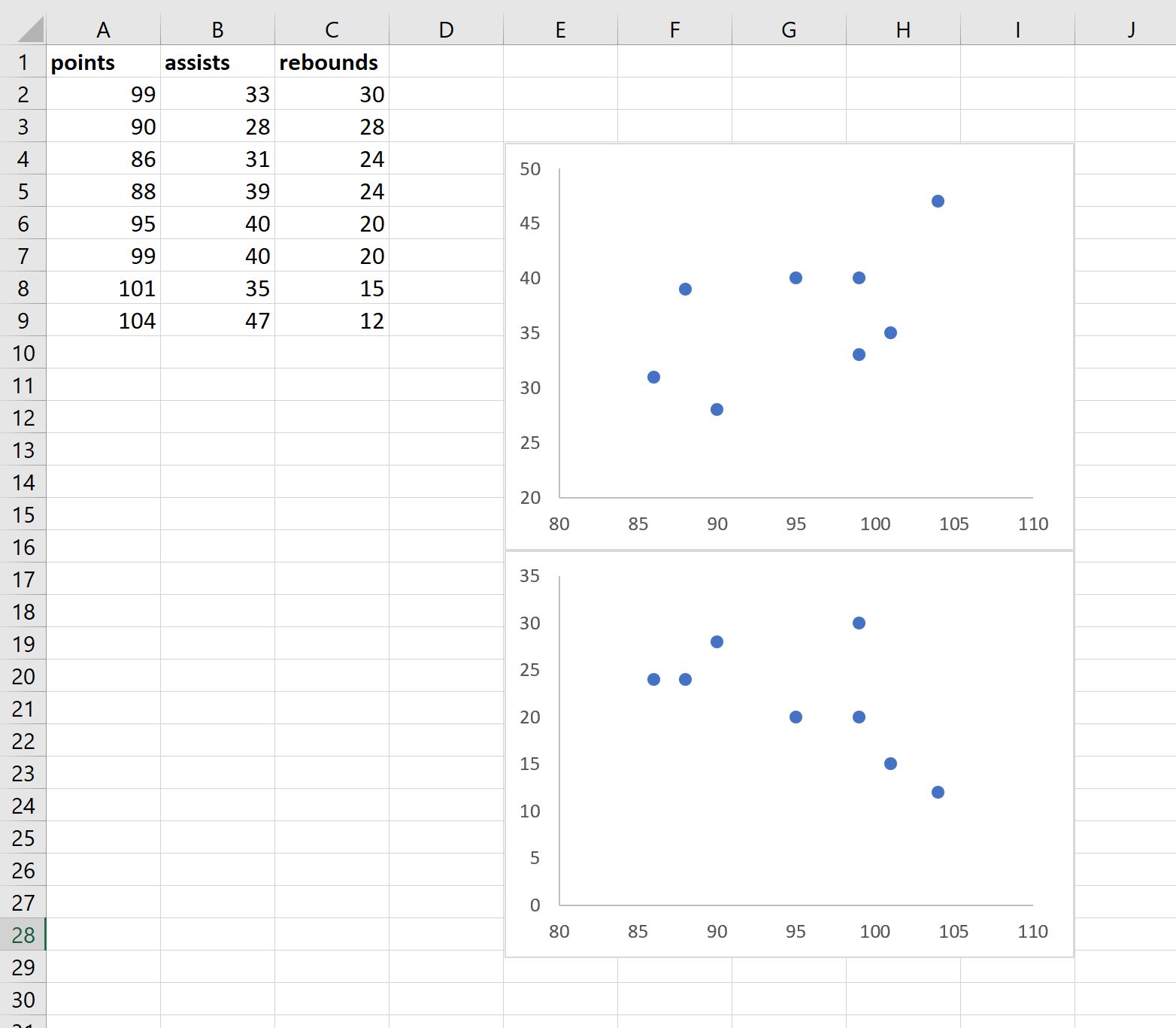
Затем повторите те же самые шаги для переменных очков и подборов и поместите диаграмму рассеяния под существующую диаграмму рассеяния:
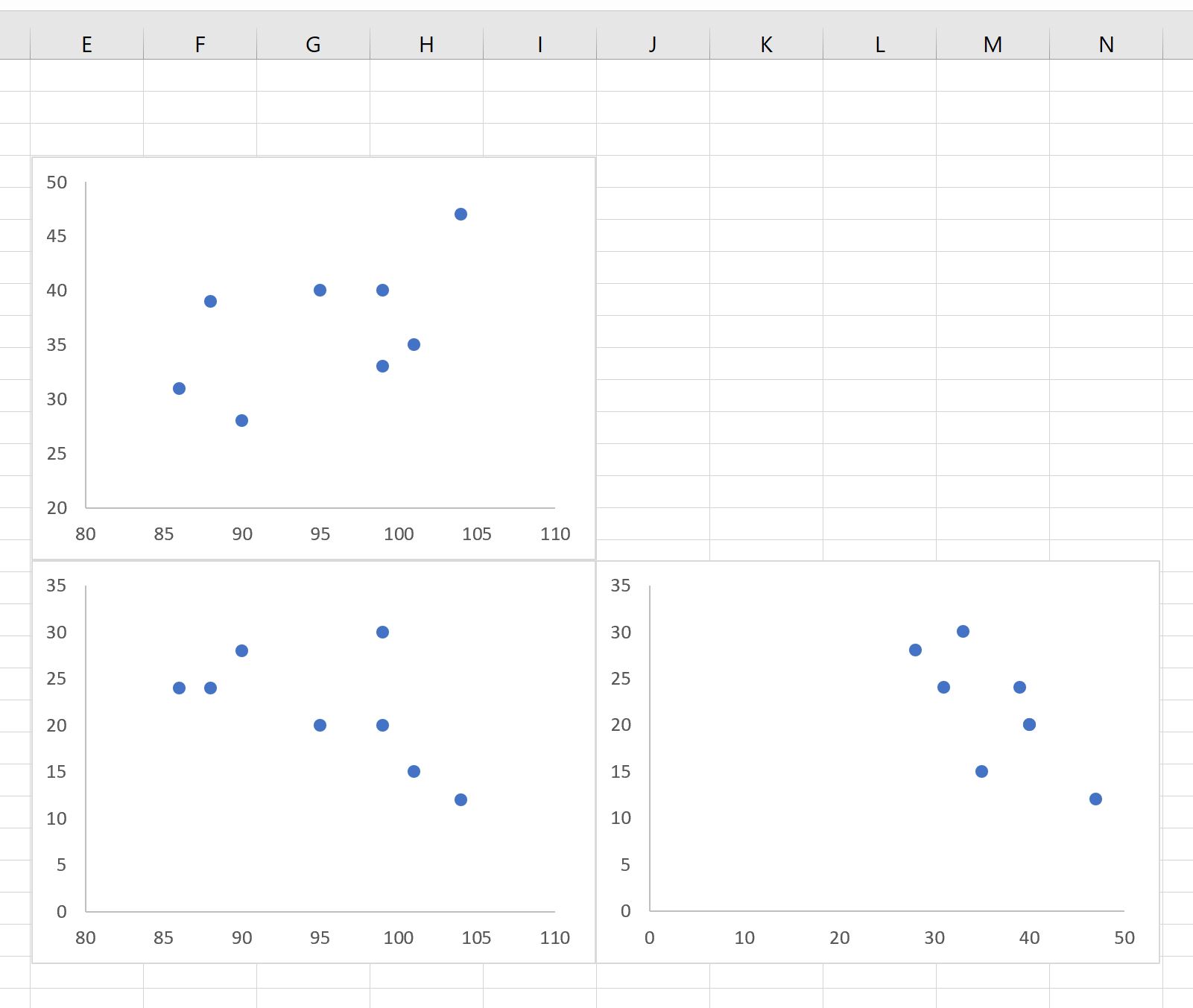
Наконец, повторите эти шаги для переменных передач и подборов и поместите диаграмму рассеяния в нижний правый угол:
Шаг 3: Пометьте диаграммы рассеяния
Наконец, введите имена переменных рядом с диаграммами рассеяния, чтобы было легко понять, какие диаграммы рассеяния представляют какие переменные:
Вот как интерпретировать сюжеты:
- Диаграмма рассеяния в верхнем левом углу представляет соотношение между очками и передачами.
- Диаграмма рассеяния в левом нижнем углу представляет соотношение между очками и подборами.
- Диаграмма рассеяния в правом нижнем углу представляет соотношение между передачами и подборами.
Примечание.Не стесняйтесь изменять цвет и размер точек на диаграммах рассеяния, чтобы они выглядели так, как вам нравится.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как создать диаграмму рассеяния с несколькими рядами в Excel
Как создать корреляционную матрицу в Excel
Как выполнить корреляционный тест в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.