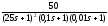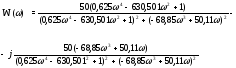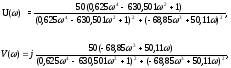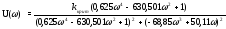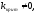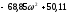Как построить годограф в excel - Word и Excel - помощь в работе с программами

Обновлено: 15.04.2023

Построение диаграммы в Microsoft Excel по таблице – основной вариант создания графиков и диаграмм другого типа, поскольку изначально у пользователя имеется диапазон данных, который и нужно заключить в такой тип визуального представления.

В Excel составить диаграмму по таблице можно двумя разными методами, о чем я и хочу рассказать в этой статье.

Способ 1: Выбор таблицы для диаграммы

Откройте необходимую таблицу и выделите ее, зажав левую кнопку мыши и проведя до завершения.

Вы должны увидеть, что все ячейки помечены серым цветом, значит, можно переходить на вкладку «Вставка».

Там нас интересует блок «Диаграммы», в котором можно выбрать одну из диаграмм или перейти в окно с рекомендуемыми.

Откройте вкладку «Все диаграммы» и отыщите среди типов ту, которая устраивает вас.

Справа отображаются виды выбранного типа графика, а при наведении курсора появляется увеличенный размер диаграммы. Дважды кликните по ней, чтобы добавить в таблицу.

Предыдущие действия позволили вставить диаграмму в Excel, после чего ее можно переместить по листку или изменить размер.

Дважды нажмите по названию графика, чтобы изменить его, поскольку установленное по умолчанию значение подходит далеко не всегда.

Не забывайте о том, что дополнительные опции отображаются после клика правой кнопкой мыши по графику. Так вы можете изменить шрифт, добавить данные или вырезать объект из листа.

Для определенных типов графиков доступно изменение стилей, что отобразится на вкладке «Конструктор» сразу после добавления объекта в таблицу.

Как видно, нет ничего сложного в том, чтобы сделать диаграмму по таблице, заранее выбрав ее на листе. В этом случае важно, чтобы все значения были указаны правильно и выбранный тип графика отображался корректно. В остальном же никаких трудностей при построении возникнуть не должно.

Способ 2: Ручной ввод данных

Преимущество этого типа построения диаграммы в Экселе заключается в том, что благодаря выполненным действиям вы поймете, как можно в любой момент расширить график или перенести в него совершенно другую таблицу. Суть метода заключается в том, что сначала составляется произвольная диаграмма, а после в нее вводятся необходимые значения. Пригодится такой подход тогда, когда уже сейчас нужно составить график на листе, а таблица со временем расширится или вовсе изменит свой формат.

На листе выберите любую свободную ячейку, перейдите на вкладку «Вставка» и откройте окно со всеми диаграммами.

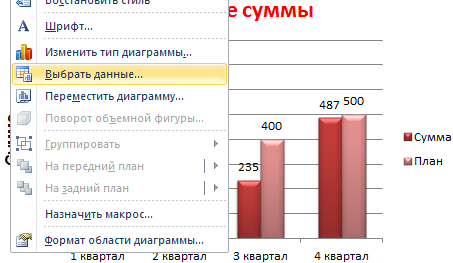
В нем отыщите подходящую так, как это было продемонстрировано в предыдущем методе, после чего вставьте на лист и нажмите правой кнопкой мыши в любом месте текущего значения.

Из появившегося контекстного меню выберите пункт «Выбрать данные».

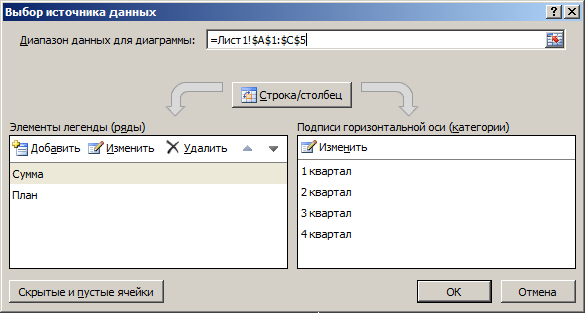
Задайте диапазон данных для диаграммы, указав необходимую таблицу. Вы можете вручную заполнить формулу с ячейками или кликнуть по значку со стрелкой, чтобы выбрать значения на листе.

В блоках «Элементы легенды (ряды)» и «Подписи горизонтальной оси (категории)» вы самостоятельно решаете, какие столбы с данными будут отображаться и как они подписаны. При помощи находящихся там кнопок можно изменять содержимое, добавляя или удаляя ряды и категории.

Обратите внимание на то, что пока активно окно «Выбор источника данных», захватываемые значения таблицы подсвечены на листе пунктиром, что позволит не потеряться.

По завершении редактирования вы увидите готовую диаграмму, которую можно изменить точно таким же образом, как это было сделано ранее.

Вам остается только понять, как сделать диаграмму в Excel по таблице проще или удобнее конкретно в вашем случае. Два представленных метода подойдут в совершенно разных ситуациях и в любом случае окажутся полезными, если вы часто взаимодействуете с графиками во время составления электронных таблиц. Следуйте приведенным инструкциям, и все обязательно получится!

График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.

Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.

График функции F(x) = X^2

Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:

Создайте строку на листе в программе, вписав туда известные значения X.

Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.

Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.

Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.

Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.

В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.

Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).

Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.

График функции y=sin(x)

y=sin(x) – вторая функция, которую мы возьмем за пример. Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.

Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.

Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.

Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.

Теперь более сложное, но не страшное действие – определение значения Y. Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.

На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.

Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.

На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.

(1)

где и полиномы комплексного переменного s, — некоторый параметр, который в дальнейшем будем называть варьируемым. (Таким параметром может служить, например, передаточный коэффициент k разомкнутой системы).

Имея характеристическое уравнение (1) с известными нулями входящих в него полиномов L(s) и D(s) можно приблизительно построить на плоскости S корневые годографы.

Для этого (1) переписываем в виде:

(2)

Учитывая, что s — комплексная переменная, (2) можно записать в виде двух уравнений: уравнения аргументов

и уравнения модулей

. (4)

Представим и в виде:

где и — коэффициент при s наивысшей степени,

, — нули полиномов и ,

m и n – порядки полиномов и .

Уравнение аргументов (3) можно переписать в следующем виде:

(Сказанное показано на рис.1)

На этом рисунке через обозначены аргументы векторов, проведенных из полюсов , аргумент вектора, проведенного из нуля .

На основании выражения (5) можно сформулировать следующие основные правила построения корневых годографов:

1. Вещественная ось плоскостей S является осью симметрии для корневых годографов и для асимптот корневых годографов.

Если число полюсов n больше числа нулей m, то (n-m) ветвей корневого годографа уйдут в бесконечность. Если число нулей больше числа полюсов, то (n-m) ветвей корневого годографа придут из бесконечности.

3. Ветви корневых годографов, находящихся в бесконечности имеют асимптоты. Число асимптот равно . Асимптоты пересекаются в одной точке вещественной оси плоскости S, причем:

, (6)

и имеют углы наклона относительно положительного направления вещественной оси плоскости S:

4. Точки вещественной оси плоскости S справа от которых находится нечетное число нулей и полюсов функции обязательно принадлежат корневым годографам, а точки этой оси справа от которых находится четное число нулей и полюсов не могут принадлежать корневым годографам.

5. В некоторых точках вещественной оси плоскости S, принадлежащих корневым годографам, корневые годографы могут, встретившись, разойтись, один в верхнюю, а другой в нижнюю части плоскости S.

Сформулированные выше правила позволяют приближенно выполнить построение корневых годографов.

Рассмотрим некоторые примеры построения корневых годографов.

Построить корневые годографы для варьируемого параметра К для замкнутой системы, если передаточная функция разомкнутой системы:

Пример 1.

Решение: Характеристическое уравнение замкнутой системы . Представим его в виде . Отсюда видно, что количество нулей равно 0, а количество полюсов равно 4. Их значения можно получить, найдя корни знаменателя. Получаем

Наносим полюса на комплексную плоскость. В соответствии с правилом 2 все корневые годографы должны уйти в бесконечность. Число асимптот равно 4-0=4. Определим точку, расположенную на вещественной оси, в которой пересекаются асимптоты –7,5

Определим углы, которые асимптоты составляют с положительным направлением вещественной оси (правило 3).

Наносим асимптоты на комплексную плоскость, как показано на рис.2. На этом же рисунке показаны корневые годографы, которые выходят из полюсов и уходят в бесконечность, неограниченно приближаясь к нарисованным асимптотам.

Рис.2

Решение: Характеристическое уравнение замкнутой системы имеет вид

Отсюда .

Приравнивая к нулю числитель и знаменатель, получим нули и полюса корневых годографов

Наносим полюса и нули на комплексную плоскость, как показано на рис.2. В соответствии с правилом 1, два корневых годографа должны закончиться в бесконечности, кроме того в соответствии с правилом 4 ни одна из точек вещественной плоскости не принадлежит корневым годографам.

В соответствии с правилом 3, корневые годографы имеют 2 асимптоты, пересекающиеся с вещественной осью в точке

Углы между асимптотами и положительным направлением вещественной оси будут равны (правило 3)

С учетом сказанного корневые годографы будут иметь вид, показанный на рис.3. Корневые годографы выйдя из полюсов P₁ и P₂ закончатся в нулях N₁ и N₂. Корневые годографы выйдя из полюсов P₃ и P₄ уйдут в бесконечность неограниченно приближаясь к асимптотам, пересекающим вещественную ось в точке –55.

Пример 3.

Решение: Характеристическое уравнение замкнутой системы

Представим его в виде

Нули корневых годографов будут:

Полюса корневых годографов будут:

Наносим нули и полюса на комплексную плоскость, как показано на рис. 4. В соответствии с правилом 4, часть вещественной оси, лежащая левее нуля N₃ будет принадлежать корневым годографам, при этом этот отрезок оси является асимптотой для годографа, уходящего в бесконечность.

Корневые годографы, построенные в соответствии с изложенными выше правилами, изображены на том же рисунке. Два корневых годографа, выйдя из полюсов P₁ и P₂ придут в нули N₁ и N₂. Корневые годографы, выйдя из полюсов P₃ и P₄ сойдутся в одной точке на вещественной оси, равной примерно 84 и, затем один закончится нуле N₃, а другой уйдет в бесконечность.

W (s) = ,

Построить годографы Михайлова и Найквиста. Определить частоту среза системы.

Определить критическое значение коэффициента усиления системы.

Решение.

А) Выписываем характеристический полином для замкнутой системы

A(s) = 50 + (30s+1) (0,4s+1)(0,01s+1) = 50+(900 +60s+1)(0,004 +0,41s+1) = 3,6 +369,24 +924,604 +60,41s+51.

В) Выделим действительную и мнимую часть.

A= U( )+jV( ), где U( ) – действительная часть, а V( ) – мнимая часть.

Г) Построим годограф Михайлова:

Д) Проверим устойчивость системы с помощью критерия Михайлова:

Из решения видно (см. рис.1 и рис.2), что годограф удовлетворяет всем условиям критерия:

W (s) = ,

Б) Раскроем скобки и выделим действительную и мнимую часть в знаменателе

W ( ) = ,

В) Умножим на сопряженное и выделим действительную и мнимую часть

где U( ) – действительная часть, а V( ) – мнимая часть.

Г) Построим годограф Найквиста:

Рис.3. Годограф Найквиста.

Д) Проверим устойчивость системы с помощью критерия Найквиста:

Критерий Найквиста: Для того чтобы система, которая в разомкнутом состоянии была устойчива, была устойчива и в замкнутом, необходимо, чтобы годограф Найквиста при изменении частоты от нуля до бесконечности не охватывал точку с координатами (-1; j0).

Из решения видно (см. рис.3), что годограф удовлетворяет всем условиям критерия:

Годограф меняет свое направление по часовой стрелке
Годографом не охватывается точка (-1; j0)
Делаем вывод, что данная разомкнутая система устойчива.

Определение критического значения коэффициента усиления системы.

А) В пункте 2 уже были выделены действительная и мнимая части

Б) Для того, чтобы найти критическое значение коэффициента усиления системы необходимо приравнять мнимую часть к нулю, а действительную к -1

= -1 (1)

= 0 (2)

В) Найдем из второго (2) уравнения

= 0

В) Подставляем в первое (1) уравнение и находим

-1

— критическое значение коэффициента усиления системы.

Определение частоты среза системы.

А) Приведем основные формулы

, где U( ) и V( ) – действительная и мнимая части соответственно.

Б) Подставляем в формулу имеющиеся данные и находим частоту среза системы

В) Найдем (при помощи Wolfram Alpha):

— частота среза системы.

1.Методы классической и современной теории автоматического управления. Том 1.

Анализ и статистическая динамика систем автоматического управления. М: Изд. МГТУ им Баумана. 2000 г.

2. Воронов А.А. Теория автоматического управления. Т. 1-3, М., Наука, 1992

Читайте также:

Как сделать обложку для альбома в вк в фотошопе

Как поменять пт на пиксели в фотошопе

Как удалить файлы с видеокамеры панасоник через компьютер

Asus motherboard как удалить

Как сделать платежную ведомость в 1с на одном листе

Источник

Задача
2

Условие
задания.

Пользуясь
критерием устойчивости Михайлова,
Найквиста определить устойчивость
одноконтурной системы управления,
имеющую в разомкнутом состоянии
передаточную функцию вида

в
формулу проставить значения К, а, b и с
по варианту.

W(s)
=,
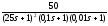
(1)

Построить
годографы Михайлова и Найквиста.
Определить
частоту среза системы.

Определить
критическое значение коэффициента
усиления системы.

Решение.

Задачи
анализа и синтеза систем управления
решаются с помощью такого мощного
математического аппарата, каким является
операционное исчисление (преобразование)
Лапласа. Задачи анализа и синтеза систем
управления решаются с помощью такого
мощного математического аппарата, каким
является операционное исчисление
(преобразование) Лапласа.
Общее
решение операторного уравнения
представляет собой сумму слагаемых,
определяемых значениями корней
характеристического полинома (многочлена):

D
(s) = d
sⁿ
d_n).

Построение
годографа Михайлова.

А)
Выписываем характеристический многочлен
для замкнутой системы, описываемой
уравнением (1)

D
(s)
= 50 + (25s+1)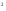(0,1s+1)(0,01s+1)
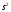
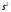
= 50+(625+50s+1)(0,001+0,11s+1)
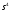
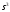
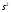
=0,625+68,85+630,501+50,11s+51.

Корни
многочлена D
(s)
могут быть: нулевыми; вещественными
(отрицательными, положительными); мнимыми
(всегда парными, сопряженными) и
комплексными сопряженными.

Б)
Преобразуем к виду s→
ωj

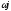
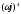
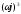
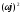
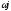
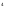
D()=0,625+68,85+630,501+50,11+51=0,625ω-68,85jω—
630,501ω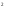+50,11jω+51

ω
– частота сигнала, j
= (1)^1/2
– мнимая
единица.
J⁴
=(-1)^4/2=1,
J³
=(-1)^3/2=-(1)^1/2=
— j,
J²
=(-1)^2/2=-1,
J
=(-1)^1/2=
j,

В)
Выделим действительную и мнимую часть.

D
= U()+jV(),
где U()
– действительная часть, а V()
– мнимая часть.

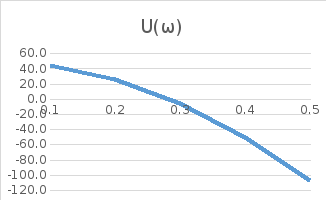
U(ω)
=0,625ω-630,501ω+51

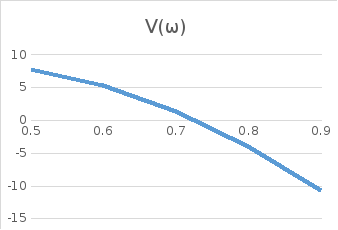
V(ω)
=ω(50,11-68,85ω)

Г)
Построим годограф Михайлова.

Построим
годограф Михайлова вблизи и сдали от
нуля, для этого построем D(jw) при изменении
w от 0 до +∞. Найдем точки пересечения
U(w)
и V(w)
с осями. Решим задачу с использованием
MicrosoftExcel.

-задаем
значения w в диапазоне от 0 до 0,0001 до 0,1,
рассчитаем в табл. Excel значения U(ω)
и
V(ω),
D(ω);
находим точки пересечения U(w)
и V(w)
с осями,

-задаем
значения w в диапазоне от 0,1 до 20, рассчитаем
в табл. Excel значения U(w)
и V(w),
D;
находим точки пересечения U(w)
и V(w)
с осями.

Таблица
2.1 – Определение действительной
и мнимой частей и самого многочлена
D(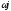)с
использованием MicrosoftExcel

ω	0,0001	0,001	0,003	0,006	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,1
U(ω)	51	51	51,0	51,0	50,9	50,7	50,4	50,0	49,4	48,7	47,9	47,0	45,9	44,7
V(ω)	0,005	0,05	0,15	0,298	0,494	0,975	1,4413	1,8942	2,333	2,7587	3,17	3,5682	3,952	4,3225
D	51,005	51,05	51,14	51,28	51,43	51,72	51,874	51,885	51,76	51,489	51,08	50,533	49,845	49,018
ω	0,1	0,2	0,3	0,5	0,7	0,8	1,0	2	5,0	7,5	10,0	12,5	15,0	20
U(ω)	44,70	25,78	-5,74	-107	-258	-352,3	-578,9	-2461	-15321	-33437	-56749	-83206	-110171	-152149
V(ω)	4,32	7,27	8,84	7,843	1,341	-3,976	-18,74	-175,2	-1471	-3497	-6384	-10131	-14740	-26538
D	49,02	33,05	3,10	-98,7	-256	-356,2	-597,6	-2636	-16792	-36934	-63133	-93337	-124911	-178687

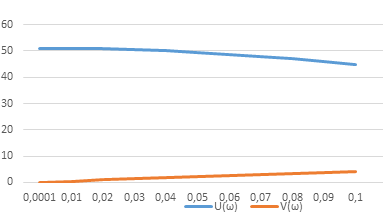
Рис.
А, Б, ….. Зависимости U(ω)
и
V(ω),
D(ω)
от ω

По
рис. А,
Б, …..находим точки пересечения U(w)
и V(w)
с осями:

при
ω
= 0 U(ω)=
…. и
V(ω)=
……

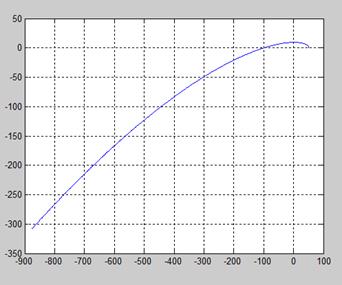
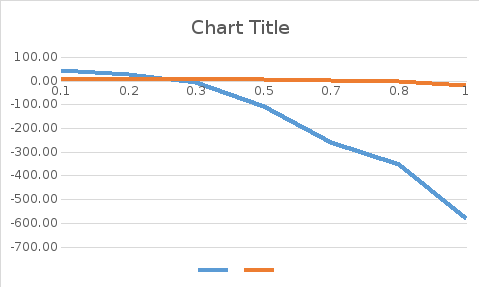
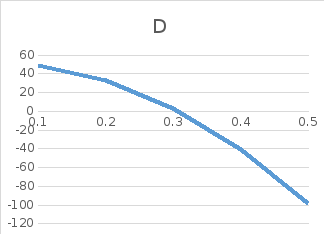
Рис.1.
Годограф Михайлова при ω = 0:000,1:0,1.

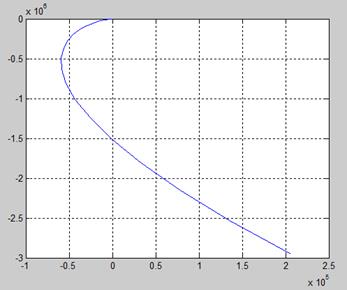
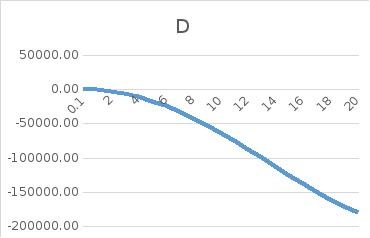
Рис.2.
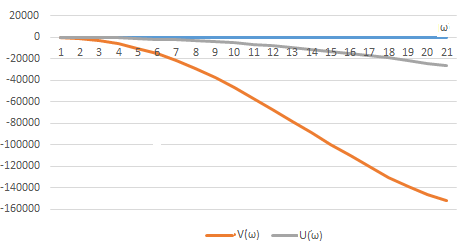
Годограф Михайлова при ω = 0,1:20

Д)
Выводы об устойчивости системы по
годографу.

Устойчивость
(как понятие) любой динамической системы
определяется ее поведением после снятия
внешнего воздействия, т.е. ее свободным
движением под влиянием начальных
условий. Система является устойчивой,
если она возвращается в исходное
состояние равновесия после прекращения
действия на систему сигнала (возмущения),
выведшего ее из этого состояния.
Неустойчивая система не возвращается
в исходное состояние, а непрерывно со
временем удаляется от него.
Для
оценки устойчивости системы необходимо
исследовать свободную составляющую
решения уравнения динамики, т.е решения
уравнения:.

D
(s)
= d
sⁿ
d_n)=0.

Проверить
устойчивость системы с помощью критерия
Михайлова:

Критерий
Михайлова: Для
устойчивой АСР необходимо и достаточно,
чтобы годограф Михайлова (см. рис.1 и
рис.2), начинаясь при w = 0 на положительной
вещественной полуоси, обходил
последовательно в положительном
направлении (против часовой стрелки)
при возрастании w от 0 до ∞ n квадрантов,
где n — степень характеристического
полинома.

Из
решения видно (см. рис.1 и рис.2), что
годограф удовлетворяет следующим
условиям критерия: Начинается
на положительной вещественной полуоси
при
w = 0. Годограф
не удовлетворяет следующим условиям
критерия:
не обходит
в положительном направлении все 4
квадранта (степень полинома n=4)
при ω.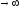

Делаем
вывод, что данная разомкнутая система
не устойчива.

Построение
годографа Найквиста.

А)
Произведем замену в формуле (1) s→
ωj

W(s)
=
=,

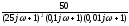
Б)
Раскроем скобки и выделим действительную
и мнимую часть в знаменателе

W()
=,

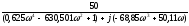
В)
Умножим на сопряженное и выделим
действительную и мнимую часть

где
U()
– действительная часть, а V()
– мнимая часть.

Г)
Построим годограф Найквиста: — зависимость
W()
от
.

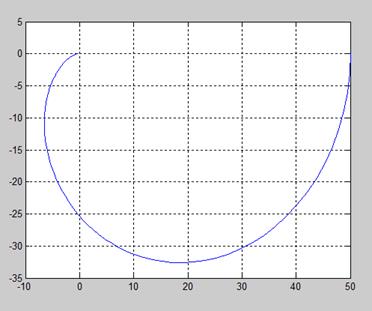
Рис.3.
Годограф Найквиста.

Д)
Проверим устойчивость системы с помощью
критерия Найквиста:

Критерий
Найквиста: Для
того чтобы система, которая в разомкнутом
состоянии была устойчива, была устойчива
и в замкнутом, необходимо, чтобы годограф
Найквиста при изменении частоты от нуля
до бесконечности не охватывал точку с
координатами (-1; j0).

Из
решения видно (см. рис.3), что годограф
удовлетворяет всем условиям критерия:

Годограф
меняет свое направление по часовой
стрелке
Годографом
не охватывается точка (-1; j0)
Делаем
вывод, что данная разомкнутая система
устойчива.

Определение
критического значения коэффициента
усиления системы.

А)
В пункте 2 уже были выделены действительная
и мнимая части

Б)
Для того, чтобы найти критическое
значение коэффициента усиления системы
необходимо приравнять мнимую часть к
нулю, а действительную к -1

=-1
(1)

=0 (2)

В)
Найдем

из второго (2) уравнения

=
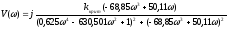
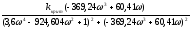
0

Числитель
должен быть равен 0.

=
0

Принимаем,
что

,
тогда

=
0

=0,853

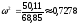
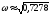
В)
Подставляем
в
первое (1) уравнение и находим

=
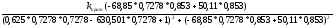
-1

Далее
произвести расчет

—
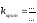
критическое значение коэффициента
усиления системы.

Литература:

1.Методы
классической и современной теории
автоматического управления. Том 1.

Анализ
и статистическая динамика систем
автоматического управления. М: Изд. МГТУ
им Баумана. 2000 г.

2.
Воронов А.А. Теория автоматического
управления. Т. 1-3, М., Наука, 1992

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание

Построение диаграммы в Excel
- Вариант 1: Построение диаграммы по таблице
- Работа с диаграммами
- Вариант 2: Отображение диаграммы в процентах
- Вариант 3: Построение диаграммы Парето
Вопросы и ответы

Microsoft Excel дает возможность не только удобно работать с числовыми данными, но и предоставляет инструменты для построения диаграмм на основе вводимых параметров. Их визуальное отображение может быть совершенно разным и зависит от решения пользователя. Давайте разберемся, как с помощью этой программы нарисовать различные типы диаграмм.

Построение диаграммы в Excel

Поскольку через Эксель можно гибко обрабатывать числовые данные и другую информацию, инструмент построения диаграмм здесь также работает в разных направлениях. В этом редакторе есть как стандартные виды диаграмм, опирающиеся на стандартные данные, так и возможность создать объект для демонстрации процентных соотношений или даже наглядно отображающий закон Парето. Далее мы поговорим о разных методах создания этих объектов.

Вариант 1: Построение диаграммы по таблице

Построение различных видов диаграмм практически ничем не отличается, только на определенном этапе нужно выбрать соответствующий тип визуализации.

Перед тем как приступить к созданию любой диаграммы, необходимо построить таблицу с данными, на основе которой она будет строиться. Затем переходим на вкладку «Вставка» и выделяем область таблицы, которая будет выражена в диаграмме.

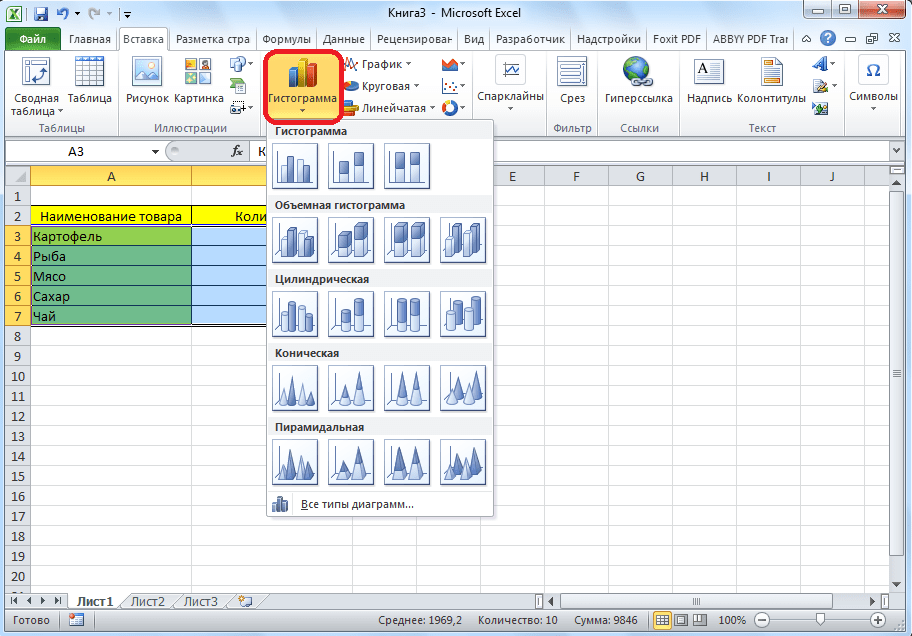
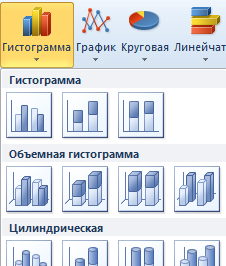
На ленте на вкладе «Вставка» выбираем один из шести основных типов:
- Гистограмма;
- График;
- Круговая;
- Линейчатая;
- С областями;
- Точечная.

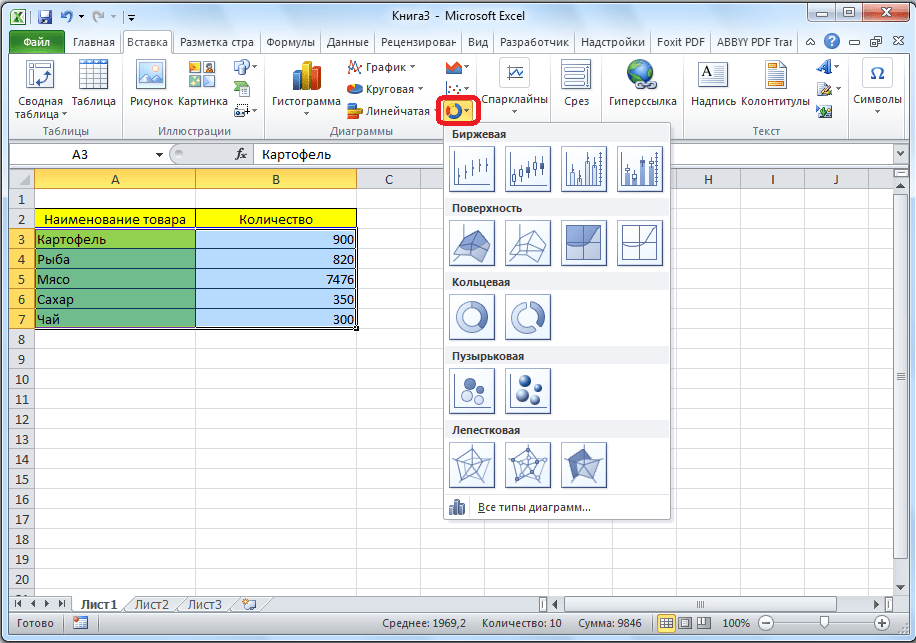
Кроме того, нажав на кнопку «Другие», можно остановиться и на одном из менее распространенных типов: биржевой, поверхности, кольцевой, пузырьковой, лепестковой.

После этого, кликая по любому из типов диаграмм, появляется возможность выбрать конкретный подвид. Например, для гистограммы или столбчатой диаграммы такими подвидами будут следующие элементы: обычная гистограмма, объемная, цилиндрическая, коническая, пирамидальная.

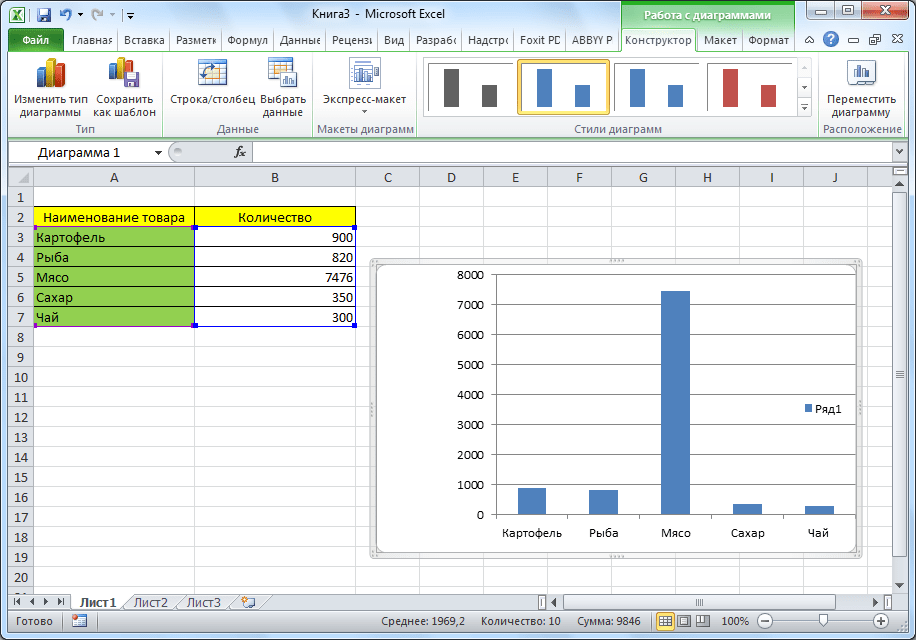
После выбора конкретного подвида автоматически формируется диаграмма. Например, обычная гистограмма будет выглядеть, как показано на скриншоте ниже:

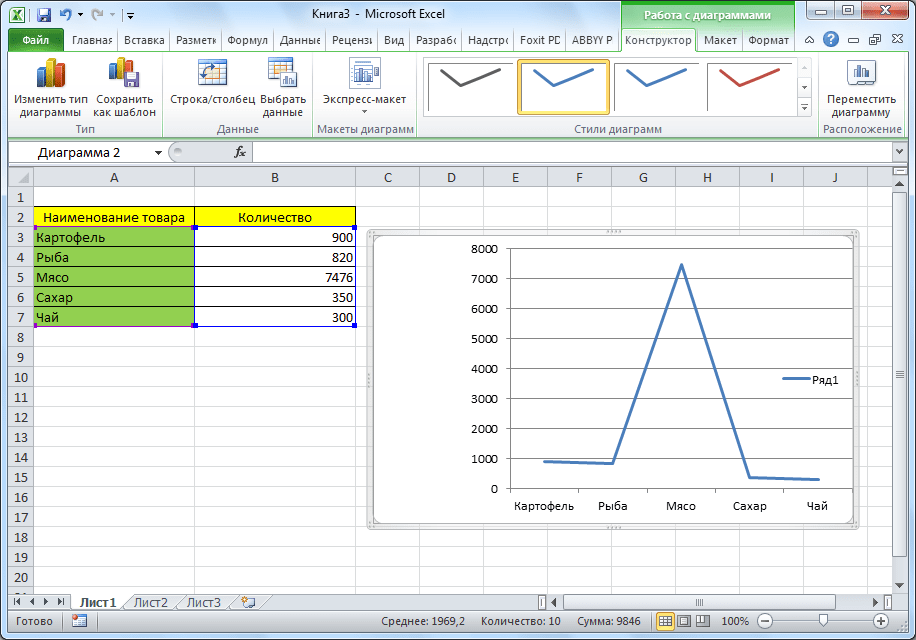
Диаграмма в виде графика будет следующей:

Вариант с областями примет такой вид:

Работа с диаграммами

После того как объект был создан, в новой вкладке «Работа с диаграммами» становятся доступными дополнительные инструменты для редактирования и изменения.

Доступно изменение типа, стиля и многих других параметров.

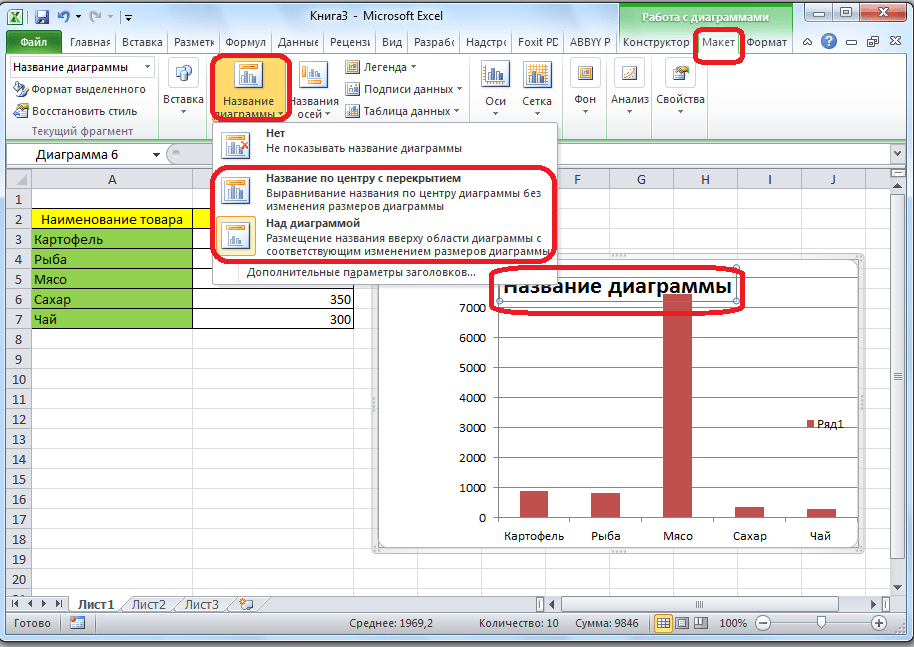
Вкладка «Работа с диаграммами» имеет три дополнительные вложенные вкладки: «Конструктор», «Макет» и «Формат», используя которые, вы сможете подстроить ее отображение так, как это будет необходимо. Например, чтобы назвать диаграмму, открываем вкладку «Макет» и выбираем один из вариантов расположения наименования: по центру или сверху.

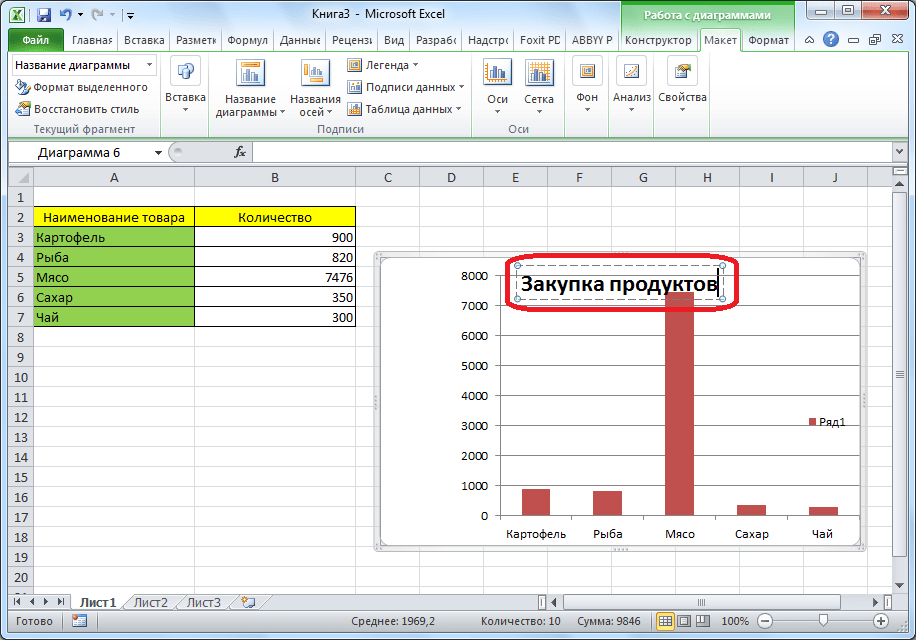
После того как это было сделано, появляется стандартная надпись «Название диаграммы». Изменяем её на любую надпись, подходящую по контексту данной таблице.

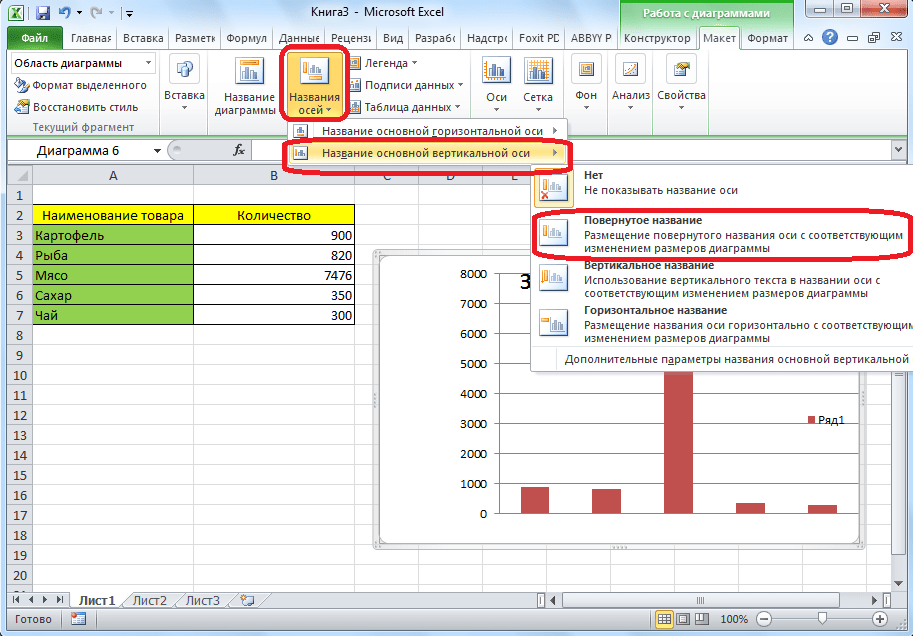
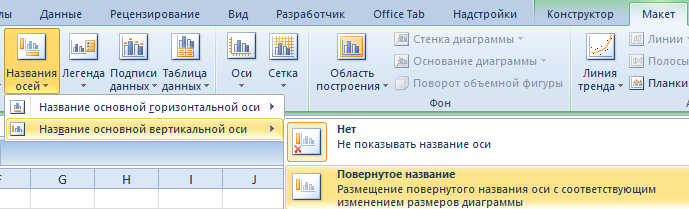
Название осей диаграммы подписываются точно по такому же принципу, но для этого надо нажать кнопку «Названия осей».

Вариант 2: Отображение диаграммы в процентах

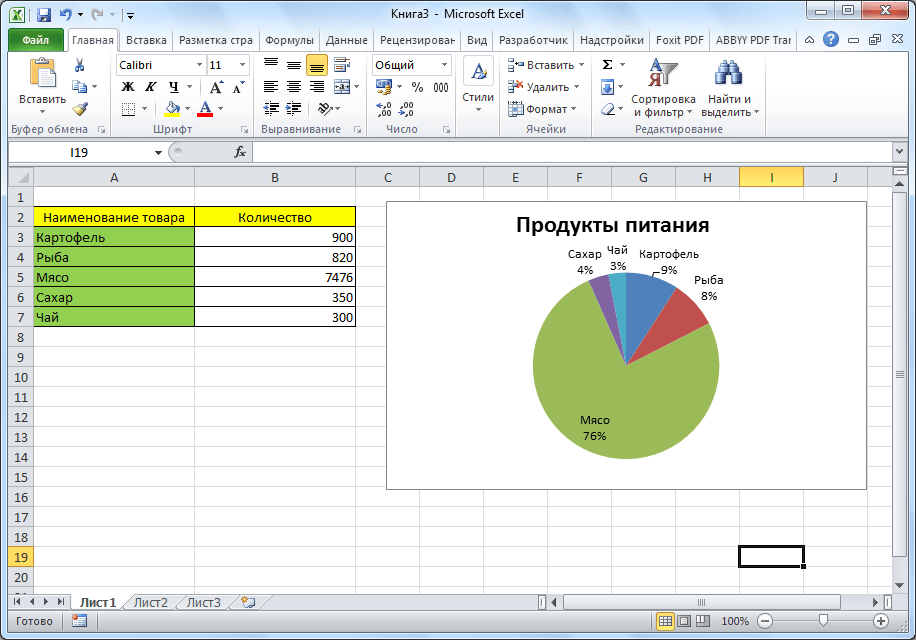
Чтобы отобразить процентное соотношение различных показателей, лучше всего построить круговую диаграмму.

Аналогично тому, как мы делали выше, строим таблицу, а затем выделяем диапазон данных. Далее переходим на вкладку «Вставка», на ленте указываем круговую диаграмму и в появившемся списке кликаем на любой тип.

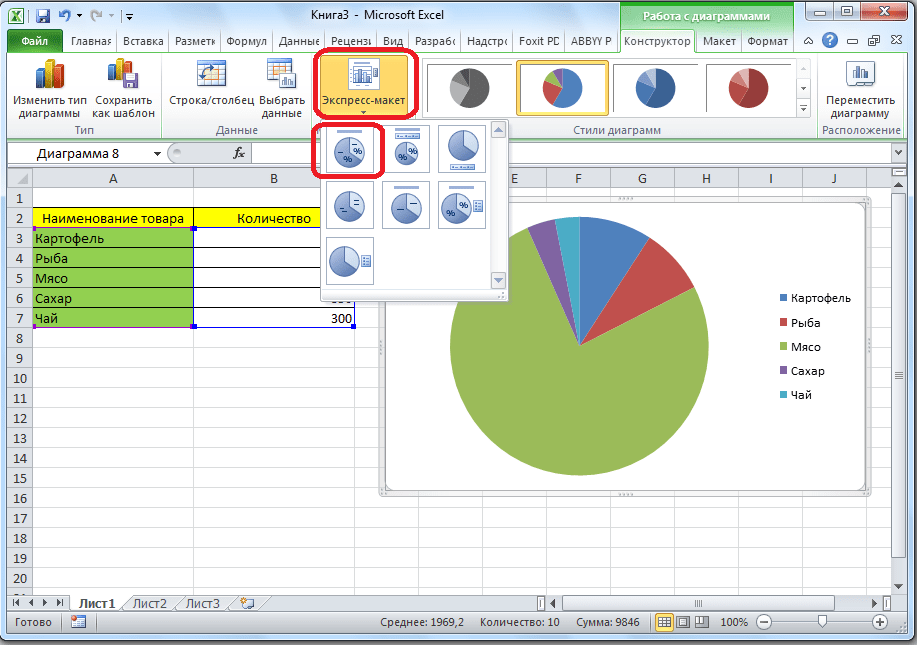
Программа самостоятельно переводит нас в одну из вкладок для работы с этим объектом – «Конструктор». Выбираем среди макетов в ленте любой, в котором присутствует символ процентов.

Круговая диаграмма с отображением данных в процентах готова.

Вариант 3: Построение диаграммы Парето

Согласно теории Вильфредо Парето, 20% наиболее эффективных действий приносят 80% от общего результата. Соответственно, оставшиеся 80% от общей совокупности действий, которые являются малоэффективными, приносят только 20% результата. Построение диаграммы Парето как раз призвано вычислить наиболее эффективные действия, которые дают максимальную отдачу. Сделаем это при помощи Microsoft Excel.

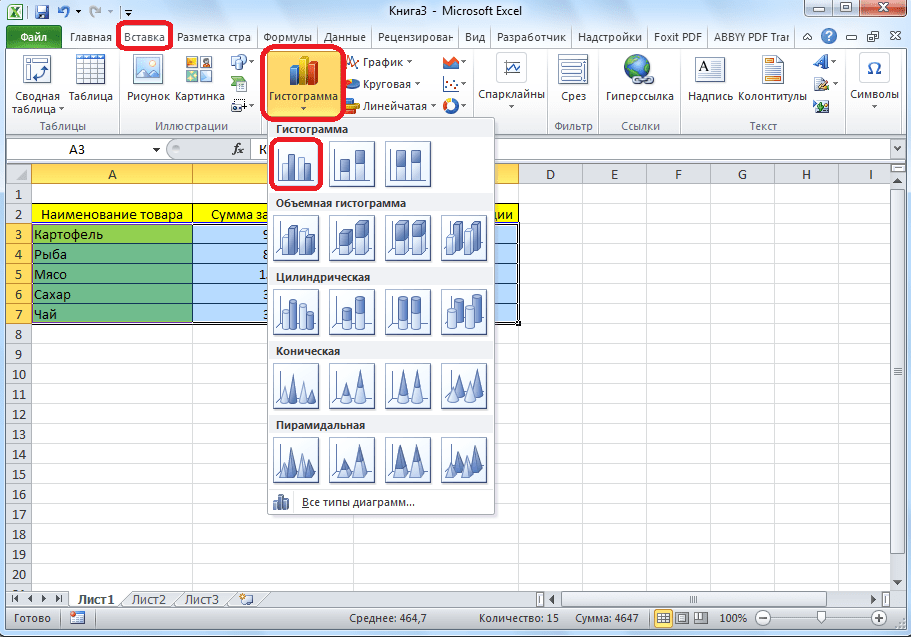
Наиболее удобно строить данный объект в виде гистограммы, о которой мы уже говорили выше.
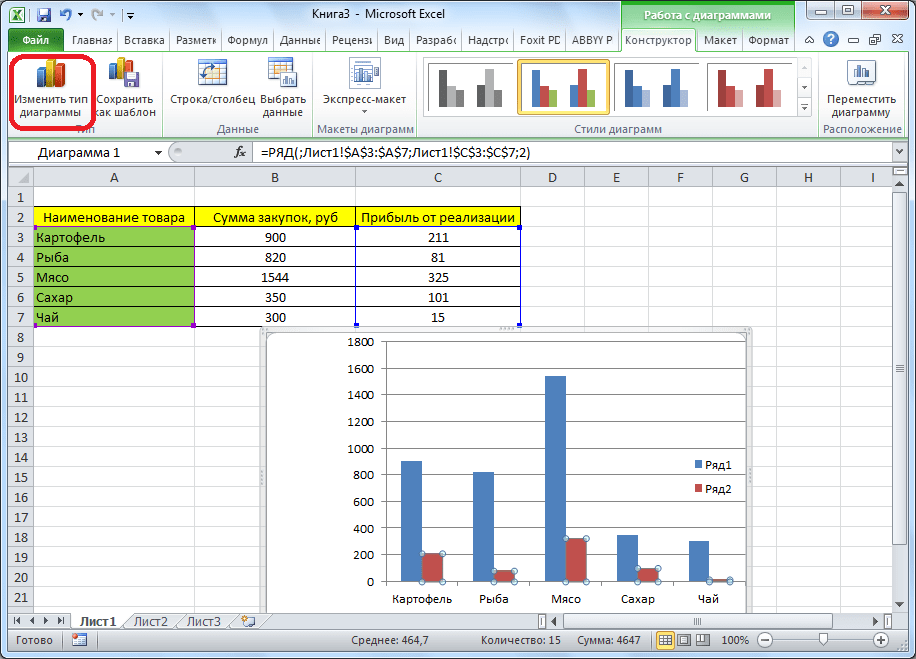
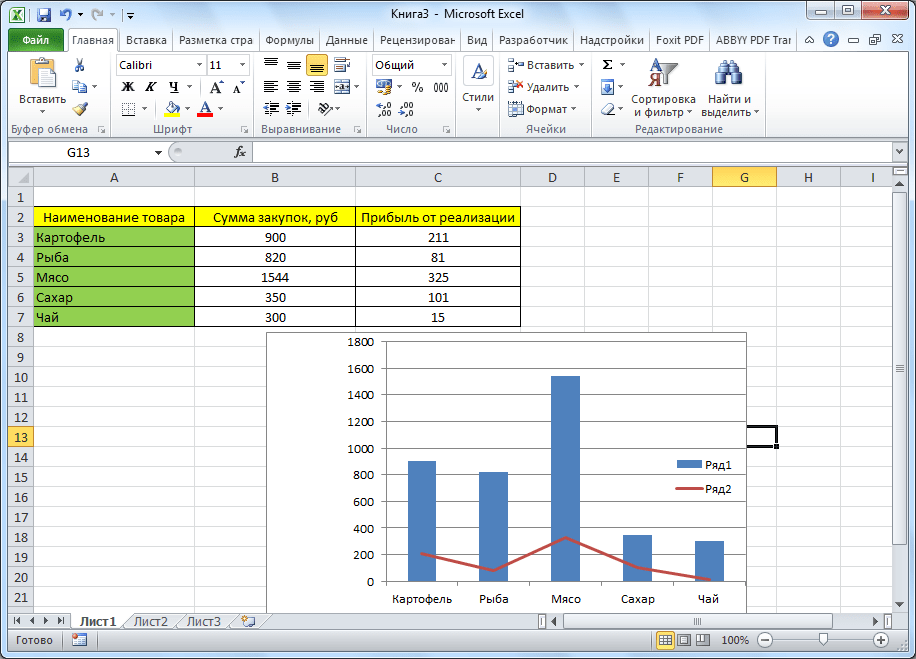
Приведем пример: в таблице представлен список продуктов питания. В одной колонке вписана закупочная стоимость всего объема конкретного вида продукции на оптовом складе, а во второй – прибыль от ее реализации. Нам предстоит определить, какие товары дают наибольшую «отдачу» при продаже.
Прежде всего строим обычную гистограмму: заходим на вкладку «Вставка», выделяем всю область значений таблицы, жмем кнопку «Гистограмма» и выбираем нужный тип.

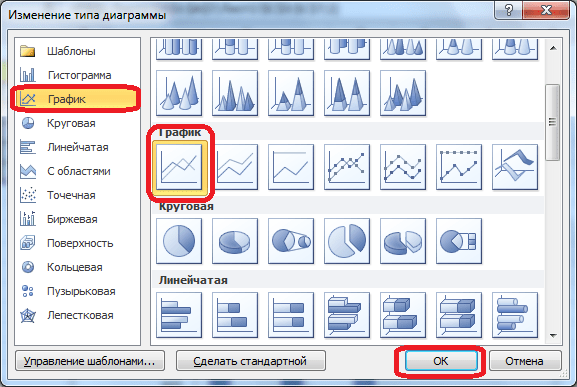
Как видим, вследствие осуществленных действий образовалась диаграмма с двумя видами столбцов: синим и красным. Теперь нам следует преобразовать красные столбцы в график — выделяем эти столбцы курсором и на вкладке «Конструктор» кликаем по кнопке «Изменить тип диаграммы».

Открывается окно изменения типа. Переходим в раздел «График» и указываем подходящий для наших целей тип.

Итак, диаграмма Парето построена. Сейчас можно редактировать ее элементы (название объекта и осей, стили, и т.д.) так же, как это было описано на примере столбчатой диаграммы.

Как видим, Excel представляет множество функций для построения и редактирования различных типов диаграмм — пользователю остается определиться, какой именно ее тип и формат необходим для визуального восприятия.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

На чтение 2 мин

Диаграмма Ганта была разработана американским инженером и консультантом Генри Гантом в 1910 году. Диаграмма используется для построения графика выполнения проектов или задач, распределенного по времени. Она выглядит как каскад горизонтальных гистограмм. Ниже, пример одной из таких диаграмм:

Как создать диаграмму Ганта в Excel

Чтобы сделать диаграмму, проделайте следующие шаги:

Для диаграммы потребуются данные:
- Название активности;
- Время начала активности;
- Количество дней продолжительности активности.

Перейдите во вкладку «Вставка» => раздел «Диаграммы» => «Гистограммы» => «Линейчатая с накоплением»;

Перейдите во вкладку «Конструктор» => в раздел «Данные» => кликните по пункту «Выбрать данные»:

В диалоговом окне, в разделе «Элементы легенды (ряды)» нажмите кнопку «Добавить». В настройках поля данных введите следующую информацию:
- «Имя ряда»: Начало;
- «Значения»: укажите диапазон данных с датами начала активностей;

Больше лайфхаков в нашем Telegram Подписаться

Кликните еще раз кнопку «Добавить» в разделе «Элементы легенды (ряды)» и в новом диалоговом окне введите следующую информацию:
- «Имя ряда»: Количество дней
- «Значения»: укажите диапазон данных с продолжительностью дней активностей;

В диалоговом окне «Выбор источника данных», в правой его части «Подписи горизонтальной оси (категории)» нажмите кнопку «Изменить»:

В появившемся окне «Подписи оси» выделите диапазон данных, включающий названия активностей:

Получившаяся диаграмма будет выглядеть примерно так, как указано на скриншоте ниже:

Для того чтобы отредактировать порядок активностей => нажмите правой клавишей мыши на значениях вертикальной оси (названия активностей), и в выпадающем меню выберите пункт «Формат оси». В диалоговом окне, в разделе «Положение оси» поставьте галочку в пункте «Обратный порядок категорий»:

Теперь, значения горизонтальной оси находятся вверху графика. Нажмите правой клавишей мыши на значениях горизонтальной оси (даты) и в выпадающем меню также выберите «Формат оси». В диалоговом окне сделайте следующие изменения:
- Перейдите в раздел «Параметры оси» => подраздел «Границы» => откорректируйте поле «Минимум» введя значение даты самой первой активности;
- В разделе «Подписи» в поле «Положение подписи» выберите значение «Вверху»:

Ваша диаграмма Ганта почти готова. Осталось только щелкнуть левой клавишей мыши по синей части диаграммы и «покрасить» в белый цвет:

Поздравляю, вы создали диаграмму Ганта!

Источник

Любую информацию легче воспринимать, если она представлена наглядно. Это особенно актуально, когда мы имеем дело с числовыми данными. Их необходимо сопоставить, сравнить. Оптимальный вариант представления – диаграммы. Будем работать в программе Excel.

Так же мы научимся создавать динамические диаграммы и графики, которые автоматически обновляют свои показатели в зависимости от изменения данных. По ссылке в конце статьи можно скачать шаблон-образец в качестве примера.

Как построить диаграмму по таблице в Excel?

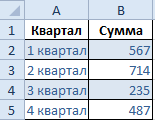
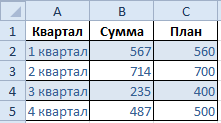
Создаем таблицу с данными.

Выделяем область значений A1:B5, которые необходимо презентовать в виде диаграммы. На вкладке «Вставка» выбираем тип диаграммы.

Нажимаем «Гистограмма» (для примера, может быть и другой тип). Выбираем из предложенных вариантов гистограмм.

После выбора определенного вида гистограммы автоматически получаем результат.
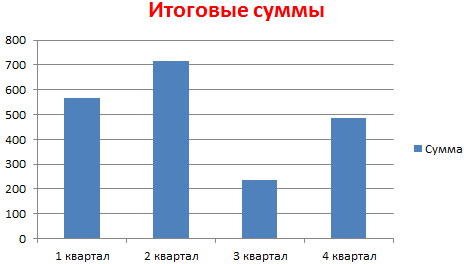
Такой вариант нас не совсем устраивает – внесем изменения. Дважды щелкаем по названию гистограммы – вводим «Итоговые суммы».

Сделаем подпись для вертикальной оси. Вкладка «Макет» — «Подписи» — «Названия осей». Выбираем вертикальную ось и вид названия для нее.

Вводим «Сумма».
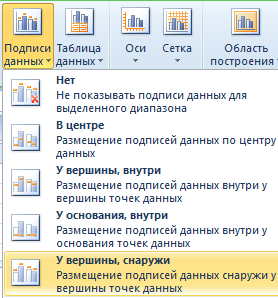
Конкретизируем суммы, подписав столбики показателей. На вкладке «Макет» выбираем «Подписи данных» и место их размещения.

Уберем легенду (запись справа). Для нашего примера она не нужна, т.к. мало данных. Выделяем ее и жмем клавишу DELETE.
Изменим цвет и стиль.

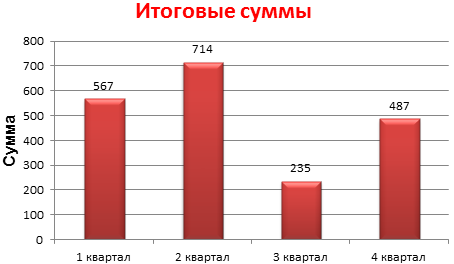
Выберем другой стиль диаграммы (вкладка «Конструктор» — «Стили диаграмм»).

Как добавить данные в диаграмму в Excel?

Добавляем в таблицу новые значения — План.

Выделяем диапазон новых данных вместе с названием. Копируем его в буфер обмена (одновременное нажатие Ctrl+C). Выделяем существующую диаграмму и вставляем скопированный фрагмент (одновременное нажатие Ctrl+V).
Так как не совсем понятно происхождение цифр в нашей гистограмме, оформим легенду. Вкладка «Макет» — «Легенда» — «Добавить легенду справа» (внизу, слева и т.д.). Получаем:

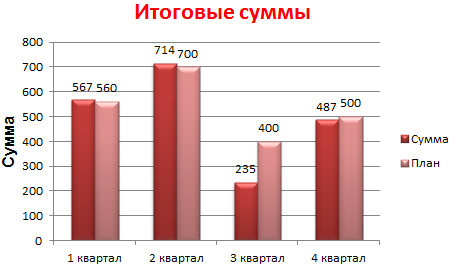
Есть более сложный путь добавления новых данных в существующую диаграмму – с помощью меню «Выбор источника данных» (открывается правой кнопкой мыши – «Выбрать данные»).

Когда нажмете «Добавить» (элементы легенды), откроется строка для выбора диапазона данных.

Как поменять местами оси в диаграмме Excel?

Щелкаем по диаграмме правой кнопкой мыши – «Выбрать данные».

В открывшемся меню нажимаем кнопку «Строка/столбец».
Значения для рядов и категорий поменяются местами автоматически.

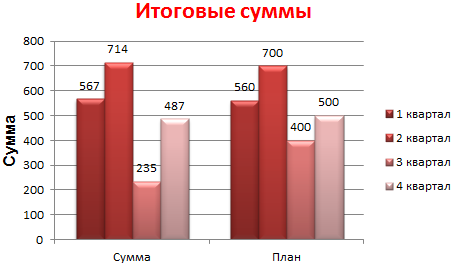
Как закрепить элементы управления на диаграмме Excel?

Если очень часто приходится добавлять в гистограмму новые данные, каждый раз менять диапазон неудобно. Оптимальный вариант – сделать динамическую диаграмму, которая будет обновляться автоматически. А чтобы закрепить элементы управления, область данных преобразуем в «умную таблицу».

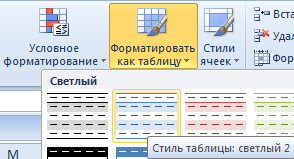
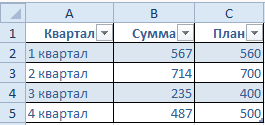
Выделяем диапазон значений A1:C5 и на «Главной» нажимаем «Форматировать как таблицу».

В открывшемся меню выбираем любой стиль. Программа предлагает выбрать диапазон для таблицы – соглашаемся с его вариантом. Получаем следующий вид значений для диаграммы:

Как только мы начнем вводить новую информацию в таблицу, будет меняться и диаграмма. Она стала динамической:

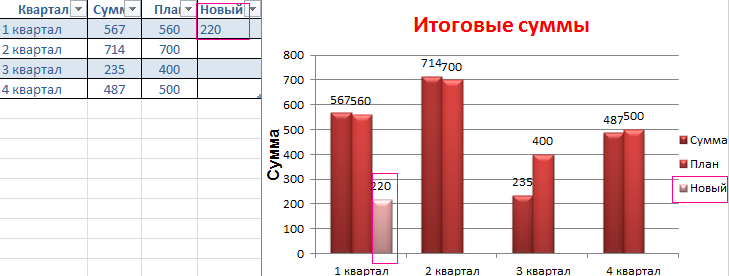
Мы рассмотрели, как создать «умную таблицу» на основе имеющихся данных. Если перед нами чистый лист, то значения сразу заносим в таблицу: «Вставка» — «Таблица».

Как сделать диаграмму в процентах в Excel?

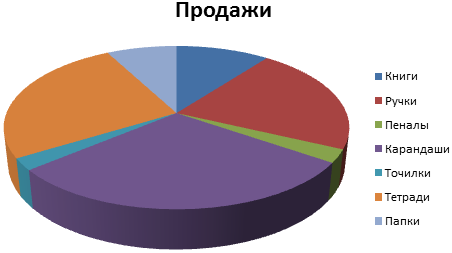
Представлять информацию в процентах лучше всего с помощью круговых диаграмм.

Исходные данные для примера:

Выделяем данные A1:B8. «Вставка» — «Круговая» — «Объемная круговая».

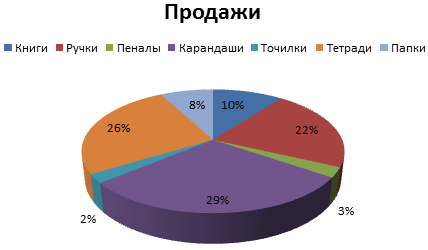
Вкладка «Конструктор» — «Макеты диаграммы». Среди предлагаемых вариантов есть стили с процентами.

Выбираем подходящий.

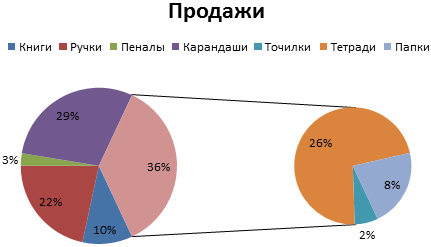
Очень плохо просматриваются сектора с маленькими процентами. Чтобы их выделить, создадим вторичную диаграмму. Выделяем диаграмму. На вкладке «Конструктор» — «Изменить тип диаграммы». Выбираем круговую с вторичной.

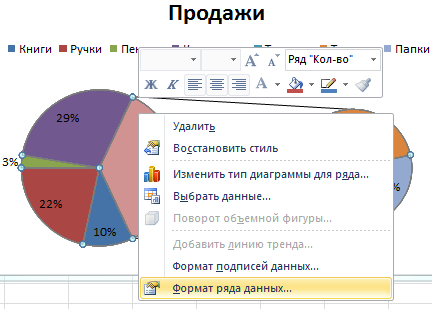
Автоматически созданный вариант не решает нашу задачу. Щелкаем правой кнопкой мыши по любому сектору. Должны появиться точки-границы. Меню «Формат ряда данных».

Задаем следующие параметры ряда:

Получаем нужный вариант:

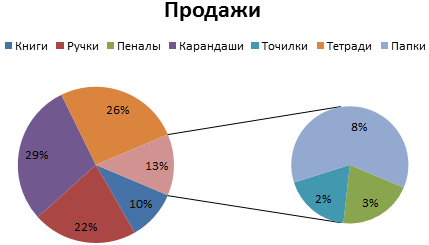
Диаграмма Ганта в Excel

Диаграмма Ганта – это способ представления информации в виде столбиков для иллюстрации многоэтапного мероприятия. Красивый и несложный прием.

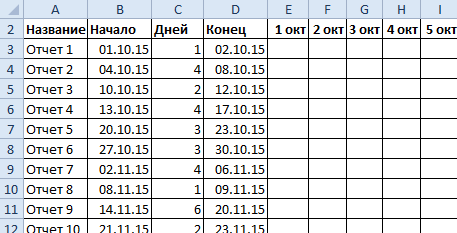
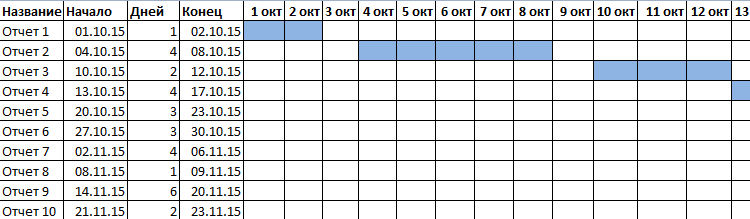
У нас есть таблица (учебная) со сроками сдачи отчетов.

Для диаграммы вставляем столбец, где будет указано количество дней. Заполняем его с помощью формул Excel.
Выделяем диапазон, где будет находиться диаграмма Ганта. То есть ячейки будут залиты определенным цветом между датами начала и конца установленных сроков.
Открываем меню «Условное форматирование» (на «Главной»). Выбираем задачу «Создать правило» — «Использовать формулу для определения форматируемых ячеек».
Вводим формулу вида: =И(E$2>=$B3;E$2<=$D3). С помощью оператора «И» Excel сравнивает дату текущей ячейки с датами начала и конца мероприятия. Далее нажимаем «Формат» и назначаем цвет заливки.

Когда вам нужно построит презентабельный отчет финансовой активности предприятия, лучше использовать средства графического представления информации.

Графическое представление информации намного эффективней и быстрей усваивается человеческим зрительным восприятием информации, чем текст и цифры. Легче проводить аналитики, лучше видно ситуацию, как в целом, так и в отдельных деталях.

Простенькая диаграмма Ганта готова. Скачать шаблон с примером в качестве образца.

Готовые примеры графиков и диаграмм в Excel скачать:

Скачать шаблоны и дашборды с диаграммами для отчетов в Excel.
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.

В программе Excel специально разрабатывались диаграммы и графики для реализации визуализации данных.

Источник