Как построить гистограмму с полигоном в excel

---

Частотный полигон — это тип диаграммы, которая помогает нам визуализировать распределение значений.

В этом руководстве объясняется, как создать полигон частот в Excel.

Пример: полигон частот в Excel

Используйте следующие шаги для создания полигона частот.

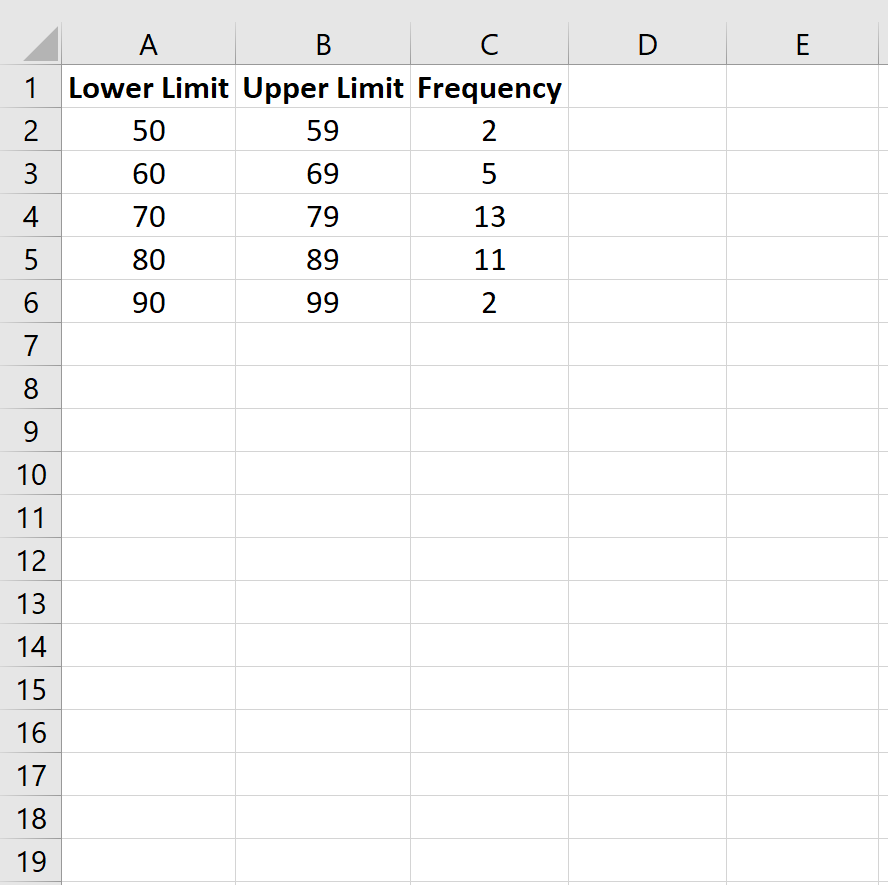
Шаг 1: Введите данные для таблицы частот.

Введите следующие данные для таблицы частоты, которая показывает количество студентов, получивших определенный балл на экзамене:

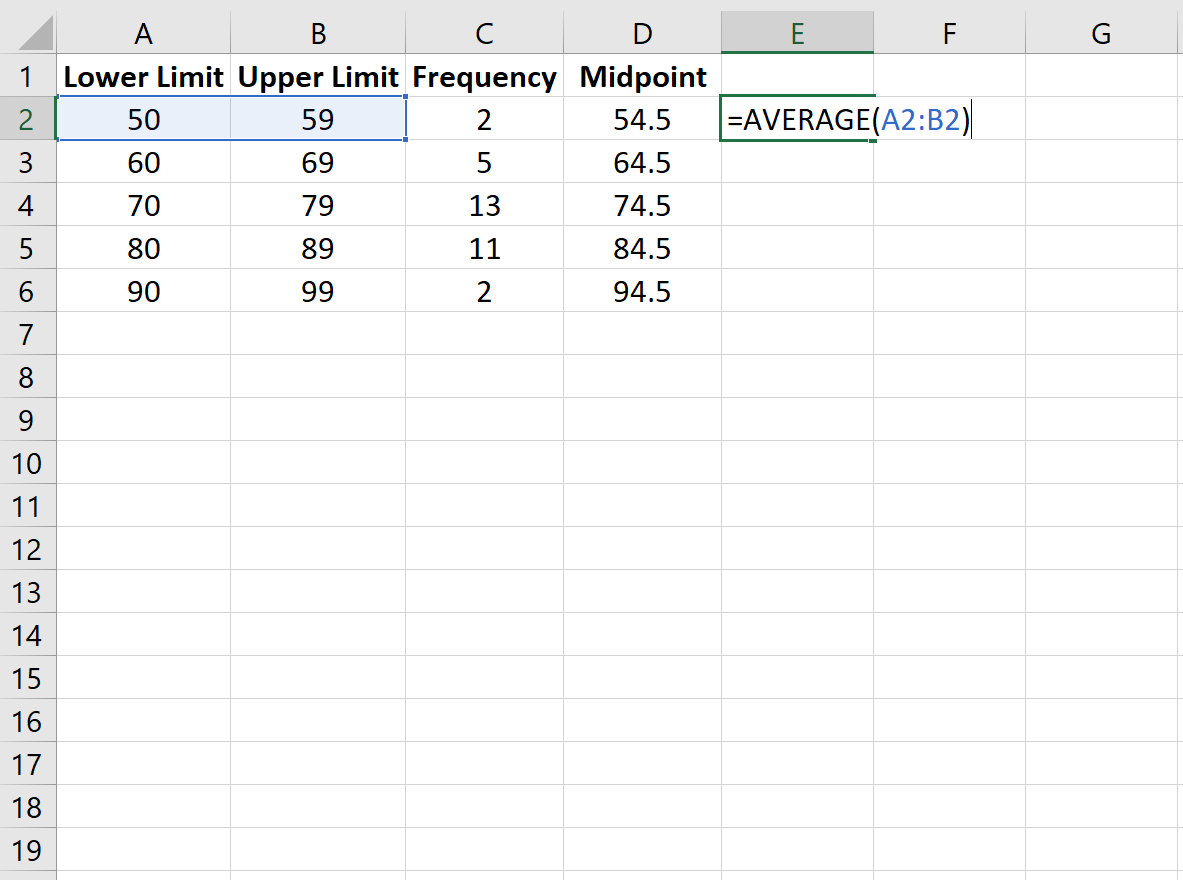
Шаг 2: Найдите среднюю точку каждого класса.

Затем используйте функцию = СРЗНАЧ() в Excel, чтобы найти среднюю точку каждого класса, которая представляет среднее число в каждом классе:

Шаг 3: Создайте полигон частот.

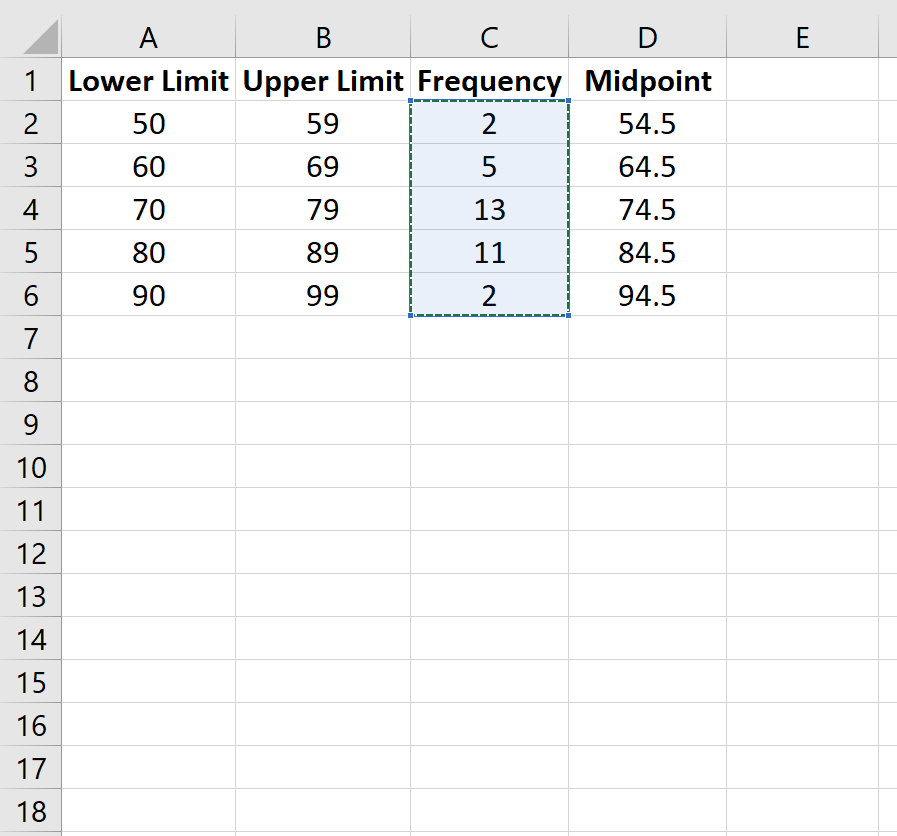
Далее мы создадим полигон частот. Выделите значения частоты в столбце C:

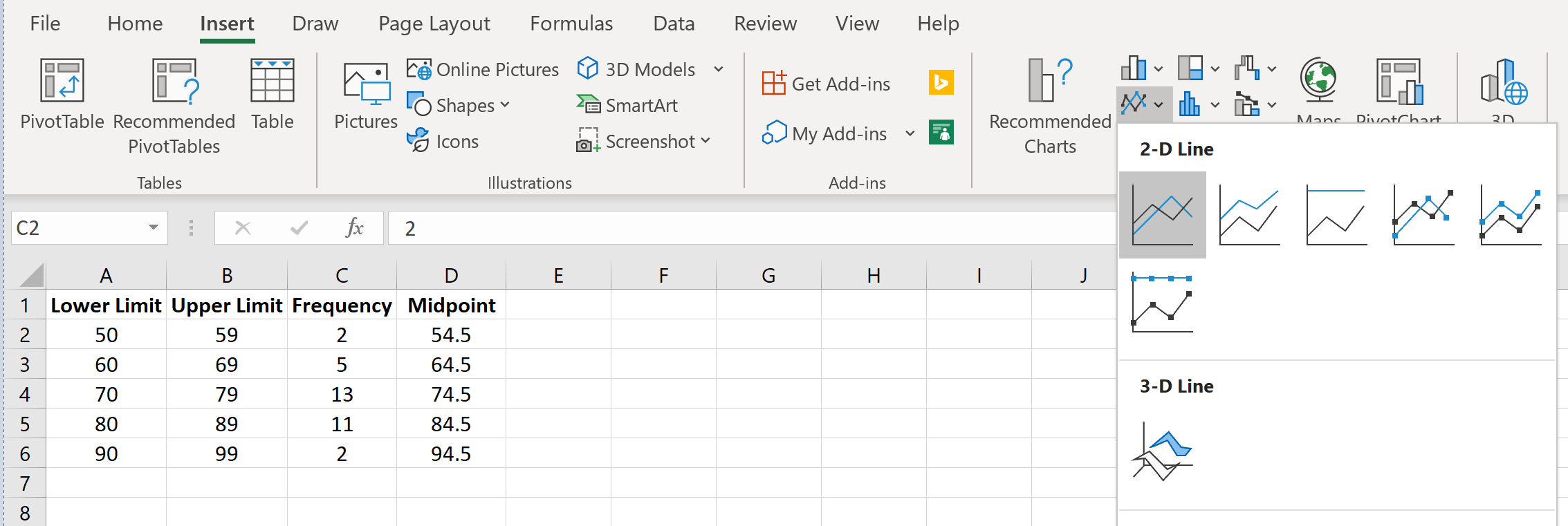
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить линию или диаграмму с областями» :

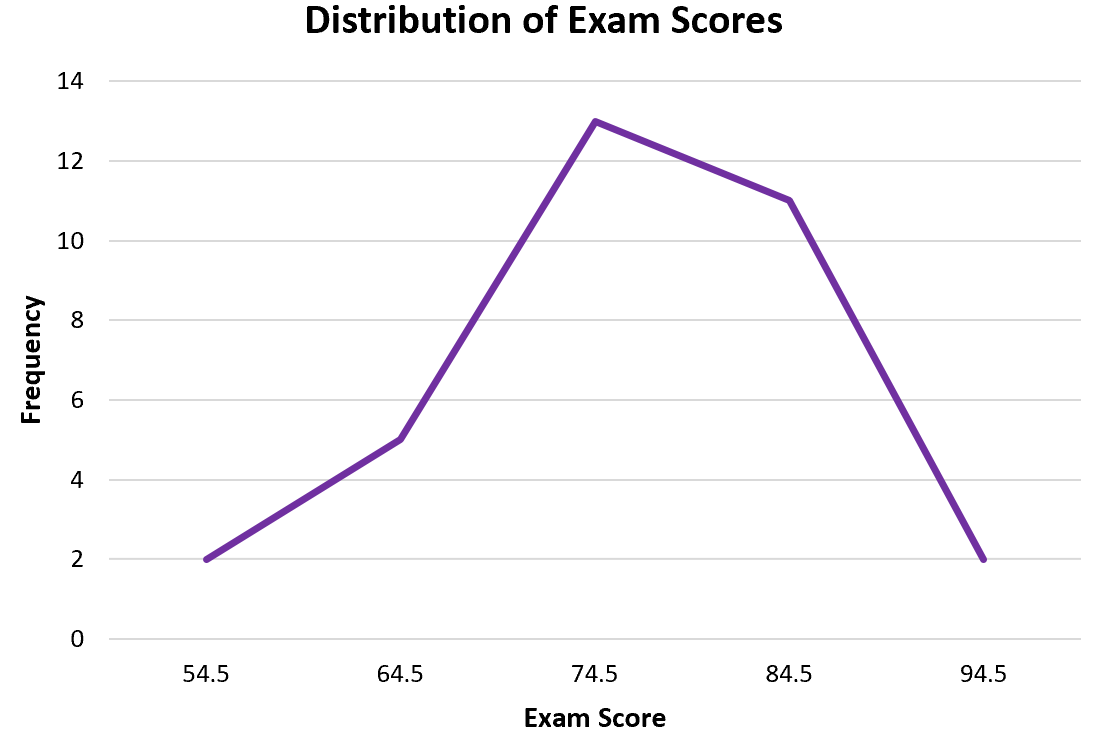
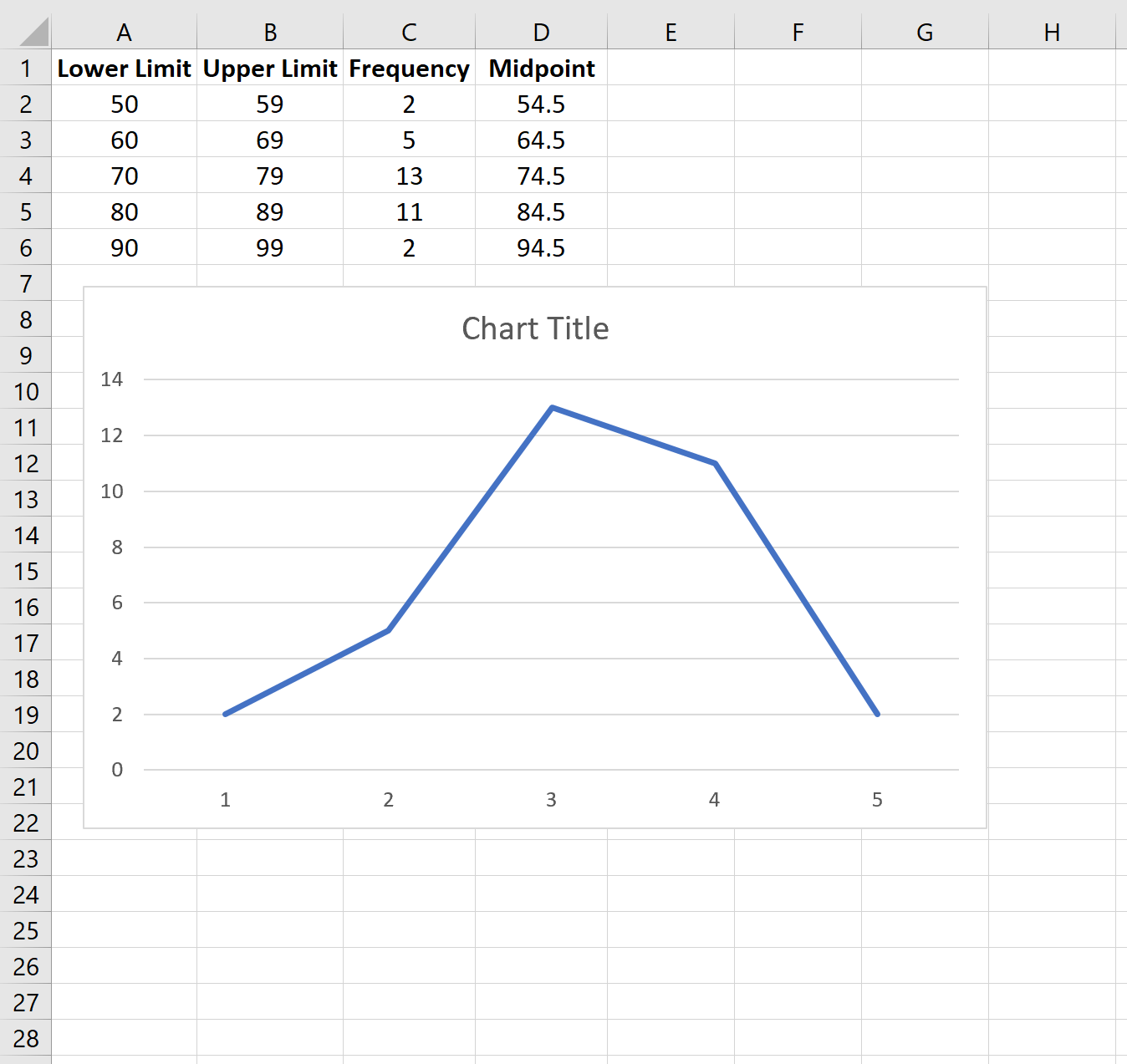
Автоматически появится полигон частот:

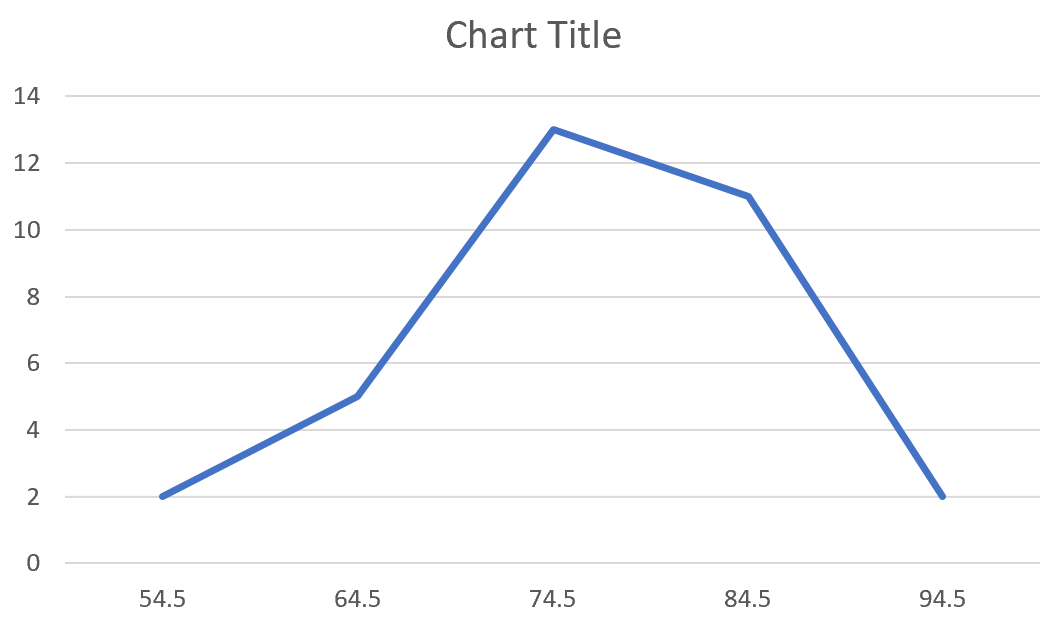
Чтобы изменить метки оси X, щелкните правой кнопкой мыши в любом месте диаграммы и выберите « Выбрать данные ». Появится новое окно. В разделе « Метки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий значения средней точки. Нажмите OK , и новые метки осей появятся автоматически:

Не стесняйтесь изменять заголовок диаграммы, добавлять метки осей и изменять цвет графика, чтобы сделать его более эстетичным.

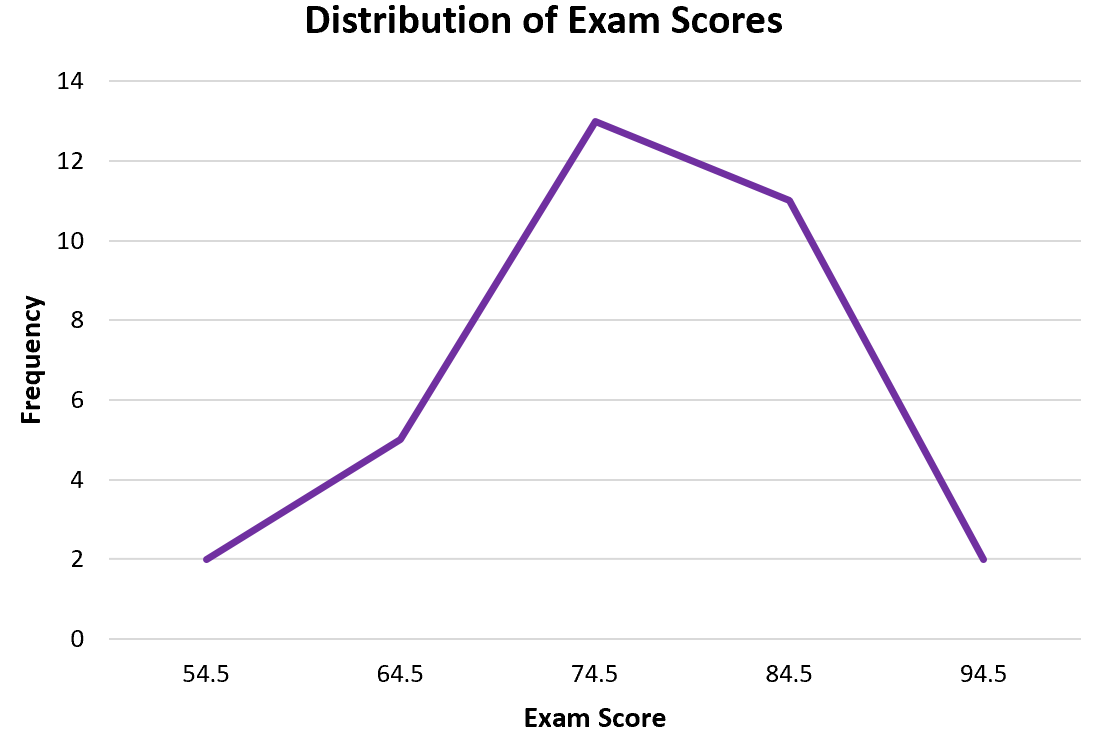
Из полигона частот легко увидеть, что большинство учащихся набрали 70-е и 80-е баллы, несколько — 60-е и еще меньше — 50-е и 90-е.

Цель:

• Совершенствование умений и навыков нахождения статистических
  характеристик случайной величины, работа с расчетами в Excel;
• применение информационно коммутативных технологий для анализа данных;
  работа с различными информационными носителями.

Ход урока

1. Сегодня на уроке мы научимся рассчитывать статистические характеристики
   для больших по объему выборок, используя возможности современных
   компьютерных технологий.
2. Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют
переменную величину, которая в зависимости от исхода испытания принимает одно
значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных
случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода,
медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических
характеристик случайной величины (полигон частот, круговые и столбчатые
диаграммы, гистограммы).

1. Рассмотрим, применение инструментов Excel для решения статистических
   задач на конкретном примере.

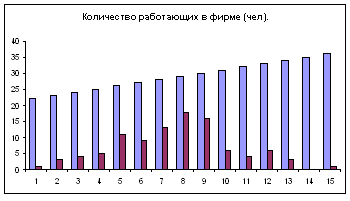
Пример. Проведена проверка в 100 компаниях. Даны значения количества
работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики: моду медиану размах ряда построить полигон частот построить столбчатую и круговую диаграммы раскрыть смысловую сторону каждой характеристики

Ход работы.

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

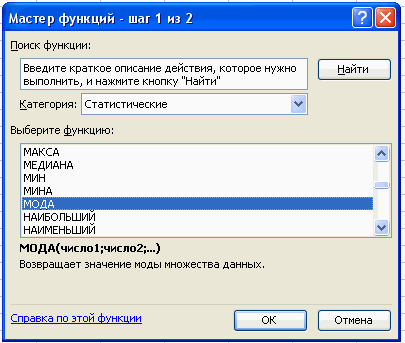
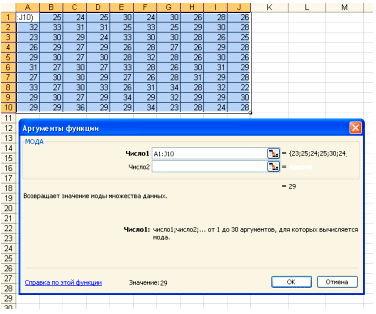
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в
появившемся окне в строке категория выберем — статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в
штате 29 человек больше всего.

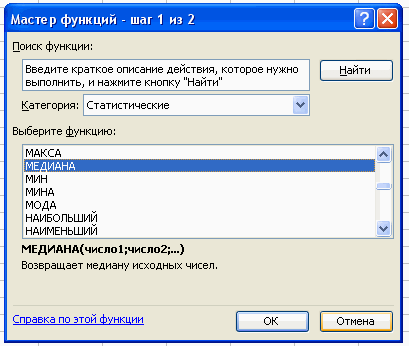
Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

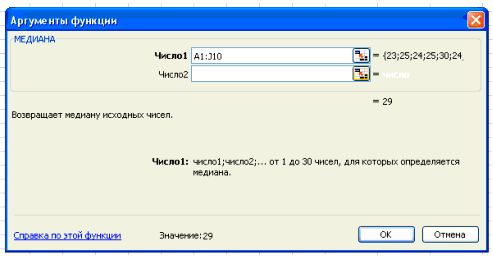
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение
сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением
случайной величины. Для вычисления размаха ряда нужно найти наибольшее и
наименьшее значения нашей выборки и вычислить их разность.

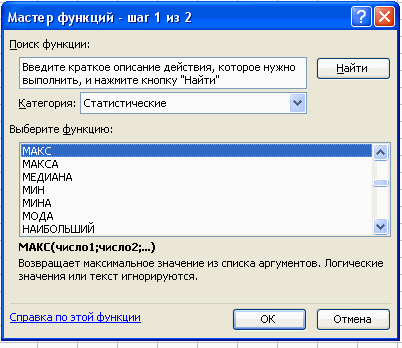
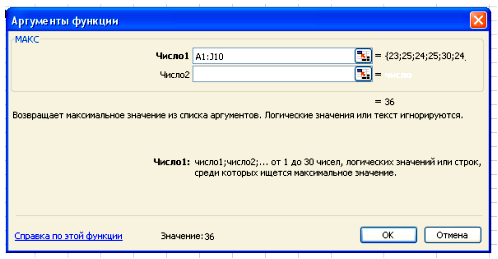
Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

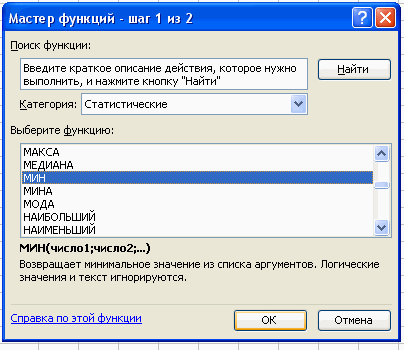
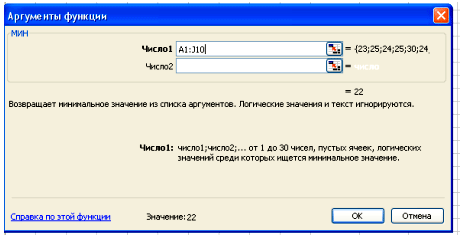
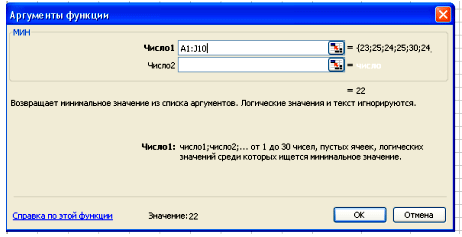
Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и
фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон
распределения, т.е. составить таблицу значений случайной величины и
соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в
фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i
случайной величины меняются от 22 до 36 включительно шагом 1.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий
ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке
встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция –
Математические — СУММА). Должно получиться 100 (количество всех фирм).

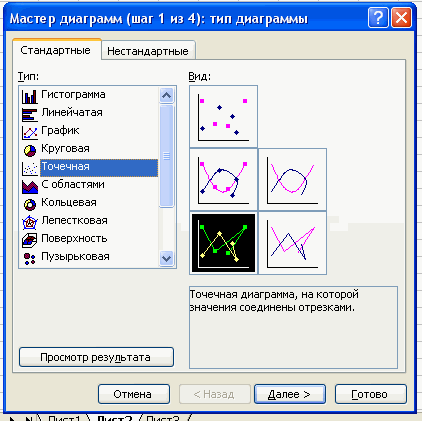
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма –
Стандартные – Точечная (точечная диаграмма на которой значения соединены
отрезками)

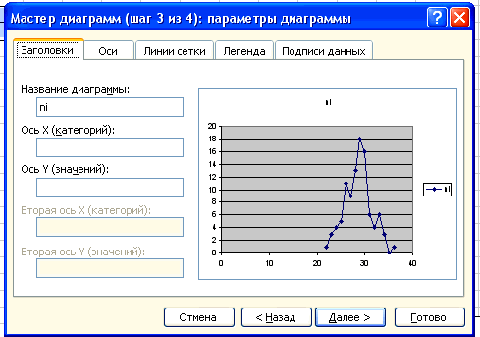
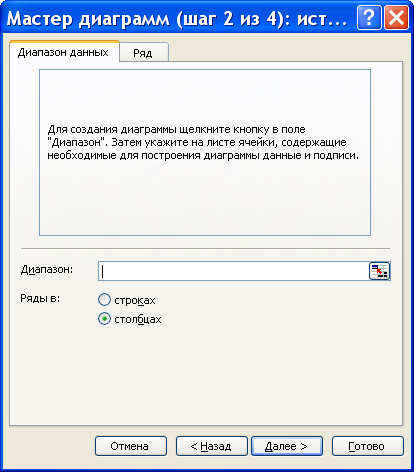
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы
(Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы
для наибольшей наглядности.

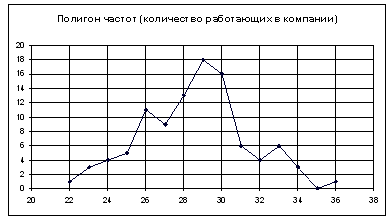
 Получаем:

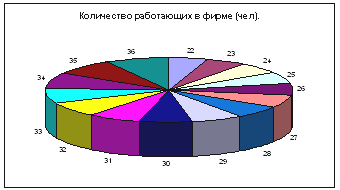
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая
нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для
анализа и обработки статистической информации.

Процедура «Гистограмма» пакета «Анализ данных. Вычисление частот и накопленных частот. Построение гистограмм.

В процедуре автоматически выполняются следующие вычисления:

находится промежуток [x_min, x_max];

выбирается число m интервалов группировки (7£ m £20);

вычисляются середины интервалов группировки , , ;

для каждого интервала  вычисляются частоты  n_j  — количество выборочных значений, которые попали в j-й интервал;

для каждого интервала  вычисляются накопленные частоты — количество выборочных значений, не превышающих верхней границы  j-го интервала;

Строится гистограмма – график ступенчатой функции , , , D_j = (a_j, b_j) , .

Для того чтобы вычислять накопленные частоты и отобразить гистограмму в листе  в листе Excel, в окне процедуры следует пометить соответствующие поля.

 

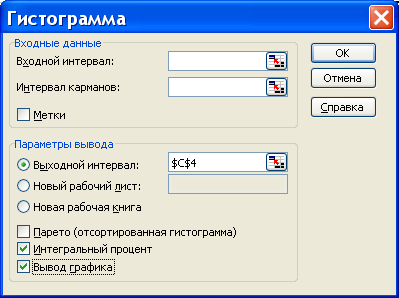
Результаты вычислений процедуры представлены в виде таблицы (ниже приведены две таблицы, первая – когда поле «Интегральный процент» не помечено, вторая – когда помечено)

Карман	Частота
114.46	1
115.581	1
116.702	6
117.823	6
118.944	12
120.065	21
121.186	23
122.307	18
123.428	5
124.549	4
Еще	2

Карман	Частота	Интегральный %
114.46	1	1.01%
115.581	1	2.02%
116.702	6	8.08%
117.823	6	14.14%
118.944	12	26.26%
120.065	21	47.47%
121.186	23	70.71%
122.307	18	88.89%
123.428	5	93.94%
124.549	4	97.98%
Еще	2	100.00%

Здесь Карман – середины интервалов группировки, Интегральный % – накопленные частоты в процентах. Для того чтобы получить числовое значение накопленных частот, следует изменить формат ячеек с «Процентного» на «Числовой».

Использование «Мастера диаграмм» для построения полигонов.

Для построения полигона накопленных частот  в поле «Диапазон» следует указать ячейки столбца «Интегральный процент» таблицы, полученной  в процедуре «Гистограммы» пакета «Анализ данных».

Для построения полигона частот можно указать ячейки столбца «Частота» таблицы, полученной  в процедуре «Гистограммы» пакета «Анализ данных». Можно –  вычислить относительные частоты  и указать в поле «Диапазон» соответствующие ячейки.

Мы объясним, что такое частотный полигон в статистике, для чего он нужен и как сделать его из гистограммы и Excel
Многоугольник частоты позволяет сравнивать данные с первого взгляда

Что такое частотный многоугольник?

Частотный многоугольник это графический инструмент, используемый на основе частотной гистограммы (т.е. другого типа графика, который выражает частоты с помощью вертикальных столбцов). Для этого различные средние точки столбцов гистограммы соединяются линией, не оставляя пространства между ними, таким образом получается геометрическая форма или многоугольник

С помощью этого графического инструмента можно быстро и легко представить количественные переменные или различные распределения, чего традиционно не делает гистограмма. Кроме того, его достоинство в том, что он виден невооруженным глазом

По этой причине он широко используется в социальных экономических науках, позволяя проводить полезные сравнения между различными результатами одного и того же процесса

Вы можете найти это полезным: Количественный метод

Характеристики частотного полигона

Частотные многоугольники образуются путем соединения средних точек каждой фазы или столбца с помощью отрезков прямых , поэтому они являются одним из видов визуального представления количественной информации. Данные в таблице всегда находятся ниже кривизны многоугольника, и его высшая точка всегда является самой высокочастотной точкой множества

Для чего нужен частотный многоугольник?

Частотные многоугольники используются, когда необходимо построить или выделить различные совместные распределения или перекрестную классификацию непрерывной количественной переменной вместе с другой качественной или дискретной количественной переменной на одном графике

Как сделать частотный многоугольник?

Частотный многоугольник возникает из гистограммы.

Как уже упоминалось, частотный многоугольник всегда получается из частотной гистограммы, когда все средние точки каждого элемента с соответствующей им частотой последовательно соединены. Для этого необходимо выполнить следующие действия:

• Сбор количественной информации о том, что подлежит изучению. Затем устанавливаются нижний и верхний пределы всех исследуемых элементов.
• Определите частоту каждого типа элементов в пределах установленных пределов и усредните эти пределы.
• Постройте график замкнутой линии, соединив средние точки полученных данных

Примеры частотных многоугольников

Для сравнения двух переменных можно использовать частотный многоугольник.Частотный полигон может быть выполнен цифровым или ручным способом

Частотный полигон в Excel

Excel позволяет графически представить загруженные данные.

Чтобы создать частотный полигон с помощью программного инструмента Microsoft Excel , необходимо выполнить следующие шаги:

• Сначала получите таблицу данных, на основе которой вы хотите построить частотный многоугольник.
• Найдите меню вставки и выберите опции graphic, затем line и, наконец, line with markers.
• Появится пустое поле.
• В поле, в диапазоне графика, поместите данные из колонки частоты.
• В том же окне на горизонтальной оси выберите опцию редактирования, чтобы поместить среднее значение.
• Нажмите кнопку accept, чтобы получить график. Помните, что это должен быть замкнутый график, поэтому нам часто придется добавлять данные для новых интервалов (в этом случае мы будем добавлять число 0 к каждому из них).

Продолжить: Инференциальная статистика

Инструменты Excel для построения гистограмм, полигонов

Процедура «Гистограмма» пакета «Анализ данных. Вычисление частот и накопленных частот. Построение гистограмм.

В процедуре автоматически выполняются следующие вычисления:

выбирается число m интервалов группировки (7 £ m £ 20);

вычисляются середины интервалов группировки , , ;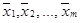

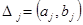
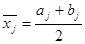
для каждого интервала вычисляются частоты n_j — количество выборочных значений, которые попали в j -й интервал;

для каждого интервала вычисляются накопленные частоты 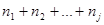— количество выборочных значений, не превышающих верхней границы j -го интервала;

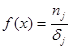
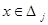
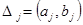
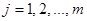
Строится гистограмма – график ступенчатой функции , , , D _j = ( a_j , b_j ) , .

Для того чтобы вычислять накопленные частоты и отобразить гистограмму в листе в листе Excel , в окне процедуры следует пометить соответствующие поля.

Результаты вычислений процедуры представлены в виде таблицы (ниже приведены две таблицы, первая – когда поле «Интегральный процент» не помечено, вторая – когда помечено)

Источник

Как сделать полигон частот в Excel

Частотный полигон — это тип диаграммы, которая помогает нам визуализировать распределение значений.

В этом руководстве объясняется, как создать полигон частот в Excel.

Пример: полигон частот в Excel

Используйте следующие шаги для создания полигона частот.

Шаг 1: Введите данные для таблицы частот.

Введите следующие данные для таблицы частоты, которая показывает количество студентов, получивших определенный балл на экзамене:

Шаг 2: Найдите среднюю точку каждого класса.

Затем используйте функцию = СРЗНАЧ() в Excel, чтобы найти среднюю точку каждого класса, которая представляет среднее число в каждом классе:

Шаг 3: Создайте полигон частот.

Далее мы создадим полигон частот. Выделите значения частоты в столбце C:

Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить линию или диаграмму с областями» :

Автоматически появится полигон частот:

Чтобы изменить метки оси X, щелкните правой кнопкой мыши в любом месте диаграммы и выберите « Выбрать данные ». Появится новое окно. В разделе « Метки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий значения средней точки. Нажмите OK , и новые метки осей появятся автоматически:

Не стесняйтесь изменять заголовок диаграммы, добавлять метки осей и изменять цвет графика, чтобы сделать его более эстетичным.

Из полигона частот легко увидеть, что большинство учащихся набрали 70-е и 80-е баллы, несколько — 60-е и еще меньше — 50-е и 90-е.

Источник

Как построить полигон частот в excel по данным таблицы пошагово

Использование Excel для расчета статистических характеристик случайной величины

Разделы: Математика

• Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
• применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

1. Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
2. Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

1. Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_iслучайной величины меняются от 22 до 36 включительно шагом 1.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Инструменты Excel для построения гистограмм, полигонов

Процедура «Гистограмма» пакета «Анализ данных. Вычисление частот и накопленных частот. Построение гистограмм.

В процедуре автоматически выполняются следующие вычисления:

выбирается число m интервалов группировки (7 £ m £ 20);

вычисляются середины интервалов группировки , , ;

для каждого интервала вычисляются частоты n_j — количество выборочных значений, которые попали в j -й интервал;

для каждого интервала вычисляются накопленные частоты — количество выборочных значений, не превышающих верхней границы j -го интервала;

Строится гистограмма – график ступенчатой функции , , , D _j = ( a_j , b_j ) , .

Для того чтобы вычислять накопленные частоты и отобразить гистограмму в листе в листе Excel , в окне процедуры следует пометить соответствующие поля.

Результаты вычислений процедуры представлены в виде таблицы (ниже приведены две таблицы, первая – когда поле «Интегральный процент» не помечено, вторая – когда помечено)

Источник