Как построить фрактал в excel - Word и Excel - помощь в работе с программами

Лабораторная работа 9

Динамический хаос и фракталы

1.
Сценарий перехода в хаос (Эта часть работы выполняется в Excel).

Логистическое уравнение
имеет следующий вид:

Это уравнение представляет собой
одномерную нелинейную систему с обратной связью. Такое уравнение может
быть исследовано в электронной таблице Excel, для чего необходимо выполнить следующие шаги:

1. В ячейку А1 поместить начальное
значение постоянной А между 0 и 4. Начать со значения А
= 2.

2. В ячейку В1 поместить начальное
значение х = 0,1.

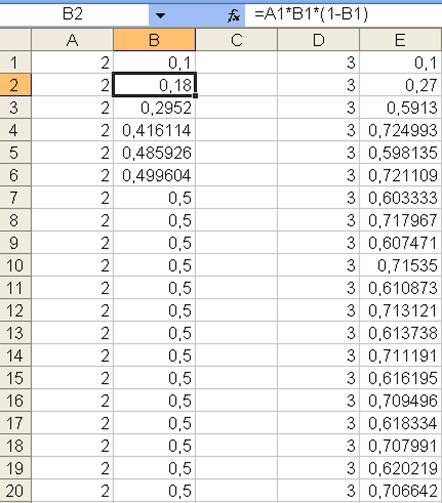
3. В ячейке В2 поместить формулу: =А1*В1*(1
– В1).

4. Скопировать ячейку В2 вниз, по
крайней мере, на 100 ячеек. Пример выполнения показан ниже (только на
20 точек).

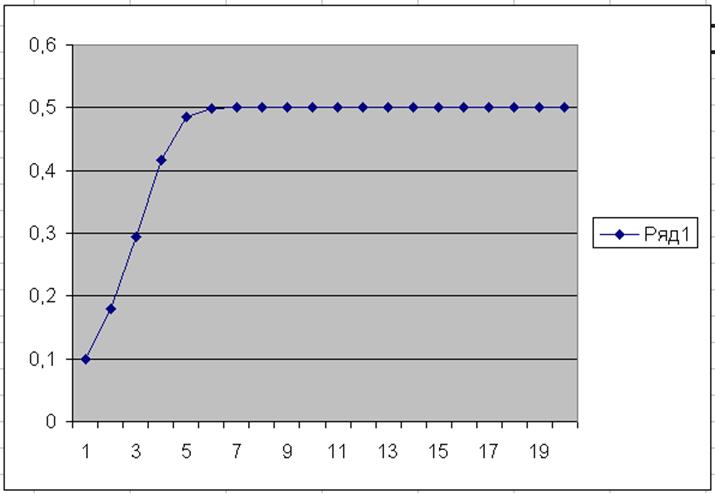
5. Построить график по данным колонки
В. Пример на рис.1.

Рис.1

6. Положить значение А = 3.
Повторить пп.2 -5.

7. Положить значение А = 3,48.
Повторить пп.2 -5.

8. Положить значение А = 3,6.
Повторить пп.2 -5.

9. Построить бифуркационную диаграмму (по
оси абсцисс -значения А; по шкале ординат — значения х).

2. Отображение Хенона описывается следующей системой
уравнений:

Построить аттрактор Хенона
следующим образом:

1.В ячейки А1 и В1
поместить начальные величины х и у, выбранные в
диапазоне от 0 до 1.

2. В ячейку А2
поместить выражение: = 1 + В1 – 1,4 * А1² .

3. В ячейку В2
поместить выражение: = 0,3*А1.

4. Скопировать А1 и
В2 вниз на 100 строк или более (чем больше, тем лучше).

5. Построить диаграмму
(аттрактор Хенона), используя значения столбца А как абсциссу, а
значения столбца В — как ординату.

3. Расчет показателя Херста с помощью
программы Fractan

1. Открыть файл «Ценные бумаги
Марков». Этот файл содержит данные по ценам акций различных
российских предприятий. Выбрать какие-либо акции (на протяжении примерно
1400 торговых дней, цену открытия или другую цену), скопировать этот
временной ряд.

2. Открыть блокнот и вставить в
него полученный временной ряд.

3. Заменить в этих данных запятую
(,) на точку (.).

4. Сохранить ряд с расширением .dat.

5. Открыть программу Fractan, вставить в него анализируемый
ряд, рассчитать показатель Херста . Оценить значение
показателя.

6. В этом же пакете произвести
расчет показателя Херста для различных временных рядов, имеющихся в
пакете.

4. Построение
странного аттрактора Лоренца

1. Открыть Matlab.

2. Запустить Simulink, выполнив в командной строке команду
simulink.

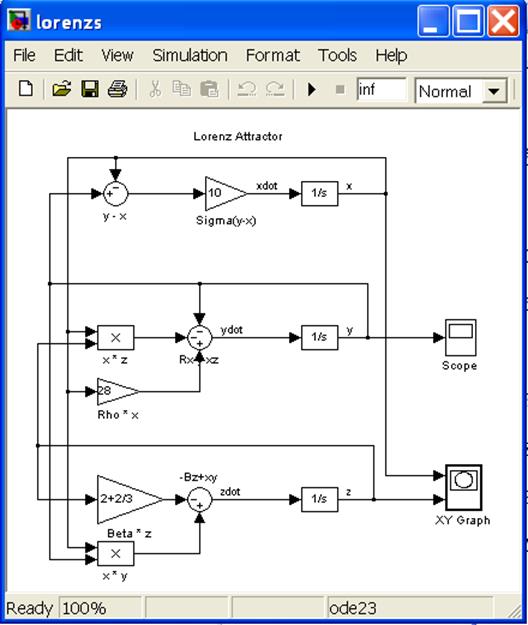
3. Выполнив File / Open
/ toolbox / simulink/ simdemos /lorenzs.mdl приходим
к окну запуска системы Лоренца (рис.2).

Рис.2

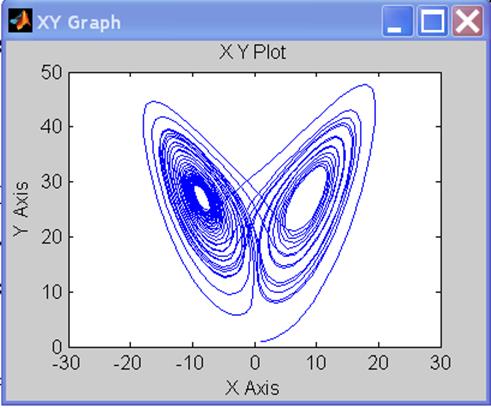
4. Запустив через Simulation, получаем аттрактор Лоренца
(рис.3).

Рис.3.

Источник

I’ve made Excel VBA code that draws and fills a fractal pattern. I know there’s a few more ways to optimize the code, just glad it works right now.

Example

Dim lng As Integer 'length of drawn lines
Dim pi As Double 'pi
Dim qpi As Double 'quarter pi
Dim rnpt() As Double 'list of avaialble points to draw from
Dim cx As Integer 'center of drawing
Dim cy As Integer
Dim stpt() As Double 'placeholder for new endpoints drawn
Dim fspt() As Double 'temp endpoints
Dim cc As Integer 'counter

'draws a 2-d bidirectional dividing fractal given a set of coordinates created in pattern()
Sub draw()


        For cnt = 1 To lng 'draws each set of lines

            t = Timer 'timer loop to prevent system freezes and lets run in background
            Do While Timer < t + 0.01
                DoEvents
            Loop

            For cnt2 = 0 To UBound(rnpt(), 2) - 1 'loops through all available points

                y = rnpt(0, cnt2) 'virtual y
                x = rnpt(1, cnt2) 'virtual x
                Z = rnpt(2, cnt2) 'z = direction


                ypa = y + WorksheetFunction.Round(Cos(Z + qpi), 0) * cnt 'extrapolates future pixels of division and checks all nearby points for collision as each pixel is drawn
                xpa = x + WorksheetFunction.Round(Sin(Z + qpi), 0) * cnt

                ypt1 = y + WorksheetFunction.Round(Cos(Z + qpi), 0) * (cnt + 1)
                xpt1 = x + WorksheetFunction.Round(Sin(Z + qpi), 0) * (cnt + 1)

                ypt2 = ypa + WorksheetFunction.Round(Cos(Z + qpi + qpi), 0)
                xpt2 = xpa + WorksheetFunction.Round(Sin(Z + qpi + qpi), 0)
                ypt3 = ypa + WorksheetFunction.Round(Cos(Z + qpi - qpi), 0)
                xpt3 = xpa + WorksheetFunction.Round(Sin(Z + qpi - qpi), 0)
                ypt4 = ypa + WorksheetFunction.Round(Cos(Z + qpi - qpi * 2), 0)
                xpt4 = xpa + WorksheetFunction.Round(Sin(Z + qpi - qpi * 2), 0)
                ypt5 = ypa + WorksheetFunction.Round(Cos(Z + qpi + qpi * 2), 0)
                xpt5 = xpa + WorksheetFunction.Round(Sin(Z + qpi + qpi * 2), 0)

                ypb = y + WorksheetFunction.Round(Cos(Z - qpi), 0) * cnt 'second division line being drawn
                xpb = x + WorksheetFunction.Round(Sin(Z - qpi), 0) * cnt

                ypt6 = y + WorksheetFunction.Round(Cos(Z - qpi), 0) * (cnt + 1)
                xpt6 = x + WorksheetFunction.Round(Sin(Z - qpi), 0) * (cnt + 1)

                ypt7 = ypb + WorksheetFunction.Round(Cos(Z - qpi + qpi), 0)
                xpt7 = xpb + WorksheetFunction.Round(Sin(Z - qpi + qpi), 0)
                ypt8 = ypb + WorksheetFunction.Round(Cos(Z - qpi - qpi), 0)
                xpt8 = xpb + WorksheetFunction.Round(Sin(Z - qpi - qpi), 0)
                ypt9 = ypb + WorksheetFunction.Round(Cos(Z - qpi - qpi * 2), 0)
                xpt9 = xpb + WorksheetFunction.Round(Sin(Z - qpi - qpi * 2), 0)
                ypt10 = ypb + WorksheetFunction.Round(Cos(Z - qpi + qpi * 2), 0)
                xpt10 = xpb + WorksheetFunction.Round(Sin(Z - qpi + qpi * 2), 0)

                'checks for missing pixels
                If Not Worksheets("sheet1").Cells(cy - ypa, cx + xpa).Interior.Color = 255 And Not fspt(2, cnt2 * 2) = 1 Then
                    f1 = 1
                End If

                'checks for collision
                If Worksheets("sheet1").Cells(cy - ypa, cx + xpa).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt1, cx + xpt1).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt2, cx + xpt2).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt3, cx + xpt3).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt4, cx + xpt4).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt5, cx + xpt5).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2) = 1
                ElseIf Not fspt(2, cnt2 * 2) = 1 Then
                    Worksheets("sheet1").Cells(cy - ypa, cx + xpa).Interior.Color = 255
                    fspt(0, cnt2 * 2) = ypa
                    fspt(1, cnt2 * 2) = xpa
                    fspt(3, cnt2 * 2) = Z + qpi
                End If

                'fills missing pixels
                If f1 = 1 Then
                    Worksheets("sheet1").Cells(cy - ypa, cx + xpa).Interior.Color = 255
                End If

                'checks for dead pixels in line 2
                If Not Worksheets("sheet1").Cells(cy - ypb, cx + xpb).Interior.Color = 255 And Not fspt(2, cnt2 * 2 + 1) = 1 Then
                    f2 = 1
                End If

                'checks for line 2 collision
                If Worksheets("sheet1").Cells(cy - ypb, cx + xpb).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2 + 1) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt6, cx + xpt6).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2 + 1) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt7, cx + xpt7).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2 + 1) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt8, cx + xpt8).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2 + 1) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt9, cx + xpt9).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2 + 1) = 1
                ElseIf Worksheets("sheet1").Cells(cy - ypt10, cx + xpt10).Interior.Color = 255 Then
                    fspt(2, cnt2 * 2 + 1) = 1
                ElseIf Not fspt(2, cnt2 * 2 + 1) = 1 Then
                    Worksheets("sheet1").Cells(cy - ypb, cx + xpb).Interior.Color = 255
                    fspt(0, cnt2 * 2 + 1) = ypb
                    fspt(1, cnt2 * 2 + 1) = xpb
                    fspt(3, cnt2 * 2 + 1) = Z - qpi
                End If

                'fills missing pixels line 2
                If f2 = 1 Then
                    Worksheets("sheet1").Cells(cy - ypb, cx + xpb).Interior.Color = 255
                End If

                'variable reset
                f1 = 0
                f2 = 0

            Next cnt2

        Next cnt

        For cc = 0 To UBound(rnpt(), 2) - 1 'adds new endpoints if no collision occured

            If Not fspt(2, cc * 2) = 1 Then
                ReDim Preserve stpt(3, UBound(stpt, 2) + 1)
                stpt(0, UBound(stpt, 2) - 1) = fspt(0, cc * 2)
                stpt(1, UBound(stpt, 2) - 1) = fspt(1, cc * 2)
                stpt(2, UBound(stpt, 2) - 1) = fspt(3, cc * 2)
            End If

            If Not fspt(2, cc * 2 + 1) = 1 Then
                ReDim Preserve stpt(3, UBound(stpt, 2) + 1)
                stpt(0, UBound(stpt, 2) - 1) = fspt(0, cc * 2 + 1)
                stpt(1, UBound(stpt, 2) - 1) = fspt(1, cc * 2 + 1)
                stpt(2, UBound(stpt, 2) - 1) = fspt(3, cc * 2 + 1)
            End If
        Next cc
End Sub

'fills pattern shapes based on radial distance from center
Sub Shader2()

Dim r As Integer 'color variables
Dim g As Integer
Dim b As Integer

Dim var As Double 'variable to adjust color
Dim rte As Integer 'square root holder for distance

Dim x As Integer 'current pixel
Dim y As Integer

Dim x2 As Integer
Dim y2 As Integer

Dim c3 As Integer

Dim y3 As Integer
Dim x3 As Integer


Dim t As Integer

Dim box() As Integer 'fill area array

Dim c As Double

Dim lim As Integer 'limit of drawing

ReDim box(2, 1) 'set initial dimensions

lim = 1499 'set limit

r = 255 'set initial color

var = (255 / (cx / 6)) 'set rate of color change by drawing diminsions

For c = 0 To 2 * pi Step pi / 180 / 2 'radial loop direction by half degrees

r = 255
g = 0
b = 0

    For c2 = 1 To cx - 1 'loop distance from center to drawing dimensions

        ReDim box(2, 1) 'reset fill area

        x = Math.Round(Sin(c) * c2, 0) 'set current pixel by current direction and distance
        y = Math.Round(Cos(c) * c2, 0)

        c3 = 1

        t3 = 0

        If Worksheets("sheet1").Cells(cy - y, cx + x).Interior.Color = 0 Then 'check for next empty pixel

            x2 = Sin(c) * (c2 + c3) 'check next pixel
            y2 = Cos(c) * (c2 + c3)

            box(0, 0) = y 'set starting pixel to array
            box(1, 0) = x

            Do While Worksheets("sheet1").Cells(cy - y2, cx + x2).Interior.Color = 0 'check while next available pixel is empty to find shape area distance from center
                x2 = Sin(c) * (c2 + c3) 'get next coordinate
                y2 = Cos(c) * (c2 + c3)

                c3 = c3 + 1 'counter for shape bisection

                rte = Math.Round(Sqr(x2 ^ 2 + y2 ^ 2), 0) 'set current distance

                If rte > lim Or c3 > 80 Then 'end loop at drawing limit
                    Exit For
                End If
            Loop

            rte = Math.Round(Sqr(x2 ^ 2 + y2 ^ 2), 0) 'set final distance

            tim = Timer 'loop to prevent freezing and allow background processes
            Do While Timer < tim + 0.01
                DoEvents
            Loop

            If rte < cx / 6 Then 'set color based on distance from center
                g = var * rte
            ElseIf rte < 2 * cx / 6 Then
                r = 255 - var * (rte - cx / 6)
            ElseIf rte < 3 * cx / 6 Then
                b = var * (rte - 2 * cx / 6)
            ElseIf rte < 4 * cx / 6 Then
                g = 255 - var * (rte - 3 * cx / 6)
            ElseIf rte < 5 * cx / 6 Then
                r = var * (rte - 4 * cx / 6)
            ElseIf rte < cx Then
                b = 255 - var * (rte - 5 * cx / 6)
            End If

            x3 = x 'save current coordinate
            y3 = y

            Worksheets("sheet1").Cells(cy - y, cx + x).Interior.Color = RGB(r, g, b) 'set current coordinate

            Do While t3 = 0 'fill shape area loop

                For cnt = 1 To UBound(box(), 2) 'for all available pixels

                    t2 = 0 'reset pixel direction counter

                    y3 = box(0, UBound(box(), 2) - cnt) 'set next available pixel
                    x3 = box(1, UBound(box(), 2) - cnt)

                    If y3 > lim Then y3 = lim 'check for drawing limits
                    If x3 > lim Then x3 = lim
                    If y3 < -lim Then y3 = -lim
                    If x3 < -lim Then x3 = -lim

                    For rad = 0 To 3 * pi / 2 Step pi / 2 'loop through four possible directions

                        'check for current color and pattern color
                        If Not Worksheets("sheet1").Cells(cy - y3 - Cos(rad), cx + x3 + Sin(rad)).Interior.Color = 255 And Not Worksheets("sheet1").Cells(cy - y3 - Cos(rad), cx + x3 + Sin(rad)).Interior.Color = RGB(r, g, b) And Not x3 = lim And Not y3 = lim And Not x3 = -lim And Not y3 = -lim Then
                            Worksheets("sheet1").Cells(cy - y3 - Cos(rad), cx + x3 + Sin(rad)).Interior.Color = RGB(r, g, b) 'set current color

                            t2 = t2 + 1 'check available pixel direction 1-4

                            'if first pixel, overwrite previous pixel, else add new pixel
                            If t2 = 1 Then
                                box(0, UBound(box(), 2) - cnt) = y3 + Cos(rad)
                                box(1, UBound(box(), 2) - cnt) = x3 + Sin(rad)
                            Else:
                                box(0, UBound(box(), 2) - 1) = y3 + Cos(rad)
                                box(1, UBound(box(), 2) - 1) = x3 + Sin(rad)
                            End If

                            ReDim Preserve box(2, UBound(box(), 2) + 1) 'add space for next loop
                        End If

                    Next rad

                    If UBound(box(), 2) - 1 > 0 Or t3 = 1 Then 'check if none remain or only one direction
                        If t2 = 0 Then 'check for remaining directions
                            If Not cnt = 1 Then 'remove dead fill pixels

                                For del = UBound(box(), 2) - cnt To UBound(box(), 2) - 2

                                    box(0, del) = box(0, del + 1)
                                    box(1, del) = box(1, del + 1)

                                Next del

                                ReDim Preserve box(2, UBound(box(), 2) - 1)

                            Else:
                                ReDim Preserve box(2, UBound(box(), 2) - 1)
                            End If

                            Exit For 'check next pixel
                        Else:
                            ReDim Preserve box(2, UBound(box(), 2) - 1) 'remove dead fill pixel
                        End If
                    Else:
                        t3 = 1 'loop break if no pixels remain
                        Exit For
                    End If

                Next cnt
            Loop
            c2 = c3 + c2 - 1 'move loop count to next shape

        End If
    Next c2
Next c

End Sub

Sub pattern()

Worksheets("sheet1").Rows.RowHeight = 8 'set excel cell area to minimum pixel dimensions and reset cell color
Worksheets("sheet1").Columns.ColumnWidth = 1
Worksheets("sheet1").Rows.Interior.Color = 0

pi = WorksheetFunction.pi 'set pi value
qpi = pi / 4 'quarter pi

cx = 2000 'sets drawing center
cy = cx
lng = 10 'sets line length drawn

ReDim rnpt(3, 2) 'creates starting point array with coordinates and direction
ReDim fspt(0, 0)

rnpt(0, 0) = 0 'adds starting points to array
rnpt(1, 0) = 0
rnpt(2, 0) = pi / 4

rnpt(0, 1) = 0
rnpt(1, 1) = 0
rnpt(2, 1) = 5 * pi / 4

stpt = rnpt 'saves points

For c1 = 1 To 180 'number of repetitions to run

    rnpt = stpt 'saves new endpoints

    ReDim fspt(4, UBound(rnpt, 2) * 2) 'adds space for possible new endpoints

    c3 = UBound(rnpt, 2) - 1 'placeholder for total number of endpoints

    ReDim stpt(3, 0) 'resets endpoint placeholder

    Call draw 'draws next set

Next c1

Call Shader2

End Sub

Источник

«Математика есть единая симфония бесконечного».

Д.Гильберт

Технологическая карта урока

Ф.И.О. учителя:
Коннова Мария Александровна

Класс: 9

Предмет: геометрия, информатика

Тема урока: Геометрия
фракталов.

Место и роль урока в
изучаемой теме: первый урок в изучаемой теме

Цели урока:

Образовательная цель: расширение общего научного кругозора. Формирование представлений о том, что наука и её концепции тесно
связаны с практикой, создают для неё общие методы, возможности решать основные
её проблемы.

Развивающая
цель: развитие математической
интуиции, фантазии и чувства гармонии; развитие внимания, восприятия,
представления, воображения, мировоззрения; расширение кругозора.

Воспитательная цель: формирование познавательного интереса к
науке учебного предмета и к методам исследования; воспитание
умения анализировать объект, вычленяя из него частные случаи; формирование
творческого сознания.

Тип
занятия: урок-исследование

Планируемые результаты.

Предметные (знания, умения,
представления): обучающийся научится объяснять что такое фрактал, определять
фрактал как «объект природы», строить фрактал в программе Excel.

Метапредметные
(познавательные, регулятивные, коммуникативные УУД):

Коммуникативные:
формирование умений работать в группе, вести дискуссию, умения выражать свои
мысли и выслушивать собеседника, воспитание сдержанности, культуры
взаимоотношений, умения работать с имеющейся информацией в необычной ситуации.

Познавательные:
приобретение опыта самостоятельного поиска и анализа информации путем
практических действий.

Регулятивные:
овладение навыками самостоятельного приобретения новых знаний, организации
учебной деятельности, постановки цели, планирования, самоконтроля и оценки
результата своей деятельности.

Личностные
(личностные УУД): самостоятельность в приобретении новых знаний и практических
умений; умение видеть математические задачи в окружающем нас мире.

Педагогические технологии: технология
проблемного диалога, технология продуктивного чтения, элементы технологии
проектной деятельности.

Методы обучения: метод научного познания,
метод исследования.

Средства обучения: раздаточный материал с
текстами из разных источников, компьютер для демонстрации фото и картинок
фракталов, природный материал, бумага, ножницы, клей, компьютеры.

Формы организации
познавательной деятельности: смысловое чтение, групповая работа, беседа.

*Этапы занятия*	*Деятельность учителя*	*Деятельность ученика*	*Формируемые УУД*	Виды работы, формы, методы, приемы	Планируемые результаты	Время
1. Мотивация учебной деятельности учащихся.	Учитель приветствует учащихся. Известно ли вам, что математика — веселая наука? Ведь ее можно увидеть во всем, что нас окружает. Математическая викторина «О математике с улыбкой» убедит вас в этом! 1) Какие геометрические фигуры дружат с солнцем? (лучи) 2) Какие математические созвездия вы знаете? (Треугольник, Циркуль ) 3) Что есть у каждого слова, растения и уравнения? (корень) 4) Назовите математические растения (тысячелистник, столетник) 5) Назовите «математические» упражнения школы фигурного катания (круг, тройка, скобка, восьмерка) 6) Какие цифры пишут летчики в небе? (8) 7) В какие цифры люди одеваются? ( костюм-двойка, тройка) Какой математический знак напоминает движение губ верблюда, когда он жует жвачку? (бесконечность) Придумайте, пожалуйста, название своей команде и эмблему, чтобы они содержали слово бесконечность и математический знак бесконечности!	Делятся на 3 команды, Включение в работу. Отвечают на вопросы	К – коммуникативные понимать позицию другого, выражать и аргументировать своё мнение, договариваться, работать в группе Л – личностные устанавливать общие правила поведения, уважать непохожих на тебя	Тест	Коммуникативные: формирование умений работать в группе, вести дискуссию	3 мин.
2. Проблемная ситуация	Вводная беседа: В 1922 году английский математик и метеоролог Льюис Фрай Ричардсон опубликовал работу, посвященную математическим предсказаниям погоды, в которой, между прочим, пародировал стихи Дж. Свифта: Блох больших кусают блошки Блошек тех – малютки-крошки, Нет конца тем паразитам, Как говорят, ad infinitum. («ad infinitum» в переводе с латыни – «до бесконечности»). Это четверостишие вполне может служить описанием того явления, о котором мы сегодня будем говорить. Ричардсон обратил внимание на то, что при исследовании турбулентности (хаотических вихрей) воздушных потоков он обнаружил каскад энергии – от больших вихрей к малым, то есть своеобразную гармонию: маленькие вихри возникают внутри больших и как бы повторяют их форму и поведение. Стихотворение Николая Заболоцкого, опубликованное в 1947 году, начинается такими строками: Я не ищу гармонии в природе. Разумной соразмерности начал, Ни в недрах скал, ни в ясном небосводе Я до сих пор, увы, не различал. Как своенравен мир ее дремучий! В ожесточенном пении ветров, Не слышит сердце правильных созвучий, Душа не чует стройных голосов. Заболоцкий искал в природе «разумную соразмерность», но представлял ее себе согласно классическим канонам – по Евклиду, а оказалось, что эта соразмерность имеет совершенно другую геометрию, о которой поэт не догадывался. Гармония и хаос. Как часто мы слышим эти слова и как редко задумываемся над их содержанием. Откуда появляется красота, почему она так волнует и радует? Существуют ли объективные законы или каждый воспринимает ее по-своему? Давайте и мы сегодня обратимся к загадкам природы, раз сегодня такой необычный у нас урок. Оглядимся вокруг и поищем ответы на вопросы?	Высказывают свои мысли аргументируя. Тем самым ставят перед собой познавательные и учебные задачи.	П – Познавательные — извлекать смысловую информацию – анализировать (в том числе выделять главное, разделять на части) и обобщать К – излагать своё мнение Р – Регулятивные -определять цель, проблему в деятельности	Беседа с учениками	Умение выражать свои мысли и выслушивать собеседника	7 мин.
3. Актуализация знаний	Учитель раздает командам тексты, содержащие информацию из разных источников и разделов науки (искусства, биологии, компьютерной графики, физики, литературы), которые они должны внимательно прочитать и остановиться на важном, ключевом для этой статьи, понятии «сложности». Что объединяет эти тексты? Учитель обобщает: иногда сложность следует понимать метафорически, что сложная система – это непременно система, способная к самоорганизации, она может быть связана с наличием большого количества и разнообразия частей, с богатством связей между этими частями, может быть обусловлена целостностью, организацией этих свойств. Вот это и является самым интересным. Есть абстрактные математические структуры – фракталы и хаос, получившие признание в 70-х годах ХХ века, и быстро стали модными. Что же такое *фрактал? Это понятие по-разному определяется в разных источниках. Прочитайте определения и свойства. Многие объекты в природе обладают свойствами фрактала, это вам еще предстоит сегодня выяснить. А пока немного истории. Фракта́л* (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения (любая часть фрактала подобна всему множеству целиком). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференциируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введён Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы». Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры. Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных свойств: · Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть на всех шкалах мы увидим одинаково сложную картину. · Является самоподобным или приближённо самоподобным. · Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.	Знакомятся с текстами. Анализируют. Делают выводы Заслушивают представителя от команды.	П – находить (в источниках достоверную информацию) Пользоваться приёмами смыслового чтения. Представлять информацию в разных формах. Р – работать по плану, сверяясь с целью. Оценивать степень и способы достижения цели. Л – осознавать целостность мира и многообразие взглядов на него. К — самостоятельно вычитывать информацию, данную в НЕявном виде — самостоятельно сопоставлять и отбирать информацию из различных источников	Работа с текстом.	Приобретение опыта самостоятельного поиска и анализа информации путем практических действий	5 мин.
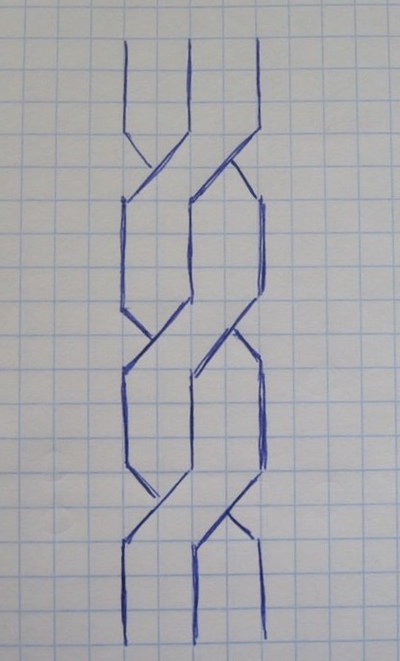
4. Совместное исследование проблемы. Первичное усвоение новых знаний.	Построить фрактал сможет любой желающий. Давайте и мы с вами немного попрактикуемся в этом. Сделаем фрактал из бумаги. Привычка мять, комкать и рвать бумагу в минуты нервного стресса или когда не дают покоя тяжкие мысли о суетном, свойственна многим людям. Почему нас так тянет к насилию над великим китайским изобретением, пусть объяснят психологи. Мы же немного поговорим о том, как наши «комкательные» порывы обратить на пользу — немного отвлечься, потренировать терпение и обогатить себя малой крупицей знания. Давайте попробуем к познанию тайны фракталов подойти с помощью небольшого эксперимента, для которого не потребуется ничего, кроме бумаги и ножниц. Итак, возьмем кусок бумажной ленты (отрежем узкую полоску бумаги от длинной стороны листа А4) и начнем складывать пополам, потом еще раз пополам и еще. Чтобы получить более-менее наглядный результат, придется ограничиться четырьмя складываниями — лента наша слишком коротка. Да, и самое главное — складывать ее придется по определенному правилу: полоску сгибать всегда в одном и том же направлении. Этапы сгиба показаны на рис. Учитель демонстрирует Теперь разогнем ленту так, чтобы в местах сгибов образовался угол 90 градусов, и разложим ленту. Вот перед нами и появился фрактал под названием «Кривая дракона». Мало кто обращает внимание, что эти удивительные фигуры присутствуют повсюду. Природа создана из самоподобных фигур, просто мы этого не замечаем. Достаточно посмотреть через увеличительное стекло на нашу кожу или листок дерева, и мы увидим фракталы. Природа является лучшим архитектором, идеальным строителем и инженером. Она устроена весьма логично, и если мы не можем найти закономерность, это не значит, что ее нет. Может быть, нужно искать в ином масштабе. С уверенностью можно сказать, что фракталы хранят еще немало секретов, которые вам только предстоит открыть. Задания командам: привести примеры объектов, обладающих, на ваш взгляд, фрактальными свойствами, в природе. Учитель демонстрирует изображения фракталов.	Делают модель фрактала из бумаги. Приводят примеры живой и неживой природы, обладающие фрактальными свойствами. Примерные ответы: 1) Кораллы, морские звезды, раковины, цветы, растения, плоды, кроны деревьев, листья, кровеносная система и бронхи человека, перья птиц 2) Границы географических объектов, береговые линии, горные хребты, снежинки, облака, молнии, снежные узоры, кристаллы, сталактиты и сталагмиты.	Р – планировать деятельность в учебной ситуации К – организовывать работу в группе, излагать своё мнение	Работа с учениками	самостоятельность в приобретении новых знаний и практических умений; умение видеть математические задачи в окружающем нас мире.	7 мин.
5. Моделирование	Вступает учитель информатики и предлагает ребятам построить фрактал при помощи программы Excel. Показывает один пример построения фрактала и рассказывает про алгоритмы построения фракталов Рассмотрим множество Мандельброта. В математике множество Мандельброта — это фрактал, который определяется как множество точек на комплексной плоскости, итеративная последовательность не уходит в бесконечность и задана формулами z₀=0, Z_n+1=Z_n²+M. Чтобы построить данную последовательность точек, т. е. фрактал, перейдем от комплексной формы записи с помощью преобразований к удобным формулам для построения. Если выражение Z_n+1=Z_n²+M переформулировать в виде итеративной последовательности значений координат комплексной плоскости x и y, то есть, приняв Z = X + iY и М = p + iq (где i — мнимая единица), то получим алгоритм с формулами (1): X_n+1=X_n²–Y_n²+p; Y_n+1=2X_nY_n+q, с параметрами p = – 0,5219; q = 0,4999. Сначала полагаем X_n = 0; Y_n = 0, и по формулам (1) получаем на первом шаге вычислений: X_n+1=0² –0²–0,5219= – 0,5219; Y_n+1=2·0·0+0,4999. Теперь полагаем X_n = X_n+1 = – 0,5219; Y_n = Y_n+1 = 0,4999, и по формулам (1) получаем на втором шаге: X_n+1 = (–0,5219)² – (0,4999)² – 0,5219 = – 0,4994…; Y_n+1 = 2·(–0,5219)·(0,4999) + 0,4999 = – 0,0218…. Затем полагаем X_n = X_n+1 = – 0,4994…; Y_n = Y_n+1 = –0,0218, и опять по формулам (1) продолжаем дальше. То есть на каждом последующем шаге вычислений (итераций) предыдущие значения X_n+1 и Y_n+1 надо подставлять в формулы (1) в качестве новых значение X_n и Y_n. В программе « Microsoft Excel» можно сделать 32000 подобных «шагов»-вычислений, а затем построить («точками») график функции Y_n+1 = f(X_n+1), который и будет похож на «пылающее солнце». Более того, меняя числовые значения параметров p и q, на том же графике можно увидеть и другие объекты; например, при p = – 0,5; q = 0,4999 вместо «солнца» получится «спиральная галактика». Представлю алгоритм, который я составила, для построения в программе «Microsoft Excel» фракталов Мандельброта «пылающее солнце» и «спиральная галактика». На практике для достижения приемлемой точности достаточно 100 итераций. См. приложение 1.	Учитель показывает как смоделировать в программе Excel фрактал на примере построения множества Мандельброта.	Р — осуществление мини-проекта.	Работа с учениками	Умение выражать свои мысли и выслушивать собеседника	5 мин.
6. Творческий этап	Учитель предлагает построить командам фракталы в программе Excel. Для каждой команды отдельный фрактал (см. приложение 2.)	Представляют мини-проект.	П – обобщать, делать выводы.	Приектная работа в группах	овладение навыками самостоятельного приобретения новых знаний, организации учебной деятельности, постановки цели, планирования, самоконтроля и оценки результата своей деятельности	13 мин.
7. Оценка результатов, рефлексия	Учитель: Давайте подведем итог занятию. Что нового, интересного вы сегодня узнали? Сможете ли вы поделиться новой информацией с друзьями или дома? Можете ли вы привести примеры, где, на ваш взгляд, можно встретить объекты, обладающие фрактальной структурой? Игра « Волшебный мешок»: у меня в пакете находится объект, обладающий структурой фрактала. Задание командам: с помощью коротких вопросов разгадать что это? (команда получает ананас)	Учащиеся приводят примеры и делятся впечатлениями. Высказывания ребят: -Очень занятно, не замечал, что фракталы встречаются настолько часто. — очень красивое явление — хм, не знал, что эти штуки называются фракталами — Давно присматривался, игрался на компе. Занятно. Получаются красивые узоры — В фильмах 3D эффекты фракталов явно используют. — вспомнила: «Неделя моды в Париже: овалы и фракталы»!!! Подумала, что за слово такое??? — я теперь понимаю что появление кубизма в европейской живописи связано с фракталами	.Р — Оценивать результат оценка-выделение и осознание обучающимися того, что уже усвоено и что еще нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы. К — умение с достаточной полнотой и точностью выражать свои мысли, владение монологической и диалогической формами речи. Л — нравственно — этическая ориентация, смыслообразование.	Оценивают результаты занятия		5 мин.

Приложение 1. Алгоритм построения в
программе “Microsoft Excel” фрактала Мандельброта
«пылающее солнце» (для 100 итераций)

Таблица 1.

1.Записать в ячейку А1
переменную X_n

2.Записать в ячейку В1
переменную Y_n.

3.Записать в ячейку D1
параметр р.

4.Записать в ячейку E1
параметр q.

5.Записать в ячейку G1
переменную X_n+1.

6.Записать в ячейку H1
переменную Y_n+1. 7.Ввести в ячейку
А2 значение 0.

8.Ввести в ячейку В2
значение 0.

9.Ввести в ячейку А3
формулу =G2.

10.Ввести в ячейку В3
формулу =H2.

11.Ввести в ячейку D2 значение
-0,5219.

12.Ввести в ячейку E2
значение 0,4999.

13.Ввести в ячейку G2
формулу =A2^2-B2^2+$D$2

14.Ввести в ячейку H2
формулу =2*A2*B2+$E$2

15.Растянуть ячейку А3 за
правый нижний уголок до A101.

16.Растянуть ячейку В3 за правый
нижний уголок до B101.

17.Растянуть ячейку G2 за
правый нижний уголок до G101.

18.Растянуть ячейку H2 за
правый нижний уголок до H101.

19.Выделить область значений
от G2 до H101.

20.Для построения фигуры
сделать следующее:

Вставка->Диаграммы->Точечная->Точечная
с гладкими кривыми

Дидактические
материалы к занятию:

Я спрашивал себя, как может книга быть бесконечной. В
голову не приходит ничего, кроме цикличного, идущего по кругу тома, тома, в
котором последняя страница повторяет первую, что и позволяет ему продолжаться
сколько угодно

Х.Л. Борхес

Пожалуй, самым интересным и удивительным считается проявление
в литературе. Самый простой и известный пример как всегда из детства – все
знают эти строки: «у попа была собака, он ее любил. Она съела кусок мяса, он ее
убил. В землю закопал, надпись написал, что у попа была собака…» и так до
бесконечности. Также примером является известная всем притча о бабочке Чжуан-
цзы: Однажды Чжуан-цзы приснилось, что он бабочка, счастливая
бабочка, что достигла исполнения желаний, и которая не знает, что она
Чжуан-цзы.
Внезапно он проснулся и тогда с испугом увидел, что он Чжуан-цзы. И неизвестно,
Чжуан-цзы ли снилось, что он бабочка, или же бабочке снится, что она
Чжуан-цзы…

Возвращаясь к прошлому, в искусстве человечества, как и в
природе, с легкостью можно найти примеры…… Яркими работами в этой системе
является рисунок Леонардо да Винчи «Всемирный потоп», гравюры японского
художника Кацусики Хокусая и работы Э. Эшера также являются ярким примером …..и
список этот можно продолжать бесконечно.

Широко распространена компьютерная графика, которая используется для
моделирования и построения разнообразных конструкций и макетов. Удивительно, но
принципы….. используются даже в
бизнесе, для анализа рынков и бирж.
….появляются на рынке достаточно часто. Абсолютно во всех временных диапазонах.
Не играет ровно никакого значения, что рассматривать: дневные, недельные,
часовые, минутные или тиковые графики — везде их можно выявить. Их природа
обманчива. Они появляются и исчезают, поэтому многим, как показывает опыт, не
под силу освоить данные инструмент выявления основной структуры рынка.

В математике под …… понимают множества точек в евклидовом
пространстве, имеющие дробную метрическую размерность, либо метрическую
размерность, отличную от топологической. И конечно, как любая другая
математическая наука, ……насыщен множеством сложнейших теоретических изысканий и
формул.

Термодинамические
процессы в живой природе идут по пути уменьшения энтропии системы, увеличения
организованности объектов. Эти свойства являются фундаментальными для живой
природы. Другие свойства живого — это рост и развитие. То есть живой объект
постепенно разворачивается в пространстве и времени, увеличивая свои размеры и
массу. (береговая линия — результат разрушения неких неживых тел (пород)).

В биологии при
изучении роста растений была выявлена такая закономерность как
«Ветвление». Ветвление возникло в процессе эволюции тела растений еще
до появление органов.

В биологии моделируют и исследуют популяции и развитие
внутренних органов.

Идеальные города
создавали в своем воображении и на бумаге художники и архитекторы прошлого.
Возможно, что-то подобное архитекторы будущего будут создавать в реальном мире.
По крайней мере, идеальный город Ромолонтино, который построил на бумаге
Леонардо да Винчи, сейчас на полном серьезе считают городом будущего.

Планы идеальных
городов причудливы, обладают некоей странной красотой

Кроме того, идеальные
города чем-то напоминают графическую поэзию или графические
музыкальные партитуры. И там, и здесь — фигуры, лабиринты, звезды…
Но в случае с городами, вместо нот или букв внутри каждой фигуры — улицы и
дома. Можно представить, как эти дивные графические объекты должны бы выглядеть
с воздуха, с неба… Если б они были построены, вид на нашу планету стал бы
поистине фантастическим!

Для демонстрации
фракталов — http://www.lookatme.ru/flow/posts/art-radar/60122-fraktalyi

Карточки с заданиями для построения
фракталов:

Приложение 2. Карточка номер 1. Написать алгоритм
построения в программе “Microsoft Excel”
фрактала Мандельброта «спиральная галактика» (для
100 итераций)
Таблица 2.(решение задачи)

1.Записать в ячейку А1
переменную X_n

2.Записать в ячейку В1
переменную Y_n.

3.Записать в ячейку D1
параметр р.

4.Записать в ячейку E1
параметр q.

5.Записать в ячейку G1
переменную X_n+1.

6.Записать в ячейку H1
переменную Y_n+1.

7.Ввести в ячейку А2
значение 0.

8.Ввести в ячейку В2
значение 0. .

9.Ввести в ячейку А3
формулу =G2.

10.Ввести в ячейку В3
формулу =H2.

11.Ввести в ячейку D2 значение
-0,5.

12.Ввести в ячейку E2
значение 0,4999.

13.Ввести в ячейку G2
формулу =A2^2-B2^2+$D$2

14.Ввести в ячейку H2
формулу =2*A2*B2+$E$2

15.Растянуть ячейку А3 за
правый нижний уголок до A101.

16.Растянуть ячейку В3 за
правый нижний уголок до B101.

17.Растянуть ячейку G2 за
правый нижний уголок до G101.

18.Растянуть ячейку H2 за
правый нижний уголок до H101.

19.Выделить область значений
от G2 до H101.

20.Для построения фигуры
сделать следующее:

Вставка->Диаграммы->Точечная->Точечная
с гладкими кривыми

Рассмотрим фрактал «кривая
Гильберта», заданный формулой (2):

y (x) = (cos^0,5x ⋅ cos 200x + |x|^0,5 − 0,7)(4
− x²)^0,01.
Найдем область допустих значений данного
выражения. Под арифметическим квадратным корнем
находится функция cos(x), значит, cos(x) ≥
0.

Представлю алгоритм, который я
составила, для построения в программе
“Microsoft Excel” фрактала «кривая Гильберта»
по данной формуле (2) в допустимой
области значений, выбрав шаг равный 0,01.

Карточка номер
2. Написать алгоритм построения в программе
“Microsoft Excel” фрактала «кривая Гильберта»

Таблица 3(решение задачи)

1.Записать в ячейку A1
переменную х.

2.Записать в ячейку B1
переменную у.

3.Записать в ячейку A2
значение -π/2, согласно области допустимых
значений XЄ[-π/2; π/2],

4.Ввести в ячейку A3
формулу =A2+0,01.

5.Растянуть ячейку А3 за
правый нижний уголок до ячейки А316
(до значения 1,57).

6.Ввести в ячейку В2
формулу

=((КОРЕНЬ(COS(A2)))*COS(200*A2)+КОРЕНЬ(ABS(A2))-0,7)*(4-A2*A2)^0,01

7.Растянуть ячейку В2 за
правый нижний уголок до ячейки В316.

8.Выделить область значений
от А2 до В316.

9.Для построения фигуры
сделать следующее:

Вставка->Диаграммы->Точечная->Точечная
с гладкими кривыми

Рассмотрим фрактал Мандельброта
«кривая Дракона», заданный системами уравнений
(3) и (4) соответственно:

Сначала полагаем X_n =
0; Y_n = 0. Задаем случайным
образом параметр m, который меняется от
0 до 1. Если m > 0,5, то
применяем систему уравнений (3) для построения
фрактала, иначе — (4). Каждое новое
значение получается из предыдущего в
зависимости от случайного числа.

Представлю алгоритм, который я
составила, для построения в программе
“Microsoft Excel” фрактала Мандельброта «кривая
Дракона».

Карточка номер 3. Написать алгоритм
построения в программе “Microsoft Excel”
фрактала Мандельброта «кривая Дракона»

Таблица 4. (решение задачи)

1. Записать в ячейку А1
номер n.

2. Записать в ячейку В1
случайную величину m.

3. В ячейку С1 записать
х.

4. В ячейку D1 записать
у.

5. В ячейку А2 записать
1.

6. В ячейку А3 ввести
формулу =A2+1

7. Растянуть А3 до
ячейки А 11363

8. В ячейку В2 записать
функцию случайного числа =СЛЧИС()

9. Растянуть ячейку В2
до В 11363

10. Ввести в ячейку С2
значение 0

11. Ввести в ячейку С3
формулу =ЕСЛИ(B3>0,5;-0,4*C2-1;0,76*C2-0,4*D2)

12. Растянуть ячейку С3
до ячейки С 11363

13. Ввести в ячейку D2
значение 0.

14. Ввести в ячейку D3
формулу =ЕСЛИ(B3>0,5;-0,4*D2+0,1;0,4*C2+0,76*D2)

15. Растянуть ячейку D3
до ячейки D11363

16. Выделить ячейки от
С2 до D11363

17. Для построения фигуры
сделать следующее:

Вставка->Диаграммы->Точечная

Источник

Технология выполнения работы

Запустить
MS
Excel
и открыть чистый лист. Дать имя книге
и сохранить файл (в дальнейшем не
забывать периодически сохранять
вносимые изменения).
Импортировать
исходные данные из файла в область
«Исходные данные» (рисунок 1.3) следующим
образом:

–открыть файл с
данными в новой книге;

Рисунок
1.3 – Расположение элементов на листе
MS
Excel
при реализации метода Херста

–если необходимо,
сделать соответствующие замены в формате
данных, чтобы преобразовать их числовую
форму (например, заменить точки,
разделяющие целую и дробную части, на
запятые);

–скопировать
полученные и преобразованные данные в
область «Исходные данные».

В область «Индексы
данных» добавить порядковые номера
исходных данных.
Построить график
исходных данных с помощью мастера
диаграмм и поместить его в одноименную
область.
Используя
мастер функций, определить объем
исследуемых данных N
и результат поместить в область
«Выходные параметры».
Вычислить
среднее
арифметическое ряда X_ср
используя формулу (1.1) и результат
поместить в область «Выходные параметры».
Вычислить
СКО ряда данных S
по формуле (1.2) следующим образом:

–вычислить
разность между каждым значением исходных
данных и X_ср,
результат поместить в область
«Промежуточные данные для СКО» в столбец
с заголовком «Хi—
X_ср»;

–возвести
в квадрат каждую из полученных разностей
и результат поместить в область
«Промежуточные данные для СКО» в столбец
с заголовком «(Х_i—
X_ср)^2»;

–используя
мастер функций, вычислить значение S
и результат поместить в область «Выходные
параметры».

Определить точки
(индексы данных), в которых будет
вычисляться функция накопленного
отклонения ряда от среднего по следующим
правилам:

–на интервале
индексов от 2 до 10 берутся точки с шагом
1;

–на интервале
индексов от 10 до 100 берутся точки с шагом
10;

–на интервале
индексов от 100 до 1000 берутся точки с
шагом 100;

–на интервале
индексов от 1000 до 10000 берутся точки с
шагом 500;

–на интервале
индексов от 10000 и более берутся точки с
шагом 5000;

–точка
с индексом N,
т.е. последняя точка.

Выбранные
индексы точек u
фиксируются
в строке «точки=u»
области «Параметр Херста в точках».

Определяется
среднее значение ряда на участках
[1;u],
где u
– выбранные
индексы точек, по формуле (1.3) и результат
заносится в строку «X_ср_u»
области «Параметр Херста в точках».
Находятся
значения функции накопленного отклонения
на участках [1;u]
по формуле (1.3)
и результат заносится в строки «Z₁»,
«Z₂»
и т.д. области «Параметр Херста в точках».

Z₁=X₁—
X_ср_u

Z₂=Z₁+X₂—
X_ср_u

Z₃=Z₂+X₃—
X_ср_u

………………..

Z_u=Z_u-1+X_u—
X_ср_u

Используя
мастер функций, находится максимальное
и минимальное значения Z
и определяется размах накопленного
отклонения на соответствующем интервале
по формуле (1.4). Результат заносится в
строку «R_u»
области «Параметр Херста в точках».
Определяется
параметр Херста в точках u
как отношение R_u/S.
Результат помещается в строку «R/S»
области «Параметр Херста в точках» для
каждой точки u.
Вычисляются
десятичные логарифмы значений: точек
u
и R/S
в этих точках. Результаты заносятся в
область «Координаты точек для фрактальной
плоскости».
Используя мастер
диаграмм, вывести фрактальную плоскость
метода Херста в одноименную область и
изобразить линию тренда.
Вычислить
угловой коэффициент аппроксимирующей
линии тренда – k.
Затем вычислить показатель Херста
Н=k-1
и результат поместить в область «Выходные
параметры».

Коэффициент
k
находится по методу наименьших квадратов
следующим образом. Пусть имеется ряд
точек с координатами (x₁;y₁),
(x₂;y₂),
… ,(x_i;y_i),
… ,(x_n;y_n),
которые аппроксимируются линейной
зависимостью, описываемой уравнением:

Y_p=kX_p+b.

Тогда
коэффициенты данного уравнения линейной
зависимости находятся как:

;

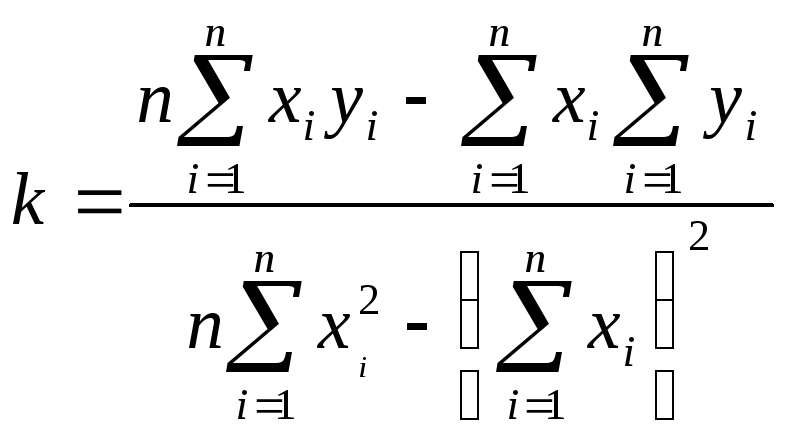
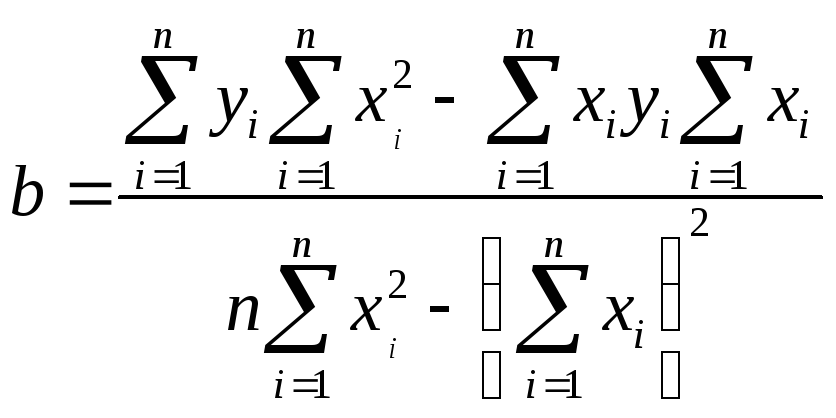
Вычислить
фрактальную размерность D
по формуле (1.6) и результат поместить в
область «Выходные
параметры».
Вычислить
степень долговременной корреляции С
по формуле (1.7) и результат
поместить в область «Выходные
параметры».
Проверить
правильность реализации метода Херста,
путем определения Н
у рядов с известными фрактальными
свойствами (таблица 1.2).

Таблица
1.2

Названия
файлов, содержащих эталонные данные

Н_т	0.1	0.5	1
Имя файла	etalon.h01	etalon.h05	etalon.h1

Оценить
погрешность нахождения Н
по формуле:

γ=(Н-Н_т)/H_т*100%,

где
Н
– экспериментальный показатель Херста,

Н_т
– теоретический показатель Херста.

Погрешность не
должна превышать 20%, в противном случае
необходимо пересмотреть реализацию
метода Херста.

Определить
фрактальные характеристики данных из
других файлов.
Составить
отчет о проделанной работе в MS
Word.

Соседние файлы в папке разное

Источник

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Онлайн
формат
Диплом
гособразца
Помощь в трудоустройстве

Видеолекции для
профессионалов

Свидетельства для портфолио
Вечный доступ за 120 рублей
311 видеолекции для каждого

ФГБОУ ВО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Кафедра информатики и вычислительной техники

ФРАКТАЛЬНАЯ ГРАФИКА В СПЕЦИАЛЬНЫХ ПРОГРАММНЫХ СРЕДСТВАХ

студентка 5 курса группы МДИ-113 Тимошина Светлана

Направление подготовки 050100 «Педагогическое образование».

Профили подготовки «Математика» и «Информатика».

Реферат проверила ______________________ Т. В. Кормилицина

Введение………………………………………………………………………. …31. Общие сведения о фракталах и фрактальной графике …. ………..…….3-5

2. Специальные программные средства. ………..………………..….…5-13

Список использованной литературы…………………………………………. 14

На сегодняшний день Фрактальная графика является второй по росту популярности из четырёх видов компьютерной графики.

Так же есть Растровая и Векторная . Одна – для создания фотореалистичных изображений; Другая – для создания сложных геометрических объектов; и Трёхмерная – как отдельный вид от предыдущих для создания объёмных зрительно-подобных изображений и объектов.

Фрактальные изображения применяются в самых разных сферах, начиная от создания обычных текстур и фоновых изображений и кончая фантастическими ландшафтами для компьютерных игр или книжных иллюстраций. Создаются фрактальные изображения путем математических расчетов. Базовым элементом фрактальной графики является сама математическая формула — это означает, что никаких объектов в памяти компьютера не хранится, и изображение строится исключительно на основе уравнений.
Таинство фрактального изображения не кроется лишь в одной удачной формуле. Не менее важны и иные аспекты. Например, цветовая настройка, фильтры трансформации и др.
Существует очень много программ по созданию фрактальных изображений. Эти программы имеют свои достоинства и недостатки. С развитием технологий количество программ увеличивается, а их качество и возможности улучшаются.

1. Общие сведения о фракталах и фрактальной графике

Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.

Фрактальная графика, как и векторная, основана на математических вычислениях. Базовыми элементами фрактальной графики являются сами математические формулы, описывающие линии и линейные поверхности, то есть никаких объектов в памяти ЭВМ не хранится и изображение строится исключительно по формулам (уравнениям).

Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.

Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.

Одним из первых описал динамические фракталы в 1918 году французский математик Гастон Жюлиа в своем объемном труде в несколько сотен страниц. Но в нем отсутствовали какие-либо изображения. Компьютеры сделали видимым то, что не могло быть изображено во времена Жюлиа. Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Квазифрактал отличается от идеальных абстрактных фракталов неполнотой и неточностью повторений структуры. Большинство встречающихся в природе фракталоподобных структур (границы облаков, линия берега, деревья, листья растений, кораллы, …) являются квазифракталами, поскольку на некотором малом масштабе фрактальная структура исчезает. Природные структуры не могут быть идеальными фракталами из-за ограничений, накладываемых размерами живой клетки и, в конечном итоге, размерами молекул.

Мультифрактал — комплексный фрактал, который может детерминироваться не одним единственным алгоритмом построения, а несколькими последовательно сменяющими друг друга алгоритмами. Каждый из них генерирует паттерн со своей фрактальной размерностью. Для описания мультифрактала вычисляют мультифрактальный спектр включающий в себя ряд фрактальных размерностей присущих элементам данного мультифрактала.

Предфрактал — это самоподобная геометрическая фигура, каждый фрагмент которой повторяется в упрощённом виде при уменьшении масштаба конечное число раз. Количество уровней масштаба, на которых наблюдается подобие, называется порядком предфрактала. При порядке, стремящемся к бесконечности, предфрактал переходит в фрактал.

Фрактальный подход нашел широкое применение во многих областях компьютерной графики, науки и искусства.

Фрактальная графика не является, строго говоря, частью векторной графики, поскольку широко использует и растровые объекты. Фракталы широко используются в растровых (AdobePhotoshop) и векторных (CorelDraw) редакторах и трехмерной (CorelBryce) графике.

2. Специальные программные средства

1. Программа Fractal Editor

Знакомство с основами фрактальной графики лучше всего начать с пакета Fractal Editor . Этот редактор (созданный фирмой Fractal Design, а теперь принадлежащий Corel) фактически представляет собой усеченный вариант программы Painter. Это отличная программа для обучения не только компьютерной графике, но прежде всего азам рисования. Малый объем требуемой памяти (для его установки необходимо всего 10 Мбайт), а также простой интерфейс, доступный даже ребенку, позволяют использовать его в школьной программе.

2. Программа Ultra Fractal

Ultra Fractal — лучшее решение для создания уникальных фрактальных изображений профессионального качества. Пакет отличается дружественным интерфейсом, многие элементы которого напоминают интерфейс Photoshop (что упрощает изучение), и сопровождается невероятно подробной и прекрасно иллюстрированной документацией с серией туториалов, в которых поэтапно рассматриваются все аспекты работы с программой. Ultra Fractal представлен двумя редакциями: Standard Edition и расширенной Animation Edition, возможности которой позволяют не только генерировать фрактальные изображения, но и создавать анимацию на их основе. Созданные изображения можно визуализировать в высоком разрешении, пригодном для полиграфии, и сохранить в собственном формате программы или в одном из популярных фрактальных форматов. Визуализированные изображения также могут быть экспортированы в один из растровых графических форматов (jpg, bmp, png и psd), а готовые фрактальные анимации — в AVI-формат.
Принцип создания фрактальных изображений достаточно традиционен, самое простое — воспользоваться одной из прилагаемых в поставке формул (сориентироваться относительно возможного вида генерируемого по выбранной формуле изображения поможет встроенный браузер), а затем подредактировать параметры формулы желаемым образом. А если эксперимент оказался неудачен, то последние действия легко отменить. Готовых фрактальных формул очень много, и число их может быть расширено путем скачивания новых формул с сайта программы. Подготовленные пользователи могут попытать счастья и в создании собственной формулы, для чего в пакете имеется встроенный текстовый редактор с поддержкой базовых шаблонов, основанных на стандартных конструкциях языка программирования фрактальных формул.
Однако не стоит думать, что таинство фрактального изображения кроется лишь в удачной формуле. Не менее важны и иные аспекты. Например, цветовая настройка, предполагающая выбор варианта окраски и точную настройку ее параметров. Настройка цвета реализована на уровне солидных графических пакетов, например градиенты можно создавать и настраивать самостоятельно, корректируя множество параметров, включая полупрозрачность, и сохранять их в библиотеке для дальнейшего использования. Применение слоев с возможностью изменения режимов их смешивания и корректировкой полупрозрачности позволяет генерировать многослойные фракталы и за счет наложения фрактальных изображений друг на друга добиваться уникальных эффектов. Использование масок непрозрачности обеспечивает маскирование определенных областей изображения. Фильтры трансформации позволяют выполнять в отношении выделенных фрагментов изображения разнообразные преобразования: масштабировать, зеркально отражать, обрезать по шаблону, искажать посредством завихрения или ряби, размножать по принципу калейдоскопа и т.д.

3. Программа Fractal Explorer

Fractal Explorer — программа для создания изображений фракталов и трехмерных аттракторов с достаточно впечатляющими возможностями. Имеет интуитивно понятный классический интерфейс, который может быть настроен в соответствии с пользовательскими предпочтениями, и поддерживает стандартные форматы фрактальных изображений (*.frp; *.frs; *.fri; *.fro; *.fr3, *.fr4 и др.). Готовые фрактальные изображения сохраняются в формате *.frs и могут быть экспортированы в один из растровых графических форматов (jpg, bmp, png и gif), а фрактальные анимации сохраняются как AVI-файлы.
Генерация фракталов возможна двумя способами — на основе базовых фрактальных изображений, построенных по входящим в поставку формулам, или с нуля. Первый вариант позволяет получить интересные результаты сравнительно просто, ведь выбрать подходящую формулу несложно, тем более что удобный файловый браузер позволит оценить качество фрактала из базы еще до создания на его основе фрактального изображения. У полученного таким путем фрактального изображения можно сменить цветовую палитру, добавить к нему фоновое изображение и определить режим смешивания фрактального и фонового слоев, а также степень прозрачности фрактального слоя. Затем можно будет подвергнуть фрактальное изображение трансформации, при необходимости масштабировать, определить размеры изображения и провести рендеринг. Создание изображения с нуля гораздо сложнее и предполагает выбор одного из двух способов. Можно выбрать тип фрактала почти из 150 вариантов. А затем уже перейти к изменению разнообразных параметров: настройке палитры, фона и пр. А можно попробовать создать свою пользовательскую формулу, воспользовавшись встроенным компилятором. Перед рендерингом готового изображения может потребоваться проведение автоматической коррекции цветового баланса и/или ручной коррекции яркости, контрастности и насыщенности.
4. Программа ChaosPro

ChaosPro — один из лучших бесплатных генераторов фрактальных изображений, с помощью которого нетрудно создать бесконечное множество удивительных по красоте фрактальных изображений. Программа имеет очень простой и удобный интерфейс и наряду с возможностью автоматического построения фракталов позволяет полностью управлять данным процессом за счет изменения большого количества настроек (число итераций, цветовая палитра, степень размытия, особенности проецирования, размер изображения и др.). Кроме того, создаваемые изображения могут быть многослойными (режимом смешивания слоев можно управлять) и к ним можно применить целую серию фильтров. Все накладываемые на строящиеся фракталы изменения тут же отражаются в окне просмотра. Созданные фракталы могут быть сохранены в собственном формате программы, либо в одном из основных фрактальных типов благодаря наличию встроенного компилятора. Или экспортированы в растровые изображения или 3D-объекты (если предварительно было получено трехмерное представление фрактала).
В списке возможностей программы:

точная цветовая настройка, обеспечивающая плавные градиентные переходы цветов друг в друга;

одновременное построение нескольких фракталов в разных окнах;

возможность создания анимации на основе фрактальных изображений с определением ключевых анимационных фаз, которые могут отличаться по любому изменяемому параметру: углам поворота и вращения, цветовым параметрам и пр.;

создание трехмерных представлений фракталов на основе обычных двумерных изображений;

поддержка многих стандартных форматов фрактальных изображений, изображения в которых могут быть импортированы и отредактированы в среде ChaosPro.

5. Программа Apophysis

Apophysis — интересный инструмент для генерации фракталов на основе базовых фрактальных формул. Созданные по готовым формулам фракталы можно редактировать и неузнаваемо изменять, регулируя разнообразные параметры. Так, например, в редакторе их можно трансформировать, либо изменив лежащие в основе фракталов треугольники, либо применив понравившийся метод преобразования: волнообразное искажение, перспективу, размытие по Гауссу и др. Затем стоит поэкспериментировать с цветами, выбрав один из базовых вариантов градиентной заливки. Список встроенных заливок достаточно внушителен, и при необходимости можно автоматически подобрать наиболее подходящую заливку к имеющемуся растровому изображению, что актуально, например, при создании фрактального фона в том же стиле, что и иные изображения некоего проекта. При необходимости несложно подрегулировать гамму и яркость, изменить фон, масштабировать фрактальный объект и уточнить его расположение на фоне. Можно также подвергнуть результат разнообразным мутациям в нужном стиле. По окончании следует задать размеры конечного фрактального изображения и записать его визуализированный вариант в виде графического файла (jpg, bmp, png).

6. Программа Mystica

Данный вид графики незаменим при создании таких сложных повторяющихся объектов, состоящих из самоподобных частей, как облака, горы, вода и т.д. Фактически, благодаря фракталу, найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Позволим заметить, что кроме графики, так же есть и живопись, и музыка. Все они построены на технологии фрактала.

Бесспорными достоинствами фрактала являются:

− Малый размер исполняемого файла при большом изображении.

− Бесконечная масштабируемость и увеличение сложности картинки.

− Незаменимость в построении сложных фигур, состоящих из однотипных элементов (облака, вода и т.д.).

− Относительная легкость в создании сложных композиций.

− Все вычисления делаются компьютером, чем сложнее изображение, тем больше загруженность ЦП и ОЗУ.

− Плохое распространение и поддержка различными системами.

− Небольшой спектр создания объектов изображений.

− Ограниченность материнских математических фигур.

В общем то, как всегда. У всего есть достоинства и недостатки. Графика тем более грешит и тем, и тем.

1. Сценарий перехода в хаос (Эта часть работы выполняется в Excel).

Логистическое уравнение имеет следующий вид:

Это уравнение представляет собой одномерную нелинейную систему с обратной связью. Такое уравнение может быть исследовано в электронной таблице Excel, для чего необходимо выполнить следующие шаги:

1. В ячейку А1 поместить начальное значение постоянной А между 0 и 4. Начать со значения А = 2.

2. В ячейку В1 поместить начальное значение х = 0,1.

3. В ячейке В2 поместить формулу: =А1*В1*(1 – В1).

4. Скопировать ячейку В2 вниз, по крайней мере, на 100 ячеек. Пример выполнения показан ниже (только на 20 точек).

5. Построить график по данным колонки В. Пример на рис.1.

6. Положить значение А = 3. Повторить пп.2 -5.

7. Положить значение А = 3,48. Повторить пп.2 -5.

8. Положить значение А = 3,6. Повторить пп.2 -5.

9. Построить бифуркационную диаграмму (по оси абсцисс -значения А; по шкале ординат — значения х).

2. Отображение Хенона описывается следующей системой уравнений:

Построить аттрактор Хенона следующим образом:

1.В ячейки А1 и В1 поместить начальные величины х и у, выбранные в диапазоне от 0 до 1.

2. В ячейку А2 поместить выражение: = 1 + В1 – 1,4 * А1 2 .

3. В ячейку В2 поместить выражение: = 0,3*А1.

4. Скопировать А1 и В2 вниз на 100 строк или более (чем больше, тем лучше).

5. Построить диаграмму (аттрактор Хенона), используя значения столбца А как абсциссу, а значения столбца В — как ординату.

3. Расчет показателя Херста с помощью программы Fractan

1. Открыть файл «Ценные бумаги Марков». Этот файл содержит данные по ценам акций различных российских предприятий. Выбрать какие-либо акции (на протяжении примерно 1400 торговых дней, цену открытия или другую цену), скопировать этот временной ряд.

2. Открыть блокнот и вставить в него полученный временной ряд.

3. Заменить в этих данных запятую (,) на точку (.).

4. Сохранить ряд с расширением .dat.

5. Открыть программу Fractan, вставить в него анализируемый ряд, рассчитать показатель Херста . Оценить значение показателя.

6. В этом же пакете произвести расчет показателя Херста для различных временных рядов, имеющихся в пакете.

4. Построение странного аттрактора Лоренца

1. Открыть Matlab.

2. Запустить Simulink, выполнив в командной строке команду simulink.

3. Выполнив File / Open / toolbox / simulink/ simdemos /lorenzs.mdl приходим к окну запуска системы Лоренца (рис.2).

Началось всё с урока информатики, когда мы выполняли задание в Excel. Результатом работы должен был быть график в виде символа бесконечности. Я закончил немного раньше и поиграл с параметрами, а график интересно себя вёл. А потом вернулся домой и сделал вот это:

Это большая таблица в Excel со сложными функциями, которые состоят из периодических. В качестве аргументов они используют друг друга, перемножаются, делятся, косинусы берутся от косинусов и синусов.

Всё сложно, формулы рандомные, делал так, как душа хотела.

И есть два параметра a и b (в верхнем левом углу), которые тоже зашиты в эти формулы и серьёзно влияют на вид графика.

Посмотрим, например, на первый график серого цвета. При a=b=1 он выглядит так:

Как он строился:

х меняется от 0 до 2580 град. с шагом 1. Далее x переводится в радианы. Для упрощения восприятия формул считаем, что х там уже в радианах.

Строим зависимость z(y)

Остальные графики — аналогично. Намешать всего в кучу с надеждой, что получится что-то красивое

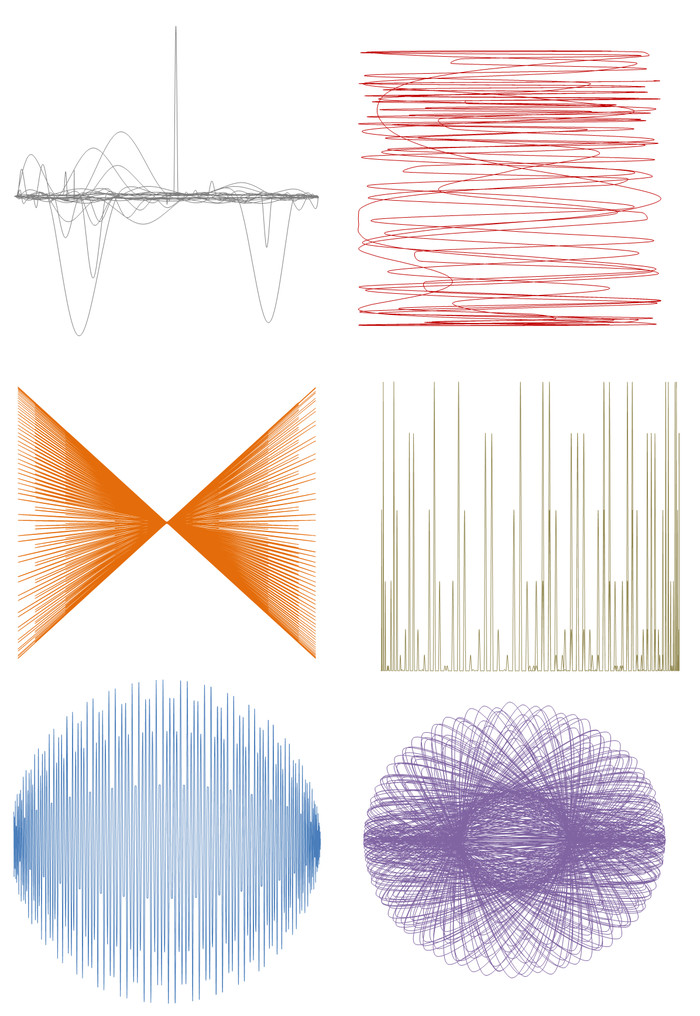
А теперь наиболее красивые картинки. Каждый график рисуется своим цветом. Если на разных картинках будут две абсолютно разные загогулины, но одинакового цвета, то это один и тот же график, только с разными параметрами a и b

Вообще при целых a (и особенно кратных 3, 6, 12. ) достаточно часто получаются особенно чёткие графики.

Продолжать можно бесконечно.

Кому интересно, вот файл:

На этом всё! Будут вопросы — пишите, постараюсь ответить.

Лига математиков

413 постов 2K подписчиков

Поставь себе матлаб для этого и отстань от экселя.

Ниче не понял но получилось интересно

О, моё почтение, дружище!

(я репетитор по информатике, мне такой пост — бальзам на душу)

4. Wolphram alpha

6. python + matplotlib

9. Excel/Google table + сеть — морской бой по сети.

Когда ещё не было этих ваших экселей, такое на осциллографе делали, только там всё «вживую» можно было менять

Ахтунг! Лиссажу на Пикабу!

А если принять a и b равным числу Пи, получится портрет Леонарда Эйлера?

Наконец-то годный пост о том, чем заняться в свободное время!
ТС, плюсую!
Вы большой молодец, спасибо за содержательный пост, пояснения и ссылки.

Я когда поступил на первый курс программистской специальности, тоже любил картиночки генерировать (и сейчас люблю)

Помню на Делфи сделал треугольник Серпинского. Фрактальная геометрия, мать её

круто, но не удивительно, учитывая то, что знающие люди могут в САПР и моделирование через эксель.

автору можно перенести функционал движка UE4 на эксель в один файл, после чего к нему сразу прилетит вертолет с нобелевской премией и каким-нибудь йен-сун-хуанем, который предложит контракт на должность CEO в какой-нибудь NVIDIA.

З.Ы. я в универе на математическом моделировании подобное писал формулами, в AnyLogic. автор может посмотреть и изучить ПО, если ему интересно.

Я так делал функцию рандом() в еще 7-й одинэске году в 2005)

В институте на паскале делали анимированные графики.

Продолжай эксперименты, может и такую картинку получишь

Ну всё, теперь читай матан, про теорию хаоса и аттракторы

Теперь осваивайте фракталы, там тоже красиво может получаться

Там в одной формуле сидит теория кротовой норы. А он её визуализировал. Что до него никто в мире не делал. Вот так, мы с лёгкостью проходим мимо открытия межпространственного перемещения, и идём копаться в песочнице .

Был когда-то очень популярный mp3-плеер WinAMP. И были к нему сторонние плагины визуализации. Один из них (название не помню) был — рай для математика-гика: в настройках задавалась форму и пачка дополнительных параметров цикличности и всего такого. Параметры a, b, c, x, y и т.д. брались из звуковой дорожки по разным частотам. Вобщем вариативности хватало. Было несколько десятков уже готовых моделей, которые переключались при проигрывании трека.

5 секунд гугления: Advanced Visualization Studio. Наверное, это он.

У меня Excel отжирал много ресурсів, а вот в MathCad или mathlab как то по лучше. Фигуры Лиссажу прикольные)
аж всплакнул. Ех молодость

на третьей картинке логотип Хабра )))

Есть вопрос, офтоп но по Excel: Пользуюсь старым Excel 2007, работа с прайс-листом и его рассылка оптовикам. Но сейчас появилась необходимость вставить информацию с ценами закупки, чтоб всегда было «под рукой». Есть какие-нибудь способы «закрыть» доступ к отдельному столбцу или в крайнем случае к отдельному листу? В гугле есть какие-то инструкции чтоб установить пароль, но я не увидел результат. Гуру экселя, посоветуйте как быть с такой задачей?

Странно, что самореферентную формулу Таппера не вспомнили)

некоторые можно даж где-то использовать для иллюстраций и графики.

Рисовать в экселе?! А че так можно было?

У меня мозг нахой щас перегорел пока понимал как делается ))))

Ни хрена не понятно, но красиво-о-о!)))

Спасибо! Получила истинное удовольствие от вашего поста!

А я такие рисоваль

Похожая штука, но в динамике, очень красиво

Не знал что на экселе можно слелать такое. А по какому учебнику занимаетесь?

Поискать зависимости между значениями a, b и получившимися графиками, нподобии того, что при a кратном 3 получается что то симпатичное, то можно писать работу и учавствовать в конференции какой-нибудь. Плюс в портфолио для поступления в универ 👍

Нобелевку этому господину

Очень здорово!у меня вопрос,возможно глупый,можно ли каким либо способом перевести екселевские графики в вектор?

Графики уж очень похожи как будто призывают дьявола! Аккуратно там.

Вот это я понимаю, современное искусство

Спасибо, скачала! ) Читала и думала — надо такое же построить )

Надеюсь, наши палаты в дурдоме будут соседними)

У меня бабушка так хуярит без exel’я.

Такие узоры порой плетет,что думаешь:

«Или проверить ее на наличие укуса паука-мутанта,либо на наличие в моче каннабиноидов».

Красота! Очень заинтересовало) хотелось бы что-то типа урока по этому поводу) а то получается, что основной рецепт — это «Намешать всего в кучу с надеждой, что получится что-то красивое».

Сама очень уважаю Exel. За время учебы в универе только в нем и оформляла лабы.

Такими темпами изучай шейдеры и цены тебе не будет

А можно как-то озвучить такие графики? Я имею в виду, связать с нотами?

Это делается в Экселе? Я не с первого раза там формулу посчитать запущу. Не было в школе уроков таких) и по работе не был нужен, кроме заполнения там отчётов

Вроде бы прочитала пост, но к сожалению он на эльфийском.

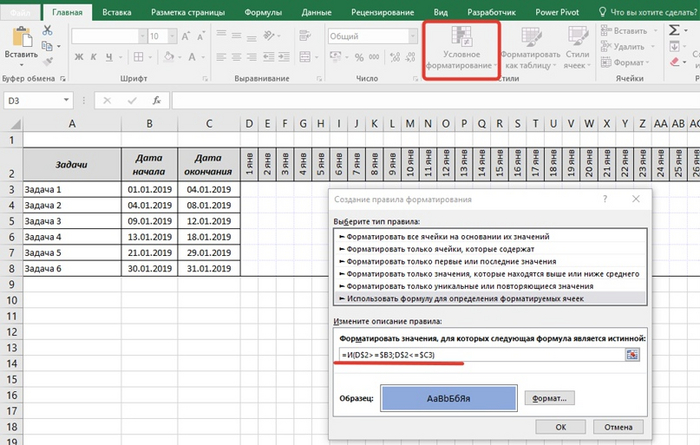
Диаграмма Ганта через условное форматирование⁠ ⁠

Допустим, у нас есть таблица с указанием сроков задач и шкала с датами в виде заголовков столбцов:

Надо закрашивать ячейки в столбцах с определенными датами, ориентируясь на даты начала и окончания задач. Для этого выполняем:

1) Выделяем весь внутренний диапазон в таблице, идем Главная — Условное форматирование — Создать правило.

2) Выбираем тип правила — Использовать формулу…

Это очень простой способ для визуализации временных периодов. Можно также сделать диаграмму Ганта именно диаграммой, но там действий по настройке диаграммы будет немного побольше.

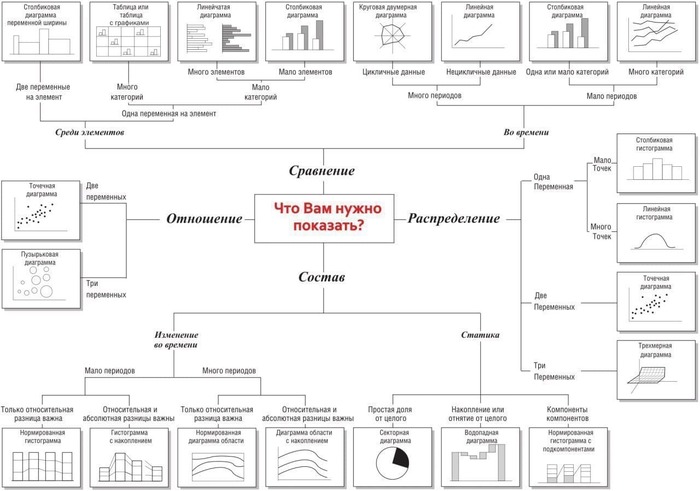
Как выбрать тип диаграммы?⁠ ⁠

Каждый, кто работает в Excel, когда-либо сталкивался с проблемой выбора подходящего типа графика, который бы визуально лучше всего отражал идеи и замысел автора.

Держите шпаргалку, которая поможет определиться, какую диаграмму выбрать для построения.

В зависимости от типа данных, диаграммы на схеме разделены на 4 основные группы:

• Сравнение (характеристики: сравнение величин, много периодов, неповторяющиеся данные);

• Распределение (характеристики: распределение величин, обычно две переменных);

• Состав (характеристики: структура величин, статика);

• Отношение (характеристики: отношение величин, обычно три переменных).

Каждая из базовых групп далее делится на множество подгрупп в зависимости от детальных параметров, что позволяет более точно выбрать тип графика.

Формула всего⁠ ⁠

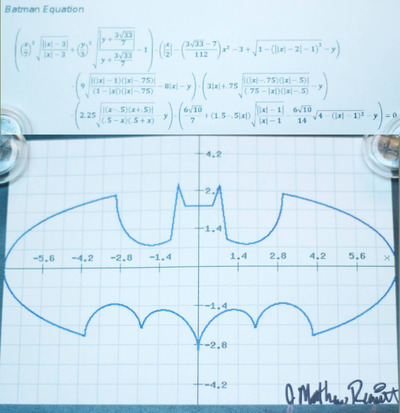
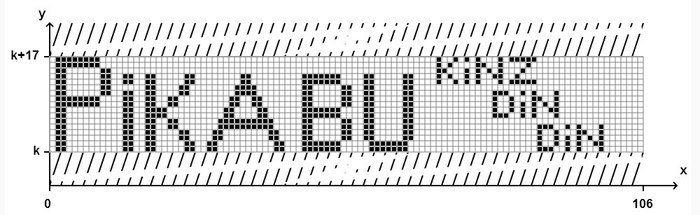
Формула Таппера- впервые формула была опубликована в 2001 году в докладе Джеффа Таппера, это самореферентная (при определённых условиях) формула, будучи отображённой на плоскости, создаёт собственное изображение.

Формула является вот таким неравенством:

Что значит «будучи отображённой на плоскости, создаёт собственное изображение»? Ну, собственно это и значит. Если отобразить это неравенство на плоскости OXY, то по оси OX оно займёт 106 пикселей (от 0 до 105), а по оси OY- 17 пикселей и будет выглядеть так:

А почему это формула всего? А дело в оси OY. Видите там слева k, k+5, k+10, k+15? Ну это значения на оси OX, просто в данном случае k= 960 939 379 918 958 884 971 672 962 127 852 754 715 004 339 660 129 306 651 505 519 271 702 802 395 266 424 689 642 842 174 350 718 121 267 153 782 770 623 355 993 237 280 874 144 307 891 325 963 941 337 723 487 857 735 749 823 926 629 715 517 173 716 995 165 232 890 538 221 612 403 238 855 866 184 013 235 585 136 048 828 693 337 902 491 454 229 288 667 081 096 184 496 091 705 183 454 067 827 731 551 705 405 381 627 380 967 602 565 625 016 981 482 083 418 783 163 849 115 590 225 610 003 652 351 370 343 874 461 848 378 737 238 198 224 849 863 465 033 159 410 054 974 700 593 138 339 226 497 249 461 751 545 728 366 702 369 745 461 014 655 997 933 798 537 483 143 786 841 806 593 422 227 898 388 722 980 000 748 404 719.

Где-то там ~~в далёкой-далёкой галактике~~ на оси OY среди бесконечного количество значений есть бесконечное количество изображений, заданных этой формулой. Т.е. там есть ВСЕ ВОЗМОЖНЫЕ изображения размером 106 на 17 пикселей.

Например, при k= 172 895 466 264 656 362 238 775 198 618 400 053 006 722 417 830 074 875 710 077 840 558 718 522 933 856 481 624 057 883 539 289 927 382 958 168 812 116 931 135 487 324 743 680 349 552 434 460 222 923 986 273 388 093 735 529 486 165 346 092 911 369 252 390 353 778 634 279 896 583 455 425 859 634 440 043 584 268 093 410 716 443 082 284 154 873 275 541 781 431 502 156 517 367 941 053 074 097 258 022 615 110 586 256 528 662 395 677 501 188 461 923 095 483 961 995 173 180 815 230 411 356 269 083 712 579 786 823 770 925 493 943 423 964 558 741 203 303 534 803 553 728 066 326 116 959 373 467 996 584 250 693 892 202 679 445 143 468 361 413 129 347 669 354 301 413 221 990 4

Изображено вот такое:

Про эту формулу есть ролик у Numberphile (у Numberphile вообще много интересного есть, рекомендую)

Я сделал код Excel VBA, который рисует и заполняет фрактальный шаблон. Я знаю, что есть еще несколько способов оптимизации кода, просто рад, что он работает прямо сейчас.

1 ответ

Public

Почему все эти переменные объявлены Public ?

Это кажется ненужным; если нужно, передавать значения между субмаринами. Публичные объявления должны быть Const в целом.

Целые

Целые числа — целые числа устарели . Согласно msdn VBA молча преобразует все целые числа в long .

Переменные имена

Ваши имена переменных не очень мне говорят о них. Я вижу, что есть куча комментариев, объясняющих их — гораздо проще назвать их описательно и полностью избежать комментариев.

Итак, теперь, когда я вижу For cnt = 1 to lineLength Я знаю, что мы рисуем строки.

Опция Явная

У вас есть несколько незанятых переменных — cnt и t , например. Лучше всего всегда объявлять переменные и давать им тип . Вы можете иметь Option Explicit автоматически, перейдя в Инструменты -> Параметры в VBE и проверка параметра Требовать переменную декларацию . Таким образом, если у вас есть какие-либо переменные, которые не определены, компилятор сообщит вам об этом.

Как я уже сказал, комментарии — «код расскажите, как, комментарии говорят вам, почему «. Код должен говорить сам за себя, если ему нужен комментарий, возможно, его нужно будет уточнить. Если нет, комментарий должен описывать , почему вы делаете что-то, а не , как вы это делаете. Ниже приведено несколько причин , чтобы избежать комментариев.

Повторяющийся код

Я вижу, что вы получаете ypt , ypt2 . ypt10 . Если вы не хотите сделать для них Class , по крайней мере, поместите их в массив для облегчения доступа —

Или что-то подобное. Похоже, вы можете определенно сократить код до кода if loop или даже select case в этом сценарии. Или еще лучше, сделайте Function , который выполняет расчет и использует его для назначения значений.

Shader2

В Sub Shader2() Я вижу, что вы вызываете c2 , но я не вижу c2 в любом месте. Option Explicit поймает это, но вместо этого вы можете использовать аргументы в своем суб

Для вашего цвета:

Хорошая идея с использованием RGB вместо Color или ColorIndex . Но поскольку цвет сохраняется как целое число, вы можете использовать его как функцию вместо

Он выглядит намного чище, как это.

Spacing

Возможно, это от копирования /вставки, но вы не отступаете весь свой код. Хорошая практика заключается в том, чтобы отступать весь ваш код таким образом Labels будет выглядеть как очевидно. Даже объявления переменных.

Вызов

Вам не нужно использовать Call , он устарел. Вместо этого просто используйте Sub argument, argument или в вашем случае, просто Shader2

шаблон

Я видел этот фрагмент кода

И я подумал, что ждать там не будет.переменная? Да, есть. Это постоянный. Отлично!

Простыни

Рабочие листы имеют свойство CodeName — окно «Свойства окна» ( F4 ) и (Name) (в верхней части) может использоваться как имя листа. Таким образом, вы можете избежать Sheets(«mySheet») и вместо этого просто использовать mySheet

Код стрелки

Думаю, я вижу довольно большую «стрелку» в Shader2 . Возможно, вы захотите попробовать сгладить это .

Рефакторинг

Это прекрасная возможность использовать Select Case . Или , вызовите функцию —

Магические числа

Что-то вроде этого

Мы бы назвали магическое число , а магические числа лучше всего определялись как константы. Таким образом, если вам когда-либо понадобится его изменить, вы можете просто изменить константу и не беспокоиться о ее обнаружении в код.

Другие

Все, что было сказано, я думаю, что вы написали здесь что-то очень творческое, и я приветствую вас. Многие из этих «улучшений» — это просто стандартные способы сделать это, но вы не узнаете их, если не придете сюда для обзора. Итак, добро пожаловать в обзор кода:)

В этой статье приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов.

Фрактал – сложная геометрическая фигура, обладающая свойством самоподобия, т.е. из всей фигуры можно выделить части, подобные целой фигуре. Примеры самоподобных множеств известны с XIX века. Термин «фрактал» (от лат. fractus — раздробленный) впервые ввел в 1975 году математик исследовательского центра IBM Бенуа Мандельброт.

Фракталы можно разделить на несколько видов:

Геометрические фракталы – строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов.
Алгебраические фракталы – строятся на основе алгебраических формул.
Стохастические фракталы – получаются, если в итерационном процессе случайным образом изменять какие-либо параметры.

Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.

Некоторые примеры алгебраических и геометрических фракталов

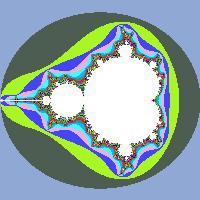
Фрактал Мандельброта

Рассмотрим последовательность комплексных чисел:

[z_ = z_k^2 + c, k = 0, 1, 2, dots, z_0 = c]

Множество точек c, для которого эта последовательность не расходится, называется множеством Мандельброта. Для построения его графической интерпретации нужно определить исходные данные:

прямоугольное окно C с разрешением (m times n) точек;
значение (r_ = 2) – минимальный радиус расходимости множества Мандельброта
максимальное число итераций (k_max)

Если точка (z_k) вышла за пределы круга радиуса (r_min) при (k lt k_max), то процесс вычисления останавливается.

Построение: для каждой точки (c_ in C (i = overline, j = overline, c_x in [-2; 1], c_y in [-2; 1,5])) запустим итерационный процесс:

[x_ = x_k^2 — y_k^2 + c_x, x_0 = c_x] [y_ = 2 x_k y_k + c_y, y_0 = c_y]

где (k = 0, 1, 2, dots, k_max) и (sqrt leqslant r_min).

Составим матрицу M , элементы которой (m_ in [1; k_max]) равны номерам итераций, на которых процесс был остановлен. Далее матрицу можно вывести на экран как растровое изображение, предварительно сопоставив каждому числу из интервала ([1, k_max]) некоторый цвет.

Если представить множество в общем виде:

то, изменяя значение N, можно получать симметричные фрактальные множества. Например, для (N = 4) и (N = 7):

Фрактал Жюлиа

Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:

[z_ = z_k^2 + c, k = 0, 1, 2, dots]

Исходные данные, этапы построения и условия остановки – те же, что и для фрактала Мандельброта, за исключением:

значение c фиксируется: (c = 0,36 + 0,36i)
начальное значение (z_0) перебирается дискретно в области (C in [-1;1] + [-1;1]i)

Julia 1

Рассматривая множество в общем виде: (z_ = z_k^N + c) и изменяя N и с, можно получать разнообразные фрактальные множества:

Julia 2
Julia 3
Julia 4

Бассейны Ньютона

Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.

Общая формула метода Ньютона имеет вид:

При выборе различных (z_0) процесс будет сходиться к различным корням (областям притяжения). Границы этих областей имеют фрактальную структуру.

Подставив (p(z)) в формулу метода, получим итерационную формулу для построения фрактала:

Итерационный процесс останавливается при:

[left| z_^3 right| leqslant r_min]

Для построения графической интерпретации также как и для фрактала Мандельброта, используется матрица, элементы которой равны номеру итерации, на которой остановился процесс.

Если записать формулу в общем виде:

[p(z) = z^N — 1] [left| z_^N — 1 right| leqslant r_min]

то можно получить изображения фракталов более сложной формы:

L-системы

В 1968 году венгерский биолог Аристид Линденмайер предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена для моделирования сложных ветвящихся структур (разнообразных растений). Эта модель получила название Lindenmayer System (Система Линденмайера или L-система).

Рекурсивная природа L-систем позволяет строить с их помощью геометрические фрактальные изображения.

L-система определяется как (G = (V, omega, P)) , где

V — алфавит – множество символов, содержащее элементы, которые могут быть замещены (переменные).
ω – строка символов из множества V, определяющая начальное состояние системы (аксиома).
P – набор правил, определяющий, как переменные могут быть замещены другими переменными и константами.

Правила применяются итеративно, начиная с аксиомы. За одну итерацию применяются одновременно все правила.

Например, L-система имеет вид:

Правила: ((A rightarrow AB) (B rightarrow BA))

После нескольких применений правил из аксиомы получаются строки:

Для построения графической интерпретации L-системы используется «черепашья графика», т.е. символам из V присваиваются команды управления некоторым простым интерпретатором («пройти вперед», «повернуться», и т. д.).

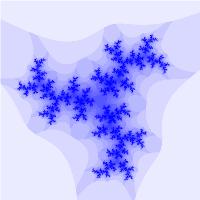
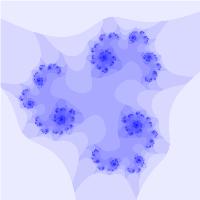
Пример некоторых фракталов, построенных с помощью L-систем — кривая дракона и растение:

Лист папоротника

Существует несколько способов построения этого фрактала.

1) Построение с помощью системы итерируемых функций (IFS)

Производится 20 итераций функции (f(x, y)). Каждое новое значение получается из предыдущего в зависимости от случайного числа, т. е. вычисляется с использованием таблицы распределения:

Вероятность	$$x’$$	$$y’$$
0,01	$$0$$	$$0,16y$$
0,85	$$0,85x + 0,04y$$	$$-0,04x + 0,85y + 1,6$$
0,07	$$0,20x — 0,26y$$	$$0,23x + 0,22y + 1,6$$
0,07	$$-0,15x + 0,28y$$	$$0,26x + 0,24y + 0,44$$

После выполнения всех итераций точка рисуется на экране.

Начальные значения x и y могут быть константами (желательно не большими, чем 1) или их можно выбирать случайным образом на отрезке ([0;1]).

Fern 1

2) Рекурсивное построение

Для построения используется процедура (псевдокод):

(R(phi) = begin cos(phi) && sin(phi) \ -sin(phi) && cos(phi) end) — матрица поворота на угол φ.

(p_0 = [x_0; y_0]) — координаты начальной точки
h – высота листа
ψ – угол отклонения листа от вертикали
side – направление изгиба ветви
δ – минимальная длина ветви ветвящегося отрезка
rec – максимальная глубина рекурсии

Рекомендуемые значения углов и коэффициентов: (phi_0 = 14,9^, phi_1 = 37,7^, phi_2 = 36,8^, phi_3 = 17,6^, k_1 = 0,0483, k_2 = 0,162, m_1 = 0,371, m_2 = 0,336, m_3 = 0,849).

Fern 2

Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1, φ2, φ3.

Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале ((-10^; 10^)), можно получить изображения:

Fern 3
Fern 4

Литература:

Программы

Здесь приведены ссылки на программы, с помощью которых были созданы иллюстрации для этой статьи.

Читайте также:

Bq 6040l magic программа для прошивки

Chrome os запустить в браузере

Программа для камеры заднего вида на андроид планшет

Как разобрать файл excel

Js как определить браузер сафари

Источник

Технология выполнения работы

2. Специальные программные средства

Лига математиков

Диаграмма Ганта через условное форматирование⁠ ⁠

Как выбрать тип диаграммы?⁠ ⁠

Формула всего⁠ ⁠

1 ответ

Public

Целые

Переменные имена

Опция Явная

Комментарии

Повторяющийся код

Shader2

Spacing

Вызов

шаблон

Простыни

Код стрелки

Рефакторинг

Магические числа

Другие

Некоторые примеры алгебраических и геометрических фракталов

Фрактал Мандельброта

Фрактал Жюлиа

Бассейны Ньютона

L-системы

Лист папоротника

Литература:

Программы