Содержание
Введение.
Глава 1.Исследование гармонических колебаний с помощью фигур Лиссажу
1.1 Гармонические колебания.
1.2 Фигуры Лиссажу.
Глава 2.Моделирование фигур Лиссажу в среде MS Excel
2.1 Анализ среды MS Excel
2.2 Построение фигур Лиссажу средствами MS Excel
2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний
Заключение
Список использованной литературы
Введение
Тема данной исследовательской работы: Моделирование фигур Лиссажу.
Настоящее исследование посвящено актуальной проблеме изучения фигур Лиссажу в курсах физики и математики.
Фигуры Лиссажу используют для сравнения гармонических колебаний, которые изучаются в курсе физики. Но в реальности провести опыты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно. В ходе математического и компьютерного моделирования фигур Лиссажу можно исследовать соотношение между частотами и фазами гармонических колебаний.
Цель работы: показать возможности применения математических функций среды MS Excel для моделирования некоторых физических явлений.
Достижение поставленной цели предполагает решение следующих задач:
1.Проанализировать литературу по теме исследования.
2.Раскрыть понятие фигуры Лиссажу.
3.Рассмотреть способы построения графиков в среде MS Excel.
4.Разработать модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
Объектом исследования являются Фигуры Лиссажу. Предмет исследования: наглядное построение фигур Лиссажу. Методы исследования: для решения поставленных задач в работе используется теоретические и эмпирические методы.
Глава 1. Исследование гармонических колебаний с помощью фигур Лиссажу
1.1. Гармонические колебания
Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Гармоническое колебание, как математическая модель участвует в множестве физических процессов, которые можно использовать для передачи информации. Многие системы совершают движение по гармоническому закону вполне естественным образом. В пример можно привести обычное раскачивание на качелях, ритмичные движения ног продолжали незатухающие колебания механического маятника, которым и являются качели.
Способы представления гармонических колебаний:[1;82-84]
- Аналитическая форма (формула):
2. Графическое представление (построение): Этот способ наглядно может показать вид и свойства данного явления.
- Гармоническое колебание изменяется во времени периодически. Период каждого совершённого колебания равен .
- Амплитуда (наибольшее значение) равна . Скорость изменения колебания во времени определяется круговой частотой , которая численно равна скорости изменения аргумента косинуса и измеряется в рад/с. — начальная фаза колебательного процесса. При совершении единичного гармонического колебания фаза особой роли не играет, а когда совершается несколько подобных колебаний, то даёт понять о местонахождении колебаний на оси времени друг относительно друга. Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная.
3. Векторное представление (делает очень наглядным фазовые и амплитудные соотношения между ними):
Эта формула выводится, если известна начальная фаза и амплитуда, т.е. значения при
Возьмём за гипотенузу прямоугольного треугольника, тогда будет в качестве его катета. Можно сказать, что сейчас гармоническому колебанию дали геометрическое представление. Такое представление гармонического колебания называют векторной диаграммой.
1.2 Фигуры Лиссажу
Фигуры Лиссажу — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Эти фигуры, впервые изученные французским учёным Жюлем Антуаном Лиссажу.
Устройство для построения фигур Лиссажу — осциллограф. Изобретение относится к радиоизмерительной технике и может быть использовано для исследования параметров электрических сигналов.
Известные способы регистрации фигур Лиссажу с помощью двух координатных регистрирующих устройств позволяют производить измерения в ограниченном диапазоне частот и при отсутствии помех. Целью изобретения является создание способа регистрации фигур Лиссажу в широком диапазоне частот и при наличии помех.
Эти фигуры используют для осциллографического метода сравнения частот.
Осциллографический метод сравнениячастот:[2;97-98]
В качестве устройства сравнения частот используется осциллограф с отключённой разверткой (Развертка— это линия, которую чертит луч на экране при отсутствии исследуемого сигнала в результате действия только одного развертывающего напряжения.), таким образом информацию получают с экрана осциллографа по изображению интерференционных фигур (фигур Лиссажу).
Измеряемый сигнал подают на вход КВО (канал вертикального отклонения), а сигнал образцового генератора известной частоты — на вход КГО (канал горизонтального отклонения). Плавным изменением частоты добиваются устойчивого изображения на экране осциллографа фигур Лиссажу. В этом методе отношение частот сравниваемых сигналов определяют путём подсчета числа пересечений фигуры Лиссажу с вертикальной осью и горизонтальной осью на экране осциллографа.
Из этой формулы можно вывести измеряемую частоту,
Закон гармонического осциллятора: [3;19]
Если закон дифференцировать по времени, то найдём закон изменения скорости при гармонических колебаниях:
Так же если повторить предыдущее действие, то найдём изменения ускорения при гармонических колебаниях:
После двух дифференцирований мы получим исходное выражение:
Перенеся слагаемые в одну сторону, то получим уравнение гармонического осциллографа:
Это уравнение встречается во всех разделах физики без исключения. Это уравнение описывает эволюцию малых отклонений динамических переменных от их устойчивых значений. Но для математика это обыкновенное уравнение 2-ого порядка с постоянными коэффициентами, в это уравнение входит функция со второй производной. Решением данного уравнения являются гармонические колебания.
Глава 2. Моделирование фигур Лиссажу в среде MS Excel
1.2. Анализ среды MS Excel
Microsoft Office Excel – это программа, предназначенная для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию.
Excel – это универсальная программа, которая позволяет работать с различными форматами данных. В Excel можно вести домашний бюджет, производить как простые, так и очень сложные расчеты, хранить данные, организовывать различные дневники, составлять отчеты, строить графики, диаграммы и многое-многое другое.
Функции MS Excel:
1.Работа с числовыми данными. Например, составление самых различных бюджетов, начиная от домашнего, как самого простого, и, заканчивая бюджетом крупной организации.
2.Работа с текстом. Разнообразный набор инструментов для работы с текстовыми данными дает возможность представить даже самые сложные текстовые отчеты.
3.Создание графиков и диаграмм. Большое количество инструментов позволяет создавать самые различные варианты диаграмм, что дает возможность представить ваши данные наиболее ярко и выразительно.
4.Организация списков и баз данных. В Microsoft Office Excel изначально была заложена структура строк и столбцов, поэтому организовать работу со списками или создать базу данных является для Excel элементарной задачей..
2.2. Построение фигур Лиссажу средствами MS Excel
В рамках данного исследования продемонстрируем построение фигур Лиссажу в табличном процессоре MS Excel, для этого понадобятся формула:
Уравнение гармонического колебания физической величины X с циклической частотой W и амплитудой А можно записать в виде формулы:,
где F-начальная фаза. Вместо W может быть использовано 2Пи/T ,где Т-период колебаний.
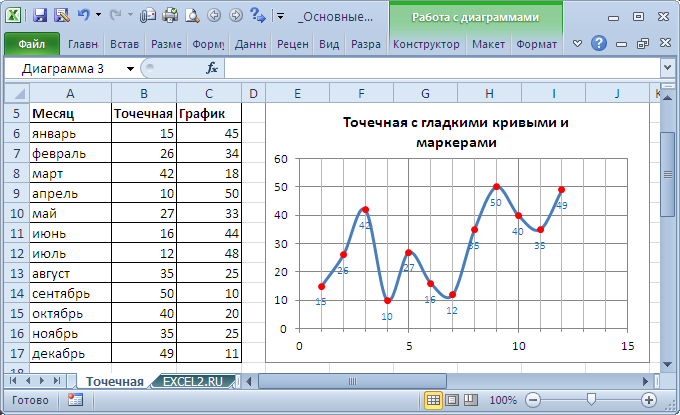
Для построения фигур Лиссажу средствами MS Excel:
1.Необходимо подготовить следующую таблицу:
- Амплитуда колебаний — это наибольшее отклонение колеблющегося тела от положения равновесия.
- Циклическая частота – скалярная величина, мера частоты вращательного или колебательного движения.
- Начальная фаза – место, откуда начинается колебательный процесс в определённый момент времени (начало отсчёта).
- Время колебаний – это время колебания системы.
- Колебание Х – это колебание системы по оси OX.
- Колебание Y – это колебание системы по оси OY.
2.Столбец F начиная с ячейки F5 и далее заполнить значениями от 0,01 до 10 с шагом 0,01
(используя функцию автозаполнения)
3.В столбец G начиная с ячейки G5 и далее ввести формулу для колебания X:
4.В столбец H начиная с ячейки H5 и далее ввести формулу для колебания Y:
5.Должна получиться вот такая таблица с данными:
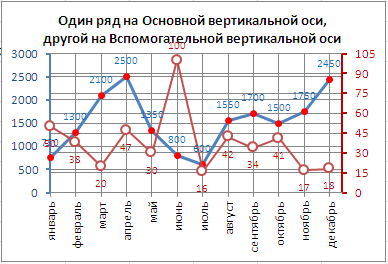
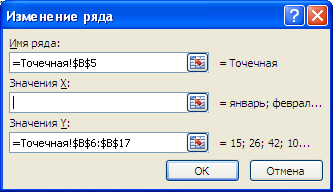
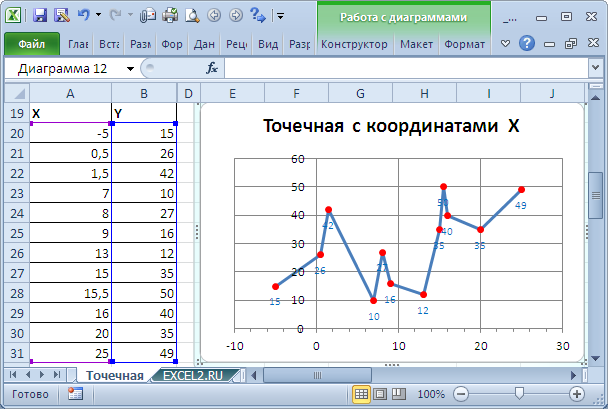
6.Теперь необходимо построить диаграмму по этим данным. Для этого нужно выделить два столбца со значениями колебаний X и Y. После этого нажимаем на пиктограмму мастера построения диаграмм.
7.Тип диаграммы выбираем «СТАНДАРТНЫЕ» — «ТОЧЕЧНАЯ» — «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров» Нажимаем «Далее». Переходим на вкладку «РЯД» и называем «Ряд 1» — Колебание X ,а «Ряд 2» — Колебание Y. Нажимаем «Далее» теперь надо подписать название диаграммы «Фигуры Лиссажу». Нажимаем «Далее» и выбираем расположение диаграммы в текущем листе.
8.Должно получиться следующее:
2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний
Анализ литературы показал, что фигуры Лиссажу применяются: в радиотехнике для сравнения частот, в осциллографе. Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причём период цикла вращения является величиной, обратной разности частот, например, при периоде оборота равен 2с. разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счёт кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Заключение
Целью данной работы являлось рассказать и наглядно показать моделирование фигур Лиссажу.
В рамках исследования были решены следующие задачи:
1.Проанализированна литература по теме «Моделирование фигур Лиссажу»
2.Было раскрыты понятия: фигуры Лиссажу, гармоническое колебание, векторная диаграмма, развертка, Microsoft Office Excel, амплитуда колебаний, циклическая частота,
3.Рассмотрели способы построения графиков в среде MS Excel.
4.Разработали модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
В рамках исследования можно считать цель достигнутой.
Список использованной литературы
- Мусин, Ю. Р. Физика: колебания, оптика, квантовая физика : учебное пособие для среднего профессионального образования / Ю. Р. Мусин. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2020. — 329 с.
- Аминев, А. В. Основы радиоэлектроники: измерения в телекоммуникационных системах : учебное пособие для среднего профессионального образования / А. В. Аминев, А. В. Блохин ; под общей редакцией А. В. Блохина. — Москва : Издательство Юрайт, 2019. — 223 с. URL: https://urait.ru/bcode/442543 .(97-98 стр.)
- Штыков, В. В. Введение в радиоэлектронику : учебник и практикум для среднего профессионального образования / В. В. Штыков. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2019. — 228 с. URL: https://urait.ru/bcode/437093 .(82-84 стр.)URL: https://urait.ru/bcode/449189 .( 19 стр.)
Использование графических возможностей Excel для решения математических задач
Возможности ЭТ Microsoft Excel весьма многогранны. Всем известно, что Excel является мощным вычислительным инструментом, позволяющим производить простые и сложные расчеты в различных областях человеческой деятельности: математике, физике, инженерных науках, экономике, технологии. Но помимо осуществления расчетов возможно применение ЭТ Excel и в других областях. Данная статья посвящена использованию Excel для построения графиков элементарных и сложных функций, изучение графических способов решения уравнений и систем уравнений, а также построения трехмерных поверхностей.
Построение графиков элементарных функций в Excel
Для построения графика функции в Excel прежде всего надо построить таблицу, в одну колонку которой занести значение аргумента функции, а в другую — значение функции при заданном значении аргумента.
Для этого в рабочем поле Excel в ячейках 1-й строки напечатаем наименование работы, во 2-ой строке – заголовок «Расчетная таблица», в 3-й – наименование колонок (столбцов) расчетной таблицы.
Начиная с ячейки А5 произведем формирование значение таблицы. Для этого необходимо в ячейку А5 ввести первое значение аргумента вычисляемой функции из заданного диапазона значений аргументов. В ячейку А6 введем второе значение аргумента, отличающееся от первого на заданный шаг изменения аргумента. Далее пометим эти ячейки и, ухватив указателем мыши квадратную точку в правом нижнем углу помеченной области ячеек, движением вниз по столбцу с нажатой левой кнопкой мыши рассчитаем значения аргумента с шагом, который вычислил Excel по указанным первым двум ячейкам (рис.1).
Пометив ячейку В5, вычисляем первое значении функции, используя Мастер формул, и если функция проста, то записываем формулу вручную. Запись формулы в ячейку вручную следует начать со знака «=» и закончить нажатием клавиши Enter. Затем, используя квадратную точку помеченной ячейки, копируем формулу в остальные ячейки.
Для построения графика заданной функции по построенной таким образом таблице необходимо воспользоваться Мастером диаграмм. Следуя указаниям Мастера, выбираем форму диаграммы Точечная.
Построение графика функции y=ax2+bx+c.
Построим график указанной функции при а-2, b=5, c=-10. Для построения графика функции будем изменять аргумент в диапазоне -5≤x≤2,5 с шагом 0,5.
Выполним последовательно все действия, описанные выше, сравнивая получаемый результат с рис.1.
Построение графика функции y=2x^2+5x-10
На этапе отладки решения задач (который всегда имеет место) возникает необходимость коррекции параметров и исходных данных графика. Для коррекции следует:
Щелчком левой кнопки мыши пометить поле графика и правой кнопки мыши вызвать всплывающее меню;
Используя команды меню, произвести необходимые коррекции графика;
Для коррекции значений в ячейках расчетной таблицы пометить мышью ячейку, удалить из нее значение либо клавишей Delete, либо использовать всплывающее меню;
Для того, чтобы вызвать всплывающее меню, необходимо пометить нужную ячейку и внутри ячейки щелкнуть правой кнопкой мыши;
В меню выбрать необходимую команду для удаления информации в ячейке;
Затем записать новую информацию, закончив запись нажатием клавиши Enter.
Построение графиков функций y=sina и y=cosa в одной системе координат.
Рассмотрим пример построения графиков функций y=sina, y=cosa в одной системе координат.
Сначала построим график одной из функций, например y=cosa, выполнив все указанные выше действия по построению графика. Следует отметить, что аргументом тригонометрических функций является угол, выраженных в радианах. Поэтому в расчетной таблице появилась колонка «Арг.Рад.», в которой угол пересчитан в радианы.
|
Построение графиков функции y=cosa, y=sina в одной координатной системе |
|
Расчетная таблица |
|
Арг.Град. |
Арг.Рад |
y=cosa |
y=sina |
|
-180 |
-3,14159 |
-1 |
-2,65359E-06 |
|
-160 |
-2,79253 |
-0,93969 |
-0,342017139 |
|
-140 |
-2,44347 |
-0,76605 |
-0,642780679 |
|
-100 |
-1,74535 |
-0,17367 |
-0,98480415 |
|
-80 |
-1,39629 |
0,173622 |
-0,984812371 |
|
-60 |
-1,04723 |
0,499972 |
-0,866041628 |
|
-40 |
-0,69817 |
0,76602 |
-0,642816948 |
|
-20 |
-0,34911 |
0,939678 |
-0,34206163 |
|
0 |
-5E-05 |
1 |
-5E-05 |
|
20 |
0,34901 |
0,939712 |
0,341967661 |
|
40 |
0,69807 |
0,766084 |
0,642740343 |
|
60 |
1,04713 |
0,500058 |
0,865991626 |
|
80 |
1,39619 |
0,17372 |
0,984795004 |
|
100 |
1,74525 |
-0,17357 |
0,984821512 |
|
120 |
2,09431 |
-0,49993 |
0,866067952 |
|
140 |
2,44337 |
-0,76599 |
0,642857281 |
|
160 |
2,79243 |
-0,93966 |
0,342111107 |
|
180 |
3,14149 |
-1 |
0,000102654 |
Для того, чтобы поместить еще один график(или несколько) в ту же координатную систему, следует:
Пометить левой кнопкой мыши поле графика и правой кнопкой мыши вызвать всплывающее меню;
Выбрать в меню команду Исходные данные;
Выбрать в окне Исходные данные команду Ряд, затем Добавить и в строках окна записать имя ряда;
Скопировать из таблицы значения ряда, пользуясь кнопкой в правом конце строк значений, предварительно удалив записи в них, если таковые имеются.
Построение графиков сложных функций в полярных координатах.
Определение полярной системы координат.
До сих пор изучалась и использовалась система координат плоскости, образованной двумя пересекающимися прямыми. Попробуем определить положение некоторой точки В в плоскости, образованной прямой и самой точкой В.
Отметим на некоторой физической плоскости (например на листе бумаги) точку В. Из некоторой точки О, которую будем называть полюсом, проведем луч в направлении слева направо и будем называть его полярной осью. Соединим полюс с точкой В и будем называть этот отрезок полярным радиусом. Отметим угол между полярной осью и полярным радиусом. Тогда местоположение точки В на плоскости определится полярным радиусом r и полярным углом а. За положительное направление полярного а будем считать направление против часовой стрелки, а полярный радиус будем считать всегда неотрицательным. Это записывается в виде В(r,a) (рис.3.).
.
Всякой точке этой системы будет соответствовать единственная пара полярных координат и наоборот – по заданной паре полярных координат определяется местоположение точки на плоскости.
Переход от полярных координат к декартовым и обратно.
Если полярную и декартову прямоугольную системы совместить так, чтобы начало их координат совпадали, полярная ось совпадала с положительным направлением оси абсцисс прямоугольной системы, то независимо от расположения точки В на плоскости получим формулы перехода от полярных координат r, a к декартовым х, у:
(1)
и от декартовых к полярным:
(2)
Уравнения (1) называются параметрическими.
Обратимся к рис.3.Задавая угол α, будем получать точки на расстоянии r от полюса, которые при достаточно большом их количестве образуют окружность. Посмотрим внимательно на рис.2. В расчетной таблице графиков функций есть данные для построения окружности в полярных координатах.
При равных значениях полярного радиуса r имеем окружность, при различных – эллипс. Если ввести коэффициенты n и m в аргумент параметрических уравнений окружности различными их значениями, то получим фигуру Лиссажу, одна из которых показана на рис.6.
|
Арг. Град |
арг. Рад. |
х=r*cosa |
y=r*sina |
|
-160 |
-2,79253 |
-0,93969 |
-0,34201996 |
|
-140 |
-2,44346 |
-0,76604 |
-0,64278757 |
|
-120 |
-2,0944 |
-0,5 |
-0,86602545 |
|
-100 |
-1,74533 |
-0,17365 |
-0,9848078 |
|
-80 |
-1,39626 |
0,173649 |
-0,98480768 |
|
-40 |
-0,69813 |
0,766045 |
-0,64278707 |
|
-20 |
-0,34907 |
0,939693 |
-0,34201934 |
|
20 |
0,349067 |
0,939692 |
0,34202122 |
|
40 |
0,698133 |
0,766044 |
0,6427886 |
|
60 |
1,047199 |
0,499999 |
0,86602613 |
|
80 |
1,396265 |
0,173647 |
0,98480803 |
|
100 |
1,745331 |
-0,17365 |
0,98480745 |
|
120 |
2,094397 |
-0,5 |
0,86602445 |
|
140 |
2,443463 |
-0,76605 |
0,64278604 |
|
160 |
2,792529 |
-0,93969 |
0,34201808 |
Построение графиков сложных тригонометрических функций, заданных полярными или параметрическими уравнениями.
Введем в параметрические уравнения окружности коэффициент n и m при аргументе а, произведем соответствующие расчеты в расчетной таблице и построим график (рис.6).
При внимательном рассмотрении кривой графика можно отметить участок, состоящий из прямых линий. Это произошло потому, что шаг задания аргумента функции слишком большой (20 градусов). При задании меньшого шага, например 1 градус, этот недостаток устраняется.
|
Арг.град. |
арг.рад. |
х=r*cos3a |
y=r*sin2a |
|
-180 |
-3,14159 |
-1 |
-6,9282E-07 |
|
-160 |
-2,79253 |
-0,5 |
0,642787308 |
|
-140 |
-2,44346 |
0,5 |
0,984807737 |
|
-100 |
-1,74533 |
0,499999 |
0,34201967 |
|
-80 |
-1,39626 |
-0,5 |
-0,3420209 |
|
-40 |
-0,69813 |
-0,5 |
-0,98480751 |
|
-20 |
-0,34907 |
0,500002 |
-0,64278631 |
|
20 |
0,349067 |
0,499997 |
0,642789371 |
|
40 |
0,698133 |
-0,5 |
0,984808204 |
|
80 |
1,396265 |
-0,5 |
0,342017139 |
|
100 |
1,745331 |
0,500005 |
-0,34202343 |
|
140 |
2,443463 |
0,499995 |
-0,98480704 |
|
160 |
2,792529 |
-0,50001 |
-0,64278424 |
Зададим полярный радиус в виде функции того же аргумента, что и параметрических уравнениях, и сформулируем задачу.
Задача. Построить график функции, заданной в полярных координатах, с полярным радиусом r=sinka при k=2.
Все технологии построения графика аналогично рассмотренной в предыдущих примерах. Для формирования расчетной таблицы данной задачи вводим столбец для расчета значений полярного радиуса (рис.7).
Заменим коэффициент k при аргументе а полярного радиуса на 3 и пересчитаем данные в расчетной таблице. Построим график по расчетной таблице (рис.8).
Для того, чтобы кривая была более достоверна, при построении этого графика был уменьшен шаг изменения аргумента.
Сравните расчетные таблицы рис. 7 и 8.
Естественно, что уменьшением шага аргумента при расчете полярного радиуса увеличивается точность построения кривой. Этот эффект появляется и необходим, когда значения коэффициента k достаточно велики (например при k=10).
Внимательно присмотревшись к графикам кривых на рисунке 7 и 8, можно заметить, что эти кривые вписаны в окружность (так как в основе лежат параметрические уравнения расчета значений координат х и у окружности). Введем в параметрические уравнения коэффициенты n и m, как это было сделано при построении фигур Лиссажу, и построим несколько кривых
|
K — лепестковая роза, K=2 |
|
Расчетная таблица |
|
Арг.град. |
арг.рад. |
х=r*cosa |
y=r*sina |
r=sin2a |
|
-180 |
-3,14159 |
6,93E-07 |
-2,4E-13 |
-6,9282E-07 |
|
-160 |
-2,79253 |
-0,60402 |
0,642787308 |
|
-140 |
-2,44346 |
-0,75441 |
-0,63302 |
0,984807737 |
|
-120 |
-2,0944 |
-0,43301 |
-0,75 |
0,866025301 |
|
-100 |
-1,74533 |
-0,05939 |
-0,33682 |
0,34201967 |
|
-80 |
-1,39626 |
-0,05939 |
0,336825 |
-0,3420209 |
|
-60 |
-1,0472 |
-0,43301 |
0,75 |
-0,86602595 |
|
-40 |
-0,69813 |
-0,75441 |
0,633022 |
-0,98480751 |
|
-20 |
-0,34907 |
-0,60402 |
0,219845 |
-0,64278631 |
|
0 |
1,00E-06 |
2E-06 |
2E-12 |
2E-06 |
|
20 |
0,349067 |
0,604024 |
0,219848 |
0,642789371 |
|
40 |
0,698133 |
0,754406 |
0,633023 |
0,984808204 |
|
60 |
1,047199 |
0,433011 |
0,749999 |
0,866023955 |
|
80 |
1,396265 |
0,05939 |
0,336821 |
0,342017139 |
|
100 |
1,745331 |
0,059392 |
-0,33683 |
-0,34202343 |
|
120 |
2,094397 |
0,433015 |
-0,75 |
-0,8660273 |
|
140 |
2,443463 |
0,754407 |
-0,63302 |
-0,98480704 |
|
160 |
2,792529 |
0,60402 |
-0,21984 |
-0,64278424 |
|
180 |
3,141595 |
-4,7E-06 |
-1,1E-11 |
4,69282E-06 |
|
K-лепестковая роза,K=3 |
|
Расчетная таблица |
|
арг.град. |
арг.рад. |
х=r*cosa |
y=r*sina |
r=sin3a |
|
-180 |
-3,14159 |
-1E-06 |
3,6E-13 |
1,03923E-06 |
|
-170 |
-2,96706 |
0,492403 |
0,086824 |
-0,499999294 |
|
-160 |
-2,79253 |
0,813797 |
0,296198 |
-0,866025109 |
|
-140 |
-2,44346 |
0,663414 |
0,55667 |
-0,866025475 |
|
-130 |
-2,26893 |
0,321394 |
0,383022 |
-0,499999928 |
|
-120 |
-2,0944 |
-1,5E-07 |
-2,7E-07 |
3,0718E-07 |
|
-110 |
-1,91986 |
-0,17101 |
-0,46985 |
0,50000046 |
|
-100 |
-1,74533 |
-0,15038 |
-0,85287 |
0,866025782 |
|
-90 |
-1,5708 |
3,27E-07 |
-1 |
1 |
|
-80 |
-1,39626 |
0,150384 |
-0,85287 |
0,866024801 |
|
-70 |
-1,22173 |
0,17101 |
-0,46985 |
0,499998762 |
|
-60 |
-1,0472 |
-8,3E-07 |
1,43E-06 |
-1,65359E-06 |
|
-50 |
-0,87266 |
-0,3214 |
0,383023 |
-0,500001626 |
|
-40 |
-0,69813 |
-0,66342 |
0,556671 |
-0,866026455 |
|
-30 |
-0,5236 |
-0,86603 |
0,499999 |
-1 |
|
-20 |
-0,34907 |
-0,8138 |
0,296197 |
-0,866024128 |
|
-10 |
-0,17453 |
-0,4924 |
0,086823 |
-0,499997596 |
|
0 |
1E-06 |
3E-06 |
3E-12 |
3E-06 |
Графическое решение уравнений и систем уравнений
К графическому способу решения уравнений и систем уравнений прибегают тогда, когда сложно или практически невозможно решить аналитически уравнение или систему уравнений.
Идея графического решения уравнений проста. Для решения следует построить график функции в прямоугольной декартовой системе координат и определить точки пересечения кривой с осью абсцисс (осью Х). Эти точки дают приблизительное значение корней заданного уравнения (т.е. значение аргумента, при котором значение функции равно нулю). Далее решения уравнения уточняется расчетным методами подстановкой найденного графически значения аргумента в исходное уравнение. Расчеты прекращаются при достижении заданной точности решения уравнения. Эту работу можно провести на компьютере.
Графическое решение уравнений вида y=ax2+bx+c.
При а≠0, b≠0. c≠0 это многочлен второй степени, геометрический образ которого – парабола. Известно, что судить о том, имеет ли данное уравнение решение, следует по значению дискриминанта Если , то уравнение имеет два различных решения, при — два равных по значению решения и при уравнение не имеет решений.
Пример. В качестве примера рассмотрим графическое решение уравнения .
Помеченные строки в расчетной таблице являются результатом уточнения прочитанного на графике решения уравнения. Для уточнения определим диапазон существования решения по графику функции и расчетной таблице, а именно:
-1,41<-1,3; -0,82<-0,7; 0,33<0,4; 1,84<1,9.
Затем в найденные диапазоны расчетной таблицы вставляем строку и производим уточнение найденного значения «методом проб и ошибок», добиваясь минимального (близкого к 0) значения функции при уточняемом значении аргумента. На рис. 10 уточненные значения решения уравнения помечены в расчетной таблице.
Графическое решение системы уравнений.
Если система уравнений легко разрешима аналитически, то не имеет смысла решать ее графически. Однако встречаются такие системы, решать которые аналитически крайне трудно. Для практических целей важно находить приблизительные решения таких систем с необходимой точностью. В таких случаях графический метод является весьма полезным средством. Поясним сказанное на примерах.
Решим систему уравнений:
Подставляя второе уравнение в первое, получим:
Решение этого уравнения представляет значительные трудности и выходит за рамки элементарной алгебры. Поэтому обратимся к графическому методу.
Графически первое уравнение представляет собой окружность с радиусом, равным 3, центром в начале координат. Второе уравнение системы графически представляет собой параболу с ветвями вниз, и осью, параллельной оси ординат.
Построим эти кривые в одной координатной системе. Начнем с построения графика окружности. Найдем у из первого уравнения системы: Таких значений два для каждого значения аргумента х. Следовательно, рассчитываем две колонки в расчетной таблице – у1 и у2. Значение аргумента х при расчете значений у первого уравнения системы должно лежать в пределах -3≤х≤3. Шаг изменения аргумента был взят равным 0,1, что определило точность построения графика функции первого уравнения системы и нахождения результата решения.
Выполняя уже знакомые нам технические операции, строим кривую второго уравнения системы. Для того чтобы график выглядел компактным, значения аргумента были взяты в меньших пределах, чем предыдущие (см. расчетную таблицу на рис.11).
|
-0,8 |
2,891366 |
-2,89137 |
1,244444 |
|
-0,6 |
2,939388 |
-2,93939 |
2,311111 |
|
-0,5 |
2,95804 |
-2,95804 |
2,777778 |
|
-0,3 |
2,984962 |
-2,98496 |
3,577778 |
|
-0,2 |
2,993326 |
-2,99333 |
3,911111 |
|
-2 |
2,236068 |
-2,23607 |
-8,88889 |
|
-1,7 |
2,471841 |
-2,47184 |
-5,75556 |
|
-1,5 |
2,598076 |
-2,59808 |
-3,88889 |
|
-1,4 |
2,6533 |
-2,6533 |
-3,02222 |
|
-1,2 |
2,749545 |
-2,74955 |
-1,42222 |
|
-1,1 |
2,791057 |
-2,79106 |
-0,68889 |
Точки пересечения кривых первого и второго уравнений системы определят ее решение. Таких точек четыре, значения их координат можно приблизительно определить на графике.
Итак, получаем графическое решение системы уравнений в виде четырех пар координат точек пересечения кривых графика:
х≈- 1,2 2) х≈- 0,5 3) х≈1,6 4) х≈2,3
у≈- 2,75 у≈2,98 у≈2,6 у≈-1,92
Полученный графический результат решения системы уравнений может быть уточнен до заданной погрешности. Для этого необходимо подставить значения координат точек пересечения, например, в первое уравнение системы: (-1,2)2+(-2,75)2=9, то 1,44+7,56 т.е. уточнить не надо.
Рис.3.
В(r,a)
O
a
А(х,у)
Y
y
O
x
a
r
X
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Обновлено: 15.04.2023
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
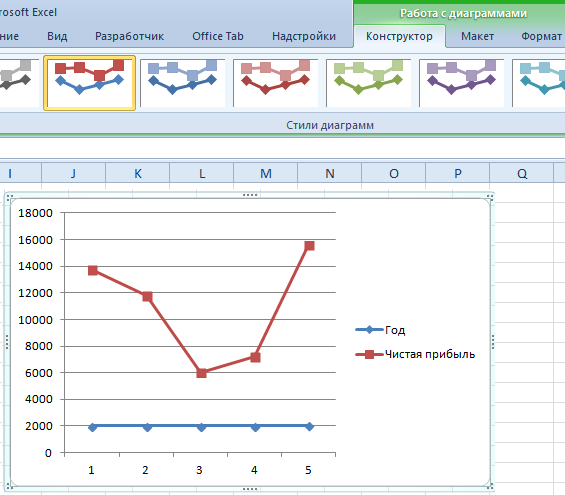
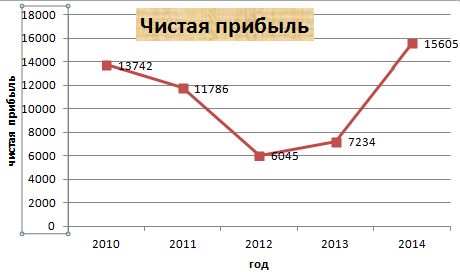
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
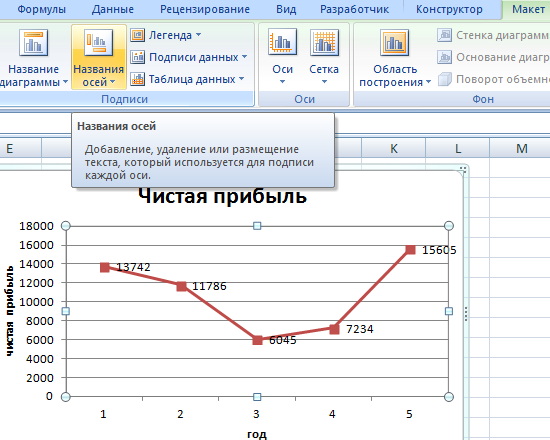
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
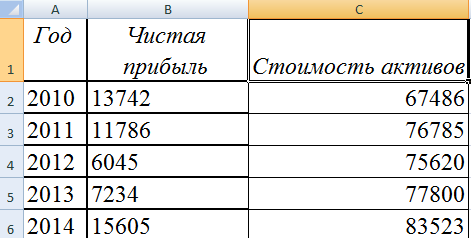
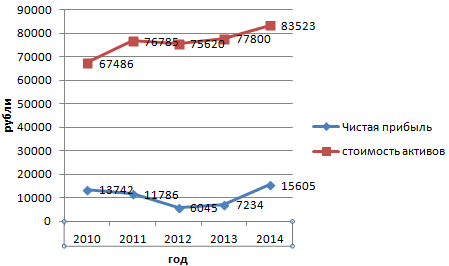
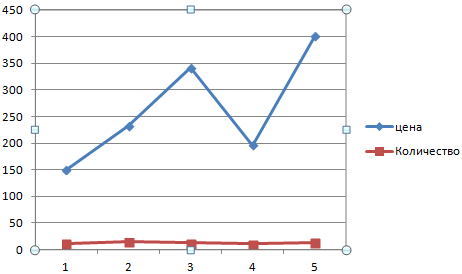
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.
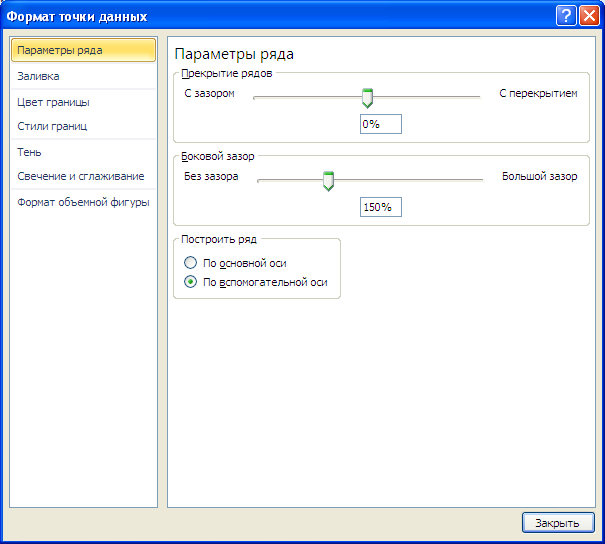
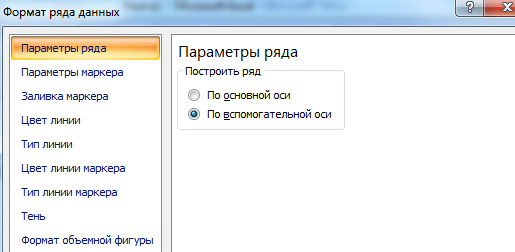
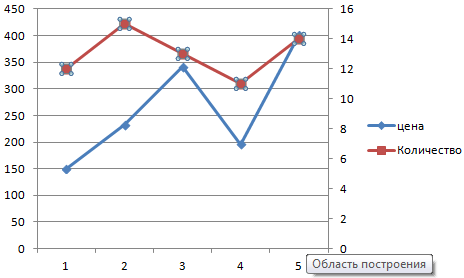
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
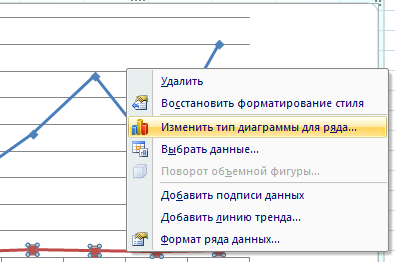
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
Пример: y=x(√x – 2). Шаг – 0,3.
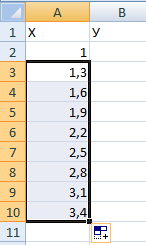
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
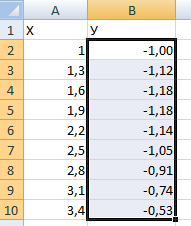
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
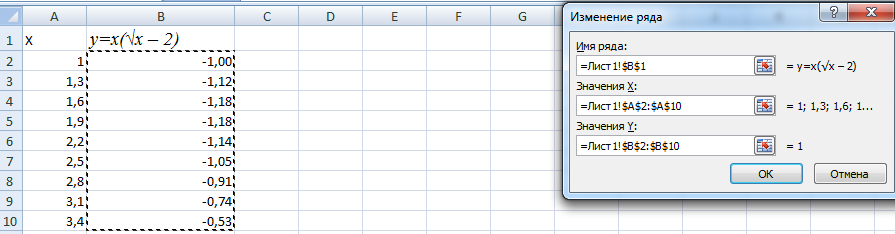
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
Наложение и комбинирование графиков
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
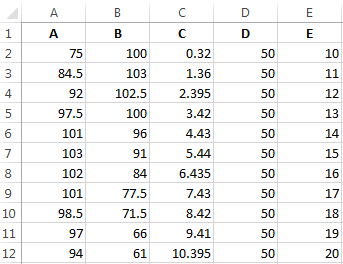
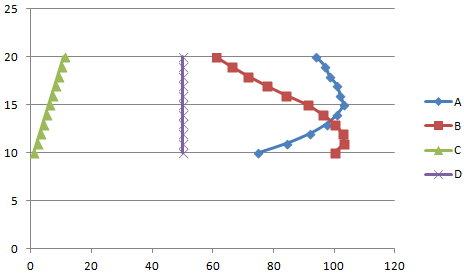
Построить график зависимости одного столбца от другого в Excel можно так:
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Готовые примеры графиков и диаграмм в Excel скачать:
Как сделать еженедельный график в Excel вместе с ежедневным.
Пример создания динамического синхронного еженедельного графика вместе с ежедневным. Синхронное отображение двух таймфреймов на одном графике.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Данная статья посвящена использованию Excel для построения графиков элементарных и сложных функций, изучение графических способов решения уравнений и систем уравнений, а также построения трехмерных поверхностей.
| Вложение | Размер |
|---|---|
| ispolzovanie_graficheskih_vozmozhnostey_excel.doc | 292 КБ |
Предварительный просмотр:
Использование графических возможностей Excel для решения математических задач
Возможности ЭТ Microsoft Excel весьма многогранны. Всем известно, что Excel является мощным вычислительным инструментом, позволяющим производить простые и сложные расчеты в различных областях человеческой деятельности: математике, физике, инженерных науках, экономике, технологии. Но помимо осуществления расчетов возможно применение ЭТ Excel и в других областях. Данная статья посвящена использованию Excel для построения графиков элементарных и сложных функций, изучение графических способов решения уравнений и систем уравнений, а также построения трехмерных поверхностей.
Построение графиков элементарных функций в Excel
Для построения графика функции в Excel прежде всего надо построить таблицу, в одну колонку которой занести значение аргумента функции, а в другую — значение функции при заданном значении аргумента.
Для этого в рабочем поле Excel в ячейках 1-й строки напечатаем наименование работы, во 2-ой строке – заголовок «Расчетная таблица», в 3-й – наименование колонок (столбцов) расчетной таблицы.
Начиная с ячейки А5 произведем формирование значение таблицы. Для этого необходимо в ячейку А5 ввести первое значение аргумента вычисляемой функции из заданного диапазона значений аргументов. В ячейку А6 введем второе значение аргумента, отличающееся от первого на заданный шаг изменения аргумента. Далее пометим эти ячейки и, ухватив указателем мыши квадратную точку в правом нижнем углу помеченной области ячеек, движением вниз по столбцу с нажатой левой кнопкой мыши рассчитаем значения аргумента с шагом, который вычислил Excel по указанным первым двум ячейкам (рис.1).
Пометив ячейку В5, вычисляем первое значении функции, используя Мастер формул, и если функция проста, то записываем формулу вручную. Запись формулы в ячейку вручную следует начать со знака «=» и закончить нажатием клавиши Enter. Затем, используя квадратную точку помеченной ячейки, копируем формулу в остальные ячейки.
Для построения графика заданной функции по построенной таким образом таблице необходимо воспользоваться Мастером диаграмм. Следуя указаниям Мастера, выбираем форму диаграммы Точечная.
Построение графика функции y=ax 2 +bx+c.
Построим график указанной функции при а-2, b=5, c=-10. Для построения графика функции будем изменять аргумент в диапазоне -5≤x≤2,5 с шагом 0,5.
Выполним последовательно все действия, описанные выше, сравнивая получаемый результат с рис.1.
Построение диаграммы в Microsoft Excel по таблице – основной вариант создания графиков и диаграмм другого типа, поскольку изначально у пользователя имеется диапазон данных, который и нужно заключить в такой тип визуального представления.
В Excel составить диаграмму по таблице можно двумя разными методами, о чем я и хочу рассказать в этой статье.
Способ 1: Выбор таблицы для диаграммы
Откройте необходимую таблицу и выделите ее, зажав левую кнопку мыши и проведя до завершения.
Вы должны увидеть, что все ячейки помечены серым цветом, значит, можно переходить на вкладку «Вставка».
Там нас интересует блок «Диаграммы», в котором можно выбрать одну из диаграмм или перейти в окно с рекомендуемыми.
Откройте вкладку «Все диаграммы» и отыщите среди типов ту, которая устраивает вас.
Справа отображаются виды выбранного типа графика, а при наведении курсора появляется увеличенный размер диаграммы. Дважды кликните по ней, чтобы добавить в таблицу.
Предыдущие действия позволили вставить диаграмму в Excel, после чего ее можно переместить по листку или изменить размер.
Дважды нажмите по названию графика, чтобы изменить его, поскольку установленное по умолчанию значение подходит далеко не всегда.
Не забывайте о том, что дополнительные опции отображаются после клика правой кнопкой мыши по графику. Так вы можете изменить шрифт, добавить данные или вырезать объект из листа.
Для определенных типов графиков доступно изменение стилей, что отобразится на вкладке «Конструктор» сразу после добавления объекта в таблицу.
Как видно, нет ничего сложного в том, чтобы сделать диаграмму по таблице, заранее выбрав ее на листе. В этом случае важно, чтобы все значения были указаны правильно и выбранный тип графика отображался корректно. В остальном же никаких трудностей при построении возникнуть не должно.
Способ 2: Ручной ввод данных
Преимущество этого типа построения диаграммы в Экселе заключается в том, что благодаря выполненным действиям вы поймете, как можно в любой момент расширить график или перенести в него совершенно другую таблицу. Суть метода заключается в том, что сначала составляется произвольная диаграмма, а после в нее вводятся необходимые значения. Пригодится такой подход тогда, когда уже сейчас нужно составить график на листе, а таблица со временем расширится или вовсе изменит свой формат.
На листе выберите любую свободную ячейку, перейдите на вкладку «Вставка» и откройте окно со всеми диаграммами.
В нем отыщите подходящую так, как это было продемонстрировано в предыдущем методе, после чего вставьте на лист и нажмите правой кнопкой мыши в любом месте текущего значения.
Из появившегося контекстного меню выберите пункт «Выбрать данные».
Задайте диапазон данных для диаграммы, указав необходимую таблицу. Вы можете вручную заполнить формулу с ячейками или кликнуть по значку со стрелкой, чтобы выбрать значения на листе.
В блоках «Элементы легенды (ряды)» и «Подписи горизонтальной оси (категории)» вы самостоятельно решаете, какие столбы с данными будут отображаться и как они подписаны. При помощи находящихся там кнопок можно изменять содержимое, добавляя или удаляя ряды и категории.
Обратите внимание на то, что пока активно окно «Выбор источника данных», захватываемые значения таблицы подсвечены на листе пунктиром, что позволит не потеряться.
По завершении редактирования вы увидите готовую диаграмму, которую можно изменить точно таким же образом, как это было сделано ранее.
Вам остается только понять, как сделать диаграмму в Excel по таблице проще или удобнее конкретно в вашем случае. Два представленных метода подойдут в совершенно разных ситуациях и в любом случае окажутся полезными, если вы часто взаимодействуете с графиками во время составления электронных таблиц. Следуйте приведенным инструкциям, и все обязательно получится!
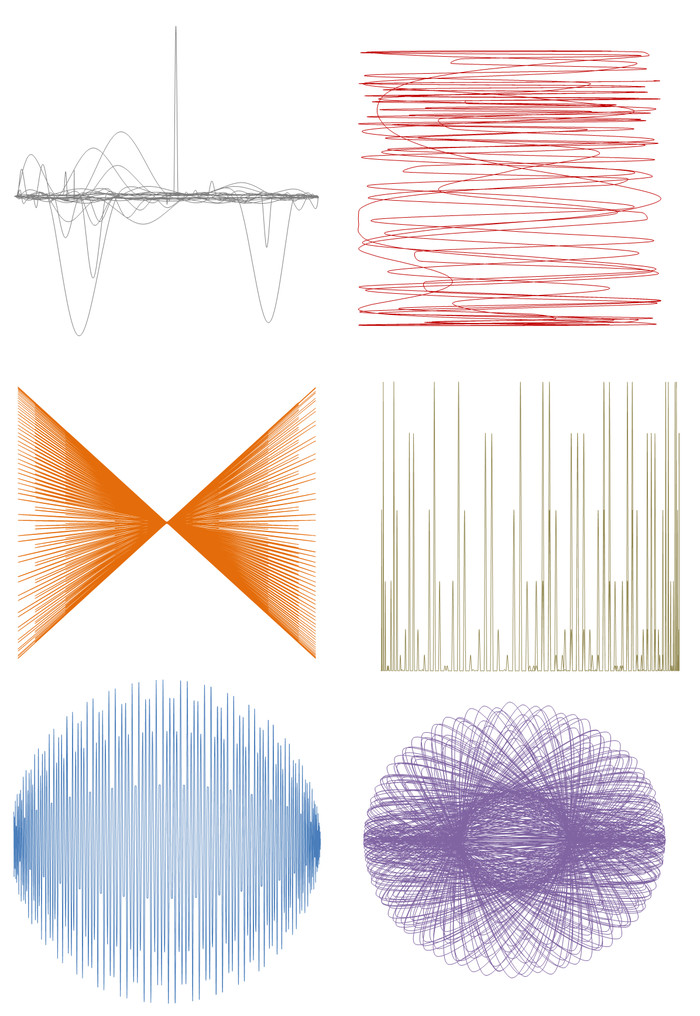
Началось всё с урока информатики, когда мы выполняли задание в Excel. Результатом работы должен был быть график в виде символа бесконечности. Я закончил немного раньше и поиграл с параметрами, а график интересно себя вёл. А потом вернулся домой и сделал вот это:
Это большая таблица в Excel со сложными функциями, которые состоят из периодических. В качестве аргументов они используют друг друга, перемножаются, делятся, косинусы берутся от косинусов и синусов.
Всё сложно, формулы рандомные, делал так, как душа хотела.
И есть два параметра a и b (в верхнем левом углу), которые тоже зашиты в эти формулы и серьёзно влияют на вид графика.
Посмотрим, например, на первый график серого цвета. При a=b=1 он выглядит так:
Как он строился:
х меняется от 0 до 2580 град. с шагом 1. Далее x переводится в радианы. Для упрощения восприятия формул считаем, что х там уже в радианах.
Строим зависимость z(y)
Остальные графики — аналогично. Намешать всего в кучу с надеждой, что получится что-то красивое
А теперь наиболее красивые картинки. Каждый график рисуется своим цветом. Если на разных картинках будут две абсолютно разные загогулины, но одинакового цвета, то это один и тот же график, только с разными параметрами a и b
Вообще при целых a (и особенно кратных 3, 6, 12. ) достаточно часто получаются особенно чёткие графики.
Продолжать можно бесконечно.
Кому интересно, вот файл:
На этом всё! Будут вопросы — пишите, постараюсь ответить.
Лига математиков
382 поста 1.8K подписчика
Поставь себе матлаб для этого и отстань от экселя.
Ниче не понял но получилось интересно
О, моё почтение, дружище!
(я репетитор по информатике, мне такой пост — бальзам на душу)
4. Wolphram alpha
6. python + matplotlib
9. Excel/Google table + сеть — морской бой по сети.
Когда ещё не было этих ваших экселей, такое на осциллографе делали, только там всё «вживую» можно было менять
Ахтунг! Лиссажу на Пикабу!
Наконец-то годный пост о том, чем заняться в свободное время!
ТС, плюсую!
Вы большой молодец, спасибо за содержательный пост, пояснения и ссылки.
Я когда поступил на первый курс программистской специальности, тоже любил картиночки генерировать (и сейчас люблю)
Помню на Делфи сделал треугольник Серпинского. Фрактальная геометрия, мать её
круто, но не удивительно, учитывая то, что знающие люди могут в САПР и моделирование через эксель.
автору можно перенести функционал движка UE4 на эксель в один файл, после чего к нему сразу прилетит вертолет с нобелевской премией и каким-нибудь йен-сун-хуанем, который предложит контракт на должность CEO в какой-нибудь NVIDIA.
З.Ы. я в универе на математическом моделировании подобное писал формулами, в AnyLogic. автор может посмотреть и изучить ПО, если ему интересно.
Я так делал функцию рандом() в еще 7-й одинэске году в 2005)
В институте на паскале делали анимированные графики.
Продолжай эксперименты, может и такую картинку получишь
Ну всё, теперь читай матан, про теорию хаоса и аттракторы
Теперь осваивайте фракталы, там тоже красиво может получаться
Там в одной формуле сидит теория кротовой норы. А он её визуализировал. Что до него никто в мире не делал. Вот так, мы с лёгкостью проходим мимо открытия межпространственного перемещения, и идём копаться в песочнице .
Был когда-то очень популярный mp3-плеер WinAMP. И были к нему сторонние плагины визуализации. Один из них (название не помню) был — рай для математика-гика: в настройках задавалась форму и пачка дополнительных параметров цикличности и всего такого. Параметры a, b, c, x, y и т.д. брались из звуковой дорожки по разным частотам. Вобщем вариативности хватало. Было несколько десятков уже готовых моделей, которые переключались при проигрывании трека.
5 секунд гугления: Advanced Visualization Studio. Наверное, это он.
У меня Excel отжирал много ресурсів, а вот в MathCad или mathlab как то по лучше. Фигуры Лиссажу прикольные)
аж всплакнул. Ех молодость
на третьей картинке логотип Хабра )))
Есть вопрос, офтоп но по Excel: Пользуюсь старым Excel 2007, работа с прайс-листом и его рассылка оптовикам. Но сейчас появилась необходимость вставить информацию с ценами закупки, чтоб всегда было «под рукой». Есть какие-нибудь способы «закрыть» доступ к отдельному столбцу или в крайнем случае к отдельному листу? В гугле есть какие-то инструкции чтоб установить пароль, но я не увидел результат. Гуру экселя, посоветуйте как быть с такой задачей?
Странно, что самореферентную формулу Таппера не вспомнили)
некоторые можно даж где-то использовать для иллюстраций и графики.
Рисовать в экселе?! А че так можно было?
У меня мозг нахой щас перегорел пока понимал как делается ))))
Очень красиво. Я только вбивать цифры и символы могу
Блин, была же целая книга с реалистичными пейзажами. Эх, разве теперь вспомнишь.
А я такие рисоваль
Не знал что на экселе можно слелать такое. А по какому учебнику занимаетесь?
Ни хрена не понятно, но красиво-о-о!)))
Похожая штука, но в динамике, очень красиво
Спасибо! Получила истинное удовольствие от вашего поста!
Нобелевку этому господину
О. На Спктруме 48к в бейсике такие же хрени выделывал! Было дело)))
Очень здорово!у меня вопрос,возможно глупый,можно ли каким либо способом перевести екселевские графики в вектор?
Никогда ещё математика не выглядела для меня так красиво
Графики уж очень похожи как будто призывают дьявола! Аккуратно там.
Вот это я понимаю, современное искусство
Спасибо, скачала! ) Читала и думала — надо такое же построить )
Надеюсь, наши палаты в дурдоме будут соседними)
У меня бабушка так хуярит без exel’я.
Такие узоры порой плетет,что думаешь:
«Или проверить ее на наличие укуса паука-мутанта,либо на наличие в моче каннабиноидов».
Красота! Очень заинтересовало) хотелось бы что-то типа урока по этому поводу) а то получается, что основной рецепт — это «Намешать всего в кучу с надеждой, что получится что-то красивое».
Сама очень уважаю Exel. За время учебы в универе только в нем и оформляла лабы.
Такими темпами изучай шейдеры и цены тебе не будет
А можно как-то озвучить такие графики? Я имею в виду, связать с нотами?
Это делается в Экселе? Я не с первого раза там формулу посчитать запущу. Не было в школе уроков таких) и по работе не был нужен, кроме заполнения там отчётов
Вроде бы прочитала пост, но к сожалению он на эльфийском.
Мне кажется, что найдена формула перемещения во времени))
Как выбрать тип диаграммы?
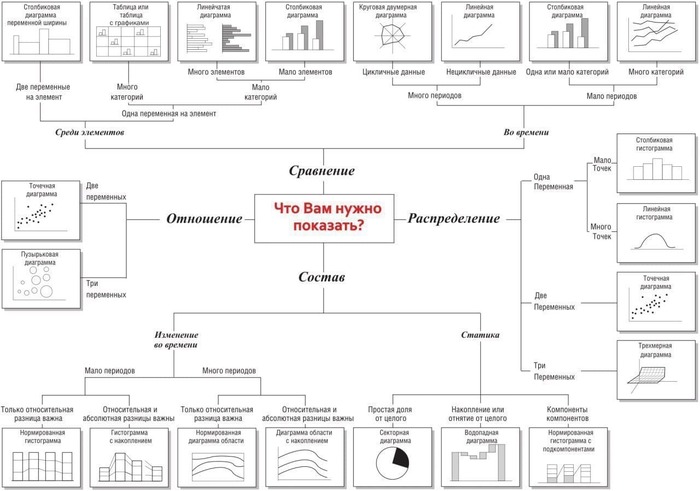
Каждый, кто работает в Excel, когда-либо сталкивался с проблемой выбора подходящего типа графика, который бы визуально лучше всего отражал идеи и замысел автора.
Держите шпаргалку, которая поможет определиться, какую диаграмму выбрать для построения.
В зависимости от типа данных, диаграммы на схеме разделены на 4 основные группы:
• Сравнение (характеристики: сравнение величин, много периодов, неповторяющиеся данные);
• Распределение (характеристики: распределение величин, обычно две переменных);
• Состав (характеристики: структура величин, статика);
• Отношение (характеристики: отношение величин, обычно три переменных).
Каждая из базовых групп далее делится на множество подгрупп в зависимости от детальных параметров, что позволяет более точно выбрать тип графика.
Формула всего
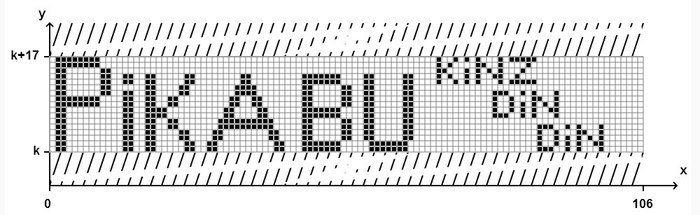
Формула Таппера- впервые формула была опубликована в 2001 году в докладе Джеффа Таппера, это самореферентная (при определённых условиях) формула, будучи отображённой на плоскости, создаёт собственное изображение.
Формула является вот таким неравенством:
Что значит «будучи отображённой на плоскости, создаёт собственное изображение»? Ну, собственно это и значит. Если отобразить это неравенство на плоскости OXY, то по оси OX оно займёт 106 пикселей (от 0 до 105), а по оси OY- 17 пикселей и будет выглядеть так:
А почему это формула всего? А дело в оси OY. Видите там слева k, k+5, k+10, k+15? Ну это значения на оси OX, просто в данном случае k= 960 939 379 918 958 884 971 672 962 127 852 754 715 004 339 660 129 306 651 505 519 271 702 802 395 266 424 689 642 842 174 350 718 121 267 153 782 770 623 355 993 237 280 874 144 307 891 325 963 941 337 723 487 857 735 749 823 926 629 715 517 173 716 995 165 232 890 538 221 612 403 238 855 866 184 013 235 585 136 048 828 693 337 902 491 454 229 288 667 081 096 184 496 091 705 183 454 067 827 731 551 705 405 381 627 380 967 602 565 625 016 981 482 083 418 783 163 849 115 590 225 610 003 652 351 370 343 874 461 848 378 737 238 198 224 849 863 465 033 159 410 054 974 700 593 138 339 226 497 249 461 751 545 728 366 702 369 745 461 014 655 997 933 798 537 483 143 786 841 806 593 422 227 898 388 722 980 000 748 404 719.
Где-то там в далёкой-далёкой галактике на оси OY среди бесконечного количество значений есть бесконечное количество изображений, заданных этой формулой. Т.е. там есть ВСЕ ВОЗМОЖНЫЕ изображения размером 106 на 17 пикселей.
Например, при k= 172 895 466 264 656 362 238 775 198 618 400 053 006 722 417 830 074 875 710 077 840 558 718 522 933 856 481 624 057 883 539 289 927 382 958 168 812 116 931 135 487 324 743 680 349 552 434 460 222 923 986 273 388 093 735 529 486 165 346 092 911 369 252 390 353 778 634 279 896 583 455 425 859 634 440 043 584 268 093 410 716 443 082 284 154 873 275 541 781 431 502 156 517 367 941 053 074 097 258 022 615 110 586 256 528 662 395 677 501 188 461 923 095 483 961 995 173 180 815 230 411 356 269 083 712 579 786 823 770 925 493 943 423 964 558 741 203 303 534 803 553 728 066 326 116 959 373 467 996 584 250 693 892 202 679 445 143 468 361 413 129 347 669 354 301 413 221 990 4
Изображено вот такое:
Про эту формулу есть ролик у Numberphile (у Numberphile вообще много интересного есть, рекомендую)
Читайте также:
- Как узнать ip компьютера через cmd
- Настройки эквалайзера для идеального звука realtek
- Написать bat файл показывающий содержимое своего параметра если параметр каталог
- Методы настройки и сопровождения системного программного обеспечения компьютерных систем
- Можно ли выносить временную папку mysql на ramdisk в памяти
Рассмотрим построение в MS EXCEL 2010 диаграмм с несколькими рядами данных, а также использование вспомогательных осей и совмещение на одной диаграмме диаграмм различных типов.
Построение диаграмм с одним рядом данных рассмотрено в статье Основы построения диаграмм в MS EXCEL. Начинающим пользователям также целесообразно перед прочтением ознакомиться со статьей Основные типы диаграмм.
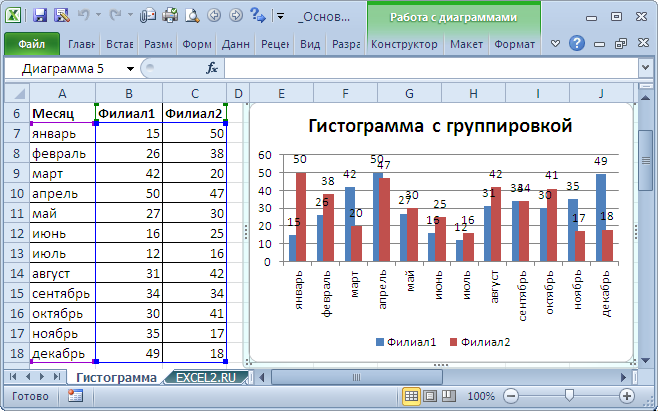
ГИСТОГРАММА
Построим Гистограмму с группировкой на основе таблицы с двумя числовыми столбцами, близких по значениям.
Выделите любую ячейку таблицы (см. файл примера ), на вкладке Вставка, в группе Диаграммы нажмите кнопку Гистограмма, в выпавшем меню выберите Гистограмма с группировкой.
MS EXCEL построит оба ряда с использованием только основных осей (чтобы в этом убедиться, дважды кликните сначала по столбцу одного ряда, затем по одному из столбцов по другого. В окне Формат ряда данных на вкладке Параметры ряда будет указано по какой оси отложены значения ряда). Т.к. значения у обоих рядов близки, то такое решение нам подходит.
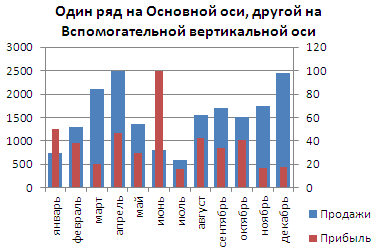
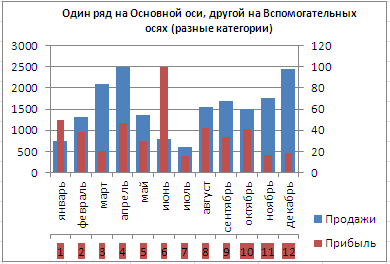
Для рядов, у которых значения существенно различаются (на порядок и больше) один из рядов нужно строить с использованием Вспомогательной вертикальной оси.
Для этого достаточно выбрать для одного из рядов построение на вспомогательной оси (дважды кликнув на один из столбцов), а затем настроить ширину столбцов (боковой зазор), чтобы отображались оба ряда.
Если не настроить ширину столбцов, то эту диаграмму можно спутать с диаграммой Гистограмма с пополнением (столбцы, относящие к одной категории «ставятся» друг на друга).
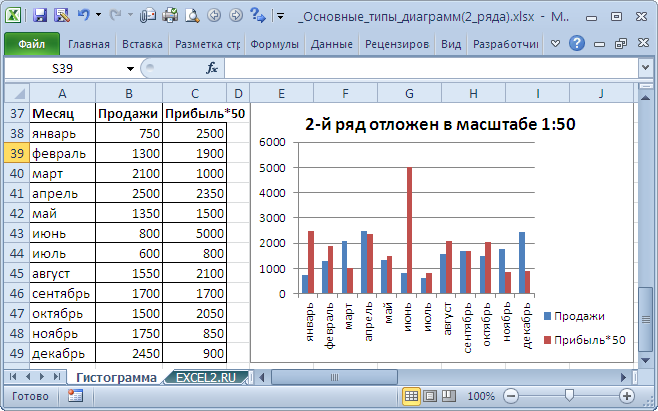
Другой возможностью отображения на диаграмме двух рядов со значительно различающимися значениями, является масштабирование самих значений в таблице-источнике.
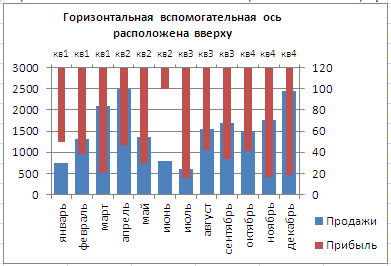
Горизонтальную вспомогательную ось можно расположить даже вверху. При этом столбцы разных рядов будут оригинально пересекаться.
Теперь изменим подписи по горизонтальной оси (категории).
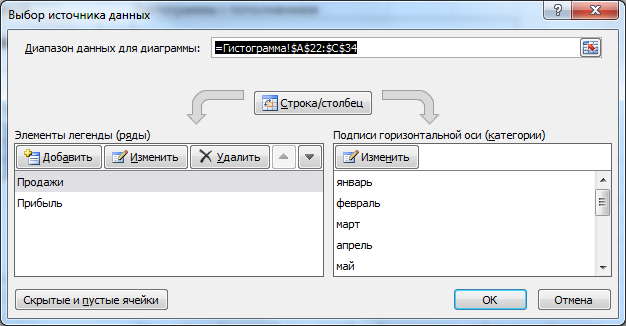
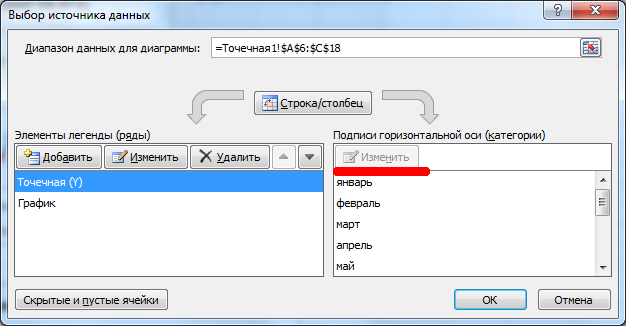
В окне Выбор источника данных видно, что для обоих рядов подписи горизонтальной оси одинаковы, т.к. категории одинаковы для обоих рядов (столбец Месяц).
Кликните сначала по ряду Продажи, затем по Прибыль — подписи по горизонтальной оси будут одинаковы.
При желании это также можно изменить. В окне Выбор источника данных выделите ряд Прибыль, нажмите кнопку Изменить расположенную справа, удалите ссылку на ячейки. Теперь у ряда Прибыль вместо названия категорий будут просто порядковые числа 1, 2, 3,… Однако, они не будут отображаться на диаграмме, т.к. отображается пока только Основная горизонтальная ось.
Теперь в меню Оси (вкладка Макет, группа Оси) выберите Вспомогательная горизонтальная ось и установите ее Слева направо. В окне формата Вспомогательной вертикальной оси измените точку пересечения оси (установите Автовыбор). Получим вот такую диаграмму.
Хотя техническая возможность отображения 2-х различных категорий существует, конечно, таких диаграмм нужно избегать, т.к. их сложно воспринимать. Категории должны быть одинаковыми для всех рядов на диаграмме. Естественно, такой трюк сработает только для двух групп рядов, т.к. имеется всего 2 типа оси: основная и вспомогательная.
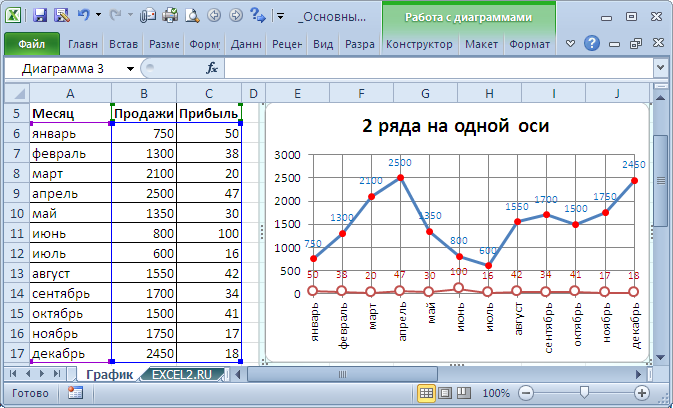
ГРАФИК
Диаграмма График во многом аналогична Гистограмме с группировкой: к ней применимы те же идеи по отображению двух рядов со значительно отличающимися значениями, что и к Гистограмме.
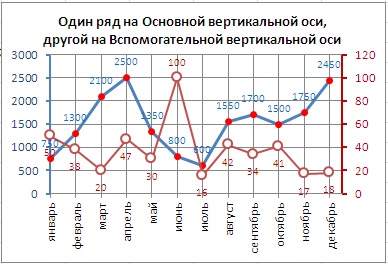
После размещения рядов на разных осях получим вот такую диаграмму (линии вертикальных осей выделены цветами, соответствующими цветам рядов).
Примечание. Если провести горизонтальные линии сетки к вспомогательной оси, то они, естественно, могут не совпасть с линиями к основной оси, т.к. масштабы осей (величины основных делений вертикальных осей) могут не совпадать. Это может «перегрузить» диаграмму.
Вообще, к использованию вспомогательных вертикальных осей, а тем более вспомогательных горизонтальных осей для Гистограммы и Графика нужно подходить обдуманно: ведь диаграмма должна «читаться» — быть понятной без дополнительных комментариев.
ТОЧЕЧНАЯ
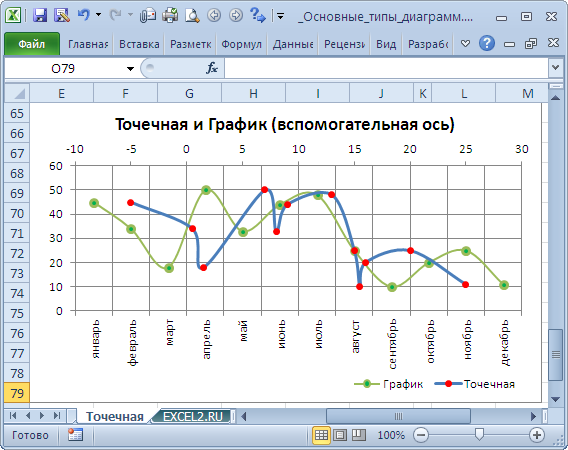
Визуально Точечная диаграмма похожа на диаграмму типа График (если конечно у Точечной диаграммы точки соединены линиями).
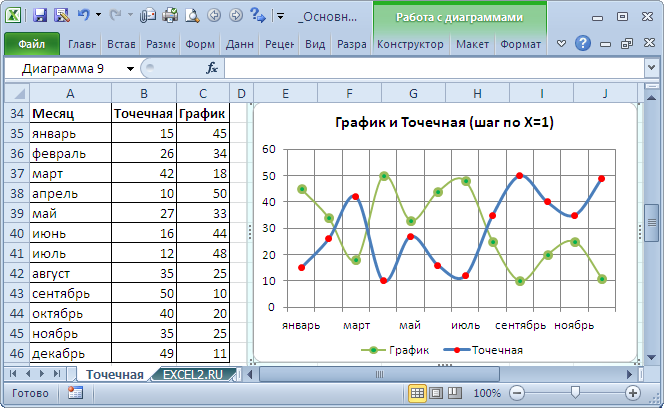
Различие состоит в том, что для построения Графика в качестве координаты Х всегда используется последовательность 1, 2, 3, … (с подписями — категориями), а для Точечной значения по горизонтальной оси м.б. любыми числами (см. статью График vs Точечная).
Примечание. Если для построения Точечной диаграммы не указана ссылка на значения Х (или ссылка указывает на текстовые значения), то в качестве координат по Х будет использована та же последовательность 1, 2, 3, …, что и для Графика.
Исходя из вышесказанного, при построении диаграммы Точечная целесообразно указывать числовые значения по Х. В противном случае нужно просто использовать График, т.к. для него можно задавать любые подписи по Х (в том числе и текстовые), что для Точечной диаграммы сделать нельзя (только числа).
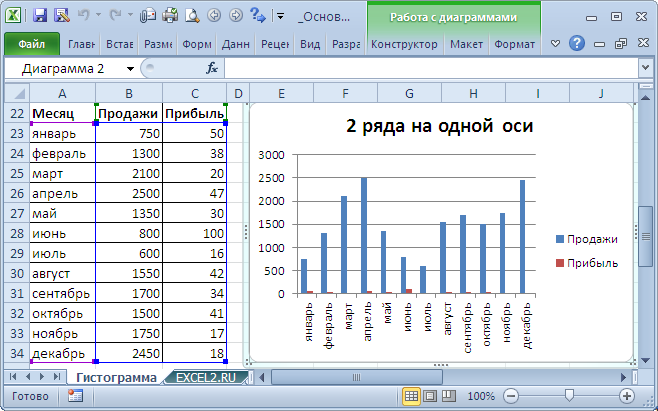
Теперь о совмещении разных типов диаграмм с Точечной. Если для Точечной диаграммы не используется координата Х, то на диаграмме она выглядит как График.
Подписи по горизонтальной оси берутся от Графика. В окне Выбор источника данных видно, что для ряда отображаемого Точечной диаграммой подписи горизонтальной оси одинаковы изменить/ удалить нельзя.
Кроме того, График может быть только на основной оси и поменять это нельзя.
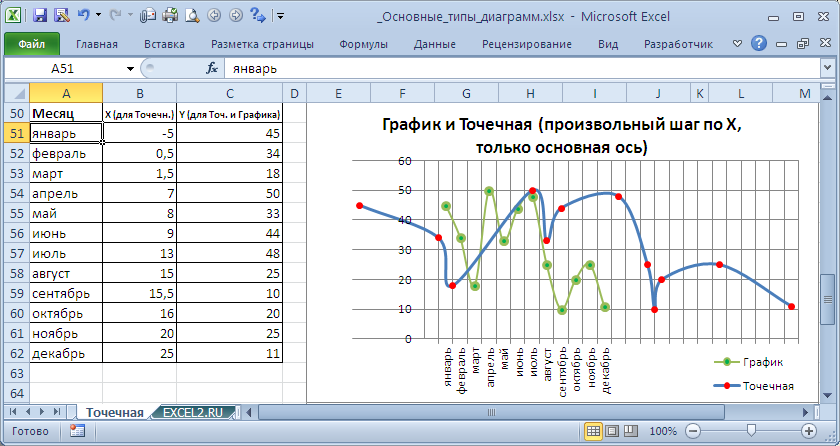
Если для Точечной диаграммы используется координата Х и оба ряда отложены по одной (основной) оси, то получается не очень красивая диаграмма.
Это связано с тем, что при совмещении с Точечной диаграммой (на одной оси и когда у Точечной указаны значения по Х), диаграмма типа График становится как бы главной:
- на горизонтальной оси отображаются подписи только для Графика;
- вертикальная сетка не отображается для отрицательных значений Х (т.к. График строится только для Х=1, 2, 3, …);
- у Графика невозможно изменить Ось с Основной на Вспомогательную (у Точечной можно).
Если Точечную построить на вспомогательной оси, то диаграмма изменится.
Подписи для Точечной (значения по Х) теперь отображаются сверху.
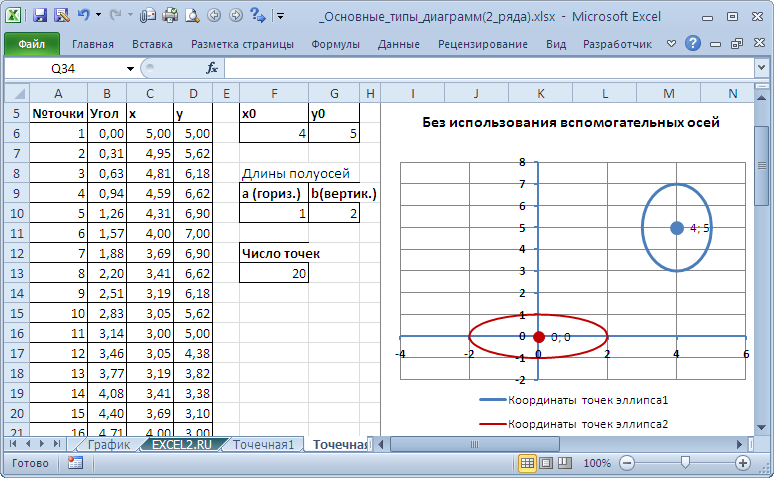
Теперь рассмотрим построение 2-х рядов данных, которые используют диаграмму Точечная.
Сначала построим 2 эллипса с различными координатами центра и размерами полуосей без использования вспомогательных осей.
Примечание. Фактически на диаграмме 4 ряда данных: точка центра представляет отдельный ряд.
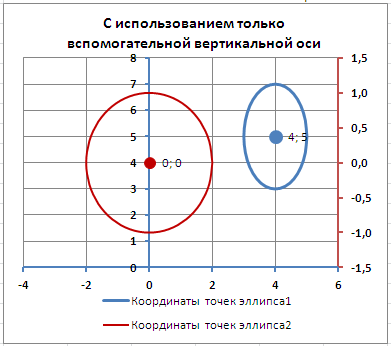
Дважды кликнем по бордовому эллипсу и выберем построение ряда на вспомогательной оси (сделаем то же и центра эллипса).
Теперь координаты Y для бордового эллипса откладываются по правой вертикальной оси (можно ее для наглядности выделить также бордовым цветом).
Добавим Вспомогательную горизонтальную ось (в меню Оси (вкладка Макет, группа Оси) выберите Вспомогательная горизонтальная ось и установите ее По умолчанию).
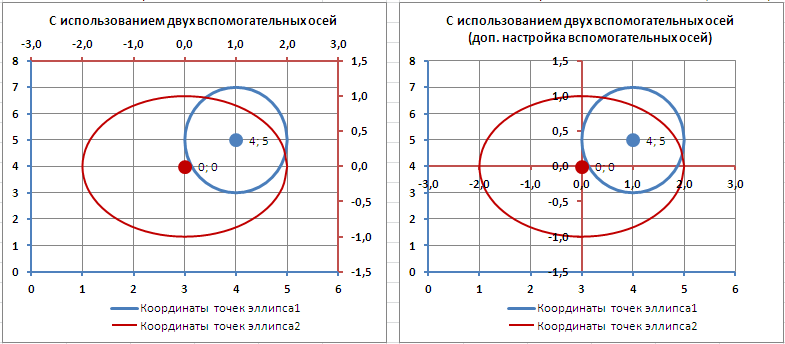
Наверное, для диаграммы типа Точечная использование вспомогательных осей наиболее оправдано – это позволяет отображать на одной диаграмме различные по масштабу кривые.
КРУГОВАЯ
В статье Основные типы диаграмм показано, что разместить несколько рядов в круговой диаграмме технически можно, но, как правило, не целесообразно.
Совмещение разных типов диаграмм
Про совмещение Графика и Точечной диаграммы рассказано выше (см. раздел Точечная).
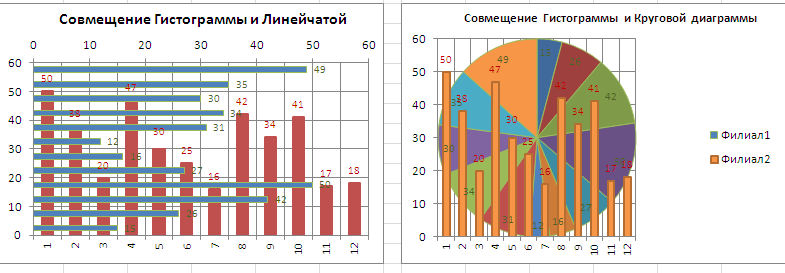
Совмещением Линейчатой и Гистограммы не стоит заниматься, т.к. выглядит это достаточно странно, почти также странно, как и совмещение Гистограммы с Круговой (см. также статью Основные типы диаграмм, раздел Круговая).
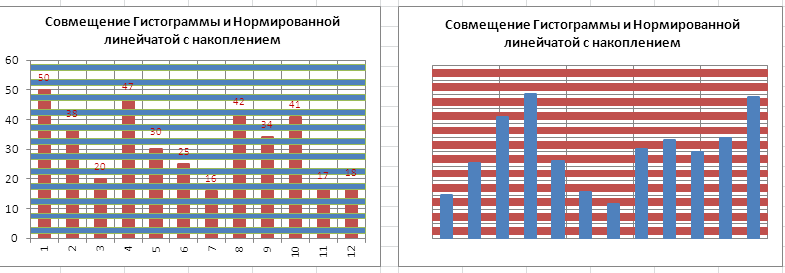
Оригинальностью совмещения могут также похвастаться Гистограмма и Нормированная линейчатая с накоплением.
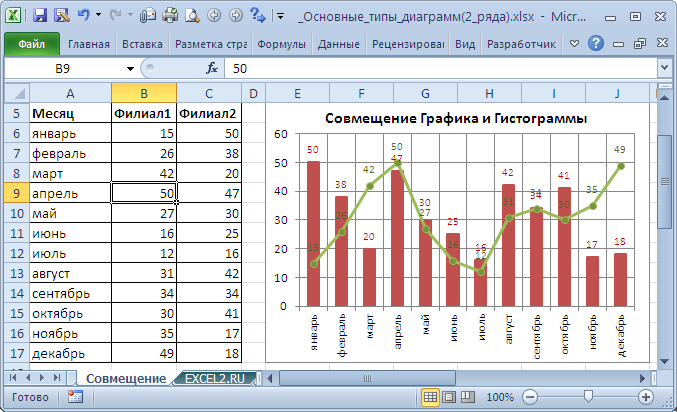
Наверное, единственными типами диаграмм, которые стоит совмещать, являются График и Гистограмма (категории должны быть одинаковыми для обоих рядов).
Для такой диаграммы постройте сначала Гистограмму с группировкой с двумя рядами (см. раздел Гистограмма в начале этой статьи). Затем выделите нужный ряд и нажмите кнопку Изменить тип диаграммы (вкладка Конструктор). Выбрав График или График с Маркерами нажмите ОК.
Если масштабы значений у рядов существенно отличаются, то можно настроить вспомогательную вертикальную ось (см. раздел Гистограмма).
В этой статье мы собрали 12 необычных диаграммам Excel со ссылками на краткие инструкции по их построению.
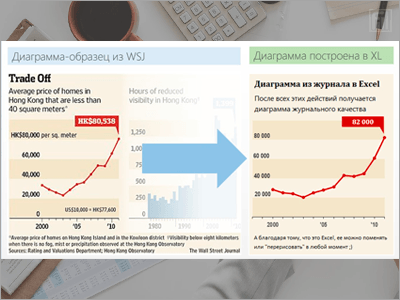
1. Диаграмма по мотивам Wall Street Journal
Какое-то время назад для того, чтобы показать неограниченность рисования в Excel, делал ряд статей, а файлы Excel к ним не прикладывал. Решил, что пора «рассекретить» хитрые диаграммы. Встретил диаграмму, созданную дизайнерами Wall Street Journal. И тут же ее воспроизвел в Excel. Подробнее >>
2. Диаграмма темпов роста в Excel
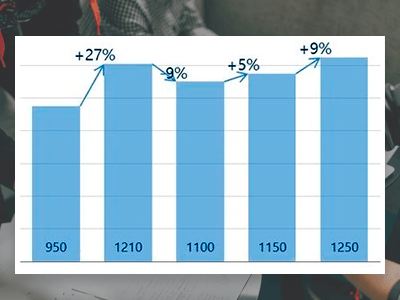
Как в Excel создать диаграмму с динамикой темпов роста, где изменения показателей показаны стрелками? Все просто — рисуем столбцы и добавляем к ним полосы повышения и понижения. Плюс рисуем графики с накоплением — первый для роста, второй график — уровень подписи. Подробнее >>
3. Линейчатая диаграмма с эффектами
На этот раз напишу о простой линейчатой диаграмме. Простой по содержанию, но необычной по оформлению. Весь секрет — пользоваться вспомогательными осями и разными типами диаграмм в одном пространстве. Подробнее >>
4. Как цветом показать на графике рост или падение последнего значения
Итак, задача: показать тенденцию последнего месяца (квартала, года, периода). В стандартных графиках можно настроить такое представление, чтобы на конце линии была красная стрелка, если у нас спад, и зеленая — если подъем. При желании можно настроить так, чтобы отличать сильный спад/подъем от незначительного, и другие нюансы. Подробнее >>
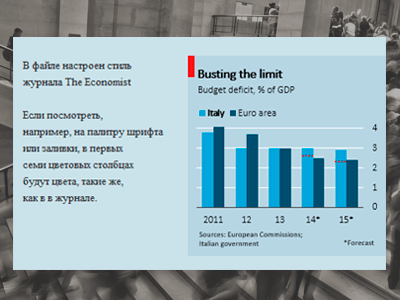
5. Диаграмма по мотивам The Economist
Обнаружил в журнале The Economist за октябрь 2014 года интересную гистограмму с меткой на столбцах. Тут же ее воспроизвел в Excel — вроде все получилось, кроме шрифтов. Подробнее >>
6. Диаграмма в виде колб
Хочу осветить тему: как «мониторить» выполнение планов компании? На одном из проектов я разработал такой интересный отчет: первая колба — год. Наполнение — сколько дней в году прошло в процентах. Следующие колбы — это контрольные показатели (может быть сколько угодно много). 100% — это план ЗА ГОД. Наполнение — как внутри года выполнен факт. Вот и смотрим: сколько прошло времени и как мы сработали. Минус — сезонность не учитывается. Плюс — взгляд со стороны. Подробнее >>
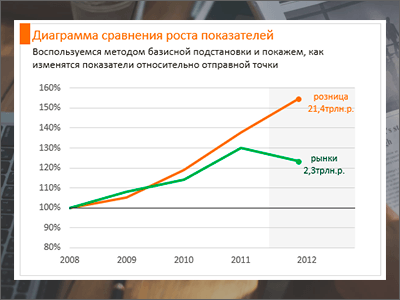
7. Диаграмма сравнения роста показателей
Как в Excel показать сравнить рост двух различных показателей? Можно «просто» сравнить данные. Правда, если они не сопоставимы, то особо ничего не увидишь. Но есть еще один способ, пожалуй, самый наглядный: методом базисной подстановки, который любит The Economist. Подробнее >>
8. Диаграмма с горизонтальной «зеброй»
Как построить в Excel диаграмму журнального качества с зеброй вместо горизонтальных линий? Есть несколько способов, с одним из которых можно ознакомиться благодаря приложенному файлу. Диаграмма построена по мотивам Wall Street Journal. Подробнее >>
9. График с вертикальной «зеброй»
Как на графике выделить данные с помощью вертикальной «зебры»? В таблицу, на основе которой строится график, необходимо добавить дополнительную строку с координатами фоновых столбцов. Немного манипуляций и все получится. Подробнее >>
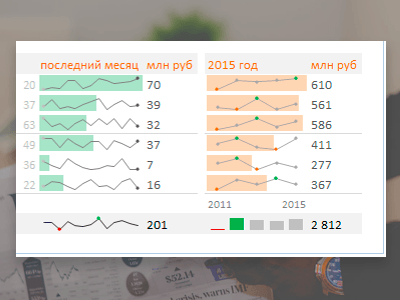
10. Спарклайны и микрографики
Как мы делаем отчеты? В виде здоровых (и нездоровых, кстати, тоже) таблиц. Что из них понятно людям, имеющим малый опыт работы с большими объемами данных? Ничего. Далее рассмотрен пример, как показать структуру продаж за месяц и за год, и тут же показать динамику по месяцам и годам. Подробнее >>
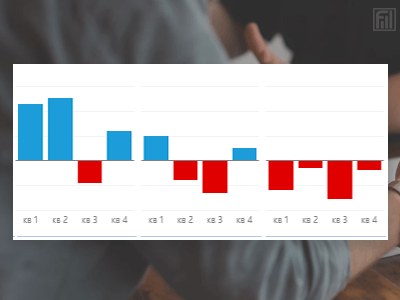
11. Как показать на диаграмме отрицательные значения другим цветом
Недавно встретил такую ситуацию: пользователь для обозначения отрицательных значений на диаграмме строил таблицу с ЕСЛИ(). Где минусы — одни блоки, где плюсы — другие. Так делать не нужно! Ведь в Excel есть стандартная возможность настраивать цвет блоков. Подробнее >>
12. Прокрутка в Excel
А напоследок предлагаем способ, как показать все диаграммы отчета, используя прокрутку в Excel. Подробнее >>
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
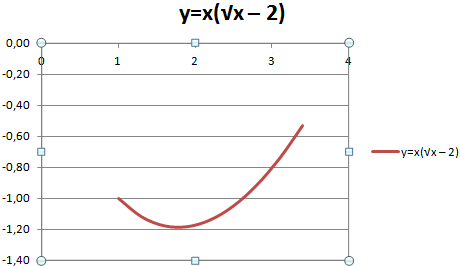
Пример: y=x(√x – 2). Шаг – 0,3.
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
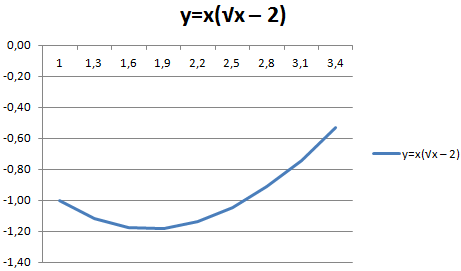
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
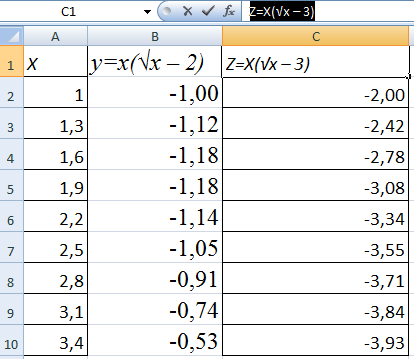
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
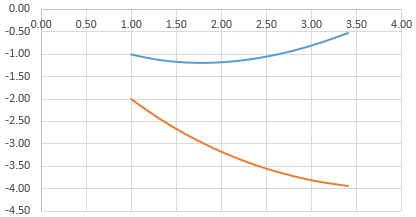
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Готовые примеры графиков и диаграмм в Excel скачать:
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.