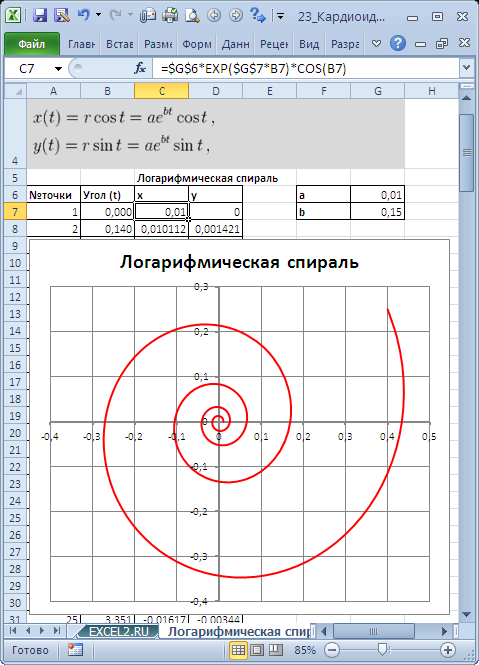
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см.
файл примера
):
х=2*а*cos(t)-а*cos(2*t)
y=2*а*sin(t)-а*sin(2*t)
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье
Эллипс и окружность в MS EXCEL
построены окружность и эллипс.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Может ли Excel строить сложные кривые?
|
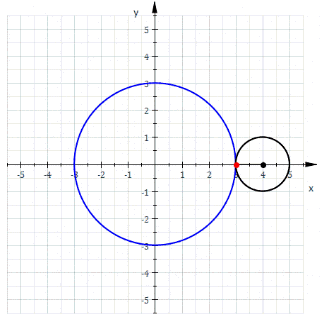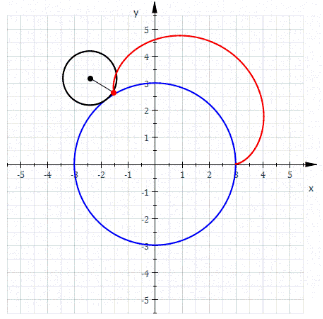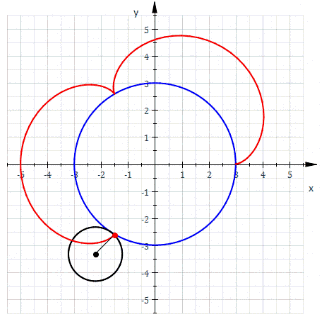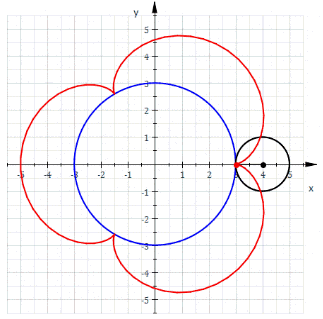
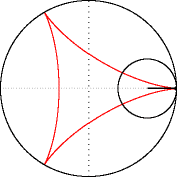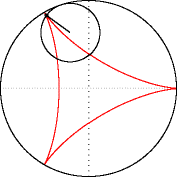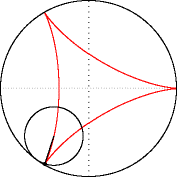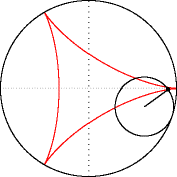
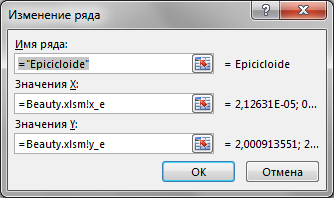
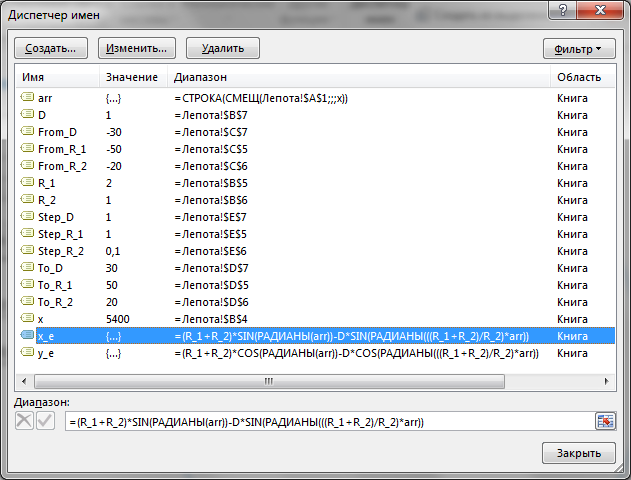
Меня трудно чем-то удивить в Excel, но когда я впервые увидел вот этот сайт, то у меня чуть глаз не выпал на клавиатуру. Очень рекомендую вам пройти по ссылке и поглазеть. В моём личном рейтинге эта команда (там двое мужчин и девушка) является №1 в мире по Excel. Сегодня я вам покажу нечто из их арсенала (с моими некоторыми адаптациями). Посмотрим на то, как при помощи точечной диаграммы с гладкими кривыми строить ТАКИЕ сложные вещи, что, когда глядишь на это в первый раз, просто не веришь, что это вообще можно нарисовать в Excel. Ну, например, как вам это: Дело в том, что мы все привыкли, что такие графики строятся по точкам, которые рассчитываются в ячейках таблицы. Тут же используется реально очень крутой трюк, который позволяет строить графики любых сложнейших функций, не используя ни диапазоны с точками XY, ни какие-либо макросы. Всё что вам нужно — это точечная диаграмма с гладкими кривыми, несколько констант и несколько именованных формул. Те граждане, кто пока плохо понимает, зачем это всё надо, сейчас просто откроют файлик, включат макросы и нажмут кнопку Старт, потому что это ПРОСТО КРАСИВО. На это можно смотреть минут 15 и всё равно будет интересно. Дольше смотреть не рекомендую, так как глаза и мозг устанут. Смотреть красоту ТУТА с теми, кому интересно, как это устроено, продолжаем разговор. В принципе абсолютно без разницы, какой график строить. Я взял циклоидальные кривые, так как они очень красивы, разнообразны и сложны. Эпициклоиды и гипоциклоиды (подмножество циклоидальных кривых) строятся по следующим параметрическим формулам: Эпициклоиды строятся так: Гипоциклоиды так: Знаки у R1 и R2 относительно друг друга определяют тип кривой (по какой поверхности круга R1 — по внутренней или внешней — будет катиться круг R2). Обратите внимание, что t — это угод в радианах. Напоминаю, что углы в 5′ и 365′ — разные углы. Если мы заглянем в ряды данных диаграммы, то увидим это: Сердце решения располагается тут: Как видите, большинство именованных диапазонов просто сылаются на конкретные ячейки и ничего сложного из себя не представляют. Кроме трёх диапазонов: arr, x_e, y_e. Можно заметить, что x_e и y_e — это то, на что ссылается ряд данных в диаграмме, и, что это формулы, описывающие кривые, которые я приводил выше. А вот ИД arr надо осмыслить: =СТРОКА( СМЕЩ( Лепота!$A$1; ; ; x) )X у нас равен 5400. Функция СМЕЩ() сформирует диапазон A1:A5400. А формула СТРОКА() будет вычислена для каждой строки данного диапазона, поэтому в результате мы получим массив чисел от 1 до 5400. Этот массив, будучи переданным в x_e, y_e тоже породит соответствующие массивы. Обратите внимание, что arr пропускается через функцию РАДИАНЫ(). Таким образом мы градусы (1..5400) переводим в радианы. Если честно, то я не знал, что ТАК можно Вот собственно и всё. А тот макрос, который у меня есть в книге, он просто случайным образом, но плавно меняет параметры R1, R2, D в пределах от From до To с шагом Step. P.S. Любителям WinAPI с его Sleep рекомендую обратить внимание на конструкцию Application.Wait Now + 1 / 24 / 60 / 60 / 2 Ну а теперь залипайте дальше на лицезрение циклоид |
Категория: Графики и диаграммы | Добавил: dsb75 (18.09.2015) |
| Просмотров: 13712 | Комментарии: 13 | Теги: гипоциклоиды, именованные диапазоны, Диаграммы, циклоиды, СМЕЩ, эпициклоиды | Рейтинг: 4.3/6 |
| Всего комментариев: 12 | |
|
Порядок вывода комментариев: Здравствуйте, Денис. 1. Вообще-то, X = R * cos (t); Y = R * sin (t). В вашем примере оси X и Y перепутаны местами, если брать за основу картинку из статьи, циклоида на диаграмме строится от вертикальной оси против часовой стрелки. Попробуйте ввести на листе разные значения угла, меньше 360 (45, 90, 180, 270) — увидите, о чём я. На красоту не влияет, конечно. 2. Попробуйте ставить в ячейку х значения 1 и 5400 и сохранять книгу, размер файла изменится в несколько раз. Диапазоны значений не хранятся на листе, но диаграмма хранит весь диапазон значений в файле. Для уменьшения размера можно кодом VBA присваивать x 5400 после открытия и 1 перед закрытием. 3. Ни в одной из статей вашего сайта нет ни одного вызова Windows API, да и фраза «Любителям WinAPI с его Sleep» позволяет предположить, что сами вы к его любителям не относитесь. Можно полюбопытствовать, откуда у вас такое принципиальное (практически — религиозное Для корректности сравнения скоростей из вашего кода выкинуты строки: Код ActiveSheet.Calculate ‘ не нужна, если есть DoEvents Application.Wait Now + 1 / 24 / 60 / 60 / 2 ‘ просто не нужна На всякий случай: комментарий категорически не является насмешкой или наездом, у вас отличный сайт и редкие педагогические способности, статьи, написанные столь доходчивым языком редко где найдёшь.
Спасибо за содержательный комментарий. Успехов вам! Использование Sleep вместо Application.Wait является шагом вперёд, осознанным или нет — второй вопрос. При выполнении програмной задержки состояние приложения можно разделить: — по загрузке процессора: грузит / не грузит; Так вот, Application.Wait находится в худшем из четырёх возможных сочетаний этих состояний. Пусть надо выполнить програмную задержку dDelay сек. Тогда варианты: ‘ вариант 0: не реагирует на события, загрузка процессора (в современном мире — одного из ядер) — 100% ‘ вариант 1: не реагирует на события, загрузка процессора — 0% ‘ вариант 2: реагирует на события, загрузка процессора — 100% ‘ вариант 3: сочетает достоинства и недостатки двух предыдущих, (не мгновенно) реагирует на события, загрузка процессора — больше 0% Ни один из этих вариантов не является идеальным с точки зрения потоков, обработки сообщений, машинного времени и пр.
Долгая история
Давайте, о себе любимом напишу подробно позже и в почту. Пока в догонку об убогости Application.Wait: https://yadi.sk/i/7NQT-OFN3Kv2BK Коротко: Application.Wait не предназначен для организации задержек, не кратных 1 сек., в частности — менее 1 сек. Поэтому он у вас в Beauty на самом деле не работал, можно было апостроф в начале строки не ставить
Ещё раз про морковь или возвращаясь к непечатному. Доброго здоровья, Денис. Глядя на процедуру расчёта и вывода циклоиды (Sub DrawCycloide) я задался вопросом: какую часть времени занимает расчёт значений для её вывода, а какую — собственно, графический вывод. Профилировать процедуру напрямую по таймеру в контрольных точках смысла не имело: слишком маленькие интервалы приведут к слишком большим погрешностям. Поэтому решено было нивелировать (свести к нулю) время расчёта, чтобы осталось только время, занимаемое графическим выводом. Как нивелировать? Перевести в машинный код, естественно 1. Первым делом к ранее выложенному здесь Beauty free.xlsm был прикручен «спидометр» — код, отображающий на форме количество выводимых циклоид в секунду. 2. Далее, через экспорт-импорт, форма из книги Beauty free speed.xlsm была перемещена в «классический» проект VB. Что понравилось: форма встала в проект VB сразу «как влитая», никаких допиливаний и танцев с бубном не понадобилось. Естественно, ссылки на ячейки рабочего листа заменены константами. 3. Наконец, была проведена переработка проекта с целью замены объекта UserForm VBA объектом Form VB: 4. И её дальнейшая оптимизация: Примечания. Итоги. Практический вывод. P. S. Всё вышенаписанное стоило писать месяца полтора назад. Руки дошли только сейчас, однако. |
|
Добавлять комментарии могут только зарегистрированные пользователи.
[
Регистрация
|
Вход
]
Построение
графиков 3-х видов в электронной таблице
Excel
1.
Построить несколько графиков параметрически
заданной функции при разных значениях
конcтант
а, b,
.
Оси графика – х и y,
которые зависят от аргумента t
или .
|
№ |
Название кривой |
Вид |
Параметрические |
Диапазон аргумента |
Кол-во граф. |
Значения |
|
1 |
Циклоида |
|
x = a(t — sin
y = a(1 — cos |
t 0 6
шаг |
5 |
a = 1; |
|
2 |
Циклоида |
|
x = a(t — sin
y = a(1 — cos |
t 0 6
шаг |
6 |
a = 2
= 0.4; |
|
3 |
Трохоида |
|
x = at — bsin
y = a — bcos |
t 0 10
шаг |
5 |
a = -1
b |
|
4 |
Эпитрохоида |
|
x = acos
y = asin |
t 0 10
шаг |
6 |
a = 0;
b = 2 |
|
5 |
Гипотрохоида |
|
x = acos
y = asin |
t 0 10
шаг |
6 |
a = 0;
b = 2 |
|
6 |
Декартов лист |
|
x = at / (1 + t3)
y = a |
t -6 6
шаг |
6 |
a = 1; |
|
7 |
Циссоида |
|
x = a
y = a |
t -6 6
шаг |
6 |
a = 1; |
|
8 |
Строфоида |
|
x = a y = at(t2 — 1) / (t2 + 1) |
t -6 6
шаг |
6 |
a = 1; |
|
9 |
Конхоида Никомеда |
|
x = a + bcos
y = atg |
t 0
шаг |
5 |
a = 2
b |
|
10 |
Улитка Паскаля |
|
x = acos2
y = a |
t 0 2
шаг |
6 |
a = 1; b |
|
11 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a
b = 1; |
|
12 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 10
Шаг |
6 |
a = 3;
= 0.5; |
|
13 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a = 1;
= 0.5; |
|
14 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a = 7;
= 0.5; |
|
15 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 2
Шаг |
6 |
a
b = 1.5; |
|
16 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 6
Шаг |
6 |
a b = 1 |
|
17 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 2
Шаг |
6 |
a = 1;
= 0.5; |
|
18 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 10
Шаг |
6 |
a = 5;
= 0.2; |
|
19 |
Спираль |
|
x = atcos
y = btsin |
t 0 10
Шаг |
6 |
a
b = -2; |
|
20 |
Гиперболич. спираль |
|
x = (acos
y = (b |
t -6 6
Шаг |
5 |
a = 2
b = 1; |
|
21 |
Гиперболич. спираль |
|
x = (acos
y = (b |
t 0.5 20
Шаг |
5 |
a = 3
b = 1; |
|
22 |
Астроида |
|
x = acos3
y = b |
t 0 8
Шаг |
5 |
a
b = 1; |
|
23 |
Астроида |
|
x = acos3
y = a |
t 0 8
Шаг |
5 |
a
b = 0; |
|
24 |
Астроида |
|
x = acos3
y = a |
t 0 8
Шаг |
5 |
a
b = 0.5; |
|
25 |
Эвольвента |
|
x = acos
y = a |
t -10 10
Шаг |
4 |
a |
|
26 |
Эвольвента |
|
x = acos
y = a |
t 0 20
Шаг |
4 |
a |
|
27 |
Эллипс |
|
x = acos
y = b |
t 0 2
Шаг |
5 |
a
b = 1; |
|
28 |
Эллипс |
|
x = acos(c
y = b |
t 0 2
Шаг |
5 |
a
b = 1; |
|
29 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
history 16 апреля 2015 г.
- Группы статей
- Диаграммы и графики
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Как построить эпициклоиду в excel
0 Спам
Ещё раз про морковь или возвращаясь к непечатному. Доброго здоровья, Денис.
Глядя на процедуру расчёта и вывода циклоиды (Sub DrawCycloide) я задался вопросом: какую часть времени занимает расчёт значений для её вывода, а какую — собственно, графический вывод. Профилировать процедуру напрямую по таймеру в контрольных точках смысла не имело: слишком маленькие интервалы приведут к слишком большим погрешностям. Поэтому решено было нивелировать (свести к нулю) время расчёта, чтобы осталось только время, занимаемое графическим выводом. Как нивелировать? Перевести в машинный код, естественно . Но всё по порядку.
1. Первым делом к ранее выложенному здесь Beauty free.xlsm был прикручен «спидометр» — код, отображающий на форме количество выводимых циклоид в секунду.
Результат здесь: https://yadi.sk/i/EtolJiGL3LhgpJ
2. Далее, через экспорт-импорт, форма из книги Beauty free speed.xlsm была перемещена в «классический» проект VB. Что понравилось: форма встала в проект VB сразу «как влитая», никаких допиливаний и танцев с бубном не понадобилось. Естественно, ссылки на ячейки рабочего листа заменены константами.
Исходник: https://yadi.sk/d/YsNL93Ph3MxWPV
Результат: https://yadi.sk/d/T3u021U-3MxWRv
3. Наконец, была проведена переработка проекта с целью замены объекта UserForm VBA объектом Form VB:
Исходник: https://yadi.sk/d/KCgRKEN33MxYGC
Результат: https://yadi.sk/d/6Odb1BKA3MxYHB
Примечания.
1. Шаги 3 и 4 не имеют отношения к поднятому вопросу, но, раз были проделаны — решил выложить
2. Если у вас нет установленного VB, можно сразу смотреть результаты, вирусов в них нет
Итоги.
Преимущество в скорости компилятора над интерпретатором в доказательствах не нуждалось, вопрос был в количественной оценке. Считая, что время графического вывода в любом случае превалирует над временем расчёта, ожидал прироста быстродействия в 20%-30%. После запуска откомпилированного на шаге 2 проекта получил прирост в скорости в 2,5 раза на своей системе. Медленно: в два с половиной раза. То есть, в коде книги Excel расчёт шёл, примерно, в 1,5 раза дольше вывода. Во сколько именно раз поднялась скорость вычислений данные действия не показывают, но, оценочно — в 8 — 10 раз.
Практический вывод.
Если ваш код VBA содержит сложные расчёты — вынести их в отдельную внешнюю процедуру, подключаемую как DLL или OCX ещё как имеет смысл.
P. S. Всё вышенаписанное стоило писать месяца полтора назад. Руки дошли только сейчас, однако.
0
Аналогично
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
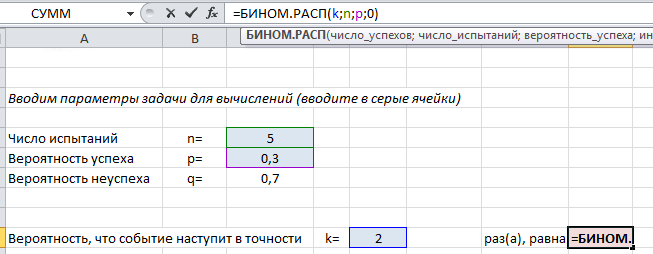
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
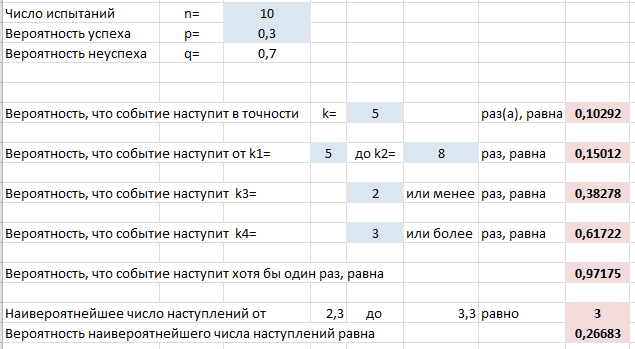
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
-
Группы статей
- Диаграммы и графики
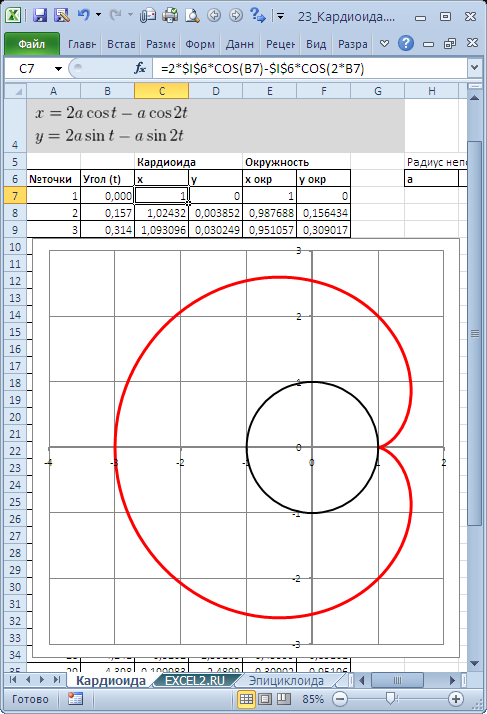
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
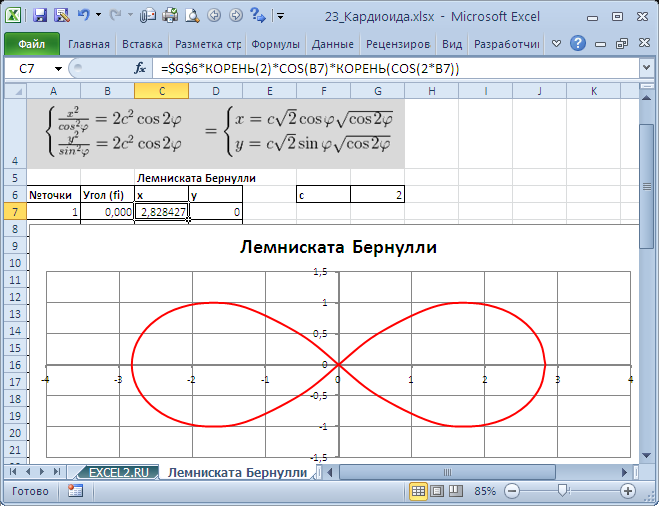
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
источники:
http://excel2.ru/articles/ploskie-algebraicheskie-krivye-v-ms-excel
http://pedsovet.su/excel/48255_krasivye_grafiki_v_excel
Практическая работа: Построение графиков средствами приложения Excel.
Цель: научиться
строить графики в Excel; развить самостоятельность при получении практических
навыков на ПК; развить навыки мыслительной деятельности.

графиков функций, заданных в параметрическом виде или в полярной системе
координат.
Параметрическое
представление кривой на плоскости – это две функции, явно выражающие обе
координаты x и y через значение
некоторого производящего параметра:
Задание 1:
Построить окружность, координаты точек которой вычисляются по формулам:
1)
Для построения полной окружности радиуса R=100 необходимо создать таблицу, в которой
значение параметра t меняется от 0 до 2π с шагом 0,1 (для заполнения ячеек используйте функцию Автозапонения).
2)

нахождения координат x и y (см. выше) и скопировать формулу для всех значений t
3)
Для построения графика выделить столбцы x и y таблицы и выбрать тип диаграммы Точечная.
Получаем диаграмму:
Подпишите
название диаграммы Окружность.
ЗАДАНИЯ для
самостоятельного выполнения:
|
t∈[0;5π] |
|
Астроида x=2sin3(t) y=2cos3(t) t∈[0;2π] |
|
|
|
Дельтоида
y=2sin(t)−sin(2t) t∈[0;2π] |
|
x=16sin3(t) y=13cos(t)−5cos(2t)−2cos(3t)−cos(4t) t∈[0;2π] |
|
|
|
Гипоциклоида x=4,4(cos(t)+cos(1,1t)/1,1) y=4,4(sin(t)−sin(1,1t)/ 1,1) t∈[0;20π] |
|
Гипоциклоида 2 x=24,8(cos(t)+cos(6,2t)/6,2) y=24,8(sin(t)−sin(6,2t)/6,2) t∈[0;10π] |
|
|
|
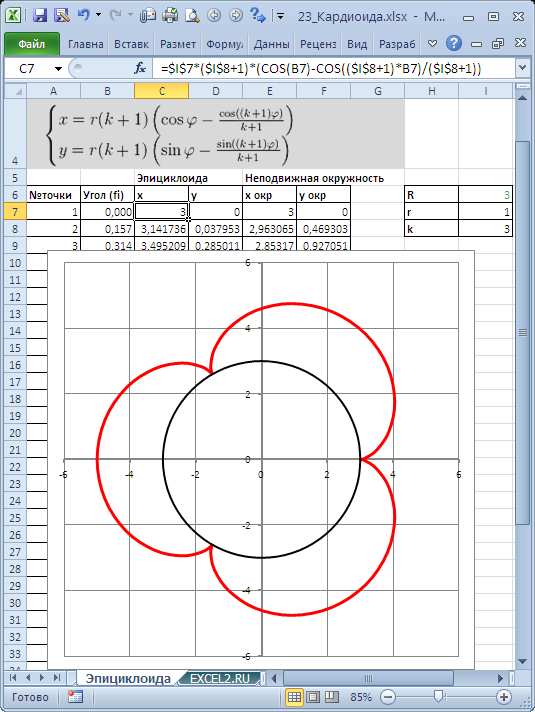
Эпициклоида x=6,2(cos(t)−cos(3,1t)/3,1) y=6,2(sin(t)−sin(3,1t)/ 3,1) t∈[0;20π] |
|
Бабочка x=sin(t)(ecos(t)−2cos(4t)+sin5(1t/12)) y=cos(t)(ecos(t)−2cos(4t)+sin5(1t/12)) t∈[0;12π] |
|
|
|
n- лепестковая n – определяет число лепестков |
|
Фигура Лиссажу
y=sin(6t) t∈[0;2π] |
|
|
Указания
к оформлению работы:
1)
Расчёты функций делать на одном Листе,
обозначая функции для разных фигур: x1,y1; x2,y2; x3,y3 и т.д.
2)
Все графики подписать и расположить каждый на
отдельном Листе. Листы переименовать по названию фигуры: Окружность,
Спираль, Астроида и т.д.


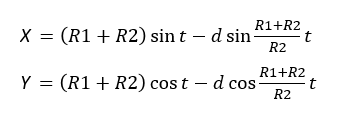

 Зачем делать столь глубокие выводы на единичных фактах? Я дурачился. Но вы правы в том, что WinAPI я не знаю, но никаких религиозных запретов на этой почве перед собой не воздвигаю. Просто часто sleep — единственное, что видишь у VBA-шников, но в Excel особой необходимости в нем нет. То есть, если вам нужно сделать паузу, то нефиг городить огород с winapi. Файл ваш посмотрел — офигенно. Дома посмотрю подробнее. Вот для этого и winapi не грех применять
Зачем делать столь глубокие выводы на единичных фактах? Я дурачился. Но вы правы в том, что WinAPI я не знаю, но никаких религиозных запретов на этой почве перед собой не воздвигаю. Просто часто sleep — единственное, что видишь у VBA-шников, но в Excel особой необходимости в нем нет. То есть, если вам нужно сделать паузу, то нефиг городить огород с winapi. Файл ваш посмотрел — офигенно. Дома посмотрю подробнее. Вот для этого и winapi не грех применять  , так что лучше прочитать её «по диагонали» и никогда так не делать.
, так что лучше прочитать её «по диагонали» и никогда так не делать. 














