Эллипс и окружность в EXCEL
history 29 марта 2015 г.
-
Группы статей
- Диаграммы и графики
Построим окружность и эллипс.
Вычислим х и y для эллипса из уравнения в параметрической форме: x=a*cos(t) и y=b*sin(t), где а и b — большая и малая полуось. При а=b получим окружность. Зададим угол от 0 до 2*ПИ() в 20 (21) точках.
Выберем тип диаграммы Точечная с гладкими кривыми и маркерами.
Т.к. MS EXCEL автоматически подбирает масштаб координатных осей, то для того чтобы форма эллипса и окружности соответствовала заданной, необходимо зафиксировать максимальное, минимальное значение и цену деления оси.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Как построить эллипс в экселе по уравнению
В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
по горизонтали — значения х, по вертикали — значения у.
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.
=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
Как строить графики в Excel
В электронной таблице Excel можно производить вычисления, используя формулы, а на основе их результатов строить различные диаграммы, в частности, графики. С их помощью в книге отображаются колебания и изменения данных во времени, показывается зависимость одних значений от других. Такой метод визуализации очень облегчает восприятие числовой информации.
В электронной таблице Excel можно производить вычисления, используя формулы, а на основе их результатов строить различные диаграммы, в частности, графики. С их помощью в книге отображаются колебания и изменения данных во времени, показывается зависимость одних значений от других. Такой метод визуализации очень облегчает восприятие числовой информации.
Пошаговый процесс создания диаграммы
График включает в себя множество элементов, при этом одни из них по умолчанию отображаются на рисунке, другие можно добавить/удалить и настроить в ручном режиме. При построении графика в Excel пользователь выбирает нужный вариант из нескольких его видов. Например, простой (и объемный) показывает изменение кого-то значения во времени (прибыль по месяцам и т.д.), с накоплением – изменение составляющей целого значения с течением времени, а нормированный с накоплением – изменение доли каждого значения с течением времени. Каждый из них также может быть с маркером или без него, но рисуются они одинаково.
Создание графика происходит после подготовки исходной таблицы.
С простым содержимым
На простейшем примере рассмотрим, как отображаются конкретные события в разные промежутки времени:
- Выделить всю таблицу.
- В главном меню книги перейти в раздел «Вставка», кликнуть по пункту «График» – в выпадающем меню будет показано 6 рисунков.
- Если клацнуть по тому или иному виду, на листе сразу появится результат.
- На рисунке будет 2 линии (кривая и прямая). Прямая не несет никакой смысловой нагрузки, поэтому ее следует удалить, выделив кликом левой кнопки мышки и нажав «Del».
Важно! При наведении курсора на любую диаграмму всплывает подсказка, для каких данных ее лучше использовать.
Теперь нужно придать графику красивый вид:
- Поскольку есть только одна кривая, справа стоит удалить легенду «прибыль, руб.». Выделить ее кликом мышки и нажать «Del».
- Перейти в раздел «Макет», где с помощью опции «Подписи данных» определить расположение цифр.
- Подписать оси с помощью одноименной опции.
- Использование дополнительных параметров опции «Название диаграммы» поможет переместить или вовсе удалить заголовок, изменить его стиль, добавить заливку, градиент или тень и т.д.
- Чтобы на горизонтальной оси вместо порядковых чисел были года 2015-2019, выделить числа кликом, вызвать контекстное меню правой кнопкой мышки и «Выбрать данные». Изменить подписи, указав диапазон годов.
Если нужно перенести созданный рисунок на другой лист книги, следует перейти на вкладку «Конструктор», где на верхней панели справа есть опция «Переместить…». В новом окне клацнуть по пункту «На отдельном листе» и подтвердить действие нажатием на «Ок».
С несколькими кривыми
Несмотря на то, что данных будет больше, принцип построения остается прежним:
- Выделить всю таблицу – «Вставка» – «График» – выбор желаемого варианта рисунка.
- Удалить нижнюю прямую, но оставить легенду справа, иначе ничего не будет понятно. Добавить заголовок, подписи данных, названия осей, придать рисунку другой стиль по желанию.
С последующим добавлением дополнительной оси
Если единицы измерения значений одинаковы, нарисовать график в Excel можно вышеописанным способом. Когда нужно представить на рисунке данные разных типов, чтобы показать их зависимость друг от друга, придется добавлять вспомогательную ось.
- Построить график по данным таблицы.
- Выделить ось, для которой будет добавлена еще одна. Клацнуть по ней правой кнопкой мышки, из контекстного меню выбрать «Формат ряда данных». В новом открывшемся окне во вкладке «Параметры ряда» отметить пункт «По вспомогательной оси».
- После закрытия настроек появится на рисунке вторая ось, которая автоматически подстроится под значения кривой.
Также существует другой способ добавления оси – через изменение типа диаграммы:
- Выделить кликом ось. Из выпадающего меню выбрать пункт «Изменить тип диаграммы для ряда».
- Щелкнуть по одному из видов из множества диаграмм – «Ок».
- На рисунке появится дополнительная ось для другого типа измерений.
Важно! Программа позволяет добавить только одну дополнительную ось.
С функцией
В качестве примера будет использоваться функция y=x(√x — 2) с шагом 0,3.
- Составить таблицу с исходными данными. Первая ячейка столбца X – это 1, вторая – содержимое первой ячейки + 0,3. Формула имеет следующий вид: =A2+0,3. При помощи маркера заполнения протянуть вычисление вниз.
- В столбце Y прописать формулу для расчета: =A2*(КОРЕНЬ(A2)-2). Протянуть ее вниз до B
- Выделить стороннюю ячейку, щелкнув по ней мышкой. Далее перейти по пути «Вставка» – «График» – выбор рисунка.
- Кликнуть по пустому месту в окне диаграммы правой кнопкой мышки и выбрать данные.
- Выделить диапазон данных. Нажать «Добавить». Откроется окно с изменением ряда.
- Задать название ряда – функция, значения X и Y – первый и второй столбец соответственно. Нажать «Ок».
- В пустой области диаграммы отобразится результат.
- На оси X вместо значений из таблицы стоят порядковые числа. Чтобы отредактировать их, нужно кликнуть по числам правой кнопкой мышки и выбрать данные.
- Для изменения подписи горизонтальной оси клацнуть по соответствующей кнопке и выделить диапазон с нужными значениями в таблице. График преобразится.
С наложением нескольких функций
Построить несколько графиков в Excel по табличным данным совсем несложно. Для этого нужно добавить еще один столбец с функцией z=x(√x — 4).
- В первую ячейку столбца Z вписать формулу =A2*(КОРЕНЬ(A2)-4). Размножить ее по остальным ячейкам.
- Выделить числа из столбца Z, скопировать их (Ctrl+C) и вставить (Ctrl+V) на область диаграммы. Некорректное название ряда и отображение цифр на оси редактируются посредством опции «Выбрать данные».
С зависимостью между данными
В результате должна отобразиться зависимость содержимого одного столбца от содержимого другого, то есть, другими словами, это зависимость функции от изменения аргумента.
Есть условие: A=f(E); B=f(E); C=f(E); D=f(E). Необходимо построить диаграмму стандартным способом.
В пункте выбора источника данных следует добавить элементы легенды:
- Первый ряд: название – A, значения X – числа из столбца A, значения Y – числа из столбца E.
- Второй ряд: название – B, значения X – числа из столбца B, значения Y – числа из столбца E.
- Третий ряд: название – C, значения X – числа из столбца C, значения Y – числа из столбца E.
источники:
http://krivaksin.ru/trehmernyie-grafiki-funktsiy-v-excel/
http://sysadmin-note.ru/article/kak-stroit-grafiki-v-excel/
Построим окружность и эллипс.
Вычислим х и y для эллипса из уравнения в параметрической форме: x=a*cos(t) и y=b*sin(t), где а и b — большая и малая полуось. При а=b получим окружность. Зададим угол от 0 до 2*ПИ() в 20 (21) точках.
Выберем тип диаграммы Точечная с гладкими кривыми и маркерами.
Т.к. MS EXCEL автоматически подбирает масштаб координатных осей, то для того чтобы форма эллипса и окружности соответствовала заданной, необходимо зафиксировать максимальное, минимальное значение и цену деления оси.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Изучим графические
возможности пакета Excel по построению
графиков функций в трехмерном пространстве.
Пример 1. Построить
верхнюю часть эллипсоида:
Для построения
поверхности необходимо разрешить
заданное уравнение относительно
переменной z.

Так как в условии речь
идет о верхней части эллипсоида, то
рассмотрим ОДЗ положительной части
уравнения:
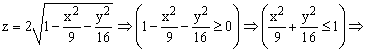
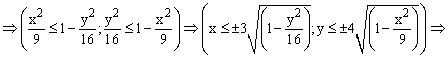
Приступим к построению
поверхности. В диапазон B1:J1 введем
последовательность значений переменной
y: -4, -3, …,4, а в диапазон ячеек А2:А14
последовательность значений переменой
x: -3, -2,5,…3.
В ячейку В2 введем
формулу = 2*(1-($A2^2)/9-(B$1^2)/16)^0,5.
Знак $, стоящий
перед буквой в имени ячейки, дает
абсолютную ссылку на столбец с данным
именем, а знак $, стоящий перед цифрой
— абсолютную ссылку на строку с этим
именем. Поэтому при копировании формулы
из ячейки В2 в ячейки диапазона
B2:J14 в них будет найдено значение z
при соответствующих значениях x, y.
Т.о. создается таблица значений z.
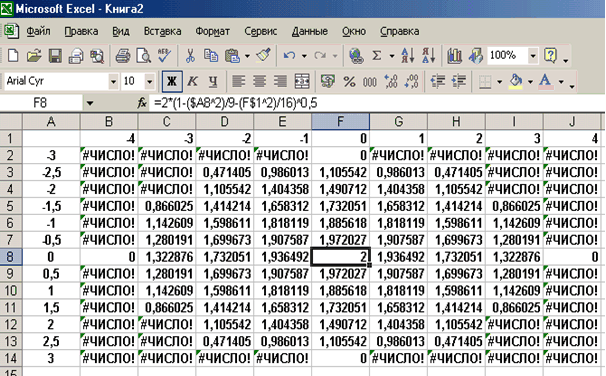
Рис. 2.19. Образцы
заполнения таблицы для построения
поверхности
Перейдем к построению
поверхности. Выделим диапазон ячеек
A1:J14, содержащий таблицу значений
функции и ее аргументов, вызовем Мастер
диаграмм и тип диаграммы Поверхность,
далее заполним диалоговые окна так как
было описано в лабораторной работе по
построению графиков функций. После
нажатия кнопки Готово получим
изображение заданной поверхности.
|
|
|
Рис. 2.20. Образцы
построения поверхностей
Пример
2. Построить поверхность z = x2-y2
при x, y [-1;1].
В диапазон B1:L1
введем последовательность значений
переменной x: -1, -0.8, …,1, а в диапазон
ячеек А2:А12 последовательность
значений переменой y. В ячейку В2
введем формулу = $A2^2-B$1^2 и скопируем
ее в ячейки диапазона B2:L12. На рисунке
2 изображена заданная поверхность.
Самостоятельная
работа
Задание 1. Построить
верхнюю (четные варианты) или нижнюю
(нечетные варианты) часть эллипсоида,
заданного уравнением:
Таблица 2.20
Варианты для самостоятельного выполнения
|
№ |
a |
b |
c |
№ |
a |
b |
c |
|
1 |
1 |
2 |
3 |
18 |
1.5 |
1.25 |
1.95 |
|
2 |
2 |
0.9 |
1.1 |
19 |
4 |
5 |
6 |
|
3 |
2 |
1 |
3 |
20 |
6 |
5 |
4 |
|
4 |
0.71 |
0.75 |
1.21 |
21 |
4 |
6 |
5 |
|
5 |
1.72 |
2.9 |
3.1 |
22 |
1 |
5 |
6 |
|
6 |
2 |
3 |
5 |
23 |
5 |
6 |
1 |
|
7 |
3 |
5 |
4 |
24 |
5 |
1 |
6 |
|
8 |
5 |
3 |
4 |
25 |
7.1 |
7.5 |
4.21 |
|
9 |
5 |
4 |
3 |
26 |
7.2 |
8.9 |
1 |
|
10 |
5.71 |
4.75 |
4.21 |
27 |
1 |
3 |
7 |
|
11 |
2.72 |
3.9 |
5.1 |
28 |
7 |
3 |
1 |
|
12 |
2 |
3 |
7 |
29 |
1 |
1 |
2 |
|
13 |
7 |
4 |
2 |
30 |
1.5 |
2.78 |
3.45 |
|
14 |
7 |
2 |
4 |
31 |
5.1 |
7.1 |
1.2 |
|
15 |
1.5 |
0.78 |
1.45 |
32 |
6.1 |
3.1 |
2.2 |
|
16 |
3.1 |
3.2 |
5.3 |
33 |
5 |
3 |
1.1 |
|
17 |
1.25 |
1.95 |
1.5 |
34 |
2.5 |
2.78 |
4.5 |
Задание
2. Построить однополостный (четные
варианты) или двуполостный (нечетные
варианты) гиперболоид, заданный
уравнением:
Таблица 2.21
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статья «Использование Excel при решении математических
задач» (учитель математики школы №38 г.Казани Васина Д.А., статья опубликованна
на сайте Казанское образование http://kros.ru/_educ/conferens-5.4-21.php
в 2008 году и с журнале МО и НРТ от 2008 года «Информатизация образования:
поиски и находки»)
Любому человеку в ходе практической деятельности
приходится совершать операции над количественными данными, которые
осуществляются в соответствии с математическими законами. Поэтому для человека,
который не свяжет дальнейшую жизнь с математикой, наиболее важным является
практический аспект математики. Для него это прикладная наука, близкая к
технологии. Здесь наиболее важным является умение провести необходимые
вычисления. Математическая теория изменяется сравнительно медленно, однако
технология применения математических методов претерпела значительно более существенные
изменения. Буквально за последние десятилетия пройден путь от расчетов в уме и на
бумаге к применению счетов, арифмометров, калькуляторов и далее — к расчетам на
компьютере. Поэтому в настоящее время специалист, даже хорошо знающий
математику, но не умеющий применять математические методы на компьютере, не
может считаться специалистом современного уровня.
Использование компьютера при проведении расчетов
сдвигает акценты в математической подготовке специалиста. Если раньше основное
внимание было сосредоточено на математических методах, которые предусматривали
проведение расчетов вручную, то теперь, с появлением специализированных
математических программ, необходимо научиться проводить требуемые вычисления на
компьютере.
Для решения задач на компьютерах чаще всего
применяется метод решения «в лоб», опирающийся на основное определение и
использующий самый общий подход. Снижается значение частных случаев,
различных свойств описываемых математических объектов, ориентированных на
облегчение решений вручную.
Например, при решении вручную квадратного уравнения ax2+bx+c=0 помимо
общего
решения требовалось знать решения для частых случаев:
когда квадратное уравнение разлагается на множители, когда b —четное,
когда а = 1, по формулам Виета. При этом было принято считать, что
решение «рационально», если для него используется, подходящая частная формула. В
настоящее время при применении компьютера, по-видимому, рациональным следует
считать решение с использованием общих подходов, по общей формуле. В то же
время традиционное преподавание классической математики все еще ориентировано
на дальнейшую работу с карандашом и бумагой.
Наиболее важной отличительной особенностью предлагаемого
материала должно являться рассмотрение основных разделов курса математики не в
традиционном изложении, а с перспективой дальнейшего применения компьютера. Причем,
в отличие от курсов, информатики, изложение материала должно вестись не «от
пакетов программ и их возможностей», а «от математических задач к способам их
решения на компьютере». При этом основное внимание должно быть сосредоточено на
реализации способов решения математических задач, на том, как решать типовые
задачи.
Компьютерный математический анализ данных предполагает
некоторое математическое преобразование данных с помощью определенных
программных средств. Следовательно, необходимо иметь представление как о
математических методах обработки данных, так и о соответствующих программных
средствах, то есть необходимо опираться на определенный программный пакет.
Существует значительное количество специализированных
математических пакетов, таких как MatLab, MatbCad, Math, Mathematica, Maple и др. Все
они охватывают основные разделы математики и позволяют производить подавляющее
большинство необходимых. математических расчетов. Однако освоение этих пакетов
самостоятельно — достаточно трудоемкая задача. В то же время в курс
информатики в большинстве вузов включено изучение электронной таблицы Excel. Поэтому
представляется оправданным реализовать в старших классах подход, основанный на
применении математических методов именно с помощью пакета Excel. Конечно, Excel сильно
уступает специализированным математическим пакетам. Тем не менее большое
количество математических задач может быть решено с его помощью.
Изложение учебного материала в 10 — 11-х классах
может осуществляться в следующей последовательности (из расчета 1час в неделю –
факультативный или элективный курс) 1. Основные операции в Excel — 12 часов
Запуск Excel, окно Excel, открытие таблицы, создание новой
рабочей книги, ввод данных, выделение блока ячеек, построение диаграмм,
редактирование диаграмм, копирование, автозаполнение, автосуммирование, ввод
математических формул, копирование формул, печать результатов, форматирование
рамки таблицы, работа с простейшими базами данных, отмена действий, сохранение
— результатов, закрытие рабочей книги, завершение работы, получение справочной
информации, сообщение об ошибках
2. Построение графиков функций 4 часа
Линейная, квадратичная, кубическая, обратная
пропорциональность, со знаком корня, модуля, дробно-рациональная,
тригонометрическая, логарифмическая, показательная функции.
3. Построение кривых 2 порядка — 2 часа
Построение окружности, эллипса.
4. Графическое решение систем уравнений — 2 часа
5 Построение плоскости — 1 час
6. Построение поверхностей второго порядка в
пространстве-3 часа
Построение эллипсоида, гиперболоида, параболоида,
конуса.
7. Решение уравнений с одним неизвестным —2 часа
8. Элементы линейной алгебры — 10 часов
Операции с матрицами, решение систем линейных уравнений.
9 Элементы математического анализа — 8 часов
Производная, определенный интеграл, числовые и
функциональные ряды.
10 Элементы теории вероятности 10 часов
Понятие случайного событии, вероятности
события, условная вероятность, перестановка, сочетания, размещение
11. Элементы статистики — 10 часов
Понятие математической статистики, выборочный метод, выборочная
функция распределения, выборочная характеристика, проверка статистических
гипотез.
Итого — 64 часа.
В
социально-гуманитарном классе можно осуществлять в следующей последовательности
(из расчета 1час в неделю во 2 половине 10 класса и в 1 половине 11 класса –
факультативный или элективный курс)
1. Основные операции в Excel — 12 часов
Запуск Excel, окно Excel, открытие таблицы, создание новой
рабочей книги, ввод данных, выделение блока ячеек, построение диаграмм,
редактирование диаграмм, копирование, автозаполнение, автосуммирование, ввод
математических формул, копирование формул, печать результатов, форматирование
рамки таблицы, работа с простейшими базами данных, отмена действий, сохранение
— результатов, закрытие рабочей книги, завершение работы, получение справочной
информации, сообщение об ошибках
2. Построение графиков функций 4 часа
Линейная, квадратичная, кубическая, обратная
пропорциональность, со знаком корня, модуля, дробно-рациональная,
тригонометрическая, логарифмическая, показательная функции.
3. Построение кривых 2 порядка — 2 часа
Построение окружности, эллипса.
4. Элементы теории вероятности 10 часов
Понятие случайного событии, вероятности
события, условная вероятность, перестановка, сочетания, размещение
5. Элементы статистики — 10 часов
Понятие математической статистики, выборочный метод,
выборочная функция распределения, выборочная характеристика, проверка статистических
гипотез.
Итого — 64 часа.
К этому курсу имеется приложение, где подробно описаны
разделы 2 – 6. Для лучшего восприятия материала, все названия клавиш, кнопок,
диалоговых окон и их полей, команды меню в приложении выделены специальным
стилем.
Приложение
Построение
графика линейной функции.
Пример 1
Рассмотрим построение прямой в Ехсеl на примере
у = 2х +1. Пусть необходимо построить отрезок прямой, лежащий в I
квадранте (х € [0; 3] ) с шагом Δ = 0,25.
Решение. Задача построения прямой (как и любой диаграммы в Ехсеl)
обычно разбивается на несколько этапов. Пусть после запуска пакета открыт
чистый рабочий лист.
Этап 1. Ввод данных. Прежде чем строить прямую необходимо составить
таблицу данных (х и у) для значениями х, а второй
соответствующими показателями у. Для этого в ячейку А1 вводим
слово Аргумент, а в ячейку В1 ее построения в рабочем окне
таблицы Ехсеl. Для этого значения х и у
следует представить в виде таблицы, где столбцами являются соответствующие
показатели. Пусть в рассматриваемом примере первый столбец будет— слово Прямая.
Начнем с введения значений аргумента. В ячейку А2
вводится первое значение аргумента — левая граница диапазона (0). В
ячейку АЗ вводится второе значение аргумента — левая граница диапазона
плюс шаг построения (0,25). Затем, выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения аргумента (за правый нижний угол блока
протягиваем до ячейки А14).
Далее вводим значения прямой. В ячейку В2
вводим ее уравнение: =2*А2 + 1, предварительно переключившись на
английский язык (Аlt+Shift). Обращаем внимание, что уравнение прямой
должно быть преобразовано к виду уравнения с угловым коэффициентом. Затем
автозаполнением копируем эту формулу в диапазон В2:В14.
В результате должна быть получена следующая таблица (рис.
1.1-а).
Этап 2. Выбор типа диаграммы. На панели инструментов Стандартная
необходимо нажать кнопку Мастер диаграмм (обычно четвертая-пятая
справа). В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип
диаграммы указать тип диаграммы.
В диалоговом окне Мастер диаграмм (шаг 1 из 4): тип
диаграммы слева приведен список типов диаграмм, справа дается вид
вариантов подтипов. Для указания типа диаграммы необходимо вначале выбрать тип
в левом списке (с помощью указателя мыши и щелчка левой кнопкой), а затем
выбрать подтип диаграммы в правом окне (щелчком левой кнопки мыши на выбранном
подтипе).
В
рассматриваемом примере выберем тип — График, вид — График с
маркерами (левую среднюю диаграмму в правом окне). После чего нажимаем кнопку Далее
в диалоговом окне.
Этап
З. Указание диапазона. В появившемся диалоговом окне Мастер диаграмм (шаг 2 из
4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и
в поле Диапазон указать, интервал данных, то есть ввести ссылку на
ячейки, содержащие данные, которые необходимо представить на диаграмме.
Определение диапазона (интервала)
данных является самым ответственным моментом построения диаграммы. Здесь
необходимо указать только те данные, которые должны быть изображены на
диаграмме (в нашем примере — значения точек прямой). Кроме того, для введения
поясняющих надписей (легенды), они также должны быть включены в диапазон (в
примере — Прямая).
Для этого с помощью клавиши Delete необходимо очистить рабочее поле Диапазон
и, убедившись, что в нем остался только мигающий курсор, навести указатель мыши
на левую верхнюю ячейку данных (В1), нажать левую кнопку мыши и, не
отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей
выносимые на диаграмму данные (В14), затем отпустить левую кнопку мыши.
В рабочем поле должна появиться запись: =Лист1!$В$1:$В$14. Здесь
наиболее важным для нас является указание диапазона В1:В14, что
подтверждает правильное введение интервала данных Если с первого раза не
удалось получить требуемую запись в поле Диапазон, действия необходимо
повторить.
Если диалоговое
окно закрывает столбцы с данными, его можно отодвинуть, дотянув за строку
заголовка указателем мыши (при нажатой левой кнопке).
Далее необходимо указать в строках или столбцах
расположены ряды данных. В примере значения точек прямой расположены в столбце,
поэтому переключатель Ряды в с помощью указателя мыши следует установить
в положение столбцах (черная точка должна стоять около слова столбцах).
Этап 4. Ввод подписей по оси Х (горизонтальной). В диалоговом окне Мастер
диаграмм (шаг 2 из 4); источник данных диаграммы необходимо выбрать
вкладку Ряд (щелкнув на ней указателем мыши) и в поле Подписи оси Х
указать диапазон подписей (в примере — Аргумент). Для этого следует
активизировать поле Подписи оси X, щелкнув в нем указателем мыши, и,
наведя его на левую верхнюю ячейку подписей (А2), нажать левую кнопку
мыши, затем, не отпуская ее, протянуть указатель мыши к правой нижней ячейке,
содержащей выносимые на ось Х подписи (А14), затем отпустить левую кнопку
мыши. В рабочем поле должна появиться запись: =Лист1!$А$2:$А$14. Здесь,
как и для данных, наиболее важным для нас является указание диапазона A2:A14, что подтверждает правильное введение
интервала подписей .
После появления требуемой записи диапазона необходимо нажать
кнопку Далее
Этап 5. Введение заголовков. В третьем окне Мастер
диаграмм (шаг 3 из 4): параметры диаграммы требуется ввести заголовок
диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки,
щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы
указателем мыши, ввести с клавиатуры в поле название: Прямая. Затем
аналогичным образом ввести в рабочие поля Ось Х (категорий) Ось
У (значений) соответствующие названия: Аргумент и Значения .
Далее в данном окне необходимо выбрать
вкладку Легенда и указать необходима ли Легенда (расшифровка кривых).
Щелчком мыши устанавливаем флажок в поле Добавить легенду.
После чего нажать
кнопку Далее.
Этап 6. Выбор
места размещения. В четвертом
окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы необходимо
указать место размещения диаграммы. Для этого переключатель Поместить
диаграмму на листе установить в нужное положение (на отдельном или текущем
листе). В примере устанавливаем переключатель в положение имеющемся
(щелчком указателя мыши черную точку устанавливаем слева от слова имеющемся).
Этап 7. Завершение. Если диаграмма в демонстрационном
поле имеет желаемый вид, необходимо нажать кнопку Готово. В противном
случае следует нажать кнопку Назад и изменить установки.
Нажимаем кнопку Готово и на
текущем листе должна появиться диаграмма
|
1.1) |
y=2x+1 |
||||||||
|
А |
В |
|
|||||||
|
1 |
аргумент |
прямая |
|||||||
|
2 |
0 |
1 |
|||||||
|
3 |
0,25 |
1,5 |
|||||||
|
4 |
0,5 |
2 |
|||||||
|
5 |
0,75 |
2,5 |
|||||||
|
6 |
1 |
3 |
|||||||
|
7 |
1,25 |
3,5 |
|||||||
|
8 |
1,5 |
4 |
|||||||
|
9 |
1,75 |
4,5 |
|||||||
|
10 |
2 |
5 |
|||||||
|
11 |
2,25 |
5,5 |
|||||||
|
12 |
2,5 |
6 |
|||||||
|
13 |
2,75 |
6,5 |
|||||||
|
14 |
3 |
7 |
Пример 2
Построение прямой 3х +2у-4=0 в
диапазоне х € [-1; 3] с шагом Δ = 0,25
Пример 3
Построение прямой, пересекающую ось ординат в точке
А(0;2),а ось абсцисс в точке В(3;0), в диапазоне . х € [-1; 4] с
шагом Δ = 0,25
Пример 4
Построение прямой , проходящую через точки А(0;3) и
В(2;2), в диапазоне х € [-1; 4] с шагом Δ = 0,25
Построение квадратичной параболы
Пример
1.
В
качестве примера рассмотрим построение параболы вида у = х2
в диапазоне х € [-3; 3] с шагом Δ = 0,5.
|
2.1) |
y=x2 |
||||||||
|
A |
B |
|
|||||||
|
1 |
аргумент |
парабола |
|||||||
|
2 |
-3 |
9 |
|||||||
|
3 |
-2,5 |
6,25 |
|||||||
|
4 |
-2 |
4 |
|||||||
|
5 |
-1,5 |
2,25 |
|||||||
|
6 |
-1 |
1 |
|||||||
|
7 |
-0,5 |
0,25 |
|||||||
|
8 |
0 |
0 |
|||||||
|
9 |
0,5 |
0,25 |
|||||||
|
10 |
1 |
1 |
|||||||
|
11 |
1,5 |
2,25 |
|||||||
|
12 |
2 |
4 |
|||||||
|
13 |
2,5 |
6,25 |
|||||||
|
14 |
3 |
9 |
|||||||
Пример 2
Построение параболы х2 =8у в
диапазоне х € [-2,25; 2,25] с шагом Δ = 0,25.
Пример 3
Построение параболы у =х2 +2 х —3
в диапазоне х € [-6; 4] с шагом Δ = 0,5
Пример 4
Построение
параболы у=( х +2) 2 –3 в диапазоне х €
[-7; 3] с шагом Δ = 0,5
Построение кубической параболы
Пример 1
В качестве
примера рассмотрим построение кубической параболы у = х3 в
диапазоне х € [-2; 2] с шагом Δ = 0,25.
|
3.1) |
y=x3 |
|
||||||
|
A |
B |
|||||||
|
1 |
аргумент |
куб.парабола |
||||||
|
2 |
-2 |
-8 |
||||||
|
3 |
-1,75 |
-5,359375 |
||||||
|
4 |
-1,5 |
-3,375 |
||||||
|
5 |
-1,25 |
-1,953125 |
||||||
|
6 |
-1 |
-1 |
||||||
|
7 |
-0,75 |
-0,421875 |
||||||
|
8 |
-0,5 |
-0,125 |
||||||
|
9 |
-0,25 |
-0,015625 |
||||||
|
10 |
0 |
0 |
||||||
|
11 |
0,25 |
0,015625 |
||||||
|
12 |
0,5 |
0,125 |
||||||
|
13 |
0,75 |
0,421875 |
||||||
|
14 |
1 |
1 |
||||||
|
15 |
1,25 |
1,953125 |
||||||
|
16 |
1,5 |
3,375 |
||||||
|
17 |
1,75 |
5,359375 |
||||||
|
18 |
2 |
8 |
Пример 2
Построение
кубической параболы у =( х-2)3 в диапазоне х € [-2;
6] с шагом Δ = 0,25.
Пример 3
Построение
кубической параболы у = -х3 +1 в диапазоне х € [-2;
2] с шагом Δ = 0,25.
Построение графика обратной
пропорциональности

шагом ∆= 0,5.
|
4.1) |
у=1/х |
|||||||||
|
A |
B |
|||||||||
|
1 |
аргумент |
гипербола |
||||||||
|
2 |
0,1 |
10 |
||||||||
|
3 |
0,6 |
1,6666667 |
||||||||
|
4 |
1,1 |
0,9090909 |
||||||||
|
5 |
1,6 |
0,625 |
||||||||
|
6 |
2,1 |
0,4761905 |
||||||||
|
7 |
2,6 |
0,3846154 |
||||||||
|
8 |
3,1 |
0,3225806 |
||||||||
|
9 |
3,6 |
0,2777778 |
||||||||
|
10 |
4,1 |
0,2439024 |
||||||||
|
11 |
4,6 |
0,2173913 |
||||||||
|
12 |
5,1 |
0,1960784 |
||||||||
|
13 |
5,6 |
0,1785714 |
||||||||
|
14 |
6,1 |
0,1639344 |
||||||||
|
15 |
6,6 |
0,1515152 |
||||||||
|
16 |
7,1 |
0,1408451 |
||||||||
|
17 |
7,6 |
0,1315789 |
||||||||
|
18 |
8,1 |
0,1234568 |
||||||||
|
19 |
8,6 |
0,1162791 |
||||||||
|
20 |
9,1 |
0,1098901 |
||||||||
|
21 |
9,6 |
0,1041667 |
||||||||
|
22 |
10,1 |
0,0990099 |
Пример 2
Построение гиперболы у =2/х в диапазоне х
€ [0,1; 5,1] с шагом Δ = 0,25
Пример 3
Построение гиперболы у =-3/(4х) в диапазоне х
€ [0,1; 4,6] с шагом Δ = 0,3
Построение
графика функции y=n√x
Пример 1
В качестве примера рассмотрим построение графика у
=√6х в диапазоне х € [0; 4] с шагом Δ = 0,25.
|
5.1) |
у2=6х |
||||||||
|
у=√6х |
|||||||||
|
А |
В |
|
|||||||
|
1 |
аргумент |
корень |
|||||||
|
2 |
0 |
0 |
|||||||
|
3 |
0,25 |
1,2247449 |
|||||||
|
4 |
0,5 |
1,7320508 |
|||||||
|
5 |
0,75 |
2,1213203 |
|||||||
|
6 |
1 |
2,4494897 |
|||||||
|
7 |
1,25 |
2,7386128 |
|||||||
|
8 |
1,5 |
3 |
|||||||
|
9 |
1,75 |
3,2403703 |
|||||||
|
10 |
2 |
3,4641016 |
|||||||
|
11 |
2,25 |
3,6742346 |
|||||||
|
12 |
2,5 |
3,8729833 |
|||||||
|
13 |
2,75 |
4,0620192 |
|||||||
|
14 |
3 |
4,2426407 |
|||||||
|
15 |
3,25 |
4,4158804 |
|||||||
|
16 |
3,5 |
4,5825757 |
|||||||
|
17 |
3,75 |
4,7434165 |
|||||||
|
18 |
4 |
4,8989795 |
Пример 2
Построение графика у =3√х в диапазоне х
€ [0; 8] с шагом Δ = 0,5
Пример 3
Построение графика у =√(х+2) в диапазоне х
€ [-2; 14] с шагом Δ = 0,5
Пример 4
Построение графика у =-√х+2 в диапазоне х
€ [0; 8] с шагом Δ = 0,5
Построение
графика функции y=│x│
Пример 1
В качестве примера рассмотрим построение графика у
= х в диапазоне х € [-7; 7] с шагом Δ = 1.
|
6.1) |
y= x |
|
|||||||
|
A |
B |
||||||||
|
1 |
аргумент |
модуль |
|||||||
|
2 |
-7 |
7 |
|||||||
|
3 |
-6 |
6 |
|||||||
|
4 |
-5 |
5 |
|||||||
|
5 |
-4 |
4 |
7 |
||||||
|
6 |
-3 |
3 |
|||||||
|
7 |
-2 |
2 |
|||||||
|
8 |
-1 |
1 |
|||||||
|
9 |
0 |
0 |
|||||||
|
10 |
1 |
1 |
|||||||
|
11 |
2 |
2 |
|||||||
|
12 |
3 |
3 |
|||||||
|
13 |
4 |
4 |
|||||||
|
14 |
5 |
5 |
|||||||
|
15 |
6 |
6 |
|||||||
|
16 |
7 |
7 |
Пример 2
Построение графика у =│х-1│ в диапазоне х
€ [-4; 6] с шагом Δ = 0,5
Пример 3
Построение графика у =│х +2│ в диапазоне х
€ [-5; 7] с шагом Δ = 0,5
Пример 4
Построение графика у = │х2-1│ в
диапазоне х € [-4,5; 4,5] с шагом Δ = 0,5.
Построение
графика дробно-рациональной функции
Пример 1
Рассмотрим
построение графика функции у=( х2 -1)/( х-1) в диапазоне х
€ [-5; 5] с шагом Δ = 0,5.
Решение. Открываем чистый рабочий лист (команда Вставка ►Лист).
Этап 1. Ввод данных. Для построения необходимо составить таблицу данных (х
и у) для значениями х, а второй соответствующими показателями у.
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1
ее построения в рабочем окне таблицы Ехсеl.
Для этого значения х и у следует представить в виде таблицы, где
столбцами являются соответствующие показатели. Пусть в рассматриваемом примере
первый столбец будет— слово Прямая.(Заметим, что этот график можно легко
построить, если упростить правую часть . Но в Ехсеl мы
этого делать не будем.)
Начнем с введения значений аргумента. В ячейку А2
вводится первое значение аргумента — левая граница диапазона (-5). В
ячейку АЗ вводится второе значение аргумента — левая граница диапазона
плюс шаг построения (-4,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением
получаем все значения аргумента (за правый нижний угол блока протягиваем до
ячейки А22).
Далее вводим значения прямой. В ячейку В2
необходимо ввести ее уравнение: =(A2^2-1)/(A2-1), предварительно переключившись на английский
язык (Аlt+Shift). Затем автозаполнением копируем эту формулу
в диапазон В2:В22.
В результате должна быть получена таблица
В ячейке В14 появляется # ДЕЛ/О! (при х=1, у – не
существует, так как на ноль делить нельзя).
Этап 2. Выбор типа диаграммы. На панели инструментов Стандартная
необходимо нажать кнопку Мастер диаграмм (обычно четвертая-пятая
справа). В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип
диаграммы указать тип диаграммы.
В диалоговом окне Мастер диаграмм (шаг 1 из 4): тип
диаграммы слева приведен список типов диаграмм, справа дается вид
вариантов подтипов. Для указания типа диаграммы необходимо вначале выбрать тип
в левом списке (с помощью указателя мыши и щелчка левой кнопкой), а затем
выбрать подтип диаграммы в правом окне (щелчком левой кнопки мыши на выбранном
подтипе).
В
рассматриваемом примере выберем тип — График, вид — График с
маркерами (левую среднюю диаграмму в правом окне). После чего нажимаем кнопку Далее
в диалоговом окне
.Этап
3. Указание диапазона. В появившемся диалоговом окне Мастер
диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку
Диапазон данных и в поле Диапазон указать, интервал данных, то
есть ввести ссылку на ячейки, содержащие данные, которые необходимо представить
на диаграмме.
Определение диапазона (интервала)
данных является самым ответственным моментом построения диаграммы. Здесь
необходимо указать только те данные, которые должны быть изображены на
диаграмме (в нашем примере — значения точек прямой). Кроме того, для введения
поясняющих надписей (легенды), они также должны быть включены в диапазон (в
примере — Прямая).
Для этого с помощью клавиши Delete необходимо очистить рабочее поле Диапазон
и, убедившись, что в нем остался только мигающий курсор, навести указатель мыши
на левую верхнюю ячейку данных (В1), нажать левую кнопку мыши и, не
отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей
выносимые на диаграмму данные (В22), затем отпустить левую кнопку мыши.
В рабочем поле должна появиться запись: =Лист1!$В$1:$В$22. Здесь
наиболее важным для нас является указание диапазона В1:В22, что
подтверждает правильное введение интервала данных
Если с первого раза не удалось
получить требуемую запись в поле Диапазон, действия необходимо
повторить.
Если диалоговое
окно закрывает столбцы с данными, его можно отодвинуть, дотянув за строку
заголовка указателем мыши (при нажатой левой кнопке).
Далее необходимо указать в строках или столбцах
расположены ряды данных. В примере значения точек прямой расположены в столбце,
поэтому переключатель Ряды в с помощью указателя мыши следует установить
в положение столбцах (черная точка должна стоять около слова столбцах).
Этап 4. Ввод подписей по оси Х (горизонтальной). В диалоговом окне Мастер
диаграмм (шаг 2 из 4); источник данных диаграммы необходимо выбрать
вкладку Ряд (щелкнув на ней указателем мыши) и в поле Подписи оси Х
указать диапазон подписей (в примере — Аргумент). Для этого следует
активизировать поле Подписи оси X, щелкнув в нем указателем мыши, и,
наведя его на левую верхнюю ячейку подписей (А2), нажать левую кнопку
мыши, затем, не отпуская ее, протянуть указатель мыши к правой нижней ячейке,
содержащей выносимые на ось Х подписи (А22), затем отпустить левую
кнопку мыши. В рабочем поле должна появиться запись: =Лист1!$А$2:$А$22. Здесь,
как и для данных, наиболее важным для нас является указание диапазона A2:A22, что подтверждает правильное введение
интервала подписей .
После появления требуемой записи диапазона необходимо нажать
кнопку Далее
Этап 5. Введение заголовков. В третьем окне Мастер
диаграмм (шаг 3 из 4): параметры диаграммы требуется ввести заголовок
диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки,
щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы
указателем мыши, ввести с клавиатуры в поле название: Прямая. Затем
аналогичным образом ввести в рабочие поля Ось Х (категорий) Ось
У (значений) соответствующие названия: Аргумент и Значения .
Далее в данном окне необходимо выбрать
вкладку Легенда и указать необходима ли Легенда (расшифровка кривых).
Щелчком мыши устанавливаем флажок в поле Добавить легенду.
После чего нажать
кнопку Далее.
Этап 6. Выбор
места размещения. В четвертом
окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы необходимо
указать место размещения диаграммы. Для этого переключатель Поместить
диаграмму на листе установить в нужное положение (на отдельном или текущем
листе). В примере устанавливаем переключатель в положение имеющемся
(щелчком указателя мыши черную точку устанавливаем слева от слова имеющемся).
Этап 7. Завершение. Если диаграмма в демонстрационном
поле имеет желаемый вид, необходимо нажать кнопку Готово. В противном
случае следует нажать кнопку Назад и изменить установки.
Нажимаем кнопку Готово и на
текущем листе должна появиться диаграмма
|
7.1) |
y=(x2-1)/(x-1) |
|
|||||
|
A |
B |
||||||
|
1 |
аргумент |
прямая |
|||||
|
2 |
-5 |
-4 |
|||||
|
3 |
-4,5 |
-3,5 |
|||||
|
4 |
-4 |
-3 |
|||||
|
5 |
-3,5 |
-2,5 |
|||||
|
6 |
-3 |
-2 |
|||||
|
7 |
-2,5 |
-1,5 |
|||||
|
8 |
-2 |
-1 |
|||||
|
9 |
-1,5 |
-0,5 |
|||||
|
10 |
-1 |
0 |
|||||
|
11 |
-0,5 |
0,5 |
|||||
|
12 |
0 |
1 |
|||||
|
13 |
0,5 |
1,5 |
|||||
|
14 |
1 |
#ДЕЛ/0! |
|||||
|
15 |
1,5 |
2,5 |
|||||
|
16 |
2 |
3 |
|||||
|
17 |
2,5 |
3,5 |
|||||
|
18 |
3 |
4 |
|||||
|
19 |
3,5 |
4,5 |
|||||
|
20 |
4 |
5 |
|||||
|
21 |
4,5 |
5,5 |
|||||
|
22 |
5 |
6 |
Пример 2
Построение графика у=(
х-1)/( х2 -1) в диапазоне х € [0; 4] с шагом Δ = 0,2
Построение
графиков тригонометрических функций.
Пример 1

качестве примера рассмотрим построение графика у =sinx в диапазоне х
€ [-5; 5] с шагом Δ = 0,5
|
8.1) |
y=sinx |
||||||||
|
А |
В |
||||||||
|
1 |
аргумент |
синусоида |
|||||||
|
2 |
-5 |
0,9589243 |
|||||||
|
3 |
-4,5 |
0,9775301 |
|||||||
|
4 |
-4 |
0,7568025 |
|||||||
|
5 |
-3,5 |
0,3507832 |
|||||||
|
6 |
-3 |
-0,14112 |
|||||||
|
7 |
-2,5 |
-0,5984721 |
|||||||
|
8 |
-2 |
-0,9092974 |
|||||||
|
9 |
-1,5 |
-0,997495 |
|||||||
|
10 |
-1 |
-0,841471 |
|||||||
|
11 |
-0,5 |
-0,4794255 |
|||||||
|
12 |
0 |
0 |
|||||||
|
13 |
0,5 |
0,4794255 |
|||||||
|
14 |
1 |
0,841471 |
|||||||
|
15 |
1,5 |
0,997495 |
|||||||
|
16 |
2 |
0,9092974 |
|||||||
|
17 |
2,5 |
0,5984721 |
|||||||
|
18 |
3 |
0,14112 |
|||||||
|
19 |
3,5 |
-0,3507832 |
|||||||
|
20 |
4 |
-0,7568025 |
|||||||
|
21 |
4,5 |
-0,9775301 |
|||||||
|
22 |
5 |
-0,9589243 |
Пример 2
Построение графика у = cosx в диапазоне х
€ [-5; 5] с шагом Δ = 0,5
Пример 3
Построение графика
у=tgx в диапазоне х € [-1,5; 1,5] с шагом Δ = 0,15
Пример 4
Построение графика у=ctgx
в диапазоне х € [0,1; 2,95] с шагом Δ = 0,15
Построение
графика логарифмической функции
Пример 1
Построение графика
у=log5x в диапазоне х € [0,1; 5,1] с шагом Δ =
0,25
|
9.1) |
у=log5x |
||||||||
|
A |
B |
||||||||
|
1 |
аргумент |
логарифм |
|||||||
|
2 |
0,1 |
-1,4306766 |
|
||||||
|
3 |
0,35 |
-0,6522912 |
|||||||
|
4 |
0,6 |
-0,3173938 |
|||||||
|
5 |
0,85 |
-0,1009787 |
|||||||
|
6 |
1,1 |
0,0592195 |
|||||||
|
7 |
1,35 |
0,1864655 |
|||||||
|
8 |
1,6 |
0,2920297 |
|||||||
|
9 |
1,85 |
0,3822363 |
|||||||
|
10 |
2,1 |
0,4609916 |
|||||||
|
11 |
2,35 |
0,5308781 |
|||||||
|
12 |
2,6 |
0,5936926 |
|||||||
|
13 |
2,85 |
0,6507359 |
|||||||
|
14 |
3,1 |
0,7029797 |
|||||||
|
15 |
3,35 |
0,7511693 |
|||||||
|
16 |
3,6 |
0,7958889 |
|||||||
|
17 |
3,85 |
0,8376049 |
|||||||
|
18 |
4,1 |
0,8766955 |
|||||||
|
19 |
4,35 |
0,9134716 |
|||||||
|
20 |
4,6 |
0,9481921 |
|||||||
|
21 |
4,85 |
0,9810746 |
|||||||
|
22 |
5,1 |
1,0123041 |
Пример 2
Построение графика
у=lg(x+2) в диапазоне х € [0,1; 4,1] с шагом Δ = 0,25
Пример 3
Построение графика
у=2log¼x в диапазоне х € [0,1; 5.1] с шагом Δ =
0,25
Построение
графика показательной функции.
Пример 1
Построение графика
у=2x в
диапазоне х € [-5; 5] с шагом Δ = 0,5
|
10.1) |
y=2x |
|
|||||||
|
A |
B |
||||||||
|
1 |
аргумент |
показат.функция |
|||||||
|
2 |
-5 |
0,03125 |
|||||||
|
3 |
-4,5 |
0,0441942 |
|||||||
|
4 |
-4 |
0,0625 |
|||||||
|
5 |
-3,5 |
0,0883883 |
|||||||
|
6 |
-3 |
0,125 |
|||||||
|
7 |
-2,5 |
0,1767767 |
|||||||
|
8 |
-2 |
0,25 |
|||||||
|
9 |
-1,5 |
0,3535534 |
|||||||
|
10 |
-1 |
0,5 |
|||||||
|
11 |
-0,5 |
0,7071068 |
|||||||
|
12 |
0 |
1 |
|||||||
|
13 |
0,5 |
1,4142136 |
|||||||
|
14 |
1 |
2 |
|||||||
|
15 |
1,5 |
2,8284271 |
|||||||
|
16 |
2 |
4 |
|||||||
|
17 |
2,5 |
5,6568542 |
|||||||
|
18 |
3 |
8 |
|||||||
|
19 |
3,5 |
11,313708 |
|||||||
|
20 |
4 |
16 |
|||||||
|
21 |
4,5 |
22,627417 |
|||||||
|
22 |
5 |
32 |
|||||||
Пример 2
Построение графика у=(¼)x в диапазоне х € [-5; 5] с шагом Δ = 0,5
Построение кривых второго порядка на
плоскости
1.Построение окружности.
Пример 1
В качестве примера
рассмотрим построение верхней полуокружности х2 + у2
= 4 в диапазоне х € [-2; 2] с шагом ∆ = 0,25.
Решение. Открываем чистый рабочий лист (команда
Вставка ►Лист).
Этап 1.
Ввод данных. Составляем таблицу данных (х и у). Пусть первый
столбец будет значениями х, а второй соответствующими показателями у.
Для этого в ячейку А1 вводим слово Аргумент, а в ячейку В1
— слово Окружность. В ячейку А2 вводится первое значение аргумента —
левая граница диапазона (-2). В ячейку АЗ вводится второе
значение аргумента — левая граница диапазона плюс шаг построения (-1,75).
Затем, выделив блок ячеек А2.-АЗ, автозаполнением получаем все значения
аргумента (за правый нижний угол блока протягиваем до ячейки А18).
Далее вводим значения верхней полуокружности. В ячейку
В2 необходимо ввести ее уравнение, разрешенное относительно у =
√4 — х2. Для этого табличный курсор необходимо поставить в
ячейку В2 и на панели инструментов Стандартная нажать кнопку Вставка
функции (fx). В появившемся диалоговом окне Мастер
функций-шаг 1 из 2 слева в поле Категория указаны виды функций.
Выбираем вид Математические. Справа в поле Функция выбираем
функцию Корень. Нажимаем кнопку ОК. Появляется диалоговое окно Корень.
В рабочее поле вводим подкоренное выражение: 4 -А2^2 Нажимаем кнопку ОК.
В ячейке В2 появляется 0. Теперь необходимо скопировать функцию из
ячейки В2. Автозаполнением копируем эту формулу в диапазон В2:В 18.
В результате должна
быть получена таблица данных для построения верхней полуокружности.
Этап 2. Выбор
типа диаграммы. На панели
инструментов Стандартная необходимо нажать кнопку Мастер диаграмм.
В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы
выберем тип — График, вид — График с маркерами (левую среднюю
диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом
окне.
Этап 3. Указание диапазона. В появившемся диалоговом окне Мастер диаграмм (шаг
2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон
данных и в поле Диапазон указать интервал данных.
Для этого с помощью
клавиши Delete необходимо очистить рабочее поле Диапазон и,
убедившись, что в нем остался только мигающий курсор, навести указатель на
левую верхнюю ячейку данных (В1), нажать левую кнопку мыши и, не
отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей
выносимые на диаграмму данные (В 18), затем отпустить левую
кнопку мыши.
Далее необходимо указать в строках или
столбцах расположены ряды данных. Переключатель Ряды в с помощью
указателя мыши следует установить в положение столбцах (черная точка должна
стоять около слова столбцах).
Этап 4. Ввод подписей по оси Х (горизонтальной). В диалоговом окне Мастер
диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать
вкладку Ряд (щелкнув на ней указателем мыши) и в поле Подписи оси Х
указать диапазон подписей (в примере — Аргумент). Для этого следует
активизировать поле Подписи оси X, щелкнув в нем указателем мыши, и,
наведя указатель мыши на левую верхнюю ячейку подписей (А2), нажать
левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней
ячейке, содержащей выносимые на ось Х подписи (А18), затем отпустить
левую кнопку мыши.
После появления требуемой записи диапазона необходимо
нажать кнопку Далее.
Этап 5. Введение заголовков. В
третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого
необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши.
Щелкнув в рабочем поле Название диаграммы указателем мыши,
ввести с клавиатуры в поле название: График полуокружности. Затем
аналогичным образом ввести в рабочие поля Ось Х (категорий) и Ось У
(значений) соответствующие названия: Аргумент и Значения.
После чего нажать
кнопку Далее.
Этап 6.
Завершение. Необходимо нажать
кнопку Готово.
На текущем листе должна появиться следующая
диаграмма
|
1.1) |
х2+у2=4 |
|||||||
|
у=√(4-х2) |
||||||||
|
А |
В |
|
||||||
|
1 |
аргумент |
окружность |
||||||
|
2 |
-2 |
0 |
||||||
|
3 |
-1,75 |
0,968245837 |
||||||
|
4 |
-1,5 |
1,322875656 |
||||||
|
5 |
-1,25 |
1,5612495 |
||||||
|
6 |
-1 |
1,732050808 |
||||||
|
7 |
-0,75 |
1,854049622 |
||||||
|
8 |
-0,5 |
1,936491673 |
||||||
|
9 |
-0,25 |
1,984313483 |
||||||
|
10 |
0 |
2 |
||||||
|
11 |
0,25 |
1,984313483 |
||||||
|
12 |
0,5 |
1,936491673 |
||||||
|
13 |
0,75 |
1,854049622 |
||||||
|
14 |
1 |
1,732050808 |
||||||
|
15 |
1,25 |
1,5612495 |
||||||
|
16 |
1,5 |
1,322875656 |
||||||
|
17 |
1,75 |
0,968245837 |
||||||
|
18 |
2 |
0 |
Пример 2
Построение
окружности х2 + у2 = 4 в диапазоне х € [-2;
2] с шагом ∆ = 0,25
2.Построение эллипса.
Пример 1
В
качестве примера рассмотрим построение верхней половины эллипса х2
/9+ у2 /4= 1
. и
диапазоне х € [-3,5; 3,5] с шагом ∆ = 0,5.
|
2.1) |
х2/9+у2/4=1 |
|||||||
|
у=√(4(1-х2/9)) |
|
|||||||
|
А |
В |
|||||||
|
1 |
аргумент |
эллипс |
||||||
|
2 |
-3,5 |
#ЧИСЛО! |
||||||
|
3 |
-3 |
0 |
||||||
|
4 |
-2,5 |
1,1055416 |
||||||
|
5 |
-2 |
1,490712 |
||||||
|
6 |
-1,5 |
1,7320508 |
||||||
|
7 |
-1 |
1,8856181 |
||||||
|
8 |
-0,5 |
1,9720266 |
||||||
|
9 |
0 |
2 |
||||||
|
10 |
0,5 |
1,9720266 |
||||||
|
11 |
1 |
1,8856181 |
||||||
|
12 |
1,5 |
1,7320508 |
||||||
|
13 |
2 |
1,490712 |
||||||
|
14 |
2,5 |
1,1055416 |
||||||
|
15 |
3 |
0 |
||||||
|
16 |
3,5 |
#ЧИСЛО! |
||||||
Пример 2
Построение эллипса х2
/4+ у2 = 1 в диапазоне х € [-2,25; 2,25] с
шагом ∆ = 0,25
Графическое решение систем уравнений.
Пример 1.Пусть необходимо найти
решение системы
Y=sinx
Y=cosx
в диапазоне х € [0; 3]
с шагом ∆ == 0,2.
Решение. Для построения диаграмм прежде всего необходимо
ввести данные в рабочую таблицу. Вводим в ячейку А1 слово Аргумент.
Затем в ячейку А2 — первое значение аргумента — 0. Далее будем
вводить приращения аргумента с шагом 0,2. Введем в ячейку АЗ сумму левой
границы диапазона плюс шаг (0,2). Затем, выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения аргумента (за правый нижний угол блока
протягиваем до ячейки А17).
Далее требуется ввести значения функции (в примере
синуса). В ячейку В1 вводим слово Синус и устанавливаем
табличный курсор в ячейку В 2. Здесь должно оказаться значение синуса,
соответствующее значению аргумента в ячейке А2. Для получения значения
синуса воспользуемся специальной функцией: нажмем на панели инструментов кнопку
Вставка функции (fx). В появившемся диалоговом окне Мастер функций-шаг 1 из 2
слева в поле Категория указаны виды функций.
Выбираем Математические. Справа в поле Функция
выбираем функцию SIN. Нажимаем кнопку ОК. Появляется
диалоговое окно SIN. Наведя указатель мыши на серое
поле окна, при нажатой левой кнопке сдвигаем его вправо, чтобы открыть столбец
данных (А). Указываем значение аргумента синуса щелчком мыши на ячейке А2.
Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
необходимо скопировать функцию из ячейки В2 в ячейки ВЗ:В17.
Осуществляем это автозаполнением (за правый нижний угол ячейки В2
протягиваем до ячейки В 17). Значения синуса получены.
Аналогично
получаем значения косинуса. В ячейку С1 вводим имя функции Косинус.
Устанавливаем табличный курсор в ячейку С2. Для получения значения
косинуса нажимаем на панели инструментов кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер
функций-шаг 1 из 2 слева в поле Категория выбираем Математические.
Справа в поле Функция выбираем функцию С0S. Нажимаем ОК. Появляется
диалоговое окно С0S. Наведя указатель мыши на серое поле при нажатой
левой кнопке сдвигаем его вправо, чтобы открыть столбец аргумента (А).
Указываем значение аргумента косинуса щелчком мыши на ячейке А2. Нажимаем
кнопку ОК. В ячейке С2 появляется 1. Автозаполнением
копируем формулу (за правый нижний угол ячейки С2 протягиваем до ячейки С17).
Значения косинуса получены.
Далее по введенным в рабочую таблицу данным необходимо
построить диаграмму. Щелчком указателя мыши по кнопке на панели инструментов
вызываем Мастер диаграмм. В появившемся диалоговом окне выбираем тип
диаграммы График, вид — левый верхний. После нажатия кнопки Далее с
помощью мыши указываем диапазон данных — В1:С17. Проверяем положение
переключателя Ряды в: столбцах— выбираем вкладку Ряд
и с помощью мыши вводим диапазон подписей оси x:А2:А17.Нажав кнопку Далее, вводим название
диаграммы — Система, название осей х и у: Аргумент
и Значения, соответственно. Нажимаем кнопку Готово. Получена
диаграмма кривых синуса и косинуса (рис. 1.23). Как видно из диаграммы, система
имеет решение (есть точка пересечения), и оно единственное (в заданном
диапазоне имеется только одна точка пересечения). Таким образом, решением
системы в заданном диапазоне являются координаты точки пересечения кривых. Для
их нахождения необходимо навести указатель мыши на точку пересечения и щелкнуть
левой кнопкой. Появляется надпись с указанием искомых координат: Ряд «Косинус».
Точка «0,8». Значение: 0,69670671. Здесь Точка «0,8» соответствует х,
а Значение: 0,69670671 —у. Таким образом, приближенное решение системы х=
0,8; у = 0,697
|
1) |
|
||||||||
|
y=cosx |
|||||||||
|
|
|||||||||
|
A |
B |
C |
|||||||
|
1 |
аргумент |
синус |
косинус |
||||||
|
2 |
0 |
0 |
1 |
||||||
|
3 |
0,2 |
0,1986693 |
0,9800666 |
||||||
|
4 |
0,4 |
0,3894183 |
0,921061 |
||||||
|
5 |
0,6 |
0,5646425 |
0,8253356 |
||||||
|
6 |
0,8 |
0,7173561 |
0,6967067 |
||||||
|
7 |
1 |
0,841471 |
0,5403023 |
||||||
|
8 |
1,2 |
0,9320391 |
0,3623578 |
||||||
|
9 |
1,4 |
0,9854497 |
0,1699671 |
||||||
|
10 |
1,6 |
0,9995736 |
-0,0291995 |
||||||
|
11 |
1,8 |
0,9738476 |
-0,2272021 |
||||||
|
12 |
2 |
0,9092974 |
-0,4161468 |
||||||
|
13 |
2,2 |
0,8084964 |
-0,5885011 |
||||||
|
14 |
2,4 |
0,6754632 |
-0,7373937 |
||||||
|
15 |
2,6 |
0,5155014 |
-0,8568888 |
||||||
|
16 |
2,8 |
0,3349882 |
-0,9422223 |
||||||
|
17 |
3 |
0,14112 |
-0,9899925 |
Пример 2. Найти решение системы
графически:
y =lnx
y =-2x+1
в диапазоне х € [0.2;
3] с шагом ∆ == 0,2
Построение плоскости
Пример
Рассмотрим
построение плоскости в Ехсе! на примере уравнения 2х+4у— 2z + 2 = 0. Пусть необходимо построить
часть плоскости, лежащей в I
квадранте (х € [0; 6] с шагом ∆ = 0,5, у € [0; 6] с шагом ∆ = 1).
Решение. Вначале необходимо разрешить
уравнение относительно переменной z. В примере z = х + 2y + 1.
Введем значения переменной х в
столбец А. Для этого в ячейку А1 вводим х. В ячейку А2
вводится первое значение аргумента — левая граница диапазона(0). В ячейку АЗ
вводится второе значение аргумента — левая граница диапазона плюс шаг
построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением
получаем все значения аргумента (за правый нижний угол блока протягиваем до
ячейки А14).
Значения
переменной у вводим в строку 1. Для этого в ячейку В1
вводится значение переменной — левая граница диапазона (0). В ячейку С1
вводится значение переменной — левая граница диапазона плюс шаг построения (1).
Затем, выделив блок ячеек В1;С1, автозаполнением получаем все
значения аргументав правый нижний угол блока протягиваем до ячейки Н1).
Далее
вводим значения переменной г. В ячейку В2 вводим ее уравнение = $А2 +
2*В$1 + 1, предварительно переключившись на английский язык . Обращаем
внимание, что символы $ предназначены для фиксации адреса столбца А —
переменной х: и строки 1 — переменной у. Затем автозаполнением
(протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2,
после чего в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена
таблица.
На
панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм.
В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграмм
указываем тип диаграммы — Поверхность, и вид — Проволочная
(прозрачная) поверхность (правую верхнюю диаграмму в правом окне).
После чего нажимаем кнопку Далее в диалоговом окне.
В
появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4); источник данных
диаграммы необходимо выбрать вкладку Диапазон данных и в поле
Диапазон указать интервал данных В2:Н14.
Далее
необходимо указать в строках или столбцах расположены ряды данных. Это определит
ориентацию осей х и у. В примере переключатель Ряды в
с помощью указателя мыши установим в положение столбцах. Выбираем
вкладку Ряд и в поле Подписи оси Х указываем диапазон подписей.
Для этого следует активизировать поле Подписи оси X, щелкнув в нем
указателем мыши, и ввести диапазон подписей оси х — А2:А14.
Далее вводим значения подписей оси у.
Для этого в рабочем поле Ряд указываем первую запись Ряд 1 и в
рабочее поле Имя, активировав его указателем мыши, вводим первое
значение переменной у — 0. Затем в поле Ряд указываем вторую
запись Ряд 2 и в рабочее поле Имя вводим второе значение
переменной у — 1. Повторяем таким образом до последней записи — Ряд
7. В результате вкладка Ряд будет иметь следующий вид (рис. 13.1-а)
После появления требуемых записей необходимо нажать кнопку Далее. В
третьем окне требуется ввести заголовок диаграммы и названия осе этого
необходимо выбрать вкладку Заголовки, щелкнув на ней указателем. Щелкнув
в рабочем поле Название диаграммы, ввести с клавиатуры в данное поле
название: Плоскость. Затем аналогичным образом ввести в рабочие поля Ось
х (категорий), Ось y (рядов данных) и Ось z (значений) соответствующие названия: х, у
и z. Далее нажать кнопку Готово, и после
небольшого редактирования будет по, следующая диаграмма
|
2х+4у-2z+2=0 |
||||||||
|
z=x+2y+1 |
||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
|
|
1 |
xy |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
2 |
0 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
|
3 |
0,5 |
1,5 |
3,5 |
5,5 |
7,5 |
9,5 |
11,5 |
13,5 |
|
4 |
1 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
|
5 |
1,5 |
2,5 |
4,5 |
6,5 |
8,5 |
10,5 |
12,5 |
14,5 |
|
6 |
2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
|
7 |
2,5 |
3,5 |
5,5 |
7,5 |
9,5 |
11,5 |
13,5 |
15,5 |
|
8 |
3 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
9 |
3,5 |
4,5 |
6,5 |
8,5 |
10,5 |
12,5 |
14,5 |
16,5 |
|
10 |
4 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
|
11 |
4,5 |
5,5 |
7,5 |
9,5 |
11,5 |
13,5 |
15,5 |
17,5 |
|
12 |
5 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
13 |
5,5 |
6,5 |
8,5 |
10,5 |
12,5 |
14,5 |
16,5 |
18,5 |
|
14 |
6 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
|
15 |
6,5 |
7,5 |
9,5 |
11,5 |
13,5 |
15,5 |
17,5 |
19,5 |
|
|
||||||||
Построение поверхностей второго порядка в пространстве.
1. Построение эллипсоида.
Пример
Рассмотрим
построение эллипсоида в Ехсе! на примере уравнения:
X2/9+y2/4+z2=1
Пусть необходимо построить верхнюю часть эллипсоида,
лежащую в диапазонах:
x € [-3; З], у € [-2; 2] с шагом ∆= 0,5 для обеих
переменных.
|
1.) |
х2/9+у2/4+z2=1 |
|||||||||
|
z=√(1-x2/9-y2/4) |
||||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
|
1 |
x |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
|
2 |
-3 |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
0 |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
|
3 |
-2,5 |
#ЧИСЛО! |
#ЧИСЛО! |
0,2357023 |
0,4930066 |
0,5527708 |
0,4930066 |
0,235702 |
#ЧИСЛО! |
#ЧИСЛО! |
|
4 |
-2 |
#ЧИСЛО! |
#ЧИСЛО! |
0,5527708 |
0,7021791 |
0,745356 |
0,7021791 |
0,552771 |
#ЧИСЛО! |
#ЧИСЛО! |
|
5 |
-1,5 |
#ЧИСЛО! |
0,433013 |
0,7071068 |
0,8291562 |
0,8660254 |
0,8291562 |
0,707107 |
0,433013 |
#ЧИСЛО! |
|
6 |
-1 |
#ЧИСЛО! |
0,571305 |
0,7993053 |
0,9090593 |
0,942809 |
0,9090593 |
0,799305 |
0,571305 |
#ЧИСЛО! |
|
7 |
-0,5 |
#ЧИСЛО! |
0,640095 |
0,8498366 |
0,9537936 |
0,9860133 |
0,9537936 |
0,849837 |
0,640095 |
#ЧИСЛО! |
|
8 |
0 |
0 |
0,661438 |
0,8660254 |
0,9682458 |
1 |
0,9682458 |
0,866025 |
0,661438 |
0 |
|
9 |
0,5 |
#ЧИСЛО! |
0,640095 |
0,8498366 |
0,9537936 |
0,9860133 |
0,9537936 |
0,849837 |
0,640095 |
#ЧИСЛО! |
|
10 |
1 |
#ЧИСЛО! |
0,571305 |
0,7993053 |
0,9090593 |
0,942809 |
0,9090593 |
0,799305 |
0,571305 |
#ЧИСЛО! |
|
11 |
1,5 |
#ЧИСЛО! |
0,433013 |
0,7071068 |
0,8291562 |
0,8660254 |
0,8291562 |
0,707107 |
0,433013 |
#ЧИСЛО! |
|
12 |
2 |
#ЧИСЛО! |
#ЧИСЛО! |
0,5527708 |
0,7021791 |
0,745356 |
0,7021791 |
0,552771 |
#ЧИСЛО! |
#ЧИСЛО! |
|
13 |
2,5 |
#ЧИСЛО! |
#ЧИСЛО! |
0,2357023 |
0,4930066 |
0,5527708 |
0,4930066 |
0,235702 |
#ЧИСЛО! |
#ЧИСЛО! |
|
14 |
3 |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
0 |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
#ЧИСЛО! |
|
|
||||||||||
2.Построение гиперболоида.
Пример
Рассмотрим построение
двухполостного гиперболоида вида X2/9+y2/4-z2=-1
|
2.) |
х2/9+у2/4-z2=-1 |
|||||||||
|
z=√(1+x2/9+y2/4) |
||||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
|
1 |
x |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
|
2 |
-3 |
1,732051 |
1,600781 |
1,5 |
1,436141 |
1,414214 |
1,436141 |
1,5 |
1,600781 |
1,732051 |
|
3 |
-2,5 |
1,641476 |
1,502313 |
1,394433 |
1,325498 |
1,301708 |
1,325498 |
1,394433 |
1,502313 |
1,641476 |
|
4 |
-2 |
1,563472 |
1,416667 |
1,301708 |
1,227577 |
1,20185 |
1,227577 |
1,301708 |
1,416667 |
1,563472 |
|
5 |
-1,5 |
1,5 |
1,346291 |
1,224745 |
1,145644 |
1,118034 |
1,145644 |
1,224745 |
1,346291 |
1,5 |
|
6 |
-1 |
1,452966 |
1,293681 |
1,166667 |
1,083333 |
1,054093 |
1,083333 |
1,166667 |
1,293681 |
1,452966 |
|
7 |
-0,5 |
1,424001 |
1,261062 |
1,130388 |
1,044164 |
1,013794 |
1,044164 |
1,130388 |
1,261062 |
1,424001 |
|
8 |
0 |
1,414214 |
1,25 |
1,118034 |
1,030776 |
1 |
1,030776 |
1,118034 |
1,25 |
1,414214 |
|
9 |
0,5 |
1,424001 |
1,261062 |
1,130388 |
1,044164 |
1,013794 |
1,044164 |
1,130388 |
1,261062 |
1,424001 |
|
10 |
1 |
1,452966 |
1,293681 |
1,166667 |
1,083333 |
1,054093 |
1,083333 |
1,166667 |
1,293681 |
1,452966 |
|
11 |
1,5 |
1,5 |
1,346291 |
1,224745 |
1,145644 |
1,118034 |
1,145644 |
1,224745 |
1,346291 |
1,5 |
|
12 |
2 |
1,563472 |
1,416667 |
1,301708 |
1,227577 |
1,20185 |
1,227577 |
1,301708 |
1,416667 |
1,563472 |
|
13 |
2,5 |
1,641476 |
1,502313 |
1,394433 |
1,325498 |
1,301708 |
1,325498 |
1,394433 |
1,502313 |
1,641476 |
|
14 |
3 |
1,732051 |
1,600781 |
1,5 |
1,436141 |
1,414214 |
1,436141 |
1,5 |
1,600781 |
1,732051 |
|
|
||||||||||
3.Построение параболоида.
Пример
Рассмотрим построение
гиперболического параболоида вида X2/9-y2/4=2z
|
3.) |
х2/9-у2/4=2z |
|||||||||
|
z=x2/18-y2/8 |
||||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
|
1 |
x |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
|
2 |
-3 |
0 |
0,21875 |
0,375 |
0,46875 |
0,5 |
0,46875 |
0,375 |
0,21875 |
0 |
|
3 |
-2,5 |
-0,152778 |
0,065972 |
0,222222 |
0,315972 |
0,347222 |
0,315972 |
0,222222 |
0,065972 |
-0,152778 |
|
4 |
-2 |
-0,277778 |
-0,059028 |
0,097222 |
0,190972 |
0,222222 |
0,190972 |
0,097222 |
-0,059028 |
-0,277778 |
|
5 |
-1,5 |
-0,375 |
-0,15625 |
0 |
0,09375 |
0,125 |
0,09375 |
0 |
-0,15625 |
-0,375 |
|
6 |
-1 |
-0,444444 |
-0,225694 |
-0,06944 |
0,024306 |
0,055556 |
0,024306 |
-0,069444 |
-0,225694 |
-0,444444 |
|
7 |
-0,5 |
-0,486111 |
-0,267361 |
-0,11111 |
-0,01736 |
0,013889 |
-0,017361 |
-0,111111 |
-0,267361 |
-0,486111 |
|
8 |
0 |
-0,5 |
-0,28125 |
-0,125 |
-0,03125 |
0 |
-0,03125 |
-0,125 |
-0,28125 |
-0,5 |
|
9 |
0,5 |
-0,486111 |
-0,267361 |
-0,11111 |
-0,01736 |
0,013889 |
-0,017361 |
-0,111111 |
-0,267361 |
-0,486111 |
|
10 |
1 |
-0,444444 |
-0,225694 |
-0,06944 |
0,024306 |
0,055556 |
0,024306 |
-0,069444 |
-0,225694 |
-0,444444 |
|
11 |
1,5 |
-0,375 |
-0,15625 |
0 |
0,09375 |
0,125 |
0,09375 |
0 |
-0,15625 |
-0,375 |
|
12 |
2 |
-0,277778 |
-0,059028 |
0,097222 |
0,190972 |
0,222222 |
0,190972 |
0,097222 |
-0,059028 |
-0,277778 |
|
13 |
2,5 |
-0,152778 |
0,065972 |
0,222222 |
0,315972 |
0,347222 |
0,315972 |
0,222222 |
0,065972 |
-0,152778 |
|
14 |
3 |
0 |
0,21875 |
0,375 |
0,46875 |
0,5 |
0,46875 |
0,375 |
0,21875 |
0 |
|
|
||||||||||
4.Построение конуса.
Пример
Построение верхней части конуса
X2/4+y2/9-z2 /4=0
лежащую в диапазонах:
x € [-6; 6], у € [-4; 4] с шагом ∆= 1 для обеих
переменных
|
4.) |
х2/4+у2/9-z2/4=0 |
|||||||||
|
z=√(4*(x2/4+y2/9)) |
||||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
|
1 |
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
2 |
-6 |
6,565905 |
6,324555 |
6,146363 |
6,0369234 |
6 |
6,036923 |
6,146363 |
6,324555 |
6,565905 |
|
3 |
-5 |
5,666667 |
5,385165 |
5,174725 |
5,0442487 |
5 |
5,044249 |
5,174725 |
5,385165 |
5,666667 |
|
4 |
-4 |
4,807402 |
4,472136 |
4,21637 |
4,055175 |
4 |
4,055175 |
4,21637 |
4,472136 |
4,807402 |
|
5 |
-3 |
4,013865 |
3,605551 |
3,282953 |
3,0731815 |
3 |
3,073181 |
3,282953 |
3,605551 |
4,013865 |
|
6 |
-2 |
3,333333 |
2,828427 |
2,403701 |
2,1081851 |
2 |
2,108185 |
2,403701 |
2,828427 |
3,333333 |
|
7 |
-1 |
2,848001 |
2,236068 |
1,666667 |
1,2018504 |
1 |
1,20185 |
1,666667 |
2,236068 |
2,848001 |
|
8 |
0 |
2,666667 |
2 |
1,333333 |
0,6666667 |
0 |
0,666667 |
1,333333 |
2 |
2,666667 |
|
9 |
1 |
2,848001 |
2,236068 |
1,666667 |
1,2018504 |
1 |
1,20185 |
1,666667 |
2,236068 |
2,848001 |
|
10 |
2 |
3,333333 |
2,828427 |
2,403701 |
2,1081851 |
2 |
2,108185 |
2,403701 |
2,828427 |
3,333333 |
|
11 |
3 |
4,013865 |
3,605551 |
3,282953 |
3,0731815 |
3 |
3,073181 |
3,282953 |
3,605551 |
4,013865 |
|
12 |
4 |
4,807402 |
4,472136 |
4,21637 |
4,055175 |
4 |
4,055175 |
4,21637 |
4,472136 |
4,807402 |
|
13 |
5 |
5,666667 |
5,385165 |
5,174725 |
5,0442487 |
5 |
5,044249 |
5,174725 |
5,385165 |
5,666667 |
|
14 |
6 |
6,565905 |
6,324555 |
6,146363 |
6,0369234 |
6 |
6,036923 |
6,146363 |
6,324555 |
6,565905 |
|
|
||||||||||
Решение систем
линейных уравнений
|
|
||||||
|
4x-5y=40 |
проверка |
|||||
|
А |
В |
С |
D |
|||
|
1 |
3 |
2 |
7 |
7 |
||
|
2 |
4 |
-5 |
40 |
40 |
||
|
3 |
0,2173913 |
0,0869565 |
5 |
|||
|
4 |
0,173913 |
-0,1304348 |
-4 |
|||
|
x=5, y=-4 |
||||||
|
|
||||||
|
2×1+4×2-2×3-3×4=18 |
||||||
|
2×1+4×2-2×3-3×4=19 |
||||||
|
2×1+4×2-2×3-3×4=20 |
||||||
|
проверка |
||||||
|
A |
B |
C |
D |
E |
F |
|
|
1 |
1 |
2 |
3 |
-2 |
6 |
6 |
|
2 |
2 |
4 |
-2 |
-3 |
18 |
18 |
|
3 |
3 |
2 |
-1 |
2 |
4 |
4 |
|
4 |
2 |
-3 |
2 |
1 |
-8 |
-8 |
|
5 |
-0,0299145 |
0,1538462 |
0,0811966 |
0,2393162 |
1 |
|
|
6 |
0,1538462 |
-0,0769231 |
0,1538462 |
-0,2307692 |
2 |
|
|
7 |
0,2521368 |
-0,1538462 |
0,0299145 |
-0,017094 |
-1 |
|
|
8 |
0,017094 |
-0,2307692 |
0,2393162 |
-0,1367521 |
-2 |
|
|
(1;2;-1;-2) |
Элементы теории вероятности
Перестановка
Пример 1 Сколькими способами
можно расставить шесть различных книг на полке?
Решение 1. Устанавливаем
табличный курсор в свободную ячейку, например в А1. Здесь должно
оказаться значение числа перестановок
2. Для получения значения числа
перестановок воспользуемся специальной функцией: нажимаем на панели
инструментов кнопку Вставка функции (fx).
3. В появившемся диалоговом
окне Мастер функций-шаг 1 из 2 слева в поле Категория указаны
виды функций. Выбираем Математические. Справа в поле Функция
выбираем функцию ФАКТР. Нажимаем на кнопку ОК.
4.. Появляется диалоговое окно ФАКТР.
В рабочее поле Число вводим с клавиатуры число переставляемых объектов
(в примере — 6). Нажимаем на кнопку ОК.
5. В ячейке А1 появляется искомое
число перестановок — 720. Следовательно П6 = 6! = 1x2x3x4x5x6
= 720.
Пример 2
1. Сколькими способами
можно .рассадить за столом 7 человек гостей?
2. Сколько различных восьмизначных
чисел можно составить из цифр 1,2,3,4,5, 6/7,8?
3. Сколько различных комбинаций
букв можно составить из всех букв слова «бухгалтер»?
4. Сколько различных слов можно
составить из всех букв слова: 1) колобок;
. 2) пудель (если принять, что с «ь»
слова не начинаются).
Пример построения графика круга (либо овала) в Excel.
Для построения графика использованы параметрические уравнения x = x0 + R*cos(t) и y = y0 + R*sin(t).
Также посчитана площадь фигуры.
Скачать пример — circle-elliplse-plot.xlsx
То же в Python:
import matplotlib.pyplot as plt
import math
xz = 4
yz = 4
rx = 2
ry = 1
x=[]
y=[]
for i in range (1,1000):
x.append((xz+rx*math.sin(i)))
y.append((yz+ry*math.cos(i)))
plt.scatter(x,y)
plt.show()
С помощью графика можно наглядно показать зависимость одних данных от других, а также проследить изменение значений. Такой метод визуализации очень востребован и используется как в учебных и деловых презентациях, так и в области точных наук и различных исследований. Давайте разберемся, как можно построить и настроить график в Microsoft Excel.
Содержание
- Как построить график
- Редактирование графика
- Добавление в график вспомогательной оси
- Как построить график функции
- Заключение
Как построить график
- Для создания графика в программе Эксель, в первую очередь, потребуется ее основа с информацией. Другими словами, сначала необходимо создать таблицу и внести в неё все значения, на базе которых будет строиться график. Или же можно открыть файл, который содержит таблицу.
- Переходим во вкладку «Вставка». Выделяем всю таблицу или только ту часть, которую необходимо отразить в виде графика. Нажимаем на кнопку «График».
- На выбор будет предоставлены различные варианты графиков.
- График. Привычные нам простые линии.
- График с накоплением. При выборе данного варианта будет отображаться динамика изменения вклада каждого значения с течением времени или по категориям данных, которые разделены на равные интервалы.
- Нормированный график с накоплением. Если выбрать данный вариант, будет отображаться динамика вклада каждой величины в процентах с течением времени или по категориям данных, которые разделены на равные интервалы.
- График с маркерами (обычный, с накоплением или нормированный с накоплением). Будут отображаться конкретные значения данных на графике.
- Объёмный график. Имеет кроме высоты и длины, еще и глубину. Кривая графика изображается в виде ленты.
- График с областями (обычный, с накоплением, нормированный с накоплением). Сами принцип построения линий в зависимости от выбранного подвида аналогичен описанным выше вариантам. Однако, в данном случае, график представляет из себя не просто линии, а закрашенные области согласно построенными линиям.
- Объемный график с областями (обычный, с накоплением, нормированный с накоплением). Все то же самое, что и в варианте выше, только в трехмерном исполнении.
- Выбираем из перечисленных вариантов наиболее понравившийся или тот, что лучше всего отобразит необходимую информацию, и щелкаем по нему.
- Об остальном позаботится Эксель, выведя результат в виде готового графика в отдельном окне, которое, к тому же, можно изменять по размерам путем растягивания или сжатия, а также, перемещать внутри листа.
Редактирование графика
Чтобы улучшить внешний вид и упростить восприятие данных, график можно отредактировать как целиком, так и изменить его отдельные элементы.
- Если необходимо изменить название графика, щелкаем по нему, чтобы выделить. Теперь правой кнопкой мыши вызываем контекстное меню, где выбираем “Изменить текст”.
Редактируем название, после чего щелкаем мышкой в любом свободном месте графика за пределами названия, чтобы сохранить его.
- Чтобы изменить размер шрифта названия, в контекстном меню выбираем пункт “Шрифт…”.
Откроется окно, в котором можно задать параметры шрифта, в том числе, его размер.
- Название можно перемещать внутри графика на своей усмотрение. Для этого наводим на область названия курсор, затем зажимаем левую кнопки мыши, двигаем его в нужное место и отпускаем кнопку.
- Чтобы вносить более существенные корректировки, необходимо перейти во вкладку «Конструктор», если вы находитесь не в ней.
В некоторых случаях, когда размеры окна с программой сжаты по ширине, возможно, вам не удастся найти требуемую вкладку, так как она скрыта. Вы можете либо растянуть размеры окна, либо нажать на небольшую стрелку вправо, чтобы раскрыть скрытые элементы и выбрать среди них тот, что нужен.
- В данной вкладке представлены широкие возможности по редактированию внешнего вида графика. Одной из главных кнопок здесь является “Добавить элемент диаграммы”.
Нажатие на нее раскрывает список, который позволяет скорректировать все элементы, отображающиеся на графике.
- Давайте попробуем изменить расположение названия. Для этого щелкаем по пункту “Название диаграммы”. Здесь мы видим все варианты, предложенные программой. Выбирать название с наложением не особо рекомендуется, так как в данном случае оно может в определенных случаях перекрывать собой часть полезной информации, отображаемой на графике.
- В дополнительных параметрах названия можно настроить границы, заливку, выравнивание, а также определить заливку и контуры самого текста.
Открыть их можно путем выбора соответствующего пункта в списке, или просто двойным щелчком мыши по элементу на самом графике.
- Для того, чтобы подписать наименование осей, нажимаем «Название осей». Здесь есть возможность выбрать вертикальную или горизонтальную ось. Допустим, мы выбрали добавить основную горизонтальную ось.
Задать ей имя и изменить расположение можно также, как это делается для название (описано выше). Также, можно в дополнительных параметрах настроить формат названия оси.
- При необходимости добавляем вертикальную ось и настраиваем ее.
- Аналогичным образом в разделе “Добавить элемент диаграммы” настраиваются другие параметры, такие как подписи данных, легенда, сетка, линии и т.д.
- У пользователя также есть возможность воспользоваться быстрой настройкой графика, воспользовавшись шаблонами, которые предлагает программа. Для этого, находясь во вкладке “Конструктор”, нужно нажать кнопку “Экспресс-макет”.
Здесь будут представлены все доступные варианты оформления.
- Помимо этого в Эксель предусмотрены разнообразные стили оформления графика. Просто выберите тот, что вам больше нравится, и щелкните по нему.
- После этого программа автоматически внесет соответствующие изменения.
Добавление в график вспомогательной оси
Нередко возникает необходимость на одной диаграмме разместить несколько графиков. В этом нет никакой сложности, если они имеют одинаковые меры исчисления. Но порой приходится совмещать несколько графиков с различными мерами исчисления, к примеру, чтобы показать зависимость одних данных от других. Делается это следующим образом.
- Первые шаги такие же, как и описанные выше. Выделяем таблицу, переходим во вкладку “Вставка” и выбираем наиболее подходящий вариант графика.
- В полученной диаграмме построено несколько графиков в соответствии с количеством столбцов выделенной таблицы. Теперь нужно нажать правой кнопкой мыши на тот, для которого необходима вспомогательная ось. Внизу появившегося списка выбираем «Формат ряда данных…».
- Откроются настройки формата данных, в котором выбираем “Построить ряд по вспомогательной оси”.
- После этого будет добавлена вспомогательная ось, и график перестроится. Далее можно скорректировать название, подписи данных, легенду, и выбрать для них подходящее место.
Примечание: в диаграмму можно добавить только одну дополнительную ось, что ограничивает возможность построения графиков для трёх и более различных мер исчисления.
Как построить график функции
Эта возможность в Excel может здорово сократить время выполнения некоторых задач, например, по алгебре. Поэтому, давайте подробнее рассмотрим такой вариант и в качестве примера возьмем функцию y=x²+5.
- Как и полагается для всех диаграмм, сперва составляем исходную таблицу. В левый столбец записываем значение х с нужным шагом, а в правый – формулу, которая будет рассчитывать значение у. В таблице это будет выглядеть так:
- Рассчитав значение для первой ячейки, нужно протянуть формулу на остальные строки таблицы. Для этого наводим курсор на правый нижний угол ячейки, он меняет вид на крестик, теперь зажав левую кнопку тянем выделение до нижней ячейки, чтобы скопировать формулу и автоматически рассчитать значения по ней для оставшихся строк.
- Выделив таблицу, переходим во вкладку «Вставка», где нажимаем на кнопку “Точечная” и из вариантов, выданных всплывающим окном, лучше всего подходит под нашу задачу вид “Точечная с гладкими кривыми и маркерами”.
- После того, как сформируется диаграмма, привычным способом ее редактируем и удаляем за ненадобностью лишние элементы.
Заключение
Наряду с работой данных в табличном виде, в программе Microsoft Excel можно строить графики. Программа предлагает большое разнообразие видов и подвидов, которые прекрасно покрывают потребности пользователей в предоставлении информации в наиболее наглядном виде, значительно облегчающем ее восприятие.
|
35 / 35 / 9 Регистрация: 16.07.2012 Сообщений: 253 |
|
|
1 |
|
Построить эллипс в екселе задан уравнением19.06.2013, 21:56. Показов 13878. Ответов 3
Построить эллипс в екселе задан уравнением x2/9+ y2/4= 1
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
19.06.2013, 21:56 |
|
3 |
|
866 / 510 / 162 Регистрация: 30.03.2013 Сообщений: 1,048 |
|
|
19.06.2013, 22:52 |
2 |
|
Вариант.
1 |
|
35 / 35 / 9 Регистрация: 16.07.2012 Сообщений: 253 |
|
|
19.06.2013, 23:04 [ТС] |
3 |
|
Вариант. спасибо большое,я конечно извиняюсь просто сделал ошибку в уравнении а исправить уже не мог. Можете сделать для x2/9+ y2/4= 1 Заранее благодарен=)
0 |
|
866 / 510 / 162 Регистрация: 30.03.2013 Сообщений: 1,048 |
|
|
19.06.2013, 23:18 |
4 |
|
График построен для этого x2/9+ y2/4= 1 уравнения.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
19.06.2013, 23:18 |
|
Помогаю со студенческими работами здесь Построить эллипс Построить цепную линию, заданную уравнением Построить конус, заданный уравнением, в matlab. Построить линию, заданную уравнением x^2+y^2-4xy-3=0 Построить линию, заданную… Построить прозрачный эллипс
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 4 |

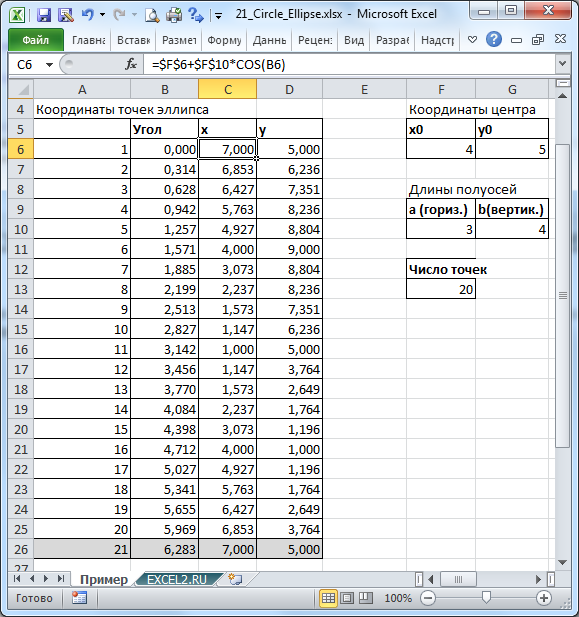
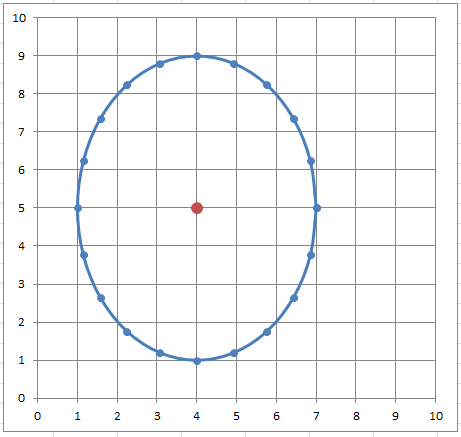
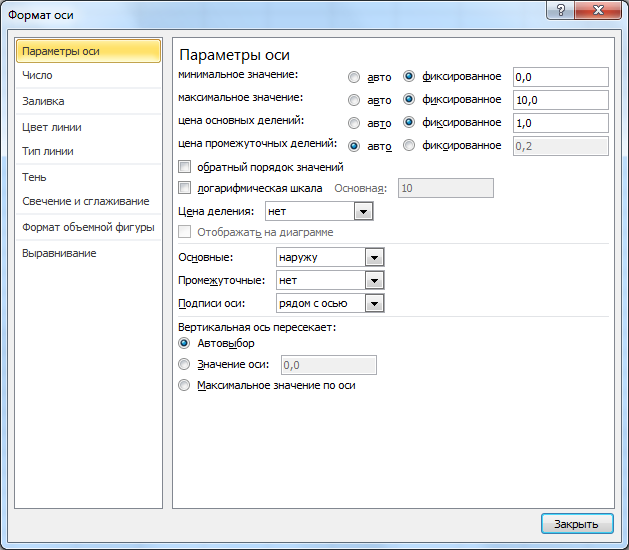
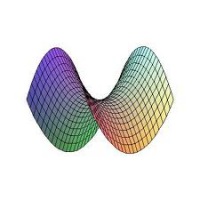
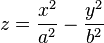
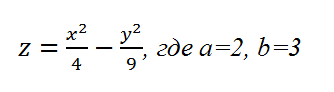
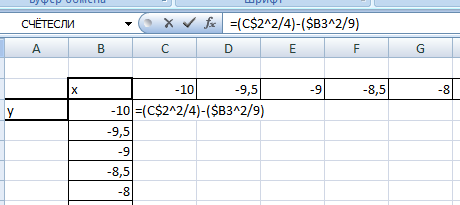

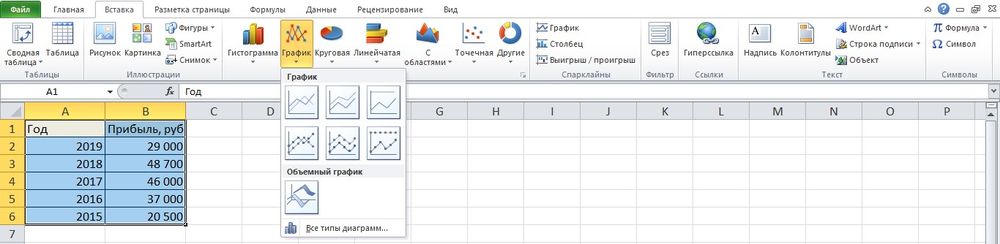
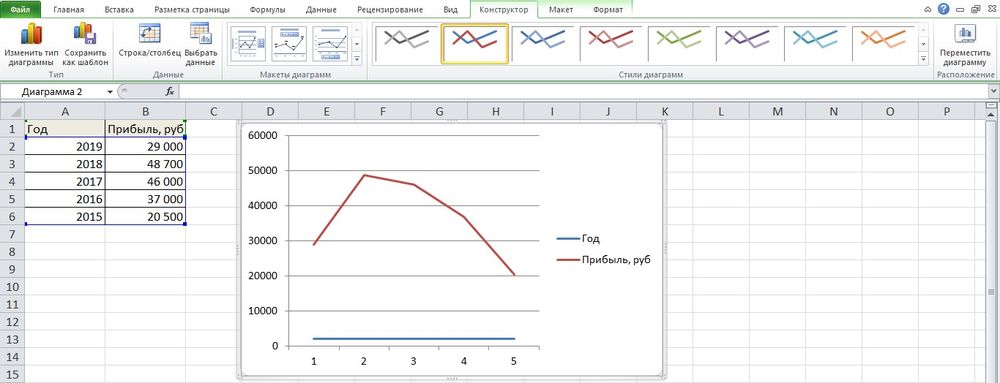
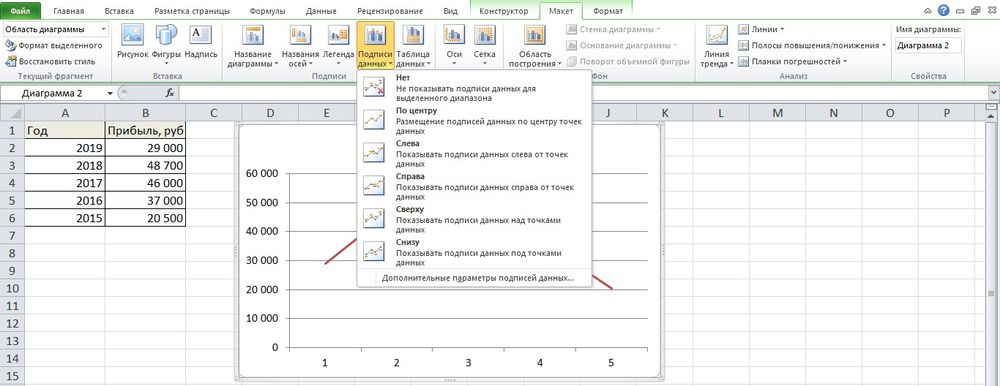
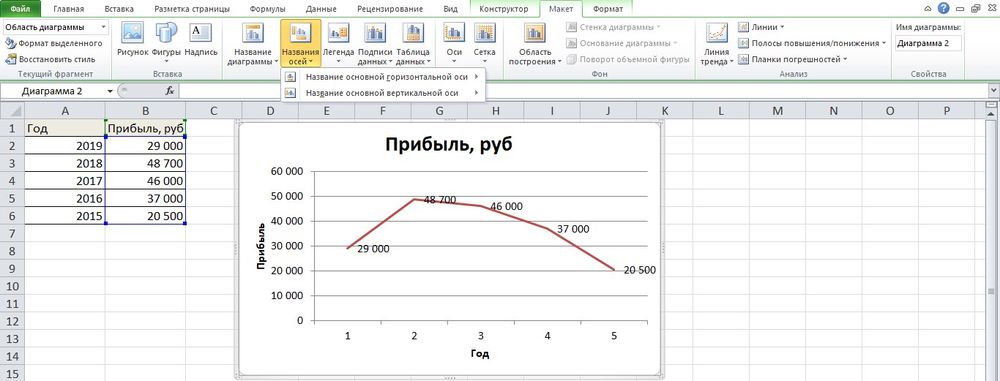
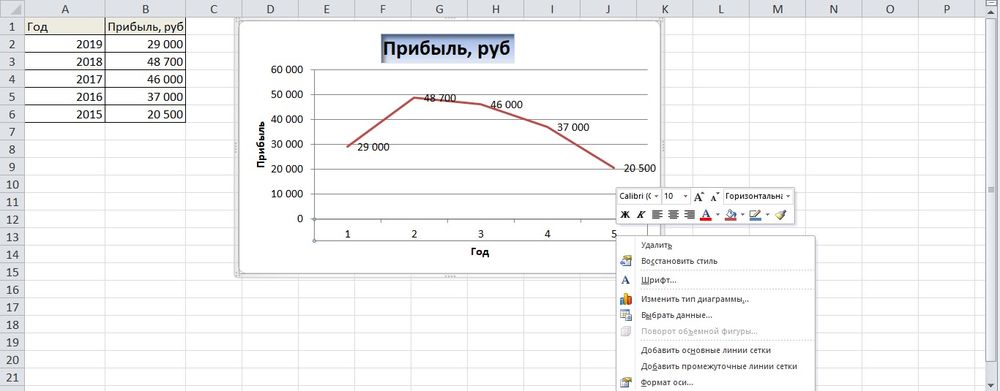
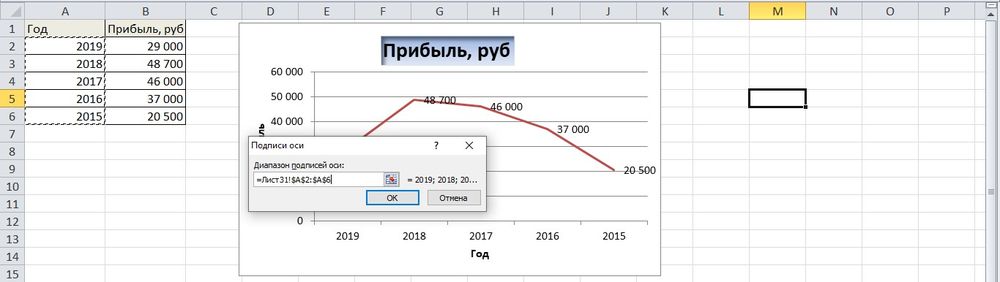
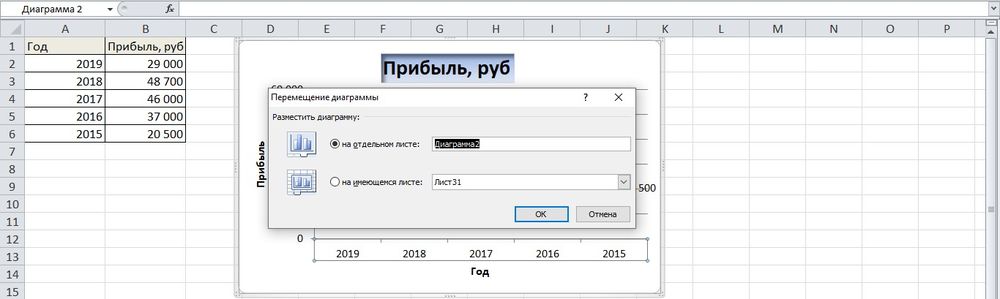

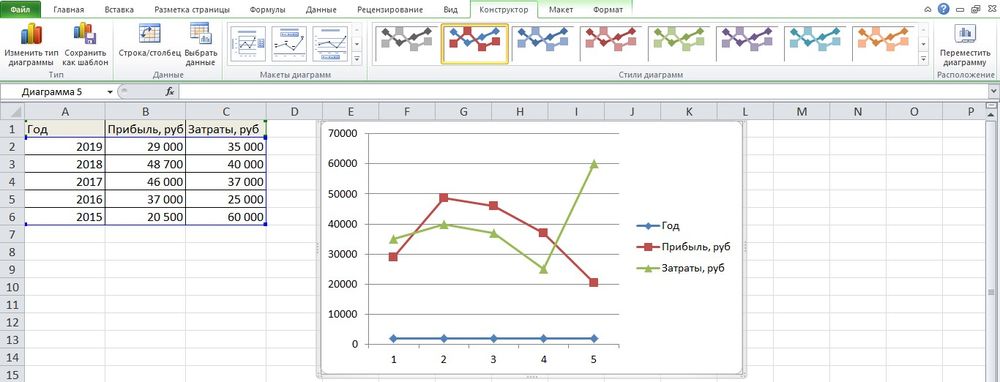
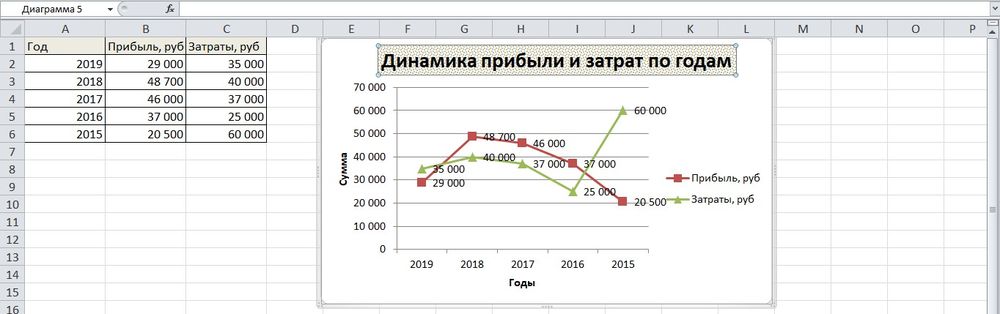
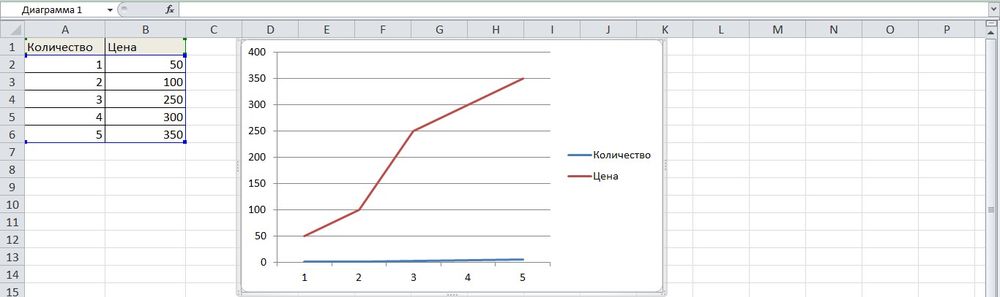
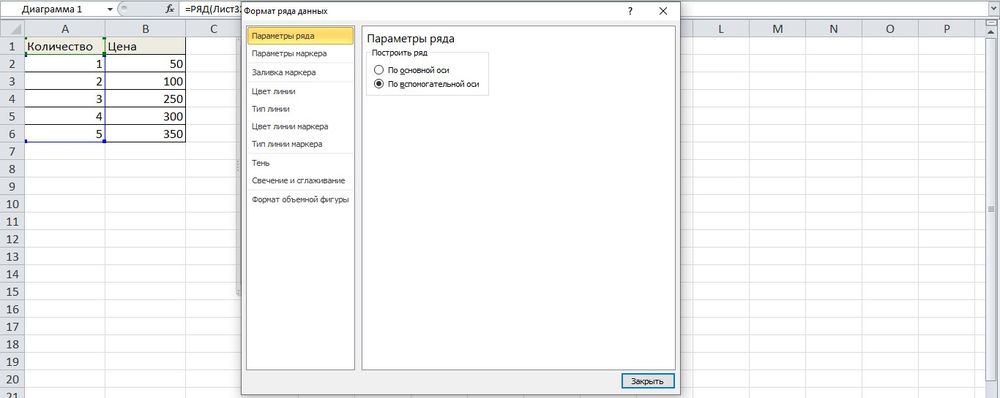
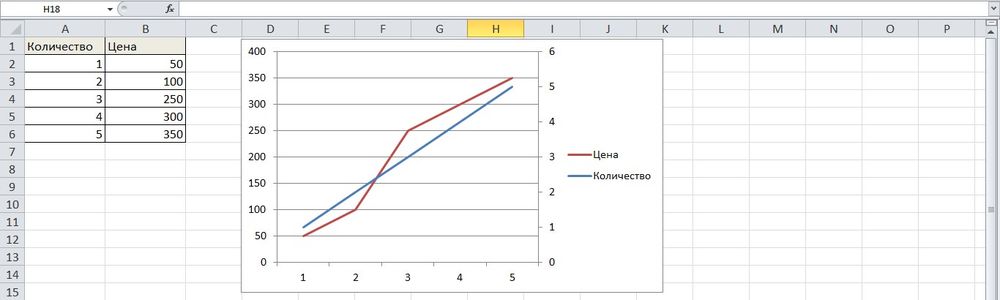
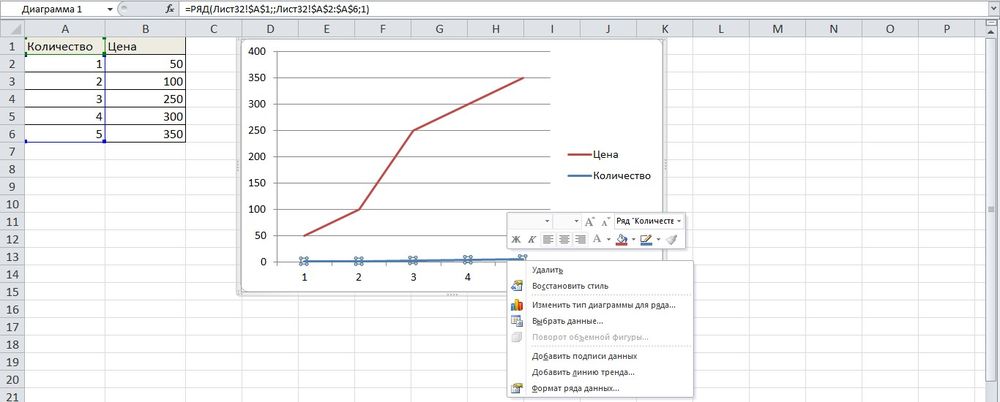
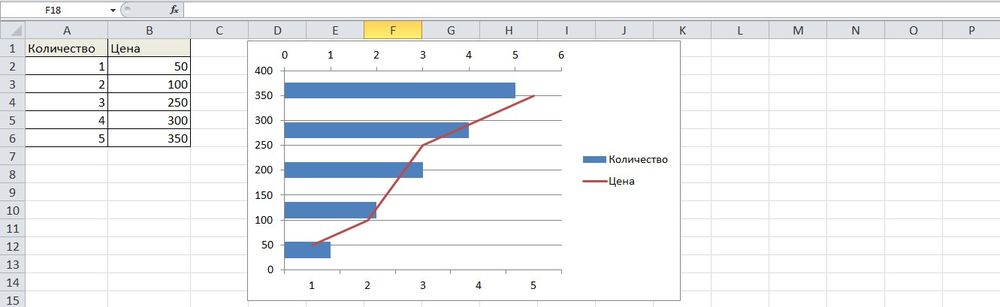
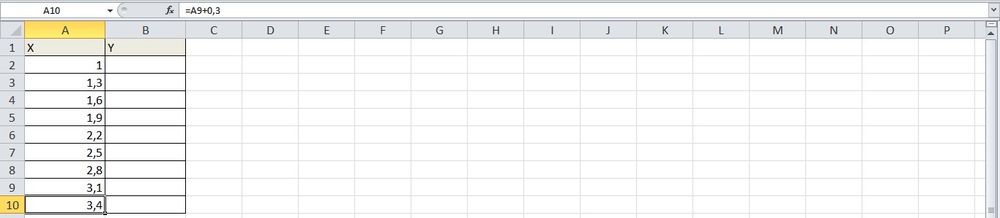
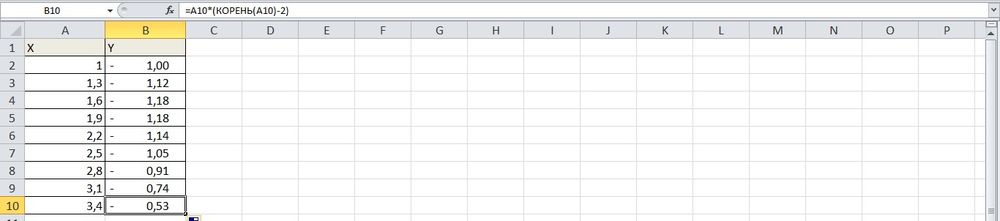
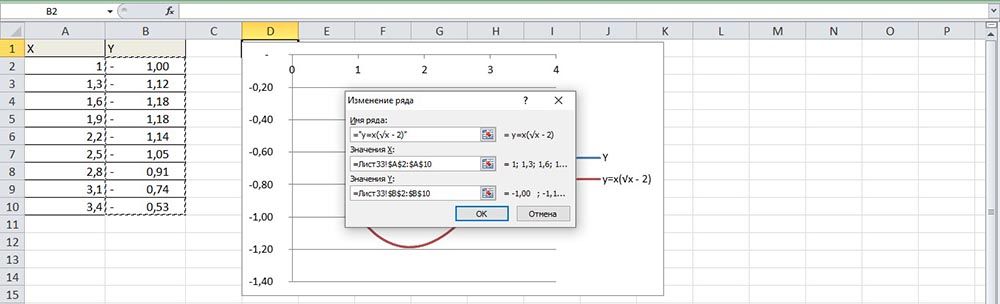
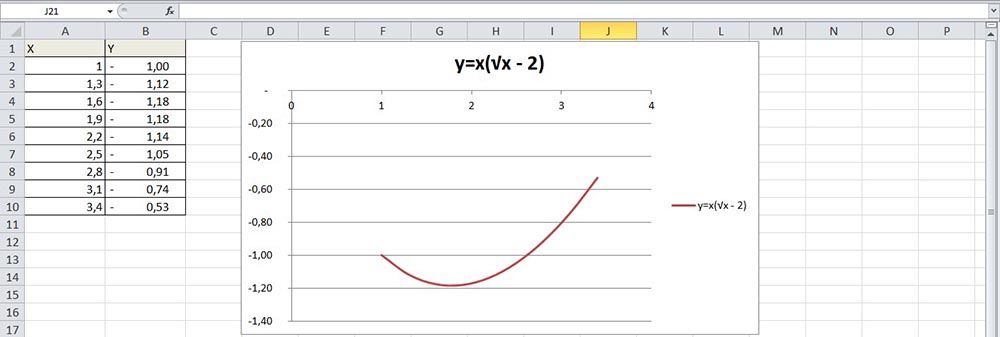
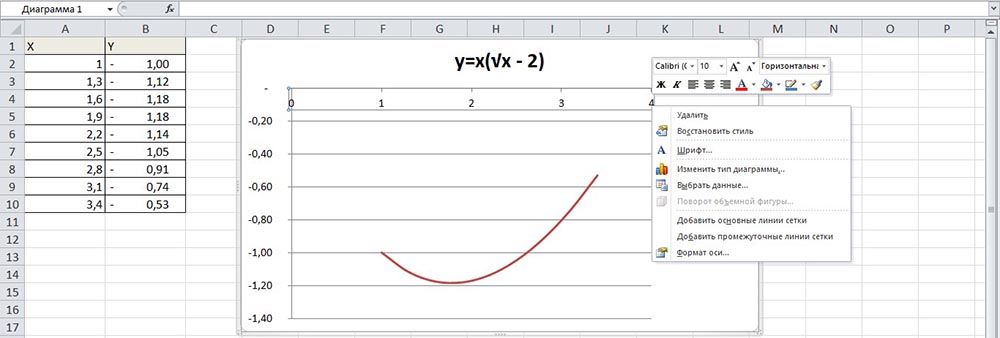
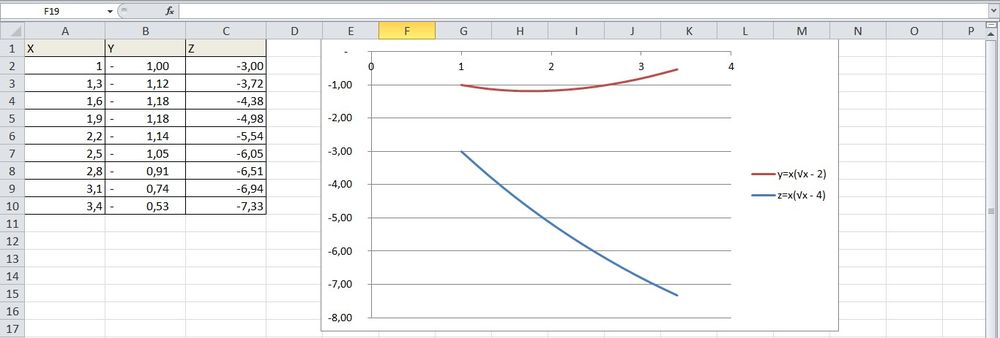
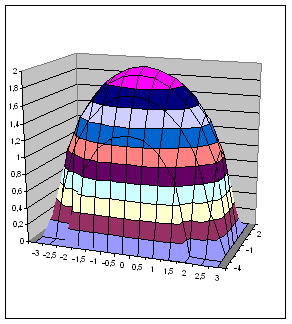






















 Редактируем название, после чего щелкаем мышкой в любом свободном месте графика за пределами названия, чтобы сохранить его.
Редактируем название, после чего щелкаем мышкой в любом свободном месте графика за пределами названия, чтобы сохранить его.
 Откроется окно, в котором можно задать параметры шрифта, в том числе, его размер.
Откроется окно, в котором можно задать параметры шрифта, в том числе, его размер.

 В некоторых случаях, когда размеры окна с программой сжаты по ширине, возможно, вам не удастся найти требуемую вкладку, так как она скрыта. Вы можете либо растянуть размеры окна, либо нажать на небольшую стрелку вправо, чтобы раскрыть скрытые элементы и выбрать среди них тот, что нужен.
В некоторых случаях, когда размеры окна с программой сжаты по ширине, возможно, вам не удастся найти требуемую вкладку, так как она скрыта. Вы можете либо растянуть размеры окна, либо нажать на небольшую стрелку вправо, чтобы раскрыть скрытые элементы и выбрать среди них тот, что нужен.
 Нажатие на нее раскрывает список, который позволяет скорректировать все элементы, отображающиеся на графике.
Нажатие на нее раскрывает список, который позволяет скорректировать все элементы, отображающиеся на графике.

 Открыть их можно путем выбора соответствующего пункта в списке, или просто двойным щелчком мыши по элементу на самом графике.
Открыть их можно путем выбора соответствующего пункта в списке, или просто двойным щелчком мыши по элементу на самом графике.
 Задать ей имя и изменить расположение можно также, как это делается для название (описано выше). Также, можно в дополнительных параметрах настроить формат названия оси.
Задать ей имя и изменить расположение можно также, как это делается для название (описано выше). Также, можно в дополнительных параметрах настроить формат названия оси.


 Здесь будут представлены все доступные варианты оформления.
Здесь будут представлены все доступные варианты оформления.












 Построить астроиду-кривую, заданную параметрическим уравнением
Построить астроиду-кривую, заданную параметрическим уравнением