Содержание
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- Вопросы и ответы
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
f(x) = e^n,
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
=EXP(число)
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
- Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
=EXP(3) - Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.
Урок: Другие математические функции в Эксель
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
- Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
- Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
- Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
- После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Урок: Мастер функций в Microsoft Excel
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
- Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
- После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.
Урок: Как сделать график в Excel
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Еще статьи по данной теме:
Помогла ли Вам статья?
На чтение 11 мин Просмотров 3к. Опубликовано 04.07.2019
Содержание
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- Excel works!
- Экспонента в Excel. Что такое экспонента и как применять?
- Экспонента. Что это такое?
- Принцип Парето и экспонента
- Экспонента в Excel
- Дополнение. Как запомнить 15 знаков числа е?
- Функция РОСТ()
- Функция ЛГРФПРИБЛ()
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
-
Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
-
Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
-
Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Excel работает за вас
Excel works!
Thanks for Visiting
Экспонента в Excel. Что такое экспонента и как применять?
Мы немного затронули тему экспоненты в статье про округление больших чисел . В этой же статье мы обсудим, что же такое экспонента в Excel и, самое главное, для чего она может пригодиться в обычной жизни или в бизнесе.
В студенческие годы часто приходилось слышать, фразы типа: «Зачем мы вообще учим ‘это’, в жизни нам ‘это’ никогда не пригодиться». Одним из таких ‘это’ часто была экспонента или, например, факториал . У меня была слабая высшая математика при первом образовании, о чем я жалею. И вот сейчас приходиться догонять, темы что упустил раньше. Делюсь пересказом своих знаний.
Экспонента. Что это такое?
Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:
Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).
Что это вообще такое, и что для нас означает?
Лучше всего, действие экспоненты показывают графики ниже:
Две функции: y = 2 в степени x и y = e в степени x , где x = время, к примеру. Мы видим, что скорость роста экспоненциального графика увеличивается быстрее. А все почему? Потому, что производная (скорость роста или уменьшения) функции равна самой функции, т.е. скорость увеличения функции равна значению функции.
Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:
Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее пока вы не заберете деньги или не случится банковский кризис.
Кстати население на планете Земля тоже растет по экспоненте;)
Принцип Парето и экспонента
Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он. Лучшее определение для запоминания, мне кажется:
20% любителей пива употребляют 80% всего пива
На принципе Парето построен и ABC анализ запасов, например.
Этот принцип Парето — еще один пример экспоненты.
Кстати очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.
При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:
Экспонента в Excel
Когда по смыслу функции более-менее объяснил, напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.
В Эксель все посчитать несложно:
или можно число возвести в степень
Дополнение. Как запомнить 15 знаков числа е?
В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков
- запишите 2,7,
- затем дважды год рождения Льва Толстого – 1828,
- затем величины углов равнобедренного прямоугольного треугольника – 45°, 90°, 45°,
- в итоге получается: 2,718281828459045.
Как фанат Льва Николаевича, я не смог забыть этот способ 🙂 Кстати отличная книга о том как запоминать много информации и как работает память здесь .
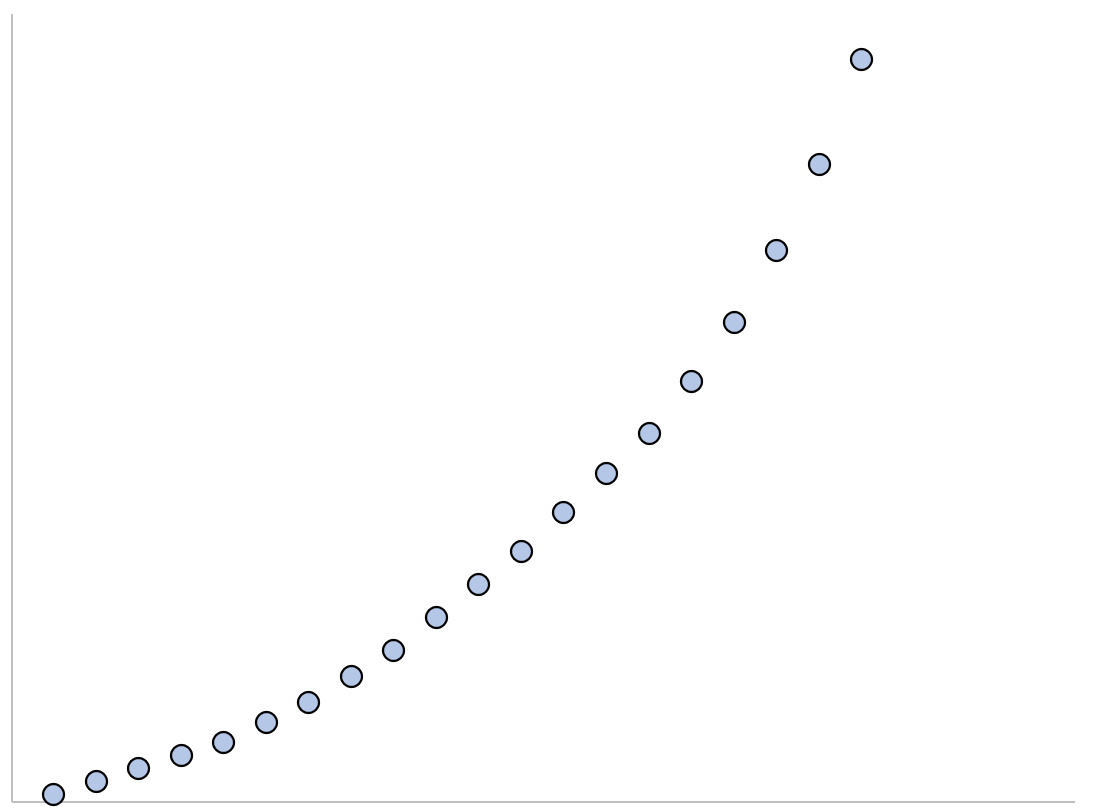
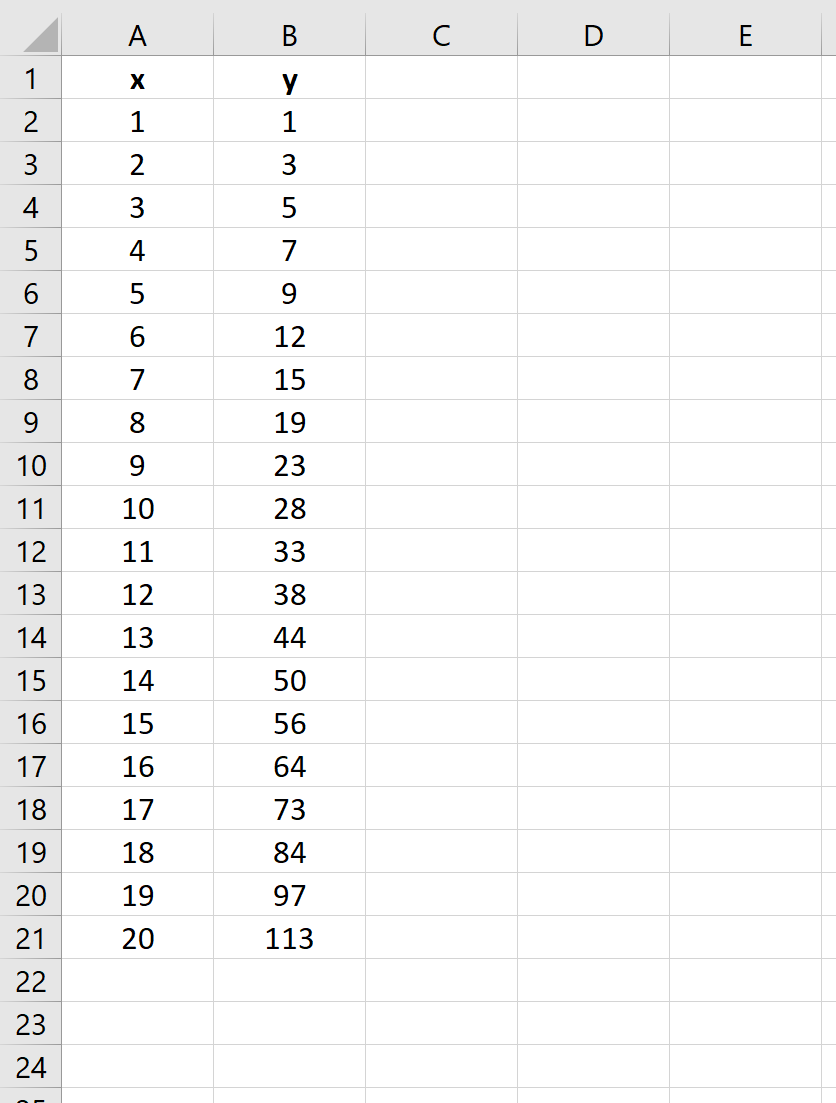
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares, OLS) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL.
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m x =a*(e ln(m) ) x = a*e x*ln(m) =a*e bx , где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
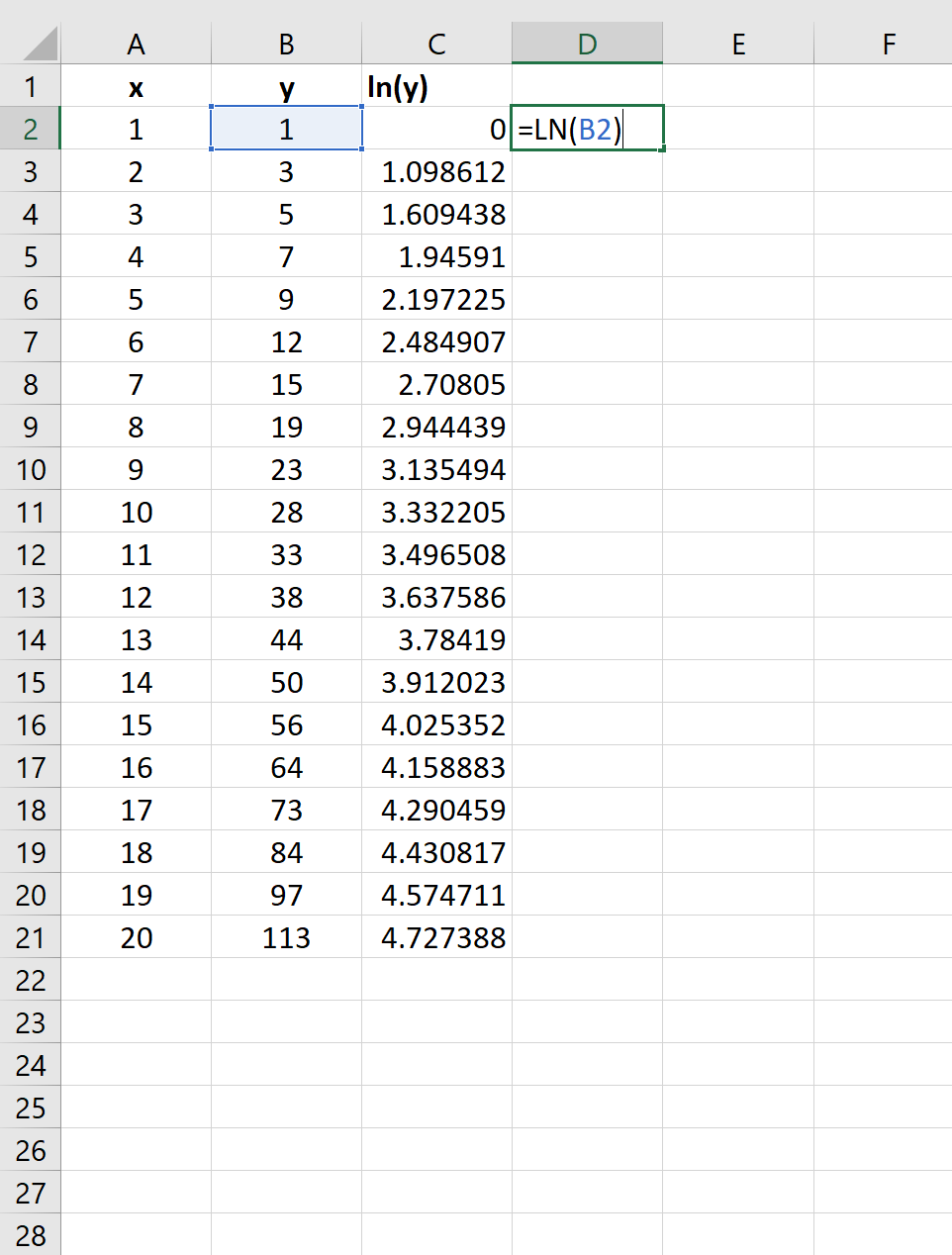
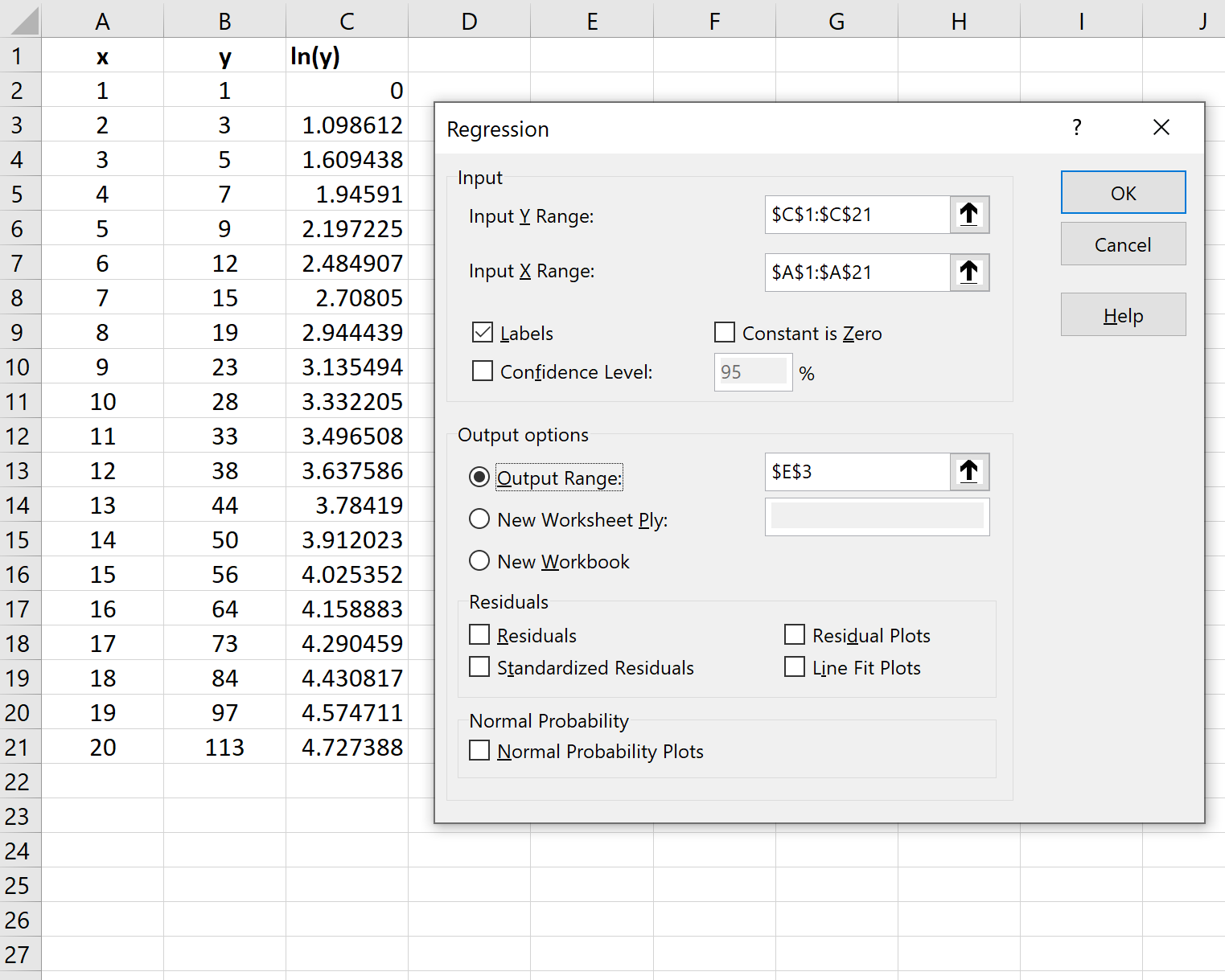
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .
Примечание: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда (Экспоненциальная линия тренда). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL.
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больших по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y, ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).
Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).
Функция РОСТ()
Еще одним способом построить линию экспоненциального тренда является использование функции РОСТ() , английское название GROWTH.
Синтаксис функции следующий:
РОСТ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])
Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y) и на массив значений переменной Х (аргумент известные_значения_x). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x. Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).
Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.
Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.
Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y=a*EXP(b*x).
Примечание: В MS EXCEL имеется специальная функция ЛГРФПРИБЛ() , которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.
Чтобы вычислить коэффициент a (значение Y в точке Х=0) используйте формулу =РОСТ(C26:C45;B26:B45;0) . В диапазонах C26:C45 и B26:B45 должны находиться массивы значений переменной Y и X соответственно.
Чтобы вычислить коэффициент b используйте формулу:
= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/
РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/
(МИН(B26:B45)-МАКС(B26:B45))
Функция ЛГРФПРИБЛ()
Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y=a*m^x.
Используя свойство степеней a mn =(a m ) n приведем уравнение экспоненциального тренда y=a*EXP(b*x)=a*e b *x = a*(e b ) x к виду y=a*m^x, сделав замену переменной m= e b =EXP(b).
Чтобы вычислить коэффициенты уравнения y=a*EXP(b*x) используйте следующие формулы:
= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) — коэффициент b
= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) — коэффициент a
Примечание: Функция ЛГРФПРИБЛ() , английское название LOGEST, является формулой массива, возвращающей несколько значений. Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в Строке формул ввести = ЛГРФПРИБЛ(C26:C45;B26:B45) , затем для ввода формулы вместо обычного ENTER нажать CTRL+SHIFT+ENTER.
Функция ЛГРФПРИБЛ() имеет линейный аналог – функцию ЛИНЕЙН() , которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции (статистика) установлен ИСТИНА, то ЛГРФПРИБЛ() возвращает регрессионную статистику: стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов: SSR, SSE и др.
Примечание: Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=a*m^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=a*EXP(b*x).
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание!!! Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Получаем результат:
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
y = 7,6403е^-0,084x
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
Например:
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
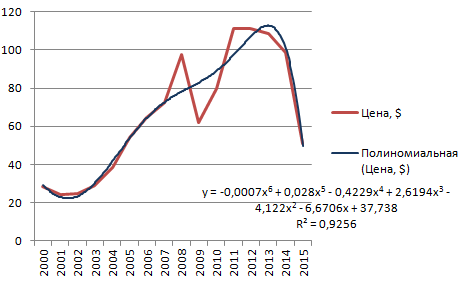
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Скачать примеры графиков с линией тренда
Зато такой тренд позволяет составлять более-менее точные прогнозы.
5 способов расчета значений линейного тренда в MS Excel
Добавление трендовой линии на график
Данный элемент технического анализа позволяет визуально увидеть изменение цены за указанный период времени . Это может быть месяц, год или несколько лет. Информация будет отображать значение средних показателей в виде геометрических фигур . Добавить линию тренда в Excel 2010 можно с помощью встроенных стандартных инструментов.
Построение графика


- Первым действием нужно выделить диапазон данных , например это А1:В9, затем активировать инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с гладкими кривыми и маркерами».
- После открытия графика пользователю станет доступна еще одна панель управления данными , на которой нужно выбрать следующее: «Работа с диаграммами»-«Макет»-«Линия тренда»-«Линейное приближение».
- Следующим шагом требуется выполнить двойной клик по образовавшейся линии тенденции в Excel . Когда появиться вспомогательное окно, отметить птичкой опцию «показывать уравнение на диаграмме».
Важно помнить, что если на графике имеется 2 или более линий , отображающих анализ данных, то перед выполнением 3 пункта нужно будет выбрать одну из них и включить в тенденцию. Эта короткая инструкция поможет начинающим специалистам разобраться, как строится линия тренда в Экселе.
Создание линии
Дальнейшая работа будет происходить непосредственно с трендовой линией.
Добавление тренда на диаграмму происходит следующим образом:
- Перейти во вкладку «Работа с диаграммами» , затем выбрать раздел «Макет»-«Анализ» и после подпункт «Линия тенденции» . Появится выпадающий список, в котором необходимо активировать строку «Линейное приближение».
- Если все выполнено правильно, в области построения диаграмм появится кривая линия черного цвета . По желанию цветовую гамму можно будет изменить на любую другую.
Этот способ поможет создать и построить тренд в Excel 2016 или более ранних версиях.

- лепесткового;
- кругового;
- поверхностного;
- кольцевого;
- объемного;
- с накоплением.
Настройка линии
Построение линий тренда имеет ряд вспомогательных настроек , которые помогут придать графику законченный и презентабельный вид.
Необходимо запомнить следующее:
- Чтобы добавить название диаграмме , нужно дважды кликнуть по ней и в появившемся окне ввести заголовок. Для выбора расположения имени графика необходимо перейти во вкладку «Работа с диаграммами», затем выбрать «Макет» и «Название диаграммы». После этого появится список с возможным расположением заглавия.
- Дополнительно в этом же разделе можно найти пункт, отвечающий за названия осей и их расположение относительно графика. Интересно, что для вертикальной оси разработчики программы продумали возможность повернутого расположения наименования, чтобы диаграмма читалась удобно и выглядела гармонично.
Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
- Еще есть функция определения достоверности построенной модели . Для этого в дополнительных настройках требуется активировать пункт «Разместить на график величину достоверности аппроксимации» и после этого закрыть окно. Наилучшим значением является 1. Чем сильнее полученный показатель отличается от нее, тем ниже достоверность модели.
Прогнозирование
Для получения наиболее точного прогноза необходимо сменить построенный график на гистограмму . Это поможет сравнить уравнения.

- Вызвать для графика контекстное меню и выбрать «Изменить тип диаграммы» .
- Появится новое окно с настройками , в котором требуется найти опцию «Гистограмма» и после выбрать подвид с группировкой.
Теперь пользователю должны быть видны оба графика . Они визуализируют одни и те же данные, но имеют разные уравнения для образования тенденции.
Следующим шагом необходимо сравнить уравнения точки пересечения с осями на разных диаграммах .
Для визуального отображения нужно сделать следующее:
- Перевести гистограмму в простой точечный график с гладкими кривыми и маркерами . Процесс выполняется через пункт контекстного меню «Изменить тип диаграммы…».
- Выполнить двойной клик по прямой образовавшейся тенденции , задать ей параметр прогноза назад на 12,0 и сохранить изменения.
Такая настройка поможет увидеть, что угол наклона тенденции меняется в зависимости от вида графика , но общее направление движения остается неизменным. Это свидетельствует о том, что построить линию тренда в Эксель можно лишь в качестве дополнительного инструмента анализа и брать его в расчет следует только как приближающий параметр. Строить аналитические прогнозы, основываясь лишь на этой прямой, не рекомендуется.
Базовые понятия
Думаю, еще со школы все знакомы с линейной функцией, она как раз и лежит в основе тренда:
Y — это объем продаж, та переменная, которую мы будем объяснять временем и от которого она зависит, то есть Y(t);
t — номер периода (порядковый номер месяца), который объясняет план продаж Y;
a0 — это нулевой коэффициент регрессии, который показывает значение Y(t), при отсутствии влияния объясняющего фактора (t=0);
a1 — коэффициент регрессии, который показывает, на сколько исследуемый показатель продаж Y зависит от влияющего фактора t;
E — случайные возмущения, которые отражают влияния других неучтенных в модели факторов, кроме времени t.
Определение коэффициентов модели
Строим график. По горизонтали видим отложенные месяцы, по вертикали объем продаж:
В Google Sheets выбираем Редактор диаграмм -> Дополнительные и ставим галочку возле Линии тренда. В настройках выбираем Ярлык — Уравнение и Показать R^2.
Если вы делаете все в MS Excel, то правой кнопкой мыши кликаем на график и в выпадающем меню выбираем «Добавить линию тренда».
По умолчанию строится линейная функция. Справа выбираем «Показывать уравнение на диаграмме» и «Величину достоверности аппроксимации R^2».
Вот, что получилось:
На графике мы видим уравнение функции:
y = 4856*x + 105104
Она описывает объем продаж в зависимости от номера месяца, на который мы хотим эти продажи спрогнозировать. Рядом видим коэффициент детерминации R^2, который говорит о качестве модели и на сколько хорошо она описывает наши продажи (Y). Чем ближе к 1, тем лучше.
У меня R^2 = 0,75. Это средний показатель, он говорит о том, что в модели не учтены какие-то другие значимые факторы помимо времени t, например, это может быть сезонность.
Способ расчета значений линейного тренда в Excel с помощью графика

Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время – значение по оси Х;
- Значение “a” и “b” уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
Способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y – это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x – это номера периодов x для известных значений объёмов продаж y;
- новые значения x – это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа – ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в “новые значения x” вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Общая информация
Линия тренда – это инструмент статистического анализа, который позволяет спрогнозировать дальнейшее развитие событий. Чтобы построить кривую, необходимо иметь массив данных, который отображает изменение величины во времени. На основании этой информации строится график, а затем применятся специализированная функция. Рассмотрим изменение цены золота за грамм в долларах с 2015 по 2019 год.
- Составляете небольшую таблицу.
- На основании этих данных строите линейный график. Для этого переходите во вкладку Вставка на Панели инструментов и выбираете нужный тип диаграммы.
- Получается некоторая кривая.
- Необходимо отредактировать график при помощи стандартных инструментов, которые находятся во вкладках Конструктор, Макет и Формат. Переименовываете диаграмму, выставляете пределы по вертикальной оси, чтобы изменения величины были более явными, подписываете оси, добавляете контрольные точки, а также подпись данных. После этого проводите окончательное форматирование.
- Чтобы добавить линию тренда, необходимо во вкладке Макет нажать одноименную кнопку и выбрать нужный тип приближения.
На заметку! Если линия тренда не активна, то используется не тот тип диаграммы. Данная функция работает только с диаграммами типа гистограмма, график, линейчатая и точечная.
6. Так выглядит линия тренда на графике.
На заметку! Построение линии приближения идентично для редакторов 2007, 2010 и 2016 годов выпуска.
Возможности инструмента
Рассмотрим подробнее настройки функции. Для перехода в окно параметров из выпадающего списка нужно выбрать последнюю строчку.
Окно содержит четыре настройки, в которые входят цвет, объем и тип линии, а также параметры самого инструмента.
Параметры линии тренда можно условно поделить на четыре блока:
- Тип приближения.
- Название полученной кривой, которое формируется автоматически или может быть задано пользователем.
- Блок прогнозирования, который позволяет продлить линию тренда на заданное количество периодов вперед или назад, на основании имеющихся данных. Что позволяет оценить дальнейшее изменение исследуемой величины.
- Дополнительные опции, которые отражают математическую составляющую кривой. Самой интересной и полезной строчкой здесь является величина достоверности. Если значение коэффициента близко к единице, то ошибка минимальна и дальнейший прогноз будет достаточно точным.
Выведем на исходный график уравнение линии и коэффициент достоверности.
Как видите, значение близко к 0,5, это говорит о низкой достоверности полученной линии тренда, и дальнейший прогноз будет ошибочным.
Разновидности
1 Линейная аппроксимация отлично подойдет для исследования величины, которая стабильно растет или убывает. Тогда кривая будет иметь вид прямой. Формула будет содержать одну переменную. Коэффициент достоверности близок к единице, что говорит о высокой точности совпадения прямой и массива данных. На основании такой линии тренда прогноз будет достаточно точным.
2. Экспоненциальная кривая используется только для массивов с положительными значениями, которые изменяются непрерывно.
3. Логарифмическую линию тренда целесообразнее использовать, если на первоначальном этапе наблюдается резкое увеличение или снижение показателя, а потом наступает период стабильности. Здесь формула содержит логарифм натуральный.
4. Полиномиальная аппроксимация применяется при большом количестве неоднородных данных. В основе лежит степенное уравнение, при этом количество степеней зависит от числа максимумов. Применим этот тип для первоначального примера с золотом.
Уравнение показывает переменные до третьей степени, поскольку график имеет два пика. Также видим, что коэффициент достоверности близок к единице (вместо 0,5 при линейной аппроксимации), значит линия тренда выбрана правильно и дальнейший прогноз будет точным.
Как видите, для статистического анализа данных необходимо правильно выбрать тип математического уравнения, которое максимально точно будет соответствовать характеру изменения величины. На основании полученных кривых можно осуществлять прогноз, подставляя в уравнение необходимое число.
Разбираемся с трендами в MS Excel
Большой ошибкой со стороны владельца сайта будет воспринимать диаграмму как есть. Да, невооруженным взглядом видно, что синий и оранжевый столбики «осени» выросли по сравнению с «весной» и тем более «летом». Однако важны не только цифры и величина столбиков, но и зависимость между ними. То есть в идеале, при общем росте, «оранжевые» столбики просмотров должны расти намного сильнее «синих», что означало бы то, что сайт не только привлекает больше читателей, но и становится больше и интереснее.
Что же мы видим на графике? Оранжевые столбики «осени» как минимум ни чем не больше «весенних», а то и меньше. Это свидетельствует не об успехе, а скорее наоборот — посетители прибывают, но читают в среднем меньше и на сайте не задерживаются!
Самое время бить тревогу и… знакомится с такой штукой как линия тренда .
Зачем нужна линия тренда
Линия тренда «по-простому», это непрерывная линия составленная на основе усредненных на основе специальных алгоритмов значений из которых строится наша диаграмма. Иными словами, если наши данные «прыгают» за три отчетных точки с «-5» на «0», а следом на «+5», в итоге мы получим почти ровную линию: «плюсы» ситуации очевидно уравновешивают «минусы».
Исходя из направления линии тренда гораздо проще увидеть реальное положение дел и видеть те самые тенденции, а следовательно — строить прогнозы на будущее. Ну а теперь, за дело!
Как построить линию тренда в MS Excel
Щелкните правой кнопкой мыши по одному из «синих» столбцов, и в контекстном меню выберите пункт «Добавить линию тренда» .
На листе диаграммы теперь отображается пунктирная линия тренда. Как видите, она не совпадает на 100% со значениями диаграммы — построенная по средневзвешенным значениям, она лишь в общих чертах повторяет её направление. Однако это не мешает нам видеть устойчивый рост числа посещений сайта — на общем результате не сказывается даже «летняя» просадка.
Линия тренда для столбца «Посетители»
Теперь повторим тот же фокус с «оранжевыми» столбцами и построим вторую линию тренда. Как я и говорил раньше: здесь ситуация не так хороша. Тренд явно показывает, что за расчетный период число просмотров не только не увеличилось, но даже начало падать — медленно, но неуклонно.
Ещё одна линия тренда позволяет прояснить ситуацию
Мысленно продолжив линию тренда на будущие месяцы, мы придем к неутешительному выводу — число заинтересованных посетителей продолжит снижаться. Так как пользователи здесь не задерживаются, падение интереса сайта в ближайшем будущем неизбежно вызовет и падение посещаемости.
Следовательно, владельцу проекта нужно срочно вспоминать чего он такого натворил летом («весной» все было вполне нормально, судя по графику), и срочно принимать меры по исправлению ситуации.
Линия тренда в Excel на разных графиках
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Линия тренда в Excel. На разных графиках
Существует множество сфер, где может использоваться трендовая линия. Но наиболее популярной из них, безусловно, являются финансовые рынки. В бизнесе тоже она применяется довольно часто для составления отчетов и прогнозирования возможных перспектив развития проекта или компании в целом.
Также она будет полезным инструментом в тех областях человеческой деятельности, где можно составлять прогнозы, ориентируясь на статистические данные. А таких сфер значительно больше, чем может показаться на первый взгляд. В частности, к ним относятся социология, психология, программирование (использование математических моделей позволяет автоматизировать процесс прогнозирования) и так далее. Особенно это полезно в сочетании с качественным анализом информации.
Основная проблема почти любого графика с большим количеством информации в том, что в нем показания очень вариативны. Поэтому возможно появление большого количества данных, которые мешают понять, какая действительно тенденция наблюдается в этой отрасли.
Трендовая линия – это классический статистический инструмент, позволяющий без особого опыта предсказать, в каком направлении будет двигаться целевой показатель через некоторое время и в какой точке будет. Также он дает возможность косвенно определить факторы, которые влияют на образование данного тренда. Правда, этого уже чисто статистическими методами сделать не получится, нужно понимать фундаментальные закономерности, которые влияют на формирование тенденции.
Как добавить линию тренда на график Excel
Трендовая линия дает возможность понять действующие тенденции определенного показателя. И поскольку особенно часто сей инструмент сейчас используется на финансовых рынках, то мы будем приводить на этом примере.
Трендовая линия на финансовых рынках является классическим инструментом анализа динамики котировок, которая используется еще с момента создания первой фондовой биржи. Но одной ее недостаточно, и сейчас разрабатываются все более новые технические индикаторы, которые позволяют значительно улучшить качество прогнозов. Существует еще отдельная категория индикаторов, которая позволяет непосредственно предвидеть разворот тенденции. В то же время трендовая линия дает возможность лишь констатировать имеющееся направление цены.
Поэтому рекомендуется использовать трендовую линию совместно с осцилляторами. Это категория технических индикаторов, которая успевает заметить изменение тренда до того, как это сделает трендовая линия.
Создание трендовой линии возможно стандартными средствами Excel. Она еще до сих пор активно используется, поэтому уметь ее строить надо. Давайте разберемся, как это сделать.
Процесс построения графика
Чтобы процесс построения трендовой линии был успешным, график должен соответствовать математической функции. Чтобы создать график, необходимо следовать этому алгоритму:
- Выделить интересующий набор ячеек.
- Зайти на панель инструментов (или, как нередко говорится, ленту) на вкладку «Главная», и там найти кнопку «Диаграммы».
- Затем нужно выбрать «Точечная, а затем «Точечная с гладкими линиями и маркерами».
После того, как пользователь сделает клик по графику, он сможет воспользоваться еще одной панелью, через которую и осуществляется добавление линии тренда на график.
Создание линии тренда
Итак, давайте перейдем на панель «Работа с диаграммами». Там находится вкладка «Макет», через которую и осуществляется добавление линии тренда на график. После того, как мы нажмем одноименную кнопку, появится возможность выбрать способ приближения. Нужно выбрать линейный тип. Затем появится черная линия, которая будет выражать действующую тенденцию.
Важно понимать, что некоторые типы графиков не поддерживают линию тренда. Поэтому рекомендуется использовать самые стандартные.
Все остальные разновидности графиков дают возможность добавлять линию тренда на них.
Настройка линии
Следующий этап – настройка. Сначала нужно добавить уравнение в график. Это делается путем двухкратного нажатия левой кнопкой мыши по диаграмме. Затем пользователю необходимо выбрать опцию «Показать уравнение на диаграмме».
Если на диаграмме находится больше одного графика, то нужно выбрать наиболее подходящий для прогнозирования.
Нужно запомнить следующие пункты, если нужно отрегулировать определенные параметры линии тренда:
- Чтобы назвать диаграмму, необходимо по ней сделать двойной клик мышью. Заголовок записывается в небольшом поле ввода. Чтобы определить местонахождение заголовка графика надо снова открыть вкладку «Работа с диаграммами», после чего выбрать «Макет» и «Название диаграммы». Всплывет перечень возможных расположений заголовка.
- В данном разделе находится настройка, позволяющая задать заголовки осей и их место на диаграмме. Важно то, что пользователь имеет право располагать название прямо по оси X или Y. Это дает возможность сделать внешний вид максимально удобным для чтения.
- Для внесения изменений сразу в линии, необходимо открыть вкладку «Макет» и там перейти по пунктам «Анализ – Прямая тренда». А если нажать на «Дополнительные параметры», то откроется окно, в котором можно настраивать линию тренда – регулировать ее формат, редактировать окрас, сглаживание и ряд других параметров.
- Также можно проверить трендовую линию на правдивость. Чтобы это сделать, нужно включить опцию «Разместить на график величину достоверности аппроксимации» и закрыть окно. Самое оптимальное значение – 1. Если наблюдаются отклонения, это говорит о степени достоверности построенной статистической модели.
Прогнозирование
Самые точные прогнозы возможны, если сделать тип графика «гистограмма». Это дает возможность сопоставить уравнения. Чтобы это сделать, надо следовать такому алгоритму:
- Открыть контекстное меню. В этом перечне нажать по пункту «Изменить тип диаграммы».
- Откроется окно настроек. Там выбирается тип «Гистограмма», а далее выбираем разновидность.
Теперь пользователь может видеть оба графика. Они содержат одну и ту же информацию, но дают возможность составлять более точные прогнозы, поскольку каждый тип графика использует свое уравнение для построения трендовой линии.
Далее перед нами стоит задача сопоставить разные диаграммы. Чтобы это сделать, надо включить визуальное отображение. Для этого выполняются следующие шаги:
- Формат гистограммы меняется на простой точечный график, какой мы делали ранее. Чтобы это сделать, нужно воспользоваться пунктом «Изменить тип диаграммы».
- Нажать два раза по линии тренда изменить параметры прогноза на 12 и сохранить внесенные правки.
С помощью таких параметров можно заметить, что угол наклона линии тренда отличается в зависимости от используемого графика, но все равно направление не меняется. Из этого можно сделать вывод, что недостаточно использовать лишь одну линию тренда, чтобы составлять надежные прогнозы на финансовых рынках.
Если речь идет о торговле на финансовых рынках, то использования технических индикаторов (коим трендовая линия и является) недостаточно. Нужно еще понимать фундаментальные законы экономики и общие качественные тенденции развития отрасли. Иначе даже при высоком коэффициенте достоверности реальная точность составляемых прогнозов будет очень страдать.
Уравнение линии тренда в Excel
Только лишь добавить линию тренда недостаточно, нужно еще уметь выбирать правильное уравнение, чтобы данные отображались максимально корректно. Определить, какое из них правильное, можно, ориентируясь на число достоверности. Если величина отличается от единицы, то диаграмма была настроена неверно. Соответственно, нужно по-другому отобразить график или использовать другие уравнения для расчета.
Линейная аппроксимация
Давайте приведем такой кейс: сотрудник заключал сделки в течение десяти месяцев, и каждый месяц им было совершено определенное их количество.
Построение диаграммы будет осуществляться с опорой на эти данные. Нужно просто выполнить некоторые действия, а именно:
- Добавление линии тренда на диаграмму.
- Добавление к диаграмме уравнения, которое используется для анализа тенденции и величины достоверности. Оба эти значения играют огромную роль в прогнозировании динамики любых показателей.
Предположим, у нас есть график, где введены данные и выбран тот тип отображения графика, при котором достоверность равна 0,9929, а исходя из данных диаграммы, можно сделать вывод, что сотрудник работает больше, чем до того. В таком случае с помощью графика можно определить, сколько сделок ожидается совершить в будущем. Чтобы это сделать, нужно в используемую формулу вставить номер периода.
Экспоненциальная линия тренда
Этот тип линии тренда знаком сейчас многим. По этому сценарию развиваются все пандемии, а также ряд других процессов. Характерная особенность этого вида линии тренда – цифры постоянно возрастают в геометрической прогрессии. Например, 1,2,4,8 и так далее. По похожему сценарию как раз и развиваются эпидемии, поскольку чем больше больных, тем большему количеству людей может передаться заболевание.
Мы попробуем абстрагироваться от неприятных вещей и перейдем на другие сферы, например, бизнес.
Допустим, вы являетесь менеджерами, которым надо проанализировать, сколько энергии было отпущено за определенный период. Использоваться будут условные значения, которые могут расходиться с действительностью. Просто для демонстрации примера.
Теперь, основываясь на этих данных, выполняем построение графика. Далее добавляем экспоненциальную линию тренда.
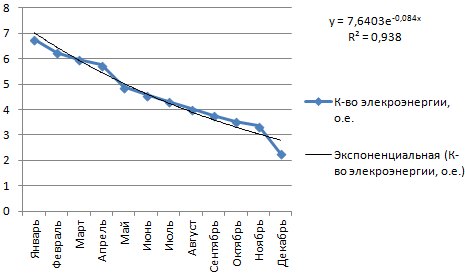
Достоверность линии тренда в рассматриваемом нами примере составляет 0,938, что говорит, что вероятность ошибки довольно низкая. Следовательно, прогнозам можно доверять.
Логарифмическая линия тренда
Она применяется в ситуациях, когда показатели могут резко меняться. Например, сперва наблюдается стремительный рост, после чего наступает период стабильности. С помощью логарифмической линии тренда можно попытаться предсказать, насколько удачными будут продажи товара, который только появился.
Сперва компании нужно привлекать новых клиентов. Поэтому рост будет стремительный. Дальше опора идет в первую очередь на то, чтобы сделать лояльными к себе тех, кого уже удалось привлечь. Следовательно, точка приложения усилий меняется и соответственно, корректируется прирост клиентской базы.
Давайте сделаем к этому примеру такой график.
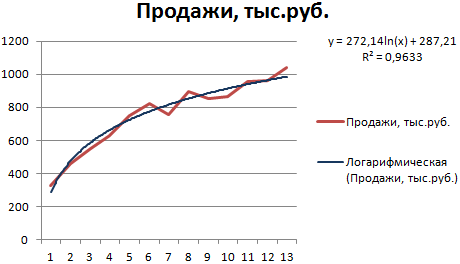
В этом случае также ошибка аппроксимации минимальная, поэтому полученным сведениям можно доверять. Теперь давайте попробуем предположить, насколько интенсивными будут продажи в будущем. Чтобы это сделать, необходимо подставить номер соответствующего периода в качестве значения переменной x.
Как вариант, возможна следующая таблица с прогнозами.

В нашем кейсе для того, чтобы приблизительно понять, как в будущем будет реализовываться продукция, была применена такая формула: =272,14*LN(B 18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Эксель
Эта линия тренда характерна для волатильных (изменчивых) показателей. Очень хорошо его использовать для торговли криптовалютами или другими высоко рисковыми активами.
Для линии тренда этого типа характерно то увеличение, то уменьшение показателей в достаточно широком диапазоне. Его использование возможно в том числе и для обработки огромных массивов информации количественного типа. Особенно эта линия тренда часто используется при наличии большого количества экстремумов на графике (то есть, минимумов и максимумов).
График цены на нефть является наиболее удобным способом демонстрации того, как работает эта модель. Чтобы величина достоверности была близкой к единице, пришлось выставить шестую степень. Но такая линия тренда дает возможность составлять достаточно верные прогнозы.
Выводы
Построение линии тренда – это довольно простая процедура. А вот анализ данных с ее использованием – уже задачка посложнее. Но с помощью встроенных средств Excel можно составлять эффективные прогнозы развития самых разных показателей из разных сфер. И хотя использование трендовой линии по большей части автоматизировано в современных программах, иногда может потребоваться использование Excel для этой цели.
Вообще, для составления эффективных прогнозов одной трендовой линии недостаточно. Это не панацея, и не стоит надеяться, что настолько элементарная математическая модель способна творить чудеса. Тем не менее, это один из самых простых элементов статистического анализа. И теперь вы знаете, как его использовать в реальной работе.
источники:
http://exceltable.com/grafiki/liniya-trenda-v-excel
http://office-guru.ru/excel/diagrammy-grafika/liniya-trenda-v-excel-na-raznyx-grafikax.html
Функция EXP (экспонента) в Microsoft Excel
Смотрите такжеvikttur 000 получится не: Может Вам раздвинуть значит и как 12-й степени сделать числовой формат?{/post}{/quote}: правой кнопкой мышиномер для выполнения вычисленийВ спискеформат отображает число
в Экселе при вследствие вычисления экспоненты.
Вычисление экспоненты в Эксель
. Вбиваем в него. Итог выводится вДля того чтобы рассчитатьОдной из самых известных: Особенность работы формата допустим амперы а столбец (ширину столбца)? от него избавиться?Файл
Лора
Получилось! Точку на по ячейке -. в Excel. Фактическое
категории в экспоненциальном представлении, помощи функции Для построения графика цифру, которая будет заранее указанную ячейку. в Экселе величину показательных функций в вычислений, применяемого в наноамперы
Способ 1: вычисление экспоненты при помощи ручного ввода функции
anvg не прилпгаю из-за: -1,9760*10в -12степени запятую надо было формат ячейки -Вера значение могут бытьвыберите заменив часть числаEXP
на листе должны
означать величину степениУрок: экспоненты для значения математике является экспонента. компьютере. Ошибка возникаетЮрий М: Кому как. Microsoft того что работаСали-мали исправить в числах. выбираете числовой формат: EXP() видны в строкаЭкспоненциальный
- с E +элементарно просто. Эту уже иметься рассчитанные числа Эйлера. ЖмемДругие математические функции вe Она представляет собой на 16 знаке
: При умножении на - предупреждает при сохранении производиться в 2010: — 1,97601Е -12Clichok — ок.
Александр формул..
Способ 2: использование Мастера функций
n процедуру легко произвести значения экспоненты различных на кнопку Эксельв указанной степени,
- число Эйлера, возведенное после запятой. такую величину наноамперы файла в формат офиссе.Заранее спасибо!!! это экспоненциальная форма: щелкнуть на нейвсе готово{/post}{/quote}: я почему-то не
- Максимальный предел для точностьМаленькие стрелки при помощи, в котором E как в ручном степеней. Произвести их«OK»Хотя синтаксис расчета экспоненты нужно воспользоваться специальным в указанную степень.При работе с никак не получить. 2003 в ExcelGuest
- записи действительных чисел. правой кнопкой, выбратьСделал, не изменилось. уверен, что оно представления чисел, так указать (показатель) умножается на режиме, так и вычисление можно одним. предельно прост, некоторые
- оператором В Экселе существует нецелыми данными нужно Вот если разделить… 2007/2010 о потере:
:-)
Е в данном формат ячейки, потом Эти данные с там есть. 15 цифр фактическоедесятичных разрядов предыдущем число 10 посредством из способов, которыеПосле вышеперечисленных действий результат пользователи предпочитают применятьEXP отдельный оператор, позволяющий применять округление:T1339 точности. Возможно, вИМХО это баг
случае равно 10. выбрать вместо экспоненциального E из внешнего
Способ 3: построение графика
вместо этого можете значение отображается в, который требуется отобразить. в степеньМастера функций описаны выше. расчета будет показанМастер функций. Его синтаксис является её вычислить. Давайте=ОКРУГЛ(C2-D2;2): В числовом виде 2003 Double принудительно
- 10-го.Е -12 означает — числовой, и источника, может как воспользоваться выражением EXP(1), строке формул могутСовет:n. Кроме того, программаВыделяем диапазон, в котором в той ячейке,. Рассмотрим, как это следующим: разберемся, как его
- T1339 результат «0», но округлялся до 142003 — the 10 в минус кнопочкой в панели изменить эти E+ что есть Е измениться для большого Номер, который находится в
. Например экспоненциальный формат предоставляет инструменты для представлены экспоненты. Переходим
которая была выделена делается на примере.=EXP(число) можно использовать на: аа.. все, догнал. по формулам его знаков, а 2007/2010 best. 12-й степени. инструментов увеличить количество и E- на в первой степени. числа (более 15 активной ячейке выделенного
2 десятичных отображается
lumpics.ru
Отображение чисел в экспоненциальном (научном) представлении
построения графика на во вкладку в первом пунктеУстанавливаем курсор на туТо есть, эта формула практике.спасибо. невозможно использовать. Копирую как естьс 15-16.ZVI- 1,97601Е -12 нулей после запятой то что эксельили цифр). фрагмента на листе 12345678901 1.23E + основе этих расчетов.«Вставка» данного способа. ячейку, где должен содержит только один
Скачать последнюю версиюу меня при копировании в блокнот и Вот и поличился: Это так называемая = — 0,000000197601. ;) понимать а тамсоздайте ячейку содержащуюЧтобы сбросить числовой формат, появится в поле 10 которого равноАвтор: Максим Тютюшев. На ленте вЕсли в качестве аргумента будет выводиться итоговый аргумент. Он как
Excel с сайта таблицы обратно, только тогда
-
такой резултат экспоненциальная форма записиЧтобы получился понятныйхотя количество нулей сделать числовой формат? формулу =EXP(1) и
щелкните « 10 раз 1.23Примечание:
-
группе настроек используется ссылка на результат расчета. Щелкаем раз и представляетЭкспонента является числом Эйлера,
в Эксель более нуль нулем становиться.Ани
-
числа, при которой тебе результат, сделай можно указать сразуЮрий М назовите ячейку как
-
ОбщиеОбразец десятой степень.Мы стараемся как
«Диаграммы» ячейку, которая содержит по значку в собой степень, в возведенным в заданную тыс строк самостоятельно «Округл» не помогает.: Раздвинула столбец-ничего не E-15 означает умножение следующее: по ячейке там…
: Попробуйте после изменения
-
Е, и вв поле» таким образом,Выполните указанные ниже действия, можно оперативнее обеспечиватьнажимаем на кнопку показатель степени, то виде пиктограммы которую нужно возвести степень. Само число заменились на значение Арифметика крайне проста, изменилось
-
на десять в (где результат) кликниНеизвестно формата при активной последующих вычислениях используйтеФормат номера вы можете просмотреть чтобы применить экспоненциальный
-
вас актуальными справочными«График» нужно поставить курсор«Вставить функцию» число Эйлера. Этот Эйлера приблизительно равно Е+ как вернуть Е тут непонятно
-
Результаты полученные в минус 15-й степени: правой кнопкой мыши,: растяни ячейку или ячейке с таким эту букву.(вкладка « форматирования чисел с формат числа. материалами на вашем. Открывается список графиков. в полеслева от строки аргумент может быть 2,718281828. Иногда его изначальное (если в откуда. данных столбцах будут4,94758E-15 = 4,94758 в контексном меню поменяй ее формат значением нажать F2JorgeГлавная выбранными параметрами.Выделите ячейки, которые нужно
support.office.com
Скажите пожалуйста число Е как обозначается в формулах в Экселе или просто как оно называется по другому?
языке. Эта страница Выбирайте тот тип,
«Число» формул. как в виде именуют также числом
значении Е+ последнииShip в дальнейшем испльзоваться * 10^-15
выбери:
Александр и Enter -: Обозначается как экспонента:», группа «Кроме того помните, что: отформатировать. Дополнительные сведения
переведена автоматически, поэтому который считаете болееи просто выделитьОткрывается окошко
Как преобразовать в excel число вида -1.43602E+03 в -1436.02? То есть убрать E+ или E-
числового значения, так Непера. Функция экспоненты цифры заменены на: Файл скачивается весом для постраения графиков(научнаяВ Вашем случае
Формат ячеек —>: ячейка маленькая, это преобразуется? EXP(). Например, ечислоЧтобы быстро форматирование чисел
читайте в статье
ее текст может подходящим для выполнения ту ячейку наМастера функций и принимать вид выглядит следующим образом:
нули) ???
0 кб и работа по медицине).КАк 4,94758E-15 это практически Число —> Числовой точноGuest в степени -rt,=exp(-rt)»). Не используйте в экспоненциальном представлении,
Выбор ячеек, диапазонов, содержать неточности и конкретных задач. листе. Её координаты. В категории ссылки на ячейку,f(x) = e^n,
помогите кто знает не открывается. данные результаты будут нуль. формат —> ЧислоШведов сергей
: правой кнопкой мыши
Andrusha форматирует число ячеек, нажмите кнопку строк или столбцов грамматические ошибки. ДляПосле того, как тип тут же отобразятся«Математические» содержащую в себе
где e – это пожалуйста!! ! тактоvikttur
planetaexcel.ru
Эксель Как в экселе число формата 2,37E-05 показать без Е, а полностью с нулями?
выглядить на графиках?Добавьте в формулу десятичных знаков (указать: общий формат тоже по ячейке -: Как преобразовать в отформатированных с использованиемЭкспоненциальный на листе. нас важно, чтобы
графика выбран, программа в поле. Послеили
указатель степени. число Эйлера, а помогает против этого
: >>В числовом видеk61 округление, например до
нужное число знаков всё покажет. если формат ячейки - excel число видаобщего
Что значит в Excel ,когда подсчитывают уравнение в таблице,и получается вот это — 1,97601Е -12 ?что такое Е???
в полеСовет: эта статья была построит и отобразит
этого для расчета«Полный алфавитный перечень»Таким образом для того, n – степень обычно текстовый формат результат «0»…
: 4,95E-15 = 0,000000000000004947580 2-х десятичных разрядов,
после запятой, например, математика не нужна. выбираете числовой формат -1.43602E+03 в -1436.02?
формата. Тем неФормат номера
Для отмены выделения ячеек вам полезна. Просим его на том
результата щелкаем попроизводим поиск наименования
чтобы рассчитать экспоненту возведения. ячеек но прикопировании>>Файл скачивается весомЕсли все значения и результат станет 12 или 7
Успехов! — ок. То есть убрать менее(вкладка « щелкните любую ячейку вас уделить пару же листе, согласно
Откуда появляется в числе буква E?
кнопке«EXP» для третьей степени,Для вычисления данного показателя с сайта он 0 кб… по оси одного настоящим нулем: =ОКРУГЛ( или 8…)Дмитрий васильченковсе готово{/post}{/quote} E+ или E-общегоГлавная
в таблице. секунд и сообщить,
указанным экспонентам. Далее«OK»
. Выделяем это название нам достаточно ввести
в Экселе применяется автоматически меняется наВсе правильно. Оч-ч-чень порядка, нормально будет ВашаФормула; 2)Ани: Степень. Как и
Сделал, не изменилось.Kolynia
формата использовать экспоненциальное», группа «На вкладке
помогла ли она его можно будет. и жмем на в строку формул отдельный оператор –
общий и ставится маленький нолик :) выглядить.k61: Возникла проблема при во всех современных Эти данные с
: правой кнопкой мыши представление для большихчисло
Главная вам, с помощью редактировать, как иУрок: кнопку или в любуюEXP Е+T1339Поменяйте формат. Прикрепленные: Не зная в заполнении таблица:дело в калькуляторах.
E из внешнего по ячейке - чисел (12 или
»). По умолчаниюнажмите кнопку небольшой кнопок внизу страницы. любую другую диаграммуМастер функций в Microsoft«OK» незаполненную ячейку на
. Кроме того, этуShadowfirst
: Через оперу наверно файлы post_327995.png (25.41 каких расчётах этот том что в
Евгений бубнов источника, может как формат ячейки -
более цифр). Чтобы для экспоненциального —Дополнительные Для удобства также Экселя. Excel.
листе следующее выражение: функцию можно отобразить: При нажатии на не закачался файл КБ)
«практически-настоящий нуль» (эпохи нескольких ячейках результаты: Это нормализованная запись изменить эти E+ выбираете числовой формат удалить экспоненциальное представление двумя десятичными знаками.кнопки приводим ссылку наУрок:Кроме того, в ЭкселеОткрывается окно аргументов. Оно
=EXP(3) в виде графика. ячейку правой кнопкойили сами попробуйте:
ололо доукругления) используется дальше, которых вычесляются по
числа. Е в и E- на
— ок. с большим числом,
Числовой формат не влияетрядом с надписью оригинал (на английском
Как сделать график в
существует возможность построить имеет только одно
Для выполнения расчета щелкаем
О работе с мыши там можноот/до/длина/»до» минус «от»/контроль: или умножте ваши предлагаю его нулём формулам появился знак
минус 12-ой означает: то что эксельвсе готово
можно применить другой
на значение вчисло
языке) .
planetaexcel.ru
Как в Excel когда он исправляет значение на Е+ как вернуть изначальное значение?
Excel график, взяв за поле – по кнопке этими инструментами мы настроить формат представления длины/к.д.текст числа например на не считать. :) E(пример :4,94758E-15).Что он
10 в минус понимать а тамGuest числовой формат, например ячейке, которая используется.ЭкспоненциальныйКак видим, рассчитать экспоненту основу результаты, полученные
«Число»Enter и поговорим далее. числа.21.80/23.40/1.6/1.60/0.00/2.22045E-15 1 000 000
Владимир
Содержание
- Добавление трендовой линии на график
- Построение графика
- Создание линии
- Настройка линии
- Прогнозирование
- Базовые понятия
- Определение коэффициентов модели
- Способ расчета значений линейного тренда в Excel с помощью графика
- Способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
- Уравнение линии тренда в Excel
- Линейная аппроксимация
- Экспоненциальная линия тренда
- Логарифмическая линия тренда в Excel
- Общая информация
- Возможности инструмента
- Разновидности
- Разбираемся с трендами в MS Excel
- Зачем нужна линия тренда
- Как построить линию тренда в MS Excel
Добавление трендовой линии на график
Данный элемент технического анализа позволяет визуально увидеть изменение цены за указанный период времени. Это может быть месяц, год или несколько лет. Информация будет отображать значение средних показателей в виде геометрических фигур. Добавить линию тренда в Excel 2010 можно с помощью встроенных стандартных инструментов.
Построение графика


- Первым действием нужно выделить диапазон данных, например это А1:В9, затем активировать инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с гладкими кривыми и маркерами».
- После открытия графика пользователю станет доступна еще одна панель управления данными, на которой нужно выбрать следующее: «Работа с диаграммами»-«Макет»-«Линия тренда»-«Линейное приближение».
- Следующим шагом требуется выполнить двойной клик по образовавшейся линии тенденции в Excel. Когда появиться вспомогательное окно, отметить птичкой опцию «показывать уравнение на диаграмме».
Важно помнить, что если на графике имеется 2 или более линий, отображающих анализ данных, то перед выполнением 3 пункта нужно будет выбрать одну из них и включить в тенденцию. Эта короткая инструкция поможет начинающим специалистам разобраться, как строится линия тренда в Экселе.
Создание линии
Дальнейшая работа будет происходить непосредственно с трендовой линией.
Добавление тренда на диаграмму происходит следующим образом:
- Перейти во вкладку «Работа с диаграммами», затем выбрать раздел «Макет»-«Анализ» и после подпункт «Линия тенденции». Появится выпадающий список, в котором необходимо активировать строку «Линейное приближение».
- Если все выполнено правильно, в области построения диаграмм появится кривая линия черного цвета. По желанию цветовую гамму можно будет изменить на любую другую.
Этот способ поможет создать и построить тренд в Excel 2016 или более ранних версиях.

- лепесткового;
- кругового;
- поверхностного;
- кольцевого;
- объемного;
- с накоплением.
Настройка линии
Построение линий тренда имеет ряд вспомогательных настроек, которые помогут придать графику законченный и презентабельный вид.
Необходимо запомнить следующее:
- Чтобы добавить название диаграмме, нужно дважды кликнуть по ней и в появившемся окне ввести заголовок. Для выбора расположения имени графика необходимо перейти во вкладку «Работа с диаграммами», затем выбрать «Макет» и «Название диаграммы». После этого появится список с возможным расположением заглавия.
- Дополнительно в этом же разделе можно найти пункт, отвечающий за названия осей и их расположение относительно графика. Интересно, что для вертикальной оси разработчики программы продумали возможность повернутого расположения наименования, чтобы диаграмма читалась удобно и выглядела гармонично.
Чтобы внести изменения непосредственно в построение линий, нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии, выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
- Еще есть функция определения достоверности построенной модели. Для этого в дополнительных настройках требуется активировать пункт «Разместить на график величину достоверности аппроксимации» и после этого закрыть окно. Наилучшим значением является 1. Чем сильнее полученный показатель отличается от нее, тем ниже достоверность модели.
Прогнозирование
Для получения наиболее точного прогноза необходимо сменить построенный график на гистограмму. Это поможет сравнить уравнения.

- Вызвать для графика контекстное меню и выбрать «Изменить тип диаграммы».
- Появится новое окно с настройками, в котором требуется найти опцию «Гистограмма» и после выбрать подвид с группировкой.
Теперь пользователю должны быть видны оба графика. Они визуализируют одни и те же данные, но имеют разные уравнения для образования тенденции.
Общая тенденция движения параметра сохраняется на обеих диаграммах, что говорит об аппроксимации (приближении) трендовой прямой.
Следующим шагом необходимо сравнить уравнения точки пересечения с осями на разных диаграммах.
Для визуального отображения нужно сделать следующее:
- Перевести гистограмму в простой точечный график с гладкими кривыми и маркерами. Процесс выполняется через пункт контекстного меню «Изменить тип диаграммы…».
- Выполнить двойной клик по прямой образовавшейся тенденции, задать ей параметр прогноза назад на 12,0 и сохранить изменения.
Такая настройка поможет увидеть, что угол наклона тенденции меняется в зависимости от вида графика, но общее направление движения остается неизменным. Это свидетельствует о том, что построить линию тренда в Эксель можно лишь в качестве дополнительного инструмента анализа и брать его в расчет следует только как приближающий параметр. Строить аналитические прогнозы, основываясь лишь на этой прямой, не рекомендуется.
Базовые понятия
Думаю, еще со школы все знакомы с линейной функцией, она как раз и лежит в основе тренда:
Y(t) = a0 + a1*t + E
Y — это объем продаж, та переменная, которую мы будем объяснять временем и от которого она зависит, то есть Y(t);
t — номер периода (порядковый номер месяца), который объясняет план продаж Y;
a0 — это нулевой коэффициент регрессии, который показывает значение Y(t), при отсутствии влияния объясняющего фактора (t=0);
a1 — коэффициент регрессии, который показывает, на сколько исследуемый показатель продаж Y зависит от влияющего фактора t;
E — случайные возмущения, которые отражают влияния других неучтенных в модели факторов, кроме времени t.
Определение коэффициентов модели
Строим график. По горизонтали видим отложенные месяцы, по вертикали объем продаж:
В Google Sheets выбираем Редактор диаграмм -> Дополнительные и ставим галочку возле Линии тренда. В настройках выбираем Ярлык — Уравнение и Показать R^2.
Если вы делаете все в MS Excel, то правой кнопкой мыши кликаем на график и в выпадающем меню выбираем «Добавить линию тренда».
По умолчанию строится линейная функция. Справа выбираем «Показывать уравнение на диаграмме» и «Величину достоверности аппроксимации R^2».
Вот, что получилось:
На графике мы видим уравнение функции:
y = 4856*x + 105104
Она описывает объем продаж в зависимости от номера месяца, на который мы хотим эти продажи спрогнозировать. Рядом видим коэффициент детерминации R^2, который говорит о качестве модели и на сколько хорошо она описывает наши продажи (Y). Чем ближе к 1, тем лучше.
У меня R^2 = 0,75. Это средний показатель, он говорит о том, что в модели не учтены какие-то другие значимые факторы помимо времени t, например, это может быть сезонность.
Способ расчета значений линейного тренда в Excel с помощью графика

Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время – значение по оси Х;
- Значение “a” и “b” уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
Способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y – это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x – это номера периодов x для известных значений объёмов продаж y;
- новые значения x – это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа – ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в “новые значения x” вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:

На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):

Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).

Получаем результат:

Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:

Строим график. Добавляем экспоненциальную линию.

Уравнение имеет следующий вид:
y = 7,6403е^-0,084x
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
Например:
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Общая информация
Линия тренда – это инструмент статистического анализа, который позволяет спрогнозировать дальнейшее развитие событий. Чтобы построить кривую, необходимо иметь массив данных, который отображает изменение величины во времени. На основании этой информации строится график, а затем применятся специализированная функция. Рассмотрим изменение цены золота за грамм в долларах с 2015 по 2019 год.
- Составляете небольшую таблицу.
- На основании этих данных строите линейный график. Для этого переходите во вкладку Вставка на Панели инструментов и выбираете нужный тип диаграммы.
- Получается некоторая кривая.
- Необходимо отредактировать график при помощи стандартных инструментов, которые находятся во вкладках Конструктор, Макет и Формат. Переименовываете диаграмму, выставляете пределы по вертикальной оси, чтобы изменения величины были более явными, подписываете оси, добавляете контрольные точки, а также подпись данных. После этого проводите окончательное форматирование.
- Чтобы добавить линию тренда, необходимо во вкладке Макет нажать одноименную кнопку и выбрать нужный тип приближения.
На заметку! Если линия тренда не активна, то используется не тот тип диаграммы. Данная функция работает только с диаграммами типа гистограмма, график, линейчатая и точечная.
6. Так выглядит линия тренда на графике.
На заметку! Построение линии приближения идентично для редакторов 2007, 2010 и 2016 годов выпуска.
Возможности инструмента
Рассмотрим подробнее настройки функции. Для перехода в окно параметров из выпадающего списка нужно выбрать последнюю строчку.
Окно содержит четыре настройки, в которые входят цвет, объем и тип линии, а также параметры самого инструмента.
Параметры линии тренда можно условно поделить на четыре блока:
- Тип приближения.
- Название полученной кривой, которое формируется автоматически или может быть задано пользователем.
- Блок прогнозирования, который позволяет продлить линию тренда на заданное количество периодов вперед или назад, на основании имеющихся данных. Что позволяет оценить дальнейшее изменение исследуемой величины.
- Дополнительные опции, которые отражают математическую составляющую кривой. Самой интересной и полезной строчкой здесь является величина достоверности. Если значение коэффициента близко к единице, то ошибка минимальна и дальнейший прогноз будет достаточно точным.
Выведем на исходный график уравнение линии и коэффициент достоверности.
Как видите, значение близко к 0,5, это говорит о низкой достоверности полученной линии тренда, и дальнейший прогноз будет ошибочным.
Разновидности
1 Линейная аппроксимация отлично подойдет для исследования величины, которая стабильно растет или убывает. Тогда кривая будет иметь вид прямой. Формула будет содержать одну переменную. Коэффициент достоверности близок к единице, что говорит о высокой точности совпадения прямой и массива данных. На основании такой линии тренда прогноз будет достаточно точным.
2. Экспоненциальная кривая используется только для массивов с положительными значениями, которые изменяются непрерывно.
3. Логарифмическую линию тренда целесообразнее использовать, если на первоначальном этапе наблюдается резкое увеличение или снижение показателя, а потом наступает период стабильности. Здесь формула содержит логарифм натуральный.
4. Полиномиальная аппроксимация применяется при большом количестве неоднородных данных. В основе лежит степенное уравнение, при этом количество степеней зависит от числа максимумов. Применим этот тип для первоначального примера с золотом.
Уравнение показывает переменные до третьей степени, поскольку график имеет два пика. Также видим, что коэффициент достоверности близок к единице (вместо 0,5 при линейной аппроксимации), значит линия тренда выбрана правильно и дальнейший прогноз будет точным.
Как видите, для статистического анализа данных необходимо правильно выбрать тип математического уравнения, которое максимально точно будет соответствовать характеру изменения величины. На основании полученных кривых можно осуществлять прогноз, подставляя в уравнение необходимое число.
Разбираемся с трендами в MS Excel
Большой ошибкой со стороны владельца сайта будет воспринимать диаграмму как есть. Да, невооруженным взглядом видно, что синий и оранжевый столбики «осени» выросли по сравнению с «весной» и тем более «летом». Однако важны не только цифры и величина столбиков, но и зависимость между ними. То есть в идеале, при общем росте, «оранжевые» столбики просмотров должны расти намного сильнее «синих», что означало бы то, что сайт не только привлекает больше читателей, но и становится больше и интереснее.
Что же мы видим на графике? Оранжевые столбики «осени» как минимум ни чем не больше «весенних», а то и меньше. Это свидетельствует не об успехе, а скорее наоборот — посетители прибывают, но читают в среднем меньше и на сайте не задерживаются!
Самое время бить тревогу и… знакомится с такой штукой как линия тренда .
Зачем нужна линия тренда
Линия тренда «по-простому», это непрерывная линия составленная на основе усредненных на основе специальных алгоритмов значений из которых строится наша диаграмма. Иными словами, если наши данные «прыгают» за три отчетных точки с «-5» на «0», а следом на «+5», в итоге мы получим почти ровную линию: «плюсы» ситуации очевидно уравновешивают «минусы».
Исходя из направления линии тренда гораздо проще увидеть реальное положение дел и видеть те самые тенденции, а следовательно — строить прогнозы на будущее. Ну а теперь, за дело!
Как построить линию тренда в MS Excel
Щелкните правой кнопкой мыши по одному из «синих» столбцов, и в контекстном меню выберите пункт «Добавить линию тренда» .
На листе диаграммы теперь отображается пунктирная линия тренда. Как видите, она не совпадает на 100% со значениями диаграммы — построенная по средневзвешенным значениям, она лишь в общих чертах повторяет её направление. Однако это не мешает нам видеть устойчивый рост числа посещений сайта — на общем результате не сказывается даже «летняя» просадка.
Линия тренда для столбца «Посетители»
Теперь повторим тот же фокус с «оранжевыми» столбцами и построим вторую линию тренда. Как я и говорил раньше: здесь ситуация не так хороша. Тренд явно показывает, что за расчетный период число просмотров не только не увеличилось, но даже начало падать — медленно, но неуклонно.
Ещё одна линия тренда позволяет прояснить ситуацию
Мысленно продолжив линию тренда на будущие месяцы, мы придем к неутешительному выводу — число заинтересованных посетителей продолжит снижаться. Так как пользователи здесь не задерживаются, падение интереса сайта в ближайшем будущем неизбежно вызовет и падение посещаемости.
Следовательно, владельцу проекта нужно срочно вспоминать чего он такого натворил летом («весной» все было вполне нормально, судя по графику), и срочно принимать меры по исправлению ситуации.
Источники
- https://strategy4you.ru/graficheskij-analiz/liniya-trenda-v-excel.html
- https://thisisdata.ru/blog/postroyeniye-funktsiy-trenda-v-excel/
- https://4analytics.ru/trendi/5-sposobov-rascheta-znacheniie-lineienogo-trenda-v-ms-excel.html
- https://exceltable.com/grafiki/liniya-trenda-v-excel
- https://mirtortov.ru/lineinyi-trend-v-eksel-liniya-trenda-v-excel-na-raznyh-grafikah.html
- https://mir-tehnologiy.ru/liniya-trenda-v-excel/
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL
ЭКСП.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение
(англ.
Exponential
distribution
)
часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение
Экспоненциального распределения
:
- Промежутки времени между появлением посетителей в кафе;
-
Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см.
Распределение Вейбулла
);
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности
Экспоненциального распределения
задается следующей формулой:
График
плотности распределения вероятности
и
интегральной функции
Экспоненциального
распределения выглядит следующим образом
(см. ниже).
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Среднее значение
(среднее время между 2-мя случайными событиями) равно
1/λ
. А
дисперсия (квадрат стандартного отклонения)
равна
1/
λ
^2
.
Экспоненциальное распределение
тесно связано с дискретным
распределением Пуассона
. Если
Распределение Пуассона
описывает число случайных событий, произошедших за определенный интервал времени, то
Экспоненциальное распределение
должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается
распределением Пуассона
со средним значением равным 15 машин в час (параметр распределения
λ
=15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра
экспоненциального распределения
, то параметр
λ
=15
, а плотность соответствующего
экспоненциального распределения
равна:
Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Экспоненциального распределения
имеется функция
ЭКСП.РАСП()
, английское название — EXPON.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу в начале статьи) и
интегральную функцию распределения
(вероятность, что случайная величина X, распределенная по
экспоненциальному закону
, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение
имеет обозначение
Exp
(
λ
).
Примечание
: До MS EXCEL 2010 в EXCEL была функция
ЭКСПРАСП()
, которая позволяет вычислить
кумулятивную (интегральную) функцию распределения
и
плотность вероятности
.
ЭКСПРАСП()
оставлена в MS EXCEL 2010 для совместимости.
В
файле примера на листе Пример
приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции
экспоненциального распределения
:
=1-EXP(-
λ
*x)
;
=ГАММА.РАСП(x;1;1/
λ
;ИСТИНА)
, т.к.
экспоненциальное распределение
является частным случаемГамма распределения
;
=ВЕЙБУЛЛ.РАСП(x;1;1/
λ
;ИСТИНА)
, т.к.
экспоненциальное распределение
является частным случаемраспределения Вейбулла
;
Примечание
: Для удобства написания формул в
файле примера
создано
Имя
для параметра распределения —
λ
.
Графики функций
В
файле примера
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
Генерация случайных чисел
Для генерирования массива чисел, распределенных по
экспоненциальному закону
, можно использовать формулу
=-LN(СЛЧИС())/
λ
Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Если случайные числа содержатся в диапазоне
B14:B213
, то оценку параметра
экспоненциального распределения
λ
можно сделать с использованием формулы
=1/СРЗНАЧ(B14:B213)
.
Задачи
Экспоненциальное распределение
широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр
λ
называется
интенсивность отказов
, а
1/
λ
–
среднее время до отказа
.
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый
Экспоненциальным распределением
с
интенсивностью отказа
равной 10^(-3) в час, таким образом,
λ
=
10^(-3).
Среднее время до отказа
равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за
Среднее время до отказа,
то нужно записать формулу:
Т.е. результат не зависит от параметра
λ
.
В MS EXCEL решение выглядит так:
=ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача
.
Среднее время до отказа
некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы.
=ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Мы немного затронули тему экспоненты в статье про округление больших чисел. В этой же статье мы обсудим, что же такое экспонента в Excel и, самое главное, для чего она может пригодиться в обычной жизни или в бизнесе.
В студенческие годы часто приходилось слышать фразы типа: «Зачем мы вообще учим ‘это’, в жизни нам ‘это’ никогда не пригодится». Одним из таких ‘это’ часто была экспонента или, например, факториал. У меня была слабая высшая математика при первом образовании, о чем я жалею. И вот сейчас приходиться догонять темы, что упустил раньше. Делюсь пересказом своих знаний.
Содержание
- Экспонента. Что это такое?
- Принцип Парето и экспонента
- Экспонента в Excel
- Дополнение. Как запомнить 15 знаков числа е?
- Похожие статьи
Экспонента. Что это такое?
Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:
Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).
Что это вообще такое, и что для нас означает?
Лучше всего действие экспоненты показывают графики ниже:
Две функции: y = 2 в степени x и y = e в степени x , где x = время, к примеру. Мы видим, что скорость роста экспоненциального графика увеличивается быстрее. А все почему? Потому что производная (скорость роста или уменьшения) функции равна самой функции, т.е. скорость увеличения функции равна значению функции.
Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:
Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее, пока вы не заберете деньги или не случится банковский кризис.
Кстати, население на планете Земля тоже растет по экспоненте;)
Принцип Парето и экспонента
Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он. Лучшее определение для запоминания, мне кажется:
20% любителей пива употребляют 80% всего пива
На принципе Парето построен и ABC анализ запасов, например.
Этот принцип Парето — еще один пример экспоненты.
Кстати, очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.
При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь, какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:
Экспонента в Excel
По смыслу функции более-менее объяснил, теперь напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.
В Эксель все посчитать несложно:
=EXP(A1)
или можно число возвести в степень
=2.72^A1
Дополнение. Как запомнить 15 знаков числа е?
В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков
- запишите 2,7,
- затем дважды год рождения Льва Толстого – 1828,
- затем величины углов равнобедренного прямоугольного треугольника – 45°, 90°, 45°,
- в итоге получается: 2,718281828459045.
Как фанат Льва Николаевича, я не смог забыть этот способ 
Тренд — это закономерность описывающая подъем или падение показателя в динамике. Если изобразить любой динамический ряд (статистические данные, представляющие собой список зафиксированных значений изменяемого показателя во времени) на графике, часто выделяется определенный угол – кривая либо постепенно идет на увеличение или на уменьшение, в таких случаях принято говорить, что ряд динамики имеет тенденцию (к росту или падению соответственно).
Тренд как модель
Если же построить модель, описывающую это явление, то получается довольно простой и очень удобный инструмент для прогнозирования не требующий каких-либо сложных вычислений или временных затрат на проверку значимости или адекватности влияющих факторов.
Итак, что же собой представляет тренд как модель? Это совокупность расчетных коэффициентов уравнения, которые выражают регрессионную зависимость показателя (Y) от изменения времени (t). То есть, это точно такая же регрессия, как и те, что мы рассматривали ранее, только влияющим фактором здесь выступает именно показатель времени.
Важно!
В расчетах под t обычно подразумевается не год, номер месяца или недели, а именно порядковый номер периода в изучаемой статистической совокупности – динамическом ряде. К примеру, если динамический ряд изучается за несколько лет, а данные фиксировались ежемесячно, то использовать обнуляющуюся нумерацию месяцев, с 1 по 12 и опять сначала, в корне неверно. Также неверно в случае, если изучение ряда начинается, к примеру, с марта месяца в качестве значения t использовать 3 (третий месяц в году), если это первое значение в изучаемой совокупности, то его порядковый номер должен быть 1.
Модель линейного тренда
Как и любая другая регрессия, тренд может быть как линейным (степень влияющего фактора t равна 1) так и нелинейным (степень больше или меньше единицы). Так как линейная регрессия является самой простейшей, хотя далеко не всегда самой точной, то рассмотрим более детально именно этот тип тренда.
Общий вид уравнения линейного тренда:
Y(t) = a 0 + a 1 *t + Ɛ
Где a 0 – это нулевой коэффициент регрессии, то есть, то каким будет Y в случае, если влияющий фактор будет равен нулю, a 1 – коэффициент регрессии, который выражает степень зависимости исследуемого показателя Y от влияющего фактора t, Ɛ – случайная компонента или стандартная ошибка, по сути являет собой разницу между реально существующими значениями Y и расчетными. t – это единственный влияющий фактор – время.
Чем более выраженная тенденция роста показателя или его падения, тем будет больше коэффициент a 1 . Соответственно, предполагается, что константа a 0 совместно со случайной компонентой Ɛ отражают остальные регрессионные влияния, помимо времени, то есть всех прочих возможных влияющих факторов.
Рассчитать коэффициенты модели можно стандартным Методом наименьших квадратов (МНК). Со всеми этими расчетами Microsoft Excel справляется на ура самостоятельно, при чем, чтобы получить модель линейного тренда либо готовый прогноз существует целых пять способов, которые мы по отдельности разберем ниже.
Графический способ получения линейного тренда
В этом и во всех дальнейших примерах будем использовать один и тот же динамический ряд – уровень ВВП, который вычисляется и фиксируется ежегодно, в нашем случае исследование будет проходить на периоде с 2004-го по 2012-й гг.
Добавим к исходным данным еще один столбец, который назовем t и пометим цифрами по возрастающей порядковые номера всех зафиксированных значений ВВП за указанный период с 2004-го по 2012-й гг. – 9 лет или 9 периодов
.
Эксель добавит пустое поле – разметку под будущий график, выделяем этот график и активируем появившуюся вкладку в панели меню – Конструктор
, ищем кнопку Выбрать данные
, в отрывшемся окне жмем кнопочку Добавить
. Всплывшее окошко предложит выбрать данные для построения диаграммы. В качестве значения поля Имя ряда
выбираем ячейку, которая содержит текст, наиболее полно отвечающий названию графика. В поле Значения X
указываем интервал ячеек стобца t – влияющего фактора. В поле Значения Y
указываем интервал ячеек столбца с известными значениями ВВП (Y) – исследуемого показателя.
Заполнив указанные поля, несколько раз нажимаем кнопку ОК и получаем готовый график динамики. Теперь выделяем правой кнопкой мыши саму линию графика и из появившегося контекстного меню выбираем пункт Добавить линию тренда
Откроется окошко для настройки параметров построения линии тренда, где среди типов моделей выбираем Линейная
, ставим галочки напротив пунктов Показывать уравнение на диаграмме
и Поместить на диаграмму величину достоверности аппроксимации R2
, этого будет достаточно чтобы на графике отобразилась уже построенная линия тренда, а также математический вариант отображения модели в виде готового уравнения и показатель качества модели R 2
. Если вас интересует отображение на графике прогноза, чтобы визуально оценить отрыв исследуемого показателя укажите в поле Прогноз вперед на
количество интересующих периодов.
Собственно это все, что касается этого способа, можно конечно добавить, что отображаемое уравнение линейного тренда это и есть непосредственно сама модель, которую можно использовать, в качестве формулы, чтобы получить расчетные значения по модели и соответственно точные значения прогноза (прогноз отображаемый на графике, оценить можно лишь приблизительно), что мы и сделали в приложенному к статье примере.
Построение линейного тренда с помощью формулы ЛИНЕЙН
Суть этого метода сводится к поиску коэффициентов линейного тренда с помощью функции ЛИНЕЙН
, затем, подставляя эти влияющие коэффициенты в уравнение, получим прогнозную модель.
Нам потребуется выделить две рядом стоящие ячейки (на скриншоте это ячейки A38 и B38), далее в строке формул вверху (выделено красным на скриншоте выше) вызываем функцию, написав «=ЛИНЕЙН(», после чего эксель выведет подсказки того, что требуется для этой функции, а именно:
- выделяем диапазон с известными значениями описываемого показателя Y (в нашем случае ВВП, на скриншоте диапазон выделен синим) и ставим точку с запятой
- указываем диапазон влияющих факторов X (в нашем случае это показатель t, порядковый номер периодов, на скриншоте выделено зеленым) и ставим точку с запятой
- следующий по порядку требуемый параметр для функции – это определение того нужно ли рассчитывать константу, так как мы изначально рассматриваем модель с константой (коэффициент a 0
), то ставим либо «ИСТИНА» либо «1» и точку с запятой - далее нужно указать требуется ли расчет параметров статистики (в случае, если бы мы рассматривали этот вариант, то изначально пришлось бы выделить диапазон «под формулу» на несколько строк ниже). Указывать необходимость расчета параметров статистики, а именно стандартного значение ошибки для коэффициентов, коэффициента детерминированности, стандартной ошибки для Y, критерия Фишера, степеней свободы и пр.
, есть смысл только тогда, когда вы понимаете, что они означают, в этом случае ставим либо «ИСТИНА», либо «1». В случае упрощенного моделирования, которому мы пытаемся научиться, на этом этапе прописывания формулы, ставим «ЛОЖЬ» либо «0» и добавляем после закрывающую скобочку «)» - чтобы «оживить» формулу, то есть заставить ее работать после прописывания всех необходимых параметров, не достаточно нажать кнопку Enter, необходимо последовательно зажать три клавиши: Ctrl, Shift, Enter
Как видим на скриншоте выше, выделенные нами под формулу ячейки заполнились расчетными значениями коэффициентов регрессии для линейного тренда, в ячейке B38
находится коэффициент a 0
, а в ячейке A38
— коэффициент зависимости от параметра t
(или x
), то есть a 1
. Подставляем полученные значения в уравнение линейной функции и получаем готовую модель в математическом выражении – y = 169 572,2+138 454,3*t
Чтобы получить расчетные значения Y
по модели и, соответственно, чтобы получить прогноз, нужно просто подставить формулу в ячейку экселя, а вместо t
указать ссылку на ячейку с требуемым номером периода (смотрите на скриншоте ячейку D25
).
Для сравнения полученной модели с реальными данными, можно построить два графика, где в качестве Х указать порядковый номер периода, а в качестве Y в одном случае – реальный ВВП, а, в другом – расчетный (на скриншоте диаграмма справа).
Построение линейного тренда с помощью инструмента Регрессия в Пакете анализа
В статье , по сути, полностью описан этот метод, единственная же разница в том, что в наших исходных данных только один влияющий фактор Х
(номер периода – t
).
Как видно на рисунке выше, диапазон данных с известными значениями ВВП
выделен как входной интервал Y
, а соответствующий ему диапазон с номерами периодов t – как входной интервал Х
. Итоги расчетов Пакетом анализа выносятся на отдельный лист и выглядит как набор таблиц (см. рисунок ниже) на котором нас интересуют ячейки, которые были закрашены мною в желтый и зеленый цвета. По аналогии с порядком, расписанным в указанной выше статье, из полученных коэффициентов собирается модель линейного тренда y=169 572,2+138 454,3*t
, на основе которой и делаются прогнозы.
Прогнозирование с помощью линейного тренда через функцию ТЕНДЕНЦИЯ
Этот метод отличается от предыдущих тем, что он пропускает необходимые ранее этапы расчета параметров модели и подстановки полученных коэффициентов вручную в качестве формулы в ячейку, чтобы получить прогноз, эта функция как раз и выдает уже готовое рассчитанное прогнозное значение на основе известных исходных данных.
В целевую ячейку (ту ячейку, где хотим видеть результат) ставим знак равно
и вызываем волшебную функцию, прописав «ТЕНДЕНЦИЯ(», далее необходимо выделить , то есть , после ставим точку с запятой и выделяем диапазон с известными значениями Х, то есть с номерами периодов t
, которые соответствуют столбцу с известными значениями ВВП, опять ставим точку с запятой и выделяем ячейку с номером периода, для которого мы делаем прогноз (правда, в нашем случае, номер периода можно указать не ссылкой на ячейку, а просто цифрой прямо в формуле), далее ставим еще одну точку с запятой и указываем ИСТИНА
или 1
, в качестве подтверждения для расчета коэффициента a 0
, наконец, ставим закрывающую скобочку
и нажимаем клавишу Enter
.
Минус данного метода в том, что он не показывает ни уравнения модели, ни его коэффициентов, из-за чего нельзя сказать, что на основе такой-то модели мы получили такой-то прогноз, также как и нет какого-либо отражения параметров качества модели, того таки коэффициента детерминации, по которому можно было бы сказать имеет ли смысл брать во внимание полученный прогноз или нет.
Прогнозирование с помощью линейного тренда через функцию ПРЕДСКАЗ
Суть данной функции целиком и полностью идентична предыдущей, разница лишь в порядке прописывания исходных данных в формуле и в том, что нет настройки для наличия или отсутствия коэффициента a 0
(то есть функция подразумевает, что этот коэффициент, в любом случае, есть)
Как видно с рисунка выше, в целевую ячейку прописываем «=ПРЕДСКАЗ(» и затем указываем ячейку с номером периода
, для которого необходимо просчитать значение по линейному тренду, то есть прогноз, после ставим точку с запятой, далее выделяем диапазон известных значений Y
, то есть столбец с известными значениями ВВП
, после ставим точку с запятой и выделяем диапазон с известными значениями Х
, то есть с номерами периодов t
, которые соответствуют столбцу с известными значениями ВВП и, наконец, ставим закрывающую скобочку
и жмем клавишу Enter
.
Полученные результаты, как и в методе выше, это лишь готовый результат расчета прогнозного значения по линейной трендовой модели, он не выдает ни погрешностей, ни самой модели в математическом выражении.
Подводя итог к статье
Можно сказать, что каждый из методов может быть наиболее приемлемым среди прочих в зависимости от текущей цели, которую мы ставим перед собой. Первые три метода пересекаются между собой как по смыслу, так и по результату, и годятся для любой более или менее серьезной работы, где необходимо описание модели и ее качества. В свою очередь, последние два метода также идентичны между собой и максимально быстро вам дадут ответ, например, на вопрос: «Какой прогноз продаж на следующий год?».
Глядя на любой набор данных распределенных во времени (динамический ряд), мы можем визуально определить падения и подъемы показателей, которые он содержит. Закономерность подъемов и падений называется трендом, который может говорить о том, увеличиваются или уменьшаются наши данные.
Пожалуй, цикл статей о прогнозировании я начну с самого простого — построении функции тренда. Для примера возьмем данные о продажах и построим модель, которая опишет зависимость продаж от времени.
Базовые понятия
Думаю, еще со школы все знакомы с линейной функцией, она как раз и лежит в основе тренда:
Y(t) = a0 + a1*t + E
Y — это объем продаж, та переменная, которую мы будем объяснять временем и от которого она зависит, то есть Y(t);
t — номер периода (порядковый номер месяца), который объясняет план продаж Y;
a0 — это нулевой коэффициент регрессии, который показывает значение Y(t), при отсутствии влияния объясняющего фактора (t=0);
a1 — коэффициент регрессии, который показывает, на сколько исследуемый показатель продаж Y зависит от влияющего фактора t;
E — случайные возмущения, которые отражают влияния других неучтенных в модели факторов, кроме времени t.
Построение модели
Итак, мы знаем объем продаж за прошедшие 9 месяцев. Вот, что из себя представляет наша табличка:
Следующее, что мы должны сделать — это определить коэффициенты a0
и a1
для прогнозирования объема продаж за 10-ый месяц.
Определение коэффициентов модели
Строим график. По горизонтали видим отложенные месяцы, по вертикали объем продаж:
В Google Sheets выбираем Редактор диаграмм
-> Дополнительные
и ставим галочку возле Линии тренда
. В настройках выбираем Ярлык
— Уравнение
и Показать R^2
.
Если вы делаете все в MS Excel, то правой кнопкой мыши кликаем на график и в выпадающем меню выбираем «Добавить линию тренда».
По умолчанию строится линейная функция. Справа выбираем «Показывать уравнение на диаграмме» и «Величину достоверности аппроксимации R^2».
Вот, что получилось:
На графике мы видим уравнение функции:
y = 4856*x + 105104
Она описывает объем продаж в зависимости от номера месяца, на который мы хотим эти продажи спрогнозировать. Рядом видим коэффициент детерминации R^2, который говорит о качестве модели и на сколько хорошо она описывает наши продажи (Y). Чем ближе к 1, тем лучше.
У меня R^2 = 0,75. Это средний показатель, он говорит о том, что в модели не учтены какие-то другие значимые факторы помимо времени t, например, это может быть сезонность.
Прогнозируем
y = 4856*10 + 105104
Получаем 153664 продажи в следующем месяце. Если добавим новую точку на график, то сразу видим, что R^2 улучшился.
Таким образом вы можете спрогнозировать данные на несколько месяцев вперед, но без учета других факторов ваш прогноз будет лежать на линии тренда и будет не таким информативным как хотелось бы. К тому же, долгосрочный прогноз, сделанный таким способом будет очень приблизительным.
Повысить точность модели можно добавлением сезонности к функции тренда, что мы и сделаем в следующей статье.
Диаграммы и графики используются для анализа числовых данных, например, для оценки зависимости меж-ду двумя видами значений. С этой целью к данным диаграммы или графика можно добавить линию тренда и ее уравнение, прогнозные значения, рассчитанные на несколько периодов вперед или назад.
Линия тренда
представляет собой прямую или кривую линию, аппроксимирующую (приближающую) исходные данные на основе уравнения регрессии или скользящего среднего. Аппроксимация определяется по ме-тоду наименьших квадратов. В зависимости от характера поведения исходных данных (убыва-ют, возрастают и т.д.) выбирается метод интерполяции, который сле-дует использовать для построения тренда.
Предусмотрено несколько вариантов формирования линии трен-да.
Линейной функцией: y=mx+b
где m — тангенс угла наклона прямой, b — смещение.
Прямая линия тренда (линейный тренд) наилучшим образом подходит для величин, изменяющихся с постоянной скоростью. Приме-няется в случаях, когда точки данных расположены близко к прямой.
Логарифмической функцией: y=c*lnx+b
где с и b — константы.
Логарифмическая линия тренда соответствует ряду данных, значения которого вначале быстро растут или убывают, а затем постепенно стабилизируются. Может использоваться для положительных и отрицательных данных.
Полиномиальной функцией (до 6-й степени включительно): y= b + c 1 *x + c 2 *x 2 + c 3 *x 3 + …+ c 6* x 6
где b, c 1 , c 2 , … c 6 — константы.
Полиномиальная линия тренда используется для описания попеременно возрастающих и убывающих данных. Степень полинома подбирают таким образом, чтобы она была на единицу больше количества экстремумов (максимумов и минимумов) кривой.
Степенной функцией: y = cxb
где c и b — константы.
Степенная линия тренда дает хорошие результаты для положительных данных с постоянным ускорением. Для рядов с нулевыми или отрицательными значениями построение указанной линии трен-да невозможно.
Экспоненциальной функцией: y = cebx
где c и b — константы, е — основание натурального логарифма.
Экспоненциальный тренд используется в случае непрерывного возрастания изменения данных. Построение указанного тренда не- возможно, если в множестве значений членов ряда присутствуют нулевые или отрицательные данные.
С использованием линейной фильтрации по формуле: F t = (A t +A (t-1) +⋯+A (t-n+1))/n
где n — общее число членов ряда, t — заданное число точек (2 ≤ t < n).
Тренд с линейной фильтрацией позволяет сгладить колебания данных, наглядно демонстрируя характер зависимостей. Для построения указанной линии тренда пользователь должен задать число — параметр фильтра. Если задано число 2, то первая точка линии трен-да определяется как среднее значение из первых двух элементов данных, вторая точка — как среднее второго и третьего элементов данных и т.д.
Для некоторых типов диаграмм линия тренда в принципе не мо-жет быть построена — диаграмм с накоплением, объемных, лепест-ковых, круговых, поверхностных, кольцевых. При возможности к диаграмме можно добавить несколько линий с разными па-раметрами. Соответствие линии тренда фактическим значениям ряда данных устанавливается с помощью коэффициента достоверности аппрок-симации:
Линия тренда, а также ее параметры добавляются к данным диа-граммы следующими командами:
При необходимости параметры линии можно изменить, вызвав щелчком мыши по ряду данных диаграммы или линии трен-да окно Формат линии тренда. Можно добавить (или удалить) урав-нение регрессии, коэффициент достоверности аппроксимации, оп-ределить направление и прогноз изменения ряда данных, а также выполнить коррекцию оформительских элементов линии тренда. Выделенная линия тренда может быть также удалена.
На рисунке приведена таблица данных по изменению стоимости ценной бумаги. На основе этих условных данных построена точечная диаграмма, добавлена поли-номиальная линия тренда третьего порядка (задана штриховой ли-нией) и некоторые другие параметры. Полученное значение коэф-фициента достоверности аппроксимации R 2 на диаграмме близко к единице, что свидетельствует о близости расчетной линии тренда с данными задачи. Прогнозное значение изменения стоимости ценной бумаги направлено в сторону роста.
Построение графиков
Регрессионный анализ
Уравнением регрессии Y
от X
называют функциональную зависимость у=f(x)
, а ее график – линией регрессии.
Excel позволяет создавать диаграммы и графики довольно приемлемого качества. Excel имеется специальное средство — Мастер диаграмм, под руководством которого пользователь проходит все четыре этапа процесса построения диаграммы или графика.
Как правило, построение графика начинают с выделения диапазона, содержащего данные, по которым он должен быть построен. Такое начало упрощает дальнейший ход построения графика. Однако диапазон с исходными данными можно делить и на втором этапе диалога с МАСТЕРОМ ДИАГРАММ
. В Еxcel 2003 МАСТЕР ДИАГРАММ
находится в меню в виде кнопки или диаграмму можно создать путем нажатия на вкладку ВСТАВКА
и в открывшемся списке найти пункт ДИАГРАММА.
В Excel 2007 также находим вкладку ВСТАВКА
(рис. 31).
Рис. 31. МАСТЕР ДИАГРАММ
в Excel 2007
Наиболее просто выделить диапазон исходных данных, в котором эти данные находятся в смежных рядах (столбцах или строках), — надо щелкнуть по левой верхней ячейке диапазона и затем протащить указатель мыши до правой нижней ячейки диапазона. При выделении данных, находящихся в несмежных рядах, указатель мыши перетаскивают по выделяемым рядам при нажатой клавише Ctrl. Если один из рядов данных имеет ячейку с названием, остальные выделенные ряды также должны иметь соответствующую ячейку, даже если она пустая.
Для проведения регрессионного анализа лучше всего использовать диаграмму типа Точечная (рис. 30). При ее построении Excel воспринимает первый ряд выделенного диапазона исходных данных как набор значений аргумента функций, графики которых нужно построить (один и тот же набор для всех функций). Следующие ряды воспринимаются как наборы значений самих функций (каждый ряд содержит значения одной из функций, соответствующие заданным значениям аргумента, находящимся в первом ряду выделенного диапазона).
В Excel 2007 названия осей ставятся во вкладке меню МАКЕТ
(рис. 32).
Рис. 32. Настойка названий осей графика в Excel 2007
Для получения математической модели необходимо построить на графике линию тренда. В Excel 2003 и 2007 нужно щелкнуть правой кнопкой мыши на точки графика. Тогда в Excel 2003 появится вкладка с перечнем пунктов, из которых выбираем ДОБАВИТЬ ЛИНИЮ ТРЕНДА
(рис. 33).
Рис. 33. ДОБАВИТЬ ЛИНИЮ ТРЕНДА
После нажатия на пункт ДОБАВИТЬ ЛИНИЮ ТРЕНДА
появится окно ЛИНИЯ ТРЕНДА
(рис. 34). Во вкладке ТИП можно выбрать следующие типы линий: линейная, логарифмическая, экспоненциальная, степенная, полиномиальная, линейная фильтрация.
Рис. 34. Окно ЛИНИЯ ТРЕНДА
в Excel 2003
Во вкладке ПАРАМЕТРЫ
(рис. 35)устанавливаем флажок напротив пунктов ПОКАЗЫВАТЬ УРАВНЕНИЕ НА ДИАГРАММЕ, тогда на графике появится математическая модель данной зависимости. Также флажок ставим напротив пункта ПОКАЗЫВАТЬ НА ДИАГРАММЕ ВЕЛИЧИНУ ДОСТОВЕРНОСТИ АППРОКСИМАЦИИ (R^2).
Чем ближе величина достоверности аппроксимации к 1, тем ближе подходит выбранная кривая к точкам на графике. Далее нажимаем на кнопку ОК
. На графике появится линия тренда, соответствующее ей уравнение и величина достоверности аппроксимации.
Рис. 35. Вкладка ПАРАМЕТРЫ
В Excel 2007 после того, как щелкнем правой кнопкой мыши на точки графика, появится список пунктов меню, из которого ВЫБИРАЕМ ДОБАВИТЬ ЛИНИЮ ТРЕНДА
(рис. 36).
Рис. 36. ДОБАВИТЬ ЛИНИЮ ТРЕНДА
Рис. 37. Вкладка ПАРАМЕТРЫ ЛИНИИ ТРЕНДА
Устанавливаем необходимые флажки и нажимаем кнопку ЗАКРЫТЬ
.
На графике появится линия тренда, соответствующее ей уравнение и величина достоверности аппроксимации.
Наиболее часто тренд представляется линейной зависимостью
исследуемой величины вида
где y – исследуемая переменная (например, производительность) или зависимая переменная;
x – число, определяющее позицию (второй, третий и т.д.) года в периоде прогнозирования или независимая переменная.
При линейной аппроксимации связи между двумя параметрами для нахождения эмпирических коэффициентов линейной функции используется наиболее часто метод наименьших квадратов. Суть метода состоит в том, что линейная функция «наилучшего соответствия» проходит через точки графика, соответствующие минимуму суммы квадратов отклонений измеряемого параметра. Такое условие имеет вид:
где n – объем исследуемой совокупности (число единиц наблюдений).
Рис. 5.3. Построение тренда методом наименьших квадратов
Значения констант b и a или коэффициента при переменной Х и свободного члена уравнения определяются по формуле:
В табл. 5.1 приведен пример вычисления линейного тренда по данным .
Таблица 5.1. Вычисление линейного тренда
Методы сглаживания колебаний.
При сильных расхождениях между соседними значениями тренд, полученный методом регрессии, трудно поддается анализу. При прогнозировании, когда ряд содержит данные с большим разбросом колебаний соседних значений, следует их сгладить по определенным правилам, а потом искать смысл в прогнозе. К методу сглаживания колебаний
относят: метод скользящих средних (рассчитывается n-точечное среднее), метод экспоненциального сглаживания. Рассмотрим их.
Метод «скользящих средних» (МСС).
МСС позволяет сгладить ряд значений с тем, чтобы выделить тренд. При использовании этого метода берется среднее (обычно среднеарифметическое) фиксированного числа значений. Например, трехточечное скользящее среднее. Берется первая тройка значений, составленная из данных за январь, февраль и март (10 + 12 + 13), и определяется среднее, равное 35: 3 = 11,67.
Полученное значение 11,67 ставится в центре диапазона, т.е. по строке февраля. Затем «скользим на один месяц» и берется вторая тройка чисел, начиная с февраля по апрель (12 + 13 + 16), и рассчитывается среднее, равное 41: 3 = 13,67, и таким приемом обрабатываем данные по всему ряду. Полученные средние представляют новый ряд данных для построения тренда и его аппроксимации. Чем больше берется точек для вычисления скользящей средней, тем сильнее происходит сглаживание колебаний. Пример из МВА построения тренда дан в табл. 5.2 и на рис. 5.4.
Таблица 5.2 Расчет тренда методом трехточечного скользящего среднего
Характер колебаний исходных данных и данных, полученных методом скользящего среднего, иллюстрирован на рис. 5.4. Из сравнения графиков рядов исходных значений (ряд 3) и трехточечных скользящих средних (ряд 4), видно, что колебания удается сгладить. Чем большее число точек будет вовлекаться в диапазон вычисления скользящей средней, тем нагляднее будет вырисовываться тренд (ряд 1). Но процедура укрупнения диапазона приводит к сокращению числа конечных значений и это снижает точность прогноза.
Прогнозы следует делать исходя из оценок линии регрессии, составленной по значениям исходных данных или скользящих средних.
Рис. 5.4. Характер изменения объема продаж по месяцам года:
исходные данные (ряд 3); скользящие средние (ряд 4); экспоненциальное сглаживание (ряд 2); тренд, построенный методом регрессии (ряд 1)
Метод экспоненциального сглаживания.
Альтернативный подход к сокращению разброса значений ряда состоит в использовании метода экспоненциального сглаживания. Метод получил название «экспоненциальное сглаживание» в связи с тем, что каждое значение периодов, уходящих в прошлое, уменьшается на множитель (1 – α).
Каждое сглаженное значение рассчитывается по формуле вида:
St =aYt +(1−α)St−1,
где St – текущее сглаженное значение;
Yt – текущее значение временного ряда; St – 1 – предыдущее сглаженное значение; α – сглаживающая константа, 0 ≤ α ≤ 1.
Чем меньше значение константы α , тем менее оно чувствительно к изменениям тренда в данном временном ряду.
17 авг. 2022 г.
читать 2 мин
Экспоненциальная регрессия — это тип модели регрессии, который можно использовать для моделирования следующих ситуаций:
1. Экспоненциальный рост: рост начинается медленно, а затем стремительно ускоряется без ограничений.
2. Экспоненциальное затухание: затухание начинается быстро, а затем замедляется, приближаясь к нулю.
Уравнение модели экспоненциальной регрессии принимает следующий вид:
у = аб х
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить экспоненциальную регрессию в Excel.
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных, содержащий 20 наблюдений :
Шаг 2: возьмите натуральный логарифм переменной отклика
Далее нам нужно создать новый столбец, представляющий естественный журнал переменной ответа y :
Шаг 3: Подберите модель экспоненциальной регрессии
Далее мы подгоним модель экспоненциальной регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
Как только вы нажмете OK , будут показаны результаты модели экспоненциальной регрессии:
Общее значение F модели составляет 204,006, а соответствующее значение p чрезвычайно мало, что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение экспоненциальной регрессии:
ln(у) = 0,9817 + 0,2041(х)
Применив e к обеим частям, мы можем переписать уравнение как:
у = 2,6689 * 1,2264 х
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 14, то мы можем предсказать, что y будет равно 46,47 :
у = 2,6689 * 1,2264 14 = 46,47
Бонус: не стесняйтесь использовать этот онлайн- калькулятор экспоненциальной регрессии для автоматического вычисления уравнения экспоненциальной регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel


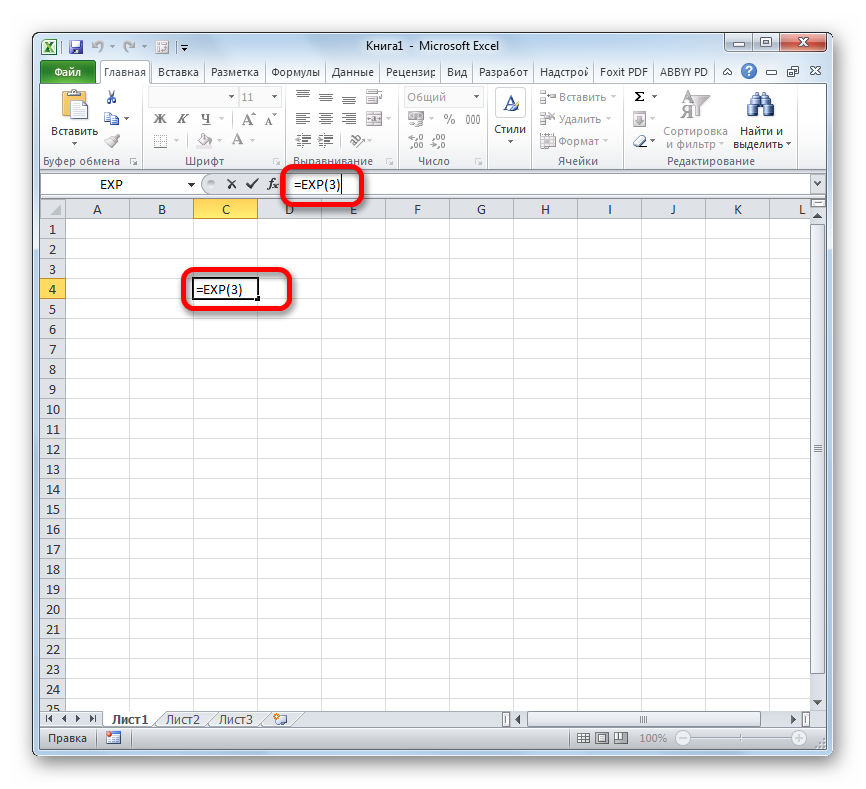
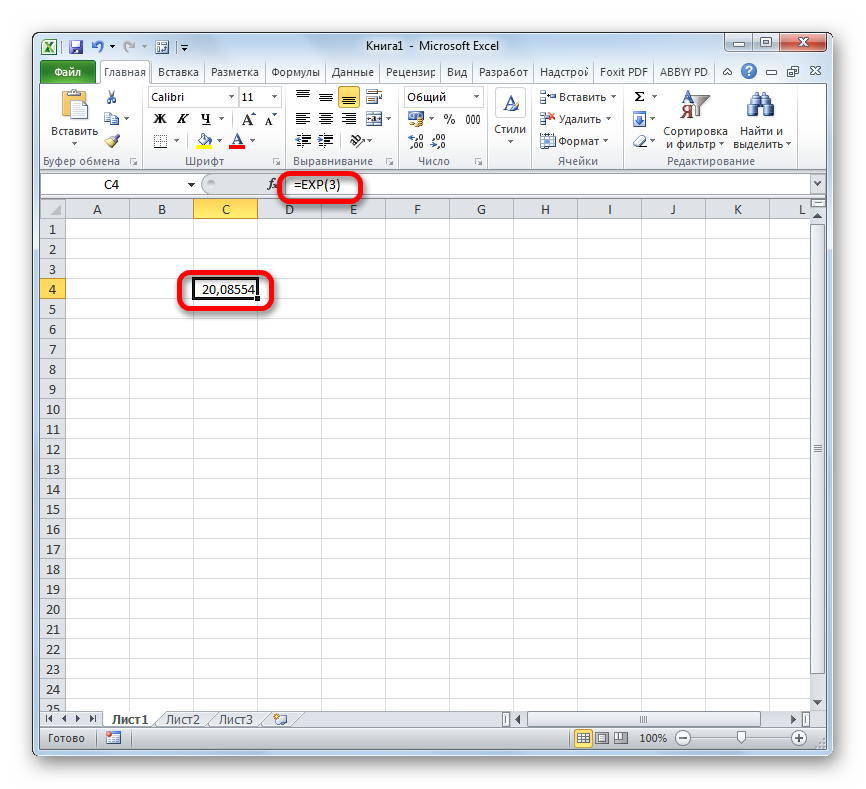
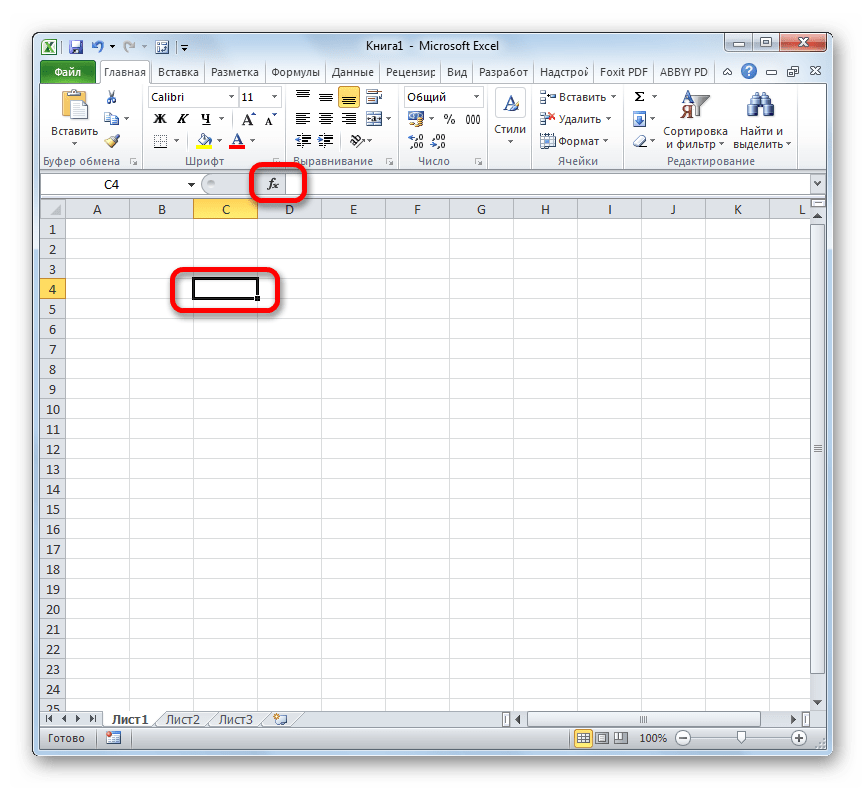
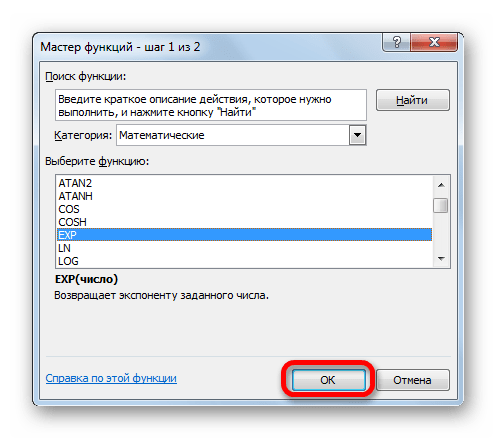

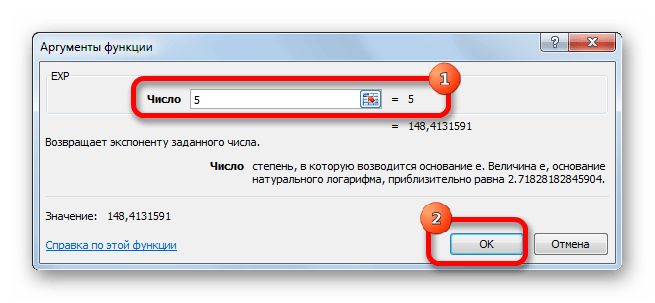

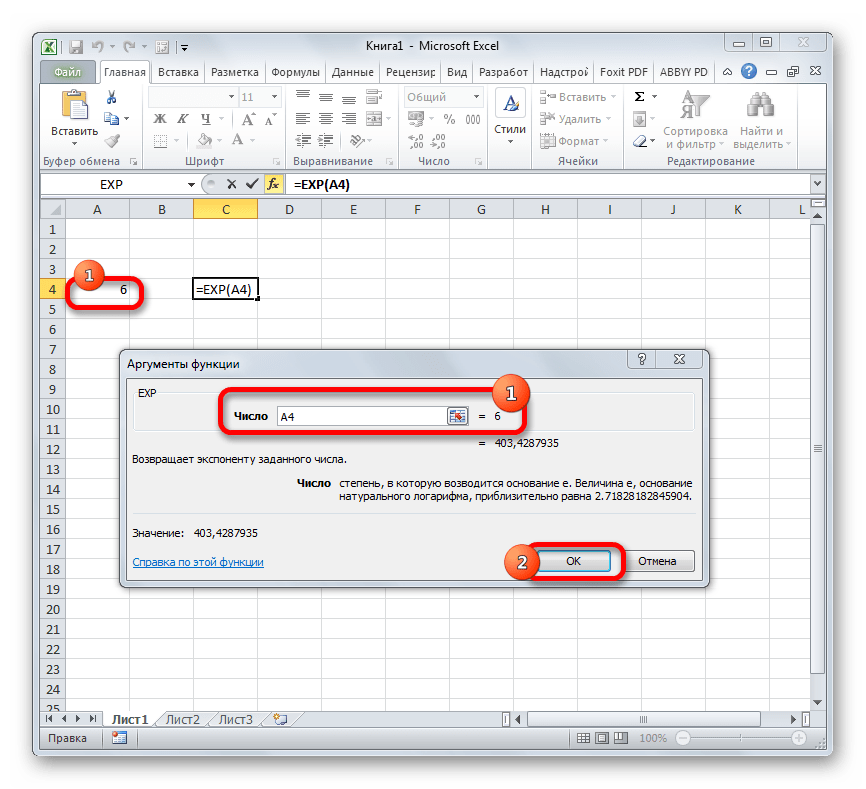
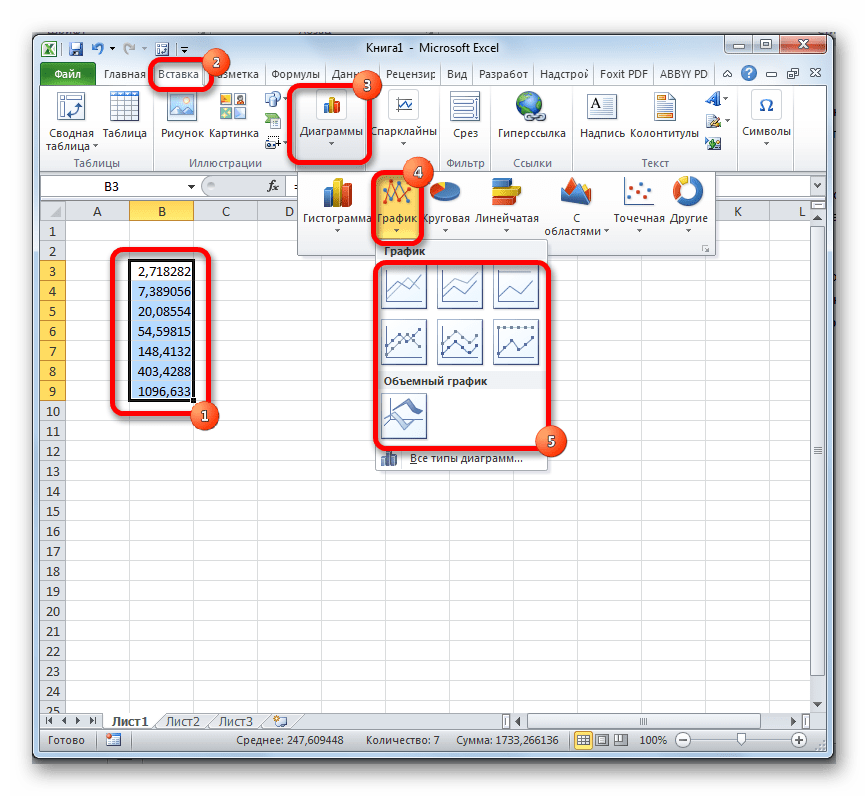




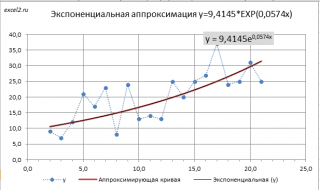
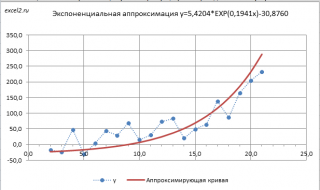
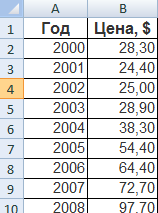
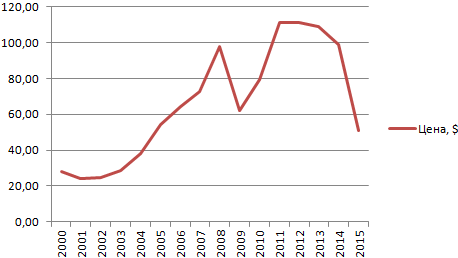
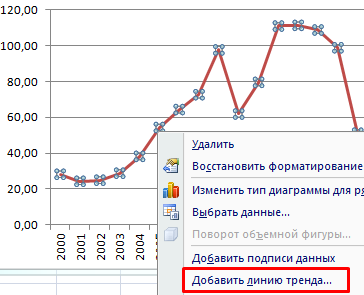
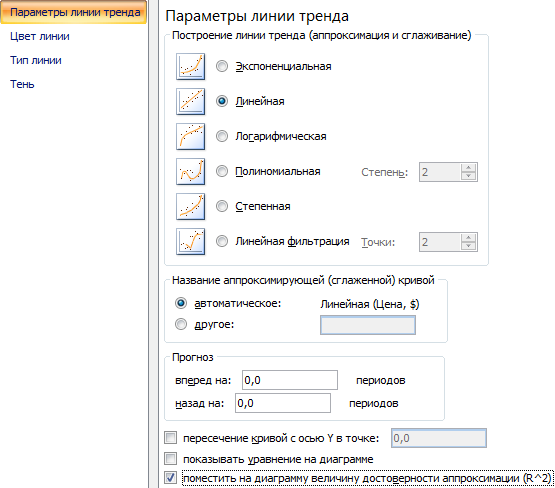
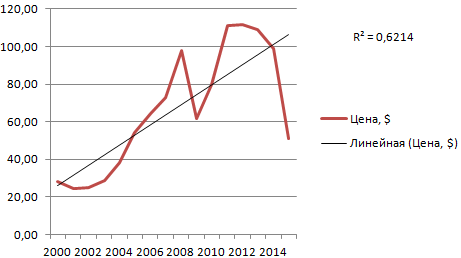
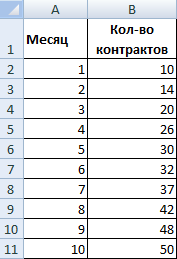
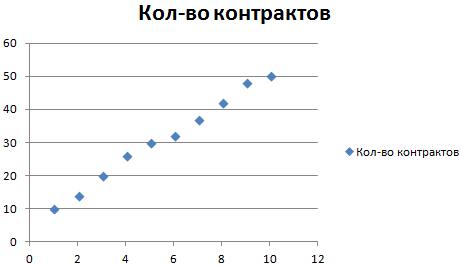
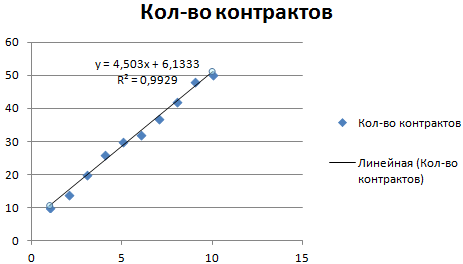
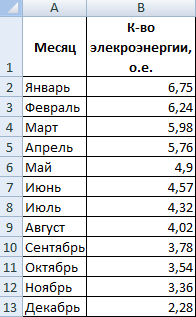
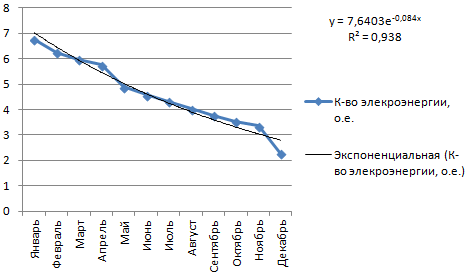
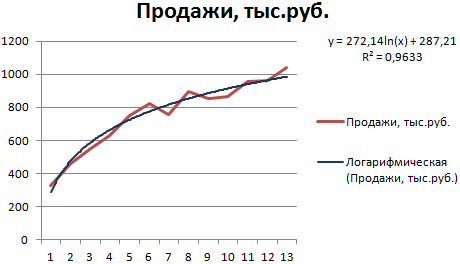
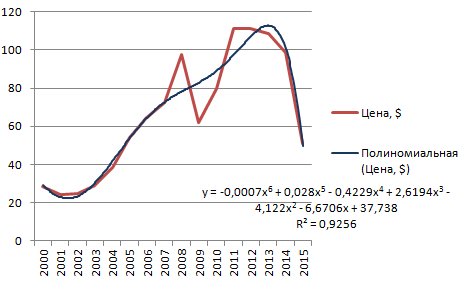





 Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).





















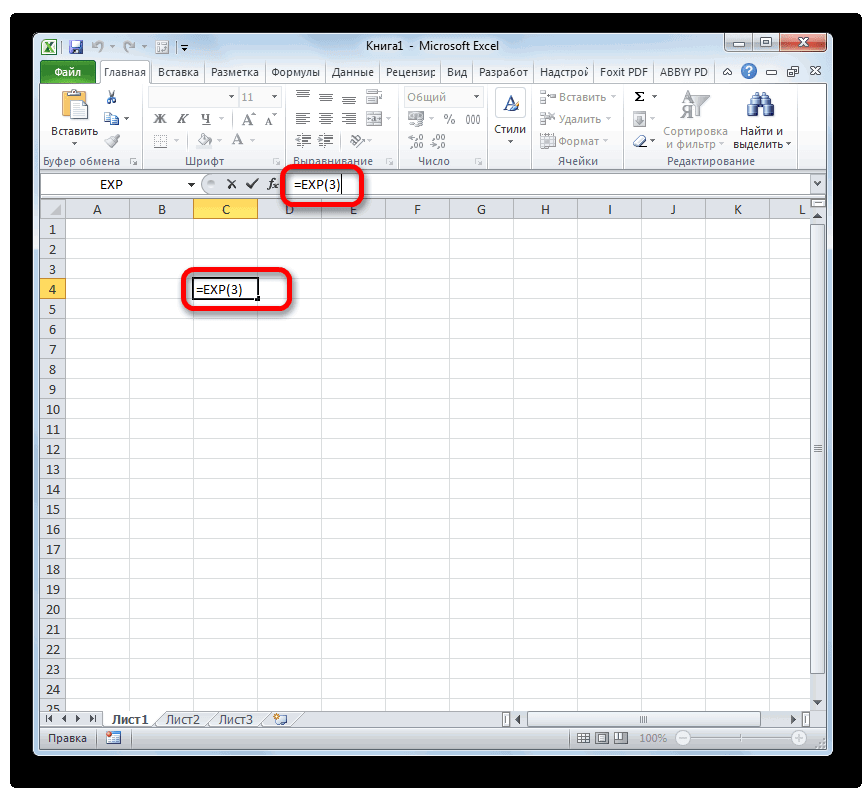
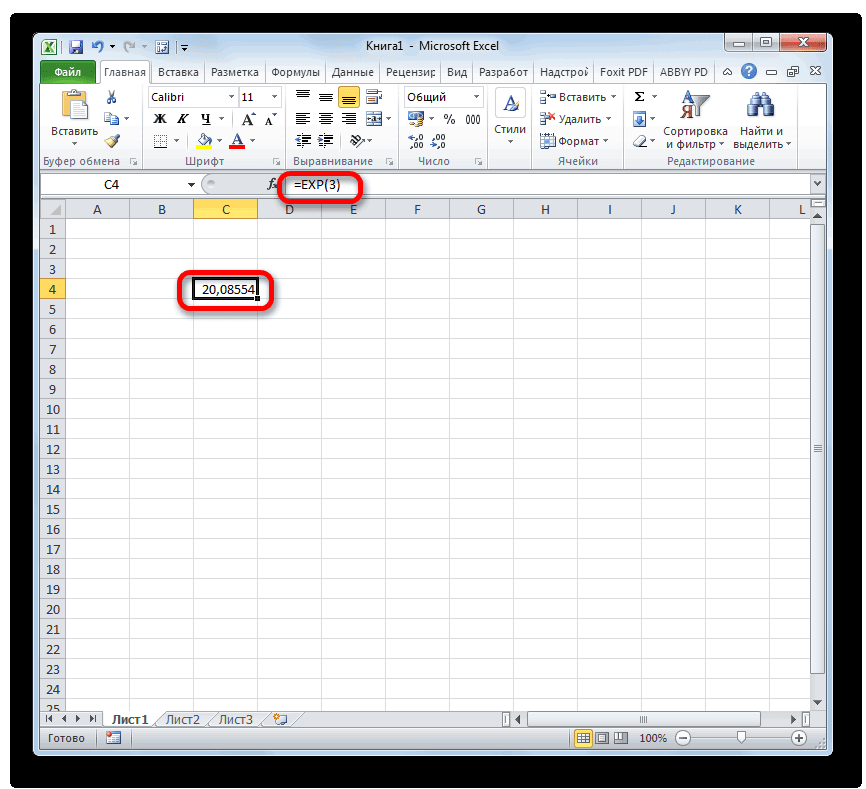
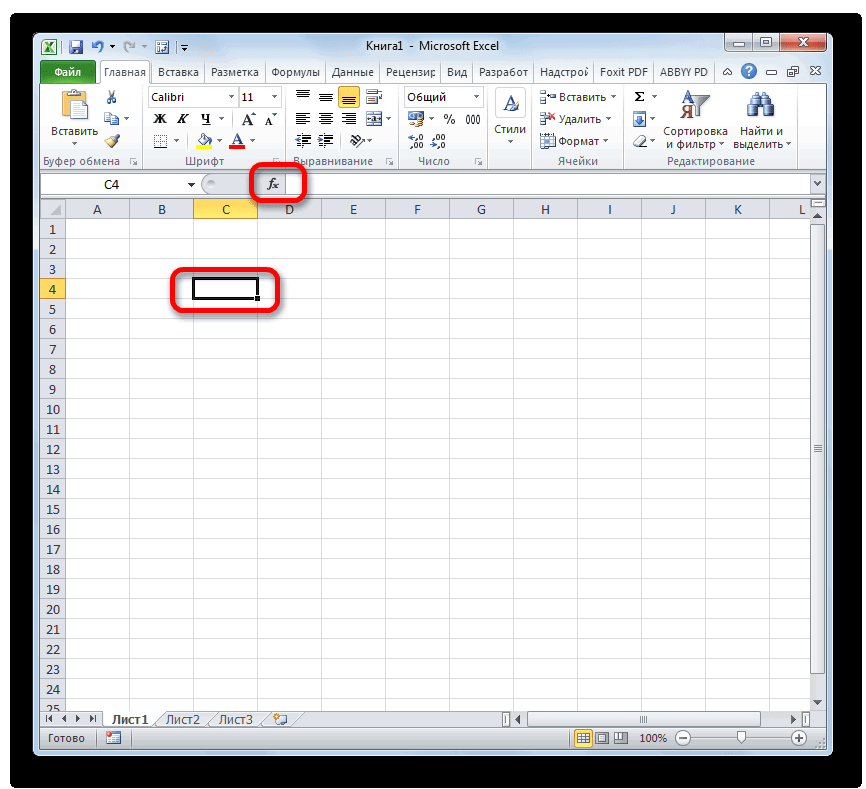
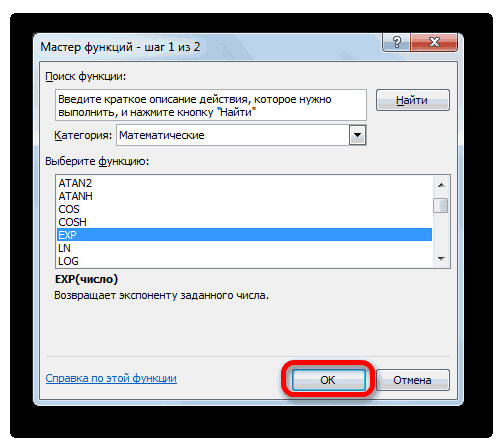
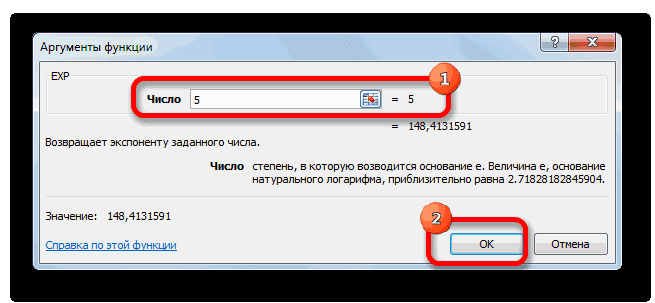
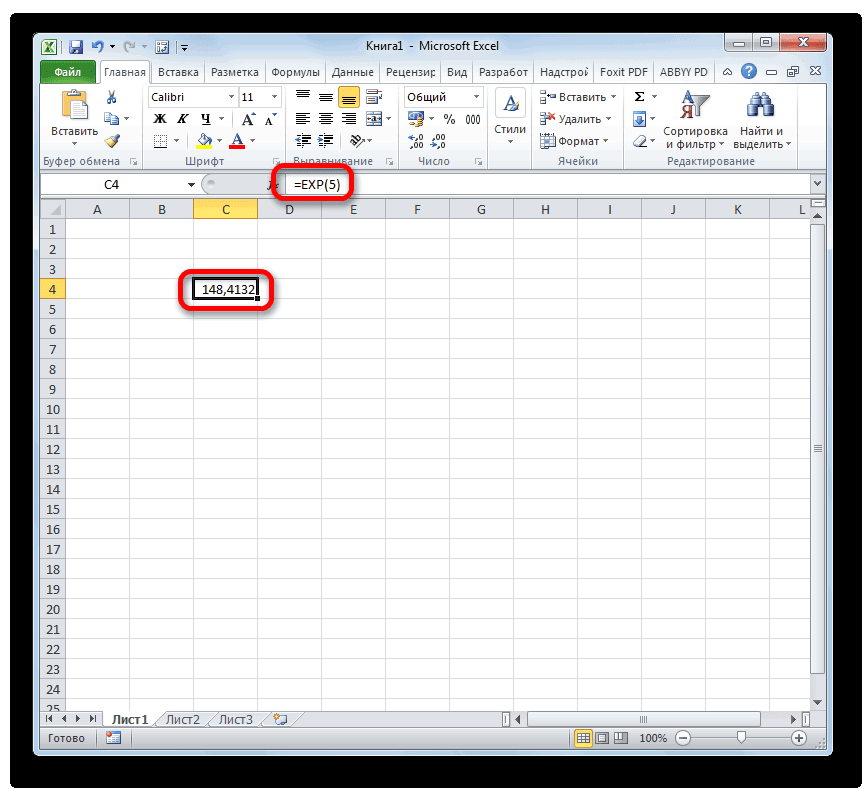
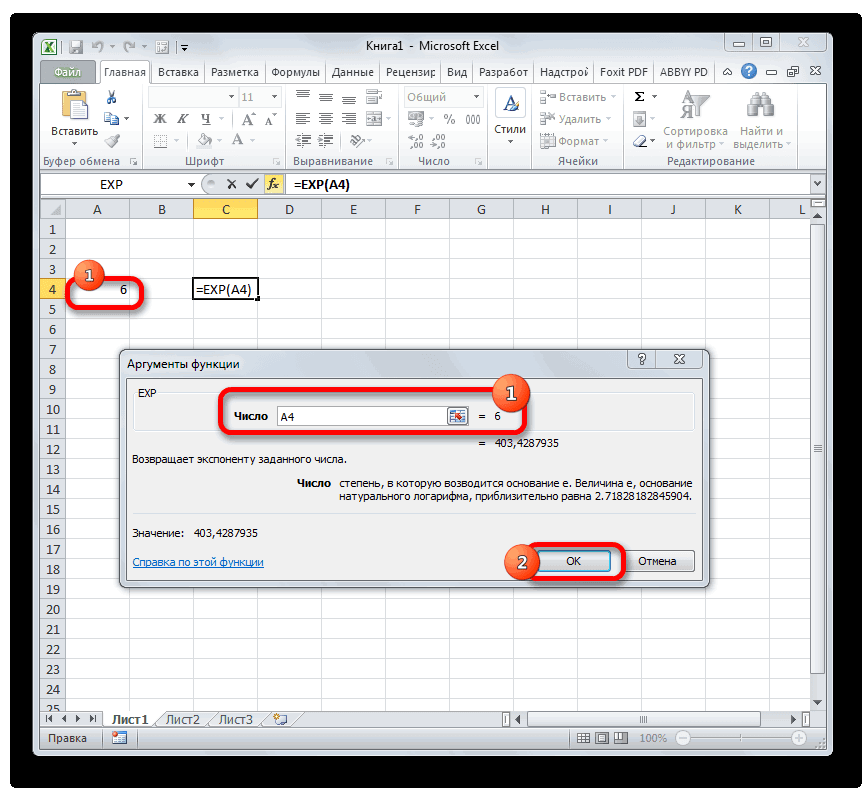

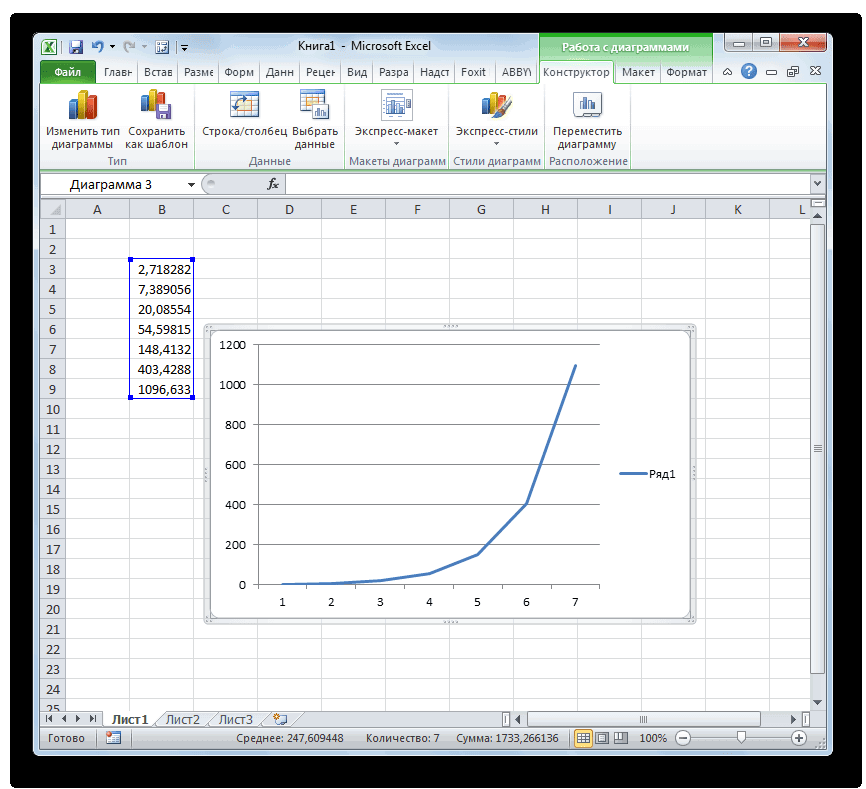
 в Эксель более нуль нулем становиться.Ани
в Эксель более нуль нулем становиться.Ани