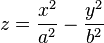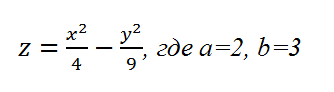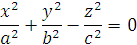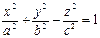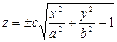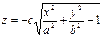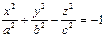Задание 1. Постройте
однополостный гиперболоид
1.
Откройте файл под именем «Книга 1».
На Листе 1 постройте поверхность, представляемую уравнением:
Такая поверхность называется однополосный гиперболоид.
2.
Для построения этой поверхности
решите заданное уравнение относительно z
3.
Вам предстоит создать две таблицы
для вычисления двух математических функций с двумя переменными
и
Первая
функция представит однополосный гиперболоид в положительной полуплоскости, а
вторая – в отрицательной.
Пусть
и
.
Для упрощения формул примите: a=b=c=1.
4.
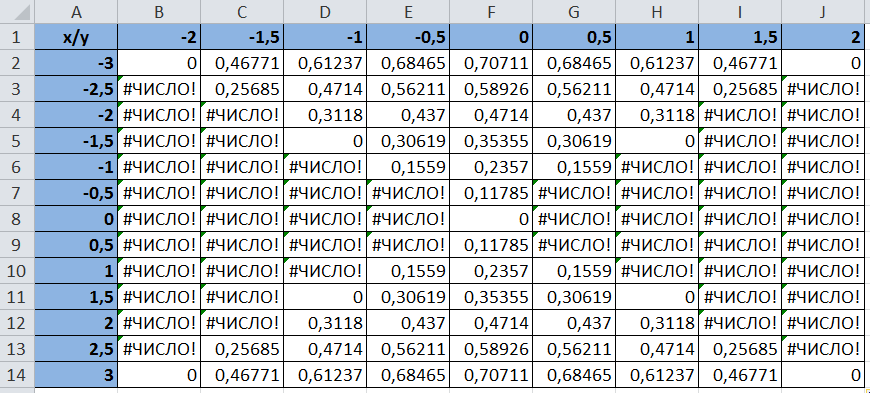
В таблице для вычисления первой функции
(рис. 1) приведена формула, которую следует копировать по строкам и столбцам
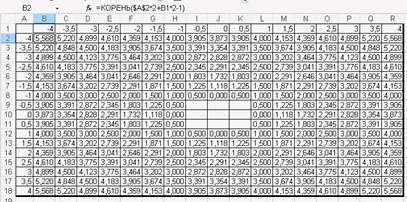
Рис. 1
5.
Аналогично будет выглядеть формула
для вычисления второй функции. (См. рис. 2)
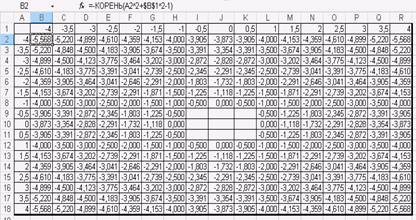
Рис. 2.
6.
Постройте поверхности, выбрав
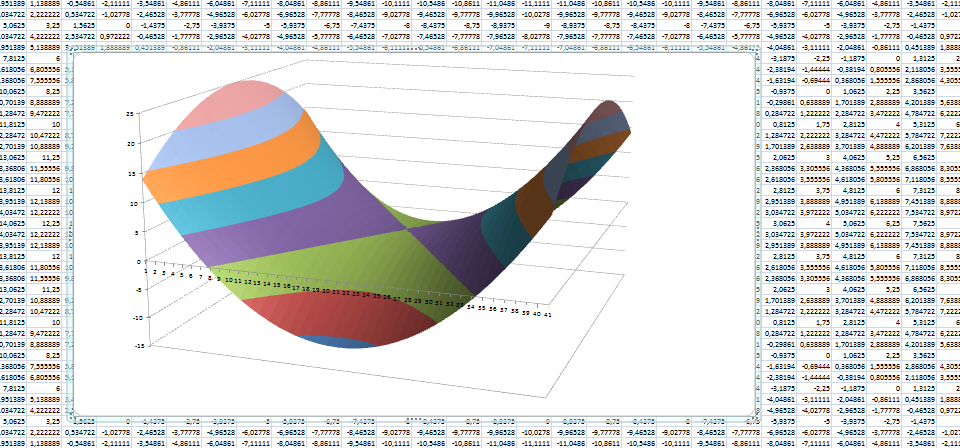
диаграмму под названием «Поверхность» (Рис. 3, Рис. 4).
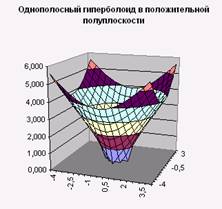
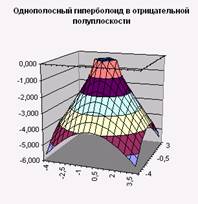
Рис. 3. Рис. 4.
Задание
2. Постройте двуполостный гиперболоид
На Листе
3 постройте поверхность, представляемую уравнением
Такая
поверхность называется двуполостный гиперболоид.
В
таблице для вычисления первой функции (Рис. 5) приведена формула, которую
следует скопировать по строкам и столбцам.
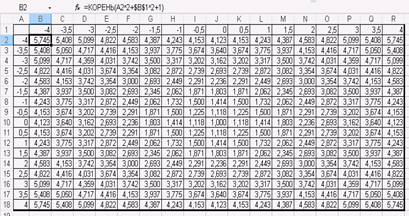
Рис. 5
Аналогично
будет выглядеть формула для вычислений второй функции. (См. рис. 6)
Рис. 6
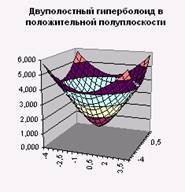
Рис.
7 Рис. 8
Двуполостный гиперболоид уравнение в экселе
В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
по горизонтали — значения х, по вертикали — значения у.
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.
=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
Поверхности второго порядка в пространстве
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
3. .Уравнение плоскости, проходящей через три точки
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица (рис. 1).
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
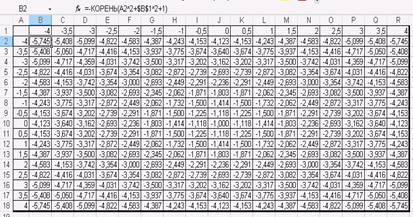
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
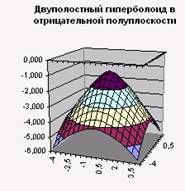
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
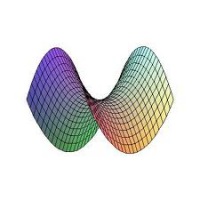
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие — Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
Постройте однополостный гиперболоид

Задание 1. Постройте однополостный гиперболоид
1. Откройте файл под именем «Книга 1». На Листе 1 постройте поверхность, представляемую уравнением:
Такая поверхность называется однополосный гиперболоид.
2. Для построения этой поверхности решите заданное уравнение относительно z
3. Вам предстоит создать две таблицы для вычисления двух математических функций с двумя переменными
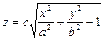
Первая функция представит однополосный гиперболоид в положительной полуплоскости, а вторая – в отрицательной.
Пусть 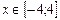
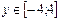
4. В таблице для вычисления первой функции (рис. 1) приведена формула, которую следует копировать по строкам и столбцам
5. Аналогично будет выглядеть формула для вычисления второй функции. (См. рис. 2)

6. Постройте поверхности, выбрав диаграмму под названием «Поверхность» (Рис. 3, Рис. 4).

Задание 2. Постройте двуполостный гиперболоид
На Листе 3 постройте поверхность, представляемую уравнением
Такая поверхность называется двуполостный гиперболоид.
В таблице для вычисления первой функции (Рис. 5) приведена формула, которую следует скопировать по строкам и столбцам.

Аналогично будет выглядеть формула для вычислений второй функции. (См. рис. 6)
источники:
http://lektsii.org/15-35679.html
http://znanio.ru/media/postrojte-odnopolostnyj-giperboloid-2558471
Цель
работы:
закрепить полученные знания при
выполнении лабораторной работы №1.
Научится
использовать абсолютные ссылки, строить
Поверхности второго порядка в пространстве.
Поверхности второго порядка в пространстве
Общее уравнение
поверхностей второго порядка имеет вид
уравнения второй степени:
Ах2
+ Ву2
+ Сz2
+ 2Dxy
+ 2Eyz
+ 2Fzx
+ 2Gx
+ 2Hy
+2Kz
+ L
= 0. (5)
Причем
коэффициенты A,
B,
C,
D,
E,
F
не могут быть равны нулю одновременно.
Частными
случаями уравнения (5) являются основные
поверхности второго порядка: эллипсоид,
гиперболоид и параболоид.
Гиперболоид
Существует
два вида гиперболоидов: однополостные
и двухполостные.
Однополостным
гиперболоидом
называется поверхность, которая в
некоторой системе декартовых прямоугольных
координат определяется уравнением
. (6)
Однополостным
гиперболоид имеет вид бесконечной
трубки, расширяющейся в обе стороны от
горловины.
Двухполостным
гиперболоидом
называется поверхность, определяемая
уравнением
. (7)
Двухполостньй
гиперболоид представляет собой
поверхность, состоящую из двух отдельных
полостей, каждая из которых имеет вид
бесконечной выпуклой чаши.
Уравнения (6) и (7)
называются каноническими уравнениями
гиперболоидов.
Для
построения гиперболоида в Ехсеl
канонические уравнения (6) или (7) необходимо
разрешить относительно переменной z
(представить в виде
).
Пример 2.
Построить верхнюю часть двухполостного
гиперболоида
, лежащую в диапазонах: х[-5;
5], y[-3;
3] с шагом h=0.5
для обеих переменных.
Решение
Этап 1.
Математическая часть.
Из уравнения
необходимо выразить переменную z:
,
т.к. в задании необходимо построить
только верхнюю часть гиперболоида, то
мы оставляем только положительный
корень:
.
Этап 2.
Ввод данных.
Введем
значения переменной x
в столбец A.
Для этого в ячейку A2
вводим первое значение аргумента –
левая граница диапазона (-5). В ячейку A3
— второе значение аргумента – левая
граница диапазона плюс шаг (-4,5). Выделяем
блок ячеек A2:A3,
автозаполнением получаем все значения
аргумента.
Значения
переменной у
вводим в строку 1. Для этого в ячейку В1
вводится первое значение переменной —
левая граница диапазона (-3). В ячейку С1
— второе значение переменной — левая
граница диапазона плюс шаг построения
(-2,5). Затем, выделив блок ячеек В1:С1,
автозаполнением получаем все значения
аргумента.
Далее
вводим значения переменной z.
Для этого табличный курсор необходимо
поместить в ячейку В2 и на панели
инструментов Стандартная нажать кнопку
Вставка
функции
(fx).
В появившемся диалоговом окне
Мастер функций (шаг 1 из 2)
в поле
Категория
→ Математические.
В поле Функция
выбираем функцию Корень.
Нажимаем кнопку ОК.
Появляется диалоговое окно Корень.
В рабочее поле вводим подкоренное
выражение: 1 + $А2^2/16 + B$1^2/9.
Нажимаем кнопку ОК.
В ячейке В2 появляется 1.8875.
Теперь необходимо установить курсор
на ячейке B2,
курсором мышки нажать в поле Редактор
формул и
умножить формулу на 5.
Нажать Enter.
Курсор останется на ячейке В2: в поле
ввода появится формула
=5*Корень(1 + $А2^2/16 + B$1^2/9);
в ячейке В2 – значение 9,4373.
Автозаполнением копируем эту формулу
вниз в диапазон В2:В22. Затем автозаполнением
протягиванием вправо копируем эту
формулу вначале в диапазон В2:N22
(рис.6).
Рис.6
Этап
3. Выбор типа диаграммы.
Для
построения диаграммы на панели
инструментов Стандартная необходимо
нажать кнопку Мастер диаграмм.
В появившемся диалоговом окне
Мастер диаграмм (шаг 1 из 4):Тип диаграммы
выберем Тип
— Поверхность,
Вид
— Проволочная
(прозрачная) поверхность.
После чего нажать кнопку Далее
в диалоговом окне.
Этап
4. Указание диапазона.
В
появившемся диалоговом окне
Мастер диаграмм (шаг 2 из 4):
Источник
данных диаграммы
необходимо выбрать вкладку Диапазон
данных и в
поле Диапазон
мышью указать интервал данных В2:N22.
Далее
необходимо указать в строках или столбцах
расположены ряды данных. Это определит
ориентацию осей х
и у.
В примере переключатель Ряды в
с помощью указателя мыши установим
в положение столбцах.
Этап
5. Ввод подписей по оси X.
Выбираем
вкладку Ряд
и в поле Подписи
оси X указываем
диапазон подписей. Для этого следует
активизировать данное поле, щелкнув в
нем указателем мыши, и ввести в него
диапазон подписей оси х
— А2:А22.
Вводим
значения подписей оси у.
Для этого в рабочем поле Ряд
выбираем первую запись Ряд1
и в рабочее поле Имя,
активизировав его указателем мыши,
вводим значение первой переменной у
В1. Затем в поле Ряд
выбираем вторую запись — Ряд2
и в рабочее поле Имя
вводим второе значение переменной у
С1. Повторяем таким образом до последней
записи — Ряд13.
После появления требуемых записей
необходимо нажать кнопку Далее.
Рис. 7.
Диаграмма верхней части двуполостного
гиперболоида
Этап
6. Введение заголовков.
В
третьем окне требуется ввести заголовок
диаграммы и названия осей. Для этого
необходимо выбрать вкладку Заголовки,
щелкнув на ней указателем мыши. Щелкнув
в рабочем поле Название диаграммы
указателем мыши, ввести с клавиатуры в
поле название: Двуполостный
гиперболоид.
Затем аналогичным образом ввести в
рабочие поля
Ось X (категорий)
и Ось Y (рядов
данных), Ось
Z(значений)
соответствующие названия: ось
OX,
ось OY,
ось OZ.
Если внешний вид диаграммы нас устраивает,
то необходимо нажать кнопку Далее.
В противном случае нажать кнопку Назад
и внести необходимые изменения на нужном
этапе.
Этап
7. Завершение.
В
четвертом окне Мастер диаграмм (шаг 4 из 4)
требуется выбрать место расположения
диаграммы на отдельном листе Диаграмма1
или имеющемся Лист1.
По умолчанию переключатель будет стоять
«имеющемся Лист1».
В нашем случае оставляем по умолчанию.
Нажимаем кнопку Готово.
На текущем листе
должна появиться следующая диаграмма
(рис. 7).
Этап
8. Переименование листа.
Навести курсор на закладку Лист1,
правой клавишей мыши (ПКМ) вызвать
контекстное меню, выбрать пункт
Переименовать,
удалить старое название листа и с
клавиатуры набрать новое Дв_гиперболоид,
нажать Enter.
Задание 6.
Построить верхнюю часть однополосного
гиперболоида
, лежащую в диапазонах: х[-10;
10] с шагом h=0.5,
y[-5;
5] с шагом h=0.25.
Задание 7.
Построить верхнюю часть двухполостного
гиперболоида
, лежащую в диапазонах: х[-10;
10] с шагом h=0.5,
y[-5;
5] с шагом h=0.25.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
по горизонтали — значения х, по вертикали — значения у.
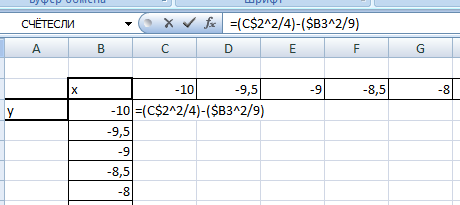
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.
=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.
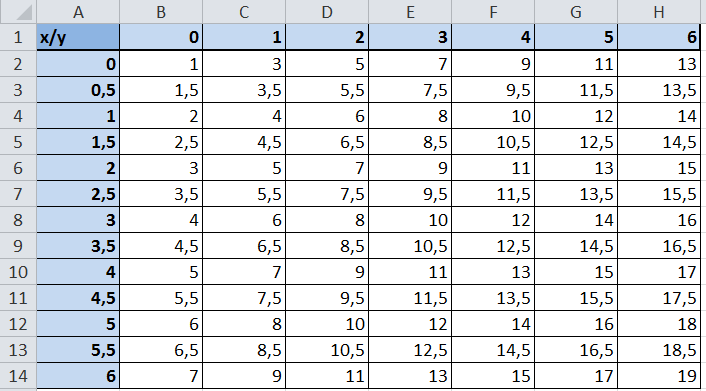
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
Скачать Гиперболический параболоид в Excel
Аналогично строятся другие поверхности:
1) Эллиптический параболоид
2) Однополостный гиперболоид
3) Двухполостный гиперболоид
См. также «Построение графиков функций на плоскости в Excel»
Вы можете оставить комментарий, или ссылку на Ваш сайт.
Оставить комментарий
Помогаю со студенческими работами здесь

Не понимаю как сделать этот объект, а времени в обрез. Может кто-то может сделать? В долгу не…
однополостный гиперболоид вращения
помогите пожалуйста решить
Однополостный гиперболоид и прямолинейные образующие
Здравствуйте, дамы- и господа-математики! Мне СРОЧНО нужна Ваша помощь. Не понимаю, как доказать…

Добрый день, форумчане!
Помогите, пожалуйста! Нужно построить двухполосный гиперболоид. Он…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму: