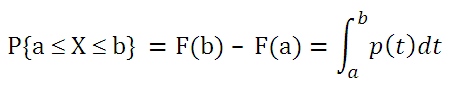Как построить дискретный график excel - Word и Excel - помощь в работе с программами

Рассмотрим Равномерное дискретное распределение, построим график функции распределения, вычислим среднее значение и дисперсию. Сгенерируем случайные значения (выборку) с помощью функции MS EXCEL

СЛУЧМЕЖДУ()

. На основании выборки оценим среднее и стандартное отклонение распределения.

Равномерное дискретное распределение (англ. Discrete uniform distribution)

имеет место, например, при подбрасывании симметричной монеты. Пусть если выпал «орёл», то случайная величина принимает значение 1, если выпала «решка» — то 0. Т.к. вероятность наступления событий одинакова и всего 2 возможных исхода, то вероятность случайной величины принять значение 1 (или 0) равна 1/2=0,5.

Распределение называется равномерным, т.к. вероятность любого исхода одинакова.

Примечание

: В данном случае, когда возможно всего 2 исхода,

равномерное распределение

является частным случаем

Распределения Бернулли

с параметром

p

=

q

=1-

p

=0,5.

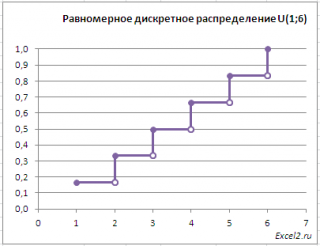
Другой пример. Результат бросания симметричной игральной кости является

равномерной дискретной случайной величиной

, т.к. количество точек на грани кубика принимает одно из 6 равновероятных значений. Вероятность выпадения каждой из шести граней равна 1/6.

Для этого примера

функция распределения

будет выглядеть следующим образом.

Примечание

: Для построения графика использованы идеи из статьи про

ступенчатый график

СОВЕТ

: Подробнее о

Функции распределения

см. статью

Функция распределения и плотность вероятности в MS EXCEL

Математическое ожидание и дисперсия

В

файле примера на листе График

приведен расчет

математического ожидания

по формуле =(a+b)/2.

Дисперсия (квадрат стандартного отклонения)

для

равномерного дискретного распределения

может быть вычислена по формуле =((b-a+1)^2-1)/12.

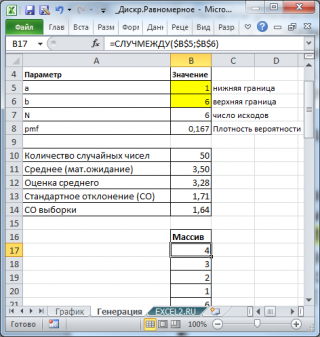
Генерация случайных значений

Случайные числа, имеющие

равномерное дискретное распределение

, можно сгенерировать с помощью функции MS EXCEL

СЛУЧМЕЖДУ()

. В функции можно задать нижнюю и верхнюю границу интервала [a; b]. Функцией будут сгенерированы

целые

случайные числа из указанного интервала (см.

файл примера лист Генерация

).

Обратите внимание, что массив случайных чисел, сгенерированных с помощью функции

СЛУЧМЕЖДУ()

, автоматически обновится при пересчете листа. Пересчет листа в MS EXCEL производится при вводе нового значения в ячейку или при нажатии клавиши

F9

.

Примечание

: Подробнее про функцию

СЛУЧМЕЖДУ()

см. статью

Функция СЛУЧМЕЖДУ() — Случайное число из заданного интервала в MS EXCEL

Чтобы сгенерировать

нецелые

случайные числа, например из интервала [1,1; 2,5], необходимо записать формулу =

СЛУЧМЕЖДУ(1,1*10;2,5*10)/10

.

Множитель 10 отражает тот факт, что

нецелые

случайные числа будут сгенерированы с точностью до десятых. Если интервал задан с точностью до сотых, то нужно использовать множитель 100.

Как видно из формулы — границы интервала также могут быть нецелыми числами. Хотя, конечно, можно сгенерировать числа, например, с точностью до сотых с помощью формулы =

СЛУЧМЕЖДУ(10*100;20*100)/100

. В этом случае случайные числа будут принадлежать интервалу [10;20] и иметь вид 10,37; 16,08; 15,43 и т.д.

Оценка среднего и стандартного отклонения

Сгенерируем 50 чисел (выборку) и разместим их в диапазоне

B17:B66

. Нижнюю и верхнюю границу интервала возьмем [1; 6] и разместим их в диапазоне

B5:B6

.

Математическое ожидание

этого распределения

=(B5+B6)/2

и равно (6+1)/2=3,5.

Стандартное отклонение

распределения равно =

КОРЕНЬ(((B6-B5+1)^2-1)/12)

=1,71

Чтобы оценить

математическое ожидание

воспользуемся значениями выборки

=СУММ(B17:B66)/СЧЁТ(B17:B66)

.

Оценить

стандартное отклонение

можно с помощью формулы

=СТАНДОТКЛОН.В(B17:B66)

в MS EXCEL 2010 или =

СТАНДОТКЛОН(B17:B66)

для более ранних версий.

Чтобы оценить

дисперсию

используйте формулу

=ДИСП.В(B17:B66)

в MS EXCEL 2010 или

=ДИСП(B17:B66)

для более ранних версий. Также можно использовать формулу

=СТАНДОТКЛОН.В(B17:B66)^2

.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

Источник

Содержание

2.2. Методика построения вариационных рядов и их графиков с помощью электронных таблиц Excel
Функция распределения и плотность вероятности в EXCEL
Генеральная совокупность и случайная величина
Функция распределения
Непрерывные распределения и плотность вероятности
Вычисление плотности вероятности с использованием функций MS EXCEL
Вычисление вероятностей с использованием функций MS EXCEL
Обратная функция распределения (Inverse Distribution Function)

2.2. Методика построения вариационных рядов и их графиков с помощью электронных таблиц Excel

Построим дискретный вариационный ряд по затратам труда на 1 ц зерна.

Открываем лист Excel, в ячейку А1 записываем условное обозначение результативного признака – у, а в ячейки А2:А31 значения затрат труда на 1 ц зерна. В ячейки В2:В3 введём наименьшее и следующее за ним значения признака 0,7 и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем мышью правый нижний угол выделительной рамки и потянем вниз до значения 1,5 (наибольшее значение признака). В ячейках В2:В10 получим варианты признака в ранжированном порядке. Для определения частот проделаем следующие шаги:

1.Поставим курсор в ячейку С2.

2.Выберем Вставка, Функция.

Выберем в категории Статистические функции функцию Частота и нажмём ОК.

3.В поле данных укажем ячейки А2:А31, а в поле интервалов В2:В10.

4.Нажмём кнопку ОК.

5.Выделим ячейки С2:С10.

6.Нажмём F2, а затем комбинацию клавиш Shift+Ctrl+Enter.

В ячейках С2:С10 появятся частоты.

Вычислим накопленные частоты, которые потребуются для дальнейших расчётов, путём последовательного суммирования локальных частот (нарастающим итогом). Так, первая плюс вторая частоты дают накопленную частоту второго варианта (1+2=3); прибавляя к ней третью частоту, получим накопленную частоту третьего варианта (3+4=7) и т.д.

Скопируем полученный в Excel вариационный ряд и построим таблицу.

Дискретный вариационный ряд распределения затрат труда на 1 ц зерна

Построим полигон распределения частот с помощью Мастера диаграмм. Выберем точечную диаграмму, соединим полученные точки отрезками, а крайние точки с осью абсцисс в точках, отстоящих от крайних на расстоянии шага.

Р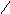ис. 1. Полигон распределения сельскохозяйственных предприятий по затратам труда на 1 ц зерна

Рассмотрим построение интервального вариационного ряда.

Рис. 2. Построение интервального вариационного ряда

На листе Excel в ячейку А1 записываем условное обозначение факторного признака – х, в ячейки А2:А31 – значения факторного признака – урожайности озимой пшеницы. Произведём сортировку данных, для чего выделяем диапазон данных, выбираем Данные – Сортировка и в появившемся окне «Сортировка диапазона» указываем «по возрастанию», нажимаем ОК. Данные в ячейках А2:А31 расположатся в ранжированном порядке по возрастанию признака. По формуле Стерджесса определяем количество групп (интервалов). Для вычисления десятичного логарифма lg30 выбираем Мастер функций – Математические – LOG10. В появившемся окне в поле Число записываем число 30, десятичный логарифм которого необходимо найти. Нажатием ОК получаем этот логарифм 1,477121. . Подставляя числовые данные в формулу (1), получим число групп (интервалов) 5,9, округляем до 6. По формуле (2) определяем величину интервалов – шаг с такой же точностью, с которой даны исходные данные (в данном случае с точностью до десятых: (30-20)/6≈1,7. Следовательно, совокупность надо разбить на 6 интервалов. Получаем шаг 1,7. Озаглавим следующие столбцы в Excel словами «Интервалы», «Частоты», «Накопленные частоты», «Середины интервалов». В ячейку В2 вписываем минимальное значение признака Х_min=20, в ячейку В3 формулу =В2+1,7, т.е. минимальное значение плюс шаг. Копируем эту формулу на 5 строк вниз. В результате в этих шести строках (В3:В8) получим верхние границы всех интервалов. Нижними границами интервалов будут данные в соседних верхних ячейках, т.е. для первого интервала нижней границей будет содержание ячейки В2, для второго В3 и для шестого В7.

Для расчёта частот выберем Сервис — Анализ данных – Гистограмма и нажмём ОК. В появившемся окне «Гистограмма» в поле «Входной интервал» копируем исходные данные (ячейки А2:А31), в поле «Интервал карманов» — верхние границы интервалов (ячейки В3:В8), в поле «Выходной интервал» ячейки частот (С3:С8), нажимаем ОК. В ячейки D3:D8 будут записаны частоты для всех шести интервалов. Накопленные частоты подсчитываем нарастающим итогом.

Для построения диаграммы необходимо найти середины интервалов. Для этого вводим формулу расчёта середины интервала: 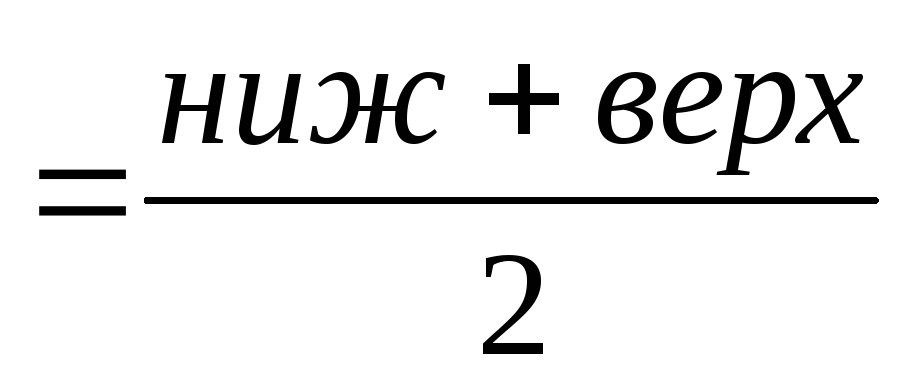, рассчитаем середину первого интервала. Копируем формулу для остальных пяти групп.

Для построения диаграммы выделяем массив частот и середин интервалов. Далее в Мастере диаграмм выбираем вид диаграммы — гистограмму определённого вида. Нажимаем кнопку Далее. В появившемся окне выбираем вкладку Ряд, удаляем ряд 1, а в поле «Подписи оси х» копируем середины интервалов. Нажимаем далее, в появившемся окне выбираем вкладку Заголовки. В поле «ось х (категорий)» вписываем название факторного признака (в данном случае урожайность, ц/га), в поле «Ось у (значений)» вписываем частоты. Нажимаем Далее, Готово. Появится диаграмма, состоящая из столбиков, отделённых друг от друга некоторым зазором. Щёлкаем правой кнопкой мыши на одном из столбиков диаграммы. В раскрывающемся списке элементов щёлкаем по кнопке Формат рядов данных. В появившемся диалоговом окне активизируем вкладку Параметры и в поле Ширина зазора устанавливаем значение 0. Нажимаем ОК, в результате чего гистограмма принимает стандартный вид.

Источник

Функция распределения и плотность вероятности в EXCEL

history 13 октября 2016 г.

Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта ]]> www.excel2.ru ]]> . Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL .

Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.

Генеральная совокупность и случайная величина

Пусть у нас имеется генеральная совокупность (population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.

Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.

Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.

В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.

Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной . По определению, любая случайная величина имеет функцию распределения , которая обычно обозначается F(x).

Функция распределения

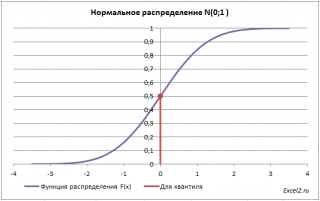
Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X файл примера ):

В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения ( Cumulative Distribution Function , CDF ).

Приведем некоторые свойства Функции распределения:

Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
Функция распределения – неубывающая функция;
Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x ₁ Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .

Непрерывные распределения и плотность вероятности

В случае непрерывного распределения случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для непрерывной случайной величины равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой функции плотности распределения p(x) . Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение функции распределения на этом интервале:

Как видно из формулы выше плотность распределения р(х) представляет собой производную функции распределения F(x), т.е. р(х) = F’(x).

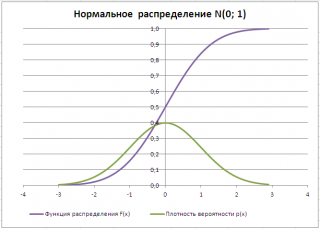
Типичный график функции плотности распределения для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):

Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .

В литературе Функция плотности распределения непрерывной случайной величины может называться: Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF) .

Чтобы все усложнить, термин Распределение (в литературе на английском языке — Probability Distribution Function или просто Distribution ) в зависимости от контекста может относиться как Интегральной функции распределения, так и кее Плотности распределения.

Из определения функции плотности распределения следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины , распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда =5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.

Напомним, что плотность распределения является производной от функции распределения , т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что плотность распределения >1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере экспоненциального распределения ).

Примечание : Площадь, целиком заключенная под всей кривой, изображающей плотность распределения , равна 1.

Примечание : Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения . Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная ). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная , д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности , то параметр интегральная , д.б. ЛОЖЬ.

Примечание : Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже «функция вероятностной меры» (см. функцию БИНОМ.РАСП() ).

Вычисление плотности вероятности с использованием функций MS EXCEL

Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение.

Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .

Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).

Вычисление вероятностей с использованием функций MS EXCEL

1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).

2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению , приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.

3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению , примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА) .

Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.

Обратная функция распределения (Inverse Distribution Function)

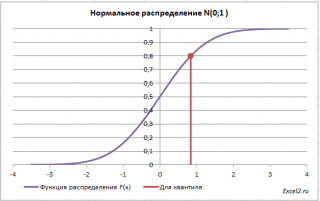
Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.

Вероятность этого события равна 0,5.

Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение =НОРМ.СТ.ОБР(0,5) =0.

Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.

Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения , а не плотность распределения . Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная , который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение .

Обратная функция распределения вычисляет квантили распределения , которые используются, например, при построении доверительных интервалов . Т.е. в нашем случае число 0 является 0,5-квантилем нормального распределения . В файле примера можно вычислить и другой квантиль этого распределения. Например, 0,8-квантиль равен 0,84.

В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).

Примечание : При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .

Источник

Построим дискретный вариационный ряд
по затратам труда на 1 ц зерна.

Открываем лист Excel,
в ячейку А1 записываем условное обозначение
результативного признака – у, а в ячейки
А2:А31 значения затрат труда на 1 ц зерна.
В ячейки В2:В3 введём наименьшее и
следующее за ним значения признака 0,7
и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем
мышью правый нижний угол выделительной
рамки и потянем вниз до значения 1,5
(наибольшее значение признака). В ячейках
В2:В10 получим варианты признака в
ранжированном порядке. Для определения
частот проделаем следующие шаги:

1.Поставим курсор в ячейку С2.

2.Выберем Вставка,
Функция.

Выберем в категории
Статистические функции
функцию Частота и
нажмём ОК.

3.В поле данных
укажем ячейки А2:А31, а в поле интервалов
В2:В10.

4.Нажмём кнопку ОК.

5.Выделим ячейки
С2:С10.

6.Нажмём F2,
а затем комбинацию клавиш Shift+Ctrl+Enter.

В ячейках С2:С10 появятся
частоты.

Вычислим накопленные
частоты, которые потребуются для
дальнейших расчётов, путём последовательного
суммирования локальных частот (нарастающим
итогом). Так, первая плюс вторая частоты
дают накопленную частоту второго
варианта (1+2=3); прибавляя к ней третью
частоту, получим накопленную частоту
третьего варианта (3+4=7) и т.д.

Скопируем полученный
в Excel
вариационный ряд и построим таблицу.

Таблица 2

Дискретный вариационный ряд распределения
затрат труда на 1 ц зерна

Варианты	Частоты	Накопленные частоты
0,7	1	1
0,8	2	3
0,9	4	7
1,0	5	12
1,1	6	18
1,2	4	22
1,3	3	25
1,4	3	28
1,5	2	30

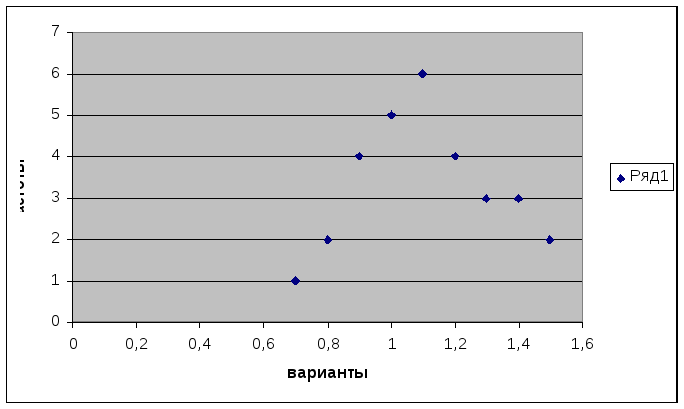
Построим
полигон распределения частот с помощью
Мастера
диаграмм.
Выберем точечную диаграмму, соединим
полученные точки отрезками, а крайние
точки с осью абсцисс в точках, отстоящих
от крайних на расстоянии шага.

Рис.
1. Полигон распределения сельскохозяйственных
предприятий по затратам труда на 1 ц
зерна

Рассмотрим
построение интервального вариационного
ряда.

Рис. 2. Построение интервального
вариационного ряда

На
листе Excel в ячейку А1 записываем условное
обозначение факторного признака – х,
в ячейки А2:А31 – значения факторного
признака – урожайности озимой пшеницы.
Произведём сортировку данных, для чего
выделяем диапазон данных, выбираем
Данные – Сортировка и в появившемся
окне «Сортировка диапазона» указываем
«по возрастанию», нажимаем ОК. Данные
в ячейках А2:А31 расположатся в ранжированном
порядке по возрастанию признака. По
формуле Стерджесса определяем количество
групп (интервалов). Для вычисления
десятичного логарифма lg30 выбираем
Мастер функций – Математические –
LOG10. В появившемся окне в поле Число
записываем число 30, десятичный логарифм
которого необходимо найти. Нажатием ОК
получаем этот логарифм 1,477121. . Подставляя
числовые данные в формулу (1), получим
число групп (интервалов) 5,9, округляем
до 6. По формуле (2) определяем величину
интервалов – шаг с такой же точностью,
с которой даны исходные данные (в данном
случае с точностью до десятых:
(30-20)/6≈1,7. Следовательно, совокупность
надо разбить на 6 интервалов. Получаем
шаг 1,7. Озаглавим следующие столбцы в
Excel словами «Интервалы», «Частоты»,
«Накопленные частоты», «Середины
интервалов». В ячейку В2 вписываем
минимальное значение признака Х_min=20,
в ячейку В3 формулу =В2+1,7, т.е. минимальное
значение плюс шаг. Копируем эту формулу
на 5 строк вниз. В результате в этих шести
строках (В3:В8) получим верхние границы
всех интервалов. Нижними границами
интервалов будут данные в соседних
верхних ячейках, т.е. для первого интервала
нижней границей будет содержание ячейки
В2, для второго В3 и для шестого В7.

Для
расчёта частот выберем Сервис — Анализ
данных – Гистограмма и нажмём ОК. В
появившемся окне «Гистограмма» в поле
«Входной интервал» копируем исходные
данные (ячейки А2:А31), в поле «Интервал
карманов» — верхние границы интервалов
(ячейки В3:В8), в поле «Выходной интервал»
ячейки частот (С3:С8), нажимаем ОК. В ячейки
D3:D8 будут записаны частоты для всех
шести интервалов. Накопленные частоты
подсчитываем нарастающим итогом.

Для
построения диаграммы необходимо найти
середины интервалов. Для этого вводим
формулу расчёта середины интервала:
,
рассчитаем середину первого интервала.
Копируем формулу для остальных пяти
групп.

Для
построения диаграммы выделяем массив
частот и середин интервалов.
Далее в
Мастере диаграмм выбираем вид диаграммы
— гистограмму определённого вида.
Нажимаем кнопку Далее. В появившемся
окне выбираем вкладку Ряд, удаляем ряд
1, а в поле «Подписи оси х» копируем
середины интервалов. Нажимаем далее, в
появившемся окне выбираем вкладку
Заголовки. В поле «ось х (категорий)»
вписываем название факторного признака
(в данном случае урожайность, ц/га), в
поле «Ось у (значений)» вписываем частоты.
Нажимаем Далее, Готово. Появится
диаграмма, состоящая из столбиков,
отделённых друг от друга некоторым
зазором. Щёлкаем правой кнопкой мыши
на одном из столбиков диаграммы. В
раскрывающемся списке элементов щёлкаем
по кнопке Формат рядов данных. В
появившемся диалоговом окне активизируем
вкладку Параметры и в поле Ширина зазора
устанавливаем значение 0. Нажимаем ОК,
в результате чего гистограмма принимает
стандартный вид.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как построить вариационный ряд в Excel

Вариационный ряд может быть:

— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).

— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.

Рассмотрим пример построения дискретного вариационного ряда.

Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения

Решение.

Алгоритм построения вариационного ряда:

1) Откроем таблицы Excel.

2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.

3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.

4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).

Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.

6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER

Рис.1.2 Пример 1. Построение вариационного ряда

7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.

Построим полигон:

1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).

2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.

Рис.1.3. Пример 1. Построение полигона частот

Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel

Следующая тема: Построение интервального вариационного ряда в Excel.

Источник

Хитрости »

15 Декабрь 2015 41782 просмотров

Ступенчатый график как правило используется для отображения динамики показателей по временным промежуткам. Предположим есть примерно такой отчет по выручке:

Для отражения повышения/понижения выручки за сутки требуется создать такой график:

Построить его можно несколькими способами. В этой статье я хочу рассказать про два из них.
Скачать пример

Tips_Charts_StepChart.xls (56,0 KiB, 3 684 скачиваний)

Способ 1: Применяем планки погрешностей

Для начала потребуется добавить столбец с формулой для погрешностей. Запишем в ячейку с первым значением(на скрине это C2, напротив 1 апр 2015) значение 0, а в следующую ячейку формулу:

=B3-B2

.

Теперь копируем ячейку с формулой, выделяем данные в столбце С, начиная с С3 и до конца данных в таблице и вставляем скопированную формулу. Или можно просто протянуть эту формулу до конца таблицы.
Теперь выделяем первые два столбца таблицы вместе с заголовками(Дата и Выручка) и вставляем новую диаграмму:

Excel 2003:
Вставка(Insert) —Диаграмма(Chart) —Точечная(Scatter) —С прямыми отрезками(Scatter with straight lines)
Excel 2007 и выше:
вкладка Вставка(Insert) -группа Диаграммы(Charts) —Точечная(Scatter) —С прямыми отрезками(Scatter with straight lines):

Далее необходимо добавить планки погрешностей:

Excel 2007-2010:
вкладка Макет(Layout) —Предел/Планки погрешностей(Error Bars) —Дополнительные параметры планок погрешностей(More Error Bars Options…)
Excel 2013
жмем справа от диаграммы кнопку со знаком «плюс» и ставим флажок Предел погрешностей(Error Bars)

Осталось дело за малым: на вкладке Макет(Layout) -группа кнопок Текущий фрагмент(Current Selection) выбираем Планки погрешностей по оси X(X Error Bars) -и сразу жмем там же кнопку Формат выделенного(Format Selection)(расположена сразу под вып.списком).
Указываем следующие параметры:

Направление(Display) —Плюс(Plus);
Конечный стиль(End Style) —Без точки(No Cap);
Величина погрешности(Error Amount) —фиксированное значение(Fixed value) — 1С величиной погрешности для горизонтальных планок чуть подробнее: 1 выбираем, т.к. у нас данные указаны в таблице ежедневные. Т.е. шаг оси между данными получается 1(один день). Если бы данные поступали каждые 20 дней и в таблице они были бы занесены тоже с промежутком через каждые 20 дней — то фиксированное значение необходимо было бы указать 20.

Далее, не закрывая окно свойств ряда идем на вкладку Макет(Layout) -группа кнопок Текущий фрагмент(Current Selection) —Планки погрешностей по оси Y(Y Error Bars). Здесь указываем:

Направление(Display) —Минус(Minus);
Конечный стиль(End Style) —Без точки(No Cap);
Величина погрешности(Error Amount) —пользовательская(Custom). Жмем Укажите значения(Specify Value) и в появившемся окне для Отрицательные значения ошибки(Negative Error Value) указываем столбец с теми формулами, которые записаны у нас в столбце С (в примере C2:C23). Ок. Закрыть.

И пара последних косметических штришков:

Вот график и построен. Остается лишь навести красоту. Например, увеличить ширину линий, изменить цвет. Чтобы увеличить ширину линий можно сразу при установке планок погрешностей после установления основных параметров перейти к свойствам Цвет линии(Line Color)(для задания нужного цвета) и Тип линии(Line Style)(для задания нужной ширины).

Если же не сделали этого сразу, то это можно сделать в любой момент: вкладка Макет(Layout) -группа кнопок Текущий фрагмент(Current Selection) —Планки погрешностей по оси X(X Error Bars). И так для любого ряда.
Так же можно изменить форматы для других элементов диаграммы: область построения, подписи данных и т.д. Сделать это можно, выделив любой из элементов -правая кнопка мыши —Формат «имя элемента»(Format «имя элемента»)
Пример результата графика через погрешности приведен в самом начале статьи.

Способ 2: «Растягиваем» данные

Этот прием основан на том, что стандартные графики строятся на перепадах данных и если значения будут одинаковые — то линия графика будет горизонтальная. Однако нужна и вертикальная и тут как раз и хитрость: мы для каждого дня будем записывать ДВА значения сумм выручки, вместо одного. Тогда мы получим желаемое.
Для этого надо будет выделить два отдельных столбца. В приложенном к статье примере это столбцы D и E. Копируем заголовки и в столбец D(начиная с ячейки D2) записываем формулу:
=ИНДЕКС($A$2:$B$23;ЦЕЛОЕ(СТРОКА()-СТРОКА(A2)/2);1)
=INDEX($A$2:$B$23,INT(ROW()-ROW(A2)/2),1)
в столбец E так же прописываем формулу, но чуть другую:
=ИНДЕКС($A$2:$B$23;ЦЕЛОЕ(СТРОКА(A1)-СТРОКА(B1)/2)+1;2)
=INDEX($A$2:$B$23,INT(ROW(A1)-ROW(B1)/2)+1,2)

Эти формулы надо будет скопировать на количество строк, большее в два раза, чем исходные данные. Как вариант можно протягивать формулу до тех пор, пока формула не вернет значение ошибки #ССЫЛКА!(#REF!). А теперь останется только вставить на основании этих данных диаграмму типа График:

Excel 2003:
Вставка(Insert) —Диаграмма(Chart) —График(Line) —График(Line)
Excel 2007 и выше:
вкладка Вставка(Insert) -группа Диаграммы(Charts) —График(Line) —График(Line)

Все, график готов. Теперь останется так же как и в первом способе навести при необходимости красоту на свое усмотрение через изменение свойств элементов диаграммы.

Статья помогла? Поделись ссылкой с друзьями!

Видеоуроки

Поиск по меткам

Access
apple watch
Multex
Power Query и Power BI
VBA управление кодами
Бесплатные надстройки
Дата и время
Записки
ИП
Надстройки
Печать
Политика Конфиденциальности
Почта
Программы
Работа с приложениями
Разработка приложений
Росстат
Тренинги и вебинары
Финансовые
Форматирование
Функции Excel
акции MulTEx
ссылки
статистика

Источник