Построение модели «Циклоида» в среде MS Excel, описывающей процесс вращения колеса с учетом различных факторов для проведения компьютерного эксперимента на уроках информатики и физики
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Сиврюк В.С. 1
1МБОУ СОШ №13 г. Белгорода
Лебедева Т.Ю. 1Новогрудская О.П. 1
1МБОУ СОШ №13 г. Белгорода
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
В наш бурный 21 век мы редко задумываемся над тем, что значит слово – изобретение. Новые идеи и новые технологии внедряются в практику, новшества устаревают так быстро, что о многих из них мы забываем, едва успев к ним привыкнуть.
Но есть изобретения, которые не устареют никогда. К ним относится самое обычное, известное всем с раннего детства колесо. Оно является великим и древнейшим изобретением человечества.
Колесо – одно из важнейших открытий человечества в области механики. История колеса, по определению ученых-историков, начиналась еще в бронзовом веке. Первый датированный документ об использовании колеса для перевозки – месопотамская мозаика (3200 г. до н.э.). Вот только предназначалось оно не для транспортировки. Его использовали в бытовых целях.
Н а протяжении многих веков человечество использует для изготовления различных керамических приспособлений глину. Вместе с тем, раньше в далекой истории практически в каждом доме стоял гончарный круг, колесо. Без него глина так и осталась бы просто природным материалом. До сих пор остается непонятным, что из них было придумано первым – гончарный каменный круг, имеющий форму колеса, положенного горизонтально, или колесо в повозке для передвижения. Изобретение гончарного круга по времени также относится к бронзовому веку. Параллельно колесо начали использовать для изготовления посуды из глины и в Древнем Египте, через несколько сотен лет египтяне даже стали делать посуду на быстро вращающихся кругах, что повлияло на разнообразие формообразования древней посуды и ее качество.
Д авным-давно для перемещения громоздких грузов на относительно большие расстояния использовались обычные бревна. На первый взгляд, революционный по тем временам способ, но у него был один существенный недостаток – требовалось подкладывать под бревна много каменных роликов, небольших колес. При этом они все время выскальзывали из-под бревен. Но древние люди решили эту проблему – они соорудили специальную платформу из досок. Им удалось закрепить на ней ролики таким образом, что давящий сверху груз не выталкивал их из-под досок, а, наоборот, прижимал к земле.
Еще через 1500 лет наши предки оснастили колесо деревянными спицами. На такой шаг их подтолкнула военная необходимость. Не удивительно, что первыми, кто использовал колесо с деревянными спицами, были египтяне. Произошло это примерно в 2000 г. до нашей эры. Они применили его в своих знаменитых колесницах.
А вот идея заключить колеса в металлические обода и тем самым уберечь их от быстрого износа, принадлежит кельтам. В 1000 г. до н.э. они оснастили такими усовершенствованными колесами свои колесницы. Примечательно, что колеса, оснащенные спицами из дерева, оставались неизменными аж до начала 19 в. В то время изобретатель Ф. Бауэр запатентовал первые спицы, изготовленные из металла. Он просто взял длинную проволоку, продел ее много раз через обод колеса и закрепил на обоих концах ступицы. Классическим примером его изобретения является велосипедное колесо.
Следующим прорывом в эволюции колеса стало изобретение шины. Идея ее создания принадлежит У.Томпсону, свое изобретение он запатентовал в 1845 г. Однако, в 1888 г. его разработку усовершенствовал шотландский ветеринар Д. Данлоп. Для изготовления шин он использовал твердую резину.
П остепенно колесо стали применять и в других устройствах. Со временем оно нашло свое применение для водяных устройств. Использовались два вида таких колес: подливное (для медленно текущих рек) и наливное (на быстрых горных речках). При строительстве люди стали пользоваться грузоподъемным блоком, основу которого также составляет колесо. Позднее колесо нашло еще одно применение – для прядения шерсти была создана прялка. По историческим данным, она была изобретена около 1 тыс. до н. э. в Индии и близлежащих районах Азии.
Проблемная ситуация. В этом учебном году мне предстоит сдавать ОГЭ по математике и информатике, в ходе освоения которой важнейшим разделом является «Моделирование в электронных таблицах». Знания школьников проверяются в задании №14 КИМ ОГЭ по информатике на самом экзамене. Кроме того, эта программа пригодится мне в будущей профессии для проведения расчетов, составления таблиц и диаграмм. Для того, чтобы лучше разобраться и понять суть этой программы, узнать ее новые функции, я решила создать компьютерную модель физического процесса.
Цель проекта: создать компьютерную модель в среде электронных таблиц, для наглядного восприятия движения колеса и проведения компьютерного эксперимента на уроках информатики и физики.
Способ достижения цели (задачи).
Постановка задачи.
Оценка информации и выбор плана создания модели.
Создание компьютерной модели в электронной таблице.
Контрольный расчет (проверка адекватности модели).
Вычисленный эксперимент и интерпретация результатов (получение решения задачи при помощи модели)
Провести занятия в 9-10 классах с использованием компьютерной модели (в том числе в рамках наставничества).
Начать работу над формированием пополняемый банк моделей физических процессов.
Результат проекта.
Разработана компьютерная модель движения колеса, в электронной таблице для практических занятий по информатике при изучении темы «Моделирование в электронных таблицах» в 9 классе.
Учащиеся смогут получить в динамике наглядные запоминающиеся иллюстрации физических экспериментов и явлений, воспроизвести их тонкие детали, которые могут ускользать при наблюдении реальных экспериментов.
Повысится мотивация к изучению урока информатики.
Критерии приемки результата проекта.
Компьютерная модель содержит практический материал для 9, 10 классов.
Материал разбит по степени сложности.
Модель достаточно наглядна.
В каждом классе проведены не менее 2-х занятий с использованием компьютерной модели.
Пользователи результата проекта: обучающиеся, учителя информатики, физики.
Основная часть
Это древнее изобретение человечества имеет некоторые тайны. Кроме того, оказывается, что его модель может быть применена к объекту, который весьма отличается от колеса как по внешнему виду, так и по некоторым свойствам. Построенная модель объяснит эти странные свойства. С каким объектом может быть связано колесо? Попробуем это установить путем моделирования.
1 этап. Постановказадачи. Что собой представляет колесо? Это плоский диск в форме цилиндра. Оно сплошное, жёсткое, идеально круглое. Что делает колесо? Катится по ровной горизонтальной поверхности равномерно без проскальзывания и трения.
2 этап. Создание формализованноймодели.
И спользуем чертёж. Пусть начало координат находится там, где в начале отсчёта времени находился центр колеса. Допустим, что колесо катится вправо без проскальзывания. Скорость, с которой центр колеса перемещается вперёд, равна V0 . Радиус колеса R0. Рассматривать будем точку А, отстоящую от центра колеса на расстоянии r. Существенные параметры: радиус; скорость перемещения оси в горизонтальном положении.
Положение материальной точки в пространстве описывается координатами. При вращательном движенииизменяютсядвекоординатыхиy.Свяжемкоординатысрадиусомокружности,покоторой движетсяточка.
Д вижение точки А можно разбить на два – вращательное (вокруг оси) и поступательное (вместе с осью колеса). Скорость вращения колеса через скорость поступательного движения вперёд V0 и его радиус R0:
Для ее координат можно записать уравнения:
Эта пара уравнений, которая выражает координаты одной точки через набор коэффициентов и параметр, называется уравнением, заданным в параметрической форме, или параметрическим уравнением.
3 этап. Создание компьютерной модели. Компьютерныйэксперимент.
|
A |
B |
C |
|
|
1 |
Траектория точки колеса |
||
|
2 |
Скорость качения Vo |
2 |
|
|
3 |
Угловая скорость |
= V0/R0 |
|
|
4 |
Радиус колеса Rо |
1 |
|
|
5 |
Расстояние до точки r |
1 |
|
|
6 |
Время |
x |
y |
|
7 |
0 |
=V*A8+Rt*SIN(W*A8) |
=Rt*COS(W*A8) |
|
8 |
0,1 |
=V*A9+Rt*SIN(W*A9) |
=Rt*COS(W*A9) |
Получили такую табличную модель, на основе которой построим график для проведения эксперимента и исследования.
Такая кривая имеет имя – ЦИКЛОИДА.
4 этап. Анализ и корректировкамодели
Увеличив скорость до 10, получили график. Он выглядит не гладким ,а угловатым. Картинка искажена.
Почему это происходит, ведь колесо осталось круглым? Происходит это потому, что точки, в которых вычисляется траектория, стоят слишком редко и не попадают на период кривой, который уменьшился в 10 раз. Еще увеличив скорость колеса, мы получили кривую которая теряет периодичность.
Рассмотрев случай, когда расстояние r (от точки до центра колеса) становится больше радиуса колеса, получили следующую кривую, на которой появляется петелька.
Кактакоеможетбыть?Этопроисходит,еслиуколесаестьвыступ.Например,уколесапоездаили колеса трамвая. С помощью такого выступа колесо «цепляется» за рельс и вагон не соскакивает с дороги. Значит, точки на выступе в какой-то момент начинают ехать «назад» по отношению к оси колеса. Это движение назад тем заметнее, чем больше радиус выступа. Например, при r = 3 мывидим такую картину: почти четверть оборота точка едетназад!
Рассмотрим полученный график «вверх ногами».
На что это похоже? Выходит наша модель – ЦИКЛОИДА описывает ещё один объект – морское волнение.
Описание процесса создания модели в MSExcel
1 . Подготовка области определения и области значения с использованием формул, записанных на формальном языке физики:
2. Построение точечной диаграммы, демонстрирующей визуальное представление графика движения точки А, находящейся ниже обода колеса:
3. Проведение эксперимента, связанного с изменением угловой скорости, радиуса колеса и расстояния до точки А:
3 .1
3 .2
3 .3
3 .4
Заключение
В результате проделанной работы была построена физическая компьютерная модель движения колеса в среде электронных таблиц, проведен компьютерный эксперимент для дальнейшего использования на уроках информатики и физики и во внеурочное время.
Был сделан интересный вывод о том, что одна и та же модель может описывать как движение точки, расположенной на разном удалении от центра, так и волновые процессы.
Наша модель – ЦИКЛОИДА описывает ещё один объект – морское волнение.
Список использованных источников и литературы
Печатные источники
1. Медведьев Л.Н. Модель колеса./ «В мир информатики» №№ 62, 66, 70, 71), «Информатика» №1/ 2005, № 5/2006, № 6/2006, № 23/ 2006).
2. Бешенков С.А., Ракитина Е.А. Моделирование и формализация. Методическое пособие. М.: Бином. Лаборатория Знаний, 2002.
3. Энциклопедия для детей. Математика. Том 11. – М.: Аванта+, 2001.
Интернет-источники
1. Великое изобретение или история колеса | Контент-платформа Pandia.ru
Просмотров работы: 656
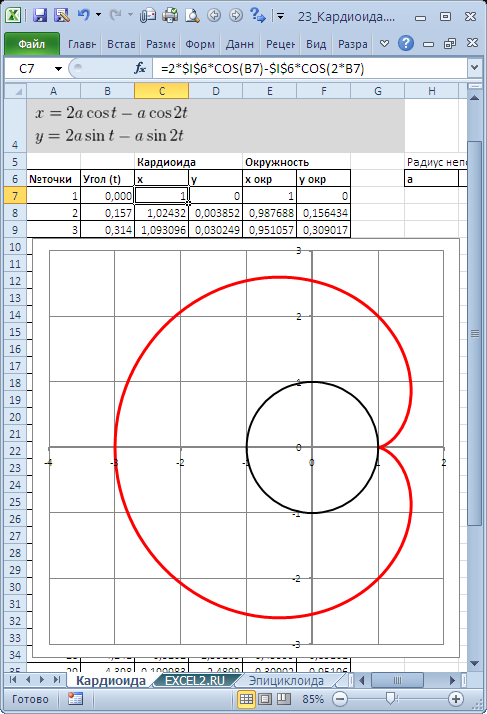
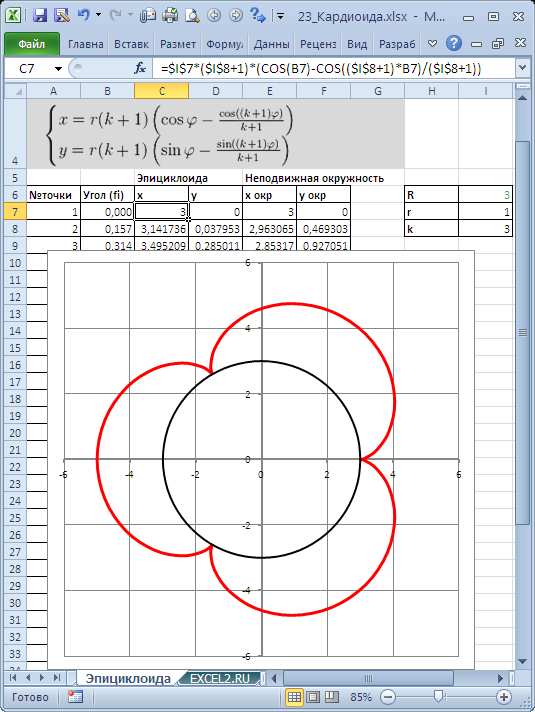
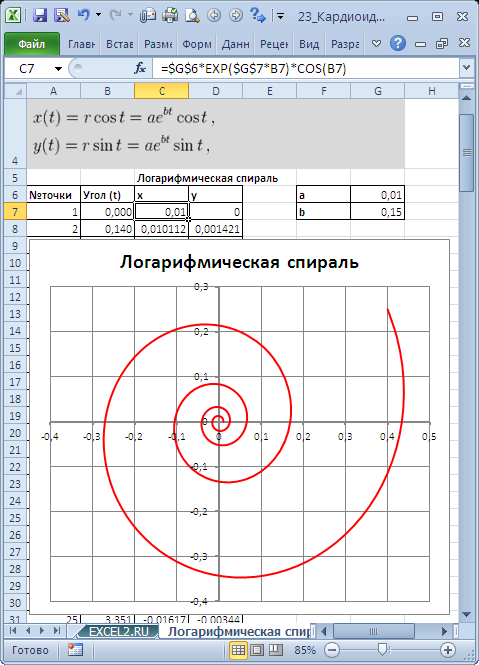
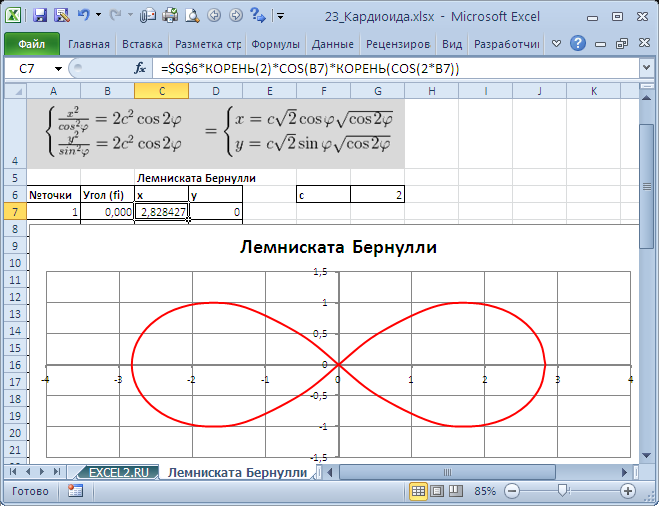
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см.
файл примера
):
х=2*а*cos(t)-а*cos(2*t)
y=2*а*sin(t)-а*sin(2*t)
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье
Эллипс и окружность в MS EXCEL
построены окружность и эллипс.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Построение
графиков 3-х видов в электронной таблице
Excel
1.
Построить несколько графиков параметрически
заданной функции при разных значениях
конcтант
а, b,
.
Оси графика – х и y,
которые зависят от аргумента t
или .
|
№ |
Название кривой |
Вид |
Параметрические |
Диапазон аргумента |
Кол-во граф. |
Значения |
|
1 |
Циклоида |
|
x = a(t — sin
y = a(1 — cos |
t 0 6
шаг |
5 |
a = 1; |
|
2 |
Циклоида |
|
x = a(t — sin
y = a(1 — cos |
t 0 6
шаг |
6 |
a = 2
= 0.4; |
|
3 |
Трохоида |
|
x = at — bsin
y = a — bcos |
t 0 10
шаг |
5 |
a = -1
b |
|
4 |
Эпитрохоида |
|
x = acos
y = asin |
t 0 10
шаг |
6 |
a = 0;
b = 2 |
|
5 |
Гипотрохоида |
|
x = acos
y = asin |
t 0 10
шаг |
6 |
a = 0;
b = 2 |
|
6 |
Декартов лист |
|
x = at / (1 + t3)
y = a |
t -6 6
шаг |
6 |
a = 1; |
|
7 |
Циссоида |
|
x = a
y = a |
t -6 6
шаг |
6 |
a = 1; |
|
8 |
Строфоида |
|
x = a y = at(t2 — 1) / (t2 + 1) |
t -6 6
шаг |
6 |
a = 1; |
|
9 |
Конхоида Никомеда |
|
x = a + bcos
y = atg |
t 0
шаг |
5 |
a = 2
b |
|
10 |
Улитка Паскаля |
|
x = acos2
y = a |
t 0 2
шаг |
6 |
a = 1; b |
|
11 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a
b = 1; |
|
12 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 10
Шаг |
6 |
a = 3;
= 0.5; |
|
13 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a = 1;
= 0.5; |
|
14 |
Эпициклоида |
|
x = (a + b)cos
y = (a + b) |
0 2
Шаг |
6 |
a = 7;
= 0.5; |
|
15 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 2
Шаг |
6 |
a
b = 1.5; |
|
16 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 6
Шаг |
6 |
a b = 1 |
|
17 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 2
Шаг |
6 |
a = 1;
= 0.5; |
|
18 |
Гипоциклоида |
|
x = (b — a)cos
y = (b — a) |
0 10
Шаг |
6 |
a = 5;
= 0.2; |
|
19 |
Спираль |
|
x = atcos
y = btsin |
t 0 10
Шаг |
6 |
a
b = -2; |
|
20 |
Гиперболич. спираль |
|
x = (acos
y = (b |
t -6 6
Шаг |
5 |
a = 2
b = 1; |
|
21 |
Гиперболич. спираль |
|
x = (acos
y = (b |
t 0.5 20
Шаг |
5 |
a = 3
b = 1; |
|
22 |
Астроида |
|
x = acos3
y = b |
t 0 8
Шаг |
5 |
a
b = 1; |
|
23 |
Астроида |
|
x = acos3
y = a |
t 0 8
Шаг |
5 |
a
b = 0; |
|
24 |
Астроида |
|
x = acos3
y = a |
t 0 8
Шаг |
5 |
a
b = 0.5; |
|
25 |
Эвольвента |
|
x = acos
y = a |
t -10 10
Шаг |
4 |
a |
|
26 |
Эвольвента |
|
x = acos
y = a |
t 0 20
Шаг |
4 |
a |
|
27 |
Эллипс |
|
x = acos
y = b |
t 0 2
Шаг |
5 |
a
b = 1; |
|
28 |
Эллипс |
|
x = acos(c
y = b |
t 0 2
Шаг |
5 |
a
b = 1; |
|
29 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Может ли Excel строить сложные кривые?
|
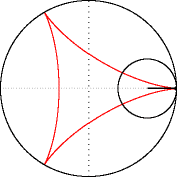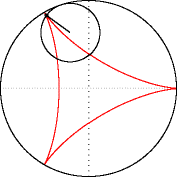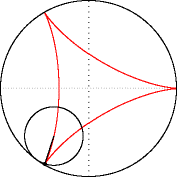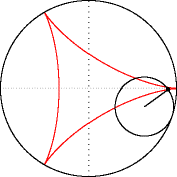
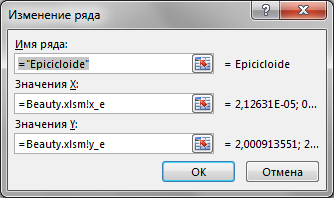
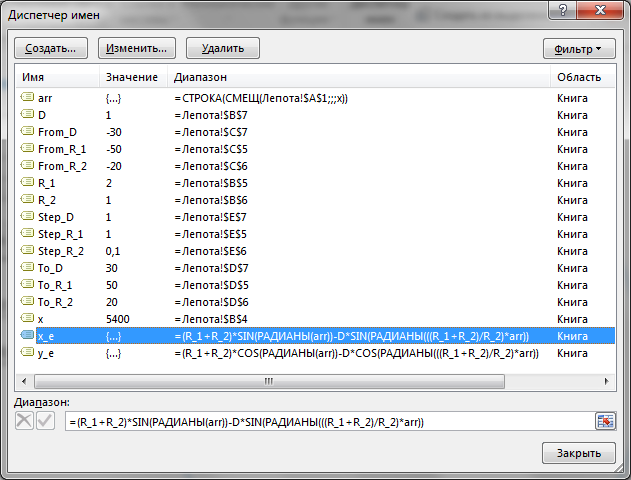
Меня трудно чем-то удивить в Excel, но когда я впервые увидел вот этот сайт, то у меня чуть глаз не выпал на клавиатуру. Очень рекомендую вам пройти по ссылке и поглазеть. В моём личном рейтинге эта команда (там двое мужчин и девушка) является №1 в мире по Excel. Сегодня я вам покажу нечто из их арсенала (с моими некоторыми адаптациями). Посмотрим на то, как при помощи точечной диаграммы с гладкими кривыми строить ТАКИЕ сложные вещи, что, когда глядишь на это в первый раз, просто не веришь, что это вообще можно нарисовать в Excel. Ну, например, как вам это: Дело в том, что мы все привыкли, что такие графики строятся по точкам, которые рассчитываются в ячейках таблицы. Тут же используется реально очень крутой трюк, который позволяет строить графики любых сложнейших функций, не используя ни диапазоны с точками XY, ни какие-либо макросы. Всё что вам нужно — это точечная диаграмма с гладкими кривыми, несколько констант и несколько именованных формул. Те граждане, кто пока плохо понимает, зачем это всё надо, сейчас просто откроют файлик, включат макросы и нажмут кнопку Старт, потому что это ПРОСТО КРАСИВО. На это можно смотреть минут 15 и всё равно будет интересно. Дольше смотреть не рекомендую, так как глаза и мозг устанут. Смотреть красоту ТУТА с теми, кому интересно, как это устроено, продолжаем разговор. В принципе абсолютно без разницы, какой график строить. Я взял циклоидальные кривые, так как они очень красивы, разнообразны и сложны. Эпициклоиды и гипоциклоиды (подмножество циклоидальных кривых) строятся по следующим параметрическим формулам: Эпициклоиды строятся так: Гипоциклоиды так: Знаки у R1 и R2 относительно друг друга определяют тип кривой (по какой поверхности круга R1 — по внутренней или внешней — будет катиться круг R2). Обратите внимание, что t — это угод в радианах. Напоминаю, что углы в 5′ и 365′ — разные углы. Если мы заглянем в ряды данных диаграммы, то увидим это: Сердце решения располагается тут: Как видите, большинство именованных диапазонов просто сылаются на конкретные ячейки и ничего сложного из себя не представляют. Кроме трёх диапазонов: arr, x_e, y_e. Можно заметить, что x_e и y_e — это то, на что ссылается ряд данных в диаграмме, и, что это формулы, описывающие кривые, которые я приводил выше. А вот ИД arr надо осмыслить: =СТРОКА( СМЕЩ( Лепота!$A$1; ; ; x) )X у нас равен 5400. Функция СМЕЩ() сформирует диапазон A1:A5400. А формула СТРОКА() будет вычислена для каждой строки данного диапазона, поэтому в результате мы получим массив чисел от 1 до 5400. Этот массив, будучи переданным в x_e, y_e тоже породит соответствующие массивы. Обратите внимание, что arr пропускается через функцию РАДИАНЫ(). Таким образом мы градусы (1..5400) переводим в радианы. Если честно, то я не знал, что ТАК можно Вот собственно и всё. А тот макрос, который у меня есть в книге, он просто случайным образом, но плавно меняет параметры R1, R2, D в пределах от From до To с шагом Step. P.S. Любителям WinAPI с его Sleep рекомендую обратить внимание на конструкцию Application.Wait Now + 1 / 24 / 60 / 60 / 2 Ну а теперь залипайте дальше на лицезрение циклоид |
Категория: Графики и диаграммы | Добавил: dsb75 (18.09.2015) |
| Просмотров: 13711 | Комментарии: 13 | Теги: гипоциклоиды, именованные диапазоны, Диаграммы, циклоиды, СМЕЩ, эпициклоиды | Рейтинг: 4.3/6 |
| Всего комментариев: 12 | |
|
Порядок вывода комментариев: Здравствуйте, Денис. 1. Вообще-то, X = R * cos (t); Y = R * sin (t). В вашем примере оси X и Y перепутаны местами, если брать за основу картинку из статьи, циклоида на диаграмме строится от вертикальной оси против часовой стрелки. Попробуйте ввести на листе разные значения угла, меньше 360 (45, 90, 180, 270) — увидите, о чём я. На красоту не влияет, конечно. 2. Попробуйте ставить в ячейку х значения 1 и 5400 и сохранять книгу, размер файла изменится в несколько раз. Диапазоны значений не хранятся на листе, но диаграмма хранит весь диапазон значений в файле. Для уменьшения размера можно кодом VBA присваивать x 5400 после открытия и 1 перед закрытием. 3. Ни в одной из статей вашего сайта нет ни одного вызова Windows API, да и фраза «Любителям WinAPI с его Sleep» позволяет предположить, что сами вы к его любителям не относитесь. Можно полюбопытствовать, откуда у вас такое принципиальное (практически — религиозное Для корректности сравнения скоростей из вашего кода выкинуты строки: Код ActiveSheet.Calculate ‘ не нужна, если есть DoEvents Application.Wait Now + 1 / 24 / 60 / 60 / 2 ‘ просто не нужна На всякий случай: комментарий категорически не является насмешкой или наездом, у вас отличный сайт и редкие педагогические способности, статьи, написанные столь доходчивым языком редко где найдёшь.
Спасибо за содержательный комментарий. Успехов вам! Использование Sleep вместо Application.Wait является шагом вперёд, осознанным или нет — второй вопрос. При выполнении програмной задержки состояние приложения можно разделить: — по загрузке процессора: грузит / не грузит; Так вот, Application.Wait находится в худшем из четырёх возможных сочетаний этих состояний. Пусть надо выполнить програмную задержку dDelay сек. Тогда варианты: ‘ вариант 0: не реагирует на события, загрузка процессора (в современном мире — одного из ядер) — 100% ‘ вариант 1: не реагирует на события, загрузка процессора — 0% ‘ вариант 2: реагирует на события, загрузка процессора — 100% ‘ вариант 3: сочетает достоинства и недостатки двух предыдущих, (не мгновенно) реагирует на события, загрузка процессора — больше 0% Ни один из этих вариантов не является идеальным с точки зрения потоков, обработки сообщений, машинного времени и пр.
Долгая история
Давайте, о себе любимом напишу подробно позже и в почту. Пока в догонку об убогости Application.Wait: https://yadi.sk/i/7NQT-OFN3Kv2BK Коротко: Application.Wait не предназначен для организации задержек, не кратных 1 сек., в частности — менее 1 сек. Поэтому он у вас в Beauty на самом деле не работал, можно было апостроф в начале строки не ставить
Ещё раз про морковь или возвращаясь к непечатному. Доброго здоровья, Денис. Глядя на процедуру расчёта и вывода циклоиды (Sub DrawCycloide) я задался вопросом: какую часть времени занимает расчёт значений для её вывода, а какую — собственно, графический вывод. Профилировать процедуру напрямую по таймеру в контрольных точках смысла не имело: слишком маленькие интервалы приведут к слишком большим погрешностям. Поэтому решено было нивелировать (свести к нулю) время расчёта, чтобы осталось только время, занимаемое графическим выводом. Как нивелировать? Перевести в машинный код, естественно 1. Первым делом к ранее выложенному здесь Beauty free.xlsm был прикручен «спидометр» — код, отображающий на форме количество выводимых циклоид в секунду. 2. Далее, через экспорт-импорт, форма из книги Beauty free speed.xlsm была перемещена в «классический» проект VB. Что понравилось: форма встала в проект VB сразу «как влитая», никаких допиливаний и танцев с бубном не понадобилось. Естественно, ссылки на ячейки рабочего листа заменены константами. 3. Наконец, была проведена переработка проекта с целью замены объекта UserForm VBA объектом Form VB: 4. И её дальнейшая оптимизация: Примечания. Итоги. Практический вывод. P. S. Всё вышенаписанное стоило писать месяца полтора назад. Руки дошли только сейчас, однако. |
|
Добавлять комментарии могут только зарегистрированные пользователи.
[
Регистрация
|
Вход
]
Коткова Лидия Леонидовна
учитель информатики
ГОУ СОШ № 728 г.Москвы
Урок по теме «Моделирование физического процесса.Циклоида»
Цель: формирование умения построения графической модели в Excel .
Необходимые знания и умения к данному уроку.
Учащиеся должны знать понятия моделирования, модели, формы информационных моделей. Уметь в электронной таблице Excel заполнять ячейки, работать с формулами, строить диаграммы.
- Организационный момент.
- Постановка задачи.
- Эксперимент.
- Историческая справка о циклоиде.
- Практическая работа: построение графика кривой в Excel .
- Повторение.
- Задание на дом.
1. Организационный момент (учащиеся сидят за партами). Мы продолжаем изучение темы моделирование. Напомните, что означает моделирование, что называется моделью? Сегодня вы будете строить графическую модель, но сначала вспомним, какие графические модели нам известны? (графы, графики, чертежи, схемы и т.д.).
2. Постановка задачи. Возьмём колесо, обруч, круг. Зафиксируем точку круга. Будем катить круг по прямой. Какую кривую опишет зафиксированная точка круга? Следите внимательно за траекторией точки (в большинстве учащиеся отвечают, что точка опишет окружность , но кто-то догадается и скажет, что точка опишет дугу ).
У читель показывает на большом экране :
( нажмите кнопку «Движение» )
3. Эксперимент. Проверим наше предположение. Прикрепим к обручу или кругу кусок мела и покатим вдоль стены, мел будет вычерчивать «кругообразную» кривую, называемую циклоидой . Одному обороту обруча соответствует одна «арка» циклоиды, если обруч будет катиться дальше, то будут получаться еще и еще арки той же циклоиды.
У читель показывает на большом экране :
( нажмите кнопку «Движение» )
4. Историческая справка о циклоиде. Первым из учёных обратил внимание на циклоиду Николай Кузанский в XV веке, но серьёзное исследование этой кривой началось только в XVII веке. Название циклоида придумал Галилей (во Франции эту кривую сначала называли рулеттой). Содержательное исследование циклоиды провёл современник Галилея Мерсенн.
Паскаль писал о циклоиде: « … является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.».
Эта кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Бернулли и другие корифеи науки XVII—XVIII веков.
Циклоида имеет ряд удивительных свойств:
ü «Перевёрнутая» циклоида является кривой скорейшего спуска. Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.
ü Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов.
Итак, циклоида — плоская кривая, описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой.
Координаты точки окружности в данный момент времени вычисляются по формулам:
x = a ( t — sin t ) ,
y = a (1- cos t ) ,
где а — радиус окружности.
Обратите внимание на то, как надо правильно ввести формулу (это для ячейки В2).
6. Повторение. Итак, вы сегодня построили графическую модель кривой, которую описывает некоторая точка окружности, катящейся без скольжения по неподвижной прямой.
ü Как называется эта к ривая?
ü Какие интересные свойства циклоиды вы запомнили?
ü Предположем, что катится гимнастический обруч. Внешняя и внутренняя точки обруча будут описывать одинаковые кривые?
7. Домашнее задание . Поищите в справочниках, интернете, какие существуют ещё интересные кривые. Модели каких кривых мы можем построить в электронной таблице Excel ?
Циклоида как построить в excel
0 Спам
Ещё раз про морковь или возвращаясь к непечатному. Доброго здоровья, Денис.
Глядя на процедуру расчёта и вывода циклоиды (Sub DrawCycloide) я задался вопросом: какую часть времени занимает расчёт значений для её вывода, а какую — собственно, графический вывод. Профилировать процедуру напрямую по таймеру в контрольных точках смысла не имело: слишком маленькие интервалы приведут к слишком большим погрешностям. Поэтому решено было нивелировать (свести к нулю) время расчёта, чтобы осталось только время, занимаемое графическим выводом. Как нивелировать? Перевести в машинный код, естественно . Но всё по порядку.
1. Первым делом к ранее выложенному здесь Beauty free.xlsm был прикручен «спидометр» — код, отображающий на форме количество выводимых циклоид в секунду.
Результат здесь: https://yadi.sk/i/EtolJiGL3LhgpJ
2. Далее, через экспорт-импорт, форма из книги Beauty free speed.xlsm была перемещена в «классический» проект VB. Что понравилось: форма встала в проект VB сразу «как влитая», никаких допиливаний и танцев с бубном не понадобилось. Естественно, ссылки на ячейки рабочего листа заменены константами.
Исходник: https://yadi.sk/d/YsNL93Ph3MxWPV
Результат: https://yadi.sk/d/T3u021U-3MxWRv
3. Наконец, была проведена переработка проекта с целью замены объекта UserForm VBA объектом Form VB:
Исходник: https://yadi.sk/d/KCgRKEN33MxYGC
Результат: https://yadi.sk/d/6Odb1BKA3MxYHB
Примечания.
1. Шаги 3 и 4 не имеют отношения к поднятому вопросу, но, раз были проделаны — решил выложить
2. Если у вас нет установленного VB, можно сразу смотреть результаты, вирусов в них нет
Итоги.
Преимущество в скорости компилятора над интерпретатором в доказательствах не нуждалось, вопрос был в количественной оценке. Считая, что время графического вывода в любом случае превалирует над временем расчёта, ожидал прироста быстродействия в 20%-30%. После запуска откомпилированного на шаге 2 проекта получил прирост в скорости в 2,5 раза на своей системе. Медленно: в два с половиной раза. То есть, в коде книги Excel расчёт шёл, примерно, в 1,5 раза дольше вывода. Во сколько именно раз поднялась скорость вычислений данные действия не показывают, но, оценочно — в 8 — 10 раз.
Практический вывод.
Если ваш код VBA содержит сложные расчёты — вынести их в отдельную внешнюю процедуру, подключаемую как DLL или OCX ещё как имеет смысл.
P. S. Всё вышенаписанное стоило писать месяца полтора назад. Руки дошли только сейчас, однако.
0
Аналогично


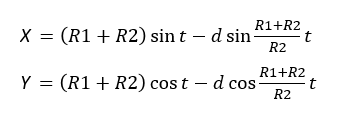
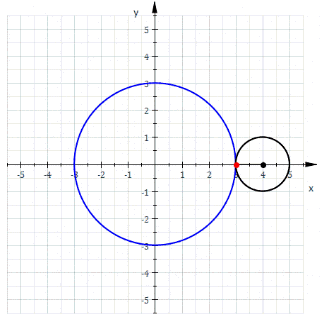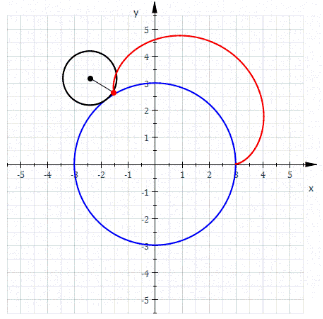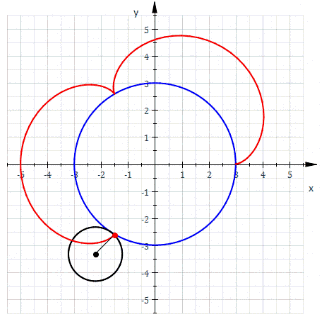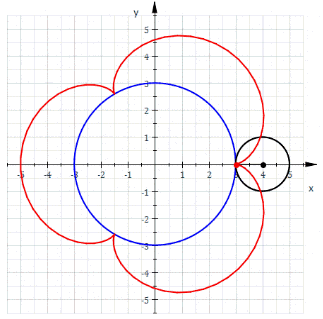

 Зачем делать столь глубокие выводы на единичных фактах? Я дурачился. Но вы правы в том, что WinAPI я не знаю, но никаких религиозных запретов на этой почве перед собой не воздвигаю. Просто часто sleep — единственное, что видишь у VBA-шников, но в Excel особой необходимости в нем нет. То есть, если вам нужно сделать паузу, то нефиг городить огород с winapi. Файл ваш посмотрел — офигенно. Дома посмотрю подробнее. Вот для этого и winapi не грех применять
Зачем делать столь глубокие выводы на единичных фактах? Я дурачился. Но вы правы в том, что WinAPI я не знаю, но никаких религиозных запретов на этой почве перед собой не воздвигаю. Просто часто sleep — единственное, что видишь у VBA-шников, но в Excel особой необходимости в нем нет. То есть, если вам нужно сделать паузу, то нефиг городить огород с winapi. Файл ваш посмотрел — офигенно. Дома посмотрю подробнее. Вот для этого и winapi не грех применять  , так что лучше прочитать её «по диагонали» и никогда так не делать.
, так что лучше прочитать её «по диагонали» и никогда так не делать. 