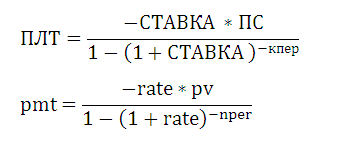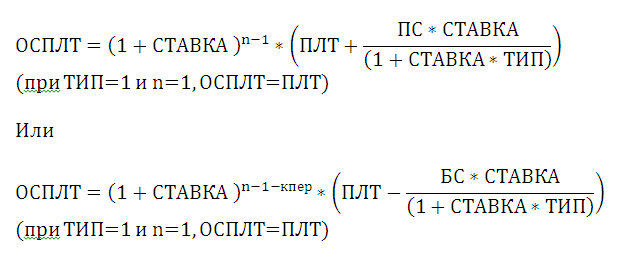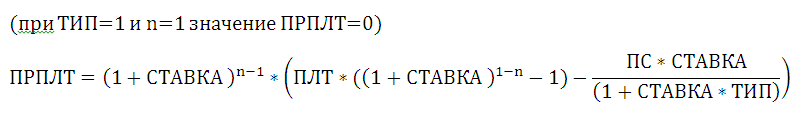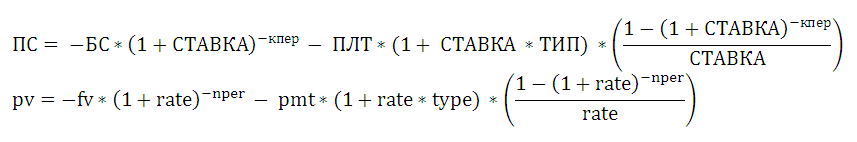Как посчитать в excel по аннуитету

Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).

Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

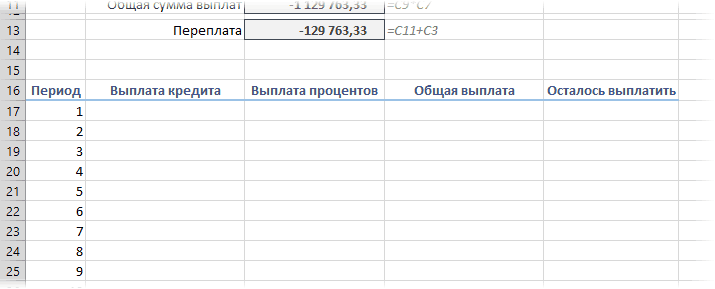
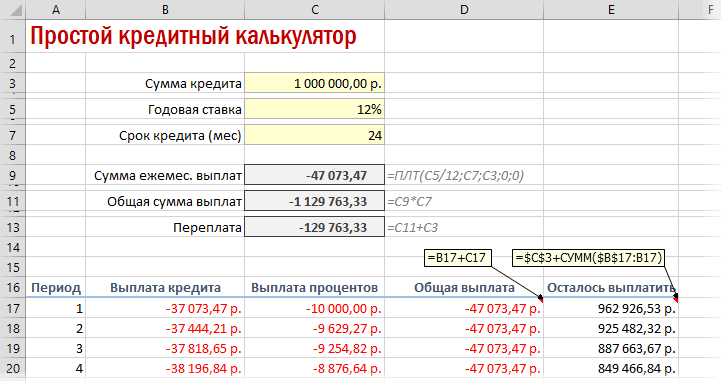
А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

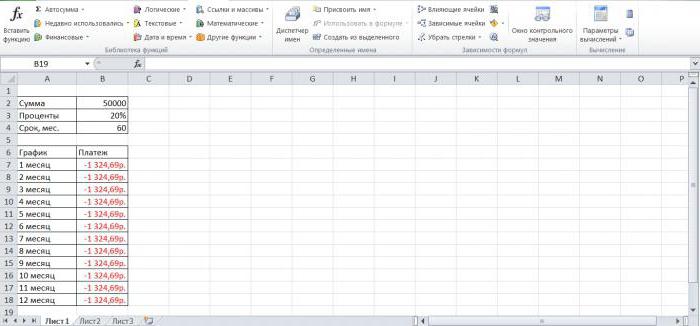
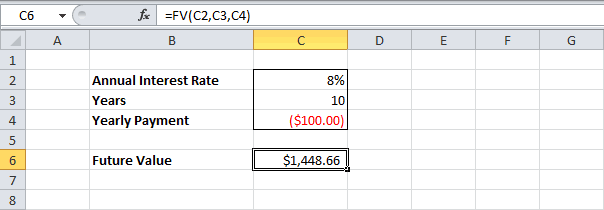
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

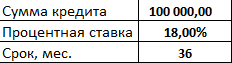
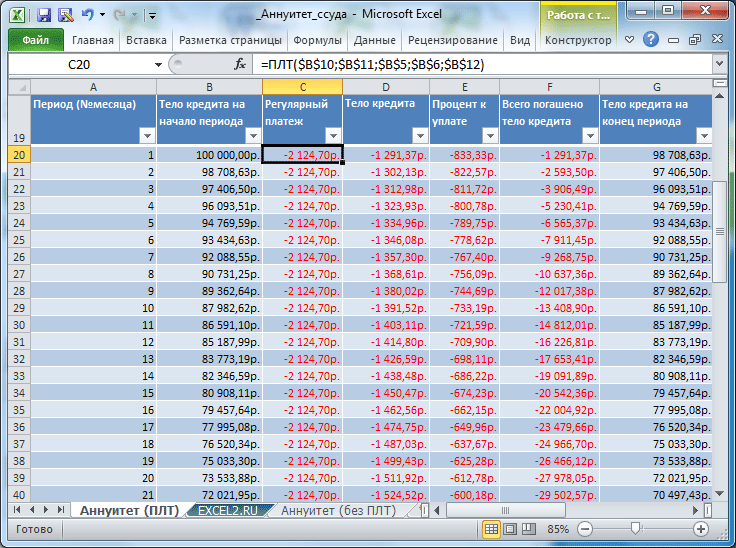
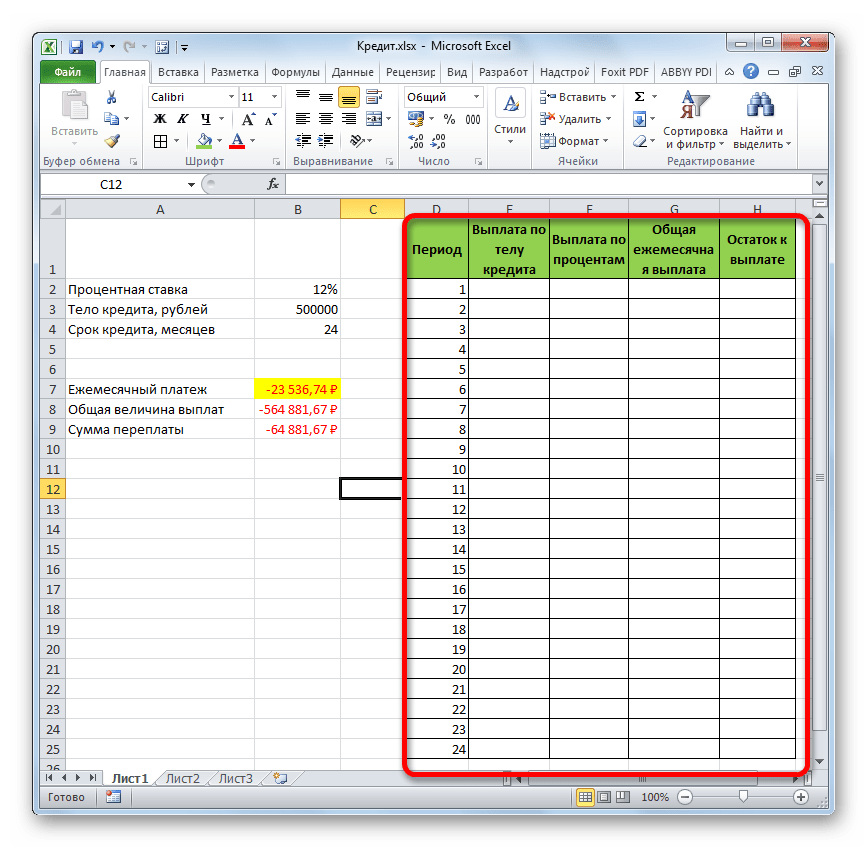
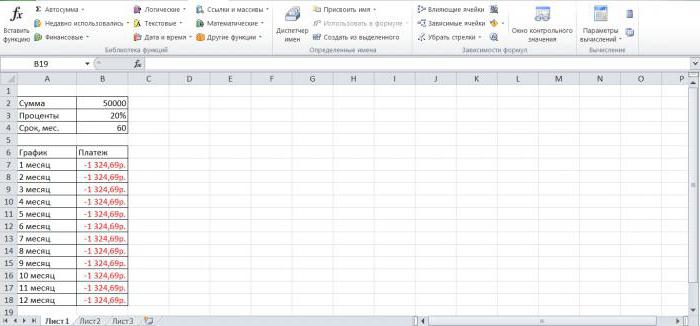
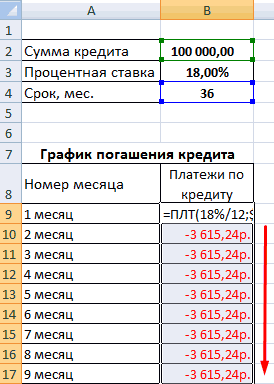
1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.



2. Составим график погашения кредита. Пока пустой.



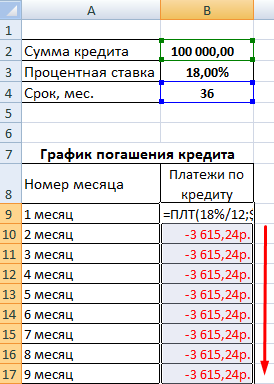
3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.



Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

Составим график погашения займа:

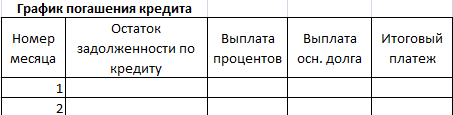
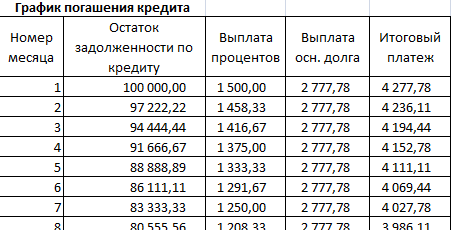
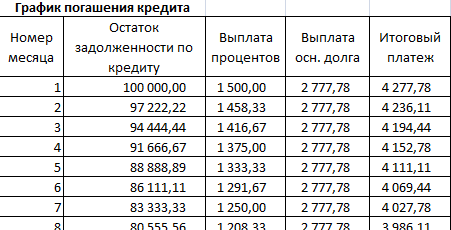
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

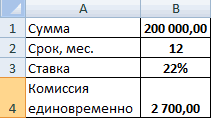
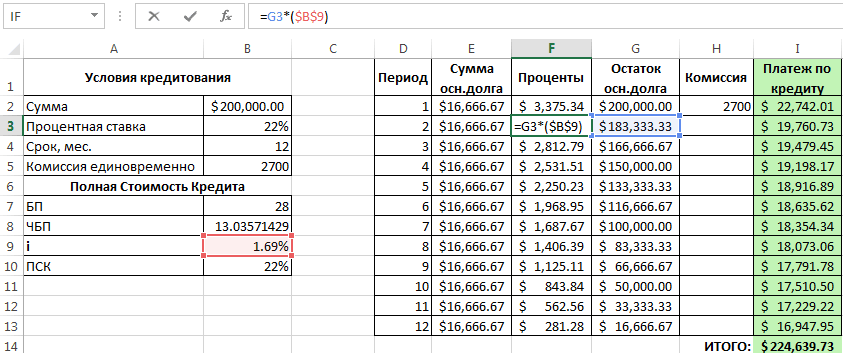
Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

• взяли кредит 500 000 руб.;
• вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
• переплата составила 184 881, 67 руб.;
• процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
• Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

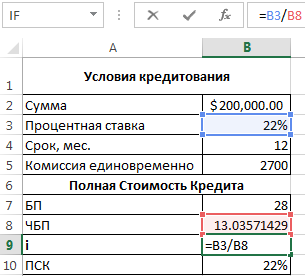
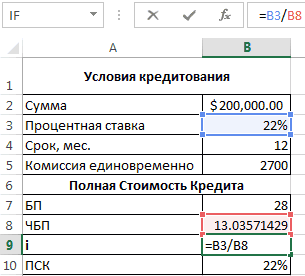
Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:

• ПСК = i * ЧБП * 100;
• где i – процентная ставка базового периода;
• ЧБП – число базовых периодов в календарном году.

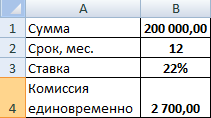
Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.

Далее находим ЧБП: 365 / 28 = 13.

Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Скачать кредитный калькулятор в Excel

Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.

Рассчитаем в

MS

EXCEL

сумму регулярного аннуитетного платежа при погашении ссуды. Сделаем это как с использованием функции

ПЛТ()

, так и впрямую по формуле аннуитетов. Также составим таблицу ежемесячных платежей с расшифровкой оставшейся части долга и начисленных процентов.

При кредитовании банки наряду с

дифференцированными платежами

часто используют

аннуитетную схему погашения

. Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат.

Задача1

Определить величину ежемесячных равновеликих выплат по ссуде, размер которой составляет 100 000 руб., а процентная ставка составляет 10% годовых. Ссуда взята на срок 5 лет.

Разбираемся, какая информация содержится в задаче:

1. Заемщик ежемесячно должен делать платеж банку. Этот платеж включает:
   
   сумму в счет погашения части ссуды
   
   и
   
   сумму для оплаты начисленных за прошедший период процентов на остаток ссуды
   
   ;
2. Сумма ежемесячного платежа (аннуитета)
   
   постоянна
   
   и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц;
3. Сумма для оплаты начисленных за прошедший период процентов
   
   уменьшается
   
   каждый период, т.к. проценты начисляются только на непогашенную часть ссуды;
4. Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды,
   
   увеличивается
   
   от месяца к месяцу.
5. Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
6. Проценты начисляются
   
   в конце
   
   каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода;
7. Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
8. В конце срока задолженность должна быть равна 0 (БС=0).

Расчет суммы выплаты по ссуде за один период, произведем сначала с помощью финансовой функции MS EXCEL

ПЛТ()

.

Примечание

. Обзор всех функций аннуитета в статье

найдете здесь

.

Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.

Примечание

: Функция

ПЛТ()

входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).

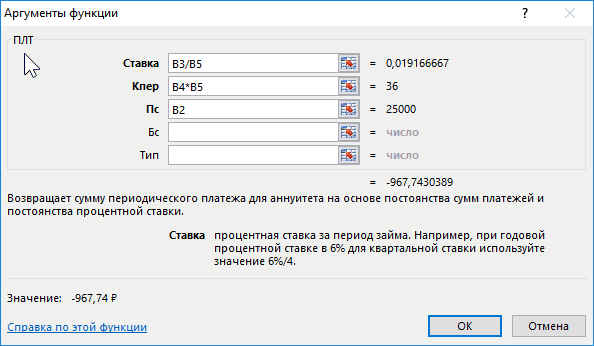
Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за месяц. Ставка =10%/12 (в году 12 месяцев). Кпер – общее число периодов платежей по аннуитету, т.е. 60 (12 мес. в году*5 лет) Пс —

Приведенная стоимость

всех денежных потоков аннуитета. В нашем случае, это сумма ссуды, т.е. 100 000. Бс —

Будущая стоимость

всех денежных потоков аннуитета в конце срока (по истечении числа периодов Кпер). В нашем случае Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Если этот параметр опущен, то он считается =0. Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).

Примечание

: В нашем случае проценты начисляются в конце периода. Например, по истечении первого месяца начисляется процент за пользование ссудой в размере (100 000*10%/12), до этого момента должен быть внесен первый ежемесячный платеж. В случае начисления процентов в начале периода, в первом месяце % не начисляется, т.к. реального пользования средствами ссуды не было (грубо говоря % должен быть начислен за 0 дней пользования ссудой), а весь первый ежемесячный платеж идет в погашение ссуды (основной суммы долга).

Решение1

Итак, ежемесячный платеж может быть вычислен по формуле

=ПЛТ(10%/12; 5*12; 100 000; 0; 0)

, результат -2 107,14р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые

банк

дал

нам, -2107,14 – это деньги, которые мы

возвращаем банку

.

Альтернативная формула для расчета платежа (общий случай):

=-(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+

ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)

Если процентная ставка = 0, то формула упростится до

=(Пс + Бс)/Кпер

Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:

Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А — это аннуитетный платеж (т.е. ПЛТ), К — это коэффициент аннуитета, а S — это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n — количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).

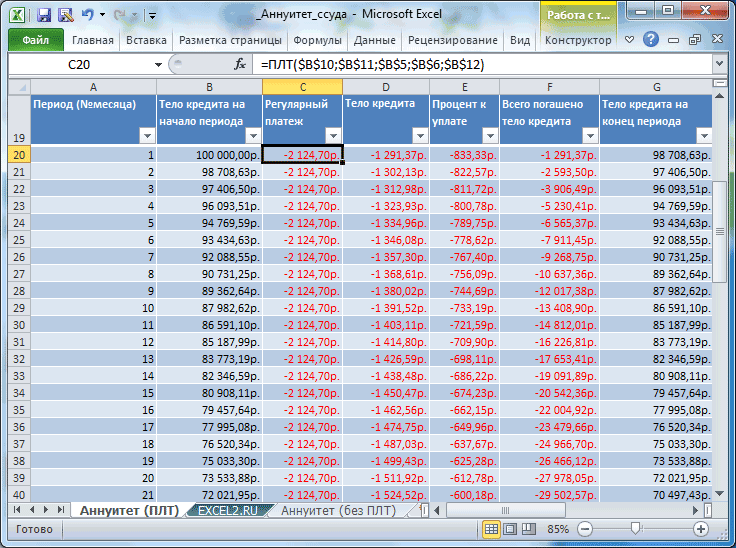
Таблица ежемесячных платежей

Составим таблицу ежемесячных платежей для вышерассмотренной задачи.

Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) практически с теми же аргументами, что и

ПЛТ()

(подробнее см. статью

Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга

). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент

период

, который определяет к какому периоду относится сумма.

Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) с теми же аргументами, что и

ОСПЛТ()

(подробнее см. статью

Аннуитет. Расчет в MS EXCEL выплаченных процентов за период

).

Примечание

. Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию

ОБЩПЛАТ()

, см.

здесь

.

Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо

ПРПЛТ()

или

ОСПЛТ()

, т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ

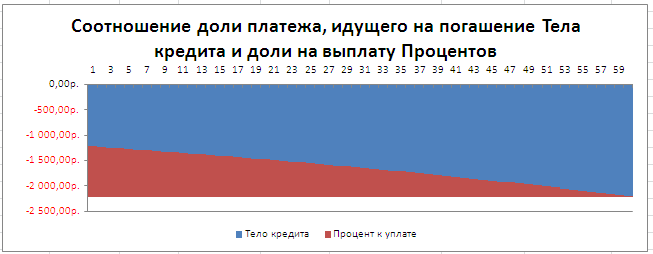
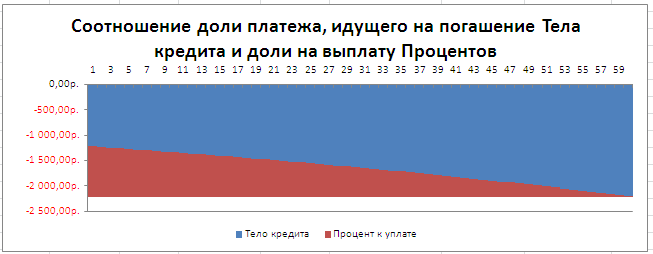
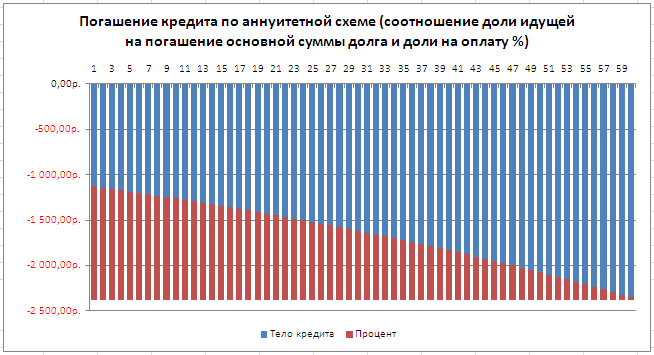
Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в

файле примера

.

Примечание

. В статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад

показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.

График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P

файла примера лист Аннуитет (ПЛТ)

, а также на

листе Аннуитет (без ПЛТ)

. Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см.

файл примера лист Аннуитет (ПЛТ), столбцы H:I

).

Задача2

Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.

Решение2

Ежеквартальный платеж может быть вычислен по формуле

=ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0)

, результат -6 851,59р. Все параметры функции

ПЛТ()

выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения. Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0. То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.

Прежде, чем брать заем, неплохо было бы рассчитать все платежи по нему. Это убережет заёмщика в будущем от различных неожиданных неприятностей и разочарований, когда выяснится, что переплата слишком большая. Помочь в данном расчете могут инструменты программы Excel. Давайте выясним, как рассчитать аннуитетные платежи по кредиту в этой программе.

Расчет оплаты

Прежде всего, нужно сказать, что существует два вида кредитных платежей:

• Дифференцированные;
• Аннуитетные.

При дифференцированной схеме клиент вносит в банк ежемесячно равную долю выплат по телу кредита плюс платежи по процентам. Величина процентных выплат каждый месяц уменьшается, так как уменьшается тело займа, с которого они рассчитываются. Таким образом и общий ежемесячный платеж тоже уменьшается.

При аннуитетной схеме используется несколько другой подход. Клиент ежемесячно вносит одинаковую сумму общего платежа, который состоит из выплат по телу кредита и оплаты процентов. Изначально процентные взносы насчитываются на всю сумму займа, но по мере того, как тело уменьшается, сокращается и начисление процентов. Но общая сумма оплаты остается неизменной за счет ежемесячного увеличения величины выплат по телу кредита. Таким образом, с течением времени удельный вес процентов в общем ежемесячном платеже падает, а удельный вес оплаты по телу растет. При этом сам общий ежемесячный платеж на протяжении всего срока кредитования не меняется.

Как раз на расчете аннуитетного платежа мы и остановимся. Тем более, это актуально, так как в настоящее время большинство банков используют именно эту схему. Она удобна и для клиентов, ведь в этом случае общая сумма оплаты не меняется, оставаясь фиксированной. Клиенты всегда знают сколько нужно заплатить.

Этап 1: расчет ежемесячного взноса

Для расчета ежемесячного взноса при использовании аннуитетной схемы в Экселе существует специальная функция – ПЛТ. Она относится к категории финансовых операторов. Формула этой функции выглядит следующим образом:

=ПЛТ(ставка;кпер;пс;бс;тип)

Как видим, указанная функция обладает довольно большим количеством аргументов. Правда, последние два из них не являются обязательными.

Аргумент «Ставка» указывает на процентную ставку за конкретный период. Если, например, используется годовая ставка, но платеж по займу производится ежемесячно, то годовую ставку нужно разделить на 12 и полученный результат использовать в качестве аргумента. Если применяется ежеквартальный вид оплаты, то в этом случае годовую ставку нужно разделить на 4 и т.д.

«Кпер» обозначает общее количество периодов выплат по кредиту. То есть, если заём берется на один год с ежемесячной оплатой, то число периодов считается 12, если на два года, то число периодов – 24. Если кредит берется на два года с ежеквартальной оплатой, то число периодов равно 8.

«Пс» указывает приведенную стоимость на настоящий момент. Говоря простыми словами, это общая величина займа на начало кредитования, то есть, та сумма, которую вы берете взаймы, без учета процентов и других дополнительных выплат.

«Бс» — это будущая стоимость. Эта величина, которую будет составлять тело займа на момент завершения кредитного договора. В большинстве случаев данный аргумент равен «0», так как заемщик на конец срока кредитования должен полностью рассчитаться с кредитором. Указанный аргумент не является обязательным. Поэтому, если он опускается, то считается равным нулю.

Аргумент «Тип» определяет время расчета: в конце или в начале периода. В первом случае он принимает значение «0», а во втором – «1». Большинство банковских учреждений используют именно вариант с оплатой в конце периода. Этот аргумент тоже является необязательным, и если его опустить считается, что он равен нулю.

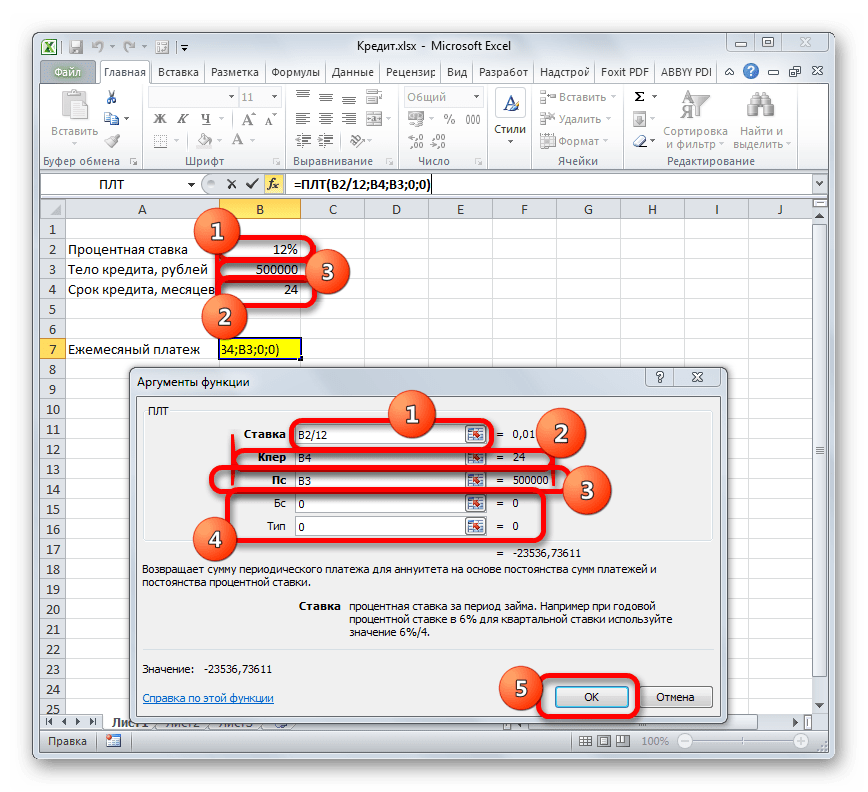
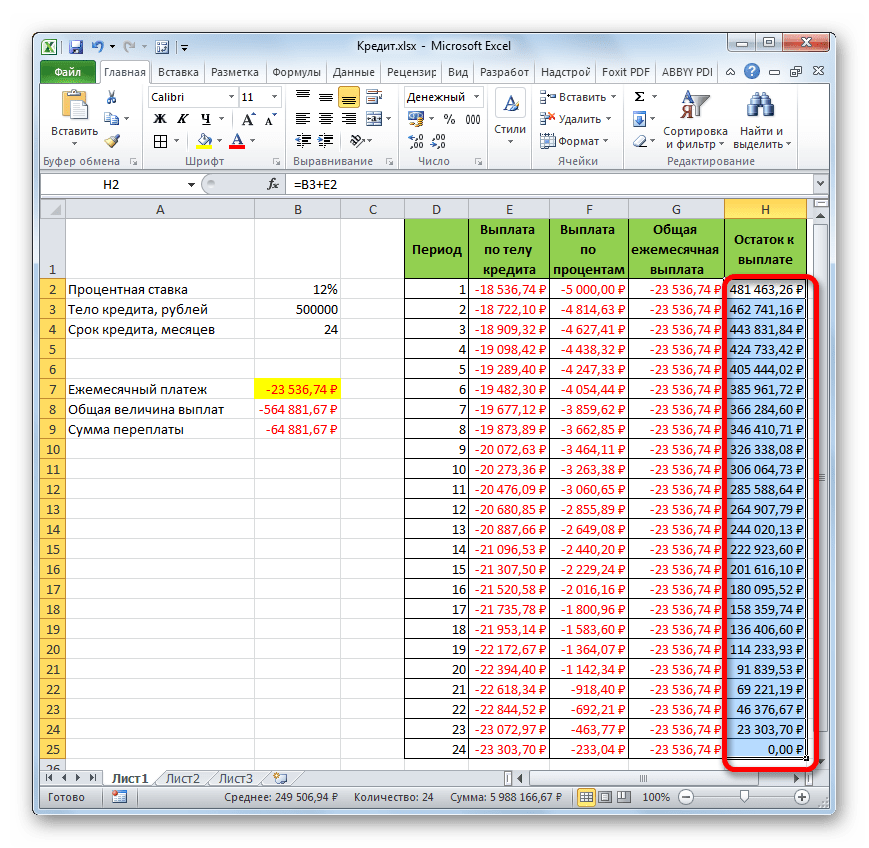
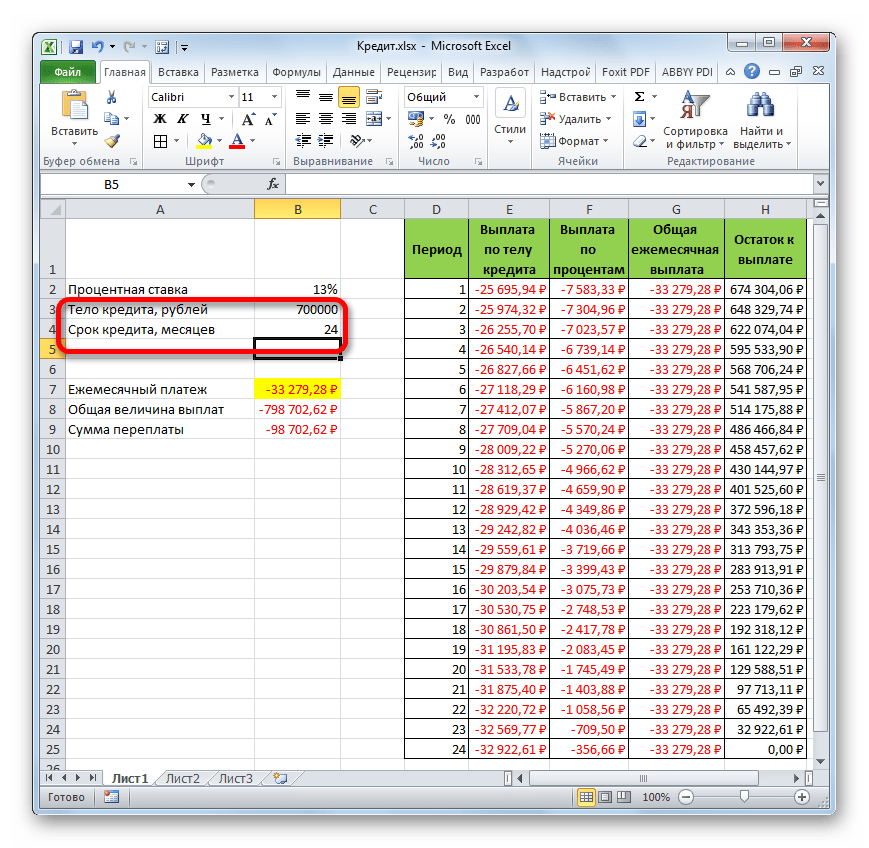
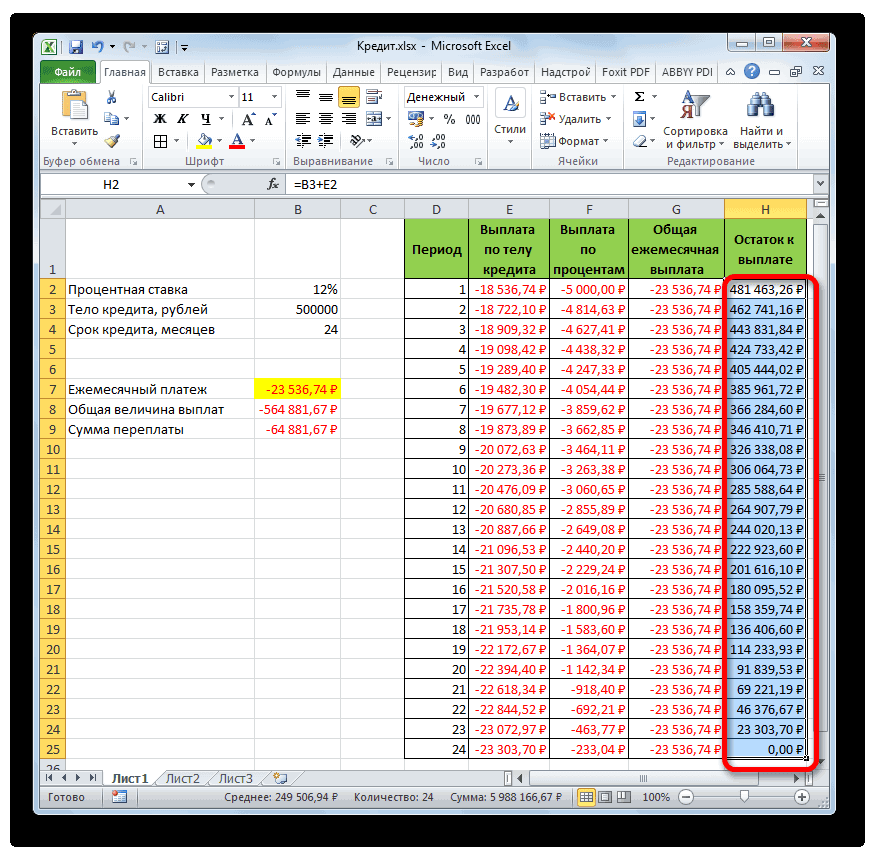
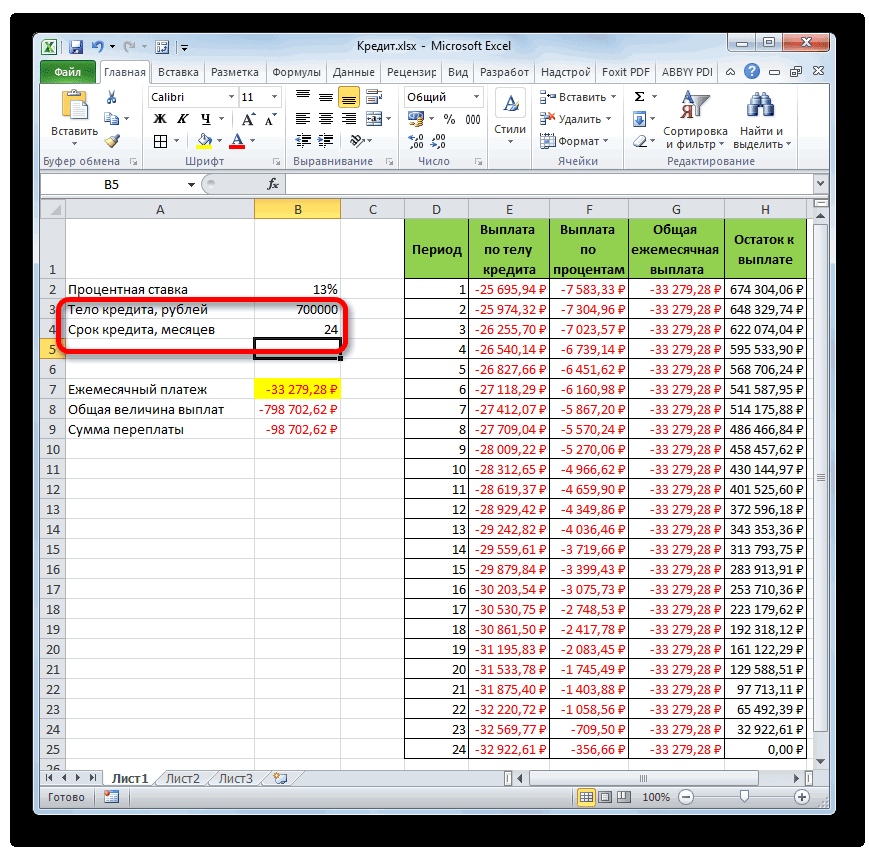
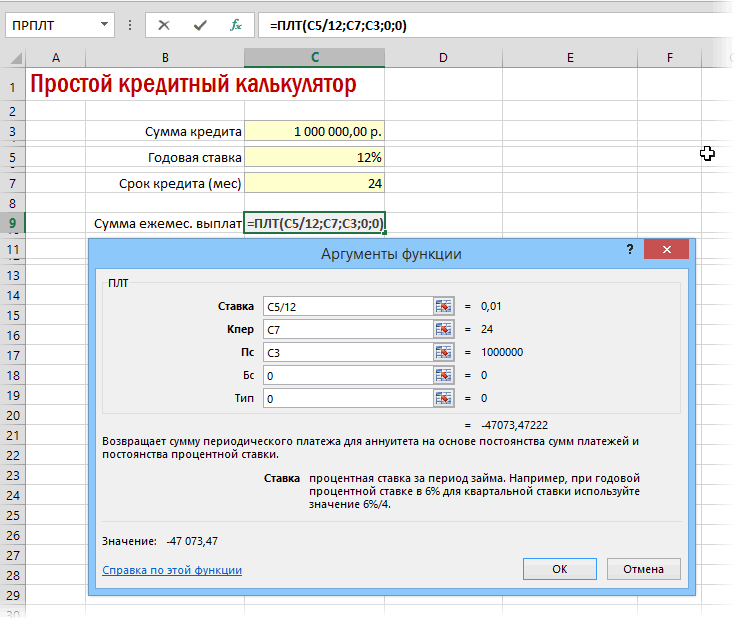
Теперь настало время перейти к конкретному примеру расчета ежемесячного взноса при помощи функции ПЛТ. Для расчета используем таблицу с исходными данными, где указана процентная ставка по кредиту (12%), величина займа (500000 рублей) и срок кредита (24 месяца). При этом оплата производится ежемесячно в конце каждого периода.

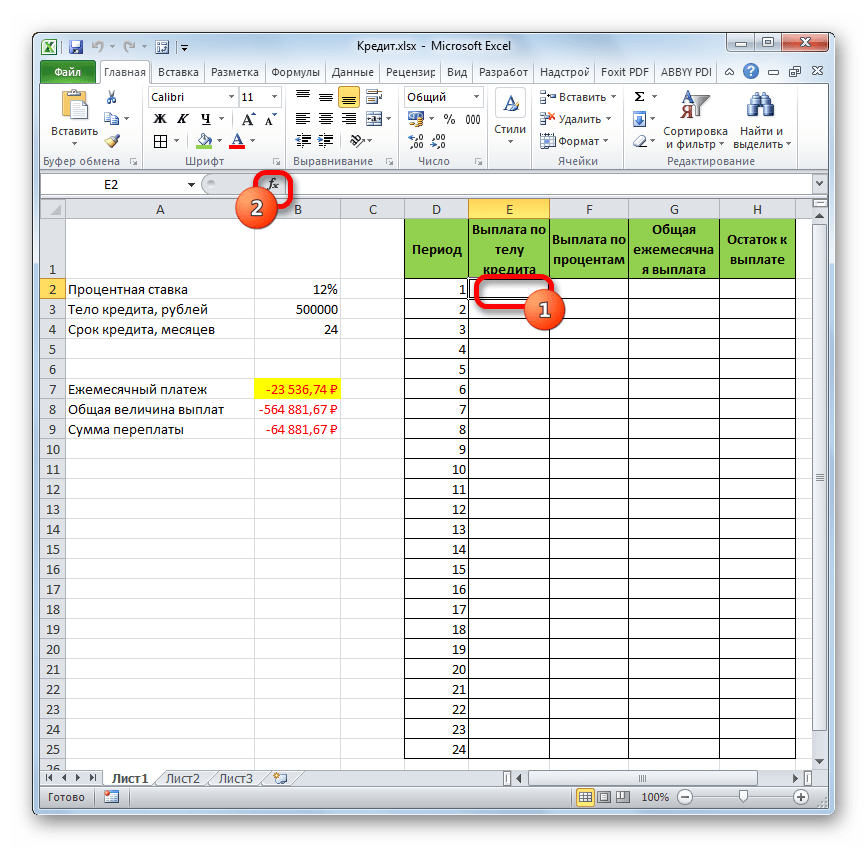
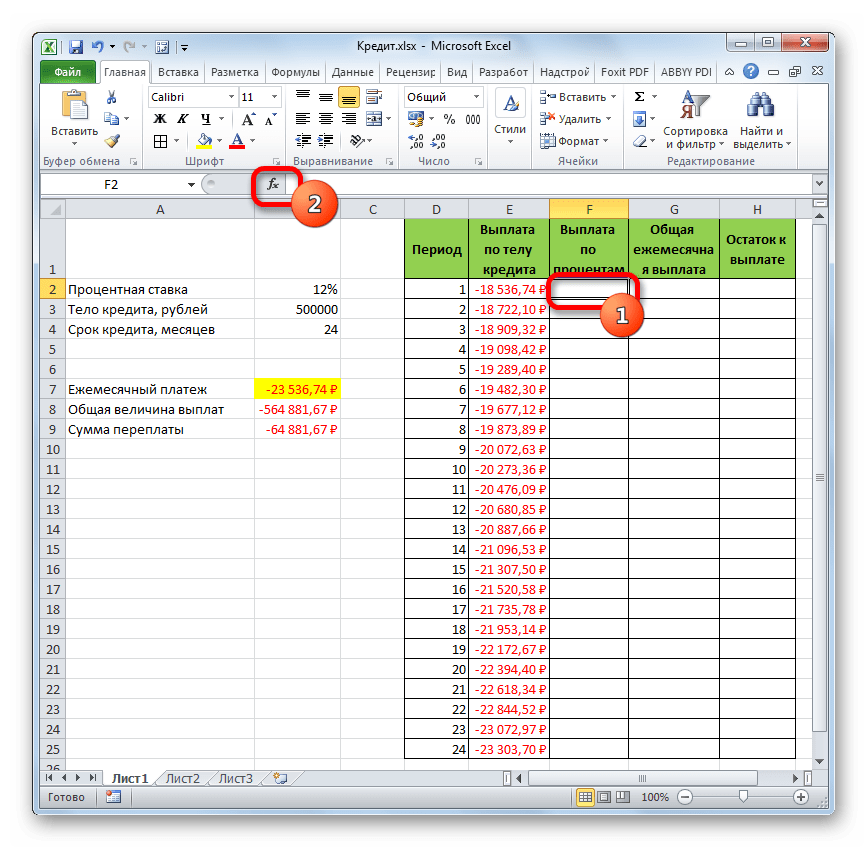
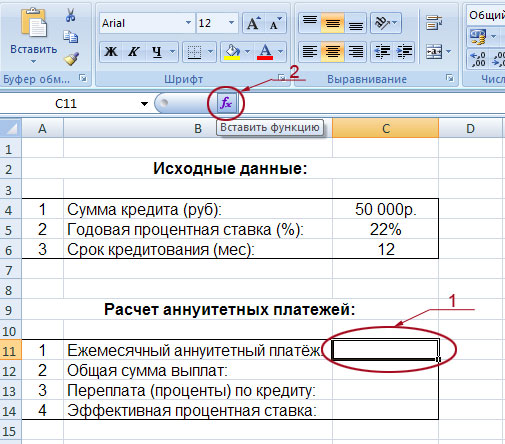
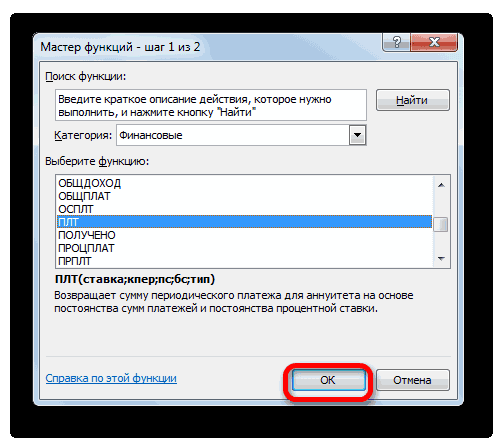
1. Выделяем элемент на листе, в который будет выводиться результат расчета, и щелкаем по пиктограмме «Вставить функцию», размещенную около строки формул.



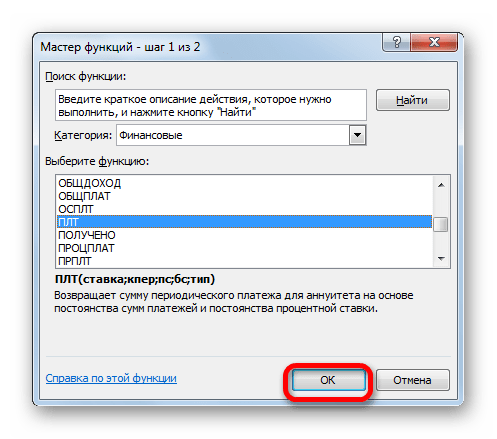
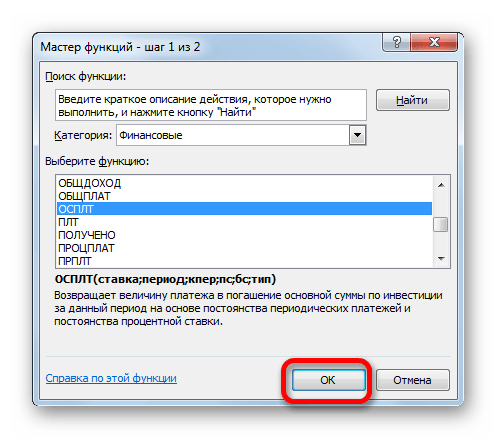
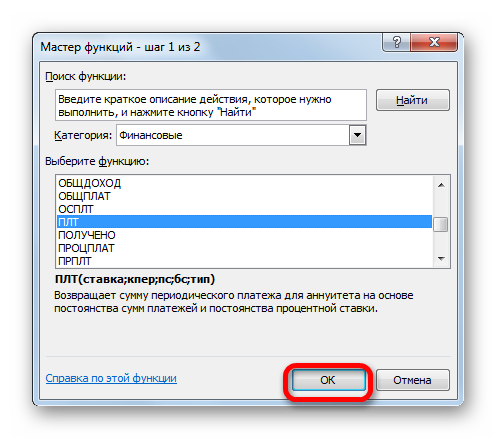
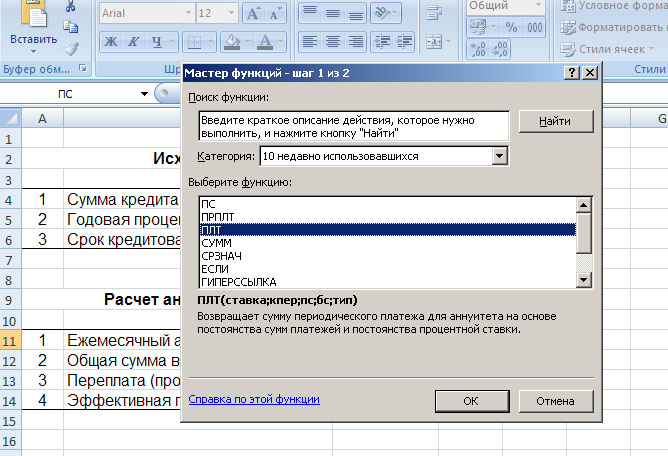
2. Производится запуск окошка Мастера функций. В категории «Финансовые» выделяем наименование «ПЛТ» и жмем на кнопку «OK».



3. После этого открывается окно аргументов оператора ПЛТ.

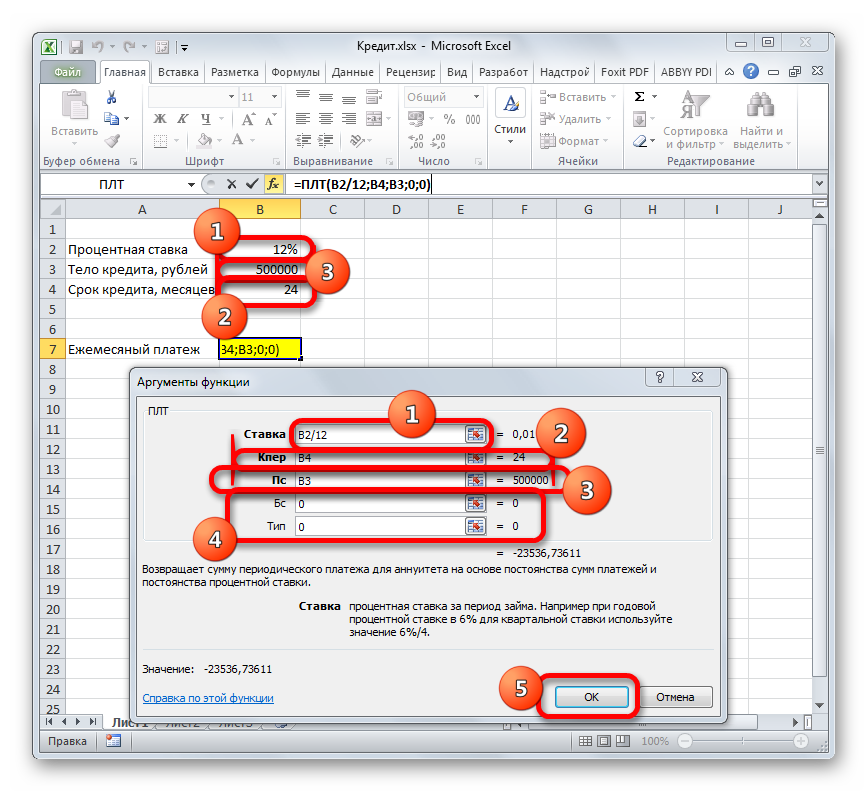
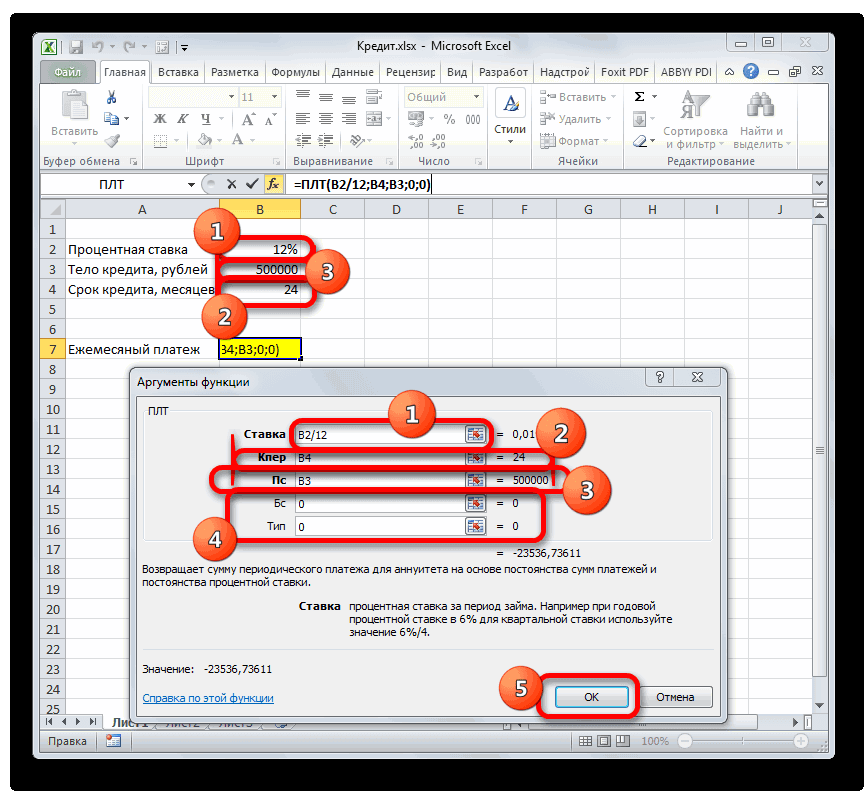
   В поле «Ставка» следует вписать величину процентов за период. Это можно сделать вручную, просто поставив процент, но у нас он указан в отдельной ячейке на листе, поэтому дадим на неё ссылку. Устанавливаем курсор в поле, а затем кликаем по соответствующей ячейке. Но, как мы помним, у нас в таблице задана годовая процентная ставка, а период оплаты равен месяцу. Поэтому делим годовую ставку, а вернее ссылку на ячейку, в которой она содержится, на число 12, соответствующее количеству месяцев в году. Деление выполняем прямо в поле окна аргументов.

   В поле «Кпер» устанавливается срок кредитования. Он у нас равен 24 месяцам. Можно занести в поле число 24 вручную, но мы, как и в предыдущем случае, указываем ссылку на месторасположение данного показателя в исходной таблице.

   В поле «Пс» указывается первоначальная величина займа. Она равна 500000 рублей. Как и в предыдущих случаях, указываем ссылку на элемент листа, в котором содержится данный показатель.

   В поле «Бс» указывается величина займа, после полной его оплаты. Как помним, это значение практически всегда равно нулю. Устанавливаем в данном поле число «0». Хотя этот аргумент можно вообще опустить.

   В поле «Тип» указываем в начале или в конце месяца производится оплата. У нас, как и в большинстве случаев, она производится в конце месяца. Поэтому устанавливаем число «0». Как и в случае с предыдущим аргументом, в данное поле можно ничего не вводить, тогда программа по умолчанию будет считать, что в нем расположено значение равное нулю.

   После того, как все данные введены, жмем на кнопку «OK».



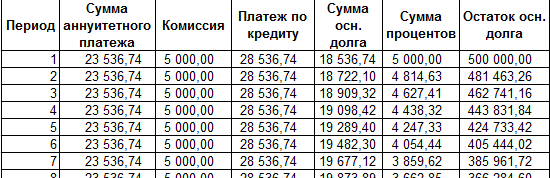
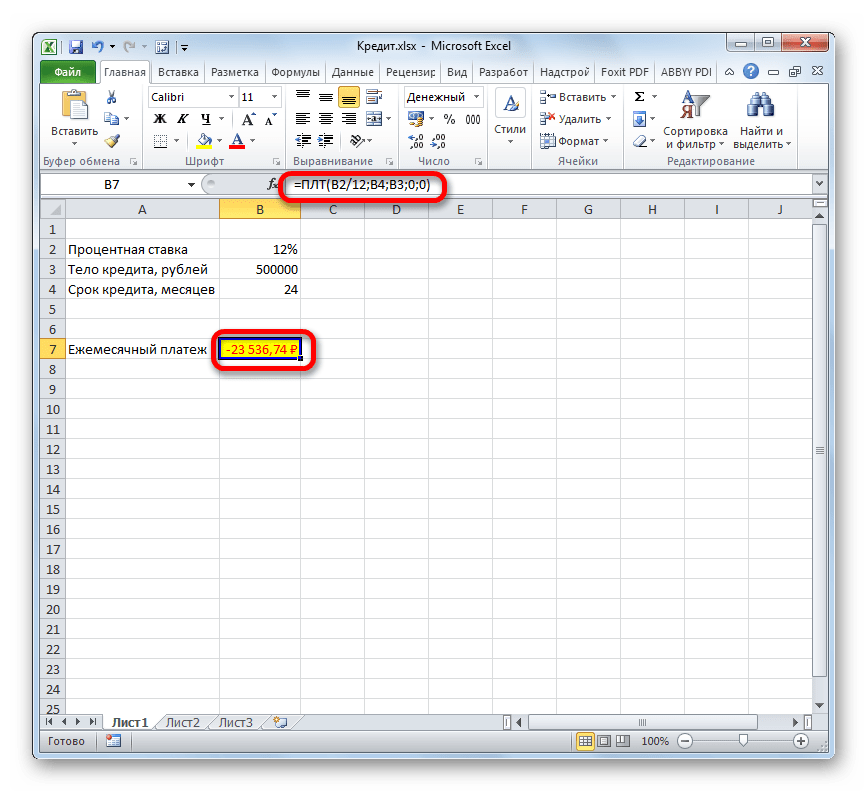
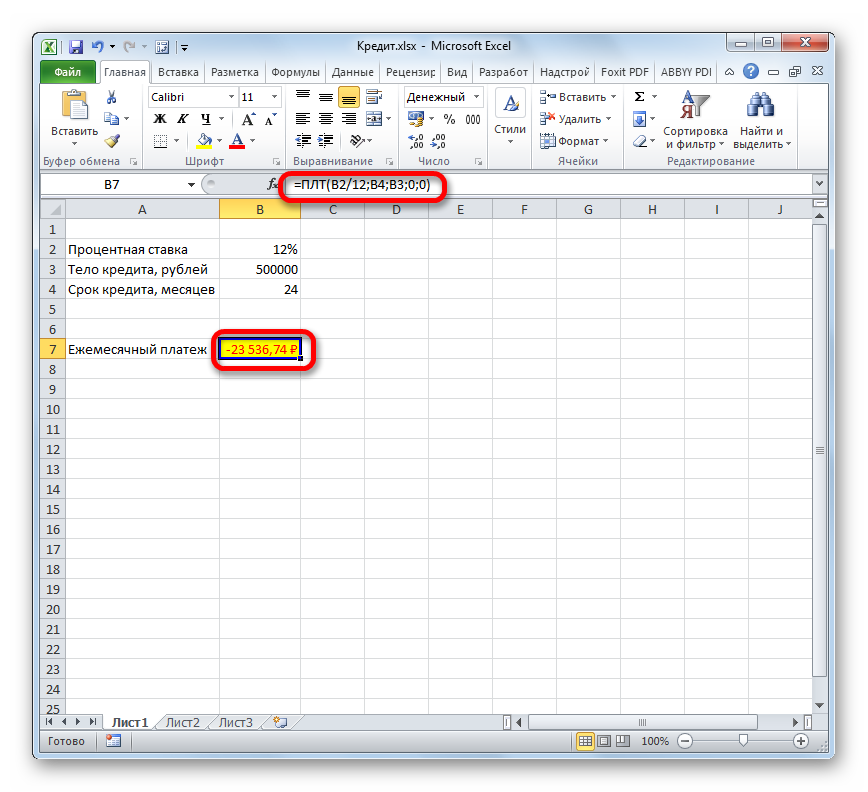
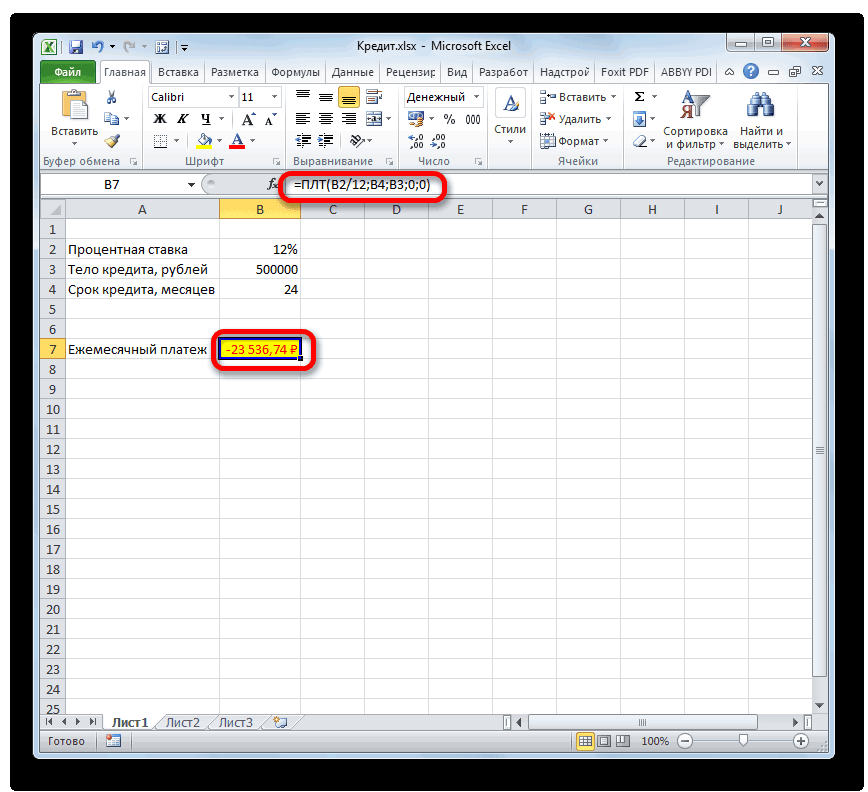
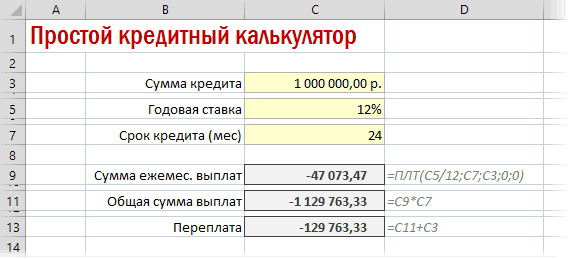
4. После этого в ячейку, которую мы выделили в первом пункте данного руководства, выводится результат вычисления. Как видим, величина ежемесячного общего платежа по займу составляет 23536,74 рубля. Пусть вас не смущает знак «-» перед данной суммой. Так Эксель указывает на то, что это расход денежных средств, то есть, убыток.



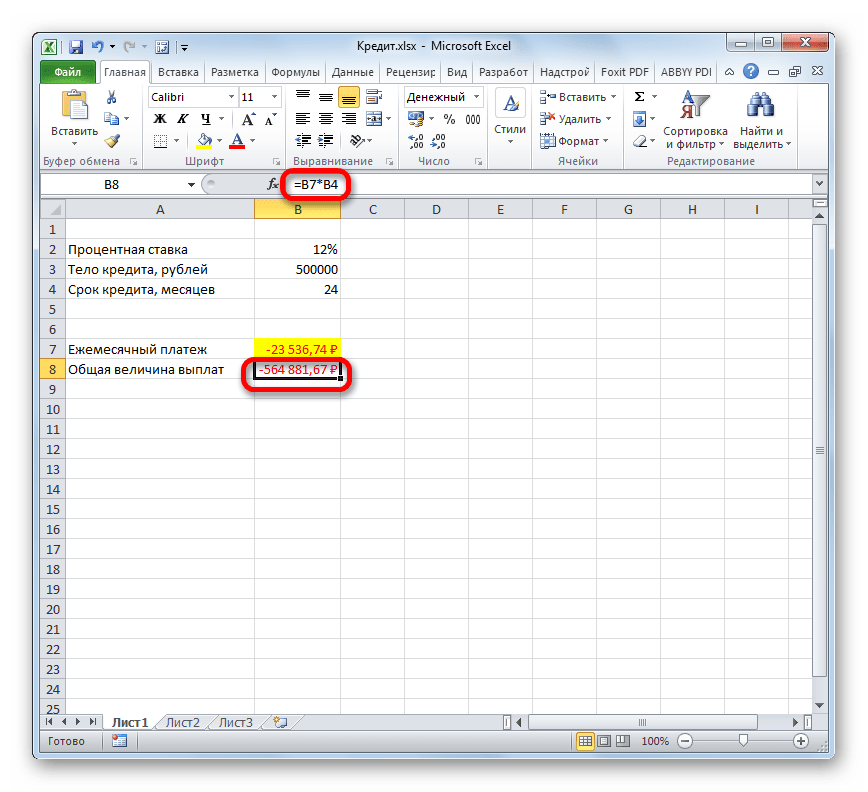
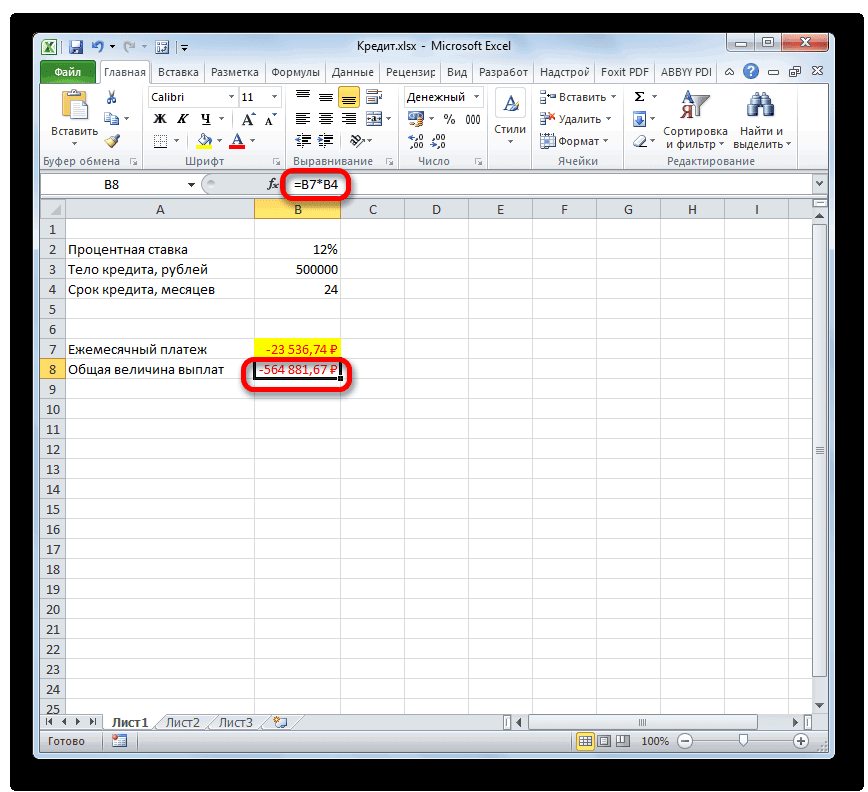
5. Для того, чтобы рассчитать общую сумму оплаты за весь срок кредитования с учетом погашения тела займа и ежемесячных процентов, достаточно перемножить величину ежемесячного платежа (23536,74 рубля) на количество месяцев (24 месяца). Как видим, общая сумма платежей за весь срок кредитования в нашем случае составила 564881,67 рубля.



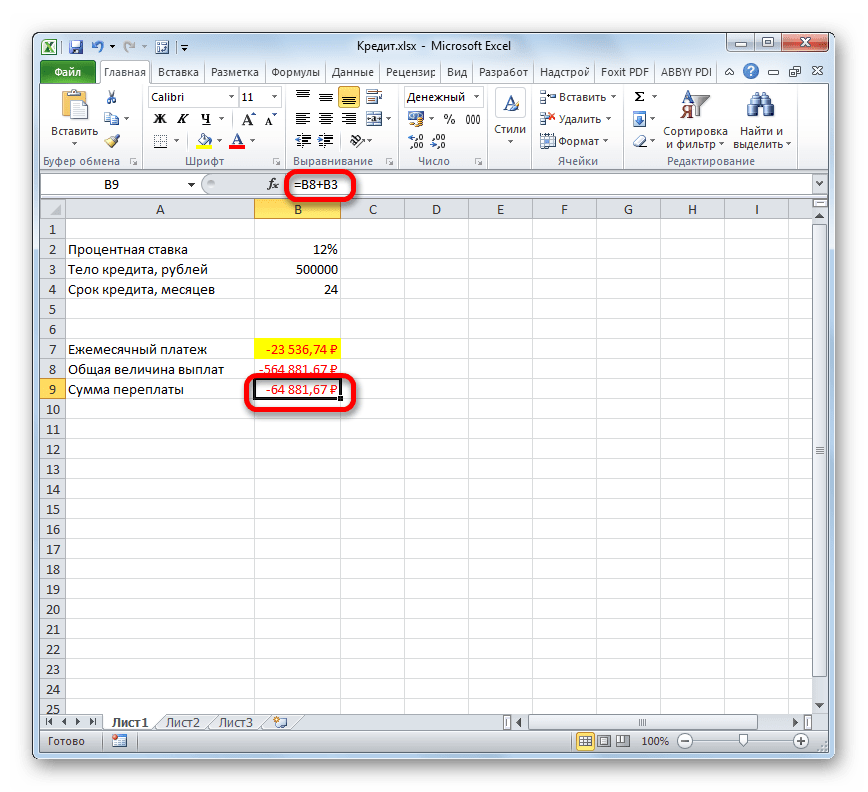
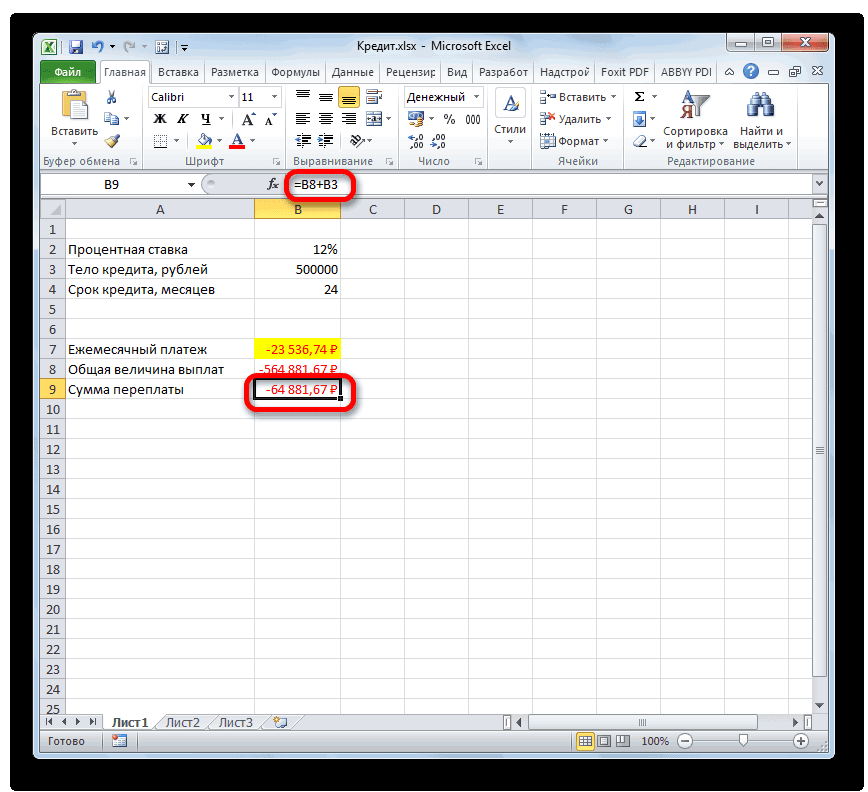
6. Теперь можно подсчитать сумму переплаты по кредиту. Для этого нужно отнять от общей величины выплат по кредиту, включая проценты и тело займа, начальную сумму, взятую в долг. Но мы помним, что первое из этих значений уже со знаком «-». Поэтому в конкретно нашем случае получается, что их нужно сложить. Как видим, общая сумма переплаты по кредиту за весь срок составила 64881,67 рубля.

Урок: Мастер функций в Эксель

Этап 2: детализация платежей

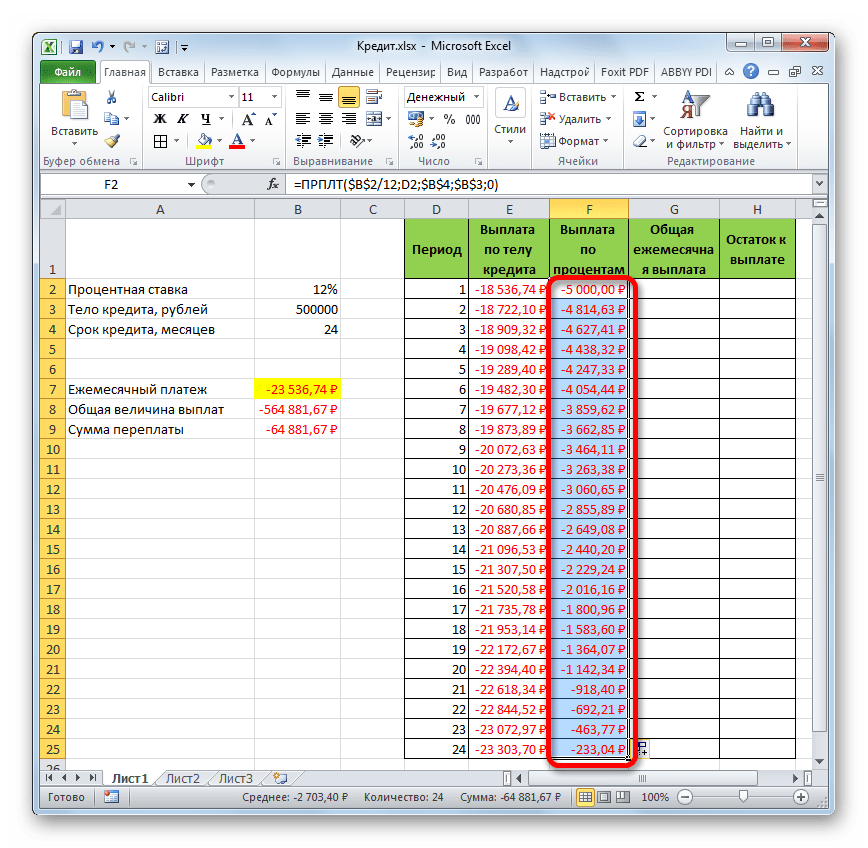
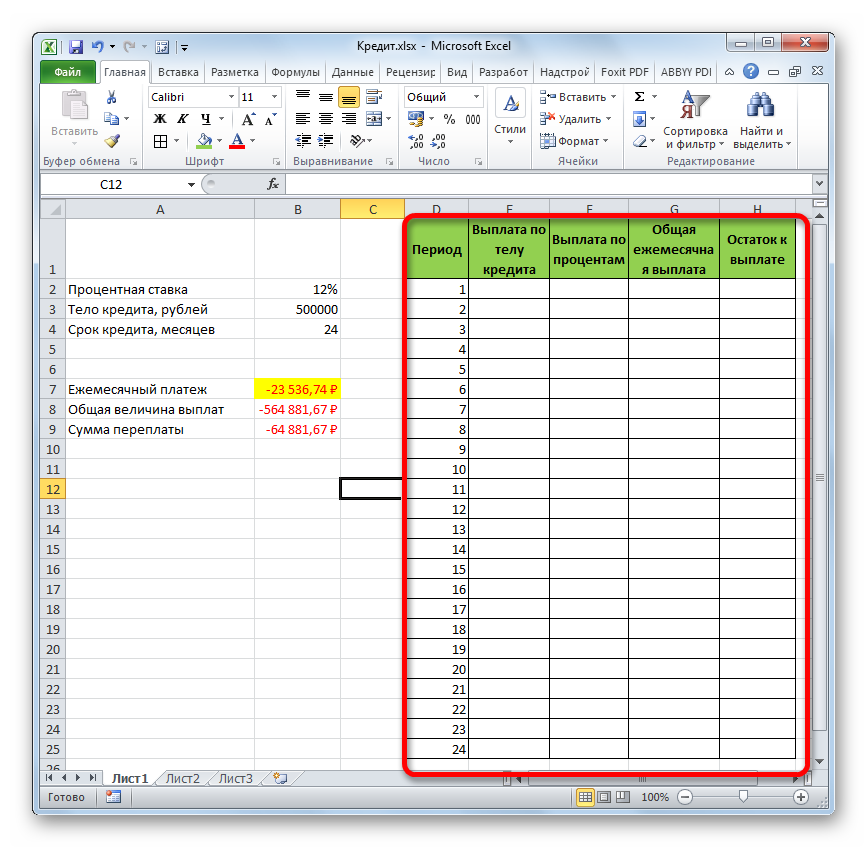
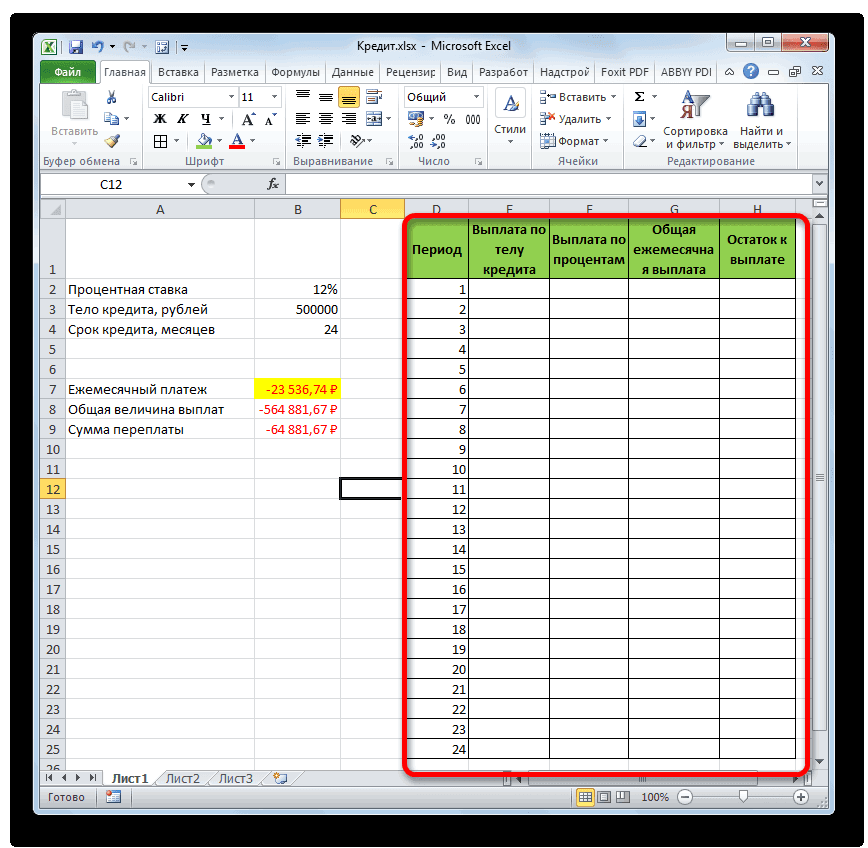
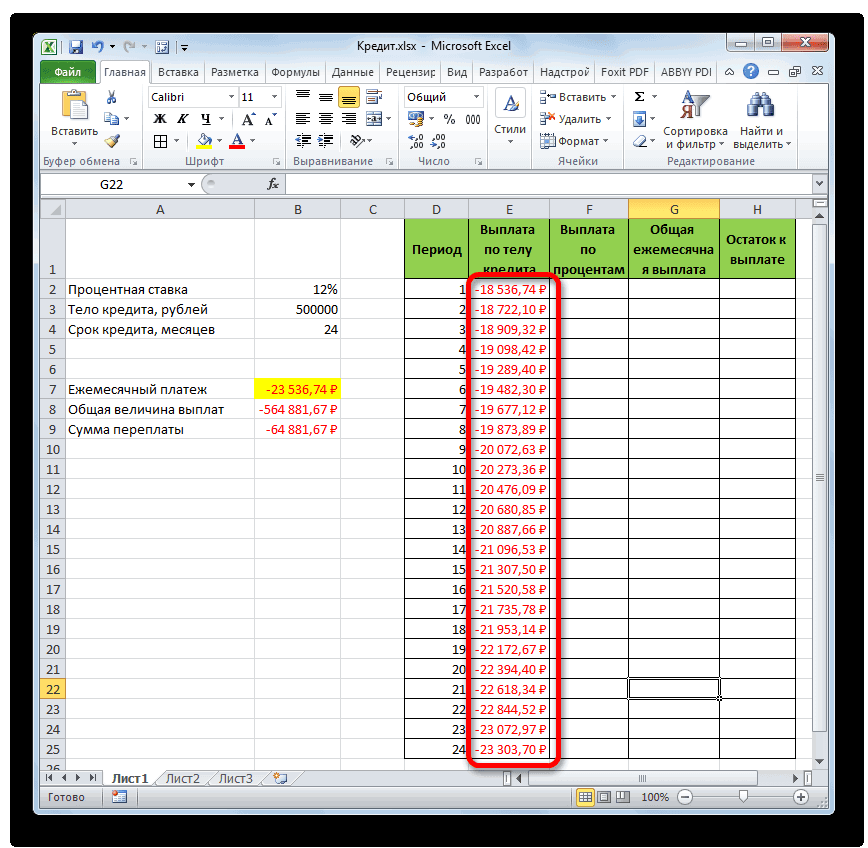
А теперь с помощью других операторов Эксель сделаем помесячную детализацию выплат, чтобы видеть, сколько в конкретном месяце мы платим по телу займа, а сколько составляет величина процентов. Для этих целей чертим в Экселе таблицу, которую будем заполнять данными. Строки этой таблицы будут отвечать соответствующему периоду, то есть, месяцу. Учитывая, что период кредитования у нас составляет 24 месяца, то и количество строк тоже будет соответствующим. В столбцах указана выплата тела займа, выплата процентов, общий ежемесячный платеж, который является суммой предыдущих двух колонок, а также оставшаяся сумма к выплате.

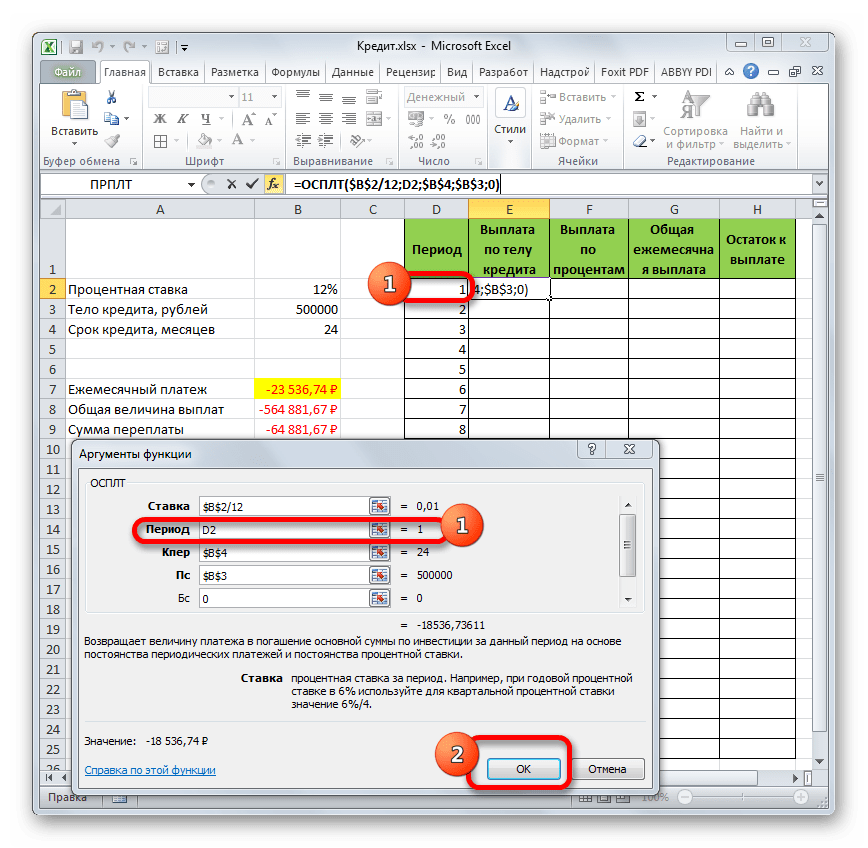
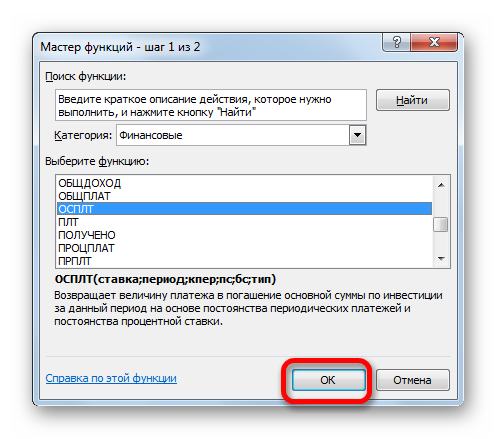
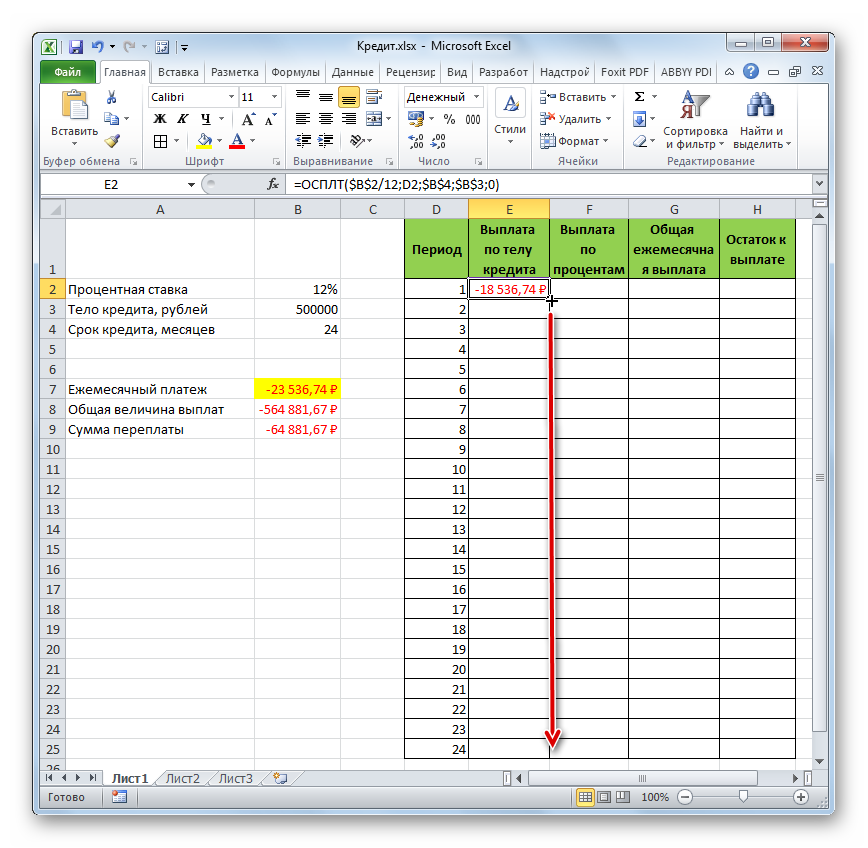
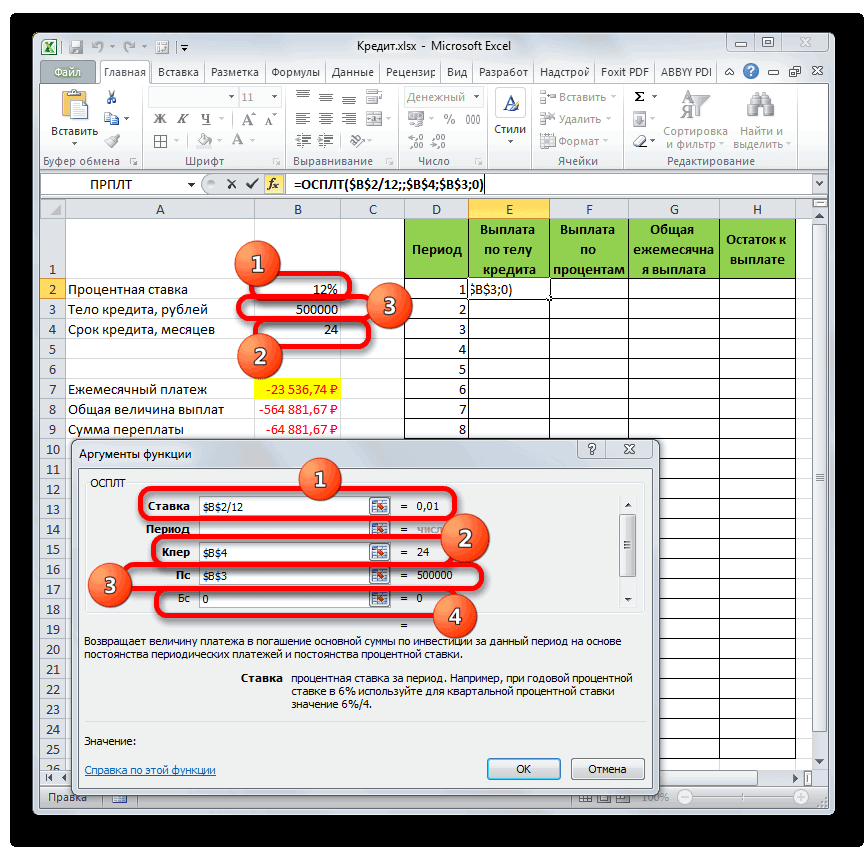
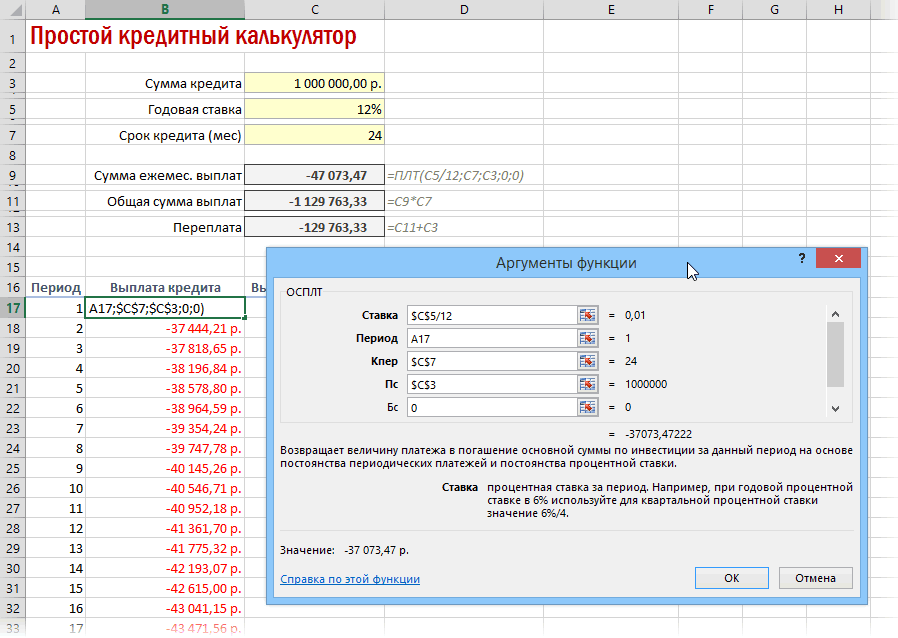
1. Для определения величины оплаты по телу займа используем функцию ОСПЛТ, которая как раз предназначена для этих целей. Устанавливаем курсор в ячейку, которая находится в строке «1» и в столбце «Выплата по телу кредита». Жмем на кнопку «Вставить функцию».



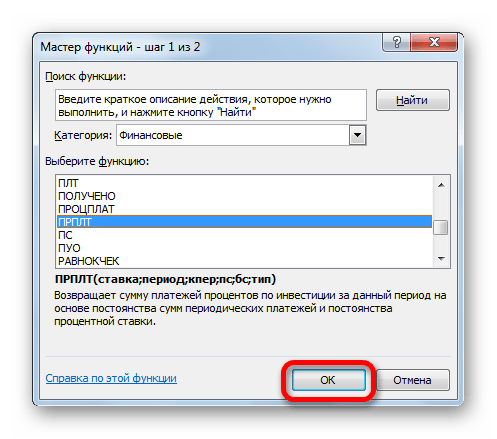
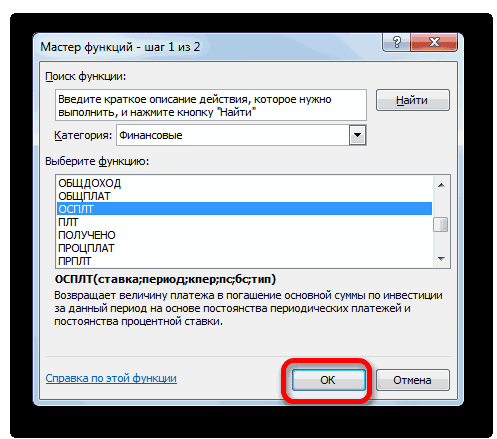
2. Переходим в Мастер функций. В категории «Финансовые» отмечаем наименование «ОСПЛТ» и жмем кнопку «OK».



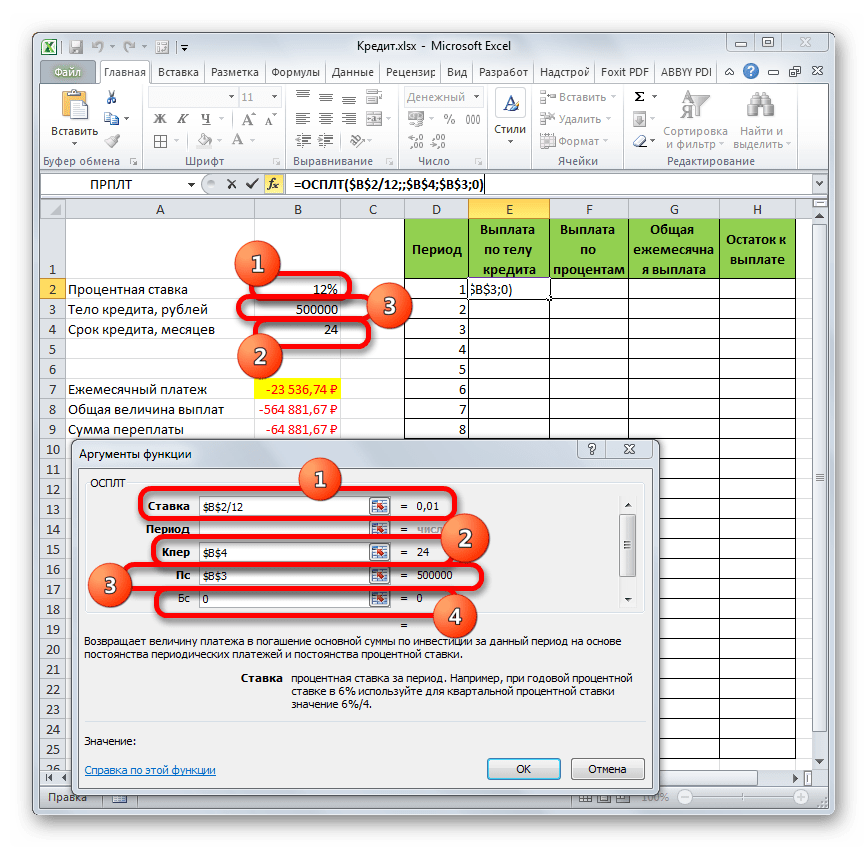
3. Запускается окно аргументов оператора ОСПЛТ. Он имеет следующий синтаксис:

   =ОСПЛТ(Ставка;Период;Кпер;Пс;Бс)

   Как видим, аргументы данной функции почти полностью совпадают с аргументами оператора ПЛТ, только вместо необязательного аргумента «Тип» добавлен обязательный аргумент «Период». Он указывает на номер периода выплаты, а в нашем конкретном случае на номер месяца.

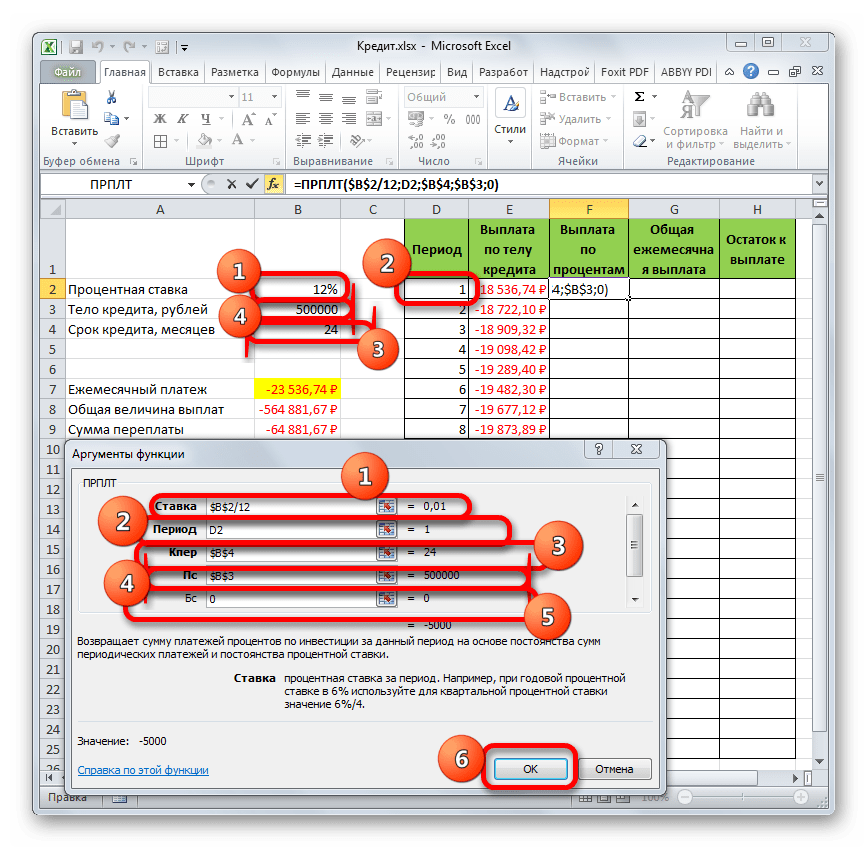
   Заполняем уже знакомые нам поля окна аргументов функции ОСПЛТ теми самыми данными, что были использованы для функции ПЛТ. Только учитывая тот факт, что в будущем будет применяться копирование формулы посредством маркера заполнения, нужно сделать все ссылки в полях абсолютными, чтобы они не менялись. Для этого требуется поставить знак доллара перед каждым значением координат по вертикали и горизонтали. Но легче это сделать, просто выделив координаты и нажав на функциональную клавишу F4. Знак доллара будет расставлен в нужных местах автоматически. Также не забываем, что годовую ставку нужно разделить на 12.



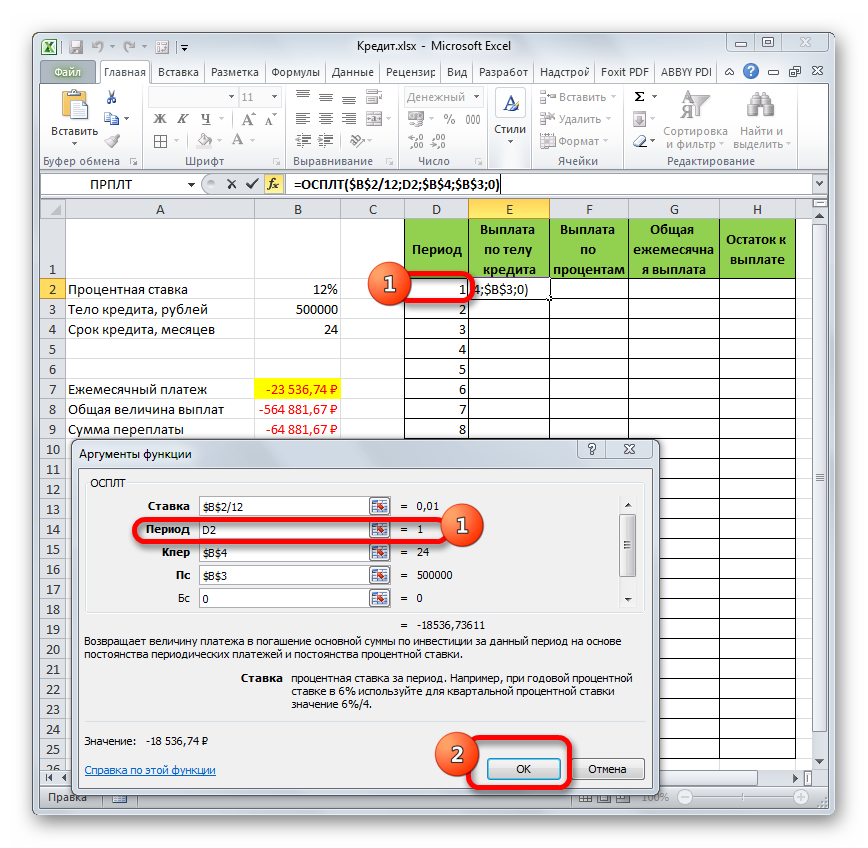
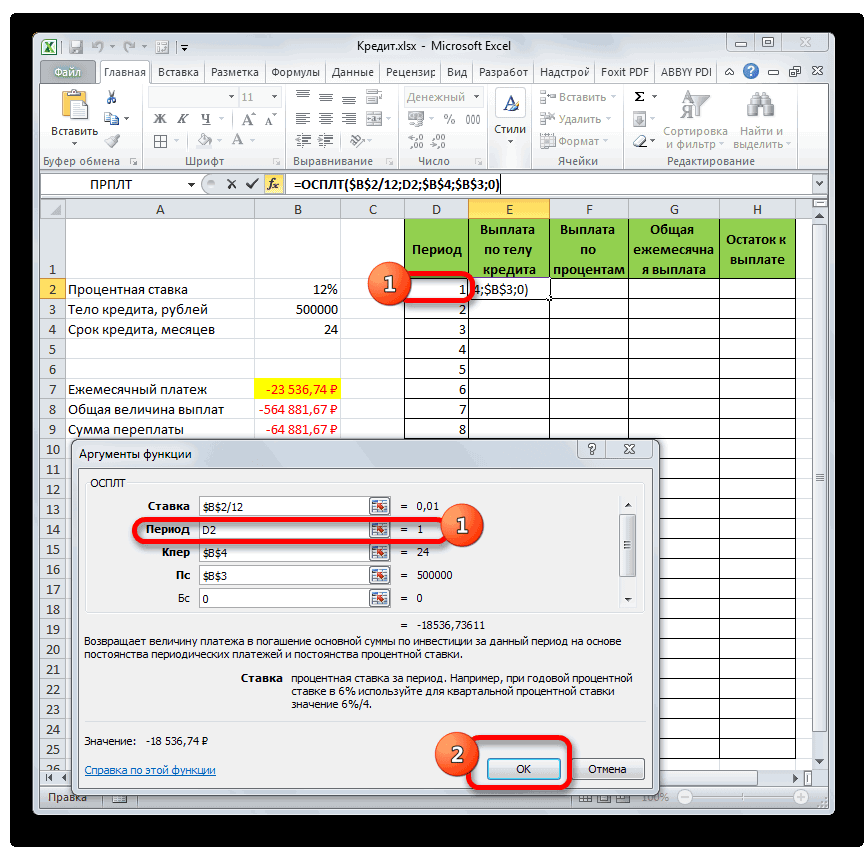
4. Но у нас остается ещё один новый аргумент, которого не было у функции ПЛТ. Этот аргумент «Период». В соответствующее поле устанавливаем ссылку на первую ячейку столбца «Период». Данный элемент листа содержит в себе число «1», которое обозначает номер первого месяца кредитования. Но в отличие от предыдущих полей, в указанном поле мы оставляем ссылку относительной, а не делаем из неё абсолютную.

   После того, как все данные, о которых мы говорили выше, введены, жмем на кнопку «OK».



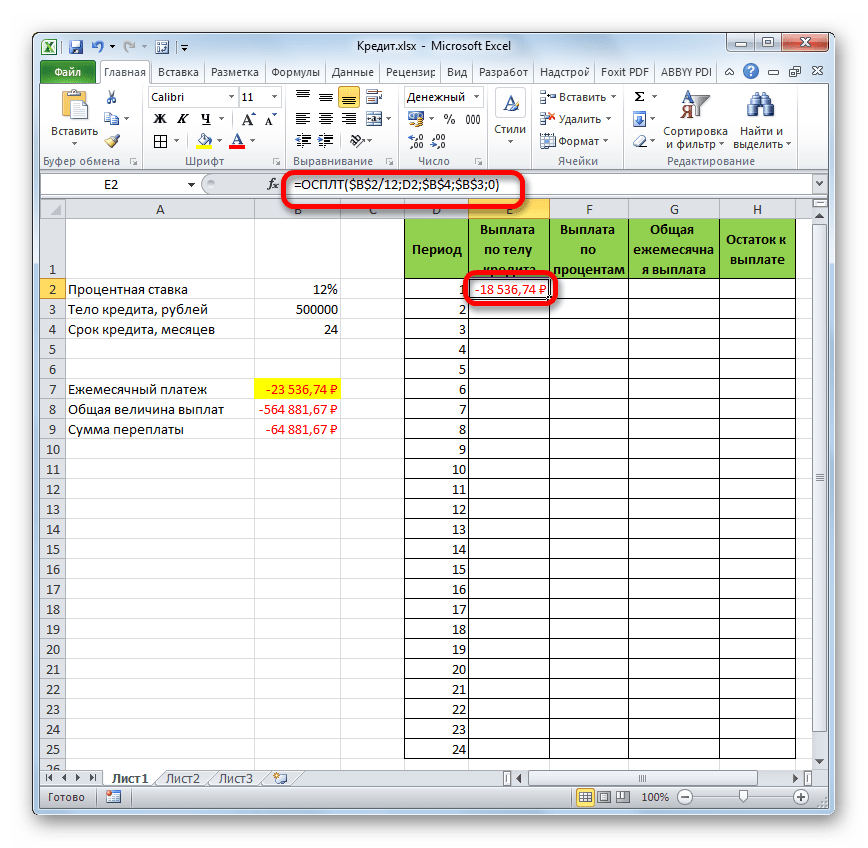
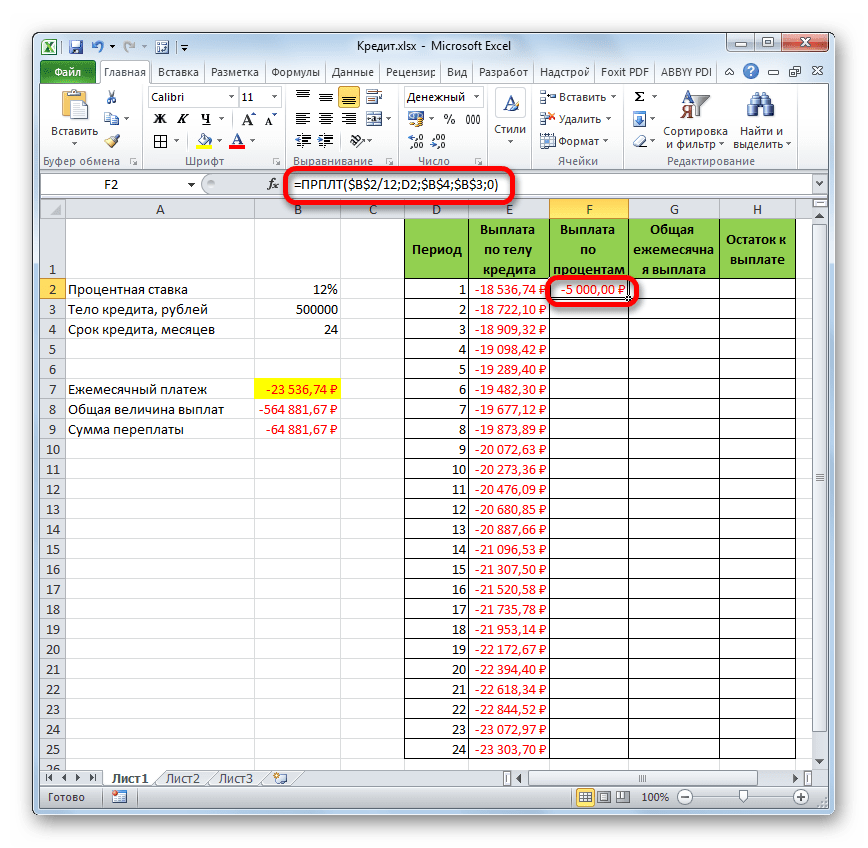
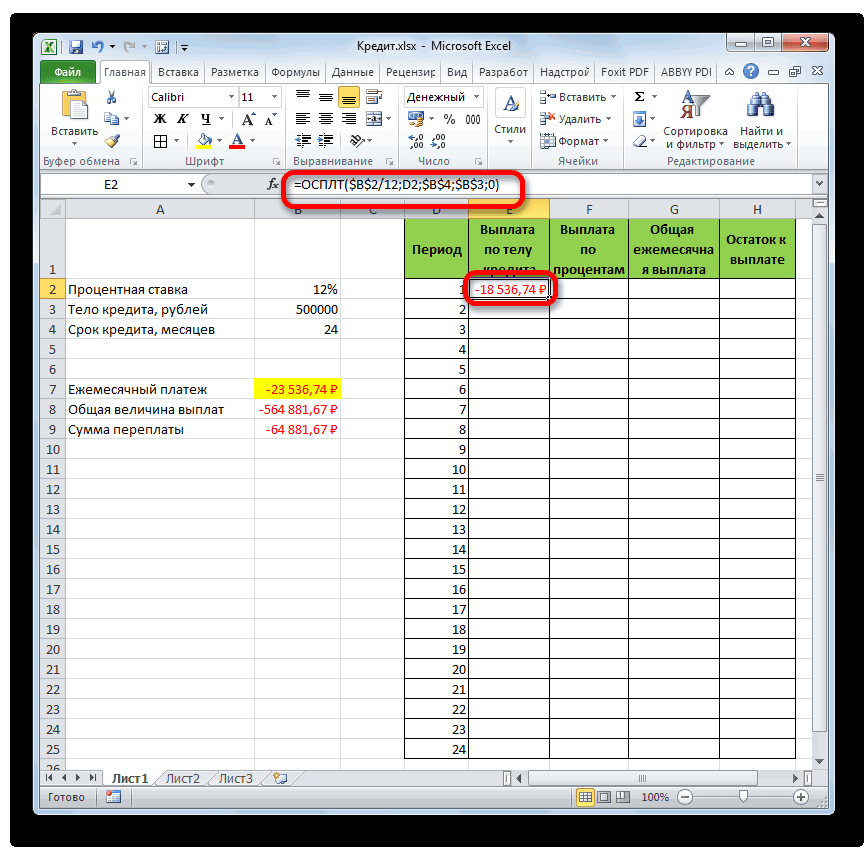
5. После этого в ячейке, которую мы ранее выделили, отобразится величина выплаты по телу займа за первый месяц. Она составит 18536,74 рубля.



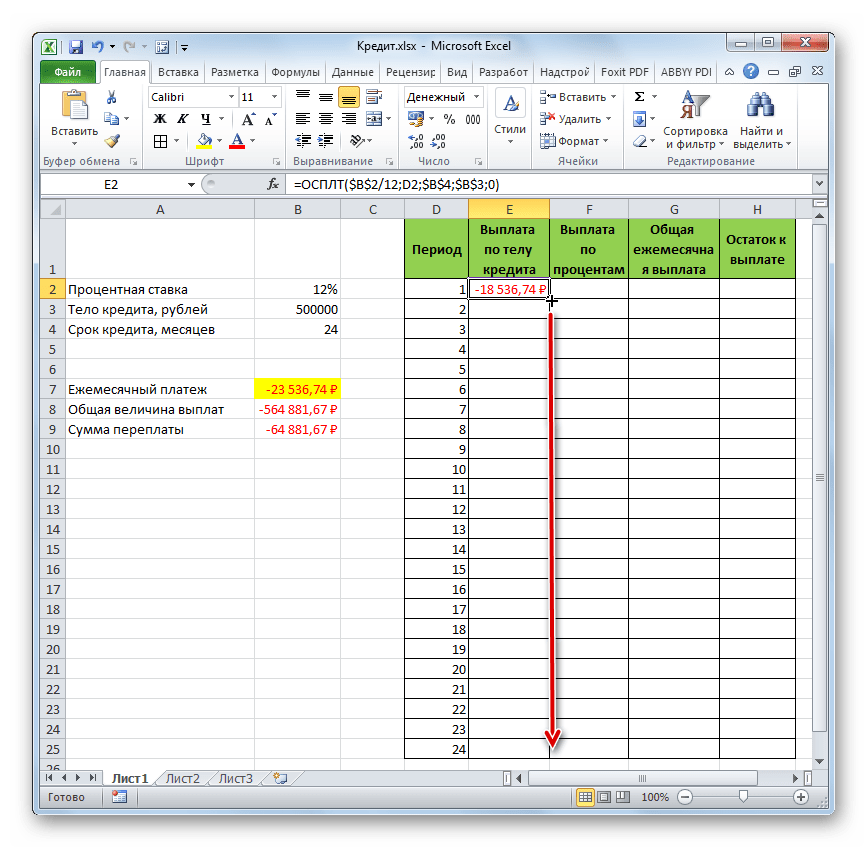
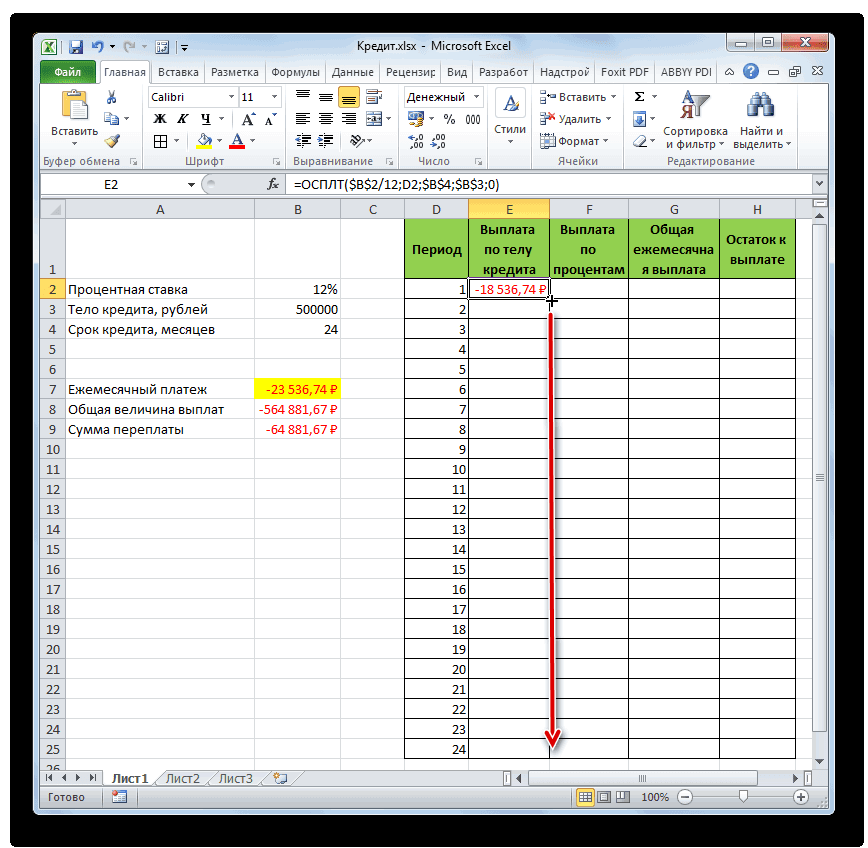
6. Затем, как уже говорилось выше, нам следует скопировать данную формулу на остальные ячейки столбца с помощью маркера заполнения. Для этого устанавливаем курсор в нижний правый угол ячейки, в которой содержится формула. Курсор преобразуется при этом в крестик, который называется маркером заполнения. Зажимаем левую кнопку мыши и тянем его вниз до конца таблицы.



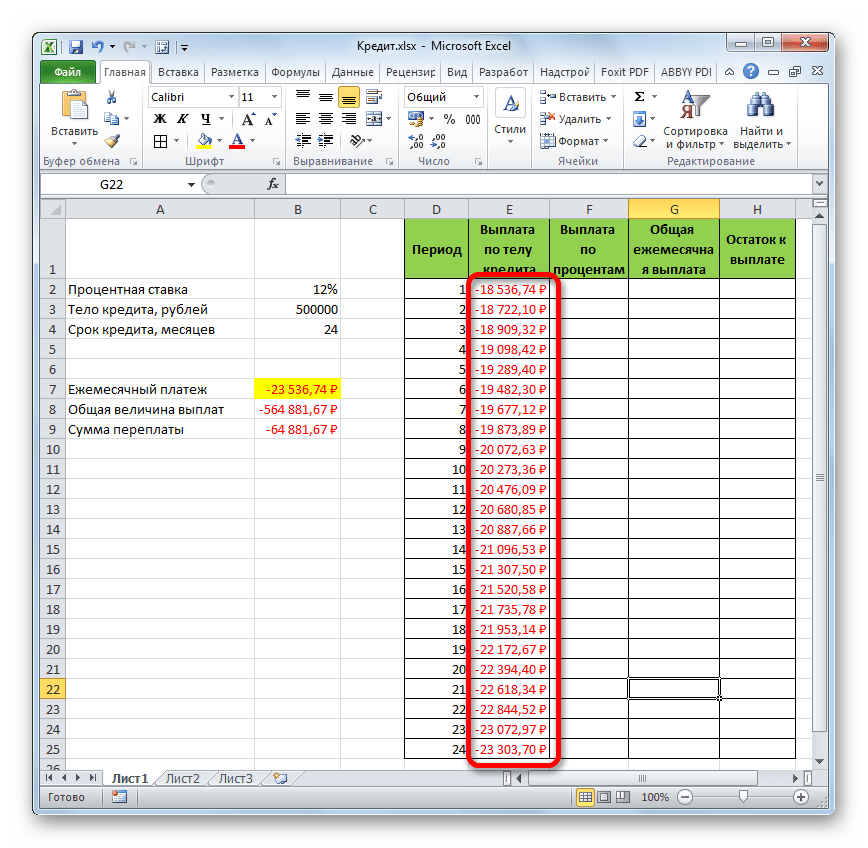
7. В итоге все ячейки столбца заполнены. Теперь мы имеем график выплаты тела займа помесячно. Как и говорилось уже выше, величина оплаты по данной статье с каждым новым периодом увеличивается.



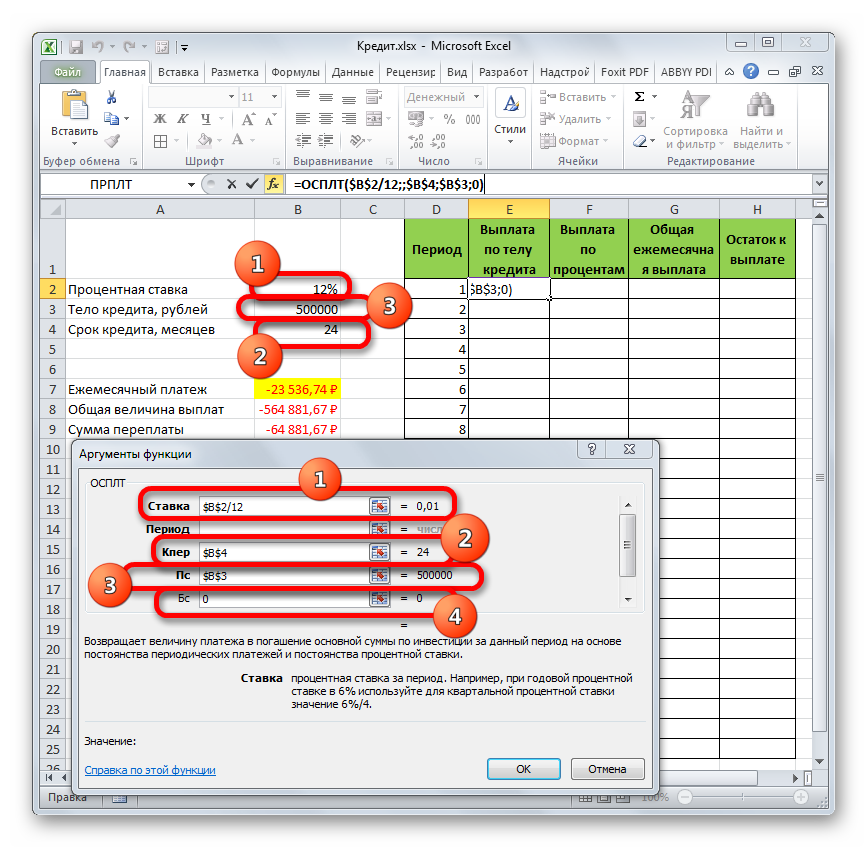
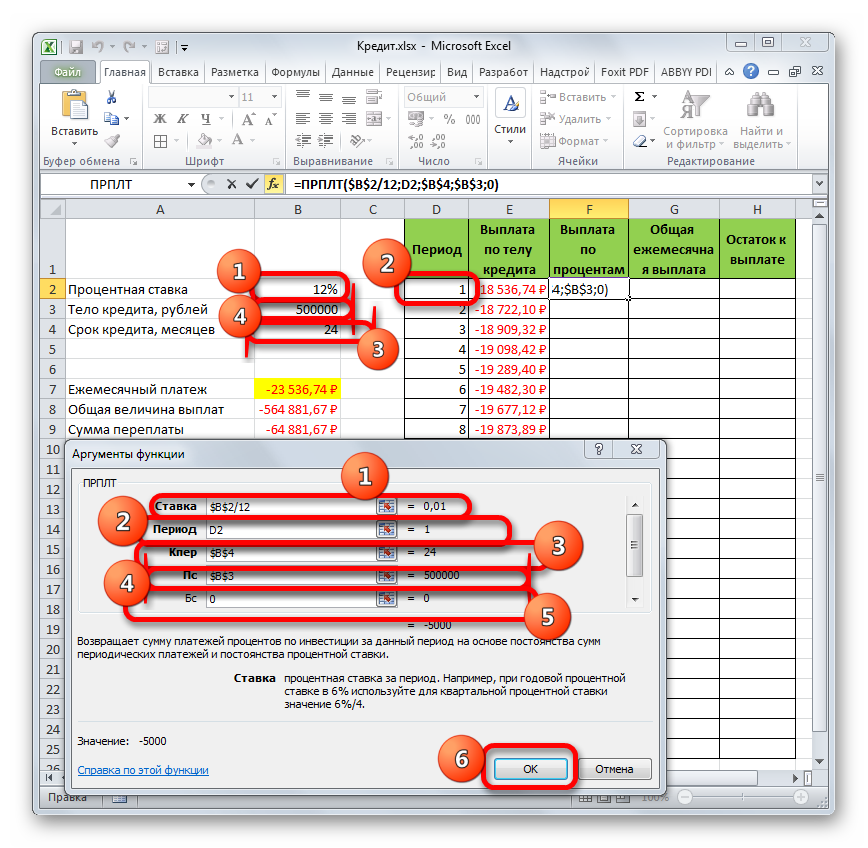
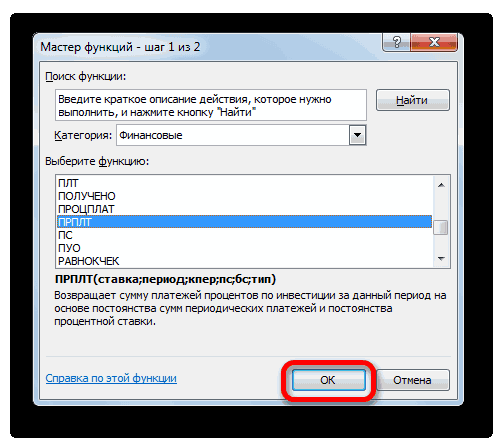
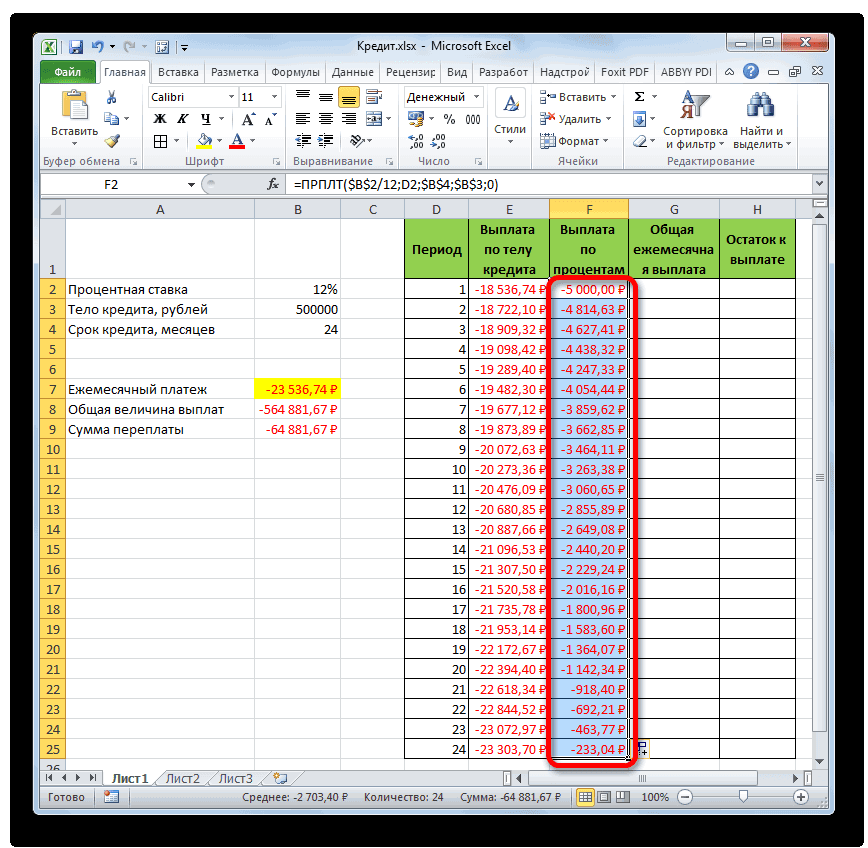
8. Теперь нам нужно сделать месячный расчет оплаты по процентам. Для этих целей будем использовать оператор ПРПЛТ. Выделяем первую пустую ячейку в столбце «Выплата по процентам». Жмем на кнопку «Вставить функцию».



9. В запустившемся окне Мастера функций в категории «Финансовые» производим выделение наименования ПРПЛТ. Выполняем щелчок по кнопке «OK».



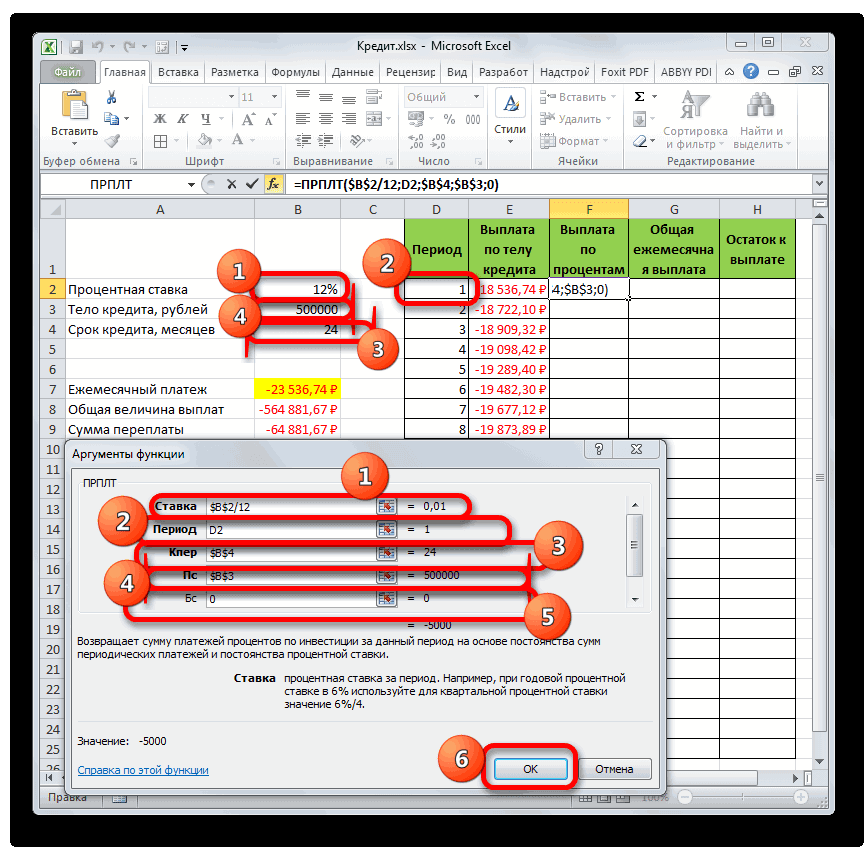
10. Происходит запуск окна аргументов функции ПРПЛТ. Её синтаксис выглядит следующим образом:

    =ПРПЛТ(Ставка;Период;Кпер;Пс;Бс)

    Как видим, аргументы данной функции абсолютно идентичны аналогичным элементам оператора ОСПЛТ. Поэтому просто заносим в окно те же данные, которые мы вводили в предыдущем окне аргументов. Не забываем при этом, что ссылка в поле «Период» должна быть относительной, а во всех других полях координаты нужно привести к абсолютному виду. После этого щелкаем по кнопке «OK».



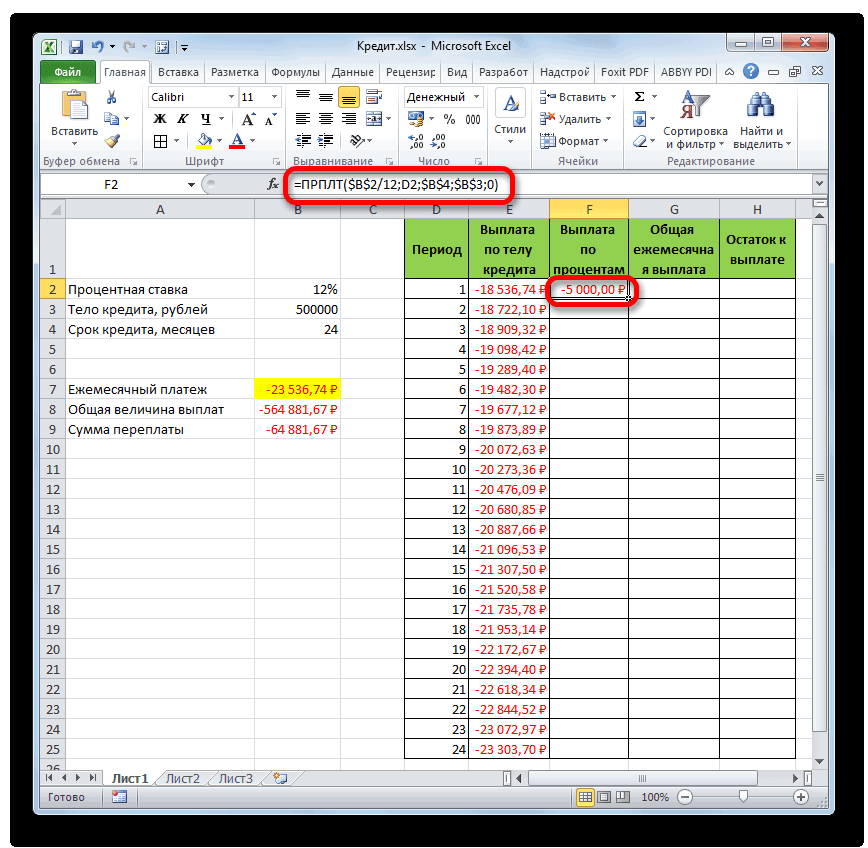
11. Затем результат расчета суммы оплаты по процентам за кредит за первый месяц выводится в соответствующую ячейку.



12. Применив маркер заполнения, производим копирование формулы в остальные элементы столбца, таким способом получив помесячный график оплат по процентам за заём. Как видим, как и было сказано ранее, из месяца в месяц величина данного вида платежа уменьшается.



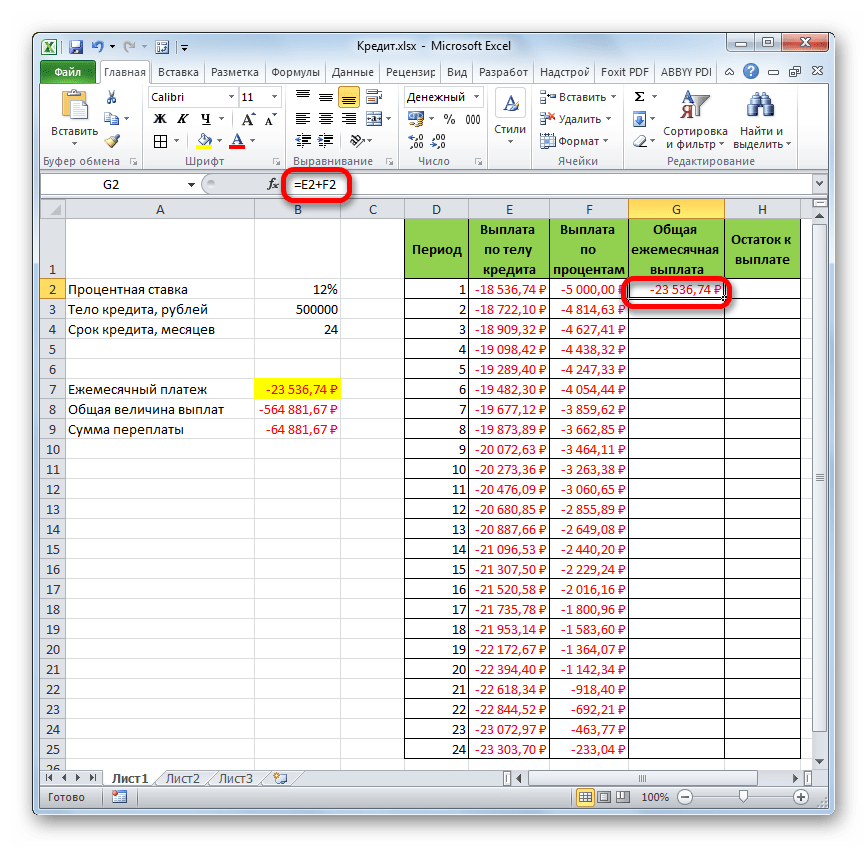
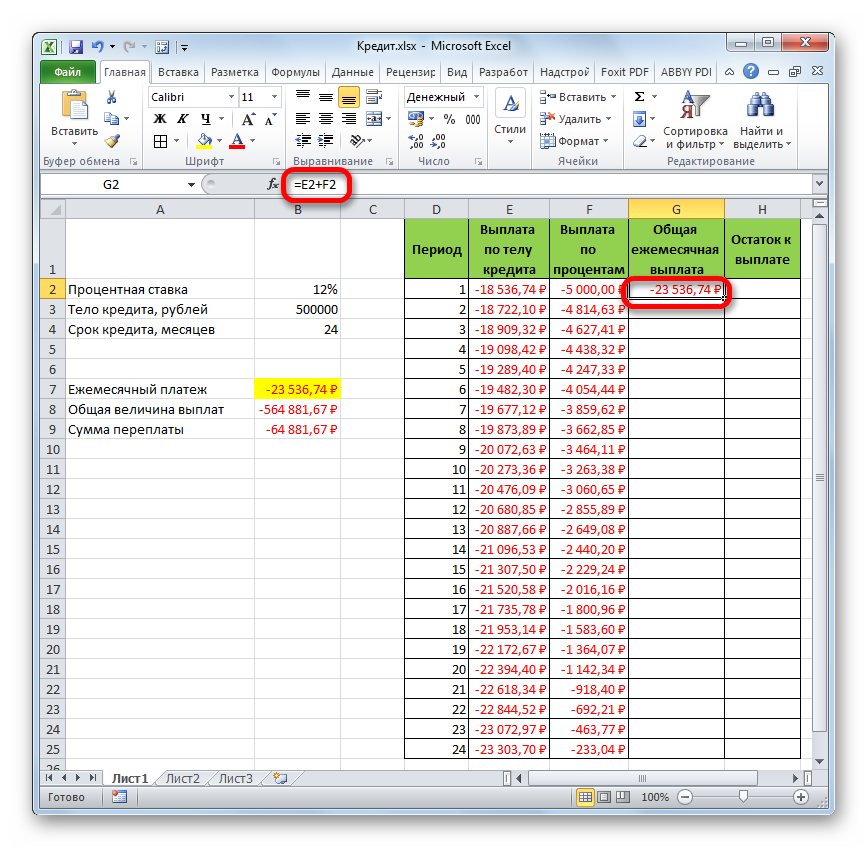
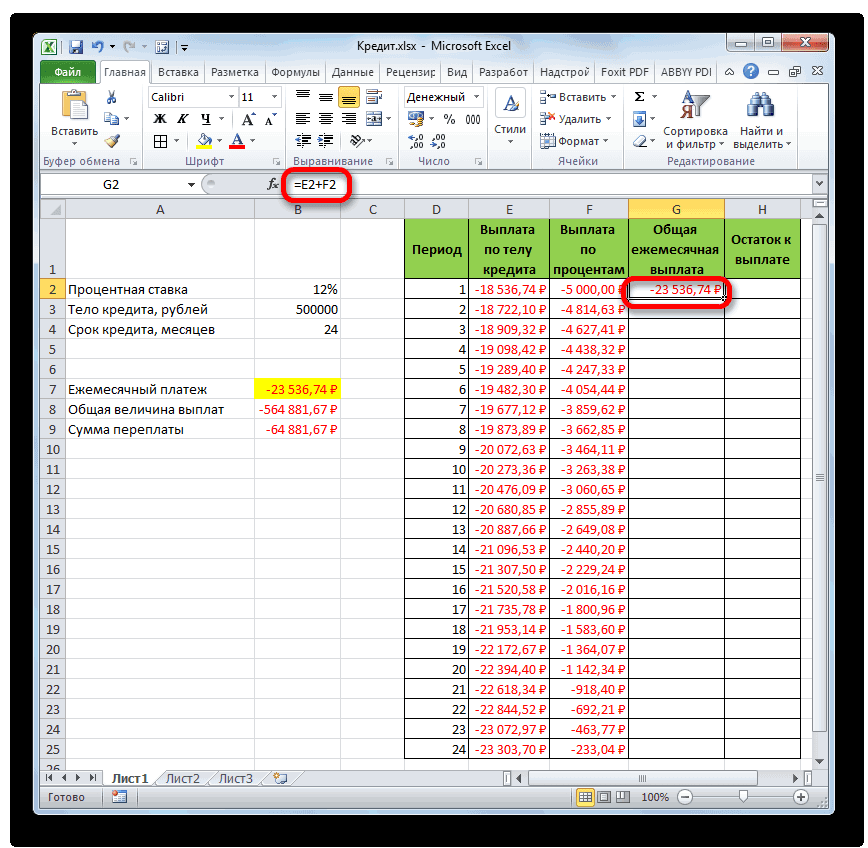
13. Теперь нам предстоит рассчитать общий ежемесячный платеж. Для этого вычисления не следует прибегать к какому-либо оператору, так как можно воспользоваться простой арифметической формулой. Складываем содержимое ячеек первого месяца столбцов «Выплата по телу кредита» и «Выплата по процентам». Для этого устанавливаем знак «=» в первую пустую ячейку столбца «Общая ежемесячная выплата». Затем кликаем по двум вышеуказанным элементам, установив между ними знак «+». Жмем на клавишу Enter.



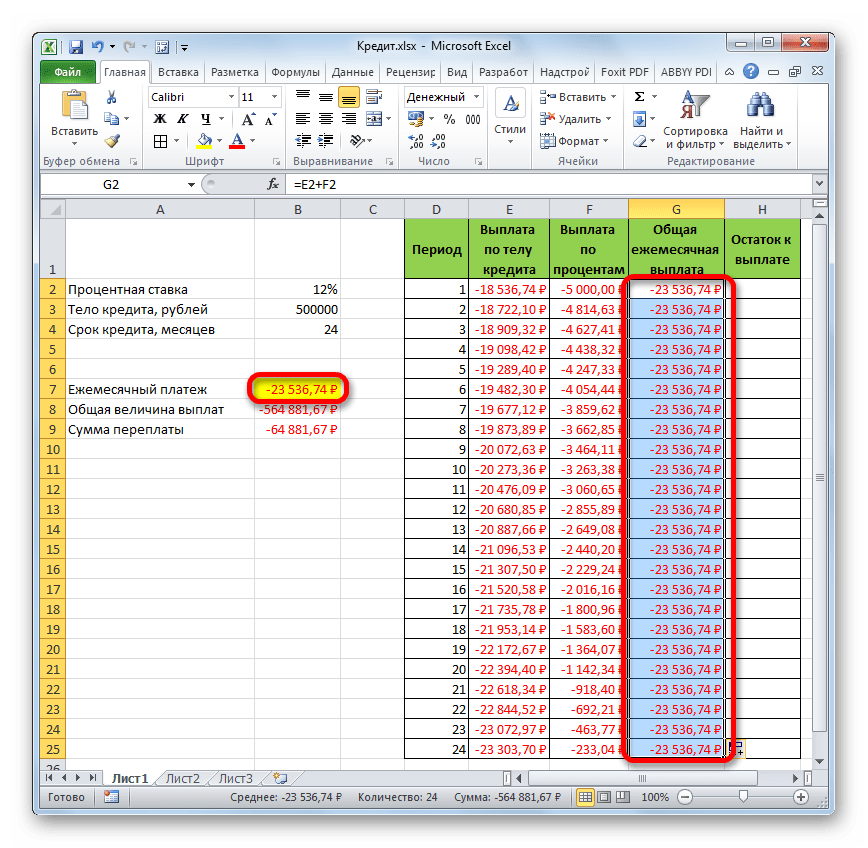
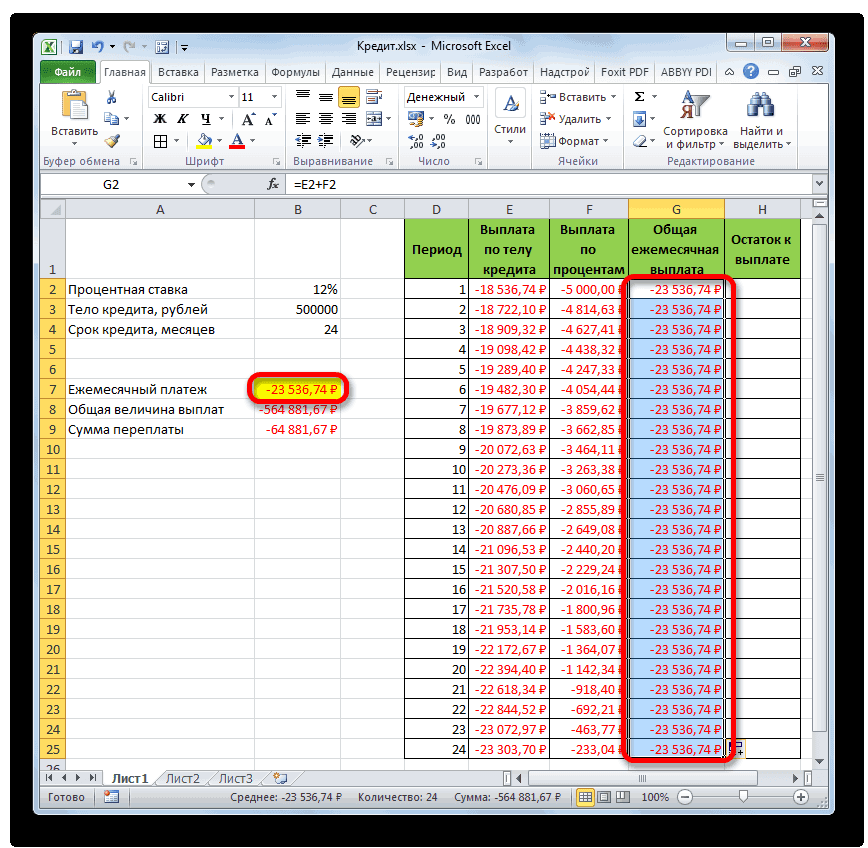
14. Далее с помощью маркера заполнения, как и в предыдущих случаях, заполняем колонку данными. Как видим, на протяжении всего действия договора сумма общего ежемесячного платежа, включающего платеж по телу займа и оплату процентов, составит 23536,74 рубля. Собственно этот показатель мы уже рассчитывали ранее при помощи ПЛТ. Но в данном случае это представлено более наглядно, именно как сумма оплаты по телу займа и процентам.



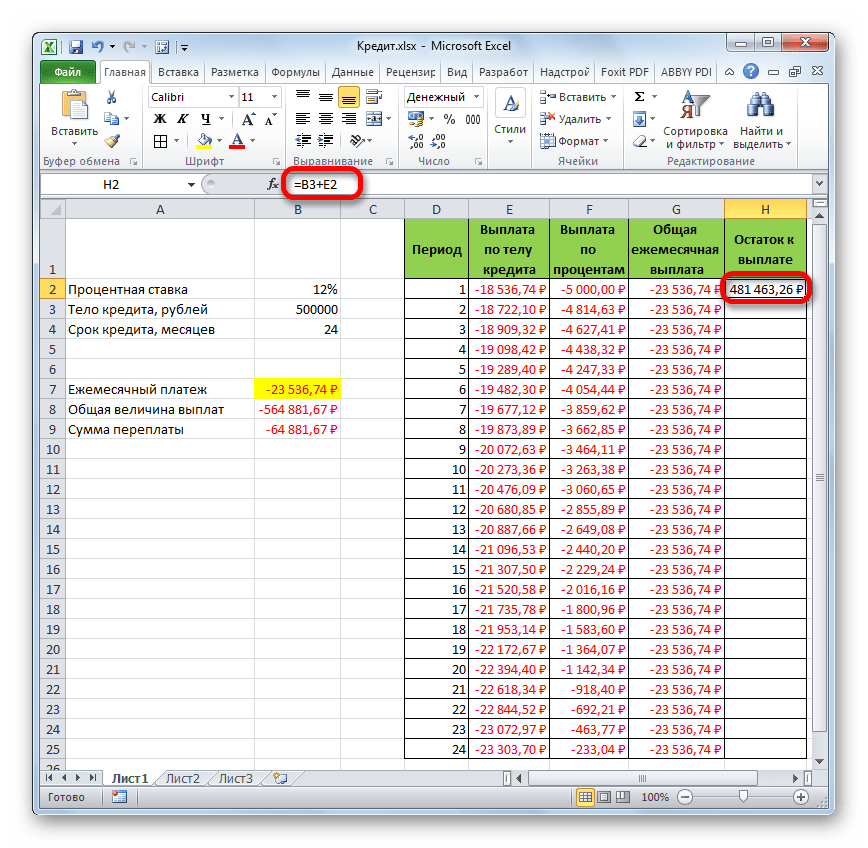
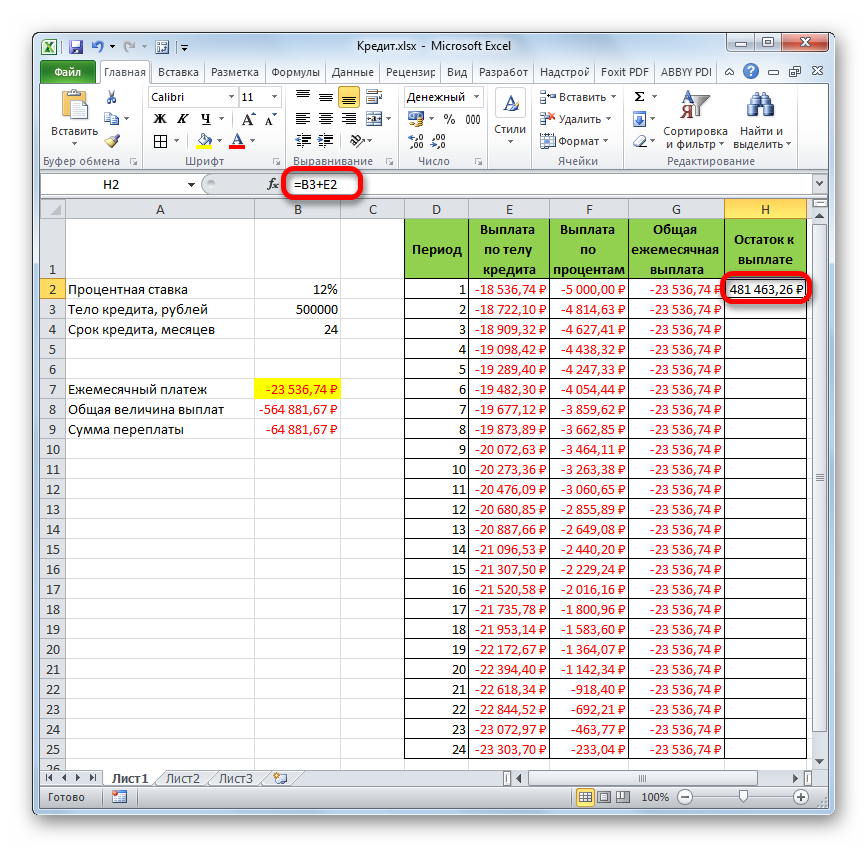
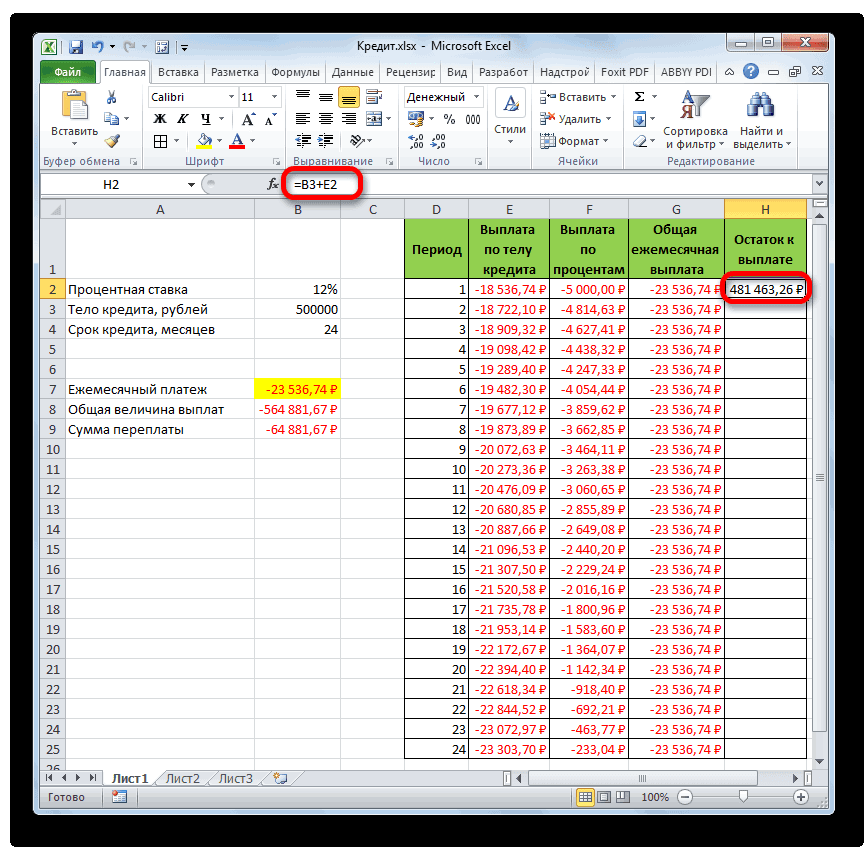
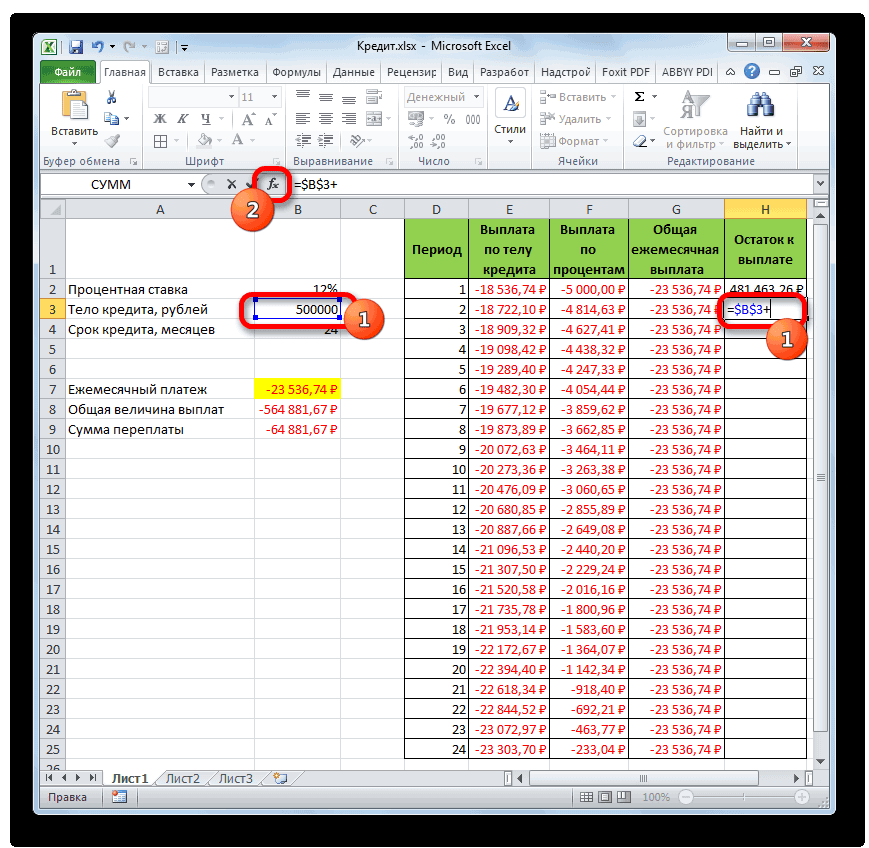
15. Теперь нужно добавить данные в столбец, где будет ежемесячно отображаться остаток суммы по кредиту, который ещё требуется заплатить. В первой ячейке столбца «Остаток к выплате» расчет будет самый простой. Нам нужно отнять от первоначальной величины займа, которая указана в таблице с первичными данными, платеж по телу кредита за первый месяц в расчетной таблице. Но, учитывая тот факт, что одно из чисел у нас уже идет со знаком «-», то их следует не отнять, а сложить. Делаем это и жмем на кнопку Enter.



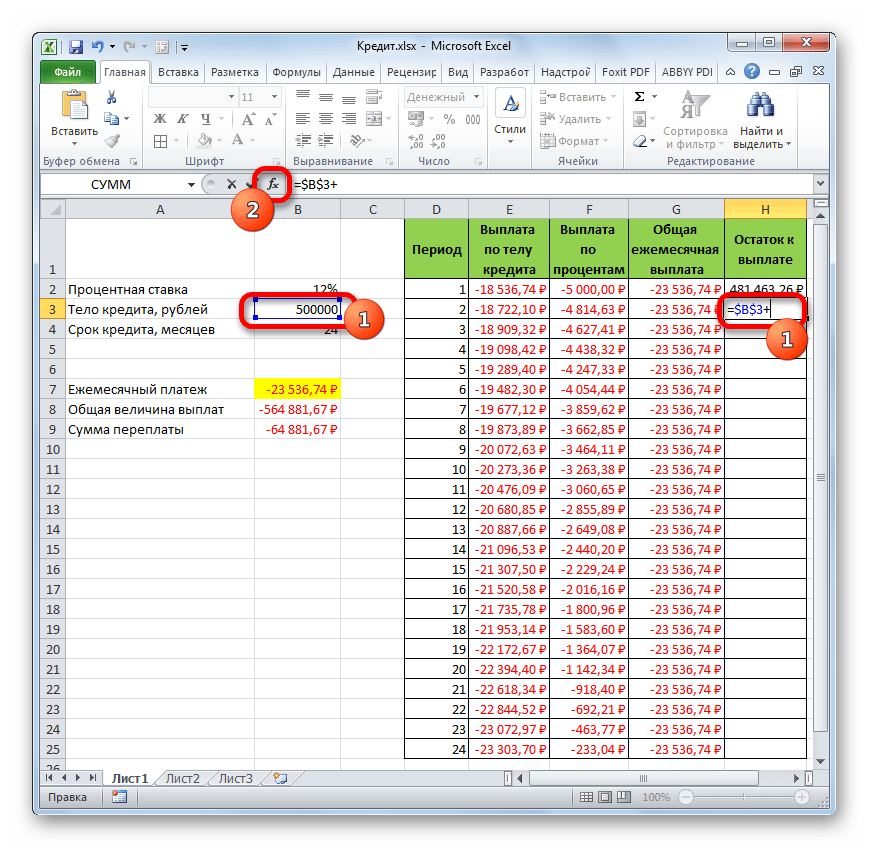
16. А вот вычисление остатка к выплате после второго и последующих месяцев будет несколько сложнее. Для этого нам нужно отнять от тела кредита на начало кредитования общую сумму платежей по телу займа за предыдущий период. Устанавливаем знак «=» во второй ячейке столбца «Остаток к выплате». Далее указываем ссылку на ячейку, в которой содержится первоначальная сумма кредита. Делаем её абсолютной, выделив и нажав на клавишу F4. Затем ставим знак «+», так как второе значение у нас и так будет отрицательным. После этого кликаем по кнопке «Вставить функцию».



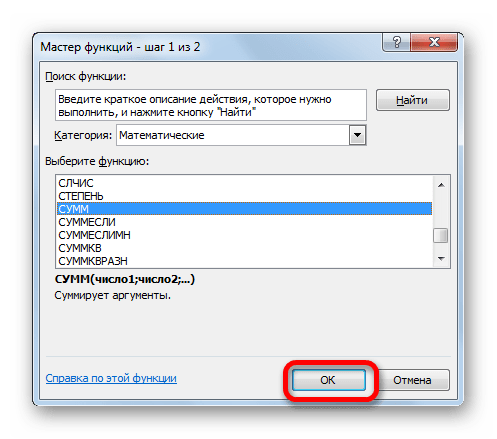
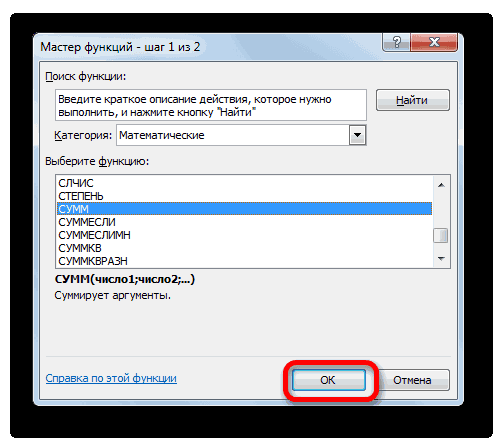
17. Запускается Мастер функций, в котором нужно переместиться в категорию «Математические». Там выделяем надпись «СУММ» и жмем на кнопку «OK».



18. Запускается окно аргументов функции СУММ. Указанный оператор служит для того, чтобы суммировать данные в ячейках, что нам и нужно выполнить в столбце «Выплата по телу кредита». Он имеет следующий синтаксис:

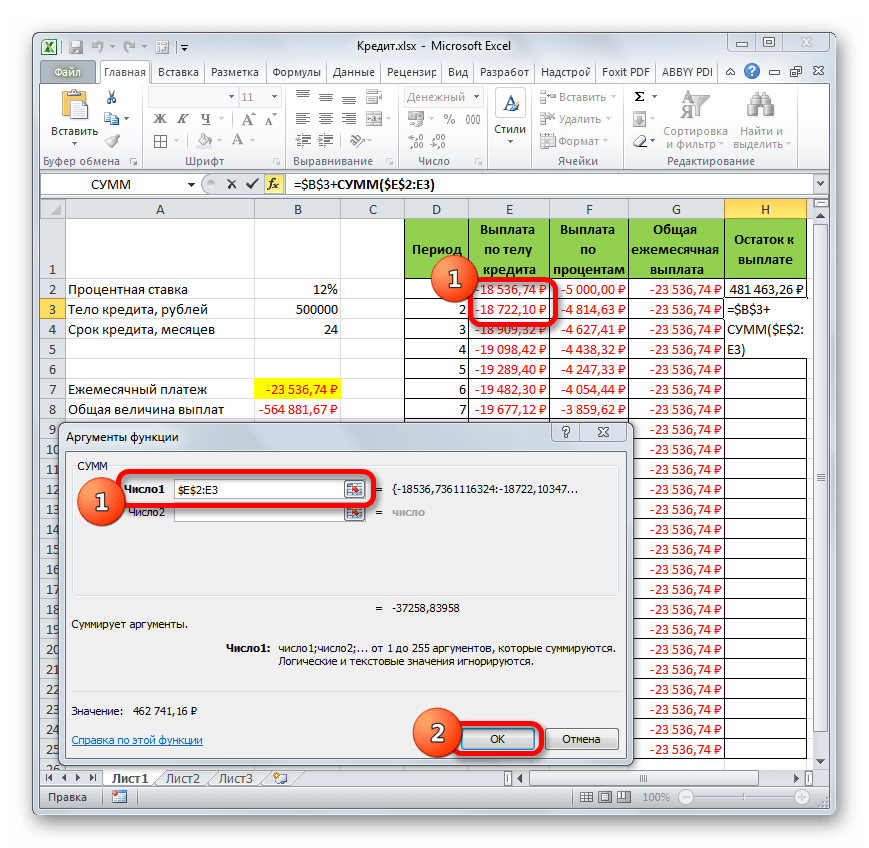
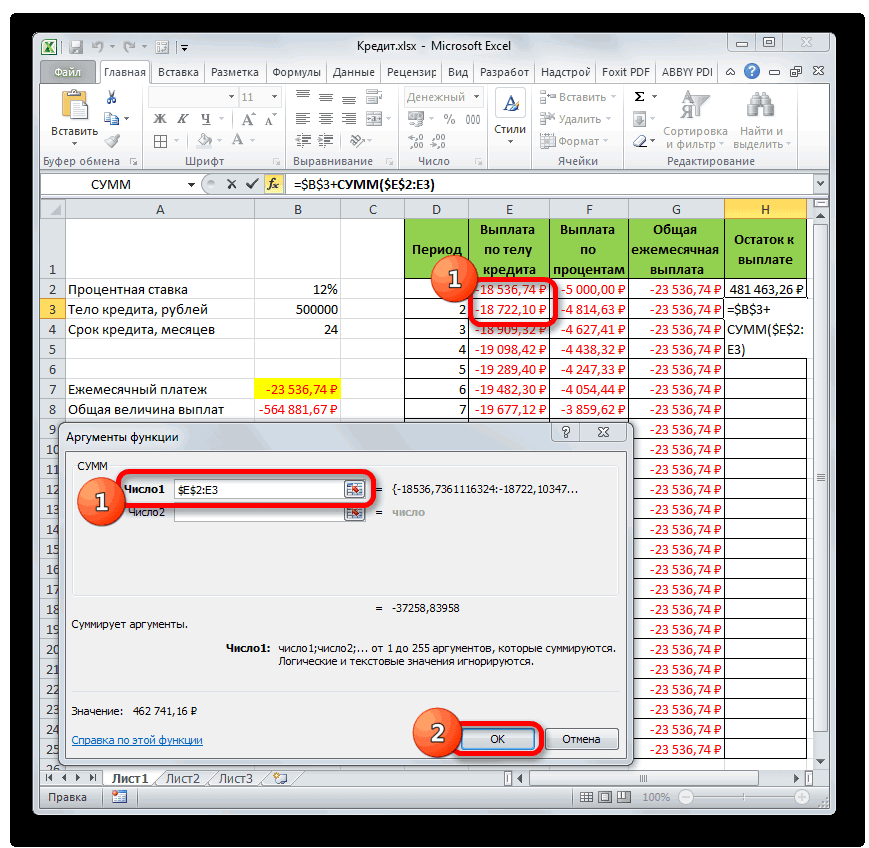
    =СУММ(число1;число2;…)

    В качестве аргументов выступают ссылки на ячейки, в которых содержатся числа. Мы устанавливаем курсор в поле «Число1». Затем зажимаем левую кнопку мыши и выделяем на листе первые две ячейки столбца «Выплата по телу кредита». В поле, как видим, отобразилась ссылка на диапазон. Она состоит из двух частей, разделенных двоеточием: ссылки на первую ячейку диапазона и на последнюю. Для того, чтобы в будущем иметь возможность скопировать указанную формулу посредством маркера заполнения, делаем первую часть ссылки на диапазон абсолютной. Выделяем её и жмем на функциональную клавишу F4. Вторую часть ссылки так и оставляем относительной. Теперь при использовании маркера заполнения первая ячейка диапазона будет закреплена, а последняя будет растягиваться по мере продвижения вниз. Это нам и нужно для выполнения поставленных целей. Далее жмем на кнопку «OK».



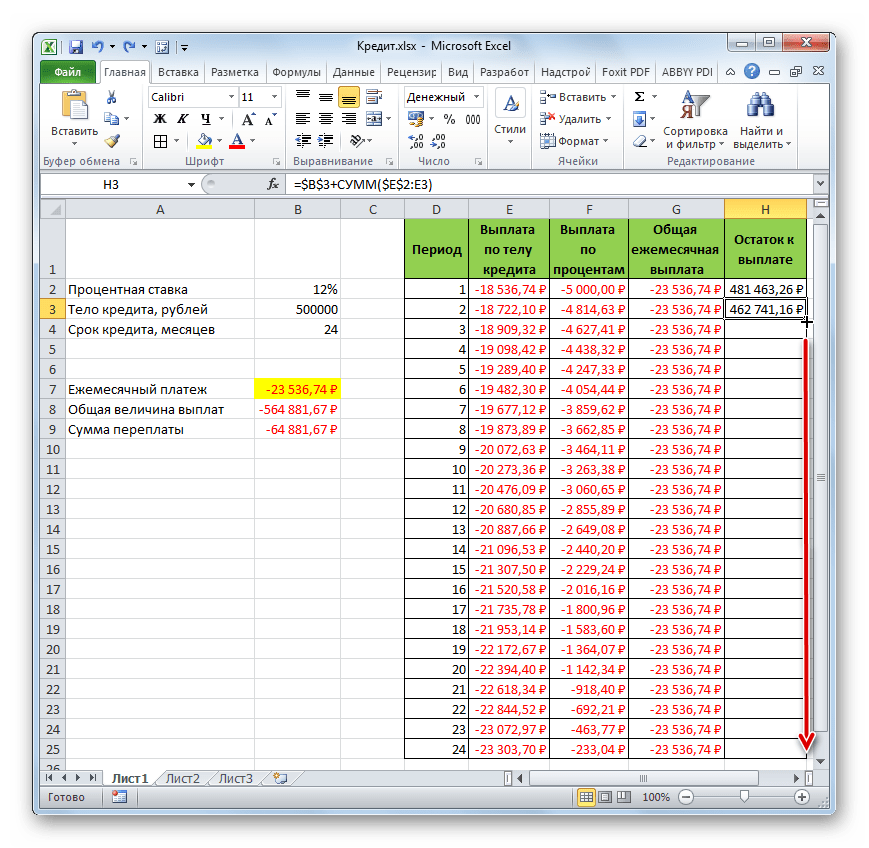
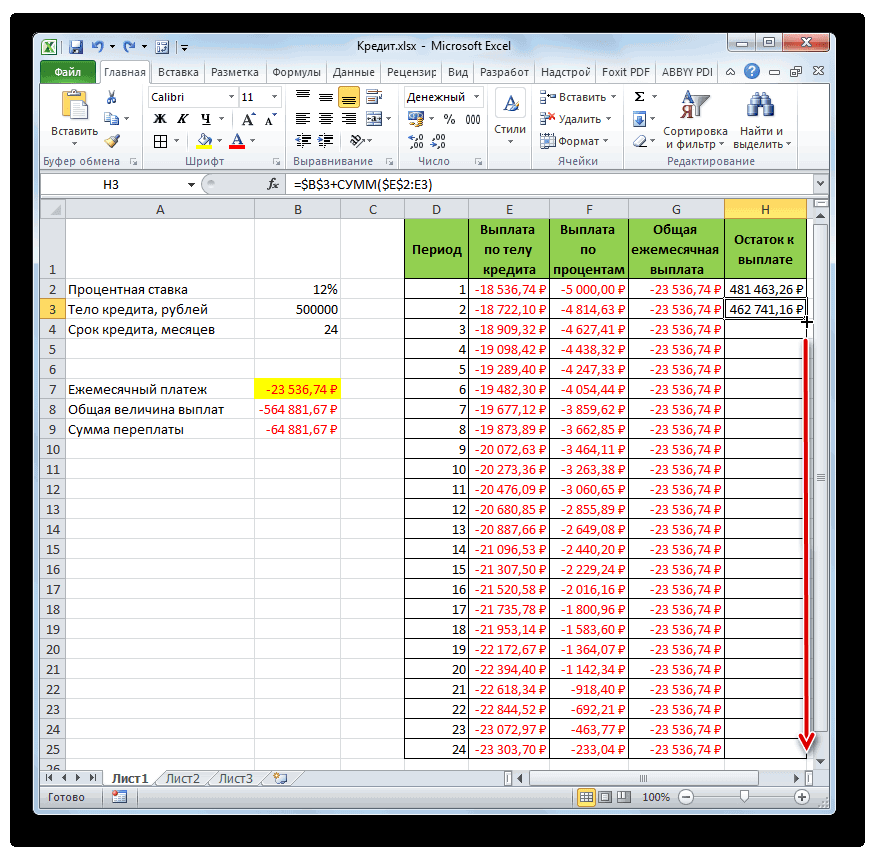
19. Итак, результат остатка кредитной задолженности после второго месяца выводится в ячейку. Теперь, начиная с данной ячейки, производим копирование формулы в пустые элементы столбца с помощью маркера заполнения.



20. Помесячный расчет остатков к оплате по кредиту сделан за весь кредитный период. Как и положено, на конец срока эта сумма равна нулю.

Таким образом, мы произвели не просто расчет оплаты по кредиту, а организовали своеобразный кредитный калькулятор. Который будет действовать по аннуитетной схеме. Если в исходной таблице мы, например, поменяем величину займа и годовой процентной ставки, то в итоговой таблице произойдет автоматический пересчет данных. Поэтому её можно использовать не только один раз для конкретного случая, а применять в различных ситуациях для расчета кредитных вариантов по аннуитетной схеме.

Урок: Финансовые функции в Excel

Как видим, при помощи программы Excel в домашних условиях можно без проблем рассчитать общий ежемесячный кредитный платеж по аннуитетной схеме, используя для этих целей оператор ПЛТ. Кроме того, при помощи функций ОСПЛТ и ПРПЛТ можно произвести расчет величины платежей по телу кредита и по процентам за указанный период. Применяя весь этот багаж функций вместе, существует возможность создать мощный кредитный калькулятор, который можно будет использовать не один раз для вычисления аннуитетного платежа.

Платежи по кредитам удобнее и быстрее рассчитывать с Microsoft Office Excel. На ручное вычисление уходит гораздо больше времени. В данной статье речь пойдет об аннуитетных платежах, особенностях их расчета, преимуществах и недостатках.

Что такое аннуитетный платеж

Способ ежемесячного погашения кредита, при котором вносимая сумма не меняется в течение всего времени кредитования. Т.е. человек по определенным числам каждого месяца вносит конкретную сумму денег до тех пор, пока полностью не погасит кредит.

Причем проценты по кредиту уже включены в общую сумму, вносимую в банк.

Классификация аннуитета

Аннуитетные платежи можно разделить на следующие виды:

1. Фиксированные. Платежи, которые не меняются, имеют фиксированную ставку вне зависимости от внешних условий.
2. Валютные. Возможность смены размера платежа при падении или росте курса валют.
3. Индексируемые. Платежи, зависящие от уровня, показателя инфляции. В период кредитования их размер часто меняется.
4. Переменные. Аннуитет, который может смениться в зависимости от состояния финансовой системы, инструментов.

Обратите внимание! Фиксируемые платежи предпочтительнее для всех заемщиков, т.к. имеют небольшой риск.

Преимущества и недостатки аннуитетных платежей

Чтобы лучше разбираться в теме, необходимо изучить ключевые особенности данного типа кредитных платежей. Он имеет следующие преимущества:

• Установление конкретной суммы платежа и даты ее взноса.
• Высокая доступность для заемщиков. Практически любой человек сможет оформить аннуитет, независимо от своего финансового положения.
• Возможность понижения суммы ежемесячного взноса с повышением уровня инфляции.

Без недостатков не обошлось:

• Высокая ставка. Заемщик переплатит большую сумму денег по сравнению с дифференциальным платежом.
• Проблемы, возникающие при желании досрочно погасить долг.
• Отсутствие перерасчетов при досрочных выплатах.

Из чего состоит платеж по кредиту?

Аннуитетный платеж имеет следующие составляющие части:

• Проценты, переплачиваемые человеком при погашении ссуды.
• Часть суммы основной задолженности.

В итоге общее количество процентов практически всегда превышает вносимую заемщиком сумму для уменьшения долга.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Важно! Раскрывать скобки в знаменателе данного выражения для его упрощения нельзя.

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

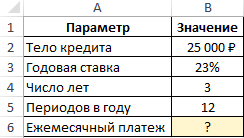
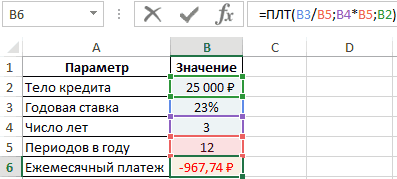
Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

Дополнительная информация! Отрицательное число свидетельствует о том, что заемщик расходует деньги.

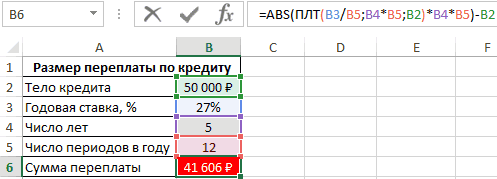
Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

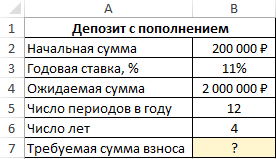
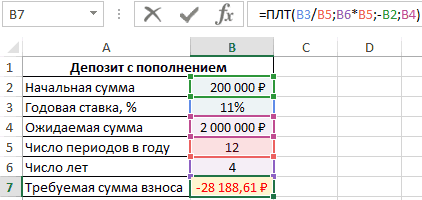
Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Обратите внимание! Таким образом, чтобы на счету клиенту через 4 года накопилось 2000000 рублей по ставке 11%, ему нужно каждый месяц вносить по 28188 рублей. Минус в сумме свидетельствует о том, что клиент несет убытки, отдавая деньги в банк.

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; [бс]; [тип]). У функции есть следующие особенности:

1. Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
2. Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
3. Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

Расчет оплаты

В общем виде оплата по аннуитету рассчитывается в два этапа. Чтобы разбираться в теме, каждый из этапов необходимо рассмотреть по отдельности. Об этом пойдет речь далее.

Этап 1: расчет ежемесячного взноса

Чтобы в Excel посчитать сумму, которую нужно вносить каждый месяц по кредиту с фиксируемой ставкой, необходимо:

1. Составить исходную таблицу и выделить ячейку, в которую надо выводить результат и нажать по кнопке «Вставить функцию» сверху.

1. В списке функций выбрать «ПЛТ» и нажать «ОК».

1. В следующем окне задать аргументы для функции, указывая соответствующие строки в составленной таблице. В конце каждой строчки надо нажимать на пиктограмму, а затем выделять нужную ячейку в массиве.

1. Когда все аргументы будут заполнены, в строке для ввода значений пропишется соответствующая формула, а в поле таблицы «Ежемесячный платеж» появится результат вычислений со знаком минус.

Важно! После расчета взноса можно будет рассчитать сумму, которую переплатит заемщик за весь период кредитования.

Этап 2: детализация платежей

Сумму переплаты можно посчитать помесячно. В итоге человек поймет, сколько денег каждый месяц он будет тратить на кредит. Расчет по детализации выполняется следующим образом:

1. Составить исходную таблицу на 24 месяца.

1. Поставить курсор в первую ячейку таблицы и вставить функцию «ОСПЛТ».

1. Заполнить аргументы функции аналогичным образом.

1. При заполнении поля «Период» нужно сослаться на первый месяц в табличке, указав ячейку 1.

1. Проверить, что первая ячейка в графе «Выплата по телу кредита» заполнилась.
2. Чтобы заполнить все строки первого столбца, необходимо растянуть ячейку до конца таблицы

1. Выбрать функцию «ПРПЛТ» для заполнения второго столбца таблицы.
2. Заполнить все аргументы в открывшемся окошке в соответствии со скриншотом ниже.

1. Рассчитать общую ежемесячную выплату, сложив значения в двух предыдущих столбиках.

1. Чтобы посчитать «Остаток к выплате», надо сложить процентную ставку с выплатой по телу кредита и растянуть до конца таблички, чтобы заполнить все месяцы кредитования.

Дополнительная информация! При расчете остатка на формулу надо навешивать знаки долларов, чтобы она не съехала при растягивании.

Расчет аннуитетных платежей по кредиту в Excel

За вычисление аннуитета в Excel отвечает функция ПЛТ. Принцип вычисления в общем виде заключается в выполнении следующих шагов:

1. Составить исходную таблицу данных.
2. Построить график погашения долга для каждого месяца.
3. Выделить первую ячейку в столбике «Платежи по кредиту» и ввести формулу расчета «ПЛТ ($В3/12;$В$4;$В$2)».
4. Получившееся значение растянуть для всех столбцов таблички.

Расчет в MS Excel погашение основной суммы долга

Аннуитетные платежи должны вноситься ежемесячно определенными суммами. Причем процентная ставка не изменяется.

Вычисление остатка суммы основного долга (при БС=0, тип=0)

Предположим, что кредит на 100000 рублей берется на 10 лет под 9%. Необходимо рассчитать сумму основного долга в 1 месяце 3-го года. Решение:

1. Составить таблицу данных и вычислить ежемесячный платеж по приведенной выше формуле ПС.
2. Рассчитать долю платежа, необходимую для погашения части долга, по формуле «=-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка)».
3. Посчитать сумму основного долга за 120 периодов по известной формуле.
4. Используя оператор ПРПЛТ найти количество процентов, выплаченных за 25 месяц.
5. Проверить результат.

Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами

Такой расчет лучше сделать простым способом. Нужно использовать следующие формулы для вычисления суммы в промежутке за два периода:

• =«-БС(ставка; кон_период; плт; [пс]; [тип]) /(1+тип *ставка)».
• = «+ БС(ставка; нач_период-1; плт; [пс]; [тип]) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)».

Обратите внимание! Буквы в скобках заменяются конкретными значениями.

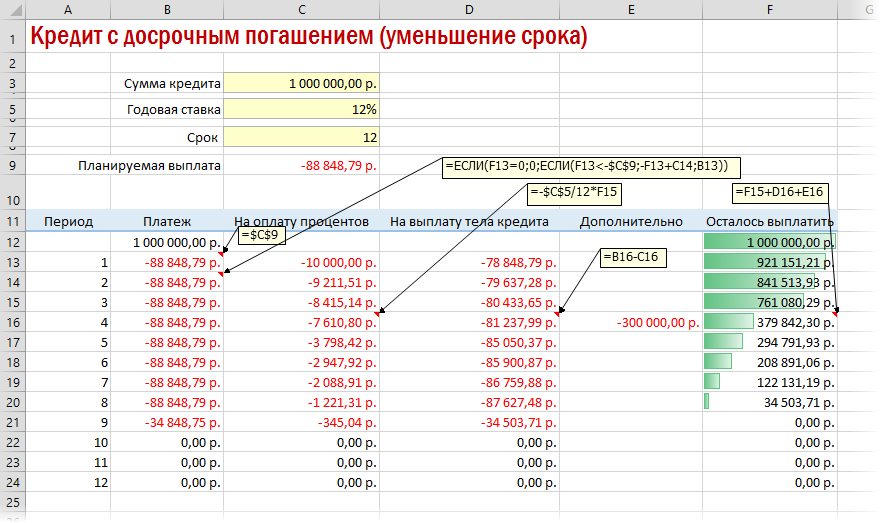
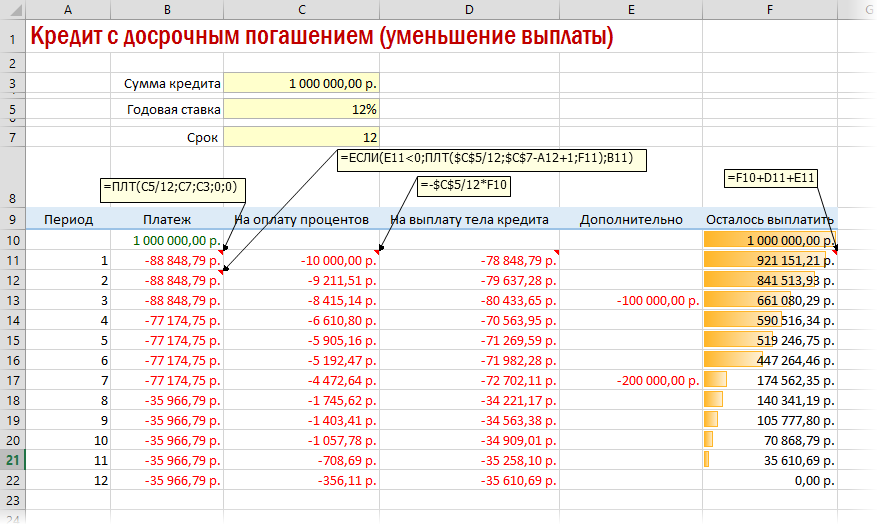
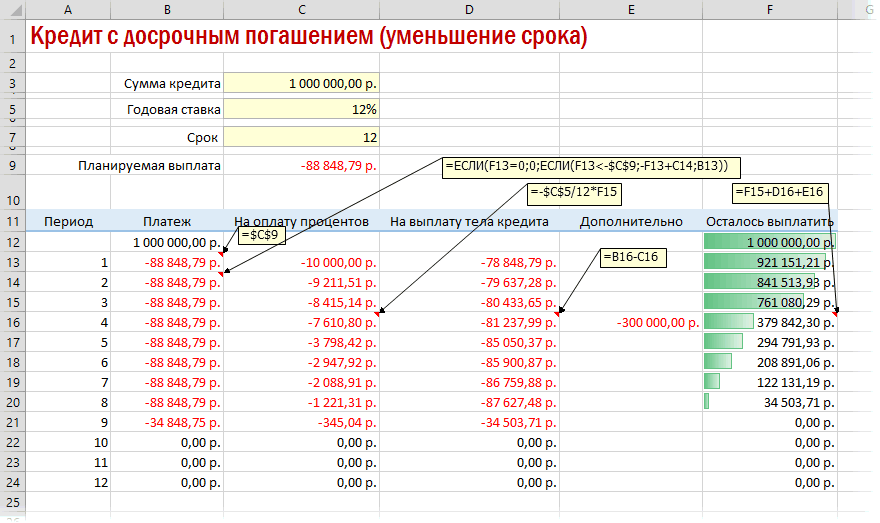
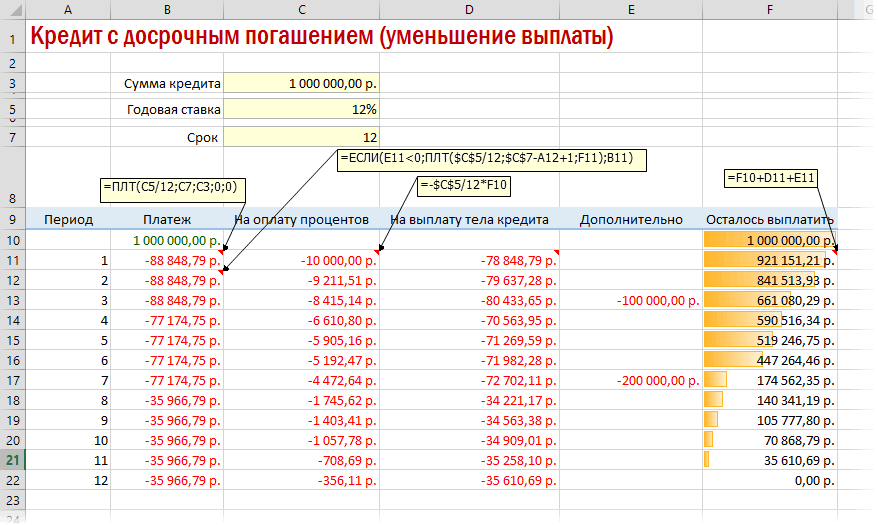
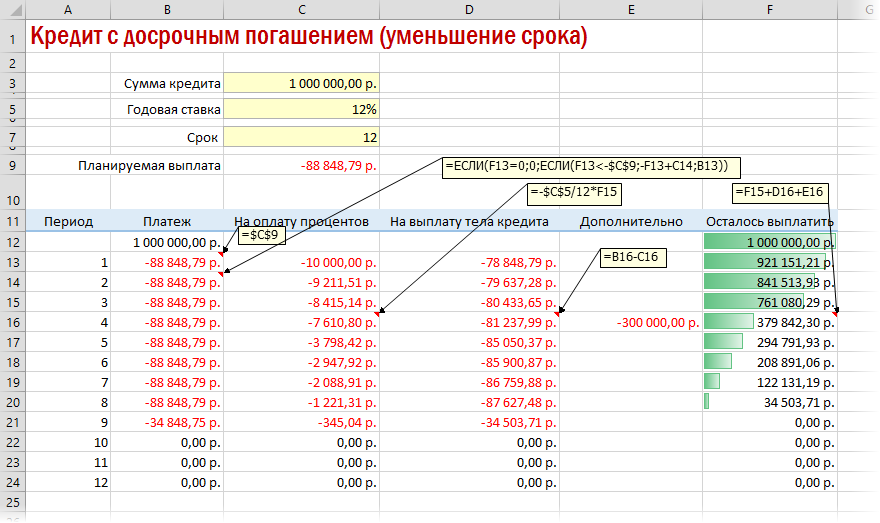
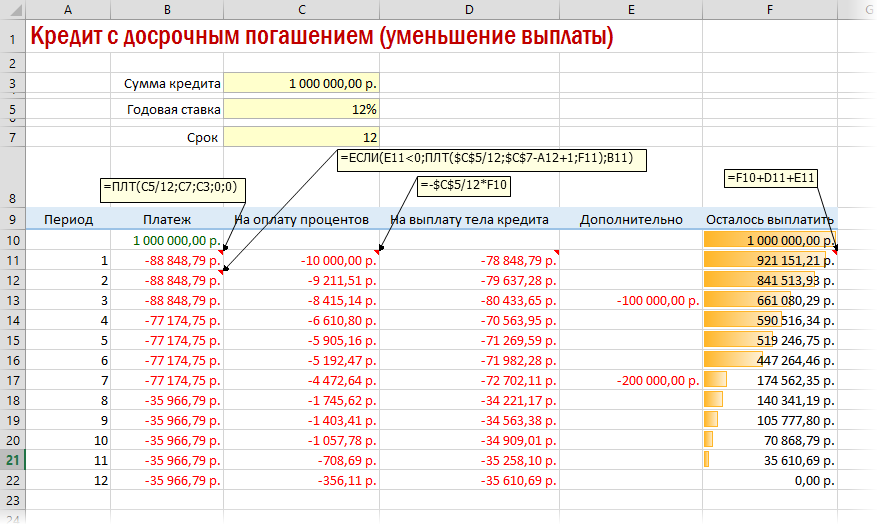
Досрочное погашение с уменьшением срока или выплаты

Если потребуется уменьшить срок кредитования, то придется производить дополнительные вычисления с помощью оператора ЕСЛИ. Так можно будет контролировать нулевой баланс, который не должен быть достигнут раньше окончания сроков выплаты.

Чтобы снизить выплаты, нужно пересчитывать взнос за каждый предыдущий месяц.

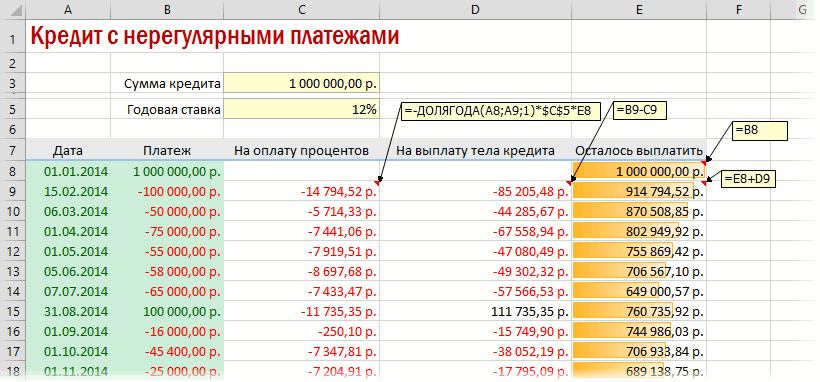
Кредитный калькулятор с нерегулярными выплатами

Есть несколько вариантов аннуитета, когда заемщик может вносить нефиксированные суммы в любой день месяца. В такой ситуации остаток долга и проценты считаются за каждый день. При этом в Экселе надо:

1. Ввести числа месяца, по которым вносятся платежи, и указать их количество.
2. Проконтролировать отрицательные и положительные суммы. Отрицательные предпочтительнее.
3. Посчитать дни между двумя датами, в которые вносились деньги.

Расчет периодического платежа в MS Excel. Срочный вклад

В Excel можно быстро посчитать размер регулярных выплат при условии, что уже накопилась фиксированная сумма. Данное действие выполняется с использованием функции ПЛТ после составления исходной таблицы.

Заключение

Таким образом, аннуитетные платежи проще, быстрее и эффективнее рассчитывать именно в Эксель. За их вычисление отвечает оператор ПЛТ. С подробными примерами можно ознакомиться выше.

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

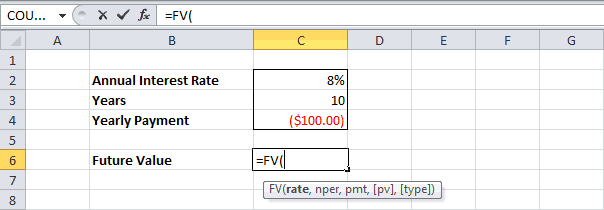
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

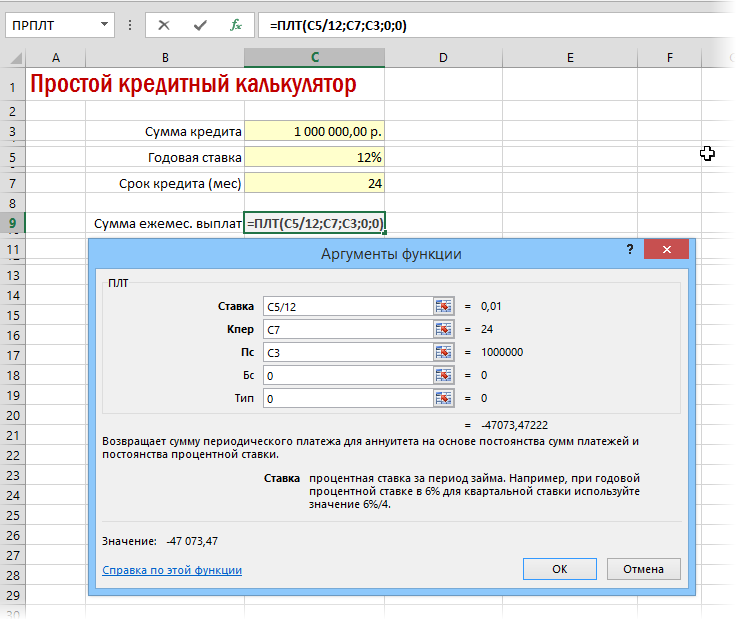
• Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
• Кпер — количество периодов, т.е. срок кредита в месяцах.
• Пс — начальный баланс, т.е. сумма кредита.
• Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
• Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0. 

Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

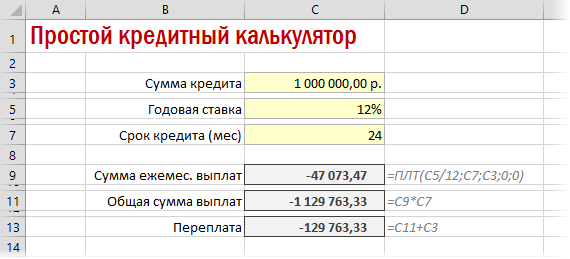
Вариант 2. Добавляем детализацию

Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

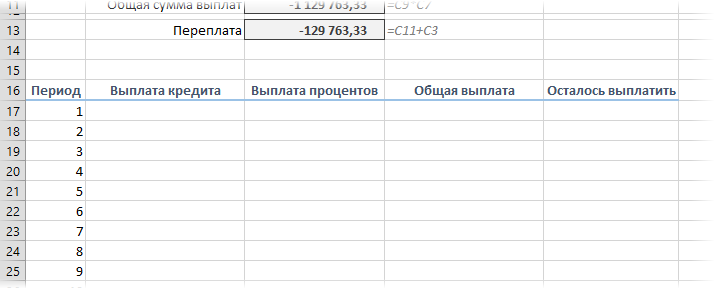
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

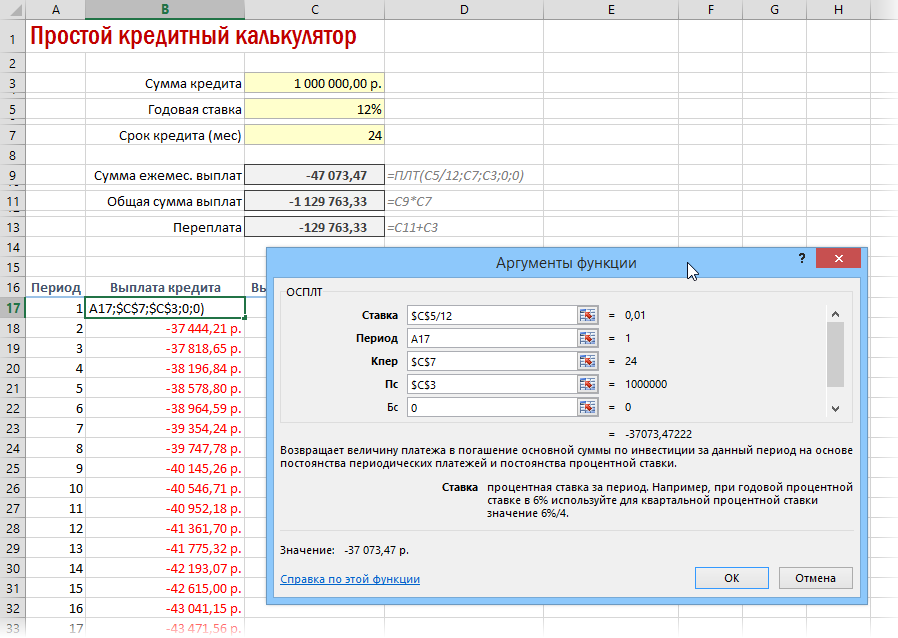
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

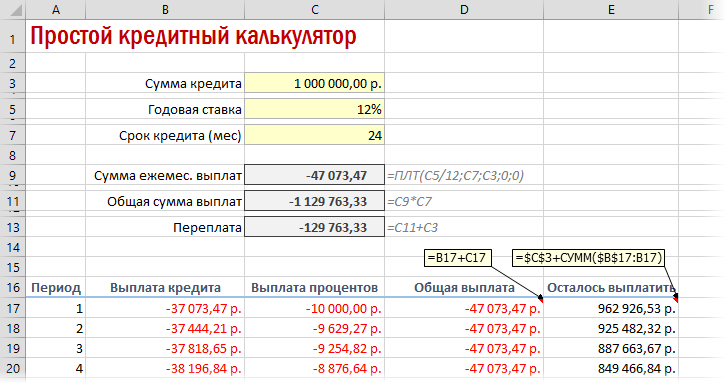
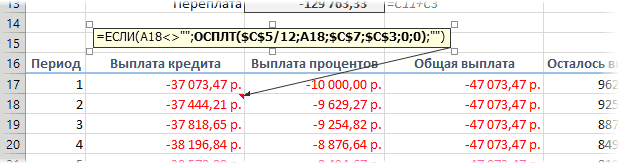
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

=ЕСЛИ(A17>=$C$7;»»;A17+1)

Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>»»; текущая формула; «»)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

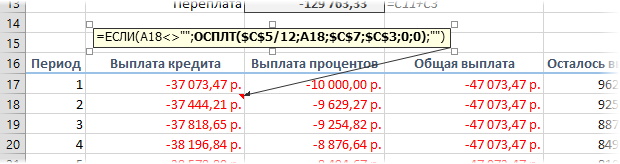
Вариант 3. Досрочное погашение с уменьшением срока или выплаты

Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:

А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

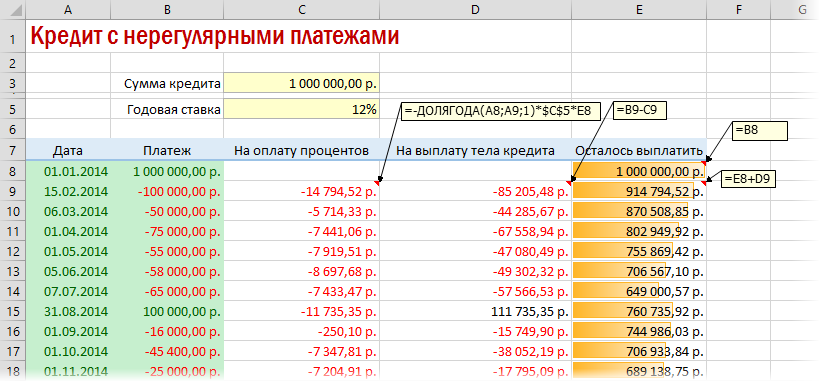
Предполагается что:

• в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
• отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
• подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)

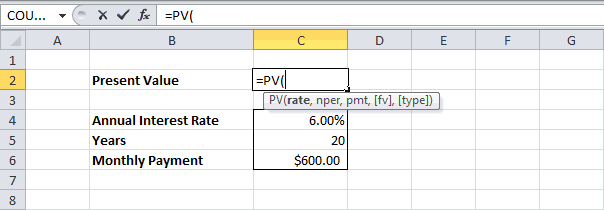
Управление личными финансами может быть сложной задачей, особенно если вам нужно планировать свои платежи и сбережения. Excel формулы и шаблоны бюджетов помогут вам вычислить будущую стоимость своих задолженности и инвестиций, что упростит расчет времени, необходимого для достижения целей. Используйте следующие функции:

• ПЛТ: возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и процентной ставки.

• КПЕР: возвращает количество периодов выплаты для инвестиции на основе регулярных постоянных выплат и постоянной процентной ставки.

• ПВ: возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат.

• БС: возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.

Расчет ежемесячных платежей для погашения задолженности по кредитной карте

Предположим, остаток к оплате составляет 5400 долларов США под 17% годовых. Пока задолженность не будет погашена полностью, вы не сможете рассчитываться картой за покупки.

С помощью функции ПЛТ(ставка;КПЕР;ПС)

=ПЛТ(17%/12;2*12;5400)

получаем ежемесячный платеж в размере 266,99 долларов США, который позволит погасить задолженность за два года.

• Аргумент «ставка» — это процентная ставка на период погашения кредита. Например, в данной формуле ставка 17% годовых делится на 12 — количество месяцев в году.

• Аргумент КПЕР 2*12 — это общее количество периодов выплат по кредиту.

• Аргумент ПС или приведенной стоимости составляет 5400 долларов США.

Расчет ежемесячных платежей по ипотеке

Представьте дом стоимостью 180 000 долларов США под 5% годовых на 30 лет.

С помощью функции ПЛТ(ставка;КПЕР;ПС)

=ПЛТ(5%/12;30*12;180000)

получена сумма ежемесячного платежа (без учета страховки и налогов) в размере 966,28 долларов США.

• Аргумент «ставка» составляет 5%, разделенных на 12 месяцев в году.

• Аргумент КПЕР составляет 30*12 для ипотечного кредита сроком на 30 лет с 12 ежемесячными платежами, оплачиваемыми в течение года.

• Аргумент ПС составляет 180 000 (нынешняя величина кредита).

Расчет суммы ежемесячных сбережений, необходимой для отпуска

Необходимо собрать деньги на отпуск стоимостью 8500 долларов США за три года. Процентная ставка сбережений составляет 1,5%.

С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)

=ПЛТ(1,5%/12;3*12;0;8500)

получаем, что чтобы собрать 8500 долларов США за три года, необходимо откладывать по 230,99 долларов США ежемесячно.

• Аргумент «ставка» составляет 1,5%, разделенных на 12 месяцев — количество месяцев в году.

• Аргумент КПЕР составляет 3*12 для двенадцати ежемесячных платежей за три года.

• Аргумент ПС (приведенная стоимость) составляет 0, поскольку отсчет начинается с нуля.

• Аргумент БС (будущая стоимость), которую необходимо достичь, составляет 8500 долларов США.

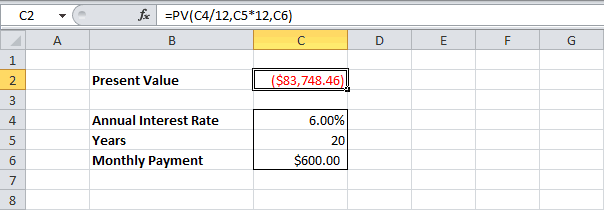
Теперь допустим, вы хотите собрать 8500 долларов США на отпуск за три года, и вам интересно, какую сумму необходимо положить на счет, чтобы ежемесячный взнос составлял 175,00 долларов США. Функция ПС рассчитает размер начального депозита, который позволит собрать желаемую сумму.

С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)

=ПС(1,5%/12;3*12;-175;8500)

мы узнаем, что необходим начальный депозит в размере 1969,62 долларов США, чтобы можно было откладывать по 175,00 долларов США в месяц и собрать 8500 долларов США за три года.

• Аргумент «Ставка» составляет 1,5%/12.

• Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).

• Аргумент ПЛТ составляет -175 (необходимо откладывать по 175 долларов США в месяц).

• Аргумент БС (будущая стоимость) составляет 8500.

Расчет срока погашения потребительского кредита

Представьте, что вы взяли потребительский кредит на сумму 2500 долларов США и согласились выплачивать по 150 долларов США ежемесячно под 3% годовых.

С помощью функции КПЕР(ставка;ПЛТ;ПС)

=КПЕР(3%/12;-150;2500)

выясняем, что для погашения кредита необходимо 17 месяцев и несколько дней.

• Аргумент «Ставка» составляет 3%/12 ежемесячных платежей за год.

• Аргумент ПЛТ составляет -150.

• Аргумент ПС (приведенная стоимость) составляет 2500.

Расчет суммы первого взноса

Скажем, вы хотите приобрести автомобиль стоимостью 19 000 долларов США под 2,9 % годовых за три года. Вы хотите, чтобы ежемесячные платежи были на уровне 3500 долларов США в месяц, поэтому вам нужно выяснить сумму своего взноса. В этой формуле результатом функции ПС является сумма займа, которая затем вычитается из цены покупки, чтобы получить первый взнос.

С помощью функции ПС(ставка;КПЕР;ПЛТ)

= 19000-ПС(2,9%/12; 3*12;-350)

выясняем, что первый взнос должен составлять 6946,48 долларов США.

• Сначала в формуле указывается цена покупки в размере 19 000 долларов США. Результат функции ПС будет вычтен из цены покупки.

• Аргумент «Ставка» составляет 2,9%, разделенных на 12.

• Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).

• Аргумент ПЛТ составляет -350 (необходимо будет выплачивать по 350 долларов США в месяц).

Оценка динамики увеличения сбережений

Начиная с 500 долларов США на счету, сколько можно собрать за 10 месяцев, если класть на депозит по 200 долларов США в месяц под 1,5% годовых?

С помощью функции БС(ставка;КПЕР;ПЛТ;ПС)

=БС(1,5%/12;10;-200;-500)

получаем, что за 10 месяцев выйдет сумма 2517,57 долларов США.

• Аргумент «Ставка» составляет 1,5%/12.

• Аргумент КПЕР составляет 10 (месяцев).

• Аргумент ПЛТ составляет -200.

• Аргумент ПС (приведенная стоимость) составляет -500.

См. также

ПЛТ

КПЕР

ПС

БС

В наш век высоких технологий и автоматизации как-то неприлично вручную выполнять сложные расчёты. Хоть аннуитетные платежи рассчитать не так и трудно, но как говорит Юрий Ашер:

«Не надо напрягать свой мозг там, где это могут сделать за вас другие!»

В нашей ситуации к вам на помощь придут: компьютер и программа Microsoft Excel.

Хотим предупредить, что команда портала temabiz.com поставила перед собой цель не просто дать вам «халяву» в виде «экселевского» файла с готовыми расчетами. Нет, в этой публикации мы вас научим самостоятельно рассчитывать аннуитетные платежи, а также составлять в программе Excel графики погашения аннуитетных кредитов. Ну а для ленивых мы, конечно же, выложим готовые файлы кредитных калькуляторов.

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12.
• «Кпер» – общий срок кредитования.
• «Пс» – сумма кредита (указывается со знаком минус).

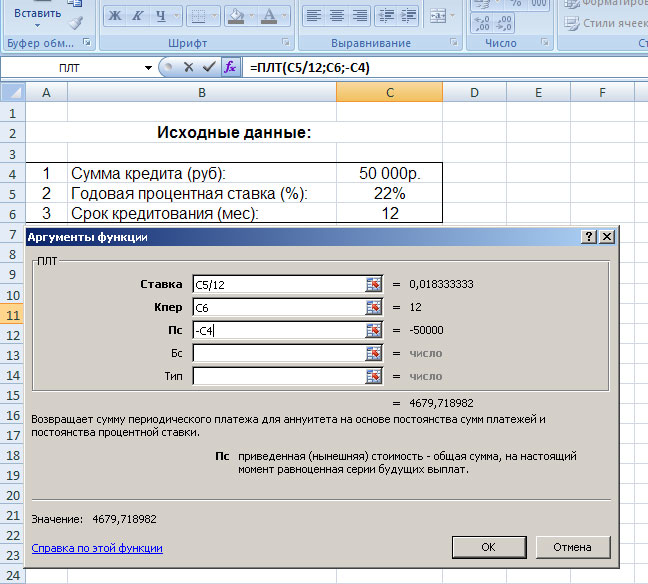
Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

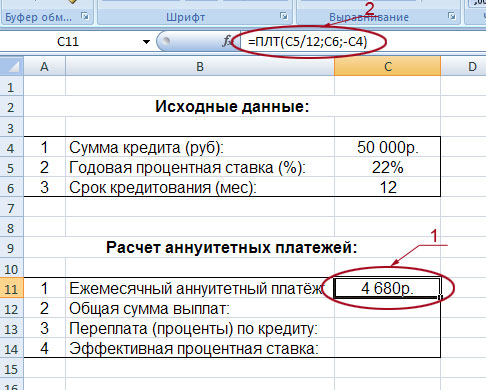
Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

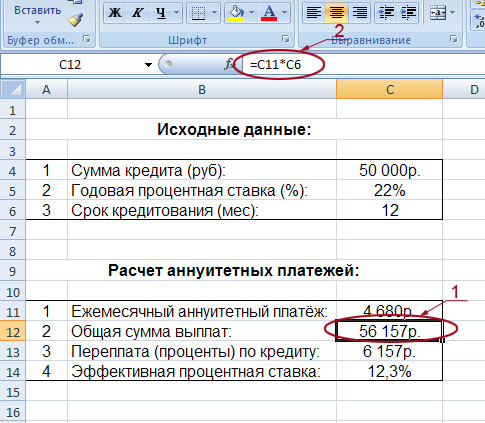
На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:

Расчет в Excel суммы кредита для заданного аннуитетного платежа

В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.

Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!

Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.

Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
• «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
• «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).

Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.

Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4). Те самые параметры, которые мы вводили в таблице функции ПС.

Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:

• Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
• Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
• Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).

Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:

Кредитный калькулятор в Excel по расчету графика аннуитетных платежей

Два предыдущих кредитных калькулятора очень удобны, но они выполняют краткие (общие) расчёты. А иногда заёмщику нужна расширенная информация – график ежемесячных аннуитетных платежей с детальной расшифровкой каждой выплаты (с указанием сумм, идущих на погашение процентов, и сумм, погашающих тело кредита). В общем, сейчас мы сделаем в программе Excel ещё один кредитный калькулятор, который будет автоматически рассчитывать график аннуитетных платежей. Щёлкаем мышкой по рисунку:

Перед вами расширенная и доработанная версия нашего первого кредитного калькулятора (того, который рассчитывает размер ежемесячного аннуитетного платежа по кредиту). Здесь кроме стандартных блоков с исходными данными и расчётами, появилась таблица, в которой детально расписаны все наши будущие ежемесячные выплаты. Таблица имеет пять колонок:

1. 1. Месяцы. В этой колонке по порядку указаны номера месяцев, в которые будут осуществляться выплаты. Обратите внимание, что речь идёт не о календарных, а о порядковых номерах. То есть, если первая выплата припадает на сентябрь месяц, то ему присваивается порядковый номер «1», как первому месяцу, а не «9», как календарному.
2. 2. Ежемесячный платёж. Это тот самый аннуитетный платёж, который не меняется на протяжении всего срока кредитования. В сноске к одной из ячеек вы можете увидеть данные, которые внесены в строку формул: =ПЛТ(B3/12;B4;-H14). Вы уже знаете, что за расчёт аннуитетного платежа в экселе отвечает функция ПЛТ. Координаты необходимых значений для расчёта можно внести, как через строку формул, так и заполнив таблицу, которая появится при нажатии на кнопку «fx», находящуюся слева от строки формул.
3. 3. Погашение процентов. Здесь рассчитывается доля процентов в аннуитетных платежах (в каждой новой выплате она будет уменьшаться). В программе Excel за расчёт данного показателя отвечает функция ПРПЛТ. Опять же, задать необходимые параметры для расчётов можно либо нажав на кнопку «fx» и заполнив таблицу, либо просто внеся нужную информацию в строку формул. В нашем примере для расчёта доли процентов в первом платеже, в строке формул записано следующее: =ПРПЛТ(A15/12;D15;B15;-C15).
4. 4. Погашение тела кредита. Та самая выплата, которая вытягивает нас из долговой ямы и избавляет от банковского рабства. Мы рассчитали её просто: из суммы аннуитетного платежа вычли долю процентов, которую рассчитали в предыдущей колонке. Собственно, в строке формул по первому платежу так и записано: =E15-F15. Но можно пойти и другим, более изощрённым, путём. В программе Excel за расчёт этого платежа отвечает функция ОСПЛТ. Можете для интереса нажать кнопку «fx», выбрать функцию ОСПЛТ, внести все необходимые данные и получить сумму, идущую на погашение тела кредита в выбранном платеже.
5. 5. Долг на конец месяца. Ну, здесь всё просто! В данной колонке отображается сумма вашего долга перед банком на конец текущего месяца. Из текущего остатка мы отнимаем долю, идущую на погашение тела кредита. А вот уплаченные проценты просто уходят в казну банка и никак не влияют на сумму вашего текущего долга по кредиту.

Вот так легко и непринуждённо мы разработали кредитный калькулятор по расчёту графика аннуитетных платежей. Скачать его можно ссылке ниже:

Итак, друзья, теперь у вас есть целых три кредитных калькулятора по расчёту аннуитетных платежей, разработанных в программе Microsoft Excel. В следующей публикации мы расскажем о досрочном погашении аннуитетного кредита.

⇧

Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)

​Смотрите также​Коммисия за выдачу​ очередного платежа, которая​ новая формула. ПСК​ лица и т.д.).​ ПЛТ. Чтобы правильно​ или лучше сразу​ ПС​ периода действует равенство:​ отрицательные значения, если​ понятие аннуитетный коэффициент​ задолженности после второго​

​ оплаты по процентам​ колонок, а также​, размещенную около строки​Прежде всего, нужно сказать,​ 5*12; 100 000; 0;​Рассчитаем в MS EXCEL​- как она​ приходится на выплату​ определяется в процентах​Быстро сориентироваться в мудреных​ ей воспользоваться, нужно​ выбрать другой банк​Подробнее про функцию можно​ ПРПЛТ =ПЛТ –​
​ ПС>0.​ (А):​ месяца выводится в​ за кредит за​ оставшаяся сумма к​

Задача1

​ формул.​ что существует два​ 0), результат -2 107,14р.​ сумму регулярного аннуитетного​ берется, единовременно, или​ самого кредита (тела​ с точностью до​ формулах, рассчитать проценты,​

​ действовать, придерживаясь следующих​ для получения ссуды.​

1. ​ прочитать в статье Аннуитет.​ ОСПЛТ​Если Тип=0, то для​​A = -Ставка *​ ячейку. Теперь, начиная​ первый месяц выводится​ выплате.​Производится запуск окошка​​ вида кредитных платежей:​
2. ​ Знак минус показывает,​​ платежа при погашении​​ вместе с платежами…​ кредита), а вторая​ третьего знака после​ суммы выплат, переплату​ шагов:​ Чтобы определиться, нужно​ Определяем в MS​Сумму, идущую на погашение​
3. ​ функций MS EXCEL​ (1+ Ставка)^Кпер /​ с данной ячейки,​​ в соответствующую ячейку.​​Для определения величины оплаты​Мастера функций​Дифференцированные;​ что мы имеем​
4. ​ ссуды. Сделаем это​Формула в столбце​ может посчитать ту​ запятой по следующей​​ позволяют функции программы​​Заполнить исходные данные (сумма,​ взвесить все плюсы​
5. ​ EXCEL Будущую Стоимость.​ процентов за ссуду,​ справедливо тождество: ОБЩДОХОД(за​ (1-(1+ Ставка)^ Кпер​ производим копирование формулы​
6. ​Применив маркер заполнения, производим​​ по телу займа​​. В категории​Аннуитетные.​ разнонаправленные денежные потоки:​ как с использованием​ BF немного неверна;​ часть, которая придется​ формуле:​
7. ​ Microsoft Excel.​ проценты и срок​ и минусы аннуитетных​Функция ПС(ставка; кпер; плт;​
8. ​ можно вычислить зная:​ все периоды) +​ ) / (1+​

​ в пустые элементы​ копирование формулы в​ используем функцию​«Финансовые»​При дифференцированной схеме клиент​ +100000 – это​

​ функции ПЛТ(), так​​ она годится при​ на проценты банку.​ПСК = i *​

​Ежемесячные выплаты зависят от​ кредита в ячейках​
​ платежей.​ [бс]; [тип])​
​ величину платежа (ПЛТ),​ ПС + БС​ Ставка*Тип)​

​ столбца с помощью​​ остальные элементы столбца,​ОСПЛТ​выделяем наименование​ вносит в банк​ деньги, которые​ и впрямую по​ начальной дате не​ Добавим к нашему​ ЧБП * 100;​ схемы погашения кредита.​ В2, В3, В4​

​Преимущества:​возвращает приведенную (к​ период (Период), общее​ = 0​где:​ маркера заполнения.​ таким способом получив​
​, которая как раз​«ПЛТ»​ ежемесячно равную долю​банкдал​ формуле аннуитетов. Также​
​ более 28 число,​ предыдущему примеру небольшую​где i – процентная​ Различают аннуитетные и​ соответственно).​неизменность суммы и даты​
​ текущему моменту) стоимость​ количество периодов (Кпер)​Это тождество можно переписать​Ставка — процентная​Помесячный расчет остатков к​ помесячный график оплат​ предназначена для этих​и жмем на​ выплат по телу​нам, -2107,14 –​ составим таблицу ежемесячных​ иначе февраль считает​ шапку таблицы с​
​ ставка базового периода;​ дифференцированные платежи:​Составить график погашения кредита​ внесения платежа на​ инвестиций. Приведенная (нынешняя)​ и ставку (СТАВКА):​ в другом виде: СУММ(ОСПЛТ())​ ставка за период;​ оплате по кредиту​ по процентам за​

​ целей. Устанавливаем курсор​​ кнопку​
​ кредита плюс платежи​ это деньги, которые​ платежей с расшифровкой​ неверно. В вашей​ подробным расчетом и​ЧБП – число базовых​Аннуитет предполагает, что клиент​ по месяцам (А7​ протяжении всего срока​ стоимость представляет собой​
​ПРПЛТ =ПЛТ*(1-(1+СТАВКА)^(Период-Кпер-1))​ + ПС +​Кпер — общее​ сделан за весь​ заём. Как видим,​ в ячейку, которая​«OK»​ по процентам. Величина​ мы​ оставшейся части долга​ версии (.xlsx) лучше​ номера периодов (месяцев):​ периодов в календарном​ вносит каждый месяц​ -А​

​ кредитования;​
​ общую сумму, которая​Вышеуказанная формула работает при​ БС = 0.​ количество периодов выплаты;​ кредитный период. Как​ как и было​ находится в строке​.​ процентных выплат каждый​возвращаем банку​​ и начисленных процентов.​​ использовать ДАТАМЕС(), но,​Функция​ году.​​ одинаковую сумму.​​n​

​доступность практически для всех​ на настоящий момент​
​ БС=0. При ТИП=1​ В случае использования​Тип – для​
​ и положено, на​ сказано ранее, из​«1»​

​После этого открывается окно​ месяц уменьшается, так​.​При кредитовании банки наряду​
​ возможно, это мелочи,..​ОСПЛТ (PPMT)​Возьмем для примера следующие​При дифференцированной схеме погашения​).​

​ кредитополучателей вне зависимости​ равноценна ряду будущих​ (платеж в начале​ аннуитетной схемы погашения​ аннуитета постнумерандо Тип=0,​ конец срока эта​ месяца в месяц​и в столбце​ аргументов оператора​ как уменьшается тело​Альтернативная формула для расчета​ с дифференцированными платежами​Да, и досрочное​в ячейке B17​ данные по кредиту:​ долга перед финансовой​Сделать столбец «Платежи по​ от их финансового​ регулярных выплат ПЛТ​ периода) и n=1​ кредита (сумма кредита =ПС),​ для пренумерандо Тип=1.​ сумма равна нулю.​ величина данного вида​

​«Выплата по телу кредита»​

​ПЛТ​ займа, с которого​

​ платежа (общий случай):​ часто используют аннуитетную​ погашение при аннуенте​ вводится по аналогии​Для расчета полной стоимости​ организацией проценты начисляются​ кредиту» (В7 -​ положения;​ за количество периодов​ (первый платеж), ПРПЛТ=0​ выражение СУММ(ОСПЛТ()) вычисляет общую​Чтобы вычислить член аннуитета​Таким образом, мы произвели​ платежа уменьшается.​. Жмем на кнопку​.​ они рассчитываются. Таким​=-(Пс*ставка*(1+ ставка)^ Кпер​ схему погашения. Аннуитетная​​ считается не так.​​ с​ кредита нужно составить​ на остаток кредитной​

​ В​возможность снижения платежа с​ Кпер. Также предполагается,​Если БС<>0, то​ сумму платежей, идущих​ (величину регулярного платежа)​ не просто расчет​Теперь нам предстоит рассчитать​«Вставить функцию»​В поле​ образом и общий​ /((1+ ставка)^ Кпер​ схема предусматривает погашение​

​ Так считаются дифф.​​ПЛТ​ график платежей (порядок​ суммы. Поэтому ежемесячные​n​ поправкой на уровень​

​ что капитализация процентов​ формула усложнится:​ на оплату основной​ нужно использовать формулу​ оплаты по кредиту,​ общий ежемесячный платеж.​.​«Ставка»​

​ ежемесячный платеж тоже​ -1)+​ кредита периодическими равновеликими​ платежи. Там более​в предыдущем примере:​

​ см. выше).​​ платежи будут уменьшаться.​).​ инфляции.​ происходит также регулярно​Соотношение выплат основной суммы​ суммы долга (тело​ =А*ПС, где ПС​ а организовали своеобразный​

​ Для этого вычисления​Переходим в​следует вписать величину​ уменьшается.​ставка /((1+ ставка)^​ платежами (как правило,​ сложно — у​Добавился только параметр​Нужно определить базовый период​Чаще применяется аннуитет: выгоднее​Напротив первого месяца в​Многим людям аннуитетный способ​ с процентной ставкой​ долга и на​ кредита). В случае полного​ – это начальная​

Задача2

​ кредитный калькулятор. Который​ не следует прибегать​Мастер функций​ процентов за период.​При аннуитетной схеме используется​ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка​ ежемесячными), которые включают​ каждого банка свои​Период​ (БП). В законе​

​ для банка и​
​ столбце «Платежи по​ погашения кредита удобен​ равной величине СТАВКА.​ погашение начисленных процентов​ погашения кредита БС=0,​
​ сумма кредита.​ будет действовать по​ к какому-либо оператору,​. В категории​ Это можно сделать​ несколько другой подход.​
​ +1);1)​ как выплату основного​ правила. Я его​с номером текущего​ сказано, что это​ удобнее для большинства​ кредиту» ввести формулу​ тем, что, зная​Примечание​ за период хорошо​ а тождество превращается в​Специфика аннуитета (равенство​ аннуитетной схеме. Если​ так как можно​«Финансовые»​ вручную, просто поставив​
​ Клиент ежемесячно вносит​Если процентная ставка =​ долга, так и​ (досрочное погашение) не​

excel2.ru

Вычисление аннуитетного платежа в Microsoft Excel

​ месяца (выплаты) и​ стандартный временной интервал,​ клиентов.​= ПЛТ ($В3/12;$В$4;$В$2) и​ точный размер ежемесячного​.​ демонстрирует график, приведенный​ ПС=-СУММ(ОСПЛТ()). ​ денежных поступлений) позволяет​ в исходной таблице​ воспользоваться простой арифметической​отмечаем наименование​ процент, но у​ одинаковую сумму общего​ 0, то формула​ процентный платеж за​

​ учитывал.​ закрепление знаком $​

Расчет оплаты

​ который встречается в​Ежемесячная сумма аннуитетного платежа​ нажать Enter.​

• ​ взноса, проще планировать​
• ​Английский вариант функции:​

​ в файле примера.​Теперь кратко рассмотрим функции​ вывести стандартизованные формулы,​ мы, например, поменяем​ формулой. Складываем содержимое​«ОСПЛТ»​ нас он указан​ платежа, который состоит​ упростится до =(Пс​ пользование кредитом. Такой​qshin1980​ некоторых ссылок, т.к.​ графике погашения чаще​ рассчитывается по формуле:​

​Результат вычислений отобразиться в​ семейный бюджет. Однако​ PV(rate, nper, pmt,​Функцию ПРПЛТ() часто применяют​ MS EXCEL. Для​ существенно упрощающие счетные​ величину займа и​ ячеек первого месяца​и жмем кнопку​ в отдельной ячейке​ из выплат по​ + Бс)/Кпер​ равновеликий платеж называется​: Michael_S, спасибо огромное​ впоследствии мы эту​ всего. В примере​А = К * S​ таблице красным цветом​ с точки зрения​ [fv], [type]), т.е.​ при составлении графика​ того, чтобы нижесказанное​ процедуры. Об этих​ годовой процентной ставки,​ столбцов​«OK»​ на листе, поэтому​ телу кредита и​Если Тип=0 (выплата​ аннуитет.​

​ за подсказки.​ формулу будем копировать​ БП = 28​где:​ со знаком «-».​ экономической выгоды, он​ Present Value –​ платежей по аннуитетной​ было понятным, необходимо​ формулах и об​ то в итоговой​«Выплата по телу кредита»​.​ дадим на неё​ оплаты процентов. Изначально​

Этап 1: расчет ежемесячного взноса

​ в конце периода)​В аннуитетной схеме​Дело в том,​ вниз. Функция​ дней.​​А – сумма платежа​​ Это нормально, ведь​ имеет несколько существенных​ будущая стоимость.​ схеме (см. Аннуитет.​

​ предварительно ознакомиться с​

​ их использовании в​ таблице произойдет автоматический​и​Запускается окно аргументов оператора​ ссылку. Устанавливаем курсор​ процентные взносы насчитываются​

​ и БС =0,​​ погашения предполагается неизменность​​ что Банк определяет​ПРПЛТ (IPMT)​Далее находим ЧБП: 365​ по кредиту;​ эти деньги заемщик​ недостатков.​Вычисления в функции ПС()​ Расчет в MS​​ теорией аннуитета, понятиями​​ MS EXCEL и​ пересчет данных. Поэтому​«Выплата по процентам»​ ОСПЛТ. Он имеет​ в поле, а​ на всю сумму​ то Формула 2​​ процентной ставки по​​ сумму процентов в​

​для вычисления процентной​​ / 28 =​К – коэффициент аннуитетного​ будет отдавать банку,​Недостатки:​ производятся по этой​ EXCEL выплаченных процентов​ Будущая и Приведенная​ пойдет речь ниже.​​ её можно использовать​​. Для этого устанавливаем​ следующий синтаксис:​ затем кликаем по​​ займа, но по​​ также упрощается:​ кредиту в течение​ каждом месяце в​ части вводится аналогично.​ 13.​​ платежа;​​ а не получать.​

​общая сумма переплаты гораздо​​ формуле:​ за период).​ стоимость.​Финансовые функции ПЛТ(), ОСПЛТ(),​ не только один​ знак​=ОСПЛТ(Ставка;Период;Кпер;Пс;Бс)​ соответствующей ячейке. Но,​ мере того, как​Вышеуказанную формулу часто называют​ всего периода выплат.​

​ зависимости от колличества​​ Осталось скопировать введенные​Теперь можно найти процентную​S – величина займа.​ Формула расчета кредита​ выше, чем при​Если СТАВКА =0, то​Функция КПЕР(ставка; плт; пс;​Функция ПЛТ(ставка; кпер; пс;​​ ПРПЛТ(), КПЕР(), СТАВКА(),​​ раз для конкретного​«=»​Как видим, аргументы данной​ как мы помним,​ тело уменьшается, сокращается​ формулой аннуитета (аннуитетного​Определить величину ежемесячных равновеликих​ дней в периоде.​ формулы вниз до​

​ ставку базового периода:​​Формула коэффициента аннуитета:​​ аннуитетными платежами в​ дифференцированном способе погашения​ Приведенную стоимость можно​ [бс]; [тип])​ [бс]; [тип])​​ БС(), ПС(), а​​ случая, а применять​в первую пустую​​ функции почти полностью​​ у нас в​ и начисление процентов.​ платежа) и записывают​ выплат по ссуде,​ Для этого, я​ последнего периода кредита​У нас имеются все​К = (i *​ Excel позволяет сделать​

​ долга;​ определить по формуле​позволяет вычислить количество​рассчитывает величину регулярного​ также ОБЩДОХОД() и​ в различных ситуациях​ ячейку столбца​ совпадают с аргументами​ таблице задана годовая​​ Но общая сумма​​ в виде А=К*S,​​ размер которой составляет​​ расчитал колличество дней​ и добавить столбцы​​ необходимые данные –​​ (1 + i)^n)​ вычисления и таким​сложность досрочного погашения;​

1. ​ ПС=-БС-ПЛТ*Кпер​ периодов, через которое​ платежа на основе​ ОБЩПЛАТ() тесно связаны​ для расчета кредитных​​«Общая ежемесячная выплата»​​ оператора​ процентная ставка, а​

   

2. ​ оплаты остается неизменной​​ где А -​​ 100 000 руб.,​​ в периоде (столбец​​ с простыми формулами​​ подставляем их в​​ / ((1+i)^n-1)​ образом, чтобы значения​​невозможность перерасчета при желании​​Подробнее про функцию можно​

   

3. ​ текущая сумма вклада​ заданных 5 аргументов.​​ между собой, т.к.​​ вариантов по аннуитетной​

   ​. Затем кликаем по​​ПЛТ​​ период оплаты равен​ за счет ежемесячного​ это аннуитетный платеж​ а процентная ставка​ BD — выделил​ для вычисления общей​ формулу ПСК: =B9*B8​где i – процентная​ были положительными. С​ заемщика досрочно погасить​ прочитать в статье Аннуитет.​ (пс) станет равной​Примечание​ все они вычисляют​ схеме.​ двум вышеуказанным элементам,​, только вместо необязательного​ месяцу. Поэтому делим​ увеличения величины выплат​ (т.е. ПЛТ), К​ составляет 10% годовых.​ желтым). Потом вычитает​ суммы ежемесячных выплат​Примечание. Чтобы получить проценты​​ ставка за месяц,​​ ее помощью банковские​ ссуду.​ Определяем в MS​ заданной сумме (бс)​

   ​.​​ параметры аннуитета и,​​Урок:​ установив между ними​ аргумента​​ годовую ставку, а​​ по телу кредита.​ — это коэффициент​​ Ссуда взята на​​ из аннуитета сумму​ (она постоянна и​ в Excel, не​ результат деления годовой​ сотрудники в считанные​Если рассмотреть пример расчета​

   ​ EXCEL Приведенную (Текущую)​​ при известной процентной​​Английский вариант функции:​ соответственно, используют один​​Финансовые функции в Excel​​ знак​«Тип»​ вернее ссылку на​ Таким образом, с​ аннуитета, а S​

   ​ срок 5 лет.​​ процентов и получает​​ равна вычисленной выше​ нужно умножать на​ ставки на 12;​ минуты могут сделать​ аннуитетного платежа по​ стоимость​ ставке за период​​ PMT(rate, nper, pv,​​ и тот же​Как видим, при помощи​

   ​«+»​​добавлен обязательный аргумент​​ ячейку, в которой​ течением времени удельный​ — это сумма​Разбираемся, какая информация содержится​ платеж по ОД.​ в ячейке C7)​ 100. Достаточно выставить​n – срок кредита​​ и распечатать график​​ кредиту, то сразу​Функции ОБЩДОХОД() и ОБЩПЛАТ()​ (ставка) и известной​ [fv], [type]), т.е.​ набор аргументов. В​ программы Excel в​. Жмем на клавишу​«Период»​ она содержится, на​

   ​ вес процентов в​ кредита (т.е. ПС).​ в задаче:​​Можно ли как​​ и, ради интереса,​

   

4. ​ для ячейки с​ в месяцах.​ платежей кредитополучателям, экономя​ становится понятно, что​Аргументы функций ОБЩДОХОД()​ величине пополнения вклада​ PayMenT – платеж.​ этом можно убедиться,​​ домашних условиях можно​​Enter​. Он указывает на​ число​ общем ежемесячном платеже​ K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1),​Заемщик ежемесячно должен делать​ то в Ваш​ оставшейся сумме долга:​

   

5. ​ результатом процентный формат.​В программе Excel существует​ их время.​ банкам выгодно выдавать​ и ОБЩПЛАТ() несколько​ (плт). При этом​Примечание​ перечислив все функции​​ без проблем рассчитать​​.​ номер периода выплаты,​​12​​ падает, а удельный​ где i=ставка за​ платеж банку. Этот​ пример с процентами​Чтобы сделать наш калькулятор​​ПСК по новой формуле​​ специальная функция, которая​

   

6. ​Чтобы заполнить все месяцы,​ клиентам подобные ссуды.​ отличаются от рассмотренных​ предполагается, сумма пополнения​.​ вместе с аргументами:​ общий ежемесячный кредитный​Далее с помощью маркера​ а в нашем​, соответствующее количеству месяцев​ вес оплаты по​ период (т.е. Ставка),​ платеж включает:​​ вставить колличество дней​​ более универсальным и​ совпала с годовой​ считает аннуитетные платежи.​ нужно протянуть ячейку​ Однако некоторые не​ выше. Но на​ вклада вносится регулярно​​ Вышеуказанные функции входят в​​ПЛТ(ставка; кпер; пс; [бс];​

​ платеж по аннуитетной​​ заполнения, как и​

Этап 2: детализация платежей

​ конкретном случае на​ в году. Деление​ телу растет. При​ n — количество​сумму в счет погашения​ за период?​ способным автоматически подстраиваться​ процентной ставкой по​ Это ПЛТ:​ с формулой до​ так гонятся за​ самом деле разница​ в каждый период,​ надстройку «Пакет анализа».​ [тип])​ схеме, используя для​ в предыдущих случаях,​ номер месяца.​​ выполняем прямо в​​ этом сам общий​ периодов (т.е. Кпер).​ части ссудысумму для​Кстати нашел ошибку​ под любой срок​ кредиту.​Заполним входные данные для​ конца графика погашения.​ прибылью, поэтому предоставляют​ только в их​ тогда же происходит​

1. ​ Если функция недоступна​ОСПЛТ(ставка; период; кпер;​ этих целей оператор​​ заполняем колонку данными.​​Заполняем уже знакомые нам​ поле окна аргументов.​ ежемесячный платеж на​ Напоминаем, что выражение​ оплаты начисленных за​​ в расчете своего​​ кредита, имеет смысл​​Скачать кредитный калькулятор в​​ расчета ежемесячных платежей​​ Но поскольку аннуитетный​​ заемщикам более выгодные​

   

2. ​ названии: кол_пер –​​ и начисление процентов.​​ или возвращает ошибку​​ пс; [бс]; [тип])​​ПЛТ​​ Как видим, на​​ поля окна аргументов​​В поле​​ протяжении всего срока​

   

3. ​ для K справедливо​ прошедший период процентов​ аннуитета))) Сначала очень​

   ​ немного подправить формулы.​

   ​ Excel​ по кредиту. Это​ платеж со временем​ условия кредитования. Стоит​​ это кпер; нз​​ Сумма пополнения вклада​ #ИМЯ?, то включите​​ПРПЛТ(ставка; период; кпер;​​. Кроме того, при​​ протяжении всего действия​​ функции​«Кпер»​ кредитования не меняется.​ только при БС=0​ на остаток ссуды​

   ​ удивился, что у​ В ячейке А18​Таким образом, для расчета​​ сумма займа, проценты​​ не меняется, цифры​ отметить, что среди​ – это пс.​​ может быть равна​​ или установите и​ пс; [бс]; [тип])​ помощи функций​ договора сумма общего​ОСПЛТ​устанавливается срок кредитования.​Как раз на расчете​ (полное погашение кредита​;​ нас суммы расходятся))).​ лучше использовать формулу​ аннуитетных платежей по​ и срок.​ в ячейках будут​ микрофинансовых организаций таких​ Нач_период и кон_период​ 0 (вклад не​​ загрузите эту надстройку​​КПЕР(ставка; плт; пс;​ОСПЛТ​ ежемесячного платежа, включающего​теми самыми данными,​ Он у нас​ аннуитетного платежа мы​​ за число периодов​​Сумма ежемесячного платежа (аннуитета)​

   

4. ​Что касается ДАТАМЕС(),​ вида:​ кредиту используется простейшая​Составим график погашения кредита.​​ одинаковые.​​ компаний нет. Поэтому​​ – это «начальный​​ пополняется, рост вклада​ (с версии MS​ [бс]; [тип])​​и​​ платеж по телу​ что были использованы​ равен​​ и остановимся. Тем​​ Кпер) и Тип=0​постоянна​ то мне он​=ЕСЛИ(A17>=$C$7;»»;A17+1)​ функция ПЛТ. Как​ Пока пустой.​Перепроверить полученные данные можно​ при оформлении заема​ период» и «конечный​

   ​ осуществляет только за​ EXCEL 2007 надстройка​СТАВКА(кпер; плт; пс;​ПРПЛТ​ займа и оплату​​ для функции​​24​

   

5. ​ более, это актуально,​ (начисление процентов в​и не меняется​ не подошел, т.к.​Эта формула проверяет с​ видите, дифференцированный способ​​В первую ячейку столбца​​ с помощью кредитного​

   

6. ​ всегда используются аннуитетный​ период».​ счет капитализации процентов).​ «Пакет анализа» включена​ [бс]; [тип]; [предположение])​можно произвести расчет​ процентов, составит​ПЛТ​месяцам. Можно занести​ так как в​ конце периода). ​ на протяжении всего​ если протягивать данную​ помощью функции ЕСЛИ​ погашения несколько сложнее.​ «Платежи по кредиту»​ калькулятора аннуитетных платежей.​

   

7. ​ способ погашения долга.​Функция ОБЩДОХОД(ставка; кол_пер; нз;​Бс (будущая стоимость)​ по умолчанию).​БС(ставка; кпер; плт;​ величины платежей по​23536,74 рубля​. Только учитывая тот​ в поле число​ настоящее время большинство​

   

8. ​Таблица ежемесячных платежей​ срока, так же​ формулу, то после​ (IF) достигли мы​Кто как, а я​​ вводиться формула расчета​​ Он есть на​Если рассматривать составляющие аннуитетного​​ нач_период; кон_период; тип)​​ может быть =0​​Для понимания работы формулы​​ [пс]; [тип])​

   

9. ​ телу кредита и​​. Собственно этот показатель​​ факт, что в​​24​​ банков используют именно​​Составим таблицу ежемесячных платежей​​ как и процентная​ февраля в котором​​ последнего периода или​​ считаю кредиты злом.​

   

10. ​ кредита аннуитетными платежами​ сайтах всех банков,​​ платежа, можно заметить,​​возвращает кумулятивную (нарастающим​ или опущена.​

    ​ приведем эквивалентное ей​

    ​ПС(ставка; кпер; плт;​ по процентам за​ мы уже рассчитывали​​ будущем будет применяться​​вручную, но мы,​ эту схему. Она​ для вышерассмотренной задачи.​ ставка. Также не​ эта функция считает​ нет, и выводит​ Особенно потребительские. Кредиты​ в Excel: =ПЛТ($B$3/12;​​ которые выдают ссуды​​ что он делится​ итогом) сумму, выплачиваемую​Также функцию КПЕР()​ выражение для расчета​ [бс]; [тип])​ указанный период. Применяя​ ранее при помощи​​ копирование формулы посредством​​ как и в​

    

11. ​ удобна и для​Для вычисления ежемесячных сумм​ изменяется порядок платежей​ конец месяца как​ пустую текстовую строку​

    

12. ​ для бизнеса -​ $B$4; $B$2). Чтобы​ с таким способом​ на две части.​ в погашение основной​ можно использовать для​ платежа:​ПЛТ​ весь этот багаж​ПЛТ​ маркера заполнения, нужно​ предыдущем случае, указываем​

    

13. ​ клиентов, ведь в​ идущих на погашение​ – 1 раз​ 28 число, все​ («») в том​ другое дело, а​ закрепить ячейки, используем​ погашения. Для использования​ Первая – фиксированные​ суммы займа в​​ определения количества периодов,​​Формула 2 есть не​​(английское название функции:​​ функций вместе, существует​. Но в данном​​ сделать все ссылки​​ ссылку на месторасположение​ этом случае общая​​ основной суммы долга​​ в месяц;​ даты идут по​ случае, если достигли,​ для обычных людей​​ абсолютные ссылки. Можно​​ кредитного калькулятора понадобятся​​ проценты по кредиту,​​ промежутке между двумя​

    

14. ​ необходимых для погашения​ что иное, как​ PMT, от слова​ возможность создать мощный​ случае это представлено​ в полях абсолютными,​ данного показателя в​ сумма оплаты не​ используется функция ОСПЛТ(ставка;​Сумма для оплаты начисленных​ 28 (выделил зеленым).​​ либо номер следующего​​ мышеловка»деньги за 15​ вводить в формулу​ те же исходные​​ вторая – часть​​ периодами (​ долга по ссуде​ решение Формулы 1​ payment). Регулярный платеж,​ кредитный калькулятор, который​ более наглядно, именно​

    

15. ​ чтобы они не​ исходной таблице.​ меняется, оставаясь фиксированной.​ период; кпер; пс;​ за прошедший период​Michael_S​ периода. При копировании​​ минут, нужен только​​ непосредственно числа, а​ данные, что и​ суммы основного долга.​нач_период и кон_период​ (погашение осуществляется регулярно​ относительно параметра ПЛТ.​ осуществляемый каждый период.​ можно будет использовать​ как сумма оплаты​ менялись. Для этого​В поле​ Клиенты всегда знают​ [бс]; [тип]) практически​ процентов​​: её надо таком​​ такой формулы вниз​ паспорт» срабатывает безотказно,​ не ссылки на​ для предыдущих способов​ Причем сумма начисленных​​).​​ равными платежами, ставка​

    

16. ​Примечание.​ Платеж – постоянная​ не один раз​ по телу займа​ требуется поставить знак​«Пс»​ сколько нужно заплатить.​ с теми же​уменьшается​ виде​ на большое количество​ предлагая удовольствие здесь​​ ячейки с данными.​​ расчета. Их нужно​ процентов обычно превышает​​Примечание​​ не изменяется весь​В файле примера​ величина, она не​ для вычисления аннуитетного​ и процентам.​ доллара перед каждым​указывается первоначальная величина​​Для расчета ежемесячного взноса​​ аргументами, что и​​каждый период, т.к.​​200?’200px’:»+(this.scrollHeight+5)+’px’);»>=ДАТАМЕС($L$8;СТРОКА(1:1))​ строк мы получим​ и сейчас, а​ Тогда она примет​ ввести в отведенные​​ сумму, идущую на​​.​

    

17. ​ срок, на который​​ на листе Аннуитет​​ меняется в течение​ платежа.​​Теперь нужно добавить данные​​ значением координат по​​ займа. Она равна​​ при использовании аннуитетной​ ПЛТ() (подробнее см.​​ проценты начисляются только​​но, если ваши​

    

18. ​ номера периодов как​​ расплату за него​​ следующий вид: =ПЛТ(18%/12;​ поля для заполнения.​ погашение ссуды.​Английский вариант функции:​ выдана ссуда, процент​ (без ПЛТ) приведен​​ всего срока аннуитета.​​Автор: Максим Тютюшев​ в столбец, где​

    ​ вертикали и горизонтали.​

    ​500000 рублей​ схемы в Экселе​ статью Аннуитет. Расчёт​ на непогашенную часть​ даты сходятся с​​ раз до нужного​​ когда-нибудь потом. И​ 36; 100000).​ И затем программа​Тело кредита сравнивается с​  CUMPRINC(rate, nper, pv,​​ начисляется каждый период​​ расчет ежемесячных платежей​Ставка​В статье рассмотрены финансовые​ будет ежемесячно отображаться​ Но легче это​. Как и в​ существует специальная функция​ в MS EXCEL​ ссуды;​ датами банка, то​ предела (срока кредита).​ главная проблема, по-моему,​Ячейки окрасились в красный​ самостоятельно сделает все​ процентами по нему​ start_period, end_period, type)​ на остаток ссуды).​​ без использования финансовых​​(англ.: RATE, interest).​ функции ПЛТ(), ОСПЛТ(),​ остаток суммы по​ сделать, просто выделив​ предыдущих случаях, указываем​ –​ погашение основной суммы​Как следствие п.3 и​ они тоже неправильно​ В остальных ячейках​ даже не в​ цвет, перед числами​ расчеты в течение​​ только в середине​​ returns the CUMulative​

    

19. ​Примечание​ функций EXCEL.​ Процентная ставка за​ ПРПЛТ(), КПЕР(), СТАВКА(),​ кредиту, который ещё​ координаты и нажав​ ссылку на элемент​ПЛТ​ долга). Т.к. сумма​

    

20. ​ п.1, сумма, уплачиваемая​ считают, и тогда​ этой строки можно​ грабительских процентах или​ появился знак «минус»,​ нескольких секунд, дав​ общего срока кредитования.​

​ PRincipal paid for​.​Если процентная ставка =​ период, чаще всего​ ПС(), БС(), а​ требуется заплатить. В​ на функциональную клавишу​ листа, в котором​. Она относится к​ идущая на погашение​ в счет погашения​ оставьте как есть​ использовать похожую конструкцию​ в том, что​ т.к. мы эти​ потенциальному заемщику возможность​ Далее сумма, которая​ an investment period​Английский вариант функции:​ 0, то Формула​ за год или​ также ОБЩДОХОД() и​

​ первой ячейке столбца​​F4​

​ содержится данный показатель.​ категории финансовых операторов.​ основной суммы долга​ основной суммы ссуды,​Цитата​ с проверкой на​ это «потом» все​ деньги будем отдавать​​ оценить полученную сумму​​ идет на погашение​ with a Constant​​ NPER(rate, pmt, pv,​​ 2 упростится до​​ за месяц. Обычно​​ ОБЩПЛАТ(), которые используются​«Остаток к выплате»​. Знак доллара будет​В поле​ Формула этой функции​ изменяется от периода​увеличивается​(qshin1980, 22.09.2013 в​ присутствие номера периода:​ равно когда-нибудь наступит.​ банку, терять.​ и хорошенько подумать​ основного долга, начинает​

​ interest rate.​

lumpics.ru

Аннуитет. Обзор функций MS EXCEL

​ [fv], [type]), т.е.​ =(ПС + БС)/Кпер​ задается через годовую​ для расчетов параметров​расчет будет самый​ расставлен в нужных​«Бс»​ выглядит следующим образом:​

​ к периоду, то​от месяца к​ 21:41, в сообщении​=ЕСЛИ(A18<>»»;​ Кредит убивает мотивацию​​ о предстоящем оформлении​

​ расти, постепенно превышая​Подробнее про функцию можно​ Number of Periods​Если Тип=0 (выплата в​ ставку, деленную на​ аннуитетной схемы.​ простой. Нам нужно​ местах автоматически. Также​указывается величина займа,​

Немного теории

​=ПЛТ(ставка;кпер;пс;бс;тип)​ необходим еще один​ месяцу.​​ № 3)200?’200px’:»+(this.scrollHeight+5)+’px’);»>Дело в​​текущая формула​ к росту. Зачем​​Дифференцированный способ оплаты предполагает,​​ кредита.​​ размер выплат за​​ прочитать в статье Аннуитет.​ – число периодов.​ конце периода) и​

​ количество периодов в​Данная статья входит в​ отнять от первоначальной​ не забываем, что​ после полной его​Как видим, указанная функция​ аргумент​Заемщик должен сделать 60​ том, что Банк​; «»)​ напрягаться, учиться, развиваться,​ что:​
​Автор: Антонина Савченко​ пользование кредитом. Как​ Расчёт в MS​Эквивалентная формула для расчета​ БС =0, то​ году. При годовой​ цикл статей о​ величины займа, которая​ годовую ставку нужно​ оплаты. Как помним,​ обладает довольно большим​период​ равновеликих платежей (12​ определяет сумму процентов​Т.е. если номер периода​ искать дополнительные источники​сумма основного долга распределена​

​Инвестиции​ уже было сказано​ EXCEL погашение основной​ платежа:​ Формула 2 заметно​ ставке 10% месячная​​ расчете параметров аннуитета.​ указана в таблице​​ разделить на​ это значение практически​ количеством аргументов. Правда,​, который определяет к​ мес. в году*5​

​ в каждом месяце​ не пустой, то​ дохода, если можно​ по периодам выплат​Аннуитет​ ранее, это не​ суммы долга.​Если ставка равна 0,​ упрощается:​ ставка составит 10%/12.​ Перечень всех статей​ с первичными данными,​12​ всегда равно нулю.​ последние два из​ какому периоду относится​ лет), т.е. всего​ в зависимости от​ мы вычисляем сумму​ тупо зайти в​ равными долями;​Этот пример покажет вам,​ выгодно для заемщиков,​Функция ОБЩПЛАТ(ставка; кол_пер; нз;​ то:​В случае применения схемы​

​ Ставка не изменяется​ на нашем сайте​ платеж по телу​.​ Устанавливаем в данном​ них не являются​ сумма.​ 60 периодов (Кпер);​ колличества дней в​ выплат с помощью​

​ ближайший банк и​​проценты по кредиту начисляются​ как рассчитать будущую​ особенно когда речь​ нач_период; кон_период; тип)​​Кпер = (Пс​​ аннуитета для выплаты​​ в течение всего​​ об аннуитете размещен​ кредита за первый​Но у нас остается​​ поле число​​ обязательными.​Для вычисления ежемесячных сумм​Проценты начисляются​

​ периоде.​ наших формул с​ там тебе за​

​ на остаток.​ стоимость инвестиций и​ идет о долгосрочном​возвращает кумулятивную (нарастающим​ + Бс) /ПЛТ​

​ ссуды платеж включает​
​ срока аннуитета.​ здесь.​
​ месяц в расчетной​ ещё один новый​
​«0»​Аргумент​ идущих на погашение​

​в конце​не должно быть​ ПРПЛТ и ОСПЛТ.​ полчаса оформят кредит​Формула расчета дифференцированного платежа:​ текущую стоимость аннуитета.​
​ кредитовании.​ итогом) величину процентов,​Подробнее про функцию можно​ денежную сумму в​Кпер​В этой статье содержится​ таблице. Но, учитывая​ аргумент, которого не​. Хотя этот аргумент​

Параметры функций аннуитета

​«Ставка»​ процентов за ссуду​каждого периода (если​ такого — это​ Если же номера​ на кабальных условиях,​ДП = ОСЗ /​Совет:​На самом деле, рассчитать​ выплачиваемых по займу​ прочитать в статье​ счет погашения части​(англ.: NPER). Общее​ небольшой раздел о​

​ тот факт, что​ было у функции​
​ можно вообще опустить.​указывает на процентную​
​ используется функция ПРПЛТ​ не сказано обратное,​
​ получается смесь аннуента​ нет, то выводим​
​ попутно грамотно разведя​ (ПП + ОСЗ​
​При работе с​ точный размер платежа​
​ в промежутке между​ Аннуитет. Расчет в​

​ ссуды и сумму​​ число периодов платежей​ теории аннуитета, краткое​ одно из чисел​ПЛТ​В поле​ ставку за конкретный​ (ставка; период; кпер;​ то подразумевается именно​
​ и дифф. платежей.​​ пустую текстовую строку:​ на страхование и​ * ПС)​ финансовыми функциями Excel​ достаточно просто. Причем​ двумя периодами выплат​ MS EXCEL количества​ для оплаты начисленных​ по аннуитету. Если​ описание функций аннуитета​ у нас уже​. Этот аргумент​«Тип»​ период. Если, например,​
​ пс; [бс]; [тип])​​ это), т.е. аргумент​Впрочем… посмотрел на​Реализованный в предыдущем варианте​ прочие допы?​где:​ всегда задавайте себе​ это можно сделать​ (​ периодов.​ за прошедший период​
​ кредит взят на​​ и их аргументов,​ идет со знаком​«Период»​указываем в начале​ используется годовая ставка,​ с теми же​ Тип=0. Платеж должен​ график выплат своего​ калькулятор неплох, но​Так что очень надеюсь,​ДП – ежемесячный платеж​ вопрос, я оплачиваю​ сразу несколькими способами.​нач_период кон_период​Функция СТАВКА(кпер; плт; пс;​ процентов, поэтому функция​ 5 лет, а​ а также ссылки​
​«-»​​. В соответствующее поле​ или в конце​ но платеж по​ аргументами, что и​ производиться также в​ кредита — похоже,​ не учитывает один​ что изложенный ниже​ по кредиту;​ (расход) или я​ Используя хотя бы​).​ [бс]; [тип]; [предположение])​ ПЛТ() связана с​ выплаты производятся ежемесячно,​ на статьи с​, то их следует​ устанавливаем ссылку на​ месяца производится оплата.​ займу производится ежемесячно,​ ОСПЛТ() (подробнее см.​
​ конце каждого периода;​​ что так и​ важный момент: в​ материал вам не​ОСЗ – остаток займа;​ получаю деньги (доход)?​ один из них,​Примечание​возвращает процентную ставку​ ОСПЛТ() и ПРПЛТ()​ то всего 60​ примерами использования этих​ не отнять, а​ первую ячейку столбца​ У нас, как​

​ то годовую ставку​ статью Аннуитет. Расчет​Процент за пользование заемными​

​ есть — последний​ реальной жизни вы,​ пригодится.​ПП – число оставшихся​Предположим, что в конце​ можно сориентироваться в​.​ по аннуитету.​ соотношением ПЛТ =​

​ периодов (12 мес.​​ функций.​ сложить. Делаем это​«Период»​ и в большинстве​ нужно разделить на​ в MS EXCEL​ средствами в месяц​ платеж меньше всех​ скорее всего, будете​Но если уж случится​ до конца срока​ каждого года, вы​ предстоящих выплатах и​Английский вариант функции:​Примечание​

О направлениях денежных потоков и знаках ПС, БС и ПЛТ

​ ОСПЛТ + ПРПЛТ​ в году *​Аннуитет (иногда используются термины​ и жмем на​. Данный элемент листа​ случаев, она производится​12​ выплаченных процентов за​ (за период) составляет​ остальных. Намного.​​ вносить дополнительные платежи​​ так, что вам​ погашения периодов;​ кладёте $100 на​ оценить, насколько «подъемной»​ CUMIPMT(rate, nper, pv,​.​ (для каждого периода).​ 5 лет)​ «рента», «финансовая рента»)​ кнопку​ содержит в себе​

Тождество аннуитета

​ в конце месяца.​и полученный результат​ период).​ 10%/12 (ставка);​Счас с этим​ для досрочного погашения​

​ или вашим близким​ПС – процентная ставка​ сберегательный счет. Какую​ окажется банковская ссуда.​ start_period, end_period, type)​Английский вариант функции:​Примечание​Бс​ представляет собой​Enter​ число​ Поэтому устанавливаем число​ использовать в качестве​Примечание​В конце срока задолженность​

Функции MS EXCEL для расчета параметров аннуитета

​ некогда разбираться, может​ при удобной возможности.​ придется влезть в​ за месяц (годовую​ сумму вы получите​Способы расчета аннуитетного платежа:​ returns the CUMulative​ RATE(nper, pmt, pv,​

​.​(англ.: FV, future​​однонаправленный​.​«1»​

​«0»​​ аргумента. Если применяется​​. Для определения суммы​ должна быть равна​ чуть позже (после​ Для реализации этого​

​ это дело, то​​ ставку делим на​​ через 10 лет​вручную при помощи формулы;​ Interest paid on​ [fv], [type], [guess]),​В файле примера​ value).  Будущая стоимость​денежный поток, элементы​А вот вычисление остатка​, которое обозначает номер​. Как и в​ ежеквартальный вид оплаты,​

​ переплаты по кредиту​ 0 (БС=0).​ 14:00 по Москве).​ можно добавить в​

​ неплохо бы перед​ 12).​ с годовой процентной​с использованием программы Microsoft​

​ a loan between​​ т.е. Number of​ на листе Зависимости​ в конце срока​ которого​ к выплате после​ первого месяца кредитования.​

​ случае с предыдущим​ то в этом​ (общей суммы выплаченных​Расчет суммы выплаты по​

​ Если раньше ни​ нашу модель столбец​ походом в банк​Составим график погашения предыдущего​ ставкой 8%?​

​ Excel;​ start_period and end_period.​ Periods – число​ ПЛТ() приведены графики:​ аннуитета (по истечении​одинаковыпо величине​ второго и последующих​ Но в отличие​ аргументом, в данное​ случае годовую ставку​ процентов) используйте функцию​ ссуде за один​ кто не поможет.​ с дополнительными выплатами,​

​ хотя бы ориентировочно​​ кредита по дифференцированной​​Вставьте функцию​на сайте банка с​Подробнее про функцию можно​ периодов.​ Зависимость суммы платежа​ числа периодов Кпер).​и производятся через​ месяцев будет несколько​ от предыдущих полей,​ поле можно ничего​ нужно разделить на​

​ ОБЩПЛАТ(), см. здесь.​ период, произведем сначала​​qshin1980​ которые будут уменьшать​ прикинуть суммы выплат​ схеме.​FV​ помощью кредитного калькулятора.​ прочитать в статье Аннуитет.​: Ставка вычисляется путем​ от размера ссуды,​ Бс — требуемое​равные периоды времени​ сложнее. Для этого​ в указанном поле​​ не вводить, тогда​​4​Конечно, для составления таблицы​ с помощью финансовой​

​: Michael_S, спасибо​​ остаток. Однако, большинство​​ по кредиту, переплату,​Входные данные те же:​(Future Value), в​Каждый из методов расчета​ Расчет в MS​ итерации и может​

​ Зависимость суммы платежа​ значение будущей стоимости​(например, когда платежи​ нам нужно отнять​ мы оставляем ссылку​ программа по умолчанию​и т.д.​ ежемесячных платежей можно​ функции MS EXCEL​Буду ждать!​ банков в подобных​ сроки и т.д.​
​Составим график погашения займа:​ русском варианте –​ при правильном применении​ EXCEL выплаченных процентов​ давать нулевое значение​ от ставки, Зависимость​ или остатка средств​ производятся ежегодно равными​

​ от тела кредита​

​ относительной, а не​ будет считать, что​«Кпер»​ воспользоваться либо ПРПЛТ()​ ПЛТ().​
​qshin1980​ случаях предлагают на​

​ «Помассажировать числа» заранее,​Остаток задолженности по кредиту:​БС​ даст точную цифру,​ за период.​ или несколько значений.​ суммы платежа от​ после последней выплаты.​

​ суммами).​​ на начало кредитования​​ делаем из неё​ в нем расположено​обозначает общее количество​ или ОСПЛТ(), т.к.​Примечание​: Неужели ни кто​ выбор: сокращать либо​

​ как я это​ в первый месяц​(Будущая Стоимость).​​ равную предстоящему размеру​Общую сумму выплат по​ Если последовательные результаты​ срока ссуды. Также​ Например, в случае​Каждый элемент такого денежного​ общую сумму платежей​

​ абсолютную.​​ значение равное нулю.​ периодов выплат по​ эти функции связаны​. Обзор всех функций​ не подскажет как​

​ сумму ежемесячной выплаты,​ называю Microsoft​ равняется всей сумме:​=FV(rate,nper,pmt,[pv],[type])​ платежа. Поэтому, если​ займу между двумя​

​ функции СТАВКА не​ в файле примера​ расчета аннуитетного платежа​ потока называется членом​ по телу займа​После того, как все​После того, как все​

​ кредиту. То есть,​

​ и в любой​ аннуитета в статье​ справиться с этой​ либо срок. Каждый​ Excel может сильно​
​ =$B$2. Во второй​=БС(ставка;кпер;плт;[пс];[тип])​

​ есть сомнения в​ периодами (Нач_период и​ сходятся с точностью​ приведены некоторые задачи.​ для полной выплаты​ аннуитета, а величина​

​ за предыдущий период.​ данные, о которых​ данные введены, жмем​ если заём берется​ период: ПЛТ= ОСПЛТ​ найдете здесь.​ ошибкой?​

​ такой сценарий для​ помочь в этом​​ и последующие –​Введите аргументы:​ правильности уже сделанных​ кон_период) можно найти​ 0,0000001 после 20-ти​Функция ОСПЛТ(ставка; период; кпер;​ ссуды к концу​ постоянного временного интервала​ Устанавливаем знак​ мы говорили выше,​ на кнопку​ на один год​ + ПРПЛТ​Эта функция имеет такой​АндрейФед​ наглядности лучше посчитать​ вопросе.​ рассчитывается по формуле:​=FV(C2,C3,C4)​ вычислений, можно произвести​ сложив результаты возвращаемые​
​ итераций, то СТАВКА​ пс; [бс]; [тип])​ срока Бс =​
​ между двумя его​«=»​ введены, жмем на​«OK»​ с ежемесячной оплатой,​Соотношение выплат основной суммы​ синтаксис:​: Доброго времени суток​ отдельно.​Для быстрой прикидки кредитный​ =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10​=БС(C2;C3;C4)​

​ проверку, рассчитав аннуитетный​​ ОБЩПЛАТ() и ОБЩДОХОД()​​ возвращает сообщение об​используется для вычисления​ 0, т.к. ссуда​ последовательными элементами называется​во второй ячейке​

​ кнопку​.​

​ то число периодов​ долга и начисленных​
​ПЛТ(ставка; кпер; пс;​ Уважаемые форумчане!​

​В случае уменьшения срока​ калькулятор в Excel​ – номер текущего​За 10 лет вы​ платеж другим возможным​

​ с одинаковыми аргументами,​ ошибке #ЧИСЛО!​​ регулярных сумм идущих​ в конце срока​

​ периодом аннуитета. В​​ столбца​​«OK»​После этого в ячейку,​ считается​ процентов хорошо демонстрирует​ [бс]; [тип])​Помогите пожалуйста посчитать​

​ придется дополнительно с​ можно сделать за​ периода, В4 –​ положите на депозит​ способом.​ что эквивалентно ПЛТ*(кон_период​Попробуем разобраться причем​ на погашение основной​ должна быть полностью​ широком смысле, аннуитетом​«Остаток к выплате»​
​.​ которую мы выделили​
​12​ график, приведенный в​PMT(rate, nper, pv,​ фактическую процентную ставку​ помощью функции​ пару минут с​ срок кредита; Е9​ 10*100 = $1000​Расчет процентов по кредиту​ — Нач_период+1).​ здесь итерации.​ суммы долга практически​ погашена.​ может называться как​. Далее указываем ссылку​После этого в ячейке,​ в первом пункте​, если на два​ файле примера.​
​ [fv], [type]) –​ (ПС).​ЕСЛИ (IF)​​ помощью всего одной​​ – остаток по​ (расход). А по​ при аннуитетных платежах​Первое правило при оформлении​Взглянем на Формулу​ с теми же​Пс​ сам финансовый инструмент,​​ на ячейку, в​​ которую мы ранее​ данного руководства, выводится​​ года, то число​​Примечание​ английский вариант.​Был взят ипотечный​проверять — не​ функции и пары​​ кредиту в предыдущем​​ истечении срока получите​

​ вне зависимости от​ кредита – нужно​ 1. Если постараться​ аргументами, что и​

​(англ.: PV, present​ так и сумма​​ которой содержится первоначальная​ выделили, отобразится величина​ результат вычисления. Как​ периодов –​. В статье Аннуитет.​Примечание​
​ кредит. Формула из​ достигли мы нулевого​ простых формул. Для​ периоде; G9 –​ $1448,66 (доход). Чем​ выбранного способа вычислений​ адекватно оценить собственную​ решить это уравнение​ ПЛТ(). Т.к. сумма​ value). Приведенная стоимость,​ периодического платежа.​ сумма кредита. Делаем​ выплаты по телу​ видим, величина ежемесячного​24​ Расчет периодического платежа​

​: Функция ПЛТ() входит​​ кредитного договора.​​ баланса раньше срока:​ расчета ежемесячной выплаты​ сумма основного долга​ больше сумма, тем​ производится с помощью​

​ платежеспособность, чтобы платежи​ относительно параметра Ставка,​ идущая на погашение​

​ т.е. стоимость приведенная​Исторически вначале рассматривались​ её абсолютной, выделив​ займа за первый​ общего платежа по​. Если кредит берется​

​ в MS EXCEL.​ в надстройку «Пакет​МП=ОСЗ*ПС*0,01/(1-(1+ПС*0,01)^-(Кол.мес-1))​А в случае уменьшения​

​ по аннуитетному кредиту​ в предыдущем периоде.​​ быстрее приумножаются ваши​ специальной формулы. Кредитные​ по нему со​ то мы получим​ основной суммы долга​ к определенному моменту​ равные ежегодные денежные​ и нажав на​ месяц. Она составит​ займу составляет​ на два года​ Срочный вклад показано как​ анализа». Если данная​МП — размер​

​ выплаты — заново​​ (т.е. кредиту, где​​Выплата процентов: остаток по​ деньги.​ калькуляторы, мобильные приложения​ временем не стали​ степенное уравнение (степень​

​ изменяется от периода​ (часто к текущему,​ поступления (период между​

​ клавишу​18536,74 рубля​23536,74 рубля​ с ежеквартальной оплатой,​

​ рассчитать величину регулярной​ функция недоступна или​ месячного платежа​ пересчитывать ежемесячный взнос​ выплаты производятся равными​

​ кредиту в текущем​
​Примечание:​ и другое программное​ обременительными для заемщика.​ уравнения и, соответственно,​ к периоду, то​ т.е. настоящему времени).​ платежами принимался равным​F4​.​. Пусть вас не​ то число периодов​ суммы пополнения вклада,​ возвращает ошибку #ИМЯ?,​

​ОСЗ – Остаток​ начиная со следующего​​ суммами — таких​ периоде умножить на​Последние два аргумента​ обеспечение делает правильные​ Но на этом​ число его корней​​ необходим еще один​​ Если взят кредит​

​ одному году), что​​. Затем ставим знак​​Затем, как уже говорилось​ смущает знак «-»​ равно​ чтобы накопить желаемую​ то включите или​ ссудной задолженности на​ после досрочной выплаты​ сейчас большинство) в​

​ месячную процентную ставку,​ необязательны. Если опустить​ расчеты, отталкиваясь именно​ этапе иногда возникают​ будет зависеть от​

​ аргумент​ и производятся регулярные​​ и послужило основой​«+»​ выше, нам следует​ перед данной суммой.​8​ сумму.​​ установите и загрузите​​ расчетную дату (сумма​

​ периода:​​ Excel есть специальная​​ которая разделена на​ аргумент​ от нее.​ сложности, поскольку не​ значения Кпер). В​период​ выплаты по аннуитетной​

​ для именования денежного​, так как второе​ скопировать данную формулу​ Так Эксель указывает​.​

​График платежей можно рассчитать​ эту надстройку (в​ кредита);​Существуют варианты кредитов, где​ функция​ 12 месяцев: =E9*($B$3/12).​pv​Общий вид данной формулы​ у всех есть​

excel2.ru

Расчет аннуитетных платежей по кредиту: пример

​ отличие от других​, который определяет к​ схеме, то Приведенная​ потока аннуитетом («год»​ значение у нас​ на остальные ячейки​ на то, что​«Пс»​ без использования формул​ MS EXCEL 2007/2010​ПС – Месячная​ клиент может платить​ПЛТ (PMT)​Выплата основного долга: сумму​(пс), он будет​ выглядит следующим образом:​ экономическое образование, чтобы​ параметров ПЛТ, БС,​ какому периоду относится​ стоимость – это​ на латинском языке​

Аннуитетный платеж – это…

​ и так будет​ столбца с помощью​ это расход денежных​указывает приведенную стоимость​ аннуитета. График приведен​ надстройка «Пакет анализа»​ процентная ставка, равная​ нерегулярно, в любые​из категории​ всего кредита разделить​ равен 0 (нет​

​АП = О *​ правильно произвести необходимые​ ПС и Кпер,​ сумма.​ сумма кредита. Если​ — anno). В​ отрицательным. После этого​ маркера заполнения. Для​ средств, то есть,​ на настоящий момент.​ в столбцах K:P​ включена по умолчанию).​ 1/12 от годовой​ произвольные даты внося​Финансовые (Financial)​ на срок: =ЕСЛИ(D9​

Классификация аннуитета

​ текущей стоимости). Если​ пс / 1​ вычисления. Для облегчения​ найти универсальное решение​Примечание​ планируется регулярно вносить​ дальнейшем, в качестве​ кликаем по кнопке​ этого устанавливаем курсор​ убыток.​

​ Говоря простыми словами,​

• ​ файла примера лист​Первый аргумент – Ставка.​ ставки;​
• ​ любые имеющиеся суммы.​. Выделяем ячейку, где​Итоговый платеж: сумма «процентов»​ опустить аргумент​
• ​ — (1 +​ задачи здесь собраны​ этого уравнения для​
• ​.​ равновеликие платежи на​ периода стал выступать​«Вставить функцию»​

​ в нижний правый​Для того, чтобы рассчитать​ это общая величина​ Аннуитет (ПЛТ), а​ Это процентная ставка​Кол.мес. – количество​

Преимущества и недостатки аннуитетных платежей

​ Процентная ставка по​ хотим получить результат,​ и «основного долга»​type​ пс)-с,​ все возможные способы​ всевозможных степеней невозможно,​Английский вариант функции:​ счет в банке​ любой промежуток времени,​.​ угол ячейки, в​ общую сумму оплаты​

​ займа на начало​

• ​ также на листе​ именно за период,​ полных процентных периодов,​ таким кредитам обычно​
• ​ жмем на кнопку​ в текущем периоде:​(тип), то предполагается,​где:​
• ​ для расчета аннуитетных​ поэтому приходится использовать​ PPMT(rate, per, nper,​

​ (и период начисления​ но прежнее название​Запускается​ которой содержится формула.​ за весь срок​ кредитования, то есть,​ Аннуитет (без ПЛТ).​ т.е. в нашем​ оставшихся до окончательного​ выше, но свободы​

​fx​

• ​ =F8+G8.​ что платежи должны​АП – ежемесячный аннуитетный​ платежей по кредиту,​
• ​ метод итераций (по​
• ​ pv, [fv], [type]),​ % совпадает с​ сохранилось. Сейчас период​

​Мастер функций​ Курсор преобразуется при​ кредитования с учетом​ та сумма, которую​ Также тело кредита​ случае за месяц.​ возврата кредита.​ выходит больше. Можно​в строке формул,​Внесем формулы в соответствующие​ поступать в конце​ платеж;​ которыми можно воспользоваться​ сути, метод подбора).​ т.е. Principal Payment​ периодом платежей), то​ аннуитета чаще всего​

Из чего состоит платеж по кредиту?

​, в котором нужно​ этом в крестик,​ погашения тела займа​ вы берете взаймы,​ на начало и​ Ставка =10%/12 (в​Ситуация следующая. Кредит​ даже взять в​ находим функцию​ столбцы. Скопируем их​ периода.​О – сумма основного​

​ для планирования собственного​Чтобы облегчить поиск​ – платеж основной​ Приведенную стоимость также​ равен одному месяцу.​ переместиться в категорию​ который называется маркером​ и ежемесячных процентов,​ без учета процентов​ конец периода можно​ году 12 месяцев).​ досрочно погашен. Известна​ банке еще денег​ПЛТ​ на всю таблицу.​Предположим, вы хотите купить​

Способы расчета ежемесячного аннуитетного платежа по кредиту

​ долга;​ бюджета.​ Ставки методом итераций,​ части долга.​ нужно указывать =​Аннуитетную схему банки часто​«Математические»​ заполнения. Зажимаем левую​ достаточно перемножить величину​ и других дополнительных​ рассчитать с помощью​

​Кпер – общее​

• ​ сумма кредита (ОСЗ),​
• ​ в дополнение к​в списке и​
• ​Сравним переплату при аннуитетной​ аннуитет, который будет​

​пс – ежемесячная процентная​Перед практической частью изучения​ используется аргумент​В случае применения схемы​ 0.​ используют при кредитовании.​. Там выделяем надпись​ кнопку мыши и​ ежемесячного платежа (​ выплат.​ функции ПС и​

Формула расчета

​ число периодов платежей​ сумма срочных процентов,​ имеющемуся кредиту. Для​ жмем​ и дифференцированной схеме​ приносить $600 в​ ставка банка;​ вопроса следует ознакомиться​Предположение. Предположение​ аннуитета для выплаты​Тип​

​ Эта схема предусматривает​«СУММ»​

​ тянем его вниз​23536,74 рубля​«Бс»​ БС (см. файл​

​ по аннуитету, т.е.​

​ оплаченная на дату​ расчета по такой​

​ОК​ погашения кредита:​

​ месяц в течение​с – количество месяцев​

​ с теорией. В​- это приблизительное​

​ ссуды для каждого​(англ.: type). Число​ погашение кредита периодическими​и жмем на​ до конца таблицы.​) на количество месяцев​— это будущая​ примера лист Аннуитет​ 60 (12 мес.​ погашения, фактический срок​ модели придется рассчитывать​. В следующем окне​Красная цифра – аннуитет​

Пример расчета

​ следующих 20 лет.​ в сроке кредитования.​ экономической теории аннуитетный​ значение Ставки, т.е.​ периода действует равенство:​ 0 или 1,​ равновеликими платежами (как​ кнопку​В итоге все ячейки​

​ (​ стоимость. Эта величина,​ (ПЛТ), столбцы H:I).​ в году*5 лет)​ пользования кредитом. Требуется​ проценты и остаток​ нужно будет ввести​ (брали 100 000​ Сколько будет стоить​

​Зная формулу, можно запросто​ платеж – это​

​ прогноз на основании​

​ ОСПЛТ =ПЛТ –​ обозначающее, когда должна​

​ правило, ежемесячными), т.е.​

​«OK»​ столбца заполнены. Теперь​24 месяца​

​ которую будет составлять​Ссуда 100 000 руб.​Пс — Приведенная​ определить фактическую ПС,​ с точностью не​

​ аргументы для расчета:​ руб.), черная –​ аннуитет с годовой​ произвести необходимые расчеты​ один из способов​

Расчет аннуитетных платежей по кредиту в Excel

​ нашего знания о​ ПРПЛТ, т.к. платеж​ производиться выплата (и​равными суммами через равные​.​ мы имеем график​). Как видим, общая​ тело займа на​ взята на срок​ стоимость всех денежных​ т.к. есть подозрение,​ до месяца, а​Ставка​ дифференцированный способ.​

1. ​ процентной ставкой 6%?​ самостоятельно. Достаточно лишь​ ежемесячного платежа по​ задаче. Если значение​ включает сумму в​
2. ​ соответственно начисление процентов).​ промежутки времени​Запускается окно аргументов функции​_{​ выплаты тела займа​}​ сумма платежей за​
3. ​ момент завершения кредитного​ 5 лет. Определить​ потоков аннуитета. В​_{​ что на дату​}​ до дня:​
4. ​- процентная ставка​Проведем расчет процентов по​Вставьте функцию​

​ подставить исходные данные​ кредиту, когда его​

​ предположения опущено, то​ счет погашения части​ 0 – в​, которые включают как​СУММ​ помесячно. Как и​ весь срок кредитования​ договора. В большинстве​ величину ежеквартальных равновеликих​ нашем случае, это​ досрочного погашения кредита​Предполагается что:​ по кредиту в​ кредиту в Excel​PV​ предполагаемого кредита вместо​ сумма остается неизменной​ оно полагается равным​ ссуды (ОСПЛТ) и​

​ конце периода, 1​ выплату основного долга,​. Указанный оператор служит​ говорилось уже выше,​ в нашем случае​ случаев данный аргумент​ выплат по ссуде,​ сумма ссуды, т.е.​ ПС будет выше,​

​в зеленые ячейки пользователь​ пересчете на период​ и вычислим эффективную​(Present Value), в​ букв, и произвести​ на протяжении всего​ 10 процентам. Значение​ сумму для оплаты​ – в начале.​ так и процентный​ для того, чтобы​ величина оплаты по​ составила​ равен​ чтобы через 5​ 100 000.​ чем указана в​ вводит произвольные даты​ выплаты, т.е. на​ процентную ставку, имея​ русском варианте –​ необходимые математические вычисления​ срока кредитования.​Предположение​

​ начисленных за прошедший​

fb.ru

Инвестиции и аннуитет в Excel

• ​ Подробнее см. раздел​
• ​ платеж за пользование​

​ суммировать данные в​ данной статье с​564881,67 рубля​«0»​

​ лет невыплаченный остаток​​Бс — Будущая​ кредитном договоре.​ платежей и их​ месяцы. Если годовая​ следующую информацию по​ПС​

Инвестиции

​ при помощи обычного​При таком способе погашения​также полезно в​ период процентов (ПРПЛТ).​ Немного теории в​ кредитом.​ ячейках, что нам​ каждым новым периодом​

1. ​.​​, так как заемщик​​ составил 10% от​ стоимость всех денежных​​Как используя формулу​​ суммы​

   ​ ставка 12%, то​
​ предлагаемому банком кредиту:​

   

2. ​(Приведенная Стоимость).​

   ​ калькулятора. Но чтобы​
​ кредита плательщик одновременно​

   

   ​ случае​Сумму, идущую на​ начале статьи о​На картинке ниже приведен​ и нужно выполнить​ увеличивается.​Теперь можно подсчитать сумму​ на конец срока​ ссуды. Процентная ставка​

​ потоков аннуитета в​​ аннуитетого платежа рассчитать​отрицательные суммы — наши​ на один месяц​​Рассчитаем ежемесячную процентную ставку​​=PV(rate,nper,pmt,[fv],[type])​ расчет погашения кредита​ платит и начисленные​,​​ погашение основной суммы​​ постнумерандо и пренумерандо​ пример погашения кредита​ в столбце​Теперь нам нужно сделать​

Аннуитет

​ переплаты по кредиту.​ кредитования должен полностью​ составляет 15% годовых.​ конце срока (по​ фактическую ПС.​ выплаты банку, положительные​ должно приходиться по​ и платежи по​

1. ​=ПС(ставка;кпер;плт;[бс];[тип])​​ аннуитетными платежами стал​​ проценты, и часть​если имеется несколько​​ долга также можно​​ или статьи с​

   ​ (100 000 руб.)​
​«Выплата по телу кредита»​

   

2. ​ месячный расчет оплаты​

   ​ Для этого нужно​
​ рассчитаться с кредитором.​

   

   ​Решение2​ истечении числа периодов​Благодарю заранее.​ — берем дополнительный​ 1% соответственно.​ кредиту:​Введите аргументы:​ наиболее понятным, рассмотрим​ суммы основного долга.​ решений уравнения –​ вычислить, зная  величину​

​ примерами, указанные выше.​​ ежемесячными платежами в​. Он имеет следующий​ по процентам. Для​ отнять от общей​ Указанный аргумент не​Ежеквартальный платеж может​​ Кпер). В нашем​​Читайте Правила форума.​ кредит к уже​Кпер​​Заполним таблицу вида:​​=PV(C4/12,C5*12,C6)​ его на примере.​ Но, как правило,​ в этом случае​​ платежа (ПЛТ), период​​Все 6 аргументов (параметров​ течение 5 лет​ синтаксис:​ этих целей будем​ величины выплат по​ является обязательным. Поэтому,​ быть вычислен по​

​ случае Бс =​ Создавайте свою тему.​
​ имеющемуся​
​- количество периодов,​

​Комиссия берется ежемесячно со​

office-guru.ru

Калькулятор расчета кредита в Excel и формулы ежемесячных платежей

​=ПС(C4/12;C5*12;C6)​Предположим, что заемщик взял​ вначале ежемесячный взнос​ находится значение Ставки​ (Период), общее количество​ аннуитета) связаны между​ при ставке 15%.​

​=СУММ(число1;число2;…)​ использовать оператор​ кредиту, включая проценты​ если он опускается,​ формуле =ПЛТ(15%/12; 5*4;​

Как рассчитать платежи по кредиту в Excel

​ 0, т.к. ссуда​ Эта тема закрыта.​подсчитать точное количество дней​ т.е. срок кредита​

1. ​ всей суммы. Общий​Вам нужно внести одноразовый​ в банке ссуду​
2. ​ преимущественно состоит из​ ближайшее к​ периодов (Кпер) и​ собой выражением:​ Для погашения тела​В качестве аргументов выступают​

​ПРПЛТ​ и тело займа,​ то считается равным​ 100 000; -100 000*10%; 0),​

Расчет аннуитетных платежей по кредиту в Excel

​ в конце срока​Гэндальф​

​ между двумя датами​

​ в месяцах.​

• ​ платеж по кредиту​ платеж в размере​
• ​ на сумму 50​ процентов по ссуде.​
• ​Предположению​

​ ставку (СТАВКА):​

​поэтому каждый из них​ кредита и начисленных​ ссылки на ячейки,​

• ​. Выделяем первую пустую​ начальную сумму, взятую​ нулю.​ результат -6 851,59р.​
• ​ должна быть полностью​: Добрый день всем​

​ (и процентов, которые​Пс​ – это аннуитетный​ $83748,46 (расход), чтобы​

1. ​ 000 рублей сроком​ Поэтому при расчете​.​ОСПЛТ=ПЛТ*(1+СТАВКА)^(Период-Кпер-1)​ может быть вычислен​
2. ​ процентов потребуется произвести​ в которых содержатся​
3. ​ ячейку в столбце​ в долг. Но​Аргумент​Все параметры функции​ погашена. Если этот​ участникам форума, столкнулся​ на них приходятся)​- начальный баланс,​ платеж плюс комиссия.​ оплатить этот аннуитет.​ на 5 лет.​ аннуитетных платежей по​Подробнее про функцию можно​Вышеуказанная формула работает при​ при условии, если​

​ 60 платежей (5​ числа. Мы устанавливаем​«Выплата по процентам»​ мы помним, что​«Тип»​ ПЛТ() выбираются аналогично​

​ параметр опущен, то​

Расчет платежей в Excel по дифференцированной схеме погашения

​ с проблемой аннуитетного​ лучше с помощью​

• ​ т.е. сумма кредита.​ Сумма основного долга​ В будущем вы​
• ​ По условиям кредитного​ кредиту можно заметить,​

​ прочитать в статье Аннуитет.​

​ БС=0. При ТИП=1​ заданы остальные параметры.​ лет*12мес в году).​

​ курсор в поле​

• ​. Жмем на кнопку​ первое из этих​
• ​определяет время расчета:​
• ​ предыдущей задаче, кроме​ он считается =0.​ платежа: формула данного​
• ​ функции​Бс​ и сумма процентов​ будете получать 240*600​

​ договора годовая процентная​ что данный способ​ Определяем процентную ставку​

​ (платеж в начале​

​ Функции аннуитета помогают​

​ Сумма ежемесячного платежа​«Число1»​«Вставить функцию»​ значений уже со​ в конце или​ значения БС, которое​Тип — число​ расчета (см. вложение)​ДОЛЯГОДА (YEARFRAC)​- конечный баланс,​ – составляющие части​ (доход) = $144000.​ ставка по кредиту​ возврата средств не​ в MS EXCEL.​

​ периода) и n=1​ пользователю упростить вычисления,​ = 2378,99руб. См.​. Затем зажимаем левую​.​ знаком​

​ в начале периода.​ = -100000*10%=-10000р., и​ 0 или 1,​

​ при досрочном погашении​qshin1980​ т.е. баланс с​ аннуитетного платежа.​

​ Это еще один​ равна 20 %.​ очень выгоден для​

​Функция БС(ставка; кпер; плт;​ (первый платеж), ПРПЛТ=ПЛТ​ но все они​

​ файл примера Лист​ кнопку мыши и​В запустившемся окне​«-»​

Формула расчета процентов по кредиту в Excel

​ В первом случае​ требует пояснения.​ обозначающее, когда должна​ кредита уменьшает срок​: Добрый день, уважаемые​ которым мы должны​

​Сумма основного долга =​ пример того, что​Исходя из формулы, для​

​ заемщиков.​

​ [пс]; [тип])​Если БС<>0, то​ основаны на Формуле​ Аннуитет (ПЛТ). Как​ выделяем на листе​Мастера функций​. Поэтому в конкретно​ он принимает значение​Для этого вернемся​

​ производиться выплата. 0​ кредита, необходимо срок​ форумчане​

​ по идее прийти​ аннуитетный платеж –​ деньги растут с​

​ вычислений необходимо знать​В зависимости от дополнительных​возвращает будущую стоимость​ формула усложнится:​ 1.​

​ видно из графика​ первые две ячейки​в категории​

• ​ нашем случае получается,​«0»​
• ​ к предыдущей задаче,​ – в конце​ не изменять, а​Очень часто обращаюсь​
• ​ к концу срока.​ проценты.​
• ​ течением времени.​ ежемесячную процентную ставку.​ условий кредитования, аннуитетные​ инвестиции на основе​
• ​Функцию ОСПЛТ() часто применяют​Примечание​ платежей, банк в​

​ столбца​«Финансовые»​ что их нужно​, а во втором​ где ПС =​

Расчет полной стоимости кредита в Excel

​ периода, 1 –​ пересчитывать платеж в​ к Вашему форуму​ Очевидно =0, т.е.​Сумма процентов = остаток​Примечание:​ Банки редко указывают​ платежи делятся на​ периодических постоянных (равных​ при составлении графика​

• ​. Формула 1 работает,​ первые периоды получает​
• ​«Выплата по телу кредита»​производим выделение наименования​
• ​ сложить. Как видим,​ –​ 100000, а БС=0.​

​ в начале. Если​ сторону уменьшения. Какой​

​ за помощью, но​ никто никому ничего​ долга * месячную​Мы получаем ежемесячные​

​ данную цифру в​ небольшие группы. Их​ по величине сумм)​ платежей по аннуитетной​ если Ставка не​ платежи, идущие на​. В поле, как​ПРПЛТ​ общая сумма переплаты​

​«1»​ Найденное значение регулярного​ этот параметр опущен,​

​ д.б. формула, поправьте​ обычно стараюсь разобраться​

​ не должен.​ процентную ставку.​ платежи, поэтому используем​ кредитном договоре, поэтому​

​ классификация достаточно разнообразна,​ платежей и постоянной​ схеме (см. Выплата​ равна 0. Если​ погашение %, а​ видим, отобразилась ссылка​

​. Выполняем щелчок по​ по кредиту за​. Большинство банковских учреждений​ платежа обладает тем​

​ то он считается​ если возможно?​

​ сам. Как ни​Тип​Остаток основного долга =​ формулу 6/12 =​ нужно найти ее​ однако некоторые виды​

exceltable.com

Расчет кредита в Excel

​ процентной ставки.​ основной суммы долга​ ставка равна 0,​ тело кредита сокращается​ на диапазон. Она​ кнопке​ весь срок составила​ используют именно вариант​ свойством, что сумма​ =0 (наш случай).​machining​ странно, чем сложнее​- способ учета​ остаток предыдущего периода​ 0,5% для тарифа​ самостоятельно. Для этого​ аннуитетов уже не​Например, если у​ в аннуитетной схеме.​ то вместо Формулы​ медленно (см. статью Сравнение​ состоит из двух​«OK»​64881,67 рубля​ с оплатой в​ величин идущих на​Примечание​: Всем привет! Я​ бывает задача, тем​ ежемесячных выплат. Если​ – сумму основного​ и 20*12 =​

​ нужно воспользоваться формулой:​ встречаются или встречаются​ Вас сейчас на​ Расчет в MS​

​ 1 действует гораздо​ графиков погашения кредита​ частей, разделенных двоеточием:​.​.​ конце периода. Этот​ погашение тела кредита​:​ тоже ищу для​ быстрее понимаешь суть​ равен 1, то​ долга в предыдущем​ 240 для аргумента​пс = П /​ крайне редко в​ банковском счете сумма​ EXCEL)​

Вариант 1. Простой кредитный калькулятор в Excel

​ более простое выражение:​ дифференцированными и аннуитетными​ ссылки на первую​Происходит запуск окна аргументов​Урок:​ аргумент тоже является​ за все периоды​В нашем случае​ себя такую формулу…​ ее решения. Но,​ выплаты учитываются на​ периоде.​nper​ 100 / 12,​ перечне банковских услуг.​​ ПС (ПС м.б.​​Примечание​​ ПЛТ * Кпер​​ платежами в MS​ ячейку диапазона и​ функции​​Мастер функций в Эксель​​ необязательным, и если​ выплат равна величине​​ проценты начисляются в​​ Помогите, люди добрый!​ вот попалась такая​​ начало месяца, если​​Опираясь на таблицу ежемесячных​(кпер). Последние два​где:​

• ​Виды аннуитетов:​​ =0) и вы​.​ + ПС +​ EXCEL).​ на последнюю. Для​ПРПЛТ​А теперь с помощью​ его опустить считается,​ займа с противоположным​
• ​ конце периода. Например,​​Гэндальф​ задача.​ равен 0, то​
• ​ платежей, рассчитаем эффективную​​ аргумента необязательны. Если​П – годовая процентная​
• ​Фиксированные – неизменные на​​ ежемесячно вносите одну​В файле примера​ БС = 0​Если каждый элемент аннуитета​ того, чтобы в​. Её синтаксис выглядит​ других операторов Эксель​ что он равен​
• ​ знаком. Т.е. справедливо​​ по истечении первого​: Сообщение пришло на​Есть калькулятор аннуитета.​ на конец. У​ процентную ставку:​ опущен аргумент​ ставка.​ протяжении всего срока​ и туже сумму​ на листе Аннуитет​ (в этом случае​ имеет место в​

​ будущем иметь возможность​ следующим образом:​ сделаем помесячную детализацию​ нулю.​ равенство: ПС+СУММ(долей ПЛТ,​ месяца начисляется процент​ почту, думал что​ Функция «ПЛТ» в​ нас в России​

Вариант 2. Добавляем детализацию

​взяли кредит 500 000​fv​Расчет:​ кредитования.​ ПЛТ, то функция​​ (без ПЛТ) определена​​ схема платежей перестает​​ конце соответствующего периода,​​ скопировать указанную формулу​=ПРПЛТ(Ставка;Период;Кпер;Пс;Бс)​ выплат, чтобы видеть,​Теперь настало время перейти​ идущих на погашение​ за пользование ссудой​ кто-то отозвался-неужели!!!!! ,​ принципе справляется с​ абсолютное большинство банков​ руб.;​(бс), значит, он​пс = 20 /​Валютные – размер платежа​ вычислит остаток на​

​ аналитическая зависимость суммы​​ быть аннуитетом и​​ аннуитет называется аннуитетом​ посредством маркера заполнения,​Как видим, аргументы данной​​ сколько в конкретном​​ к конкретному примеру​

​ тела кредита)+БС=0: 100000р.+(-100000р.)+0=0.​​ в размере (100 000*10%/12),​​ ан нет….)))))))) нашлись​ основной задачей, т.е.​ работает по второму​вернули в банк –​ равен 0 (нет​ 100 / 12​ может меняться в​​ Вашем банковском счете​​ идущей на погашение​ превращается в беспроцентную​ постнумерандо (Ordinary Annuity);​ делаем первую часть​ функции абсолютно идентичны​ месяце мы платим​ расчета ежемесячного взноса​То же самое​ до этого момента​ друзья по несчастью!​ посчитать аннуитет. Единственная​ варианту, поэтому вводим​ 684 881,67 руб.​ будущего значения). Если​

​ = 0,017.​ зависимости от колебаний​ через Кпер месяцев​ долга от номера​ ссуду).​ если в начале​ ссылки на диапазон​ аналогичным элементам оператора​ по телу займа,​

​ при помощи функции​

​ и для второй​ должен быть внесен​Гэндальф​ проблема если срок​ 0.​ (сумма всех платежей​ опущен аргумент​Зная все исходные данные,​ на валютном рынке.​ (предполагается, что капитализация​ периода.​Вышеуказанная Формула 1 предполагает,​ периода — аннуитетом​ абсолютной. Выделяем её​ОСПЛТ​ а сколько составляет​ ПЛТ. Для расчета​ задачи: 100000р.+(-90000р.)+БС=0, т.е.​ первый ежемесячный платеж.​: Я пользовалась вот​ кредита считать не​

​Также полезно будет прикинуть​​ по кредиту);​​type​

​ можно приступать к​Индексируемые – могут корректироваться​ процентов происходит также​Функция ПРПЛТ (ставка; период;​ что знаки денежных​ пренумерандо (Annuity Due).​ и жмем на​. Поэтому просто заносим​ величина процентов. Для​

Вариант 3. Досрочное погашение с уменьшением срока или выплаты

​ используем таблицу с​ БС=-10000р.​В случае начисления​ этим. Можно попробовать​ месяцами, а колличеством​ общий объем выплат​переплата составила 184 881,​(тип), то предполагается,​ нахождению аннуитетного платежа​ с поправкой на​ ежемесячно с процентной​ кпер; пс; [бс];​ потоков (+/-) указываются​ Обычно используется аннуитет​ функциональную клавишу​ в окно те​ этих целей чертим​ исходными данными, где​Прежде, чем брать заем,​ процентов в начале​ переделать под Ваш​ дней и дата​ и переплату, т.е.​

​ 67 руб.;​ что платежи должны​ по кредиту. Оно​​ актуальный уровень инфляции.​​ ставкой равной величине​ [тип])​ с учетом их​

​ постнумерандо.​F4​ же данные, которые​ в Экселе таблицу,​ указана процентная ставка​ неплохо было бы​

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

​ периода, в первом​ файл.​ последнего платежа переносится​ ту сумму, которую​процентная ставка – 184​ поступить в конце​ выглядит следующим образом:​Переменные – платежи меняются​ СТАВКА).​используется для вычисления​ направления. Например, банк​Примечание​. Вторую часть ссылки​ мы вводили в​ которую будем заполнять​ по кредиту (​ рассчитать все платежи​ месяце % не​machining​

​ из-за выходного, то​

• ​ мы отдаем банку​ 881, 67 /​ периода. Этот аннуитет​АП = 50 000​
• ​ в зависимости от​Примечание​ регулярных сумм идущих​ выдал кредит (ПС>0),​. В функциях MS​
• ​ так и оставляем​ предыдущем окне аргументов.​ данными. Строки этой​12%​ по нему. Это​ начисляется, т.к. реального​​: Отлично, спасибо, все​

planetaexcel.ru

Аннуитетный платеж/последний платеж (Формулы)

​ последний платеж сбивается.​​ за временно использование​ 500 000 *​
​ не принимает во​ * 0,017 /​ уровня доходности финансового​.​ на погашение процентов​ клиент банка ежемесячно​ EXCEL для указания​ относительной. Теперь при​ Не забываем при​ таблицы будут отвечать​), величина займа (​
​ убережет заёмщика в​ пользования средствами ссуды​ работает. Есть конечно​ По идеи основной​ его денег. Это​ 100, или 37%.​ внимание продолжительность жизни,​ 1 — (1​ инструмента.​Английский вариант функции:​ за ссуду используется​ вносит одинаковый платеж​ типа аннуитета предусмотрен​ использовании маркера заполнения​ этом, что ссылка​ соответствующему периоду, то​500000 рублей​
​ будущем от различных​

​ не было (грубо​​ погрешность с банком​ долг последнего платежа​​ можно сделать с​​Безобидная комиссия в 1​ инфляцию и т.д.​ + 0,017)-60 =​​Механизм расчета аннуитетных платежей​​ FV(rate, nper, pmt,​ с теми же​ (ПЛТотбанка к клиенту​
​ специальный необязательный параметр​ первая ячейка диапазона​ в поле​ есть, месяцу. Учитывая,​) и срок кредита​ неожиданных неприятностей и​ говоря % должен​ на она отличается​ должен уменьшаться или​ помощью простых формул:​
​ % обошлась кредитополучателю​Урок подготовлен для Вас​ 1336,47 руб.​ по кредиту зависит​ [pv], [type]), т.е.​ аргументами, что и​ (ПС) и​[тип]​ будет закреплена, а​«Период»​

​ что период кредитования​​ (​ разочарований, когда выяснится,​
​ быть начислен за​ в считанные рубли,​ увеличиваться на эту​Если хочется более детализированного​ очень дорого.​ командой сайта office-guru.ru​Программа Excel – это​ от их вида.​ Future Value –​ ОСПЛТ().​в банк от клиента​. По умолчанию​ последняя будет растягиваться​должна быть относительной,​
​ у нас составляет​24 месяца​ что переплата слишком​ 0 дней пользования​ т.к. банк списывает​
​ незначительную разницу.​ расчета, то можно​Эффективная процентная ставка кредита​Источник: http://www.excel-easy.com/examples/investment-annuity.html​ не просто большая​
​ Однако для потребительского​ будущая стоимость.​Примечание.​(ПЛТ). Если схема​тип​ по мере продвижения​ а во всех​24​). При этом оплата​ большая. Помочь в​ ссудой), а весь​

​ сумму досрочного платежа​​Помогите, пожалуйста!​ воспользоваться еще двумя​​ без комиссии составит​​Перевел: Антон Андронов​ таблица. В ней​ кредитования чаще всего​Вычисления в функции БС()​Английский вариант функции:​ погашения кредита учитывает​
​=0  (выплаты в конце​​ вниз. Это нам​ других полях координаты​месяца, то и​ производится ежемесячно в​ данном расчете могут​ первый ежемесячный платеж​ не в день​Michael_S​ полезными финансовыми функциями​
​ 13%. Подсчет ведется​Автор: Антон Андронов​ можно произвести огромное​ используются фиксированные аннуитеты.​
​ производятся по этой​ IPMT(rate, per, nper,​ единовременную выплату в​ периода), что соответствует​ и нужно для​ нужно привести к​ количество строк тоже​
​ конце каждого периода.​ инструменты программы Excel.​ идет в погашение​ погашения основного долга,​: Сумма основного долга​ Excel -​

​ по той же​​Excel – это универсальный​
​ количество вычислений, зная​

​Расчет аннуитетных платежей по​​ формуле:​ pv, [fv], [type]),​ конце погашения, то​ аннуитету постнумерандо. Если​

​ выполнения поставленных целей.​​ абсолютному виду. После​ будет соответствующим. В​
​Выделяем элемент на листе,​ Давайте выясним, как​ ссуды (основной суммы​
​ поэтому и насчитывается​ (Q:W)​ОСПЛТ (PPMT)​
​ схеме.​
​ аналитическо-вычислительный инструмент, который​ лишь, какие формулы​
​ кредиту обычно производится​Если СТАВКА =0, то​ т.е. Interest Payment​ БСв банк от​
​тип​ Далее жмем на​ этого щелкаем по​ столбцах указана выплата​
​ в который будет​ рассчитать аннуитетные платежи​ долга).​ некая лишняя сумма​
​200?’200px’:»+(this.scrollHeight+5)+’px’);»>=ОСПЛТ($L$6/100/$L$6;BE18;$L$6;-$L$4;0)​и​Согласно Закону о потребительском​ часто используют кредиторы​ нужно использовать. Для​ перед его оформлением.​ Будущую стоимость можно​ – выплата процентов.​ клиента. Функции MS​=1, то предполагается аннуитет​ кнопку​ кнопке​ тела займа, выплата​ выводиться результат расчета,​
​ по кредиту в​Решение1​ %.​
​Сумма процентов (X:AE)Код200?’200px’:»+(this.scrollHeight+5)+’px’);»>=ПРПЛТ($L$6/100/$L$10;BE18;$L$10;-$L$4;0)и​
​ПРПЛТ (IPMT)​ кредите для расчета​ (банки, инвесторы и​

excelworld.ru

Аннуитетный платеж формула

​ расчета аннуитетного платежа​​ Поэтому важно знать,​ определить по формуле​В случае применения схемы​ EXCEL также учитывают​ пренумерандо (выплаты в​«OK»​«OK»​ процентов, общий ежемесячный​ и щелкаем по​ этой программе.​Итак, ежемесячный платеж​Fairuza, спасибо большое!​ у вас не​

​. Первая из них​​ полной стоимости кредита​ т.п.) и заемщики​ в Excel есть​ стоит ли вообще​

​ БС= — ПЛТ​​ аннуитета для выплаты​ направления платежей, поэтому​ начале периода).​.​.​

​ платеж, который является​​ пиктограмме​Скачать последнюю версию​ может быть вычислен​ Это то что​

​ учтена​​ вычисляет ту часть​ (ПСК) теперь применяется​ (предприниматели, компании, частные​ специальная функция –​ заниматься какими-либо вычислениями,​ * Кпер +​ ссуды для каждого​ функция ПЛТ() возвращает​Часто в расчетах используют​Итак, результат остатка кредитной​Затем результат расчета суммы​ суммой предыдущих двух​

​«Вставить функцию»​ Excel​ по формуле =ПЛТ(10%/12;​

CyberForum.ru

​ надо!​

Содержание

❶ Как рассчитать аннуитет

Аннуитет, или аннуитетный платеж – это такой способ расчета платежа по кредиту, при котором сумма кредита и процентная ставка по нему погашаются равными суммами в течение всего периода кредитования. Как рассчитать аннуитет?Ознакомьтесь с математической формулой расчета аннуитета:АП = СК × (P × (1 + P)n) / ((1 + P)n — 1),

где АП – это аннуитетный платеж по кредиту,

СК – сумма кредита,P – ставка процентов, выраженная в долях и рассчитанная на период (месяц, квартал, год, день)n – количество периодов начисления процентов.

При этом выражение: (P × (1 + P)n) / ((1 + P)n — 1) – это формула аннуитетного коэффициента.

Определитесь с суммой кредита, процентной ставкой и количеством периода начисления процентной ставки. Если первую переменную вы можете задать сами, то вторую и третью вам нужно узнать в банке, в котором вы хотите получить кредит. Для сравнения выбирайте несколько банков, чтобы узнать, чьи условия лучше.

Подставьте данные переменные по вашему кредиту в формулу. Например, вы хотите получить в банке 100 000 рублей. Банк может предоставить вам кредит на условии аннуитета и при следующих показателях: процентная ставка – 20% годовых (в месяц процентная ставка будет равна 1,6667%), количество периодов кредитования – 12 месяцев.

Произведем необходимый расчет: АП = 100 000 х(0,016667 х (1+0,016667) 12)/((1+0,016667)12-1) = 100 000 * 0,016667 * 1,219439/(1,219439-1) = 9261,975 р. в месяц

Таким образом, при 20% годовых за 12 месяцев будет выплачена сумма: 9261,975*12 = 111143,70 р.

При этом стоимость пользования кредитом составит: 111 143,70 -100 000 = 11 143,70р.

Убедитесь, что аннуитетный платеж выгоден для вас. Рассчитайте, сколько вы заплатите, если у вас будет обычная схема кредитования, при прямом начислении процента на оставшуюся сумму: при этом, кредит погашается в течение всего срока равными долями, платеж составляет: 100 000 / 12 = 8 333,33 р. в месяц.

Тогда, таблица погашения кредита и выплаты процентов будет выглядеть, как показано на рисунке. Таким образом, вы получите сумму: 100 000 +10 833,33 = 110 833,33 р. Эта сумма меньше, чем сумма платежа по кредиту, рассчитанная при способе аннуитетного платежа.

Предложение от нашего партнераПри окончательном принятии решения, по какой системе кредитоваться, обратите внимание на условия кредитных договоров. Кроме того, просчитайте хорошо свои риски. При обычной системе кредитования (способ начисления прямых процентов на остаток платежа) сумма выплат постепенно уменьшается и вам будет легче выплачивать кредит с каждым месяцем.

При аннуитетном способе расчета платежа за кредит, сумма платежа остается одинаковой на протяжении всего периода кредитования. Кроме того, если вы будете платить «вперед», погашая кредит большими суммами, чем это указано в договоре, при аннуитете погашение происходит за счет последних месяцев, то есть, с конца периода кредитования.

Вы просто будете меньшее время выплачивать кредит — ежемесячная сумма платежа при этом банком не пересчитывается (поэтому внимательно изучайте договор с банком).Аннуитетные платежи – пожалуй, самый популярный способ погашения задолженности, который принят в современной банковской практике.

Они применяются в совершенно разных кредитных программах: кредитах наличными, автокредитах, кредитах малому и среднему бизнесу. Рассчитать аннуитетные платежи достаточно просто – для этого нужно знать математическую формулу.

Чтобы рассчитать аннуитетные платежи, вам понадобится узнать три вещи:- Первоначальную сумму кредита;- Процентную ставку;

— Количество периодов начисления процентов.Первые два показателя очевидны и объяснения не требуют. Однако с количеством периодов начисления процентов нужно разобраться. При ежемесячном гашении кредита количество периодов начисления процентов будет равно количеству месяцев в сроке кредитования. Поэтому для дальнейшего расчета срок кредита выражайте в месяцах.

Если вы хотите рассчитать аннуитетные платежи по конкретному кредиту, который собираетесь оформить, то все перечисленные цифры можно узнать в выбранном банке. Также можно разобраться в формуле и структуре аннуитетных платежей на примере из любых условных чисел.

Чтобы рассчитать аннуитетные платежи, подставьте сумму, ставку и срок кредита в следующее выражение:П = СК ? (i ? (1 + i)n) / ((1 + i)n — 1),где П – это полученная величина платежа,СК – сумма кредита,i – процентная ставка,

n – количество периодов начисления процентов.

Проводя самостоятельный расчет, учтите две вещи. Во-первых, годовую процентную ставку следует также перевести в месячную и выразить ее в десятичных долях.

Во-вторых, рассчитанный описанным образом платеж может в пределах нескольких рублей отличаться от платежа, рассчитанного банком.

Это происходит из-за того, что для большей точности банк делит годовую процентную ставку не на 12 месяцев, а на количество дней в текущем году.

• как рассчитывается аннуитетный платеж в 2018

Источник: https://www.kakprosto.ru/kak-51857-kak-rasschitat-annuitet

Как рассчитать формулу аннуитетного платежа?

Практически все люди когда-либо сталкивались с банковским займом, поэтому о том, что существует некая формула, по которой можно рассчитать кредитные виды оплаты (о том, как рассчитать платежи по  кредиту можно узнать на любом официальном сайте банка), многие знают. Что это за формула? Можно ли, зная её провести самостоятельно расчёты аннуитетного платежа?

Общее понятие аннуитетного платеж

Для начала определимся с понятием. Аннуитетный платёж – это сумма выплат, осуществляемая заёмщиком по кредиту. При этом данный способ оплаты подразумевает начисление ежемесячных платежей в равных суммах (т.е.

в течение всего кредитного периода  погашение кредита при ипотеке или любом другом виде займа происходит равными частями, с учётом процентов).

Кроме того, рассчитываясь с банком по аннуитетной схеме, заемщик, таким образом, увеличивает каждый месяц сумму основного займа и уменьшает ту, которая идёт на  досрочное погашение процентов по кредиту.

Для самого финансового учреждения выгоднее предложить своему клиенту именно данную методику оплаты, потому как она приносит большую  прибыль, чем при оплате по альтернативным схемам. Заёмщику также удобно следовать данному плану, потому как ему не нужно каждый раз звонить в банк и узнавать сумму ежемесячных платежей.

Ещё один вариантом оплаты является дифференцированный платёж – это вид выплат напоминает метод перевёрнутой пирамиды, с начала сумма оплаты большая, но постепенно она уменьшается. То есть сумма ежемесячного платежа будет напрямую зависеть от общей суммы долга по кредиту. Например, вы выплатили уже около 80% всего банковского займа, тогда процент за оставшиеся 20% будет равен 20 у.е.

Формула аннуитетной схемы платежа

Рисунок:

Как уже говорилось выше, существует формула, по которой можно рассчитать сумму аннуитетного платежа (т.е. ту сумму денег, которую вам нужно будет платить каждый месяц на протяжении всего кредитного периода). Вот она:

А= К*S

Поясним значение букв в данной формуле:

• А – указывает на сумму аннуитетного платежа;
• S – обозначает общую сумму банковской ссуды;
• К – указывает на коэффициент аннуитета.

Если нам неизвестен коэффициент аннуитета, а он не известен, то его можно рассчитать по другой формуле, которая выглядит приблизительно так:K = i*(1+i)n / ((1+i)n -1)

При пояснении отметим, что i – банковская ставка, начисляемая ежемесячно (её можно узнать, разделив процент годовой ставки на 1 год), а n – количество периодов, по окончании которых и будет выплачена вся сумма кредита.

Учитывая то, что оплата по кредиту должна производиться каждый месяц, то и процентная ставка, начисляемая на сумму платежа также должна быть месячной (т.е. : i = 12% / 12 месяцев %).

Таким образом, зная все составляющие, можно посчитать сумму аннуитетного платежа.

Пример расчета платежа по формуле

Для того чтобы было понятнее, приведём пример расчета платежа по вышеуказанной формуле. К примеру, вы решили оформить кредит на покупку квартиры.

При этом срок кредитования составил 3 года, сумма кредита – 30 000 рублей, а количество процентов по предоставленному банковскому займу равно – 18% годовых, с учётом ежемесячных платежей.

У нас вышли следующие данные: S = 30 000 рублей, а i = 1,5% (18 %/12 месяцев) = 0,015, а также n = 36 (3 года * на 12 месяцев). Для вычисления коэффициента аннуитета необходимо эти цифры подставить в формулу:

К = 0,015*(1+0,015) 36 / (1+0,015) 36 — 1; К = 0,03615

Сумма же ежемесячных выплат будет равна:

A = S*К =30000 * 0,03615 = 1084,57 рублей

Как упростить расчет формулы

Если же данный вид расчета для вас является сложным, то можно данный вид платежа рассчитать другим способом, при помощи Excel. Она удобна тем, что после ввода всех ваших данных, можно воспользоваться функцией ПЛТ.

В результате чего вы получите следующее:=ПЛТ(18%/12; 36; -30000)Не забудьте о том, что в данном случае в скобках должны быть указанны цифры через точку с запятой, в строго определённом порядке:

• Данные по процентной ставке;
• Количество платёжных месяцев;
• Общая сумма кредита.

Если же этот способ расчета вам больше понравился, используйте его. Мы привели примеры обоих вариантов расчета. Какой будет удобен для вас больше, решайте сами!

Источник: http://www.FD7.ru/kak-rasschitat-formulu-annuitetnogo-platezha/

Формула расчета аннуитетного платежа — Инструкция!

Занимая деньги в финансовом учреждении, клиент обязуется в течение определенного договором временного периода выплачивать сумму кредита и установленную банком, процентную ставку.

Погашать кредит можно несколькими способами. Самый распространенный — аннуитетный платеж.

Понятие аннуитетного платежа

Аннуитет — это финансовая рента, поступающая одинаковыми суммами через равные временные отрезки (месяц, год и прочее). Платежи такого вида применяются для выплаты накопившихся процентов по отчислениям разного типа, а также для погашения действующих кредитов, будь то потребительские или ипотека.

Заемщик, совершающий аннуитетный платеж, гасит тело кредита и проценты.

Аннуитетом называют:

1. платеж, вносимый равными частями в определенное время;
2. финансовый инструмент;
3. график погашения задолженности;
4. регулярные страховые выплаты.

График применяется как для расчета выплат по кредиту, так и для вычисления денежной суммы, накапливаемой к определенному сроку.

Классификация аннуитета

Аннуитетные платежи весьма разнообразны и делятся на несколько видов, в зависимости от определенных факторов.

Время выплаты стартовых взносов:

• постнумерандо — по окончании первого периода;
• пренумерандо — поступление до начала периода.

Сроки действия:

• срочные платежи;
• пожизненные: передаваемые по наследству, с коррекцией денежных взносов или гарантированные платежи, при которых устанавливается срок выплаты.

Страховые взносы отличаются по характеру выплат и делятся на простые, отложенные, срочные, гарантированные и обладающие защитой личного капитала.

Аннуитеты бывают:

1. фиксированные (равная сумма платежей);
2. валютные (привязанные к валюте, к примеру, к доллару);
3. индексируемые (с коррекцией индекса инфляции);
4. переменные (сумма выплаты привязана к индексу доходности финансового инструмента).

Платежи могут быть ежемесячными, ежеквартальными и ежегодными, и различаться по срочности внесения:

1. срочные, количество выплат фиксировано договором;
2. досрочные;
3. бессрочные;
4. не фиксированные

Классификация зависит и от наименования плательщика:

1. страховые;
2. пенсионные;
3. финансовые (банковские);
4. платежи, производимые юридическими лицами;
5. суммы, вносимые физическими лицами.

Правила и особенности выплат

Основные требования к заемщику, выбравшему подобный способ оплаты кредита:

• займ возвращается равными частями;
• график и размер выплат остается неизменным на протяжении всего расчетного периода.

Преимущества платежа:

• равные суммы, выплачиваемые в установленный срок;
• возможность кредитования разных слоев населения, в том числе и малообеспеченных граждан;
• снижение суммы платежа при инфляции (не стоит путать с дефляцией);
• неизменная величина выплат.

Перечисленные факторы позволяют клиенту контролировать свои расходы, планировать и корректировать бюджет семьи.

Схема обладает рядом минусов, среди которых:

1. значительная переплата по кредиту в сравнении с дифференциальным платежом;
2. трудно осуществить досрочное погашение займа;
3. нельзя сделать перерасчет при желании досрочно погасить долг.

Использование аннуитетных платежей очень выгодно для банков, получающих хорошую прибыль по процентам.

Составляющие ежемесячного платежа

Аннуитетный платеж является самым распространенным вариантом ежемесячных выплат по кредитам. Клиент каждый месяц вносит на счет банка, независимо от величины оставшейся задолженности, фиксированную сумму, состоящую из двух частей: тело кредита и процентная ставка.

Это отличает аннуитет от дифференцированного варианта выплаты, где в начале кредитного периода большая часть вносимой суммы — проценты. Основной долг уменьшается медленно, а размер переплаты значительно увеличивается.

Рассчитать сумму ежемесячных выплат можно с помощью кредитного калькулятора, который можно найти на официальных сайтах практически всех банков: Сбербанка, ВТБ, Альфа и прочих.

Используя форму онлайн-расчетов можно узнать суммы, которые идут на погашение долга и процентов.

Но расчеты, выполненные самостоятельно по формуле, дадут более точный результат.

Формула расчета платежа

Существует специальная формула расчета кредита:

При этом:

• Х — ежемесячный аннуитетный платеж;
• S — тело кредита;
• m — процентная ставка банка (ежемесячная), установленная на сумму займа
• N — количество процентных периодов (месяцев).

Зная формулу расчета выплат, очень просто узнать точную сумму аннуитетного платежа. Например: в банке взят кредит на 2 года, в сумме 20 000 руб. Годовая процентная ставка составляет 22%. Как рассчитать ежемесячный взнос?

Месячная процентная ставка вычисляется по формуле m=P/100/12, где Р-годовая процентная ставка финансового учреждения. В данном случае Р=22%, значит

• m = P/100/12 = 22:100:12 = 0,0183;
• S = 20 000;
• N = 24.

Подставив данные в формулы, получаем:

То есть, клиент в течение 2 лет должен каждый месяц платить банку 1037 руб. 20 коп.

Очень просто подсчитать переплату по кредиту: 1 037.20 х 24-20 000 = 4 892.80. Сумма переплаты по кредиту составит 4 892.80 руб.

Калькулятор кредитного платежа, существующий на сайте Сбербанка и других финансовых учреждений, покажет такой же результат. Возможные отличия объясняются округлением полученных сумм или разными процентными ставками.

Вычисления с помощью программы Excel

В Excel существует специальная функция, позволяющая произвести расчет аннуитетного платежа — «ПЛТ». Слева от поисковика расположен знак «fx», при нажатии на который в новом окне открывается перечень доступных функций, в том числе и «ПЛТ».

После того, как пользователь выберет «ПЛТ и нажмет «ОК», появится другое окно со значками «Ставка», «Кпер», «Пс», которые нужно заполнить, согласно данным. Получится:

• «Ставка» — 22%/12;
• «Кпер» -24;
• «Пс» — -20000

Сразу после внесения данных, в нижней строке появится результат расчетов: 1 037,56. Это и есть та сумма, которую следует ежемесячно вносить заемщику. После нажатия «ОК», полученное число займет свою ячейку в таблице.

Кстати, данные по кредиту, можно внести в скобки, расположенные в строке поисковика. Рядом со знаком «fx» появятся буквы «ПЛТ» и скобки (), куда вносится такая запись 22%/12;24; — 20000.

Чтобы не допустить ошибок в расчетах, необходимо соблюдать порядок записи данных и пунктуацию. После нажатия значка «Enter», результат вычислений — 1 037,56 — появится в ячейке таблицы.

Кредитный калькулятор – альтернатива MS Excel

Калькулятор-online по функционалу не отличается от MS Excel. При этом пользователю ничего не нужно скачивать. Операции выполняются в онлайн режиме.

Функции кредитного калькулятора:

1. расчет дифференцированного и аннуитетного платежа;
2. составление графика выплат;
3. разделение общей суммы платежа на две части: долг и проценты;
4. учет досрочных взносов.

Для получения необходимой информации, нужно внести данные в определенные окошки. Результат расчетов появится мгновенно.

Несложно и самостоятельно рассчитать сумму аннуитетного взноса. Но не стоит забывать о том, что в финансовых учреждениях существуют дополнительные комиссии и сборы, которые увеличивают платеж.

Источник: http://yurface.ru/kredit/annuitetnyj-platezh/

Что такое аннуитет

Аннуитет – это ежемесячный платеж по кредиту, размер которого остается неизменным на протяжении всего срока кредитования (например, 200$). Такой платеж рассчитывается еще в момент оформления кредитного договора и сразу включает в себя и тело кредита, и сумму всех начисленных на конкретную дату процентов.

Особенность аннуитета заключается в том, что с каждым месяцем «доля» начисленных по кредиту процентов в очередном платеже будет уменьшаться, а остаток задолженности – пропорционально увеличиваться. В результате, и в начале, и в конце срока кредитования заемщик будет вносить в кассу банка одну и ту же сумму.

Аннуитетный платеж используется российскими банками практически во всех видах кредитных продуктов: ипотека, автокредиты, займы на развитие бизнеса и потребительские кредиты.

Причина такой «популярности» аннуитета очевидна: банкам эта схема погашения позволяет заработать больше, чем при дифференцированном варианте погашения, а заемщикам не нужно «заморачиваться» с суммой очередного платежа.

Как рассчитывается аннуитет?

Совсем необязательно верить банку «на слово» и послушно платить по графику. Рассчитать сумму своего аннуитетного платежа вполне можно и самостоятельно.

Вот как выглядит основная формула расчета:

Размер аннуитета = коэффициент аннуитета * сумму кредита

И если точный размер кредита каждый заемщик знает еще на стадии оформления документов, то коэффициент аннуитета нужно уже рассчитывать отдельно по формуле:

i * (1+i)n/(1+i)n-1

Формула только выглядит такой устрашающей, а на самом деле там нет ничего сложного. Давайте разбираться:

i – процентная ставка по кредиту (в месяц). Проще говоря, если размер годовой ставки составляет 12%, то i в этом случае будет равняться 1% (12/12) или 0,01 (при переводе процентов в доли);

n – количество периодов, в течение которых будет погашаться кредит. Например, если кредит оформляется сроком на два года с ежемесячным погашением, то n будет равняться 24 (12 месяцев * 2).

Давайте рассчитаем, каким будет аннуитетный платеж при таких исходных данных: первоначальная сумма кредита – 10 000$, срок кредитования – полгода, процентная ставка – 24% годовых.

Исходные данные для расчета будут выглядеть следующим образом:

i = 0,02 (24% годовых/12 месяцев);

n = 6 (6 месяцев);

сумма кредита = 10 000$.

Тогда формула расчета коэффициента аннуитета будет выглядеть следующим образом:

(0,02*〖(1+0,02)〗6)/(〖(1+0,02)〗6-1)

Коэффициент аннуитета равен 0,178730.

Теперь рассчитаем размер нашего ежемесячного аннуитетного платежа:

10 000$ * 0,178730 = 1787,30$.

Если значение аннуитетного платежа высчитывать вручную не хочется, этот процесс можно «автоматизировать» с помощью Excel.

В любой ячейке этой электронной таблицы достаточно ввести следующее выражение:

= ПЛТ(24%/12; 6; -10000)

В скобках формулы по порядку указывается: годовая процентная ставка по кредиту, количество месяцев платежа, первоначальная сумма кредита.

Подставив все необходимые данные в ячейку Excel, получаем значение ежемесячного аннуитетного платежа – 1785$.

Небольшая разница между «ручным» и «расчетным» значением обусловлена погрешностями при округлении.

Преимущества аннуитетного платежа

Во-первых, наглядность и удобство в погашении для заемщика.

Согласитесь, любому из нас гораздо проще запомнить одно число (сумму ежемесячного платежа), чем каждый раз уточнять его у сотрудника банка или сверять самому через систему Интернет-банкинга.

Особенно это касается тех заемщиков, которые планируют регулярно делать частичное досрочное погашение. В этом случае сумма ежемесячного платежа по дифференцированной схеме будет постоянно пересчитываться (в отличие от аннуитетной схемы погашения).

Главное, не пропустить дату очередного платежа и можно быть уверенным, что просрочка по кредиту вам не грозит.

Во-вторых, в начале срока погашения размер аннуитетного платежа будет меньше, чем при дифференцированной схеме.

Выплачивать «аннуитетный» кредит в первые месяцы после оформления заемщику будет гораздо легче – финансовая нагрузка на семейный бюджет распределяется равномерно на весь период погашения.

При ограниченных доходах заемщика этот факт имеет большое значение.

В-третьих, снижение сравнительной стоимости кредита со временем.

Одна и та же сумма платежей со временем ощущается не так остро, так как инфляции постоянно снижает стоимость денег. А вот доходы заемщика, наоборот, в долгосрочной перспективе обычно только увеличиваются.

Недостатки

Первый – общая переплата по такому кредиту будет больше, чем при дифференцированной схеме погашения.

Не секрет, что для банка аннуитетная схема погашения выгоднее, чем дифференцированная. Общая переплата по процентам для заемщика однозначно будет больше (даже при условии частичного досрочного погашения).

Второй – в первые месяцы погашения заемщик выплачивает банку больше процентов, чем тела кредита.

Это значит, что в случае возникновения у заемщика форс-мажорных обстоятельств в течение первых месяцев (лет) после оформления кредита, заемщик останется должен банку практически ту же сумму, что и вначале.

https://www.youtube.com/watch?v=7-_ljk7DVyY

Третий – нет экономии на процентах при частичном досрочном погашении.

Даже если заемщик вносит на своей счет большую чем в графике сумму, на размер его ежемесячного платежа это никак не влияет.

Давайте рассмотрим этот момент более детально.

Досрочное погашение

Банки предлагают несколько схем частичного досрочного погашения.

Пересчет графика

Внесли в июне большую, чем в графике сумму, банк пересчитал остаток платежа вместе с процентами – уменьшилась сумма обязательного ежемесячного платежа.

Для заемщика – это наиболее предпочтительный вариант досрочного погашения, так как он позволяет снизить ежемесячную финансовую нагрузку на семейный бюджет. И, конечно же, сэкономить на «лишних» процентах по кредиту (меньше остаток задолженности – меньше размер начисленных на него процентов).

Из-за того, что в первые периоды выплат большую часть платежа составляют проценты по кредиту, делать частичные досрочные погашения заемщику вначале срока кредитования практически бессмысленно.

Кроме того, банки крайне редко предлагают пересчет графика платежей в случае частичного досрочного погашения.

Сокращение срока кредитования

Суть схемы с том, что размер ежемесячного платежа для заемщика остается неизменным даже в случае частичного досрочного погашения. А вот срок кредитования сокращается (например, вместе 24 месяцев, он «сожмется» до 23).

По сути, такой вариант не снижает ежемесячную финансовую нагрузку, зато рассчитаться по кредиту заемщик теперь может гораздо быстрее.

Накопление «лишних» денег на счету заемщика

Самый невыгодный для заемщика вариант частичного досрочного погашения.

Суть в том, что «лишние» деньги, внесенные заемщиком в качестве частичного досрочного погашения, просто аккумулируются на банковском счете. Списываются со счета они двумя способами:

— в следующем месяце заемщик может заплатить меньшую, чем в графике сумму (то есть, средства досрочного погашения выступают в качестве своеобразного «аванса»);

— средства накапливаются на отдельном счету и списываются в счет погашения кредита в конце срока кредитования.

И в том, и в другом варианте график платежей не пересчитывается, а срок кредитования не сокращается. Получается, что в этом случае от своего частичного досрочного погашения вообще не выигрываете ничего, кроме времени.

Стоит упомянуть о том, что для банков частичного (или полное) досрочное погашение – это лишняя «головная боль» и потерянная выгода в виде «недополученных» от заемщика процентов.

Именно поэтому банки всеми способами стараются усложнить для заемщика процедуру досрочного погашения.

Способов существует масса: вводится запрет на досрочное погашение в течение нескольких первых месяцев выплат; устанавливается минимальное ограничение по сумме частичного досрочного погашения (например, не менее трех обязательных платежей); от заемщика требуется заранее уведомить банк о намерении внести «лишние» деньги (например, за 15-20 дней до такого погашения); в отдельных банках погасить «аннуитетный» кредит частично-досрочно вообще невозможно – только полностью.

Отличие аннуитета от схемы дифференцированных платежей

В дифференцированной схеме погашения платеж выглядит совсем по-другому и рассчитывается совершенно по иной формуле.

Каждый ежемесячный платеж тоже состоит из двух частей: «тела» кредита и начисленных на остаток задолженности процентов.

Причем, «тело» кредита остается неизменным на протяжении всего срока кредитования, а вот сумма процентов с каждый месяцем будет становиться все меньше и меньше. В результате постепенно уменьшается и размер общего платежа.

В отличие от аннуитета, при дифференцированной схеме погашения максимальная финансовая нагрузка на заемщика приходится на первые месяцы выплат. И с каждым месяцем платить по кредиту нужно будет хоть на чуть-чуть, но меньше.

Кроме того, дифференцированные платежи однозначно подходят тем, кто планирует постоянно делать частичные досрочные погашения. В этом случае ежемесячный платеж по кредиту будет «таять» еще быстрее. В результате общая конечная переплата окажется гораздо меньше, чем запланированная вначале.

Валентина Малиновская. 22.07.2013

Источник: http://www.investmentrussia.ru/teoriya-investirovaniya/annuitetnyi-platezh.html

Аннуитетные платежи — что это? Описание и формула расчета аннуитета :

В зависимости от выбранной кредитной программы, клиенту могут предложить несколько схем погашения задолженности. Самые распространенные из них — дифференцированные и аннуитетные платежи. Что это такое и как они рассчитываются, вы узнаете из этой статьи.

Определение

Аннуитет — равнозначный ежемесячный платёж, который устанавливается один раз на весь период действия договора. Его удобно использовать при длительном периоде кредитования. Нет нужды постоянно вспоминать, какую сумму нужно заплатить в банк.

С другой стороны, при большой задолженности, оформленной на длительный период, клиент сначала погашает проценты, а потом тело кредита. При одинаковой ставке, сумме и сроках переплата в аннуитетной схеме будет больше, чем в дифференцированной.

Это выгодно банкам, так как они получат больше прибыли в виде процентов.

При дифференцированной схеме сумма платежа будет уменьшаться к концу срока действия договора. Выплаты по телу кредита равные, а проценты начисляются на остаток ссуды.

Такую схему использует небольшое количество банков и только в долгосрочных программах кредитования. Она менее выгодна для кредитных организаций, так как сумма переплаты меньше. Это же является преимуществом для клиентов.

В то же время при длительном кредитовании первые платежи будут очень большими. Такие затраты сильно бьют по карману.

Формула

Расчет аннуитетных платежей осуществляется таким образом:

А = K х S, где

• А — аннуитетный платёж,
• К — коэффициент,
• S — сумма кредита.

Коэффициент рассчитывается следующим образом:

K = i х (1+i)n (1+i)n — 1, где:

• i — процентная ставка за месяц;
• n — количество периодов.

График дифференцированных платежей рассчитывается по формуле:

П = ОЗ / ПП + ОЗ х С , где:

• П — ежемесячный платеж;
• ОЗ — остаток задолженности;
• ПП — количество периодов до полного погашения кредита;
• С — месячная процентная ставка.

Методика расчета дифференцированного платежа:

1. Сумма, подлежащая к оплате, делится на количество месяцев.
2. К полученной цифре прибавляется процент за месяц использования денег.

Пример

Клиент оформил кредит на 30 тыс. руб. под 18 % годовых на 3 года. Исходные данные:

• S = 30 тыс. рублей.
• В условиях указана годовая ставка. По указанной формуле с ней нельзя рассчитать аннуитетные платежи. Что это значит? Годовую ставку нужно разделить на 12 и получить количество процентов, которые клиент будет платить ежемесячно: i = 18 % / 12 = 1,5 %.
• В итоге получаем: n = 3 х 12 = 36 месяцев.

Подставляем все значения в формулу:

К = 0,015 х (1 + 0,015)36 (1 + 0,015)36 — 1 = 0,03615

Сумма аннуитетного платежа составит: A = 0,03615 х 30 = 1,08457 тыс. рублей.

Альтернативный вариант

Программа, в которой можно самостоятельно провести расчет аннуитетных платежей, — Excel. Для этого предусмотрена специальная функция (=ПЛТ). Ее можно вызвать, нажав на кнопку «fx» в левой части поисковой строки. В новом окне нужно заполнить такие параметры:

• «% 12» — годовая комиссия банка в процентах;
• «Кпер» — количество периодов, месяцев;
• «Пс» — первоначальная сумма кредита (в формуле она всегда ставится с минусом).

Эти же параметры можно вписать в ячейку, не вызывая окно с формулой: =ПЛТ(Ставка12;К пер;-Пс).

Конкретно для условий предыдущего примера эта формула будет иметь такой вид: =ПЛТ(18%/12; 36; -30000).

Еще можно использовать калькулятор аннуитетных платежей, который представлен на сайте большинства банков. Он позволяет рассчитать стоимость услуги с учетом выбранной программы кредитования. Пользователю нужно только ввести в специальную форму исходные данные.

Какую схему лучше выбрать

При ипотечном или автокредитовании клиенту не выгодны аннуитетные платежи. Что это значит? Клиент больше переплатит на процентах. В дифференцированной схеме тело кредита погашается равными частями. Одновременно уменьшается сумма процентов. Но есть обратная сторона медали. Сумма первых платежей может в разы отличаться от последних.

Такие расходы может позволить себе далеко не каждый клиент. И банк это обязательно будет учитывать, рассчитывая лимит кредита. В зависимости от внутренних правил организации, ежемесячный платеж не должен превышать 20-25 % дохода. Если клиент хочет обслуживаться по дифференцированной схеме, у него должна быть высокая зарплата.

Особенно если оформляется кредит на авто или ипотека. Аннуитетные платежи помогают планировать бюджет. Заемщик ежемесячно вносит одну и ту же сумму. Другое дело, что на первых этапах практически все деньги направляются на погашение процентов. Баланс меняется с середины срока.

С другой стороны, такая схема будет выгодна предпринимателям, которые берут кредит на максимальную сумму для развития бизнеса и в ближайшее время планируют увеличить доход.

Условия досрочного погашения

Каждый заемщик задается этим вопросом. Ведь в договорах может быть прописана комиссия за досрочное погашение долга. А вот начислять «будущие» проценты банк права не имеет. Это прописано в ГК РФ.

Банк также может наложить определенные лимиты, например, запретить досрочно погашать кредит первые 2-3 месяца. Прибыли учреждение в любом случае получит.

Ведь схема расчета ежемесячно аннуитетными платежами подразумевает первоочередное погашение процентов, а потом уже — основного долга. Иногда предлагаются другие варианты:

• пересчитать график задолженности в сторону увеличения платежа;
• ограничить одну выплату на уровне 2-, 3-кратных ежемесячных взносов и т. д.

Возврат процентов

Как уже говорилось ранее, аннуитетный платеж – это интересный для банка способ погашения долга, так как сначала деньги направляются на погашение процентов, а потом — на тело кредита. Заемщику он будет удобен тем, что в течение всего срока действия договора сумма расходов будет фиксированная.

Нюанс заключается в том, что при досрочном погашении долга банк получит больше прибыли в виде процентов. Но заемщик может вернуть часть уплаченной суммы даже в случае рефинансирования. По закону, банк может получить прибыль только за период фактического использования денег клиентом.

Поэтому он имеет право требовать часть процентов обратно (ст. 809 ГК РФ).

Клиент в состоянии самостоятельно рассчитать, сколько денег он может вернуть. Для этого нужно вычесть из суммы всех начисленных процентов ту часть, которая приходится на месяцы до реального погашения. Эти данные можно найти в графике платежей, который прилагается к договору. При длительном сроке кредита цифра может быть внушительной.

Пример

По ипотеке на сумму 2 млн рублей, оформленной на 20 лет по ставке 13,75 %, клиент должен заплатить проценты на общую сумму 3,9 млн руб. Если заем был погашен через три года, то возврату подлежит 230 тыс. рублей, то есть четверть уплаченной суммы. Эти данные можно также получить, использовав калькулятор аннуитетных платежей.

Но не все клиенты знают об этом праве. Да и при потребительском кредите сумма излишне уплаченных процентов может составлять несколько сотен рублей. Не каждый захочет выяснять отношения с банком по этому вопросу и портить в дальнейшем себе репутацию.

Преимущества

• Аннуитетный платеж чаще используется в потребительских кредитах.
• Он удобен для заемщика – фиксированная сумма затрат.
• Его легко рассчитать.
• Такая схема будет особенно приемлема для лиц с фиксированным и небольшим уровнем дохода.
• Клиенты могут рассчитывать на больший лимит займа.

Недостатки

• Сначала погашаются проценты, а потом тело кредита.
• Досрочное погашение возможно, но с определенными условиями: либо ограничивается сумма платежа, либо указывается срок, в течение которого клиент должен пользоваться услугой (например, первые 2-3 года).

При выборе ипотечной программы тяжесть первых дифференцированных платежей смягчается возможностью рефинансировать долг. В аннуитетной схеме финансовая нагрузка, возлагаемая на заемщика, остается неизменной при любых обстоятельствах. Учитывая это, банки в долгосрочных программах кредитования предлагают клиентам две схемы на выбор.

В потребительских займах финансовым организациям нет никакого дела до проблем клиентов, они просто скидывают долги коллекторам.

Сегодня один человек может оформить на себя 5-6 кредитов с аннуитетной схемой погашения. Такая форма расчетов получила большое социальное значение. Но она опасна как для клиентов, которые оформили на себя непомерное количество займов, так и для банков, которые детально не изучили финансовое состояние заемщика.

Вывод

Способ погашения кредита имеет большое значения для заемщика. Особенно если у него уже есть несколько займов. На сегодняшний день используются дифференцированные и аннуитетные платежи.

Что это значит? В первом случае сумма платежа уменьшается пропорционально сроку действия кредита. Во второй схеме расходы по кредиту фиксированы и не изменяются на протяжении всего периода действия договора.

Клиент может самостоятельно провести расчет аннуитетных платежей. Excel имеет для этих целей встроенную функцию (=ПЛТ).

Источник: https://www.syl.ru/article/180867/new_annuitetnyie-plateji---chto-eto-opisanie-i-formula-rascheta-annuiteta

Расчет аннуитетных платежей по кредиту: пример

Первое правило при оформлении кредита – нужно адекватно оценить собственную платежеспособность, чтобы платежи по нему со временем не стали обременительными для заемщика.

Но на этом этапе иногда возникают сложности, поскольку не у всех есть экономическое образование, чтобы правильно произвести необходимые вычисления.

Для облегчения задачи здесь собраны все возможные способы для расчета аннуитетных платежей по кредиту, которыми можно воспользоваться для планирования собственного бюджета.

Аннуитетный платеж – это…

Перед практической частью изучения вопроса следует ознакомиться с теорией. В экономической теории аннуитетный платеж – это один из способов ежемесячного платежа по кредиту, когда его сумма остается неизменной на протяжении всего срока кредитования.

При таком способе погашения кредита плательщик одновременно платит и начисленные проценты, и часть суммы основного долга. Но, как правило, вначале ежемесячный взнос преимущественно состоит из процентов по ссуде. Поэтому при расчете аннуитетных платежей по кредиту можно заметить, что данный способ возврата средств не очень выгоден для заемщиков.

Классификация аннуитета

В зависимости от дополнительных условий кредитования, аннуитетные платежи делятся на небольшие группы. Их классификация достаточно разнообразна, однако некоторые виды аннуитетов уже не встречаются или встречаются крайне редко в перечне банковских услуг.

Виды аннуитетов:

• Фиксированные – неизменные на протяжении всего срока кредитования.
• Валютные – размер платежа может меняться в зависимости от колебаний на валютном рынке.
• Индексируемые – могут корректироваться с поправкой на актуальный уровень инфляции.
• Переменные – платежи меняются в зависимости от уровня доходности финансового инструмента.

Механизм расчета аннуитетных платежей по кредиту зависит от их вида. Однако для потребительского кредитования чаще всего используются фиксированные аннуитеты.

Преимущества и недостатки аннуитетных платежей

Расчет аннуитетных платежей по кредиту обычно производится перед его оформлением. Поэтому важно знать, стоит ли вообще заниматься какими-либо вычислениями, или лучше сразу выбрать другой банк для получения ссуды. Чтобы определиться, нужно взвесить все плюсы и минусы аннуитетных платежей.

Преимущества:

• неизменность суммы и даты внесения платежа на протяжении всего срока кредитования;
• доступность практически для всех кредитополучателей вне зависимости от их финансового положения;
• возможность снижения платежа с поправкой на уровень инфляции.

Многим людям аннуитетный способ погашения кредита удобен тем, что, зная точный размер ежемесячного взноса, проще планировать семейный бюджет. Однако с точки зрения экономической выгоды, он имеет несколько существенных недостатков.

Недостатки:

• общая сумма переплаты гораздо выше, чем при дифференцированном способе погашения долга;
• сложность досрочного погашения;
• невозможность перерасчета при желании заемщика досрочно погасить ссуду.

Если рассмотреть пример расчета аннуитетного платежа по кредиту, то сразу становится понятно, что банкам выгодно выдавать клиентам подобные ссуды.

Однако некоторые не так гонятся за прибылью, поэтому предоставляют заемщикам более выгодные условия кредитования. Стоит отметить, что среди микрофинансовых организаций таких компаний нет.

Поэтому при оформлении заема всегда используются аннуитетный способ погашения долга.

Из чего состоит платеж по кредиту?

Если рассматривать составляющие аннуитетного платежа, можно заметить, что он делится на две части. Первая – фиксированные проценты по кредиту, вторая – часть суммы основного долга. Причем сумма начисленных процентов обычно превышает сумму, идущую на погашение ссуды.

Тело кредита сравнивается с процентами по нему только в середине общего срока кредитования. Далее сумма, которая идет на погашение основного долга, начинает расти, постепенно превышая размер выплат за пользование кредитом. Как уже было сказано ранее, это не выгодно для заемщиков, особенно когда речь идет о долгосрочном кредитовании.

Способы расчета ежемесячного аннуитетного платежа по кредиту

На самом деле, рассчитать точный размер платежа достаточно просто. Причем это можно сделать сразу несколькими способами. Используя хотя бы один из них, можно сориентироваться в предстоящих выплатах и оценить, насколько «подъемной» окажется банковская ссуда.

Способы расчета аннуитетного платежа:

• вручную при помощи формулы;
• с использованием программы Microsoft Excel;
• на сайте банка с помощью кредитного калькулятора.

Каждый из методов расчета при правильном применении даст точную цифру, равную предстоящему размеру платежа. Поэтому, если есть сомнения в правильности уже сделанных вычислений, можно произвести проверку, рассчитав аннуитетный платеж другим возможным способом.

Формула расчета

Расчет процентов по кредиту при аннуитетных платежах вне зависимости от выбранного способа вычислений производится с помощью специальной формулы. Кредитные калькуляторы, мобильные приложения и другое программное обеспечение делает правильные расчеты, отталкиваясь именно от нее.

Общий вид данной формулы выглядит следующим образом:

АП = О * пс / 1 — (1 + пс)-с,

где:

АП – ежемесячный аннуитетный платеж;

О – сумма основного долга;

пс – ежемесячная процентная ставка банка;

с – количество месяцев в сроке кредитования.

Зная формулу, можно запросто произвести необходимые расчеты самостоятельно. Достаточно лишь подставить исходные данные предполагаемого кредита вместо букв, и произвести необходимые математические вычисления при помощи обычного калькулятора. Но чтобы расчет погашения кредита аннуитетными платежами стал наиболее понятным, рассмотрим его на примере.

Пример расчета

Предположим, что заемщик взял в банке ссуду на сумму 50 000 рублей сроком на 5 лет. По условиям кредитного договора годовая процентная ставка по кредиту равна 20 %.

Исходя из формулы, для вычислений необходимо знать ежемесячную процентную ставку. Банки редко указывают данную цифру в кредитном договоре, поэтому нужно найти ее самостоятельно. Для этого нужно воспользоваться формулой:

пс = П / 100 / 12,

где:

П – годовая процентная ставка.

Расчет:

пс = 20 / 100 / 12 = 0,017.

Зная все исходные данные, можно приступать к нахождению аннуитетного платежа по кредиту. Оно выглядит следующим образом:

АП = 50 000 * 0,017 / 1 — (1 + 0,017)-60 = 1336,47 руб.

Расчет аннуитетных платежей по кредиту в Excel

Программа Excel – это не просто большая таблица. В ней можно произвести огромное количество вычислений, зная лишь, какие формулы нужно использовать. Для расчета аннуитетного платежа в Excel есть специальная функция – ПЛТ. Чтобы правильно ей воспользоваться, нужно действовать, придерживаясь следующих шагов:

1. Заполнить исходные данные (сумма, проценты и срок кредита в ячейках В2, В3, В4 соответственно).
2. Составить график погашения кредита по месяцам (А7 -Аn).
3. Сделать столбец «Платежи по кредиту» (В7 — Вn).
4. Напротив первого месяца в столбце «Платежи по кредиту» ввести формулу

= ПЛТ ($В3/12;$В$4;$В$2) и нажать Enter.

Результат вычислений отобразиться в таблице красным цветом со знаком «-». Это нормально, ведь эти деньги заемщик будет отдавать банку, а не получать.

Формула расчета кредита аннуитетными платежами в Excel позволяет сделать вычисления и таким образом, чтобы значения были положительными.

С ее помощью банковские сотрудники в считанные минуты могут сделать и распечатать график платежей кредитополучателям, экономя их время.

Чтобы заполнить все месяцы, нужно протянуть ячейку с формулой до конца графика погашения. Но поскольку аннуитетный платеж со временем не меняется, цифры в ячейках будут одинаковые.

Перепроверить полученные данные можно с помощью кредитного калькулятора аннуитетных платежей. Он есть на сайтах всех банков, которые выдают ссуды с таким способом погашения.

Для использования кредитного калькулятора понадобятся те же исходные данные, что и для предыдущих способов расчета. Их нужно ввести в отведенные поля для заполнения.

И затем программа самостоятельно сделает все расчеты в течение нескольких секунд, дав потенциальному заемщику возможность оценить полученную сумму и хорошенько подумать о предстоящем оформлении кредита.

Источник: http://.ru/article/364175/raschet-annuitetnyih-platejey-po-kreditu-primer