Рассчитаем Будущую стоимость инвестиции для различных способов начисления процента: по формуле простых процентов, сложных процентов и формуле аннуитета.
Будущая стоимость (Future Value), является суммой, в которую в будущем превратится определенная сумма денег, инвестированная ранее под известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Будущей стоимости, также как и
Приведенной (Текущей) стоимости
важен, так как, платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту.
Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты:
простые проценты
,
сложные проценты
или
аннуитет
(в
файле примера
приведено решение задачи для каждого из методов).
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты, начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
При начислении простых процентов формула для расчета будущей стоимости (FV) инвестиций имеет следующий вид:
FV = PV * (1+i*n)
где PV —
настоящая (приведенная) стоимость
(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц (=годовая ставка/12)); n – количество периодов времени, в течение которых начисляются проценты.
Как видно из формулы FV (в MS EXCEL используется аббревиатура БС) это ни что иное, как
наращенная сумма
с использованием простых процентов. Про вычисление наращенной суммы при постоянной и переменной ставке можно прочитать в статье
Простые проценты в MS EXCEL
.
Примечание
. В MS EXCEL нет отдельной функции для расчета Будущей стоимости по методу Простых процентов. Функция
БС()
используется только для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить
БС()
рассчитать Будущую стоимость и по методу простых процентов (см.
файл примера
).
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования
простых процентов
изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент» (см.
файл примера
). Формула для расчета Будущей стоимости в случае начисления по сложным процентам имеет следующий вид:
FV = PV * (1+i)^n
где PV —
настоящая (приведенная) стоимость
(сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). Предполагается, что процентная ставка не изменяется в течение всего срока инвестирования; n – количество периодов времени, в течение которого начисляются проценты.
Про вычисление Будущей стоимости по сложным процентам можно прочитать в статье
Сложные проценты в MS EXCEL
. В этой статье разобраны случаи применения функции
БС()
и формула капитализации m раз в год. В статье
Сложные проценты в MS EXCEL. Переменная ставка
разобраны случаи применения функции
БЗРАСПИС()
для расчета будущей стоимости при переменной ставке. В статье
Непрерывные проценты
Будущая стоимость рассчитывается при непрерывном начислении процентов.
Аннуитет
Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Будущей стоимости существенно усложняется См. статью
Аннуитет. Определяем в MS EXCEL Будущую Стоимость
.
В случае, если сумма начальной инвестиции =0 и нужно определить Будущую стоимость периодических равновеликих платежей, то это можно сделать по формуле (см.
файл примера
):
FV = PMT * (((1+i)^n)-1) / i
где PMT – размер платежа при аннуитете; i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). В формуле предполагается, что проценты начисляются в конце периода; n – количество периодов времени, в течение которых начисляются проценты (и делаются платежи).
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
БС — одна из финансовых функций, возвращающая будущую стоимость инвестиции на основе постоянной процентной ставки. В функции БС можно использовать как периодические постоянные платежи, так и единый общий платеж.

Воспользуйтесь средством Excel Formula Coach для расчета будущей стоимости серии платежей. При этом вы узнаете, как использовать функцию БС в формуле.
Excel Formula Coach также можно использовать для расчета будущей стоимости единого общего платежа.
Синтаксис
БС(ставка;кпер;плт;[пс];[тип])
Дополнительные сведения об аргументах функции БС и других функциях, связанных с аннуитетами, см. в описании функции ПС.
Аргументы функции БС описаны ниже.
-
Ставка — обязательный аргумент. Процентная ставка за период.
-
Кпер — обязательный аргумент. Общее количество периодов платежей по аннуитету.
-
Плт — обязательный аргумент. Выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
-
Пс — необязательный аргумент. Приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент «пс» опущен, предполагается значение 0. В этом случае аргумент «плт» является обязательным.
-
Тип Необязательный. Число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.
|
Тип |
Выплата |
|---|---|
|
0 |
В конце периода |
|
1 |
В начале периода |
Замечания
-
Убедитесь, что единицы измерения аргументов «ставка» и «кпер» используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента «ставка» и 4*12 — в качестве аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% в качестве аргумента «ставка» и 4 — в качестве аргумента «кпер».
-
Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.
Примеры
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
0,06 |
Годовая процентная ставка |
|
|
10 |
Количество платежей |
|
|
-200 |
Объем платежей |
|
|
-500 |
Стоимость на текущий момент |
|
|
1 |
Платежи осуществляются в начале периода (0 означает, что платежи осуществляются в конце периода) |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4; A5; A6) |
Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5. |
2 581,40 ₽ |
Пример 2
|
Данные |
Описание |
|
|---|---|---|
|
0,12 |
Годовая процентная ставка |
|
|
12 |
Количество платежей |
|
|
-1000 |
Объем платежей |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4) |
Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A4. |
12 682,50 ₽ |
Пример 3
|
Данные |
Описание |
|
|---|---|---|
|
0,11 |
Годовая процентная ставка |
|
|
35 |
Количество платежей |
|
|
-2000 |
Объем платежей |
|
|
1 |
Платежи осуществляются в начале года (0 означает конец года) |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4;; A5) |
Будущая стоимость инвестиций с условиями, указанными в ячейках A2:A4. |
82 846,25 ₽ |
Пример 4
|
Данные |
Описание |
|
|---|---|---|
|
0,06 |
Годовая процентная ставка |
|
|
12 |
Количество платежей |
|
|
-100 |
Объем платежей |
|
|
-1000 |
Стоимость на текущий момент |
|
|
1 |
Платежи осуществляются в начале года (0 означает конец года) |
|
|
Формула |
Описание |
Результат |
|
=БС(A2/12; A3; A4; A5; A6) |
Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5. |
2 301,40 ₽ |
Нужна дополнительная помощь?
Функция БС в Excel рассчитывает будущую стоимость инвестиции при условии, что процентная ставка является константой (не меняется с течением времени), и возвращает соответствующее значение. Функцию можно использовать в случаях, когда по окончанию срока выполняется единый платеж, а также при разбиении общей суммы на несколько фиксированных платежей.
Примеры использования финансовой функции БС в Excel
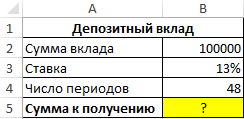
Пример 1. Вкладчик сделал депозит с ежемесячной капитализацией на сумму 100 000 рублей под 13% годовых сроком на 4 года. Какую сумму средств он сможет снять со своего депозитного счета по окончанию действия договора с банком?
Исходные данные:
Формула для расчета:
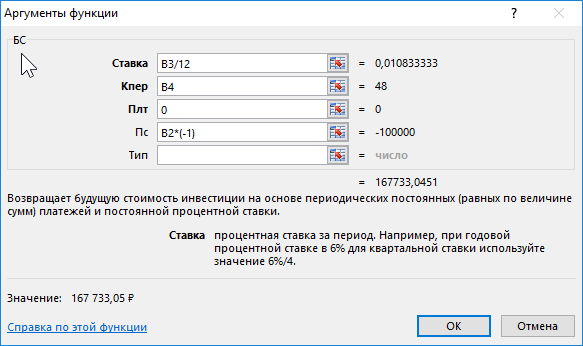
Описание аргументов:
- B3/12 – ставка за период (капитализация выполняется ежемесячно);
- B4 – число периодов капитализации вклада;
- 0 – сумма выплаты за период капитализации (неизвестная величина в рамках данной задачи, поэтому значение 0);
- B2*(-1) – начальная сумма вклада (инвестиция, которая должна являться отрицательным числом).
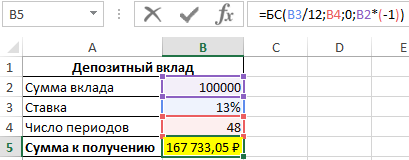
Результаты расчета:
Спустя 4 года вкладчик получит 167 733 рубля.
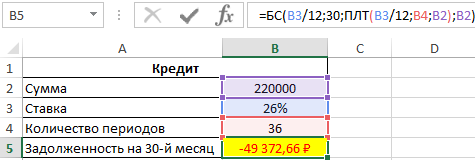
Расчет суммы долга по кредиту по состоянию на 30-й период погашения
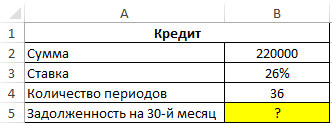
Пример 2. Заемщик взял кредит в банке под 26% годовых на сумму 220 000 рублей сроком на 3 года с ежемесячным фиксированным платежом. Какой будет сумма задолженности заемщика по окончанию 30-го периода выплат?
Исходные данные:
Формула для расчета:
=БС(B3/12;30;ПЛТ(B3/12;B4;B2);B2)
Описание аргументов:
- B3/12 – месячная процентная ставка;
- 30 – номер периода для расчета остатка задолженности;
- ПЛТ(B3/12;B4;B2) – функция, возвращающая сумму ежемесячного платежа;
- B2 – тело кредита.
Полученный результат:
Фактическая задолженность за кредит по окончанию 30-го месяца составит примерно 49372 рубля.
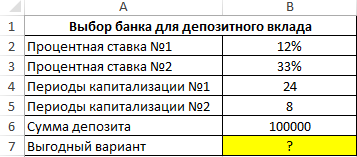
Сравнительный инвестиционный анализ условий депозита в банке
Пример 3. Вкладчик получил предложения по депозитному вкладу от двух банков с различными условиями:
- Ставка – 12% годовых, капитализация – ежемесячная.
- Ставка – 33% годовых, капитализация – ежеквартальная.
Определить, какое из предложений является более выгодным, если сумма вклада – 100000 рублей, срок действия договора – 2 года.
Исходные данные:
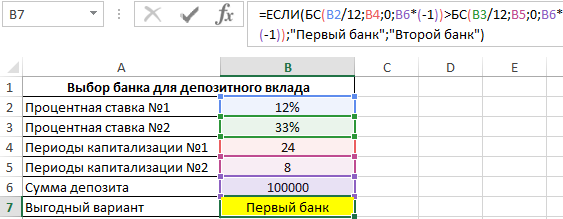
Формула для расчета:
С помощью функции ЕСЛИ определяем, в каком случае будущая стоимость окажется больше и возвращаем соответствующее значение. Полученный результат:
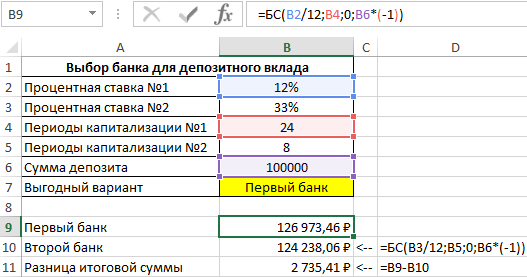
Выведем результаты расчетов функций БС и разницу сумм:
Как видно, несмотря на высокую годовую ставку, первый банк сделал более выгодное предложение, поскольку по условиям предложенного договора капитализация является ежемесячной. То есть, чем чаще происходит капитализация, тем быстрее увеличивается сумма вклада.
Особенности использования финансовой функции БС в Excel
Функция БС используется наряду с прочими финансовыми функциями (ПС, ПЛТ, КПЕР и другими) и имеет следующий синтаксис:
=БС(ставка;кпер;плт;[пс];[тип])
Описание аргументов:
- ставка – аргумент, принимающий числовое или процентное значение ставки за указанный период. Обязательный для заполнения. Если по условию используется годовая ставка, необходимо выполнить пересчет по следующей формуле: R=Rg/n, где Rg – годовая ставка, n – число периодов.
- кпер – числовое значение, характеризующее число периодов оплаты. Аргумент обязателен для заполнения. Если кредит был взят на период 3 года, выплаты по которому должны производиться каждый месяц, аргумент кпер должен принять значение 3*12=36 (12 – месяцы в году).
- плт – числовое значение, характеризующее фиксированную сумму выплаты за каждый период. Аргумент обязателен для заполнения. Если выплата за период является неизвестной величиной, аргумент плт может принимать значение 0, но при этом следующий аргумент задается явно.
- [пс] – приведенная стоимость на данный момент. Например, когда заемщик берет кредит у финансовой организации, тело кредита является приведенной на текущий момент стоимостью. По умолчанию аргумент [пс] принимает значение 0, а плт должен иметь отличное от нуля значение.
- [тип] – числовое значение, характеризующее тип выплат: в конце или начале периода. Принимает только два значения: 0 (если явно не указан) и 1.
Примечание 1:
- При указании аргумента ставка можно использовать процентный формат данных (например 17%) и числовой аналог (0,17).
- Расходные операции (текущая стоимость, выплата за период) должны быть указаны со знаком «-», то есть являться отрицательными числами.
- Функция БС использует в расчетах следующую формулу:
- Данная функция может быть использована для расчета баланса на конец периода и остаточной суммы задолженности по кредиту на текущий момент.
- Если процентная ставка меняется со временем, для расчетов следует использовать формулу БЗРАСПИС.
- Аргументы функции могут являться числовыми значениями или текстовыми данными, которые могут быть преобразованы в числа. Если один или несколько аргументов функции БС принимают текстовые строки, не содержащие числовые значения, будет возвращен код ошибки #ЗНАЧ!.
Примечание 2: функция БС также применяется для определения остатка задолженности по кредиту с аннуитетным графиком выплат, при этом дополнительные проценты и комиссии учтены не будут. Аннуитетный график предполагает фиксированную сумму погашения для каждого периода выплат (состоит из процентов и тела кредита).
Функция FV — это финансовая функция в Excel, которая определяет будущую стоимость инвестиций, взносов или запланированных платежей на основе периодических постоянных платежей с фиксированной процентной ставкой. Эта функция FV также может рассчитать будущие значения единовременной выплаты в Excel.
Синтаксис и аргументы функции
БС (ставка, кол-во, вып., [Pv], [тип])
(1) Оценить: Необходимые. Процентная ставка за период. Это постоянно на протяжении всей жизни инвестиции.
Допустим, вы получаете годовую процентную ставку 6%, вы можете изменить его следующим образом:
- Для полугодовых платежей вам необходимо преобразовать его в полугодовую процентную ставку: 3% (= 6% / 2);
- Для ежеквартальных выплат вам необходимо конвертировать ее в квартальную процентную ставку: 1.5% (= 6% / 4);
- Для ежемесячных выплат вам необходимо конвертировать ее в ежемесячную процентную ставку: 0.5% (= 6% / 12).
(2) Кпер: Необходимые. Общее количество периодов выплат. Предположим, вам нужно заплатить за 3 лет, вы можете изменить его следующим образом:
- Для ежеквартальных платежей общее количество периодов платежей составляет 12 (= 3 * 4);
- Для ежемесячных платежей общее количество периодов платежей составляет 36 (= 3 * 12).
(3) ПМТ: Необходимые. Постоянная оплата в каждом периоде. Это закреплено на всю жизнь инвестирования.
(4) Пв: Необязательный. Текущая стоимость ваших инвестиций или единовременный платеж в настоящее время. Если он не указан, функция FV рассчитает его как 0.
(5) Тип: Необязательный. Значение указывает время платежа. Есть два типа:
- 0 или не указано: платеж в конце каждого периода;
- 1: выплата в начале каждого периода.
Возвращаемое значение
Численная величина.
Функция FV вернет будущую стоимость инвестиции на основе периодических постоянных платежей и фиксированной процентной ставки.
Примечания по использованию
(1) Процентная ставка: Убедитесь, что процентная ставка соответствует срокам выплаты.
(2) Постоянная выплата в каждый период: если для вывода средств, должно быть отрицательным; в то время как для полученных денежных средств он должен быть положительным.
Примеры формул
Пример 1. Рассчитайте будущую стоимость паушальных инвестиций в Excel
Предполагая, что в настоящее время на вашем банковском счете есть 10,000 XNUMX долларов. Теперь вы хотите сохранить деньги в виде срочного депозита в размере 3 лет, а его годовая сложная процентная ставка составляет 5%. По этому депозиту будут начисляться проценты ежегодно. Теперь вы можете применить функцию FV, чтобы легко узнать, сколько денег вы получите от срочного депозита через 3 года.
В этом примере приведенная стоимость, которую вы заплатите, составляет 10,000 5 долларов, процентная ставка — 3%, периоды выплат — 0, а платеж за период — XNUMX. Вы можете рассчитать будущую стоимость этой единовременной инвестиции с помощью одной из формул ниже.:
= FV (C5; C6,0; -C4)
= FV (5%; 3,0; -10000)
Пример 2: Расчет будущей стоимости аннуитета
Предположим, вы планируете купить аннуитетный продукт сейчас. В этом аннуитетном продукте вам нужно заплатить $2,500 в год с фиксированной годовой процентной ставкой 6%, и его жизнь 30 лет. Если вы купите этот аннуитетный продукт, сколько денег вы сможете получить обратно через 30 лет?
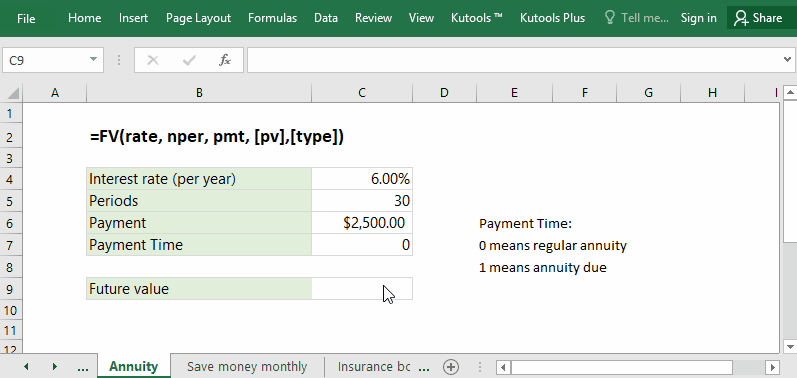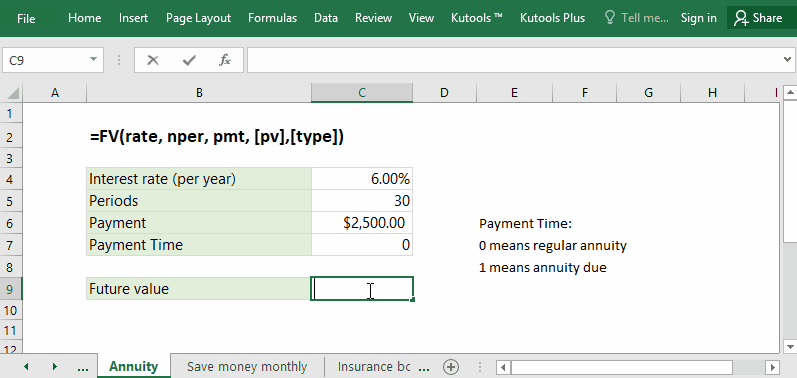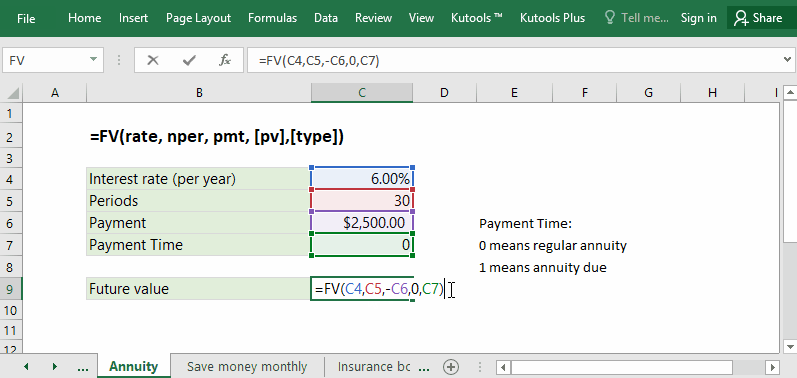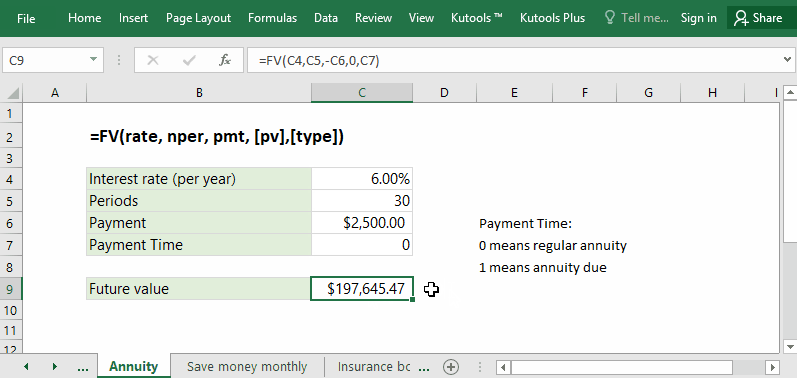
В примере приведенная стоимость равна 0, процентная ставка по аннуитету — 6.00%, периоды выплат — 30, а выплаты составляют 2,500 долларов в год. Поэтому вы можете применить одну из формул ниже легко вычислить будущую стоимость вашего аннуитета.
= FV (C4; C5; -C6,0; C7)
= БС (6%; 30; -2500; 0; 0)
Пример 3: Расчет будущей стоимости постоянных ежемесячных платежей
Допустим, вы собираетесь ежемесячно откладывать деньги на продолжение обучения. Вы планируете экономить $500 в месяц, а годовая процентная ставка составляет 4%, и вы будете выполнять этот план за 5 лет. Таким образом, вы также можете применить FV future, чтобы рассчитать, сколько основной суммы и процентов вы получите от этого плана.
В этом примере приведенная стоимость — 0, процентная ставка — 4.00% / 12, периоды выплат — 12 * 5, ежемесячный платеж — 500.00 долларов США, поэтому вы можете использовать формулу = БС (4% / 12, 5 * 12, -500, 1) Чтобы выяснить суть принципа и интереса:
=FV(C5/C7,C6*C7,-C8,C9)
= БС (4% / 12, 5 * 12, -500, 1)
Лучшие инструменты для работы в офисе
Kutools for Excel — Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
Комментарии (0)
Оценок пока нет. Оцените первым!
Будущая стоимость является оборотной стороной временных изменений денег. Будущая стоимость говорит о том, сколько будет стоить известная сумма денег (или известная серия выплат) через некоторый промежуток времени. Синтаксис функции БС следующий: БС(ставка;кпер;плт;пс;тип).
Будущая стоимость платежей
В этом примере мы предположим, что открыли накопительный счет для своего ребенка, чтобы к окончанию школы насобирать ему сумму, необходимую для платного обучения в университете. Начиная со следующего месяца, вы будете ежемесячно откладывать 50 долларов на этот счет под 3% годовых. Следующая формула показывает, что к совершеннолетию у вашего сына на счету будет 14297,02 долларов (рис. 1): =БС(,03/12;18*12;-50;0;0).
Рис. 1. Вычисление будущей суммы платежей
Годовую процентную ставку 3% мы преобразуем в месячную; 18 лет также преобразуем в месяцы. Приведенная стоимость отсутствует, так как вы только что открыли счет. Аргумент Тип равен нулю, так как вносить суммы вы начинаете со следующего месяца.
Будущая стоимость суммы вклада
В следующем примере вычисляется будущая стоимость суммы денег, которая не будет пополняться, и с нее не будут сниматься деньги. Предположим, что вы открыли пенсионный счет, внесли на него 20 тысяч долларов и планируете через 15 лет выйти на пенсию (рис. 2): =БС(,08;15;0;-20000;0).
Рис. 2. Вычисление будущей стоимости вклада
В данном примере предполагается, что пенсионный вклад гарантирует получение 8% годовых. Значение -20000 представляет двадцать тысяч долларов, уходящих от вас в банк. В результате мы получаем 63443,38 долларов — эту сумму вы получите через 15 лет при выходе на пенсию.
Округление в финансовых формулах
При использовании финансовых формул проблема округления значений ощущается особенно остро. Excel предлагает несколько функций для выполнения этой задачи: ОКРУГЛ, ОКРУГЛВНИЗ И ОКРУГЛВВЕРХ. Чтобы предотвратить накопительные ошибки, округляйте только конечный получаемый результат. Другими словами, избегайте округления промежуточных данных. Обычно результаты финансовых расчетов отображаются в виде чисел с двумя десятичными разрядами или вообще без таковых. В промежуточных расчетах это предполагает получение результатов с точностью до цента или доллара.
В отдельных случаях вычисления базируются на приблизительных данных или данных, полученных в результате эмпирического анализа или подбора параметров. Поэтому уже давно обычной практикой стало применение округленных значений (чтобы не утруждать себя вводом длинных значений). Предположим, что вы арендуете торговое помещение площадью 1537 квадратных метров по цене 43,55 долларов за квадратный метр. Простое умножение приводит к получению суммы $66936,35.
Однако вы знаете, что арендная плата может изменяться (скажем, в диапазоне от 42 до 45 долларов). В результате конечная сумма аренды будет колебаться в небольших пределах. Чтобы избежать излишней неточности, конечную сумму можно округлить до ближайших ста или даже тысячи долларов. Одна из потенциальных опасностей, привнесенная современными технологиями, — это быть обманутым видимой точностью на самом деле приблизительных оценок.
Будущая стоимость платежей и суммы вклада
Также можно вычислить будущую стоимость и уже существующего вклада, на который периодически будут добавляться (или сниматься) деньги. В предлагаемом примере мы собираемся вносить ежемесячные платежи в сумме 900 долларов по закладной на сумму 150 тысяч долларов. Процентная ставка составляет 5,75% годовых. Следующая формула вычисляет, сколько мы останемся должны через пять лет: =БС(,0575/12;5*12;-900;150000;0).
Платежи вносятся ежемесячно, поэтому все остальные аргументы мы соотносим с месяцами — количество лет умножается, а процентная ставка делится на 12. Текущий баланс показан как приход денег, хотя на самом деле они не поступают в настоящий момент — это движение было, когда мы изначально покупали дом. Так как область определения задачи распространяется на пять будущих лет, начиная с текущего момента, совершенно не имеет значения, когда на самом деле был выполнен начальный платеж.
Лучше представить себе данную задачу следующим образом. Некто одолжил вам 150 тысяч долларов, чтобы выкупить закладную на дом, хотя на самом деле этого не произошло. Вычисленное значение — 137435,10 — это сумма выходного потока по истечении пяти лет.