Основная идея
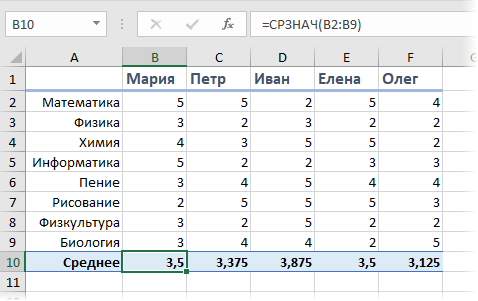
Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:
Свободное место, допустим, только одно, и наша задача — выбрать достойного.
Первое, что обычно приходит в голову — это рассчитать классический средний балл с помощью стандартной функции Excel СРЗНАЧ (AVERAGE).
На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется «Программирование», а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень. Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.
Средневзвешенное — это среднее с учетом различной ценности (веса, важности) каждого из элементов.
В бизнесе средневзвешенное часто используется в таких задачах, как:
- оценка портфеля акций, когда у каждой из них своя ценность/рисковость
- оценка прогресса по проекту, когда у задач не равный вес и важность
- оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности
- и т.д.
Расчет средневзвешенного формулами
Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:
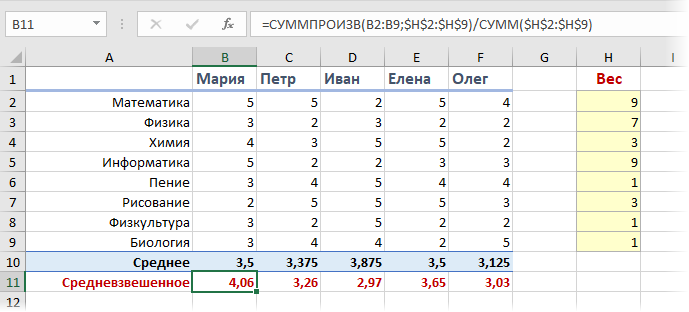
Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в двух указанных диапазонах — оценки абитурента и вес каждого предмета — а затем суммирует все полученные произведения. Потом полученная сумма делится на сумму всех баллов важности, чтобы усреднить результат. Вот и вся премудрость.
Так что берем Машу, а Иван пусть поступает в институт физкультуры 
Расчет средневзвешенного в сводной таблице
Поднимем ставки и усложним задачу. Допустим, что теперь нам нужно подсчитать средневзвешенное, но не в обычной, а в сводной таблице. Предположим, что у нас есть вот такая таблица с данными по продажам:
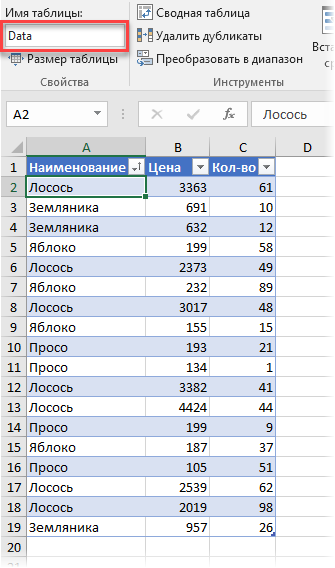
Обратите внимание, что я преобразовал ее в «умную» таблицу с помощью команды Главная — Форматировать как таблицу (Home — Format as Table) и дал ей на вкладке Конструктор (Design) имя Data.
Заметьте, что цена на один и тот же товар может различаться. Наша задача: рассчитать средневзвешенные цены для каждого товара. Следуя той же логике, что и в предыдущем пункте, например, для земляники, которая продавалась 3 раза, это должно быть:
=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33
То есть мы суммируем стоимости всех сделок (цена каждой сделки умножается на количество по сделке) и потом делим получившееся число на общее количество этого товара.
Правда, с реализацией этой нехитрой логики именно в сводной таблице нас ждет небольшой облом. Если вы работали со сводными раньше, то, наверное, помните, что можно легко переключить поле значений сводной в нужную нам функцию, щелкнув по нему правой кнопкой мыши и выбрав команду Итоги по (Summarize Values By):
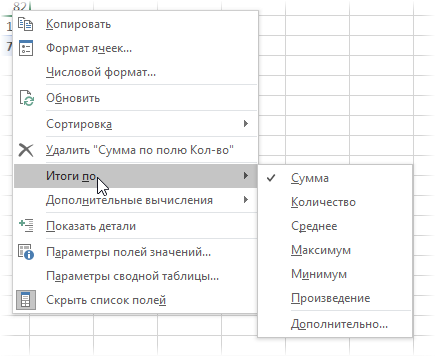
В этом списке есть среднее, но нет средневзвешенного 
Можно частично решить проблему, если добавить в исходную таблицу вспомогательный столбец, где будет считаться стоимость каждой сделки:
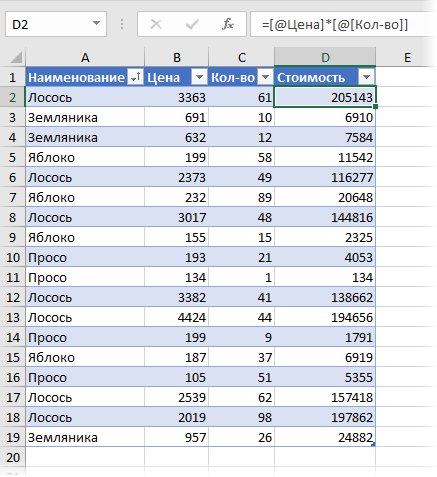
Теперь можно рядом закинуть в область значений стоимость и количество — и мы получим почти то, что требуется:
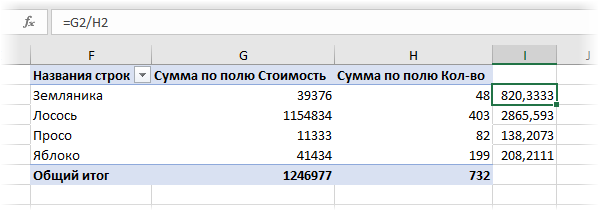
Останется поделить одно на другое, но сделать это, вроде бы, простое математическое действие внутри сводной не так просто. Придется либо добавлять в сводную вычисляемое поле (вкладка Анализ — Поля, элементы, наборы — Вычисляемое поле), либо считать обычной формулой в соседних ячейках или привлекать функцию ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GET.PIVOT.DATA), о которой я уже писал. А если завтра изменятся размеры сводной (ассортимент товаров), то все эти формулы придется вручную корректировать.
В общем, как-то все неудобно, трудоемко и нагоняет тоску. Да еще и дополнительный столбец в исходных данных нужно руками делать. Но красивое решение есть.
Расчет средневзвешенного в сводной таблице с помощью Power Pivot и языка DAX
Если у вас Excel 2013-2016, то в него встроен супермощный инструмент для анализа данных — надстройка Power Pivot, по сравнению с которой сводные таблицы с их возможностями — как счеты против калькулятора. Если у вас Excel 2010, то эту надстройку можно совершенно бесплатно скачать с сайта Microsoft и тоже себе установить. С помощью Power Pivot расчет средневзвешенного (и других невозможных в обычных сводных штук) очень сильно упрощается.
1. Для начала, загрузим нашу таблицу в Power Pivot. Это можно сделать на вкладке Power Pivot кнопкой Добавить в модель данных (Add to Data Model). Откроется окно Power Pivot и в нем появится наша таблица.
2. Затем щелкните мышью в строку формул и введите туда формулу для расчета средневзвешенного:
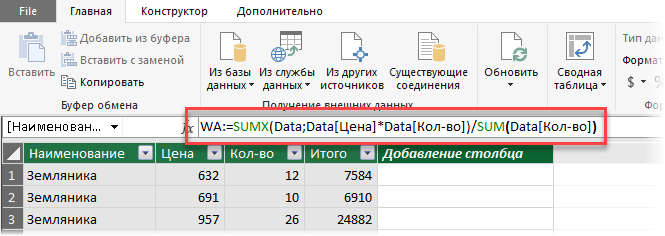
Несколько нюансов по формуле:
- В Power Pivot есть свой встроенный язык с набором функций, инструментов и определенным синтаксисом, который называется DAX. Так что можно сказать, что эта формула — на языке DAX.
- Здесь WA — это название вычисляемого поля (в Power Pivot они еще называются меры), которое вы придумываете сами (я называл WA, имея ввиду Weighted Average — «средневзвешенное» по-английски).
- Обратите внимание, что после WA идет не равно, как в обычном Excel, а двоеточие и равно.
- При вводе формулы будут выпадать подсказки — используйте их.
- После завершения ввода формулы нужно нажать Enter, как и в обычном Excel.
3. Теперь строим сводную. Для этого в окне Power Pivot выберите на вкладке Главная — Сводная таблица (Home — Pivot Table). Вы автоматически вернетесь в окно Excel и увидите привычный интерфейс построения сводной таблицы и список полей на панели справа. Осталось закинуть поле Наименование в область строк, а нашу созданную формулой меру WA в область значений — и задача решена:
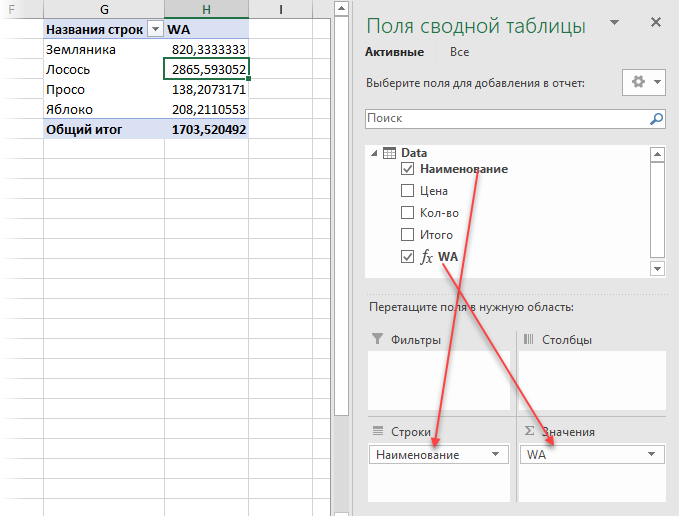
Вот так — красиво и изящно.
Общая мораль: если вы много и часто работаете со сводными таблицами и вам их возможности «тесноваты» — копайте в сторону Power Pivot и DAX — и будет вам счастье!
Ссылки по теме
- Что умеет функция СУММПРОИЗВ на самом деле
- Зачем нужна функция ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ
- Настройка вычислений в сводных таблицах
Skip to content
В этом руководстве демонстрируются два простых способа вычисления средневзвешенного значения в Excel — с помощью функции СУММ (SUM) или СУММПРОИЗВ (SUMPRODUCT в английском варианте).
В одной из предыдущих статей мы обсудили три основные функции для вычисления среднего в Excel, которые очень просты и просты в использовании.
Но что, если некоторые значения более важны, чем другие, и, следовательно, вносят больший вклад в конечное среднее значение? Например, если вы участвуете в экзаменах и все экзамены имеют одинаковый вес, они одинаково важны, то для вас важно именно среднее значение оценки.
Однако в реальной жизни это не всегда так. Например, если вы изучаете программирование, то насколько важны для вас оценки по истории и физкультуре по сравнению с оценками по профильным дисциплинам?
Некоторые задачи всегда важнее других. Некоторые экзамены важнее других.
В таких ситуациях вам как раз и необходимо рассчитывать средневзвешенное значение.
- Что такое средневзвешенное значение?
- Формулы для средневзвешенного значения в Excel
- Пример 1. Функция СУММ.
- Пример 2. Функция СУММПРОИЗВ
- Пример 3. Средневзвешенная цена.
Хотя Microsoft Excel не предоставляет специальной функции взвешенного среднего, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что показано в следующих примерах.
Что такое средневзвешенное значение?
Оно является своего рода средним арифметическим, в котором некоторые элементы набора данных имеют большую значимость, чем другие. Другими словами, каждому исходному показателю присваивается определенный вес.
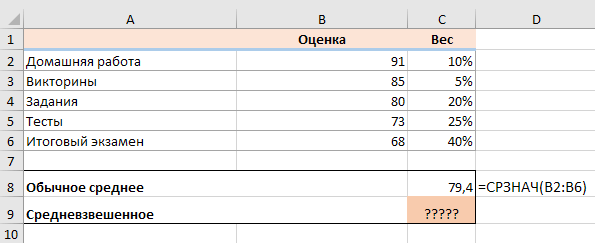
Оценки учащихся часто рассчитываются с использованием этого подхода, что видно на следующем скриншоте. Обычное среднее значение легко вычисляется с помощью СРЗНАЧ . Однако мы хотим, чтобы итог учитывал значимость каждого вида занятий, указанного в столбце C.
В математике и статистике вы вычисляете взвешенное среднее значение, умножая каждое число в наборе на его вес, затем складываете произведения и делите итог сложения произведений на сумму всех весомостей.
В этом примере, чтобы посчитать средневзвешенную итоговую оценку, вы умножаете каждый полученный балл на соответствующий процент (преобразованный в десятичную дробь), складываете эти 5 произведений вместе и делите это число на итог сложения пяти весов:
((91 * 0,1) + (85 * 0,05) + (80 * 0,2) + (73 * 0,25) + (68 * 0,4)) / (0,1 + 0,05 + 0,2 + 0,25 + 0,4) = 74,8
Обычная средняя оценка (79,4) и средневзвешенная (74,8) — это разные величины.
Формулы для средневзвешенного значения в Excel
В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.
Пример 1. Функция СУММ.
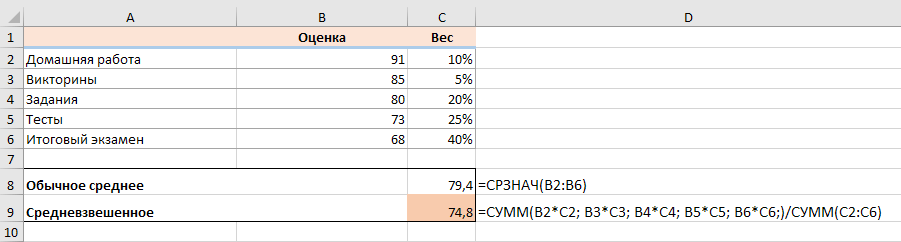
Если у вас есть базовые знания о ней , приведенная ниже формула вряд ли потребует какого-либо объяснения:
=СУММ(B2*C2; B3*C3; B4*C4; B5*C5; B6*C6)/СУММ(C2:C6)
По сути, он выполняет те же вычисления, что и описанные выше, за исключением того, что вы предоставляете ссылки на ячейки вместо чисел.
Посмотрите на рисунок чуть ниже: формула возвращает точно такой же результат, что и вычисления, которые мы делали минуту назад. Обратите внимание на разницу между нормальным средним, возвращаемым при помощи СРЗНАЧ в C8, и средневзвешенным (C9).
Несмотря на то, что формула эта очень проста и понятна, но она не подходит, если вы хотите усреднить большое количество элементов. Ведь придётся перечислять множество аргументов, что довольно утомительно.
В этом случае вам лучше использовать функцию СУММПРОИЗВ (SUMPRODUCT в английской версии). Об этом – ниже.
Пример 2. Функция СУММПРОИЗВ
Она идеально подходит для нашей задачи, так как предназначена для сложения произведений чисел. А это именно то, что нам нужно.
Таким образом, вместо умножения каждого числа на показатель его значимости по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом контексте массив представляет собой непрерывный диапазон ячеек), а затем делите результат на итог сложения весов:
= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )
Предполагая, что величины для усреднения находятся в ячейках B2: B6, а показатели значимости — в ячейках C2: C6, наша формула будет такой:
=СУММПРОИЗВ(B2:B6; C2:C6) / СУММ(C2:C6)
Итак, формула умножает 1- е число в массиве 1 на 1- е в массиве 2 (в данном примере 91 * 0,1), а затем перемножает 2- е число в массиве 1 на 2- е в массиве 2 (85 * 0,15). в этом примере) и так далее. Когда все умножения выполнены, Эксель складывает произведения. Затем делим полученное на итог весов.
Чтобы убедиться, что функция СУММПРОИЗВ дает правильный результат, сравните ее с формулой СУММ из предыдущего примера, и вы увидите, что числа идентичны.
В нашем случае сложение весов дает 100%. То есть, это просто процент от итога. В таком случае верный результат может быть получен также следующими способами:
=СУММ(B2*C2; B3*C3; B4*C4; B5*C5; B6*C6)
{=СУММ(B2:B6*C2:C6)}
Это формула массива, не забудьте, что вводить ее нужно при помощи комбинации клавиш CTRL+SHIFT+ENTER.
=СУММПРОИЗВ(B2:B6;C2:C6)
Но при использовании функции СУММ или СУММПРОИЗВ веса совершенно не обязательно должны составлять 100%. Однако, они также не должны быть обязательно выражены в процентах.
Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:
Видите, в этом случае мы обошлись без процентов.
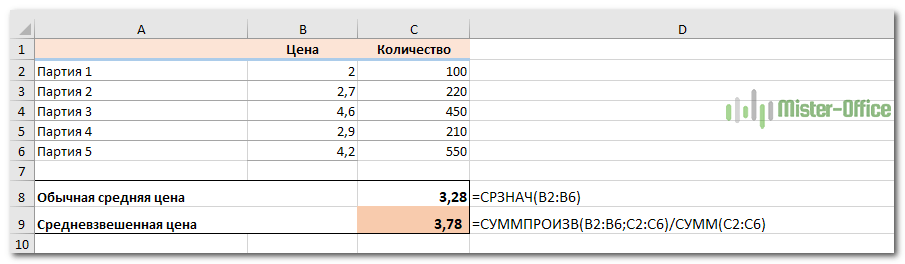
Пример 3. Средневзвешенная цена.
Еще одна достаточно часто встречающаяся проблема – как рассчитать средневзвешенную цену товара. Предположим, мы получили 5 партий товара от различных поставщиков. Мы будем продавать его по одной единой цене. Но чтобы ее определить, нужно знать среднюю цену закупки. В тот здесь нам и пригодится расчет средневзвешенной цены. Взгляните на этот простой пример. Думаю, вам все понятно.
Итак, средневзвешенная цена значительно отличается от обычной средней. На это повлияли 2 больших партии товара по высокой цене. А формулу применяем такую же, как и при расчете любого взвешенного среднего. Перемножаем цену на количество, складываем эти произведения, а затем делим на общее количество товара.
Ну, это все о формуле средневзвешенного значения в Excel.
Рекомендуем также:
Excel для Microsoft 365 для Mac Excel 2021 для Mac Excel 2019 для Mac Excel 2016 для Mac Excel для Mac 2011 Еще…Меньше
В Excel существует несколько способов найти среднее для набора чисел. Например, можно воспользоваться функцией для расчета простого среднего, взвешенного среднего или среднего, исключающего определенные значения.
Чтобы научиться вычислять средние значения, используйте предоставленные образцы данных и описанные ниже процедуры.
Копирование примера данных
Чтобы лучше понять описываемые действия, скопируйте пример данных в ячейку A1 пустого листа.
-
Создайте пустую книгу или лист.
-
Выделите приведенный ниже образец данных.
Примечание: Не выделяйте заголовки строк или столбцов (1, 2, 3… A, B, C…) при копировании данных примера на пустой лист.
Выбор примеров данных в справке
Качество изделия
Цена за единицу
Количество заказанных изделий
10
35
500
7
25
750
9
30
200
10
40
300
8
27
400
5
20
200
Среднее качество изделий
Средняя цена изделия
Среднее качество всех изделий с оценкой качества выше 5
-
Нажмите клавиши
+C.
-
Выделите на листе ячейку A1, а затем нажмите клавиши
+V.
Расчет простого среднего значения
-
Выделите ячейки с A2 по A7 (значения в столбце «Качество изделия»).
-
На вкладке Формулы щелкните стрелку рядом с кнопкой Автоумма
и выберитесреднее значение .
Результат — 8,166666667.
Расчет среднего для несмежных ячеек
-
Выберите ячейку, в которой должно отображаться среднее значение, например ячейку A8, которая находится слева ячейки с текстом «Среднее качество изделия» в примере данных.
-
На вкладке Формулы щелкните стрелку рядом с кнопкой Автоумма
кнопку Среднее инажмите клавишу RETURN.
-
Щелкните ячейку, которая содержит только что найденное среднее значение (ячейка A8 в этом примере).
Если используется образец данных, формула отображается в строка формул, =СС00(A2:A7).
-
В строке формул выделите содержимое между скобками (при использовании примера данных — A2:A7).
-
Удерживая нажатой клавишу
, щелкните ячейки, для чего нужно вычесть среднее значение, и нажмите клавишу RETURN. Например, выберите A2, A4 и A7 и нажмите клавишу RETURN.
Выделенная ссылка на диапазон в функции СРЗНАЧ заменится ссылками на выделенные ячейки. В приведенном примере результат будет равен 8.
Расчет среднего взвешенного значения
В приведенном ниже примере рассчитывается средняя цена за изделие по всем заказам, каждый из которых содержит различное количество изделий по разной цене.
-
Выделите ячейку A9, расположенную слева от ячейки с текстом «Средняя цена изделия».
-
На вкладке Формулы нажмите кнопку Вставить функцию, чтобы открыть панель Построитель формул.
-
В списке построителя формул дважды щелкните функцию СУММПРОИЗВ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СУММПРОИЗВ.
-
Щелкните поле рядом с надписью массив1 и выделите на листе ячейки с B2 по B7 (значения в столбце «Цена за единицу»).
-
Щелкните поле рядом с надписью массив2 и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество заказанных изделий»).
-
В строке формул установите курсор справа от закрывающей скобки формулы и введите /
Если строка формул не отображается, в меню Вид выберите пункт Строка формул.
-
В списке построителя формул дважды щелкните функцию СУММ.
-
Выделите диапазон в поле число1, нажмите кнопку DELETE и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество изделий»).
Теперь в строке формул должна содержаться следующая формула: =СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7).
-
Нажмите клавишу RETURN.
В этой формуле общая стоимость всех заказов делится на общее количество заказанных изделий, в результате чего получается средневзвешенная стоимость за единицу — 29,38297872.
Расчет среднего, исключающего определенные значения
Вы можете создать формулу, которая исключает определенные значения. В приведенном ниже примере создается формула для расчета среднего качества всех изделий, у которых оценка качества выше 5.
-
Выделите ячейку A10, расположенную слева от ячейки с текстом «Среднее качество всех изделий с оценкой качества выше 5».
-
На вкладке Формулы нажмите кнопку Вставить функцию, чтобы открыть панель Построитель формул.
-
В списке построителя формул дважды щелкните функцию СРЗНАЧЕСЛИ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СРЗНАЧЕСЛИ.
-
Щелкните поле рядом с надписью диапазон и выделите на листе ячейки с A2 по A7 (значения в столбце «Цена за единицу»).
-
Щелкните поле рядом с надписью условие и введите выражение «>5».
-
Нажмите клавишу RETURN.
Такая формула исключит значение в ячейке A7 из расчета. В результате будет получено среднее качество изделий, равное 8,8.
Совет: Чтобы использовать функцию СРЗНАЧЕСЛИ для расчета среднего без нулевых значений, введите выражение «<>0» в поле условие.
Чтобы научиться вычислять средние значения, используйте предоставленные образцы данных и описанные ниже процедуры.
Копирование примера данных
Чтобы лучше понять описываемые действия, скопируйте пример данных в ячейку A1 пустого листа.
-
Создайте пустую книгу или лист.
-
Выделите приведенный ниже образец данных.
Примечание: Не выделяйте заголовки строк или столбцов (1, 2, 3… A, B, C…) при копировании данных примера на пустой лист.
Выбор примеров данных в справке
Качество изделия
Цена за единицу
Количество заказанных изделий
10
35
500
7
25
750
9
30
200
10
40
300
8
27
400
5
20
200
Среднее качество изделий
Средняя цена изделия
Среднее качество всех изделий с оценкой качества выше 5
-
Нажмите клавиши
+C.
-
Выделите на листе ячейку A1, а затем нажмите клавиши
+V.
Расчет простого среднего значения
Рассчитаем среднее качество изделий двумя разными способами. Первый способ позволяет быстро узнать среднее значение, не вводя формулу. Второй способ предполагает использование функции «Автосумма» для расчета среднего значения и позволяет вывести его на листе.
Быстрый расчет среднего
-
Выделите ячейки с A2 по A7 (значения в столбце «Качество изделия»).
-
На строка состояния щелкните стрелку всплывающее меню
(если вы используете образец данных, вероятно, область содержит текст Sum=49),а затем выберите среднее .
Результат — 8,166666667.
Примечание: Если строка состояния не отображается, в меню Вид выберите пункт Строка состояния.
Расчет среднего с отображением на листе
-
Выберите ячейку, в которой должно отображаться среднее значение, например ячейку A8, которая находится слева ячейки с текстом «Среднее качество изделия» в примере данных.
-
На панели инструментов Стандартная под названием книги щелкните стрелку рядом с кнопкой
кнопку Среднее и нажмите клавишу RETURN.
Результат составляет 8,166666667 — это средняя оценка качества всех изделий.
Совет: Если вы работаете с данными, в которые перечислены числа в строке, выберите первую пустую ячейку в конце строки, а затем щелкните стрелку рядом с кнопкой
.
Расчет среднего для несмежных ячеек
Существует два способа расчета среднего для ячеек, которые не следуют одна за другой. Первый способ позволяет быстро узнать среднее значение, не вводя формулу. Второй способ предполагает использование функции СРЗНАЧ для расчета среднего значения и позволяет вывести его на листе.
Быстрый расчет среднего
-
Выделите ячейки, для которых вы хотите найти среднее значение. Например, выделите ячейки A2, A4 и A7.
Совет: Чтобы выбрать несмещные ячейки, щелкните их, удерживая
клавишу.
-
На строка состояния щелкните стрелку всплывающее меню
и выберите среднеезначение .
В приведенном примере результат будет равен 8.
Примечание: Если строка состояния не отображается, в меню Вид выберите пункт Строка состояния.
Расчет среднего с отображением на листе
-
Выберите ячейку, в которой должно отображаться среднее значение, например ячейку A8, которая находится слева ячейки с текстом «Среднее качество изделия» в примере данных.
-
На панели инструментов Стандартная под названием книги щелкните стрелку рядом с кнопкой
кнопку Среднее и нажмите клавишу RETURN.
-
Щелкните ячейку, которая содержит только что найденное среднее значение (ячейка A8 в этом примере).
Если используется образец данных, формула отображается в строка формул, =СС00(A2:A7).
-
В строке формул выделите содержимое между скобками (при использовании примера данных — A2:A7).
-
Удерживая нажатой клавишу
, щелкните ячейки, для чего нужно вычесть среднее значение, и нажмите клавишу RETURN. Например, выберите A2, A4 и A7 и нажмите клавишу RETURN.
Выделенная ссылка на диапазон в функции СРЗНАЧ заменится ссылками на выделенные ячейки. В приведенном примере результат будет равен 8.
Расчет среднего взвешенного значения
В приведенном ниже примере рассчитывается средняя цена за изделие по всем заказам, каждый из которых содержит различное количество изделий по разной цене.
-
Выделите ячейку A9, расположенную слева от ячейки с текстом «Средняя цена изделия».
-
На вкладке Формулы в разделе Функция выберите пункт Построитель формул.
-
В списке построителя формул дважды щелкните функцию СУММПРОИЗВ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СУММПРОИЗВ.
-
В разделе Аргументы щелкните поле рядом с надписью массив1 и выделите на листе ячейки с B2 по B7 (значения в столбце «Цена за единицу»).
-
В разделе Аргументы щелкните поле рядом с надписью массив2 и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество заказанных изделий»).
-
В строке формул установите курсор справа от закрывающей скобки формулы и введите /
Если строка формул не отображается, в меню Вид выберите пункт Строка формул.
-
В списке построителя формул дважды щелкните функцию СУММ.
-
В разделе Аргументы щелкните диапазон в поле число1, нажмите кнопку DELETE и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество изделий»).
Теперь в строке формул должна содержаться следующая формула: =СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7).
-
Нажмите клавишу RETURN.
В этой формуле общая стоимость всех заказов делится на общее количество заказанных изделий, в результате чего получается средневзвешенная стоимость за единицу — 29,38297872.
Расчет среднего, исключающего определенные значения
Вы можете создать формулу, которая исключает определенные значения. В приведенном ниже примере создается формула для расчета среднего качества всех изделий, у которых оценка качества выше 5.
-
Выделите ячейку A10, расположенную слева от ячейки с текстом «Среднее качество всех изделий с оценкой качества выше 5».
-
На вкладке Формулы в разделе Функция выберите пункт Построитель формул.
-
В списке построителя формул дважды щелкните функцию СРЗНАЧЕСЛИ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СРЗНАЧЕСЛИ.
-
В разделе Аргументы щелкните поле рядом с надписью диапазон и выделите на листе ячейки с A2 по A7 (значения в столбце «Цена за единицу»).
-
В разделе Аргументы щелкните поле рядом с надписью условие и введите выражение «>5».
-
Нажмите клавишу RETURN.
Такая формула исключит значение в ячейке A7 из расчета. В результате будет получено среднее качество изделий, равное 8,8.
Совет: Чтобы использовать функцию СРЗНАЧЕСЛИ для расчета среднего без нулевых значений, введите выражение «<>0» в поле условие.
Дополнительные сведения
Расчет суммы с нарастающим итогом
Вычисление процентов
Функция СРЗНАЧ
Нужна дополнительная помощь?
Среднее арифметическое значение — самый известный статистический показатель. В этой заметке рассмотрим его смысл, формулы расчета и свойства.
Средняя арифметическая как оценка математического ожидания
Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.
Формула матожидания имеет следующий вид:
где M(X) – математическое ожидание
xi – это случайные величины
pi – их вероятности.
То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.
Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.
Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.
Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.
где xi – значения переменной,
n – количество значений.
Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).
Свойства средней арифметической (математического ожидания)
Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.
Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).
Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.
M(X+Y+Z) = M(X) + M(Y) + M(Z)
Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.
Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.
M(aX) = aM(X)
К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.
Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).
M(a) = a
Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.
Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
M(XY) = M(X)M(Y)
Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.
Среднее арифметическое чисел в Excel рассчитывают с помощью функции СРЗНАЧ. Выглядит примерно так.
У этой формулы есть замечательное свойство. Если в диапазоне, по которому рассчитывается формула, присутствуют пустые ячейки (не нулевые, а именно пустые), то они исключается из расчета.
Вызвать функцию можно разными способами. Например, воспользоваться командой автосуммы во вкладке Главная:
После вызова формулы нужно указать диапазон данных, по которому рассчитывается среднее значение.
Есть и стандартный способ для всех функций. Нужно нажать на кнопку fx в начале строки формул. Затем либо с помощью поиска, либо просто по списку выбрать функцию СРЗНАЧ (в категории «Статистические»).
Средняя арифметическая взвешенная
Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.
Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:
Теперь преобразуем формулу до удобного вида.
Подставим значения.
Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.
Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.
где x – анализируемый показатель; f – вес.
Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.
Формула средневзвешенного значение в Excel
Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.
Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.
Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:
=СУММПРОИЗВ(B3:B5;C3:C5)/СУММ(C3:C5)
Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.
Физический смысл средней арифметической
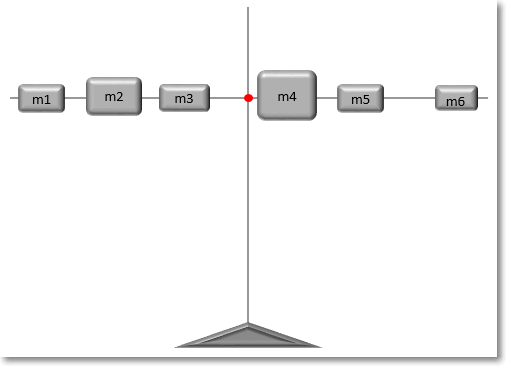
Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.
Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (mi), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.
И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.
Поделиться в социальных сетях:
Microsoft Excel
трюки • приёмы • решения
Как в Excel рассчитать средневзвешенное значение
Функция Excel СРЗНАЧ вычисляет среднее значение набора данных. Часто пользователям нужно рассчитать средневзвешенное. Вы можете потратить целый день на поиски, но не найдете функцию, позволяющую сделать такой расчет. Можно, однако, рассчитывать средневзвешенные, создав формулу, которая использует функции СУММПРОИЗВ и СУММ.
На рис. 96.1 показан обычный лист, который содержит цены на бензин в течение 30 дней. Например, цена составляла $2,48 первые пять дней. Затем она снизилась до $2,41 в течение двух дней. Далее цена еще снизилась до $2,39 в течение трех дней и т. д.
Рис. 96.1. Формула в ячейке В16 вычисляет средневзвешенную цену на бензин
Ячейка В15 содержит формулу, которая использует функцию СРЗНАЧ: =СРЗНАЧ(B4:B13) . Если вы проанализируете ее, то увидите, что формула не возвращает точный результат. Скорее, цены должны быть взвешены по фактору количества дней, в течение которых каждая цена была в силе. Другими словами, средневзвешенное является соответствующим типом расчета. Следующая формула, указанная в ячейке В16 , делает то, что нужно: =СУММПРОИЗВ(B4:B13;C4:C13)/СУММ(C4:C13) .
Эта формула умножает каждую цену на соответствующее количество дней, а затем складывает все, что получилось. Результат делится на количество дней. Вы можете легко переделать эту формулу для других видов расчета средневзвешенного.
Средневзвешенная цена в MS EXCEL
Рассчитаем средневзвешенную цену товара без использования вспомогательных столбцов. Также рассчитаем средневзвешенную цену с условием.
Пусть дана таблица продаж партий одного товара (см. файл примера ). В каждой партии указано количество проданного товара (столбец А) и его цена (столбец В).
Найдем средневзвешенную цену. В отличие от средней цены, вычисляемой по формуле СРЗНАЧ(B2:B8) , в средневзвешенной учитываются «вес» каждой цены (в нашем случае в качестве веса выступают значения из столбца Количество). Т.е. если продали одну крупную партию товара по очень низкой цене (строка 2), а другие небольшие партии по высокой, то не смотря, что средняя цена будет высокой, средневзвешенная цена будет смещена в сторону низкой цены.
Средневзвешенная цена вычисляется по формуле.
=СУММПРОИЗВ(B2:B8;A2:A8)/СУММ(A2:A8)
Если в столбце «весов» (А) будут содержаться одинаковые значения, то средняя и средневзвешенная цены совпадут.
Средневзвешенная цена с условием
Если требуется найти средневзвешенную цену не для всего массива данных, а для определенной группы значений, то формула усложнится. Покажем на примере.
Пусть имеется таблица партий товара от разных поставщиков.
Формула для вычисления средневзвешенной цены для Поставщика1:
К аргументам функции СУММПРОИЗВ() добавился 3-й аргумент: —($B$7:$B$13=B17)
Если выделить это выражение и нажать F9, то получим массив <1:1:1:1:0:0:0>. Т.е. значение 1 будет только в строках, у которых в столбце поставщик указан Поставщик1. Теперь сумма произведений не будет учитывать цены от другого поставщика, т.к. будут умножены на 0. Сумма весов для Поставщика1 вычисляется по формуле СУММЕСЛИ($B$7:$B$13;B17;$D$7) .
Решение приведено в файле примера на листе Пример2 .
Как посчитать средневзвешенное значение в Excel? Какая нужна формула?
Средневзвешенное значение (средняя взвешенная) в отличие от среднего значения учитывает вес (важности) каждого из элементов совокупности.
Как в программе Эксель (Excel) можно сделать расчёт средней взвешенной?
Какую формулу нужно написать?
Средневзвешенное значение можно посчитать по следующей формуле:
x1, x2, x3, . xn — это значения (цена, оценка, курс валюты и т.д.).
w1, w2, w3, . wn — вес каждого значения.
То есть нужно каждое значение умножить на его вес и просуммировать все произведения, а затем разделить всё это на сумму всех весов.
В программе Excel нет специальной функции, с помощью которой можно посчитать средневзвешенное значение.
Для его расчёта можно использовать комбинацию из 2 других функций: СУММПРОИЗВ и СУММ.
Вот несложный пример расчёта средневзвешенного значения в Excel:
Есть несколько товаров, которые имеют разную цену. За 1 день было продано сколько-то штук каждого из товаров. Нужно посчитать средневзвешенную цену продажи.
1) Составляем таблицу.
Здесь всё понятно — пишем название товара, рядом — соответствующее количество и цену.
2) Теперь ставим курсор в ту ячейку, куда нужно записать формулу для средневзвешенного.
Переходим на вкладку панели инструментов «Формулы», там нажимаем на «Математические» и в списке выбираем «СУММПРОИЗВ».
В качестве первого аргумента этой функции указываем столбец с количеством (С), в качестве второго аргумента указываем столбец с ценой (D).
3) Теперь в строке формул после функции СУММПРОИЗВ ставим символ деления (/) и добавляем функцию СУММ.
Здесь достаточно указать в 1 аргументе столбец с количеством (С).
4) В результате получится средневзвешенная цена.
Взвешенное среднее значение
В этом курсе:
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
Обычно при вычислении среднего значения все числа задаются равным значимости; числа добавляются одновременно, а затем поделяются на количество чисел. При использовании взвешенного среднего значения одному или нескольким числам присваивается более значимое значение или толщина.
Вычисление среднего взвешенного значения
Используйте функции СУММПРОИЗВ и сумм, чтобы найти взвешенное среднее значение, которое зависит от веса, примененного к значениям.
Например, отгрузка 10 вариантов Карандашов составляет 20 центов на каждый вариант. Но вторая отгрузка 40 долларов на один случай, поскольку карандашы имеют высокий спрос. Если средние затраты для каждой отгрузки таким образом (0,20 + 0.30)/2 = 0,25, результат будет неточным.
Математический ввод не учитывает, что количество коробок составляет более 30 центов, чем 20 центов. Чтобы получить правильное среднее значение, используйте эту формулу для получения результата (28 центов на каждую отгрузку).
Формула выполняет деление общей стоимости двух заказов на общее количество заказанных коробок.
СРЕДНЕВЗВЕШ
Данная функция является частью надстройки MulTEx
- Описание, установка, удаление и обновление
- Полный список команд и функций MulTEx
- Часто задаваемые вопросы по MulTEx
Скачать MulTEx
Расчет средневзвешенного значения, в том числе на основании критерия
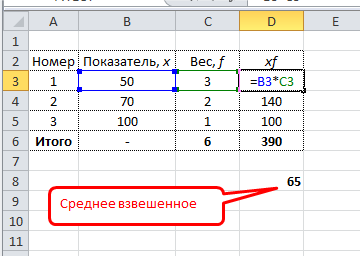
Функция рассчитывает средневзвешенное значение. Средневзвешенное значение, это значение, которое определяет «важность» того или иного значения на основании числовой шкалы. Т.е. чем большее число шкалы указано для значения — тем больший вес(ценность) при расчетах это значение имеет. Например, при оценке знаний слушателя можно использовать промежуточные тесты и итоговые экзамены. Экзамены при этом имеют большее значение, чем промежуточные тесты. Если не брать в расчет вес экзамена или теста, то можно применить вычисление обычного среднего при помощи встроенной в Excel СРЗНАЧ (AVERAGE) . Но по сути в данном случае те слушатели, которые сдали на отлично тесты могут одновременно полностью провалить экзамены. А экзамены для нас куда важнее и фактически при использовании обычных средних итогов мы получим неверную картину. Для примера возьмем следующую таблицу слушателей и их оценок по тестам и экзаменам: 
Если верить средним показателям самый «одаренный» слушатель — Андрей. Но если присмотреться видно, что Андрей не сдал ни одного экзамена даже на 4. Это значит, что он по факту нам не подходит. В то же время на основании средневзвешенного значения Сергей наиболее подходящий кандидат. И если изучить его результаты, то видно, что какие-то тесты он хоть и сдавал на 3, но экзамены сданы минимум на 4. А в столбце Вес у нас указано, что экзамены имеют куда большее значение, нежели тесты.
Так же средневзвешенное можно применять для общей оценки компетенций сотрудников или кандидатов на определенные должности.
Стандартных функций для расчета средневзвешенного в Excel нет. Функция СРЕДНЕВЗВЕШ позволяет без лишних ухищрений вычислить средневзвешенное значение для таблиц.
Вызов команды через стандартный диалог:
Мастер функций—Категория «MulTEx»— СРЕДНЕВЗВЕШ
Вызов с панели MulTEx:
Сумма/Поиск/Функции — Математические — СРЕДНЕВЗВЕШ
Синтаксис:
=СРЕДНЕВЗВЕШ( C2:C9 ; $B$2:$B$9 )
=СРЕДНЕВЗВЕШ( $B$2:$B$20 ; $C$2:$C$20 ; A3 ; $A$2:$A$20 )
=СРЕДНЕВЗВЕШ( $B$2:$B$20 ; $C$2:$C$20 ;»*блок*»; $A$2:$A$20 )
Значения ( $B$2:$B$20 ) — указывается диапазон со значениями, среднее для которых необходимо подсчитать с учетом веса каждого показателя.
Вес( $C$2:$C$20 ) — указывается ссылка на диапазон, в котором указана значимость каждого показателя. Должен состоять только из одного столбца и должен быть равен по количеству строк диапазону Значения.
Критерий( A3 ) — необязательный. Ссылка на ячейку с критерием или непосредственно критерий в текстовом представлении. В критерии допускается указание специальных символов подстановки — * и ? . Т.е. указав в качестве Критерия » *затрат* » средневзвешенное будет рассчитано для всех ячеек, в столбце критериев которых встречается слово » затрат «(затраты, данные по затратам и т.п.).
Так же данный аргумент может принимать в качестве критерия символы сравнения( , =, <>, ):
- «>0» — будут рассчитаны средневзвешенные для всех ячеек в столбце значений, критерии для которых в диапазоне критериев больше нуля;
- «>=2» — будут рассчитаны средневзвешенные для всех ячеек в столбце значений, критерии для которых в диапазоне критериев больше или равно двум;
- » — будут рассчитаны средневзвешенные для всех ячеек в столбце значений, критерии для которых в диапазоне критериев меньше нуля;
- » — будут рассчитаны средневзвешенные для всех ячеек в столбце значений, критерии для которых в диапазоне критериев меньше или равно 60;
- «<>0″ — будут рассчитаны средневзвешенные для всех ячеек в столбце значений, критерии для которых в диапазоне критериев не равно нулю;
- «<>« — будут рассчитаны средневзвешенные для всех ячеек в столбце значений, критерии для которых в диапазоне критериев не пустые
Вместо нуля может быть любое число или текст. Так же можно добавить ссылку на ячейку со значением: «<>«& D$1
ДиапазонКритерия( $A$2:$A$20 ) — необязательный. Указывается ссылка на диапазон значений, среди которых просматривать критерии. Обязателен к указанию, если указан аргумент критерий . Должен состоять только из одного столбца и должен быть равен по количеству строк диапазону Значения .
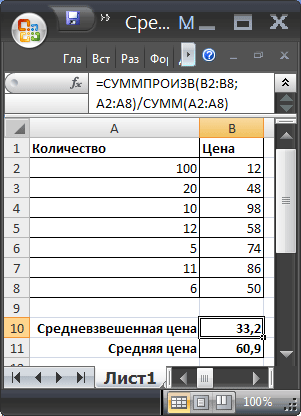
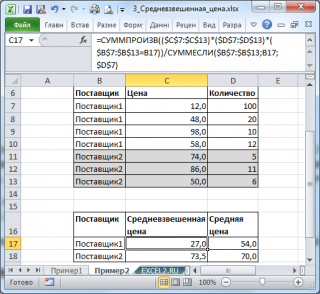
Если с простой таблицей(с расчетом средневзвешенных оценок) все выглядит достаточно логично и понятно, то с критериями чуть сложнее. Для примера возьмем таблицу товаров, продаваемых за разные периоды. Цена товара в разные дни могла изменяться и нам необходимо определить средневзвешенную цену на каждый товар, в зависимости от его продаваемости по той или иной цене: 
Т.е. по сути критерием веса для каждого товара у нас является общая стоимость продаж каждого товара. Стандартными функциями пришлось бы сначала количество каждого товара умножить на цену(определив общую стоимость), далее просуммировать полученную общую стоимость по каждому отдельному товару и её разделить на общее количество этого товара. Звучит не очень просто, а вычислять руками еще сложнее. Функция СРЕДНЕВЗВЕШ делает это опять же самостоятельно — надо просто дополнительно указать критерий(наименование товара) и столбец, в котором этот критерий искать(столбец наименований товара): 
Здесь функция для каждого отдельного наименования товара вычислила средневзвешенное. Т.е. для всех строк, где в столбце А записано «Сканер» записано одно и то же значение средневзвешенного. Так же можно сначала в отдельном столбце создать список уникальных наименований товаров(при помощи функции MulTEx —Диапазоны —Работа с дубликатами) и к этим данным применить формулу СРЕДНЕВЗВЕШ:





 +C.
+C. и выберитесреднее значение .
и выберитесреднее значение . (если вы используете образец данных, вероятно, область содержит текст Sum=49),а затем выберите среднее .
(если вы используете образец данных, вероятно, область содержит текст Sum=49),а затем выберите среднее .
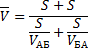
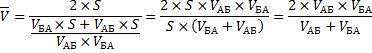








 Скачать MulTEx
Скачать MulTEx