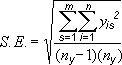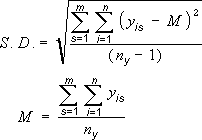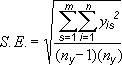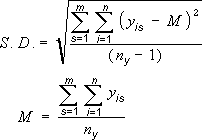С использованием встроенных функций
Excel расчет доверительного
интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа —
уровень значимости используемый для
вычисления уровня надежности.
(,
т.е.
означает надежности);
станд_откл
— стандартное отклонение, предполагается
известным;
размер — размер выборки.
Лабораторная работа
1
Тема: Обработка прямых
измерений в Excel (2 часа ).
Задание:
Обработать заданный набор экспериментальных
данных методом Стьюдента, построить
экспериментальные кривые методом
наименьших квадратов.
|
Пример |
Используемуе |
|
|
|
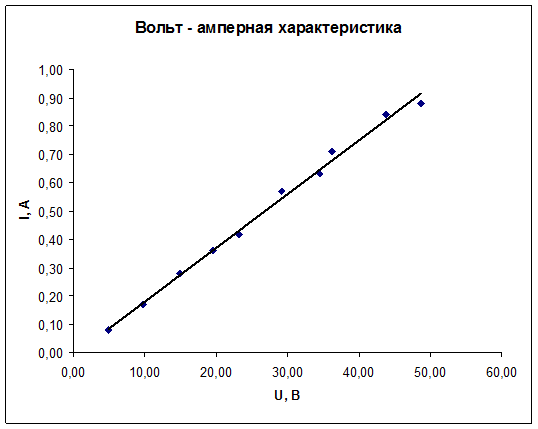
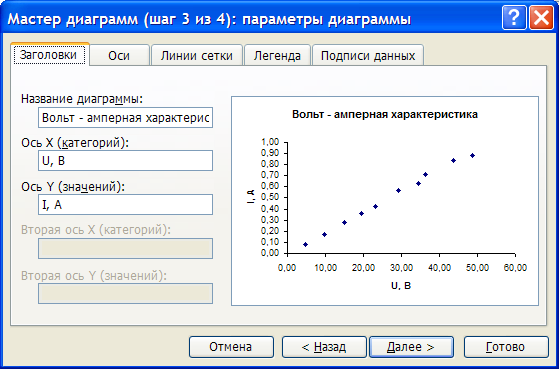
Для построения графика используем
мастер диаграмм.
Расчет
погрешности при косвенных измерениях
При измерении
величины косвенным методом предполагается,
что известна математическая модель
связывающая искомую
величину
с величинами
,
измеряемыми непосредственно. Далее
предполагается, выполнена обработка
всех прямых измерений, т. е. определены
доверительные интервалы для величин
:
Погрешность величины у
определяется по формуле:
где
.
Расчет косвенной
погрешности в Maple
Рассмотрим расчет погрешности на примере
функции одной переменной
,
где
Таким образом, найден доверительный
интервал величины
.
В случае, если определяемая в косвенном
измерении величина, является функцией
нескольких переменных, рекомендуем:
-
вычисление погрешности оформить в виде
процедуры
>dy:=proc(y, dx) ……код
процедуры
…… end proc
Код процедуры учащийся должен составить
самостоятельно на основе примера,
рассмотренного выше.
-
параметр dx считать массивом из N
переменных -
для определения списка аргументов и
их количества величины y
можно использовать операторы op() и
nops():
-
Лабораторная работа 2 Тема: Обработка косвенных измерений в Maple (4 часа).
Задание:
Написать программу нахождения погрешности
косвенного измерения в среде Maple.
Выполнение задания
1. Ввести выборку значений измеряемых
величин в матричном виде
2. Определить размерность выборки
3. Задать уровень значимости и определить
степень доверия:
4. Вычислить среднее значение выборки
измеряемой величины:
a) с помощью операций
суммирования
б) с помощью встроенных функций
5. Вычислить значения среднеквадратичного
отклонения.
а) с помощью операций суммирования
,
в) с помощью встроенных функций
6. Вычислить доверительный интервал:
а) Задать коэффициент Стьюдента для
данных размерности выборки и степени
доверия:
.
б) Вычислить абсолютную случайную
погрешность
.
в) Вычислить верхнюю и нижнюю границы
доверительного интервала.
.
7. Учесть приборные погрешности:
а) Задать приборные погрешности
.
б) Вычислить абсолютную случайную
погрешность с учетом приборных
погрешностей
.
8. Представить результат:
а) Абсолютная погрешность:
,
б) Относительная погрешность:
,
в) Верхняя и нижняя границы доверительного
интервала.
.
Примечание. Вычисления провести:
а) в обычном виде,
(См. Дов_инт_01)
б) с помощью операций суммирования,
(См. Дов_инт_02)
в) с помощью встроенных функций.
(См. Дов_инт_03)
2. Вычисление косвенных погрешностей
Выполнение задания
1. Провести аналитические вычисления:
а) Ввести выражение для исследуемой
функции:
,
б) Получить выражение для среднего
значения величины исследуемой функции:
,
в) Получить выражение косвенной
погрешности исследуемой функции в общем
виде и для значения :
,
,
1. Провести численные вычисления:
а) Ввести численные значения постоянных,
б) Ввести средние значения и доверительные
интервалы переменных,
в) Вычислить относительные погрешности
переменных,
г) Вычислить среднее значение исследуемой
функции:
,
г) Вычислить косвенную погрешность
(абсолютную погрешность) исследуемой
функции
,
г) Вычислить относительную погрешность
исследуемой функции
,
в) Вычислить верхнюю и нижнюю границы
доверительного интервала исследуемой
функции:
.
(См. Косв_погр).
3. Построение графиков. Полиномиальная
регрессия
Выполнение задания
1. Ввод выборок значений величин :
2. Вычислить верхнюю и нижнюю границы
доверительного величины Y:
.
3. Полиномиальная регрессия:
а) Задать степень полинома k:
б) Задать число точек данных:
.
в) Задать регрессионную зависимость:
.
г) Определить коэффициенты уравнения
регрессии
:
,
.
4. Построить графики:
а) точечных график данных,
б) кривую регрессии,
в) доверительные интервалы величины Y.
(См. Постр_граф).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Добавление, изменение и удаление отрезков ошибок на диаграмме
- Добавление и удаление отрезков ошибок
- Формулы для расчета величины погрешности
- Добавление, изменение и удаление отрезков ошибок на диаграмме в Office 2010
- Выражение погрешности в виде процентной доли, стандартного отклонения или стандартной ошибки
- Выражение погрешностей в виде пользовательских значений
- Добавление полос повышения и понижения
- Расчет случайной погрешности средствами Excel
Добавление, изменение и удаление отрезков ошибок на диаграмме
Планки погрешностей на создаваемых диаграммах помогают быстро определять пределы погрешностей и стандартные отклонения. Их можно отобразить для всех точек или маркеров данных в ряду данных как стандартную ошибку, относительную ошибку или стандартное отклонение. Можно задать собственные значения для отображения точных величин погрешностей. Например, отобразить положительную и отрицательную величины погрешностей в 10 % в результатах научного эксперимента можно следующим образом:
Планки погрешностей можно использовать на плоских диаграммах с областями, гистограммах, линейчатых диаграммах, графиках, точечных и пузырьковых диаграммах. На точечных и пузырьковых диаграммах планки погрешностей можно изобразить для значений X и Y.
Примечание: Следующие процедуры применяются к Office 2013 и более поздним версиям. Ищете инструкции по Office 2010?
Добавление и удаление отрезков ошибок
Щелкните в любом месте диаграммы.
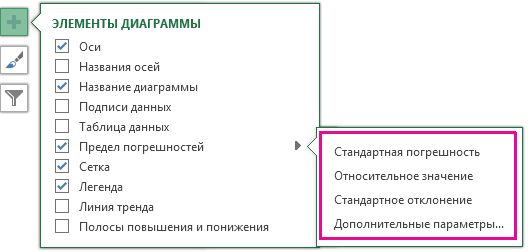
Нажмите кнопку «Элементы диаграммы 
Чтобы изменить отображаемую сумму ошибки, щелкните стрелку рядом с полосами ошибок и выберите нужный вариант.
Выберите предопределенный параметр планок погрешностей, такой как Стандартная погрешность, Относительное отклонение или Стандартное отклонение.
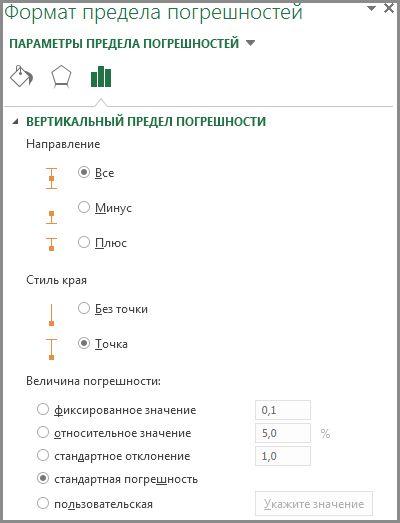
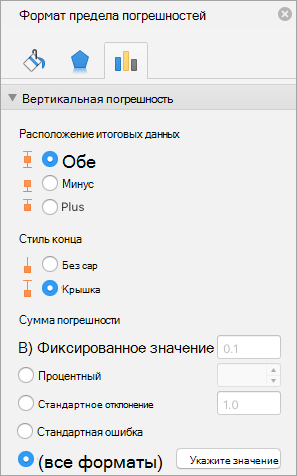
Выберите пункт Дополнительные параметры, чтобы задать собственные величины пределов погрешностей, а затем выберите нужные параметры в разделе Вертикальный предел погрешностей или Горизонтальный предел погрешностей. Здесь также можно изменить направление и стиль концов пределов погрешностей или создать собственные пределы погрешностей.
Примечание: Направление планок погрешностей зависит от типа диаграммы. Для точечных диаграмм могут отображаются и горизонтальные, и вертикальные планки погрешностей. Чтобы удалить планки погрешностей, выделите их и нажмите клавишу DELETE.
Формулы для расчета величины погрешности
Пользователи часто спрашивают, как в Excel вычисляется величина погрешности. Для вычисления стандартной погрешности и стандартного отклонения, которые отображаются на диаграмме, используются указанные ниже формулы.
i = номер точки в ряду s;
m = номер ряда для точки y на диаграмме;
n = число точек в каждом ряду;
yis = значение данных ряда s и i-й точки;
ny = суммарное число значений данных во всех рядах.
i = номер точки в ряду s;
m = номер ряда для точки y на диаграмме;
n = число точек в каждом ряду;
yis = значение данных ряда s и i-й точки;
ny = суммарное число значений данных во всех рядах;
M = среднее арифметическое.
Добавление, изменение и удаление отрезков ошибок на диаграмме в Office 2010
В Excel можно отобразить столбцы ошибок, использующие стандартную сумму ошибок, процент от значения (5 %) или стандартное отклонение.
Стандартные ошибки и стандартное отклонение используют следующие уравнения для вычисления сумм ошибок, отображаемых на диаграмме.
i = номер точки в ряду s;
m = номер ряда для точки y на диаграмме;
n = число точек в каждом ряду;
yis = значение данных ряда s и i-й точки;
ny = суммарное число значений данных во всех рядах.
i = номер точки в ряду s;
m = номер ряда для точки y на диаграмме;
n = число точек в каждом ряду;
yis = значение данных ряда s и i-й точки;
ny = суммарное число значений данных во всех рядах;
M = среднее арифметическое.
На двухмерной диаграмме, линейчатой диаграмме, столбце, линии, хи (точечной) или пузырьковой диаграмме выполните одно из следующих действий:
Чтобы добавить гистограммы во все ряды данных на диаграмме, щелкните область диаграммы.
Чтобы добавить панели ошибок в выбранную точку данных или ряд данных, щелкните нужные точки данных или ряды данных или выполните следующие действия, чтобы выбрать ее из списка элементов диаграммы:
Щелкните в любом месте диаграммы.
Будут отображены средства Работа с диаграммами, включающие вкладки Конструктор, Макет и Формат.
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Элементы диаграммы, а затем выберите нужный элемент диаграммы.
На вкладке «Макет » в группе «Анализ » щелкните » Панели ошибок».
Выполните одно из указанных ниже действий.
Выберите предопределенный параметр панели ошибок, например «Панели ошибок со стандартной ошибкой «, «Отрезки ошибок с процентом» или «Отрезки ошибок» со стандартным отклонением.
Щелкните «Дополнительные параметры панели ошибок», а затем в разделе «Вертикальные полосы ошибок» или «Горизонтальные панели ошибок » выберите нужные параметры отображения и количества ошибок.
Примечание: Направление гистограммы зависит от типа диаграммы. Для точечных диаграмм по умолчанию отображаются горизонтальные и вертикальные полосы ошибок. Вы можете удалить один из этих столбцов ошибок, выбрав их и нажав клавишу DELETE.
На двухстрочной области, линейчатой диаграмме, столбце, линии, хи (точечной) или пузырьковой диаграмме щелкните отрезки ошибок, точку данных или ряд данных с полосами ошибок, которые вы хотите изменить, или выполните следующие действия, чтобы выбрать их из списка элементов диаграммы:
Щелкните в любом месте диаграммы.
Будут отображены средства Работа с диаграммами, включающие вкладки Конструктор, Макет и Формат.
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Элементы диаграммы, а затем выберите нужный элемент диаграммы.
На вкладке «Макет » в группе «Анализ » щелкните » Панели ошибок» и выберите пункт «Дополнительные параметры панели ошибок».
В разделе «Отображение» щелкните направление и стиль конца панели ошибок, которые вы хотите использовать.
На двухстрочной области, линейчатой диаграмме, столбце, линии, хи (точечной) или пузырьковой диаграмме щелкните отрезки ошибок, точку данных или ряд данных с полосами ошибок, которые вы хотите изменить, или выполните следующие действия, чтобы выбрать их из списка элементов диаграммы:
Щелкните в любом месте диаграммы.
Будут отображены средства Работа с диаграммами, включающие вкладки Конструктор, Макет и Формат.
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Элементы диаграммы, а затем выберите нужный элемент диаграммы.
На вкладке «Макет » в группе «Анализ » щелкните » Панели ошибок» и выберите пункт «Дополнительные параметры панели ошибок».
В разделе «Сумма ошибки» выполните одно или несколько из следующих действий:
Чтобы использовать другой метод для определения количества ошибок, щелкните нужный метод и укажите сумму ошибки.
Чтобы определить количество ошибок с помощью пользовательских значений, нажмите кнопку «Пользовательский» и выполните следующие действия.
Нажмите кнопку «Указать значение».
В полях «Положительное значение ошибки» и «Отрицательное значение ошибки» укажите диапазон листа, который вы хотите использовать в качестве значений количества ошибок, или введите значения, которые вы хотите использовать, разделив их запятыми. Например, введите 0.4, 0.3, 0.8.
Совет: Чтобы указать диапазон листа, можно нажать кнопку «Свернуть 
Примечание: В Microsoft Office Word 2007 или Microsoft Office PowerPoint 2007 диалоговом окне «Настраиваемые панели ошибок» кнопка «Свернуть диалоговое окно» может не отображаться, а введите только значения количества ошибок, которые вы хотите использовать.
На двухстрочной области, панели, столбце, линии, хи (точечной) или пузырьковой диаграмме щелкните гистограмму, точку данных или ряд данных с отрезками ошибок, которые нужно удалить, или выполните следующие действия, чтобы выбрать их из списка элементов диаграммы:
Щелкните в любом месте диаграммы.
Будут отображены средства Работа с диаграммами, включающие вкладки Конструктор, Макет и Формат.
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Элементы диаграммы, а затем выберите нужный элемент диаграммы.
Выполните одно из указанных ниже действий.
На вкладке « Макет» в группе «Анализ » щелкните » Панели ошибок» и выберите пункт » Нет».
Нажмите клавишу DELETE.
Совет: Вы можете удалить полосы ошибок сразу после их добавления на диаграмму, нажав кнопку «Отменить» на панели быстрого доступа или нажав клавиши CTRL+Z.
Выполните одно из следующих действий:
Выражение погрешности в виде процентной доли, стандартного отклонения или стандартной ошибки
На диаграмме выберите ряд данных, к которому нужно добавить панели ошибок.
Например, щелкните одну из линий графика. Будут выделены все маркер данных этого ряд данных.
На вкладке «Деиговка диаграммыn» нажмите кнопку «Добавить элемент диаграммы».
Наведите указатель мыши на панели ошибок и выполните одно из следующих действий:
Применение стандартной ошибки с использованием следующей формулы:
s — номер ряда;
I — номер точки в ряду s;
m — количество рядов для точки y на диаграмме;
n — количество точек в каждом ряду;
y — значение данных ряда s и I-й точки;
n y — общее число значений данных во всех рядах.
Применение процентной доли значения к каждой точке данных в ряду данных
Применение кратного стандартного отклонения с использованием следующей формулы:
s — номер ряда;
I — номер точки в ряду s;
m — количество рядов для точки y на диаграмме;
n — количество точек в каждом ряду;
y — значение данных ряда s и I-й точки;
n y — общее число значений данных во всех рядах;
M — арифметическое среднее.
Выражение погрешностей в виде пользовательских значений
На диаграмме выберите ряд данных, к которому нужно добавить панели ошибок.
На вкладке «Конструктор диаграммы » нажмите кнопку «Добавить элемент диаграммы» и выберите пункт «Дополнительные параметры гистограммы».
В области «Формат гистограмм» на вкладке «Параметры панели ошибок» в разделе «Сумма ошибки» нажмите кнопку «Настраиваемое» и выберите команду «Указать значение».
В разделе Величина погрешности выберите пункт Настраиваемая, а затем — пункт Укажите значение.
В полях Положительное значение ошибки и Отрицательное значение ошибки введите нужные значения для каждой точки данных, разделенные точкой с запятой (например, 0,4; 0,3; 0,8), и нажмите кнопку ОК.
Примечание: Значения погрешностей можно также задать в виде диапазона ячеек из той же книги Excel. Чтобы указать диапазон ячеек, в диалоговом окне Настраиваемые планки погрешностей очистите содержимое поля Положительное значение ошибки или Отрицательное значение ошибки и укажите нужный диапазон ячеек.
Добавление полос повышения и понижения
На диаграмме выберите ряд данных, в который нужно добавить отрезки вверх и вниз.
На вкладке «Конструктор диаграмм » нажмите кнопку «Добавить элемент диаграммы», наведите указатель мыши на полосы вверх и вниз, а затем щелкните «Стрелки вверх /вниз».
В зависимости от типа диаграммы, некоторые параметры могут быть недоступны.
Источник
Расчет случайной погрешности средствами Excel
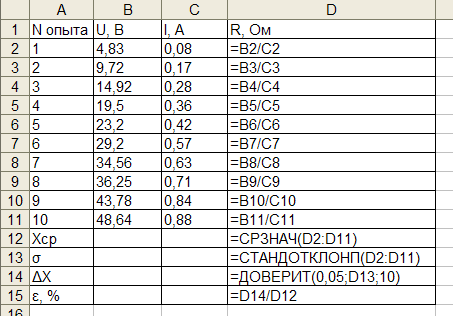
С использованием встроенных функций Excel расчет доверительного интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа — уровень значимости используемый для вычисления уровня надежности.
( 


станд_откл — стандартное отклонение, предполагается известным;
размер — размер выборки.
Задание: Обработать заданный набор экспериментальных данных методом Стьюдента, построить экспериментальные кривые методом наименьших квадратов.
Предположим, в ходе эксперимента по измерению электросопротивления были получены следующие данные:
Используя для определения сопротивления закон Ома 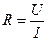
| Используемуе формулы |
 |
| Результат расчета |
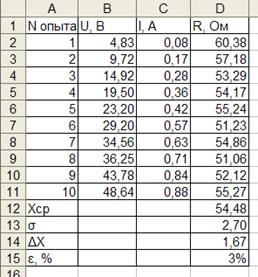 |
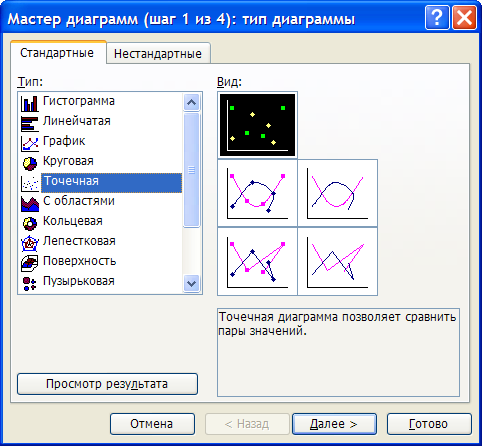
Для построения графика используем мастер диаграмм.
Полученные экспериментальные данные следует аппроксимировать. Для выполнения этой процедуры в Excel предусмотрен мастер, добавляющий линию тренда, производящий аппроксимацию и сглаживание.
В меню «Диаграмма» выберите пункт «Добавить линию тренда…».
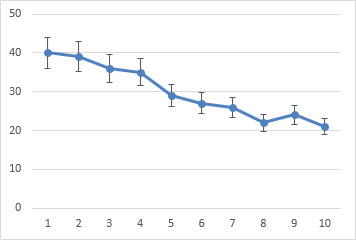
В результате, должен получиться следующий график.
Задание 1.
Просчитать погрешность измерений и построить график ее распределения.
| Задание 1 | Задание 2 | Задание 3 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 4 | Задание 5 | Задание 6 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
| Задание 7 | Задание 8 | Задание 9 |
| № опыта | № опыта | № опыта |
| 10,3 | 13,55 | 12,65 |
| 10,277 | 13,527 | 12,627 |
| 10,325 | 13,575 | 12,675 |
| 10,285 | 13,535 | 12,635 |
| 10,297 | 13,547 | 12,647 |
| 10,31 | 13,56 | 12,66 |
| 10,35 | 13,6 | 12,7 |
| 10,35 | 13,6 | 12,7 |
| 10,29 | 13,54 | 12,64 |
| 10,38 | 13,63 | 12,73 |
| Задание 10 | Задание 11 | Задание 12 |
| № опыта | №опыта | № опыта |
| 26,65 | 24,65 | 18,3 |
| 26,627 | 24,627 | 18,277 |
| 26,675 | 24,675 | 18,325 |
| 26,635 | 24,635 | 18,285 |
| 26,647 | 24,647 | 18,297 |
| 26,66 | 24,66 | 18,31 |
| 26,7 | 24,7 | 18,35 |
| 26,7 | 24,7 | 18,35 |
| 26,64 | 24,64 | 18,29 |
| 26,73 | 24,73 | 18,38 |
| Задание 13 | Задание 14 | Задание 15 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 16 | Задание 17 | Задание 18 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
Задание 2.
Определить является ли 3-е измерение промахом.
Источник
С использованием встроенных функций Excel расчет доверительного интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2; . )
число1, число2, . — аргументы, для которых вычисляется стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа — уровень значимости используемый для вычисления уровня надежности.
( , т.е. означает надежности );
станд_откл — стандартное отклонение, предполагается известным;
размер — размер выборки.
Задание: Обработать заданный набор экспериментальных данных методом Стьюдента, построить экспериментальные кривые методом наименьших квадратов.
Предположим, в ходе эксперимента по измерению электросопротивления были получены следующие данные:
Используя для определения сопротивления закон Ома произведем обработку данной серии экспериментальных данных.
| Используемуе формулы |
 |
| Результат расчета |
 |
Для построения графика используем мастер диаграмм.
Полученные экспериментальные данные следует аппроксимировать. Для выполнения этой процедуры в Excel предусмотрен мастер, добавляющий линию тренда, производящий аппроксимацию и сглаживание.
В меню «Диаграмма» выберите пункт «Добавить линию тренда…».
В результате, должен получиться следующий график.
Задание 1.
Просчитать погрешность измерений и построить график ее распределения.
| Задание 1 | Задание 2 | Задание 3 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 4 | Задание 5 | Задание 6 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
| Задание 7 | Задание 8 | Задание 9 |
| № опыта | № опыта | № опыта |
| 10,3 | 13,55 | 12,65 |
| 10,277 | 13,527 | 12,627 |
| 10,325 | 13,575 | 12,675 |
| 10,285 | 13,535 | 12,635 |
| 10,297 | 13,547 | 12,647 |
| 10,31 | 13,56 | 12,66 |
| 10,35 | 13,6 | 12,7 |
| 10,35 | 13,6 | 12,7 |
| 10,29 | 13,54 | 12,64 |
| 10,38 | 13,63 | 12,73 |
| Задание 10 | Задание 11 | Задание 12 |
| № опыта | №опыта | № опыта |
| 26,65 | 24,65 | 18,3 |
| 26,627 | 24,627 | 18,277 |
| 26,675 | 24,675 | 18,325 |
| 26,635 | 24,635 | 18,285 |
| 26,647 | 24,647 | 18,297 |
| 26,66 | 24,66 | 18,31 |
| 26,7 | 24,7 | 18,35 |
| 26,7 | 24,7 | 18,35 |
| 26,64 | 24,64 | 18,29 |
| 26,73 | 24,73 | 18,38 |
| Задание 13 | Задание 14 | Задание 15 |
| № опыта | № опыта | № опыта |
| 10,3 | 15,55 | 25,65 |
| 10,277 | 15,527 | 25,627 |
| 10,325 | 15,575 | 25,675 |
| 10,285 | 15,535 | 25,635 |
| 10,297 | 15,547 | 25,647 |
| 10,31 | 15,56 | 25,66 |
| 10,35 | 15,6 | 25,7 |
| 10,35 | 15,6 | 25,7 |
| 10,29 | 15,54 | 25,64 |
| 10,38 | 15,63 | 25,73 |
| Задание 16 | Задание 17 | Задание 18 |
| № опыта | №опыта | № опыта |
| 27,65 | 23,65 | 17,3 |
| 27,627 | 23,627 | 17,277 |
| 27,675 | 23,675 | 17,325 |
| 27,635 | 23,635 | 17,285 |
| 27,647 | 23,647 | 17,297 |
| 27,66 | 23,66 | 17,31 |
| 27,7 | 23,7 | 17,35 |
| 27,7 | 23,7 | 17,35 |
| 27,64 | 23,64 | 17,29 |
| 27,73 | 23,73 | 17,38 |
Задание 2.
Определить является ли 3-е измерение промахом.
Формула погрешности
- Формула погрешности
Формула погрешности (оглавление)
- Формула погрешности
- Примеры формулы допустимой погрешности (с шаблоном Excel)
- Калькулятор формулы ошибки поля
Формула погрешности
В статистике мы рассчитываем доверительный интервал, чтобы увидеть, куда упадет значение данных выборочной статистики. Диапазон значений, которые находятся ниже и выше выборочной статистики в доверительном интервале, называется границей ошибки. Другими словами, это в основном степень ошибки в статистике выборки. Чем выше погрешность, тем меньше будет достоверность результатов, поскольку степень отклонения в этих результатах очень высока. Как следует из названия, погрешность — это диапазон значений выше и ниже фактических результатов. Например, если мы получаем ответ в опросе, в котором 70% людей ответили «хорошо», а допустимая погрешность составляет 5%, это означает, что в целом от 65% до 75% населения считают, что ответ «хороший»,
Margin of Error = Z * S / √n
- Z — Z счет
- S — стандартное отклонение населения
- n — Размер выборки
Другая формула для расчета погрешности:
Margin of Error = Z * √((p * (1 – p)) / n)
- p — доля образца (доля образца, которая является успешной)
Теперь, чтобы найти желаемую оценку z, вам нужно знать доверительный интервал выборки, потому что оценка Z зависит от этого. Ниже приведена таблица, чтобы увидеть отношение доверительного интервала и z балла:
| Доверительный интервал | Z — Оценка |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Как только вы знаете доверительный интервал, вы можете использовать соответствующее значение z и рассчитать предел погрешности оттуда.
Примеры формулы допустимой погрешности (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчёт Margin of Error.
Вы можете скачать этот шаблон Margin of Error здесь — Шаблон Margin of Error
Формула погрешности — пример № 1
Допустим, мы проводим опрос, чтобы увидеть, каков балл, который получают студенты университетов. Мы выбрали 500 учеников случайным образом и задали их оценку. Среднее значение составляет 2, 4 из 4, а стандартное отклонение составляет, скажем, 30%. Предположим, что доверительный интервал составляет 99%. Рассчитайте погрешность.
Решение:
Погрешность рассчитывается по формуле, приведенной ниже
Граница ошибки = Z * S / √n
- Погрешность = 2, 58 * 30% / √ (500)
- Погрешность = 3, 46%
Это означает, что с вероятностью 99% средний балл учащихся составляет 2, 4 плюс или минус 3, 46%.
Формула погрешности — пример № 2
Допустим, вы запускаете новый продукт для здоровья на рынке, но вы не знаете, какой вкус понравится людям. Вы путаетесь между ароматом банана и ванили и решили провести опрос. Для вас это 500 000 человек, что является вашим целевым рынком, и из этого вы решили спросить мнение 1000 человек, и это будет образец. Предположим, что доверительный интервал составляет 90%. Рассчитайте погрешность.
Решение:
Как только опрос закончен, вы узнали, что банану понравился 470 человек, а 530 попросили аромат ванили.
Погрешность рассчитывается по формуле, приведенной ниже
Граница ошибки = Z * √ ((p * (1 — p)) / n)
- Погрешность = 1, 65 * √ ((0, 47 * (1 — 0, 47)) / 1000)
- Погрешность = 2, 60%
Таким образом, мы можем сказать, что с 90% уверенностью, что 47% всех людей любили банановый аромат плюс или минус 2, 60%.
объяснение
Как обсуждалось выше, предел погрешности помогает нам понять, подходит ли размер выборки для вашего опроса или нет. В случае, если погрешность слишком велика, возможно, размер нашей выборки слишком мал, и нам нужно его увеличить, чтобы результаты выборки более точно соответствовали результатам совокупности.
Существуют некоторые сценарии, в которых предел погрешности не будет иметь большого значения и не поможет нам в отслеживании ошибки:
- Если вопросы опроса не разработаны и не помогают получить требуемый ответ
- Если люди, отвечающие на опрос, имеют некоторую предвзятость в отношении продукта, для которого проводится опрос, то и результат будет не очень точным
- Если выбранная выборка является надлежащим представителем населения, в этом случае также результаты будут далеко.
Кроме того, одно большое предположение здесь состоит в том, что население обычно распределено. Таким образом, если размер выборки слишком мал и распределение населения не является нормальным, z-оценка не может быть рассчитана, и мы не сможем найти предел погрешности.
Актуальность и использование формулы ошибки
Всякий раз, когда мы используем выборочные данные, чтобы найти какой-то релевантный ответ для набора населения, возникает некоторая неопределенность и вероятность того, что результат может отличаться от фактического результата. Допустимая погрешность скажет нам, что каков уровень отклонения, это образец выборки. Нам необходимо минимизировать погрешность, чтобы результаты наших выборок отражали реальную историю данных о населении. Поэтому, чем ниже погрешность, тем лучше будут результаты. Запас погрешности дополняет и дополняет имеющуюся у нас статистическую информацию. Например, если опрос показал, что 48% людей предпочитают проводить время дома в выходные дни, мы не можем быть настолько точными, и в этой информации отсутствуют некоторые элементы. Когда мы ввели здесь предел погрешности, скажем, 5%, то результат будет интерпретирован как 43-53% людей, которым понравилась идея быть дома в выходные дни, что имеет полный смысл.
Калькулятор формулы ошибки поля
Вы можете использовать следующий калькулятор Margin of Error
Рекомендуемые статьи
Это было руководство по формуле ошибки. Здесь мы обсудим, как рассчитать погрешность, а также на практических примерах. Мы также предоставляем калькулятор Margin of Error с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
- Руководство по формуле амортизации прямой линии
- Примеры формулы удвоения времени
- Как рассчитать амортизацию?
- Формула для центральной предельной теоремы
- Альтман Z Оценка | Определение | Примеры
- Формула амортизации | Примеры с шаблоном Excel
Often in statistics, we’re interested in estimating a population parameter using a sample.
For example, we might want to know the mean height of students at a particular school. If the school has 1,000 total students, it might take too long to measure every student so instead we could take a simple random sample of 50 students and calculate the mean height of students in this sample.
And while the mean height of students in the sample might be a good estimate of the true population mean, there is no guarantee that the sample mean is exactly equal to the population mean. In other words, there exists some uncertainty.
One way to account for uncertainty is create a confidence interval, which is a range of values that we believe contains the true population parameter.
For example, if the mean height of students in the sample is 67 inches, our confidence interval for the true mean height of all students in the population might be [65 inches, 69 inches], which means we’re confident that the true mean height of students in the population is between 65 and 69 inches.
A confidence interval is composed of two parts:
Point estimate – often this is a sample mean or sample proportion.
Margin of error – a number that represents the uncertainty of the point estimate.
The formula to create a confidence interval is:
Confidence Interval = point estimate +/- margin of error
Margin of Error Formula
If you’re creating a confidence interval for a population mean, then the formula for the margin of error is:
Margin of error: Z * σ / √n
Where:
Z: Z-score
σ: Population standard deviation
n: Sample size
Note: If the population standard deviation is unknown, then you can replace Z with tn-1, which is the t critical-value that comes from the t distribution table with n-1 degrees of freedom.
And if you’re creating a confidence interval for a population proportion, then the formula for the margin of error is:
Margin of error: Z * √(p*(1-p)) / n)
Where:
Z: Z-score
p: Sample proportion
n: Sample size
Note that the Z-score you’ll use for this calculation is dependent on you chosen confidence level. The following table shows the Z-scores associated with common confidence levels:
| Confidence Level | Z-score |
|---|---|
| 80% | 1.282 |
| 85% | 1.44 |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.576 |
Next, we’ll walk through two examples of how to calculate the margin of error in Excel.
Example 1: Margin of Error for a Population Mean
Suppose we want to find the mean height of a certain plant. It is known that the population standard deviation, σ, is 2 inches. We collect a random sample of 100 plants and find that the sample mean is 14 inches. Find a 95% confidence interval for the true mean height of this certain plant.
Since we’re finding a confidence interval for the mean height, the formula we will use for the margin of error is: Z * σ / √n
The following image shows how to calculate the margin of error for this confidence interval:
The margin of error turns out to be 0.392.
Thus, the confidence interval for the true mean height of plants would be 14 +/ 0.392 = [13.608, 14.392].
Example 2: Margin of Error for a Population Proportion
Suppose we want to know what percentage of individuals in a certain city support a candidate named Bob. In a simple random sample of 200 individuals, 120 said they supported Bob (i.e. 60% support him). Find a 99% confidence interval for the true percentage of people in the entire city who support Bob.
Since we’re finding a confidence interval for the mean height, the formula we will use for the margin of error is: Z * √(p*(1-p)) / n)
The following image shows how to calculate the margin of error for this confidence interval:
The margin of error turns out to be 0.089.
Thus, the confidence interval for the true percentage of individuals in this city that support Bob is 0.6 +/- 0.089 = [ 0.511, 0.689].
Notes on Finding the Appropriate Z-Score or t-Score
If you’re finding the confidence interval for a population mean and you’re unsure of whether or not to use a Z-Score or a t-Score for the margin of error calculation, refer to this helpful diagram to help you decide:
Also, if you don’t have a helpful table that shows you which Z-Score or t-Score to use based on your confidence interval, you can always use the following commands in Excel to find the correct Z-Score or t-Score to use:
To find Z-Score: =NORM.INV(probability, 0, 1)
For example, to find the Z-Score associated with a 95% confidence level, you’d type =NORM.INV(.975, 0, 1), which turns out to be 1.96.
To find t-Score: =T.INV(probability, degrees of freedom)
For example, to find the t-Score associated with a 90% confidence level and 12 degrees of freedom, you’d type =T.INV(.95, 12), which turns out to be 1.78.