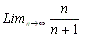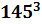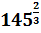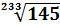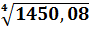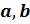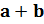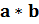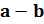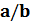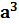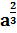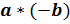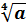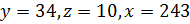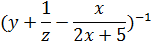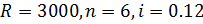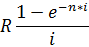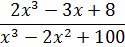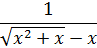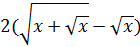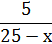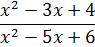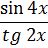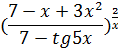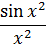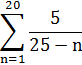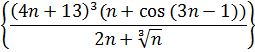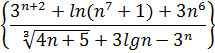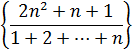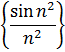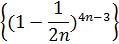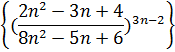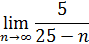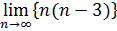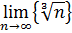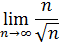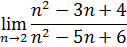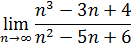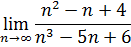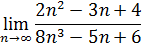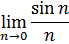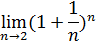Напомним, что функция f(x) имеет предел в точке а тогда и только тогда, когда в этой точке существуют левый и правый пределы, причем они равны. В математике для нахождения пределов функций применяются специальные приемы, в частности такой, как разложением числителя и знаменателя на сомножители и некоторые другие. Используя электронную таблицу можно применить следующую технологию:
1. В ячейку рабочего листа ввести формулу, соответствующую выражению функциональной зависимости, в которой значение аргумента указывается адресной ссылкой на ячейку, которая содержит аргумент.
2. В ячейку, предназначенную для записи аргумента функции, ввести число, максимально близкое к точке, в которой вычисляется предел функции.
Пример 10 . Найти предел
1. Введите в ячейку рабочего листа (А6 см. рис. 16) значение близкое к 2, например 1,99999999999.
2. В ячейку В6 – введите формулу =(A6^2-5*A6+6)/(A6^2-3*A6+2). После вычисления в ячейке В6 будет отображено приближенное значение предела функции.
На рисунке приведен также пример вычисления предела Обратите внимание на то, что значение х в ячейке А11 задано достаточно большое.
Упражнение 16 . Используя Excel, найдите предел функции в точке х= 0.
Подсчет ЧИСЕЛ попадающих в интервал в EXCEL
history 19 апреля 2013 г.
- Группы статей
- Подсчет Чисел
- Проверка данных
- Подсчет с множественными условиями
Подсчет чисел, попадающих в интервал – стандартная задача: используйте функцию СЧЕТЕСЛИМН() . Усложним задачу, сделаем интервал легко настраиваемым.
В качестве примера подсчета чисел возьмем список с числовыми значениями от 4 до 30 (См. файл примера ).
Будем подсчитывать значения, попадающие в интервал, например, (4;15]. Причем, границы интервала «включает [ ]» и «не включает ( )» будем выбирать из Выпадающего (раскрывающегося) списка .
Примечание : решение без выбора интервалов = СЧЁТЕСЛИМН(A2:A12;»>»&D2;A2:A12;» Предполагается, что границы интервала введены в ячейки D2 и F2 . Эти ячейки не должны быть пустыми, даже если одна из границ =0. Если в диапазоне A2:A12 содержатся числовые значения в текстовом формате , то они будут проигнорированы.
Для настройки границ интервала используем Проверку данных с типом данных Список . В качестве источника укажем для левой границы >;>= и для правой СЧЁТЕСЛИМН(A2:A12;C2&D2;A2:A12;E2&F2)
Как правило, люди пользуются лишь ограниченным количеством формул Excel, хотя есть ряд функций, о которых люди незаслуженно забывают. При этом они могут здорово помочь в решении множества задач. Чтобы ознакомиться с математическими функциями, необходимо открыть вкладку «Формулы» и найти там пункт «Математические». Мы рассмотрим некоторые из этих функций, потому что каждая из возможных формул в Excel имеет свое практическое применение.
Содержание
- Математические функции случайных чисел и возможных комбинаций
- Функция СЛУЧМЕЖДУ
- Функция СЛЧИС
- Функция ЧИСЛКОМБ
- Функция ФАКТР
- Функции преобразования чисел
- Функция ABS
- Функция РИМСКОЕ
- Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ
- Иные математические функции
- Функция ЗНАК
- Функция Число ПИ
- Функция ПРОИЗВЕД
Математические функции случайных чисел и возможных комбинаций
Это функции, позволяющие работать со случайными числами. Надо сказать, что по-настоящему случайных чисел не бывает. Все они генерируются по определенным закономерностям. Тем не менее, для решения прикладных задач генератор даже не совсем случайных чисел бывает очень полезным. К математическим функциям, которые генерируют случайные числа, относятся СЛУЧМЕЖДУ, СЛЧИС, ЧИСЛКОМБ, ФАКТР. Давайте каждую из них рассмотрим более подробно.
Функция СЛУЧМЕЖДУ
Это одна из самых часто используемых функций этой категории. Она генерирует случайное число, которое вписывается в определенный предел. Важно учитывать, что если диапазон слишком узкий, числа могут быть одинаковыми. Синтаксис очень прост: =СЛУЧМЕЖДУ(нижнее значение; верхнее значение). В качестве параметров, передаваемых пользователем, могут выступать как числа, так и ячейки, в которых есть определенные цифры. Обязательный ввод каждого аргумента.
Первая цифра в скобках – минимальное число, ниже которого генератор не будет работать. Соответственно, вторым является максимальное число. За пределами этих значений эксель не будет искать случайное число. Аргументы могут быть одинаковыми, но в таком случае будет генерироваться только одно число.
Величина этого числа постоянно изменяется. Каждый раз при редактировании документа значение получается другим.
Функция СЛЧИС
Данная функция генерирует случайное значение, границы которого автоматически устанавливаются на уровне 0 и 1. Можно использовать и несколько формул с применением этой функции, а также использовать одну функцию несколько раз. Модификации показаний в этом случае не будет.
Никаких дополнительных параметров передавать этой функции не нужно. Следовательно, ее синтаксис максимально простой: =СЛЧИС(). Возможно возвращение и дробных случайных значений. Для этого необходимо воспользоваться функцией СЛЧИС. Формула будет следующей: =СЛЧИС()*(максимальный предел-минимальный предел)+минимальный предел.
Если распространить формулу на все ячейки, то можно задать любое количество случайных чисел. Для этого необходимо использовать маркер автозаполнения (квадратик в левом нижнем углу выделенной ячейки).
Функция ЧИСЛКОМБ
Эта функция относится к такому разделу математики, как комбинаторика. Она определяет количество уникальных комбинаций при определенном количестве объектов в выборке. Активно используется, например, в статистических исследованиях в социономических науках.Синтаксис функции следующий: =ЧИСЛКОМБ(размер набора, количество элементов). Давайте рассмотрим эти аргументы более подробно:
- Размер набора – это общее количество элементов в выборке. Это может быть количество людей, товара и так далее.
- Количество элементов. Этот параметр обозначает ссылку или число, демонстрирующие полное количество объектов, которое должно в итоге получиться. Главное требование к величине этого аргумента – он всегда должен быть меньшим в сравнении с предыдущим.
Ввод всех аргументов – обязательнен. Помимо всего прочего, все они должны быть положительными по модальности. Давайте приведем небольшой пример. Допустим, у нас есть 4 элемента – ABCD. Задача следующая: подобрать комбинации таким образом, чтобы числа не повторялись. При этом их расположение не учитывается. То есть, программе будет все равно, это комбинация AB или BA.
Давайте теперь введем формулу, которая нам нужна для получения этих комбинаций: =ЧИСЛКОМБ(4;2). В результате, будет выведено 6 возможных комбинаций, состоящих из разных значений.
Функция ФАКТР
В математике есть такое понятие, как факториал. Под этим значением подразумевается число, которое получается в результате умножения всех натуральных чисел до этого числа. Например, факториалом числа 3 будет число 6, а факториалом числа 6 станет число 720. Обозначается факториал восклицательным знаком. А с помощью функции ФАКТР становится возможным нахождение факториала. Синтаксис формулы: =ФАКТР(число). Факториал соответствует количеству вероятных комбинаций значений, входящих в набор. Например, если у нас есть три элемента, то максимальное количеством комбинаций в этом случае будет 6.
Функции преобразования чисел
Преобразование чисел – это выполнение определенных операций с ними, которые не относятся к арифметическим. Например, превращение числа в римское, возвращение его модуля. Эти возможности реализуются с помощью функций ABS и РИМСКОЕ. Давайте их рассмотрим более подробно.
Функция ABS
Напоминаем, что модуль – это расстояние до нуля на оси координат. Если представить горизонтальную прямую с отмеченными на ней числами с шагом в 1, то можно увидеть что от числа 5 до нуля и от числа -5 до нуля будет одинаковое количество ячеек. Это расстояние и называется модулем. Как мы можем увидеть, модулем числа -5 является 5, поскольку необходимо пройти 5 ячеек, чтобы дойти до нуля.
Чтобы получить модуль числа, необходимо воспользоваться функцией ABS. Ее синтаксис очень простой. Достаточно в скобках написать число, после чего будет возвращено значение. Синтаксис следующий: =ABS(число). Если ввести формулу =ABS(-4), то в результате этих операций будет получено 4.
Функция РИМСКОЕ
Эта функция сделать из числа в арабском формате римское. Эта формула имеет два аргумента. Первый обязательный, а второй можно и не записывать:
- Число. Это непосредственно число, или ссылка на содержащую значение в этом форме ячейку. Важное требование – этот параметр должен быть выше нуля. Если число содержит разряды после запятой, то после его перевода в римский формат, дробная часть попросту отсекается.
- Формат. Этот аргумент уже не обязательно использовать. Задает формат представления. Каждому числу соответствует определенный внешний вид числа. Есть несколько возможных параметров, которые могут использоваться в качестве этого аргумента:
- 0. В этом случае значение показывается в своем классическом виде.
- 1-3 – разные виды отображения римских чисел.
- 4. Облегченный способ показа римского числа.
- Истина и Ложь. В первой ситуации число представляется в стандартном виде, а во втором – упрощенном.
Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ
Это довольно сложная функция, дающая возможность подвести промежуточные итоги на основе значений, которые ей переданы в качестве аргументов. Можно создать эту функцию через стандартный функционал Excel, а также возможно ее ручное применение.
Это довольно сложная в использовании функция, поэтому про нее нужно рассказать отдельно. Синтаксис этой функции такой:
- Номер функции. Этот аргумент – число в границах от 1 до 11. Это число показывает на ту функцию, которая будет применяться для подведения итогов определенного диапазона. Например, если нам требуется складывать числа, то нужно указать в качестве первого параметра число 9 или 109.
- Ссылка 1. Это тоже обязательный параметр, который дает ссылку на диапазон, учитываемый для подведения итогов. Как правило, люди используют лишь один диапазон.
- Ссылка 2, 3… Далее идет определенное количество ссылок на диапазон.
Максимальное количество аргументов, которые может содержать эта функция – 30 (номер функции + 29 ссылок).
Важное замечание! Вложенные итоги игнорируются. То есть, если в каком-то диапазоне уже применялась функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ, то она игнорируется программой.
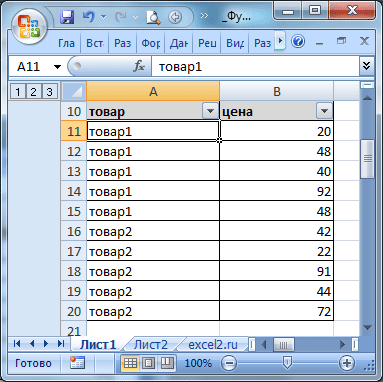
Следует также учитывать, что использование этой функции для подведения промежуточных итогов для горизонтальных массивов с данными не рекомендуется, поскольку она не предназначена для этого. В этом случае результаты могут оказаться неправильными. Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ нередко совмещается с автофильтром. Предположим, у нас есть такой набор данных.
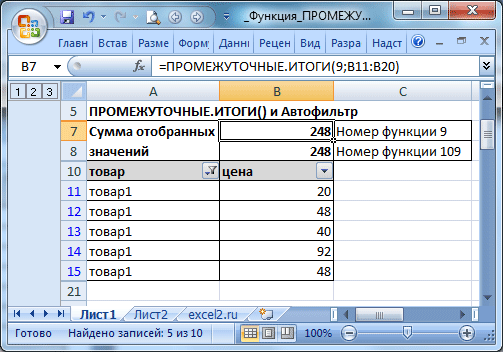
Давайте попробуем применить к нему автофильтр и отобрать лишь ячейки, маркируемые, как «Товар1». Далее поставим задачу определить с помощью функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ промежуточную сумму этих товаров. Здесь нам нужно применять код 9, как показано на скриншоте.
Далее функция автоматически отбирает те строки, которые не включаются в результат фильтра и не включает их в расчеты. Это дает много дополнительных возможностей. Кстати, есть встроенная функция Excel, которая называется Промежуточные итоги. Какая разница между этими инструментами? Дело в том, что функция автоматически убирает из выборки все строки, которые не отображаются на данный момент. При этом не учитывается код номер_функции.
Кстати, этот инструмент позволяет много чего делать, а не только осуществлять определение суммы значений. Вот перечень кодов с функциями, которые применяются для подведения промежуточных итогов.
1 – СРЗНАЧ;
2 – СЧЁТ;
3 – СЧЁТЗ;
4 – МАКС;
5 – МИН;
6 – ПРОИЗВЕД;
7 – СТАНДОТКЛОН;
8 – СТАНДОТКЛОНП;
9 – СУММ;
10 – ДИСП;
11 – ДИСПР.
Также можно добавить 100 к этим номерам, и функции будут те же. Но есть одна разница. Разница в том, что в первом случае скрытые ячейки не будут учитываться, а во втором – да.
Иные математические функции
Математика – непростая наука, которая включает множество формул для самых разнообразных задач. Excel включает почти все. Рассмотрим лишь три из них: ЗНАК, Число Пи, ПРОИЗВЕД.
Функция ЗНАК
С помощью этой функции пользователь может определить, число положительное или отрицательное. Может использоваться, например, для группировки клиентов на тех, которые имеют долги в банке и на тех, кто на данный момент или не оформлял заем или погасил его.
Синтаксис функции следующий: =ЗНАК(число). Видим, что здесь только один аргумент, ввод которого обязательный. После проверки числа функция возвращает значение -1, 0 или 1 в зависимости от того, какой знак был. Если число оказалось отрицательное, то будет -1, а если положительное – 1. Если же в качестве аргумента попался ноль, то он же и возвращается. Функция используется в сочетании с функцией ЕСЛИ или в любом другом подобном случае, когда нужно осуществить проверку числа.
Функция Число ПИ
Число ПИ является самой известной математической константой, которая равняется 3,14159… С помощью данной функции можно получить округленную до 14 знаков после запятой версию данного числа. Она не имеет аргументов и у нее следующий синтаксис: =ПИ().
Функция ПРОИЗВЕД
Функция, похожая по принципу на СУММ, только вычисляет произведение всех чисел, переданных ей в качестве аргументов. Можно указать до 255 чисел или диапазонов. Важно учитывать, что функция не учитывает текстовые, логические и любые другие значения, которые не используются в арифметических операциях. Если же в качестве аргумента используется логическое значение, то значению ИСТИНА соответствует единица, а значению ЛОЖЬ – нуль. Но важно понимать, что если в диапазоне будет логическое значение, то результат будет неправильный. Синтаксис формулы следующий: =ПРОИЗВЕД(число 1; число 2…).
Видим, что здесь приводятся числа через точку с запятой. Обязательный аргумент один – первое число. В принципе, можно и не использовать эту функцию при небольшом количестве значений. Тогда нужно последовательно перемножить все числа и ячейки. Но когда их много, то в ручном режиме это будет занимать довольно много времени. Чтобы его сэкономить, и существует функция ПРОИЗВЕД.
Таким образом, у нас есть огромное количество функций, которые используются довольно редко, но при этом они могут составить хорошую службу. Не стоит забывать, что данные функции можно сочетать между собой. Следовательно, набор возможностей, которые открываются, значительно расширяется.
Оцените качество статьи. Нам важно ваше мнение:
Технологию приближенного вычисления предела числовой последовательности рассмотрим на примере.
Пример. Пусть требуется найти предел числовой последовательности .
— полагая, что в ячейке А2 будет находиться число n, в ячейку рабочего листа В2 введите формулу “= A2/(A2+1)”;
— в ячейку А2 введите большое число, примерно равное 1*10 30 , или несколько больше, например 1* 10 100 . После ввода числа в ячейке В2 отобразится приближенное значение предела числовой последовательности (см.рис. 12)
1. Известно, что число е является пределом последовательности Вычислите приближенно значение числа е.
2. Найдите предел
3. Найдите предел последовательности
Напомним, что функция f(x) имеет предел в точке а тогда и только тогда, когда в этой точке существуют левый и правый пределы, причем они равны. В математике для нахождения пределов функций применяются специальные приемы, в частности такой, как разложением числителя и знаменателя на сомножители и некоторые другие. Используя электронную таблицу можно применить следующую технологию:
1. В ячейку рабочего листа ввести формулу, соответствующую выражению функциональной зависимости, в которой значение аргумента указывается адресной ссылкой на ячейку, которая содержит аргумент.
2. В ячейку, предназначенную для записи аргумента функции, ввести число, максимально близкое к точке, в которой вычисляется предел функции.
Пример 10 . Найти предел
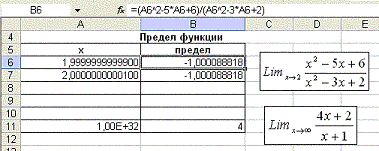
1. Введите в ячейку рабочего листа (А6 см. рис. 16) значение близкое к 2, например 1,99999999999.
2. В ячейку В6 – введите формулу =(A6^2-5*A6+6)/(A6^2-3*A6+2). После вычисления в ячейке В6 будет отображено приближенное значение предела функции.
На рисунке приведен также пример вычисления предела Обратите внимание на то, что значение х в ячейке А11 задано достаточно большое.
Упражнение 16 . Используя Excel, найдите предел функции в точке х= 0.
Подсчет чисел, попадающих в интервал – стандартная задача: используйте функцию СЧЕТЕСЛИМН() . Усложним задачу, сделаем интервал легко настраиваемым.
В качестве примера подсчета чисел возьмем список с числовыми значениями от 4 до 30 (См. файл примера ).
Будем подсчитывать значения, попадающие в интервал, например, (4;15]. Причем, границы интервала «включает [ ]» и «не включает ( )» будем выбирать из Выпадающего (раскрывающегося) списка .
Примечание : решение без выбора интервалов = СЧЁТЕСЛИМН(A2:A12;»>»&D2;A2:A12;» Предполагается, что границы интервала введены в ячейки D2 и F2 . Эти ячейки не должны быть пустыми, даже если одна из границ =0. Если в диапазоне A2:A12 содержатся числовые значения в текстовом формате , то они будут проигнорированы.
Для настройки границ интервала используем Проверку данных с типом данных Список . В качестве источника укажем для левой границы >;>= и для правой СЧЁТЕСЛИМН(A2:A12;C2&D2;A2:A12;E2&F2)
Источник
Моделирование числовых последовательностей и рядов
Числовые последовательности представляют собой множества чисел. Если каждому числу n из натурального ряда чисел 1,2,3, …, n…поставлено в соответствие вещественное число xn, то множество чисел x1, x2, x3, …,xn … называют числовой последовательностью. Числа x1, x2, x3, … называют, членами последовательности, xn— n-нымили общим элементом, а число n –его номером.
Таким образом, последовательность представляет собой множество пронумерованных элементов. Последовательность задана, если известен способ получения любого ее элемента. Последовательность обозначается символом n>. Например, символ <1>обозначает последовательность чисел 1, 1/2, 1/3, 1/4, …, 1/n. В общем случае для создания массива элементов последовательности нужно выполнить следующие действия:
1. Создать массив, содержащий множество чисел натурального ряда;
2. Ввести в ячейку формулу последовательности, делая в ней адресные ссылки на ячейки, содержащие номера элементов последовательности
3. Скопировать введенную формулу во все другие ячейки массива.
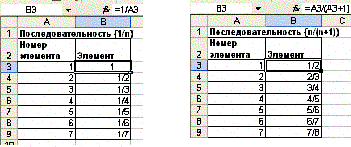
Пример создания последовательности <1>, и последовательности .
Для создания наиболее часто встречающихся последовательностей, таких как арифметическая или геометрическая прогрессия, табличный процессор имеет специальный инструмент “Прогрессия”, который находится: линейка Главная →Редактирование→Заполнить→Прогрессия.
Технология вычисления пределов числовых последовательностей
Технологию приближенного вычисления предела числовой последовательности рассмотрим на примере.Пусть требуется найти предел числовой последовательности
Технология моделирования числовых рядов
Числовым рядом называется бесконечная последовательность чисел u1, u2 , …, un…, соединенных знаком сложения
Ряд считается заданным, если известен его общий член un=f(n). Сумма n первых членов ряда называется частичной суммой ряда. Для вычисления частичной суммы ряда в электронной таблице нужно выполнить следующие шаги:
1. Вычислить n первых членов числовой последовательности
2. Вычислить сумму членов числовой последовательности
Численное вычисление пределов функций
В математике для нахождения пределов функций применяются специальные приемы, в частности такой, как разложением числителя и знаменателя на сомножители и некоторые другие. Используя электронную таблицу, можно применить следующую технологию:
Ø В ячейку рабочего листа ввести формулу, соответствующую выражению функциональной зависимости, в которой значение аргумента указывается адресной ссылкой на ячейку, которая содержит аргумент
Ø В ячейку, предназначенную для записи аргумента функции, ввести число, максимально близкое к точке, в которой вычисляется предел функции.
Пример.
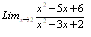
Найти предел функции
Подбор параметра
Реализация различных экономических и финансовых проектов и задач, зачастую требует решения проблемы подбора одного параметра так, чтобы другой параметр принял требуемое значение. То есть, если известен целевой показатель вычисления формулы, но не известны входные значения, позволяющие получить его, то в MSExcel используется инструмент Подбор параметра. Этот инструмент является средством решения задач анализа данных «что если», когда путем перебора одного значения достигается необходимое значение исследуемой функции (критерии оптимальности).
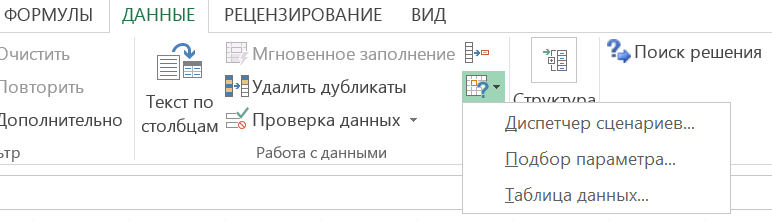
Итак, для того, чтобы определить значение, удовлетворяющее требуемому значению критерия оптимальности, необходимо вывести инструмент Подбор параметра в списке команд «Анализ «что-если»»в группе команд Работа с данными ленты ДАННЫЕ (рис.5).
Рис.5. Работа с данными (Анализ «что если»)
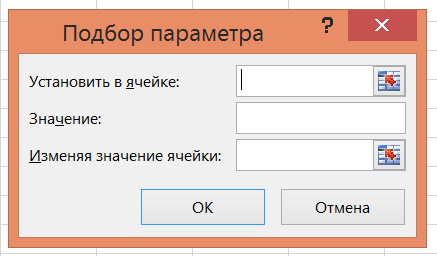
Для того, чтобы применить инструмент Подбор параметра (рис. 6) необходимо настроить соответствующие поля диалогового окна:
1. Установить в ячейке — ссылка на ячейку с исследуемой формулой;
2. Значение — планируемое значение, в виде частного экстремума;
3. Изменяя значение ячейки — ссылка на ячейку с подбираемым параметром;
4. Нажать ОК.
Рис. 6.Окно Подбор параметра
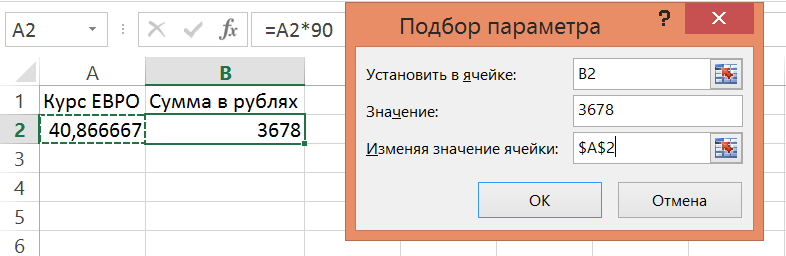
Пример 1. Требуется определить, каким должен быть курс евро, чтобы имея в наличии 3678 рублей, купить 90 евро.
Решение (уравнение для упомянутой задачи имеет вид х * 90 = 3678, где х — искомый курс доллара, для которого в MSExcel создадим модель):
1. В ячейке А2 должно быть подобрано значение курса доллара (предварительно ячейка пустая).
2. В ячейку B2 вводим формулу: =А2 * 90, предварительный итог которой 0.
3. Запустив инструментПодбор параметра, необходимо в поле Установить в ячейке указать ссылку на ячейку B2, в поле Значение ввести 3678, а в поле Изменяя значение ячейки указать ссылку на ячейку А2 (рис. 7) (ответ: 40,866667).
Рис. 7. Результат решения примера 1
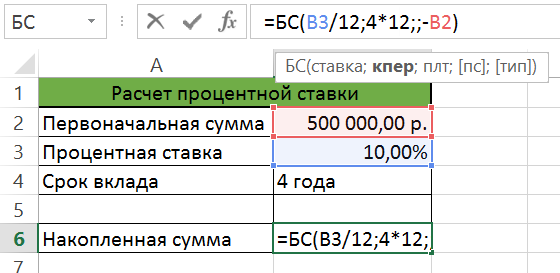
Пример 2. Определить, под какую процентную ставку необходимо сделать вклад в банк в сумме 500000 рублей, с ежемесячным начислением процентов, чтобы за 4 года накопить на счету 1000000 рублей? Модель задачи представлена на рисунке 8.
С помощью встроенной финансовой функции (БС), позволяющей вычислять будущую стоимость, определим ее значение при условных 10% (744 677,05 р.).
Рис. 8.Расчет процентной ставки
1. Установите курсор в ячейку B6, где расположена функция (формула) и запустите инструмент Подбор параметра.
2. В поле Установить в ячейке, должна быть ссылка на ячейку B6.
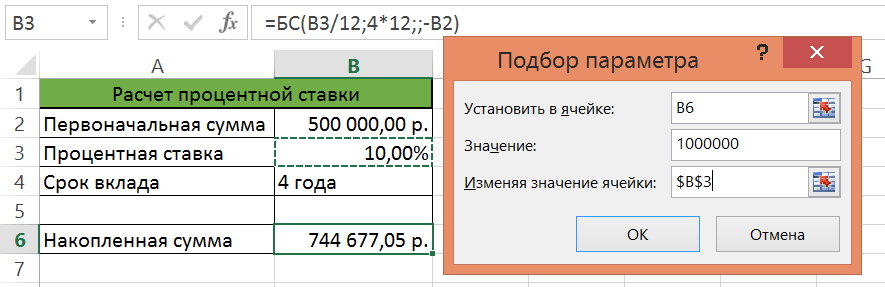
3. В поле Значение введите 1000000.
4. В поле Изменяя значение ячейки установите ссылку на ячейку В3 (рис9) (ответ: 17,45%).
Рис. 9. Подбор параметрарасчета процентной ставки
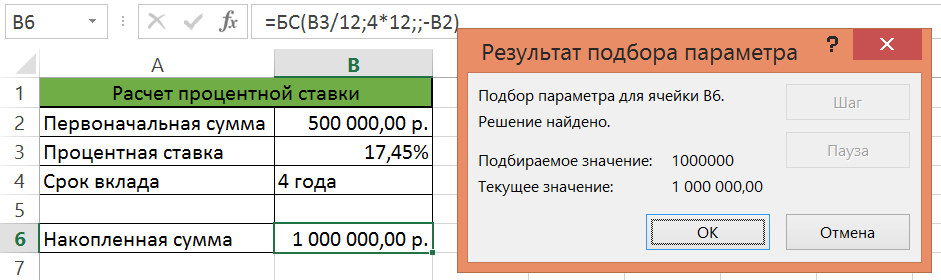
В результате получим искомое значение процентной ставки 17,45% (рис. 10).
Рис. 10.Расчет процентной ставки после подбора параметра
Итак, инструмент Подбор параметра, подбирает конкретный показатель, при котором требуемый результат достигает определенного значения.
Практический раздел
1. Математические операции в Excelс числами
2. Математические операции в Excelсо значениями в ячейках
3. Формулы в Excelвручную
4. Формулы в Excel с помощью функцийExcel
5. Вычисление значений математических функций в Excel
6. Вычисление сумм последовательностей
7. Вычисление пределов последовательностей
8. Подбор параметра под заданное значение в Excel
9. Задачи для самостоятельного решения
Указания студентам
· Выполните с 1 по 5 задания в рабочем файле, с точностью до двух знаков после запятой.
· Значения запишите в числовом и экспоненциальном форматах.
· Занесите соответствующие результаты вычислений в сводную таблицу ответов, находящуюся в конце рабочего файла.
· Номера заданий с 6 по 10 рекомендуются в качестве домашнего задания.
Задание1.Математические операции в Excel
Произвести математические операции с помощью Excel.
1. 135+243
2. 135*243
3. 135-243
4. 135/243
5.
6.
7.
8.
9.
10. -35/28,5
Задание2.
Произвести математические операции с помощью Excel, по заданным значениям
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Задание 3.Формулы в Excel
1. Задать в Excel формулу вручную и найти значение выражения при
2. Задать в Excel формулу вручную и найти значение выражения при
3. Задать в Excel формулу вручную и найти значение выражения при
4. Задать в Excel формулу вручную и найти значение выражения при
5. Задать в Excel формулу вручную и найти значение выражения при x=0.0002543
6. Задать в Excel формулу вручную и найти значение выражения при x=0.0002543
7. Задать в Excel формулу вручную и найти значение выражения при x=0.0002543
8. Задать в Excel формулу вручную и найти значение выражения при x=678
9. Задать в Excel формулу вручную и найти значение выражения при x=-15,25
10. Задать в Excel формулу вручную и найти значение выражения при x=0.00025
Задание 4.
Используя функции Excel, задать формулы для вычисления следующих выражений и вычислить их
3.При х=0,990077
5. При x=0.0002543
10. При x=2853,006
Если в результате компьютер выдает «ошибку», пояснить ее происхождение и указать как нужно изменить значение x.
Задание 5.Вычисление значений функций в Excel
Вычислите значений функции y(x)=k*f(x) для всех значений переменной х на отрезке [a;b] с шагом c при заданном k, где f(x) из задания 5
I (номер варианта)
k
a
b
с
Задание 6.
1. Найти суммудвадцати первых членов числовой последовательности
2. Найти сумму первых 9 членов числовой последовательности
3. Найти сумму 30 первых членов числовой последовательности
4. Найти сумму с 10 по 15 членов числовой последовательности
5. Найти сумму30 первых членов числовой последовательности
6. Найти сумму 30 первых членов числовой последовательности
7. Найти сумму 30 первых членов числовой последовательности
8. Найти сумму 30 первых членов числовой последовательности
9. Найти сумму 30 первых членов числовой последовательности
10. Найти сумму 30 первых членов числовой последовательности
Задание 7.
1. Найти приближенное значение предела числовой последовательности
2. Найти приближенное значение предела числовой последовательности
3. Найти приближенное значение предела числовой последовательности
4. Найти приближенное значение предела числовой последовательности
5. Найти приближенное значение предела числовой последовательности
6. Найти приближенное значение предела числовой последовательности
7. Найти приближенное значение предела числовой последовательности
8. Найти приближенное значение предела числовой последовательности
9. Найти приближенное значение предела числовой последовательности
10. Найти приближенное значение предела числовой последовательности
Пояснениезаданию 7.Предположим, что в ячейке А30 расположено значение n, которое стремится к бесконечности. В ячейке В30 вводим формулу для вычисления n–го члена. Далее в ячейке А30 запишем достаточно большое число, например, 10^100. В ячейке В30 появиться примерное значение предела.
Задание 8.Подбор параметра под заданное значение в Excel
1. Известно, что длина окружности первого круга составляет 100, а площадь второго круга составляет 1000. С помощью инструмента Подбор параметра определить во сколько раз радиус первого круга отличается от радиуса второго. Ответ дать с двумя знаками после запятой.
2. Дана формула линейной функции: y=b + ax. Известно, чтоа=10, b=20. Протабулировать функцию на интервале значений xот 1 до 10 с шагом 1. С помощью инструмента Подбор параметра, изменяя значение b определить, чему равен y в точке x=10, если в точке x=6 значение y=100.
3. Площадь первого круга составляет 1500, площадь второго круга составляет 100. С помощью инструмента Подбор параметра определить во сколько раз радиус первого круга отличается от радиуса второго.
4. Дана формула линейной функции: y=2b — ax . Известно, чтоа=25, b=10. Протабулировать функцию на интервале значений xот -3 до 5 с шагом 0,5. С помощью инструмента Подбор параметра, изменяя значение b определить, чему равен y в точке x=5,если в точке x=1 значение y=-10.
5. Найти решение уравнения 2,84x^2-14,7=0. Ответ дать с двумя знаками после запятой.
6. Найти решение уравнения x^2-11,7x+3=0. Ответ дать с двумя знаками после запятой.
7. Дана формула линейной функции: y=a – bx+3 . Известно, чтоа=10, b=20. Протабулировать функцию на интервале значений x от -2 до +2 с шагом 0,2. С помощью инструмента Подбор параметра, изменяя значение b определить, чему равен y в точке x=2, если в точке x=0,2 значение y=15.
8. Найти решение уравнения x^2-8,2x+6=0. Ответ дать с двумя знаками после запятой.
9. Известно, что площадь первого прямоугольника (a1*b1) равна 135, а площадь второго прямоугольника (a2*b2) равна 195. С помощью инструмента Подбор параметра определить во сколько раз отличается сторона а1 от стороны а2, если стороны b1 и b2 равны по 3,75. Ответ дать с двумя знаками после запятой.
10. Известно, что площадь первого прямоугольного треугольника (a1*b1/2) равна 156, а площадь второго прямоугольника (a2*b2/2) равна 185. С помощью инструмента Подбор параметра определить во сколько раз отличается сторона а1 от стороны а2, если стороны b1 и b2 равны по 4,15. Ответ дать с двумя знаками после запятой.
11. Найти корни уравнения cos(x)+sin(x)=0 на отрезке [-2,5;2,5]. В ответе записать большее значение. Построить график.
12. 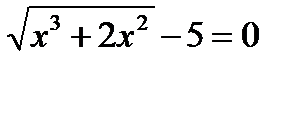
Дата добавления: 2018-04-05 ; просмотров: 6726 ; Мы поможем в написании вашей работы!
Источник
Подсчет максимального и минимального значения выполняется известными функциями МАКС и МИН. Бывает, что вычисления нужно произвести по группам или в зависимости от условия, как в СУММЕСЛИ.
Долгое время в Excel не было аналога СУММЕСЛИ или СРЗНАЧЕСЛИ для расчета максимального и минимального значения, поэтому использовали формулу массивов.
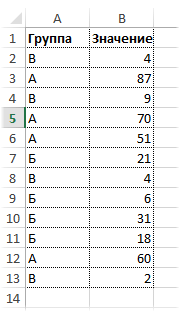
Пусть имеются данные
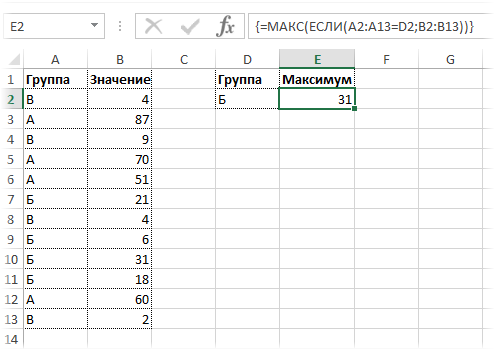
Нужно подсчитать максимальное значение в указанной группе. Название группы (критерий) введем в отдельную ячейку (D2). Пусть для начала это будет группа Б. Рядом введем следующую формулу:
=МАКС(ЕСЛИ(A2:A13=D2;B2:B13))
Это формула массивов, поэтому ввести ее нужно комбинацией Ctrl + Shift + Enter.
Теперь, меняя название группы, можно без всяких фильтров и сводных таблиц видеть максимальное значение внутри этой группы.
Как это работает? Очень просто. Первым делом нужно указать диапазон, который будет использоваться в качестве аргумента функции МАКС, то есть только те ячейки, которые соответствуют указанной группе. Так как мы заранее позаботились об удобстве использования функции, то название группы указали не внутри формулы, а в отдельной ячейке (гораздо легче менять группу). Тогда формула для нужного диапазона выглядит так.
ЕСЛИ(A2:A13=D2;B2:B13)
Указанное выражение отбирает только те значения, для которых название группы совпадает с условием в ячейке D2. Вот, как это видит Excel
На следующем этапе укажем функцию МАКС, аргументом которой выступает полученный выше массив. Excel воспринимает примерно так.
Видно, что максимальное значение внутри массива равно 31. Его и мы и увидим в ячейке с формулой. Нужно только не забыть итоговую функцию ввести комбинацией клавиш Ctrl + Shift + Enter, иначе ничего не получится. В строке формул формула массива отображается внутри фигурных скобок. Добавляются сами, специально дорисовывать не нужно.
Если функцию МАКС заменить на МИН, то по указанному условию (названию группы) будет выдаваться минимальное значение.
Функции Excel 2016 МАКСЕСЛИ (MAXIFS) и МИНЕСЛИ (MINIFS)
В MS Excel добавили новые статистические функции — МАКСЕСЛИ и МИНЕСЛИ. Обе функции имеют возможность учитывать несколько условий и некоторое время в их названиях в конце были буквы -МН. Потом убрали, хотя в скриншотах ниже используется вариант названий с -МН.
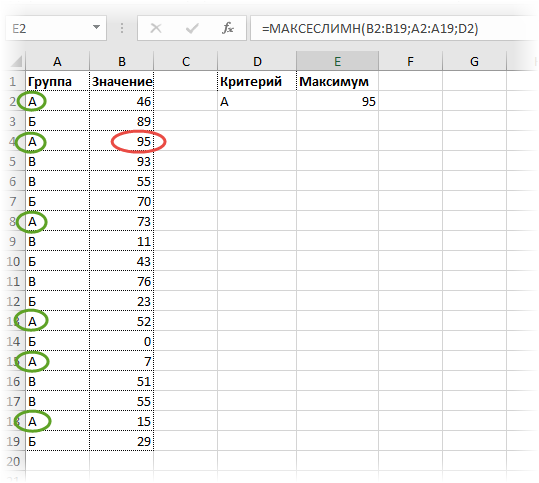
Есть ряд значений, каждое из которых входит в некоторую группу. Нужно рассчитать максимальное значение по группе А. Используем формулу МАКСЕСЛИ.
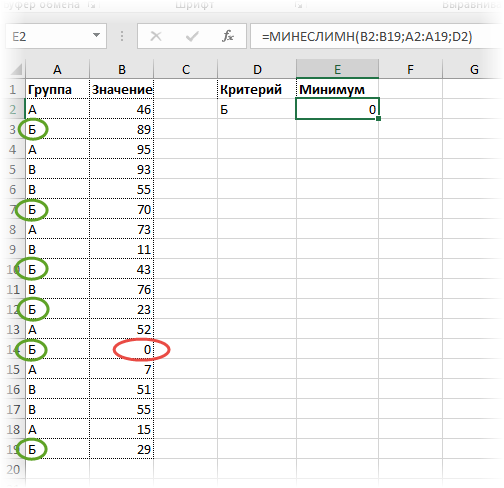
Все очень просто. Как и у СУММЕСЛИМН вначале указываем диапазон, где находится искомое максимальное значение (колонка В), затем диапазон с критериями (колонка А) и далее сам критерий (в ячейке D2). Можно указать сразу несколько условий. Таким же способом легко рассчитать минимальное значение по условию. Найдем, к примеру, минимум внутри группы Б.
Ниже показан
ролик, как рассчитать максимальное и минимальное значение по условию.
Поделиться в социальных сетях: