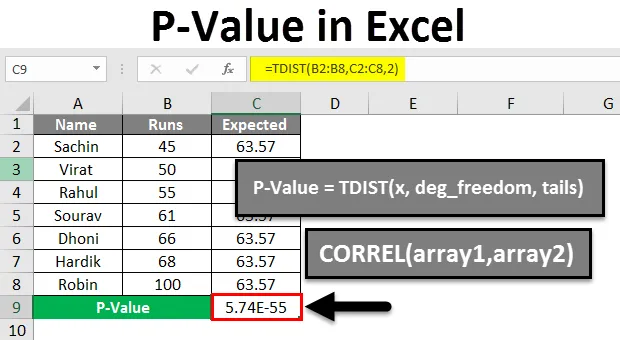
Excel’s primary function is running calculations for you and analyzing data sets in many different ways. One of the most useful tools is calculating a p-value, or a probability value.
Jump To:
- How to find the p-value in Excel
- Method 1. Find the p-value using T-Test
- Method 2. Find the p-value using Data Analysis
- Things you may want to know about the p-value
Probability is a key concept in statistical hypothesis testing and may help you in many projects. Finances, physics, economics, and other fields all benefit from calculating p-values, and Microsoft’s software makes it easy to do just that. Forget complex calculations and let Excel handle the math.
In this article, you can learn how to calculate probability values or p-values in different versions of Excel.
How to find the p-value in Excel
There are currently 2 ways of finding the probability value in Excel: the T-Test function and the Data Analysis tool. We’ve set up an example below for both approaches. We recommend you try the one more suitable for your project and skill level.
Disclaimer: For this article, we’ll be using the most recent Microsoft Excel 2019. Some steps may be different in earlier or later versions of the software.
Let’s get right into it.
Method 1. Find the p-value using T-Test
The guide below gives step-by-step instructions for using the T-Test function in order to calculate the p-value.
- Open the Excel document you want to work with or create a new one. Make sure there’s already data in the workbook before you proceed.
- Select any cell outside of your data set. Input the following formula: =T.Test(
- Type in the first argument. In our example, this would be the entire Before (kg) column. The formula should change accordingly, automatically inputting the cells.
- Next, type a comma (,) and select the second argument. In the example we set up, this would be the After (kg) column, further completing the function.
- Type another comma (,) after the second argument. Here, double-click on the One-tailed distribution from the options.
- Type another comma (,) and double-click on Paired.
- Now, all elements the function needs have been selected. Use the ) symbol to close the bracket, and then press Enter.
- The selected cell will display the p-value immediately.
So, what does this mean? In this example, the p-value is low. This means that the research can safely conclude that the test didn’t result in significant weight-loss. This doesn’t mean the null hypothesis is correct, only that it hasn’t been disproven.
Method 2. Find the p-value using Data Analysis
The Data Analysis tool allows you to play with your data in a number of different ways. This includes finding the p-value of your data set. Follow the instructions below to learn how.
To keep things simple, we’ll be using the same data set as in the previous method.
- Open the Excel document you want to work with or create a new one. Make sure there’s already data in the workbook before you proceed.
- Switch to the Data tab in the ribbon header interface, and then click on Data Analysis from the Analysis group.
- If you don’t have this option, navigate to File → Options → Add-ins and click on the Go button. Select Analysis ToolPak and click OK. The option should appear on your ribbon now.
- In the pop-up window, scroll down and select t-Test: Paired Two Sample for Means, and then click OK.
- Enter your arguments. Make sure to place a “$” symbol before each digit, excluding the “:” symbol between two cells. Your setup should look similar to this example:
- You should leave the Alpha text box on the default value. If you changed it, change it back to 0.05.
- Select the Output Range option and type the cell you want to use in the field. For example, if you want to use the A9 cell to display the p-value, type in $A$9.
- The final table will contain a number of calculations, and the p-value result. You can use this table to get interesting facts about your data.
Things you may want to know about the p-value
Calculating and finding p-values is a complex process. Probability is one of the hardest fields to tackle, even for experienced and educated individuals. Here are some things to note when working with p-values in Excel:
- The data in your table is important if the p-value is 0.05 (5 percent). However, the data you have is more relevant if it is less than 0.05 (5%).
- If the p-value is more than 0.1 (10%), the data in your table is insignificant.
- You may change the alpha value to a different number; however, most people tend to fluctuate between 0.05 (5%) and 0.10 (10%).
- Choose two-tailed testing instead of one-tailed testing if it’s better for your hypothesis.
- P-values can’t identify data variables. If a correlation is identified, the p-value calculation isn’t able to detect the cause(s) behind it.
Final thoughts
If you need any further help with Excel, don’t hesitate to reach out to our customer service team, available 24/7 to assist you. Return to us for more informative articles all related to productivity and modern-day technology!
Would you like to receive promotions, deals, and discounts to get our products for the best price? Don’t forget to subscribe to our newsletter by entering your email address below! Receive the latest technology news in your inbox and be the first to read our tips to become more productive.
You may also like
» What is Flash Fill in Excel? How do I use it?
» Excel for mac
» How to Calculate Break-Even Analysis in Excel
- P-значение в Excel
Excel P-Value (Содержание)
- P-значение в Excel
- Как рассчитать P-значение в Excel?
P-значение в Excel
- P-значения в Excel можно назвать значениями вероятности, они используются для понимания статической значимости результатов.
- Значение P используется для проверки правильности нулевой гипотезы. Если нулевая гипотеза считается неправдоподобной согласно P-значению, то это приводит нас к мысли, что альтернативная гипотеза может быть верной. По сути, это позволяет нам выяснить, были ли предоставленные результаты случайными или они демонстрируют, что мы тестируем две несвязанные вещи. Таким образом, P-Value — это следователь, а не судья.
- P-значение — это число от 0 до 1, но о них проще думать в процентах (т. Е. Для Pvalue 0, 05 — 5%. Меньшее Pvalue приводит к отклонению нулевой гипотезы).
- Поиск P-значения для корреляции в Excel — это относительно простой процесс, но для этой задачи не существует ни одной функции, мы также увидим пример для этой же задачи.
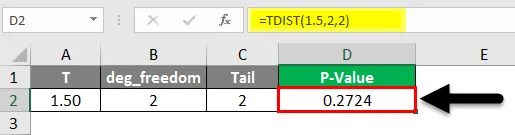
- Формула для вычисления P-значения: TDIST (x, deg_freedom, tails)
Нулевая гипотеза:
- Когда мы сравниваем две вещи друг с другом, то нулевая гипотеза — это предположение, что между двумя вещами нет никакой связи.
- Прежде чем сравнивать две вещи друг с другом, мы должны доказать, что существует какая-то связь между этими двумя.
- Когда значение P отвергает нулевую гипотезу, мы можем сказать, что оно имеет хорошие шансы на то, что обе вещи, которые мы сравниваем, имеют некоторую связь друг с другом.
Как рассчитать P-значение в Excel?
Давайте разберемся, как рассчитать P-Value в Excel, используя несколько примеров.
Вы можете скачать этот шаблон Excel P-Value здесь — Шаблон Excel P-Value
P-значение в Excel — пример № 1
В этом примере мы рассчитаем P-значение в Excel для заданных данных.
- Что касается скриншота, мы можем видеть ниже, мы собрали данные некоторых игроков в крикет против прогонов, которые они сделали в определенной серии.
- Теперь, для этого нам нужен еще один хвост, мы должны получить ожидаемые пробеги, которые должен был забить каждый игрок с битой.
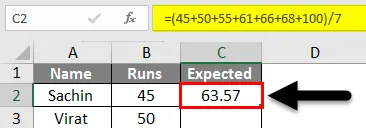
- Для столбца ожидаемых пробегов мы найдем средние пробеги для каждого игрока, разделив нашу сумму подсчетов на сумму пробегов следующим образом.
- Здесь мы нашли ожидаемое значение, разделив нашу сумму отсчетов на сумму прогонов. В основном средний и в нашем случае это 63, 57 .
- Как видно из таблицы, мы добавили столбец для ожидаемых прогонов, перетащив формулу, использованную в ячейке C3.
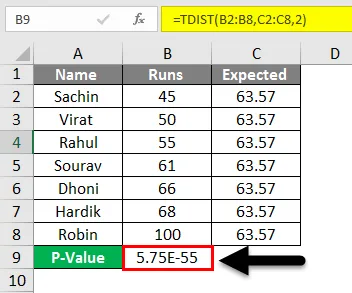
Теперь, чтобы найти P-значение для этого конкретного выражения, формулой для этого является TDIST (x, deg_freedom, tails).
Так вот,
- х = диапазон наших данных, которые запускаются
- deg_freedom = диапазон данных наших ожидаемых значений.
- tails = 2, так как мы хотим получить ответ для двух хвостов.
- На изображении выше мы видим, что полученные результаты составляют почти 0.
- Таким образом, для этого примера мы можем сказать, что у нас есть веские доказательства в пользу нулевой гипотезы.
P-значение в Excel — пример № 2
- Здесь для давайте предположим некоторые значения, чтобы определить поддержку против квалификации доказательств.
- Для нашей формулы = TDIST (x, deg_freedom, tails).
- Здесь, если мы возьмем x = t (тестовая статистика), deg_freedom = n, tail = 1 или 2.
- Здесь, как мы можем видеть результаты, если мы видим в процентах, это 27, 2%.
Точно так же вы можете найти P-значения для этого метода, когда предоставляются значения x, n и tails.
P-значение в Excel — пример № 3
Здесь мы увидим, как рассчитать P-значение в Excel для корреляции.
- В то время как в Excel нет формулы, которая дает прямое значение P-значения, связанного с корреляцией.
- Таким образом, мы должны получить P-значение из корреляции, корреляция — это r для P-значения, как мы уже обсуждали ранее, чтобы найти P-Valuepvalue, которое мы должны найти после получения корреляции для заданных значений.
- Чтобы найти корреляцию, формула является CORREL (массив1, массив2)
- Из уравнения корреляции мы найдем тестовую статистику r. Мы можем найти т для P-значения.
- Чтобы вывести t из r, формула t = (r * sqrt (n-2)) / (sqrt (1-r 2)
- Теперь предположим, что n (№ наблюдения) равно 10 и r = 0, 5
- На изображении выше мы нашли t = 1.6329…
- Теперь, чтобы оценить значение значимости, связанное с t, просто используйте функцию TDIST.
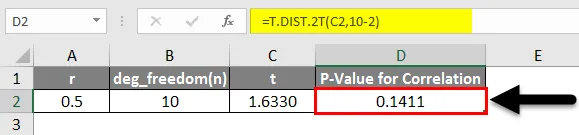
= t.dist.2t (т, степень_свободы)
- Таким образом, P-значение, которое мы нашли для данной корреляции, составляет 0, 1411.
- С помощью этого метода мы можем найти P-значение из корреляции, но после нахождения корреляции мы должны найти t и затем после того, как мы сможем найти P-значение.
A / B тестирование:
- A / B-тестирование — это скорее обычный пример, чем превосходный пример P-Value.
- Здесь мы рассмотрим пример запуска продукта, организованного телекоммуникационной компанией:
- Мы собираемся классифицировать данные или привлекать людей с историческими данными и данными наблюдений. Исторические данные в смысле ожидаемых людей согласно прошлым событиям запуска.
Тест: 1 Ожидаемые данные :
Всего посетителей: 5000
Помолвлено: 4500
Слева: 500
Тест: 2 Наблюдаемые данные :
Всего посетителей: 7000
Занято: 6000
Слева: 1000
- Теперь, чтобы найти х 2, мы должны использовать формулу хи-квадрат, в математическом отношении ее сложение (наблюдаемые данные — ожидаемые) 2 / ожидаемые
- Для наших наблюдений его х 2 = 1000
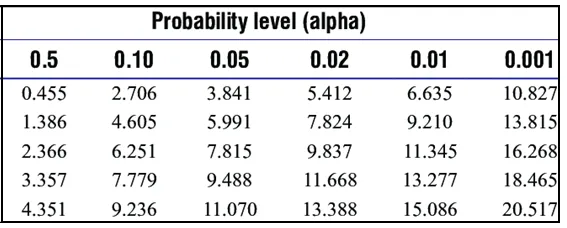
- Теперь, если мы проверим наш результат с помощью диаграммы хи-квадрат и просто пробежимся, наш счет хи-квадрат 1000 со степенью свободы 1.
- В соответствии с приведенной выше таблицей хи-квадрат, и идея в том, что мы будем двигаться слева направо, пока не найдем счет, соответствующий нашим оценкам. Наше приблизительное значение P — это значение P в верхней части таблицы, выровненное по столбцу.
- Для нашего теста оценка очень высока, чем самое высокое значение в данной таблице 10, 827. Таким образом, мы можем предположить, что значение P для нашего теста составляет не менее 0, 001.
- Если мы проведем наш счет через GraphPad, мы увидим, что его значение составляет менее 0, 00001.
Что нужно помнить о P-Value в Excel
- P-Value включает в себя измерение, сравнение, тестирование всего, что составляет исследование.
- P-значения — это далеко не все исследования, они только помогают вам понять вероятность того, что ваши результаты окажутся случайными и измененными условиями.
- Это на самом деле не говорит вам о причинах, величине или для определения переменных.
Рекомендуемые статьи
Это было руководство по P-Value в Excel. Здесь мы обсудили, как рассчитать P-Value в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Как использовать SUM в Excel?
- MS Excel: СРЕДНЯЯ функция
- Лучшие примеры функции SUMIF
- Руководство к Excel БОЛЬШАЯ функция
Теория “p-values” и нулевая гипотеза может показаться сложной на первый взгляд, но понимание концепций поможет вам ориентироваться в мире статистики. К сожалению, эти термины часто неправильно используются в популярной науке, поэтому всем необходимо понимать основы.
< p>Вычисление “p-значения” модели и доказательство/опровержение нулевой гипотезы на удивление просто с MS Excel. Есть два способа сделать это. Давайте углубимся.
Нулевая гипотеза — это утверждение, также называемое позицией по умолчанию, утверждающее, что взаимосвязь между наблюдаемыми явлениями не существует. Нулевая гипотеза может также применяться к ассоциациям между двумя экспериментальными группами. В ходе исследования вы проверяете эту гипотезу и пытаетесь ее опровергнуть.
Например, вы хотите посмотреть, дает ли конкретная причудливая диета значительные результаты. Нулевая гипотеза в данном случае состоит в том, что между испытуемыми нет существенной разницы». вес до и после диеты. Альтернативная гипотеза состоит в том, что диета действительно имела значение. Альтернатива — это то, что попытаются доказать исследователи.
“p-значение” представляет вероятность того, что статистическая сводка будет равна или больше наблюдаемого значения, когда нулевая гипотеза верна для конкретной статистической модели. Хотя “p-значение” часто выражается в виде десятичного числа, обычно лучше описывать его в процентах. Например, значение “p-value” 0,1 должно быть представлено как 10%.
Низкое значение “p-значение” означает, что доказательства против нулевой гипотезы сильны. Это также означает, что ваши данные важны. С другой стороны, высокое “значение p” означает, что нет убедительных доказательств против гипотезы. Чтобы доказать, что причудливая диета работает, исследователям необходимо найти низкое “p-значение”
Статистически значимый результат — это такой результат, который маловероятен, если нулевая гипотеза верна. Уровень значимости обозначается греческой буквой “альфа” и оно должно быть больше “p-value” чтобы результат был статистически значимым.
Многие исследователи используют “p-значение” для лучшего и более глубокого понимания данных эксперимента. Некоторые известные научные области, в которых используется значение “p-value” включают социологию, уголовное правосудие, психологию, финансы и экономику.
Поиск значения p в Excel 2010
Вы можете найти “р-значение” набора данных в MS Excel с помощью теста “T-Test” или с помощью функции “Анализ данных” инструмент. Во-первых, мы рассмотрим “T-Test” функция. Вы увидите пять студентов колледжа, которые соблюдали 30-дневную диету, и сопоставимые данные об их весе до и после диеты.
ПРИМЕЧАНИЕ. В этой статье рассматриваются функции p-value для MS Excel 2010 и 2016, но шаги должны применяться ко всем версиям. Однако макет графического пользовательского интерфейса (GUI) меню и многого другого будет отличаться.
Функция T-теста
Выполните следующие действия, чтобы вычислить “p-значение” с помощью функции T-Test.
- Создайте и заполните таблицу. Наша таблица выглядит следующим образом:
- Нажмите на любую ячейку за пределами таблицы.
< img src=»/wp-content/uploads/2022/06/1ef3347516be459ba15580224cbc478d.png» /> - Тип”=T.Test(“(включите открывающую скобку) в ячейку.
- После открывающей скобки введите в первом аргументе. В этом примере это “Перед диетой” столбец. Диапазон должен быть ”B2:B6.” Пока функция выглядит так: T.Test(B2:B6.
- Далее введите второй аргумент. Программа «После диеты» столбец вместе с его результатами является вторым аргументом, и вам нужен следующий диапазон: “C2:C6.” Давайте добавим его в формулу: T.Test(B2:B6,C2:C6.
- Введите запятую после второго аргумента. Параметры одностороннего распределения и двустороннего распределения автоматически появятся в раскрывающемся меню. Продолжайте и выберите “одностороннее распределение”, дважды щелкнув по нему.< бр>
- Введите еще одну запятую. Для простоты использования полный код приведен ниже.
- Дважды щелкните значок Параметр «Пара» в следующем раскрывающемся меню.
- Теперь, когда у вас есть все необходимые элементы, вам нужно вставить закрывающую скобку. Формула для этого примера выглядит следующим образом: =T.Test(B2:B6,C2:C6,1,1)
- Нажмите “Ввод”. Теперь в ячейке отображается значение “p-value” немедленно. В нашем случае значение равно “0,133905569” или “13.3905569%.”
Более 5%, это “p-значение” не дает убедительных доказательств против нулевой гипотезы. В нашем примере исследование не доказало, что диета помогла испытуемым значительно похудеть. Результаты не обязательно означают, что нулевая гипотеза верна, а только то, что она еще не была опровергнута.
Маршрут анализа данных
«Анализ данных»; позволяет делать много интересных вещей, в том числе “p-значение” расчеты. Мы будем использовать ту же таблицу, что и в предыдущем методе, чтобы упростить процесс.
Вот как использовать “Анализ данных” инструмент.
- Поскольку у нас уже есть “вес” различия в “D” столбец, мы пропустим вычисление разницы. Для будущих таблиц используйте следующую формулу: =”Ячейка 1”-“Ячейка 2”.
- Далее нажмите “Данные” в главном меню.
- Выберите инструмент “Анализ данных”.
- Прокрутите список вниз и выберите “t-Test: два образца в паре для средних значений”
< img src=»/wp-content/uploads/2022/06/b3c8545a8ccf465a320b19b78794cf5f.png» /> - Нажмите “ОК”< br>
- Появится всплывающее окно. Это выглядит так:
- Введите первый диапазон/аргумент. В нашем примере это “$B$2:$B$6“как “B2:B6.”
- Введите второй диапазон/аргумент. В данном случае это “$C$2:$C$6“как в “C2:C6”
- Оставьте значение по умолчанию в “Alpha” текстовое поле (0,05).
- Нажмите “Вывод Диапазон” и выберите желаемый результат. Если это “A8″ введите следующее:”$A$8.”
- Нажмите <эм>“ОК”
- Excel рассчитает “p-значение” и ряд других параметров. Итоговая таблица может выглядеть так:
Как видите, односторонний “p-значение” такое же, как и в первом случае (0,133905569). Поскольку оно выше 0,05, к этой таблице применима нулевая гипотеза, а доказательства против нее слабые.
Поиск значения p в Excel 2016
Как и в предыдущих шагах, давайте рассмотрим расчет “p-Value” в Excel 2016.
- Мы будем использовать тот же пример, что и выше, поэтому создайте таблицу, если хотите продолжить.
- Теперь в ячейке “A8&rdquo ; введите следующее: =T.Test(B2:B6, C2:C6.
- Затем в ячейке A8 введите “запятую” после “C6” и выберите “Одностороннее распределение”
- Затем введите еще одну “запятую” и выберите “В паре”
- Теперь уравнение должно выглядеть следующим образом: =T.Тест(B2:B6, C2:C6,1,1).
- Наконец нажмите “Enter”, чтобы показать результат.
Результаты могут отличаться на несколько знаков после запятой в зависимости от ваших настроек и доступного места на экране. .
Что нужно знать о значении p
Вот несколько ценных советов относительно “p-value” расчеты в Excel.
- Если значение “p-value” равно 0,05 (5%), данные в вашей таблице “значительны” Если он меньше 0,05 (5%), данные являются “высокозначимыми”
- В случае “p-значения” больше 0,1 (10%), данные в вашей таблице “несущественны” Если он находится в диапазоне 0,05–0,10, у вас есть “минимально значимый” данные.
- Вы можете изменить “альфа” значение, хотя наиболее распространенными вариантами являются 0,05 (5%) и 0,10 (10%).
- В зависимости от вашей гипотезы выбор “двухстороннего тестирования” может быть лучшим выбором. В приведенном выше примере “одностороннее тестирование” означает, что мы исследуем, потеряли ли испытуемые вес после диеты, что нам и нужно было выяснить точно. Но «двухвостый» тест также будет проверять, значительно ли они прибавили в весе.
- “p-значение” не может идентифицировать переменные. Другими словами, если он находит корреляцию, он не может распознать причины, лежащие в ее основе.
p– Демистификация ценности
Каждый статистик должен знать все тонкости проверки нулевой гипотезы и знать значение “p-value” означает. Эти знания также пригодятся исследователям во многих других областях.

Многие проверки гипотез в статистике приводят к статистике z-теста. Как только мы находим эту статистику z-теста, мы обычно находим связанное с ней значение p. Если это p-значение меньше определенного альфа-уровня (например, 0,10, 0,05, 0,01), то мы отклоняем нулевую гипотезу теста и делаем вывод, что наши результаты значимы.
В этом руководстве показано несколько примеров того, как найти p-значение по z-значению в Excel с помощью функции НОРМ.РАСП , которая принимает следующие аргументы:
НОРМ.РАСП (x, среднее, стандартное_отклонение, кумулятивное)
куда:
- x — интересующая нас z-оценка.
- среднее — это среднее значение распределения — мы будем использовать «0» для стандартного нормального распределения.
- standard_dev — это стандартное отклонение распределения — мы будем использовать «1» для стандартного нормального распределения.
- cumulative принимает значение «TRUE» (возвращает CDF) или «FALSE» (возвращает PDF) — мы будем использовать «TRUE», чтобы получить значение кумулятивной функции распределения.
Давайте рассмотрим пару примеров.
Пример 1. Нахождение значения P по Z-показателю (двусторонний тест)
Компания хочет знать, отличается ли средний срок службы батареи нового типа от текущей стандартной батареи, средний срок службы которой составляет 18 часов. При случайной выборке из 100 новых батарей они обнаружили, что средний срок службы составляет 19 часов при стандартном отклонении в 4 часа.
Проведите двусторонний тест гипотезы, используя альфа-уровень 0,05, чтобы определить, отличается ли средний срок службы новой батареи от среднего срока службы текущей стандартной батареи.
Шаг 1: Сформулируйте гипотезы.
Нулевая гипотеза (H 0 ): μ = 18
Альтернативная гипотеза: (Ha): μ ≠ 18
Шаг 2: Найдите статистику z-теста.
Статистика теста z = (x-μ) / (с/√n) = (19-18) / (4/√100) = 2,5
Шаг 3: Найдите p-значение статистики z-теста с помощью Excel.
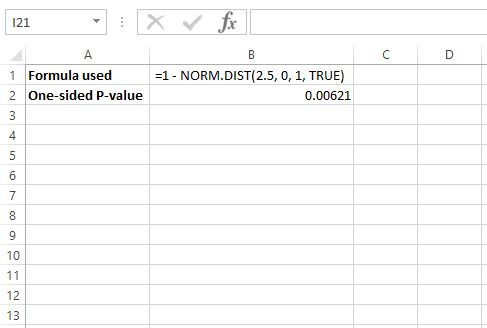
Чтобы найти значение p для z = 2,5, мы будем использовать следующую формулу в Excel: = 1 – НОРМ.РАСП(2,5, 0, 1, ИСТИНА)
Это говорит нам о том, что одностороннее p-значение равно 0,00621 , но поскольку мы проводим двусторонний тест, нам нужно умножить это значение на 2, поэтому p-значение будет 0,00612 * 2 = 0,01224 .
Шаг 4: Отклонить или не отклонить нулевую гипотезу.
Поскольку p-значение 0,01224 меньше, чем выбранный нами альфа-уровень 0,05 , мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что средний срок службы новой батареи значительно отличается от среднего срока службы текущей стандартной батареи.
Пример 2. Нахождение значения P по Z-показателю (односторонний тест)
Ботаник считает, что средняя высота определенного растения составляет менее 14 дюймов. Она случайным образом выбирает 30 растений и измеряет их. Она находит, что средний рост составляет 13,5 дюймов со стандартным отклонением 2 дюйма.
Проведите тест односторонней гипотезы, используя альфа-уровень 0,01, чтобы определить, действительно ли средняя высота этого растения меньше 14 дюймов.
Шаг 1: Сформулируйте гипотезы.
Нулевая гипотеза (H0): μ≥ 14
Альтернативная гипотеза: (Ha): μ < 14
Шаг 2: Найдите статистику z-теста.
Статистика теста z = (x-μ) / (с/√n) = (13,5-14) / (2/√30) = -1,369
Шаг 3: Найдите p-значение статистики z-теста с помощью Excel.
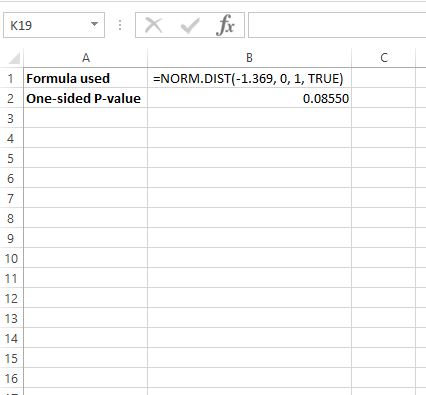
Чтобы найти значение p для z = -1,369, мы будем использовать следующую формулу в Excel: =НОРМ.РАСП(-1,369, 0, 1, ИСТИНА)
Это говорит нам о том, что одностороннее значение p равно 0,08550 .
Шаг 4: Отклонить или не отклонить нулевую гипотезу.
Поскольку p-значение 0,08550 больше, чем выбранный нами альфа-уровень 0,01 , мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что средняя высота этого определенного вида растений составляет менее 14 дюймов.
Для получения дополнительных руководств по статистике в Excel обязательно ознакомьтесь с нашим полным списком руководств по Excel .
Рассмотрим использование MS EXCEL при проверке статистических гипотез о среднем значении распределения в случае известной дисперсии. Вычислим тестовую статистику
Z
0
, рассмотрим процедуру «одновыборочный z-тест», вычислим Р-значение (Р-
value
).
Проверка гипотез
(Hypothesis testing) тесно связана с построением
доверительных интервалов
. При первом знакомстве с
процедурой проверки гипотез
рекомендуется начать с изучения
построения соответствующего доверительного интервала
.
СОВЕТ
: Для
проверки гипотез
нам потребуется знание следующих понятий:
-
дисперсия и стандартное отклонение
,
-
выборочное распределение статистики
,
-
уровень доверия/ уровень значимости
,
-
стандартное нормальное распределение
и
его квантили
.
Формулировка задачи.
Из
генеральной совокупности
имеющей
нормальное распределение
с неизвестным μ и известной
дисперсией
σ
2
взята
выборка
размера n. Необходимо проверить
статистическую гипотезу
о равенстве неизвестного μ заданному значению μ
0
(англ. Inference on the mean of a population, variance known).
Примечание
: Требование о
нормальности
исходного распределения, из которого берется
выборка
, не является строгим. Н
0
, необходимо, чтобы были выполнены условия применения
Центральной предельной теоремы
.
Статистическая гипотеза
– это некое утверждение о неизвестных параметрах распределения. Процедура проверки гипотез зависит от оцениваемого параметра распределения и условий задачи. Сначала рассмотрим общий подход при
проверке гипотез
, затем рассмотрим конкретный пример.
Обычно формулируют 2 гипотезы:
нулевую
Н
0
и
альтернативную
Н
1
. В нашем случае
нулевой гипотезой
будет равенство μ и μ
0
, а
альтернативной гипотезой
– их отличие.
Нулевая гипотеза
отвергается только в том случае, если на это достаточно оснований. В этом случае принимается
альтернативная гипотеза
.
Чтобы понять, достаточно ли у нас оснований для отклонения
нулевой гипотезы
, из распределения делают
выборка.
Сначала проведем
проверку гипотезы
, используя
доверительный интервал
, а затем с помощью вышеуказанной процедуры
z-тест
.
В конце вычислим
Р-значение
и также используем его для
проверки гипотезы
.
Итак,
нулевая гипотеза
Н
0
утверждает, что неизвестное
среднее значение
распределения μ равно μ
0
. Соответствующая
альтернативная гипотеза
Н
1
утверждает обратное: μ не равно μ
0
. Это пример
двусторонней проверки
, т.к. неизвестное значение может быть как больше, так и меньше μ
0
.
Если упрощенно, то
проверка гипотезы
заключается в сравнении 2-х величин: вычисленного на основании
выборки среднего значения
Х
ср
и заданного μ
0
. Если эти значения «отличаются больше, чем можно было бы ожидать исходя из случайности», то
нулевую гипотезу
отклоняют.
Поясним фразу «отличаются больше, чем можно было бы ожидать исходя из случайности». Для этого, вспомним, что распределение
Выборочного среднего (статистика Х
ср
)
стремится к
нормальному распределению
со
средним значением
μ и
стандартным отклонением
равным σ/√n, где σ –
стандартное отклонение распределения
, из которого берется
выборка
(не обязательно
нормальное
), а n – объем
выборки
(подробнее см.
статью про ЦПТ
). В нашем случае
стандартное отклонение
σ известно.
В задачах
проверки гипотез
также задается
уровень доверия
(вероятность), который определяет порог между утверждением «мало вероятно» и «вполне вероятно» или «может быть обусловлено случайностью» и «не может быть обусловлено случайностью». Обычно используют значения
уровня доверия
90%; 95%; 99%, реже 99,9% и т.д.
Примечание
:
Уровень доверия
равен (1-α)
,
где α –
уровень значимости
. И наоборот, α=(
1-уровень доверия
)
.
Таким образом, знание распределения
статистики
Х
ср
и заданного
уровня доверия
, позволяют нам формализовать с помощью математических выражений фразу «отличаются больше, чем можно было бы ожидать исходя из случайности». В этом нам поможет
доверительный интервал
(как строится
доверительный интервал
нам
известно из этой статьи
).
Если
среднее выборки
попадает в
доверительный интервал,
построенный относительно μ
0
, то для отклонения нулевой гипотезы оснований нет.
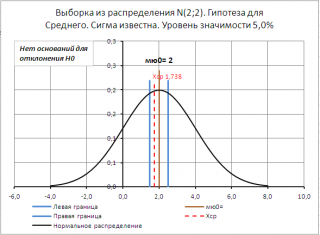
Для визуализации процедуры
проверки гипотез
в
файле примера на листе Сигма известна
создана
диаграмма
.
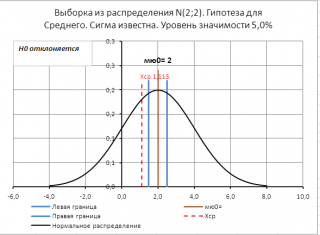
Если μ
0
не попадает в
доверительный интервал,
то нулевая гипотеза отклоняется.
Теперь рассмотрим проверку гипотез с помощью процедуры
z
-тест
.
Z-тест
Кроме
доверительного интервала
для
проверки гипотез
существует также и другой эквивалентный подход —
z
-тест:
-
На основе
выборки
вычисляюттестовую статистику
. Выбор
тестовой статистики
делают в зависимости от оцениваемого параметра распределения и условий задачи. В нашем случае
тестовой статистикой
является случайная величина z=
, где
–среднее выборки
(обозначим Х
ср
). Значение, которое приняла
z-
статистика
, обычно обозначают Z
0
;
z
-статистика
, как и любая другая случайная величина, имеет свое распределение. В процедуре
проверки гипотез
это распределение называют «
эталонным распределением
», англ. Reference distribution. В нашем случае
тестовая статистика
имеетстандартное нормальное распределение
;
-
Также исследователь устанавливает требуемый
уровень значимости
– это допустимая для данной задачи
ошибка первого рода
, т.е. вероятность отклонить
нулевую гипотезу
, когда она верна (
уровень значимости
обозначают буквой α и чаще всего выбирают равным 0,1; 0,05 или 0,01); -
С помощью
эталонного распределения
для заданного
уровня значимости
вычисляют соответствующиеквантили этого распределения
. В нашем случае, при проверке
двухсторонней гипотезы
, необходимо будет вычислить
верхний α/2-квантиль стандартного
нормального распределения,
т.е. такое значение случайной величины
z
,
что
P
(
z
>=
Z
α
/2
)=α/2
; -
И наконец, значение
тестовой статистики
Z
0
сравнивают с вычисленными на предыдущем шаге
квантилями
и делают
статистический вывод
: Имеются ли основания, чтобы отвергнуть
нулевую гипотезу
? В нашем случае проверки двусторонней гипотезы, Н
0
отвергается если: |Z
0
|>Z
α
/2
.
Примечание
: Подробнее про
квантили
распределения можно прочитать в статье
Квантили распределений MS EXCEL
.
В MS EXCEL
верхний
α
/2-квантиль стандартного нормального распределения
вычисляется по формуле
=НОРМ.СТ.ОБР(1-α/2)
Учитывая симметричность
стандартного нормального распределения
относительно оси ординат,
верхний
α
/2-квантиль
равен обычному α
/2-квантилю
со знаком минус:
=-НОРМ.СТ.ОБР(α/2)
Примечание
: Еще раз подчеркнем связь процедуры
z
-теста
с построением
доверительного интервала
. Т.к.
z
-статистика
распределена по
стандартному нормальному закону,
то можно ожидать, что 1-α значений
z
-статистики
будет попадать в интервал между -Z
α/2
и Z
α/2
. Например, для
уровня доверия
95% в интервал между -1,960 и 1,960 будет попадать примерно 95% значений Z
0
, вычисленных на основе
выборки
. Если Z
0
не попало в указанный интервал, то это считается маловероятным событием и
нулевая гипотеза
отвергается.
В случае
односторонней гипотезы
речь идет об отклонении μ только в одну сторону: либо больше либо меньше μ
0
. Если
альтернативная гипотеза
звучит как μ>μ
0
, то гипотеза Н
0
отвергается в случае Z
0
> Z
α
. Если
альтернативная гипотеза
звучит как μ<μ
0
, то гипотеза Н
0
отвергается в случае Z
0
< -Z
α
.
Вычисление Р-значения
При
проверке гипотез
большое распространение также получил еще один эквивалентный подход, основанный на вычислении
p
-значения
(p-value). Поясним его на основе
односторонней гипотезы
Н
1
: μ>μ
0
.
Напомним, что если Н
1
утверждает, что μ>μ
0
, то
односторонняя гипотеза
Н
0
отвергается в случае если Z
0
> Z
α
. Эти значения
z
-статистики
имеют размерность анализируемой случайной величины, но их трудно интерпретировать. Преобразуем неравенство Z
0
> Z
α
так, чтобы его можно было проще интерпретировать.
Напомним, что Z
α
– это положительная величина и она равна
верхнему
α
-квантилю стандартного нормального распределения
(такому значению случайной величины z, что P(z>=Z
α
)=α). Неравенство Z
0
> Z
α
означает, что если Z
0
, вычисленное на основе
выборки
, будет слишком велико, т.е. больше Z
α
, то эта ситуация считается маловероятным событием и появляется основание для отклонения
нулевой гипотезы
.
Поэтому, логично вычислить вероятность события, что
z
-статистика
примет значение z>=Z
0
и сравнить ее с вероятностью, что z=>Z
α
. Вероятность события z=>Z
α
(по определению
верхнего квантиля
) – это просто α. Вероятность события, что
z
-статистика
примет значение z>=Z
0
равна 1-Ф(Z
0
), где Ф(z) –
интегральная функция стандартного нормального распределения
.
В MS EXCEL эта функция вычисляется по формуле
=1-НОРМ.СТ.РАСП(Z
0
;ИСТИНА)
Примечание
: В MS EXCEL для вычисления
p-значения
имеется специальная функция
Z.TEСT()
, которая эквивалентна выражению
=1-НОРМ.СТ.РАСП(Z
0
;ИСТИНА)
.
Про функцию
Z.TEСT()
см.
ниже
.
Таким образом, неравенство Z
0
> Z
α
эквивалентно неравенству P(z>= Z
0
)<α или в других обозначениях 1-Ф(Z
0
)<α. Величина 1-Ф(Z
0
) называется
p
-значением.
СОВЕТ
: Лучше понять вышесказанное помогут графики
функции стандартного нормального распределения
из статьи
Квантили распределений MS EXCEL
.
Теперь, если
p-значение
меньше чем заданный
уровень значимости α
, то
нулевая гипотеза
отвергается и принимается
альтернативная гипотеза
. И наоборот, если
p-значение
больше α, то
нулевая гипотеза
не отвергается. Другими словами, если
p-значение
меньше
уровня значимости
α, то это свидетельство того, что значение
z
-статистики
, вычисленное на основе
выборки
при условии истинности
нулевой гипотезы
, приняло маловероятное значение Z
0
.
Для другой односторонней гипотезы (μ<μ
0
)
p-значение
вычисляется как Ф(Z
0
) или
=НОРМ.СТ.РАСП(Z
0
;ИСТИНА)
. Соответственно,
p-значение
для односторонней гипотезы μ<μ
0
вычисляется по формуле
=1-Z.TEСT(
выборка
; μ
0
; σ)
, где
выборка
– ссылка на диапазон, содержащий значения
выборки
.
В случае двусторонней гипотезы,
p
-значение
вычисляется по формуле =2*(1-Ф(|Z
0
|)).
В качестве примера проверим гипотезу Н
0
: μ=μ
0
, при этом
альтернативная
односторонняя гипотеза
Н
1
: μ<μ
0
. Известно, что
среднее выборки
размера 60 равно 1,851;
стандартное отклонение
=2; μ
0
=2,3;
уровень значимости
равен 0,05. Решение:
Z
0
=(1,851-2,3)/(2/КОРЕНЬ(60))=-1,739
p-значение
=НОРМ.СТ.РАСП(-1,739;ИСТИНА)=0,04
Нулевая гипотеза
отклоняется, т.к. 0,04<0,05.
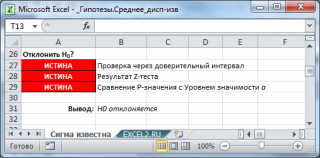
Эквивалентность этих трех подходов для проверки гипотез (
проверка через доверительный интервал
,
z
-тест
и
p-значение
) продемонстрирована в
файле примера
: во всех случаях, когда
z-тест
дает заключение о необходимости отклонить
нулевую гипотезу
, Х
ср
не попадает в соответствующий
доверительный интервал,
а
p
-значение
меньше уровня значимости.
Функция
Z.ТЕСТ()
MS EXCEL для процедуры
z-тест
существует специальная функция
Z.ТЕСТ()
, которая на самом деле вычисляет
p-значение
в случае
односторонней альтернативной гипотезы μ
>μ
0
:
=Z.TEСT(
выборка
; μ
0
; σ)
, где
выборка
– ссылка на диапазон, содержащий n значений
выборки, σ
– известное
стандартное отклонение
распределения, из которого делается
выборка
.
Функция
Z.ТЕСТ()
эквивалентна формуле
=1- НОРМ.СТ.РАСП((СРЗНАЧ(
выборка
)- μ
0
) / (σ/√n);ИСТИНА)
Выражение
(СРЗНАЧ(
выборка
)- μ
0
) / (σ/√n)
– это значение
тестовой статистики
, т.е. Z
0
.
Эту же функцию можно использовать для вычисления
p
-значения
в случае проверки
двусторонней гипотезы
, записав формулу:
=2 * МИН(Z.TEСT(
выборка
; μ
0
; σ); 1 — Z.TEСT(
выборка
; μ
0
; σ)
Для вычисления
p
-значения
в случае
односторонней альтернативной гипотезы μ
<μ
0
используйте формулу:
=1-Z.TEСT(
выборка
; μ
0
; σ)
σ — третий аргумент функции
Z.ТЕСТ()
должен быть всегда указан, т.к. это соответствует вышерассмотренной процедуре
z-теста
.