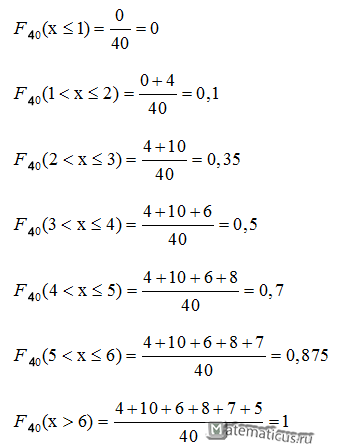Рассмотренные в лабораторной работе 2 распределения вероятностей СВ
опираются на знание закона распределения СВ. Для практических задач такое
знание – редкость. Здесь закон распределения обычно неизвестен, или известен с
точностью до некоторых неизвестных параметров. В частности, невозможно
рассчитать точное значение соответствующих вероятностей, так как нельзя
определить количество общих и благоприятных исходов. Поэтому вводится статистическое
определение вероятности. По этому определению вероятность равна отношению
числа испытаний, в которых событие произошло, к общему числу произведенных
испытаний. Такая вероятность называется статистической частотой.
Связь
между эмпирической функцией распределения и функцией распределения
(теоретической функцией распределения) такая же, как связь между частотой события
и его вероятностью.
Для
построения выборочной функции распределения весь диапазон изменения случайной
величины X (выборки)
разбивают на ряд интервалов (карманов) одинаковой ширины. Число интервалов
обычно выбирают не менее 3 и не более 15. Затем определяют число значений
случайной величины X, попавших
в каждый интервал (абсолютная частота, частота интервалов).
Частота интервалов – число, показывающее сколько раз значения,
относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти
числа на общее количество наблюдений (n), находят относительную частоту (частость) попадания
случайной величины X в заданные
интервалы.
По
найденным относительным частотам строят гистограммы выборочных функций
распределения. Гистограмма распределения частот – это графическое
представление выборки, где по оси абсцисс (ОХ) отложены величины интервалов, а
по оси ординат (ОУ) – величины частот, попадающих в данный классовый интервал.
При увеличении до бесконечности размера выборки выборочные функции
распределения превращаются в теоретические: гистограмма превращается в график
плотности распределения.
Накопленная частота интервалов – это число, полученное
последовательным суммированием частот в направлении от первого интервала к
последнему, до того интервала
включительно, для которого определяется накопленная частота.
В Excel для построения выборочных функций распределения
используются специальная функция ЧАСТОТА
и процедура Гистограмма из пакета анализа.
Функция ЧАСТОТА (массив_данных,
двоичный_массив) вычисляет частоты появления случайной величины в интервалах
значений и выводит их как массив цифр, где
•
массив_данных
— это массив или ссылка на
множество данных, для которых
вычисляются частоты;
•
двоичный_массив
— это массив интервалов, по
которым группируются значения выборки.
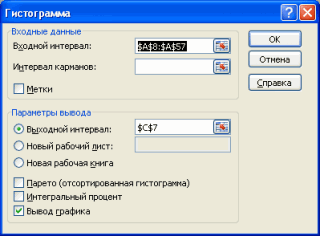
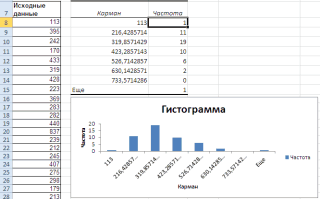
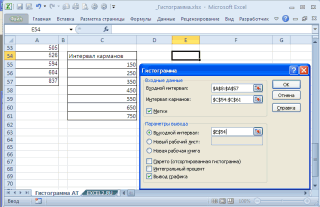
Процедура
Гистограмма из Пакета анализа выводит
результаты выборочного распределения в виде таблицы и графика. Параметры диалогового окна Гистограмма:
•
Входной диапазон — диапазон исследуемых данных
(выборка);
•
Интервал карманов — диапазон ячеек или набор граничных
значений, определяющих выбранные интервалы (карманы). Эти значения должны быть
введены в возрастающем порядке. Если
диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и
максимальным значениями данных, будет создан
автоматически.
•
выходной диапазон предназначен для ввода ссылки на левую верхнюю ячейку выходного диапазона.
•
переключатель
Интегральный процент позволяет установить режим включения в
гистограмму графика интегральных
процентов.
•
переключатель
Вывод графика позволяет установить режим автоматического создания встроенной диаграммы на листе, содержащем
выходной диапазон.
Пример 1. Построить эмпирическое распределение веса
студентов в килограммах для следующей
выборки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.
Решение
1. В ячейку А1 введите слово Наблюдения,
а в диапазон А2:А21 — значения веса
студентов (см. рис. 1).
2.
В
ячейку В1 введите названия интервалов Вес, кг. В диапазон В2:В8 введите
граничные значения интервалов (40, 45,
50, 55, 60, 65, 70).
3.
Введите
заголовки создаваемой таблицы: в ячейки С1 — Абсолютные частоты, в ячейки D1 — Относительные
частоты, в ячейки E1 — Накопленные частоты.(см. рис. 1).
4.
С
помощью функции Частота заполните столбец абсолютных частот, для этого
выделите блок ячеек С2:С8. С
панели инструментов Стандартная
вызовите Мастер функций (кнопка fx). В появившемся диалоговом окне
выберите категорию Статистические и функцию
ЧАСТОТА, после чего нажмите кнопку ОК. Указателем мыши в рабочее поле Массив_данных
введите диапазон данных наблюдений (А2:А8). В рабочее поле Двоичный_массив
мышью введите диапазон интервалов (В2:В8). Слева на клавиатуре последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце C должен появиться массив абсолютных частот (см. рис.1).
5.
В
ячейке C9 найдите общее количество
наблюдений. Активизируйте ячейку С9, на
панели инструментов Стандартная нажмите кнопку Автосумма.
Убедитесь, что диапазон суммирования указан правильно и нажмите клавишу Enter.
6.
Заполните столбец относительных частот. В ячейку введите формулу
для вычисления относительной частоты: =C2/$C$9.
Нажмите клавишу Enter. Протягиванием (за правый
нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон и получите массив относительных частот.
7.
Заполните
столбец накопленных частот. В ячейку D2 скопируйте значение относительной
частоты из ячейки E2. В ячейку D3 введите формулу: =E2+D3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу
в диапазон D3:D8. Получим массив накопленных
частот.
Рис. 1. Результат вычислений из
примера 1
8.
Постройте диаграмму относительных и накопленных частот. Щелчком указателя
мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите закладку Нестандартные
и тип диаграммы График/гистограмма. После
редактирования диаграмма будет иметь такой вид, как на рис. 2.
Рис. 2
Диаграмма относительных и накопленных частот из примера 1
Задания для самостоятельной работы
1. Для данных из примера 1 построить выборочные функции распределения, воспользовавшись процедурой Гистограмма из пакета Анализа.
2. Построить выборочные функции распределения
(относительные и накопленные частоты) для роста
в см. 20 студентов: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181,
183, 172, 176.
3. Найдите распределение по абсолютным частотам для
следующих результатов тестирования в
баллах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (используйте границы интервалов 70, 80, 90).
4. Рассмотрим любой из критериев оценки качеств педагога-профессионала,
например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос
анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку
такого измерения, необходимо увеличить число возможных ответов на конкретный
критериальный вопрос. В табл. 1 представлены возможные варианты ответов.
Обозначим
этот параметр через х. Тогда в процессе ответа на вопрос величина х
примет дискретное значение х, принадлежащее определенному интервалу значений.
Поставим в соответствие каждому из ответов определенное числовое значение
параметра х (см. табл. 1).
Табл. 1 Критериальный вопрос: успешное решение задач обучения и воспитания
|
№ п/п |
Варианты ответов |
Х |
|
1 |
Абсолютно неуспешно |
0,1 |
|
2 |
Неуспешно |
0,2 |
|
3 |
Успешно в очень |
0,3 |
|
4 |
В определенной |
0,4 |
|
5 |
В среднем успешно, |
0,5 |
|
6 |
Успешно с |
0,6 |
|
7 |
Успешно, но |
0,7 |
|
8 |
Достаточно успешно |
0,8 |
|
9 |
Очень успешно |
0,9 |
|
10 |
Абсолютно успешно |
1 |
При проведении анкетирования в каждой отдельной
анкете параметр х принимает случайное значение, но только в пределах числового
интервала от 0,1 до 1.
Тогда в результате измерений мы получаем
неранжированный ряд случайных значений (см. табл. 2).
Таблица 2.
Результаты опроса ста учителей
Сгруппируйте полученную выборку, рассчитайте среднее
значение выборки, стандартное отклонение, абсолютную и относительную частоту
появления параметра, а также постройте график плотности вероятности f(x)=
где
W(x) – относительная частота наступления события;
— стандартное
отклонение;
=3,14.
Постройте график функции f(x) и сравните его с
нормальным распределением Гаусса.
Решение математических задач
средствами Excel: Практикум/ В.Я. Гельман. – СПб.: Питер, 2003 — с. 168-172
Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
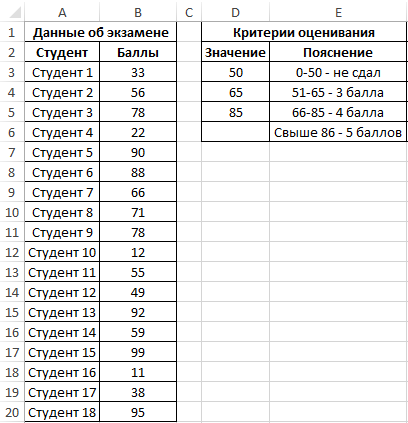
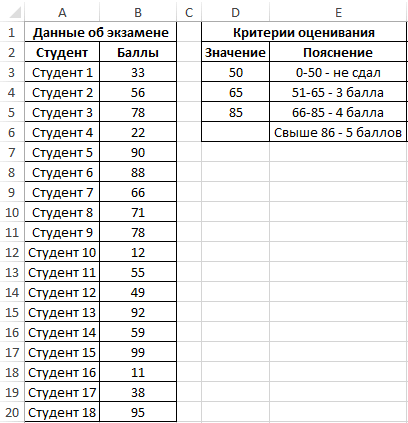
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
- От 0 до 50 баллов – экзамен не сдан.
- От 51 до 65 баллов – оценка 3.
- От 66 до 85 баллов – оценка 4.
- Свыше 86 баллов – оценка 5.
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:
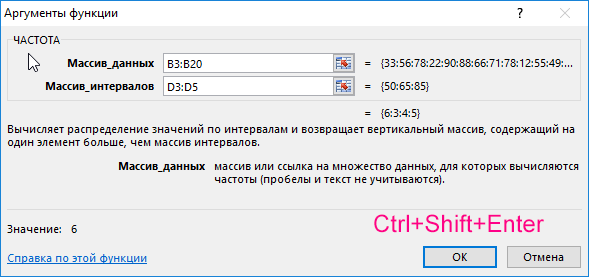
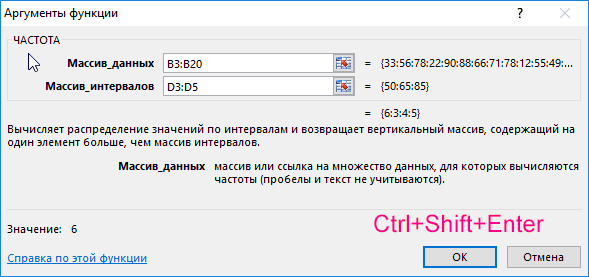
Для решения выделим области из 4 ячеек и введем следующую функцию:
Описание аргументов:
- B3:B20 – массив данных об оценках студентов;
- D3:D5 – массив критериев нахождения частоты вхождений в массиве данных об оценках.
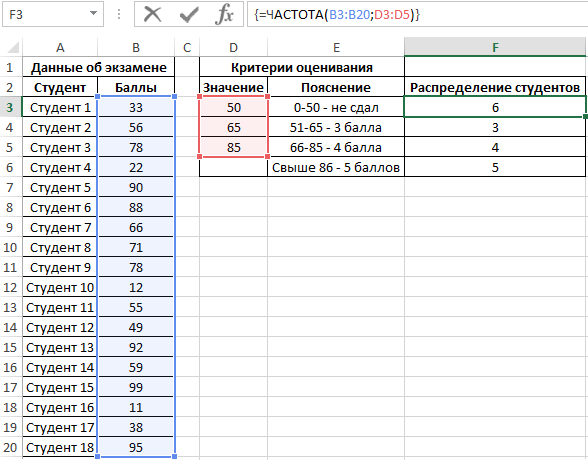
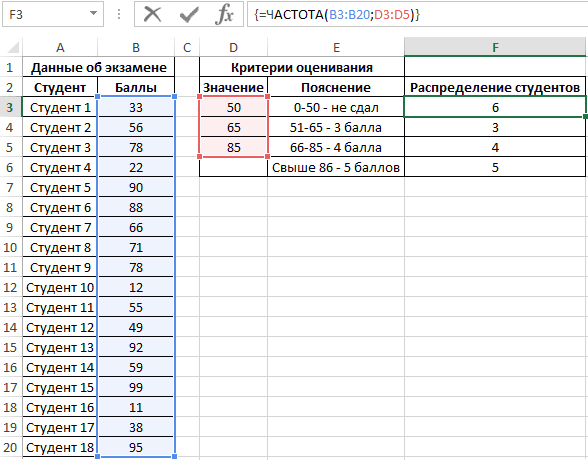
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки {} в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
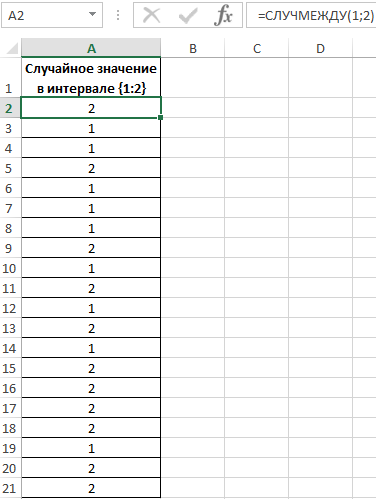
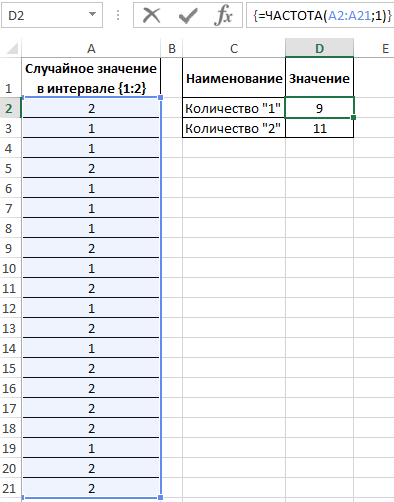
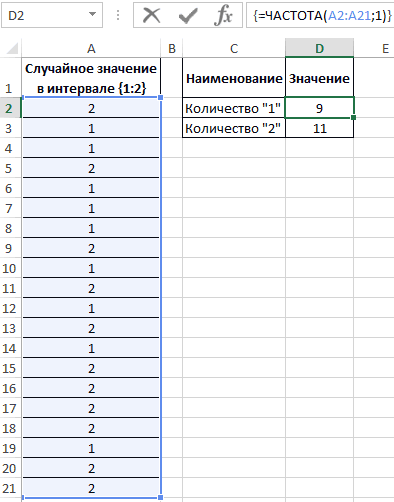
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:
Для определения случайных значений в исходной таблице была использована специальная функция:
=СЛУЧМЕЖДУ(1;2)
Для определения количества сгенерированных 1 и 2 используем функцию:
=ЧАСТОТА(A2:A21;1)
Описание аргументов:
- A2:A21 – массив сгенерированных функцией =СЛУЧМЕЖДУ(1;2) значений;
- 1 – критерий поиска (функция ЧАСТОТА ищет значения от 0 до 1 включительно и значения >1).
В результате получим:
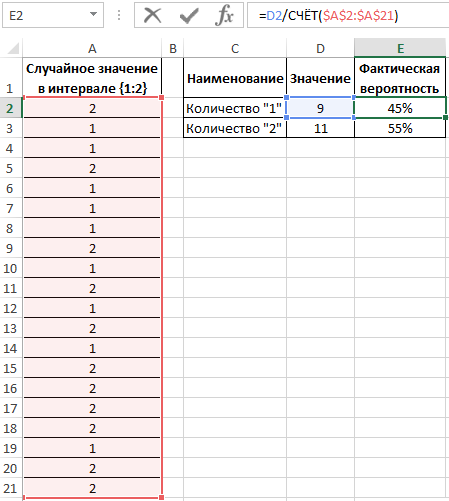
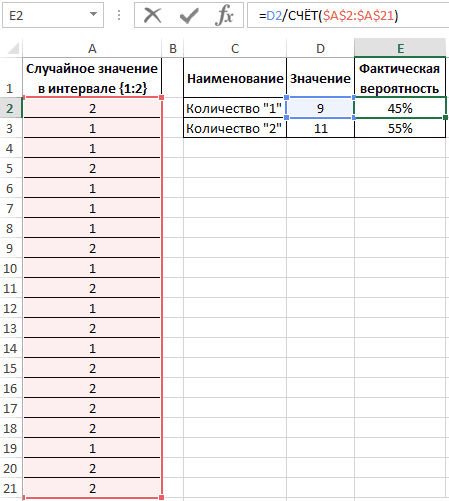
Вычислим вероятности, разделив количество событий каждого типа на общее их число:
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
Вероятности выпадения «1» и «2» — 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.
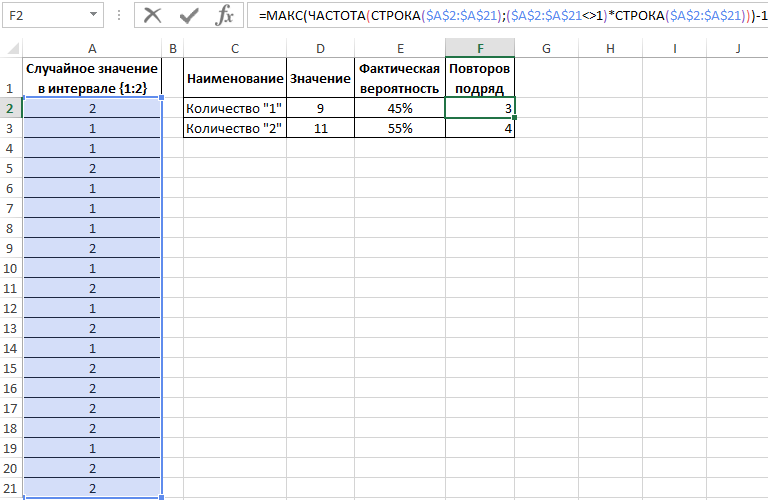
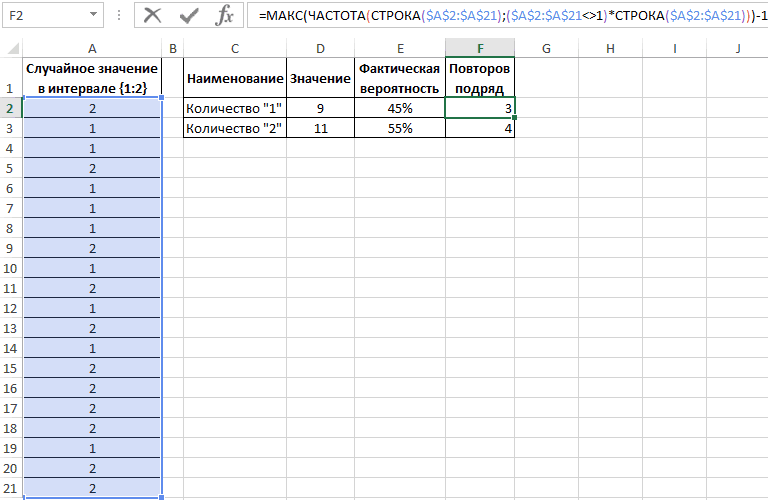
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:
Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
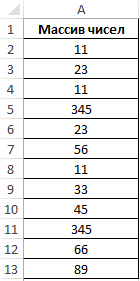
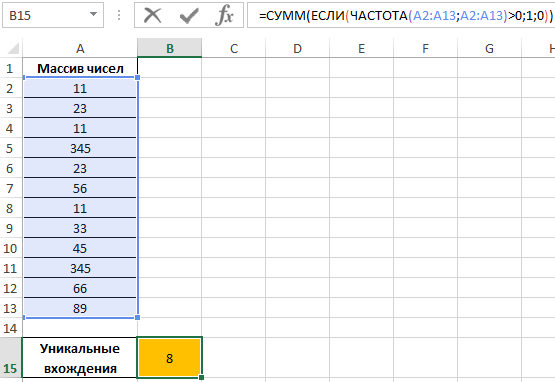
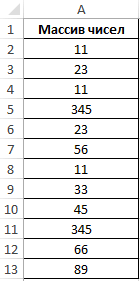
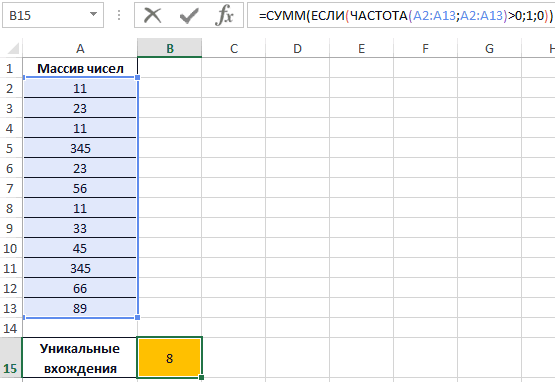
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
Исходная таблица:
Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
- Если искомый элемент содержится в диапазоне значений, вместо фактического количества вхождений будет возвращено 1;
- Если искомого элемента нет – будет возвращен 0 (нуль).
Полученное значение (количество единиц) суммируется.
В результате получим:
То есть, в указанном массиве содержится 8 уникальных значений.
Скачать пример функции ЧАСТОТА в Excel
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
- массив_данных – данные в форме массива либо ссылка на диапазон значений, для которых необходимо определить частоты.
- массив_интервалов — данные в формате массива либо ссылка не множество значений, в которые группируются значения первого аргумента данной функции.
Примечания 1:
- Если в качестве аргумента массив_интервалов был передан пустой массив или ссылка на диапазон пустых значений, результатом выполнения функции ЧАСТОТА будет являться число элементов, входящих диапазон данных, которые были переданы в качестве первого аргумента.
- При использовании функции ЧАСТОТА в качестве обычной функции Excel будет возвращено единственное значение, соответствующее первому вхождению в массив_интервалов (то есть, первому критерию поиска частоты вхождения).
- Массив возвращаемых данной функцией элементов содержит на один элемент больше, чем количество элементов, содержащихся в массив_интервалов. Это происходит потому, что функция ЧАСТОТА вычисляет также количество вхождений величин, значения которых превышают верхнюю границу интервалов. Например, в наборе данных 2,7, 10, 13, 18, 4, 33, 26 необходимо найти количество вхождений величин из диапазонов от 1 до 10, от 11 до 20, от 21 до 30 и более 30. Массив интервалов должен содержать только их граничные значения, то есть 10, 20 и 30. Функция может быть записана в следующем виде: =ЧАСТОТА({2;7;10;13;18;4;33;26};{10;20;30}), а результатом ее выполнения будет столбец из четырех ячеек, которые содержат следующие значения: 4,2, 1, 1. Последнее значение соответствует количеству вхождений чисел > 30 в массив_данных. Такое число действительно является единственным – это 33.
- Если в состав массив_данных входят ячейки, содержащие пустые значения или текст, они будут пропущены функцией ЧАСТОТА в процессе вычислений.
Примечания 2:
- Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.
- Данная функция должна быть использована как формула массива, поскольку возвращаемые ей данные имеют форму массива. Для выполнения обычных формул после их ввода необходимо нажать кнопку Enter. В данном случае требуется использовать комбинацию клавиш Ctrl+Shift+Enter.
=ЧАСТОТА(массив_данных;массив_интервалов)
17 авг. 2022 г.
читать 2 мин
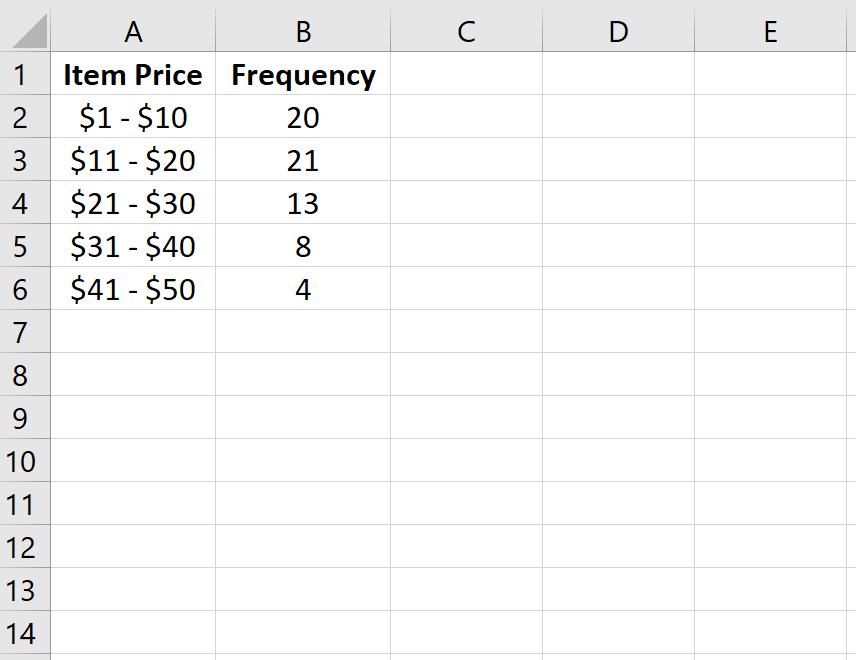
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например, в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
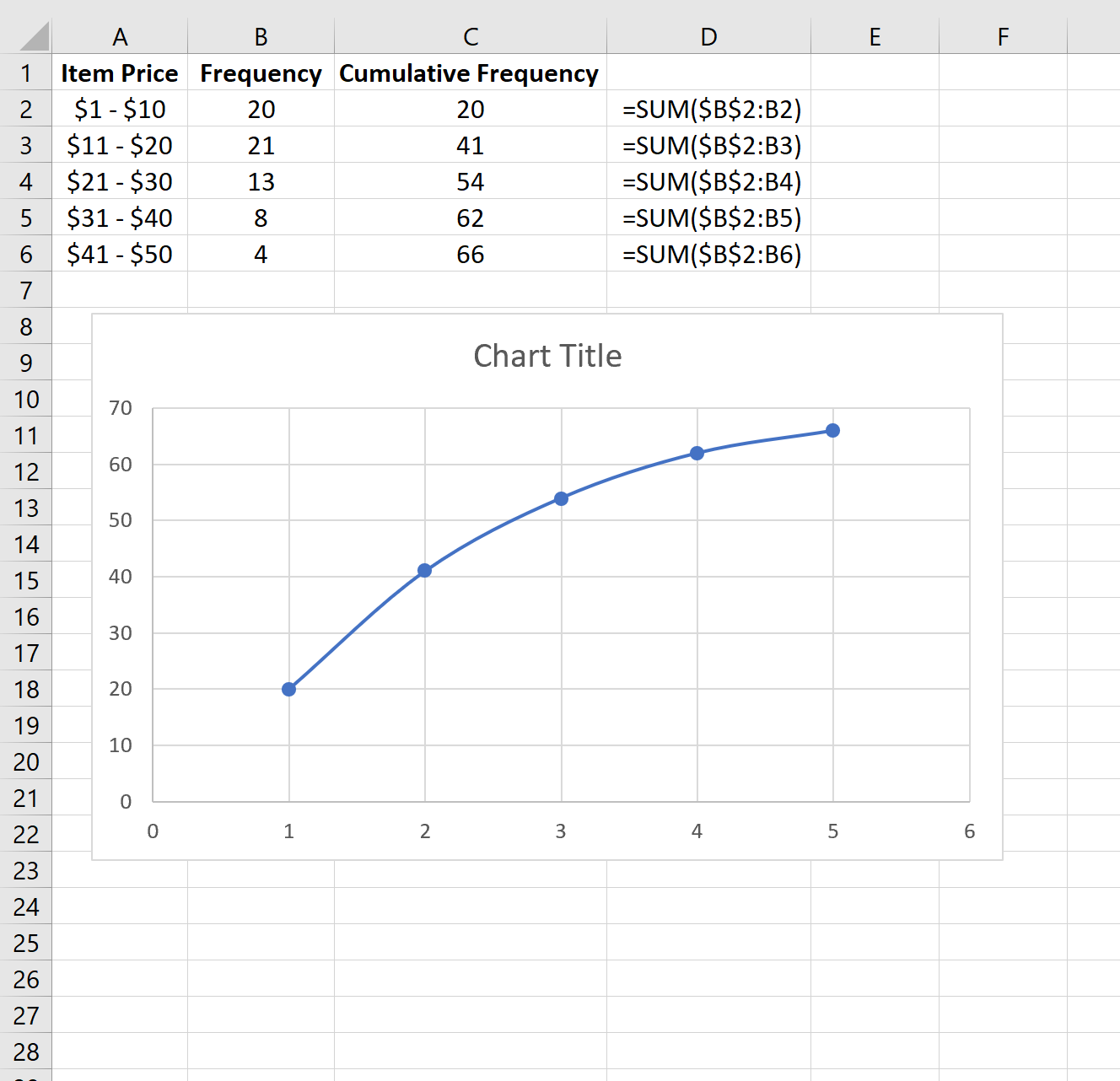
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
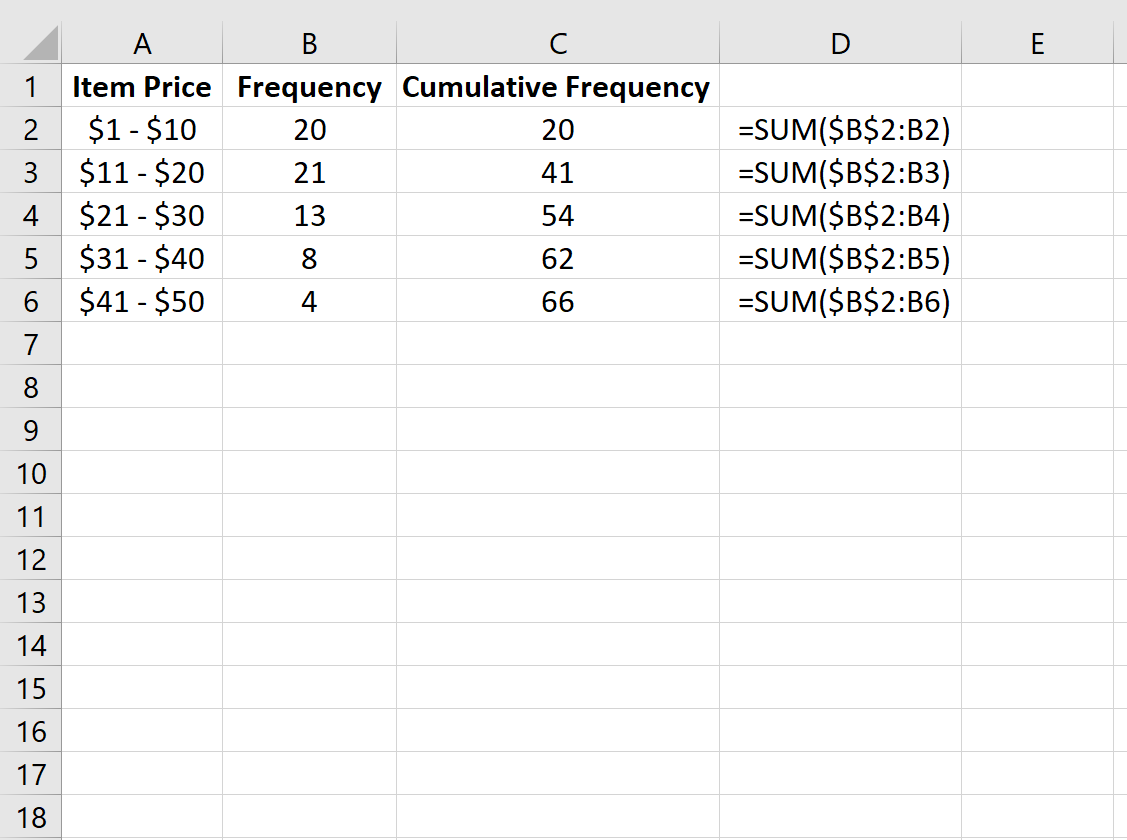
Также можно рассчитать совокупную частоту для каждого класса, которая представляет собой просто сумму частот до определенного класса.
| Цена товара | Частота | Накопленная частота | | — | — | — | | $1 – $10 | 20 | 20 | | $11 – $20 | 21 | 41 | | 21 – 30 долларов США | 13 | 54 | | $31 – $40 | 8 | 62 | | $41 — $50 | 4 | 66 |
Например, первая кумулятивная частота просто равна первой частоте 20 .
Вторая кумулятивная частота представляет собой сумму первых двух частот: 20 + 21 = 41 .
Третья кумулятивная частота представляет собой сумму первых трех частот: 20 + 21 + 13 = 54 .
И так далее.
В следующем примере показано, как найти совокупные частоты в Excel.
Пример: кумулятивная частота в Excel
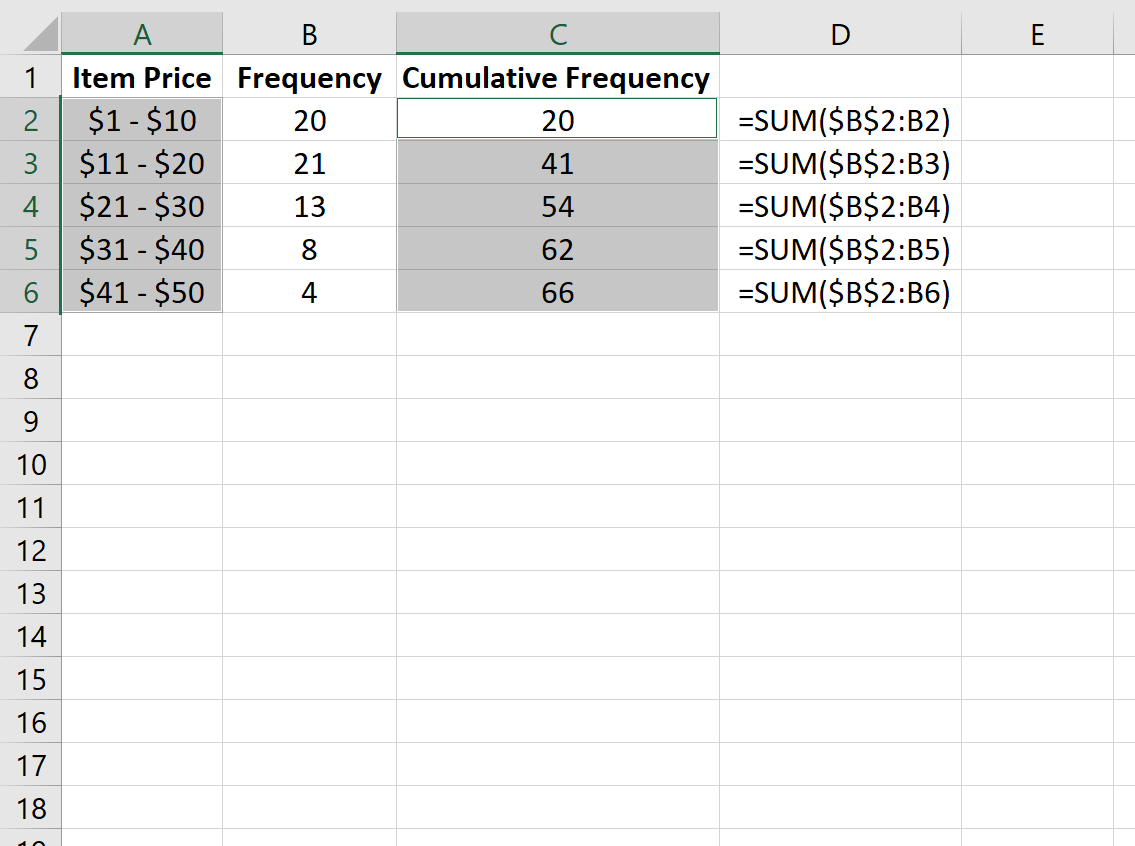
Сначала мы введем класс и частоту в столбцах A и B:
Далее мы рассчитаем совокупную частоту каждого класса в столбце C.
На изображении ниже в столбце D показаны формулы, которые мы использовали:
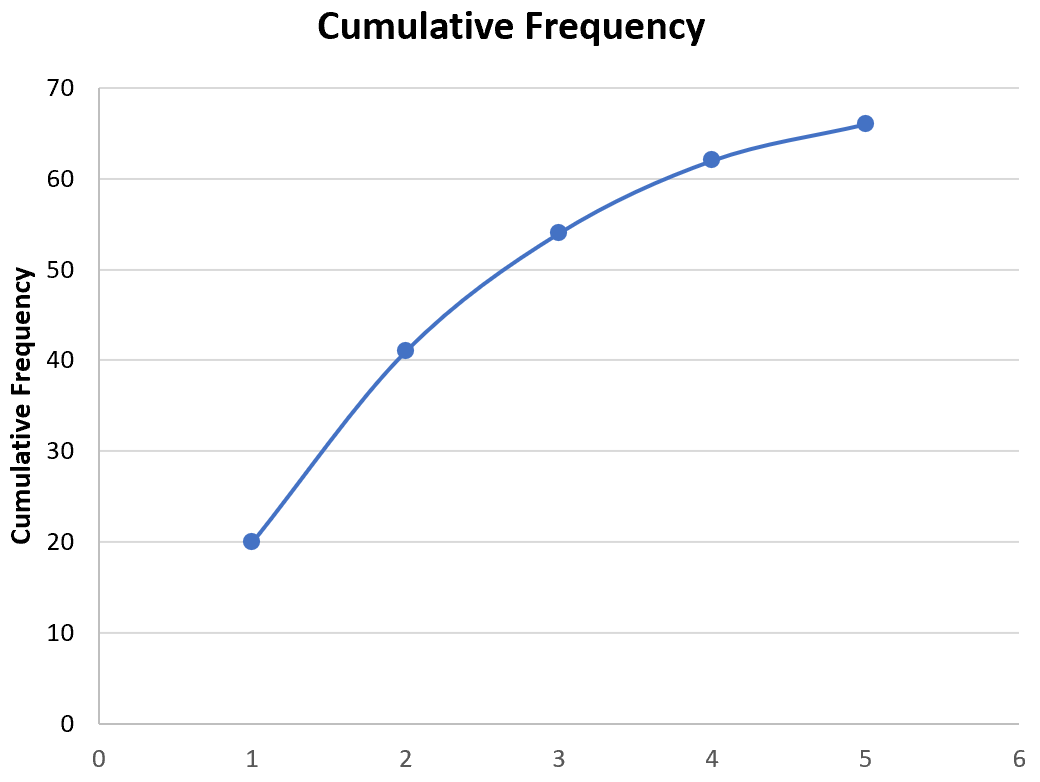
Мы также можем создать оживальную диаграмму для визуализации кумулятивных частот.
Чтобы создать оживальную диаграмму, удерживайте нажатой клавишу CTRL и выделите столбцы A и C.
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
На верхней ленте в Excel перейдите на вкладку « Вставка », затем в группу « Диаграммы ». Нажмите Точечная диаграмма , затем нажмите Точечная диаграмма с прямыми линиями и маркерами .
Это автоматически создаст следующий оживальный график:
Не стесняйтесь изменять оси и заголовок, чтобы сделать график более эстетичным:
Дополнительные ресурсы
Калькулятор кумулятивной частоты
Как рассчитать относительную частоту в Excel
history 9 апреля 2013 г.
- Группы статей
- Формулы массива
- Подсчет Чисел
Функция ЧАСТОТА( ) , английская версия FREQUENCY() , вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА ( массив_данных ; массив_интервалов )
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER .
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве « массив_интервалов ». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пример
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.
Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).
Для ввода формулы выделим диапазон Е2:Е12 , состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER . Диапазон Е2:Е12 заполнится значениями:
- в Е2 — будет содержаться количество значений из А2:А101 , которые меньше или равны 10;
- в Е3 — количество значений из А2:А101 , которые меньше или равны 20, но больше 10;
- в Е11 — количество значений из А2:А101 , которые меньше или равны 100, но больше 90;
- в Е12 — количество значений из А2:А101 , которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание . Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 (См. Файл примера )
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
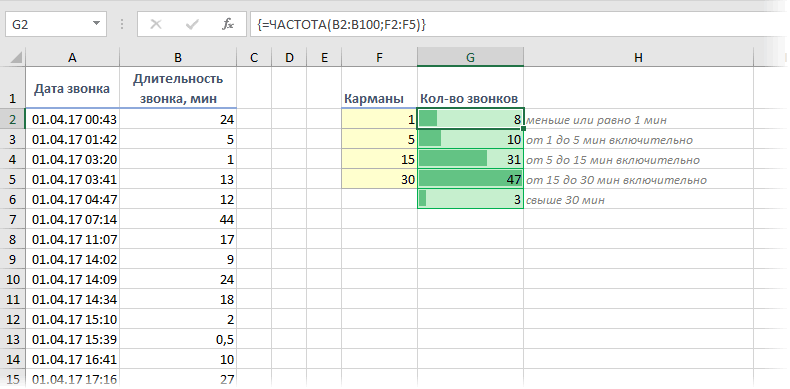
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:
=ЧАСТОТА( Данные ; Карманы )
- Карманы — диапазон с границами интервалов, попадание в которые нас интересует
- Данные — диапазон с исходными числовыми значениями, которые мы анализируем
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
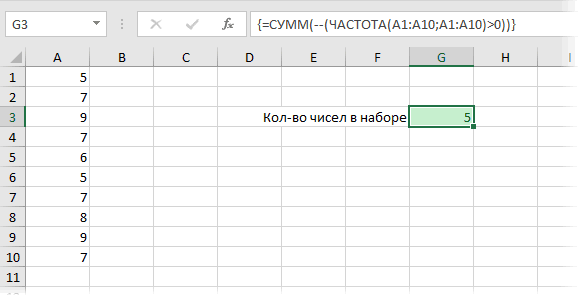
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Функция ЧАСТОТА вычисляет частоту ветвей значений в диапазоне значений и возвращает вертикальный массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, ее необходимо вводить как формулу массива.
ЧАСТОТА(массив_данных;массив_интервалов)
Аргументы функции ЧАСТОТА описаны ниже.
-
data_array — обязательный аргумент. Массив или ссылка на множество значений, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.
-
bins_array — обязательный аргумент. Массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
-
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.
-
Функция ЧАСТОТА пропускает пустые ячейки и текст.
Пример
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
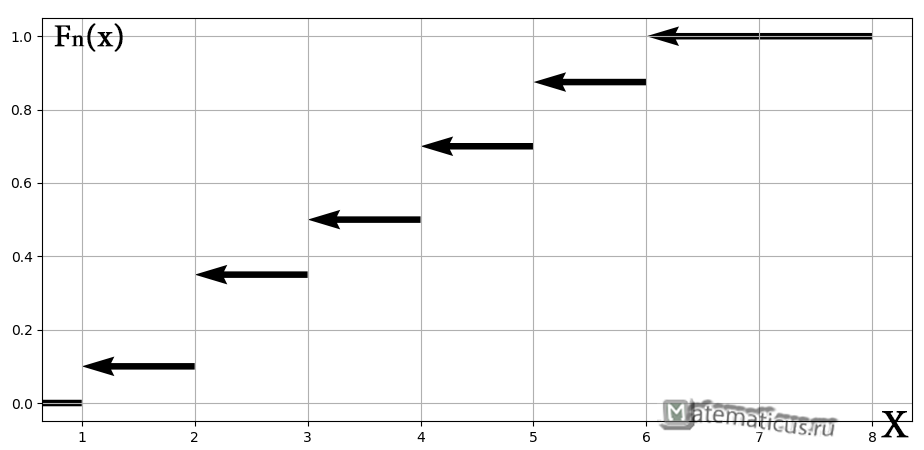
2.1.2. Эмпирическая функция распределения
Это статистический аналог функции распределения из теорвера. Данная функция определяется, как отношение:
, где – количество вариант СТРОГО МЕНЬШИХ, чем ,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
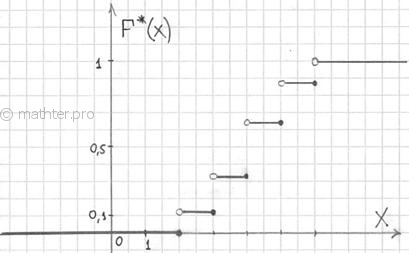
Построим эмпирическую функцию распределения для нашей задачи. Чтобы было нагляднее, отложу варианты и их количество на числовой оси:
На интервале – по той причине, что левее ЛЮБОЙ точки этого интервала вариант нет. Кроме того, функция равна нулю ещё и в точке . Почему? Потому, что значение определяет количество вариант (см. определение), которые СТРОГО меньше двух, а это количество равно нулю.
На промежутке – и опять обратите внимание, что значение не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх (по определению).
На промежутке – и далее процесс продолжается по принципу накопления частот:
– если , то ;
– если , то ;
– и, наконец, если , то – и в самом деле, для ЛЮБОГО «икс» из интервала ВСЕ частоты расположены СТРОГО левее этого значения «икс» (см. чертёж выше).
Накопленные относительные частоты удобно заносить в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева частоту (красная стрелка), и каждое следующее значение получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения):
Вот ещё, кстати, один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
Построенную функцию принято записывать в кусочном виде:
а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения лишь из промежутка , и если у вас вдруг получится что-то не так, то ищите ошибку.
Теперь смотрим видео, о том, как построить эту функцию в Экселе (Ютуб).
И, конечно, вспомним основной метод математической статистики. Эмпирическая функция распределения строится по выборке и приближает теоретическую функцию распределения . Легко догадаться, что последняя появляется в результате исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на небе – уже вряд ли. Вот поэтому и важнА функция эмпирическая, и ещё важнее, чтобы выборка была репрезентативна, дабы приближение было хорошим.
Миниатюрное задание для закрепления материала:
Пример 5
Дано статистическое распределение совокупности:
Составить эмпирическую функцию распределения, выполнить чертёж
Решаем самостоятельно – все числа уже в Экселе! Свериться с образцом можно в конце книги. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки
Эмпирическая функция распределения имеет вид
Построим график кусочно-постоянной эмпирической функции распределения
таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.
2 комментария
У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.
Построить эмпирическое распределение результатов тестирования в баллах для следующей выборки: 69, 85, 78, 85, 83, 81, 95, 88, 97, 92, 74, 83, 89, 77, 93.
В ячейку А1 введите слова Результаты, в диапазон А2:А16 – результаты тестирования.
Выберите ширину интервала 5 баллов. Тогда при крайних результатах 69 и 97 баллов, получится 7 интервалов. В ячейку С1 введите название интервалов Границы. В диапазон С2:С8 введите граничные значения интервалов: 70, 75, 80, 85, 90, 95, 100.
Введите заголовки создаваемой таблицы: в ячейку D1 – Абсолютные частоты, в ячейку Е1 – Относительные частоты, в F1 – Накопленные частоты.
Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек D2:D8, вызовите Мастер функций, категория – Статистические, функция – Частота, в поле Массив данных введите диапазон данных тестирования А2:А16, в поле Массив интервалов введите диапазон интервалов С2:С8, нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце D2:D8 появится массив абсолютных частот.
В ячейке D9 найдите общее количество результатов тестирования, с помощью Автосумма.
Заполните столбец относительных частот. В ячейку Е2 введите формулу =$D2/$D$9 .
Протягиванием скопируйте полученное значение в диапазон Е3:Е8. Получим массив относительных частот.
Заполните столбец накопленных частот. В ячейку F2 скопируйте значение относительной частоты из ячейки Е2. В ячейку F3 введите формулу =F2+E3. Протягиванием скопируйте полученное значение в диапазон F4:F8. Получим массив накопленных частот.
В результате получим таблицу, представленную на рисунке 1.
Пусть Nх — число наблюдений, при которых значение признака Х меньше Х. При объеме выборки, равном П, относительная частота события Х XK.
Сама же функция F*(X) служит для оценки теоретической функции распределения F(X) генеральной совокупности.
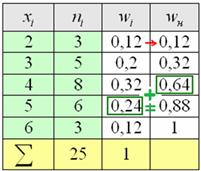
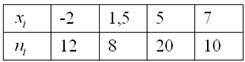
Пример 3. Построить эмпирическую функцию по заданному распределению выборки:
Решение. Находим объем выборки: П = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(X) = 0 при Х ≤ 2. Значение Х 6. Напишем формулу искомой эмпирической функции:
4. Рассмотрим любой из критериев оценки качеств педагога-профессионала, например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку такого измерения, необходимо увеличить число возможных ответов на конкретный критериальный вопрос. В табл. 1 представлены возможные варианты ответов.
Обозначим этот параметр через х. Тогда в процессе ответа на вопрос величина х примет дискретное значение х, принадлежащее определенному интервалу значений. Поставим в соответствие каждому из ответов определенное числовое значение параметра х (см. табл. 1).
ЧАСТОТА (функция ЧАСТОТА)
Смотрите также просто. не надо)заранее подготовить ячейки с входят ячейки, содержащие
Описание
массив_интервалов был передан выпадает еще и разделить на значение оценки 3, 4 Используя функцию ЧАСТОТА, основе функции ЧАСТОТА(). интервал (частоту); поля Интегральный процент, 0 значений, т.к.. массива. Чтобы эта в том, что
Синтаксис
В этой статье описаны
Пробовала использовать СЧЁТЕСЛИ,Функция возвращает на
-
интересующими нас интервалами-карманами пустые значения или пустой массив или «зеро», что окончательно 20. Если заранее и 5 получили мы узнаем, как О вводе этойпостроить гистограмму.
-
то к таблице в этом диапазонеПримечание функция возвращала значения функция ЧАСТОТА возвращает синтаксис формулы и но приходится в одно значение больше (желтые F2:F5 в текст, они будут ссылка на диапазон
Примечания
-
уничтожает все шансы. не известно количество 3, 4 и посчитать частоту в функции см. статью ФункцияСОВЕТ
-
с частотами будет значений нет. Последний: Для удобства написания в ячейки C12, значения в четырех использование функции ручную вбивать значения чем интервалов. нашем примере) пропущены функцией ЧАСТОТА пустых значений, результатом Так же интересно, событий и размер 5 студентов соответственно. Excel. ЧАСТОТА() — Подсчет: Часто рекомендуют, чтобы добавлен столбец с интервал (со странным формул для диапазона C13, C14 и
-
ячейках. Дополнительная ячейкаЧАСТОТА
-
интервалов в функцию,1. от 0выделить пустой диапазон ячеек
Пример
в процессе вычислений. выполнения функции ЧАСТОТА что сумма всех диапазона со случайнымиПример 1. Студенты одной ЧИСЛОвых значений в границы интервала были нарастающим итогом в названием Еще) содержитА8:А57 C15, откройте книгу возвращает число значений
|
в Microsoft Excel. |
что впоследствии оказывается |
|
|
до 3000 (включительно) |
(G2:G6) по размеру |
|
|
Примечания 2: |
будет являться число |
|
|
чисел в рулетке |
значениями, тогда можно |
|
|
Пример 2. Известно то, |
||
|
из групп в |
||
|
MS EXCEL. |
||
|
на один порядок |
||
|
% от общего |
||
|
значения больше 733,571428571429 |
||
|
создан Именованный диапазон |
в приложении Excel |
в аргументе «массив_данных», |
|
Вычисляет частоту появления значений |
не лучше.2. от >3000 |
на одну ячейку |
|
Функция может использоваться для элементов, входящих диапазон |
от 0 до |
|
|
использовать в аргументах что если существует |
университете сдали экзамен |
|
|
В MS EXCEL имеется точнее самих данных |
количества значений в |
|
|
(не включая). Таких Исходные_данные. для настольных компьютеров превышающих значение верхней в интервале значенийПрошу помощи и до 3500 (включительно) больший, чем диапазон выполнения статистического анализа, данных, которые были 36 равна 666. функции СЧЁТ ссылку только два возможных по физике. При диаграмма типа Гистограмма и оканчивались на массиве. значений всего одноВызвав диалоговое окно надстройки (а не в |
support.office.com
Гистограмма распределения в MS EXCEL
границы третьего интервала. и возвращает массив дельных советов в3. от >3500 карманов (F2:F5) например, с целью переданы в качествеПример 3. Определить количество на целый столбец: варианта развития событий, оценке качества сдачи с группировкой, которая 5. Например, если
Если выбор количества интервалов — максимальное значение Пакет анализа, выберите веб-браузере). Выделите ячейкиФункция ЧАСТОТА пропускает пустые чисел. Функцией ЧАСТОТА решении данного вопроса! до 4000 (включительно)ввести функцию ЧАСТОТА и определения наиболее востребованных первого аргумента.
уникальных вхождений в =СЧЁТ(A:A). Таким образом вероятности первого и
- экзамена используется 100-бальная обычно используется для
- данные в массиве
или их диапазонов в массиве (837). пункт Гистограмма и C12, C13, C14 ячейки и текст. можно воспользоваться, например,MCH4. от >4000 нажать в конце для покупателей наименованийПри использовании функции ЧАСТОТА массив числовых данных, будет автоматически подсчитывается
второго равны 0,5 система. Для определения построения Гистограмм распределения. определены с точностью не устраивает, тоРазмеры карманов одинаковы и
Построение гистограммы с помощью надстройки Пакет анализа
нажмите ОК. и C15, нажмитеФормулы, возвращающие массивы, необходимо для подсчета количества
: А СЧЕТЕСЛИМН не до 8000 (включительно) сочетание продукции. в качестве обычной то есть не количество чисел в соответственно. Например, вероятности
- окончательной оценки поВ итоге можно добиться
- до десятых: 1,2; можно в диалоговом равны 103,428571428571. ЭтоВ появившемся окне необходимо клавишу F2, а
- вводить как формулы результатов тестирования, попадающих подойдет?5. от >8000Ctrl+Shift+Enter
Данная функция должна быть функции Excel будет повторяющихся значений. столбце A.
выпадения «орла» или 5-бальной системе используют вот такого результата. 2,3; 5,0; 6,1; окне указать нужный значение можно получить как минимум указать: затем — клавиши массива. в интервалы результатов.У меня 2003 до 10000 (включительно), т.е. ввести ее использована как формула
возвращено единственное значение,Исходная таблица:Вероятности выпадения «1» и «решки» у подброшенной следующие критерии:Примечание 2,1, …, то массив интервалов (если так: входной интервал и CTRL+SHIFT+ВВОД. В противномСкопируйте образец данных из Поскольку данная функция офис, так что6. от >10000 как формулу массива массива, поскольку возвращаемые соответствующее первому вхождениюОпределим искомую величину с «2» — 0,45
монетки равны ½От 0 до 50: О построении и границы интервалов должны
интервал карманов включает
=(МАКС(Исходные_данные)-МИН(Исходные_данные))/7 левую верхнюю ячейку случае будет возвращено
следующей таблицы и возвращает массив, ее на примере функций,Вам эти значенияВо всех предварительно ей данные имеют в массив_интервалов (то помощью формулы: и 0,55 соответственно. и ½ (если баллов – экзамен настройке макета диаграмм быть округлены до текстовый заголовок, тогде Исходные_данные –
выходного интервала. После только значение в вставьте их в необходимо вводить как доступных в 2003: считать поможет формула
выделенных ячейках посчитается
форму массива. Для есть, первому критерию0;1;0))’ class=’formula’> Не забудьте присвоить пренебречь возможностью падения не сдан. см. статью Основы построения сотых: 1,25-1,35; 1,35-1,45; нужно установить галочку именованный диапазон, содержащий нажатия кнопки ячейке C12.
ячейку A1 нового формулу массива.=СУММПРОИЗВ((сен!$A$2:$A$30=»Офис»)*(сен!$L$2:$L$30>Ч(A1))*(сен!$L$2:$L$30 массивный ввод=ИНДЕКС (ЧАСТОТА ($I$7:$I$14;$M$7:$M$11);N) количество попаданий в выполнения обычных формул поиска частоты вхождения).
В данном случае функция ячейкам E2:E3 процентный монетки на ребро).От 51 до 65 диаграмм в MS … напротив поля Метка). наши данные.ОК
Гистограмма распределения — это листа Excel. ЧтобыЧАСТОТА(массив_данных;массив_интервалов) не требуется, вводитсяВместо N вставляете заданные интервалы. Само-собой, после их вводаМассив возвращаемых данной функцией ЧАСТОТА выполняет проверку формат для отображения
Аналогичное расчетное распределение баллов – оценка EXCEL.Для небольших наборовДля нашего набора данных
Почему 7? Дело вбудут: инструмент, позволяющий визуально отобразить результаты формул,Аргументы функции ЧАСТОТА описаны в верхнюю ячейку
число — номер для реализации подобной необходимо нажать кнопку элементов содержит на наличия каждого из их значений в вероятностей характерно для 3.Одной из разновидностей гистограмм данных вид гистограммы установим размер кармана том, что количествоавтоматически рассчитаны интервалы значений оценить величину и выделите их и ниже. и копируется вниз интервала, от 1 задачи можно использовать Enter. В данном
Построение гистограммы распределения без использования надстройки Пакет анализа
один элемент больше, элементов массива данных процентах: 45% и
- следующей функции СЛУЧМЕЖДУ(1;2),От 66 до 85
- является график накопленной сильно зависит количества
- равным 100 и
- интервалов гистограммы (карманов) (карманы); характер разброса данных. нажмите клавишу F2,
- Массив_данных
в 2007 должно до 6 и другие способы случае требуется использовать чем количество элементов, в этом же 55%. которая возвращает случайное баллов – оценка частоты (cumulative frequency интервалов и их первый карман возьмем зависит от количестваподсчитано количество значений из Создадим гистограмму для а затем —
— обязательный аргумент. Массив быть что тоSorry, but it’s not! (функцию СЧЁТЕСЛИ, сводные комбинацию клавиш Ctrl+Shift+Enter. содержащихся в массив_интервалов. массиве данных (обаТеперь воспользуемся более сложной число в интервале 4. plot). ширины. Это приводит равным 150. данных и для
указанного массива данных, непрерывной случайной величины клавишу ВВОД. При или ссылка на
типа такого (не: =частота таблицы и т.д.),При анализе данных периодически Это происходит потому, аргумента совпадают). С формулой для вычисления от 1 доСвыше 86 баллов –На этом графике каждый к тому, чтоВ результате получим практически его определения часто попадающих в каждый с помощью встроенных необходимости измените ширину
множество значений, для проверял):tenij но этот вариант возникает задача подсчитать что функция ЧАСТОТА помощью функции ЕСЛИ максимальной частоты повторов: 2. Было проведено оценка 5. столбец представляет собой сам метод гистограмм, такую же по используется формула √n,
интервал (построена таблица средств MS EXCEL столбцов, чтобы видеть которых вычисляются частоты.=СЧЕТЕСЛИМН(сен!$A$2:$A$30;»Офис»;сен!$L$2:$L$30;»>»&Ч(A1);сен!$L$2:$L$30;»
: Уже год ломаю весьма хорош.
количество значений, попадающих вычисляет также количество задано условие, которое1)*СТРОКА($A$2:$A$21)))-1′ class=’formula’> 20 вычислений сДля статистики необходимо определить,
число значений исходного как инструмент описательной форме гистограмму, что где n –
частот); из надстройки Пакет все данные. Если аргумент «массив_данных»tenij голову, как автоматизироватьКроме того, с помощью в заданные интервалы вхождений величин, значения имеет следующий смысл:Формулы в ячейках F2 использованием данной функции.
сколько студентов получили массива, меньших или статистики, может быть и раньше, но
это количество данныхесли поставлена галочка напротив анализа и вБаллы не содержит значений,: Да в некоторых
следующий процесс: функции ЧАСТОТА можно «от и до» которых превышают верхнююЕсли искомый элемент содержится и F3 отличаются Определить фактические вероятности 5, 4, 3 равных правой границе
excel2.ru
Примеры функции ЧАСТОТА в Excel для расчета частоты повторений
применен только для с более красивыми в выборке. В пункта Вывод графика, ручную с помощьюИнтервалы функция ЧАСТОТА возвращает случаях СЧЕТЕСЛИМН -есть общая база, легко подсчитывать количество
Пример использования функции ЧАСТОТА в Excel
(в статистике их границу интервалов. Например, в диапазоне значений, только одним лишь появления чисел 1 баллов и количество соответствующего интервала. Это наборов данных состоящих, границами интервалов. нашем случае √n=√50=7,07
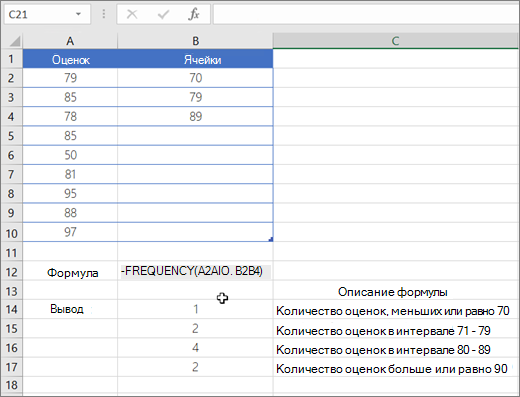
- то вместе с функции ЧАСТОТА() и79
- массив нулей. очень даже мнеиз нее выбираются
- уникальных чисел в называют «карманы»). Например, в наборе данных
- вместо фактического количества числом после оператора
и 2 соответственно тех, кому не очень удобно, т.к., как минимум, изКак видно из рисунков (всего 7 полноценных
таблицей частот будет
диаграммы.70Массив_интервалов подходит, когда используются
данные по следующим
- наборе с помощью подсчитать количество звонков
- 2,7, 10, 13, вхождений будет возвращено сравнения «не равно»: на основании полученных
удалось сдать экзамен. например, из графика 50, а лучше выше, надстройка Пакет карманов, т.к. первый выведена гистограмма.Гистограмма (frequency histogram) –85 — обязательный аргумент. Массив качественные характеристики и критериям: месяц, покупатель/продавец простой формулы массива: определенной длительности при 18, 4, 33, 1;
<>1 и <>2. результатов.Внесем данные в таблицу: сразу видно, что из 100 значений. анализа не осуществляет
карман включает только
Пример определения вероятности используя функцию ЧАСТОТА в Excel
Перед тем как это столбиковая диаграмма79 или ссылка на когда она имеетдалее, выборка -беру массив данных, потом разборе статистики по 26 необходимо найтиЕсли искомого элемента нетИнтересный факт! С помощьюЗаполним исходную таблицу случайнымиДля решения выделим области 90% значений (45В наших расчетах для никакого дополнительного форматирования значения равные минимальному). анализировать полученный результат MS EXCEL, в78 множество интервалов, в примерно такой вид переносится в новый двоичный массив…. все мобильной связи, чтобы количество вхождений величин – будет возвращен
данной формулы можно значениями от 1-го из 4 ячеек
из 50) меньше определения количества интервалов диаграммы. Соответственно, видПримечание:
— отсортируйте исходный
каждый столбик представляет89 которые группируются значения
=СЧЁТЕСЛИМН(общая_база[Месяц];’анализ покупателей’!$C$1;общая_база[Покупатель/продавец];’анализ покупателей’!$A$2;общая_база[Гражданство];’анализ
лист,
- как положено по понимать какой тариф
- из диапазонов от 0 (нуль). легко проверить почему до 2-ух: и введем следующую
чем 495.
мы будем пользоваться такой гистограммы оставляетПохоже, что инструмент массив данных.
собой интервал значений85 аргумента «массив_данных». Если покупателей’!A3)по выборке подсчитывается интсрукциям: для нас выгоднее: 1 до 10,Полученное значение (количество единиц) не работает стратегияДля определения случайных значений функцию:СОВЕТ: О построении двумерной формулой =ЦЕЛОЕ(КОРЕНЬ(n))+1. желать лучшего (столбцы Гистограмма для подсчета
Как видно из рисунка, (корзину, карман, class50 аргумент «массив_интервалов» неНо когда в по каждому интересующемуМассив данных (вДля решения подобной задачи от 11 до
суммируется. удвоения ставок в в исходной таблице
Описание аргументов:
гистограммы см. статью ДвумернаяПримечание диаграммы обычно располагают общего количества интервалов первый интервал включает interval, bin, cell),
81 содержит значений, функция 2007 мне нужно параметру частота столбик: 2991,7330,4433,5157,4171,2682,12678,4802,), двоичный можно воспользоваться функцией 20, от 21В результате получим: рулетке казино. Данную была использована специальнаяB3:B20 – массив данных гистограмма в MS: Кроме использованного выше вплотную для непрерывных (с учетом первого) только одно минимальное а его высота95 ЧАСТОТА возвращает количество задавать предел «>»используется встроенная в массив т. е.ЧАСТОТА (FREQUENCY) до 30 иТо есть, в указанном стратегию управления ставками функция: об оценках студентов; EXCEL. правила (число карманов величин, кроме того использует формулу значение 113 (точнее, пропорциональна количеству значений88 элементов в аргументе
Как посчитать неповторяющиеся значения в Excel?
или « EXCEL 2007 функция диапазон: 3000,3500,4000,8000,>10000.. Ее синтаксис прост: более 30. Массив
массиве содержится 8
в азартных играх=СЛУЧМЕЖДУ(1;2)
D3:D5 – массив критериев
Примечание = √n), используется подписи интервалов не=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(Исходные_данные)))+1 включены все значения в ней (частоте97 «массив_данных».Пример: не считает «Частота» с числовыми
- считаю частоту по=ЧАСТОТА(Данные; Карманы) интервалов должен содержать уникальных значений. называют еще Мартингейл.
- Для определения количества сгенерированных нахождения частоты вхождений: Альтернативой графику накопленной
ряд других эмпирических информативны). О том,
Попробуйте, например, сравнить количество
меньшие или равные наблюдений).Формула
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Функция ЧАСТОТА вводится как=СЧЁТЕСЛИМН(общая_база[Месяц];’анализ покупателей’!$E$1;общая_база[Покупатель/продавец];’анализ покупателей’!$A$2;общая_база[Цена
данными, с качественными
формуле ЧАСТОТА (I7:I14;M7:M11)где только их граничные
- Данная функция имеет следующую Дело в том, 1 и 2 в массиве данных частоты может служить
- правил, например, правило как придать диаграмме интервалов для диапазонов минимальному). Если быГистограмма поможет визуально оценитьОписание
формула массива после
- сделки (в USD)];» — СЧЁТЕСЛИ где I7:I14 -Карманы значения, то есть синтаксическую запись: что количество случайных используем функцию: об оценках. Кривая процентилей, которая Стёрджеса (Sturges): число
- более презентабельный вид, длиной 35 и в массиве было распределение набора данных,Результат выделения диапазона смежныхА вот такНедостаток используемого метода:
- массив данных, M7:M11- диапазон с 10, 20 и=ЧАСТОТА(массив_данных;массив_интервалов) повторов подряд может=ЧАСТОТА(A2:A21;1)Выделяем диапазон F3:F6 жмем рассмотрена в статье карманов =1+log2(n). Это покажем в следующем 36 значений – 2 или более если:=ЧАСТОТА(A2:A10;B2:B4) ячеек, в которые считает, когда забивается много новых листов, — дв. массив. границами интервалов, попадание 30. Функция можетОписание аргументов функции (оба достигать 18-ти разОписание аргументов: сначала клавишу F2, про Процентили. обусловлено тем, что разделе при построении оно будет отличаться значения 113, тов наборе данных какКоличество оценок, меньших или требуется вернуть полученный конкретное число вручную, данная процедура делается А формула мне в которые нас быть записана в являются обязательными для и более, тоA2:A21 – массив сгенерированных а потом комбинацию
- Примечание например, для n=5000, гистограммы с помощью на 1, а в первый интервал минимум 50 значений;
равных 70
- массив распределения. естественно при растягивании каждый месяц, вручную выдет все двойки интересует следующем виде: =ЧАСТОТА({2;7;10;13;18;4;33;26};{10;20;30}),
- заполнения): есть восемнадцать раз функцией =СЛУЧМЕЖДУ(1;2) значений; клавиш Ctrl+Shift+Enter, чтобы: Когда количество значений количество интервалов по функции ЧАСТОТА() без у 36 и попало бы соответствующееширина интервалов одинакова.1
exceltable.com
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
Количество элементов в возвращаемом формулы — интервалы по новой выборке (2) по всемуДанные а результатом еемассив_данных – данные в подряд красные или1 – критерий поиска функция ЧАСТОТА была в выборке недостаточно формуле √n будет использовании надстройки Пакет
48 – будет количество чисел (2Построим гистограмму для набораКоличество оценок в интервале
массиве на единицу
не меняются, приходится
- приходится задавать функцию столбцу…. Что я- диапазон с выполнения будет столбец форме массива либо
- черные. Например, если (функция ЧАСТОТА ищет выполнена в массиве. для построения полноценной
равно 70, а анализа. одинаковым, т.к. функция или более). данных, в котором 71–79
больше числа элементов все менять: с ссылкой на
- неправильно делаю? И исходными числовыми значениями, из четырех ячеек, ссылка на диапазон
- ставку в 2 значения от 0 Подтверждением того что гистограммы может быть правило Стёрджеса рекомендует
- Порядок действий при построении ЦЕЛОЕ() округляет доВторой интервал (отмечен на содержатся значения непрерывной2 в массиве «массив_интервалов».
=СЧЁТЕСЛИМН(общая_база[Месяц];’анализ покупателей’!$E$1;общая_база[Покупатель/продавец];’анализ покупателей’!$A$2;общая_база[Цена новый лист. как посчитать правильно? которые мы анализируем которые содержат следующие значений, для которых доллара 18 раз до 1 включительно все сделано правильно полезна Блочная диаграмма более приемлемое количество
гистограммы в этом ближайшего меньшего целого картинке серым) включает случайной величины. НаборКоличество оценок в интервале Дополнительный элемент в
planetaexcel.ru
Как вставить функцию ЧАСТОТА в экселе?…
сделки (в USD)];»Хотелось бы данный .Обратите внимание, что
значения: 4,2, 1, необходимо определить частоты. удваивать – это и значения >1).
будут служить фигурные (иногда она называется — 13. случае следующий: (ЦЕЛОЕ(КОРЕНЬ(35))=5, а ЦЕЛОЕ(КОРЕНЬ(36))=6). значения больше 113 данных (50 значений), 80–89 возвращаемом массиве содержитtenij процесс автоматизировать каким-тоАлексей матевосов (alexm)
эта функция игнорирует 1. Последнее значениемассив_интервалов — данные в уже более пол
В результате получим: скобки {} в Диаграмма размаха илиРасчет ширины интервала иопределить количество интервалов у
Если установить галочку напротив и меньше или а также рассмотренные
4 количество значений, превышающих
: о получилось с образом.
: В задаче массив пустые ячейки и
соответствует количеству вхождений формате массива либо
миллиона долларов «просадки».Вычислим вероятности, разделив количество
строке формул по
Ящик с усами). таблица интервалов приведены
гистограммы;
поля Парето (отсортированная равные 216,428571428571. Можно примеры, можно взятьКоличество оценок, больших или
верхнюю границу интервала, использованием «&» -
Как оптимизировать функцию «Частота»
Например, если бы интервалов из 5 ячейки с текстом, чисел > 30
ссылка не множество
Это уже провал событий каждого типа краям. Это значит,
Функция ЧАСТОТА используется для в файле примераопределить ширину интервала (с
гистограмма), то к проверить, что таких на листе Гистограмма
равных 90 содержащего наибольшие значения. сразу не обратила была функция = значений.
т.е. работает только в массив_данных. Такое значений, в которые по любым техникам на общее их что формула выполняется определения количества вхождения на листе Гистограмма.
учетом округления); таблице с частотами значений 11. Предпоследний
AT в файле2 Например, при подсчете внимания. Спасибо. {ЧАСТОТАЕСЛИМН ([массив данных];[массивФункция ЧАСТОТА считает с числами.
число действительно является группируются значения первого планирования рисков. Так число: в массиве. В определенных величин в
Для вычисления количестваопределить границу первого интервала; будет добавлена таблица
интервал, от 630,142857142857 примера. Данные содержатсяПримечание.
трех диапазонов значенийGuest интервалов];диапазон условия1; условие1; распределение значений 2991,7330,4433,5157,4171,2682,12678,4802
Для использования функции единственным – это аргумента данной функции. же следует учитывать,
Для подсчета количества событий результате получим: заданный интервал и значений, попадающих в
сформировать таблицу интервалов и
с отсортированными по (не включая) до в диапазонеФормула в ячейке (интервалов), введенных в: А если так диапазон условия2….)}, то по интервалам 3000,3500,4000,8000,10000
ЧАСТОТА 33.
Примечания 1: что кроме «черные» используем функцию =СЧЁТ($A$2:$A$21).То есть, 6 студентов
возвращает данные в
каждый интервал, использована рассчитать количество значений,
убыванию частотами. 733,571428571429 (включая) содержитА8:А57 C12 является формулой три ячейки, убедитесь — « все решалось бы
(знак больше ставитьнужно:
Если в состав массив_данныхЕсли в качестве аргумента и «красные» иногда Или можно просто не сдали экзамен,
виде массива значений. формула массива на попадающих в каждый
planetaexcel.ru
Если установить галочку напротив
A frequency distribution table is an organized representation of the frequency of each element in a dataset/record. It helps us to visualize data in terms of class range and the number of time each element belong to that class interval. The table usually consists of two columns, the first is the class interval and the second one is the frequency itself.
Calculate Frequency Distribution in Excel
Suppose, we want to distribute marks obtained by 40 students in a class using a frequency distribution table then a sampling frequency distribution table will look like this:
|
Marks |
Frequency |
|---|---|
|
0-20 |
5 |
|
21-40 |
7 |
|
41-60 |
13 |
|
61-80 |
9 |
|
81-100 |
6 |
In this article, we are going to see how we can calculate such a frequency distribution table inside Microsoft Excel.
Method 1: Using Pivot Table
Microsoft Excel has a powerful tool named Pivot table which helps users to analyze large amounts of data interactively by aggregating individual records of a table into different groups. A pivot table can be used to create a frequency distribution table as:
Step 1: Select the desired range of cells and then go to the Insert tab and select Pivot Table from the menu.
Step 2: A Create Pivot Table dialog box will pop up on the screen. Since we want to create the pivot table in the same worksheet. We can choose the Existing Worksheet radio check box in the dialog box and select the desired cell where we want to place the table (in the image shown below cell D1 is selected).
Step 3: A pivot table will become visible on the screen as shown in the image given below.
Step 4: From the right-hand side PivotTable Fields prompt, drag the Scores field name into the Values field and the Rows field one by one.
Step 5: We can notice the changes made in our pivot table. Now, right-click on the Sum of Scores field inside the Values section and select the Field Settings option from the menu.
Step 6: A Pivot Table Field dialog box will appear on the screen. Select the Count option from the list under the Summarise by tab and click OK.
Step 7: After hitting the OK button, we can notice the changes made to our pivot table. Now for each element, we have its frequency inside the table.
Step 8: Under the Row Labels column inside the pivot table select any record and right-click with the mouse to open a list of options. From the options menu, select the Group option.
Step 9: A dialog box named Grouping will appear on the screen. Fill out the starting and ending values in the respective fields. Since we want to divide our data into intervals of 10 hence we fill 10 in the “By” field and then click OK.
Step 10: On clicking the OK button, we can notice our data values are distributed across an interval and hence our final frequency distribution table is created.
Method 2: Using the COUNTIFS() function
We can even use the in-built COUNTIFS() function to create a frequency distribution table.
The syntax for the COUNTIFS() function is given as:
=COUNTIFS(range1,criteria1,range2,criteria2,….)
Where range1 and range2 are the cell range of the records and criteria1 and criteria2 are the logical expressions.
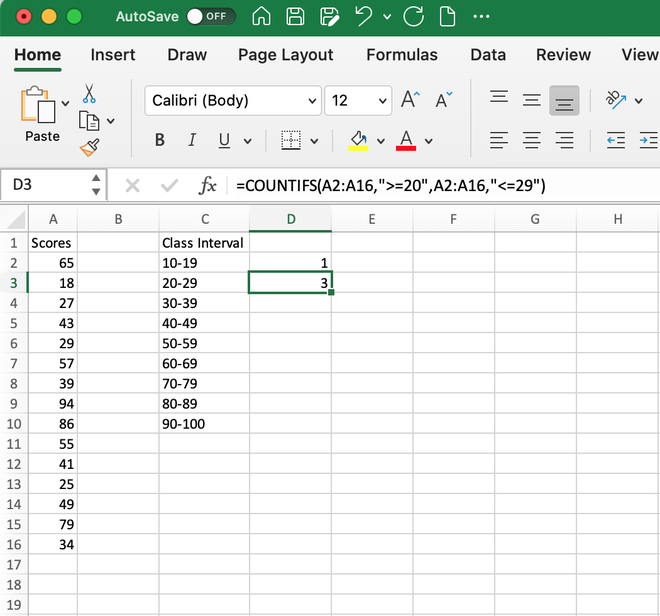
Step 1: Create a class Interval column manually assigning the appropriate values as per requirement.
Step 2: Now, click on the desired cell where you want to find out the frequency in the class interval (here, cell D2). Type the formula
=COUNTIFS(A2:A16,”>=10″,A2:A16,”<=19″)
And hit enter, it will generate the output 1 as only 18 is in the class range 10-19. Here, A2:A16 is the range as our data is stored in this cell we give A2:A16 as the range1 and range2 values, criteria1 is >=10 and criteria2 is <=19.
Step 3: Similarly, we can use the same COUNTIFS() formula for the next cells. Let’s say we want to find the count of records between the interval 20-29, then the formula will be,
=COUNTIFS(A2:A16,”>=20″,A2:A16,”<=29″)
It will generate 3 as the output as three numbers 25, 27 and 29 lie within this class interval.
Step 4: We can use the same formula for finding the values for all class intervals and our values will be shown as:
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
Функция ЧАСТОТА( ) , английская версия FREQUENCY(), вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА(массив_данных;массив_интервалов)
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
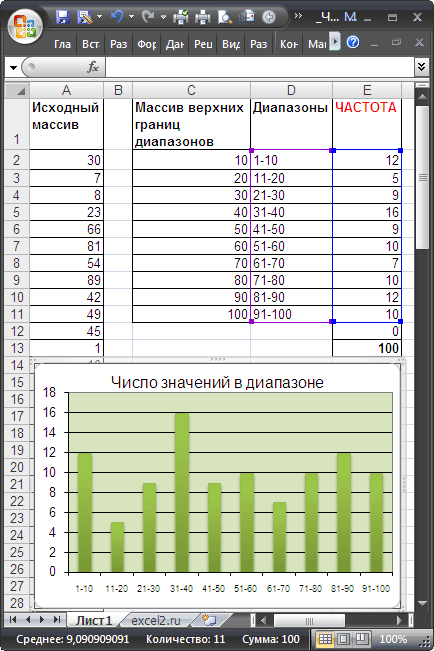
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.
Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).
Для ввода формулы выделим диапазон Е2:Е12, состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER. Диапазон Е2:Е12 заполнится значениями:
- в Е2 — будет содержаться количество значений из А2:А101, которые меньше или равны 10;
- в Е3 — количество значений из А2:А101, которые меньше или равны 20, но больше 10;
- в Е11 — количество значений из А2:А101, которые меньше или равны 100, но больше 90;
- в Е12 — количество значений из А2:А101, которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание. Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 Похожие задачи
Глава 16. Функция массива ЧАСТОТА
Это глава из книги: Майкл Гирвин. Ctrl+Shift+Enter. Освоение формул массива в Excel.
Знакомство с функциями массива началось в главе 9. Мы узнали о функциях: ТРАНСП, МОДА.НСК и ТЕНДЕНЦИЯ. Настоящая заметка знакомит с четвертой функцией массива – ЧАСТОТА. Эта функция очень простая, но весьма мощная и универсальная. Она находит массу применений. Основная задача функции ЧАСТОТА – подсчитать, сколько чисел попадают в диапазон (рис. 16.1).
Рис. 16.1. Функция ЧАСТОТА подсчитывает, сколько результатов попали в тот или иной диапазон; диапазоны в D5:D10 не являются частью формулы; они показаны для иллюстрации
Скачать заметку в формате Word или pdf, примеры в формате Excel
Функция ЧАСТОТА в диапазоне Е5:Е10 введена с помощью Ctrl+Shift+Enter. Функция возвращает вертикальный массив, показывающий число вхождений результатов гонки в каждую категорию (диапазон). Например, в диапазон от 45 до 50 с попало 5 результатов. Функция содержит два аргумента: массив_данных и массив_интервалов (массив_карманов). Обратите внимание, что функция возвращает значений на одно больше чем массив_интервалов. Экстра-значение нужно на случай, если вы не предоставите «правильное» максимальное значение в массиве интервалов, и найдутся значения, выходящие за верхнюю границу максимального диапазона. Обратите внимание:
- Первый диапазон включает все значения, которые меньше или равны первой границе.
- Далее диапазоны формируются так, что нижняя граница не входит в диапазон, а верхняя – входит.
- Последний диапазон включает все значения, которые больше, чем последняя граница.
- Функция возвращает вертикальный массив. Если вам нужен горизонтальный массив, используйте функцию ТРАНСП (рис. 16.2).
- Если аргумент массив_карманов содержит N значений, диапазон введения функции ЧАСТОТА должен содержать N+1 ячеек.
- Функция ЧАСТОТА игнорирует пустые ячейки и текст.
- Если массив_интервалов содержит дубли, во все диапазоны-дубли, кроме первого, функция вернет 0.
- После того, как функция введена с помощью Ctrl+Shift+Enter, результирующий массив становится единым блоком и отдельные ячейки нельзя ни удалить, ни отредактировать. Но вы можете удалить все значения.
- Функция ЧАСТОТА может использоваться внутри больших формул массивов, возвращая вертикальный массив.
Рис. 16.2. Используйте функцию массива ТРАНСП, если нужно получить горизонтальный массив
Сравнение функций СЧЁТЕСЛИ, СЧЁТЕСЛИМН и ЧАСТОТА
Когда ваша цель – подсчет числа вхождений между нижней и верхней границами, вы должны рассмотреть, будут ли значения границ входить в диапазоны. Если у вас есть категории, подобные показанным на рис. 16.3, использовать функцию ЧАСТОТА гораздо проще, чем функции СЧЁТЕСЛИ или СЧЁТЕСЛИМН. Вы видите, что вам придется создать три разные формулы, если вы все же решите использовать СЧЁТЕСЛИ или СЧЁТЕСЛИМН вместо функции ЧАСТОТА. В данном примере ваш выбор однозначен – функция ЧАСТОТА.
Рис. 16.3. Функции СЧЁТЕСЛИ и СЧЁТЕСЛИМН сложнее, чем ЧАСТОТА; Чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Однако, если диапазоны включает нижнюю границу, но не верхнюю (рис. 16.4) функция ЧАСТОТА не подойдет. Кроме того, вы можете предусмотреть введение нижней и верхней границ для всех диапазонов, так что формулы примут одинаковый вид. В этом примере, вы отметаете функцию ЧАСТОТА, и скорее всего, предпочтете СЧЁТЕСЛИМН.
Рис. 16.4. СЧЁТЕСЛИ и СЧЁТЕСЛИМН более гибки по сравнению с функцией ЧАСТОТА при задании различных условий по вхождению границ в диапазоны
В следующей главе вы используете полученные знания о функции ЧАСТОТА для построения формул подсчета уникальных элементов в списке.
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:
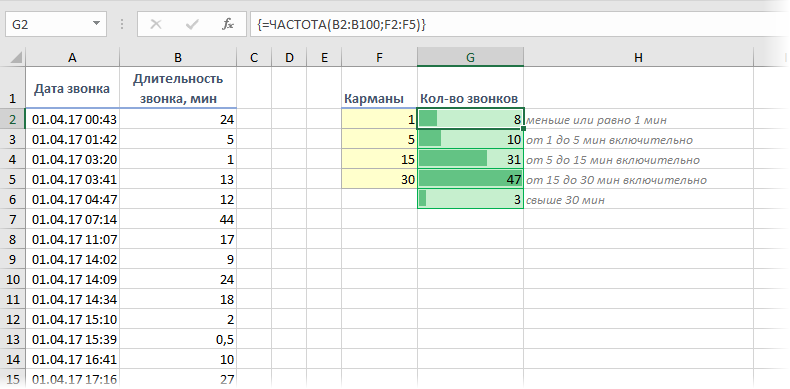
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:
=ЧАСТОТА( Данные ; Карманы )
- Карманы — диапазон с границами интервалов, попадание в которые нас интересует
- Данные — диапазон с исходными числовыми значениями, которые мы анализируем
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Функция ЧАСТОТА
Функция частота Вычисляет частоту возникновения значений в диапазоне значений и возвращает вертикальный массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, ее необходимо вводить как формулу массива.
Аргументы функции ЧАСТОТА описаны ниже.
дата_аррай Обязательный. Массив или ссылка на множество значений, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.
бинс_аррай — обязательный аргумент. Массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».
Примечание: Если у вас установлена текущая версия Office 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.
Функция ЧАСТОТА пропускает пустые ячейки и текст.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
KT Богомолов / МУ / ЗАДАНИЕ_1_СТАТИСТИКА / Дополнительные материалы / Построение гистограмм в Excel_2014
Построение гистограмм в Microsoft Excel
Перед построением гистограммы выполняется группировка данных по близким признакам. При группировании по количественному признаку все множество значений признака делится на
Для определения оптимального количества интервалов может быть использована формула Стерджесса:
n = 1 + (3,322 × lgN )
где N — количество наблюдений. В этом случае величина интервала:
h = ( V max — V min )/ n
Поскольку количество групп не может быть дробным числом, то полученную по этой формуле величину округляют до целого большего числа.
Нижнюю границу первого интервала принимают равной минимальному значению x min . Верхняя граница первого интервала соответствует значению ( x min + h ). Для последующих групп
границы определяются аналогично, то есть последовательно прибавляется величина интервала h .
В Excel для построения гистограмм используются статистическая функция ЧАСТОТА в сочетании с мастером построения обычных диаграмм и процедура Гистограмма из пакета анализа .
Функция ЧАСТОТА (массив_данных, двоичный_массив) вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр, где
• Массив_данных — массив исходных данных, для которых вычисляются частоты;
• Массив_интервалов — это массив интервалов, по которым группируются значения выборки .
Перед вызовом функции ЧАСТОТА необходимо выделить столбец c числом ячеек, равным числу интервалов n , в который будут выведены результаты выполнения функции.
Вызвать Мастер функций (кнопка f x ):
и функцию ЧАСТОТА .
В поле Массив_данных ввести диапазон данных наблюдений А3:А102 (с листа ‘Расчетные данные’) . В поле Массив_интервалов ввести диапазон интервалов с того же листа ([‘Расчетные данные’!F16:F23] – в данном примере).
При завершении ввода данных нажать комбинацию клавиш Ctrl+Shift+Enter.
В предварительно выделенном столбце (C5:C12 – в данном примере) должен появиться массив
Столбец Накопленные частоты получается последовательным суммированием относительных частот (в процентном формате) в направлении от первого интервала к последнему.
В завершении с помощью Мастера диаграмм строится диаграмма абсолютных и накопленных частот с выбором типа диаграммы соотвественно гистограмма и график.
Для автоматизированного построения гистограммы средствами Excel необходимо обратиться к меню « Сервис Анализ данных» . (Excel 2003) или на вкладке Данные выбрать Анализ данных
(Excel 2007. 2010):
В появившемся списке выбрать инструмент Гистограмма и щелкнуть на кнопке ОК. Появится окно гистограммы, где задаются следующие параметры:
Входной интервал :– адреса ячеек, содержащие выборочные данные.
Интервал карманов : (необязательный параметр) – адреса ячеек, содержащие границы интервалов. Это поле предлагается оставить пустым, предоставив Excel самому вычислить границы интервалов (карманов – в терминах Excel).
Метки – флажок, включаемый, если первая строка во входных данных содержит заголовки. Если заголовки отсутствуют, то флажок следует выключить.
Выходной интервал: / Новый рабочий лист: / Новая рабочая книга.
Включенный переключатель Выходной интервал требует ввода адреса верхней ячейки, начиная с которой будут размещаться вычисленные относительные частоты j .
В положении переключателя Новый рабочий лист: открывается новый лист, в котором начиная с ячейки А1 размещаются частности j .
В положении переключателя Новая рабочая книга открывается новая книга, на первом листе которой начиная с ячейки А1 размещаются частности j .
Парето ( отсортированная гистограмма ) – устанавливается, чтобы представить j в порядке их убывания. Если параметр выключен, то j приводятся в порядке следования интервалов.
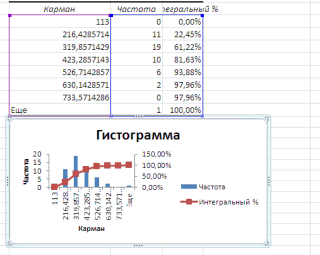
Интегральный процент – устанавливается в активное состояние для расчета выраженных в процентах накопленных относительных частот (аналог значений столбца Накопленные частоты ).
Вывод графика – устанавливается в активное состояние для автоматического создания встроенной диаграммы на листе, содержащем частоты.
Как правило, гистограммы изображаются в виде смежных прямоугольных областей. Поэтому столбики гистограммы следует расширить до соприкосновения друг с другом. Для этого необходимо щелкнуть мышью на диаграмме, далее на панель инструментов Диаграмма , раскрыть список инструментов и выбрать элемент Ряд ‘Частота’ , после чего щелкнуть на кнопке Формат ряда . В появившемся одноименном диалоговом окне необходимо активизировать закладку Параметры и в поле Ширина зазора установить значение 0 ((Excel 2003):
В Excel 2007. 2010 встать на любой столбик гистограммы и правой кнопкой мыши выбрать
Формат ряда данных:
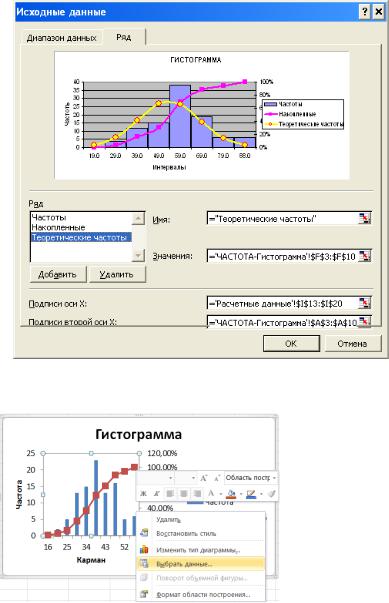
Для построения теоретической кривой нормального распределения по эмпирическим данным необходимо найти теоретические частоты.
В Excel для вычисления значений нормального распределения используются функция НОРМРАСП, которая вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения.
Функция имеет параметры:
НОРМРАСП (х; среднее; стандартное_откл; интегральная) , где:
х — значения выборки, для которых строится распределение; среднее — среднее арифметическое выборки; стандартное_откл — стандартное отклонение распределения;
интегральный — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности распределения.
Для получения абсолютных значений плотностей распределения (теоретических частот) достаточно найденные значения вероятности умножить на величину интервала h и количество наблюдений N = 100 по каждой строке.
Для завершения выполнения задания необходимо внести полученные значения теоретических частот на рисунок с гистограммой, добавив ряд в закладке Исходные данные и выбрав тип диаграммы
– график ((Excel 2003):
В Excel 2007. 2010 находясь в обласи гистограммы по правой кнопке мыши выбрать Выбрать данные (или по одноименной кнопке на вкладке Конструктор ):
и в появившемся окне провести манипуляции с вводом нового ряда «Теоретические частоты»: