Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции МЕДИАНА в Microsoft Excel.
Описание
Возвращает медиану заданных чисел. Медиана — это число, которое является серединой множества чисел.
Синтаксис
МЕДИАНА(число1;[число2];…)
Аргументы функции МЕДИАНА описаны ниже.
-
Число1, число2,… Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 чисел, для которых требуется определить медиану.
Замечания
-
Если в наборе имеется ряду чисел, медиана вычисляет среднее значение двух чисел в середине. См. вторую формулу в примере.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят в возникновению ошибок.
Примечание: Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
-
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
-
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
-
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
1 |
||
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
6 |
||
|
Формула |
Описание |
Результат |
|
=МЕДИАНА(A2:A6) |
Медиана пяти чисел в диапазоне A2:A6. Так как имеется пять значений, третье из них является медианой. |
3 |
|
=МЕДИАНА(A2:A7) |
Медиана шести чисел в диапазоне A2:A6. Так как имеется шесть чисел, медианой является средняя точка между третьим и четвертым числами. |
3,5 |
Нужна дополнительная помощь?
Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.
Примеры использования функции МЕДИАНА в Excel
Пример 1. При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.
Исходные данные:
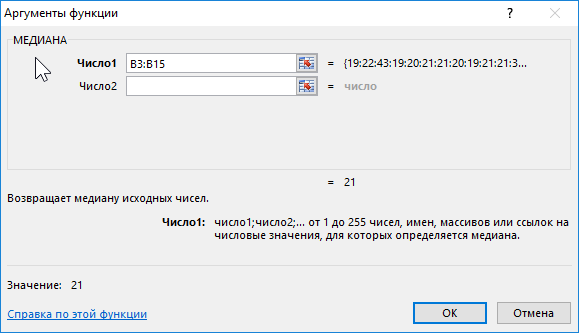
Формула для расчета:
Описание аргумента:
- B3:B15 – диапазон исследуемых возрастов.
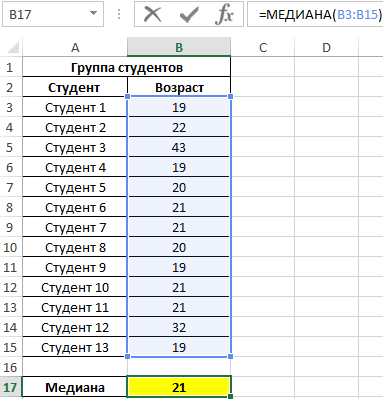
Полученный результат:
То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.
Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения
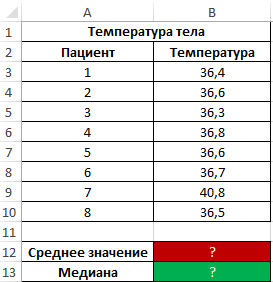
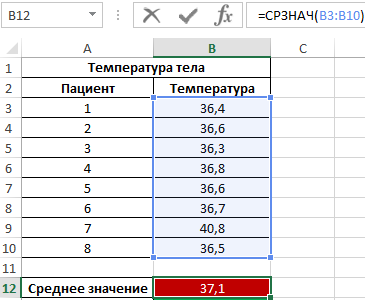
Пример 2. Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.
Исходные данные:
Формула для нахождения среднего значения:
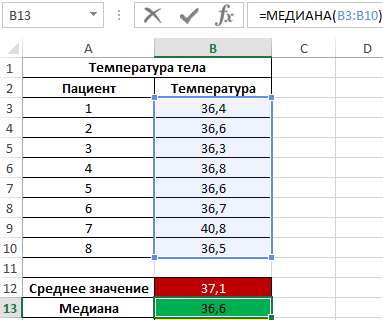
Формула для нахождения медианы:
Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.
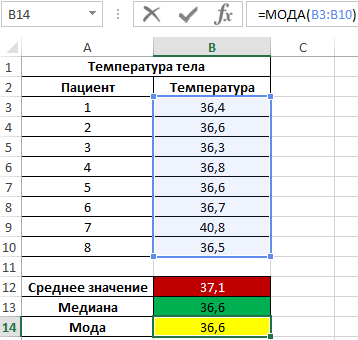
Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:
То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.
Пример расчета медианы при статистическом анализе в Excel
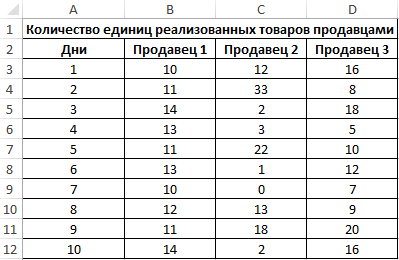
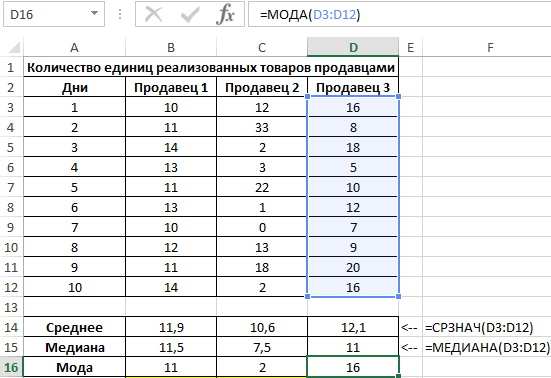
Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.
Исходная таблица данных:
Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:
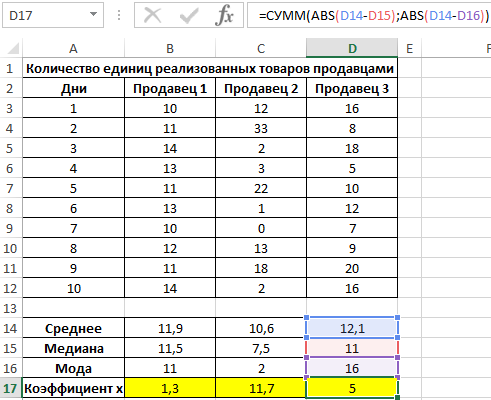
Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:
- av – среднее значение;
- med – медиана;
- mod – мода.
Рассчитаем значение коэффициента x для первого продавца:
Аналогично проведем расчеты для остальных продавцов. Полученные результаты:
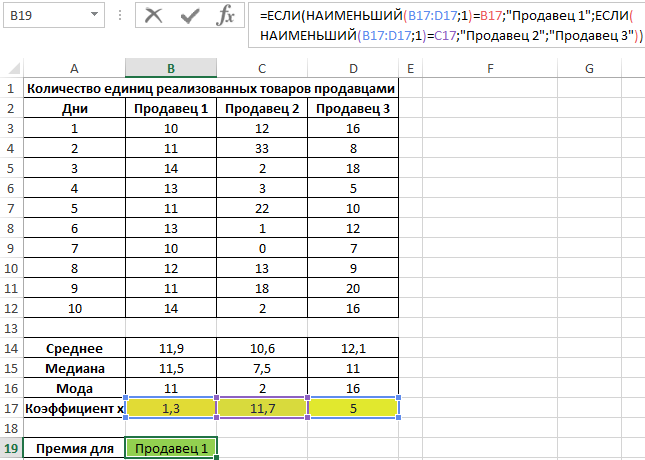
Определим продавца, которому будет выдана премия:
Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.
Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.
Особенности использования функции МЕДИАНА в Excel
Функция имеет следующий синтаксис:
=МЕДИАНА(число1;[число2];…)
Описание аргументов:
- число1 – обязательный аргумент, характеризующий первое числовое значение, содержащееся в исследуемом диапазоне;
- [число2] – необязательный второй (и последующие аргументы, всего до 255 аргументов), характеризующий второе и последующие значения исследуемого диапазона.
Примечания 1:
- При расчетах удобнее передавать сразу весь диапазон исследуемых значений вместо последовательного ввода аргументов.
- В качестве аргументов принимаются данные числового типа, имена, содержащие числа, данные ссылочного типа и массивы (например, =МЕДИАНА({1;2;3;5;7;10})).
- При расчете медианы учитываются ячейки, содержащие пустые значения или логические ИСТИНА, ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно. Например, результат выполнения функции с логическими значениями в аргументах (ИСТИНА;ЛОЖЬ) эквивалентен результату выполнения с аргументами (1;0) и равен 0,5.
- Если один или несколько аргументов функции принимают текстовые значения, которые не могут быть преобразованы в числовые, или содержат коды ошибок, результатом выполнения функции будет код ошибки #ЗНАЧ!.
- Для определения медианы выборки могут быть использованы другие функции Excel: ПРОЦЕНТИЛЬ.ВКЛ, КВАРТИЛЬ.ВКЛ, НАИБОЛЬШИЙ Примеры использования:
- =ПРОЦЕНТИЛЬ.ВКЛ(A1:A10;0,5), поскольку по определению медиана – 50-я процентиль.
- =КВАРТИЛЬ.ВКЛ(A1:A10;2), так как медиана – 2-я квартиль.
- =НАИБОЛЬШИЙ(A1:A9;СЧЁТ(A1:A9)/2), но только если количество чисел в диапазоне является нечетным числом.
Примечания 2:
- Если в исследуемом диапазоне все числа распределены симметрично относительно среднего значения, среднее арифметическое и медиана для данного диапазона будут эквивалентны.
- При больших отклонениях данных в диапазоне («разбросе» значений) медиана лучше отражает тенденцию распределения значений, чем среднее арифметическое. Отличным примером является использование медианы для определения реального уровня зарплат у населения государства, в котором чиновники получают на порядок больше обычных граждан.
- Диапазон исследуемых значений может содержать:
Скачать примеры функции МЕДИАНА для статистического анализа в Excel
- Нечетное количество чисел. В этом случае медианой будет являться единственное число, разделяющее диапазон на два подмножества больших и меньших значений соответственно;
- Четное количество чисел. Тогда медиана вычисляется как среднее арифметическое для двух числовых значений, разделяющих множество на два указанных выше подмножества.
Для различных аналитических целей часто требуется получить средний уровень различных показателей: средний возраст, средняя зарплата и т.д. Первое, что приходит на ум – это найти простое среднее арифметическое. Но всегда ли это правильно? В этой статье разберемся, что такое медиана, среднее арифметическое и мода. А также научимся считать их в Excel.
- Среднее арифметическое
- Медиана – чем отличается от среднего значения
- Что лучше – медиана или среднее значение
- Что такое мода
- Средневзвешенное значение
Среднее арифметическое
Среднее арифметическое значение – это сумма всех элементов выборки, поделенная на количество этих элементов.
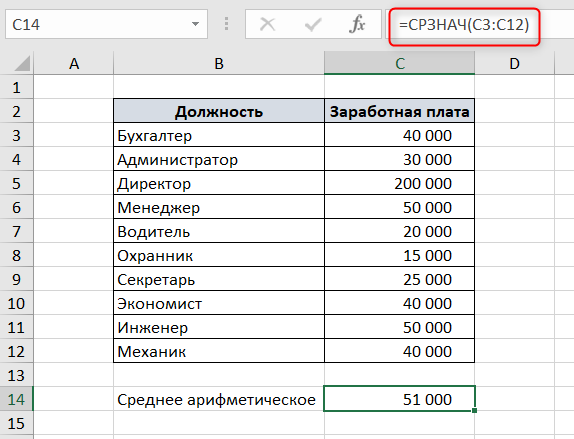
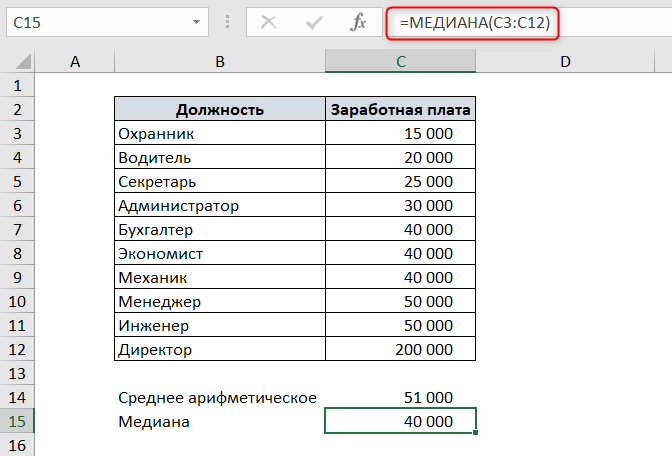
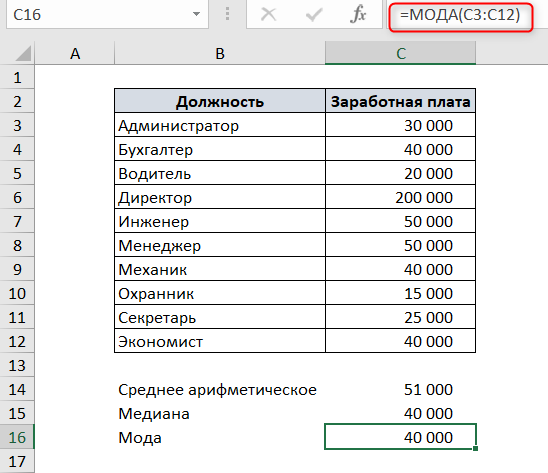
Например, есть список должностей и заработных плат. Чтобы посчитать среднюю заработную плату в Excel, воспользуемся функцией СРЗНАЧ.
Медиана – чем отличается от среднего значения
Медиана – это середина набора чисел, отсортированного по возрастанию.
Другими словами, 50% наблюдений ниже медианы и 50% наблюдений выше медианы. Медиана всегда равно удалена от начала и от конца набора чисел.
Если набор чисел состоит из нечетного количества элементов, то медианой будет число, которое находится в середине.
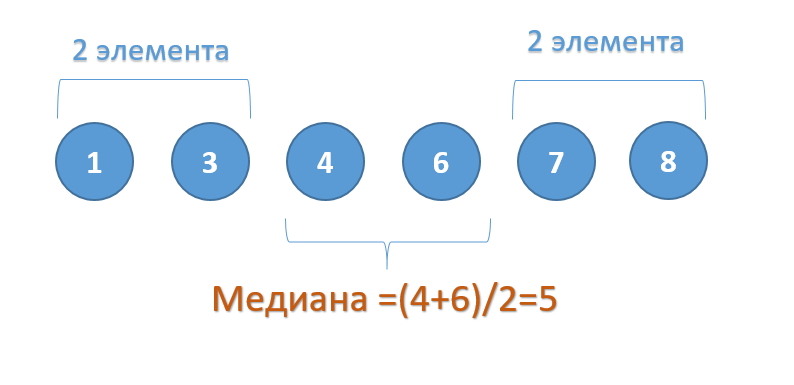
Если набор чисел состоит из четного числа элементов, то медиана будет равна среднему арифметическому между двумя центральными элементами списка.
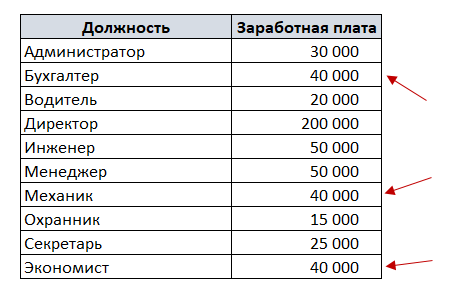
Чтобы наглядно увидеть, чем отличается медиана от среднеарифметического значения на нашем первом примере с зарплатой, отсортируем список по возрастанию.
Поскольку в списке 10 элементов – четное количество – то медианой будет среднее арифметическое 5 и 6 элементов.
Чтобы посчитать медиану в Excel, воспользуемся функцией МЕДИАНА. В качестве аргументов функция принимает числовые значения ряда данных.
Как видите, медиана не равна среднему значению.
Что лучше – медиана или среднее значение
На этот вопрос однозначного ответа нет, все зависит от целей вашего анализа.
Основные отличия медианы от среднего арифметического:
- Медиана в отличие от среднего арифметического игнорирует выбросы данных (выбросы – это значения, которые значительно отличаются от основного массива выборки).
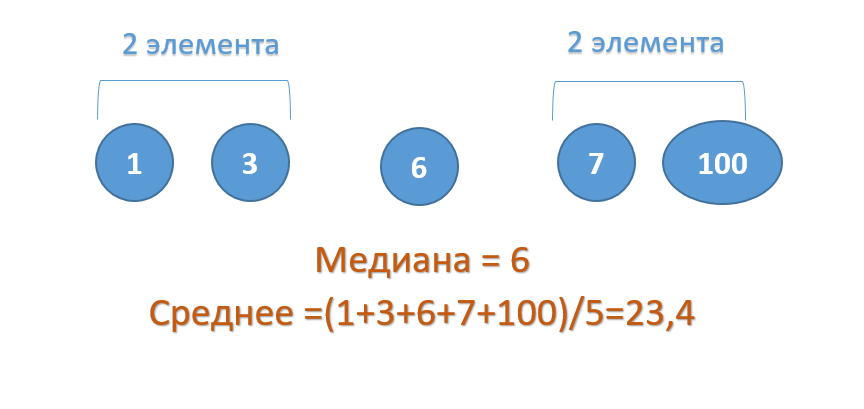
Рассмотрим пример:
В данном примере число 100 – это выброс, т.к. оно значительно отличается от основной других чисел в ряду. И при расчете среднего арифметического это число 100 исказило среднее – оно стало значительно больше остальных чисел.
Медиана же останется неизменной, даже если вместо 100 мы укажем 1000, т.к. середина ряда все равно будет число 6.
Это свойство медианы – игнорировать выбросы – особенно полезно, когда нужно посчитать среднюю зарплату или средний возраст. В целом, медиана более точно определяет середину выборки, чем среднее арифметическое, поскольку устойчива к искажениям.
- Свойство медианы игнорировать выбросы, на самом деле, не всегда полезно. Оно может скрыть из виду важные моменты, тогда как среднее арифметическое, завысив или занизив среднее, поможет обратить на них внимание.
В нашем примере с заработной платой среднее арифметическое заработных плат выше, чем медиана. Это может обратить внимание на то, что одна из заработных плат (в данном случае – директора) сильно отличается от заработных плат других сотрудников.
- Если ряд данных имеет нормальное или близкое к нормальному распределение, то медиана или среднее значение будут равны или близки друг к другу.
- Если среднее значение больше медианы, то распределение положительно искажено (т.е. имеет выбросы в сторону больших значений). И наоборот, если среднее значение меньше медианы, то выборка отрицательно искажена (преобладают меньшие значения).
Что такое мода
Мода – это наиболее часто встречающееся значение выборки.
В нашем примере мода – это заработная плата 40000, т.к. это значение встречается 3 раза, в то время, как остальные значения – один или два раза.
Чтобы посчитать моду в Excel, используем функцию МОДА.
Для чего считать моду? Пример использования моды на коммерческом предприятии: для планирования производства обуви необходимо определить размер, который наиболее часто приобретают покупатели.
Средневзвешенное значение
Средневзвешенное значение отличается от среднего арифметического тем, что каждому элементу ряда присваивается «вес» — или как бы «значимость» его в ряду.
Для того, что определить средневзвешенное, сумма элементов ряда, умноженная на их «вес», делится на количество элементов.
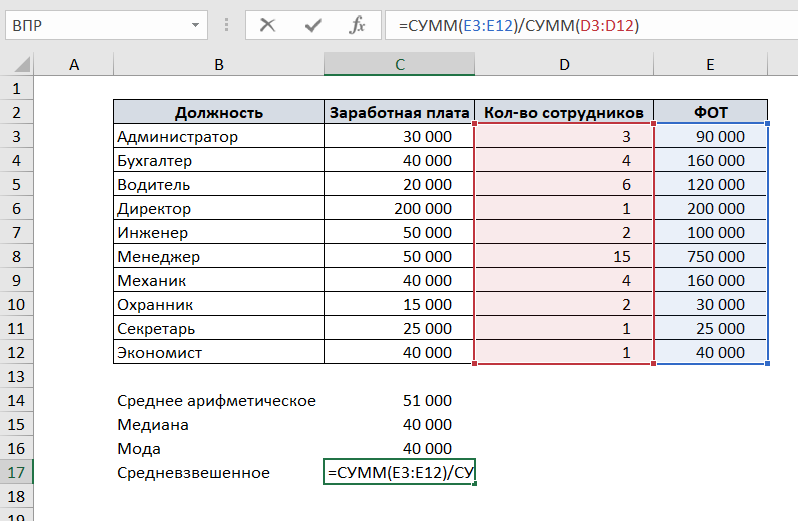
Рассмотрим на том же примере с зарплатой. Добавим к таблице два столбца: количество сотрудников и ФОТ (в этом столбце умножим заработную плату одного сотрудника на количество сотрудников).
Чтобы посчитать средневзвешенную заработную плату, разделим сумму всех зарплат сотрудников на сумму количества сотрудников.
Таким образом, зарплату каждого сотрудника мы «взвесили» на количество сотрудников каждой должности.
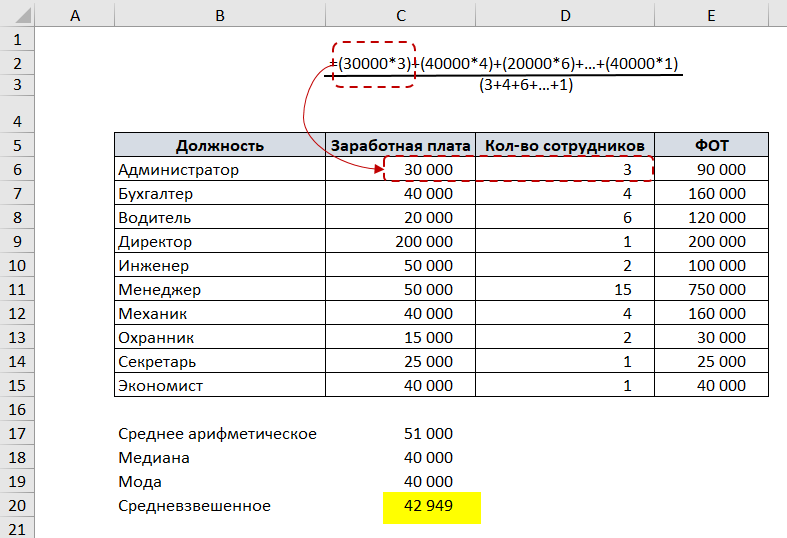
Если разложить формулу средневзвешенного подобно, то получается:
Для данного примера медиана, среднее арифметическое, средневзвешенное и мода отличаются.
Таким образом, в этом статье мы разобрались, что такое медиана, среднее арифметическое и мода и узнали, при помощи каких функций их можно посчитать в Excel.
Сообщество Excel Analytics | обучение Excel
Канал на Яндекс.Дзен
Вам может быть интересно:
Для вычисления медианы в Excel вы можете использовать встроенную функцию МЕДИАНА. Попробуем разобраться, что такое медиана, и рассмотрим методы ее вычисления для выборки или распределения случайных чисел.
Медиана выборки
Следовательно, медиана — это число, которое выражает центр набора определенной серии чисел. Следовательно, половина чисел в указанном ряду будет больше, чем рассчитанное медианное значение, а вторая половина числового ряда будет меньше. Для определения медианы необходимо отсортировать числовые значения выборки. Следовательно, медиана выборки цифр 2, 2, 3, 5, 6, 7, 8 будет 5. В этом случае выборка состоит из семи значений: три цифры больше, чем полученная медиана, и три менее.
Важно! Если выборка состоит из четного числа целых цифровых значений, медиана будет представлена в виде десятичной дроби. Следовательно, медиана выборки из серий 2, 2, 3, 5, 6, 7, 8, 10 составляет 5,5.
Расчет медианы для выборки с использованием функций Excel выполняется с помощью соответствующей функции МЕДИАНА. В скобках формулы можно ввести до 255 значений, из которых нужно рассчитать медиану.
Функция МЕДИАНА с выборкой из семи чисел
Медиана не всегда совпадает со средним числовым значением представленного ряда. Как правило, совпадение происходит только тогда, когда есть тождество, симметричное относительно среднего.
Примечание! Медиана не равна среднему. Выборочное среднее чисел 2, 2, 3, 5, 6, 7, 300 соответствует значению 46,42857, в то время как медиана по-прежнему равна 5, поскольку соотношение между числами больше 5 и меньше не изменилось.
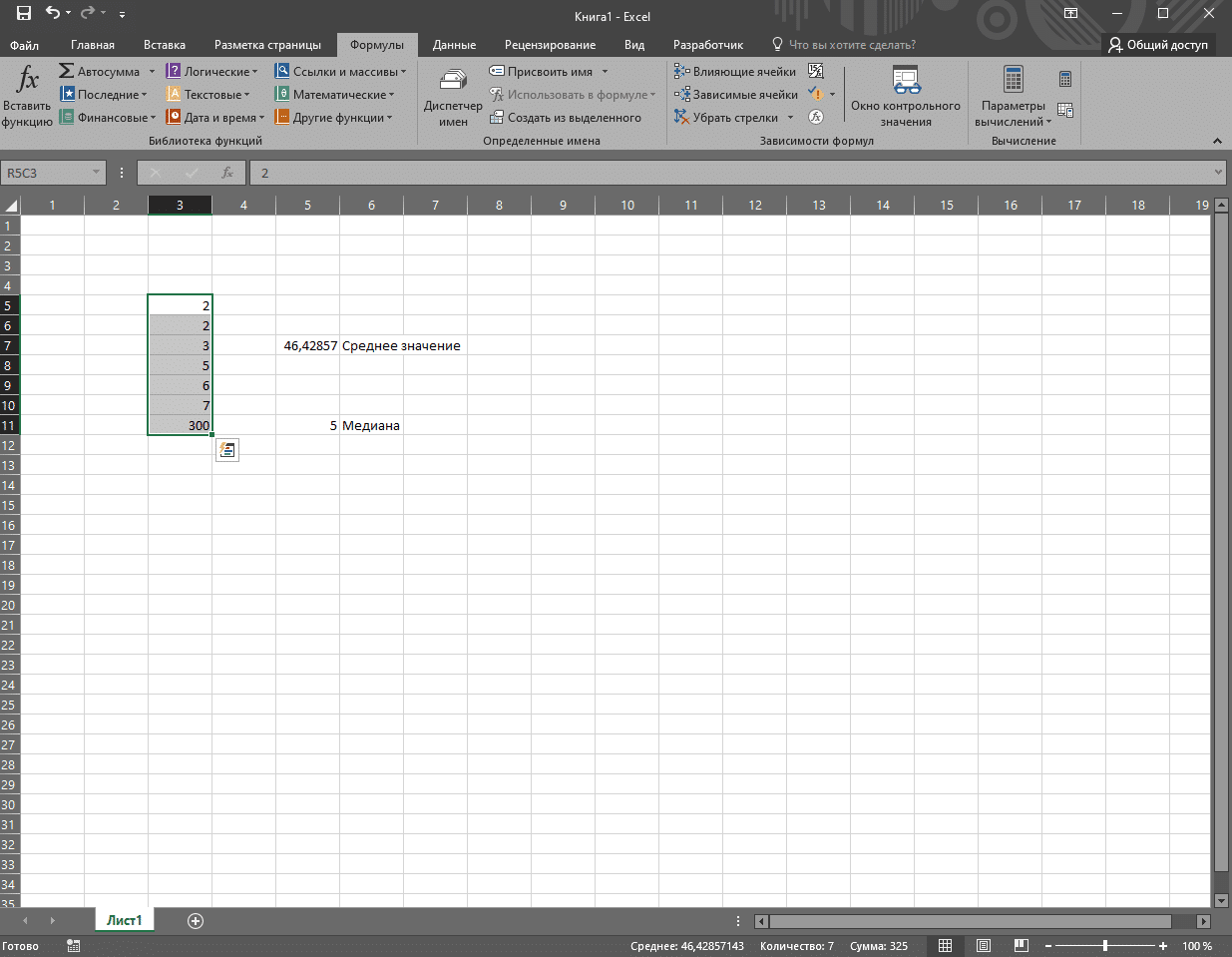
Медиана непрерывного распределения
Теперь рассмотрим вычисление медианы в случае непрерывного распределения. Медианная экспонента является результатом решения функции распределения случайных непрерывных числовых значений. Если известен показатель степени функции распределения (то есть функция плотности), то среднее значение можно вычислить по следующей формуле:
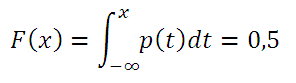
При решении этого уравнения аналитическим методом с логнормальным распределением LnN (µ; σ; 2) можно вычислить медианное значение по формуле = EXP (µ). Учитывая, что µ = 0, медиана будет равна 1. В Excel результат медианы для логнормального распределения, представленный формулой LnN (0; 1), вычисляется с помощью функции = LOGNORM.OBR (0,5; 0; 1).
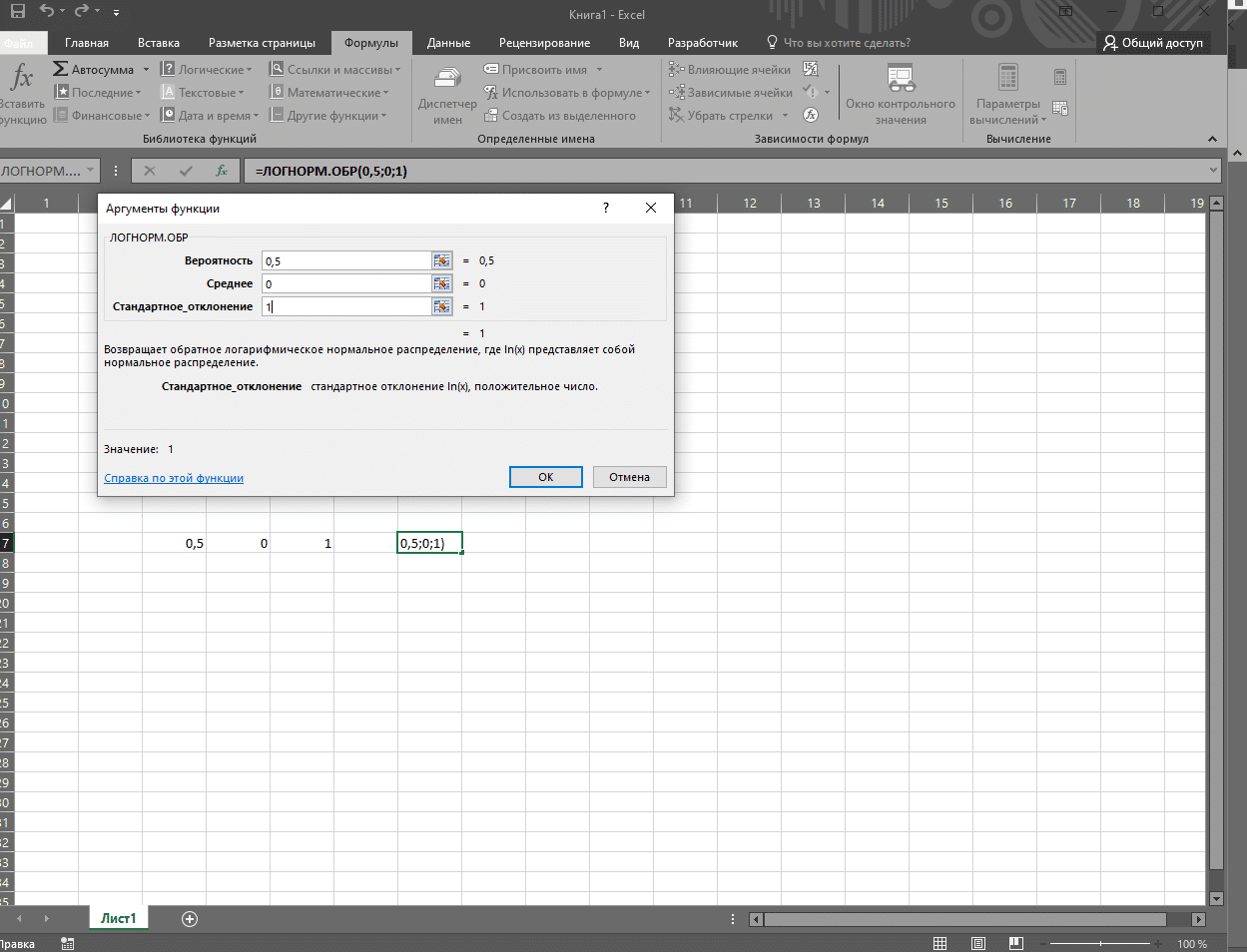
Функция МЕДИАНА
Используя функцию МЕДИАНА в Excel, вы можете вычислить среднюю точку набора чисел. Синтаксическим выражением является формула = МЕДИАНА (число 1; [число 2]…). Аргументами являются число 1, число 2 и т.д. До числа 255. Первое значение является обязательным, следующие — необязательными, но они помогают вычислить медиану.
Следует отметить! В качестве аргументов можно использовать не только числовые значения, но и ссылки, имена, массивы. Если ссылка или массив частично представлены в виде текста или в выделении присутствуют пустые ячейки, эти значения не учитываются в процессе расчета. Использование текстового формата в аргументах приводит к ошибкам в функции.
Среднее значение ряда чисел
Рассмотрим вариант расчета средних значений определенного ряда чисел. Например, это может быть средняя температура воздуха в определенный день в году, выполнение задач сотрудниками и так далее. Для выполнения этого расчета требуются три важных параметра:
- Медиана — это среднее значение ряда чисел. Кроме того, половина чисел больше медианы, а другая половина меньше. Например, медиана ряда чисел 2, 2, 3, 5, 6, 7, 9 равна 5.
- Среднее значение — это среднее арифметическое, которое рассчитывается путем сложения всех чисел заданного ряда и деления этой суммы на количество показателей, то есть 2 + 2 + 3 + 5 + 6 + 7 + 9 = 34/7. В этом случае среднее значение соответствует 4,857143.
- Индикаторный режим — это выбор числа, которое встречается чаще других в серии чисел. В представленном ряду чисел 2, 2, 3, 5, 6, 7, 9 этому показателю соответствует цифра 2.
Эти параметры не меняют своих значений при симметричном распределении числового ряда, а при асимметричном распределении они могут изменяться.
Вычисление значений непрерывного ряда
При определении среднего значения непрерывного числового ряда необходимо выполнить определенный порядок действий:
- Вы должны активировать ячейку справа или под строкой или строкой, в которой представлены значения.
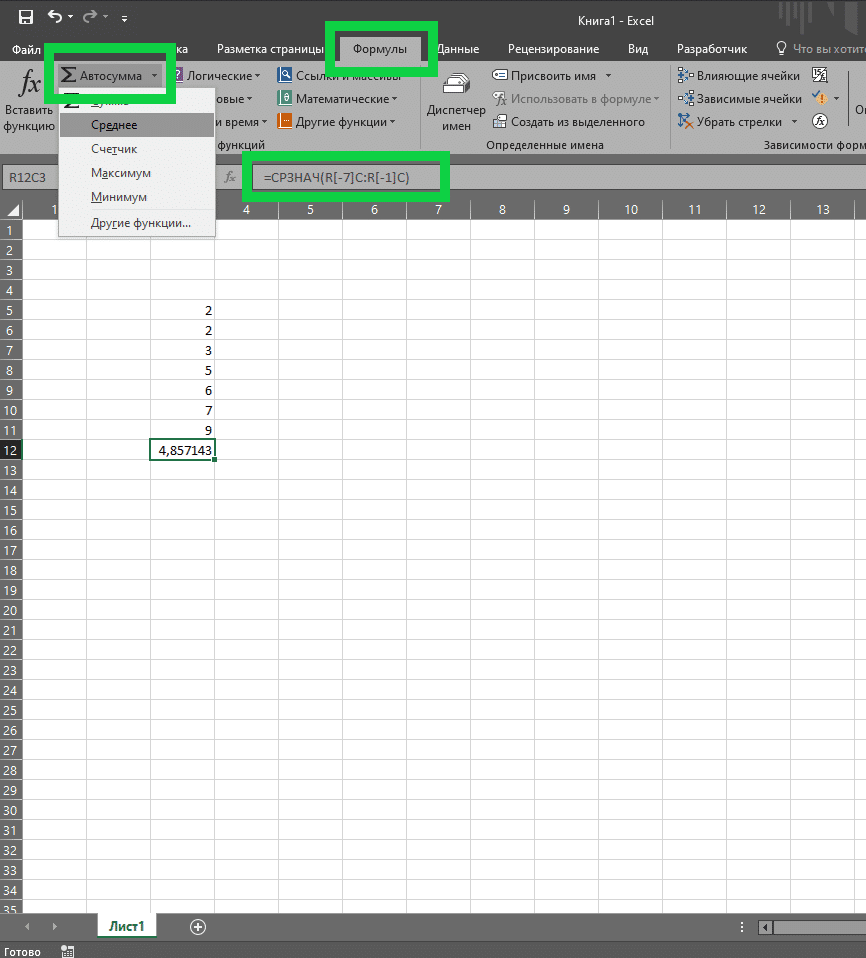
- На вкладке «Основные» выберите параметр «Автосумма», который находится в группе инструментов «Редактировать».
- Также эта функция находится на вкладке «Формулы».
- Рядом с кнопкой Автосумма, обозначенной значком Σ, находится стрелка со встроенным меню. Выбираем показатель «Средний». Это значение также можно получить, выполнив функцию СРЕДНЕЕ.
Среднее взвешенное значение
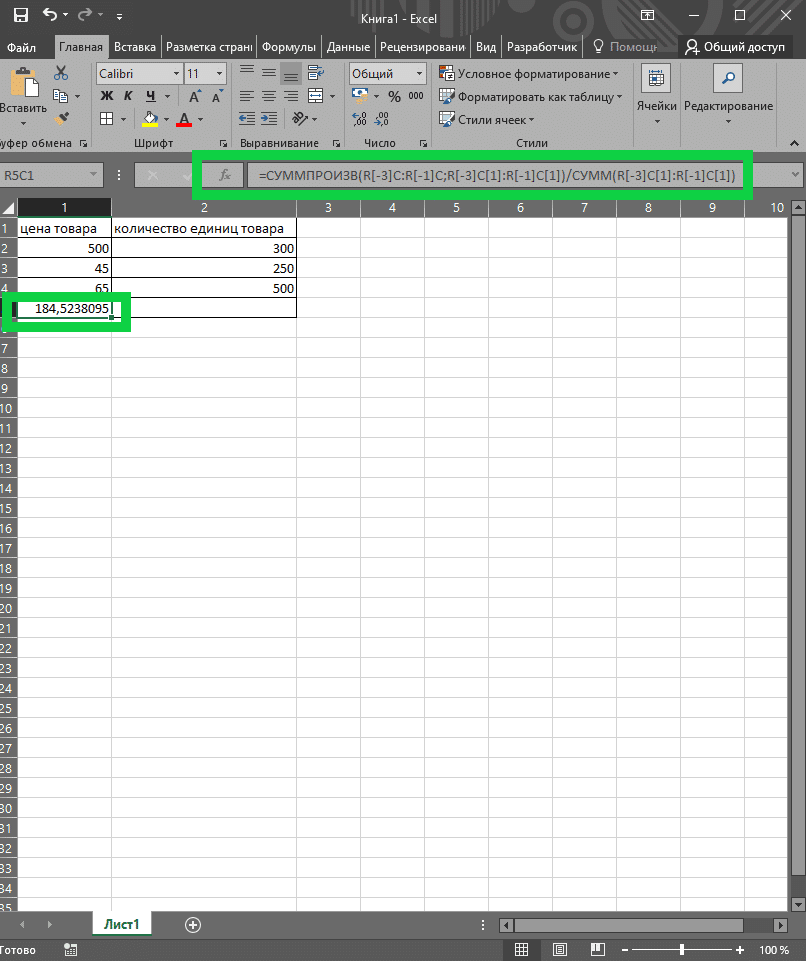
В этом случае вам придется использовать несколько функций: СУММ и СУММПРОИЗВ. Попробуем посчитать среднюю себестоимость единицы товара, если товаров три и количество осуществленных продаж. Синтаксис формулы выглядит следующим образом: = СУММПРОИЗВ (R [-3] C: R [-3] C [1]: R [-1] C [1]) / СУММ (R [-3] C [1]: R [-1] C [1]). После выполнения данной функции получаем среднюю себестоимость единицы товара 184,5238095
Вычисление без учета нулевых значений
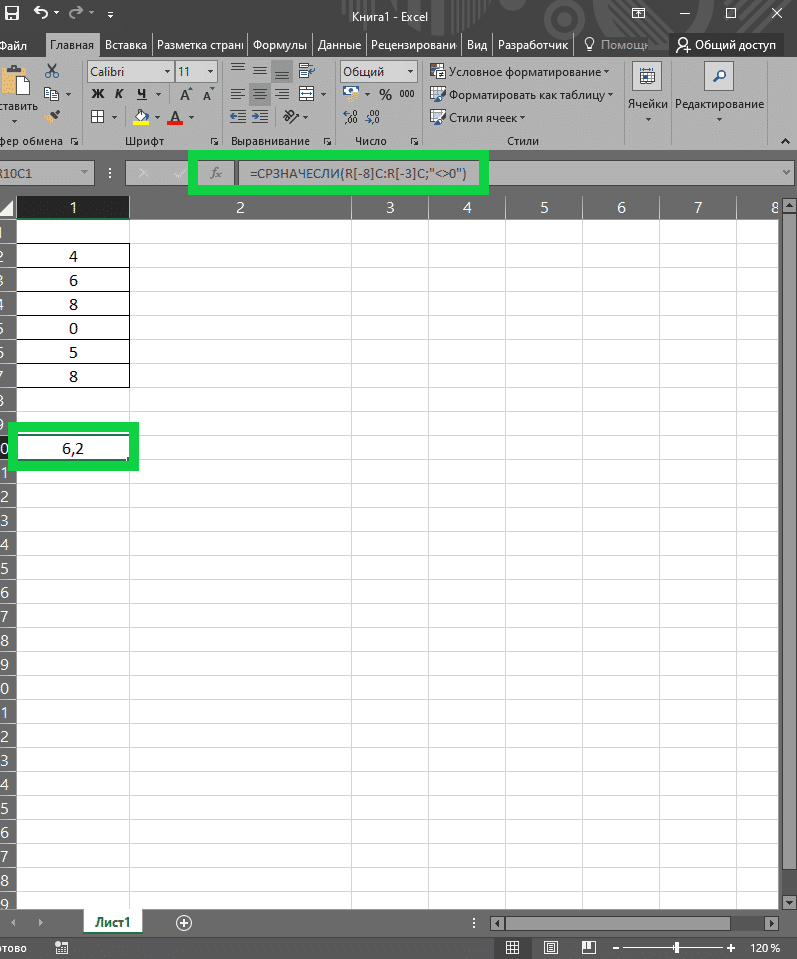
Чтобы исключить нулевые значения в процессе расчета, нужно использовать две функции: ЕСЛИ и СРЕДНИЙ. Давайте посмотрим на пример. В представленных числовых рядах 4, 6, 8, 0, 5, 8 необходимо найти среднее значение, но с условием исключения нулевого значения. Функция будет иметь следующий синтаксис: = СРЗНАЧЕСЛИ (A2: A7; « 0»). Следовательно, результат функции без нуля будет 6.2.
Полезные видео
Изучите основы вычисления медианы в Excel, посмотрев некоторые руководства на YouTube
В учебнике показано, как использовать функцию МЕДИАНА для вычисления медианы числовых значений в Excel.
Медиана является одним из трех основных показателей центральной тенденции, который обычно используется в статистике для нахождения центра выборки данных или совокупности, например, для расчета типичной заработной платы, дохода домохозяйства, цены на жилье, налога на недвижимость и т. д. В этом уроке вы узнаете общую концепцию медианы, чем она отличается от среднего арифметического, и как ее вычислить в Excel.
Проще говоря, медиана — это среднее значение в группе чисел, отделяющее более высокую половину значений от более низкой половины. С технической точки зрения, это центральный элемент набора данных, упорядоченный по порядку величины.
В наборе данных с нечетным числом значений медиана является средним элементом. Если имеется четное количество значений, медиана является средним значением двух средних.
Например, в группе значений {1, 2, 3, 4, 7} медиана равна 3. В наборе данных {1, 2, 2, 3, 4, 7} медиана равна 2,5.
По сравнению со средним арифметическим, медиана менее восприимчива к выбросам (чрезвычайно высоким или низким значениям) и, следовательно, является предпочтительной мерой центральной тенденции асимметричного распределения. Классическим примером является медианная заработная плата, которая дает лучшее представление о том, сколько люди обычно зарабатывают, чем средняя заработная плата, поскольку последняя может быть искажена небольшим количеством аномально высоких или низких заработков. Для получения дополнительной информации см. Среднее значение против медианы: что лучше?
Microsoft Excel предоставляет специальную функцию для нахождения медианы числовых значений. Его синтаксис следующий:
МЕДИАНА(число1, [number2]…)
Где Number1, number2, … — числовые значения, для которых вы хотите вычислить медиану. Это могут быть числа, даты, именованные диапазоны, массивы или ссылки на ячейки, содержащие числа. Номер 1 обязателен, последующие номера необязательны.
В Excel 2007 и более поздних версиях функция МЕДИАНА принимает до 255 аргументов; в Excel 2003 и более ранних версиях можно указать не более 30 аргументов.
4 факта, которые вы должны знать о Excel Median
- Если общее количество значений нечетное, функция возвращает среднее число в наборе данных. Когда общее количество значений четное, возвращается среднее значение двух средних чисел.
- Ячейки с нулевыми значениями (0) включаются в расчеты.
- Пустые ячейки, а также ячейки, содержащие текст и логические значения, игнорируются.
- Учитываются логические значения ИСТИНА и ЛОЖЬ, введенные непосредственно в формулу. Например, формула МЕДИАНА(ЛОЖЬ, ИСТИНА, 2, 3, 4) возвращает 2, то есть медиану чисел {0, 1, 2, 3, 4}.
МЕДИАНА — одна из самых простых и удобных функций в Excel. Однако есть еще некоторые хитрости, не очевидные для новичков. Скажем, как вычислить медиану на основе одного или нескольких условий? Ответ в одном из следующих примеров.
Формула Excel МЕДИАНА
Для начала давайте посмотрим, как использовать классическую формулу МЕДИАНА в Excel, чтобы найти среднее значение в наборе чисел. В образце отчета о продажах (см. скриншот ниже) предположим, что вы хотите найти медиану чисел в ячейках C2:C8. Формула будет такой простой:
=МЕДИАНА(C2:C8)
Как показано на снимке экрана выше, формула одинаково хорошо работает для чисел и дат, поскольку в терминах Excel даты также являются числами.
Формула Excel MEDIAN IF с одним критерием
К сожалению, в Microsoft Excel нет специальной функции для вычисления медианы на основе условия, как это делается для среднего арифметического (функции СРЗНАЧЕСЛИ и СРЗНАЧЕСЛИМН). К счастью, вы можете легко построить собственную формулу МЕДИАНА ЕСЛИ следующим образом:
МЕДИАНА(ЕСЛИ(критерии_диапазонзнак равнокритерии, медианный_диапазон))
В нашем образце таблицы, чтобы найти медианную сумму для определенного товара, введите название товара в какую-нибудь ячейку, скажем, E2, и используйте следующую формулу, чтобы получить медиану на основе этого условия:
=МЕДИАНА(ЕСЛИ($A$2:$A$10=$E2, $C$2:$C$10))
Формула указывает Excel вычислять только те числа в столбце C (Сумма), для которых значение в столбце A (Элемент) соответствует значению в ячейке E2.
Обратите внимание, что мы используем символ $ для создания абсолютных ссылок на ячейки. Это особенно важно, если вы собираетесь копировать формулу медианы, если в другие ячейки.
Наконец, поскольку вы хотите проверить каждое значение в указанном диапазоне, сделайте его формулой массива, нажав Ctrl + Shift + Enter. Если все сделано правильно, Excel заключит формулу в фигурные скобки, как показано на снимке экрана ниже.
В динамическом массиве Excel (365 и 2021) он также работает как обычная формула.
Формула Excel Median IFS с несколькими критериями
Развивая предыдущий пример, давайте добавим в таблицу еще один столбец (Статус), а затем найдем медианную сумму для каждого товара, но будем считать только заказы с указанным статусом. Другими словами, мы будем рассчитывать медиану на основе двух условий — названия товара и статуса заказа. Чтобы выразить несколько критериев, используйте две или более вложенных функции ЕСЛИ, например:
МЕДИАНА(ЕСЛИ(критерии_диапазон1знак равнокритерии1ЕСЛИ(критерии_диапазон2знак равнокритерии2, медианный_диапазон)))
С критерии1 (Элемент) в ячейке F2 и критерии2 (Статус) в ячейке G2 наша формула принимает следующий вид:
=МЕДИАНА(ЕСЛИ($A$2:$A$10=$F2, ЕСЛИ($D$2:$D$10=$G2,$C$2:$C$10)))
Поскольку это формула массива, не забудьте нажать Ctrl + Shift + Enter, чтобы завершить ее правильно. Если все сделано правильно, вы получите примерно такой результат:
Вот как вы вычисляете медиану в Excel. Чтобы поближе познакомиться с формулами, обсуждаемыми в этом руководстве, вы можете загрузить наш образец книги ниже. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Практическая рабочая тетрадь
Формула МЕДИАНА Excel — примеры (файл .xlsx)